Feasibility of Using Real-Time MRI to Measure Joint Kinematics in 1.5T and Open-Bore 0.5T Systems

Abstract

Purpose

To test the feasibility and accuracy of measuring joint motion with real-time MRI in a 1.5T scanner and in a 0.5T open-bore scanner and to assess the dependence of measurement accuracy on movement speed.

Materials and Methods

We developed an MRI-compatible motion phantom to evaluate the accuracy of tracking bone positions with real-time MRI for varying movement speeds. The measurement error was determined by comparing phantom positions estimated from real-time MRI to those measured using optical motion capture techniques. To assess the feasibility of measuring in vivo joint motion, we calculated 2D knee joint kinematics during knee extension in six subjects and compared them to previously reported measurements.

Results

Measurement accuracy decreased as the phantom’s movement speed increased. The measurement accuracy was within 2 mm for velocities up to 217 mm/s in the 1.5T scanner and 38 mm/s in the 0.5T scanner. We measured knee joint kinematics with small intraobserver variation (variance of 0.8° for rotation and 3.6% of patellar width for translation).

Conclusion

Our results suggest that real-time MRI can be used to measure joint kinematics when 2 mm accuracy is sufficient. They can also be used to prescribe the speed of joint motion necessary to achieve certain measurement accuracy.

ACCURATE MEASUREMENTS of in vivo joint motions are needed to understand normal and pathological joint mechanics and to effectively diagnose and treat musculoskeletal disorders. For example, altered patellofemoral joint kinematics are thought to play a role in the development of patellofemoral pain (1,2). Abnormal tibiofemoral kinematics result following a tear of the anterior cruciate ligament (3), and may play a role in the development of osteoarthritis (4). Methods to quantify joint kinematics in vivo enable us to identify these abnormal motions and evaluate treatments for musculoskeletal disorders.

Current techniques to study joint kinematics provide valuable information about the mechanics and alignment of joints. Direct bone motion has been measured in cadaveric specimens (5–8); however, these experiments may not accurately reflect natural joint behavior due to the difficulty in reproducing the complex pattern of muscle forces that arise during normal motion. Therefore, techniques to study in vivo joint motions are necessary. Conventional methods to obtain measurements of joint motion during active, dynamic tasks typically use optoelectronic or magnetic tracking of skin-based markers (9). These methods are noninvasive, but motion of skin and soft tissue relative to the bones can introduce displacements between the markers and bones as large as 13 mm during walking (10). Soft-tissue motion limits the ability of skin-based markers to accurately capture the internal motion of joints. Techniques to directly measure internal joint structures in vivo overcome these limitations. Such methods include medical imaging techniques or using markers rigidly attached to the bones. Previous studies have used optical markers attached to implanted bone pins to measure three-dimensional (3D) knee joint kinematics with reported accuracies of 0.5 mm (11). While these experiments enable highly accurate measurements of bone motion during functional tasks, the technique is invasive, difficult to perform, and does not provide information about the surrounding soft tissues in the joint. Fluoroscopy and biplane radiography have been used to directly measure bone motion during dynamic, weight-bearing tasks. Since these are projective imaging modalities, 3D registration must typically be performed to make clinically relevant measurements. These techniques can either perform marker-based registration, which involves the implantation of radiopaque bone markers (12–14) or intensity-based registration using a 3D model (12,15–18), often derived from CT images. Marker-based registration techniques have reported in-plane accuracy’s of 0.06 mm (13) to 1.0 mm (12) and out-of-plane accuracy’s of 0.06 mm (13) to 2.1 mm (12). Intensity-based registration techniques have reported in-plane accuracy’s of 0.42 mm (16) to 1.74 mm (12) and out-of-plane accuracy’s of 1.58 mm (12) to 5.6 mm (16). The measurement accuracy is often dependent on the bones being studied and the number of image planes used in the registration process. While fluoroscopy and biplane radiography offer highly accurate measurements of in vivo 3D bone motion, the techniques expose subjects to ionizing radiation and they provide no information describing the motion of the surrounding soft tissues.

Magnetic resonance imaging (MRI) is a powerful tool used to noninvasively image bone and soft tissues. The ability to correlate joint kinematics with data describing the motion of muscles and other soft tissues will serve to test the accuracy of biomechanical models and offer a more complete understanding of the function of the musculoskeletal system. MRI has been used to measure 2D knee joint alignment in subjects holding static positions (19–21). Additionally, static measurements of 3D knee joint alignment at different angles of knee flexion have been assessed using MRI in both unloaded (22) and loaded conditions (23–25). The reported measurement accuracy of estimated 3D joint kinematics from unloaded static MRI scans is 0.39 mm (22). To image joints under an applied load the scan time has been minimized to as little as 36 seconds (26) to reduce muscle fatigue and studies have measured 3D joint kinematics in a supine position accurate to within 0.88 mm (23) to 1.8 mm (25). Much faster MR imaging techniques have been developed, enabling joint kinematics to be assessed during a more continuous motion (27). For example, kinematic MRI can acquire images at frame rates of ≈1–1.4 frames/s (28). Many studies have used these techniques to perform qualitative (28,29) and quantitative (30,31) analyses of 2D knee joint kinematics during active joint motion. The advantage of these techniques is that, due to the short imaging time, more knee flexion angles can be imaged and higher loads can be applied to the joints. However, subjects often remain static during each image acquisition and it is unclear whether the joint alignment in a static posture accurately reflects the joint kinematics during a dynamic motion. Cine phase contrast MRI (cine-PC MRI) can be used to noninvasively measure joint kinematics during active, dynamic motions with a frame rate of ≈14 frames/s (3,32–36). Validation studies have reported tracking accuracies up to 0.36–0.55 mm for in-plane measurements and 0.21–1.83 mm for out-of-plane measurements (35). Cine-PC MRI has also been used with a 3D model-based tracking technique to measure 3D joint kinematics with an accuracy of 2.82 mm (32). This technique enables accurate measurements of 3D joint motion, but often requires at least 100 precise repetitions of the desired movement to obtain the necessary motion data. Thus, cine-PC MRI is limited to studying joint motion under minimally loaded conditions in subjects who can produce repeatable movement. Loaded joint kinematics are different from those occurring during unloaded movement (37,38), and in many musculoskeletal disorders, pain or instability arises during highly loaded movements such as deep knee flexion. In vivo measurements of bone motions under weight-bearing conditions are needed to characterize joint kinematics and treat certain musculoskeletal disorders.

Recent advances in MR technology have resulted in the implementation of real-time image acquisition (39–43). This technique produces a time series of single image slices. The imaging plane can be continuously defined and updated in real-time to follow an object if out-of-plane motion occurs. Real-time MRI can acquire a plane of image data quickly with reconstructed image display rates of 24 frames/s (44). This high rate of image acquisition and display minimizes the risk of muscle fatigue during highly loaded motions, allowing data to be obtained under weight-bearing conditions. Furthermore, in contrast to cine-PC MRI, only one motion cycle is required, enabling the imaging of subjects with musculoskeletal or neurological disorders who cannot perform many consecutive repetitions of a certain movement. Real-time phase contrast MRI has been used to measure muscle velocities with an accuracy of 2cm/s (42); however, a study investigating the accuracy of measuring bone motion using real-time imaging techniques has yet to be performed.

While real-time MRI has been used to image musculoskeletal motion during dynamic tasks, it is still unclear how movement speed affects measurement accuracy. The accuracy of measuring the position of a moving object using real-time MRI depends on the image acquisition frame rate, the image resolution, and the signal-to-noise ratio (SNR) of the images. These parameters depend on the magnitude and slew rate of the available gradients, the scanner field strength, and the homogeneity of the primary magnetic field. Therefore, the accuracy of using real-time imaging sequences to measure joint kinematics will depend highly on the type of scanner used. Implementing real-time imaging capabilities on open-bore scanners allows for studies of joint kinematics with a more realistic range of motion and higher applied joint loads than those obtained in closed-bore scanners (24,29). However, it is important to understand whether the gradient strength and slew-rates of these scanners limit image acquisition speed and resolution for real-time applications.

The goal of this study was to establish the feasibility of using real-time MRI to measure joint kinematics. We performed a phantom study to: 1) determine the accuracy of measuring object positions using real-time MRI, 2) assess how movement speed affects measurement accuracy, and 3) compare the measurement accuracies obtained using real-time MRI in a 1.5T closed-bore scanner to those obtained using a 0.5T upright, open-MRI scanner. We performed an in vivo study to establish the feasibility of using real-time MRI to estimate 2D patellofemoral joint kinematics.

MATERIALS AND METHODS

Phantom Study

We developed an MRI-compatible velocity phantom with a known and repeatable motion trajectory. The phantom consisted of a hollow, 3.8 cm diameter polypropylene sphere (Product Components, Martinez, CA) filled with olive oil to be representative of the fat in bone marrow. It was rigidly attached to a rotating wooden bar (Fig. 1b). The wooden bar was connected to a 24V DC gear motor with encoder (Maxon Motor, Sachseln, Switzerland) by a 2.7 m long driveshaft made of filament wound epoxy tubing (Tap Plastics, Mountain View, CA). This long driveshaft allowed the motor to be placed far enough from the scanner that it was not affected by the magnetic field (Fig. 1c). The speed of rotation of the phantom was controlled through a proportional-integral-derivative motor controller (Procyon Engineering, Santa Clara, CA), and once set, remained constant throughout the duration of the trial. The trajectory of the phantom center was a circle with radius 25.5 mm.

Figure 1.

a: Photograph of the 0.5T open-bore scanner. b: Front view of motion phantom. The dashed line represents the path traced by the sphere center during movement. To balance the weight of the sphere, a counterweight was placed an equal distance from the center of rotation. The speed-controlled motor is connected to the driveshaft. c: Diagram of motion phantom in the open-bore scanner (side view). This figure represents a slice through the center of the scanner, showing the phantom (from the side) positioned at the center of the magnet.

The position trajectory of the phantom was measured in a motion capture laboratory using standard 3D optical motion capture techniques (EVaRT, Motion Analysis, Santa Rosa, CA) that are accurate to within 0.2–0.3 mm. A single marker was placed on the center of the sphere and its position was recorded during several cycles to ensure position and velocity repeatability. The phantom velocity was found to vary by only 0.01 rad/s (translational velocity = 0.26 mm/s) within a full rotation. The positions of the phantom measured from the motion capture system were used to provide a gold standard with which to compare the position trajectories measured from real-time MRI.

The accuracy of tracking the phantom using real-time MRI was found in two scanners: a 1.5T GE Excite HD MRI scanner and a 0.5T GE Signa SP open-MRI scanner (GE Healthcare, Milwaukee, WI). The gradient strength, slew rate, and field homogeneity of the scanners are different (Table 1), resulting in different real-time image acquisition speeds.

Table 1.

Description of the MR Hardware Parameters for the 1.5T Closed-Bore MRI Scanner and the 0.5T Open-Bore MRI Scanner

	1.5T	0.5T
Gradient Strength (mT/m)	40	12
Slew Rate (T/m/s)	150	16
Homogeneity (ppm)	2	10

In long readout spiral acquisitions, magnetic field inhomogeneity can cause image blur. The field homogeneity of the open-MRI scanner was measured as 10 ppm with a cylindrical field of view (FOV) (28 × 28 × 20cm³) and was comparable to previous measurements (12 ppm) of field homogeneity in 0.5T open scanners (45). Field homogeneity in the 1.5T closed-bore MRI scanner was estimated at 2 ppm based on previous measurements (46).

Accounting for the MR hardware constraints and field homogeneity, real-time, single-slice spiral imaging sequences designed to image large joints, such as a knee, were implemented in both MRI scanners (Table 2) using the RTHawk System (47). The total acquisition time of each image was 85 ms (12 images/s) and 171 ms (6 images/s) in the 1.5T and 0.5T scanner, respectively. High acquisition speed is achieved using efficient k-space sampling with variable density readouts (48). Six spiral interleaves (acquisitions) are used to form one image in the 0.5T scanner and four interleaves are used to form one image in the 1.5T scanner. Continuous image reconstruction is done with a sliding window algorithm (49) to achieve high frame rates for smooth temporal visualization. The reconstructed frame rates are 47 frames/s in the 1.5T scanner and 35 frames/s in the 0.5T scanner. Sliding window reconstruction can be applied when multiple incomplete acquisitions are used to construct an image. Once the first full dataset is acquired and an image is formed, the next image is formed by replacing the first acquisition with the most recently acquired acquisition instead of creating it from the next set of independent acquisitions. This allows one to increase the frame rate without sacrificing spatial resolution, since all images are formed using only acquired data. The sampling rate for both scanners is 4 μs (125 kHz BW) and the TE was 4 ms and 3.8 ms in the 1.5T scanner and 0.5T scanner, respectively. The TE was minimized to avoid deliberate T2 weighting. In the 1.5T scanner we used a spectral-spatial excitation that either images fat or water. The real-time system used allows for dynamic fieldmap calculation and correction to compensate for the changes in the magnetic field relative to the position of the imaged object.

Table 2.

Description of the Spiral Real-Time Sequences Implemented on the 1.5T Closed-Bore MRI Scanner and the 0.5T Open-Bore MRI Scanner

	1.5T	0.5T
Field of View (cm)	20	16
Pixel Size (mm)	1.8	1.9
TR (ms)	21.4	28.5
Readout Length (ms)	12.2	16
Image Acq. Time (ms)	85	171
Number of Interleaves	4	6
Recon. Frame Rate (fr/s)	47	35
Slice thickness (mm) (fwhm)	4.7	5.0

In both scanners, a body coil was used for RF transmission and a 5-inch receive-only surface coil was used for signal reception. In the open-bore scanner, the coil was positioned vertically and the phantom rotated within the coil center. However, this configuration was not possible in the 1.5T scanner since the drive shaft could not enter from the side (as shown in Fig. 1). Therefore, the phantom was positioned so that it rotated in a plane perpendicular to the main magnetic field in the 1.5T scanner and a 5-inch receive-only surface coil was placed horizontally, under the phantom. This caused the images to lose signal from the phantom when it was at the top of its trajectory; however, the complete contour of the phantom could be seen in all images. We acquired real-time MR images of the phantom rotating at up to 19 different speeds, ranging from 1 rad/s to 10 rad/s in 0.5 rad/s increments. This corresponds to translational velocities of the phantom center of 25.5 mm/s to 255 mm/s. We chose the image plane to go through the center of the sphere and be oriented such that only in-plane motion occurred.

We calculated the SNR of the real-time images by computing the ratio of the signal in the phantom to the standard deviation (SD) of the noise in the image background. We measured this ratio at 20 locations in three images obtained from both scanners and found the average and the SD of the image SNR for each scanner. We also calculated the contrast-to-noise ratio (CNR) of the images by subtracting the signal of the air surrounding the phantom from the signal in the phantom, then dividing by the SD of the noise.

To facilitate comparisons with the optically measured trajectory of the phantom, we measured the position trajectory of the phantom centroid from the real-time images (MatLab, The MathWorks, Inc., Natick, MA). The centroid was computed by first thresholding each image to identify all pixels corresponding to the phantom, then computing the voxel intensity-weighted area centroid (C_x*, C_y*) of the sphere using the following equation:

$$(C_x\ast ,C_y\ast )=\left(\frac{{\displaystyle \sum _{i=1\dots n}}{x}_i{E}_i}{{\displaystyle \sum _{i=1\dots n}}{E}_i},\frac{{\displaystyle \sum _{i=1\dots n}}{y}_i{E}_i}{{\displaystyle \sum _{i=1\dots n}}{E}_i}\right),$$

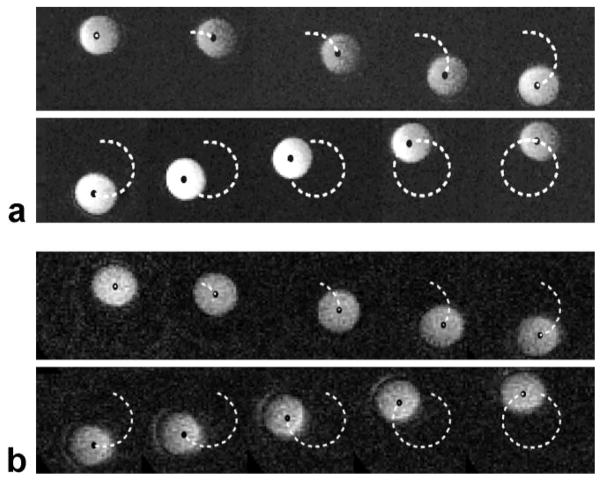
where (x_i, y_i) are the spatial coordinates and E_i is the intensity of each of the n pixels belonging to the phantom. This was performed for each frame of the real-time image sequence (Fig. 2). No assumptions about the shape of the phantom or trajectory were used in the algorithm. Using the frame rate of the sequence we computed the time corresponding to each position measurement, resulting in a position trajectory consisting of the position of the centroid of the sphere as a function of time.

Figure 2.

a: Sample real-time images of the phantom rotating in the 1.5T scanner. The black dot represents the area centroid of the phantom. The dashed line represents the path traced by the phantom center (ie, the recorded position of the centroid of the sphere at each frame in the real-time MRI sequence). Due to constraints on coil position, the images lose signal as the phantom moves far from the coil; however, the tracking algorithm was still able to identify the pixels corresponding to the phantom. b: Sample real-time images of the phantom rotating in the 0.5T open-MRI scanner. The black dot represents the area centroid of the phantom. The dashed line represents the path traced by the phantom center.

To determine the accuracy of tracking an object using real-time MRI, the position trajectory measured from the real-time images (measured trajectory) was compared to the position trajectory determined using the optical motion capture system (gold-standard trajectory). For each of the tested phantom velocities, the position trajectory was measured from the real-time images for three complete revolutions of the phantom. The root-mean-square (RMS) error between the measured position trajectory and the gold-standard trajectory was calculated and the average RMS error of the three measured trajectories was found.

In Vivo Study

We used the same real-time imaging sequences in both scanners (Table 2) to image the patellofemoral joint in a group of six healthy female subjects (age: 26 ± 2 years, height: 1.66 ± 0.07 m, weight: 59 ± 7 kg). Prior to scanning, the subjects were informed about the nature of the study and provided consent according to the policies of the Institutional Review Board.

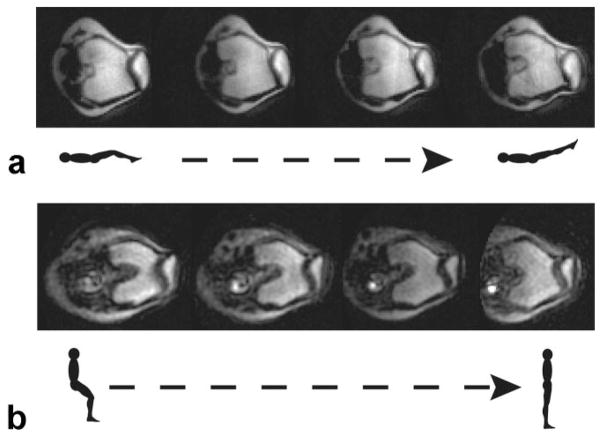
To assess the in vivo image quality, we obtained oblique-axial real-time images during knee flexion in both scanners (Fig. 3). In the 1.5T closed-bore scanner, we acquired images of supine, unloaded knee flexion as the subjects continuously flexed and extended their knees from 30° to 0° of knee flexion and back at a rate of 6°/s. In the 0.5T scanner we acquired images as the subjects maintained an upright, weight-bearing position, stabilized by a custom-built backrest (50). The subjects performed continuous knee flexion from 0°–60° and back at a rate of 6°/s. The speed of motion of the subjects was chosen to be representative of the slow phantom speeds to ensure sufficient measurement accuracy. In both scanners an oblique–axial plane through the widest portion of the patella was imaged. This plane was defined from a sagittal view of the knee as the subjects knees were maintained in ≈30° of knee flexion. Since the knee moves during deep flexion, the image plane was continuously translated to ensure that every frame in the time series captured the widest portion of the patella, while keeping the posterior femoral condyles in the image.

Figure 3.

a: Sample real-time MR images of the patellofemoral joint during knee flexion in the 1.5T scanner. These are oblique–axial views through the knee as the subject lies supine and moves her knee from 30° of knee flexion to full extension. b: Sample real-time MR images of the patellofemoral joint during upright, weight-bearing knee flexion in the 0.5T open-MRI scanner. These are oblique axial images through the knee as the subject rises from a weight-bearing squat (from 60° of knee flexion to a straight-leg position).

We calculated the SNR and CNR of the in vivo images, distinguishing between the signal in the patella and that in the femur. We calculated the CNR of the images by subtracting the signal of the surrounding soft tissues from the signal in each bone, and then dividing by the SD of the noise.

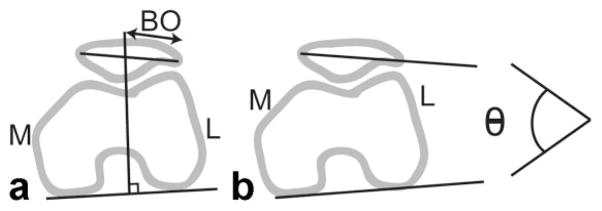
To assess the feasibility of measuring joint motion from these images, we estimated 2D patellofemoral joint kinematics during knee flexion/extension from the images obtained in each scanner. Clinical measurements of 2D patellar motion were estimated by manually identifying bony landmarks in each image frame. The medial/lateral position of the patella was described by the bisect offset (33,51) and is reported as the percentage of the patella lateral to the midline of the femur. Patellar tilt is a measure of the medial/lateral angle between the patella and the posterior femoral condyles (52) (Fig. 4). To assess the intraobserver repeatability, one observer measured bisect offset and patellar tilt three times from two different image sets corresponding to a complete extension cycle in two subjects. Each measurement was separated by at least 1 day. The variance of the results was then computed. To assess interobserver repeatability, two examiners measured kinematics from three different image sets corresponding to a complete extension cycle in three subjects. The average RMS difference between measurements was found.

Figure 4.

a: Diagram of bisect offset (BO) measurement, which defines the lateral position of the patella relative to the femur. b: Diagram of patellar tilt angle (Θ), which measures the angle between the patella and the posterior femoral condyles.

Patellofemoral joint kinematics were measured during weight-bearing knee extension in the 0.5T scanner for all subjects. To account for differences in scan plane orientation that may affect the kinematic measurements, the kinematics of each subject were computed during two different knee extension trials. These kinematics were averaged and smoothed with a low-pass filter (53). The average and SD of the kinematic measurements during weight-bearing knee extension from all six subjects were computed.

RESULTS

Phantom Study

The SNR and the CNR of the images from the 1.5T closed-bore scanner were significantly larger (P < 0.01) than the SNR and CNR of images from the 0.5T open-bore scanner (Table 3).

Table 3.

Measurements of Signal-to-Noise (SNR) Ratio and Contrast-to-Noise (CNR) Ratio of the Real-Time Images

	SNR	CNR
1.5T MRI Scanner
Phantom	42.1 ± 1.0	40.2 ± 0.9
In Vivo
Patella	57.6 ± 5.8	45.5 ± 4.2
Femur	54.2 ± 7.3	42.1 ± 5.8
0.5T MRI Scanner
Phantom	12.5 ± 1.4	10.8 ± 1.2
In Vivo
Patella	31.8 ± 5.2	22.6 ± 4.4
Femur	28.1 ± 3.8	18.8 ± 3.1

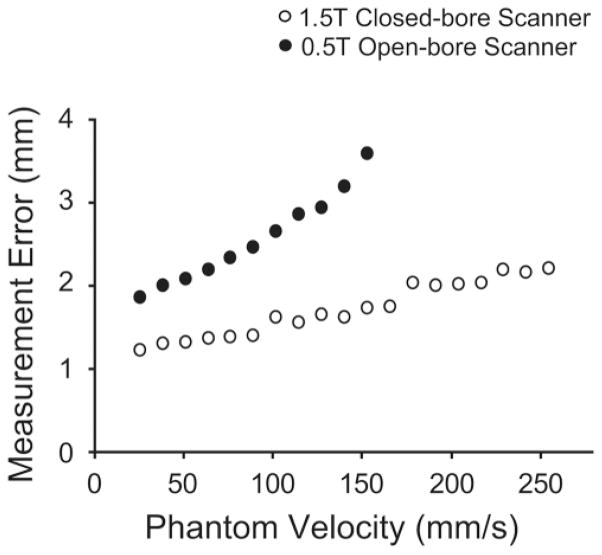
In the 1.5T scanner we were able to track the phantom to within 2 mm for velocities slower than 217 mm/s (Fig. 5). The measurement error increased with increasing phantom velocity, although this increase was not as dramatic as in the 0.5T scanner. The measurement error (2.2 mm) of tracking the phantom moving at 255 mm/s was 80% larger than the error (1.2 mm) in tracking the phantom moving at 26 mm/s.

Figure 5.

Plot of measurement (RMS) errors of the phantom position trajectory measured from real-time MRI for different speeds of phantom motion. The measurement errors increased with phantom speed in both scanners. The measurement error was smaller in the 1.5T scanner than in the 0.5T scanner for all phantom speeds.

In the open-bore 0.5T MRI scanner the phantom positions could be tracked to within 2 mm for phantom velocities under 38 mm/s and to within 3 mm for phantom velocities of 127 mm/s or slower (Fig. 5). At speeds of 153 mm/s, measurement error (3.6 mm) was 89% larger than the error (1.9 mm) at phantom speeds of 26 mm/s. Due to motion artifact, the image quality degraded significantly for velocities faster than 153 mm/s. Therefore, we did not measure the phantom trajectory for faster phantom velocities in this scanner.

With comparable measurement accuracy, we could track the phantom in the 1.5T scanner while it moved three times faster than it had moved in the 0.5T scanner. Furthermore, the measurement errors for a given phantom speed were, on average, 72% smaller in the 1.5T scanner compared to the errors seen in the 0.5T scanner, although this difference was more pronounced at faster movement speeds.

In Vivo Study

The SNR and the CNR of the in vivo images were higher (P < 0.01) than those of the phantom in both scanners (Table 3). The SNR and CNR of the in vivo images from the 1.5T closed-bore scanner were significantly larger (P < 0.01) than those of images from the 0.5T open-bore scanner.

The measurements of 2D kinematics (Fig. 6) were repeatable in both scanners. In the 1.5T scanner the intraobserver repeatability was 1.7% and 0.37° for bisect offset and patellar tilt, respectively. In the 0.5T open-bore scanner the intraobserver repeatability in bisect offset was 3.6% and the repeatability in patellar tilt was 0.8°. In the open-bore scanner the RMS difference between measurements by two different observes was 5.8% for bisect offset and 3.2° for patellar tilt.

Figure 6.

Plots of 2D patellofemoral joint kinematics measured from real-time MRI. The solid line represents the average of the six subjects and the shaded region, ±1 SD. These kinematics were obtained during weight-bearing knee extension. The black dots are values measured using kinematic MRI of subjects in a prone posture (31). a: Relationship between knee flexion angle and lateral translation of the patella relative to the femur (bisect offset). b: Relationship between knee flexion angle and patellar tilt. The values obtained in this study are within 1 SD of these previously reported kinematics for all knee flexion angles, except for patellar tilt at 36°.

The rate of knee flexion of the subjects corresponds to velocities slower than 38 mm/s. Measurements of the phantom moving at these speeds are accurate to within 1.2 mm in the 1.5T scanner and 1.9 mm in the 0.5T scanner.

To ensure that our in vivo kinematic measurements are consistent with accepted values, we compared the real-time measured kinematics to those previously measured in 12 asymptomatic subjects using kinematic MRI (31). For all knee flexion angles our measurements of bisect offset are within 1 SD of the previous measurements. For all knee flexion angles except 36°, our average measurements of patellar tilt are within 1 SD of previous measurements (Fig. 6).

DISCUSSION

Real-time MR imaging of joints during dynamic tasks can offer insight into the musculoskeletal system that cannot be achieved through static or quasi-static imaging techniques. The results of this study suggest that it is feasible to use real-time MRI in either scanner to measure the internal motions of slowly moving joints when 2 mm accuracy is sufficient. Bone and soft tissue movement can be captured with real-time MRI, resulting in quantitative measurements of in vivo joint mechanics. Through the use of a 0.5T open-bore MRI scanner, bone and soft tissue motion can be captured during upright, weight-bearing tasks, such as squats or stair climbs. The ability to study subjects during the highly loaded movements that often elicit pain or instability will make this technique useful for many clinical and research applications. The trade-off with using such a scanner is that the speed of motion must be slower to achieve acceptable levels of measurement accuracy.

Quantitative kinematic measurements of objects moving at physiologically relevant speeds can be obtained using real-time MRI. Based on our phantom study, we can compute the maximum rates of knee flexion that result in measurements accurate to within 2 mm. Assuming a revolute (purely rotational) joint and that the patella lies within 10 cm of the center of rotation of the knee, the maximum rate of knee flexion that can be accurately imaged in the 1.5T scanner is 124°/s. Applying the same approximations to the maximum velocity able to be imaged in the open-bore scanner, the rate of knee flexion that results in a 2 mm tracking accuracy is 22°/s. To put this in perspective, the range of knee flexion/extension angular velocities during the single-support phase of walking at normal speeds (1.4 m/s) was measured in our laboratory using optical motion capture techniques to be between 0–100°/s. While real-time MRI cannot be used to directly measure kinematics during walking, knee flexion and extension at velocities comparable to those occurring during the weight-bearing phase of walking can be studied with this technique in a 1.5T scanner. A limitation of real-time MRI is that it cannot be used to obtain kinematic measurements of joints moving at very fast velocities, such as those that occur during fast running.

Despite using real-time MRI sequences with comparable pixel sizes, there were marked differences in tracking accuracy between images from the two scanners. These differences arise from several factors. The SNR and CNR of the real-time images taken with the 1.5T scanner are significantly larger than those of the images from the 0.5T scanner, due to the higher field strength. The frame rate of the sequence used in the 1.5T scanner is faster than the frame rate of the 0.5T scanner sequence, resulting in less motion artifact. This is due to the gradient speed in the 0.5T scanner. Finally, the magnetic field in the 1.5T scanner is more homogeneous than the 0.5T open-bore scanner, resulting in less image blur. Although using the open-bore scanner results in less accurate measurements than those from images acquired in the 1.5T scanner, the ability to study load-bearing joints during dynamic, weight-bearing conditions over a wide range of motion may provide a better understanding of in vivo joint mechanics. While the 0.5T open-bore scanner is not as common as the traditional closed-bore scanner, it has many applications in musculoskeletal imaging. There are a variety of open-MR systems, and it is likely that they will have comparable trade-offs in measurement accuracy compared to closed-bore MRI scanners.

The goal of the phantom study was to investigate the in-plane accuracy of the real-time MR images. To reduce the influence of other factors affecting tracking accuracy, we chose a spherical phantom and constrained the phantom to in-plane motion. This simplified the tracking problem by eliminating the need for image segmentation or registration, thereby reducing the effect of image processing errors on our measured in-plane tracking accuracy. If real-time MRI is used to quantify 3D joint motion, then additional evaluations of the combined accuracy of the images and the specific image analysis algorithms used to quantify 3D motion must be performed.

Our in vivo study confirmed that real-time MRI can be used to measure physiologically relevant 2D joint kinematics during slow movements. A limitation of the study is that the phantom does not entirely reflect the in vivo conditions, as there are no structures representing the fat, cartilage, skin, and other soft tissues surrounding the bone. However, the SNR and CNR of the in vivo images were higher than the images of the phantom, suggesting that the in vivo measurement accuracy at a given speed of motion may be better than that of the phantom. Furthermore, our kinematic measurements obtained with real-time MRI are in good agreement with those computed using previously established MR imaging techniques (31). Future studies will investigate techniques to estimate 3D joint kinematics using real-time MRI and will be tested using a cadaveric phantom that more accurately represents a joint in vivo and will provide an improved assessment of tracking accuracy.

Other methods of measuring joint kinematics can be used to measure faster motions with greater accuracy. Biplane radiography enables measurements of joint kinematics with an accuracy up to 0.4 mm during fast movements (15), making it desirable for many applications. However, radiography involves ionizing radiation and does not capture the motion of soft tissues, such as muscles, ligaments, or cartilage.

The advantages of using MRI over radiographic methods are that it is entirely noninvasive and it allows for simultaneous imaging of soft tissues (42). MRI can be used to obtain experimental data describing the motion of bones, the contraction of skeletal muscle, and the moment arms of muscles during joint movement. These data provide information about normal and abnormal function of the musculoskeletal system and can serve to test the accuracy of biomechanical models (54). The accuracy of measuring object positions using real-time MRI is comparable to some other MR-based methods of measuring bone motion in vivo, such as dynamic MRI. This technique has been shown to measure positions of the pelvis and femur to within 1.8–3.3 mm (43). Cine-PC MRI enables more accurate kinematic measurements to be obtained (0.36–0.55 mm in-plane accuracy) (35) compared to real-time MRI. However, the ability to image highly loaded movements in subjects who may not be able to perform precise repetitions of a movement makes real-time MRI desirable for many clinical applications. Furthermore, as MR technology and hardware improves, it may become possible to achieve faster frame rates and better image resolution with real-time MRI. These developments will likely improve the measurement accuracy and allow for faster movements to be studied.

Real-time MRI addresses several of the limitations affecting current techniques to measure joint movement. Our results demonstrate the promise of using real-time MRI to quantify joint kinematics in vivo, thereby furthering our understanding of the function of the musculoskeletal system during highly loaded, dynamic tasks.