Viewpoint: Rigor and reproducibility in analysis of vascular calcification

Summary Abstract

Clinical and pre-clinical studies of cardiovascular calcification often require interpretation of images from histopathology, CT scans, intravascular ultrasound, and positron emission tomography. To avoid potential pitfalls in biological inferences, investigators should know what happens to data in image processing algorithms, the limitations of cross-sectional images in studying mechanostability, and how smoothing algorithms can mask partial-volume artifacts in PET images.

Years ago, a head-on collision sent a motorcyclist to intensive care with multiple limb fractures. A cardiologist was paged to evaluate the unconscious patient for a dangerously low value of cardiac index, suggesting severe cardiac injury. On evaluation, pulse, blood pressure, and cardiac output were normal despite the extremely low cardiac index. How could that be? It turned out that this low value was the result of a common error: failure to scrutinize “adjustments” in processed data. Cardiac index is a type of processed data, which is derived from cardiac output divided by body surface area, which is, in turn, derived from height and weight. On assessing this “adjustment,” the cardiologist found that the patient’s weight included the casts on his arms and leg. Though it’s obvious that casts don’t require perfusion, this is an example of blindly following protocol, in this case resulting in a gross overestimate of weight, overestimate of body surface area and underestimate of cardiac index. The moral of the story is that blind adherence to adjustment protocols may cause clinical errors. Does this happen in research?

Corrections, adjustments, and technical limitations are common in imaging of pre-clinical and clinical vascular calcification, such as x-ray computed tomography (CT), intravascular ultrasound (IVUS), and, fused positron emission tomography (PET)-CT using the bone-seeking ¹⁸F-fluoride PET tracer. There is growing interest in using such imaging methods to infer molecular and cellular mechanisms of vascular calcification. However, colleagues in the engineering and imaging have cautioned about inherent technical limitations and effects of post-acquisition processing, such as resolution, truncation, thresholding, partial volume effects, and smoothing algorithms. This commentary provides examples of pitfalls in image interpretation that may affect rigor, reproducibility, and validity of studies.

Truncation and thresholding algorithms in CT imaging of coronary calcification

Calcium deposits in most vascular structures are non-invasively detectable by plain x-ray, fluoroscopy, ultrasound, or CT scanning. For coronary calcification, ultra-fast or electron-beam CT and multi-detector CT are used clinically to compensate for phasic cardiac and respiratory motion. Known to patients as “calcium scans,” their results are expressed as a single number, the “calcium score.” The algorithm for this score, developed by Agatston and colleagues in 1990,¹ has been the standard for decades.

As with the cardiac index scenario above, it is important to examine how these scores are derived. Raw data from CT scans consist of values of radiographic density in Hounsfield units (H.U.) for each pixel in each slice of the scan. As an aside, “pixel,” a unit of area, is the more familiar term, but “voxel,” the corresponding unit of volume, is more appropriate for scan slices. For calcified tissue, radiographic density ranges from 130 to about 3000 H.U. Thus, only voxels with a density value of ≥ 130 H.U. are counted as positive for calcium mineral. In addition, to exclude random noise, only contiguous voxels occupying more than 1 mm² are counted as positive. Such contiguous groups are termed “lesions.” These aspects of the Agatston protocol are reasonable.

Where the protocol deviates is in determination of mass of calcium. Ordinarily, mass would be the sum of radiographic density values for all positive voxels across all slices, corresponding with integrating density over volume. A simple formula for calcium mass would be Σ D_j where D is density, and the summation is over values of j from 1 to the number of voxels over all slices, with voxel size then converted to cubic millimeters. Interestingly, the Agatston approach instead uses a different - and very unusual - approach, where the data are processed through three unusual steps before summation. This approach is illustrated using a hypothetical lesion in Fig. 1. First, two digits are truncated from each value of radiographic density (Fig. 1A). Second, an upper threshold of 4 is applied for all voxels having density values of 500–3000 HU (Fig. 1B). Third, values of all voxels in a given lesion are replaced with the peak density number (PDN) in that lesion (in Fig. 1B, it is 4). This number is then multiplied by the lesion area to generate the “lesion score.” A total coronary calcium score is derived by adding up all lesion scores in all slices.

Figure 1. The standard Agatston processing method and its effects on hypothetical values of density for a single lesion.

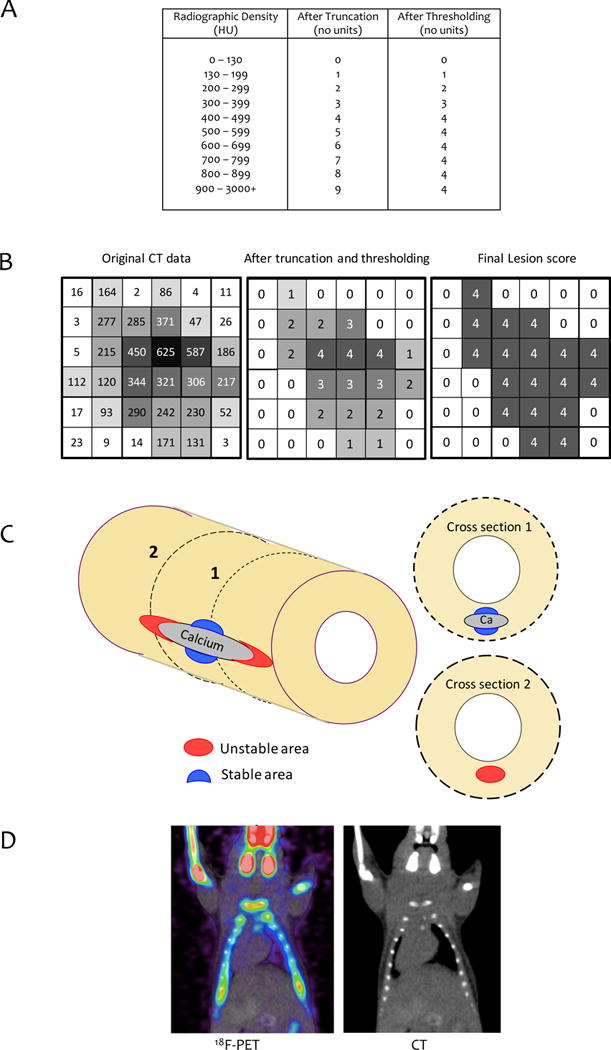
(A) Agatston method’s truncation and thresholding algorithm. (B) Hypothetical example. Left: Hypothetical values of radiographic density (H.U.) for 36 voxels of a CT scan. Middle: After truncation and thresholding, per Fig. 1A. Right: After peak density step of Agatston method. (C) Diagram of high (red) and low (blue) stress zones near a hypothetical calcium deposit subject to longitudinal stretch. Section 1 shows an example of a cross section just beyond the longitudinal edge of a calcium deposit that would miss the calcification causing the high-risk, unstable zone. Section 2 shows a cross-section through the center of a calcium deposit that would find calcification in association with a low-risk, stable zone. (D) Spillover effect. ¹⁸F-PET and CT images of mouse chest and head. Note greater area and intensity of PET signal compared with the CT scan of the skull, clavicles, ribs and limb bones.

Unfortunately, this process sacrifices rigor and reproducibility for no clear reason. The truncation step introduces high amplitude, random noise, specifically, random subtraction of values ranging from 0 to 99 HU from the original radiographic density values. For example, for a voxel value of 256 HU, truncation subtracts 56 HU, reducing it by over 20% of its value. Moreover, applying the upper threshold of 4 introduces nonlinearity. Moreover, the use of a PDN, introduces false homogeneity, resembling pixelation; it also introduces high sensitivity to noise, as noted by Shinbane and Budoff.² For instance, if a patient had a single coronary calcified lesion in a single slice, with an area of 500 mm² and a highest density of 199 H.U., the PDN would be 1 (after truncating 99), and the patient’s calcium score would be 500 (PDN × area). If the scan were repeated a week later, and imaging noise were to cause a 0.5% increase the one most dense voxel from 199 to 200, the new maximal CT number would be 2 (dropping the last two digits of 200), and the new calcium score would be 1,000. Such a doubling of the calcium score in one week would alarm both patient and doctor, making clinical use of the Agatston method problematic.

In similar ways, use of the method in clinical research is likely to reduce rigor and reproducibility. For instance, artifactual nonlinearity would falsely diminish correlation coefficients and raise p values, thus masking potentially important relationships. One may ask why this algorithm is used, since it seems to have no purpose. It may have simplified calculations, but, in this computerized age, simplifying calculations has no value. Nevertheless, the algorithm has remained the standard in most clinical studies of coronary calcification. Future studies may benefit from quantifying calcium mineral density and volume without Agatston’s data-reduction steps and comparing them to the Agatston calcium score.

Calcification and rupture risk by IVUS

Another valuable tool for imaging coronary calcification is intravascular ultrasound (IVUS). Studies using IVUS³ suggest that culprit lesions, which are presumably rupture-prone, are associated with “spotty calcification,” multiple calcium deposits measuring ≤ 90° or about 2 mm in arc length, whereas clinically stable lesions are associated with deposits of greater arc length. This finding is consistent with the concept of compliance mismatch. The amplitude of von Mises (rupture-promoting) stress increases at sites of interface between materials of differing compliance. Biomechanical analyses using finite element analysis^{4, 5} have shown that von Mises stress is increased in a region of tissue at the edge of a rigid deposit facing the direction of tensile stress. In an artery or plaque exposed to longitudinal stress from blood pressure pulsations, this would correspond to the tissue adjacent to each longitudinal end of a calcium deposit. Simultaneously, rupture stress is decreased below normal levels at the ends of the deposit perpendicular to the direction of tensile stress. Thus, calcium deposits both destabilize and stabilize the artery wall.

An important corollary is that the magnitude of von Mises stress (and risk of plaque rupture) would be expected to increase with the surface area of calcium deposits. But surface area does not increase linearly with progression of calcification; surface area and rupture risk increase up to a limit where deposits are forced, by the size of the artery, to coalesce, thus reducing surface area and decreasing risk. Based on the work of Ehara et al.,³ that critical size may be an arc length of 90° or about 2.5 mm. This concept may create a nonlinear relationship between coronary calcification and cardiovascular mortality.⁶

These concepts, the compliance mismatch phenomenon, dependence on direction of stress, and the nonlinear relationship of surface area with calcification progression, together with the dependence of rupture risk on underlying tissue strength, may explain why prior reports have shown only stabilization or destabilization with coronary calcification. Furthermore, studies based on cross-sectional imaging (histopathology or IVUS) may not recognize longitudinal proximity to a calcium deposit. A cross-section through the center of a large calcium deposit would find low stress associated with calcification; whereas a cross-section just beyond the longitudinal end of the calcium deposit would miss the association of high stress with calcification (Fig. 1C), Similarly, given the bell-shaped relationship of surface area with degree of calcification, the relationship of risk to calcification may depend on the stage of disease.

Partial volume effects and spillover in fused ¹⁸F-fluoride PET-CT images

Because fluoride, taken up by calcium mineral, binds to growing crystals of hydroxyapatite, its positron-emitting isotope, ¹⁸F-fluoride, is used for PET imaging of skeletal disease, sometimes in combination with CT scans. In exciting recent work, Dweck and colleagues⁷ demonstrated that uptake of ¹⁸F-fluoride in human coronaries colocalizes with culprit lesions. On close examination, some regions of positive PET signal extend beyond the corresponding regions on fused PET-CT. It has been proposed that such regions of PET-only positivity represent a molecular-level metabolic process generating micro-sized calcium deposits.⁸ However, this same extension of PET-only positivity beyond CT-positivity is also seen in PET-CT of skeletal bone (Fig. 1D) and tumors.⁹ In these cases, the part of the PET signal beyond the actual object is known to be a technical artifact known as spillover or the partial-volume effect.⁹ As described by Soret et al.,⁹ for any region of ¹⁸F-fluoride tracer uptake that is almost as large as a voxel and that is embedded in a colder background, the partial volume effect spreads out and dilutes the signal. It causes dispersion of the signal, not loss of it. A small calcium deposit will look larger, but less active on PET than it actually is. It generally occurs for objects whose size is less than 3 times the full-width-half-maximum of the image resolution, and the effect may be reduced by use of newer, time-of-flight acquisition.¹⁰ In some fused PET-CT images, a small CT signal is accompanied by a minimal or absent PET signal. This may appear to indicate metabolic inactivity. However, in tumor PET imaging, such an effect is attributed to a tissue-fraction effect – if a voxel contains an interface between two tissues, then the signal is averaged for the two components in that voxel. Thus, both partial-volume and tissue-fraction effects may be masked by smoothing algorithms, which make the image appear more precise than it really is.

Other technical considerations include motion blurring of PET-CT co-registration¹¹ and differences in reconstruction algorithms, which have varying signal-to-noise ratios.^12–14 Iterative reconstruction in PET may improve accuracy of detection of calcified boundaries confounded by partial-volume effects, and, in CT, reconstruction may reduce noise and improve spatial resolution. In both modalities, iterative methods may enhance the lower limit of detection. Therefore, before drawing biological inferences from fused PET-CT images, it is necessary to consider technical causes, such as resolution differences, partial volume effects, tissue fraction effects, and spillover, masked by smoothing algorithms.

Concluding remarks

For rigor and reproducibility, it is essential to recognize technical limitations of imaging modalities and the pitfalls of data adjustments and processing algorithms. Like processed food, processed data warrant close inspection of the ingredients.