Simultaneous tracking of spin angle and amplitude beyond classical limits

Abstract

Measurement of spin precession is central to extreme sensing in physics,^1,2 geophysics,³ chemistry,⁴ nanotechnology⁵ and neuroscience,⁶ and underlies powerful magnetic resonance spectroscopies.⁷ Because there is no spin-angle operator, any measurement of spin precession is necessarily indirect, e.g., inferred from spin projectors F_α at different times. Such projectors do not commute, and thus quantum measurement back-action (QMBA) necessarily enters the spin measurement record, introducing errors and limiting sensitivity. Here we show how to reduce this disturbance below $\delta F_{\alpha }\sim \sqrt{N},$ the classical limit for N spins, by directing the QMBA almost entirely into an unmeasured spin component. This generates a planar squeezed state⁸ which, because spins obey non-Heisenberg uncertainty relations,^9,10 allows simultaneous precise knowledge of spin angle and amplitude. We use high-dynamic-range optical quantum non-demolition measurements^11–13 applied to a precessing magnetic spin ensemble, to demonstrate spin tracking with steady-state angular sensitivity 2.9 dB beyond the standard quantum limit, simultaneous with amplitude sensitivity 7.0 dB beyond Poisson statistics.¹⁴ This method for the first time surpasses classical limits in non-commuting observables, and enables orders-of-magnitude sensitivity boosts for state-of-the-art sensing^15–18 and spectroscopy.^19,20

Spin-based magnetometers monitor precession of the collective spin F of a magnetically-sensitive atomic ensemble,^1,3,21 while atomic clocks² and other atomic sensors²² use pseudo-spin systems with equivalent quantum descriptions: all are described by the SU(2) Lie algebra. Many optical interferometers are also SU(2) systems.²³ These SU(2) systems obey different uncertainty relations than do position/momentum or harmonic oscillator systems, with dramatic consequences for their quantum sensitivity limits. The classical quantity to be measured manifests as precession rate dψ/dt about a known axis, which we take to be x. This signal is not directly observable, because there is no quantum mechanical operator for spin angle ψ. Rather, it must be estimated, e.g. from F_z = |F_ρ| cos ψ, where |F_ρ| is the spin amplitude in the y–z plane, itself an observable to be measured. While some theoretical models assume F_ρ to be precisely known a priori, this assumption cannot be applied to most systems of interest – relaxation necessarily adds noise not knowable a priori.²⁴ We thus require a multi-component measurement: of amplitude and angle, or equivalently F_y and F_z, in both cases requiring tracking of non-commuting observables.

Similarly, magnetic resonance techniques²⁰ employ simultaneous amplitude and angle tracking to correlate spin relaxation rate, which indicates the physical environment,¹⁹ with precession frequency, which indicates the chemical shift or, in imaging, the spin location.⁷ In these applications, joint angle-amplitude dynamics contain the important signal.

For simple harmonic oscillator systems, it is well known that QMBA couples angle and amplitude, or equivalently the quadratures X and P, as required to preserve the Heisenberg uncertainty relation δXδP ≥ 1/2 (we take ħ = 1 throughout). This limits angle tracking to the standard quantum limit²⁵ (SQL), with uncertainty δψ = N^−1/2, where here N is the mean number of excitations. In contrast, uncertainty principles do not prevent tracking spin systems beyond the SQL. As the spin components F_y and F_z precess about the x axis, they are governed by the Robertson (not Heisenberg) uncertainty relation⁹

$$\delta F_y\delta F_z\ge \frac{1}{2}\left|\langle \left[F_y,F_z\right]\rangle \right|=\frac{1}{2}\left|\langle F_x\rangle \right|.$$ (1)

In normal sensor operation, 〈F_x〉 is set to zero, to allow large polarization in the F_y−F_z plane. Because it is a constant of the motion, 〈F_x〉 remains zero for all time, and Eq. (1) places no limit on how precisely F_y and F_z can be simultaneously known or tracked. Arithmetic uncertainty relations¹⁰ then set the relevant limit, var(F_y) + var(F_z) ~ N^2/3, far below var(F_z) ~ N, the SQL. Because N is typically ~ 10⁶ in cold atom systems and ~ 10¹² in atomic vapors, this N^1/3 advantage extends the quantum limits by orders of magnitude. Spin states with two sub-classical spin uncertainties have been studied theoretically as planar squeezed states.⁸

Our discussion thus far indicates only the absence of uncertainty-principle barriers to precision spin tracking. We now outline a proof, given in Methods, that continuous quantum non-demolition (QND) measurement achieves this goal. The state evolution is illustrated in Fig. 1 a) and summarized here: F_z is coupled to an optical “meter” variable S_z via the QND interaction H_eff = gF_zS_z, where g is a coupling constant. The interaction with N_L photons imprints a signal proportional to F_z on the meter, which when measured reduces var(F_z) by an amount Δ_m ~ g²N_Lvar²(F_z). This same interaction rotates F about F_z by a random angle θ ≡ gS_z , which increases var(F_y) by Δ_d ~ g²N_Lvar(F_x), much smaller than Δ_m, given that var(F_z) ≫ 1. Combining these effects, there is a net reduction of var(F_z) + var(F_y), the total variance in the plane of precession. Precessing and under continuous measurement, F_z and F_y alternate roles as the measured and disturbed variable, and each experiences a net uncertainty reduction. When N_L reaches 1/(g²N), the measurement benefit Δ_m ~ N is of order the initial variance, while the in-plane back-action Δ_d ~ 1 is still negligible. Probing with this N_L also induces a negligible loss of coherence, so that the sensitivity to both angular and radial perturbations improves beyond classical limits. It is important to note that the QMBA is not eliminated in this method, rather it is directed almost entirely to the F_x variable, which is never measured and acts as a depository for quantum uncertainty. A similar approach has been proposed for harmonic oscillators using auxiliary negative-mass oscillators to create uncertainty depositories.^26,27

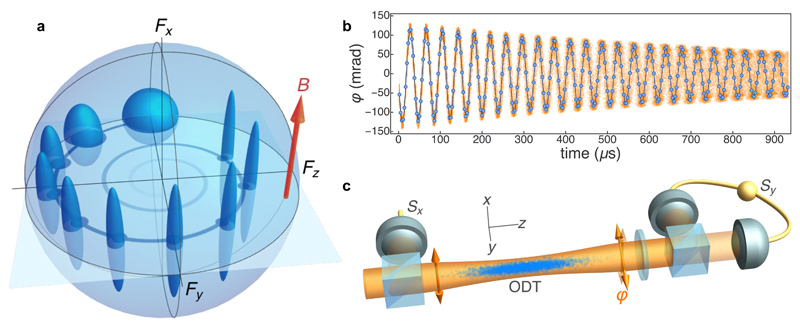
Fig. 1. Simultaneous, precise tracking of spin angle and amplitude.

a) Bloch-sphere representation of the atomic state evolution. Ellipsoids show uncertainty volumes (not to scale) as the state evolves anti-clockwise from an initial, F_y-polarized state with isotropic uncertainty. An x-oriented magnetic field B drives a coherent spin precession in the F_y–F_z plane. Quasi-continuous measurement of F_z produces a reduction in F_z and F_y variances, with a corresponding increase in var(F_x). b) Observed Faraday rotation angle φ ∝ F_z versus time. Each circle shows the rotation angle from one V-polarized pulse. A magnetic field of 37.6 mG produces the observed oscillation, while dephasing due to residual magnetic gradients and off-resonant scattering of probe photons cause the decay of coherence. Blue circles show a single, representative trace, overlaid on 453 repetitions of the experiment shown as orange dots. The time zero corresponds to the first probe pulse; the end of optical pumping is 58 µs earlier. c) Experimental geometry: 1.9 × 10⁶ cold ⁸⁷Rb atoms are confined in a weakly-focused single beam optical dipole trap (ODT). Transverse optical pumping is used to produce F_y polarisation. On-axis, 0.6 µs pulses with mean photon number 2.74 × 10⁶ experience Faraday rotation by an angle φ ∝ F_z. A polarimeter consisting of waveplates, a polarising beamsplitter, high-quantum-efficiency photodiodes, and charge-sensitive amplifiers measures the output Stokes component S_y. A reference detector before the atoms measures input Stokes component S₀ = |S_x|. The rotation angle is computed as φ = arcsin(S_y/S_x).

Realizing this in-principle advantage requires control of measurement dynamics²⁸ and incoherent effects,²⁹ as well as low-noise non-destructive detection with high dynamic range.³⁰ We use an ensemble of N = 1.9 × 10⁶ cold ⁸⁷Rb atoms held in an optical dipole trap. The atoms are initially prepared in the F_y-polarized state by optical pumping and, due to an applied B-field in the x direction, precess coherently in the F_y−F_z plane with Larmor period T_L ≈ 38 μs. The “meter” variable is the polarisation of ~ 1 μs, off-resonance optical pulses, which experience Faraday rotation by an angle φ = gF_z on the Poincare sphere as they propagate through the atomic cloud. We probe the atoms with V-polarized optical pulses, interspersed with Hpolarized compensation pulses to dynamically decouple the spin alignment,^12,13 i.e., to produce the effective hamiltonian H_eff = gF_zS_z without tensor light shifts. Earlier experiments have demonstrated sub-projection noise Faraday rotation measurements of either angular¹³ or amplitude¹⁴ variables. To measure both, we use high dynamic-range, shot-noise-limited optoelectronics³⁰ and nonlinear signal reconstruction to achieve sub-projection-noise readout sensitivity for rotation up to φ ≈ 100 mrad. See Methods.

A representative sequence of measured Faraday rotation angles φ(t_k) for QND measurements spread over 1 ms is shown in Fig. 1 b), and is well described by a free induction decay model that we use to estimate F_z and F_y at a time t_e

$$\phi \left(t\right)=g\left[F_z\left(t_{\text{e}}\right)\text{cos}{\omega }_{\text{L}}{t}_{\text{r}}-F_y\left(t_{\text{e}}\right)\text{sin}{\omega }_{\text{L}}{t}_{\text{r}}\right]e^{-t_{\text{r}}/T_2}+{\phi }_0$$ (2)

where t_r ≡ t − t_e. The coupling constant g is found by an independent calibration, while the Larmor frequency ω_L, the coherence time T₂, and the offset φ₀ are found by fitting to the measured φ(t_k) over the the range t_e − Δt ≤ t_k ≤ t_e + Δt, where Δt = 270 μs (see Methods).

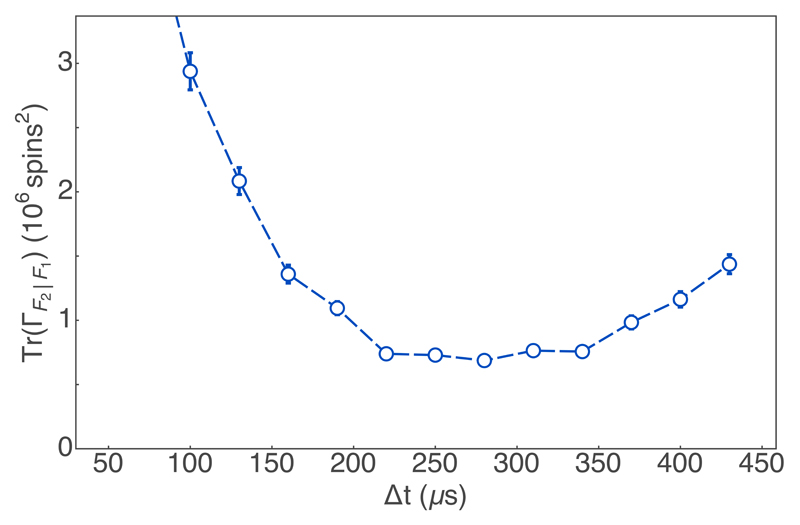
With these parameters fixed, we then use Eq. (2) to obtain a predictive estimate ${\mathbf{\text{F}}}_1=\left(F_y^{\left(1\right)},F_z^{\left(1\right)}\right)$ at time t_e using the measurements {φ(t_k)}_{te−Δt≤tk<te} from an interval Δt immediately before t_e; and to obtain a confirming estimate ${\mathbf{\text{F}}}_2=\left(F_y^{\left(2\right)},F_z^{\left(2\right)}\right)$ using {φ(t_k)}_{te<tk≤te+Δt} from the interval Δt after t_e. Because the classical parameters g, ω_L, T₂ and φ₀, are fixed beforehand, these are two linear, least-squares estimates of the vector F obtained from disjoint data sets. Estimating F for several values of t_e gives a predictive trajectory and a confirming one. We gather statistics over 453 repetitions of the experiment. Empirically, we find Δt = 270 μs minimizes the total conditional variance Tr(Γ_F2|F1) (see Methods), reflecting a trade-off of photon shot noise versus scattering-induced decoherence and magnetic-field technical noise.

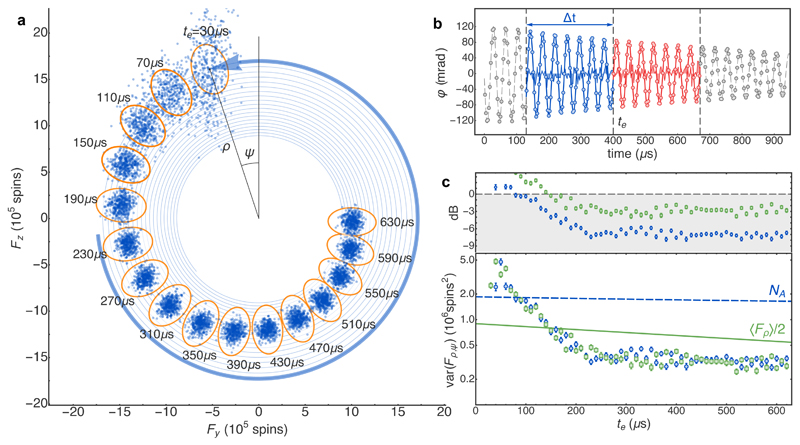
Fig. 2 a) shows the resulting mean predictive trajectory 〈F₁〉, which spirals slowly toward the origin due to residual magnetic field gradient, and the discrepancy between the trajectories, F₂−F₁. The scatter of this discrepancy rapidly decreases with increasing t_e , as more probe pulses become available for estimating F₁, and reaches a steady state after about 250 μs of probing, at which point the number of pulses used for estimation is limited by Δt. With the optimum Δt = 270 μs, N_p = 90 and the total number of photons used to estimate F is N_L = N_p . n_L = 2.47 × 10⁸.

Fig. 2. Experimental results.

a) Measured trajectories in the F_y–F_z phase space at different estimation times t_e. For each of the 453 traces shown in Fig. 1 b), the function of Eq. (2) is fit to the data to find predictive and confirming estimates F₁, F₂, respectively, for (F_y , F_z) at time t_e. Fits for F₁ and F₂ use disjoint sets of data covering the ranges t_e − Δt ≤ t_k < t_e and t_e < t_k ≤ t_e + Δt, respectively. A single fit is a tightly-wound spiral shown as a thin blue line and the thick arrow shows the trajectory from t = 0 to t = t_e = 30 µs. For clarity, we show results for t_e values spaced by 40 µs, slightly more than one Larmor period. Each point shows 〈F₁〉 + 100ℱ, where 〈F₁〉 is the mean over the 453 repetitions, and $ℱ\equiv {\mathbf{\text{F}}}_{\text{2}}-{\text{Γ}}_{2,1}{\text{Γ}}_1^{-1}{\mathbf{\text{F}}}_{\text{1}}$ is the error of the best linear prediction (see SI). The factor 100 provides magnification for visualization purposes. Orange ellipses, with radial and azimuthal radii of 2σ, where $\sigma \hspace{0.17em}=\hspace{0.17em}100\sqrt{\text{CL}}$, show the relevant classical limits: Poisson (radial, CL = N) and SQL (azimuthal, CL = 〈F_ρ〉/2). b) Fits to estimate (F_y, F_z) for t_e = 400 µs and a measurement time Δt = 270 µs. Blue (red) shows fits based on prior (posterior) data. Shaded regions show fit residuals ×10. c) Evolution of tracking precision for different t_e. Blue circles and green squares show radial and azimuthal components of Γ_F2|F1. Error bars show the ±1 standard error in the variance for 453 repetitions. Dashed blue and solid green curves show Poisson and SQL variances. These decrease during probing due to loss of coherence and loss of atoms. No readout noise has been subtracted.

To quantify the measurement uncertainty, we compute the vector conditional covariance ${\Gamma }_{{\mathbf{\text{F}}}_2|{\mathbf{\text{F}}}_1}={\Gamma }_{{\mathbf{\text{F}}}_2}-{\Gamma }_{{\mathbf{\text{F}}}_2{\mathbf{\text{F}}}_1}{\Gamma }_{{\mathbf{\text{F}}}_1}^{-1}{\Gamma }_{{\mathbf{\text{F}}}_1{\mathbf{\text{F}}}_2}$ where Γ_v matrix for vector v, and Γ_uv indicates the cross-covariance matrix for u and v. Defining the polar coordinate system (F_y, F_z) = ρ(−sin ψ, cos ψ), we identify the radial and azimuthal variances, var(F_ρ) ≡ ρ̂^TΓ_F2|F1ρ̂ and var(F_ψ) ≡ ψ̂^TΓ_F2|F1ψ̂, respectively, where ρ̂ ≡ (−sin ψ, cos ψ)^T and ψ̂ ≡ (− cos ψ, − sin ψ)^T are radial and azimuthal unit vectors.

As shown in Fig. 2 c), var(F_ψ) drops below the SQL of 〈F_ρ〉/2 after ≈ 150 μs of probing, and remains below it to the limit of the experiment. No read out noise has been subtracted. Considering the steady-state region t_e ≥ 270 μs, var(F_ψ) is on average 2.9 dB below the SQL, and var(F_ρ) is on average 7.0 dB below the Poissonian variance N, to give a precision surpassing classical limits in both dynamical variables. For any given value of t_e, var(F_ρ) and var(F_ψ) have standard errors of ≈ 0.3 dB, implying high statistical significance even without combining results for different t_e.

We have shown how quantum measurement back-action can be almost completely evaded in spin-based sensors and spectroscopies, allowing simultaneous tracking of spin angle and amplitude beyond classical limits, using the physics of planar squeezed states.⁸ Our method is very close to practical application in the highest-performance atomic sensors: Tracking of atomic spin precession by non-destructive optical measurement is already used in the highest-sensitivity magnetic field measurements¹ and is also being developed for optical lattice clocks.¹⁵ The method is compatible with multi-pass¹⁷ and cavity build-up methods,¹⁸ that greatly reduce incoherent scattering, the limiting factor in our experiment. Together, these advances promise orders-of-magnitude sensitivity improvement in extreme sensing, in applications ranging from studies of macromolecular dynamics⁴ and geophysics,³ to non-invasive measurements of single-neurons⁶ and brain dynamics.¹⁶

Methods

A. Faraday rotation probing of atomic spins

The effective atom-light interaction is given by the hamiltonian

$$H_{\text{eff}}=g{S}_z{F}_z$$ (3)

which describes a quantum non-demolition measurement of the collective atomic spin F_z, where the operators $F_{\alpha }\equiv {\displaystyle {\sum }_i{f}_{\alpha }^{\left(i\right)}}$ (with α = x, y, z) describe the collective atomic spin, with $f_{\alpha }^{\left(i\right)}$ the spin orientation of individual atom spins. The optical polarization of the probe pulses is described by the Stokes operators $S_k=\frac{1}{2}\left(a_L^{†},a_R^{†}\right){\sigma }_k{\left(a_L,a_R\right)}^T,$ with Pauli matrices σ_k. The coupling constant g depends on the detuning from the resonance, the atomic structure and the geometry of the atomic ensemble and probe beam and is independently measured.^31–34,50

An input S_x-polarized optical pulse interacting with the atoms experiences a rotation by an angle φ = gF_z because of the interaction given by eq. (3). The transformation produced by the measurement on S_y is

$$S_y^{\prime }=S_y\text{cos}\phi +S_x\text{sin}\phi$$ (4)

In our experiment we measure S_x at the input by picking off a fraction of the optical pulse and sending it to a reference detector, and $S_y^{\prime }$ using a fast home-built balanced polarimeter.³⁵ Both signals are recorded on a digital oscilloscope.

From the record of S_x and $S_y^{\prime }$ , we calculate φ̂, the estimator for φ:

$$\begin{array}{l}\widehat{\phi }=\text{arcsin}\left(\frac{S_y^{\prime }}{S_x}\right)\\ =\text{arcsin}\left(\text{sin}\phi +\frac{S_y}{S_x}\sqrt{1-{\text{sin}}^2\phi }\right)\\ =\phi +\frac{S_y}{S_x}+\frac{1}{2}{\left(\frac{S_y}{S_x}\right)}^2\text{tan}\phi +O{\left(\frac{S_y}{S_x}\right)}^3.\end{array}$$ (5)

We note that due to shot noise S_y/S_x is normally distributed with zero mean and variance 1/(2S_x) ~ 5×10⁻⁷. The term containing tan φ thus describes a distortion of the signal at the ~ 10⁻⁶ level, which is negligible in the experiment.

B. Quantum limits for spin variances

Different classical limits provide benchmarks for the radial and azimuthal components of a spin precessing in the F_y−F_z plane. In general, these benchmarks describe the minimal noise of quantum states describing uncorrelated particles. For our system of N spin-1 atoms, the lowest noise uncorrelated state is the coherent spin state defined as a pure product state in which each atom is fully polarized in the same direction. If this direction is ŷ cos θ − ẑ sin θ, then the azimuthal component F_θ = − F_y sin θ + F_z cos θ has variance

$$\text{var}(F_{\psi }{)}_{\text{SQL}}=\frac{\langle F_{\rho }\rangle }{2}.$$ (6)

Any state that surpasses this limit implies entanglement among the atoms, and/or entanglement of the internal components of the individual atoms.^36,37

For the radial component F_ρ = F_y cos θ + F_z sin θ, the classical limit comes from the fact that accumulation of independent atoms into the ensemble is limited by Poisson statistics, var(N) = 〈N〉, so that for F = 1,

$$\text{var}(F_{\rho }{)}_{\text{Poisson}}=\langle N\rangle .$$ (7)

Noise below this level can be produced by a strong interaction among the atoms during accumulation,^38–41 or as here by precise non-destructive measurement.^34,42–47

C. Operator-level description of back-action evading measurement of two non-commuting spin observables

We consider a spin variable F, defined by commutation relations [F_x, F_y] = iF_z and cyclic permutations, precessing about the F_x axis and subjected to brief, non-destructive measurements of the F_z variable. We assume the precession during the measurement is negligible. In the measurement, the spin is coupled to the polarization of a probe pulse, described by the Stokes operators S with [S_x, S_y] = iS_z and cyclic permutations. The probe initial state is a coherent state polarized along S_x, so that $\left|\langle S_x\rangle \right|=N_{\text{L}}/2,\langle S_y\rangle =\langle S_z\rangle =0,\text{and}\text{var}\left(S_y\right)=\text{var}\left(S_z\right)=\frac{1}{2}\left|\langle S_x\rangle \right|.$. The system and meter are coupled by the quantum nondemolition hamiltonian

$$H_{\text{eff}}=g{S}_z{F}_z$$ (8)

which acts for unit time. The transformation produced is

$$S_x^{\prime }=S_x\text{cos}g{F}_z-S_y\text{sin}g{F}_z$$ (9)

$$S_y^{\prime }=S_y\text{cos}g{F}_z+S_x\text{sin}g{F}_z$$ (10)

$$S_z^{\prime }=S_z$$ (11)

$$F_x^{\prime }=F_x\text{cos}g{S}_z-F_y\text{sin}g{S}_z$$ (12)

$$F_y^{\prime }=F_y\text{cos}g{S}_z+F_x\text{sin}g{S}_z$$ (13)

$$F_z^{\prime }=F_z$$ (14)

Where primes indicate the output variables.

We assume a spin state in the F_y-F_z plane, i.e. with 〈F_x〉 = 0, and with zero initial cross-correlation, i.e. cov(F_x , F_y) = cov(F_x , F_z) = 0. Due to the zero mean of S_z , which is also independent of F, the transformation preserves these statistics in the primed variables, for example

$$\text{cov}\left(F_x^{\prime },F_y^{\prime }\right)=\text{cov}\left(F_x,F_y\right)\langle {\text{cos}}^{2}g{S}_z-{\text{sin}}^{2}g{S}_z\rangle +\left[\text{var}\left(F_x\right)+\text{var}\left(F_y\right)\right]\langle \text{cos}g{S}_z\text{sin}g{S}_z\rangle =0$$ (15)

We can compute the statistics of the output variables using

$$\begin{array}{l}\langle \text{cos}g{S}_z\rangle =\langle 1-\frac{1}{2}{g}^2\text{var}\left(S_z\right)+O{\left(g\right)}^4\rangle \\ =1-\frac{1}{4}{g}^2\left|\langle S_x\rangle \right|+O{\left(g\right)}^4\end{array}$$ (16)

and similar expansions for 〈cos² gS_z〉 and 〈sin² gS_z〉. The mean of F_y changes due to the back-action as

$$\begin{array}{l}\langle F_y^{\prime }\rangle =\langle F_y\rangle \langle \text{cos}g{S}_z\rangle +\langle F_x\rangle \langle \text{sin}g{S}_z\rangle \\ =\langle F_y\rangle \langle \text{cos}g{S}_z\rangle \\ =\langle F_y\rangle -\frac{1}{4}{g}^2\left|\langle S_x\rangle \right|\langle F_y\rangle +O{\left(g\right)}^4\end{array}$$ (17)

while the means of F_x and F_z are unchanged.

The variance of F_x is coupled to the variance of F_y , due to the rotation about F_z by a random angle gS_z :

$$\begin{array}{l}\text{var}\left(F_x^{\prime }\right)=\langle {\left(F_x\text{cos}g{S}_z-F_y\text{sin}g{S}_z\right)}^2\rangle -{\langle F_y\rangle }^2{\langle \text{sin}g{S}_z\rangle }^2\\ =\text{var}\left(F_x\right)\langle {\text{cos}}^{2}g{S}_z\rangle +\langle F_y^2\rangle \langle {\text{sin}}^{2}g{S}_z\rangle \\ =\text{var}\left(F_x\right)+g^2\left|\langle S_x\rangle \right|\left[-\frac{1}{4}\text{var}\left(F_x\right)+\frac{1}{2}\langle F_y^2\rangle \right]+O{\left(g\right)}^4\end{array}$$ (18)

and similarly

$$\begin{array}{l}\text{var}\left(F_y^{\prime }\right)=\langle {\left(F_y\text{cos}g{S}_z+F_x\text{sin}g{S}_z\right)}^2\rangle -{\langle F_y\rangle }^2{\langle \text{cos}g{S}_z\rangle }^2\\ =\langle F_y^2{\text{cos}}^{2}g{S}_z\rangle +\langle F_x^2{\text{sin}}^{2}g{S}_z\rangle -{\langle F_y\rangle }^2{\langle \text{cos}g{S}_z\rangle }^2\\ =\langle F_y^2\rangle \langle {\text{cos}}^{2}g{S}_z\rangle -{\langle F_y\rangle }^2{\langle \text{cos}g{S}_z\rangle }^2+\langle F_x^2\rangle \langle {\text{sin}}^{2}g{S}_z\rangle \\ =\text{var}\left(F_y\right)+g^2\left|\langle S_x\rangle \right|\left[-\frac{1}{4}\text{var}\left(F_y\right)+\frac{1}{2}\text{var}\left(F_x\right)\right]+O{\left(g\right)}^4\end{array}$$ (19)

after noting that, to order g³, 〈cos² gS_z〉 = 〈cos gS_z〉².

After the coupling, a projective measurement of $S_y^{\prime }$ provides information about F_z , with readout variance

$${\text{var}}_{\text{RO}}\left(F_z\right)\approx \frac{1}{2g^2\left|\langle S_x\rangle \right|}.$$ (20)

The approximation comes from a linearization of Eq. (10), which as discussed in Sec. A introduces an error at the 10⁻⁶ level, negligible in this scenario.

The resulting F_z variance, including both the prior and posterior information, is then^48,49

$$\begin{array}{l}\text{var}\left(F_z^{\prime }\right)=\frac{1}{{\text{var}}^{-1}\left(F_z\right)+{\text{var}}_{\text{RO}}^{-1}\left(F_z\right)}\\ =\frac{\text{var}\left(F_z\right)}{1+2g^2\left|\langle S_x\rangle \right|\text{var}\left(F_z\right)}\end{array}$$ (21)

expanding in g this becomes

$$\text{var}\left(F_z^{\prime }\right)=\text{var}\left(F_z\right)-2g^2\left|\langle S_x\rangle \right|{\text{var}}^2\left(F_z\right)+O{\left(g\right)}^4.$$ (22)

Collecting Eqs. (18), (19) and (22), defining $\Delta \langle F_{\alpha }\rangle \equiv \langle F_{\alpha }^{\prime }\rangle -\langle F_{\alpha }\rangle \text{and}\Delta \text{var}\left(F_{\alpha }\right)\equiv \text{var}\left(F_{\alpha }^{\prime }\right)-\text{var}\left(F_{\alpha }\right),$ and dropping terms of order O(g)⁴ we find

$$\Delta \langle F_y\rangle =-\frac{1}{2}{g}^2\left|\langle S_x\rangle \right|\langle F_y\rangle$$ (23)

$$\Delta \text{var}\left(F_x\right)=g^2\left|\langle S_x\rangle \right|\left[-\frac{1}{4}\text{var}\left(F_x\right)+\frac{1}{2}\langle F_y^2\rangle \right]$$ (24)

$$\Delta \text{var}\left(F_y\right)=g^2\left|\langle S_x\rangle \right|\left[-\frac{1}{4}\text{var}\left(F_y\right)+\frac{1}{2}\text{var}\left(F_x\right)\right]$$ (25)

$$\Delta \text{var}\left(F_z\right)=-2g^2\left|\langle S_x\rangle \right|{\text{var}}^2\left(F_z\right)$$ (26)

Considering an initial coherent spin state and choosing |〈S_x〉| = g⁻²N⁻¹, where N is the number of spins, we note that Δvar(F_z) ~ N, implying a reduction in the uncertainty of F_z comparable to its initial uncertainty. Due to the $\langle F_y^2\rangle$ term, the increase in var(F_x) is ~ N, comparable to its initial value. The other changes are ~ 1, negligible relative to the initial values. In this way we see that uncertainty is moved from F_z to F_x with negligible effect on F_y.

Larmor precession then noiselessly rotates uncertainty from F_y into F_z , uncertainty that is moved into F_x by the next measurement. This procedure reduces the uncertainty of both F_y and F_z with negligible in uence from measurement back-action.

D. Implementation in an atomic ensemble

1. Experimental set up

The experimental set up is described in detail in references .^31,50 The trap consists of a single beam laser at 1064 nm with 6.3 W of optical power, focused to a beam waist of 26 μm using an 80 mm lens. The trap is loaded with laser-cooled atoms from a magneto optical trap (MOT). After sub-doppler cooling in the final stage of the loading sequence, the trapped atoms have a temperature ~ 12 μK. The resulting atomic ensemble has an approximately Lorentzian distribution along the trap axis (which we label the z-axis) with a FWHM of w = 4 mm, and a gaussian distribution in the radial direction with of ω = 33 ± 3μm.

2. State preparation

The initial atomic state is prepared via optical pumping with circularly polarized light resonant with the F = 1 → F′ = 1 transition propagating along the y-axis. During the optical pumping stage the atoms are also illuminated with repumping light resonant with the F = 2 → F = 2′ transition using the six MOT beams, preventing accumulation of atoms in the F = 2 hyperfine level, and a small magnetic field is applied along the x-axis, with B_x = 37.6 mG, to coherently rotate the atomic spins in the y–z plane. We use a stroboscopic pumping strategy, chopping the optical pumping light into a series of τ_pump = 1.5 μs duration pulses applied synchronously with the precessing atoms for total of 200 μs, to prepare the atoms in an F_y-polarized state with high efficiency (~ 98%), resulting in a input polarized atomic ensemble with 〈F_y〉 ≃ N (see Extended Data Fig. 1). The pulse duration τ_pump ≪ T_L is chosen to optimize the optical pumping efficiency.

3. Probing

We probe the atoms via off-resonant paramagnetic Faraday-rotation using τ = 0.6 μs duration pulses of linearly polarized light with a detuning of 700 MHz to the red of the ⁸⁷Rb D₂ line. The probe pulses are V-polarized, with on average N_L = 2.74 × 10⁶ photons, and sent through the atomic cloud at 3 μs intervals. Between the probe pulses, we send H-polarized compensation pulses with on average $N_{\text{L}}^{(\text{H})}=1.49\times {10}^6$ photons through the atomic cloud. As described in detail in references,^48,51,52 the compensation pulses serve to cancel effects due to the tensor light shift, but do not otherwise contribute to the measurement. During the probing sequence, a magnetic field along the x direction drives a coherent rotation of the atoms in the y − z plane with T_L = 38 μs period. This ensures that the time taken to complete a single-pulse measurement is small compared to the Larmor precession period, i.e. τ ≪ T_L.

We correct for slow drifts in the polarimeter signal by subtracting a baseline ${\phi }_0=\frac{1}{N}{\displaystyle {\sum }_{k=1}^N{\phi }_k^{\left(i\right)}}$ from each pulse, estimated by repeating the measurement without atoms in the trap.

4. Statistics of probing inhomogeneously-coupled atoms

We consider the statistics of Faraday rotation measurements on an ensemble of N atoms, described by individual spin operators f_i. To define the SQL, we consider an ensemble in a coherent spin state, with the individual spins are independent and fully polarized in the F_y–F_z plane. We take N to be Poisson-distributed. When the spatial structure of the probe beam is taken into account, the Faraday rotation is described by the input-output relation for the Stokes component S_y

$$S_y^{(\text{out})}=S_y^{(\text{in})}+S_x^{(\text{in})}{\displaystyle \sum _{i=1}^{N}g({\mathbf{\text{x}}}_i)f_z^{(i)}}$$ (27)

where g(x_i) is the coupling strength for the ith atom, proportional to the intensity at the location x_i of the atom. $S_y^{(\text{in})}$ is has zero mean and variance $|\langle S_x^{(\text{in})}\rangle |/2$. We consider first the case in which the spin is orthogonal to the measured F_z direction, i.e. a measurement of the azimuthal component. Here the uncertainty in g(x_i) and in N make a negligible contribution, and the rotation angle $\phi =S_y^{(\text{out})}/S_x^{(\text{in})}$ has the statistics

$$\langle \phi \rangle =\langle f_z\rangle {\displaystyle \sum _{i=1}^N{\langle g({\mathbf{\text{x}}}_i)\rangle }_{{\mathbf{\text{x}}}_i}\equiv \langle N\rangle \langle f_z\rangle {\mu }_1}$$ (28)

$$\text{var}\left(\phi \right)=\text{var}\left({\phi }_0\right)+\text{var}\left(f_z\right){\langle {\displaystyle \sum _{i=1}^N{g}^2\left({\mathbf{\text{x}}}_i\right)}\rangle }_{N,{\mathbf{\text{x}}}_i}\equiv \text{var}\left({\phi }_0\right)+\langle N\rangle \text{var}\left(f_z\right){\mu }_2$$ (29)

where φ₀ is the polarization angle of the input light, subject to shot-noise fluctuations and assumed independent of F_z , and the angle brackets indicate an average over the number and positions of the atoms.

Next we consider the case in which the spin is along the measured F_z direction, i.e., a measurement of the radial component. In this case, the uncertainty in f_z is zero, and the variation in g and in N determines the measured variation

$$\langle \phi \rangle =\langle N\rangle \langle f_z\rangle {\mu }_1$$ (30)

$$\text{var}\left(\phi \right)=\text{var}\left({\phi }_0\right)+{\langle f_z\rangle }^2\text{var}\left({\displaystyle \sum _{i=1}^{N}g\left({\mathbf{\text{x}}}_i\right)}\right)\equiv \text{var}\left({\phi }_0\right)+\langle N\rangle {\langle f_z\rangle }^2{v}_2$$ (31)

We note that v₂ includes the variation of both the atom number and the coupling strength, and as such is lower-bounded by the Poisson statistics of N: v₂ ≥ 〈g²(x)〉 = μ₂.

For known 〈f_z〉 and var(f_z), measurements of 〈φ〉 and var(φ) versus N give the calibration factors μ₁ and μ₂ as described in Sections D5 and D6, respectively. To preserve the SQL $\text{var}\left(F_z\right)=\frac{1}{2}\left|\langle F_y\rangle \right|$ and similar, in the analysis leading to Fig. 2 we infer mean values as

$$\langle F^{(a)}\rangle =\frac{1}{{\mu }_1}\langle {\phi }^{(a)}\rangle$$ (32)

and covariances, including cov(A, A) = var(A), as

$$\text{cov}\left(F^{\left(a\right)},F^{\left(b\right)}\right)=\frac{1}{{\mu }_2}\text{cov}\left({\phi }^{\left(a\right)},{\phi }^{\left(b\right)}\right),$$ (33)

where F^(a,b) and φ^(a,b) are corresponding spin and angle variables. We note that because the contribution of var(φ₀) is not subtracted, this overestimates the spin variances.

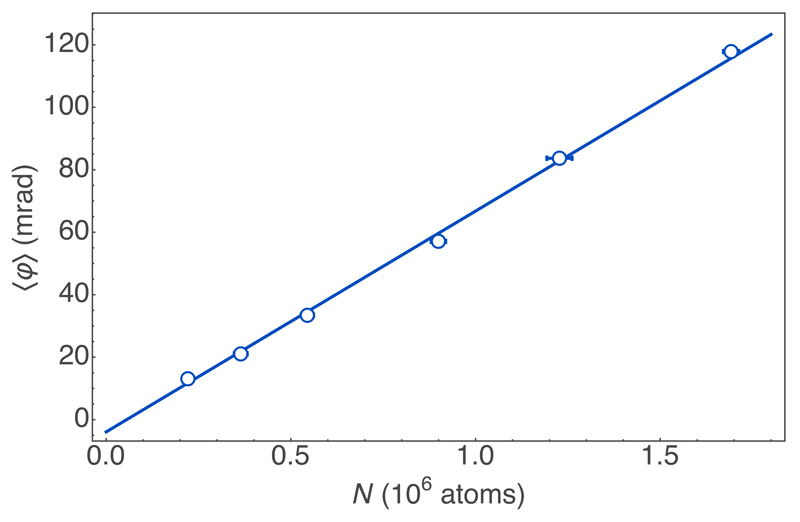
5. Measurement of calibration factor μ₁

We calibrate the measured rotation angle φ with a dispersive atom number measurements using absorption imaging, as shown in Extended Data Fig. 2. For the absorption imaging, atoms are transferred into the f = 2 hyperfine ground state by a 100 μs pulse of laser light tuned to the 5S_1/2(f = 1) → 5P_3/2(f′ = 2) transition. The dipole trap is switched off to avoid spatially dependent light shifts. An image is taken with a 100 µs pulse of circularly polarized light resonant to the 5S_1/2(f = 2) → 5P_3/2(f′ = 3) transition. We calculate the resonant interaction cross-section and take into account the finite observable optical depth. The statistical error in the absorption imaging is < 3%, including imaging noise and shot-to-shot trap loading variation.

6. Measurement of calibration factor µ₂

To measure μ₂ we prepare a F_y-polarized state by optical pumping, and then probe stroboscopically with N_p = 36 pulses of N_L = 3.15 × 10⁷ photons each in the presence of a B-field of ≈ 71.5 mG along y , producing a Larmor precession of an angle π during the 10 μs pulse repetition period. In this way, the measured variable is always ±F_z , evading back-action effects.

If φ_n is the measured Faraday rotation angle for pulse n, and ${\phi }_0^{(n)}$ is the corresponding input angle, we can define the pulse-train-averaged rotation signal as

$$\phi \equiv \frac{1}{N_{\text{p}}}{\displaystyle \sum _{n=1}^{N_{\text{p}}}{\left(-1\right)}^{n-1}{\phi }_n}$$ (34)

with variance

$$\text{var}(\phi )\equiv \text{var}({\phi }_0)+{\mu }_2{\displaystyle \sum _{n=1}^{N_{\text{p}}}\text{var}(F_{z,n})}$$ (35)

where ${\phi }_0=\frac{1}{N_{\text{p}}}{\sum }_{n=1}^{N_{\text{p}}}{\phi }_o^{(n)},$ with zero mean and variance var(φ₀) = (N_pN_L)⁻¹, and F_z,n is the value of F_z at the time of the nth probe pulse.

During the measurement, off-resonant scattering of probe photons produces both a reduction in the number of probed atoms and introduces noise into F. We note that this is a single-atom process that preserves the independence of the atomic spins. We compute the resulting evolution of the state using the covariance matrix methods reported in,⁴⁸ and specifically described for this case in Section D7, giving

$$\text{var}\left(\frac{g}{N_{\text{p}}}{\displaystyle \sum _{n=1}^{N_{\text{p}}}{F}_{z,n}}\right)={\mu }_2\frac{1}{2}\alpha N$$ (36)

where 1/2 = var(f_z) is the variance of the initial state, α = 0.86 describes the net noise reduction due to scattering.

Including the readout noise var(φ₀) and a generic technical noise a₂N² in the preparation of the coherent spin state, we have the observable variance

$$\text{var}(\phi )=\text{var}({\phi }_0)+{\mu }_2\frac{1}{2}\alpha N+a_2{N}^2,$$ (37)

in which the N scaling distinguishes the atomic quantum noise from other contributions. Experimental result shown in Extended Data Fig. 3 give μ₂ = (1.5 ± 0.2) × 10⁻¹⁴.

7. Calculation of the noise contribution α

As reported in Colangelo et al.⁴⁸ the full system is described by a state vector $V=\{F_z,S_y^{(1)},S_y^{(2)},\dots ,S_y^{(N)}\}$ and covariance matrix Γ = 〈V ∧ V + (V ∧ V)^T〉/2 − 〈V〉 ∧ 〈V〉, where $S_y^n$ is the measured photon imbalance after the n-th pulse. The QND interaction leads to a transformation of the covariance matrix

$${\Gamma }^{(n+1)}={\mathbf{\text{M}}}^{(n)}{\Gamma }^{(n)}{[{\mathbf{\text{M}}}^{(n)}]}^T$$ (38)

where M is equal to the identity matrix apart from the elements M_1,1 = −1 due to the precession by an angle π about the magnetic field, and M_n+1,1 = gS_x, where S_x = N_L/2 and N_L is the number of photons per pulse and g is the coupling constant for uniform coupling.

Off-resonant scattering of photons introduces decoherence, noise and loss in the atomic state. During the spin-noise measurement, a fraction ξ = 1 − exp(−ηN_L) = 0.01 of atoms scatter a photon during a single probe pulse, where η = 3 × 10⁻¹⁰ is the scattering rate per photon measured in an independent experiment, while a fraction χ = 1 − ξ remain in the coherent spin state. The scattered atoms are either lost from the F = 1 manifold, or return to F = 1 with probability p = 0.7 and random polarization. This has the effect of losing atomic polarization at each measurement. We calculate the effective measured polarization in terms of the initial atom number. We assume that the fraction p of scattered atoms the return to F = 1 have a random polarization and that the scattering rate η is independent of the atomic state.

After each pulse, the atomic part of the covariance matrix transforms according to

$${\Gamma }_{\text{at}}^{(n+1)}\text{=}\chi {\Gamma }_{\text{at}}^{(n)}+\frac{2}{3}p(1-\chi )N^{(n)}𝕀$$ (39)

where 𝕀 is the identity matrix. This follows from Eq.(A.6) of⁴⁸ assuming Γ_∧ = NΓ_λ. We note that we have

$$N^{(n+1)}=1-(1-\chi )(1-p)N^{(n)}=(\chi +p-\chi p)N^{(n)}$$ (40)

which, assuming that N⁽⁰⁾ = N, gives

$$N^{(n)}={(\chi +p-\chi p)}^{n}N$$ (41)

Including these terms, we get a linear transformation of the covariance matrix after the n-th pulse

$${\Gamma }^{(n+1)}={\mathbf{\text{DM}}}^{(n)}{\Gamma }^{(n)}{[{\mathbf{\text{M}}}^{(n)}]}^T{\mathbf{\text{D}}}^T+{\mathbf{\text{N}}}^{(\mathbf{\text{n}})}$$ (42)

where D is a zero matrix apart from the element ${\mathbf{\text{D}}}_{1,1}\text{=}\sqrt{\chi },$ and N⁽ⁿ⁾ is the identity matrix apart from the element ${\mathbf{\text{N}}}^{(\mathbf{\text{n}})}1,1=\frac{2}{3}p(1-\chi ){(\chi +p-\chi p)}^{n}N.$

We sum N individual polarimeter signals $S_y^{\prime (n)}$ to find the net Stokes operator $S_y^{\prime }\equiv {{\sum }_{n=1}^N(-1)}^{n-1}{S}_y^{\prime (n)}.$ This has a variance

$$\begin{array}{l}\text{var}(S_y^{\prime })={\displaystyle \sum _{n=1}^N\text{var}}(S_y^{\prime (n)})+2{\displaystyle \sum _{n\ne m}^N\text{cov}}(S_y^{\prime (n)},S_y^{\prime (m)}){(-1)}^{n-m}\\ =\mathbf{\text{P}}{\Gamma }^{(N)}\mathbf{\text{P}}\end{array}$$ (43)

with the projector P = diag(0, 1, −1, 1, −1, … , −1). When evaluated analytically using χ = 0.99, this gives

$$\text{var}(S_y^{\prime })=\text{var}(S_y,0)+\beta g^2\frac{1}{2}{\mathrm{NN}}_{\text{L}}^2$$ (44)

where β ≈ 0.1081. Noting that $\text{var}(\phi )=\text{var}(S_y^{\prime })/S_x^2$, where $S_x\equiv {\sum }_{n=1}^N{S}_x^{(n)}$ is the total input Stokes operator, dividing Eq. (44) by $S_x^2=N_{\text{L}}^2/4,$ and comparing against Eq. (37), we find that α = 8β ≈ 0.86.

E. Data analysis

1. Fitting procedure

As described in the main text, we follow a two-step fit procedure in our data analysis: we first fit Eq. 2 to the joint data set {φ(t_k)} of the first and second measurements, to estimate the classical parameters g, ω_L, T₂ and φ₀ near the measurement time t_e; then second, with the classical parameters fixed, we obtain a predictive estimate F₁ using measurements {φ(t_k)}_{te−Δt≤tk<te} from the interval Δt immediately before t_e; and a confirming estimate F₂ using {φ(t_k)}_{te<tk≤te+Δt} from the interval Δt after t_e.

2. Measurement phase

We note that, as shown in Fig. 2, the observed squeezing is independent of the choice of t_e provided that sufficient measurements are available in the interval Δt prior to t_e, indicating that the observed squeezing is not dependent on the choice of a particular phase of the spin oscillation.

3. Fit gain

Since the classical parameters g, ω_L, T₂ and φ₀ are fixed beforehand, the predictive and confirming fits to estimate F_y and F_z are linear, least-squares fits to disjoint data sets. We note that our condition for (conditional) spin squeezing is whether the conditional variance Tr(Γ_F2|_F1) is below classical limits - i.e., whether the estimate F₁ can be used to precisely predict the estimate F₂. This definition of squeezing is quite robust as regards the choice of estimators for F_y and F_z: they only need to have the right gain, i.e., the slope of the curve relating the mean estimate to the true value. The error propagation formula can then be used to find the variance of the true values in terms of the variance of the estimators.

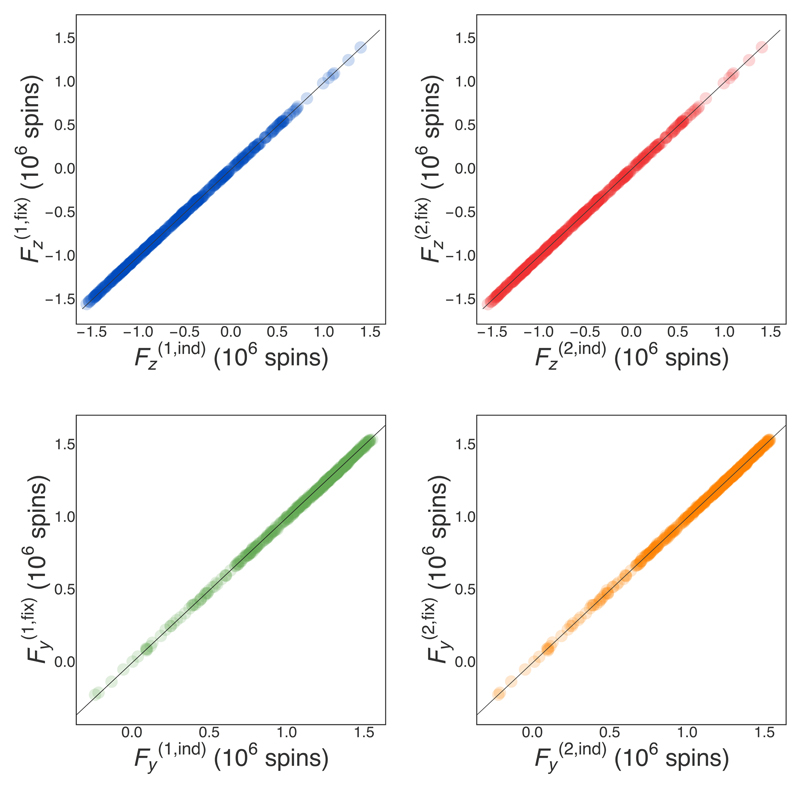
We check that the least-squares fits give the correct gain by comparing the estimated F_1,2 with the results of two independent fits using all free parameters in Eq. (2). Results, shown in Extended Data Fig. 4, show the gains are equal to within a ~ 10⁻³ fractional error, implying a similarly small ~ 10⁻³ fractional error in the inferred variances and conditional variances, with negligible effect on the squeezing results.

4. Weights

For the first fit to estimate the classical parameters, our data are weighted using an empirical function based on two observations: 1) the polarimeter signal shows increased technical noise in the optical variable at larger imbalance, i.e. when measuring a large instantaneous spin-projection along the z-axis; and 2) points closer in time to t_e should be given greater weight (minimizing errors introduced by small changes in ω_L and T₂ during the measurement). This motivates using the weight function

$$W(\phi (t_k))\equiv \frac{g(|t_k-t_e|)}{h(\phi (t_k))}$$ (45)

where $g(|t_k-t_e|)\equiv 1+A\text{exp}\left(-w\left|\frac{t_k-t_e}{T_2}\right|\right)$ and h(φ_k) = 1 + r |φ_k|. This ensures that we accurately estimated the classical parameters g, ω_L, T₂ and φ₀ at the measurement time t_e.

We numerically optimize W(φ(t_k)) varying the parameters A, w and r and minimizing the resulting Tr(Γ_F2|F1) from the predictive and confirming fits. We find an optimum with the parameters A = 15, w = 11 and r = 6, and note that the fit procedure gives similar results with variations of up to 30% in each of these parameters.

For the predictive and confirming fits, which are linear in F_y and F_z, all the points are weighted equally.

5. Optimal measurement length

The optimal measurement length Δt results from a trade off between the photon shot noise, the decoherences induced by the probing and the technical noise induced by the magnetic field. Longer measurements reduces the photon shot noise, while increasing the atomic decoherences and making the model eq. (2) less accurate. We empirically find the optimal Δt by minimizing the total variance Tr(Γ_F2|F1) for measurements with different length, as shown in Extended Data Fig. 5.

6. Conditional Covariance

Estimating F for several values of t_e gives a predictive trajectory and a confirming one. Estimations are repeated on 453 repetitions of the experiment to gather statistics. Assuming gaussian statistics, to quantify the measurement uncertainty, we compute the conditional covariance matrix

$${\Gamma }_{{\mathbf{\text{F}}}_2|{\mathbf{\text{F}}}_1}={\Gamma }_{{\mathbf{\text{F}}}_2}-{\Gamma }_{{\mathbf{\text{F}}}_2{\mathbf{\text{F}}}_1}{\Gamma }_{{\mathbf{\text{F}}}_1}^{-1}{\Gamma }_{{\text{F}}_1{\mathbf{\text{F}}}_2}$$ (46)

which quantifies the error in the best linear prediction of F₂ based on F₁.⁵³ Here Γ_v indicates the covariance matrix for vector v, and Γ_uv indicates the cross-covariance matrix for vectors u and v. The difference between the best linear prediction of F using F₁ and the confirming estimate F₂ is visualized using the vector $𝓕=\{{ℱ}_{\text{y}},{ℱ}_{\text{z}}\}={\widetilde{\mathbf{\text{F}}}}_2-{\Gamma }_{{\mathbf{\text{F}}}_2{\mathbf{\text{F}}}_1}{\Gamma }_{{\mathbf{\text{F}}}_1}^{-1}{\widetilde{\mathbf{\text{F}}}}_1,$ where ${\tilde{\text{F}}}_i={\text{F}}_i-\langle {\text{F}}_i\rangle .$ Standard errors in the estimated conditional covariance matrix are calculated from the statistics of {ℱ}.⁵⁴

Data Availability

The datasets generated and analysed during the current study are available from the corresponding author on reasonable request. The data shown in Fig. 2 and all the data used to generate plots of Extended Data are included as Source Data.

Extended Data

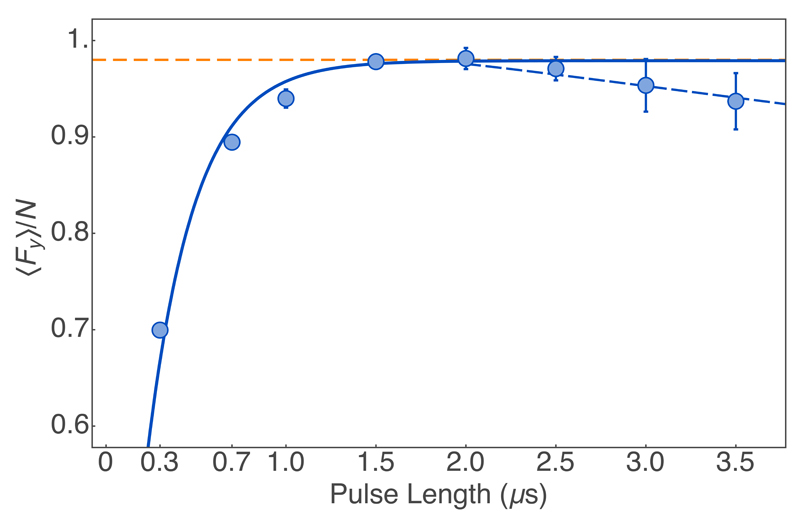
Extended Data Fig. 1.

Optical pumping efficiency. We prepare an input atomic state with 〈F_y〉 ≃ N via stroboscopic optical pumping in the presence of a small magnetic field along the x-axis. Data is fit with an exponential growing curve ∼ a(1 − e^−t/τ) (solid line) and we obtain a = 0.979 ± 0.004 and τ = 0.26 ± 0.02. Orange dashed line: Optical pumping efficiency of 98%. ±1 s.e.m. error bars are smaller than the points for most of the data.

Extended Data Fig. 2.

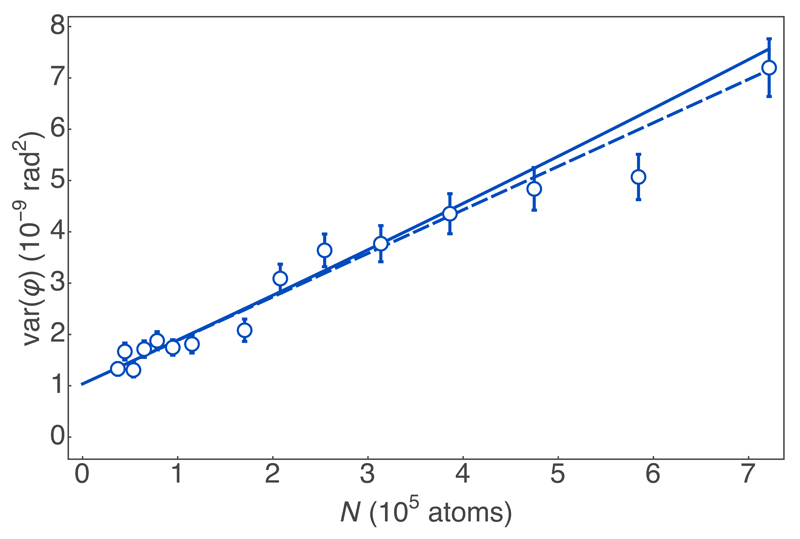
Calibration of average Faraday rotation signal. We calibrate the rotation angle φ against input atom number N, measured via absorption imaging. Solid line, the fit curve φ = a₀ + µ₁N, with we obtain µ₁ = (7.07 ± 0.04) × 10⁻⁸ and a₀ = (3.9 ± 0.3) × 10⁻³. Error bars indicate ±1 s.e.m.

Extended Data Fig. 3.

Calibration of quantum noise limited Faraday rotation probing of atomic spins. We plot the measured variance var(φ) as a function of the number of atoms N in an input coherent spins state with 〈F〉 = {0, N, 0}. Solid curve: a fit using the polynomial var(φ) = a₀ + a₁N + a₂N². The linear term a₁ = αµ₂N/2 corresponds to the atomic quantum noise from atoms in the input coherent spin state. We estimate a₀ = (11.7 ± 0.7) × 10⁻¹⁰, a₁ = (6.5 ± 0.8) × 10⁻¹⁵, and a₂ = (2.8 ± 12) × 10⁻²², consistent with negligible technical noise in the atomic state preparation. Dashed line: var(φ) = a₀ + a₁N. Error bars indicate ±1 standard error in the variance for 206 repetitions.

Extended Data Fig. 4.

Fit gain. We compare the estimated F_z and F_y from a fit using Eq. (2); first, with the classical parameters g, ω_L, T₂ and φ₀, fixed (labeled $F_{y,z}^{(\text{fix})}$) for measurements 1 and 2; and second, free to vary as independent parameters (labeled $F_{y,z}^{\text{(ind)}}$). In blue (green) F_z (F_y) of the first measurement, in red (orange) F_z (F_y) of the second measurement. A linear fit γx + δ to points of plots a-d gives γ_a = 0.9981(8), γ_b = 1.0026(8), γ_c = 0.9923(4), γ_d = 1.0007(5) and δ_a = 0.003(1), δ_b = 0.0001(9), δ_c = 0.0004(3), δ_d = −0.0023(3), where the subscripts refer to the values shown in plots a-d. A grey line y = x is plotted on both the figures.

Extended Data Fig. 5.

Tracking precision as function of Δt. An optimum is found at Δt = 270 µs. Error bars indicate ±1 standard error in the variance for 453 repetitions.