Abstract
Purpose
Myocardial perfusion can be quantified using the “dual bolus” technique, which uses two separate contrast boluses to avoid signal nonlinearity in the blood pool. This technique relies on knowing the precise ratio of contrast concentrations between the two boluses. In this study, we investigated the variability found in these ratios, as well as the error it introduces, and developed a method for correction.
Methods
Five dogs received dual bolus myocardial perfusion MRI scans. Perfusion was calculated separately using assumed contrast dilution ratios and empirically determined contrast ratios. Perfusion was compared with reference standard fluorescent microspheres. The same technique was then applied to a cohort of six patients with no significant coronary artery stenosis by cardiac catheterization.
Results
Assumed contrast dilution ratios were 10:1 for all animal and patient scans. Empirically derived contrast ratios were significantly different for animal (8.51:1 ± 1.53:1, P < 0.001) and patient scans (7.32:1 ± 2.27:1, P < 0.01). Incorporating empirically derived ratios for animal scans improved correlation with microspheres from 0.84 to 0.90 (P < 0.05).
Conclusion
Variability in dual bolus contrast concentration ratios is an important source of experimental error, especially outside of a carefully controlled laboratory setting. Empirically deriving the correct ratio is feasible and improves the accuracy of quantitative perfusion measurements.
Introduction
Myocardial perfusion has long been a marker for cardiovascular health, playing an important role in the diagnosis and management of coronary artery disease. Myocardial perfusion imaging has historically been dominated by nuclear imaging, principally single photon emission computed tomography (SPECT); however, more recently cardiac MRI has been developed as an alternative way to measure myocardial perfusion [1-3]. One of the advantages of cardiac MRI over SPECT for measuring perfusion is the ability to quantitatively measure perfusion in absolute terms (mL/min/g) instead of looking for relative differences between flow in different areas of the myocardium [4, 5]. In this regard, MRI is similar to positron emission tomography (PET), but because MRI does not depend on short-lived radioisotopes, MRI is potentially more widely available than PET perfusion imaging and avoids patient exposure to ionizing radiation. Quantification of myocardial blood flow has several advantages over visual inspection and semiquantitative techniques, including improved correlation with microspheres [6], the ability to monitor serial changes, and improved recognition of diffuse coronary artery disease [7]. However, the methods for measuring absolute perfusion are technically challenging and not widely implemented in clinical environments.
In first-pass perfusion studies, contrast agent is injected and images are taken of the ventricular blood pool and myocardium during the transit of contrast bolus. The contrast concentration over time in the blood pool is known as the arterial input function (AIF), and by modeling myocardial contrast concentration as a function of the AIF, flow in the myocardium can be calculated. MR perfusion imaging uses signal intensity over time as a surrogate for contrast concentration over time, but this assumes a linear relationship between MR signal and contrast concentration. Virtually all first-pass techniques suffer from saturation of the AIF signal during the peak of the contrast bolus, which results in underestimation of the AIF and errors in calculated flow. The Dual Bolus technique [6] addresses the problem of AIF signal saturation by using a low-dose contrast bolus to measure the AIF and a separate high-dose contrast bolus to ensure adequate myocardial signal.
Although dual bolus can effectively solve the AIF saturation problem when performed correctly, in practice it is seldom used outside of a few academic centers, in large part because it can be very difficult to implement. For any dual bolus experiment, two contrast agent mixtures of different contrast concentration but equal volume and identical delivery rate are needed: the “full” bolus used to measure signal in the myocardium and a more dilute “mini” bolus used to measure the AIF without saturation effects. There are several different proposed methods for implementing this sort of protocol, none of which has been adopted as a universal standard. One method of accommodating both bolus concentrations is to use a separate power injector for each bolus. However, obtaining a second injector is costly, and most clinical MR scanners only have access to a single injector at a time. When a second injector is not available, a preloading scheme can be used [8]. Another single injector alternative has been proposed [9], but this requires the presence of a physician for a manual contrast push. Although both of these methods avoid the cost of a second injector, they add time and complexity to the experimental setup, which is a significant hurdle in busy clinical environments where time is scarce and procedures are typically performed by MRI technicians and not dedicated cardiovascular MRI researchers. A typical clinical protocol also includes two perfusion studies (one at rest and one under stress), which would require preparation of separate lengths of tubes that are switched between the stress and rest studies. Existing microsphere validation of dual bolus has focused primarily on stress perfusion [6], and it is unclear what effect a more complicated stress/rest protocol would have on dual bolus accuracy and precision.
Not only is the experimental setup difficult for dual bolus, but care and attention to detail during this setup are crucial. In order to match the mini-bolus AIF to the full bolus myocardial signal during blood flow calculations, the mini-bolus AIF must be scaled by the ratio of contrast agent concentrations as measured at the left ventricle (LV). Accurate knowledge of this ratio is critical, because even small errors in the ratio can cause significant changes in the resulting flow. Typically, the mini-bolus is created by diluting the full bolus, and the concentration ratio at the LV is assumed to be the same as the dilution ratio. However, creating the two mixtures will always involve some degree of experimental error, which will only be magnified when performed outside of tightly controlled research environments. An alternative method proposed by Kostler et al. [10] uses a summation of smaller volume (instead of lower concentration) pre-boluses. Although this technique avoids dilution error, it is similarly susceptible to experimental error in that the summation is predicated on knowing a precise ratio of pre-bolus to full bolus volume. Finding an adjustment to the dual bolus technique so that it requires less careful setup and is more robust toward experimental error might facilitate more widespread adoption.
Fortunately, it should be possible to determine contrast concentration ratios empirically from the measured signal intensity data. Because only the peak of the AIF is saturated, the portion of the AIF after the signal peak should have minimal saturation effects. Thus, when scaled properly, the tail end of the mini-bolus AIF and the full bolus AIF should match. If this information can be used to determine the contrast ratios empirically and reduce the effects of experimental error, it would both reduce scan-to-scan variability and make dual bolus easier to implement in less controlled environments. In this study, we developed a tail matching method for empirically deriving contrast concentration ratios in dual bolus experiments. We then investigated the effect of this technique on quantitative perfusion measurements and used the empirically derived contrast ratios to examine potential sources of error in dual bolus experiments. We hypothesized that empirically derived contrast ratios improve the quantification of myocardial perfusion when using a dual bolus scan protocol.
Methods
Simulations
Our motivation for this study is predicated on the idea that dual bolus perfusion measurements are highly susceptible to small changes in full to mini-bolus contrast concentration ratios in the left ventricle. To investigate this effect, we took a representative AIF and myocardial signal intensity data from an animal experiment (described below) and adjusted the contrast ratio from 8 to 12 in increments of 1 (true dilution ratio = 10). In each case, the myocardial flow was calculated as described below.
Our experimental determination of the contrast agent dilution ratio is derived from signal ratios acquired in the LV, after peak contrast enhancement in the “tail” of the bolus where saturation effects are negligible. To confirm the assumption that saturation effects are negligible in the tail of the AIF, we simulated the passage of full and mini-bolus AIFs through the LV. The full bolus AIF contrast concentration was modeled using a gamma variate function [11, 12] in units of mmol/mL, and the mini-bolus AIF was empirically derived by dividing the full bolus AIF concentrations by 10 (the dilution factor used in the experiments described below). Both AIFs, currently defined in terms of contrast concentration, were then converted to signal intensity using a baseline blood T1 of 1500 ms (field strength of 1.5T to match our experiments), the relaxivity of gadopentetate dimeglumine (Magnevist; Bayer Healthcare, Whippany, New Jersey, USA) [13], and the SR-FLASH signal equation [5]. Simulations assumed a full bolus contrast concentration of 0.5 mmol/mL, an injection rate of 4 mL/s, and a cardiac output of 5 L/min. Additionally, to test the validity of the assumption that the scaled mini-bolus is an approximately linear representation of the unsaturated full bolus, we also modeled the ideal case of an unsaturated full bolus signal. To model this ideal signal, the linear region of SR-FLASH signal equation [5] was extrapolated to higher contrast concentrations.
Animal Imaging
A total of eight rest studies and 10 stress studies were conducted on five dogs in accordance with and after approval by our institution's animal care and use committee. Each animal was chronically instrumented with an external hydraulic occluder and cuff-type Doppler flowmeter around the left circumflex or left anterior descending coronary artery as described previously [14]. Left atrial, right atrial, and aortic catheters were placed for the administration of fluorescent microspheres, phenylephrine, and withdrawal of reference blood samples, respectively. Animals that received more than one imaging study were allowed to recover at least 48 hours between studies. All stress perfusion studies were performed under maximal adenosine vasodilation. The adenosine infusion rate for each dog (140–420 μg/kg/min) was that which produced the greatest increase in Doppler flow on a preliminary study. Except during reference blood withdrawals, the aortic catheter was used for continuous invasive blood pressure monitoring, and phenylephrine (40–80 μg/min) was given to maintain mean arterial pressure >60 mm Hg. Different levels of coronary stenosis were achieved by varying the inflation level of the coronary occluder under Doppler flowmeter guidance for each study. During image acquisition, ventilation was suspended to eliminate respiratory motion artifacts. The typical scan protocol was as follows: scouts, cine images, resting first-pass perfusion, stress first-pass perfusion. There was a minimum of 30 min between contrast injections.
All perfusion images were acquired with a 1.5T scanner (Siemens Medical Systems, Erlangen, Germany) with a saturation recovery, Cartesian, TurboFLASH sequence (repetition time = 2.21 ms, echo time = 1.39 ms, saturation recovery time = 100 ms, flip angle = 12°, slice thickness = 8 mm, in-plane resolution = 1.79 mm, acquisition matrix = 192 × 74). GRAPPA acceleration with an acceleration factor of 2 was used and no fat saturation was applied. Two or three short axis slices were scanned depending on the animal's heart rate at the time of imaging, and the midventricular slices were selected for further analysis.
Using a dual bolus protocol, two equal volume doses of gadopentetate dimeglumine (0.005 mmol/kg and 0.05 mmol/kg) were injected using separate power injectors (Medrad, Indianola, Pennsylvania, USA) at a constant rate of 4 mL/s followed by a 12 mL saline flush injected at 4 mL/s. The total volume in the lines between the saline syringe and the patient was 6.8 mL; a schematic of the experimental setup is shown in Figure 1. Immediately following the high-dose contrast injection of each study, approximately 3 × 106 microspheres (FluoSpheres Blood Flow Determination Color Kit #2, 15 μm; Invitrogen, Eugene, Oregon, USA) were injected via catheter into the left atrium with simultaneous reference blood withdrawal from the aortic catheter. Microspheres with multiple unique fluorescence spectra enabled multiple imaging studies to be performed in each animal.
Figure 1.
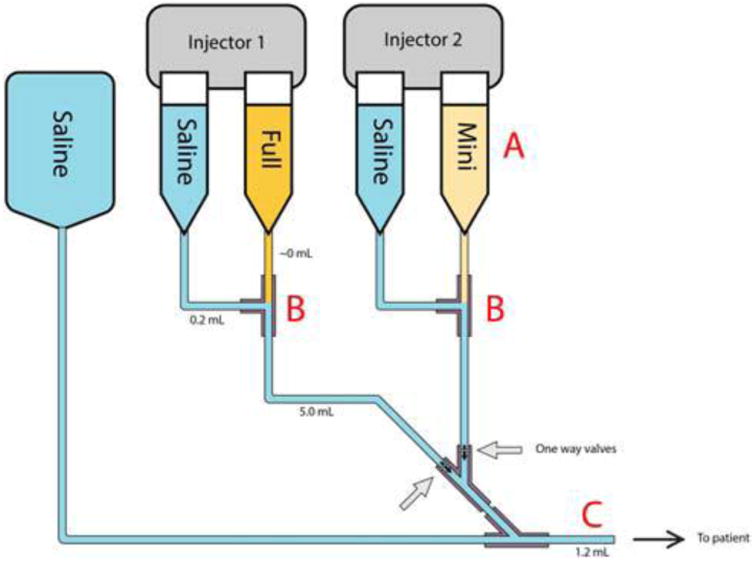
Schematic representation of a dual injector setup for dual bolus perfusion. For this study, we used specialized Y-connectors with one-way valves to prevent backflow into the mini-bolus and full bolus lines. Volumes of the different components are shown (Y-connector = 0.4 mL). Potential sources of dilution error include (A) improper dilution of mini-bolus, (B) inadvertent mixing of saline and gadolinium, and (C) retention of residual contrast agent from prior bolus in IV line.
After imaging, the animals were euthanized with an overdose of pentobarbital, and each heart was fixed in formalin. Eight-millimeter slices corresponding to image acquisition slices were sectioned into six segments following the standard American Heart Association bullseye segmentation [15]. Microsphere concentrations were quantified fluorometrically [16].
Patient Studies
Clinical records were queried to retrospectively identify patients who underwent clinically indicated adenosine stress first-pass myocardial perfusion imaging in which a dual bolus injection scheme was used. Six patients with quantitative coronary angiography showing <30% stenosis in each of the major coronary vessels were used in this study. Adenosine was infused at 140 μg/kg/min. After a minimum of 2 min infusion, equal volumes of gadolinium (Gd)- DTPA (mini-bolus 0.0075 mmol/kg, full bolus 0.075 mmol/kg) were injected using separate power injectors at a constant rate of 4 mL/s followed by 20 mL saline flush injected at 4 mL/s. The materials and design used for the dual bolus experimental setup were identical to those used in the animal study. However, scanning in the patient cohort was performed by MRI technicians during the course of normal clinical workflow, whereas in the animal study all scanning was performed by MRI research personnel. Additionally, stress scans were performed first in the patient cohort but second in the animal cohort. Adenosine infusion was stopped after completion of the first pass of contrast through the left ventricle. After a minimum of 10 minutes, rest perfusion imaging was performed using the identical imaging and contrast injection scheme as stress perfusion imaging. Perfusion images were acquired with a saturation recovery, TurboFLASH sequence (repetition time = 1.85 ms; echo time = 1.03 ms, saturation recovery time = 105 ms, flip angle = 12°, slice thickness = 10 mm, in-plane resolution = 2.375 mm, acquisition matrix = 160 × 120) on a 1.5T scanner (Siemens Medical Systems, Erlangen, Germany). Images were analyzed identically as in the animal study.
Image Analysis
Images were loaded into Medis QMass v6.5 (Medis Medical Imaging Systems, Leiden, Netherlands) for drawing epicardial contours, endocardial contours, and blood pool regions of interest. Signal intensity (SI) data from six equiangular segments of the midventricular short axis slice was extracted and averaged to generate SI curves for each American Heart Association bullseye segment. All further analyses were performed in MATLAB (MathWorks, Natick, Massachusetts, USA). A time offset was added manually to each mini-bolus to ensure temporal alignment with the corresponding full bolus. SI in each segment was normalized using the mean of the first 10 time points before contrast arrival, and the normalized baseline was then subtracted. Dual bolus correction was performed (see below for further details), and a Tofts-Kety two-compartment model that includes fitting of the blood plasma volume [17] was used to calculate Ktrans for each segment from the normalized ΔSI data. Blood flow was then calculated from Ktrans using extraction fractions [18]. An extraction fraction of 0.46 was assumed for regions with MBF less than or equal to 2.9 mL/min/g and 0.32 for higher MBF regions. Ktrans is known to vary with blood flow, and this cutoff was chosen as a rough approximation of the results reported by Ishida et al. [19].
Dual Bolus Correction
After SI normalization, SI data from the mini-bolus AIF was temporally shifted so that the arrival times of the AIF (determined visually) were identical for the full and mini-bolus. The SI data for the mini-bolus were then interpolated using a piecewise cubic spline interpolation to match the acquisition times of the full bolus AIF. Two separate scalings of the mini AIF were then performed, generating two different AIF curves. One was scaled using an assumed ratio of 10:1 for contrast concentrations in the full/mini-boluses; the other was scaled using an empirically determined concentration ratio.
To empirically derive the contrast concentration ratio, we scaled the mini-bolus SI curve such that the SI data at the tail end of the scaled AIF best overlapped with the full bolus AIF. To find the optimal matching, the tail was defined in each case as a relatively steady state period toward the end of signal acquisition. The second pass peak was avoided to minimize any potential saturation effects. In this region, SI data should be mostly unsaturated, so when scaled correctly the mini-bolus SI curve should overlap the full bolus SI curve. To achieve maximum overlap, least-squares fitting was used to find the full/mini-bolus ratio that minimized the difference between the two SI curves in this region (Fig. 2b).
Figure 2.
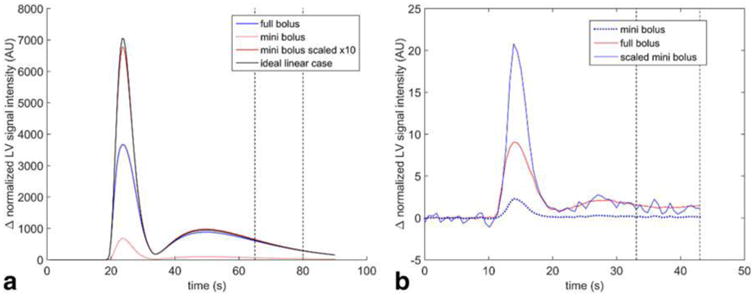
(a) Simulation of signal intensities from passage of full and mini-boluses through the left ventricle. Saturation effects are apparent during the peak of the mini-bolus but are small (5%) in the indicated portion of the tail. (b) Example AIF calculated using tail-matching. The original mini-bolus (dotted line) is scaled to minimize the difference between the mini- and full boluses in the region between 33 s and 43 s postinjection). Although the assumed contrast ratio is 10:1, the empirically derived contrast concentration ratio is 9.0:1. Because there is minimal saturation of the MR signal in this region, when scaled correctly, the mini-bolus overlaps with the full bolus in this region.
Results
Simulation
The newly scaled AIFs and resulting perfusion calculations are shown in Figure 3. Using the assumed dilution ratio of 10, the resulting flow was 2.6 mL/min/g. Adjusting the assumed ratio to 8 caused the calculated perfusion to increase 30% to 3.3 mL/min/g. Adjusting the assumed ratio to 12 caused the calculated perfusion to decrease 17% to 2.1 mL/min/g.
Figure 3.
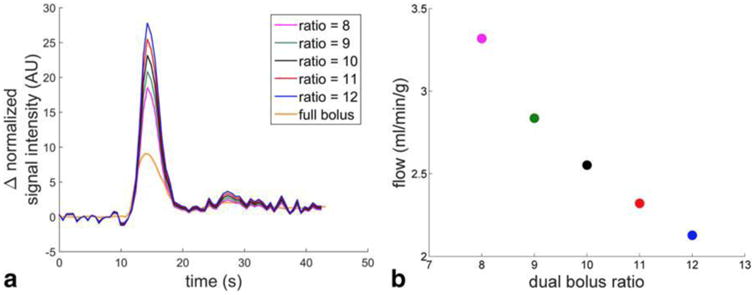
AIF and flow variability as a function of contrast concentration ratios. (a) A variety of scaled mini-bolus AIFs are plotted assuming different full/mini-bolus contrast ratios. (b) Mean perfusion in a segment of the midventricular slice using each AIF. As the assumed contrast ratio decreases, the AIF peak falls and the resulting calculated myocardial perfusion is higher.
For the saturation simulation, simulated SI curves are shown in Figure 2a. As expected, due to saturation effects on the full bolus, the peak of the scaled mini-bolus is much larger than the peak of the full bolus (84% larger). However, in the indicated segment of the tail, the mini-bolus signal intensity was only 5.1% larger. When comparing the scaled mini-bolus to the ideal unsaturated signal, the peak of the scaled mini-bolus was 96% of the height of the unsaturated peak.
Animal Study
A total of 108 midventricular myocardial segments were analyzed. Using an assumed contrast concentration ratio of 10:1, the correlation coefficient of MR perfusion with microspheres was 0.84 with a slope of 0.62. Using the tail-corrected empirically derived contrast ratios, the correlation coefficient was 0.90 with a slope of 0.82 (Figure 4). The correlation coefficients were compared as described by Zou [20] using an R implementation [21]. The 95% confidence interval for the difference between these coefficients is 0.035–0.102, indicating that the difference is statistically significant. Additionally, the slope of the best fit linear regression relating MR perfusion to microsphere perfusion changed from 0.62 to 0.82 with 95% confidence intervals of 0.54–0.69 and 0.74–0.89. These confidence intervals do not overlap, which demonstrates that the ratio of MR perfusion to microsphere perfusion is significantly closer to 1:1 when using the empirically derived contrast ratios. Without empiric correction, the correlation between Ktrans and microsphere was 0.85 with a best fit slope of 0.24. With empiric correction, the correlation coefficient was 0.89 with best fit slope of 0.30 (Fig. 4). Both the correlation coefficient and best fit slope changes were significant at P < 0.05.
Figure 4.

Myocardial blood flow in dogs before and after contrast ratio correction. Myocardial blood flow and Ktrans was calculated using both an assumed dilution ratio (a, c) and empirically calculated contrast ratios (b, d). Each plot includes both stress and rest data, and each data point represents the mean flow/Ktrans in a single midventricular segment. Use of empirically calculated ratios improved correlation with gold standard microsphere measurements.
The mean tail-corrected empirically derived contrast concentration ratio was 8.51 ± 1.53. This was significantly different than the assumed dilution ratio of 10 (P < 0.001). The mean empirically derived contrast concentration ratio was 9.40 ± 1.52 at rest and 7.78 ± 1.15 under stress. The rest empirically derived contrast ratio was not significantly different than the assumed dilution ratio (P = 0.27), whereas the stress contrast ratio was significantly lower (P < 0.001). The difference in contrast ratios between the rest and stress scans was significant (P < 0.05).
Human Study
The stress and rest flows, empirically derived contrast ratios, and flow reserves are summarized in Table 1. An example AIF is shown in Figure 5. The empirically derived contrast ratios were significantly different than the assumed dilution ratio (P < 0.01); however, the difference in contrast ratios between the rest and stress scans was not significant (P = 0.23).
Table 1. Perfusion Measurements from Patient Studies.
| Empirically Derived Ratio | Assumed Dilution Ratio | |
|---|---|---|
| Stress | ||
| Contrast ratio | 4.79 ± 0.45b | 10 |
| MRI calculated myocardial blood flow (mL/min/g) | 2.95 ± 0.67b | 1.37 ± 0.28 |
| Rest | ||
| Contrast ratio | 6.56 ± 2.98a | 10 |
| MRI calculated myocardial blood flow (mL/min/g) | 1.65 ± 0.20a | 1.06 ± 0.40 |
| Myocardial perfusion reserve | 1.86 ± 0.53 | 1.59 ± 1.07 |
P < 0.05.
P < 0.01.
Figure 5.

(a) Example patient AIF, before and after correction. Using the dilution ratio, the tail of the scaled mini-bolus is much greater than the full bolus, and the full bolus appears to be extremely saturated. When matching the tails (dashed segments), the full bolus appears less saturated, and the calculated flow is in a more normal physiologic range. (b) Mean adenosine vasodilated myocardial blood flow calculated using assumed dilution contrast ratios and empirically derived contrast ratios.
Discussion
In this study, we investigated the effect of contrast concentration ratio variability in dual bolus MR perfusion studies. Simulations confirmed the assumption that there are minimal saturation effects after the AIF peak, and we used this feature to find the empirically derived contrast concentration ratio that best matched the mini-bolus to the unsaturated portion of the full bolus. When perfusion values calculated using the empirically derived ratios were compared with perfusion values calculated using the assumed dilution ratio, using the empirically derived ratio significantly improved correlation and agreement with gold standard microsphere measurements. Furthermore, analysis of empirically derived ratios suggested that the actual ratios were on average 15% smaller than the assumed dilution ratio. These results suggest that variation in contrast concentration ratios is an important source of noise in dual bolus perfusion measurements and that this variability can be mitigated by using ratios empirically derived from the AIF tails.
Dual bolus has been shown to be accurate in an ideal setting [6], but despite the advantages of having quantitative perfusion data, dual bolus adoption has been limited in scope. A major reason for this lack of adoption is that dual bolus experiments are difficult to perform in a routine clinical setting. Setup either requires a lengthy and complex preloading scheme or use of two power injectors [6, 8, 9]. Compounding this high degree of complexity in preparation is a low tolerance for experimental error, because any change in contrast ratios has a large effect on final perfusion calculations. For example, suppose a typical experiment involves diluting 5 mL of Gd contrast with 45 mL of saline. An error of just 1 mL in drawing up the Gd contrast will produce a 20% error in the mini-bolus contrast concentration. As seen in Figure 2, this could introduce as much as 30% error into the final perfusion measurements, effectively negating any advantage of absolute quantitative analysis. This type of error is easily conceivable if, for example, a single 50-mL syringe is used to draw up both the Gd and the saline rather than using a separate 5-mL syringe to more precisely draw up the Gd. The error potentially introduced by the sensitivity of this technique to what may seem like minor experimental details may help to explain why some studies have not found a significant advantage in using pre-bolus [22] or dual bolus [23] over single bolus.
Reducing the experimental burden of using dual bolus may help both to increase its adoption and improve its accuracy. Some work has already been done in this area. Somewhat recently, a more universal method for performing dual bolus experiments was proposed [9], but it requires a physician for manual contrast push of the mini-bolus. However, the vast majority of clinical MRI scans are performed by MRI technicians, and necessitating a physician present for scans adds a logistical burden that may not be feasible in many clinical environments. Additionally, adding another variable in the rate at which the mini-bolus is pushed may further introduce variability between scans. Rather than focusing on modifying the dual bolus technique, we have instead focused on trying to improve the robustness of analysis to experimental error. Not only does this remove some complexity at the time of experiment, but it can also be applied retrospectively to existing dual bolus perfusion data.
In this study, we took advantage of the unsaturated regions of the AIF to empirically derive contrast concentration ratios at the left ventricle (Fig. 3). First, this eliminates the need to know the dilution ratio, which makes this analysis tolerant of any experimental error in mixing the mini-bolus. Second, what matters in the dual bolus experiment is not the contrast ratio at the injection site but at the site of AIF measurement (i.e., the LV). Consequently, even in the case of a precisely diluted mini-bolus, the contrast ratio in the LV can be affected by changes in cardiac output, infusion rate [relevant for any bolus pushed by hand, as in the study by Ishida et al. [9]], or residual blood contrast. Because our method determines contrast ratios from LV data, much of this variability should be incorporated into the empiric ratio. As such, this method would be expected to reduce variability and improve accuracy even in tightly controlled experimental settings.
In our animal data, we found that using empiric ratios significantly improved dual bolus MRI perfusion against gold standard microspheres, indicating that our method was successful in reducing measurement error. When applying the same technique to real world patient data, we found that empiric ratios were significantly lower than the assumed dilution ratios. Accordingly, absolute perfusion values increased when applying the empiric correction. Not only did the absolute perfusion values fall into more expected ranges for a cohort without significant coronary vessel disease, but the standard deviation of the perfusion reserve decreased by over 50%. This result suggests that using empiric ratios may increase the accuracy and precision of perfusion reserve measurements. A follow-up study using a gold standard (e.g., PET) comparison would better elucidate the accuracy of this method in real-world patient settings.
In both datasets, we found there was considerable variability in the empiric ratios. Given that the patient data were acquired in a less controlled setting, we found that empiric ratios in the clinical perfusion study deviated further from the dilution ratio. This result indicates that in real-world data, assuming a contrast concentration ratio equal to the dilution ratio may introduce significant error into perfusion measurements.
Although the tail matching technique to calculate empiric contrast ratios appears to reduce a significant source of error in dual bolus experiments, there are some important limitations to this study. First, because we did not directly measure the contrast concentrations in the LV, we cannot directly validate the accuracy of our contrast concentration ratios. Instead, we can only infer that they are more accurate than the assumed ratios based on how they affect perfusion measurements. It is likely that the empiric ratios include some degree of inaccuracy. The ratios are calculated from data toward the end of the scan, which is more likely to include respiratory motion. Also, as can be seen in Figure 2b, there is noise in the tail—especially in the mini-bolus—as it is scaled from low signal intensities. We used a broad time period to reduce noise by averaging, but still some error is bound to remain. However, the fact that the empiric ratios improved perfusion measurements against gold standard microsphere data indicates that any error introduced by the empiric approach is less than the error it reduces.
Second, we cannot determine from this study the source of variability and/or inaccuracy in the contrast ratios. Changes in cardiac output or injection kinetics, experimental error, contrast leakage or residual contrast may all play a role in changing the real contrast ratio away from the dilution ratio, and without more experimentation we cannot say what role each factor plays. Despite efforts to limit error, Figure 1 illustrates several potential sites of error in our injection set up:
Dilution error: Any errors in measuring contrast, saline, or improper mixing will lead to actual dilution ratios that differ from the assumed 1/10 dilution.
Leakage of contrast at saline/contrast T-junction: We used a specialized Y connector with one-way valves to prevent communication between the full strength and mini-bolus contrast injector systems (Injector 1, 2). However, we used commercial injector kits, which do not include one-way valves at the T-junctions between contrast and saline injection syringes.
Residual contrast in IV line: Despite the use of adequate flush, some residual contrast remains in the IV line between the Y connector and the patient after each contrast injection.
One trend we did see in our animal data was that the contrast ratios during the first (rest) perfusion injection were not significantly different than the dilution ratios, but the ratios during the second (stress) perfusion injection were 22% smaller (P < 0.001) than expected from the dilution ratio. Importantly, existing microsphere validation of dual bolus used only a single stress scan, so it is unclear what effect a stress/rest protocol has on perfusion accuracy. Some preliminary phantom experimentation suggests that residual contrast from the first full bolus remaining in the IV line may have played a role in this finding, but without more testing it is impossible to state this with certainty. In the patient cohort we saw a similar trend of smaller stress than rest contrast ratios, although the difference was not significant (P = 0.23). In this case, residual contrast would not explain the difference, because the stress scan preceded the rest scan in the patient cohort. It may be possible that other factors, such as leakage or dilution error, played a larger role in the clinical workflow, but at this point we cannot be certain what the underlying causes are. Ultimately, the causes of contrast ratio variability are multifactorial in nature. Some sources of variability may be systematic, whereas others are sporadic (e.g., human error), and sources of variability in one particular workflow or patient scan may be wholly different than those in another. Although it may be of interest to determine the relative contributions to contrast ratio error in various settings, in practice it is likely more feasible to compensate for this error via a method such as the one presented here than to try to eliminate it entirely.
Finally, an important limitation of all dual bolus experiments—including this study—is the assumption of a constant scaling factor. When applying the empiric contrast ratio to scale the mini-bolus, we are implicitly making the assumption that the entire mini-bolus can be scaled by the same ratio. First, this implies that the dispersion of the two boluses is identical, and any change in cardiac output between the full and mini-bolus may alter this. Also, the purpose of the mini-bolus is to avoid signal nonlinearity, and as seen in Figure 2, it is possible that the mini-bolus peak exhibits some nonlinearity. In an ideal case, this region would be scaled differently than the rest of the AIF. However, this would require knowing the degree of nonlinearity at the peak, which differs based on contrast dose, hemodynamics, and sequence parameters. In practice, it is impractical to determine the degree of nonlinearity, and instead a constant scaling factor is assumed for the entire AIF. As seen in Figure 2, the peak of the mini-bolus is typically similar to that of the ideal linear case, and assuming a linear response is fairly reasonable.
When considering these limitations, it is important to keep alternative methods for quantification in mind. Although dual bolus is an imperfect method, there is no perfect method for myocardial perfusion quantification. Dual sequence [8] offers a conceptually similar approach to dual bolus, but it is susceptible to T2* effects and adds time to each slice acquisition, which may reduce spatial coverage. A single low dose can be used to minimize nonlinearity, but this comes at the expense of losing signal-to-noise ratio in the myocardium. Another method, constrained alternating minimization with model [24], uses an iterative series of constrained fits to derive an AIF, but this approach has yet to be validated outside of animal models. Each method for quantification has its advantages and disadvantages, including dual bolus. One of the principle disadvantages of dual bolus is its experimental complexity, and a central aim of our proposed method is to reduce the impact of any experimental error.
In conclusion, we have demonstrated a method for improving the accuracy of dual bolus MRI perfusion experiments by empirically determining left ventricular contrast concentration ratios between the full and mini-boluses. This reduces variability due to sources such as physiological noise and increases the tolerance of the technique to experimental error while acquiring data. In a real-world clinical environment, some degree of experimental error is inevitable. Increasing the robustness of analysis techniques eases the logistical burden on clinical staff and may help to promote a more widespread adoption of dual bolus myocardial perfusion MRI.
References
- 1.Klocke FJ, Baird MG, Lorell BH, et al. ACC/AHA/ASNC guidelines for the clinical use of cardiac radionuclide imaging—executive summary: a report of the American College of Cardiology/American Heart Association Task Force on Practice Guidelines (ACC/AHA/ASNC Committee to Revise the 1995 Guidelines for the Clinical Use of Cardiac Radionuclide Imaging) J Am Coll Cardiol. 2003;42:1318–1333. doi: 10.1016/j.jacc.2003.08.011. [DOI] [PubMed] [Google Scholar]
- 2.Greenwood JP, Maredia N, Younger JF, et al. Cardiovascular magnetic resonance and single-photon emission computed tomography for diagnosis of coronary heart disease (CE-MARC): a prospective trial. Lancet. 2012;379:453–460. doi: 10.1016/S0140-6736(11)61335-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Schwitter J, Nanz D, Kneifel S, Bertschinger K, Buchi M, Knusel PR, Marincek B, Lüscher TF, von Schulthess GK. Assessment of myocardial perfusion in coronary artery disease by magnetic resonance: a comparison with positron emission tomography and coronary angiography. Circulation. 2001;103:2230–2235. doi: 10.1161/01.cir.103.18.2230. [DOI] [PubMed] [Google Scholar]
- 4.Lee DC, Johnson NP. Quantification of absolute myocardial blood flow by magnetic resonance perfusion imaging. JACC Cardiovasc Imaging. 2009;2:761–770. doi: 10.1016/j.jcmg.2009.04.003. [DOI] [PubMed] [Google Scholar]
- 5.Jerosch-Herold M. Quantification of myocardial perfusion by cardiovascular magnetic resonance. J Cardiovasc Magn Reson. 2010;12:57. doi: 10.1186/1532-429X-12-57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Christian TF, Rettmann DW, Aletras AH, Liao SL, Taylor JL, Balaban RS, Arai AE. Absolute myocardial perfusion in canines measured by using dual-bolus first-pass MR imaging. Radiology. 2004;232:677–684. doi: 10.1148/radiol.2323030573. [DOI] [PubMed] [Google Scholar]
- 7.Patel AR, Antkowiak PF, Nandalur KR, West AM, Salerno M, Arora V, Christopher J, Epstein FH, Kramer CM. Assessment of advanced coronary artery disease: advantages of quantitative cardiac magnetic resonance perfusion analysis. J Am Coll Cardiol. 2010;56:561–569. doi: 10.1016/j.jacc.2010.02.061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Gatehouse PD, Elkington AG, Ablitt NA, Yang GZ, Pennell DJ, Firmin DN. Accurate assessment of the arterial input function during high-dose myocardial perfusion cardiovascular magnetic resonance. J Magn Reson Imaging. 2004;20:39–45. doi: 10.1002/jmri.20054. [DOI] [PubMed] [Google Scholar]
- 9.Ishida M, Schuster A, Morton G, Chiribiri A, Hussain S, Paul M, et al. Development of a universal dual-bolus injection scheme for the quantitative assessment of myocardial perfusion cardiovascular magnetic resonance. J Cardiovasc Magn Reson. 2011;13:28. doi: 10.1186/1532-429X-13-28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Kostler H, Ritter C, Lipp M, Beer M, Hahn D, Sandstede J. Prebolus quantitative MR heart perfusion imaging. Magn Reson Med. 2004;52:296–299. doi: 10.1002/mrm.20160. [DOI] [PubMed] [Google Scholar]
- 11.Keijer JT, van Rossum AC, van Eenige MJ, Karreman AJ, Hofman MB, Valk J, Visser CA. Semiquantitation of regional myocardial blood flow in normal human subjects by first-pass magnetic resonance imaging. Am Heart J. 1995;130:893–901. doi: 10.1016/0002-8703(95)90092-6. [DOI] [PubMed] [Google Scholar]
- 12.Thompson HK, Jr, Starmer CF, Whalen RE, McIntosh HD. Indicator transit time considered as a gamma variate. Circ Res. 1964;14:502–515. doi: 10.1161/01.res.14.6.502. [DOI] [PubMed] [Google Scholar]
- 13.Shen Y, Goerner FL, Snyder C, Morelli JN, Hao D, Hu D, Li X, Runge VM. T1 relaxivities of gadolinium-based magnetic resonance contrast agents in human whole blood at 1.5, 3, and 7 T. Invest Radiol. 2015;50:330–338. doi: 10.1097/RLI.0000000000000132. [DOI] [PubMed] [Google Scholar]
- 14.Lee DC, Simonetti OP, Harris KR, Holly TA, Judd RM, Wu E, Klocke FJ. Magnetic resonance versus radionuclide pharmacological stress perfusion imaging for flow-limiting stenoses of varying severity. Circulation. 2004;110:58–65. doi: 10.1161/01.CIR.0000133389.48487.B6. [DOI] [PubMed] [Google Scholar]
- 15.Cerqueira MD, Weissman NJ, Dilsizian V, Jacobs AK, Kaul S, Laskey WK, Pennell DJ, Rumberger JA, Ryan T, Verani MS American Heart Association Writing Group on Myocardial Segmentation and Registration for Cardiac Imaging. Standardized myocardial segmentation and nomenclature for tomographic imaging of the heart. A statement for healthcare professionals from the Cardiac Imaging Committee of the Council on Clinical Cardiology of the American Heart Association. Circulation. 2002;105:539–542. doi: 10.1161/hc0402.102975. [DOI] [PubMed] [Google Scholar]
- 16.Glenny RW, Bernard S, Brinkley M. Validation of fluorescent-labeled microspheres for measurement of regional organ perfusion. J Appl Physiol (1985) 1993;74:2585–2597. doi: 10.1152/jappl.1993.74.5.2585. [DOI] [PubMed] [Google Scholar]
- 17.Tofts PS, Brix G, Buckley DL, et al. Estimating kinetic parameters from dynamic contrast-enhanced T(1)-weighted MRI of a diffusable tracer: standardized quantities and symbols. J Magn Reson Imaging. 1999;10:223–232. doi: 10.1002/(sici)1522-2586(199909)10:3<223::aid-jmri2>3.0.co;2-s. [DOI] [PubMed] [Google Scholar]
- 18.Pack NA, DiBella EV. Comparison of myocardial perfusion estimates from dynamic contrast-enhanced magnetic resonance imaging with four quantitative analysis methods. Magn Reson Med. 2010;64:125–137. doi: 10.1002/mrm.22282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Ishida M, Ichihara T, Nagata M, Ishida N, Takase S, Kurita T, Ito M, Takeda K, Sakuma H. Quantification of myocardial blood flow using model based analysis of first-pass perfusion MRI: extraction fraction of Gd-DTPA varies with myocardial blood flow in human myocardium. Magn Reson Med. 2011;66:1391–1399. doi: 10.1002/mrm.22936. [DOI] [PubMed] [Google Scholar]
- 20.Zou GY. Toward using confidence intervals to compare correlations. Psychol Methods. 2007;12:399–413. doi: 10.1037/1082-989X.12.4.399. [DOI] [PubMed] [Google Scholar]
- 21.Baguley T. Comparing correlations: independent and dependent (overlapping or non-overlapping) 2012 Available from: https://seriousstats.wordpress.com/2012/02/05/comparing-correlations/
- 22.Groothuis JG, Kremers FP, Beek AM, Brinckman SL, Tuinenburg AC, Jerosch-Herold M, van Rossum AC, Hofman MB. Comparison of dual to single contrast bolus magnetic resonance myocardial perfusion imaging for detection of significant coronary artery disease. J Magn Reson Imaging. 2010;32:88–93. doi: 10.1002/jmri.22231. [DOI] [PubMed] [Google Scholar]
- 23.Utz W, Greiser A, Niendorf T, Dietz R, Schulz-Menger J. Single- or dual-bolus approach for the assessment of myocardial perfusion reserve in quantitative MR perfusion imaging. Magn Reson Med. 2008;59:1373–1377. doi: 10.1002/mrm.21611. [DOI] [PubMed] [Google Scholar]
- 24.Fluckiger JU, Schabel MC, DiBella EV. Constrained estimation of the arterial input function for myocardial perfusion cardiovascular magnetic resonance. Magn Reson Med. 2011;66:419–427. doi: 10.1002/mrm.22809. [DOI] [PMC free article] [PubMed] [Google Scholar]


