The Relationship between Selection, Network Connectivity, and Regulatory Variation within a Population of Capsella grandiflora

Abstract

Interactions between genes can have important consequences for how selection shapes sequence variation at these genes. Specifically, genes that have pleiotropic effects by affecting the expression level of many other genes may be under stronger selective constraint. We used coexpression networks to measure connectivity between genes and investigated the relationship between gene connectivity and selection in a natural population of the plant Capsella grandiflora. We observed that network connectivity was negatively correlated with genetic divergence due to stronger negative selection on highly-connected genes even when controlling for variation in gene expression level. However, the presence of local regulatory variation for a gene’s expression level was also associated with reduced negative selection and lower gene connectivity. While it is difficult to disentangle the causal relationships between these factors, our results show that both connectivity and local regulatory variation are important factors for explaining variation in selection between genes.

Introduction

Variation in quantitative traits results from the combined effects of the environment and genetic variation at many genes (Lynch et al. 1998), and the ways in which these genes interact can influence how selection shapes genetic variation. Specifically, genes that have pleiotropic effects on multiple traits are likely to be under stronger negative selection than genes with less pleiotropy (Orr 2000; Stern and Orgogozo 2008). Similarly, genes with reduced pleiotropy may be more subject to weaker evolutionary constraint and thus be more free to adapt (Orr 2000; Stern and Orgogozo 2008). While these hypotheses are intuitively appealing, we lack data on the importance of pleiotropy in shaping genetic variation on a genome-wide scale. One way to estimate the pleiotropy of genes on a genome-wide scale is to use information about the strength of connections between a focal gene and other genes in a gene network, called “network connectivity” (Langfelder and Horvath 2008). The reasoning here is that genes with higher connectivity are more likely to be pleiotropic than genes with low connectivity (He and Zhang 2006).

A large body of work has shown that amino acid divergence is affected by network properties, including the number of protein–protein interactions (Fraser et al. 2002; Lemos et al. 2005; Luisi et al. 2015), protein-network centrality (Hahn and Kern 2005), pathway position (Rausher et al. 1999; Ramsay et al. 2009; Eanes 2011), metabolic network connectivity (Vitkup et al. 2006), regulatory network centrality (Jovelin and Phillips 2009), and coexpression network connectivity (Jordan et al. 2004; Carlson et al. 2006) although this pattern is certainly not observed in all cases for all types of networks (Pál et al. 2006; Hahn et al. 2004; Jordan et al. 2003). Reduced amino acid divergence in highly connected genes has been interpreted to be due to either stronger constraint on well-connected genes (Hahn and Kern 2005; Ramsay et al. 2009) or more frequent positive selection in genes on the network periphery (Kim et al. 2007; Luisi et al. 2015). Both of these explanations are possible, but they are difficult to disentangle using divergence-based approaches. The development of techniques that use both polymorphism and divergence to infer the strength of positive and negative selection hold promise for distinguishing between the relative roles of positive and negative selection in shaping divergence (Keightley and Eyre-Walker 2007; Eyre-Walker and Keightley 2009).

In this study we investigate the strength of negative and positive selection across gene coexpression networks constructed from natural variation for gene expression level. A coexpression network is an undirected graph where the nodes correspond to different genes, and genes that exhibit a significant correlation in expression level are connected. Gene connectivity is calculated as the sum of the strengths of correlations between a focal gene and all other genes (Langfelder and Horvath 2008). Coexpression networks can be generated using expression data collected across tissues or environments in the same genotype (Sekhon et al. 2014; Schmid et al. 2005; Walley et al. 2016), or using expression data from a population of genetically-distinct individuals (Mähler et al. 2017; Porth et al. 2013; Swanson-Wagner et al. 2012; Ayroles et al. 2009; Oldham et al. 2006; Lee et al. 2004) or a combination of varying genotypes and environments or tissues (Childs et al. 2011; Ficklin et al. 2010; Pierson et al. 2015). We take the second approach, investigating coexpression in a population sample, measured in one environment and tissue type, and constructing coexpression networks that summarize expression variation between individuals.

Connectivity measured in coexpression networks generated using a population sample will likely reflect, at least in part, genetic variation for gene regulation that segregates in the population. Large-effect cis-regulatory variants can reduce correlations in expression between the genes they regulate and other genes, so the presence of cis-regulatory variants may influence measurements of gene connectivity. Similarly, expression level may correlate with measures of connectivity. Because both expression level (Zhang and Yang 2015) and the presence of cis-regulatory variants (Steige et al. 2017; Li et al. 2014) have been linked to selection, accounting for these factors will be important for using coexpression networks to understand selection and pleiotropy.

Here, we evaluate the relationship between coexpression network connectivity and both positive and negative selection in the plant Capsella grandiflora. We find that connectivity is negatively correlated with amino acid divergence and show that this correlation is driven by stronger negative selection on highly connected genes, even when controlling for gene expression level. However, the relationship between negative selection and connectivity is confounded by the presence of local regulatory variation, which both reduces connectivity as measured using coexpression networks and is associated with lower levels of negative selection. Our results are consistent with two possibilities: first, highly connected genes are under stronger negative selection and thus tolerate less local regulatory variation and, second, that genes under stronger negative selection tolerate less regulatory variation and so appear to be better connected in regulatory networks.

Materials and Methods

Measuring Expression

We used leaf expression data from a population sample of 99 individuals of C. grandiflora reported in Josephs et al. (2015) and an additional 48 individuals, first reported here. All individuals descend from a sample of ∼400 plants collected from a single population located near Monodendri, Greece (population Cg-9 from St. Onge et al. 2011). We grew an individual seed collected from each wild parent in the University of Toronto greenhouses and conducted independent random crosses to generate the seeds used in the studies. These seeds were sterilized, transferred to sterile plates for stratification and germination, and transplanted to pots and grown in a growth chamber in standard conditions (additional protocol details are available described in Josephs et al. 2015).

Four weeks after transplanting, leaf tissue from all 147 individuals was collected and immediately flashes frozen in liquid nitrogen. All samples were collected sequentially. We extracted RNA from two or three samples per plant using plant RNA extraction kits (Sigma) and used a Qubit spectrophotometer to quantify RNA concentration so that the samples from each plant could be pooled such that each pool contained equal amounts of RNA from each sample. All RNA was sequenced at the Genome Quebec Innovation Centre in an Illumina HiSeq. The 99 individuals previously reported in Josephs et al. (2015) were sequenced on two flow cells with eight samples per lane (additional samples were sequenced and not reported here) with 100 bp long paired-end reads. The RNA from the previously unreported 48 individuals was sequenced in one flow cell with seven or eight samples per lane (again, additional samples were sequenced and were not included in this analysis). All RNAseq reads from these 48 individuals were 100 bp long and single ended. To avoid confounding effects from different mapping accuracy for paired- and single-end reads, we randomly selected one read per pair from paired-end data from the original 99 individuals to use for further analysis.

All sequence data were mapped using Stampy 1.0.21 (Lunter and Goodson 2011) with default settings to an exon-only reference generated from the Capsella rubella reference genome (Josephs et al. 2015; Slotte et al. 2013). Capsella rubella and C. grandiflora diverged between 50,000 and 100,000 years ago and sequence divergence between C. grandiflora and C. rubella is comparable to sequence diversity within C. grandiflora (Brandvain et al. 2013), making the C. rubella genome an appropriate reference genome here. We measured expression level for each gene by counting the number of reads that mapped to each gene using the HTSeq.scripts.count feature from HTSeq and we normalized for sequencing depth by dividing by the median expression level for each individual (Anders et al. 2015). We did not detect interactions between GC content, expression level, and lane (Josephs et al. 2015). Genes with a median expression of 0 were removed from the analysis, leaving a total of 20,570 genes. For comparisons of expression level with divergence and selection we divided read count by gene length, measured as the number of nucleotides in the coding sequence, to make expression level comparable between genes.

Measuring Gene Connectivity

The R package, WGCNA version 1.34 (Langfelder and Horvath 2008), running under R version 2.15.1 (R Core Team 2015) was used to calculate gene connectivity values using the C. grandiflora expression data. We conducted a network analysis using the following adjacency function: $a_{ij}=|cor(x_i,x_j)|$, where cor(x_i,x_j) is the correlation of gene expression in the ith and jth gene. Preliminary coexpression analysis showed that one individual was a strong outlier, so we removed it and reran the analysis on the remaining 146 individuals. Total connectivity for each gene was calculated as the sum of connection strengths (a_ij) between the focal gene and all other genes. We report and plot the average correlation coefficient per gene (the sum of correlation coefficients divided by the total number of genes) for interpretability.

Measuring Divergence and Relating It to Other Parameters

Divergence measurements from each gene were previously published in Williamson et al. (2014) and detailed methods are included there. Briefly, we found orthologs between the C. rubella reference genome and its two closest available outgroups: Neslia paniculata and Arabidopsis thaliana and aligned the protein sequences of these orthologs. These alignments were used to calculate d_N and d_S using codeml in PAML in a model where divergence was allowed to vary in the lineage leading to C. rubella (Yang 2007). Nine genes with zero synonymous substitutions were removed from the analysis so that d_N /d_S could be calculated.

We conducted Spearman correlations between connectivity and divergence and connectivity and expression for each gene (N = 13,211) using R’s cor.test() function (R Core Team 2015). Partial Spearman correlations between connectivity and divergence while accounting for expression were conducted with the pcor.test() function from the ppcor library in R. For both sets of correlations, we also conducted 1,000 permutations that randomized gene connectivity levels and compared observed correlation coefficients with those generated from permuted data. Following Drummond et al. (2006), a principal component analysis for d_S, mean expression level (log transformed), and connectivity was conducted in R using the prcomp() function, with scaling. We also used the R lm() function to construct a linear model for how principal components predict variation in d_N. We normalized the matrix of principal component loadings by squaring each value and normalizing such that all rows and columns summed to 1. These normalized principal component loadings show how much variance in each principal component was explained by d_S, connectivity, and expression.

We also investigated genes with and without eQTLs using eQTLs located within 5 kb of the genes they regulate, identified at an FDR <0.1 from Josephs et al. (2015). We tested for a difference in d_N/d_S and connectivity between genes with and without eQTLs using a Wilcoxan test with the wilcox.test() function from R (R Core Team 2015).

Measuring Positive and Negative Selection

The strength of positive and negative selection in the C. grandiflora genome was measured using single nucleotide polymorphism (SNP) data from 178 individuals collected from the same population described above and previously reported in Josephs et al. (2015) and Sicard et al. (2015). 146 of these 178 individuals overlap with the individuals used to generate coexpression networks and measure gene expression levels.

The methods for DNA extraction, sequencing, and genotyping are fully described in Josephs et al. (2015). Briefly, DNA was extracted from leaves by either a CTAB based protocol or by DNeasy Plant Mini Kit (Qiagen). We obtained whole genome sequences from each individual through 100 cycles of paired end sequencing in a Hiseq 2000 with Truseq libraries (Illumina) and three individuals were sequenced per lane. SNP genotypes were called following GATK Best Practices for Variant Quality Recalibration circa GATK 2.7 (DePristo et al. 2011) using a high confidence truth set generated by filtering SNPs for concordance with common variants (<0.11) in a species-wide sample of C. grandiflora as well as suspect realignments (transposable elements, centromeres, 600 bp intervals containing extreme Hardy Weinberg deviations, 1 kb intervals that showed evidence of three or more SNPs in a reference-to-reference mapping of 150 bp paired end reads from the reference genome line). For population genetic analysis, we downsampled to 320 alleles by randomly classifying alleles as missing, which allowed retention of 94.2% of sites.

We used SNP genotypes to estimate the strength of positive and negative selection across gene categories. For this analysis, divergence was measured from an outgroup, N. paniculata, aligned to C. rubella using LastZ with chaining, as described in (Haudry et al. 2013). We used the Joint Genome Institute’s gene annotation of the C. rubella reference genome to identify 0-fold degenerate and 4-fold degenerate sites within genes. We assigned genes into equally-sized categories based on connectivity values (low, medium–low, medium–high, and high) and calculated site frequency spectra (SFS) and divergence at 0-fold degenerate and 4-fold degenerate sites within these categories. We used SFS and divergence to estimate the fraction of 0-fold degenerate sites within each category under negative selection and measures of positive selection, α and ω, using 4-fold sites as a neutral reference and the methods described in Eyre-Walker and Keightley (2009) and Keightley and Eyre-Walker (2007). 1,000 bootstraps were conducted by resampling the genes included within each category with replacement. We used these bootstraps to construct 95% confidence intervals (Eyre-Walker and Keightley 2009) and tested for significant differences between the highest and lowest connectivity categories by randomly pairing bootstraps and calculating the proportion of pairs where one category was larger than the others. We compared bootstraps for six variables (α, ω, and 4 N_eS categories) in two datasets (all genes and the subset of genes described below), making 12 comparisons total, so we multiplied P values by 12 to account for multiple testing.

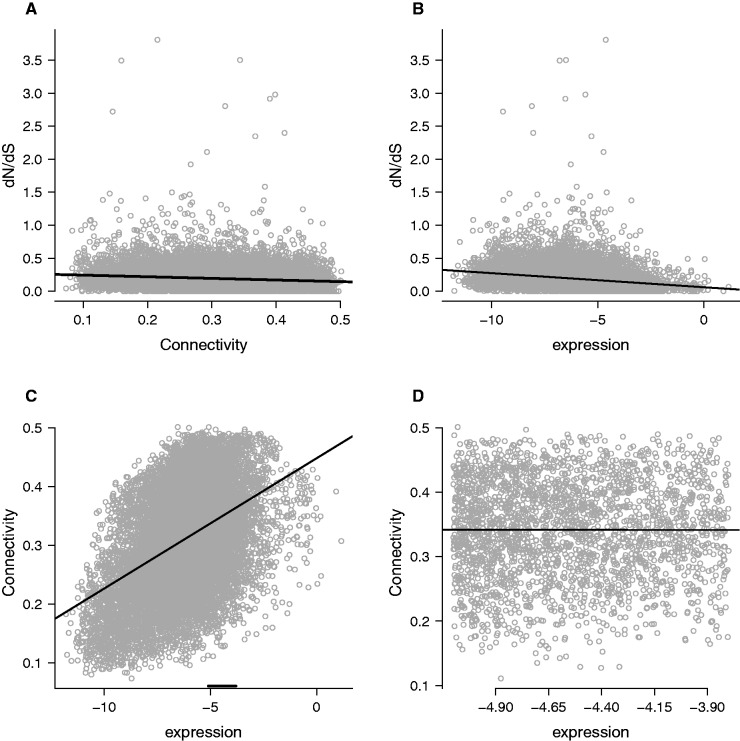
Positive and negative selection were also evaluated on a set of 2,449 genes chosen from a limited range of expression levels (-5.8 to -3.8 reads/(median read count per lane × gene length)). This region was chosen based on visual inspection of a plot of connectivity and expression level (fig. 1C). In this subset, gene expression level was not correlated with connectivity in a spearman test conducted in R with cor.test (ρ = –0.00555, P = 0.784). We used the same connectivity category cutoffs as in the full analysis, so the number of genes included in the connectivity categories were 305, 582, 735, and 827 for low, medium–low, medium–high, and high respectively.

Fig. 1.—

Correlations between protein divergence, connectivity, and expression. Each point represents one gene. (A) d_N/d_S correlates negatively with connectivity (ρ = −0.135, P < 2.2 × 10⁻¹⁶). In this and subsequent panels, we plot the fitted line from a linear model for visualization but statistical significance was determined using Spearman correlations. (B) d_N/d_S correlates negatively with expression (ρ = −0.289, P < 2.2 × 10^-16). Expression is plotted on a log scale. (C) Expression (also on a log scale) correlates positively with connectivity (ρ = 0.405, P < 2.2 × 10^-16). The window of expression level used to pick the subset of genes where expression does not correlate with connectivity is shown with a horizontal black line. (D) Within a subset of genes indicated in (C), expression and connectivity are not correlated (ρ = –0.00555, P = 0.784).

Results

We analyzed genome-wide gene expression data from the leaves of 146 C. grandiflora individuals from one large population grown in common garden. The expression data from 99 of these individuals have been previously reported (Josephs et al. 2015). For the previously unreported 47 individuals, we generated ∼1.3 billion single-end RNAseq reads, with a median of 26.7 million reads per individual (range: 19.4–44.3 million). Of these, a median of 94.2% reads mapped to genes (range: 93.1–94.9%).

Connectivity is Negatively Correlated with Nonsynonymous Divergence

Total connectivity values for each gene were calculated as the sum of correlation coefficients with all other genes. Connectivity is negatively correlated with d_N (ρ = −0.195, P < 2.2 × 10⁻¹⁶, see supplementary fig. S1A, Supplementary Material online), d_S (ρ = −0.145, P < 2.2 × 10⁻¹⁶, see supplementary fig. S1B, Supplementary Material online), and d_N/d_S (ρ = −0.135, P < 2.2 × 10⁻¹⁶, fig. 1A). The observed correlations between connectivity and d_N, d_S, and d_N /d_S were stronger than any of the correlations observed in 1,000 permutations (see supplementary fig. S2A, B, C, Supplementary Material online).

Expression level is also negatively correlated with d_S (ρ = −0.104, P < 2.2 × 10⁻¹⁶, see supplementary fig. S1C, Supplementary Material online), d_N (ρ = -0.333, P < 2.2 × 10^-16, see supplementary fig. S1D, Supplementary Material online), and d_N/d_S (ρ = −0.289, P < 2.2 × 10^-16, fig. 1B). In addition, expression level is positively correlated with connectivity (ρ = −0.405, P < 2.2 × 10^-16, fig. 1C) suggesting that expression level could explain observed divergence patterns. Partial correlations that account for expression level still show a significant, although weaker, relationship between connectivity and d_N (ρ = −0.070, P < 2 × 10^-15) and d_S (ρ = −0.112, P < 2 × 10⁻²⁵), and d_N/d_S (ρ = −0.0202, P < 0.05). The observed partial correlations between connectivity and d_N and d_S were stronger than any of the correlations observed in permuted data and the observed partial correlation between connectivity and d_N/d_S was stronger than all but 8 of 1,000 permutations (see supplementary fig. S2D, E, F, Supplementary Material online).

Experimental noise in measuring expression can make it difficult to fully remove expression’s effects in a partial correlation, potentially generating a spurious correlation between d_N or d_S and connectivity (Drummond et al. 2006). To ensure that our conclusion that connectivity affects divergence is not the result of this process, we conducted a principal component analysis to identify independent sources of variation in the explanatory variables d_S, expression level, and connectivity. A linear model based on the three principal components and all possible interactions explains ∼22.8% of the variation in d_N (table 1). The first principal component (PC1) explains 11.9% of the variation in d_N and was determined by connectivity, d_s, and expression level (see supplementary fig. S3, Supplementary Material online). The loadings of d_S, expression and connectivity on PC1 suggest that d_S contributes positively to d_N while connectivity and expression level contribute negatively to d_N (table 1).

Table 1.

Parameters and Results from Principal Components Analysis

	PC1	PC2	PC3	All
% variation in dN explained	11.13	7.47	0.78	22.79
P value	<0.001	<0.001	<0.001
Direction of effect	+	+	–
Contributions to PCs
dS	0.309	−0.948	−0.074
Expression level	−0.665	−0.271	0.696
Connectivity	−0.680	−0.166	−0.715

Connectivity Affects Positive and Negative Selection

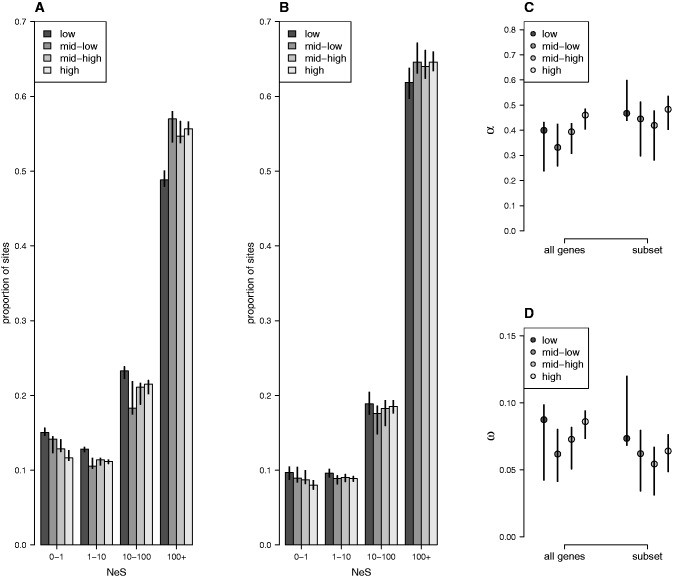
Reduced divergence in highly connected genes could be caused either by stronger negative selection or weaker positive selection on highly connected genes. To investigate these alternatives, we ranked all genes that were expressed in C. grandiflora leaf tissue and included in the previous analyses (N = 12,896) by connectivity level and divided these genes into four equally-sized categories: low connectivity, medium–low connectivity, medium–high connectivity, and high connectivity (N = 3,246 for each category). We estimated the proportion of 0-fold degenerate sites in these categories that are under various strengths of negative selection (Eyre-Walker and Keightley 2009).

Negative selection acts more strongly on genes with higher connectivity than lower connectivity (fig. 2A). For example, 0.150 (95% CIs: 0.147–0.156) of 0-fold degenerate sites in genes in the lowest connectivity category are effectively neutral (N_eS < 1) while 0.116 (95% CIs: 0.113–0.126) of 0-fold degenerate sites in genes in the highest connectivity category are effectively neutral (P <0.05, fig. 2A). There was no evidence that positive selection differs between genes with different connectivities. The proportion of fixations driven to positive selection, α, is 0.400 (95%CIs: 0.238–0.431) in the lowest connectivity category and 0.460 (95% CIs: 0.404–0.474) in the highest connectivity category (P >0.05, fig. 2C) and the rate of fixations driven by positive selection relative to neutral divergence, ω is not significantly different in genes with high connectivity (0.0874, 95% CIs: 0.0431–0.0985) than genes with low connectivity (0.0860, 95% CIs: 0.0734–0.0940, P > 0.05, fig. 2D).

Fig. 2.—

Estimates of negative and positive selection in genes of different connectivity categories, for all genes and for a subset of genes where expression is not correlated with connectivity. (A) The proportion of sites found in each bin of negative selection strength, separated by connectivity category for all genes (12,896 genes). (B) The proportion of sites located in the subset of genes (2,449 genes) where expression is not correlated with connectivity found in each bin of negative selection strength, separated by connectivity category. (C) The proportion of sites fixed by positive selection (α), and (D) the rate of adaptive substitution (ω). Error bars represent 95% confidence intervals.

Variation in expression level could also explain stronger negative selection in highly connected genes, because expression level is correlated with connectivity and genes with higher expression in leaf tissue in C. grandiflora experience stronger negative selection (Williamson et al. 2014). To control for expression level, we examined a subset of our data in which expression level and connectivity were not correlated and repeated our analysis of selection on this subset of genes using the same connectivity values to define categories as in the analysis of all expressed genes (N = 2,449, fig. 1C, D). Within this subset, negative selection was stronger on genes with higher connectivity values, although this effect was somewhat weaker than in the entire dataset: 0.0968 (95% CIs: 0.0877–0.0968) of sites in the lowest connectivity category were effectively neutral (N_eS < 1) while only 0.0800 (95% CIs: 0.0746–0.0862) of 0-fold degenerate sites in the highest connectivity category were neutral (P < 0.05, fig. 2B). In addition, both measures of positive selection, α and ω, do not differ between connectivity categories (P > 0.05, fig. 2C, D).

Local Regulatory Variation is Related to Connectivity and Selection

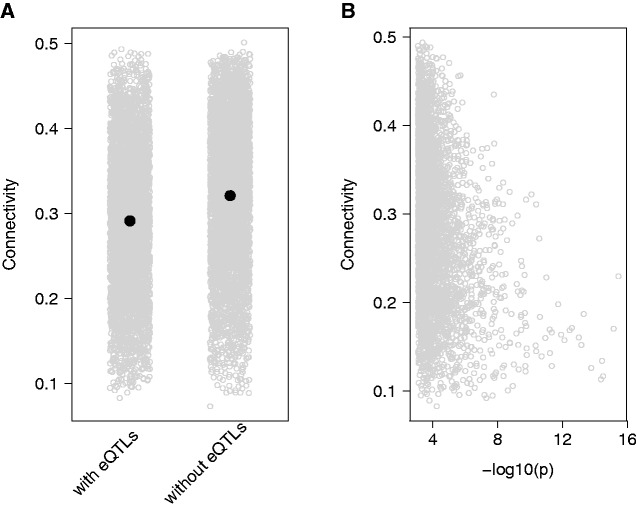
Many genes have local expression quantitative trait loci (eQTLs) that segregate within the population of C. grandiflora (Josephs et al. 2015). The presence of local eQTLs may reduce the correlation across genes between gene expression levels, thus reducing coexpression network connectivity which depends on the strength of these correlations. We separated genes into those with and without at least one eQTL located within 5 kB of the transcript, as identified in Josephs et al. (2015). We observed that the presence of an eQTL reduced gene connectivity: mean correlation coefficient for genes without eQTLs is 0.321 (n = 8,806) and the mean correlation coefficient for genes with eQTLs is 0.291 (n = 4,090), (P < 2.2 × 10⁻¹⁶, fig. 3A). Even within the set of genes with eQTLs, connectivity appears to relate to the strength of the association: a gene’s connectivity level is negatively correlated with the significance of the association for the most significant eQTL, measured as the negative log 10 of the P value (P < 2.2 × 10⁻¹⁶, ρ = -0.276, fig. 3B).

Fig. 3.—

Genes with local eQTLs have lower connectivity. (A) Black dots show mean connectivity, gray dots are values for each individual gene. Genes without an eQTL were randomly sampled to have the same number of observations as genes with an eQTL (n = 4,090). Standard errors are too small to be plotted. (B) For genes with at least one significant eQTL, connectivity is negatively correlated with the significance of the association for the strongest eQTL, measured as the negative log of the P value for the association test.

Genes with an eQTL also show evidence of reduced constraint: d_N/d_S is higher in genes with an eQTL (d_N/d_S = 0.201) than genes without an eQTL (d_N/d_S = 0.189, P = 9.9 × 10⁻⁹). The differences in divergence between genes with an eQTL and genes without an eQTL are driven by stronger negative selection on genes without an eQTL. Specifically, 0.167 of 0-fold degenerate sites in genes with eQTLs evolve neutrally (N_eS < 1, 95% CIs: 0.163–0.171) while 0.136 of 0-fold degenerate sites in genes without eQTLs evolve neutrally (95% CIs: 0.134–0.138, fig. 4A). Estimates of positive selection, α and ω do not differ between the two categories (fig. 4B, C). Overall, there is a general association between levels of constraint, connectivity and the presence of cis-regulatory variation as detected using the presence of local eQTLs. However, the direction of causality for these relationships is unclear.

Fig. 4.—

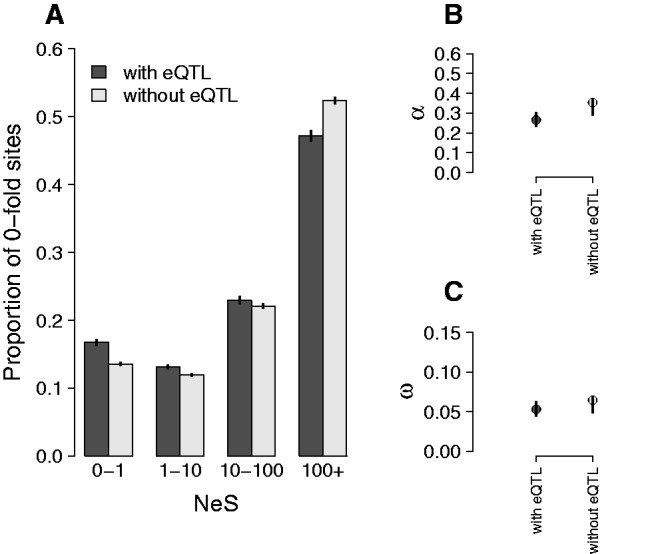
Estimates of negative and positive selection in genes with and without proximal eQTL. (A) The proportion of sites found in each bin of negative selection strength, separated by whether or not genes have eQTLs (4,090 genes have eQTLs, 8,806 genes do not). (B) The proportion of sites fixed by positive selection, and (C) the rate of adaptive substitution. Error bars represent 95% confidence intervals.

Discussion

This study investigated the relationship between connectivity and selection in the plant C. grandiflora. Connectivity is negatively associated with d_N/d_S, and this pattern is driven by stronger negative selection on highly connected genes. However, the extent of local regulatory variation, inferred by the presence of eQTLs near genes, also affects both connectivity and the strength of negative selection. Disentangling the ultimate cause of these relationships is difficult and we see two possible explanations for the observed relationship between connectivity, selection, and regulatory variation. First, the presence or absence of eQTLs could drive the observed relationship between connectivity and selection because genes under weaker negative selection may be better able to tolerate eQTLs which then, in turn, leads to reduced connectivity observed in these genes. Second, reduced constraint due to network connectivity could affect both levels of negative selection and the ability of genes to tolerate local regulatory variation.

How Methods of Network Inference Shape Evolutionary Conclusions

Our ability to distinguish between potential explanations for a correlation between connectivity and selection is mediated by our choice to use coexpression to measure connectivity. Coexpression networks are a useful tool for investigating regulatory networks using commonly available expression data. They differ from many other types of network inference such as protein–protein interaction networks, metabolic pathways, and gene regulatory networks, in that they can be estimated using observations from interactions that occur in vivo and do not require manipulative experiments. Because of this, coexpression networks have been used for a number of purposes, such as identifying genes important for tissue differentiation and other processes (Pierson et al. 2015; Ayroles et al. 2009), investigating adaptive divergence in expression (Koenig et al. 2013; Swanson-Wagner et al. 2012; Oldham et al. 2006), and understanding the forces maintaining variation within populations (Mähler et al. 2017). However, coexpression networks do not provide information about causality: high connectivity between two genes could result from the expression level of one gene affecting that of the other or from both genes responding to another stimulus.

In addition, coexpression network inference depends directly on the variation present in the sample used because connections can only be observed when there is some sort of expression regulation that differs between samples. Coexpression networks generated using a population sample collected at one time point, as done in this study, will be especially sensitive to the presence of cis-regulatory variation, compared with those generated using samples of the same genotype measured across tissues or conditions. It is unclear how sensitive coexpression networks are to sample choice, but the role of network position in shaping expression divergence has been shown to differ between coexpression networks generated using expression data from response to different stimuli (Des Marais et al. 2016). Overall, while coexpression networks are a useful tool for investigating connectivity, it is important to remember that coexpression does not imply causality and that sample choice can influence outcome.

The Underlying Causes of Variation in Divergence

Most previous work on the relationship between connectivity and selection has focused on amino acid divergence, making it difficult to separate the effects of positive and negative selection. By using polymorphism to investigate the distribution of fitness effects and an extension of the McDonald–Kreitman test to estimate positive selection, we were able to demonstrate that reduced divergence in highly connected genes is driven by negative selection. Previous applications of this approach have also shown that negative selection is often a key determinant of between-gene variation in divergence (Williamson et al. 2014; Hodgins et al. 2016). However, genes under stronger negative selection within species may also experience stronger positive selection between species, a situation that would be undetectable looking at divergence alone (Arunkumar et al. 2013). Clearly, further disentangling the relative roles of positive and negative selection in shaping d_N/d_S will continue to be important for future work investigating the mechanisms responsible for variation in selection between genes.

In addition to observing negative correlations between d_N and d_N/d_S and connectivity, we observed a significant negative correlation between d_S and connectivity that persisted after controlling for expression level with a partial correlation. There are a number of factors that could explain this result. First, there may be some relationship between mutation rate and connectivity that decreases d_S in highly connected genes. There is limited evidence that the mutation rate varies across site types and genomic region in A. thaliana (Ossowski et al. 2010) and that mutation rates are higher in certain sequence motifs in alga (Ness et al. 2015). In addition, genomic features like exons and DNAase hypersensitivity sites appear to have higher mutation rates in humans (Michaelson et al. 2012; Francioli et al. 2015). Similar patterns in plants could contribute to a relationship between mutation rate and gene expression and/or connectivity. Second, there may be stronger selection on synonymous sites in highly connected genes due to selection on codon usage (Qiu et al. 2011; Hershberg and Petrov 2008) or mRNA folding (Park et al. 2013). If this is the case, then heterogeneity in d_S will reflect variation in synonymous constraint, not mutation rate variation, and so dividing by d_S could explain why connectivity and d_N/d_S are more weakly correlated than connectivity and d_N. Third, background selection in an ancestral species can be an important determinant of variation in divergence between loci (Phung et al. 2016). Stronger background selection at constrained genes in the species ancestral to C. grandiflora, N. paniculata, and A. thaliana could reduce neutral divergence between these species at constrained genes, potentially generating a correlation between d_S and connectivity. Further work will be needed to fully explain why d_S correlates with connectivity in C. grandiflora.

The Relationship between Pleiotropy and Selection

We set out to understand whether highly pleiotropic genes are under stronger evolutionary constraint and used coexpression network connectivity as a measure of pleiotropy. There is a long history of thought on pleiotropy (Stearns 2010) and many conflicting definitions for pleiotropy (Paaby and Rockman 2013). Different definitions of pleiotropy have the potential to lead to differing conclusions about the relationship between pleiotropy and selective constraint. Our approach is not consistent with all definitions. Specifically, pleiotropy in our study is measured as the number of additional genes whose expression could be altered by variation in expression of the focal gene and we cannot make further conclusions about whether these genes ultimately contribute to the same or different traits.

Our results are consistent with a relationship between pleiotropy and negative selection: genes with higher connectivity are under stronger negative selection in C. grandiflora. However, this conclusion is confounded by the presence of local regulatory variation. Regulatory variation could drive variation in connectivity if genes with local regulatory variants appear to be less connected. Alternatively, regulatory variation could result from variation in constraint if genes under strong constraint with pleiotropic effects on the expression of other genes are less likely to be able to tolerate local regulatory variants. Distinguishing between these two possibilities will require additional experimental and analytical approaches for identifying genes with pleiotropic effects.

A number of approaches have been used to investigate the evolutionary significance of pleiotropy on a genomic scale, including investigations of GWAS variants that affect multiple traits (Pickrell et al. 2016) and experiments showing that stabilizing selection acts more strongly on mutations that affect multiple expression traits through comparisons of standing genetic variation and mutation variation (McGuigan et al. 2014a, 2014b). An additional way forward could be taking advantage of QTLs measured in the same lines across environments. If selective constraint on pleiotropic loci is widespread, QTLs with effects in multiple environments should be at lower frequency than those with more limited effects in the same way that QTLs with large effects on single traits are at lower frequency than those with small effects (Josephs et al. 2015). Using eQTLs for this analysis may be especially powerful because it would allow the investigation of hundreds to thousands of phenotypes and allow integration with network-based approaches.

Supplementary Material

Supplementary data are available at Genome Biology and Evolution online.