Estimation of anisotropic permeability in trabecular bone based on microCT imaging and pore-scale fluid dynamics simulations

Abstract

In this paper, a comprehensive framework is proposed to estimate the anisotropic permeability matrix in trabecular bone specimens based on micro-computed tomography (microCT) imaging combined with pore-scale fluid dynamics simulations. Two essential steps in the proposed methodology are the selection of (i) a representative volume element (RVE) for calculation of trabecular bone permeability and (ii) a converged mesh for accurate calculation of pore fluid flow properties. Accurate estimates of trabecular bone porosities are obtained using a microCT image resolution of approximately 10 μm. We show that a trabecular bone RVE in the order of 2 × 2 × 2 mm³ is most suitable. Mesh convergence studies show that accurate fluid flow properties are obtained for a mesh size above 125,000 elements. Volume averaging of the pore-scale fluid flow properties allows calculation of the apparent permeability matrix of trabecular bone specimens.

For the four specimens chosen, our numerical results show that the so obtained permeability coefficients are in excellent agreement with previously reported experimental data for both human and bovine trabecular bone samples. We also identified that bone samples taken from long bones generally exhibit a larger permeability in the longitudinal direction. The fact that all coefficients of the permeability matrix were different from zero indicates that bone samples are generally not harvested in the principal flow directions. The full permeability matrix was diagonalized by calculating the eigenvalues, while the eigenvectors showed how strongly the bone sample's orientations deviated from the principal flow directions. Porosity values of the four bone specimens range from 0.83 to 0.86, with a low standard deviation of ± 0.016, principal permeability values range from 0.22 to 1.45 ⋅ 10 ⁻⁸ m², with a high standard deviation of ± 0.33. Also, the anisotropic ratio ranged from 0.27 to 0.83, with high standard deviation. These results indicate that while the four specimens are quite similar in terms of average porosity, large variability exists with respect to permeability and specimen anisotropy. The utilized computational approach compares well with semi-analytical models based on homogenization theory. This methodology can be applied in bone tissue engineering applications for generating accurate pore morphologies of bone replacement materials and to consistently select similar bone specimens in bone bioreactor studies.

Highlights

• •A representative volume element (RVE) size of 2 ×2 × 2 mm³ is sufficient to represent bovine trabecular bone microstructure and corresponding fluid flow properties.
• •Using periodic boundary conditions, with a mesh size  >125,000 elements, provides the most accurate values for respective bone permeability data.
• •Comparison of bone specimens with respect to porosity does not provide accurate information about permeability.
• •For similarity between specimens based on mechanical properties, both magnitude of principal permeability and anisotropic ratio, need to be similar.
• •Comparison of permeabilities of our bovine sternum bone specimens with other bone samples from the literature, showed excellent agreement.

1. Introduction

Trabecular bone permeability has been associated with a variety of important physiological processes including bone-remodeling, modeling and fracture healing. These processes are affected by the density of blood vessels and changes of intravascular pressure (Brookes and Revell, 2012) . It is well known that permeability is directly related to fluid velocity and fluid pressure in the trabecular bone pore space and that these latter quantities have been identified as important mechanobiological cell stimuli (Klein-Nulend et al., 2005, Mullender et al., 2004, Scheiner et al., 2015) . Furthermore, for bone tissue engineering applications, design of scaffold permeability is essential to successful bone repair (Hollister, 2005; Hutmacher et al., 2007, Karande et al., 2004, Mitsak et al., 2011) bone permeability is an important design parameter for successful application of surgical techniques such as vertebroplasty (Baroud et al., 2004) and bone diagnostic techniques using ultrasound (Buchanan and Gilbert, 2007, Grimes et al., 2012) . Recently, a variety of ex vivo experimental systems have been utilized to investigate different aspects of bone physiology. These 3D bioreactor systems aim to mimic in vivo conditions including fluid flow, mechanical loading, and local drug delivery to the bone microenvironment (Aw et al., 2012) . A major challenge in utilizing bioreactors for studying bone tissue physiology is to be able to reproduce experimental results due to variability of design parameters. Bone samples are commonly harvested from different neighbouring bone sites and may vary in morphological and structural parameters such as porosity, stiffness, and permeability. The latter properties cannot be controlled experimentally and may have a significant impact on bone physiological responses and associated statistical analyses. Consequently, a large amount of experimental, theoretical and computational studies have been dedicated to accurately estimating trabecular bone permeability (Baroud et al., 2004, Grimm and Williams, 1997, Abdul Kadir and Syahrom, 2009, Nauman et al., 1999, Teo and Teoh, 2012) .

1.1. Experimental and computational estimations of bone permeability

In the field of biomedical engineering significant efforts have been made to investigate experimental and theoretical aspects of estimating bone permeability (Baroud et al., 2004, Beno et al., 2006, Kameo et al., 2010, Smit et al., 2002) . Classical phenomenological relations such as the Kozeny–Carman equation, have linked bone porosity to permeability together with some phenomenological constant characteristic for the bone sample morphology (Arramon and Nauman, 2001, Bear, 1972) . Other more sophisticated techniques use semi-analytical tools to estimate pore-scale fluid flow properties which can then be upscaled to obtain (apparent) bone permeability estimates (Abdalrahman et al., 2015) . Two interesting findings were revealed by Abdalrahman et al. Firstly, the constant appearing in the Kozeny–Carman equation is a function of bone porosity and bone specific surface (Abdalrahman et al., 2015) . Secondly, the permeability is strongly affected by the pore fluid viscosity which, in the case of polarized fluids, is strongly increased due to the presence of electrically charged pore walls and formation of diffuse double layers in the fluid (Ichikawa et al., 2002, Pollack, 2013) . Based on the latter observation, a large number of bone permeability experiments were reassessed with respect to the most typical fluids used for evaluation, i.e., (de-ionized) water or oil. It was shown that experimental data based on using oils (e.g. linseed or silicone) provide consistent values for permeability with high correlations between different bone types.

In order to estimate permeability, a number of computational models have been developed based on pore-scale imaging relating to 3D scaffold biomaterials for use in tissue engineering (Jones et al., 2009, Singh et al., 2009, Truscello et al., 2012, Van Cleynenbreugel et al., 2006) . 3D pore geometry studies most widely use the Lattice Boltzmann method or classical computational fluid dynamics (CFD) (Arramon and Nauman, 2001, Aw et al., 2012) . In order to obtain accurate morphological information about pore size and distribution, most studies employ microCT imaging (Bultreys et al., 2016) . Bone-specific computational models are often based on CFD principles using the Stokes'equation (Syahrom et al., 2013, Teo and Teoh, 2012, Tsouknidas et al., 2015, Widmer and Ferguson, 2013) . The analytical equations are most commonly solved using numerical techniques such as the Finite Element Method (FEM) or the Finite Volume Method (FVM) (Guibert et al., 2015, Teo and Teoh, 2012, Versteeg and Malalasekera, 2007, Zienkiewicz and Taylor, 1977) . Computational domain size varies depending on the achievable numerical resolution, but most sizes commonly range between 1 × 1 × 1  mm³ and 5 × 5 × 5  mm³. Convergence of numerical results is not commonly reported due to the high computational costs involved. The numerical results found in the literature vary dependent on imaging resolution and computational capacity, however are within a comparable range to experimental findings.

The objective of this paper is to develop a theoretical framework to accurately estimate trabecular bone permeability. We employ a similar approach as the one suggested in Guibert et al. (2015) to the study of bone permeability. This approach is based on performance of high resolution pore-scale imaging of four trabecular bovine bone samples in order to obtain the respective pore morphologies, together with numerical simulations of fluid flow in the vascular porosity. Suitable choice of RVE is based on a study using different volumes to calculate bone porosity, while mesh convergence studies are performed to assess variability of flow properties based on choice of mesh. In order to separate the air and solid phase of the porous bone samples we utilize the multi-threshold segmentation method proposed by Otsu (1975), which is based on the density histograms of the respective specimen. We then calculate pore-scale velocity and pressure distribution in the trabecular samples using the multiphysics finite volume solver software package arb (Daish et al., 2016, Harvie, 2012) . Subsequently, we utilize Darcy's law at the tissue scale together with numerical upscaling of pore-scale quantities. This delivers the anisotropic permeability of the respective bone samples.

We further calculate the principal (i.e., diagonalised) permeability matrix, which provides information with respect to material morphology and deviation of the specimen from principal directions. This allows determination of the anisotropy ratio, i.e., a measure of bone material anisotropy. We then compare the anisotropic permeability matrix for the four bone samples in order to estimate variability between different bone sites. The variability so calculated is an indicator of how suitable the chosen specimens are for statistical analyses when used, e.g., in a bioreactor setting in terms of characterizing fluid/solute transport behavior. Our numerical results are discussed in detail with experimental and computational results from the literature.

The paper is organised as follows: the preparation of bone specimens is discussed in Section 2.1. The microCT imaging methodology including extraction of porosity and bone specific surface is provided in 2.2, 2.3. 3D model development of the specimens is described in Section 2.4. The numerical approach used to solve the pore-scale fluid dynamical problem, and the boundary conditions utilized are described in 2.5, 2.6, respectively. The upscaling procedure of the pore-scale properties in order to obtain the tissue-scale/apparent permeability matrix of trabecular bone samples is provided in Section 2.7. The results obtained from our studies are described in Section 3 with detailed discussions provided in Section 4. Summary and conclusions are given in Section 5.

2. Experimental, theoretical and numerical methods

2.1. Bone core preparation and scanning

Four bovine trabecular bone specimens (10 mm diameter and 5 mm height) from adjacent bone sites were cored and prepared following the procedure described previously in Aw et al. (2012) and briefly summarized below. The sternum of a 13-month-old steer was harvested from a freshly slaughtered animal and kept in cold sterile saline (0.85%) prior to processing. All soft tissues were removed from the sternum, which was then manually cut into sagittal sections using a hacksaw. Bone cylinders, 10 mm in diameter, were prepared from adjacent bone sections using an industrial drilling machine (Model G0517 Mill/Drill, Grizzly Industrial, Inc., Muncy, PA) and a custom-made diamond drill bit. Bone cylinders were mounted onto a custom-made platform and milled to a 5 mm thickness using a 10 mm diameter tungsten carbide bit. The resulting bone cores consisted of uniform trabecular bone without any visible cartilage. All bone cores had the marrow removed by utilizing a pressurized dental water jet (WP-450A; Water Pik, Inc., Fort Collins, CO). The obtained cylinders were stored in 70% ethanol solution until further processing.

The samples were then dried in air and scanned in a Skyscan 1172 microCT device (Skyscan, Kontisch, Belgium). The scanning parameters are the following: source voltage 100 kV, source intensity 100 μA, 3 mm aluminum filter, average number of frames 5, rotation step 0.30, pixel size 9.87 μm. The reconstruction was made by means of the software NRecon (Skyscan, Kontisch, Belgium), with the following parameters: 20% ring artifacts correction, threshold mask 50%, Hounsfield unit scale [ −899, 1400], and smoothing algorithm boxcar asymmetrical.

All four samples were scanned and reconstructed with the same parameters. In addition, for scanning, the samples were orientated vertically. The reconstruction provided for each sample a stack of 500 8-bit images of size 1320 × 1320  pixels.

2.2. Segmentation

From the total volume represented in Fig. 1, a cubic subset of 5 × 5 × 5  mm³ is cropped through the stack of CT images and written in a three dimensional array in MATLAB (The MathWorks Inc., Natick, MA, USA). This array contains the contrast values of all pixels of the subset in terms of grey values ranging between 0 and 255. For the purpose of the fluid flow simulations described in Section 2.5, the contrast values need to be converted into average fluid volume fractions in each computational cell (ϕ), such that a cell having ϕ = 1 contains only fluid, a cell having ϕ = 0 contains only solid, and a cell with intermediate values of ϕ (0 < ϕ < 1) contains both regions of fluid and solid. The method for calculating these volume fractions from the contrast values is now described.

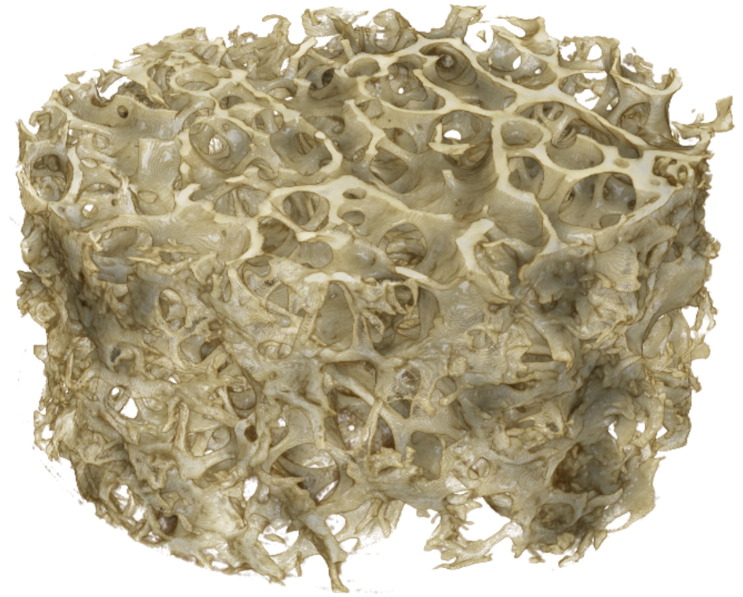
Fig. 1.

MicroCT image of cylindrical specimen n = 3 showing the porous trabecular bone morphology. Coring direction and orientation detailed in Davies et al. (2006).

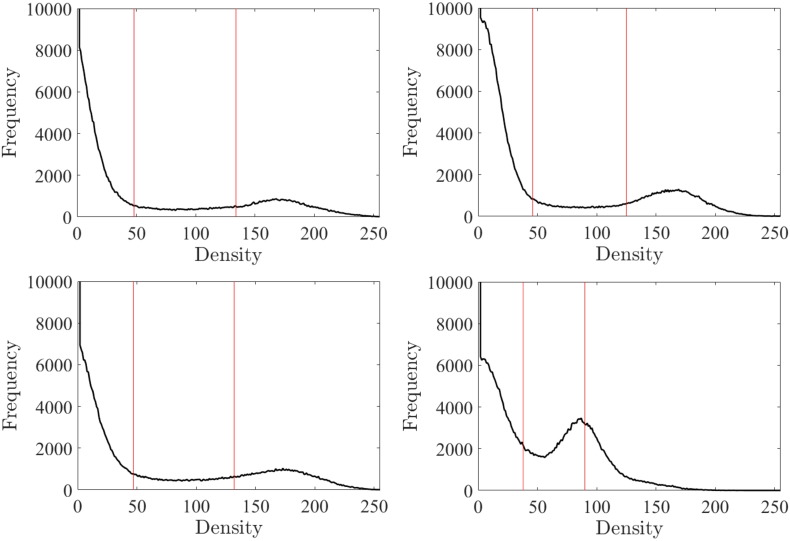
Firstly, in order to visualize the contrast values for each sample, frequency density plots are presented Fig. 2. In these histograms, two peaks can be identified: The right hand peak relates to the most frequently occurring grey values containing bone material, and the left hand peak relates to most frequently occurring air values. Two thresholds have to be set in order to segment the three phases (i.e., solid, fluid and interface regions).

Fig. 2.

Representation of grey values (GV) frequency plots for all four bovine specimens (n = 1...…4). Bone and water thresholds are chosen from these frequency values. Threshold for t_fluid and t_solid are represented by the lower and upper lines respectively.

We chose to first segment the solid-fluid interface region based on two threshold points t_solid and t_fluid, found by applying the Otsu multi-thresholding method based on the global property of the histogram (Otsu, 1975) , wherein an optimal set of thresholds t_solid and t_fluid is selected by maximizing the variance between the two classes (υ):

$$\upsilon (t_{solid},t_{fluid})=\underset{0<\omega (t)<1}{\max }\upsilon (t_1,t_2).$$ (1)

where ω(t) is the zeroth-cumulative moment of the histogram up to the t-th level, and t₁ and t₂ refer to two assumed thresholds used for separating the three phases, such that 0 < ω(t) < 1. Using this method we obtained values for t_solid and t_fluid in the ranges of 45 ± 4.7 and 120 ± 20.5 respectively. The porous solid phase is then made up of all values between t_solid and t_fluid such that:

$$\varphi =(t_{solid}-GV)/(t_{solid}-t_{fluid}).$$ (2)

In summary, the rules for the assignment of the fluid volume fraction ϕ read as:

$$\left\{\begin{array}{l}\varphi =0\text{if material is pure bone, for}GV\ge t_{solid}\\ \varphi =f(GV)\text{if}{t}_{fluid}<GV<t_{solid}\\ \varphi =1\text{if material is pure fluid, for}GV\le t_{fluid}\end{array}\right)$$ (3)

where GV is the contrast value for each pixel of the subset. This method defines a smooth transition between phases and prevents edge effects. The output of this step is a new three dimensional array containing the values for the fluid volume fraction in each voxel.

2.3. Selection of RVE

As for any porous material, an optimal RVE should be found that takes into account: (i) The microstructure of the material: Trabecular bone is a highly porous material (∼85% porosity), exhibiting 400 μm-large pores separated by 100 μm-thick trabecular struts and plates; (ii) A size which is small enough to make computational modeling feasible. The quantity classically investigated to select a suitable RVE is the porosity (Nordahl and Ringrose, 2008) . Using our segmented 5 × 5 × 5 mm³ sample, the macroscopic porosity Φ is the sum of all voxel-specific fluid volume fractions ϕ(n) over the total number of voxels (N) in the volume of interest and reads as:

$$\mathbf{\Phi }=\frac{{\sum }_{n=1}^N\varphi (n)}{N}.$$ (4)

The porosity is computed for 18 different cubic RVE sizes, with edge length ranging from 100 μm to 5000 μm. Cubic unit cells of the aforementioned edge lengths are taken from the initial volume (Fig. 3).

Fig. 3.

Bone segment selection process for each bovine specimen based on microCT imaging to develop a consistent representation of permeability: cubic segments (5 × 5 × 5 mm³) selected from each specimen using microCT are subsequently sub sampled to identify suitable RVE sizes.

Initially porosity values fluctuate significantly until stability is reached for a RVE size between 1000 μm and 2000 μm (shown in Section 3.1). The latter RVE is the optimum configuration for representing the trabecular bone microstructure and is used in subsequent simulations and discussions.

We also calculated the specific surface, based on CT analyzer software CTAn (Skyscan, Kontisch, Belgium). The specific surface represents the internal surface area per unit volume of whole bone, i.e., S_v = A_s/V, where A_s is the bone surface area and V is the volume of the RVE. In Section 2.8, we will use the value of S_v for calculating permeability based on the Kozeny–Carman equation.

2.4. Mesh creation

A regular finite volume mesh is created for each of the cubic RVEs selected in Section 2.3. Specifically, an in-house algorithm written in MATLAB transforms each 9.87 μm edge-length voxel into a cubic volume defined by 8 nodes. To each volume is allocated the material property defined in Section 2.2 for the corresponding voxel. These meshes serve as the input files for the finite volume fluid flow simulations described hereafter.

2.5. Numerical simulations of fluid flow in trabecular bone pore space

Under physiological conditions fluid flow within the vascular porosity can be assumed incompressible, non-inertial, single phase and slow, characterized by low Reynolds numbers. Hence, movement within the pore space (fluid region) is governed by the Stokes' equations (Bear and Bachmat, 1990, Durlofsky, 2005) :

$$\mathit{\nabla }\cdot \mathit{u}=0\text{and}-\nabla p-\mathit{s}=\nabla \cdot \tau \text{on}{\Omega }_f$$ (5)

while within the solid region and on the solid/fluid interface,

$$\mathit{u}=\mathbf{0}\text{on}\Gamma \text{and}{\Omega }_s.$$ (6)

Here, u is the microscale velocity field, p the microscopic pressure field, τ = −μ [∇u +(∇u)^T] the viscous stress tensor, μ the dynamic viscosity of the fluid and s an imposed pressure gradient which is implemented numerically as a body force on the fluid. Here, Ω_f,Ω_s and Γ represent the fluid and solid regions, and solid/fluid interface, respectively.

In this study, we solve a set of equations that yield the solution to Eqs. (5) and (6), over the fluid region and interface, but that are also valid within the solid phase (Daish et al., 2016, Harvie, 2012) . This allows us to solve a single set of equations (using a finite volume method with Volume of Fluid (VOF) techniques; Hirt and Nichols, 1981) over the entire bone region, using the original mesh that is associated with the scan data.

2.6. Computational domain and boundary conditions

We define the target domain following a similar methodology to that of Odsæter where the domain is assumed to be a hexahedron aligned with the local coordinate system (x,y,z) (Odsæter, 2013). The choice of boundary condition (BC) depends on the problem at hand (Odsæter, 2013). For the configuration considered in this paper, periodic boundary conditions are most suitable and can be implemented in the following way:

Periodic BCs connect opposing faces, so that the fluid flowing out at one boundary flows into the opposite boundary, which can be expressed as:

$$\mathit{u}{|}_{\partial V^{\xi ,1}}=\mathit{u}{|}_{\partial V^{\xi ,2}},\xi =x,y,z$$ (7)

where ∂V^ξ,1 and ∂V^ξ,2 denote two opposite faces on the chosen unit cell. A similar equation applies to pressure, p. i.e., $\mathit{u}{|}_{\partial p^{\xi ,1}}=\mathit{u}{|}_{\partial p^{\xi ,2}},\xi =x,y,z$. The periodic BC is, a priori more representative than for example a fixed boundary condition, for calculating accurate permeability due to the fact that it does not introduce boundary effects. However, as periodicity is introduced to the sample, it could increase computation time significantly (Guibert et al., 2015) . Using arb, we experienced no significant change in computation time. For more information regarding choice of different boundary conditions on permeability, see Daish et al. (2016).

2.7. Numerical up-scaling

Describing the entire microstructural features of heterogeneous materials is for many situations difficult if not impossible, and leads to large scale boundary value problems (Auriault, 2002) . As continuum theory has shown, it is possible in many cases to replace the heterogeneous material by a homogeneous one (Cushman, 1997). The derived macroscopic, i.e., continuum behavior should be intrinsic to the material and to the excitation, and should be independent of the macroscopic boundary conditions.

For the case of slow flow velocities, as encountered in the bone vascular pore space, it can be shown that volume averaging of the Stokes' momentum equation over a suitable RVE leads to the well-known Darcy's law (Bear and Bachmat, 1990, Whitaker, 1986):

$$\mathbf{v}=-\frac{\mathbf{k}}{\mu }\nabla P.$$ (8)

where v is the average fluid velocity (also denoted as Darcy velocity), k the intrinsic permeability matrix and ∇P the macroscale pressure gradient. In this study, ∇P is represented by s. Based on knowledge of the microscale state variables, the apparent fluid velocity can be determined based on volume averaging:

$$\mathbf{v}=⟨\mathbf{u}⟩=\frac{1}{|V|}{\int }_V\mathbf{u}dV.$$ (9)

It can be shown that k is a symmetric second order matrix (i.e., 3 × 3 matrix) with real coefficients (k_ij), which reflects the anisotropy of the pore-scale flow (Lei et al., 2015) , i.e.,

$$\mathbf{k}=\left(\begin{array}{lll}{k}_{xx}& k_{xy}& k_{xz}\\ ⋮& k_{yy}& k_{yz}\\ sym& \cdots & k_{zz}\end{array}\right).$$ (10)

In general, k is independent of the nature of the fluid and only depends on the morphology of the pore space. Hence, it is possible to derive estimates for k in terms of geometrical parameters. Note that Darcy's law is generally applicable only for laminar flow with low Reynold number (Re), i.e., 1 ≤Re < 10, with the transition between laminar and turbulent flow occurring at around Re ≈2000 to 4000 (Fung, 2013) . A great deal of effort has been spent on deriving relationships for k (Adler, 1994, Bear, 1972, Dullien, 1992).

In order to determine the six independent coefficients of permeability in Eq. (10) one requires six independent equations. For the local numerical methods these are obtained by prescribing three pressure gradients in different directions. For the periodic boundary condition used in this paper, we chose the orientations of these volumetric source terms to coincide with the x,y,z coordinate directions to deliver the following system of equations:

$$\begin{array}{ll}\hfill {({\mathbf{v}}_{\eta })}_x=& -({\tilde{k}}_{xx}{(\nabla P_{\eta })}_x+{\tilde{k}}_{xy}{(\nabla P_{\eta })}_y+{\tilde{k}}_{xz}{(\nabla P_{\eta })}_z)/\mu ,\hfill \\ \hfill {({\mathbf{v}}_{\eta })}_y=& -({\tilde{k}}_{yx}{(\nabla P_{\eta })}_x+{\tilde{k}}_{yy}{(\nabla P_{\eta })}_y+{\tilde{k}}_{yz}{(\nabla P_{\eta })}_z)/\mu ,\hfill \\ \hfill {({\mathbf{v}}_{\eta })}_z=& -({\tilde{k}}_{zx}{(\nabla P_{\eta })}_x+{\tilde{k}}_{zy}{(\nabla P_{\eta })}_y+{\tilde{k}}_{zz}{(\nabla P_{\eta })}_z)/\mu ,\hfill \end{array}$$ (11)

where s_η is the applied pressure gradient, ${\tilde{k}}_{ij}$ the macroscopic permeability coefficient for directions i ⋅ j and μ the viscosity of the fluid, in our case water, i.e., μ = 0.001  Pa⋅s. Eq. (11) delivers for each of the enforced volumetric pressure gradient terms (direction η) a respective microscopic velocity field, from which the apparent fluid velocity field can be computed based on volume averaging (Eq. (9)). This leads to nine equations for nine coefficients ${\tilde{k}}_{ij}$. Solving this system of equations gives the permeability matrix. In general this matrix is non-symmetrical, and can be symmetrized by taking the average of the cross terms:

$$\mathbf{k}=\frac{1}{2}(\tilde{\mathbf{k}}+{\tilde{\mathbf{k}}}^T).$$ (12)

2.8. Semi-analytical model of permeability

A phenomenological relationship between porosity and permeability has been established for geotechnical materials using the Kozeny–Carman relation (Bear, 1972). This equation was adopted in the bioengineering literature assuming bone behavior is isotropic (Cowin et al., 2001).

$$k=\frac{{\Phi }^3\cdot C}{\mu S_v^2}$$ (13)

where Φ is the vascular porosity of trabecular bone, S_v is the bone specific surface (1/m), μ is the viscosity of the fluid, and C is a dimensionless constant. The specific surface S_v is defined as the total amount of bone surface (A_s) within the RVE divided by the RVE volume (V):

$$S_v(\Phi )=\frac{A_s}{V}=a_1\cdot \Phi +a_2\cdot {(\Phi )}^2+a_3\cdot {(\Phi )}^3+a_4\cdot {(\Phi )}^4+a_5\cdot {(\Phi )}^5.$$ (14)

where the coefficients (a₀ = 0,a₁ = 26.23,a₂ = −81.73,a₃ = 121.80,a₄ = −92.71,a₅ = 26.55) are derived from the experimental data of Martin (1983). The constant C in Eq. (13) needs to be estimated based on experimental data or information of the particular pore morphology (Bear, 1972).

Recently, the theory of homogenization utilizing the self-consistent scheme was applied to upscale fluid flow in the vascular porosity of bone, using the classical Hagens–Poiseuille law for laminar flow in the format of a “micro-Darcy law” (Abdalrahman et al., 2015) . The so upscaled isotropic permeability depends on pore size and porosity as geometrical input. Using this approach the authors could make a link between the derived relation for a material's permeability with the Kozeny–Carman equation, which provides a definition of the constant in the latter equation. The trabecular bone permeability can be expressed as (Abdalrahman et al., 2015):

$$k=\frac{\frac{1}{6}{\Phi }^3}{\mu S_v^2\left(\frac{3}{2}+\frac{1}{6}\Phi \right)}$$ (15)

where the porosity-dependent isotropic tissue-scale permeability expression is derived by replacing C from the Kozeny–Carman equation (Eq. (13)), with a function depending only on porosity.

2.9. Characterization of bone specimen principal directions and anisotropy

Based on the finite-dimensional spectral theorem (Bronshtein and Semendyayev, 2013) , any symmetrical matrix whose entries are real, can be diagonalized. In this instance, the principal permeability matrix $\left({\mathbf{k}}^p=\left[k_1^p,k_2^p,k_3^p\right]\right)$ was found by applying the MATLAB function eig(E,D) to our full symmetric matrix k.

Anisotropy of permeability is of great importance in bioengineering. The degree of anisotropy is commonly defined by the anisotropic ratio R (Clavaud et al., 2008):

$$R=\frac{k_{\min }^p}{\sqrt{k_{int}^p\cdot k_{\max }^p}}.$$ (16)

where $k_{\min }^p,k_{int}^p$ and $k_{\max }^p$ are ordered principal permeability coefficients. If the material is transversely isotropic (i.e., the matrix defines a revolution ellipsoid) with the minimal value of the permeability along the morphological vertical direction, R defined in Eq. (16) is equivalent to the classical ratio r = k_L/k_T, where k_L and k_T are the longitudinal and transverse permeabilities, respectively.

3. Results

In this section we present the results of our study both in terms of choice of RVEs and convergence of numerical results.

3.1. Selection of RVE

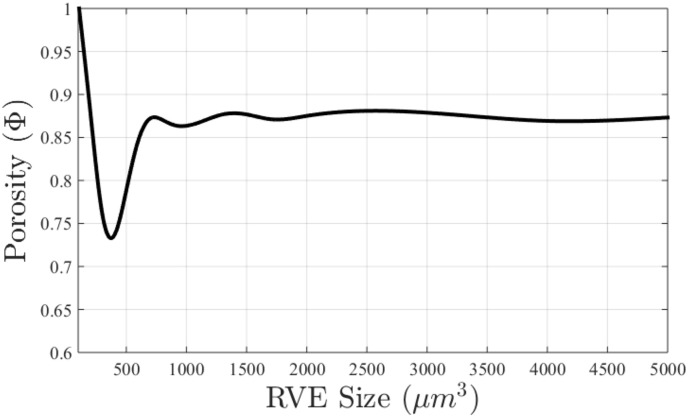
Fig. 4 shows the output from running porosity calculations on 125  unit cells of varying RVE sizes. The RVE sizes range from 10 μm to 5000 μm to assess different sub volumes of the entire specimen (5 × 5 × 5  mm³). This figure clearly shows that an average porosity of 0.86 is obtained at RVE sizes of 1 mm or above. It is noted that porosity varied between specimens from 0.83 to 0.86 [Table 1].

Fig. 4.

Plot of the porosity against the edge length ranging from 10 μm to 5000 μm for specimen n = 3, used for assessment of the best RVE size for the numerical simulations.

Table 1.

Summary of microCT data for specimens of RVE size 2 × 2 × 2 mm³: porosity (Φ) and bone specific surface (S_v); Anistropic permeability values k, principal permeability values k^p, isotropic permeability k based on Kozeny–Carman equation (Eq. (13)), and anisotropy measure R for each of the four specimen.

n	1	2	3	4	Units
Φ	0.83	0.83	0.85	0.86	−
Sv	3.98	3.52	3.43	3.31	m −1
kxx	0.67	0.39	1.19	1.05	⋅ 10 −8 m2
kyy	0.66	0.87	0.82	1.04	⋅ 10 −8 m2
kzz	0.58	0.59	0.56	0.98	⋅ 10 −8 m2
kxy	−0.08	0.24	−0.41	−0.04	⋅ 10 −8 m2
kxz	0.04	−0.14	−0.10	−0.11	⋅ 10 −8 m2
kyz	0.02	0.09	−0.02	0.03	⋅ 10 −8 m2
$k_1^p$	0.74	0.97	1.45	1.15	⋅ 10 −8 m2
$k_2^p$	0.63	0.66	0.63	1.02	⋅ 10 −8 m2
$k_3^p$	0.54	0.22	0.49	0.90	⋅ 10 −8 m2
k	0.37	0.47	0.53	0.59	⋅ 10 −8 m2
R	0.7909	0.2750	0.5127	0.8310	−

3.2. Computation of pore-scale velocity and pressure

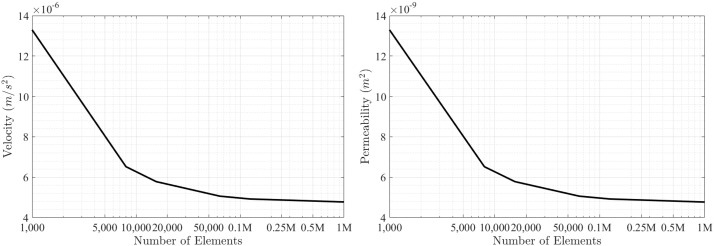
Simulations were performed on an Intel Xeon CPU E5-2650 v2 at 2.60  GHz having 16 physical cores. Computing took three hours to perform a full simulation on a single specimen of chosen RVE size and mesh resolution. Fig. 5 shows the results obtained from running arb numerical simulations on an RVE size of 2 × 2 × 2  mm³ as described in Section 2.5. First, we investigate convergence of numerical results with respect to pore-scale velocity and permeability calculations. Convergence in our numerical simulations is achieved if the state variables (i.e., the pore-scale velocity and pressure fields) do not further change with increasing the number of elements to solve the governing equations. Hence, performing numerical simulations with continuously increasing element numbers provides a means to identify a point with a nearly horizontal gradient (of a state variable) which allows estimation of the minimum number of elements required to obtain accurate numerical results. This procedure is shown in Fig. 5 (a) and (b), which indicates that for 125,000 elements convergence is achieved. Typical pore-scale velocities are in the range of 5 ⋅ 10 ⁻⁶  m/s, while the intrinsic permeability is in the order of 5 ⋅ 10 ⁻⁹  m².

Fig. 5.

Pore-scale fluid flow simulation using arb software: convergence study performed on 2 × 2 × 2 mm³ segment with outputs representing (a) velocity and (b) permeability.

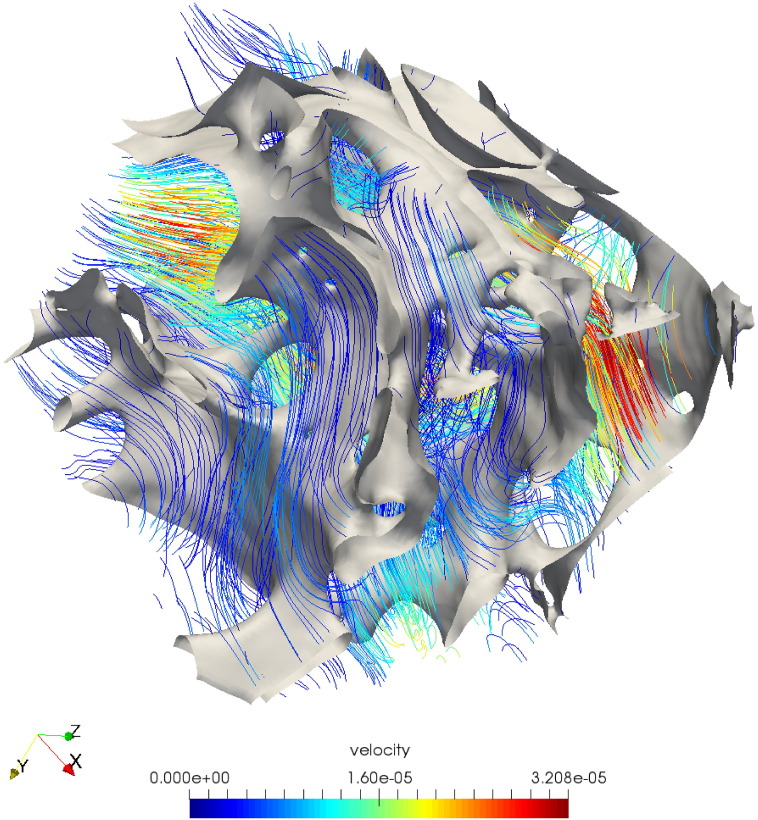
A typical vector flow plot of the pore-scale velocity field is shown in Fig. 6. This figure shows that the velocity is maximum in the middle of the pore, while it decreases to zero at the boundaries between solid and fluid.

Fig. 6.

Pore-scale fluid flow simulation using arb software: velocity streamline profile across the unit cell (2 × 2 × 2 mm³).

3.3. Up-scaled trabecular bone permeability

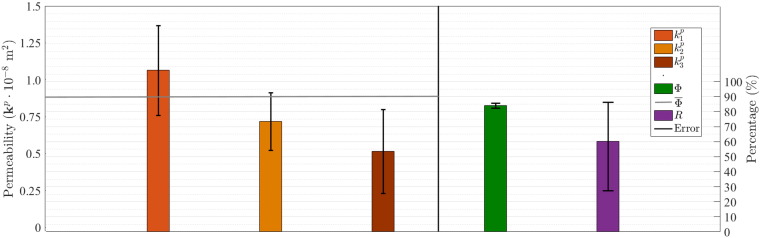
Following numerical upscaling detailed in Section 2.7, the full symmetric upscaled permeability matrix k with coefficients k_ij, is obtained and presented for each specimen in Table 1. For each specimen, the corresponding principal permeability matrices k^p are presented. The overall porosity deviation is observed as 0.016, while deviation of k diagonal and off-diagonal components varies with specimen. As is expected, the principal permeability matrices increase in value with increase in porosity.

The span of diagonal components for each individual specimen is on average 0.30 ⋅ 10 ⁻⁸  m², the standard deviation for the off diagonals is smaller at 0.25 ⋅ 10 ⁻⁸  m². The off-diagonal terms (k_xy,k_xz,k_yz) are up to an order of magnitude smaller in comparison to the diagonal permeabilities [see Table 1]. Also shown in Table 1 are the values for anisotropic ratio R (discussed in Section 4.3), which range between 0.27 and 0.83. Finally the bone specific surface S_v values (discussed in Section 2.8) range from 3.31 to 3.98  m ⁻¹.

From Table 1, we see that specimens 1 and 4 are rather isotropic (i.e., R is close to 1). However, they are different in terms of permeability, i.e., specimen 4 is almost twice as permeable $\left(k_2^p=1.02\cdot 10^{-8}{\mathrm{m}}^2\right)$ compared to the least permeable specimen 1 $\left(k_2^p=0.63\cdot 10^{-8}{\mathrm{m}}^2\right)$.

Both specimens 2 and 3 are quite anisotropic (R ≤ 0.5), with specimen 2 having the lowest R value. Specimen 3 is more permeable than specimen 2 in first and third principal directions, while the permeabilities in the second principal direction are of similar order.

The mean and SD of porosity, anisotropic ratio and principal permeability coefficients are shown in Fig. 7. One can see that the only quantity with low variability is the porosity ($\bar{\Phi }=0.84$, SD =±0.016). On the other hand, principal permeability coefficients $k_i^p$ and anisotropic ratio R exhibit large variation across the four specimens. The highest standard deviation of principal permeability is observed for the first principal direction $\left(\overline{{\mathbf{k}}_1^p}=1.08\cdot 10^{-8}{\mathrm{m}}^2,\text{SD}=\pm 0.29\right)$.

Fig. 7.

Mean values and standard deviations considering four specimens: mean porosity ($\overline{\Phi }$) = 0.84; SD =± 0.16, mean anisotropic ratio ($\overline{R}$) = 0.60; SD =± 0.26, and mean permeability $\overline{{\mathbf{k}}_i^p}$ [⋅ 10 ⁻⁸ m²] = 0.78; SD =± 0.33.

Substituting porosity and specific surface values of the four specimens (Table 1) into Eq. (15), we obtain the following k values: k = (0.37;0.47;0.53;0.59) ⋅ 10 ⁻⁸  m², for n = (1,2, 3, 4). Our bovine S_v values determined using CT An are slightly higher than those of the same porosity suggested by Martin (Eq. (14)). As such, the permeability results lie below applied model predictions of Abdalrahman et al. (2015). These k values are close to the transverse results of our specimens with the exception of specimen 4.

4. Discussion

In this section, we discuss the numerical results obtained for anisotropic permeability coefficients in the context of the bone bioengineering literature. We also compare our results with permeability values derived from semi-analytical models estimating bone permeability.

4.1. RVE size

Results obtained in Section 3.3 are based on an RVE size of 2000 μm. For this RVE size, convergence was obtained at a computational cell size of 40  μm (size length, equating to close to 125,000 elements). Utilizing smaller RVE sizes such as 600 μm we found that permeability continued to decrease significantly even with computational cell sizes as low as 10 μm (corresponding to 216,000 elements), indicating that at this RVE size, boundary effects on the RVE domain become significant, obfuscating the permeability calculation of the true bone's microstructure. Suitability of RVE size needs to be based on a comparison of calculated permeability versus mesh resolution, as well as permeability versus RVE size, showing that the RVE size is large enough that subsequent increases in mesh resolution and RVE size do not change permeability.

The RVE size versus porosity plot in Fig. 5 is obtained by choosing a fixed point in the 5 × 5 × 5  mm³ bone sample and then incrementally increasing the volume size. It can be seen that for this choice of RVE location, the porosity for ℓ_RVE = 2  mm is in good agreement with the average specimen porosity of 0.86. This indicates that this RVE size is indeed representative of the bone microstructure.

In determining an adequate RVE, it is important to perform refinement studies to check spatial convergence of simulations. While our simulations reached convergence at around 125,000 elements with only minor changes obtained at a maximum element number of 1 million elements, the simulations performed by Guibert et al. under periodic conditions reached 33.42 million elements, at a refinement level of two (Guibert et al., 2015) . As discussed in Odsæter, while periodic boundary conditions are most suitable in many applications, numerical convergence may be affected by the choice of boundary conditions (Odsæter, 2013) . The velocity magnitudes obtained in our simulations correspond well to those found by Spencer et al. in the range of 1.6 ⋅ 10 ⁻⁵ to 3.2 ⋅ 10 ⁻⁵  m/s (Spencer et al., 2013).

4.2. Comparison with experimental bone permeability data and other simulation results

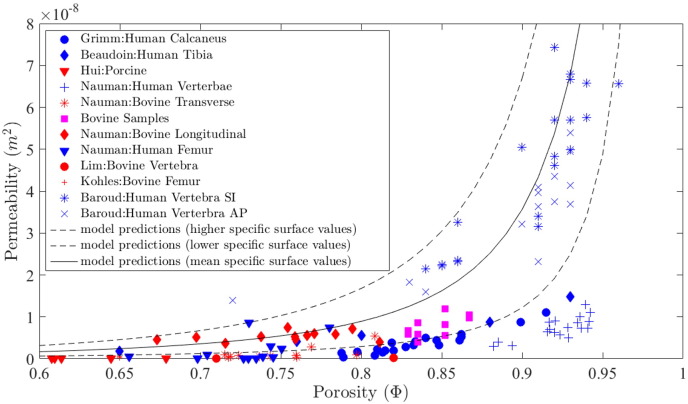
In Fig. 8, we compare our model results with a large number of experimental data from the literature and simulation results from a semi-analytical homogenization-based model (Eq. (15), Abdalrahman et al., 2015) for a wide range of porosities, i.e., 0.6 ≤ Φ ≤ 1.

Fig. 8.

Permeability findings comparison with model predictions (Abdalrahman et al., 2015) over the spread of all four specimens against model predictions.

The homogenization-based model by Abdalrahman et al. utilizes the mean specific surface function proposed by Martin (Eq. (14)) in the Kozeny–Carman equation (Eq. (13)), to deliver the mean isotropic permeability k (Fig. 8, solid line). Using upper and lower bounds for the coefficients in the specific surface function (see Abdalrahman et al., 2015 for details), one obtains the upper and lower bounds for the permeability (Fig. 8, dashed lines).

As can be observed from this figure, permeability values strongly vary with respect to bone type, location and porosity. Permeability varies between longitudinal and transverse specimens, with large deviations that can be attributed to bone specimen anisotropy. In addition, there is a clear trend in terms of increasing permeability with increasing porosity. Most of the experimental data and our own data are located within the upper and lower permeability bounds.

Based on the obtained porosity values (ranging from 0.83 to 0.86) for the four specimens in our study, we searched the literature for comparative experimental permeability data. Several groups investigated bovine trabecular bone specimens with similar porosities (Kohles et al., 2001, Nauman et al., 1999, Tae-Hong and Hong, 2000) . One study investigated permeability of porcine bone specimens (Hui et al., 1996) , and several groups investigated human trabecular bone (Baroud et al., 2004, Beaudoin et al., 1991, Grimm and Williams, 1997, Nauman et al., 1999).

Grimm and Williams, Beaudoin et al., and Nauman et al. produced values within the same range as our own, in terms of both porosity and permeability (Beaudoin et al., 1991, Grimm and Williams, 1997, Nauman et al., 1999) . Grimm and Williams achieved permeabilities for human calcaneal trabecular bone in the range of 0.4 ⋅ 10 ⁻⁹ to 11 ⋅ 10 ⁻⁹  m², for a porosity range of 0.78 to 0.92, while Beaudoin et al. achieved a mean permeability for human cancellous tibia of 0.69 ⋅ 10 ⁻⁸  m², for a mean porosity of 0.75 ± 0.17 (Beaudoin et al., 1991, Grimm and Williams, 1997) . Similarly, Nauman et al. achieved permeabilities for bovine proximal tibia specimens in the ranges of 9.51 ⋅ 10 ⁻¹⁰ to 5.47 ⋅ 10 ⁻⁹  m², and 3.74 ⋅ 10 ⁻⁹ to 7.45 ⋅ 10 ⁻⁹  m², for transverse and longitudinal specimens respectively, with porosities ranging from 0.67 to 0.81 (values extracted from Fig. 5 in Nauman et al., 1999). The data from Grimm and Williams similarly to our own, most closely follows the lower bound model prediction of Abdalrahman et al., whereas for Nauman et al., permeability values followed both mean and lower model predictions dependent on anatomical selection, i.e., longitudinal permeability values were up to 10 times larger than transverse permeability values of similar porosities. Principal permeability values of our bone specimens are in good agreement with the longitudinal bovine permeability data of Nauman et al., however for human vertebral specimens of Nauman et al., the values found for permeability lie outside the model predictions of Abdalrahman et al., and primarily lie outside of our own porosity range (see Fig. 8).

It can be clearly observed that results from Nauman et al. span a wide range of porosities due to varying bone types, i.e., varying pore morphology. This can more explicitly be observed at the lower end of the porosity scale, in the quadrupedal specimens of Lim and Hong, Hui et al., and Kohles et al., with mean porosities of 0.82, 0.49 ± 0.07 and 0.65 ± 0.09 respectively (Hui et al., 1996, Kohles et al., 2001, Tae-Hong and Hong, 2000) . Although these studies infer a good porosity to permeability relationship, they tend to lie slightly below the lower bound model predictions. Baroud et al. produced results at the opposite end of the porosity scale for human cancellous bone specimens, observing permeability values 4.45 ⋅ 10 ⁻⁸ ± 1.72  m² and 3.44 ⋅ 10 ⁻⁸ ± 1.26  m², for specimens respectively located in the longitudinal axis and in the frontal axis. Although these values lie within the model predictions of Abdahlraman et al., their average porosity is relatively high (0.90 ± 0.05), and their permeabilities show up to an order of magnitude variation (Baroud et al., 2004). From the experimental bone permeability data in the literature, it is clear that the dependence of permeability on volume fractions was complex and depended on anatomic site and flow direction. Results obtained that lie below the model predictions of Abdahlraman et al., based on the Kozeny–Carman equation, may be attributed to higher specific surface values of the varying bone types (Abdalrahman et al., 2015).

4.3. Bone specimen anisotropy

From Table 1, it can be seen that the permeability matrix of all four bone specimens is full, i.e., it contains six coefficients different from zero and consequently represents an orthotropic material. This also indicates that the bone samples were not harvested in any plane of symmetry, which for trabecular bone samples is a challenging task.

With the R values found for each specimen defining the degree of anisotropy, large variation and a wide range of behaviors are exhibited. This can be directly attributed to the way in which specimens were cored. From Table 1 it can be seen that, similarly to Clavaud et al. (2008), the permeabilities along the axis of minimum permeability $\left(k_3^p\right)$ are 1.2 to 4.9 times smaller than the mean permeability in the perpendicular plane $\left(k_1^p\right)$. For specimens n = 1, 4 the R values obtained are respectively 0.79 and 0.83, while for n = 2, 3 the R values obtained are 0.27 and 0.51. Based on Guibert et al. and Rice et al., where isotropy is suggested to be the case when R > 0.75 and 0.65 < R < 0.84 respectively, specimens n = 1,4 are much closer to being isotropic (Guibert et al., 2015, Rice et al., 1970) has the largest variation between $k_{\min }^p,k_{int}^p$ and $k_{\max }^p$ and therefore exhibits the largest degree of anisotropy.

Taking the classical ratio (r) results obtained by Nauman et al. $\left(\text{where}{k}_{\max }^p=k_L,k_{int}^p=k_{\min }^p=k_T\right)$, we can estimate the anisotropic ratio R. For bovine proximal tibia specimen, the anisotropic ratio (R = 0.39) is relatively anisotropic, more closely related to our specimen n = 2. It is important to note that a significant variation is observed between human vertebral body (R = 0.69) and human proximal femur (R = 0.21), with strong differences in k values shown in Fig. 8 (Nauman et al., 1999) . The extremely low anisotropic ratio observed by Nauman et al., for the human proximal femur data, can be explained by having a whole order of magnitude difference between the longitudinal and transverse permeability values.

As observed in Fig. 1, the bovine specimens exhibit a wide range of architecture displaying varying amounts of plate-like structures, which have a large affect on the anisotropy of the permeability (Nauman et al., 1999, Widmer and Ferguson, 2013) . This is clearly shown in the variability of R in Fig. 7.

5. Conclusion and outlook

In the current study, we described a comprehensive approach linking pore-scale imaging with large-scale fluid dynamics simulations in the pore space of trabecular bone samples, together with calculating bone intrinsic permeability based on upscaling. Only a few studies have previously explored this type of approach with respect to selection of representative volume elements and mesh sensitivity due to the large computational time required. We demonstrated that using an open-source software, arb, to calculate pore-scale fluid flow properties, in combination with MATLAB to calculate the upscaled permeability matrix and principal flow directions, it is feasible to run large scale simulations.

Based on the numerical simulation results, we demonstrated that an RVE size of ℓ_RVE = 2 mm is sufficient to represent the bovine trabecular bone microstructure and the corresponding pore scale fluid flow properties. Mesh convergence studies on pore-scale fluid dynamics simulations showed that the finite volume method converges for element numbers larger than 125,000. Utilizing a smaller number of elements can significantly compromise the accuracy of calculated fluid flow properties. Using periodic boundary conditions provides the most accurate values for respective bone permeability data. Permeability values ranged from 0.22 ⋅ 10 ⁻⁸  m² for porosities between 0.83 and 0.86. Comparison of permeabilities of our bovine sternum bone specimens with other bone samples from the literature showed good agreement. Anisotropy of our bone samples varied from highly anisotropic to highly isotropic, however results compared well with those reported in the literature for bovine.

Permeability plays a major role in the fields of biomechanics and tissue engineering. It not only influences the hydrodynamic properties of porous media, but also the ability for cells to penetrate the media, and for nutrients, oxygen and waste products to perfuse through the pore space of these materials (Dias et al., 2012, Truscello et al., 2012) . An accurate and efficient prediction of permeability is essential to the design of porous scaffolds, and to the development of highly perfusable bioreactors for stem cell seeding and expansion applications. The proposed methodology can be utilized in a number of bioengineering applications including design of accurate pore morphologies for bone replacement materials, consistent selection of bone specimen for bone bioreactor studies, hydraulic stiffening effects in whole bones, and for comparison and characterization of bone fluid flow properties.

Nomenclature

Variables

C

dimensionless constant

GV

grey value

k

intrinsic permeability tensor

$\tilde{k}$

macroscopic permeability tensor

n

normal vector

N

total number of elements

p

microscopic pressure field

P

macroscopic pressure field

r

anisotropy ratio as defined in Clavaud et al. (2008)

R

anisotropic ratio

s

imposed pressure gradient

S_v

specific surface

t

threshold

V

whole volume of RVE

n

specimen number

τ

viscous stress tensor

Ω_f

fluid region

Ω_s

solid region

Γ

solid/fluid interface

u

microscale velocity

v

macroscale velocity

δ

Kronecker operator

Δ

delta operator

μ

viscosity of the fluid phase

ϕ

microscale porosity

Φ

macroscale porosity

⟨⟩

volumetric average

$\overline{\Phi }$

mean porosity

$\overline{R}$

mean anisotropic ratio

$\overline{{\mathbf{k}}_i^p}$

mean principal permeability

∇

vector differential operator nabla

Re

Reynolds number

Abbreviations

RVE

representative volume element

hom

homogenized

ave

average

BC

boundary condition

SD

standard deviation

MicroCT

micro-computed tomography

VOI

volume of interest

sym

symmetry

Superscripts

p

principal flow direction

exp

experimental

T

transpose operator

Subscripts

n

bovine specimen

fluid

… of the fluid volume fraction

min

minimum value of …

int

intermediate value of …

max

maximum value of …

L

… in longitudinal direction

T

… in transverse direction

RVE

representative volume element

Appendix A. Supplementary data

.