Low Data Drug Discovery with One-Shot Learning

Abstract

Recent advances in machine learning have made significant contributions to drug discovery. Deep neural networks in particular have been demonstrated to provide significant boosts in predictive power when inferring the properties and activities of small-molecule compounds (Ma, J. et al. J. Chem. Inf. Model. 2015, 55, 263–274). However, the applicability of these techniques has been limited by the requirement for large amounts of training data. In this work, we demonstrate how one-shot learning can be used to significantly lower the amounts of data required to make meaningful predictions in drug discovery applications. We introduce a new architecture, the iterative refinement long short-term memory, that, when combined with graph convolutional neural networks, significantly improves learning of meaningful distance metrics over small-molecules. We open source all models introduced in this work as part of DeepChem, an open-source framework for deep-learning in drug discovery (Ramsundar, B. deepchem.io. https://github.com/deepchem/deepchem, 2016).

Short abstract

We demonstrate how one-shot learning can lower the amount of data required to make meaningful predictions in drug discovery. Our architecture, the iterative refinement long short-term memory, permits the learning of meaningful distance metrics on small-molecule space.

Introduction

The lead optimization step of drug discovery is fundamentally a low-data problem. When biological studies yield evidence that a particular molecule can modulate essential pathways to achieve therapeutic activity, the discovered molecule often fails as a potential drug for a number of reasons including toxicity, low activity, and low solubility.³ The central problem of small-molecule based drug-discovery is to optimize the candidate molecule by finding analogue molecules with increased pharmaceutical activity and reduced risks to the patient. Yet, with only a small amount of biological data available on the candidate and related molecules, it is challenging to form accurate predictions for novel compounds.

In the past few years, the field of machine-learning has produced several pivotal advances that address complex problems. Deep neural networks have solved challenging problems in visual perception,⁴ speech-recognition,⁵ language translation,⁶ and game-playing.⁷ These techniques leverage the use of multilayer neural network architectures as powerful and flexible function approximators. This capability of deep neural networks is underpinned by their ability to learn sophisticated representations of their input given large amounts of data.

These advances in deep-learning have inspired novel approaches for better understanding chemistry. For example, in 2012, Merck sponsored a Kaggle competition for improving the accuracy of molecular property prediction. The winning team used multitask deep networks and achieved a 15% improvement in relative accuracy over a random forest baseline.⁸ Following this work, many groups demonstrated that massively multitask networks can provide significant boosts in the predictive power of deep-learning models for property prediction.^1,9,10 In parallel, other groups developed sophisticated deep-architectures for processing and extracting features from molecular structures.¹¹ Graph-convolutional architectures^12,13 in particular process small-molecules as undirected graphs and build up features using learnable convolution layers. In contrast to older small-molecule featurizing algorithms, such as circular fingerprints,¹⁴ these new graph convolutional feature extracting architectures are learnable, meaning they can be modified to improve performance.

The practical effect of these innovations in drug discovery has been limited as most of the aforementioned deep-learning frameworks require large amounts of data. For example, massively multitask networks have so far been trained with millions of data points.⁹ This is in stark contrast to the state of current drug discovery pipelines, which often struggle to characterize even a few dozen compounds. Recent work has demonstrated that standard machine-learning techniques such as random forests and simple deep-networks are capable of learning meaningful chemical information from only a few hundred compounds,¹⁵ but even a hundred compounds is often too resource intensive for standard drug discovery campaigns.

Other recent advances in machine learning have demonstrated that in some circumstances, nontrivial predictors may be learned from only a few data points.¹⁶⁻¹⁸ These methods work by using related data to learn a meaningful distance metric over the space of possible inputs. This sophisticated metric is used to compare new data points to the limited available data and subsequently predict properties of these new data points. More broadly, these techniques are known as “one-shot learning” methods. For example, matching-networks¹⁸ learn a distance-metric upon images which they use to achieve impressive near-human accuracies on the one-shot character-recognition Omniglot data set.¹⁶

In this work, we mathematically adapt the standard one-shot learning paradigm to the drug discovery problem. Standard one-shot learning focuses on recognizing new-classes (say recognizing a giraffe given only one example). In drug-discovery, the challenge is rather to predict the behavior of a molecule in a new experimental system.

We introduce a new deep-learning architecture, the iterative refinement long short-term memory (LSTM), a modification of the matching-networks architecture and the residual convolutional network.¹⁹ This architecture allows for the learning of sophisticated metrics which can trade information between evidence and query molecules. We demonstrate that this architecture offers significant boosts in predictive power for a variety of problems meaningful for low-data drug discovery.

Furthermore, we take a strong open-source approach in this work. Every primitive introduced in this paper is open-sourced as part of the DeepChem² library for open-source drug discovery. In particular we provide high-quality Tensorflow²⁰ implementations of graph-convolutional primitives along with implementations of our one-shot learning models. The scripts used to generate all numbers in this paper are similarly open sourced, along with all data sets. Interested parties can reproduce all results claimed in this work with relative ease.

Methods

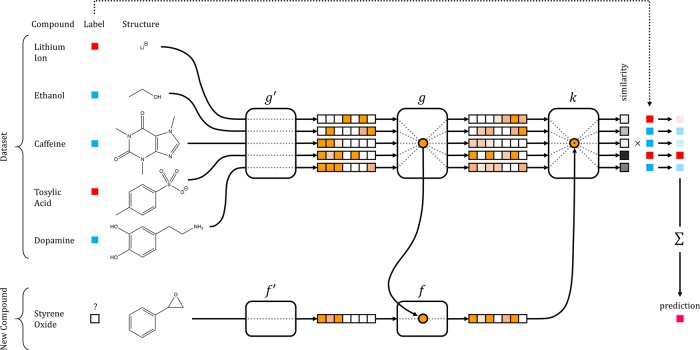
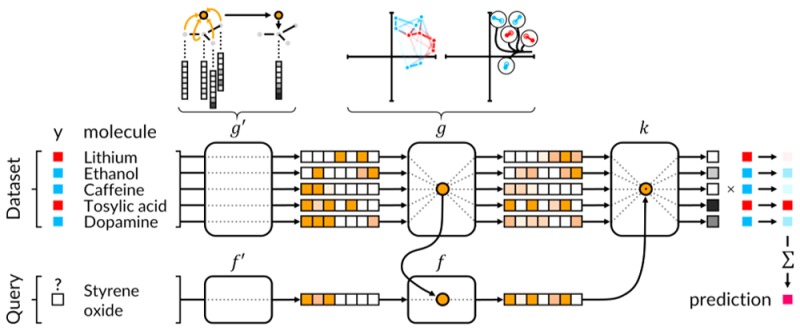
Figure 1 provides a high-level schematic of our architecture for one-shot learning in drug discovery. The remainder of this section will expand on the subcomponents that comprise such an architecture and introduce our proposed iterative refinement LSTM module.

Figure 1.

Schematic of Network Architecture for one-shot learning in drug discovery.

Mathematical Formalism

In this paper, we consider the situation in which one has multiple binary learning tasks. Some proportion of these tasks are reserved for training a one-shot learning model. The remaining tasks are those with too little data for standard machine-learning models to learn an effective classifier predicting the outcomes for these tasks (active/inactive correspond respectively to positive/negative examples for the binary classifier). The goal is to harness the information available in the training tasks to create strong classifiers for the test systems.

Mathematically, we have T tasks, each associated with a data set, S = {(x_i,y_i)}_i = 1^m, y_i ∈ {0,1} (here m = |S| is the number of data points in S). In our setting, each task typically corresponds to an experimental assay. The data points x are compounds tested in the experimental assay, while the labels y are binary experimental outcomes for the experiment (e.g., active/inactive). The learning challenge is learning to predict the experimental outcomes for new compounds tested against this assay.

We refer to the collection of available data points for a given task as a “support” set. The goal is to learn a function h, parametrized upon choice of support S that predicts the probability of any query x being active in the same system. Formally, 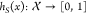, where 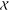is the chemical space of small-molecules. If h is specified with a neural network, fully differentiable with respect to x and S, then h can be trained end-to-end with gradient descent.

One-Shot Learning

In this section, we briefly review previously proposed techniques for one-shot learning and then introduce our new architecture for one-shot learning. We closely follow notation introduced in previous work¹⁸ to lower notational burden for readers.

Review of Prior One-Shot Techniques

Deep one-shot learning systems^17,18 use convolutional layers to encode images into continuous vectors. In the simplest one-shot learning formalism these continuous vectors are then fed into a simple nearest-neighbor classifier that labels new examples by distance-weighted combination of support set labels. Let a(x, x_i) denote some weighting function for query example x and support set element x_i with associated label y_i. Then the label h_S(x) for query compound x can be defined as

The function a is called an attention mechanism in previous work.¹⁸ Mathematically, an attention mechanism is a non-negative function a(x,x_i), with ∑_i = 1^ma(x,x_i) = 1, that forms a probability distribution over the support set. The purpose of the attention distribution a(x,·) is to reflect the model’s reasoning about the relationship between examples in support S and the query x. The final prediction of the task’s output for x can then be interpreted as the expected value of the y_i’s under the attention distribution.

The attention mechanism a depends on two embedding functions 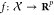and 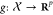which embed input examples (in small molecule space) into a continuous representation space. In past work, both f and g are standard convolutional networks, while in ours, f and g are graph-convolutional networks. The similarities between the “embedded” vectors f(x) and {g(x_i)} are computed using a similarity measure k(·,·). For example, k could be the cosine-distance between two vectors. Given a choice of similarity measure, a simple attention mechanism a can be defined by normalizing the similarity values

Note that a(x,x_i) is large when f(x) is closer to g(x_i) under metric k compared to the other g(x_j)’s. This formulation of one-shot learning has been referred to as a Siamese one-shot learning method.²¹ If f and g are circular fingerprints,¹⁴ and k is the Tanimoto distance, notice that this formula matches standard chemoinformatic similarity methods.

The simple one-shot learning formulation introduced thus far uses independent embeddings f(x) and g(x_i) with only the distance metric k linking the information from the two feature embeddings. As a result, the feature map f(x) is formed without any context about data available in support S = {x₁, ... c, x_m}. The previously introduced matching-network architecture¹⁸ addresses this problem by developing full context embeddings, in which embeddings f(x) = f(x|S) and g(x_i) = g(x_i|S) are computed using both x and S. Full context embeddings allow the embeddings for x and x_i’s to affect one another. Empirically, this modification allows for stronger one-shot learning results.

To construct f(x|S) and g(x_i|S), matching networks¹⁸ compute initial embeddings f′(x) and g′(x) using standard convolutional neural networks. (Note f′ and g′ are identical to the f and g used in the simple one-shot formulation.) The embedding g(x) is computed by placing all the g′(x_i)’s into a vector, and linking all the elements using a bidirectional LSTM^22,23 (BiLSTM), allowing each g(x_i) to be influenced by all the g′(x_j)’s.

We note that LSTM networks are a form of recurrent neural network useful for processing sequences of information. In our application, the support set S can be viewed as a sequence x₁, ...c, x_m. The BiLSTM is a modification of the basic LSTM that partially reduces dependence of the output on the ordering of the sequence.

To compute embedding f(x|S), matching networks exploit a context based attention LSTM model²⁴ (attLSTM), which is entirely order invariant with respect to the sequence. This model computes an order independent combination of its inputs.

Internally, the attLSTM contains K layers of processing which allow for transfer of information among its input. Note that both the BiLSTM and attLSTM are mechanisms for combining sequences of vectors into single vectors. However, the attLSTM is order-independent, while the BiLSTM is order dependent. The order dependence in the definition of g(x|S) is undesirable since there is no natural ordering to the elements of the support set. Furthermore, the treatment of f and g is nonsymmetric. While g(·|S) depends only on the g′, the definition of f depends on f′ and the embedding g(·|S).

Iterative Refinement LSTMs

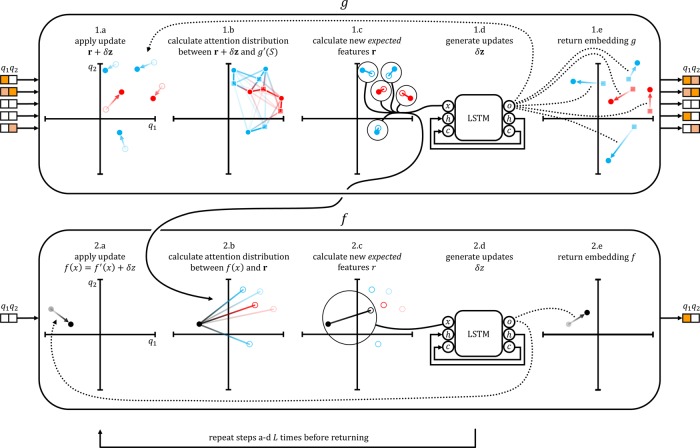
Our proposed architecture for one-shot learning preserves the context-aware design of matching networks but resolves the order dependence in the support-embedding g and the nonsymmetric treatment of the query and support noted in the previous section (Figure 2).

Figure 2.

Pictorial depiction of iterative refinement of embeddings. Inputs/outputs are two-dimensional for illustrative purposes, with q₁ and q₂ forming the coordinate axes. Red and blue points depict positive/negative samples (for illustrative purposes only). The original embedding g′(S) is shown as squares. The expected features r are shown as empty circles.

The core idea is to use an attLSTM to generate both query embedding f and support embedding g. As noted previously, the matching networks¹⁸ embedding requires the support embedding g(·|S) to define f(·|S). To resolve this issue, our architecture iteratively evolves both embeddings simultaneously.

On the first iteration, we define f(x) = f′(x) and g(S) = g′(S). Then, we iteratively update the embeddings f and g for L steps using an attention mechanism. This iteration for L steps is analogous to the K internal steps within an attLSTM, but with dual refinement of both support and query (Figure 2). This construction allows the embedding of the data set to iteratively inform the embedding of the query. The quantity L will be referred to as the depth of the IterRefLSTM. The equations below specify the full update performed over the L iterations.

1

The generated dually evolved embeddings are used to perform one-shot learning as in the simpler models explained in previous sections.

Graph Convolutions

We briefly review prior work on molecular graph convolution and then introduce a pair of new graph convolutional layers that we find useful for architectural design.

Previous Work on Molecular Graph Convolution

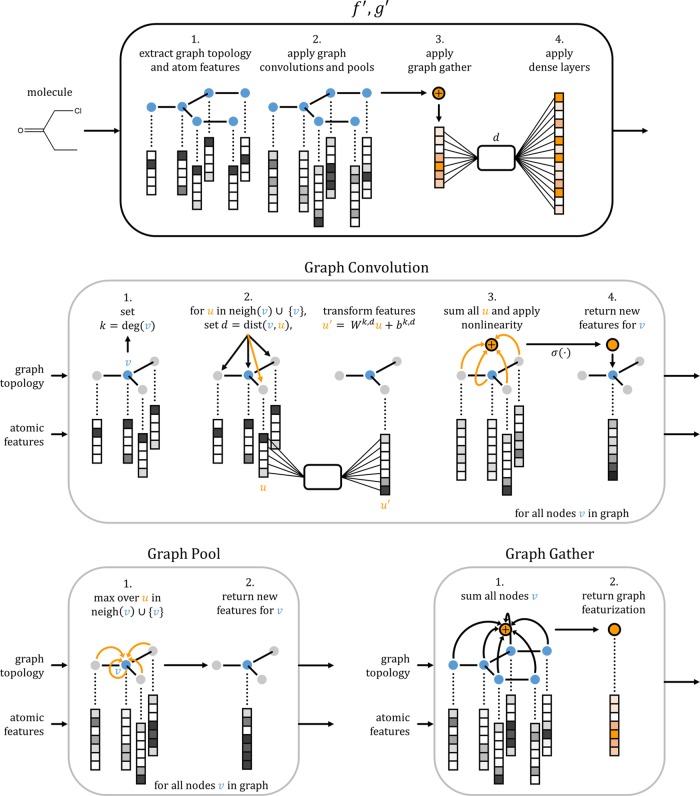
Earlier work¹² defines a generalized graph convolution layer that extends standard two-dimensional convolutions upon images to arbitrary graphs. In standard convolutional networks, an image can be viewed as a grid, where each node corresponds to a pixel. The “neighbors” of a pixel in the same receptive field are passed through a dense neural layer to compute the output value for the convolution.²⁵ Similarly, when computing the convolution output for a specific node in an arbitrary graph, all neighbors of the node are passed through a dense layer to form the new features at this node. Both convolutions exploit the “local geometry” of the system to reduce the number of learnable parameters (see Figure 3 and Appendix). Since molecules can be viewed as undirected graphs, with atoms as nodes and bonds as edges, graph convolutional architectures allow for the learning of complex functions of molecular structure.

Figure 3.

Graphical representation of the major graph operations described in this paper. For each of the operations, the nodes being operated on are shown in blue, with unchanged nodes shown in light blue. For graph convolution and graph pool, the operation is shown for a single node, v; however, these operations are performed on all nodes v in the graph simultaneously.

Graph-convolutional networks are useful for transforming small molecules into continuous vectorial representations. Such representations have emerged as a powerful way to manipulate small molecules within deep networks.²⁶ Earlier work on one-shot learning uses convolutional neural networks to encode images into continuous vectors which are then used to make one-shot predictions. By analogy, we use graph-convolutional neural networks to encode small-molecules in a form suitable for one-shot prediction.

New Layers

For the purposes of architectural design, we found it useful to introduce a pair of graph convolutional layer types, max-pooling and graph-gathering. The max-pooling operation has been used widely in the broader convolutional architecture literature,²⁵ and the graph-gather layer has been used implicitly in previous graph-convolutional architectures.¹²

Standard convolutional networks have “pooling layers”, which perform a max operation upon local receptive fields in an image.²⁵ In analogy to this pooling operation, we introduce an analogous max pool operator on a node in graph structured data that simply returns the maximum activation across the node and the node’s neighbors (see Figure 3 and Appendix). Such an operation is useful for increasing the size of downstream convolutional layer receptive fields without increasing the number of parameters.

In a graph-convolutional system, each node has a vector of descriptors. However, at prediction time, we will require a single vector descriptor of fixed size for the entire graph. We introduce a graph-gather convolutional layer which simply sums all feature vectors for all nodes in the graph to obtain a graph feature vector (see Figure 3). Note that summing feature vectors in this fashion has been done in previous architectures,¹² but we find that explicitly defining a graph-gather layer is useful for architectural design.

To facilitate the use of graph-convolutional layers in future work, we open-source our Tensorflow²⁰ implementation of graph-convolutions, graph-pooling, and graph-gathering layers as part of DeepChem.²

Model Training and Evaluation

The objective for the iterative refinement LSTM models is similar to that for the matching networks, with the key difference that a set of training tasks are specified instead of a set of training classes. Note that this distinction means our work is not a direct extension of prior work on one-shot learning; rather we seek to demonstrate that one-shot methods are capable of transferring information between related, but distinct learning tasks.

Let Tasks represent the set of all learning tasks. We split this into two disjoint sets, Train–Tasks and Test–Tasks. LetS represent a support set, and let B represent a batch of queries.

Training consists of a sequence of episodes. In each episode, a task T is randomly sampled, and then a support S and a batch of queries B (nonoverlapping) are sampled from the task. One gradient descent step minimiz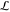ing , using ADAM²⁷ is performed for each episode. We experimented with more gradient descent steps per episode but found that sampling more supports instead improved performance. The Appendix contains numerical details of settings used for training.

At test time, the accuracy of a one-shot model is evaluated separately for each test task in Test–Tasks. For a given test task, a support of size |S| is sampled at random from data points for that task. The ROC-AUC score for the model is evaluated on the remainder of the data points for the test task (excluding the support). This procedure is reported n times for each test task (20 times in all experiments reported below), and the mean and standard deviations of ROC-AUC scores for each test task are computed.

Results and Discussion

This paper introduces the task of low data learning for drug discovery and provides an architecture for learning such models. We demonstrate that this architecture can provide strong boosts over simpler methods for low-data learning. On the Tox21 and SIDER collections, one-shot learning methods strongly dominate simpler machine learning baselines. This result is particularly interesting for the SIDER collection, since this data set consists of very high-level phenotypic side-effect observations. Given the amount of uncertainty in these predictions, the fact that one-shot learning is able to do well is a strong indication that these methods could offer strong performance on small biological data sets (for example, perhaps on a small number of drug tests done with rats).

We note that our work is not simply an application of prior work on one-shot learning to molecular data sets. The learning task undertaken by previous one-shot algorithms¹⁸ is to perform object recognition for new classes of images given only a few examples from each class. For molecules, the analogous learning challenge would be to learn the behavior of compounds in a new molecular scaffold, for a fixed experimental assay, given only a few data points from the new scaffold. Our results go further and demonstrate that iterative refinement LSTMs can generalize to new experimental assays, related but not identical to assays in the training collection. For images, the analogous step would be demonstrating that one-shot methods trained to perform object recognition, can perform, say, object localization given only limited amounts of data. Consequently, this work takes a conceptual step forward, showing that one-shot methods are capable of stronger generalization than demonstrated previously.

At the same time, it is clear that there are strong limitations to the generalization powers of current one-shot learning methods. On the MUV data sets, one-shot learning methods struggle compared to simple machine-learning baselines. This result is likely due to the presence of diverse scaffolds in the MUV collection, suggesting that one-shot learning methods may struggle to generalize to unseen molecular scaffolds. Furthermore, on the transfer learning experiment, which attempts to use the Tox21 collection to train SIDER predictors, all one-shot learning methods collapse entirely. It is clear that there is a limit to the cross-task generalization capability of one-shot models, but it is left to future work to determine the precise limits. Future work might also investigate the structure of the embeddings learned by the iterative refinement LSTM modules, to understand how these representations compare to standard techniques such as circular fingerprints. It might, for example, be possible to perform one-shot learning purely with circular fingerprints rather than learned dense embeddings.

In order to facilitate the wide adoption of these models, we have open-sourced all graph-convolutional primitives in addition to the iterative refinement LSTM models themselves as part of the DeepChem library. All scripts used to perform experiments listed in this paper have been made public as well.

The use of one-shot learning in chemistry can only be validated experimentally, but we hope that our results will provide the impetus for such work.

Experiments

This section reports experimental results for one-shot models across a number of assay collections.

Tox21

The Tox21 collection consists of 12 nuclear receptor assays related to human toxicity, first gathered for the Tox21 Data Challenge.²⁸ The winner of this challenge used a multitask deep-network²⁹ to achieve strong predictive performance.

For a low-data benchmark, we do not use the standard train/test split for this data set. Instead, we use the first nine assays as the training set, and the last three assays as the test collection. For details, see Appendix.

Results are in Table 1. All one-shot learning methods show strong boosts over the random-forest baseline, with the iterative refinement LSTM models showing a more robust boost in the presence of less data. Interestingly, the iterative refinement LSTM appears to display lower variance due to choice of support set when compared to other models, demonstrating a potential benefit of the iterative refinement process. The single-task graph convolutional baseline performs much worse than all one-shot models, demonstrating that the strong performance of one-shot models likely requires architectures that explicitly promote metric learning.

Table 1. ROC-AUC Scores of Models on Median Held-out Task for Each Model on Tox21^a.

Tox21	RF (100 trees)	Graph Conv	Siamese	AttnLSTM	IterRefLSTM
10+/10–	0.586 ± 0.056	0.648 ± 0.029	0.820 ± 0.003	0.801 ± 0.001	0.823 ± 0.002
5+/10–	0.573 ± 0.060	0.637 ± 0.061	0.823 ± 0.004	0.753 ± 0.173	0.830 ± 0.001
1+/10–	0.551 ± 0.067	0.541 ± 0.093	0.726 ± 0.173	0.549 ± 0.088	0.724 ± 0.008
1+/5–	0.559 ± 0.063	0.595 ± 0.086	0.687 ± 0.210	0.593 ± 0.153	0.795 ± 0.005
1+/1–	0.535 ± 0.056	0.589 ± 0.068	0.657 ± 0.222	0.507 ± 0.079	0.827 ± 0.001

^aNumbers reported are means and standard deviations. Randomness is over the choice of support set; experiment is repeated with 20 support sets. The Appendix contains results for all held-out Tox21 tasks. The result with highest mean in each row is highlighted. The notation 10+/10– indicates supports with 10 positive examples and 10 negative examples.

SIDER

The SIDER data set contains information on marketed medicines and their observed adverse reactions.³⁰ We originally tested on the original 5868 side effect categories, but due to lack of signal at this level of granularity we grouped the drug–SE pairs into 27 system organ classes according to MedDRA classifications.³¹ We treat the problem of predicting whether a given compound induces a side effect as an individual task (for 27 tasks in total). For the low-data benchmark, all models were trained on the first 21 tasks and tested on the last 6. For details see Appendix.

Results are in Table 2. The Siamese and IterRefLSTM methods show strong boosts over the random-forest baseline, but the AttnLSTM has poor performance on this collection (comparable to the random forest). The iterative refinement LSTM models show a robust boost in the presence of less data. As before, the iterative refinement models tend to have lower variance. The graph convolutional baseline does poorly, with performance indistinguishable from random.

Table 2. ROC-AUC Scores of Models on Median Held-out Task for Each Model on SIDER^a.

SIDER	RF (100 trees)	Graph Conv	Siamese	AttnLSTM	IterRefLSTM
10+/10–	0.535 ± 0.036	0.483 ± 0.026	0.687 ± 0.089	0.553 ± 0.058	0.669 ± 0.007
5+/10–	0.533 ± 0.030	0.473 ± 0.029	0.648 ± 0.070	0.534 ± 0.053	0.704 ± 0.002
1+/10–	0.540 ± 0.034	0.447 ± 0.016	0.544 ± 0.056	0.506 ± 0.016	0.556 ± 0.011
1+/5–	0.529 ± 0.028	0.457 ± 0.029	0.530 ± 0.050	0.505 ± 0.022	0.644 ± 0.012
1+/1–	0.506 ± 0.039	0.468 ± 0.045	0.510 ± 0.016	0.501 ± 0.022	0.697 ± 0.002

^aNumbers reported are means and standard deviations. Randomness is over the choice of support set; experiment is repeated with 20 support sets. The Appendix contains results for all held-out SIDER tasks. The result with highest mean in each row is highlighted. The notation 10+/10– indicates supports with 10 positive examples and 10 negative examples.

MUV

The MUV data set collection³² contains 17 assays designed to be challenging for standard virtual screening. The positives examples in these data sets are selected to be structurally distinct from one another. As a result, this collection is a best-case scenario for baseline machine learning (since each data point is maximally informative) and a worst-case test for the low-data methods, since structural similarity cannot be effectively exploited to predict behavior of new active compounds.

Results are in Table 3. The random forest baseline does significantly better for MUV than for the other two datsets we tested. All one-shot models struggle on this collection. The graph-convolutional baseline struggles on MUV as well, suggesting that part of the difficulty of MUV may be due to current limitations of graph convolutions. That said, these results suggest that one-shot learning methods may have some difficulties generalizing to new molecular scaffolds.

Table 3. ROC-AUC Scores of Models on Median Held-out Task for Each Model on MUV^a.

MUV	RF (100 trees)	Graph Conv	Siamese	AttnLSTM	IterRefLSTM
10+/10–	0.754 ± 0.064	0.568 ± 0.085	0.601 ± 0.041	0.504 ± 0.058	0.499 ± 0.053
5+/10–	0.730 ± 0.063	0.565 ± 0.068	0.655 ± 0.166	0.507 ± 0.052	0.663 ± 0.019
1+/10–	0.556 ± 0.084	0.569 ± 0.061	0.602 ± 0.118	0.504 ± 0.044	0.569 ± 0.012
1+/5–	0.598 ± 0.067	0.554 ± 0.089	0.514 ± 0.053	0.515 ± 0.021	0.632 ± 0.011
1+/1–	0.559 ± 0.095	0.552 ± 0.084	0.500 ± 0.0001	0.500 ± 0.027	0.479 ± 0.037

^aNumbers reported are means and standard deviations. Randomness is over the choice of support set; experiment is repeated with 20 support sets. The Appendix contains results for all held-out MUV tasks. The result with highest mean in each row is highlighted. The notation 10+/10– indicates supports with 10 positive examples and 10 negative examples.

Transfer Learning to SIDER from Tox21

The experiments thus far have tested the ability of one-shot learning methods to generalize from training tasks to closely related testing tasks. To test whether one-shot learning methods are capable of broader generalization, we trained models on the Tox21 data set collection and evaluated predictive accuracy on the SIDER collection. Note that these collections are broadly distinct, with Tox21 measuring results in nuclear receptor assays, and SIDER measuring adverse reactions from real patients.

Results are in Table 4. None of our models achieve any predictive power on this task, providing evidence that the one-shot models have limited generalization powers to unrelated systems.

Table 4. ROC-AUC Scores of Models Trained on Tox21 on Median SIDER Task for Each Model on SIDER^a.

SIDER from Tox21	Siamese	AttnLSTM	IterRefLSTM
10+/10–	0.511 ± 0.031	0.509 ± 0.014	0.509 ± 0.012

^aNote that models are evaluated on all SIDER tasks and not just the held-out SIDER tasks from previous section. Numbers reported are means and standard deviations. Randomness is over the choice of support set; experiment is repeated with 20 support sets. The result with highest mean in each row is highlighted. The notation 10+/10- indicates supports with 10 positive examples and 10 negative examples.

Appendix

Definitions of Graph Primitives

There are three major neural-network layers that are used to featurizing the molecular graphs. This is the graph convolution, h_conv(G), the graph pool, h_pool(G), and the graph gather, h_gather(G), all defined below. The graph convolution and graph pool operations definitions are given for a single node in the graph v ∈ V; however, when performing the operation on the graph, G, the operation is performed on all nodes simultaneously. This means that h_conv(G) = [h_conv(v₁), h_conv(v₂), ...], and similarly for the pool layer. Specifically, we define

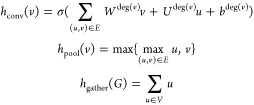where σ(·) is a nonlinearity, such as ReLU or tanh.

Convolutional Architecture in this Paper

The Graph Conv, Siamese, AttnLSTM, and IterRefLSTM models all used the same convolutional architecture, shown in the table below, with the input starting at the left, sequentially feeding into the layers to the right.

Table 5. Convolutional Network Architecture.

layer	conv	pool	conv	pool	conv	pool	dense	gather
dimension	64		128		64		128
nonlinarity	relu		relu		relu		tanh	tanh

Iterative Refinement LSTM Architecture in This Paper

The IterRefLSTM model and AttnLSTM model both use cosine similarity functions, 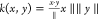. All LSTMs used in this paper have an tanh activation and hard sigmoid inner activation.

Molecular Features

For the convolutional models, all molecules were featurized into graphs by considering atoms as nodes and bonds as edges in an undirected graph. No distinction was made between bond types. RDKit³³ was used to compute basic features of atoms including atom-type, valences, formal charges, and hybridization for each atom in a given molecule. This set of features formed the initial set of atomic features fed into graph-convolutional layers.

Details of Model Training

This section provides further information on model training procedures. All code for this paper is open-sourced, so we refer interested readers to the actual code within DeepChem for exact implementation details.

One-Shot Models

When training a model on a data set collection, assays within that collection are split into training assays and testing assays. For Tox21, 9 assays are reserved for training, 3 for testing. For SIDER, 21 assays are reserved for training, and 6 for testing. For MUV, 12 assays are reserved for training, and 5 models are reserved for testing. See following Appendix sections for listings of training/testing assays for each collection.

As mentioned previously, training for one-shot models consists of a sequence of episodes. In each episode, an assay from the training assays is randomly sampled, and then a support S of size n_pos + n_neg and a batch of queries B (of size 128) are sampled from the task. In the experimental tables, we use short-hand 10+/10– or 1+/5– to respectively represent n_pos = 10, n_neg = 10 and n_pos = 1, n_neg = 5. Models were trained for 2000·n_train episodes, where n_train was the number of training assays for that data set collection. Each episode takes one gradient descent step minimizing 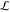, using ADAM.²⁷

At test time, the accuracy of a one-shot model is evaluated separately on each testing assay. For a given test assay, a support of size n_pos + n_neg is sampled at random from data points for that assay. The ROC-AUC score for the one-shot model is evaluated on the remainder of the data points for the test assay (excluding the support). This procedure is reported 20 times for each test assay, and the mean and standard deviations of computed ROC-AUC scores for each test assay are presented in the tables in the Appendix. For the tables in the body of the paper, the mean and standard deviations of computed ROC-AUC scores is only presented for the “median task”. That is, for the test assay whose mean ROC-AUC score (over sampled supports) is the median of the set of mean ROC-AUC scores (over all test assays).

Singletask Models

Random forests were trained on circular fingerprint representations of input molecules.¹⁴ For each test assay, supports of size n_pos + n_neg are sampled at random. The random forest model is trained on this sampled supported set and evaluated on the remainder of test assay. This procedure is repeated 20 times (note that a different random forest is trained for each newly sampled support). Means and standard deviations are reported as for one-shot models.

Singletask graph convolutional networks are trained as the random forests are, but with graph convolutional features instead of circular fingerprint representations.

Tox21 Details

Assay Details

The assays NR-AR, NR-AR-LBD, NR-AhR, NR-Aromatase, NR-ER, NR-ER-LBD, NR-PPAR-gamma, SR-ARE, SR-ATAD5 were used for training. Assays SR-HSE, SR-MMP, and SR-p53 were used for model evaluation.

Per-Assay Results

Results for each held-out assay are reported in Tables 6, 7, and 8.

Table 6. ROC-AUC Scores of Models on Tox21 Assay SR-HSE^a.

SR-HSE	RF (100 trees)	Graph Conv	Siamese	AttnLSTM	IterRefLSTM
10+/10–	0.532 ± 0.033	0.540 ± 0.025	0.767 ± 0.005	0.747 ± 0.003	0.772 ± 0.002
5+/10–	0.521 ± 0.037	0.546 ± 0.023	0.733 ± 0.098	0.716 ± 0.098	0.771 ± 0.002
1+/10–	0.525 ± 0.033	0.531 ± 0.035	0.647 ± 0.202	0.498 ± 0.046	0.671 ± 0.007
1+/5–	0.510 ± 0.041	0.537 ± 0.043	0.680 ± 0.167	0.505 ± 0.074	0.729 ± 0.003
1+/1–	0.507 ± 0.039	0.526 ± 0.0378	0.613 ± 0.187	0.507 ± 0.029	0.767 ± 0.001

^aNumbers reported are means and standard deviations. Each model is evaluated 20 times with different support sets to compute means and standard deviations. The model with highest mean in each row is highlighted. The notation 10+/10– indicates supports with 10 positive examples and 10 negative examples.

Table 7. ROC-AUC Scores of Models on Tox21 Assay SR-MMP^a.

SR-MMP	RF (100 trees)	Graph Conv	Siamese	AttnLSTM	IterRefLSTM
10+/10–	0.629 ± 0.058	0.648 ± 0.029	0.825 ± 0.006	0.801 ± 0.001	0.838 ± 0.001
5+/10–	0.634 ± 0.079	0.637 ± 0.061	0.846 ± 0.028	0.811 ± 0.003	0.847 ± 0.001
1+/10–	0.587 ± 0.068	0.541 ± 0.093	0.809 ± 0.020	0.551 ± 0.086	0.730 ± 0.003
1+/5–	0.597 ± 0.097	0.595 ± 0.086	0.687 ± 0.210	0.602 ± 0.122	0.799 ± 0.002
1+/1–	0.560 ± 0.0844	0.589 ± 0.068	0.657 ± 0.222	0.527 ± 0.090	0.835 ± 0.001

^aNumbers reported are means and standard deviations. Each model is evaluated 20 times with different support sets to compute means and standard deviations. The model with highest mean in each row is highlighted. The notation 10+/10– indicates supports with 10 positive examples and 10 negative examples.

Table 8. ROC-AUC Scores of Models on Tox21 Assay SR-p53^a.

SR-p53	RF (100 trees)	Graph Conv	Siamese	AttnLSTM	IterRefLSTM
10+/10–	0.586 ± 0.056	0.653 ± 0.021	0.820 ± 0.003	0.809 ± 0.002	0.823 ± 0.002
5+/10–	0.573 ± 0.0604	0.639 ± 0.042	0.823 ± 0.004	0.753 ± 0.173	0.830 ± 0.001
1+/10–	0.551 ± 0.067	0.597 ± 0.083	0.726 ± 0.173	0.549 ± 0.088	0.724 ± 0.008
1+/5–	0.559 ± 0.063	0.595 ± 0.073	0.745 ± 0.156	0.593 ± 0.153	0.795 ± 0.005
1+/1–	0.535 ± 0.056	0.591 ± 0.084	0.680 ± 0.197	0.507 ± 0.079	0.827 ± 0.001

^aNumbers reported are means and standard deviations. Each model is evaluated 20 times with different support sets to compute means and standard deviations. The model with highest mean in each row is highlighted. The notation 10+/10– indicates supports with 10 positive examples and 10 negative examples.

SIDER Details

Assay Details

Indications “Hepatobiliary disorders”, “Metabolism and nutrition disorders”, “Product issues”, “Eye disorders”, “Investigations,Musculoskeletal and connective tissue disorders”, “Gastrointestinal disorders”, “Social circumstances”, “Immune system disorders”, “Reproductive system and breast disorders”, “Neoplasms benign, malignant and unspecified (incl cysts and polyps)”, “General disorders and administration site conditions”, “Endocrine disorders”, “Surgical and medical procedures”, “Vascular disorders”, “Blood and lymphatic system disorders”, “Skin and subcutaneous tissue disorders”, “Congenital, familial and genetic disorders”, “Infections and infestations”,“Respiratory, thoracic and mediastinal disorders”, “Psychiatric disorders” were used for training. Indications “Renal and urinary disorders”, “Pregnancy, puerperium and perinatal conditions”, “Ear and labyrinth disorders”, “Cardiac disorders”, “Nervous system disorders”, “Injury, poisoning and procedural complications” were used for model evaluation.

Per-Assay Results

Results for each held-out assay in SIDER collection are reported in Tables 9, 10, 11, 12, 13, and 14.

Table 9. ROC-AUC Scores of Models on “Renal and Urinary Disorders”^a.

R.U.D.	RF (100 trees)	Graph Conv	Siamese	AttnLSTM	IterRefLSTM
10+/10–	0.564 ± 0.031	0.496 ± 0.035	0.729 ± 0.049	0.576 ± 0.081	0.706 ± 0.002
5+/10–	0.564 ± 0.022	0.477 ± 0.031	0.670 ± 0.119	0.540 ± 0.026	0.710 ± 0.002
1+/10–	0.540 ± 0.034	0.449 ± 0.025	0.578 ± 0.047	0.518 ± 0.025	0.575 ± 0.015
1+/5–	0.538 ± 0.045	0.457 ± 0.029	0.518 ± 0.060	0.509 ± 0.026	0.681 ± 0.010
1+/1–	0.508 ± 0.046	0.468 ± 0.045	0.503 ± 0.063	0.497 ± 0.022	0.728 ± 0.001

^aNumbers reported are means and standard deviations. Each model is evaluated 20 times with different support sets to compute means and standard deviations. The model with highest mean in each row is highlighted. The notation 10+/10- indicates supports with 10 positive examples and 10 negative examples.

Table 10. ROC-AUC Scores of Models on “Pregnancy, Puerperium and Perinatal Conditions”^a.

P.P.P.C.	RF (100 trees)	Graph Conv	Siamese	AttnLSTM	IterRefLSTM
10+/10–	0.515 ± 0.034	0.552 ± 0.028	0.694 ± 0.012	0.505 ± 0.018	0.669 ± 0.007
5+/10–	0.517 ± 0.050	0.548 ± 0.032	0.645 ± 0.073	0.545 ± 0.041	0.714 ± 0.004
1+/10–	0.529 ± 0.043	0.521 ± 0.041	0.541 ± 0.038	0.505 ± 0.026	0.539 ± 0.018
1+/5–	0.507 ± 0.044	0.538 ± 0.030	0.511 ± 0.032	0.505 ± 0.022	0.640 ± 0.011
1+/1–	0.504 ± 0.032	0.527 ± 0.027	0.510 ± 0.016	0.493 ± 0.016	0.697 ± 0.002

^aNumbers reported are means and standard deviations. Each model is evaluated 20 times with different support sets to compute means and standard deviations. The model with highest mean in each row is highlighted. The notation 10+/10– indicates supports with 10 positive examples and 10 negative examples.

Table 11. ROC-AUC Scores of Models on “Ear and Labyrinth Disorders”^a.

E.L.D.	RF (100 trees)	Graph Conv	Siamese	AttnLSTM	IterRefLSTM
10+/10–	0.527 ± 0.034	0.533 ± 0.026	0.676 ± 0.077	0.559 ± 0.070	0.661 ± 0.001
5+/10–	0.518 ± 0.038	0.486 ± 0.032	0.648 ± 0.070	0.528 ± 0.047	0.680 ± 0.001
1+/10–	0.524 ± 0.021	0.456 ± 0.018	0.547 ± 0.037	0.506 ± 0.016	0.558 ± 0.011
1+/5–	0.526 ± 0.031	0.463 ± 0.027	0.534 ± 0.064	0.504 ± 0.021	0.639 ± 0.008
1+/1–	0.509 ± 0.032	0.519 ± 0.035	0.514 ± 0.059	0.501 ± 0.022	0.689 ± 0.001

^aNumbers reported are means and standard deviations. Each model is evaluated 20 times with different support sets to compute means and standard deviations. The model with highest mean in each row is highlighted. The notation 10+/10– indicates supports with 10 positive examples and 10 negative examples.

Table 12. ROC-AUC Scores of Models on “Cardiac Disorders”^a.

C.D.	RF (100 trees)	Graph Conv	Siamese	AttnLSTM	IterRefLSTM
10+/10–	0.552 ± 0.036	0.456 ± 0.038	0.687 ± 0.089	0.532 ± 0.076	0.691 ± 0.002
5+/10–	0.560 ± 0.041	0.444 ± 0.027	0.678 ± 0.085	0.534 ± 0.053	0.704 ± 0.002
1+/10–	0.540 ± 0.029	0.422 ± 0.035	0.544 ± 0.056	0.504 ± 0.016	0.555 ± 0.012
1+/5–	0.537 ± 0.052	0.447 ± 0.035	0.536 ± 0.052	0.517 ± 0.045	0.674 ± 0.005
1+/1–	0.506 ± 0.039	0.461 ± 0.0478	0.543 ± 0.068	0.509 ± 0.029	0.704 ± 0.001

^aNumbers reported are means and standard deviations. Each model is evaluated 20 times with different support sets to compute means and standard deviations. The model with highest mean in each row is highlighted. The notation 10+/10– indicates supports with 10 positive examples and 10 negative examples.

Table 13. ROC-AUC Scores of Models on “Nervous System Disorders”^a.

N.S.D.	RF (100 trees)	Graph Conv	Siamese	AttnLSTM	IterRefLSTM
10+/10–	0.681 ± 0.077	0.367 ± 0.040	0.809 ± 0.013	0.657 ± 0.119	0.784 ± 0.006
5+/10–	0.638 ± 0.102	0.360 ± 0.035	0.791 ± 0.022	0.637 ± 0.078	0.803 ± 0.007
1+/10–	0.639 ± 0.043	0.334 ± 0.025	0.631 ± 0.115	0.511 ± 0.057	0.667 ± 0.021
1+/5–	0.604 ± 0.091	0.344 ± 0.033	0.617 ± 0.107	0.514 ± 0.080	0.775 ± 0.011
1+/1–	0.598 ± 0.100	0.437 ± 0.095	0.515 ± 0.121	0.508 ± 0.060	0.797 ± 0.002

^aNumbers reported are means and standard deviations. Each model is evaluated 20 times with different support sets to compute means and standard deviations. The model with highest mean in each row is highlighted. The notation 10+/10– indicates supports with 10 positive examples and 10 negative examples.

Table 14. ROC-AUC Scores of Models on “Injury, Poisoning and Procedural Complications”^a.

I.S.P.C.	RF (100 trees)	Graph Conv	Siamese	AttnLSTM	IterRefLSTM
10+/10–	0.535 ± 0.036	0.483 ± 0.026	0.671 ± 0.089	0.553 ± 0.058	0.667 ± 0.001
5+/10–	0.533 ± 0.0302	0.473 ± 0.029	0.589 ± 0.125	0.509 ± 0.036	0.688 ± 0.002
1+/10–	0.541 ± 0.021	0.447 ± 0.016	0.537 ± 0.045	0.510 ± 0.015	0.556 ± 0.011
1+/5–	0.529 ± 0.028	0.458 ± 0.024	0.530 ± 0.050	0.501 ± 0.021	0.644 ± 0.012
1+/1–	0.477 ± 0.029	0.475 ± 0.023	0.501 ± 0.044	0.504 ± 0.019	0.689 ± 0.001

^aNumbers reported are means and standard deviations. Each model is evaluated 20 times with different support sets to compute means and standard deviations. The model with highest mean in each row is highlighted. The notation 10+/10– indicates supports with 10 positive examples and 10 negative examples.

MUV Details

Assay Details

Assays MUV-466, MUV-548, MUV-600, MUV-644, MUV-652, MUV-689, MUV-692, MUV-712, MUV-713, MUV-733, MUV-737, MUV-810 were used for training. Assays MUV-832, MUV-846, MUV-852, MUV-858, MUV-859 were used for model evaluation.

Per-Assay Results

Results for each held-out assay in MUV collection are reported in Tables 15, 16, 17, 18, and 19.

Table 15. ROC-AUC Scores of Models on MUV-832^a.

MUV-832	RF (100 trees)	Graph Conv	Siamese	AttnLSTM	IterRefLSTM
10+/10–	0.805 ± 0.0547	0.568 ± 0.0851	0.655 ± 0.066	0.484 ± 0.058	0.500 ± 0.053
5+/10–	0.730 ± 0.063	0.565 ± 0.068	0.656 ± 0.136	0.517 ± 0.045	0.726 ± 0.025
1+/10–	0.556 ± 0.084	0.569 ± 0.061	0.610 ± 0.144	0.511 ± 0.042	0.573 ± 0.013
1+/5–	0.598 ± 0.067	0.573 ± 0.082	0.511 ± 0.179	0.529 ± 0.052	0.670 ± 0.014
1+/1–	0.559 ± 0.095	0.552 ± 0.084	0.500 ± 0.001	0.497 ± 0.030	0.463 ± 0.024

^aNumbers reported are means and standard deviations. Each model is evaluated 20 times with different support sets to compute means and standard deviations. The model with highest mean in each row is highlighted. The notation 10+/10– indicates supports with 10 positive examples and 10 negative examples.

Table 16. ROC-AUC Scores of Models on MUV-846^a.

MUV-846	RF (100 trees)	Graph Conv	Siamese	AttnLSTM	IterRefLSTM
10+/10–	0.820 ± 0.051	0.608 ± 0.079	0.601 ± 0.041	0.504 ± 0.058	0.460 ± 0.054
5+/10–	0.788 ± 0.061	0.595 ± 0.063	0.655 ± 0.166	0.494 ± 0.040	0.663 ± 0.019
1+/10–	0.700 ± 0.094	0.576 ± 0.075	0.602 ± 0.118	0.504 ± 0.045	0.598 ± 0.013
1+/5–	0.698 ± 0.106	0.554 ± 0.089	0.562 ± 0.149	0.517 ± 0.059	0.632 ± 0.011
1+/1–	0.646 ± 0.080	0.588 ± 0.077	0.500 ± 0.0001	0.496 ± 0.015	0.511 ± 0.029

^aNumbers reported are means and standard deviations. Each model is evaluated 20 times with different support sets to compute means and standard deviations. The model with highest mean in each row is highlighted. The notation 10+/10– indicates supports with 10 positive examples and 10 negative examples.

Table 17. ROC-AUC Scores of Models on MUV-852^a.

MUV-852	RF (100 trees)	Graph Conv	Siamese	AttnLSTM	IterRefLSTM
10+/10–	0.754 ± 0.064	0.657 ± 0.103	0.678 ± 0.047	0.514 ± 0.049	0.514 ± 0.048
5+/10–	0.775 ± 0.047	0.670 ± 0.068	0.765 ± 0.017	0.495 ± 0.046	0.755 ± 0.023
1+/10–	0.631 ± 0.105	0.627 ± 0.156	0.737 ± 0.097	0.574 ± 0.053	0.569 ± 0.012
1+/5–	0.632 ± 0.106	0.597 ± 0.135	0.663 ± 0.109	0.485 ± 0.022	0.727 ± 0.008
1+/1–	0.590 ± 0.134	0.614 ± 0.133	0.500 ± 0.002	0.502 ± 0.032	0.471 ± 0.032

^aNumbers reported are means and standard deviations. Each model is evaluated 20 times with different support sets to compute means and standard deviations. The model with highest mean in each row is highlighted. The notation 10+/10– indicates supports with 10 positive examples and 10 negative examples.

Table 18. ROC-AUC Scores of Models on MUV-858^a.

MUV-858	RF (100 trees)	Graph Conv	Siamese	AttnLSTM	IterRefLSTM
10+/10–	0.565 ± 0.073	0.552 ± 0.083	0.550 ± 0.143	0.516 ± 0.053	0.530 ± 0.044
5+/10–	0.564 ± 0.072	0.554 ± 0.069	0.580 ± 0.105	0.548 ± 0.051	0.629 ± 0.023
1+/10–	0.537 ± 0.089	0.552 ± 0.069	0.553 ± 0.101	0.492 ± 0.032	0.567 ± 0.014
1+/5–	0.577 ± 0.068	0.526 ± 0.050	0.486 ± 0.082	0.506 ± 0.028	0.613 ± 0.009
1+/1–	0.526 ± 0.070	0.527 ± 0.060	0.500 ± 0.009	0.500 ± 0.027	0.503 ± 0.041

^aNumbers reported are means and standard deviations. Each model is evaluated 20 times with different support sets to compute means and standard deviations. The model with highest mean in each row is highlighted. The notation 10+/10– indicates supports with 10 positive examples and 10 negative examples.

Table 19. ROC-AUC Scores of Models on MUV-859^a.

MUV-859	RF (100 trees)	Graph Conv	Siamese	AttnLSTM	IterRefLSTM
10+/10–	0.503 ± 0.0717	0.534 ± 0.084	0.514 ± 0.054	0.498 ± 0.098	0.474 ± 0.059
5+/10–	0.502 ± 0.068	0.510 ± 0.067	0.498 ± 0.051	0.507 ± 0.052	0.386 ± 0.017
1+/10–	0.530 ± 0.053	0.511 ± 0.049	0.507 ± 0.062	0.497 ± 0.076	0.412 ± 0.010
1+/5–	0.515 ± 0.074	0.513 ± 0.042	0.514 ± 0.053	0.515 ± 0.021	0.397 ± 0.010
1+/1–	0.521 ± 0.060	0.493 ± 0.065	0.500 ± 0.001	0.502 ± 0.044	0.479 ± 0.037

^aNumbers reported are means and standard deviations. Each model is evaluated 20 times with different support sets to compute means and standard deviations. No models had signal so did not highlight any models. The notation 10+/10– indicates supports with 10 positive examples and 10 negative examples.

Author Contributions

^# H.A.-T. and B.R. made an equal contribution.

The authors declare no competing financial interest.