HYDRA: revealing Heterogeneity of imaging and genetic patterns through a multiple max-margin Discriminative Analysis framework

Abstract

Multivariate pattern analysis techniques have been increasingly used over the past decade to derive highly sensitive and specific biomarkers of diseases on an individual basis. The driving assumption behind the vast majority of the existing methodologies is that a single imaging pattern can distinguish between healthy and diseased populations, or between two subgroups of patients (e.g., progressors vs. non-progressors). This assumption effectively ignores the ample evidence for the heterogeneous nature of brain diseases. Neurodegenerative, neuropsychiatric and neurodevelopmental disorders are largely characterized by high clinical heterogeneity, which likely stems in part from underlying neuroanatomical heterogeneity of various pathologies. Detecting and characterizing heterogeneity may deepen our understanding of disease mechanisms and lead to patient-specific treatments. However, few approaches tackle disease subtype discovery in a principled machine learning framework. To address this challenge, we present a novel non-linear learning algorithm for simultaneous binary classification and subtype identification, termed HYDRA (Heterogeneity through Discriminative Analysis). Neuroanatomical subtypes are effectively captured by multiple linear hyperplanes, which form a convex polytope that separates two groups (e.g., healthy controls from pathologic samples); each face of this polytope effectively defines a disease subtype. We validated HYDRA on simulated and clinical data. In the latter case, we applied the proposed method independently to the imaging and genetic datasets of Alzheimer’s Disease Neuroimaging Initiative (ADNI 1) study. The imaging dataset consisted of T1-weighted volumetric magnetic resonance images of 123 AD patients and 177 controls. The genetic dataset consisted of single nucleotide polymorphism information of 103 AD patients and 139 controls. We identified 3 reproducible subtypes of atrophy in AD relative to controls: 1) diffuse and extensive atrophy, 2) precuneus and extensive temporal lobe atrophy, as well some prefrontal atrophy, 3) atrophy pattern very much confined to the hippocampus and the medial temporal lobe. The genetics dataset yielded two subtypes of AD characterized mainly by the presence/absence of the apolipoprotein E (APOE) ε4 genotype, but also involving differential presence of risk alleles of CD2AP, SPON1 and LOC39095 SNPs that were associated with differences in the respective patterns of brain atrophy, especially in the precuneus. The results demonstrate the potential of the proposed approach to map disease heterogeneity in neuroimaging and genetic studies.

Graphical abstract

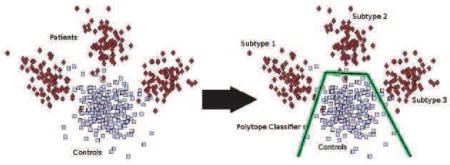
1. Introduction

Automated analysis of spatially aligned medical images has become the main framework for studying the anatomy and function of the human brain. This is typically performed by either employing voxel-based (VBA) or multivariate pattern analysis (MVPA) techniques.

VBA complements region of interest (ROI) volumetry by providing a comprehensive assessment of anatomical differences throughout the brain, while not being limited by a-priori regional hypotheses. VBA typically performs mass-univariate statistical tests on either tissue composition or deformation fields, aiming to reveal regional anatomical or shape differences (Ashburner et al., 1998; Goldszal et al., 1998; Ashburner and Friston, 2000; Davatzikos et al., 2001; Chung et al., 2001; Fox et al., 2001; Job et al., 2002; Kubicki et al., 2002; Chung et al., 2003; Studholme et al., 2004; Bernasconi et al., 2004; Giuliani et al., 2005; Job et al., 2005; Meda et al., 2008; Ashburner, 2009). However, voxel-wise methods often suffer from low statistical power and more importantly, ignore multivariate relationships in the data.

On the other hand, MVPA techniques have gained significant attention due to their ability to capture complex relationships of imaging signals among brain regions. This property allows to better characterize group differences and could potentially lead to improved diagnosis and personalized prognosis. As a consequence, machine learning methods have been used with increased success to derive highly sensitive and specific biomarkers of diseases on individual basis (Mourão Miranda et al., 2005; Klöppel et al., 2008; Davatzikos et al., 2008; Vemuri et al., 2008; Duchesne et al., 2008; Sabuncu et al., 2009; McEvoy et al., 2009; Ecker et al., 2010; Hinrichs et al., 2011; Cuingnet et al., 2011).

A common assumption behind both VBA and MVPA methods is that there is a single pattern that distinguishes the two contrasted groups. In other words, most computational neuroimaging analyses assume a single unifying pathophysiological process and perform a monistic analysis to identify it. However, this approach ignores the heterogeneous nature of diseases, which is supported by ample evidence. Typical examples of brain disorders that are characterized by a heterogeneous clinical presentation include both neurodevelopmental and neurodegenerative disorders: Autism Spectrum Disorder (ASD) comprises neurodevelopmental disorders characterized by deficits in social communication and repetitive behaviors (Geschwind and Levitt, 2007; Jeste and Geschwind, 2014); Schizophrenia and Parkinson’s Disease can be subdivided into distinct groups by separating its symptomatology to discrete symptom domains (Buchanan and Carpenter, 1994; Graham and Sagar, 1999; Koutsouleris et al., 2008; Nenadic et al., 2010; Zhang et al., 2015; Lewis et al., 2005); Alzheimer’s Disease (AD) can be separated into three subtypes on the basis of the distribution of neurofibrillary tangles (Murray et al., 2011); and Mild Cognitive Impairment (MCI) may be further classified based on the type of specific cognitive impairment (Huang et al., 2003; Whitwell et al., 2007).

Disentangling disease heterogeneity may significantly contribute to our understanding and lead to a more accurate diagnosis, prognosis, and targeted treatment. However, few research efforts have been focused on revealing the inherent disease heterogeneity. These approaches can be categorized into two distinct classes. The first class assumes an a priori subdivision of the diseased samples into coherent groups, based on independent (e.g., clinical) criteria, and opts to identify group-level anatomical or functional differences using univariate statistical methods (Huang et al., 2003; Koutsouleris et al., 2008; Nenadic et al., 2010; Whitwell et al., 2012; Zhang et al., 2015). As a consequence, multivariate relationships in the data are ignored. Moreover, and more importantly, these methods depend on an a priori disease subtype definition, which may be either difficult to obtain (e.g., from autopsy near the date of imaging), or noisy and non-specific (e.g., cognitive or clinical evaluations). Methods belonging to the second class apply multivariate clustering (typically driven by all image elements) directly to the diseased population towards segregating subsets of distinct anatomical subtypes (Graham and Sagar, 1999; Whitwell et al., 2007; Lewis et al., 2005; Noh et al., 2014). Such an approach aims to cluster brain anatomies instead of pathological patterns. Thus, it has the potential risk of estimating clusters that reflect normal inter-individual variability, some of which is due to sex, age, and other confounds, instead of highlighting disease heterogeneity.

In order to tackle the aforementioned limitations, it is necessary to develop a principled machine learning approach that is able to simultaneously identify a class of pathological samples and separate them into coherent subgroups based on multivariate pathological patterns. To the best of our knowledge, one approach has been previously proposed in this direction (Filipovych et al., 2012). That work tackled disease subtype discovery by simultaneously solving classification and clustering in a semi-supervised maximum margin framework. It jointly estimated two hyperplanes, one that separates the diseased population from the healthy one, and another hyperplane that splits the estimated diseased population into two groups. Thus, only one linear classifier was used to separate patients from controls, thereby limiting its ability to capture heterogeneous pathologic processes. Moreover, it arbitrarily assumed that exactly two disease subgroups exist, rather than attempting to determine the number of subtypes from the data.

Here, we propose a novel non-linear semi-supervised² machine learning algorithm for integrated binary classification and subpopulation clustering aiming to reveal HeterogeneitY through DiscRiminant Analysis (HYDRA). To the best of our knowledge, ours is the first algorithm to deal with anatomical/genetic heterogeneity in a supervised-clustering fashion with arbitrary number of clusters. The proposed approach is motivated by recent machine learning methods that derive non-linear classifiers through the use of multiple-hyperplanes(Fu et al., 2010; Gu and Han, 2013; Varol and Davatzikos, 2014; Kantchelian et al., 2014; Takács, 2009; Osadchy et al., 2015). Classification is performed through the separation of healthy controls from pathological samples by a convex polytope that is formed by combining multiple linear max-margin classifiers. Heterogeneity is disentangled by implicitly clustering pathologic samples through their association to single linear sub-classifiers. Multiple dimensions of heterogeneity may be captured by varying the number of estimated hyperplanes (faces of the polytope). This is in contrast to non-linear kernel classification methods which may accurately fit to heterogeneous data in terms of disease prediction, but do not provide any explicit clustering information that can be used to determine subtypes of pathology. HYDRA is a hybrid between unsupervised clustering and supervised classification methods; it can simultaneously fit maximum margin classification boundaries and elucidate disease subtypes, which is not possible with neither unsupervised clustering methods nor non-linear kernel classifiers.

Note that a preliminary version of this work was presented in (Varol et al., 2015). The current paper extends our previous work in multiple ways: i) A more sophisticated initialization scheme based on Determinental Point Processes is employed (Sec. Appendix A.1); ii) The sensitivity to initialization due to the non-convexity of the objective function has been improved by using multiple initializations and consensus strategies (Sec. Appendix A.4); iii) A symmetric version of the algorithm is developed towards accounting for the heterogeneity of the healthy controls and avoiding over-learning (Sec. 2.4). iv) A detailed description of the proposed methodology is provided. v) We extensively evaluate our method, HYDRA, by using additional (imaging and genetic) datasets and comparing it to unsupervised clustering and non-linear classification methods.

The remainder of this paper is organized as follows. In section 2, we detail the proposed approach. Next, we experimentally validate our method using synthetic (Sec. 3) and clinical (Sec. 4) data. We discuss the results in Sec. 5, while section 6 concludes the paper with our final remarks.

2. Method

In high dimensional spaces, the modeling capacity of linear Support Vector Machines (SVMs) is theoretically rich enough to discriminate between two homogeneous classes. However, while two classes are linearly separable with high probability, the resulting margin may be small. This case arises for example when one class is generated by a multimodal distribution that models a heterogeneous process (see Fig. 1a). This may be remedied by the use of non-linear classifiers, allowing for larger margins and thus, better generalization. However, while kernel methods, such as Gaussian Radial Basis Function (GRBF) kernel SVM, provide non-linearity, they lack interpretability when aiming to characterize heterogeneity.

Figure 1.

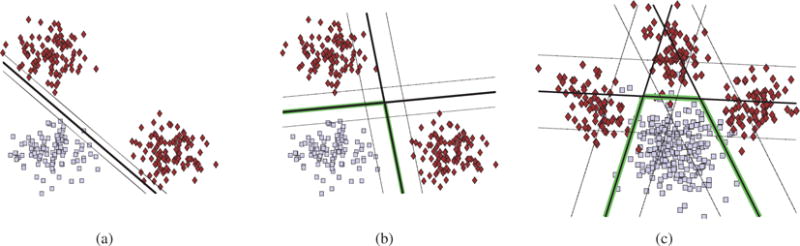
Illustrating the effect of heterogeneity when separating a positive class (denoted by gray squares) from a heterogeneous negative class (denoted by red rhombuses). (a) Linear SVM separates the positive class from a heterogeneous negative class (presence of two clusters) by a small margin. (b) Our method classifies each cluster separately, resulting in a larger margin. (c) Heterogeneity introduced by the presence of three clusters modeling distinct deviations from normality. Each deviation is captured by a different face of the convex polytope. Solid lines correspond to the classifier, dashed lines indicate margin while highlighted linear segments define the separating convex polytope.

Here, we take advantage of the previous intuition to design a novel machine learning technique that will provide larger margins while being able to elucidate heterogeneity. We introduce non-linearity using multiple linear classifiers that form locally linear hyperplanes whose linear segments separate the clusters of negative samples from the positive class (see Fig. 1b). In this way, subjects are explicitly clustered by being assigned to different hyperplanes, giving rise to interpretable directions of variability that may be useful in discovering heterogeneity.

Suppose that our dataset consists of n binary labelled d-dimensional data points ( $\mathcal{D}={\left({\mathbf{x}}_i,y_i\right)}_{i=1}^n$, x_i ∈ ℝ^d and y_i ∈ {−1, 1}). Without loss of generality, we assign the negative class to the pathological population whose heterogeneity we seek to reveal. Let us note that while there may be heterogeneity in the healthy population, we focus here on revealing disease heterogeneity. Our aim is twofold. First, we aim to estimate k hyperplanes that form a convex polytope that separates the two classes with a large margin. Second, we aim to assign each pathological sample to the hyperplane that best separates it from the normal controls. The main idea is that samples that belong to different pathological subgroups will be assigned to different hyperplanes, each of which reflects a respective pathological process (see Fig. 1c). Towards fulfilling the aforementioned aims, we introduce the proposed approach by extending standard linear maximum margin classifiers.

2.1. Large Margin Classification

For completeness, let us briefly introduce standard linear maximum margin classifiers. Maximum margin classifiers aim to estimate a hyperplane that separates the two classes by a half space, while ensuring that the distance (or margin) from the decision boundary for each sample is maximized. More formally, suppose that the set $ℱ$ comprises the set of all linear classifiers w such that for the given dataset $\mathcal{D}$ all samples are correctly classified, or ∀i, y_i(w^T x_i) + b ≥ 1. The goal is to find the classifier w belonging to the set $ℱ$ that maximizes the margin between classes. The margin is defined as the orthogonal distance between the two hyperplanes:

$${\mathbf{w}}^T\mathbf{u}+b=-1,\text{and}{\mathbf{w}}^T\mathbf{v}+b=+1,$$

where the set of points u, v that satisfy the equations, represent points from both classes with active constraints. Notice that setting $\mathbf{u}=-\frac{1+b}{{\Vert \mathbf{w}\Vert }_2^2}\mathbf{w}$ and $\mathbf{v}=\frac{1-b}{{\Vert \mathbf{w}\Vert }_2^2}\mathbf{w}$ satisfies the previous equations. Since u, v are parallel, the orthogonal distance between the hyperplanes is simply ${\Vert \mathbf{u}-\mathbf{v}\Vert }_2=\frac{2}{{\Vert \mathbf{w}\Vert }_2}$, which is the margin for SVM (Vapnik, 2000).

The optimal classifier is estimated by solving an optimization problem. However, instead of maximizing the margin, its inverse $(\frac{{\Vert \mathbf{w}\Vert }_2^2}{2})$ is typically minimized subject to the separability constraints. This results in the well known SVM objective:

$$\begin{array}{l}\underset{\mathbf{w},b,\mathit{\xi }}{\text{minimize}}\frac{{\Vert \mathbf{w}\Vert }_2^2}{2}+C{\displaystyle \sum _{i=1}^n{\xi }_i}\\ \text{subject to}\\ y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)\ge 1-{\xi }_i\text{and}{\xi }_i\ge 0\end{array}$$

where ξ = (ξ₁, …, ξ_n). The second term of the objective $\left(C{\displaystyle {\sum }_{i=1}^n{\xi }_i}\right)$ accounts for slack when classes are non-separable.

2.2. Convex Polytope Classification

Standard SVMs assume that there is a single pattern (encoded by the estimated hyperplane) that distinguishes the two classes. However, this assumption is violated in the case of heterogeneity. We aim to model heterogeneity by utilising multiple linear hyperplanes, each one corresponding to a different pathological pattern. By combining multiple linear classifiers in a piecewise fashion, we extend linear max-margin classifiers to the non-linear case. Thus, we consider the extended hypothesis class that consists of the set of sets of K hyperplanes, generalizing the geometry of the classifier to that of a convex polytope (Takács, 2009). Due to the interior/exterior asymmetry of the polytope, it is necessary to confine one class to its interior while restricting the other class to its exterior. Without loss of generality, we confine the positive class to the interior of the polytope. Thus, the search space ${ℱ}_K$ is defined as:

$$\begin{array}{r}{ℱ}_K\triangleq \{{\left\{{\mathbf{w}}_j,b_j\right\}}_{j=1}^K|\forall j,{\mathbf{w}}_j^T{\mathbf{x}}_i+b_j\ge 1\text{if}{y}_i=+1,\\ \exists j:{\mathbf{w}}_j^T{\mathbf{x}}_i+b_j\le -1\text{if}{y}_i=-1\}.\end{array}$$

In other words, ${ℱ}_K$ comprises all sets of K classifiers such that all classifiers correctly classify all members of the positive class, while for every negative sample, there is at least one classifier that correctly classifies it.

The latter gives rise to an assignment problem, where samples that have been affected by the same pathological process are assigned to the same hyperplane. This can also be seen as a clustering task since samples that have been assigned to the same hyperplane can be equivalently considered as clustered together. Thus, if ${\mathbf{S}}^{-}=[s_{i,j}]\in {\left\{0,1\right\}}^{n^{-}\times K}$ denotes the binary matrix that describes the assignment of the i-th negative class sample (n⁻ in number) to the j-th face of the polytope, then the search space becomes:

$$\begin{array}{r}{ℱ}_K({\mathbf{S}}^{-})\triangleq \{{\left\{{\mathbf{w}}_j,b_j\right\}}_{j=1}^K|\forall j,{\mathbf{w}}_j^T{\mathbf{x}}_i+b_j\ge 1\text{if}{y}_i=+1,\\ {\mathbf{w}}_j^T{\mathbf{x}}_i+b_j\le -1\text{if}{y}_i=-1\text{and}{s}_{i,j}=1\}.\end{array}$$

Given the assignment S⁻, there are K margins; each one corresponding to one face of the polytope. Analogous to the SVM formulation, the margin for the j-th face of the polytope is $\frac{2}{{\Vert {\mathbf{w}}_j\Vert }_2}$. However, due to the piecewise nature of the convex polytope, there are multiple notions of margin for the surface of the polytope. In this work, aiming to keep the problem tractable, we maximize the average margin across all the faces of the polytope: $\overline{m}=\frac{1}{K}{\displaystyle {\sum }_{j=1}^K\frac{2}{{\Vert {\mathbf{w}}_j\Vert }_2}}$. Thus, for a given dataset D and assignment S⁻ for the negative class, the objective becomes:

$$\begin{array}{l}\underset{{\{{\mathbf{w}}_j,b_j\}}_{j=1}^K}{\text{maximize}}\frac{1}{K}{\displaystyle \sum _{j=1}^K\frac{2}{{\Vert {\mathbf{w}}_j\Vert }_2}}\\ \text{subject to}\\ \begin{array}{ll}{\mathbf{w}}_j^T{\mathbf{x}}_i+b_j\ge 1& \text{if}{y}_i=+1\text{for}j=1,\dots ,K\\ {\mathbf{w}}_j^T{\mathbf{x}}_i+b_j\le -1& \text{if}{y}_i=-1\text{and}{s}_{i,j}=1\end{array}\end{array}$$

Note that, given the assignments, the objective, and the constraints are separable into K independent subproblems. Each subproblem is analogous to the SVM formulation after adding the slack terms ξ_i,j, or:

$$\begin{array}{l}\underset{{\mathbf{w}}_j,b_j,{\mathit{\xi }}_j}{\text{minimize}}\frac{{\Vert {\mathbf{w}}_j\Vert }_2^2}{2}+C{\displaystyle \sum _{i=1}^n{\xi }_{i,j}}\\ \text{subject to}\\ \begin{array}{ll}{\mathbf{w}}_j^T{\mathbf{x}}_i+b_j\ge 1-{\xi }_{i,j}\hfill & \text{if}{y}_i=+1\hfill \\ {\mathbf{w}}_j^T{\mathbf{x}}_i+b_j\le -1+{\xi }_{i,j}\hfill & \text{if}{y}_i=-1\text{and}{s}_{i,j}=1\hfill \\ {\xi }_{i,j}\ge 0\hfill & \text{for}j=1,\dots ,n\hfill \end{array}\end{array}$$

where C is a penalty parameter on the training error. If we now use the definition of the slack terms as ${\xi }_{i,j}=max\{0,1-y_i({\mathbf{w}}_j^T{\mathbf{x}}_i+b_j)\}$, and consider all hyperplanes $(\{\mathbf{W},\mathbf{b}\}\triangleq {\{{\mathbf{w}}_j,b_j\}}_{j=1}^K)$ at the same time, we get:

$$\begin{array}{l}\underset{{\{{\mathbf{w}}_j,b_j\}}_{j=1}^K}{\text{minimize}}{\displaystyle \sum _{j=1}^K\frac{{\Vert {\mathbf{w}}_j\Vert }_2^2}{2}}+C{\displaystyle \sum _{\underset{j}{i|y_i=+1}}\frac{1}{K}max\{0,1-{\mathbf{w}}_j^T{\mathbf{x}}_i-b_j\}}\\ +C{\displaystyle \sum _{\underset{j}{i|y_i=-1}}{s}_{i,j}max\{0,1+{\mathbf{w}}_j^T{\mathbf{x}}_i+b_j\}}\end{array}$$ (1)

So far, we have assumed that the assignment matrix S⁻ is known. However, this is not the case in practice and S⁻ has to be estimated too.

Attempting to solve for both {W, b} and S⁻ results in a non-convex objective function which is combinatorially difficult to optimize. Furthermore, optimization for the binary assignment S⁻ is itself non-convex since it constitutes an integer programming task. To make the problem tractable, we take two steps. First, we relax the binary assignment (s_i,j ∈ {0, 1}) to a soft assignment (s_i,j ∈ [0, 1], ${\displaystyle {\sum }_{j=1}^K{s}_{i,j}=1}$, ∀i). Given this relaxation, the objective becomes block-wise convex with respect to the groups of variables {W, b} and {S⁻}. We then use this relaxed objective function to obtain locally optimal solutions by iteratively solving for {W, b} and {S⁻}. The details of the iterative optimization are given in Appendix A.

Prediction

Once the polytope classifier {W, b} is trained, predicting the class y* of a new instance x* is straightforward:

$$y^{\ast }=\text{sign}(\underset{j}{min}{\mathbf{w}}_j^T{\mathbf{x}}^{\ast }+b_j)$$

In other words, if x* is in the interior of the polytope defined by the estimated hyperplanes ({W, b}), then it is classified as positive by all classifiers corresponding to the faces of the polytope $({\mathbf{w}}_j^T{\mathbf{x}}^{\ast }+b_j>0)$, resulting in an overall positive class prediction (y* = +1). Otherwise, if x^* is in the exterior of the polytope, then it is classified as negative by at least one classifier corresponding to a face of the polytope $({\mathbf{w}}_j^T{\mathbf{x}}^{\ast }+b_j<0)$, resulting in an overall negative class prediction (y^* = −1). Analogously, the prediction score is simply the minimum of the prediction scores of all classifiers corresponding to the faces of the polytope: $(\underset{j}{min}{\mathbf{w}}_j^T{\mathbf{x}}^{\ast }+b_j)$. Moreover, a new sample may be assigned to the existing clusters by computing the assignment index s_*,j using Eq. A.1.

2.3. HYDRA Algorithm

Given the solutions of {W, b} and S⁻ outlined in Sec. Appendix A.2 and Sec. Appendix A.3, we solve for the maximum margin convex polytope in an iterative fashion. This is the main workhorse behind the proposed framework that aims to elucidate HeterogeneitY through DiscRiminative Analysis (HYDRA) and is outlined in Algorithm 1. However, due to the non-convex nature of the problem, it is necessary to take additional steps to ensure the high quality of the solution.

Our approach towards enhancing the quality of the solution is twofold. First, particular care is taken to initialize the iterative algorithm in such a way that clustering solutions that exhibit disease-related diversity are promoted. This is made possible by employing Determinental Point Processes (DPP) (Kulesza and Taskar, 2012) to sample diverse directions of pathology, which can subsequently be used to estimate the initial clustering assignments (see Appendix A.1 for details).

Second, acknowledging the fact that, in non-convex settings, the estimated solution may vary greatly depending on the initialization, we employ a multi-initialization strategy that is coupled with a fusion step. Multiple runs of the Algorithm 1 are performed using different initializations generated by the previously described DPP sampling process, as well as different subsets of the population. The estimated clusters constitute hypotheses that capture perturbations of the underlying group topography. These clustering hypotheses are aggregated by taking into account the consensus of the respective solutions, producing the final clustering result that is free of noisy perturbations and emphasizes the underlying group structure (see Appendix A.4 for details).

2.4. Symmetric HYDRA algorithm

The algorithm that we have so far outlined is asymmetric. The patients lie on the exterior of the polytope while the controls are constrained on the interior of the polytope. This property may result in over-fitting when classifying. This can be remedied by symmetrizing the algorithm. One can run the Algorithm 1 twice, once using the actual labels Y and once using the negated labels: −Y. In that case, one can use the estimated output polytopes [W⁺, b⁺] and [W⁻, b⁻] to make predictions using the following formula:

Algorithm 1 — HYDRA

Input: X ∈ Rn×d, y ∈ {−1, +1}n (training signals), C (loss penalty), K (number of clusters/hyperplanes)

Output: W ∈ ℝd×K, b ∈ ℝ1×K (Classifier); ${\mathbf{S}}^{-}\in {\left[0,1\right]}^{n^{-}\times K}$ (Clustering Assignment)

Initialization: Initialize S− by Algorithm 2

Loop: Repeat until convergence (or a fixed number of iterations)

• Fix S− — Solve for W, b by weighted LIBSVM (sample weights set by Eq. A.2)

• Fix W, b — Solve for S− using Eq. A.1

$$y^{\ast }=\text{sin}\left(\left(\underset{j}{min}{\mathbf{w}}_j^{+T}{\mathbf{x}}^{\ast }+b_j^{+}\right)-\left(\underset{j}{min}{\mathbf{w}}_j^{-T}{\mathbf{x}}^{\ast }+b_j^{-}\right)\right),$$ (2)

where both classifiers are taken into account.

Note that the symmetric model does not affect the clustering of the patients since the two runs of Algorithm 1 are independent of each other. The difference is that the symmetric model provides two clusterings, one for the patients, and one for the controls.

3. Experiments using Simulated Data

We first validated the proposed method using synthetic data. We used a two-dimensional toy dataset to provide insight into the workings of the proposed approach. Then, we quantitatively validated the proposed approach against common clustering and classification approaches in a simulated dataset where heterogeneity has been introduced. We evaluated the ability of HYDRA to distinguish between two classes and demonstrated its potential to reveal relevant subgroups.

Let us note that for all experiments, the classification was performed using the symmetric version of HYDRA, while the clustering of the negative class was used to reveal disease heterogeneity. The final clustering was the consensus result of twenty repetitions. The primal formulation was employed when tackling low-dimensional data, while the dual formulation was preferred in the case of high-dimensional data (see Appendix B.1 for the dual formulation).

3.1. Toy Example

To illustrate the behavior of our method, we generated a synthetic two-dimensional dataset with thousand instances (see Fig. 2). The first half of the samples were drawn from a unimodal distribution, simulating the healthy control population (denoted by magenta squares). The other half consisted of a crescent-shaped cluster of points, corresponding to the heterogeneous disease group (denoted by rhombuses colored using different variants of blue). To provide a more comprehensive setting, we additionally considered two different separability cases between the two populations. In the first case (see Fig. 2a), the two classes overlapped highly, resulting in low separability. In the second case (see Fig. 2d), the two groups did not overlap and were separated by a significant margin, thus increasing separability.

Figure 2.

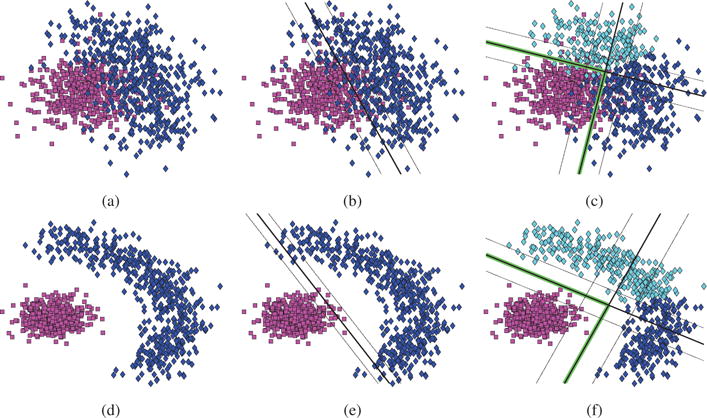
Positive (squares) and negative (rhombuses) instances in a continuous two-dimensional feature space. Instances of the two classes either (a) overlap and are not linearly separable, or (b) are highly separable. Linear SVM is used to classify the low (b) and high (e) separability toy dataset. Similarly, HYDRA (K=2) is applied to the low (c) and high (f) separability toy dataset. Dark gray lines correspond to the estimated separating hyperplanes, while light gray lines denote the estimated margins. Note the increase of the margin that is made possible through the use of multiple linear classifiers that form a convex polytope denoted by the highlighted line segments. The classes, as well as the estimated subgroups, are encoded using different colors.

To further clarify the advantages of the proposed framework, we compared the performance of HYDRA (using two hyperplanes, K = 2) against the performance of standard linear SVM. The results of the experiments are shown in Fig. 2. There are two important observations to make. First, the introduced non-linearity in HYDRA allows for improved separability between the two groups in both scenarios (see Fig. 2b, 2c, 2e and 2f). This increase is more important in the case of low-separability between classes (see Fig. 2b and 2c), where the linear SVM was not able to fully separate them. In the case of high-separability, the hyperplane that was estimated by the linear SVM effectively separated positive from negative samples. However, it did so by a relatively small margin (see Fig. 2b). On the other hand, HYDRA harnessed the non-linear structure of the data and separated them with a high margin that led to improved generalization performance (see Fig. 2f).

Second, and most importantly, HYDRA separated the negative class into two subgroups that differ from the positive class in two distinct directions. This clustering is directly related to the hyperplanes that separate the two classes. As a consequence, the obtained clustering is obtained in a supervised fashion and thus, it is driven by discriminating patterns that capture disease heterogeneity. This is in contrast to standard clustering techniques that group together samples based on appearance, which is not necessarily related to disease variability.

3.2. Simulated High-Dimensional Heterogeneous Data

Despite ample evidence of disease heterogeneity, the lack of labeled ground-truth poses a fundamental obstacle in validating the proposed approach. Thus, to overcome these limitations, we construct a simulated validation setting that allows for quantitative comparisons with other algorithms.

Aiming to replicate the common high-dimensional low sample size regime that is prevalent in neuroimaging studies, we generated a synthetic dataset with three hundred instances (or subjects) that are sampled as images with features on a 64 × 64 grid. The positive class (healthy group) was generated by randomly sampling 150 samples from a multivariate unimodal Gaussian distribution with zero mean and unit variance $(\mathcal{N}(0,1))$. The negative class (disease group) was generated by drawing 150 samples from a tri-modal distribution, where each mode simulates a different focus of disease progression (see Fig. 3a). Each focal effect had a radius of 10 pixels, with a variance of 0.5 units. To simulate the effect of disease progression, an age effect was simulated. This was generated by adding unit variance random noise to simulate progression. Therefore, there were three distinct focal effects in each subgroup, the subgroup specific effect with variance 1.5 units and the non-specific effects with unit variance. Additionally, 10% of the labels were mislabeled to simulate misdiagnosis and label noise.

Figure 3.

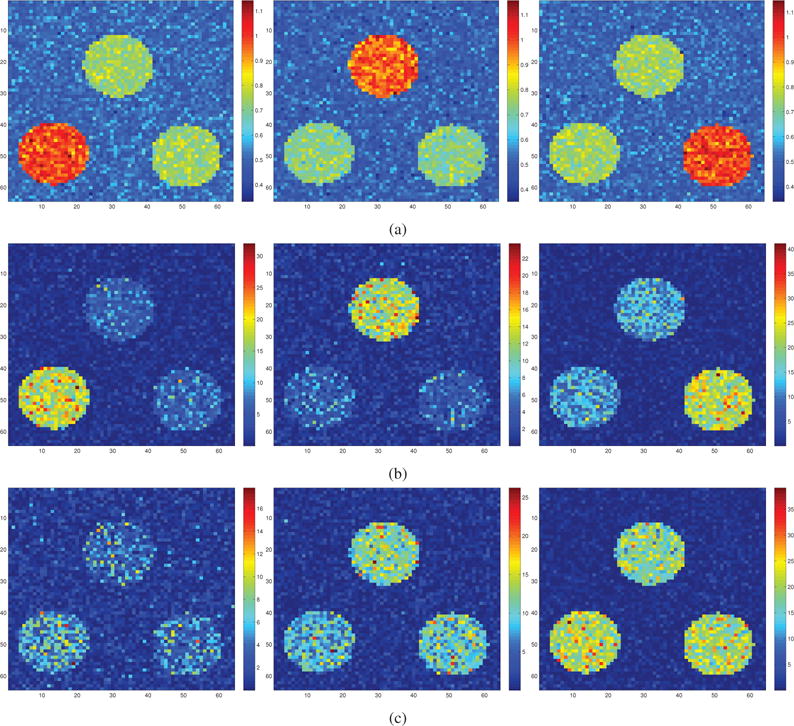
(a) Patterns of simulated heterogeneity. Mean difference images between the positive class and the three negative class subgroups, respectively. (b) The results that were obtained using HYDRA (K = 3) are visualized by performing group comparison between each estimated subgroup and the positive class. The negative logarithm of the estimated p-values is shown. (c) Similarly, the groups that were obtained using K-means (K = 3) are reported. Note that the groups estimated by HYDRA capture distinct focal effects that align well with the simulated ones, while the ones estimated by K-means mix the focal effects and recapitulate different stages of disease progression.

3.2.1. Validation Measures

HYDRA is in principle an exploratory analysis tool, aiming to reveal disease heterogeneity. However, it operates by simultaneously performing classification and clustering. Thus, it is of interest to understand how well the proposed method accomplishes each step.

To validate the classification performance, we computed the Area Under the receiver operating characteristic Curve (AUC) (Bradley, 1997). The AUC statistic summarizes the quality of the performance of a binary classifier. It is equal to the probability that a classifier will rank a randomly chosen positive instance higher than a randomly chosen negative one. Thus, an AUC equal to one indicates a perfect classifier. We calculated a distribution of AUC values by performing 100 realizations of 10-fold cross-validation. During each iteration, the data were partitioned into ten folds. Each fold was successively used as a test set while the remaining folds were used to train the method. The optimal parameter C of the method was estimated by performing a grid search over C ∈ {2⁻⁵, …, 2³} using an internal round of 10-fold cross-validation.

The clustering performance of our approach was assessed by taking into account the stability of the obtained results. The adjusted Rand Index (ARI) (Hubert and Arabie, 1985) was used to quantify the similarity between different clustering results. This index is corrected for grouping by chance, resulting in a more conservative estimation of the overlap. A value equal to one indicates a perfect clustering. We calculated the ARI in a cross-validated fashion, following the previously described cross-validation scheme. However, in our calculations we took into account only the clustering stability between training folds. Any pair of training folds shared 80% of the subjects, allowing us to compute how consistently the common subjects were placed in the same clusters despite the variations due to the ~ 10% difference in the sample composition across folds. In detail, given the optimal C value that was estimated during the inner-fold cross-validation, we trained the model, yielding a clustering of the negative subjects in the training set. This procedure was repeated for all realizations of the 10-fold cross-validation, yielding a set of clusterings of the negative subjects of the respective training sets. Finally, we computed the average pairwise ARI between the estimated clusterings.

Let us note that the classification accuracy and the clustering stability are only surrogate measures that allow us to elucidate the underpinnings of the proposed method. HYDRA does not directly target increased classification accuracy, but instead it focuses on detecting disease subgroups. Moreover, while clustering stability is desirable, it does not necessarily imply that the estimated clusters correspond to the underlying heterogeneity. Quantitatively evaluating the relevance of the clustering to the intrinsic heterogeneity is in general not feasible. However, in this simulated scenario, the ground truth was available by default. Thus, we calculated the ARI between the estimated clusters and the simulated ones. Moreover, to further assess the performance, we conducted group analysis between the estimated subgroups and the positive class. The derived p-value maps allow for the visualization of the estimated clusters and their comparison to the generated ones.

3.2.2. Comparison with existing methods

To further validate HYDRA, we compared it to common classification and clustering approaches.

As far as classification is concerned, we first compared our method against linear SVMs. In fact, our method is a generalization of the linear SVM framework. By setting the parameter K equal to one, our method reduces to a linear SVM classifier. Parameter selection (i.e., fixing C value) was performed using the same strategy as the one for the proposed framework.

Moreover, because HYDRA establishes a non-linear separation boundary between the two classes, we contrasted its performance against the GRBF kernel SVM. The free parameters were determined through a nested cross-validation strategy. A grid search was performed over the parameter space defined by the regularization parameter C (C ∈ {2⁻⁵, …, 2³}) and the parameter σ that controls the bandwidth of the RBF kernel (σ ∈ {2⁻⁵, …, 2³}).

Verifying that HYDRA achieves comparable accuracy with commonly used classifiers, thus retaining discriminative power, is important because discrimination is inextricably tied to the cluster definition. However, the main focus of the method is on discovering clusters in the abnormal cohort. To validate the clustering potential of our framework, we included the performance of the K-means clustering (Lloyd, 1982) (20 replicates were used). We also examined the potential of the approach that performs classification on top of the clustering results. In particular, we first used K-means to cluster samples from one class and then trained a linear SVM for each cluster. This procedure was performed for both the negative and positive classes. The out of sample prediction was obtained using Eq. 2. This approach (Gu and Han, 2013) is termed here K-means/SVM. Similar to the previous cases, nested cross-validation was performed for selecting the C parameter. Note also that we run K-means and HYDRA for the same value of the parameter K that varied from one to nine (K ∈ {1, …, 9}).

3.2.3. Results

The results of the cross-validated classification accuracy are reported in Fig. 4a. We note that the classification results depend on the value of the parameter K. The high dimension and low sample size setting allowed linear SVM to separate the two classes with high accuracy. However, the non-linearity that is introduced by Gaussian SVM, as well as by HYDRA and K-means/SVM, resulted in a slight improvement in the classification performance (see also Table 1). We should underline that a statistically significant improvement of the performance was observed only for HYDRA results (p-value for t-test comparison between K = 3 HYDRA results and linear SVM equals to 0.016). Lastly, we observe that the classification accuracy that was obtained by HYDRA peaks at K = 3 and relatively decreases for higher values of K. This indicates that HYDRA was able to correctly estimate the intrinsic dimensionality of the pathological class.

Figure 4.

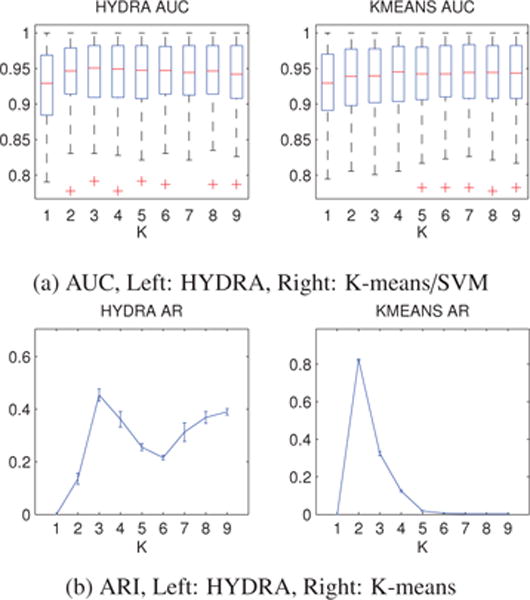
Simulated data results: (a) Cross-validated AUC for HYDRA (left) and K-means/SVM (right) binary classification. (b) Cross-validated ARI for the clustering result of HYDRA (left) and K-means (right). The results are reported for different values of the parameter K. Error bars are centered around the mean and indicate variance. Both the classification accuracy and the cluster stability were maximized at K = 3 for HYDRA, agreeing with the intrinsic dimensionality of the heterogeneous group. The classification accuracy obtained by K-means/SVM remained relatively stable for different values of K. However, the clustering stability was maximized for K = 2, demonstrating that higher reproducibility does not necessarily imply successful heterogeneity detection.

Table 1.

Table summarizing the results for the simulated dataset. Cross-validated classification accuracy is reported for Gaussian SVM, linear SVM, HYDRA, and K-means/SVM. Cross-validated cluster stability and overlap with the ground truth are reported for HYDRA and K-means.

Decoding simulated focal effects
Data	Method	K	AUC	ARI	ARI with Ground Truth
Synthetic Data	Gaussian SVM	—	0.9327 ± 0.0368	—	—
	Linear SVM	1	0.9258 ± 0.0498	—	—
	HYDRA	2	0.9404 ± 0.0471	0.1353 ± 0.1464	0.3487
		3*	0.9423 ± 0.0460	0.3620 ± 0.1514	0.6175
	K-means/SVM	2*	0.9347 ± 0.0484	0.8237 ± 0.0641	−0.0076
		3	0.9369 ± 0.0470	0.3235 ± 0.0985	0.0233

^*denotes the value of the parameter K that was chosen based on the cluster stability analysis. All models achieved comparable classification performance in terms of AUC. However, HYDRA was able to correctly identify the ground truth clusters. Note that while K-means achieved the highest reproducibility, it estimated clusters that did not correspond to the generated focal effects.

As far as the clustering reproducibility is concerned, we note a significant difference between HYDRA and K-means (see Fig. 4b). Note that K-means obtained the highest reproducibility, yet the estimated clusters did not reflect the simulated focal effects. K-means consistently grouped the data into two clusters, while HYDRA segregated the data with higher stability into three subgroups (see also Table 1). The importance of this difference was further emphasized by the fact that K-means results were significantly different from the HYDRA clustering. HYDRA clusters overlapped highly with the simulated ones while K-means results did not match the generated subgroups (see Table 1). This is because K-means, being blind to class information, was driven by global patterns that were confounded by the variations stemming from covariate effects rather than relevant heterogeneity. On the contrary, HYDRA was able to identify the heterogeneous groups by exploiting patterns that encode directions along which the two groups differ.

To further appraise the differences between the two methods, we report in Fig. 3b and Fig. 3c the group differences between the positive class and the three subgroups K-means and HYDRA estimated, respectively. By visually comparing them to the group differences for the simulated groups (see Fig. 3a), we observe that HYDRA recovered the three modes of differences with high certainty. Contrarily, K-means captured global effects that reflect the overall progression of the simulated pathology (note the relevant increase of the group differences in Fig. 3c), instead of teasing out distinct pathological directions.

Our synthetic validation setting provides two key insights. First, while all methods were able to successfully separate the two groups, only HYDRA was able to distinguish between pathological subgroups. Thus, to effectively disentangle disease heterogeneity, one should focus on discriminating patterns rather than global image appearance. Second, and most importantly, analyzing the clustering stability allows for the estimation of the intrinsic dimensionality of the pathological group. Therefore, we adopt hereafter this popular approach (Ben-Hur et al., 2002; Lange et al., 2004) to perform model selection.

4. Experiments using Clinical Data

Having shown the interest of the proposed approach in synthetic data, we next applied our method to data from the Alzheimer’s Disease Neuroimaging Initiative³ (ADNI). The ADNI was launched in 2003 as a public-private partnership, led by Principal Investigator Michael W. Weiner, MD. The primary goal of ADNI has been to test whether serial Magnetic Resonance Imaging (MRI), Positron Emission Tomography (PET), other biological markers, clinical and neuropsychological assessment can be combined to measure the progression of mild cognitive impairment and early Alzheimer’s disease⁴. Here, our goal was to investigate both the anatomical and the genetic heterogeneity in Alzheimer’s Disease.

4.1. Visualization of Heterogeneity

Anatomical heterogeneity

To visualize the neuroanatomical heterogeneity of both the anatomically and genetically-defined disease clusters, voxel-based analyses (VBA) were performed between the controls and patient groups.

To perform VBA, MRI scans were first pre-processed using previously validated and published techniques (Goldszal et al., 1998). The preprocessing pipeline includes: (1) alignment to the Anterior and Posterior Commissures plane; (2) skull-stripping (Doshi et al., 2013); (3) N3 bias correction (Sled et al., 1998); (4) tissue segmentation into gray matter (GM), white matter, cerebrospinal fluid, and ventricles using MICO (Li et al., 2014); (5) deformable mapping (Ou et al., 2011) to a standardized template space (Kabani et al., 1998); (6) formation of regional volumetric maps called RAVENS maps (Davatzikos et al., 2001), generated to enable analyses of volume data rather than raw structural data; (7) the RAVENS were normalized by individual intracranial volume to adjust for global differences in intracranial size, and smoothed for incorporation of neighborhood information using an 8-mm Full Width at Half Maximum Gaussian filter.

The GM RAVENS were used for all VBA experiments, where a general linear model (GLM) was applied voxel-wise to estimate the disease effect on the voxel value using age and sex as covariates. False Discovery Rate (FDR) correction for multiple comparisons was used for all voxel-based analyses. Only results surviving the statistical threshold at q < 0.05 are shown.

Genetic heterogeneity

In addition to anatomical heterogeneity, the genetic differences between the subgroups of AD were assessed by performing ANOVA on genetic markers, followed by a Bonferroni test for multiple comparisons. Only results surviving the statistical threshold at q < 0.05 are reported.

4.2. Anatomical Heterogeneity of Alzheimer’s Disease

4.2.1. Participants and MRI data preprocessing

The first dataset comprises MRI scans that were made available by the ADNI study⁵. T1-weighted MRI volumetric scans were obtained at 1.5 Tesla for 123 AD patients and 177 normal controls (CN) (see demographic information given in Table 2).

Table 2.

Demographic and clinical characteristics of healthy controls (CN), AD patients (left) and the estimated structural MRI driven subtypes of AD (right). MMSE stands for mini mental state examination score.

Anatomic heterogeneity in Alzheimer’s disease
	AD vs. CN (n = 300)			AD subgroups (n = 123)
	CN (n = 177)	AD (n = 123)	p-valuec	Group 1 (n = 29)	Group 2 (n = 63)	Group 3 (n = 31)	p-valued
Age (years)	75.87 ± 5.18	74.66 ± 7.39	0.09	78.93 ± 5.75	73.70 ± 7.63	72.61 ± 6.85	0.0011
Sex (female), n (%)	87 (49.15)	62 (50.4)	0.83	8 (27.5)	32 (50.7)	22 (70.9)	0.0031
MMSE	29.12 ± 1.03	23.57 ± 1.88	1.01e-100	23.96 ± 1.97	23.15 ± 1.99	24.06 ± 1.34	0.0388
APOE ε4 genotypea, n (%)	48 (27.12)	82 (66.67)	1.71e-12	21 (72.41)	38 (60.32)	23 (74.19)	0.3121
CSF Aβ (pg/mL)b	209.2 ± 53.92	143.2 ± 42.29	1.468e-14	157.3 ± 49.49	144 ± 42.59	127.9 ± 28.66	0.09907
CSF t-tau (pg/mL)b	68.21 ± 24.66	122.5 ± 58.07	2.865e-13	97.37 ± 40.17	127.4 ± 55.16	139.4 ± 71.27	0.06547
CSF p-tau (pg/mL)b	24.36 ± 13.64	40.79 ± 19.11	2.102e-09	31.26 ± 10.76	44.91 ± 23.18	42.95 ± 14.4	0.03558

^a– Denotes subjects with at least one APOE ε4 allele present.

^b– denotes the cerebrospinal fluid (CSF) concentrations of Amyloid-beta 1 to 42 peptide (Aβ), total tau (t-tau), and tau phosphorylated at the threonine 181 (p-tau).

^c– p-value estimated using two-tailed t-test to compare AD with CN.

^d– p-value estimated using analysis of variance (ANOVA) to compare the three estimated AD subgroups.

A low-level representation was extracted by automatically partitioning the MRI scans of all participants into 153 ROIs spanning the entire brain. The ROI segmentation was performed by applying a new multi-atlas label fusion method (Doshi et al., 2015). The derived ROIs were used as features for all clustering and classification methods.

Correction for age and sex effects

To remove age and sex related differences between patient groups while retaining disease-associated neuroanatomical variation, the strategy outlined in (Dukart et al., 2011) was used. Within each cross-validation training fold, we calculated voxel-level β-coefficients for age and sex in control subjects’ ROIs using partial correlation analysis. Then, all subjects were residualized using these coefficients to correct for age and sex effects not attributable to disease related factors.

4.2.2. Evaluation of results for structural MRI AD data

Classification results are reported in Fig. 5a. The standard linear SVM achieved a highly accurate classification performance (AUC for K = 1 is greater than 0.9), which emphasizes the high separability between AD patients and healthy controls. Similar to linear SVM, HYDRA was able to separate the two groups with high accuracy but, contrary to the simulated case, it did not improve on the results of linear SVM. This is most likely because the data were already linearly separable. However, the classification performance of the proposed method remained relatively stable for different values of K (no statistically significant differences between the results were found), demonstrating that HYDRA was able to retain the important discriminative information that is necessary for disease subtype clustering. Furthermore, the stable AUC at K ≥ 2 may indicate a possible plateau in the AD vs. control classification rate (Cuingnet et al., 2011). Lastly, we should emphasize that HYDRA aims to increase the margin with K, which is indeed achieved (see Supplementary Material). This has two important implications: i) that there is heterogeneity in the data; and ii) that HYDRA successfully harnesses this heterogeneity to improve the margin.

Figure 5.

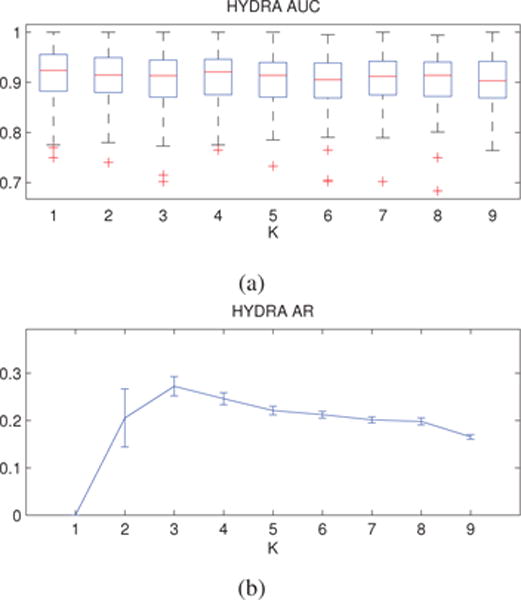
Anatomical Data: (a) Cross-validated classification accuracy. (b) Cross-validated cluster stability. Results are reported for different values of the parameter K. Error bars are centered around the mean and indicate variance. Classification accuracy remains relatively stable for different values of K (no statistically significant differences between the reported AUC values were observed). Cluster stability exhibits a distinct peak at K = 3, suggesting the existence of three distinct disease subgroups.

The clustering stability results are presented in Fig. 5b, while the AUC and ARI values for the HYDRA model at K = 1, 2, 3 are given in Table 3. The stability analysis suggests that three clusters are appropriate for capturing the intrinsic dimensionality for representing the disease heterogeneity. At finer levels (higher values of K), these three clusters are partitioned into smaller clusters, giving rise to a hierarchical structure (see Supplementary Material). This observed hierarchy provides further evidence that the data has an inherent structure that HYDRA effectively reveals.

Table 3.

Table summarizing the classification and clustering performance of HYDRA for the experiments using structural MRI and genetic data, respectively. Results are reported for three values of the parameter K. The optimal value of the parameter K that was estimated by performing model selection based on clustering stability is denoted by *. The differences in AUC were statistically insignificant between K = 1 and K = 3 for MRI data (two-tailed t-test p-value equals to 0.115) and between K = 1 and K = 2 for genetic data (two-tailed t-test p-value equals to 0.102). This suggests that discriminative signal was preserved, allowing for clinically relevant clusters to be found.

Experiment		Classification/Clustering Performance
Data	K	AUC	ARI
MRI	1	0.9149 ± 0.0563	—
	2	0.9123 ± 0.0517	0.2054 ± 0.2477
	3*	0.9021 ± 0.0572	0.2724 ± 0.1430
Genotype	1	0.7296 ± 0.1033	—
	2*	0.7047 ± 0.1105	0.7986 ± 0.2266
	3	0.6990 ± 0.1121	0.6412 ± 0.3124

The optimal clustering is visualized through the use of VBA (see Fig. 6B, 6C and 6D). The commonly performed voxel-wise group difference analysis between all healthy subjects and all patients (see Fig. 6A) provides the necessary baseline for comparison. It should be noted that the statistical significance of the group comparisons between the controls and the subgroups of AD may be biased due to sample splitting. Thus, these comparisons should serve a qualitative visualization function, rather than a quantitative one. For this reason, we do not state the statistical significance levels for these differences.

Figure 6.

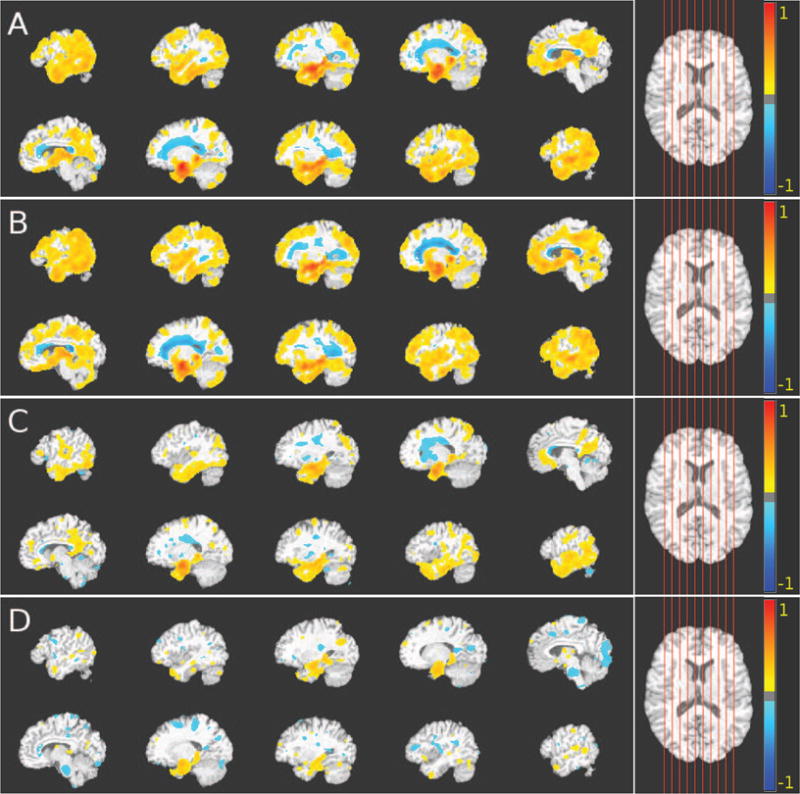
Comparison between group differences obtained using commonly applied monistic analysis and the results that were obtained using our method for heterogeneity detection in structural MRI data. The voxel-based analysis was performed using GM RAVENS. Color-maps indicate the scale for the t-statistic. Colder colors indicate relative GM volume increases (CN < pathological population), while warmer colors correspond to relative GM volume decreases (CN > pathological population). Images are displayed in radiological convention. Axial views of the VBA results obtained from GM group comparisons of (A) CN vs. AD; (B) CN vs. first AD subgroup; (C) CN vs. second AD subgroup; and (D) CN vs. third AD subgroup are shown. The first subgroup exhibited diffuse atrophy; the second subgroup was characterized by bilateral parietal lobe, precuneus, and bilateral dorsolateral frontal lobe atrophy, while the third subgroup exhibited bilateral medial temporal dominant atrophy.

We observe that at the K = 3 cluster level (see Fig. 6) the estimated subgroups are associated with distinct patterns of structural brain alterations: i) diffuse atrophy subtype (see Fig. 6B) exhibiting a typical AD pattern, similar to the one that is found by commonly applied monistic VBA (see Fig. 6A). This subtype was characterized by atrophy in nearly all cortical regions and increased lesion load in the periventricular white matter; ii) lateral parietal/temporal subtype (see Fig. 6C) in which bilateral parietal lobe, bilateral temporal cortex, bilateral dorsolateral frontal lobe, precuneus were mainly involved, and few periventricular white matter lesions were present; iii) medial temporal dominant subtype (see Fig. 6D) involving predominantly bilateral medial temporal cortex.

The estimated subgroups were associated with distinct demographic, cognitive and cerebrospinal fluid (CSF) biomarker characteristics. The first subgroup comprised 24% of AD subjects. It included relatively more male participants (21 males, 8 females) of relatively increased age (78.9 ± 5.75). Members of this group achieved a Mini Mental State Examination (MMSE⁶) score of 23.97 ± 1.97, while the frequency of APOE ε4 allele carriers was 72.4%. In addition, this group had the highest CSF Amyloid-beta 1 to 42 peptide (Aβ) concentration, 157.3 pg/mL, and the lowest CSF total tau (t-tau) and CSF tau phosphorylated at threonine 181 (p-tau) concentrations, 97.3 pg/mL and 31.2 pg/mL, respectively, on average compared to the other subgroups.

The second subgroup was the largest one, consisting of 51% of AD subjects, 60.32% of whom are APOE ε4 carriers. Both sexes were nearly equally represented (31 males and 32 females), having a mean age of 73.7 years (±7.63 standard deviation). Its members performed relatively worse in terms of MMSE (23.16 ± 1.99). The average CSF p-tau concentration for this group was the highest compared to the other subgroups at 44.9 pg/mL.

The last subgroup included the 25% of AD patients. Contrary to the previous subgroup, it was dominated by females (9 males and 22 females) of relatively younger age (72.62±6.85) with a rather higher frequency of APOE ε4 allele carriers (74.19%). MMSE performance of this subgroup was 24.06 ± 1.34. The CSF Aβ concentration was the lowest for this group at 127.9 pg/mL while the CSF t-tau concentration was the highest at 139.4 pg/mL, on average, compared to the other subgroups.

Comparing the genetic profiles of these three subgroups of AD yielded further insight on the differences between the pathologies exhibited by each subgroup. One-way ANOVA was performed for each of the single nucleotide polymorphisms (SNPs) identified in two recent genome wide association studies that reported loci associated with AD (Lambert et al., 2013) and cognitive decline (Sherva et al., 2014) (see Appendix C). Three SNPs were statistically significant different: rs10948363, which is related to gene CD2AP, rs11023139, which is related to gene SPON1, and rs7245858, which is related to gene LOC390956.

For SNP rs10948363, which is related to gene CD2AP, 58% of the first subgroup and 74% of the third subgroup were carriers of the minor G allele, while 39% of the second subgroup were carriers of this risky allele.

For SNP rs11023139, which is related to gene SPON1, 29% of the first subgroup were carriers of the minor A allele, while 2% of the second subgroup and 11% of the third subgroup were carriers of this allele.

Lastly, for SNP rs7245858, which is related to gene LOC39095, 23% of the first subgroup were carriers of the minor A allele, while 2% of the second subgroup and 4% of the third subgroups were carriers of this allele.

4.3. Genetic Heterogeneity of Alzheimer’s Disease

4.3.1. Genotype data

The second dataset comprises genotypes for 103 AD patients and 139 normal controls (see demographic information in Table 4), obtained from the ADNI study⁷. ADNI genotyping is performed using the Human610-Quad Bead-Chip (Illumina, Inc., San Diego, CA) which results in a set of 620,901 single nucleotide polymorphisms (SNPs) and copy number variation markers (for details see (Saykin et al., 2010)).

Table 4.

Demographic and clinical characteristics of healthy controls, AD patients (left) and the estimated genetic-driven subtypes of AD (right).

Genetic heterogeneity in Alzheimer’s Disease
	AD vs. CN (n = 243)			AD subgroups (n = 103)
	CN (n = 139)	AD (n = 103)	p-valuec	Group 1 (n = 68)	Group 2 (n = 35)	p-valued
Age (years)	76.19±4.85	75.04±7.59	0.15	74.46±6.56	76.18±9.27	0.27
Sex (female), n (%)	62 (44.60)	49 (47.57)	0.64	33 (48.52)	16 (45.71)	0.78
MMSE	29.16±1.01	23.54±1.95	1.85e-80	23.60±1.88	23.42±2.10	0.67
APOE ε4 genotypea, n (%)	36 (25.89)	72 (69.90)	9.56e-13	67 (98.52)	5(14.28)	8.96e-33
CSF Aβ (pg/mL)b	206.1 ± 54.61	147.2 ± 43.82	1.093e-09	133.6 ± 28.47	174.2 ± 56.04	0.0004245
CSF t-tau (pg/mL)b	71.11 ± 24.89	121.9 ± 59.62	6.456e-09	129.5 ± 57.31	107 ± 62.71	0.1738
CSF p-tau (pg/mL)b	25.02 ± 13.69	40.7 ± 19.86	1.026e-06	42.58 ± 19.92	36.95 ± 19.7	0.3051

^a– Denotes subjects with at least one APOE ε4 allele present.

^b– denotes the cerebrospinal fluid (CSF) concentrations of Amyloid-beta 1 to 42 peptide (Aβ), total tau (t-tau), and tau phosphorylated at the threonine 181 (p-tau).

^c– p-value estimated using two-tailed t-test to compare AD with CN.

^d– p-value estimated using analysis of variance (ANOVA) to compare the two estimated AD subgroups.

Due to the weak or spurious signal in most of the genome, we opted to only use SNP loci that were associated with Alzheimer’s disease or cognitive decline in recent large scale genome wide association studies (Lambert et al., 2013; Sherva et al., 2014). This resulted in a reduced set of 66 SNPs (see table in Appendix C)that were represented through the use of two binary variables encoding the presence of major-major or major-minor alleles, thus raising the total number of features to 132.

4.3.2. Evaluation of results for genotype AD data

Classification results are reported in Fig. 7a. The standard linear SVM discriminated fairly between healthy controls and AD patients (AUC for K = 1 equals to 0.72). Compared to the result that was obtained using imaging features, this highlights the difficulties associated with disease classification in the genotype domain. HYDRA was able to separate the two groups with a similar accuracy for K = 2 (AUC equals to 0.70). The classification accuracy dropped for higher values of K. However, the difference between the results for K = 1 and K = 2 was statistically insignificant (p = 0.10).

Figure 7.

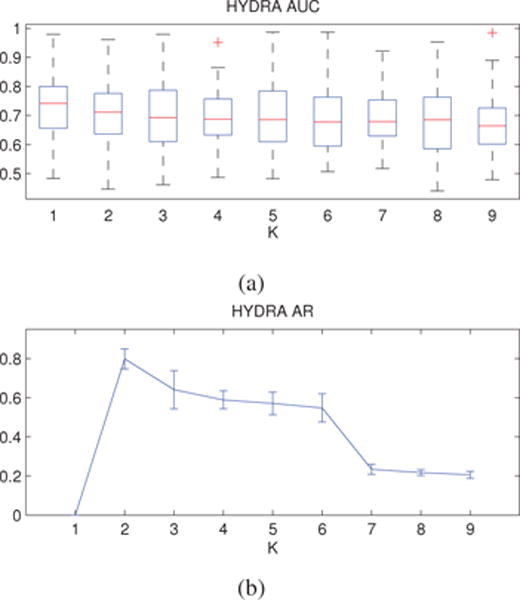
Genetic Data: (a) Cross-validated classification accuracy. (b) Cross-validated cluster stability. Results are reported for different values of the parameter K. Error bars are centered around the mean and indicate variance. Classification accuracy slightly decreases. However, the results for K = 1 and K = 2 were not statistically significant different. Cluster stability exhibited a distinct, high peak at K = 2, suggesting the existence of two distinct disease subgroups.

The clustering stability results are presented in Fig. 7b, while the AUC and ARI values for the HYDRA model at K = 1, 2, 3 are given in Table 3. The stability analysis suggested that two clusters are appropriate for capturing the intrinsic dimensionality for representing the genetic heterogeneity associated with AD. Similar to the anatomically-driven clustering results, these two clusters are successively partitioned to smaller clusters for higher values of K (see Supplementary Material), showing a hierarchical organization. This suggests that the data has structure that HYDRA reveals.

The optimal genotype clustering is visualized by contrasting the imaging phenotypes of the estimated subgroups against the healthy control population through VBA (see Fig. 8A and Fig. 8B).

Figure 8.

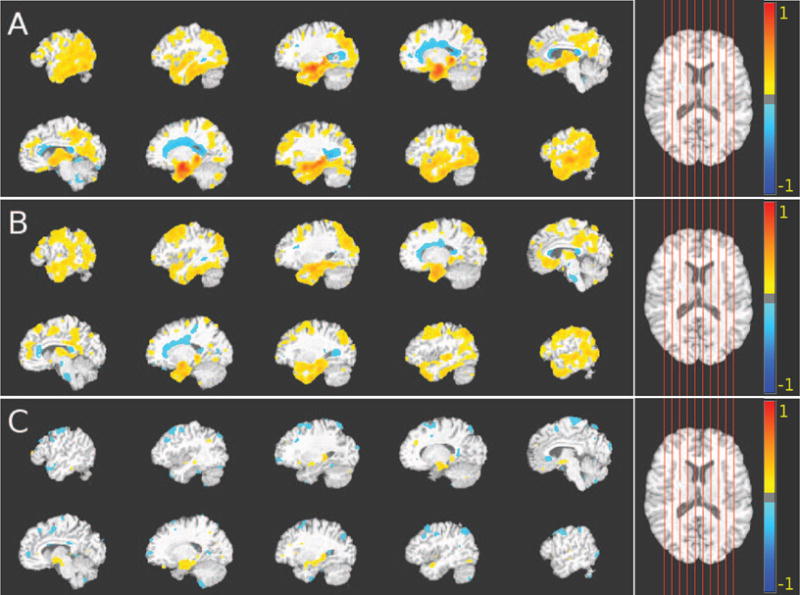
Comparison between group differences obtained using commonly applied monistic analysis and the results that were obtained using our method for heterogeneity detection in genetic data. The voxel-based analysis was performed using GM RAVENS. Color-maps indicate the scale for the t-statistic. Images are displayed in radiological convention. Axial views of the VBA results obtained from GM group comparisons of (A) CN vs. first AD subgroup; (B) CN vs. second AD subgroup; and (C) first AD subgroup vs. second AD subgroup are shown. For (A) and (B), colder colors indicate relative GM volume increases (CN < AD subgroups), while warmer colors correspond to relative GM volume decreases (CN > AD subgroups). Similarly for (C), warmer colors indicate relative GM volume increases (first AD subgroup < second AD subgroup), while colder colors correspond to relative GM volume decreases (first AD subgroup > second AD subgroup). Both groups exhibit atrophy in the temporal lobe and posterior medial cortex while white matter lesions are present in the periventricular area. However, the first AD subgroup, which mainly comprises APOE ε4 carriers, is characterized by significantly more hippocampus and entorhinal cortex atrophy and less superior frontal lobe atrophy.

We observe that at the K = 2 cluster level, the estimated subgroups were associated with distinct patterns of structural brain alterations: i) increased temporal lobe atrophy subtype (see Fig. 8A) including posterior medial cortex atrophy and increased white matter lesion load; ii) increased superior frontal lobe atrophy subtype (see Fig. 8B) including temporal lobe atrophy and periventricular white matter lesions.

The first subgroup exhibited reduced GM volumes in the hippocampus and entorhinal cortex (Fig. 8A), while the second subgroup exhibited reduced GM volumes in the superior frontal lobe (Fig. 8B). The difference between the brain images in the two subgroups are visualized in Fig. 8C.

The sex and age composition of the two estimated subgroups was similar for both cases. The proportion of the females in the first subgroup was 48.52%, while for the second one was 45.71% (see also Table 4). The average age of the first subgroup was 74.5, while for the second one was 76.2 years old.

In addition to anatomical differences, the two subgroups exhibited significantly different levels of APOE ε4 allele and CSF biomarkers. While the first subgroup was composed of 98% APOE ε4 carriers, only 14% of the second subgroup were APOE ε4 carriers. Also, the first group had lower Aβ concentration, 133.6 pg/mL, and higher t-tau and p-tau concentrations, 129.5 pg/mL and 42.5 pg/mL, respectively, on average compared to the second subgroup.

Further analysis of the genetic differences between the two subgroups yielded two additional loci of interest. While 32% of the first subgroup were carriers of the risk related A allele of the SNP rs6656401 (related to gene CR1) 49% of the second subgroup was composed of carriers of this allele.

The second locus that differed between the two subgroups was the SNP rs6733839, which is related to gene BIN1. While 72.06% of the first subgroup consisted of risk related C allele carriers of rs6733839, 85.71% of the second group comprised carriers of this allele.

However, similar to voxel-based analysis of the differences between the subgroups of AD patients, these statistical findings should be approached with care as there might be bias due to sample splitting. The statistical power needed to make a definite statement about the genetic differences between the subtypes of AD may require a much higher sample size.

5. Discussion & Conclusion

Synopsis

In this paper, we presented HYDRA, a method for disentangling heterogeneity in a principled semi-supervised machine learning framework. HYDRA aims to generalize the basic assumption of computational neuroimaging studies from a single separating pattern to many patterns, thus addressing one of the major challenges that characterizes many studies, namely the presence of heterogeneity. HYDRA attempts to find patterns associated with the underlying disease process, or more generally with the difference between two groups. These different patterns could potentially identify different dimensions of the underlying disease process and hence lead to diagnostic subcategories.

The proposed approach seamlessly integrates clustering and discrimination in a coherent framework by solving for a non-linear classifier that bears common geometric properties with convex polytopes. Discrimination is achieved by constraining one class in the interior of the polytope, while at the same time maximizing the margin between examples and class boundary. On the other hand, clustering is performed by associating disease samples to different faces of the polytope, and hence to different disease processes. Thus, each face of the polytope informs us about the distinct foci of disease effects that distinguish the patients from the healthy control subjects. This coupling between clustering and classification allows for segregating patients based on disease patterns rather than global anatomy.

In our experiments, we demonstrated the ability of the proposed approach to discern disease foci in both synthetic and clinical datasets without undermining its predictive power. Moreover, our method is endowed with improved generalization performance due to its maximum margin property of the method and the low complexity of the model (compared to standard non-linear classifiers, e.g., Gaussian kernel SVM). The latter allows it to efficiently handle small sample size high dimensionality data that are commonly encountered in neuroimaging studies by exploiting the dual model representation and operating in the inner product space.

Model selection

Choosing an appropriate number of hyperplanes, or corresponding disease subtypes, is a important and difficult model selection question. The difficulty is underlined by the fact that there is no ground truth available against which one may test a clustering result. However, we presented a strategy based on examining the clustering stability (Ben-Hur et al., 2002; Lange et al., 2004). The basic premise behind this strategy is that as one gets closer to the intrinsic dimensionality of the pathological group, the clustering algorithm should obtain similar results for different datasets generated by sampling the initial population. The group structure should remain relatively stable accounting for the fact that the datasets have been generated by the same factors.

Anatomical heterogeneity of AD

Applying the proposed framework to structural imaging data from ADNI, resulted in the definition of three AD subgroups. Our results largely agree with a recent study employing surface-based morphometry to study AD heterogeneity based on cortical thickness (Noh et al., 2014) and bear similarity to the subtypes that were recently identified in a pathologic study based on the distribution and density of neurofibrilllary tangles (Murray et al., 2011). The first subgroup is similar to the diffuse atrophy subtype reported in (Noh et al., 2014) and the typical AD group in (Murray et al., 2011). The second subgroup is comparable to the parietal dominant in (Noh et al., 2014) and the first subtype in (Murray et al., 2011). The third subgroup maps to the medial temporal subtype of (Noh et al., 2014) and the third group of (Murray et al., 2011).

The agreement of the results, despite the differences in the design of the studies, emphasizes the fact that AD should be considered as a neuroanatomically heterogeneous disease, characterized by multiple pathological dimensions. Among the pathological dimensions revealed in this study, only the first one (Fig. 6B) bore important resemblance with a typical AD pattern involving signature AD regions, while the other two (Fig. 6B and Fig. 6C) exhibited distinct pathological patterns. These dimensions may reflect distinct pathways leading to AD, associated with distinct disease processes that may constitute potential therapeutic targets.

Aiming to further elucidate the recovered pathological dimension of AD, we found that the anatomically defined clusters exhibit significant differences in their genotypes, demographic characteristics and CSF biomarker distributions.

The first subgroup comprised more male participants of relatively older age. 72.4% of its members were APOE ε4 allele carriers, while SNPs rs11023139 and rs7245858 were carried relatively more by members of this subgroup than members of the other two; 29% of the first subgroup were carriers of the minor A allele for rs11023139 and 23% of the first subgroup were carriers of the minor A allele for rs7245858, respectively (see Sec. 4.2.2). This subgroup was characterized by the most widespread pattern of atrophy, yet the most normal CSF biomarker levels. Moreover, the cognitive performance of its members was comparable to the one of the rest of the subgroups. The older age of the group, the relatively more normal levels of CSF biomarkers as well as the protective nature of rs11023139, which has been associated with a slower rate of cognitive decline (Sherva et al., 2014), suggest a protracted disease progression. The possible long disease progression may have allowed for compensatory mechanisms to develop resulting in a cognitive performance that is comparable to the other groups despite the extended atrophy.

The second subgroup was the largest one (comprising 51% of AD subjects), with a nearly equal sex proportions. However, it comprised proportionally fewer APOE ε4 carriers (60.32%), fewer carriers of the risky allele of SNP rs10948363 (39%), and almost no carriers of the minor A allele of SNP rs10948363 (2%) and SNP rs7245858 (2%). This was the group whose members performed worse in terms of MMSE.

The third subgroup included predominantly females of relatively younger age. Most of the patients (74.19%) were APOE ε4 allele carriers, while also 74% of them were carriers of the minor G allele of the SNP rs10948363, whose corresponding gene is CD2AP. CD2AP is a scaffolding protein that is involved in cytoskeletal reorganization and intracellular trafficking (Dustin et al., 1998) and has been previously associated with late onset AD (Naj et al., 2011). Moreover, a direct link between CD2AP and amyloid β toxic effects has been noted in yeast, nematodes, and rat cortical neurons after study of the role of several genes in amyloid β and tau pathways (Treusch et al., 2011). This along with the fact that this group exhibits the most abnormal levels of CSF t-tau and Aβ concentration may explain why members of this group are diagnosed as AD, despite being of younger age and exhibiting more focal atrophy. The sex difference in the population of this subgroup may result from the gender difference in the AD-promoting effect of the APOE genotype (Payami et al., 1996). Given that APOE ε4 preferably affects medial temporal lobe structures, women may have a more vulnerable medial temporal cortex than men, giving rise to this specific subtype.

Genetic heterogeneity of AD

Applying the proposed framework to genetic data from ADNI, resulted in the identification of two AD subgroups. These groups were essentially dichotomized based on the presence of APOE ε4 allele (98% of the members of the first subgroup carry it, while only 14% of the second subgroup do). However, the two groups exhibit additional genetic differences, as well as anatomical differences and distinct distributions of CSF biomarkers.

Genetic differences were found for the SNP rs6656401 (related to gene CR1) and the SNP rs6733839 (related to gene BIN1). Genetic variations at CR1 have been associated with the risk of cerebral amyloid angiopathy and decreased entorhinal cortex volume (Biffi et al., 2012; Bralten et al., 2011). Increased expression of the BIN1 gene has been recently implicated with modulating tau pathology (Chapuis et al., 2013), while BIN1 has also been associated with entorhinal and temporal pole cortex thickness (Biffi et al., 2012).

Anatomical differences were mainly found in hippocampal and entorhinal cortex, where the first group was characterized by significantly more atrophy. The anatomical differences between the subgroups may be explained by the genetic variations. APOE ε4 has been related to increased atrophy in hippocampus (Hashimoto et al., 2001; Honea et al., 2009), entorhinal (Juottonen et al., 1998) and medial frontal cortex (Fennema-Notestine et al., 2011). Given that, the first subgroup is expected to exhibit more atrophy in these areas.

The two groups were characterized by differences in the distribution of the CSF biomarkers. This difference was more significant for the CSF Aβ, which was significantly reduced in the first group. This difference may also be attributed to the effect of APOE ε4, which has been previously associated with reduced levels of CSF Aβ and t-tau(Prince et al., 2004; Sunderland et al., 2004).

While the dominant presence of APOE ε4 in the first subgroup provides the means to interpret the anatomical and CSF biomarker differences between the two subgroups, the relatively higher expression of the SNPs related to CR1 and BIN1 genes in the second subgroup (where APOE ε4 allele is less expressed) may be an indication that these genes may be part of an alternative pathway for AD pathogenesis in the absence of APOE ε4 expression. The atrophy exhibited by the second subgroup in the entorhinal cortex seen in Fig. 8B) may be a product of CR1 expression since APOE ε4 is largely absent in this subgroup. While this hypothesis remains to be validated, this underlines the value of data-driven, multivariate, exploratory techniques in forming new hypotheses.

Limitations and future work

There are some limitations to this work. First, the lack of ground truth for the clinical datasets does not allow us to quantitatively validate the proposed method. However, on the one hand, when AD patients were clustered based on imaging information, the identified patterns of abnormality aligned well with findings based on neuropathology reported in (Murray et al., 2011) and the subtypes defined based on cortical thickness in (Noh et al., 2014). Moreover, the anatomically defined subgroups also exhibited genetic differences, which provides additional evidence for the validity of the obtained clustering. On the other hand, when clustering based on genetic information, we identified subpopulations that exhibited meaningful anatomical differences. In summary, our results were consistent with the existing picture of pathological neurodegeneration and the function of the related SNPs.

Nevertheless, the sample size that is necessary for drawing reliable conclusions about the full extent of heterogeneity of AD may be higher than what was analyzed. In general, we were able to demonstrate the presence of heterogeneity in AD given the ADNI dataset. However, to be able to elucidate disease heterogeneity and map the distinct pathological processes that drive it, a wider sampling of the patient population probed in a multi-parametric fashion may be required.

Another limitation of this work is that the diseased population was studied by using either structural imaging data or genetic information. While this demonstrates the ability of the proposed framework to handle both imaging and non-imaging data, including additional information (e.g., amyloid PET imaging, tau imaging, cerebrospinal fluid biomarkers, etc) would beneficial in better characterizing the dimensions and extent of heterogeneity. Nonetheless, HYDRA can not currently handle multiple sources of information. This could be made possible by extending HYDRA through the adoption of multiple kernel techniques (Bach et al., 2004). Different kernels could be employed to encode different sources of information, allowing for their seamless integration. This extension could make HYDRA even more general, allowing its application to other exploratory problems, such as characterization of the breast cancer heterogeneity and the analysis of abnormal tissue subtypes, without being limited to the clustering of brain images.

We should note that the estimation of the subpopulations may be influenced by confounding variations due to age and sex differences. In its current form, our method does not explicitly take into account this case. Instead, we circumvent this by performing univariate covariate correction prior to feeding the data to our method. In order to tackle this shortcoming, we are currently working on extending the proposed method by explicitly modelling the effect of covariates within a unified clustering framework. However, the effect of the covariates also renders prohibitive the usage of the classification model to interpret the weight vectors of the hyperplanes (as explained in (Haufe et al., 2014)). We circumvent this by performing voxel-wise group analysis between the inferred patient clusters. However, the interpretation of the group comparison results should be made with care since the significance of the comparison may be biased due to the sample splitting. The voxel-based comparisons should serve only as a qualitative tool and not as a quantitative one. Furthermore, to avoid the circularity of assessing group differences using the same features that the groups are clustered by, we have assessed group differences using features that have not been used in the clustering. Namely, we have assessed the genetic and demographic differences between the anatomic subtypes of AD and the anatomic and demographic differences between the genetic subtypes of AD.

A possible extension of our method is towards handling regression and longitudinal studies. This could allow us to elucidate the complex nature of spatiotemporal disease dynamics as well as to reveal varying paths of normal progression. Lastly, it is straightforward to derive a one-class version of HYDRA, analogous to the work of (Sato et al., 2009), to detect and subtype outliers among controls. This could potentially shed light on the heterogenous nature of healthy phenotypes.

6. Conclusion

HYDRA aims to separate two groups by deriving a non-linear classification boundary that is constructed by using multiple linear hyperplanes. The constructed polytope allows for the revealing heterogeneity by assigning subgroups of patients to different hyperplanes. HYDRA is general; it can handle imaging and non-imaging data and can find applications in exploratory analyses other than clustering of brain images. We evaluated the performance of the method in simulated data, providing insight into its workings. Furthermore, we applied HYDRA to structural imaging and genetic dataset from ADNI, revealing disease subtypes that are consistent with the existing picture of pathological neurodegeneration and the function of the related SNPs. These results demonstrates the potential of our approach in teasing out heterogeneity.

Highlights.

• We present a novel machine learning framework for the analysis of heterogeneity in neuroimaging studies

• We propose a semi-supervised learning framework that integrates classification and clustering

• The anatomical and genetic heterogeneity of Alzheimer’s disease is explored using the proposed framework

• The anatomical and genetic subtypes that are revealed are clinically meaningful and match well with previous studies

Appendix A. Optimization

Similar to other clustering methods, HYDRA algorithm requires an initialization step followed by iterations of assignment and convex polytope solutions. To make the clustering robust, we further find the consensus of the clustering results obtained in multiple runs of HYDRA. Here we detail the techniques used for each of these steps. Initialization is found in Appendix A.1, assignment step is found in Appendix A.2, convex polytope solution is in Appendix A.3 and consensus is found in Appendix A.4.

As mentioned in the main text, HYDRA is geometrically asymmetric, requiring one of the groups to lie inside the polytope. We provide the solution for the symmetric version of HYDRA in 2.4.

Lastly, HYDRA can be solved in the dual domain if sample size is relatively lower than the dimensionality. The dual solution is in Appendix B.1.

Appendix A.1. Initialization

Due to the non-convex nature of the maximum margin polytope problem, the initialization is crucial in directing the iterative algorithm towards favorable solutions. Since we are interested in elucidating discriminative patterns between controls and patients, simply initializing by clustering the patients may not be sufficient. This is because standard clustering may group patients by following global patterns, such as the brain volume, or even more subtle patterns that nonetheless reflect normal inter-individual variability and not variability in the disease process. On the contrary, patients should be assigned to initial clusters by considering their difference map with respect to controls. In other words, since we aim to explore different directions of deviation from normal anatomy without concern for magnitude of that deviation, we initially group patients into clusters based on the regions in which they differ from the controls and not the magnitude of their difference. To achieve this, we initialize the assignments of patients into clusters by sampling K unit length hyperplanes obtained by considering the space of all pairwise differences between patients and controls. We choose K unique hyperplanes by applying Determinental Point Processes (DPP) (Kulesza and Taskar, 2012). DPP is a sampling technique that aims to obtain samples that are as diverse as possible. This type of sampling ensures that the differences we sample reflect unique biomarkers instead of repeated biomarkers with varying magnitudes. This is crucial in preventing clustering patients into groups that are not related to variability in the disease process. The steps of the initialization algorithm are given in Algorithm 2.

Algorithm 2 — Initialization — Determinental Point Processes

Input: X ∈ ℝn×d, y ∈ {−1, +1}n (training signals), K (number of clusters), m (number of hyperplanes samples to draw)

Output: ${\mathbf{S}}^{-}\in {\left[0,1\right]}^{n^{-}\times K}$ (Initial Clustering Assignment)

• Randomly draw m pairs of negative (x−) and positive (x+) samples (with replacement): ${\{{\mathbf{x}}_i^{-},{\mathbf{x}}_i^{+}\}}_{i=1}^m$

• Obtain m hyperplanes by taking the difference between members of the same pair: ${\mathbf{u}}_i=({\mathbf{x}}_i^{+}-{\mathbf{x}}_i^{-})/{\Vert {\mathbf{x}}_i^{+}-{\mathbf{x}}_i^{-}\Vert }_2$

• Sample K hyperplanes ${\{{\mathbf{w}}_j^0\}}_{j=1}^K$ from ${\left\{{\mathbf{u}}_i\right\}}_{i=1}^m$ by Determinental Point Processes (Kulesza and Taskar, 2012)

• Set rows of S− such that $s_{i,\text{arg}{min}_j{\mathbf{w}}_j^{0^T}{\mathbf{x}}_i}=1$, otherwise set si,j = 0

Appendix A.2. Assignment Step Solution

For {W, b} fixed, the problem of estimating S⁻ is an assignment problem that can be cast as a linear program (LP). The LP problem has infinite solutions when the loss function $max\{0,1+{\mathbf{w}}_j^T{\mathbf{x}}_i+b_j\}$ is equal to 0 for multiple classifiers j and for the same sample i. In this case, we choose the solution that is proportional to the margin:

$$s_{i,j}=\{\begin{array}{l}0\text{if}max\{0,1+{\mathbf{w}}_j^T{\mathbf{x}}_i+b_j\}>0\\ \frac{1+{\mathbf{w}}_j^T{\mathbf{x}}_i+b_j}{{\displaystyle {\sum }_j(1+{\mathbf{w}}_j^T{\mathbf{x}}_i+b_j)\mathbf{1}(\text{max}\{0,1+{\mathbf{w}}_j^T{\mathbf{x}}_i+b_j\}\le 0)}}\text{otherwise}\end{array}$$ (A.1)

where 1(·) is the indicator function. Let us note here that the obtained clustering is inherently different from the result that is obtained by standard clustering techniques. Instead of grouping together samples based on the similarity of their appearance, we aggregate here samples that are best separated by the same classifier. Thus, the inferred clustering is driven by discrimination. The more pronounced the pathology is, the easier it is to disentangle the underlying heterogeneity in the imaging profiles.

Appendix A.3. Convex Polytope Solution

For S⁻ fixed, the solution to {W, b} can be obtained using K calls to a modified version of LIBSVM (Chang and Lin, 2011)⁸ that allows for adaptive sample weightings. The adaptive weight c_i,j of sample i for the classifier j is calculated as:

$$c_{i,j}\{\begin{array}{cc}C{s}_{i,j}& \text{if}{y}_i=-1\\ \frac{C}{K}& \text{if}{y}_i=+1\end{array}$$ (A.2)

In case the dataset is highly unbalanced (i.e., one of the classes is over represented) samples in each class can be further weighted by their inverse relative proportion within the training set.

Appendix A.4. Consensus Solution

While DPP initialization serves as the first step in avoiding poor locally optimal solutions, consensus clustering serves as the second layer to eliminate unstable clusterings that may arise due to the non-convexity of the objective function. In noisy, or high dimensional data, the clustering obtained via Algorithm 1 may depend greatly on the initialization. To decrease this dependency and obtain stable clustering results that characterize the disease heterogeneity, we opt for a multi-initialization strategy, endowed by a fusion step. First, multiple runs of Algorithm 1 result in a number of clustering hypotheses. Then, we aim to fuse the respective hypotheses by harnessing the wisdom of the crowd to obtain an aggregate clustering. Consensus is achieved by grouping together samples that co-occur (i.e., they are assigned to the same clustering) across different clustering hypotheses. In practice, we first compute a co-occurrence matrix of the subjects based on each clustering result and then perform spectral clustering using it.

Appendix A.4.1. Co-occurrence Matrix

Given P clusterings ${\left\{{\mathbf{S}}^{-p}\right\}}_{p=1}^p$ obtained by running Algorithm 1 P times, the co-occurence matrix A is given by:

$$\begin{array}{l}{\mathbf{A}}_{i,l}={\displaystyle \sum _{p=1}^P{\displaystyle \sum _{j=1}^K{s}_{i,j}^p{s}_{l,j}^p}i,l=1\dots n,i\ne l}\\ {\mathbf{A}}_{i,l}=0i=1\dots n\end{array}$$ (A.3)

In other words, each il-th entry of the matrix enumerates the number of cases that the i-th and l-th sample were assigned to the same cluster.

Appendix A.4.2. Spectral Clustering

The consensus clustering involves the calculation of the Laplacian matrix from the co-occurrence matrix A and the computation of the K eigenvectors ([v₁ … v_k]) that correspond to the K smallest eigenvalues (λ₁ ≤ … ≤ λ_K). Then, the aggregate clustering of subjects is obtained by running K-means in the obtained subspace. The implementation of consensus clustering is outlined in Algorithm 3. It should be noted that the consensus clustering presented herein is analogous to spectral clustering (Ng et al., 2002).

Algorithm 3 — Consensus Clustering

Input: ${\{{\mathbf{S}}^{-p}\in {[0,1]}^{n^{-}\times K}\}}_{p=1}^P$ (P clusterings from Algorithm 1), K (number of clusters)

Output: ${\mathbf{S}}^{-}\in {[0,1]}^{n^{-}\times K}$ (Final Clustering Assignment)

• Compute co-occurrence matrix A using Eq. A.3

• Spectral clustering on A:

• Compute Laplacian matrix $\mathbf{L}=\text{diag}\left({\displaystyle {\sum }_{l=1}^{n^{-}}{\mathbf{A}}_{i,l}}\right)-\mathbf{A}$

• Compute the K eigenvectors (v1, …, vK) that correspond to K smallest eigenvalues of L (λ1 ≤ … ≤ λK)

• S− ← K-means([v1 … vK])

Appendix B. Dual Optimization

Due to the high dimensional, low sample size nature of neuroimaging data, it would be useful to operate in the dual domain to ease the computational burden. The dual formulation of HYDRA can be obtained by converting Eq. 1 to:

$$\underset{{\left\{{\alpha }_{i,j}\right\}}_{j=1,\dots ,K}^{i=1,\dots ,n}}{\text{maximize}}{\displaystyle \sum _{j=1}^K{\displaystyle \sum _{i=1}^n{\alpha }_{i,j}-\frac{1}{2}{\displaystyle \sum _{j=1}^K{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{l=1}^n{\alpha }_{i,j}{\alpha }_{l,j}{y}_i{y}_l{\mathbf{x}}_i^T{\mathbf{x}}_l}}}}}$$

subject to

$\begin{array}{l}{\displaystyle \sum _{i=j}^n{\alpha }_{i,j}{y}_i=0}j=1,\dots ,K\\ C/K\ge {\alpha }_{i,j}\ge 0\text{if}{y}_i=-1j=1,\dots ,K\\ C{s}_{i,j}\ge {\alpha }_{i,j}\ge 0\text{if}{y}_i=+1j=1,\dots ,K\end{array}$

The advantages of this formulation are two-fold. First, it allows us to solve for only n × K variables ${\left\{{\alpha }_{i,j}\right\}}_{j=1,\dots ,K}^{i=1,\dots ,n}$ instead of K × d variables, which may be prohibitively large. Second, via the kernel trick, we may substitute ${\mathbf{x}}_i^T{\mathbf{x}}_j$ with any kernel satisfying the Mercer condition. In terms of implementation, this formulation is readily adaptable to the weighted LIBSVM (Chang and Lin, 2011) implementation. Similar to the case of the primal problem, the weights are given by Eq. A.2.

This formulation does not affect the assignment step solution since the assignment step requires only the prediction score for each subject corresponding to the K hyperplanes. Since the hyperplanes are defined as ${\mathbf{w}}_j={\displaystyle {\sum }_{i=1}^n{y}_i{\alpha }_{i,j}{\mathbf{x}}_i}$, the prediction score for each hyperplane wj can be simply calculated as:

$${\mathbf{w}}_j^T{\mathbf{x}}_l={\displaystyle \sum _{i=1}^n{y}_i{\alpha }_{i,j}{\mathbf{x}}_i^T{\mathbf{x}}_l}$$

which can be readily obtained from the Gram matrix that stores the inner products between data points. Furthermore, the bias terms b_j can be solved in the dual by:

$$b_j=y_l-{\displaystyle \sum _{i=1}^n{\alpha }_{i,j}{y}_i{\mathbf{x}}_i^T{\mathbf{x}}_l}$$

using any labeled sample (x_l, y_l) such that C > α_i,l > 0. The solutions for {α_i,j, b_j} can be directly used in Equation A.1 to solve for the assignments S⁻. In addition, the prediction for the dual version of HYDRA is:

$$y^{\ast }=\text{sign}\left(\underset{j}{min}{\displaystyle \sum _{i=1}^n{y}_i{\alpha }_{i,j}{\mathbf{x}}_i^T{\mathbf{x}}^{\ast }+b_j}\right)$$

Appendix B.1. Dual Symmetric Prediction

In the case of the symmetric version of the algorithm, the final prediction can be obtained as:

$$\begin{array}{r}{y}^{\ast }=\text{sign}[\left(\underset{j}{min}{\displaystyle \sum _{i=1}^n{y}_i{\alpha }_{i,j}^{+}{\mathbf{x}}_i^T{\mathbf{x}}^{\ast }+b_j^{+}}\right)\\ -\left(\underset{j}{min}{\displaystyle \sum _{i=1}^n{y}_i{\alpha }_{i,j}^{-}{\mathbf{x}}_i^T{\mathbf{x}}^{\ast }+b_j^{-}}\right)]\end{array}$$

Appendix C. List of Genetics Features Used

The SNPs used as features is given in table C.5. Two features were extracted from each subject for each SNP: the presence of the major-major and the major-minor alleles. Minor allele frequency (MAF) column in table C.5 denotes the likelihood of observing the rare minor allele in the population.

Table C.5.

Genetic features used in HYDRA to classify AD from Controls and discover subtypes of AD.

Genetic features used for Control vs. AD Classification/Clustering using HYDRA
SNPs associated with cognitive decline identified in Sherva et al. (2014).
a SNP	b Chr.	c Position	d Gene	e MAF	a SNP	b Chr.	c Position	d Gene	e MAF
rs2421847	1	171557600	PRRC2C	0.04	rs4836694	9	132939792	NCS1	0.11
rs12091371	1	240605052	FMN2	0.07	rs118048115	10	122279476	PPAPDC1A	0.04
rs6738962	2	80281173	CTNNA2	0.04	rs11023139	11	14224346	SPON1	0.05
rs78022502	2	128396167	LIMS2	0.06	rs61883963	11	14338703	RRAS2	0.06
rs538867	3	39513278	MOBP	0.03	rs34162548	11	14556220	PSMA1	0.05
rs9857727	3	51095028	DOCK3	0.1	rs326946	11	110499253	ARHGAP20	0.17
rs2668205	3	165493136	BCHE	0.03	rs147845115	12	51878760	SLC4A8	0.03
rs78647349	4	5237153	STK32B	0.04	rs61144803	12	94235165	CRADD	0.04
rs340635	4	87931404	AFF1	0.03	rs1399439	12	101221239	ANO4	0.04
rs113689198	5	109111327	MAN2A1	0.03	rs143258881	13	93945858	GPC6	0.03
rs112724034	5	109221026	PGAM5P1	0.03	rs17393344	13	109473946	MYO16	0.06
rs77636885	5	110719187	CAMK4	0.03	rs115102486	14	95764564	CLMN	0.03
rs116348108	5	118435127	DMXL1	0.04	rs74006954	15	27712644	GABRG3	0.03
rs143954261	5	126729450	MEGF10	0.04	rs17301739	15	58730639	LIPC	0.07
rs146579248	5	127382302	FLJ33630	0.04	rs8045064	16	24675589	FLJ45256	0.05
rs148763909	5	153837106	SAP30L	0.03	rs9934540	16	77876763	VAT1L	0.03
rs117780815	6	124326227	NKAIN2	0.03	rs62076103	17	45888374	OSBPL7	0.07
rs9494429	6	136288895	PDE7B	0.03	rs62076130	17	45905622	MRPL10	0.06
rs75253868	6	151102830	PLEKHG1	0.04	rs4794202	17	45930539	SP6	0.08
rs58370486	7	16707861	BZW2	0.03	rs117964204	17	48692082	CACNA1G	0.04
rs73071801	7	16811139	TSPAN13	0.04	rs72832584	17	59292436	BCAS3	0.05
rs1861525	7	25161602	CYCS	0.03	rs7245858	19	51430596	LOC390956	0.04
rs17172199	7	43377276	HECW1	0.08	rs34972666	20	2384972	TGM6	0.11
rs73660619	8	3088173	CSMD1	0.06	rs75617873	22	44526105	PARVB	0.03

SNPs associated with AD identified in Lambert et al. (2013)
a SNP	b Chr.	f Position	d Gene	MAF	a SNP	b Chr.	f Position	d Gene	e MAF
rs6656401	1	207692049	CR1	0.197	rs11218343	11	121435587	SORL1	0.039
rs35349669	2	234068476	INPP5D	0.488	rs983392	11	59923508	MS4A6A	0.403
rs6733839	2	127892810	BIN1	0.409	rs10498633	14	92926952	SLC24A4 - RIN3	0.217
rs10948363	6	47487762	CD2AP	0.266	rs17125944	14	53400629	FERMT2	0.092
rs11771145	7	143110762	EPHA1	0.338	rs3865444	19	51727962	CD33	0.307
rs28834970	8	27195121	PTK2B	0.366	rs4147929	19	1063443	ABCA7	0.19
rs9331896	8	27467686	CLU	0.379	rs429358	19	44908684	APOE	0.1492
rs10792832	11	85867875	PICALM	0.358	rs7412	19	44908822	APOE	0.07392
rs10838725	11	47557871	CELF1	0.316	rs7274581	20	55018260	CASS4	0.083

Abbreviations:

^aSNP — Single nucleotide polymorphism

^bChr. — Chromosome,

^cPosition — indicates base pair location in release 19, build 135 of the human genome in the dbSNP database,

^dGene — Genes located ±100 kb of the top SNP,

^eMAF — minor allele frequency.

^fPosition — indicates base pair location in release 19, build 37 of the human genome in the dbSNP database.