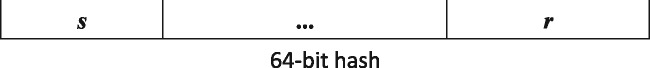ntCard: a streaming algorithm for cardinality estimation in genomics data

Abstract

Motivation

Many bioinformatics algorithms are designed for the analysis of sequences of some uniform length, conventionally referred to as k-mers. These include de Bruijn graph assembly methods and sequence alignment tools. An efficient algorithm to enumerate the number of unique k-mers, or even better, to build a histogram of k-mer frequencies would be desirable for these tools and their downstream analysis pipelines. Among other applications, estimated frequencies can be used to predict genome sizes, measure sequencing error rates, and tune runtime parameters for analysis tools. However, calculating a k-mer histogram from large volumes of sequencing data is a challenging task.

Results

Here, we present ntCard, a streaming algorithm for estimating the frequencies of k-mers in genomics datasets. At its core, ntCard uses the ntHash algorithm to efficiently compute hash values for streamed sequences. It then samples the calculated hash values to build a reduced representation multiplicity table describing the sample distribution. Finally, it uses a statistical model to reconstruct the population distribution from the sample distribution. We have compared the performance of ntCard and other cardinality estimation algorithms. We used three datasets of 480 GB, 500 GB and 2.4 TB in size, where the first two representing whole genome shotgun sequencing experiments on the human genome and the last one on the white spruce genome. Results show ntCard estimates k-mer coverage frequencies >15× faster than the state-of-the-art algorithms, using similar amount of memory, and with higher accuracy rates. Thus, our benchmarks demonstrate ntCard as a potentially enabling technology for large-scale genomics applications.

Availability and Implementation

ntCard is written in C ++ and is released under the GPL license. It is freely available at https://github.com/bcgsc/ntCard.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Many bioinformatics applications rely on counting or cataloguing fixed-length substrings of DNA/RNA sequences, called k-mers, generated from reads coming out of high-throughput sequencing platforms. This is a very important step in de novo assembly (Butler et al., 2008; Li et al., 2010; Salzberg et al., 2012; Simpson et al., 2009; Zerbino and Birney, 2008), multiple sequence alignment (Edgar, 2004), error correction (Medvedev et al., 2011; Heo et al., 2014), repeat detection (Simpson, 2014), SNP detection (Nattestad and Schatz, 2016; Shajii et al., 2016) and RNA-seq quantification analysis (Patro et al., 2014). The problem of counting k-mers has been well studied in the literature, including the Jellyfish (Marçais and Kingsford, 2011), BFCounter (Melsted and Pritchard, 2011), DSK (Rizk et al., 2013) and KMC (Deorowicz et al., 2015) algorithms. These tools need considerable computational resources and can be improved in terms of memory, disk space and runtime requirements for processing and obtaining the histogram of k-mer frequencies in large sets of DNA/RNA sequences. During the past few years, there have been many studies to improve the memory and time requirements for the k-mer counting problem. While a naïve approach would keep track of all possible k-mers in the input datasets, employing a succinct and compact data structure (Conway and Bromage, 2011), or a disk-based workflow (Deorowicz et al., 2015; Rizk et al., 2013) would reduce memory usage. Although the improved methods with efficient implementations have considerable impact on memory and time usage, they require processing all possible k-mers base-by-base and storing them in memory or disk. Therefore, the time and memory requirements for theses efficient solutions grow linearly with the input data size, and can take hours or days using terabytes of memory for large datasets. In the recent works by Chikhi-Medvedev (Chikhi and Medvedev, 2014) and Melsted-Halldórsson (Melsted and Halldórsson, 2014), the authors proposed methods to approximate the k-mer coverage histogram in large sets of DNA/RNA sequences, which are about an order of magnitude faster, and use only a fraction of the memory compared with previous k-mer counting algorithms. However, these methods still can take considerable amount of time for processing terabytes of high-throughput sequencing data, or may not provide the full histogram for k-mer abundance.

In this article, we present an efficient streaming algorithm, ntCard, for estimating the k-mer coverage histogram for large high-throughput sequencing genomics data. The proposed method requires fixed amount of memory, and runs in linear time with respect to the size of the input dataset. At its core, ntCard uses the ntHash algorithm (Mohamadi et al., 2016) to efficiently compute hash values for streamed sequences. It samples the calculated hash values to build a reduced representation multiplicity table describing the sample distribution, which it uses to statistically infer the population distribution. We compare the histograms estimated by ntCard with the exact k-mer counts of DSK (Rizk et al., 2013), and illustrate that the ntCard estimations are approximations within guaranteed intervals. We also compare the accuracy, runtime and memory usage of ntCard with the best available exact and approximate algorithms for k-mer count frequencies such as DSK (Rizk et al., 2013), KmerGenie (Chikhi and Medvedev, 2014), KmerStream (Melsted and Halldórsson, 2014) and Khmer (Irber and Brown, 2016).

2 Methods

Let’s first introduce the problem background and notations on streaming algorithms for identifying the distinct elements. Then we will derive a statistical model to estimate k-mer frequencies, and outline the generated model.

2.1 Background, notations and definitions

Streaming algorithms are algorithms for processing data that are too large to be stored in available memory, but can be examined online, typically in a single pass. There has been a growing interest in streaming algorithms in a wide range of applications, in different domains dealing with massive amounts of data. Examples include, analysis of network traffic, database transactions, sensor networks and satellite data feeds (Cormode and Garofalakis, 2005; Cormode and Muthukrishnan, 2005; Indyk and Woodruff, 2005).

Here, we propose a streaming algorithm for estimating the frequencies of k-mers in massive data produced from high-throughput sequencing technologies. Let f_i denote the number of distinct k-mers that appear i times in a given sequencing dataset. The k-mer frequency histogram is then the list of f_i, $i\ge 1$. The kth frequency moment F_k is defined as

$$F_k=\sum _{i=1}^{\infty }{i}^k.f_i$$ (1)

The numbers F_k provide useful statistics on the input sequences. For example, F₀ denotes the number of distinct k-mers appearing in the stream sequences, F₁ is the total number of k-mers in the input datasets, F₂ is the Gini index of variation that can be used to show the diversity of k-mers and $F_{\infty }$ results in the most frequent k-mer in the input reads.

There are streaming algorithms in the literature for estimating different kth frequency moments. The problem of estimating F₀, also known as distinct elements counting, has been addressed by the FM-Sketch (Flajolet and Martin, 1985) and K-Minimum Value (Bar-Yossef et al., 2002) algorithms. An F₂ estimation algorithm was first proposed in Alon et al. (Alon et al., 1999), and $F_{\infty }$ was investigated by Cormode and Muthukrishnan (Cormode and Muthukrishnan, 2005). These proposed algorithms can perform their estimations within a factor of ($1\pm \mathrm{ϵ}$) with a set probability using $O({\mathrm{ϵ}}^{-2}\hspace{0.17em}\text{log}\hspace{0.17em}(N))$ operations, where N is the number of distinct k-mers in the dataset (Melsted and Halldórsson, 2014).

2.2 Estimating k-mer frequencies, f_i

To estimate the k-mer frequencies, we use a hash-based approach similar to the KmerStream algorithm (Melsted and Halldórsson, 2014). KmerStream is based on the K-Minimum Value algorithm (Bar-Yossef et al., 2002), and it samples the data streams at different rates to select the optimal sampling rate giving the best result.

ntCard works by first hashing the k-mers in read streams, which it samples to build a reduced multiplicity table. After calculating the multiplicity table for sampled k-mers, it uses this table to infer the population histogram through a statistical model.

2.2.1 Hashing

ntCard utilizes the ntHash algorithm (Mohamadi et al., 2016) to efficiently compute the canonical hash values for all k-mers in DNA sequences. ntHash is a recursive, or rolling, hash function in which the hash value for the next k-mer in an input sequence of length l ($l\ge k$) is derived from the hash value of the previous k-mer.

$$H_i=ro{l}^1{H}_{i-1}\hspace{0.17em}\oplus \hspace{0.17em}ro{l}^{k}h(r[i-1])\hspace{0.17em}\oplus \hspace{0.17em}h(r[i+k-1])$$ (2)

This calculation is initiated for the first k-mer in the sequence using the base function

$$H_0=ro{l}^{k-1}h(r[0])\hspace{0.17em}\oplus \hspace{0.17em}ro{l}^{k-2}h(r[1])\hspace{0.17em}\oplus \hspace{0.17em}\dots \hspace{0.17em}\oplus \hspace{0.17em}h(r[k-1])$$ (3)

In the above equations ⊕ is bitwise exclusive or operation, rol is cyclic binary left rotation, and h is a seed table mapping the nucleotide letters to a pre-designed 64-bit random integers. The 64-bit random integers are designed in a way that in every bit position in the 64-bit random seeds, there is equal number of 0’s and 1’s spread randomly. The time complexity of ntHash for a sequence of length l is $O(k+l)$, compared to O(kl) for regular hash functions.

To compute the reverse-complement and consequently the canonical hash values (i.e. hash values invariant of reverse-complementation), ntHash modifies the seed table h by placing the complement nucleotide seeds within a fixed distance d of the corresponding nucleotide seeds, and then computes the hash values using

$$\begin{array}{c}{\overline{H}}_0=h(r[0]+d)\hspace{0.17em}\oplus \hspace{0.17em}ro{l}^{1}h(r[1]+d)\hspace{0.17em}\oplus \hspace{0.17em}\cdots \hspace{0.17em}\oplus \hspace{0.17em}ro{l}^{k-1}h(r[k-1]+d)\hfill \\ {\overline{H}}_i=ro{r}^1{\overline{H}}_{i-1}\hspace{0.17em}\oplus \hspace{0.17em}ro{r}^{1}h(r[i-1]+d)\hspace{0.17em}\oplus \hspace{0.17em}ro{l}^{k-1}h(r[i+k-1]+d)\hfill \end{array}$$ (4)

Where ror is a cyclic binary right rotation. We have shown earlier that ntHash has substantial speed improvement over conventional approaches, while retaining a near-ideal hash value distribution (Mohamadi et al., 2016).

2.2.2 Sampling and building the multiplicity table

After computing the hash values for k-mers in DNA streams using ntHash, ntCard segments the 64-bit hash values into three parts as shown in Figure 1. It uses the left s bits in the 64-bit hash value for its sampling criterion, picking k-mers for which these bits are zero, which results in an average sampling rate of $1/2^s$. Earlier, we have demonstrated that ntHash bits are independently and uniformly distributed (Mohamadi et al., 2016). Consequently, 1/2 of the hash values start with 0, 1/4 of them will start with two zeros, and $1/2^s$ start with s zeros. Therefore, by selecting the hash values starting with s zeros, we build our sample with the cardinality of $1/2^s$.

Fig. 1.

64-bit hash value generated by ntHash. The s left bits are used for sampling the k-mers in input datasets and the r right bits are used as resolution bit for building the reduced multiplicity table, with $r+s<64$

Also building on the statistical properties of computed hash values, we use the right r bits, called the resolution bits, to build a k-mer multiplicity table for sampled k-mers. To do so, we use an array of size $2^r$ to keep observed k-mer counts. The resolution bits of each hash value serve as the index for the count array. We note that, each entry in the array is an approximate count of the sampled k-mers, since there may be multiple k-mers with the same r bit pattern, resulting in count collisions.

Ideally, one would want a hash function that generates a unique hash value for every k-mer, say using infinite number of bits. Also, if one has access to infinite memory to hold all these values, the ideal values for s and r would be zero and infinity, respectively. Since we do not in practice have access to such resources, we use 64-bit hash values, subsample our dataset by $1/2^s$, and tabulate $2^r$ patterns (some of which with zero counts). To infer the population histogram from these measurements, we derived the following statistical model.

Let’s denote the count array with $2^r$ entries by $t^{(r)}$. If we were to extend our resolution to r + 1, we would obtain a new count array, $t^{(r+1)}$, with $2^{r+1}$ entries, twice the size of the current array $t^{(r)}$. There is a relation between the entries of the current array $t^{(r)}$ and the new count array $t^{(r+1)}$. By folding the first half of $t^{(r+1)}$ with its second half, we can construct $t^{(r)}$ using

$$t_n^{(r)}=t_n^{(r+1)}+t_{2^r+n}^{(r+1)},\forall n\in [0,\dots ,2^r-1]$$ (5)

where $t_n^{(r)}$ denotes the count for entry n in the table $t^{(r)}$.

Next, if we let $p_i^{(r)}$ be the relative frequency of counts $i\ge 0$ in table $t^{(r)}$, with ${\sum }_{i=0}^{\infty }{p}_i^{(r)}=1$, we can make the following observations. An entry of $t_i^{(r)}=0$ is only possible if $t_i^{(r+1)}=0$ and $t_{2^r+i}^{(r+1)}=0$. Since there is no a priori reason why the first and second half of $t^{(r+1)}$ should have different count distributions, we can relate the frequencies of zero counts in the two tables through

$$p_0^{(r)}={(p_0^{(r+1)})}^2$$ (6)

Similarly, a count of one in $t^{(r)}$ is only possible if the first half of $t^{(r+1)}$ is a one and the second half a zero corresponding to that entry, or vice versa, which we can write mathematically as

$$p_1^{(r)}=2p_0^{(r+1)}{p}_1^{(r+1)}$$ (7)

This can be generalized as

$$p_i^{(r)}=\sum _{i\prime =0}^i{p}_{i^{\prime }}^{(r+1)}{p}_{i-i^{\prime }}^{(r+1)}$$ (8)

Algorithm 1.

The ntCard algorithm

1: function Update(k-mer)

2:  for each read seq do

3:   for each k-mer in seq do

4:    $h\leftarrow$ntHash (k-mer) ▹ Compute 64-bit h using ntHash

5:    if$h_{64:64-s+1}=0^s$then ▹ Checking the s left bit in h

6:     $i\leftarrow h_{r:1}$ ▹ r is resolution parameter

7:     $t_i\leftarrow t_i+1$

8: function Estimate

9:  for$i\leftarrow$ 1 to $2^r$ do

10:   $p_{t[i]}\leftarrow p_{t[i]}+1$

11:  for$i\leftarrow$ 1 to t_max do

12:   $p_i\leftarrow p_i/2^r$

13:  $F_0=-\ln p_0\times 2^{s+r}$ ▹ F₀ estimate

14:  for$i\leftarrow$ 1 to t_max do

15:   ${\widehat{f}}_i\leftarrow \frac{-p_i}{p_0\ln p_0}-\frac{1}{i}{\sum }_{j=1}^{i-1}\frac{j{p}_{i-j}{\widehat{f}}_j}{p_0}$ ▹ Relative estimates

16:  for$i\leftarrow$ 1 to t_max do

17:   $f_i\leftarrow {\widehat{f}}_i\times F_0$ ▹ f_i estimates

18:  return$f,F_0$

Note that, Equations (6)–(8) can be solved for $p_i^{(r+1)}$ through the recursive formula

$$p_i^{(r+1)}=\{\begin{array}{cc}{\left(p_0^{(r)}\right)}^{1/2}\hfill & \hspace{0.17em}\text{for}\hspace{0.17em}i=0\hfill \\ \frac{p_1^{(r)}}{2p_0^{(r+1)}}\hfill & \hspace{0.17em}\text{for}\hspace{0.17em}i=1\hfill \\ \frac{1}{2p_0^{(r+1)}}\left(p_i^{(r)}-\sum _{i\prime =1}^{i-1}{p}_{i^{\prime }}^{(r+1)}{p}_{i-i^{\prime }}^{(r+1)}\right)\hfill & \hspace{0.17em}\text{for}\hspace{0.17em}i>1\hfill \end{array}$$ (9)

Now, just like extensions from a resolution of r to r + 1, resolution to r + x is also mathematically tractable. Ultimately, we would be interested in relating the observed count frequencies $p_i^{(r)}$ to the count frequencies $p_i^{(\infty )}$, and in calculating k-mer multiplicity frequencies

$${\widehat{f}}_i=\frac{p_i^{(\infty )}}{1-p_0^{(\infty )}}$$ (10)

For example, for i = 1, this can be calculated as

$${\widehat{f}}_1=\underset{x\to \infty }{\lim }\frac{\frac{p_1^{(r)}}{2^x{(p_0^{(r)})}^{\frac{2^x-1}{2^x}}}}{1-{(p_0^{(r)})}^{\frac{1}{2^x}}}=\frac{-p_1^{(r)}}{p_0^{(r)}\ln p_0^{(r)}}$$ (11)

and for i = 2 as

$${\widehat{f}}_2=\frac{-p_0^{(r)}{p}_2^{(r)}+\frac{1}{2}{(p_1^{(r)})}^2}{{(p_0^{(r)})}^2\ln p_0^{(r)}}$$ (12)

In general, for ${\widehat{f}}_i,i\ge 1$, we can write the following equation

$$\begin{array}{cc}{\widehat{f}}_i=\hfill & \frac{1}{{(p_0^{(r)})}^i\ln p_0^{(r)}}\sum _{j=0}^{i-1}\frac{{(-1)}^{i+j}{(p_0^{(r)})}^j}{i-j}(\hfill \\ \hfill & {\displaystyle \sum _{\begin{array}{l}\forall (l,u)\in {\mathbb{Z}}^2\hspace{0.17em}\mathrm{s}.\mathrm{t}.\hspace{0.17em}\\ \sum _k{u}_k=i-j\\ \sum _k{l}_k{u}_k=i\end{array}}}\prod _{k=1}^{\left|u\right|}\left(\begin{array}{c}i-j-{\sum }_{k^{\prime }=0}^{k-1}{u}_{k\prime }\\ u_k\end{array}\right){(p_{l_k}^{(r)})}^{u_k})\hfill \end{array}$$ (13)

where $u_0=0,\hspace{0.17em}{u}_k\ne u_{k\prime }$ for all $k\ne k\prime$, and $\left|u\right|=\underset{k}{\arg \max }\left\{u_k\right\}$.

This complex-looking formula can also be written in the following recursive form

$${\widehat{f}}_i=\frac{-p_i^{(r)}}{p_0^{(r)}\ln p_0^{(r)}}-\frac{1}{i}\sum _{j=1}^{i-1}\frac{j{p}_{i-j}^{(r)}{\widehat{f}}_j}{p_0^{(r)}}$$ (14)

The two terms of this equation can be interpreted as follows. The first term corresponds to count frequencies i in table $t^{(r)}$ assuming none of the entries collided with any non-zero entries through folding rounds from $\underset{x\to \infty }{\lim }(r+x)$ to r. The second term is a correction to the first term, accounting for all collisions of $(i-j),0<j<i$ and j, result of which is a count frequency of i.

Now, we can derive an estimate for F₀ by a similar approach we used for relative frequencies.

$$F_0=\underset{x\to \infty }{\lim }{2}^s(1-p_0^{(r+x)})2^{r+x}$$ (15)

This formula has three terms inside the limit, the first one, $2^s$, correcting for the subsampling we have performed. The second term is the frequency of non-zero entries in table $t^{(r+x)}$, and the third entry is the normalizing factor that was used to convert occurrences of counts in this table to their frequencies, $p_i^{(r+x)}$. Taking this limit then gives

$$F_0=-2^{s+r}\ln p_0^{(r)}$$ (16)

Using the Equations (14) and (16) we can obtain the k-mer coverage frequencies as outlined in Algorithm 1 with a binomial proportion confidence interval. The workflow of ntCard algorithm is also presented in Supplementary Figure S1.

2.3 Implementation details

Selection of the resolution parameter, r, represents a tradeoff between accuracy and computational resources. While it should not be too low to avoid poor estimates of frequency counts, it should not be too high for feasible peak memory usage. In our experience, values r > 20 work well for accurate estimates, and memory usage peaks above 1 GB for $r\ge 28$. We have set the default value to r = 27. We have also observed that estimations based on only t_r, without applying the statistical model, has higher error rates due to count collisions, as expected.

If input reads or sequences contain ambiguous bases, or characters other than $\{A,C,G,T\}$, ntCard ignores them in the hashing stage. This is performed as a functionality of ntHash algorithm. When ntHash encounters a non-ACGT character it can jump over the ambiguous base, and restarts the hashing procedure from the first valid k-mer containing only ACGT characters.ntCard is written in C ++ and parallelized using OpenMP for multi-threaded computing on a single computing node. As input, it gets the set of sequences in FASTA, FASTQ, SAM and BAM formats. The input sequences can also be in compressed formats such as.gz and.bz formats. ntCard is distributed under GNU General Public License (GPL). Documentation and source code are freely available at https://github.com/bcgsc/ntCard.

3 Results

3.1 Experimental setup

To evaluate the performance and accuracy of ntCard, we downloaded the following publicly available sequencing data.

• The Genome in a Bottle (GIAB) project (Zook et al., 2016) sequenced seven individuals using a large variety of sequencing technologies. We downloaded 2x250 bp paired-end Illumina whole genome shotgun sequencing data for the Ashkenazi mother (HG004).

• We downloaded a second H. Sapiens dataset from the 1000 Genomes Project, for the individual NA19238 (SRA:ERR309932).

• To represent a larger problem, we used the white spruce (Picea glauca) genome sequencing data that represents the genotype PG29 (Warren et al., 2015) (accession number: ALWZ0100000000 and PID: PRJNA83435).

The information of each dataset including the number of sequences, size of sequences, total number of bases and total input size of datasets is presented in Table 1. To evaluate the performance of ntCard, we compare it to KmerGenie, KmerStream and Khmer in terms of accuracy of estimates, runtime and memory usage. We also compare the accuracy of our results with DSK, which is an exact k-mer counting tool. Results were obtained on computing nodes with 48 GB of RAM and dual Intel Xeon X5650 2.66GHz CPUs with 12 cores. The operating system on each node was Linux CentOS 5.4.

Table 1.

Dataset specification

Dataset	Read number	Read length	Total bases	Size
HG004	868,593,056	250 bp	217,148,264,000	480 GB
NA19238	913,959,800	250 bp	228,489,950,000	500 GB
PG29	6,858,517,737	250 bp	1,714,629,434,250	2.4 TB

All five tools are run with their default parameters, and the parameters related to the resource usage are set in a way to utilize the maximum capacity on each computing node as described in Supplementary Data. For example, all tools are run in multi-threaded mode with the maximum number of threads available on the computer.

3.2 Accuracy

In Tables 2–4, we see the results of DSK, ntCard, KmerGenie, KmerStream, and Khmer for distinct number of k-mers, F₀, as well as the number on singletons, f₁, on three datasets. We compared the accuracy of estimated counts from ntCard, KmerGenie, KmerStream and Khmer with exact counts from DSK. We see that, for all k-mer lengths, ntCard computes F₀ and f₁ for all three datasets with error rates less than 0.7%. In comparison, the error rates of KmerGenie, KmerStream and Khmer can be up to 17%, 9% and 11%, respectively. Note that, the Khmer algorithm only estimates the total number of distinct k-mers, F₀. The full results from all algorithms other than DSK are presented in Supplementary Tables S1–S3.

Table 2.

Accuracy of algorithms in estimating F₀ and f₁ for HG004 reads

k	DSK		ntCard	KmerGenie	KmerStream	Khmer
32	f1	13,319,957,567	0.01%	0.97%	7.04%	–
	F0	16,539,753,749	0.02%	0.64%	5.12%	0.67%
64	f1	17,898,672,342	0.02%	0.35%	0.73%	–
	F0	21,343,659,785	0.00%	0.22%	0.66%	0.15%
96	f1	18,827,062,018	0.36%	0.87%	0.00%	–
	F0	22,313,944,415	0.24%	0.69%	0.05%	0.31%
128	f1	18,091,241,186	0.36%	0.76%	0.40%	–
	F0	21,555,678,676	0.25%	0.62%	0.20%	0.30%

The DSK column reports the exact k-mer counts, and columns for the other tools report percent errors.

Table 3.

Accuracy of algorithms in estimating F₀ and f₁ for NA19238 reads

k	DSK		ntCard	KmerGenie	KmerStream	Khmer
32	f1	14,881,561,565	0.00%	0.53%	6.36%	–
	F0	18,091,801,391	0.00%	0.40%	4.64%	1.82%
64	f1	19,074,667,480	0.02%	0.75%	0.68%	–
	F0	22,527,419,136	0.01%	0.77%	0.65%	1.22%
96	f1	19,420,503,673	0.22%	0.66%	0.09%	–
	F0	22,932,238,161	0.16%	0.66%	0.07%	0.46%
128	f1	17,902,027,438	0.21%	0.85%	0.19%	–
	F0	21,421,517,759	0.13%	0.76%	0.03%	1.05%

The DSK column reports the exact k-mer counts, and columns for the other tools report percent errors.

Table 4.

Accuracy of algorithms in estimating F₀ and f₁ for PG29 reads

k	DSK		ntCard	KmerGenie	KmerStream	Khmer
32	f1	27,430,910,938	0.02%	15.33%	9.41%	–
	F0	42,642,198,777	0.01%	11.02%	7.37%	8.86%
64	f1	44,344,130,469	0.04%	16.36%	2.61%	–
	F0	67,800,291,613	0.02%	11.14%	1.73%	11.18%
96	f1	43,300,244,443	0.66%	17.51%	0.73%	–
	F0	69,855,690,006	0.46%	11.13%	0.57%	9.36%
128	f1	32,089,613,024	0.40%	14.82%	0.06%	–
	F0	58,195,246,941	0.30%	8.35%	0.27%	7.39%

The DSK column reports the exact k-mer counts, and columns for the other tools report percent errors.

Compared to ntCard and KmerStream, Khmer and KmerGenie estimates for distinct number of k-mers, F₀, have the highest error rates (>7%) on PG29 data; though, for HG004 and NA19238, Khmer estimates F₀ with lower error rates, and KmerGenie has very accurate estimates with error rates <1% for all k values. On all three datasets, KmerStream has more accurate estimates for longer k-mers, where error rates increasing rapidly for shorter k-mers. Although ntCard generally has the opposite trend, it also has the most stable performance for all three datasets. Except for k = 128 bp on NA19238 and PG29, and k = 96 bp on NA19238 and HG004, ntCard consistently displays the best accuracy both for F₀ and f₁, as indicated by the bold entries in Tables 2–4.

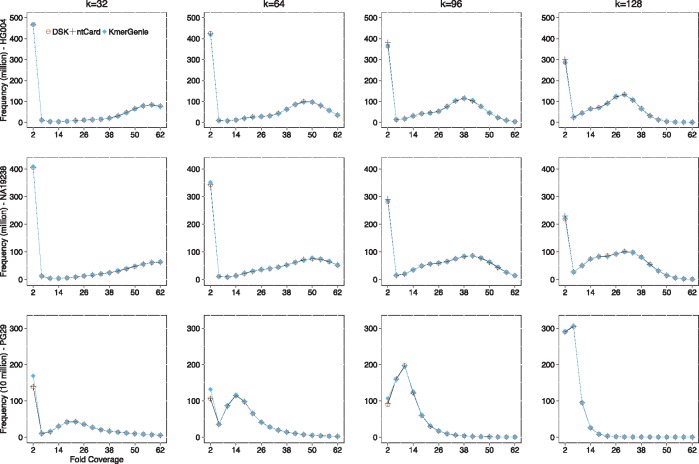
We have also evaluated the accuracy of full k-mer frequency histograms of ntCard on all three datasets with different k values. Since the KmerStream algorithm only computes estimates for F₀ and f₁ and Khmer only estimates F₀, we could only compare the accuracy of the ntCard histogram with the estimated results of KmerGenie and the exact histogram from DSK method. Figure 2 shows the k-mer frequency histograms of DSK, ntCard, and KmerGenie for all three datasets with four k values, $\{32,64,96,128\}$. Since the results of f₁ have already been presented in Tables 2–4, and since $f_2\mathrm{\dots }{f}_{62}\ll f_1$, the histograms in Figure 2 show the k-mer frequencies starting from f₂. The exact numbers of $f_1\mathrm{\dots }{f}_{62}$ for DSK, ntCard, and KmerGenie on all three datasets are presented in Supplementary Tables S4–S15. From Figure 2 and Supplementary Tables S4–S15, we can see ntCard estimates the k-mer frequency histograms for all three datasets more accurate than KmerGenie.

Fig. 2.

k-mer frequency histograms for human genomes HG004 and NA19238 (rows 1 and 2, respectively), and the white spruce genome PG29 (row 3). We have used DSK k-mer counting results as our ground truth in evaluation (orange circle data points). The k-mer coverage frequency results, $f_2\mathrm{..}{f}_{62}$ of ntCard and KmerGenie for different values of $k=32,64,96,128$ (the four columns from left to right) are shown with the symbols (+) and ($\diamond$), respectively

3.3 Runtime and memory usage

We have calculated the memory usage of all benchmarked tools. DSK uses both main memory and disk space for counting k-mers, and therefore we obtained both values for it. We should also mention that DSK was executed on compute nodes equipped with solid-state drives (SSD). This helps the runtime of DSK be greatly reduced with the SSD and multi-threaded parallelism. The memory usage for DSK on all three datasets was the same at about 20 GB of RAM, while the disk space usage was 500 GB for human genomes HG004 and NA19238, and 1 TB for the white spruce genome PG29.

The memory usage of KmerGenie to estimate the full k-mer frequency histograms for all datasets was about 200 MB of RAM. KmerStream uses 2-bit counters to estimate F₀ and f₁, resulting in lower memory requirement. The memory usage for KmerStream on all three datasets was about 65 MB of RAM. The Khmer algorithm requires the lowest amount of memory among all algorithms but only estimates F₀. It requires about 15 MB of RAM to estimate the total number of distinct k-mers in all three datasets. The memory requirement of ntCard for all three datasets was about 500 MB of RAM, although we note that it computes the full k-mer multiplicity histogram. We have also implemented a special runtime parameter to only compute the total number of distinct elements, F₀, in which case it requires about 2 MB of RAM.

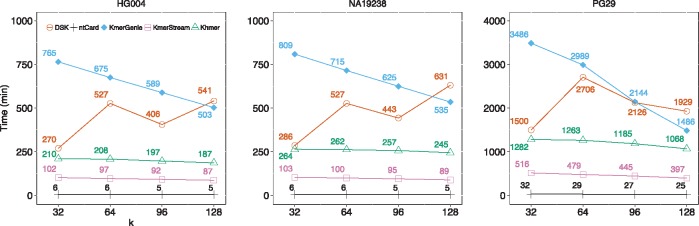
Figure 3 shows the runtime of all methods on the experimented datasets with different k values from 32 to 128. The runtime of ntCard to obtain the full k-mer frequency histograms for human genome datasets (HG004, NA19238) is about 6 mins. For KmerStream, it takes about 100 mins to obtain F₀ and f₁ on human genome datasets, while this is about 200 mins for Khmer to estimate just the total number of distinct k-mers, F₀. DSK and KmerGenie take up to 600 and 800 minutes, respectively, to compute the k-mer coverage histograms for human genome datasets. For the white spruce PG29 dataset, ntCard requires about 30 mins to estimate k-mer frequency histograms, while for KmerStream it takes about 450 mins to obtain F₀ and f₁. The Khmer takes longer time about 1200 mins to estimate F₀. DSK can take up to 2700 mins to compute the k-mer frequency histograms and this number is 3400 mins for KmerGenie to estimate k-mer coverage histograms. We should note that ntCard, KmerGenie and KmerStream algorithms have an option to pass multiple k values and compute multiple k-mer coverage histograms in a single run. This option will reduce the amortized runtime per k value, but it will increase the memory usage. From the runtime results, we see ntCard estimates the full k-mer coverage frequency histograms >15× faster than the closest competitor, KmerStream, which only computes F₀ and f₁. Supplementary Figure S2 shows the runtime performance versus the number of threads for the ntCard algorithm. In our experiments and computing environment, approximately one third of the ntCard runtime is spent on reading input datasets, and the rest on computing k-mer coverage histograms. Therefore I/O efficiency, which is system and architecture dependent, has a considerable impact on the runtime performance of ntCard.

Fig. 3.

Runtime of DSK, ntCard, KmerGenie, KmerStream and Khmer for all three datasets, HG004, NA19238 and PG29. We have calculated the runtime of all algorithms for different values of k in $\{32,64,96,128\}$. As we see in the plots, ntCard estimates the full k-mer coverage frequency histograms >15× faster than KmerStream

4 Discussion

With growing throughput and dropping cost of the next generation sequencing technologies, there is a continued need to develop faster and more effective bioinformatics tools to process and analyze data associated with them. Developing algorithms and tools that analyze these huge amounts of data on the fly, preferably without storing intermediate files, would have many benefits in a broad spectrum of genomics projects such as de novo genome and transcriptome assembly, sequence alignment, repeat detection, error correction and downstream analysis.

In this work, we introduced the ntCard streaming algorithm for estimating the k-mer coverage frequency histogram for high-throughput sequencing genomics data. It employs the ntHash algorithm for hashing all k-mers in DNA/RNA sequences efficiently, samples the k-mers in datasets based on the k-mer hashes, and reconstructs the k-mer frequencies using a statistical model. Using an amount of memory comparable to similar tools, ntCard estimates k-mer frequency histogram for massive genomics datasets, several folds faster than the state-of-the-art approaches.

Sample use cases of ntCard include tuning runtime parameters in de Bruijn graph assembly tasks such as optimal k value for the assembly, and setting parameters in applications utilizing the Bloom filter data structure. ntCard has been used in the new version of our genome assembly software package, ABySS 2.0 (Jackman et al., 2016), to determine the values for total memory size and number of hash functions. It has been also utilized to set the Bloom filter sizes in BioBloom tools (Chu et al., 2014), which is a general use fast sequence categorization tool utilizing Bloom filters. Using ntCard these tools are able to get the total number of distinct k-mers F₀, as well as the number of k-mers above a certain multiplicity threshold. The k-mer coverage histograms computed by ntCard can be also used as input to utilities like GenomeScope (http://qb.cshl.edu/genomescope/) for estimating genome sizes, sequencing error rates, repeat contents, and heterozygosity of genomes (Chikhi and Medvedev, 2014; Marçais and Kingsford, 2011; Melsted and Halldórsson, 2014; Simpson, 2014).

We expect ntCard to provide utility in efficiently characterizing certain properties of large read sets, helping quality control pipelines and de novo sequencing projects.