Blind Source Separation for Unimodal and Multimodal Brain Networks: A Unifying Framework for Subspace Modeling

Abstract

In the past decade, numerous advances in the study of the human brain were fostered by successful applications of blind source separation (BSS) methods to a wide range of imaging modalities. The main focus has been on extracting “networks” represented as the underlying latent sources. While the broad success in learning latent representations from multiple datasets has promoted the wide presence of BSS in modern neuroscience, it also introduced a wide variety of objective functions, underlying graphical structures, and parameter constraints for each method. Such diversity, combined with a host of datatype-specific know-how, can cause a sense of disorder and confusion, hampering a practitioner’s judgment and impeding further development.

We organize the diverse landscape of BSS models by exposing its key features and combining them to establish a novel unifying view of the area. In the process, we unveil important connections among models according to their properties and subspace structures. Consequently, a high-level descriptive structure is exposed, ultimately helping practitioners select the right model for their applications. Equipped with that knowledge, we review the current state of BSS applications to neuroimaging.

The gained insight into model connections elicits a broader sense of generalization, highlighting several directions for model development. In light of that, we discuss emerging multi-dataset multidimensional (MDM) models and summarize their benefits for the study of the healthy brain and disease-related changes.

I. Introduction

Blind source separation (BSS) methods [1] have been widely used in the study of the brain. They can be adapted and made compatible with a number of brain imaging, genetics, and non-imaging modalities, fueling applications to neurophysiological measurements such as magnetic resonance imaging (MRI)—both structural (sMRI) [2] and functional (fMRI) [3], [4]—magnetoencephalography (MEG) [5], electroencephalography (EEG) [6], diffusion weighted MRI (DWI) [7], copy-number variation (CNV) [8], single nucleotide polymorphism (SNP) [9], methylation [10], [11], metabolomics [12], and questionaires [13], [14] among others. Continued technological advancements in brain structure and function assessment [15]–[18] have fostered the development of a growing collection of BSS methods and tools. Their applications range from the study of human brain deficits associated with certain mental disorders to the neurophysiological associations with cognitive and behavioral measures.

Despite such wide application range, selecting the right BSS tool for a given problem—or developing a new one—can quickly turn into a daunting task if an understanding of the underlying structure of the area is missing. Our work addresses this issue. It highlights fundamental connections among BSS models and offers a novel, intuitive taxonomy, organizing BSS problems into specialized subproblems. Also, our investigation of various assumptions embedded within BSS models refines this structure, revealing hidden connections and differences.

To achieve that, we let BSS refer to any method for simultaneous model (or system) inversion of one or multiple datasets that uses only the observed measurements (or outputs). Then, we put a number of methods originating from different areas in perspective, focusing on three key properties: the number of datasets allowed, the grouping of sources within a dataset, and the use of second-, higher-, or all-order statistics. As a result, unanticipated connections and differences among seemingly unrelated methods are revealed, culminating in a new unified framework for BSS model selection and development. A hierarchy of increasing model complexity ensues, providing a sensible guide to practitioners in their domain-specific contexts. Model weaknesses and strengths, as well as key differences and shared features, stand out, exposing a high-level descriptive structure useful for researchers either interested in pursuing new, unexplored directions, or simply trying to identify candidate models for an application. These properties are finally summarized in a set of systematic, yet simple, modeling choices, exposing new insight into future directions for the area and advancing a novel unifying view.

Our unifying framework describes a new, largely under-investigated class of problems, paving a way for development of new models. These models are anticipated to be highly flexible, combining and expanding key features and subspace structures from existing models. We expect that these models will play a key role in neuroimaging research and improve how we understand the intricacies of the human brain, laying out a promising new path for future research developments that could easily extend beyond neuroimaging applications.

We introduce the unifying framework in section II. We then describe how the unifying framework specializes to different models and methods in section III. We discuss future directions in section IV and provide concluding remarks in section V.

II. A Unified Framework for Subspace Modeling and Development

The wide range of applications utilizing BSS methods to capture and analyze brain networks requires a fairly broad understanding of the area by the average researcher. The terminology and notation from different fields where methods have originally been developed makes it an even harder task. Not surprisingly, the use of a BSS tool for a certain application is often unintentionally limited to what has already been applied to a certain datatype or disease. Our belief is that users and developers of BSS tools can largely benefit from a clear and intuitive description of the underlying structure among BSS methods. This is our guiding motivation throughout.

A. The Structure of BSS Problems

The BSS problem is broadly defined as “recovering unobservable source signals s from measurements x (i.e., data), with no knowledge of the parameters θ of the generative system x = f (s, θ).” It can be organized into subproblems depending on whether x contains either single or multiple datasets, and whether or not subsets of s (within the same dataset) group together to form one or more multidimensional sources. We propose a novel taxonomy to define four general BSS subproblems, as follows:

1. Single dataset unidimensional (SDU): x consists of a single dataset whose sources are not grouped, e.g., independent component analysis (ICA) [19]–[21] and second order blind identification (SOBI) [22], [23], as in section III-A1;

2. Multiple dataset unidimensional (MDU): x consists of one or more datasets but no multidimensional sources occur within any of the datasets, although multidimensional sources containing a single source from each dataset may occur, e.g., canonical correlation analysis (CCA) [24], partial least squares (PLS) [25], and independent vector analysis (IVA) [26], [27], discussed in III-A2;

3. Single dataset multidimensional (SDM): x consists of a single dataset with one or more multidimensional sources, e.g., multidimensional independent component analysis (MICA) [28], [29] and independent subspace analysis (ISA) [30], [31], discussed in III-A3;

4. Multiple dataset multidimensional (MDM): x contains one or more datasets, each containing one or more multidimensional sources that may group further with single or multidimensional sources from the remaining datasets, e.g., multidataset independent subspace analysis (MISA) [32], [33] and joint independent subspace analysis (JISA) [34], discussed in III-A4.

Under these definitions, subproblems are contained within each other, as described in Fig. 1, revealing a natural hierarchical structure among them. Accordingly, the generative models describing data generation from sources should follow the same hierarchy. Problem specification, therefore, contributes to the description of f (·) itself and some properties of its parameters (θ) and inputs (s) in generative models. This provides a new perspective about basic connections among models following from problem specification.

Fig. 1. Venn diagram of the structure of BSS subproblems.

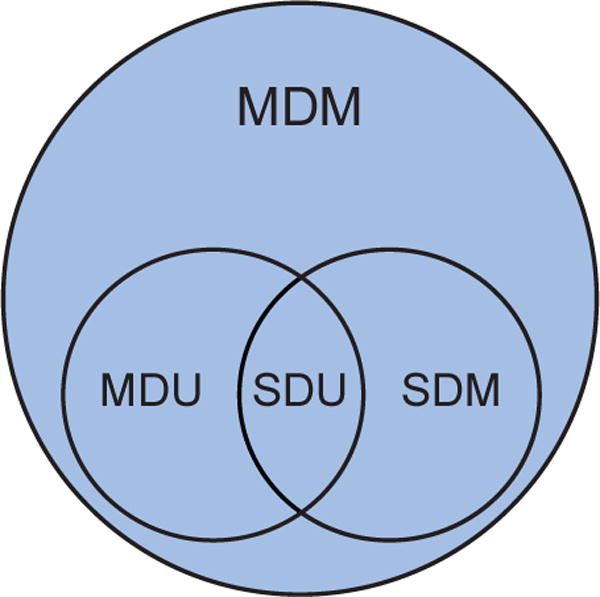
Single dataset unidimensional (SDU) problems are special cases of multiple dataset unidimensional (MDU), single dataset multidimensional (SDM), and multiple dataset multidimensional (MDM) problems, while MDU and SDM problems are special cases of MDM problems.

In the presence of noise, x = f (s, θ) + e, where the sensor noise e is typically Gaussian. Noisy system inversion has been well studied, especially in linear systems, with results such as the Wiener filter, which defines a system inversion ŝ = g(s, θ, x) that minimizes ${\Vert \mathbf{s}-\widehat{\mathbf{s}}\Vert }_2$ for known s and θ Source estimation strategies for noisy cases are different (see section II-D) and largely tailored to SDU problems. Still, noise-free BSS models are often fairly robust to noise.

B. Assumptions that Drive Model Hierarchy

A generative BSS model is completely defined only when the parameters (θ) and source signals (s) are fully described according to three sets of assumptions. The leading assumption is the presence of latent source signals in the data. Additional assumptions act to counter ill-conditions, allowing sources to be identified from data. These assumptions, combined with the problem hierarchy, induce a set of basic modeling choices, as described below and summarized in Table I.

TABLE I.

Typical choices in BSS modeling. Choices relevant to this work are color-coded to match Fig. 2.

Model Property	Choice to Make	Options
Sources	Model order	C ∈ ℕ (per dataset)
Mixture	Mapping	linear or non-linear
	Layout	fully-connected or structured
(optional)	Parameter constraints	Orthogonality, sparsity, match a template, min. total variation
Statistical Relationship	$\mathbf{Subsets}$ (which)	$\mathbf{grouping of sources}$ and K ≤ C
	Interactions (how)	graph (directed or not, acyclic/cyclic, tree/hierarchy), and/or sample dependence
	Type of Stats. (how)	$\mathbf{SOS}$, $\mathbf{HOS}$, or $\mathbf{both}$
(optional)	Source constraints	Sparsity, match a template, min. total variation

Presence of sources

Given N observations of M ≥ 1 datasets, we wish to identify an unobservable latent source random vector (r.v.) $\mathbf{s}={\left[{\mathbf{s}}_1^T\cdots {\mathbf{s}}_M^T\right]}^T,{\mathbf{s}}_m={\left[s_1\cdots s_{C_m}\right]}^T$ that relates to the observed r.v. $\mathbf{x}={\left[{\mathbf{x}}_1^T\cdots {\mathbf{x}}_M^T\right]}^T,{\mathbf{x}}_m={\left[x_1\cdots x_{V_m}\right]}^T$ via a vector function f (s, θ). Learning both s and f (·, θ) blindly—without prior knowledge of either of them—requires choosing the number of sources C_m in each dataset, with compound $\overline{C}={\displaystyle {\sum }_{m=1}^M{C}_m}$ and $\overline{V}={\displaystyle {\sum }_{m=1}^M{V}_m}$.

Mixture function

The assumptions imposed on the vector function f (·, θ) are characterized by the following properties:

1. Mapping. Mixture functions are mappings of either a linear or non-linear type. A linear function is any linear transformation by square or rectangular matrices (A) with $\mathbf{x}=\mathbf{f}\left(\mathbf{s},\mathit{\theta }\right)=\mathbf{As}={\displaystyle {\sum }_{j=1}^{\overline{C}}{\mathbf{a}}_j{s}_j}$, and $\mathit{\theta }=\mathbf{A}=\left[{\mathbf{a}}_1\cdots {\mathbf{a}}_{\overline{C}}\right]$. For quadratic functions, $\mathbf{x}=\mathbf{f}(\mathbf{s},\mathbf{A},{\mathbf{Q}}_{v,v=\mathrm{1..}\overline{V}})=\mathbf{As}+\mathbf{z}$, $\mathbf{z}={\left[z_1\cdots z_{\overline{V}}\right]}^T$, $z_v={\mathbf{s}}^T{\mathbf{Q}}_v\mathbf{s}$.

2. Layout. The layout is a cross-dataset indication of which elements of s generate which elements of x. It is fully-connected if s in all datasets contribute to all x. Otherwise, it is structured, such as in separable models where f() is either shared (e.g., same A) or dataset-specific (e.g., block-diagonal A). Tensor models, such as parallel factors (PARAFAC), offer further structured layout subtypes [35].

Statistical relationship among sources

This assumption regards which sources are (un)related, and how. Only stochastic relationships are considered since all deterministic relationships can be absorbed in f(·). Sources can also be related to themselves through sample dependence (e.g., autocorrelation).

1. Subsets. This choice determines which sources are related to each other and which are not. It leads to the notion of source groups (s_k, k = 1,…, K), i.e., related sources that go together to form one of K groups, which are broadly referred to as subspaces¹. The number of subspaces (K) and their compositions are key choices in S/MDM problems.

2. Interactions. This specifies directed (possibly causal) and/or undirected relationships among sources. Many graphical structures [36] are possible, including “self-loops” to represent sample dependence. For brevity, this work emphasizes either undirected non-causal instantaneous relations, or those based on sample dependence.

3. Type of statistics. When random variables are statistically related they are said to be dependent. There are two types of statistical dependence to choose from: linear dependence (captured by second-order statistics), and higher-order dependence (captured by higher-order statistics). Unrelated variables, however, are statistically independent, meaning their joint distribution is a product of the marginal distributions, e.g., $p\left(\mathbf{s}\right)={\displaystyle {\prod }_{i=1}^{C}p\left(s_i\right)}$. Independence implies no grouping and, thus, sources do not interact. Consequently, both second- and higher-order dependencies are absent in that case.

   Second-order statistics (SOS): This kind of statistics refers to so-called second moments. The second moment of a zero-mean random variable is E[X²], where E[ ] is the expected value operator. It captures the “scale” (or variability) of X in the form of variance or standard deviation. For pairs of variables, however, second moments become cross-moments E[X₁, X₂], which capture the level of linear relation between random variables in the form of a correlation coefficient (ρ). In simple terms, SOS measures how well a straight line explains the joint statistical relationship between two random variables. Independence implies all SOS cross-moments are zero for zero-mean sources and, therefore, uncorrelation.

   Higher-order statistics (HOS): This kind of statistics refers to higher-order moments. A higher-order moment of a zero-mean random variable is the expected-value of its p-th power, E[X^p], for p > 2. It captures other properties of the distribution of X, like skewness (p = 3) and kurtosis (p = 4). For tuples of C variables, however, higher-order moments become higher-order cross-moments $E_p\left[X_1^{q_1},\dots ,X_C^{q_C}\right]$, ${\displaystyle {\sum }_{i=1}^C{q}_i=p,}$ C ≤ p; E_p[·] is a p-order expectation. Put simply, HOS measures joint relationships among multiple random variables beyond those explained by a single straight line. Independence implies all HOS cross-moments are zero for zero-mean sources.

SOS and HOS are at the core of statistical source relationship modeling, broadly compartmentalizing the landscape of models into those capturing only one or both types of statistics. The latter case is considered more general, as depicted in Fig. 2. Often, all-order statistical information (i.e., both SOS and HOS) can be achieved by simply choosing an effective joint probability density model for the sources/subspaces.

Fig. 2. Hierarchy of linear BSS models.

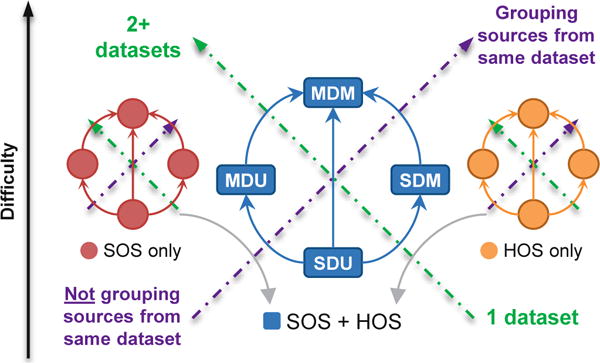
Historically, BSS models have been made more general by: A) increasing the number of datasets which can be jointly analyzed [see Layout and Subsets]; B) moving from isolated sources to groups of sources in the same dataset [see Subsets]; C) exploiting SOS, HOS, or both [see Type of Statistics]. The arrows indicate the directions of increasing difficulty, model complexity, and generality. Highly general models can address MDM problems by incorporating lenient modeling choices.

C. Terminology and Indeterminacies

We intentionally generalize the definition of BSS to include cases of simultaneous system inversion, which attempt to leverage information from multiple systems (via their outputs) to jointly infer their mixture functions and sources. Utilizing multiple datasets to infer each system may lead one to interpret the methods not as “blind” as a single-dataset BSS. However, our view is that, together, all these systems/datasets form a single larger system that needs to be identified only by the outputs provided by each of its parts. This view aligns with prior work coined as joint BSS [37], and even more so with multimodal brain data analysis.

Like seminal works from the SDU literature [38], certain restrictions apply with respect to the identifiability of SDM, SDU, and MDM models. In general, this is a result of how well the modeling choices (see Table I) match the true generative process. For example, the typical scale, sign, and permutation ambiguities from the linear independence-based SDU models [1] generalize to arbitrary invertible linear transformations of the subspaces in SDM models [28]. In linear second-order independence-based MDU models, identifiability is not attainable in cases were two or more subspaces share an identical block correlation structure [39], [40]. Recent initial work [41] developed for linear second-order independence-based MDM models suggests a combination of conditions from SDM and MDU. In the non-linear case, however, independence-based SDU models are unidentifiable if independence is the only assumption [1, Ch.14]. Additional constraints are required and Bayesian approaches offer a nice framework for that. A complete study of the identifiability conditions for each combination of modeling choices, especially in the case of MDM models, is valuable but exceeds the scope of this work. Note, however, that for noisy linear models optimizing for minimal error in s implies WA ≠ I, i.e., W is not identifiable. Conversely, identifiability of W does not guarantee identifiability of s in noisy models [1, Ch.4]. Finally, the number of components C can be estimated by model order selection approaches based on information-theoretic criteria (IC) such as Akaike’s IC (AIC) [42], Bayesian IC (BIC) [43], Kullback-Leibler IC (KIC) [44], Draper’s IC [45], or minimum description length (MDL) [46]. However, we are unaware of methods for direct estimation of the number of subspaces K and their compositions, except for post-hoc approaches using clustering [47] and non-linear correlations [31]. Also, these approaches do not generalize trivially to multiple datasets.

D. Turning Models into Algorithms

After characterizing the model based on the choices outlined above, three additional steps are typically required to translate it into an algorithm (Fig. 3): (i) define an inverse model for s ≈ y = g (x; ϕ) based on the modeling choices made for f(·), s and θ, where ϕ denotes a system inversion parameter, (ii) select a cost function J(ϕ) that is sensitive to the properties of s, and (iii) choose an optimization procedure to estimate ϕ by minimizing/maximizing J(ϕ).

Fig. 3. Steps involved in moving from a model to an algorithm.

The properties of s and θ, selected during the modeling step, impose requirements on the inverse model and cost function. The parameters ϕ of the inverse model are the inputs to the cost function and change according to the selected optimization strategy.

The inverse model results directly from the choices in the generative model. In noise-free linear BSS models, the inverse model must also be linear, in which case ϕ is also a matrix, denoted W, and y = Wx. The cost function is typically one that reflects the desired properties of s, i.e., it attains a minimum or a maximum when such properties are met (e.g. the likelihood function). It also changes with the structure of A. Thus, a numerical optimization strategy [48] is selected to identify the optimal W that approximately attains such minimum/maximum from data. Typical unconstrained optimization algorithms include line search methods, using regular, stochastic, relative [49], or natural [50] gradient descent, Newton or quasi-Newton descent [48], as well as trust-region methods [48]. Some variations allow for constraints on θ, ϕ and/or s (Table I), such as regularized optimization, null-space methods [51], interior point [48], and multiobjective [52] optimization. For example, sparsity constraints on θ = A reduce the number of sources contributing to a sensor, while low total variation of s has a smoothing and denoising effect.

Numerical optimization is key for Bayesian estimation [1, Ch.12] as well. Using priors, Bayesian methods infer the posterior distribution from the likelihood function. This offers a nice, principled strategy to incorporate constraints as prior knowledge. Then, maximization of the posterior (MAP) jointly estimates s and θ from x. Alternatively, maximization after marginalizing s out of the posterior is thought to prevent overfitting by avoiding arbitrary peaks of the joint posterior, leading to a better estimate of the posterior mass concentration. Variational Bayes (VB) approaches, such as ensemble learning [53], [54], carry out marginalization while approximating the joint posterior by a product of factors, each corresponding to a subset of the model (and noise) parameters θ. Marginalization can also simplify to the likelihood function when a “constant” prior is used for θ. When no analytical approximation is imposed on this likelihood, a general expectation-maximization (EM) approach emerges [55]: conditional expectations of s are computed in the E-step and used to update θ in the M-step (maximizing the likelihood). This was shown [56] to be particularly useful in the case of noisy models, using the Wiener filter in the E-step. Marginalization of θ following marginalization of s requires MCMC approaches for approximate integration.

E. Unified Framework

Building on the broad, general view of modeling and development in BSS problems presented above, we propose a unified framework for description of BSS models based on charting the modeling choices made for each of the three sets of assumptions outlined in II-B and the type of problem being addressed. In the following section, we illustrate the scope of this unifying framework by characterizing and reviewing a number of BSS models popular for brain data analysis.

III. Review of BSS Models for Brain Data

Following the proposed framework, in this section we review BSS models and algorithms frequently employed in brain data analysis. Throughout the description, models become progressively stronger by adopting more lenient choices, enabling simultaneous analysis of multiple datasets, allowing multidimensional sources, and exploiting both second- and higher-order statistics. High-level differences and relationships among these models become evident, as shown below. Applications to various brain data modalities are presented last.

A. BSS Models

Here, both classical algorithms and recent models are reviewed through the framework we propose. Following Table I, we first focus our attention on linear mixture models (x = As) with undirected source relationships within subspaces and/or sample dependence, and no optional constraints. In all cases, we assume that sources are zero-mean. The sections are organized by problem, following the structure in Fig. 1.

1) Single Dataset Unidimensional (SDU) Problem

The linear models for the SDU problem assume a single dataset (M = 1) generated by an invertible linear, fully-connected mixture (see Fig. 4). The classical model in this case is principal component analysis (PCA) [57]–[60], which assumes the sources s are uncorrelated, implying a diagonal source covariance matrix Σ^s. Thus, SOS dependence among estimated sources y = Wx should be zero. Eigenvalue decomposition (EVD) of Σ^x or singular value decomposition (SVD) of the observed V × N dataset X identify such diagonalizing W, assigning sources to each of the principal axes of the data, i.e., the (orthogonal) directions of maximal variability. The PCA solution is unique only up to sign ambiguities. Also, sources with equal variance are unrecoverable if A is a rotation matrix, since x would then be already uncorrelated. Its focus on the top C sources with largest variability makes it prone to error when the sources of interest have low variance.

Fig. 4. General inverse models for linear SDU, MDU, and SDM problems.

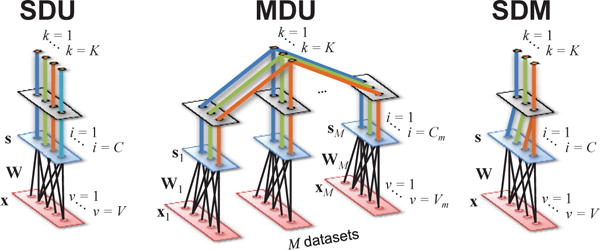
The models are presented as graphical structures where the lower layer corresponds to one 1 × V observation of the input data x. The middle layer represents the C sources s obtained by linear transformation of x through the unmixing matrix W. The top layer establishes the type of interaction between sources as described in Section II-B, forming K subspaces s_k. The problems are described in Section II-A.

A very successful model for brain data in this category is independent component analysis (ICA) [3], [7]–[9], [61]–[70]. The ICA model assumes statistical independence among the sources in s and, thus, all HOS and SOS dependence among estimated sources should be zero. Cost functions for dependence assessment are abundant [1], [71]–[73], including negentropy [19] (as in FastICA [21], [74]) and information divergence [75], [76], of which mutual information [26], [77], [78] is an important special case and a natural, general choice:

$$I\left(\mathbf{s}\right)=-h\left(\mathbf{s}\right)+{\displaystyle \sum _{i=1}^{C}h\left(s_i\right)},$$ (1)

where h(s) = −E[log p(s)] is the joint differential entropy, and p(s) and p(s_i) are the joint probability density function (pdf) of all sources and the marginal pdf, respectively. When u ≈ γ(y) = γ(Wx), where γ(·) is an element-wise non-linear transformation representing a fixed cumulative distribution function (cdf), and p(u_i) is the Uniform distribution in the [0, 1] domain, h(u_i) is zero. In this case, minimizing I(u) is equivalent to maximizing h(u), which is the popular Infomax approach [20] when the sigmoid function is chosen as the cdf.

Another successful method, particularly in the field of EEG-based brain-computer interface (BCI), is called second-order blind identification (SOBI) [22], [79]. SOBI considers the case of independent non-white stochastic source processes s_i(t), in which sample dependence occurs within each source s_i through autocorrelation ${\mathbf{R}}_{ii}^{\mathbf{s}}$ (e.g., lag-correlation ${\mathbf{R}}_{ii}^{\mathbf{s}}\left(\tau \right)$, τ ∈ [0, T ]) but not highly among different sources (e.g., ${\mathbf{R}}_{ij}^{\mathbf{s}}\left(\tau \right)\approx \mathbf{0}$, i ≠ j, ∀τ ∈ [0, T ]). This translates to high SOS of a source with itself and low SOS with other sources, i.e, R^s(τ) ≈ I for all τ. Finding W that simultaneously diagonalizes R^x(τ) for all τ is known as joint diagonalization (JD). This principle is shared by many other techniques, such as the algorithm for multiple unknown signals extraction (AMUSE) [80], which pursues exact² JD between R^x(0) and R^x(τ), for fixed τ ≠ 0, and the time-delays based separation (TDSEP) [81], which uses exact JD on two weighted averages of multiple R^x(τ). Weights-adjusted SOBI (WASOBI) [23] is a variant implementation of the SOBI model that attains better performance by optimally weighting each R^x(τ) and performing approximate JD via weighted least-squares.

Seeking to combine the ICA and SOBI models, COMBI [82] proposes a “wrapper” algorithm that runs both efficient FastICA (EFICA) [83] and WASOBI, selecting the “best” components from each [84]. Recent developments utilizing mutual information rate to combine ICA and SOBI principles have inspired unique algorithms like entropy rate bound minimization (ERBM) [85] and entropy rate minimization using an autoregressive (AR) source model driven by generalized Gaussian distribution (ERM-ARG) [86]. The use of both sample correlation and HOS of sources provides significantly better performance [26], although these have not yet been applied in BCI.

The last model we consider in this category is a simple but effective one, called group ICA (GICA) [4], [87]. GICA is a popular approach for group analysis of resting-state fMRI data [88] that implements “spatial ICA.” An actively growing research area called dynamic resting-state functional network connectivity (rs-FNC) [89]–[92] analysis has been built on top of results produced with this approach. GICA models several datasets as if they were one (by temporal concatenation), assuming the same single set of sources s (the “aggregate” spatial maps) for all M datasets (the subjects): x_m = A_ms_m, s₁ = ⋯ = s_M = s. Dataset- or subject-specific variations in s are then captured by a process called back-reconstruction [93]. While effective, this assumption is also somewhat restrictive and recent work suggests that MDU-type models may capture subject-specific source variability better than GICA when s_m are highly distinct [26], [94] across datasets.

The class of SDU models includes those that extend beyond noise-free linear unconstraint approaches. We go over some of them. Factor analysis (FA) assumes Gaussian sources with uncorrelated sensor noise [95]. Probabilistic ICA (PICA) [96] is a FastICA approach that utilizes a preprocessing step (namely, standardize each observation x_n to zero mean and unit variance) to condition the data prior to PCA reduction. This is based on an extended FA [38] to select the number of components, assuming sensor noise is very low. Expanding Bayesian methods for linear ICA [97]–[99], non-linear FA (NFA) and non-linear independent FA (NIFA) approaches [100], [101] have been proposed under a Bayesian framework too.

In tensor ICA (TICA) [102], the PARAFAC tensor model x_m = AD_ms, m = 1M, where D_m is a diagonal matrix, is used to achieve a variation of GICA. Identically to GICA on M datasets, shared sources s are recovered using PICA. However, A_m = AD_m is obtained in a post-processing step of the concatenated mixing matrices. Thus, the columns of A_m are perfectly correlated across datasets (subjects). While this can be useful for task-elicited activation in which the task stimulus timing is identical, in the case of spontaneous activity, such as resting fMRI, a model that does not assume perfectly correlated timecourses across datasets (subjects) is preferred.

The use of tensor representations is also common in cumulant-based SDU methods [103], but does not relate to modeling datasets as tensors. Instead, they seek to diagonalize second- and fourth-order cumulant tensors by applying the same transformation matrix W to all dimensions of the tensor, effectively achieving second- and fourth-order independence by driving cross-moments toward zero. As for constraints, ICA-R [104]–[106] was proposed to allow references to be incorporated and help extract certain specific patterns from data while pursuing independence. The reference “guides” the decomposition, potentially overcoming high noise issues.

2) Multiple Dataset Unidimensional Problem

MDU-type linear models assume M ≥ 1 datasets generated by a linear, structured mixture. As such, the combined mixing matrix A has a block-diagonal structure that confines sources to their respective datasets: x_m = A_ms_m, m = 1 … M. The number of sources is typically the same for all datasets (C_m = C). Although no multidimensional (grouped) sources occur within any single dataset, sources are allowed to group across datasets (see Fig. 4). The properties of these K = C cross-dataset M-dimensional source groupings (or subspaces, s_k) mark the major differences among models in this category, particularly their choice of SOS, HOS, or both to describe (un)relatedness.

SOS-only models underly classical algorithms such as canonical correlation analysis (CCA) [24] and partial least squares (PLS) [25], [107], as well as more recent models such as multiset CCA (mCCA) [108] and second-order independent vector analysis (IVA) [26], [27]. Thus, in these models, unrelated sources are linearly independent (uncorrelated) and related sources are linearly dependent (correlated). In the case of CCA and PLS, exactly M = 2 datasets are considered, meaning only corresponding sources from each dataset form related pairs. CCA seeks a particular solution that maximizes the correlation between related source pairs s_k=i = [s_1i, s_2i]^T, s_1i = W_1ix₁ and s_2i = W_2ix₂, i = 1 … C, where W_mi is the i-th row of W_m, while PLS maximizes their covariance instead. For i = 1, CCA solves the following constrained optimization [109],

$$\begin{array}{cc}\hfill \underset{{\mathbf{W}}_{1i},{\mathbf{W}}_{2i}}{\max }\hfill & {\mathbf{W}}_{1i}{\mathbf{\sum }}_{12}^{\mathbf{x}}{\mathbf{W}}_{2i}^T\hfill \\ \hfill s.t.\hfill & {\mathbf{W}}_{\mathit{mi}}{\mathbf{\sum }}_{\mathit{mm}}^{\mathbf{x}}{\mathbf{W}}_{\mathit{mi}}^T=1,\forall m\in \left\{1,2\right\},\hfill \end{array}$$ (2)

where ${\mathbf{\sum }}_{ml}^{\mathbf{x}}$ is the (cross-) covariance matrix between datasets x_m and x_l, while PLS solves a different constraint [109],

$$\begin{array}{cc}\hfill \underset{{\mathbf{W}}_{1i},{\mathbf{W}}_{2i}}{\max }\hfill & {\mathbf{W}}_{1i}{\mathbf{\sum }}_{12}^{\mathbf{x}}{\mathbf{W}}_{2i}^T\hfill \\ \hfill s.t.\hfill & {\mathbf{W}}_{mi}{\mathbf{W}}_{mi}^T=1,\forall m\in \left\{1,2\right\}.\hfill \end{array}$$ (3)

In either case, by Lagrange multipliers, the constrained optimizations reduce to generalized eigenvalue (GEV) problems Ev_i = λFv_i, where

$$\mathbf{E}=\left[\begin{array}{cc}\mathbf{0}& {\mathbf{\sum }}_{12}^{\mathbf{x}}\\ {\mathbf{\sum }}_{21}^{\mathbf{x}}& \mathbf{0}\end{array}\right],{\mathbf{F}}_{\mathit{CCA}}=\left[\begin{array}{cc}{\mathbf{\sum }}_{11}^{\mathbf{x}}& \mathbf{0}\\ \mathbf{0}& {\mathbf{\sum }}_{22}^{\mathbf{x}}\end{array}\right],{\mathbf{v}}_i=\left[\begin{array}{c}{\mathbf{W}}_{1i}^T\\ {\mathbf{W}}_{2i}^T\end{array}\right],$$

for CCA³, and F_PLS = I for PLS, both solvable by the power method (PM) of numerical linear algebra. The structure of F_PLS implies W₁₁ and W₂₁ are the left and right singular vectors of the largest singular value of ${\mathbf{\sum }}_{12}^{\mathbf{x}}$, respectively [109]. It also enables a popular variant of PM called non-linear iteration partial least squares (NIPALS) [111], which converges in a single step when either x₁ or x₂ is univariate (V_m = 1).

For i > 1, CCA requires additional constraints to enforce diagonal structure on source covariances ${\mathbf{\sum }}_{11}^{\mathbf{s}}$, ${\mathbf{\sum }}_{22}^{\mathbf{s}}$, and ${\mathbf{\sum }}_{12}^{\mathbf{s}}$

$${\mathbf{\sum }}_{ml,j\overline{j}}^{\mathbf{s}}={\mathbf{W}}_{mj}{\mathbf{\sum }}_{ml}^{\mathbf{x}}{\mathbf{W}}_{l\overline{j}}^T=0,1\le \overline{j}<j\le i,\forall m,l\in \left\{1,2\right\},$$

meaning all non-corresponding source pairs are uncorrelated. While sequential estimation in CCA simply yields the remaining eigenvectors of the GEV problem [112], the same is not always the case in PLS [109]. This is because different deflation strategies can be employed between iterations i and i+1, giving rise to a wide range of PLS variants [109], [110], [113], [114]:

Name	Deflation
PLS-SVD	${\mathbf{X}}_m^{i+1}={\mathbf{X}}_m^i-{\mathbf{W}}_{\mathit{mi}}^T{\mathbf{W}}_{\mathit{mi}}{\mathbf{X}}_m^i$
PLS Mode A	${\mathbf{X}}_m^{i+1}={\mathbf{X}}_m^i-{\mathbf{X}}_m^i{\mathbf{B}}_m^i$
PLS1/PLS2	${\mathbf{X}}_1^{i+1}={\mathbf{X}}_1^i-{\mathbf{X}}_1^i{\mathbf{B}}_1^i$, ${\mathbf{X}}_2^{i+1}={\mathbf{X}}_2^i-{\mathbf{X}}_2^i{\mathbf{B}}_1^i$

where ${\mathbf{B}}_m^i={\mathbf{X}}_m^{iT}{\mathbf{W}}_{\mathit{mi}}^T{\left({\mathbf{W}}_{\mathit{mi}}{\mathbf{X}}_m^i{\mathbf{X}}_m^{iT}{\mathbf{W}}_{\mathit{mi}}^T\right)}^{-1}{\mathbf{W}}_{\mathit{mi}}{\mathbf{X}}_m^i$, ${\mathbf{X}}_m^i$ is the m-th V_m × N data matrix, containing N observations of the measurement vector x_m at the i-th iteration, and ${\mathbf{X}}_m^1={\mathbf{X}}_m$. Alternating the PLS-SVD deflation with the basic PLS optimization in (3), for i > 1, is equivalent to sequential rank-one deflations of ${\mathbf{\sum }}_{12}^{\mathbf{x}}$ [109], or to additional orthogonal constraints ${\mathbf{W}}_{mj}{\mathbf{W}}_{m\overline{j}}^T=0,1\le \overline{j}<j\le i$, ∀m ∈ {1, 2}, all simply yielding the remaining eigenvectors of the initial GEV problem. As a result, non-corresponding source pairs are uncorrelated in PLS-SVD (as in CCA). This is generally not the case in PLS Mode A, although sources are uncorrelated to each other within the same dataset [110] (since the residual ${\mathbf{X}}_m^{i+1}$ is orthogonal to ${\mathbf{X}}_m^i$). The deflation in PLS Mode A is inspired by least squares [115], seeking to remove the variability in ${\mathbf{X}}_m^i$ explained by ${\mathbf{S}}_{\mathit{mi}}^i={\mathbf{W}}_{\mathit{mi}}{\mathbf{X}}_m^i$ (the m-th 1 × N vector containing N observations of the source s_mi) at the i-th iteration. PLS-SVD and PLS Mode A are exploratory approaches recommended for modeling unobservable relationships between datasets. PLS1 and PLS2, however, are intended for regression, univariate (V₂ = 1) and multivariate (V₂ > 1), respectively [113], with X₂ acting as the response variable and using the information contained in X₁ to make predictions about X₂. To that end, s_1i is assumed to be a good surrogate for s_2i [113], thus replacing it in the deflation of ${\mathbf{X}}_2^i$. After C deflations, a “global” multiple regression equation is derived which can be used for prediction of X₂ from new observations of X₁ [109], [112]:

$${\mathbf{x}}_{2,\text{pred}}={\mathbf{P}}_2{\left({\mathbf{W}}_1{\mathbf{P}}_1\right)}^{-1}{\mathbf{W}}_1{\mathbf{x}}_{1,\text{pred}},$$

where P₁ and P₂ are matrices whose columns are the projections ${\mathbf{p}}_{1i}={\mathbf{X}}_1^i{\mathbf{B}}_1^i$ and ${\mathbf{p}}_{2i}={\mathbf{X}}_2^i{\mathbf{B}}_1^i$, respectively, 1 ≤ i ≤ C, and W₁ contains W_1i at the i-th row.

Overall, for sources s estimated with a known inverse model g(·), [116] suggests that the generative model f() conveying optimal interpretation is the one which minimizes the data reconstruction error ‖(s) − x‖. When the L₂-norm is selected, the least squares solution ensues. For separable linear models, ${\mathbf{f}}_m\left({\mathbf{s}}_m\right)={\mathbf{X}}_m{\mathbf{X}}_m^T{\mathbf{W}}_m^T{\left({\mathbf{W}}_m{\mathbf{X}}_m{\mathbf{X}}_m^T{\mathbf{W}}_m^T\right)}^{-1}{\mathbf{W}}_m{\mathbf{X}}_m$, and, thus, ${\mathbf{A}}_m\approx {\mathbf{\sum }}_{\mathit{mm}}^{\mathbf{x}}{\mathbf{W}}_m{{\mathbf{\sum }}_{\mathit{mm}}^{\mathbf{s}}}^{-1}$. This is quite similar in nature to the PLS Mode A deflation, except that all sources s_m contribute simultaneously to the estimation of A_m. This idea was explored in source power comodulation (SPoC) [117], which pursued a CCA-type analysis between windowed variance profiles of s₁ (in dataset m = 1) and a single known fixed reference source s₂₁ (in dataset m = 2), canonical SPoC (cSPoC) [118], which pursued CCA between “envelope” transformations of s_m, and multimodal SPoC (mSPoC) [119], which pursued CCA between s₁ and temporally filtered windowed variance profiles of s₂. The key differences between CCA and SPoC-type approaches are that s₁ and s₂ can have different number of observations and at least one set of sources undergoes a non-linear transformation.

Since covariance is $E\left[s_{1i},s_{2i}\right]={\rho }_{12i}^s{\sigma }_{1i}^s{\sigma }_{2i}^s$, where ${\rho }_{12i}^s$ is correlation between s_1i and s_2i, and ${\sigma }_{1i}^s$ ${\sigma }_{2i}^s$ are their standard deviations, respectively, maximizing covariance will not necessarily maximize correlation⁴. Thus, covariance might not detect sources with high linear dependence (high correlation) if either of their standard deviations is low (possibly the case in genetic data [120]). Because PLS does not prioritize correlation over scale, we consider it “deficient” from an optimization perspective as it will always be biased by the scale of the data. Nevertheless, it may still be advantageous to rely on this property, depending on the importance of scale for a given application, such as regression, where larger scale translates into larger explained variability.

Multiset CCA (mCCA) [108] extends CCA to M ≥ 2 datasets. In this case, sources are organized into K = C subspaces, each one spanning over M datasets, forming K tuples made of one corresponding source from each dataset. The M sources contained in each subspace (s_k, k = i) share an M × M correlation matrix ${\mathbf{R}}^{{\mathbf{s}}_k}$. The solution sought in mCCA maximizes the entire correlation structure of each ${\mathbf{R}}^{{\mathbf{s}}_k}$. This is typically achieved by either minimizing its determinant $\text{det}\left({\mathbf{R}}^{{\mathbf{s}}_k}\right)$ or maximizing some norm $\Vert {\mathbf{R}}^{{\mathbf{s}}_k}\Vert$. Consequently, sources in the same subspace s_k are (potentially) highly linearly related to each other and, therefore, statistically dependent. Typical cost functions for mCCA include sum of squares of all entries of the correlation matrix (SSQCOR) and the generalized variance (GENVAR). For i = 1, SSQCOR mCCA solves the following constrained optimization [37], [108], [121], with ${\mathbf{R}}^{{\mathbf{s}}_k}={\mathbf{\sum }}^{{\mathbf{s}}_k}$, when the constraints are enforced, and k = i:

$$\begin{array}{ll}\underset{{\mathbf{W}}_{\cdot i}}{\max }& \text{tr}\left({\mathbf{\sum }}^{{\mathbf{s}}_i}{\mathbf{\sum }}^{{\mathbf{s}}_{i}T}\right),{\mathbf{\sum }}^{{\mathbf{s}}_i}={\mathbf{W}}_{\cdot i}{\mathbf{\sum }}^{\mathbf{x}}{\mathbf{W}}_{\cdot i}^T\\ s.t.& {\mathbf{W}}_{\mathit{mi}}{\mathbf{\sum }}_{\mathit{mm}}^{\mathbf{x}}{\mathbf{W}}_{\mathit{mi}}^T=1,m=1\dots M,\end{array}$$ (4)

where, tr(·) is the trace operator, ${\mathbf{\sum }}^{{\mathbf{s}}_i}$ is the cross-covariance among the i-th source from all datasets, Σ^x is the crosscovariance matrix among all datasets, and W_·i is a $M\times \overline{V}$, $\overline{V}={\displaystyle {\sum }_{m=1}^M{V}_m}$ block-diagonal matrix whose m-th block contains the row vector W_mi. GENVAR mCCA, on the other hand, solves [108]:

$$\begin{array}{cc}\underset{{\mathbf{W}}_{\cdot i}}{\min }& \text{det}\left({\mathbf{\sum }}^{{\mathbf{s}}_i}\right),{\mathbf{\sum }}^{{\mathbf{s}}_i}={\mathbf{W}}_{\cdot i}{\mathbf{\sum }}^{\mathbf{x}}{\mathbf{W}}_{\cdot i}^T\\ s.t.& {\mathbf{W}}_{\mathit{mi}}{\mathbf{\sum }}_{\mathit{mm}}^{\mathbf{x}}{\mathbf{W}}_{\mathit{mi}}^T=1,m=1\dots M,\end{array}$$ (5)

which is a function of the product of eigenvalues of R_i. For i > 1, mCCA also requires additional constraints:

$${\displaystyle {\sum }_{ml,j\overline{j}}^{\mathbf{s}}={\mathbf{W}}_{mj}{\mathbf{\sum }}_{ml}^{\mathbf{x}}{\mathbf{W}}_{l\overline{j}}^T}=0,1\le \overline{j}<j\le i,1\le m,1\le M,$$

meaning all non-corresponding source pairs are uncorrelated. Multi-block PLS approaches exist [122] but are not common in brain data analysis.

IVA is a model that seeks to minimize the mutual information between subspaces s_k [26], [27], similarly to (1):

$$I\left(\mathbf{s}\right)=-h\left(\mathbf{s}\right)+{\displaystyle \sum _{k=1}^{K}h\left({\mathbf{s}}_k\right)},$$ (6)

where K = C, h(s) = −E[log p(s)], and p(s) and p(s_k) are the joint probability density function (pdf) of all sources and the marginal subspace pdf, respectively. The choice of distribution for p(s_k) distinguishes between different IVA algorithms. In second-order IVA (IVA-G) [123], p(s_k) is modeled as multivariate Gaussian, simplifying (6) to:

$$\begin{array}{l}{I}_{\text{IVA-G}}(\mathbf{s})=\frac{\mathit{CM}\log (2\pi e)}{2}+\frac{1}{2}\log \left({\displaystyle \prod _{i=1}^C{\displaystyle \prod _{m=1}^M{\mathrm{\lambda }}_{\mathit{mi}}}}\right)\\ -{\displaystyle \sum _{m=1}^M\log \left|\text{det}({\mathbf{W}}_m)\right|}-\mathit{const},\end{array}$$ (7)

where λ_mi are the M eigenvalues of the source covariance matrices ${\displaystyle {\sum }^{{\mathbf{s}}_k}}$, k=i, and e is Napier’s constant. When W_m is constrained to be orthogonal, IVA-G is equivalent to GENVAR mCCA [123].

IVA assumes all sources are independent within each dataset, such that $p({\mathbf{s}}_m)={\displaystyle {\prod }_{i=1}^{C}p(s_{\mathit{mi}})}$, m = 1 … M. This implies that second- and higher-order cross-moments between non-corresponding sources are driven to zero and, likewise, become potentially non-zero for sources in the same subspace. For IVA-G, only SOS is considered so that independence translates to uncorrelation. Thus, IVA-G shares the same base model as CCA, PLS-SVD, and mCCA, except the latter three seek particular solutions that explicitly maximize some measure of correlation inside each subspace s_k. The relationship with IVA becomes clearer when we consider that the cost functions in these algorithms assume zero-correlation among sources in different subspaces. From an optimization theory perspective, this can be achieved, for example, by null-space methods [51], which first project into a space that satisfies the constraints (i.e., uncorrelates non-corresponding sources) and then find a solution within that space. It should be clear that the constraints in CCA, PLS-SVD, and mCCA correspond exactly to IVA-G and that maximization of correlation/covariance gives a particular solution within that space.

IVA-L [27], on the other hand, uses the multivariate Laplace distribution to model HOS dependence within subspaces. Due to its HOS nature, it leads to independence, in addition to uncorrelation, among subspaces. Uncorrelation is imposed within subspaces, however, due to the assumed identity dispersion matrix [107]:

$$\begin{array}{l}{I}_{\text{IVA-L}}(\mathbf{s})=\frac{\mathit{CM}\log (4\pi )}{2}-C\log \left(\sqrt{\pi }\mathrm{\Gamma }\left(\frac{M+1}{2}\right)\right)\\ +{\displaystyle \sum _{i=1}^C{\Vert {\mathbf{s}}_i\Vert }_2}-{\displaystyle \sum _{m=1}^M\log \left|\text{det}({\mathbf{W}}_m)\right|},\end{array}$$ (8)

with k = i, ${\Vert {\mathbf{s}}_i\Vert }_2={\mathbf{s}}_i^T{\mathbf{s}}_i=\sqrt{{\displaystyle {\sum }_{m=1}^M{\mathbf{s}}_{\mathit{mi}}^2}}$, s_mi = W_mix_m, and Γ(·) is the Gamma function. IVA can explicitly pursue independence in each dataset while retaining dependence across corresponding sources. Estimating dataset-specific W_m and dependent, rather than identical, sources s_m enables greater flexibility to capture dataset-specific variability. Under similar motivation, GIG-ICA [124] uses the source estimates s from GICA as reference for dataset-specific estimation of W_m and s_m via ICA-R, effectively using two SDU approaches to attain an MDU result.

Next, we consider the joint ICA (jICA) model [125], commonly utilized in multimodal data fusion [121], [126] and “temporal ICA” of temporally concatenated fMRI [127], [128]. Originally proposed for (but not limited to) exactly two datasets, jICA’s hallmark assumption is that the same mixing matrix A generates both datasets. It also assumes none of the sources are statistically related, i.e., $p(\mathbf{s})={\displaystyle {\prod }_{i=1}^C{\displaystyle {\prod }_{m=1}^{M}p(s_{\mathit{mi}})}}$, and that p(·) is the same for all sources. Comparing to the IVA model, this is equivalent to constraining the block-diagonal structure to A_m = A, m = 1 … M, and modeling subspaces with $p({\mathbf{s}}_k)={\displaystyle {\prod }_{m=1}^{M}p(s_{mk})}$. The key difference between such a variant of IVA and JICA is that the first uses an M-dimensional independent joint pdf for s_k while the second combines corresponding sources into a single one-dimensional pdf. Thus, JICA conveniently follows optimization of (1).

In a similar fashion, the approach of common spatial patterns (CSP) [129], [130] assumes the same generative system for two different datasets (typically from the same subject in different conditions). Like exact JD approaches for SDU models, it uses SOS from two covariance matrices, ${\displaystyle {\sum }^{{\mathbf{x}}_1}}$ and ${\displaystyle {\sum }^{{\mathbf{x}}_{+}}}\triangleq {\displaystyle {\sum }^{{\mathbf{x}}_1}}+{\displaystyle {\sum }^{{\mathbf{x}}_2}}$, to form a generalized eigenvalue problem ${\displaystyle {\sum }^{{\mathbf{x}}_1}}{\mathbf{v}}_i=\mathrm{\lambda }{\displaystyle {\sum }^{{\mathbf{x}}_{+}}}{\mathbf{v}}_i$, ${\mathbf{v}}_i={\mathbf{W}}_{1i}^T={\mathbf{W}}_{2i}^T$, and identify uncorrelated sources s₁ and s₂ with maximum variance contrast between corresponding sources. That is, for C sources, s₁₁ has maximal variance (eigenvalue) and the corresponding s₂₁ has minimal variance; likewise, s_1C has minimal variance and s_2C has maximal variance. The motivation for ${\displaystyle {\sum }^{{\mathbf{x}}_{+}}}$ stems from classification: maximizing variance contrast between corresponding sources helps enhance source-based classification of different conditions. Equivalently, maximization of the Jensen-Shannon divergence (or symmetric Kullback-Leibler (KL) divergence) leads to the same CSP solution when the sources are assumed to be uncorrelated Gaussian [131]. Extensions of CSP focus on regularizing the problem with additional constraints [132], [133], leading to GEV problems of the form ${\displaystyle {\sum }^{{\mathbf{x}}_m}{\mathbf{v}}_{\mathit{mi}}}=\mathrm{\lambda }({\displaystyle {\sum }^{{\mathbf{x}}_{+}}}+{\displaystyle {\sum }_p}{\alpha }_p{\mathbf{K}}_p){\mathbf{v}}_{\mathit{mi}}$, ${\mathbf{v}}_{\mathit{mi}}={\mathbf{W}}_{\mathit{mi}}^T$, where K_p is a positive definite penalty term representing any undesired properties detected in the data (typically, non-stationarity due to multiple subjects, sessions, or artifacts). A general regularization framework based on divergence measures is also possible, with Beta divergence offering additional robustness against outliers [131]. The benefits of regularization come at a cost: W_mi is different for each dataset and, thus, requires dataset-specific optimization. Consequently, this implies a different generative system per dataset, which places CSP closer to CCA (and mCCA) but not quite since each dataset is optimized separately rather than jointly.

Expanding on the jICA model, linked ICA (LICA) [134] applies Bayesian ICA to a “joint” TICA model, establishing a more flexible structure on the shared A. Specifically, TICA is applied to D groups of M_d datasets of equal spatial resolution. For each d = 1..D, x_dm = AD_dms_d, m = 1..M_d. Like jICA, sources s_d are assumed independent across the D groups of datasets but, like GICA, they are identical for the M_d datasets in the same group, i.e., ${\mathbf{s}}_{d1}=\cdots ={\mathbf{s}}_{d{M}_d}={\mathbf{s}}_d$. Thus, sources are modeled as $p(\mathbf{s})={\displaystyle {\prod }_{i=1}^C{\displaystyle {\prod }_{d=1}^{D}p(s_{\mathit{di}})}}$, finally combining the corresponding sources s_k, k = i, into a single one-dimensional pdf that is a weighted average of each source’s pdf: $p(s_k)={\displaystyle {\sum }_{d=1}^D{\alpha }_{d}p(s_{dk})}$, k = i, where α_d is determined by the number of observations in each s_d. As a result of the PARAFAC model, the mixing matrices from each dataset share a common structure but are not identical, unlike jICA. However, their columns are perfectly correlated, which may or may not be a benefit depending on the problem. Finally, the Bayesian strategy provides a nice framework to handle noise and employ re-estimation of the source distribution parameters, which is selected as a mixture of Gaussian (MOG) for each s_k.

To conclude, a nice example of generalization are the wide class of models contained in the IVA-Kotz family [107] (and a version that includes HOS and sample dependence [135]), which cleverly use the Kotz distribution to capture both SOS and HOS simultaneously.

3) Single Dataset Multidimensional (SDM) Problem

The linear models for the SDM problem assume a single dataset generated by an invertible linear, fully-connected mixture with multidimensional (grouped) sources occurring within the dataset (see Fig. 4), forming K ≤ C subspaces s_k. The most common model in this category was originally introduced as multidimensional ICA (MICA) [28] and later investigated under the independent subspace analysis (ISA) [30], [31], [136] nomenclature. In this model, sources in the same subspace s_k are related and, thus, statistically dependent. Sources in different subspaces are assumed independent. The simplest ISA approach post-processes ICA results to form subspaces post-hoc as in [28], [31], [47].

A more principled approach is to minimize (6), redefining s_k according to user-defined source groupings. Applying this approach, Hyvärinen et al. [136] assume W is orthogonal, using a Laplacian-like multivariate distribution for independence among subspaces and HOS-only dependence within subspaces, enforcing uncorrelation both within and among subspaces. Similarly, Silva et al. [33] use a scale-adjusted multivariate Laplace distribution and introduces reconstruction error constraints to bypass the typical PCA reduction step. Focusing only on SOS among subspaces, Lahat et al. [29] use a multivariate Gaussian distribution to model subspace dependences. Likewise, Silva et al. [137] improve on [33] by not enforcing uncorrelation within subspaces.

Stationary subspace analysis (SSA) is a model designed to find one group of sources whose mean and SOS remain unchanged over time, hence the name. KL-SSA [138] uses an AJD of Σ^s(τ), accounting for different μ^s(τ), to identify stationary sources based on KL divergence, very similar to Pham’s AJD criterion [139]. It models each window as a Gaussian source $\mathcal{N}({\mu }^{\mathbf{s}}\left(\tau \right),{\mathbf{\sum }}^{\mathbf{s}}(\tau \left)\right)$, and the collection of all windows as $\mathcal{N}({\mu }^{\mathbf{s}},{\mathbf{\sum }}^{\mathbf{s}})$. Then the sum of divergences between each window and the “aggregate” source is minimized. By definition, K = 2, though only the group of stationary sources is retrieved. Analytic SSA (ASSA) [140] approximates the KL divergence with a “variance of covariance” function, simplifying the optimization to a generalized eigenvalue problem. Like other SDM models, sources within the retrieved subspace are still unmixed. Consequently, SSA is only intended to act as a filtering tool, removing non-stationarities from the data.

4) Multiple Dataset Multidimensional Problem

MDM models were developed only recently. In linear MDM, M ≥ 1, datasets are generated by a linear, structured mixture where the combined mixing matrix A has a block-diagonal structure: x_m = A_ms_m, m = 1 … M. The number of sources C_m is typically not the same for all datasets. Multidimensional (grouped) sources occur within any single dataset and are allowed to group (or not) across datasets (see Fig. 5), forming K d_k-dimensional subspaces s_k.

Fig. 5. General inverse model for the linear MDM problem.

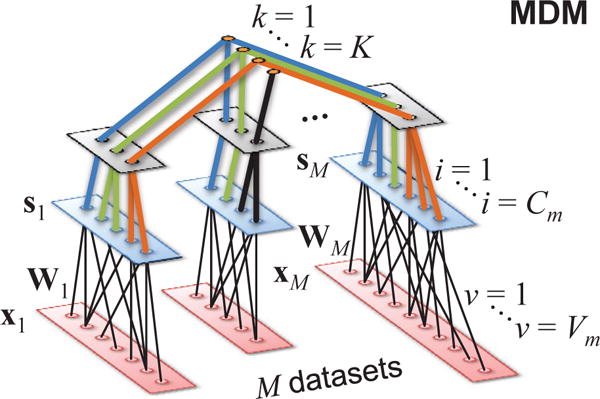
The lower layer corresponds to one V_m × 1 observation of each input data stream x_m, reflecting the different intrinsic dimensionality (V_m) of each dataset. The middle layer represents the C_m sources. The top layer establishes the K subspaces s_k, which may be dataset-specific (k = K in the figure) or span through many datasets, illustrating the different compositions permitted.

Sources in the same subspace s_k are considered statistically dependent, and independent otherwise. Thus, $p(\mathbf{s})={\displaystyle {\prod }_{k=1}^{K}p({\mathrm{s}}_k)}$, and minimization of (6) with user-defined source groupings for s_k follows. Variations include models that either exploit a) only SOS, like joint independent subspace analysis (JISA) [34], b) only HOS, like multidataset independent subspace analysis (MISA) [32], [33] (emphasizing uncorrelation within subspaces), or c) both, like MISA with SOS [137].

B. Applications and Data Modalities

The “blind” property of BSS models makes them a powerful tool in applications lacking a precise model of the measured system and with data confounded by noise of unknown characteristics. Brain imaging is an area where these properties are especially emphasized. We now briefly review some applications of BSS models to brain imaging data. The first case focuses on data from a single imaging modality (unimodal) while the other considers current attempts to identify common motifs from two or more imaging modalities (multimodal).

1) Unimodal

First we consider the analysis of a single dataset. If it contains data from a single subject, the model captures subject-specific information. If instead it contains subject-specific summaries from a certain population, then the model characterizes underlying group patterns. Both cases resort to SDU models. The second example regards the processing of two or more datasets simultaneously. When each dataset contains information from a single subject, shared or similar patterns across subjects are identified and group trends derived. Although group trends offer useful conclusions about population differences, preserving subject-specific information is crucial for clinical diagnosis and personalized treatment. Both SDU and MDU models have been used to capture inter-subject, and sometimes inter-trial, variability.

a) SDU Problem

ICA has been successfully utilized in a number of exciting applications, especially those that have proven challenging with the standard regression-type approaches [141], [142]. For fMRI [4], [143] and EEG [6], [144]–[146], ICA reveals dynamics for which a temporal model is not available [147], finding largely non-overlapping, temporally coherent brain regions without constraining the shape of the temporal response. The Infomax algorithm with a sparse prior is particularly well suited for spatial analysis [148]. Besides fMRI, the brain grey [2], [149] and white matter [149], as well as functional near-infrared spectroscopy (fNIRS) [69] have also been analyzed by ICA to study the diseased brain. In addition to its wide use for recovering spatial networks as independent components—in diffusion tensor imaging (DTI) [7], positron emission tomography (PET) [67], and even MEG [150]—ICA is also promising for temporal [128], [151] and spectral (e.g., MR spectroscopic imaging (MRSI) [70]) domains of brain imaging.

ICA was shown to be useful in modalities such as EEG and MEG. It has also been successfully applied to multi-neuronal recordings [68]. Mostly, it is used for artifact reduction [61], [152] or for real-time control in BCI applications [65]. However, for artifact reduction in MEG, SOBI was shown to be superior to other BSS methods available at the time [5] (also see [153], [154] for another comparative study).

GICA [4] of fMRI [3] is one of the most successful BSS tools for neuroimaging analysis, providing a means to handle multi-subject datasets. It enables network identification under task and rest regimes [89]. The connection patterns between these networks is very interesting and useful for differentiation [90], [155]–[157] and neurodiagnostic discovery [87].

b) MDU Problem

Both CCA and mCCA have been successfully utilized in applications ranging from single- [158] and multi-subject analysis of fMRI [159], [160], as well as BCI [161], [162]. PLS, on the other hand, has also been successfully applied to neuropsychological and MRI relationships [163], while temporal ICA was investigated in [127], [128], [151]. Finally, IVA has found great value in leveraging the success of independence-based methods while better characterizing inter-subject variability [94], [164], [165].

2) Multimodal

Multimodal analyses are intended to leverage information contained in multiple data streams by modeling the relationship among modalities. Convergent evidence suggests that combining functional and structural information is useful in clinical research [166]–[168]. Moreover, multi-modal studies often demonstrate some congruent effects across modalities and different brain pathologies [169]–[173]. Any remaining complementary information typically contributes to increased differentiation power among diseases. Unlike multimodal approaches that use one modality to constrain or filter the other, multimodal data fusion seeks hidden shared information underlying the signals from both modalities simultaneously. Multimodal data fusion applications are by and large viewed as MDU-type problems [174], [175]. However, for the most part, current neuroimaging multimodal fusion schemes have focused on pairs of modalities.

IV. Future Directions

A. Emerging Modalities

Improvements in imaging instrumentation and signal acquisition continue to provide researchers with novel and higher quality information about the physiology of the brain. Naturally, the use and combination of such emerging modalities has great potential for producing new findings and applications.

We begin with a summary of promising, emerging modalities. First, high-resolution quantitative MR imaging of tissue-specific parameters such as longitudinal relaxation (T1) provides good indication of cortical myelination [176], with the benefit of allowing direct comparison of images across scanners and sites, as well as longitudinally, for most cortical brain areas [177]. Also, a measure of local variation in grey matter called voxel-based cortical thickness (VBCT) provides higher grey matter sensitivity than typical voxel-based morphometry (VBM) [178]. Following recent breakthroughs in DWI [179], [180], crossing white matter fibers can now be resolved and tracked, providing thrilling details about the orientation and structural connectivity of fiber bundles. Similar improvements have led to ultra-fast fMRI sequences [16] at higher spatial resolution, simplifying the filtering of certain physiological noise sources, such as breathing and cardiac pulsation.

We also highlight the emergence of new devices that combine different imaging modalities. Simultaneous PET/MR devices offer multiple opportunities for multimodal research. Particularly, with the advent of functional PET (fPET) by constant infusion of 2-[(18)F]-fluorodeoxyglucose (FDG), functional changes in glucose utilization by the brain can be observed with better time resolution than traditional PET [181]. Consequently, simultaneous functional imaging using fPET and fMRI (by arterial spin labeling (ASL) and blood oxygen level dependent (BOLD) contrasts) enables the study of neurovascular coupling [182], especially in the study of drug challenges. Also, sMRI scans interleaved with PET acquisition can enable improved PET resolution and SNR following MRI-guided attenuation and partial-volume corrections, motion compensation, and reconstruction [183].

Similarly, recent advances in cap and probe design allow for high-density simultaneous fNIRS and EEG experiments with reduced motion artifacts and for extended periods of time [184], [185]. These could be combined with PET/MR systems, offering a huge opportunity for neurodiscovery, and indicating an impending need for multiple-dataset methods oriented to multimodal fusion.

B. Emerging Applications

The past decade has witnessed a growing interest in multimodal analyses, especially N-way multimodal fusion [33], [186], for their potential to leverage hidden multimodal interactions (i.e., cross-dataset dependence) and construct a more complete view of brain function and structure. More modalities typically means increased confidence in statements about the neural determinants of healthy [187] and disease states. Moreover, multiple-dataset BSS has demonstrated potential to identify endophenotypes from brain imaging data for genetic association studies, eliciting candidate biomarkers for several mental illnesses [188], [189].

While multiple-dataset BSS provides a pristine opportunity for neurodiscovery in multimodal studies of mental disorders [190], the benefits for unimodal studies involving longitudinal or multi-site data can be more immediate, as they may identify recurrent features across time and study location.

Structure-function connectivity analyses [171], [191]–[193] are also expected to largely benefit from continued research in multiple-dataset BSS. For example, graph-oriented BSS may elicit the underlying breakdown of networks into modules and meta-states [194], offering a fresh new look at connectivity.

C. Emerging Techniques

Typically, linear BSS on a V ×N dataset X = AS captures information along the dimension of N. In order to leverage information contained along the other dimension, some approaches have been exploiting the data transpose X^T as well. Utilizing a two-step approach, mCCA+jICA [190] computes mCCA among ${\mathbf{X}}_m^T$ to find ${\mathbf{A}}_m^T$ with high correlation among corresponding rows, followed by jICA on S_m; conversely, [151] uses temporal ICA on the temporally concatenated A^T that results from GICA. On the other hand, approaches like non-negative matrix factorization (NMF) [195] alternate between X and X^T at every step of the alternating least-squares (ALS) [196], [197] optimization. This approach generalizes well to the tensor case [198], [199]. Parallel ICA [9], however, alternates between ICA (on X₁ and X₂, separately) and CCA (between ${\mathbf{X}}_1^T$ and ${\mathbf{X}}_2^T$) at every step. Such techniques are likely to play an important role in the development of new methods for linear MDM problems.

V. Conclusion

We have presented a unifying view of BSS, providing new insight into the connections among many traditional and modern BSS models. The new perspective leads to a broader sense of generalization, highlighting several directions for further development. Particularly, MDM models emerge as an organic confluence of three major trends: simultaneous multi-dataset analysis, grouping of sources within a dataset, and use of all-order statistics. Therefore, they capture all key features and subspace structures common to their predecessors. Their benefit is in the flexibility to simultaneously model dataset-specific as well as cross-dataset subspace associations.

The demands from advances in multimodal brain imaging technology are likely to propel the development of BSS methods strongly into the direction of N-way multimodal fusion. However, a better and more general solution becomes possible. The availability of such advanced BSS approaches will provide novel ways to investigate inter-subject covariation across multiple populations, sites, and longitudinal inquiries.

Biographies

Rogers F. Silva (Student Member, IEEE) received the B.Sc. degree in Electrical Engineering in 2003 from the Catholic University (PUCRS), Porto Alegre, Brazil, the M.S. degree in Computer Engineering (with minors in Statistics and in Mathematics) in 2011, and the Ph.D. degree in computer engineering in 2016 (expected), both from The University of New Mexico, Albuquerque, NM, USA. He worked as an engineer, lecturer, and consultant, and is currently a senior graduate research assistant at The Mind Research Network, Albuquerque, NM, USA. As a multidisciplinary research scientist, he develops algorithms for statistical and machine learning, image analysis, numerical optimization, memory efficient large scale data reduction, and distributed analyses, focusing on multimodal, multi-subject neuroimaging data from thousands of subjects. His interests are: multimodal data fusion, statistical and machine learning, image, video and data analysis, multiobjective, combinatorial and constrained optimization, signal processing, and neuroimaging.

Sergey M. Plis received the Ph.D. degree in Computer Science in 2007 from The University of New Mexico, Albuquerque, NM, USA. He is the Director of Machine Learning at the Mind Research Network, Albuquerque, NM, USA. His research interests lie in developing novel and applying existing techniques and approaches to analyzing large scale datasets in multimodal brain imaging and other domains. He develops tools that fall within the fields of machine learning and data science.

One of his key goals is to take advantage of the strengths of imaging modalities and infer structure and patterns that are hard to obtain non-invasively and/or that are unavailable for direct observation. In the long term this amounts to developing methods capable of revealing mechanisms used by the brain to form task-specific transient interaction networks and their cognition-inducing interactions via multimodal fusion at features and interaction levels.

His ongoing work is focused on inferring multimodal probabilistic and causal descriptions of these function-induced networks based on fusion of fast and slow imaging modalities. This includes feature estimation via deep learning-based pattern recognition and learning causal graphical models.

Jing Sui (Senior Member, IEEE) received her B.S. and PhD. Degree in optical engineering with honors from Beijing Institute of Technology in 2002 and 2007 respectively. Then she worked at the Mind Research Network, NM, USA as a postdoctor fellow and got promoted to Research Scientist in 2010 and Assistant Professor of Translational Neuroscience in 2012. She is currently a full professor at the National Laboratory of Pattern Recognition & Brainnetome Center, Institute of Automation, Chinese Academy of Science (CAS). Dr Suis research interests include machine learning, multi-modal data fusion (fMRI, sMRI, DTI, EEG, genetics), pattern recognition and biomarker identification of mental illnesses. Her ongoing work in predictive data mining attempts to meet clinical challenges of making early intervention possible based on fundamental neuroimaging data. She is a recipient of One Hundred Talents plan of CAS and has been program committee member of IEEE BIBM since 2011. Now she serves as grant reviewer for China Natural Science Foundation, China Scholarship Council etc and regular reviewers for more than 30 peer-reviewed journals.

Tülay Adalı (Fellow, IEEE) received the Ph.D. degree in electrical engineering from North Carolina State University, Raleigh, NC, USA, in 1992.

She joined the faculty at the University of Maryland Baltimore County (UMBC), Baltimore, MD, USA, in 1992. She is currently a Distinguished University Professor in the Department of Computer Science and Electrical Engineering at UMBC. Her research interests are in the areas of statistical signal processing, machine learning for signal processing, and biomedical data analysis.

Prof. Adalı assisted in the organization of a number of international conferences and workshops including the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), the IEEE International Workshop on Neural Networks for Signal Processing (NNSP), and the IEEE International Workshop on Machine Learning for Signal Processing (MLSP). She was the General Co-Chair, NNSP (2001–2003); Technical Chair, MLSP (2004–2008); Program Co-Chair, MLSP (2008, 2009, and 2014), 2009 International Conference on Independent Component Analysis and Source Separation; Publicity Chair, ICASSP (2000 and 2005); and Publications Co-Chair, ICASSP 2008. She is Technical Program Co-Chair for ICASSP 2017 and Special Sessions Co-Chair for ICASSP 2018. She chaired the IEEE Signal Processing Society (SPS) MLSP Technical Committee (2003–2005, 2011–2013), served on the SPS Conference Board (1998–2006), and the Bio Imaging and Signal Processing Technical Committee (2004–2007). She was an Associate Editor for the IEEE TRANSACTIONS ON SIGNAL PROCESSING (2003–2006), the IEEE TRANSACTIONS ON BIOMEDICAL ENGINEERING (2007–2013), the IEEE JOURNAL OF SELECTED AREAS IN SIGNAL PROCESSING (2010–2013), and Elsevier Signal Processing Journal (2007–2010). She is currently serving on the Editorial Boards of the PROCEEDINGS OF THE IEEE and Journal of Signal Processing Systems for Signal, Image, and Video Technology, and is a member of the IEEE Signal Processing Theory and Methods Technical Committee. She is a Fellow of the American Institute for Medical and Biological Engineering (AIMBE), a Fulbright Scholar, recipient of a 2010 IEEE Signal Processing Society Best Paper Award, 2013 University System of Maryland Regents’ Award for Research, and an NSF CAREER Award. She was an IEEE Signal Processing Society Distinguished Lecturer for 2012 and 2013.

Marios S. Pattichis (Senior Member, IEEE) received the B.Sc. degree (high and special honors) in Computer Sciences and the B.A. degree (high honors) in Mathematics, both in 1991, M.S. degree in Electrical Engineering in 1993, and the Ph.D. degree in Computer Engineering in 1998, all from the University of Texas at Austin, Austin, TX, USA. He is currently a Professor with the Department of Electrical and Computer Engineering, University of New Mexico (UNM), Albuquerque, NM, USA. He was a founding Co-PI of COSMIAC at UNM, where he is currently Director of the image & video Processing and Communications Lab (ivPCL, ivpcl.org). His current research interests include digital image, video processing, communications, dynamically reconfigurable computer architectures, and biomedical and space image processing applications.

Dr. Pattichis is currently a Senior Associate Editor of the IEEE SIGNAL PROCESSING LETTERS. He has been an Associate Editor for the IEEE TRANSACTIONS ON IMAGE PROCESSING and the IEEE TRANSACTIONS ON INDUSTRIAL INFORMATICS, and has also served as a Guest Associate Editor for the IEEE TRANSACTIONS ON INFORMATION TECHNOLOGY IN BIOMEDICINE. He was the General Chair of the 2008 IEEE Southwest Symposium on Image Analysis and Interpretation. He was a recipient of the 2004 Electrical and Computer Engineering Distinguished Teaching Award at UNM. For his development of the digital logic design labs at UNM he was recognized by the Xilinx Corporation in 2003 and by the UNM School of Engineering’s Harrison faculty excellent award in 2006.

Vince D. Calhoun (Fellow, IEEE & AAAS) received the B.S. degree in electrical engineering from the University of Kansas, Lawrence, KS, USA, in 1991, the M.S. degrees in biomedical engineering and information systems from The Johns Hopkins University, Baltimore, MD, USA, in 1993 and 1996, respectively, and the Ph.D. degree in electrical engineering from the University of Maryland Baltimore County, Baltimore, in 2002.

He worked as a Research Engineer in the Psychiatric Neuroimaging Laboratory, Johns Hopkins, from 1993 until 2002. He then served as the Director of Medical Image Analysis at the Olin Neuropsychiatry Research Center and as an Associate Professor at Yale University. He is currently Executive Science Officer and Director of Image Analysis and MR Research at the Mind Research Network, Albuquerque, NM, USA, and is a Distinguished Professor in the Departments of Electrical and Computer Engineering (primary), Biology, Computer Science, Neurosciences, and Psychiatry at the University of New Mexico, Albuquerque. He is the author of more than 400 full journal articles and over 500 technical reports, abstracts, and conference proceedings. Much of his career has been spent on the development of data-driven approaches for the analysis of brain imaging data. He has won over $85 million in NSF and NIH grants on the incorporation of prior information into ICA for functional magnetic resonance imaging, data fusion of multimodal imaging and genetics data, and the identification of biomarkers for disease, and leads a P20 COBRE center grant on multimodal imaging of schizophrenia, bipolar disorder, and major depression.

Dr. Calhoun is a Fellow of the American Association for the Advancement of Science (AAAS), the American Institute for Medical and Biological Engineering (AIMBE), and the International Society for Magnetic Resonance in Medicine (ISMRM). He is also a member and regularly attends the Organization for Human Brain Mapping, the International Society for Magnetic Resonance in Medicine, the International Congress on Schizophrenia Research, and the American College of Neuropsychopharmacology. He is also a regular grant reviewer for NIH and NSF. He has organized workshops and special sessions at multiple conferences. He is currently chair of the IEEE Machine Learning for Signal Processing (MLSP) technical committee. He is a reviewer for many journals, is on the editorial board of the Brain Connectivity and Neuroimage journals, and serves as an Associate Editor for Journal of Neuroscience Methods and several other journals.