Abstract
The free solution electrophoretic mobilities of polyelectrolytes with different charge densities have been analyzed using data taken from the literature. The polyions include single- and double-stranded DNA oligomers, small aromatic molecules, peptides, proteins and synthetic copolymers. Mobility variations due to differences in the background electrolytes were minimized by calculating mobility ratios, dividing the mobility of each charge variant in each data set by the mobility of the most highly charged polyion in that data set. In all cases, the mobility ratios increase linearly with the logarithm of the fractional charge, not the first power of the charge as usually assumed. In addition, the mobility ratios observed for all polyelectrolytes except the synthetic copolymers exhibit a common dependence on the logarithm of fractional charge. The unique results observed for the synthetic copolymers may be due to the flexibility of their hydrocarbon backbones, in contrast to the relatively rigid hydrophilic backbones of the other polyelectrolytes. The mobilities observed for the DNA charge variants are well predicted by the Manning electrophoresis equation, while the mobilities predicted by zeta potential theories are too high. However, mobility ratios calculated from both theories agree with the observed results.
Graphical Abstract
Introduction
The free solution electrophoretic mobility of a polyelectrolyte is determined by the balance between competing electrostatic and hydrodynamic forces. Increasing the number of charged residues increases the mobility because of increased electrostatic interactions with the electric field; increasing the size of the polyion decreases the mobility because of increased solvent friction.1–5 The observedmobilities are also affected by the buffer used as the background electrolyte (BGE) because of relaxation and retardation effects that oppose the migration of the polyion in the electric field. These effects vary with the ionic strength of the solution and the identities of the counterions and coions in the BGE.1–9
If a polyion is rigid and spherical in shape and the Debye length (κ−1) is much larger than the particle radius, a, (i.e.,κa ≪ 1), the Debye-Hückel-Onsager theory predicts that the free solution mobility is directly proportional to the charge of the polyion and inversely proportional to its radius, as shown in Eq. (1).
| (1) |
Here, μ is the observed mobility, Q is the structural charge of the polyion, a is the radius and η is the viscosity of the solvent.1–3,10 In the opposite case, when the particle radius is much larger than the Debye length (κa ≫ 1), the mobility can be described by the Smoluchowski equation:
| (2) |
for polyions of any shape.1–3 Eqs. (1) and (2) are based on the linear Debye-Hückel approximation, making them valid only under certain limiting conditions.1–8,10 However, many current discussions of electrophoresis in the literature do not emphasize the limited applicability of Eqs. (1) and (2). As a result, it is often assumed that the mobility of a polyelectrolyte is directly proportional to its structural charge.
Over the years, many investigators have tested the proportionality between the mobility of a polyion and its structural charge, using capillary electrophoresis to measure the free solution mobilities of polyions containing different numbers of charged residues. Without fail, the results showed that the free solution mobility of a polyion is not linearly related to its structural charge, although the number of charge variants in each study was too small to determine the relationship unambiguously. Analytical chemists and biochemists,11–14 using relatively small polyions containing different numbers of covalently attached charged residues, found that the mobilities increased less strongly with charge density than predicted by Eqs. (1) and (2). Colloid chemists,15–18 using high molar mass copolymers containing different proportions of charged and uncharged monomers, found that the mobility increased gradually with increasing charge density before leveling off and becoming constant at high charge densities.
Recently, Stellwagen et al.19 found that the mobilities measured for the charge variants of single-stranded (ss) and double-stranded (ds) DNA oligomers in different studies could be correlated by calculating the ratio of the mobility of each charge variant, with respect to the mobility of the most highly charged DNA molecule in a given data set, and comparing the mobility ratios with the fractional charge of the DNA. Normalizing the mobilities in this manner minimizes the dependence of the mobilities on the physical properties of the BGE because these factors cancel out in the mobility ratios.20 Surprisingly, we found that the mobility ratios of the ss- and dsDNA charge variants increased linearly with the logarithm of the fractional charge, not the first power of the charge as expected from Eqs. (1) and (2). Even more surprisingly, the mobility ratios calculated for charge variants of adenosine, benzene, and naphthalene, using data taken from the literature, exhibited the same dependence on the logarithm of the fractional charge as observed for the DNA charge variants.19 Hence, the dependence of electrophoretic mobility on the logarithm of charge density appears to be valid for both large and small polyions.
In this report, we have extended the analysis to the charge variants of a positively charged protein, bovine carbonic anhydrase II,21 seven-residue peptides containing different amino acids,14 and synthetic copolymers containing different proportions of charged and uncharged monomers,15–18 using data taken from the literature. As expected, the mobility ratios calculated for these polyelectrolytes also increase approximately linearly with the logarithm of the fractional charge. The mobility ratios observed for the charge variants of all polyelectrolytes except the synthetic copolymers exhibit the same dependence on the logarithm of fractional charge. The different results observed for charge variants of the synthetic copolymers appear to be due to the flexibility and/or hydrophobicity of their hydrocarbon backbones. The mobilities and mobility ratios observed for the various polyions are also compared with values calculated from electrophoresis theories.1,2,23,24,28
Experimental
Polyelectrolyte Samples
The free solution electrophoretic mobilities of the polyelectrolyte charge variants were taken from published data in the literature. Four classes of polyelectrolytes have been compared: ss- and dsDNA oligomers containing different numbers of positive, neutral and/or negatively charged linkers between the nucleotide bases,13,19,25 small aromatic molecules containing variable numbers of phosphate, carboxylate or sulfate residues,11,12,26 a protein charge ladder created by mutating some of the positively charged lysine residues in bovine carbonic anhydrase II (called BCA for brevity),21 seven-residue peptides containing different numbers of lysine residues,14 and synthetic copolymers with varying percentages of charged and uncharged monomers.15–18 The preparation and characterization of the polyions and their charge variants are described in the original papers. For convenience, the various polyions, their approximate molar masses, the number of charge variants in each data set, the BGEs, and references to the original literature are compiled in Table 1.
Table 1.
Polyions Used in the Analysis of Mobility Ratios as a Function of Fractional Charge
| polyion | molar mass | number of variants | BGE | pH | reference |
|---|---|---|---|---|---|
| ssDNA-16a | 5.3 × 103 | 7 | 20 mM Na cacodylate | 6.7 | 13 |
| ssDNA-20,23a | ~7.1 ×103 | 2,2 | 20 mM HEPES | 7.5 | 19 |
| ssDNA-8a | 2.6 × 103 | 2 | 20 mM HEPES | 7.5 | this workb |
| dsDNA-20,23a | ~7.1 × 103 | 2,2 | 20 mM K diethyl-malonate | 7.5 | 19 |
| dsDNA-118a | 78 × 103 | 7 | 40 mM Tris acetate | 8.0 | 25 |
| dsDNA-99a | 65 × 103 | 4 | 20 mM K diethyl-malonate | 7.5 | 19 |
| benzene-COOH | ~122 | 4 | 5.5 mM Na borate | 9.2 | 12 |
| naphthalene-azo dyes | 230 – 448 | 7 | ~1 mM Na acetate | 4.75 | 11 |
| AMP, ADP, ATP, cyclic A | 330 – 510 | 4 | 40 mM Tris acetate | 8.3 | 26 |
| BCA | 29.3 × 103 | 21 | 25 mM Tris glycine | 8.4 | 21 |
| peptides | 780 – 960 | 7 | 20 mM Na citrate | 2.5 | 14 |
| polyacrylamide/acrylic acid copolymers | ~280 × 103 | 8 | 10 mM Tris chloride | 8.2 | 15 |
| polyacrylamide/Amps copolymers | ~50 × 103 | 7 | 50 mM phosphate | 6.4 | 16 |
| polyacrylamide/Amps copolymers | ~250 × 103 | 6 | 12 mM ammediol/anisic acid | 8.8 | 18 |
| Na PSS | ~ 250 ×103 | 5 | 40 mM Na borate | 8.3 | 17 |
The number at the end of the acronym corresponds to the number of bases or base pairs in the molecule.
Mobility of control oligomer estimated from Ref. (27).
Since the electrophoretic mobilities of the polyions in each study were measured under a constant set of experimental conditions, the charge of the polyion was the only variable. Mobility ratios were calculated by dividing the mobility of each charge variant, taken from figures or tables in the cited references, by the mobility of the most highly charged polyion in that data set. The charge densities of the various polyelectrolytes were taken from values given by the authors or estimated from the chemical structure of the polyion and the number of covalently attached charged residues. For simplicity, the charge densities were assumed to be spatially uniform, as though the charged groups were evenly distributed on the surface of the polyion.
Calculating the mobility ratios (i.e., fractional mobilities) of the polyion charge variants with respect to the fractional charge of the most highly charge polyion is that data set is reasonable for the DNA charge variants, because the unmodified DNAs are fully charged. For consistency, the mobility ratios and fractional charges of the other types of polyions were calculated in the same manner. The major assumption made in the analysis is that the conformation of the polyion is essentially independent of charge density, so that the frictional coefficients of the charge variants are independent of the number of charged residues.
Manning Electrophoresis Equation
Manning has used counterion condensation theory22 to derive an equation for DNA electrophoretic mobility that includes relaxation and retardation effects due to the counterions and coions in the BGE.28 This equation is based on modeling DNA as an infinitely long wire (no end effects) with point charges separated by their average distance along the contour length, b. The DNA molecules are assumed to be isolated and embedded in a solution containing excess electrolyte. The theory also assumes that no hydrodynamic interactions occur between monomers (complete free draining), so that the electrophoretic mobility is independent of molar mass. Stretches of the chain comparable in length to κ −1 are assumed to be nearly fully extended. Various terms in the equations have been evaluated in accordance with counterion condensation theory,22 taking advantage of Debye-Hückel equilibrium theory and theories of irreversible thermodynamics.28
The resulting electrophoresis equation can be written as:
| (3a) |
| (3b) |
| (3c) |
| (3d) |
where μ is the free solution mobility, z1 and z2 are the counterion and coion valences, respectively, ε is the dielectric constant of the solvent, kB is Boltzmann’s constant, T is the absolute temperature, η is the viscosity of the solution, κ is the inverse Debye length, b is the linear distance between charged residues, eo is the elementary charge, ν1 and ν2 are the numbers of counterion and coions, respectively, and λ1o and λ2o are the equivalent conductances of the counterions and coions in the BGE, respectively. Based on Eq. (3b), DNA mobilities are predicted to vary as the logarithm of the linear charge separation, b.
All parameters in Eqs. (3a–3d) are known physical constants or can be estimated from data in the literature. The parameter b can be calculated for dsDNA from the length of the oligomer (number of base pairs × rise/base pair, 3.4 Å) divided by the net charge of the oligomer. If the ssDNA oligomers are assumed to be rod-like in the relatively low ionic strength buffers used for electrophoresis, the distance between successive bases can be taken as 4.0 Å.29 Hence, the value of b is calculated to be the number of nucleotides × 4.0 Å/nucleotide divided by the net charge of the oligomer.
Zeta Potential Theories
Wiersma et al.1,30 and O’Brien and White2 have developed theories relating the electrophoretic mobilities of large spherical polyions to their zeta potentials in BGEs of various ionic strengths. The zeta potential (ζ) is defined as the electrostatic potential at the surface of hydrodynamic shear between a polyion and the solvent. Charged residues within the surface of shear are assumed to migrate with the polyion in the electric field, reducing the net charge of the polyion. Other ions in the BGE are assumed to affect the mobility by increasing the viscous drag and decreasing the effective electric field by polarization of the ionic double layer (the so-called retardation and relaxation effects). The coupled non-linear partial differential equations have been solved by assuming that each polyion is rigid, spherical, and has a radius much larger than the thickness of the double layer, so that the double layer is not distorted by the electric field. Similar calculations have been carried out for cylindrical rod-like polyions, although without including relaxation effects.23,24
Graphs of selected values of the dimensionless mobility and dimensionless zeta potential as a function of κa are available for spheres1,2,5 and rod-like polyions.23,24 For small zeta potentials and low values of κa (κa ≪ 1), the zeta potentials can be calculated from the observed mobilities according to Eq. (4):1,2,30
| (4) |
However, this relationship becomes highly non-linear at high zeta potentials and large values of κa because the retarding force acting on the polyion increases faster with increasing ζ potential than does the driving force, which is proportional to the charge Q.1,2,5,24,30–33
The relationship between the charge Q, the zeta potential and the surface charge density of a polyion is not clear. Some investigators have interpreted Q as the structural charge of the polyion decreased by any bound counterions located within the shear surface.1–3,34,35 Other investigators have explained discrepancies between theory and experiment by interpreting Q as the effective charge of the polyion after counterion condensation.16,31,32,36 Further studies are needed to clarify the relationship between these variables.
Calculations
The observed mobilities of the various polyions and their charge variants were taken from values given in the original literature (see Table 1). Observed mobility ratios were calculated from the original data by dividing the observed mobility of a given charge variant by the observed mobility of the most highly charged polyion in that data set. Calculated mobilities of the various polyions and their charge variants were determined from the Manning electrophoresis equation, Eqs. (3a–3d), or estimated from zeta potential theories by interpolating between published curves of the dimensionless mobility vs. the dimensionless zeta potential at suitable values of κa.1,2,23,24 Calculated mobility ratios were determined by dividing the calculated mobilities of the charge variants in each data set by the calculated mobility of the most highly charged polyion in that data set.
Results and Discussion
Dependence of the Mobilities and Mobility Ratios on Fractional Charge
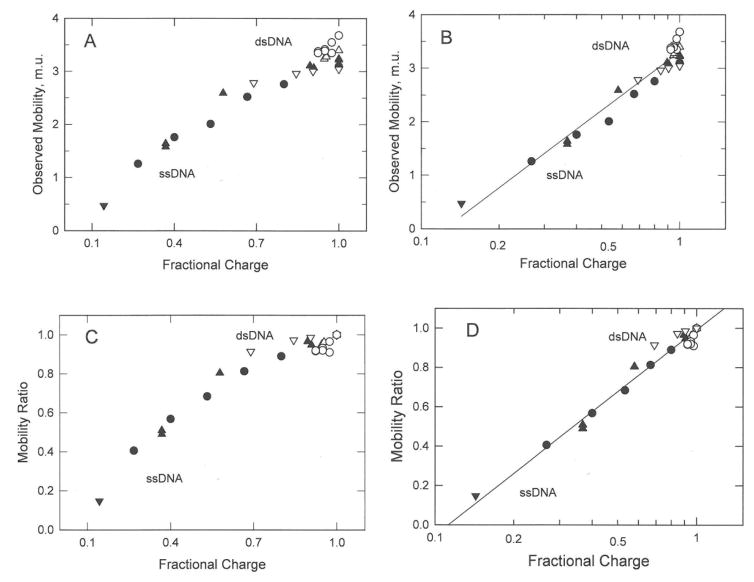
The mobilities and mobility ratios observed for ss- and dsDNA charge variants19 are plotted as a function of the fractional charge in Figures 1A and 1C, and as the logarithm of the fractional charge in Figures 1B and 1D. The mobilities and mobility ratios exhibit a curvilinear dependence on the fractional charge of the DNA, as shown in in Figures 1A and 1C and a linear dependence on the logarithm of the fractional charge, as shown in Figures 1B and 1D. The combined results indicate that the mobilities and mobility ratios of the DNA charge variants increase linearly with the logarithm of the fractional charge, not the first power of the charge as expected from Eqs. (1) and (2).
Figure 1.
Dependence of the mobilities and mobility ratios observed for ss- and dsDNA charge variants on: (A) and (C), the fractional charge of the oligomer; and (B) and (D), the logarithm of the fractional charge. The symbols in all panels correspond to: (●), ssDNA-16; (▲), ssDNA-20,23; (▼), ssDNA-8; (o), dsDNA-118; (△), dsDNA-20,23; and (▽), dsDNA-99. The mobilities in this and subsequent figures are given in mobility units, m.u. (1 m.u. = 1 × 10−4 cm2/Vs). The identities of the DNA samples, BGEs, and references to the original literature are given in Table 1. The straight lines in (B) and (D) were drawn by linear regression; r2 = 0.952 and 0.997, respectively.
The results also suggest that the single-stranded DNA charge variants were highly stretched during electrophoresis, because the mobilities and mobility ratios of the ss- and dsDNA charge variants can be described by the same straight line in Figures 1B and 1D. The ssDNA charge variants contained mixtures of negatively charged and neutral linkers or mixtures of positively and negatively charged linkers; the net charge of the oligomer was always negative. The mobilities of ssDNA charge variants containing different types of linkers were equal when their fractional charge ratios were equal. Hence, the electrophoretic mobilities observed for the ssDNA charge variants were determined by the net charge of the DNA, not by the type of linker used to modify the net charge.
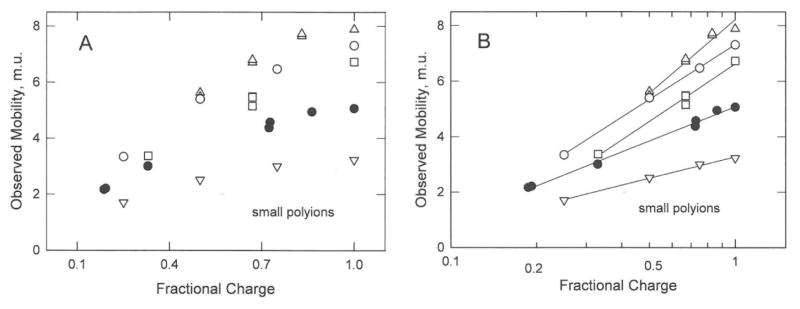
The mobilities and mobility ratios observed for carboxylate derivatives of benzene,12 sulfate derivatives of naphthalene,11 phosphate derivatives of adenosine,26 and seven-residue peptides containing different numbers of charged lysine residues14 are plotted in Figures 2A to 2D. The mobilities and mobility ratios of the charge variants of each polyion increase non-linearly with fractional charge as shown in Figures 2A and 2C, and linearly with the logarithm of the fractional charge as shown in Figures 2B and 2D. Comparison of Figures 2B and 2D illustrates another advantage of plotting the data as mobility ratios rather than mobilities. Mobility ratios minimize the effect of analyte size on the observed mobility, so that the mobility ratios of all the small polyions exhibit the same dependence on fractional charge, as shown in Figure 2D.
Figure 2.
Dependence of the mobilities and mobility ratios observed for small polyion charge variants on: (A) and (C), the fractional charge of the polyion; and (B) and (D), the logarithm of the fractional charge. The symbols in all panels correspond to: (o), benzene charge variants; (■,△), naphthalene charge variants; (▽), adenosine charge variants; and (●), seven-residue peptides (see Table 1). The straight lines in (B) connect the mobilities of the charge variants of each polyion and are meant to guide the eye. The straight line in (D) was drawn by linear regression; r2 = 0.966.
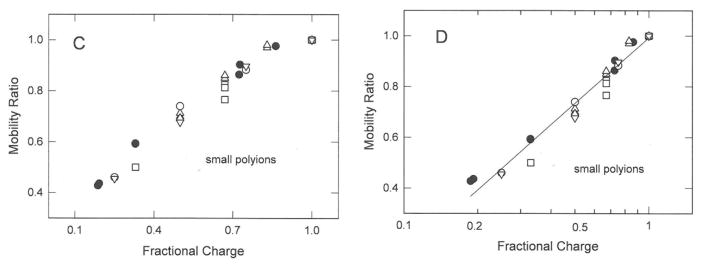
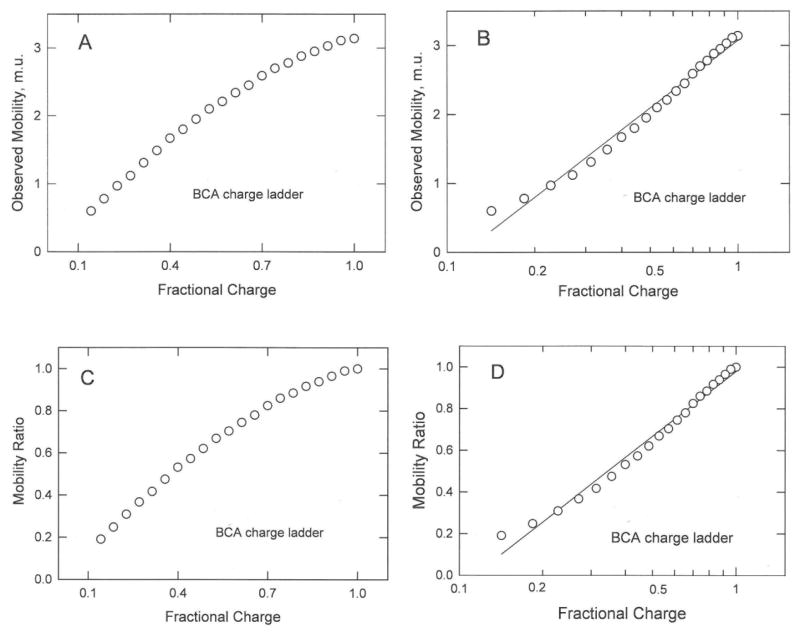
The mobilities and mobility ratios observed for a BCA “charge ladder” containing BCA molecules with different numbers of positively charged lysine residues21 are shown in Figures 3A to 3D. The mobilities and mobility ratios increase non-linearly with the fractional charge, as shown in Figures 3A and 3C, and approximately linearly with the logarithm of the fractional charge, as shown in Figures 3B and 3D. However, the mobility ratios observed for BCA charge variants containing relatively few positively charged lysine residues are somewhat higher than expected from the straight line describing the mobilities and mobility ratios of the other charge variants. It is possible that BCA mutants with very low charge densities are somewhat more globular in shape than mutants with higher charge densities, as observed for other proteins.37 Decreasing the asymmetry of mutants with very low charge densities would decrease their frictional coefficients, increasing the observed mobility.
Figure 3.
Dependence of the mobilities and mobility ratios observed for BCA charge variants on: (A) and (C), the fractional charge; and (B) and (D), the logarithm of the fractional charge. The straight lines in (B) and (D) were drawn by linear regression; r2 = 0.984 for both.
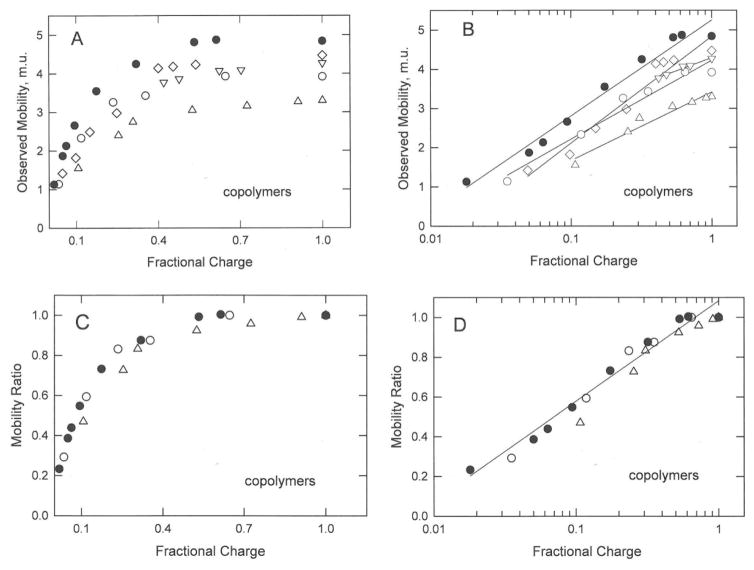
The mobilities and mobility ratios observed for synthetic copolymers of acrylamide and 2-acrylamido-2-methylpropanesulfonate (Amps),16,18 partially hydrolyzed polyacrylamides,15 and partially sulfonated polystyrenes17 are plotted in Figures 4A to 4D. The copolymers were homogeneous in average charge density but heterogeneous in molar mass and in the distribution of charged residues in the sequence. The synthetic copolymers were sufficiently large that their mobilities were independent of molar mass.15–18 The mobilities and mobility ratios observed for the copolymers describe smooth curves that increase with increasing fractional charge and level off at high values of the fractional charge, as shown in Figures 4A and 4C. However, the mobilities and mobility ratios exhibit a linear dependence on the logarithm of the fractional charge, as shown in Figures 4B and 4D. As observed for the small polyion charge variants in Figure 2D, plotting the data as mobility ratios instead of mobilities minimizes the effect of analyte size and solute/solvent interactions on the results. Hence, as shown in Figure 4D, the results clearly indicate that the mobility ratios of the synthetic copolymer charge variants exhibit a common dependence on the logarithm of fractional charge.
Figure 4.
Dependence of the mobilities and mobility ratios observed for charge variants of the synthetic copolymers on: (A) and (C), the fractional charge of the copolymer; and (B) and (D), the logarithm of the fractional charge of the copolymer. The symbols in all panels correspond to: (●), partially hydrolyzed polyacrylamides; (o,△), polyacrylamide/Amps copolymers; and (▽), polystyrene sulfonates (see Table 1). The straight lines in (B) connect the mobilities of the charge variants of each copolymer and are meant to guide the eye. The straight line in (D) was drawn by linear regression; r2 = 0.976.
Comparison of Polyion Mobility Ratios
The mobilities and mobility ratios of the charge variants of DNA, BCA, small polyions and synthetic copolymer all exhibit a linear dependence on the logarithm of the fractional charge, as shown in Figures 1–4. Hence, the conclusion appears to be inescapable: the mobilities and mobility ratios of the charge variants of various types of polyions increase linearly with the logarithm of the fractional charge, not the first power of the charge as often assumed.
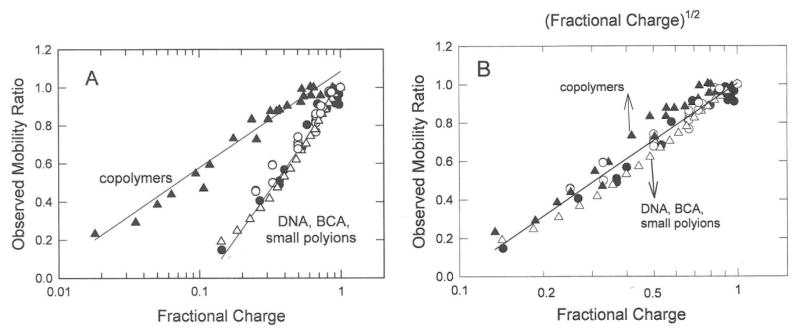
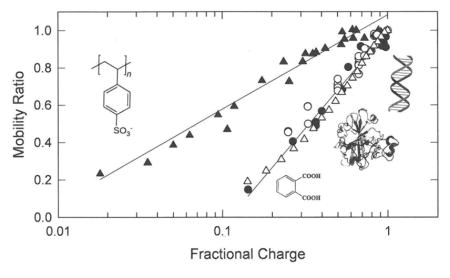
The mobility ratios of the polyion charge variants are compared with each other in Figure 5A, where the mobility ratios are plotted as a function of the logarithm of the fractional charge of the polyion. Surprisingly, the mobility ratios of the DNA, BCA, and small polyion charge variants coincide, while the mobility ratios of the synthetic copolymers are larger than observed for the other polyions at a given charge density.
Figure 5.
Comparison of the mobility ratios observed for all polyion charge variants. (A), Observed mobility ratios plotted as a function of the logarithm of the fractional charge. (B), Comparison of the observed mobility ratios of DNA, BCA and small polyions, plotted as a function of the logarithm of the fractional charge (lower axis), with mobility ratios of the copolymers plotted as a function of the square root of the logarithm of fractional charge (upper axis). The symbols in both (A) and (B) correspond to: (●), ss- and dsDNAs; (o), small polyions; (△), BCA charge variants; and (▲), synthetic copolymers. The lines were drawn by linear regression. In (A), r2 = 0.986 for DNA, peptides, BCA and small polyions and 0.976 for the copolymers; in (B), r2 = 0.948 for all polyions.
The reason for the variation in the results observed for the synthetic copolymers and the other polyions in Figure 5A is not clear, because the polyions differed significantly in their physical properties and the conditions under which the measurements were made. The DNA oligomers, peptides and small aromatic polyion charge variants were monodisperse in molar mass and contained charged residues in known locations. The BCA charge variants were monodisperse in molar mass and in the number of charged residues in each mutant; however, the charged and uncharged lysine residues were randomly distributed in the sequence. By contrast, the synthetic copolymers were polydisperse in molar mass and their average charge densities were determined either by the ratio of charged and uncharged monomers in the polymerization mixture or by partial modification of the residues in a particular copolymer sample. However, all copolymers were sufficiently large that their mobilities were independent of molar mass,15–18 making it unlikely that the differences in the mobility ratios observed for the different polyions in Figure 5A can be explained by differences in polydispersity.
Differences in shape also cannot explain the differences in the mobility ratios observed for the different polyions at the same fractional charge density. The BCA charge variants can be described as prolate ellipsoids of revolutions with small axial ratios,38 the aromatic polyions are approximately globular in shape, and the ss- and dsDNA oligomers can be described as rod-like cylinders. Regardless of the differences in shape, the mobility ratios of the charge variants of all these polyions coincide when plotted as a function of the logarithm of the fractional charge, while the mobility ratios of the synthetic copolymers are larger at the same nominal charge density.
The DNA oligomers, BCA charge mutants and small polyion charge variants are relatively rigid in conformation, with charged residues fully exposed to the solvent. By contrast, the charged moieties in the synthetic copolymers are attached to relatively flexible hydrocarbon backbones. The slopes of the lines describing the dependence of the mobility ratios of the synthetic copolymers and the other polyions on the logarithm of the fractional charge in Figure 5A differ by approximately a factor of two. Hence, it seems likely that the copolymers, especially those with relatively low charge densities, are freely jointed chains with end-to-end lengths related to the square root of the number of monomers. If so, the mobilities and mobility ratios might be related to the logarithm of the square root of the fractional charge, not the fractional charge itself. To test this hypothesis, the mobility ratios observed for the synthetic copolymers are plotted as a function of the logarithm of the square root of the fractional charge in Figure 5B and compared with the mobility ratios of the other polyions plotted as a function of the logarithm of the fractional charge. All the mobility ratios can now be described by the same straight line. The results suggest that the charge variants of the synthetic copolymers, especially those with relatively small numbers of charged groups appended to the hydrocarbon backbone, are more compact than hydrophilic polyions with the same charge density. Hence, increasing the charge density of the synthetic copolymers not only increases the interaction of the polyions with the electric field but causes a gradual expansion of the hydrocarbon backbone. As a result, the mobilities and mobility ratios of the charge variants of synthetic copolymers increase more slowly with increasing fractional charge than observed for the more rigid hydrophilic polyions.
Comparison of Observed DNA Mobilities with Values Calculated from the Manning Equation
The mobilities observed for the ss- and dsDNA charge variants are compared with the mobilities calculated from the Manning electrophoresis equation in Figure 6. The calculated mobilities are reasonably close to the observed mobilities, even though the various studies were carried out in four different BGEs, the DNAs ranged in size from 8 nucleotides to 118 base pairs, the net charge ranged from −1 to −236, and no adjustable parameters were used in the calculation. Since the DNA charge variants contained different numbers and arrangements of positive, negative and/or neutral residues, the specific arrangement of the charged residues is not important. The mobility is determined primarily by the DNA net charge.
Figure 6.
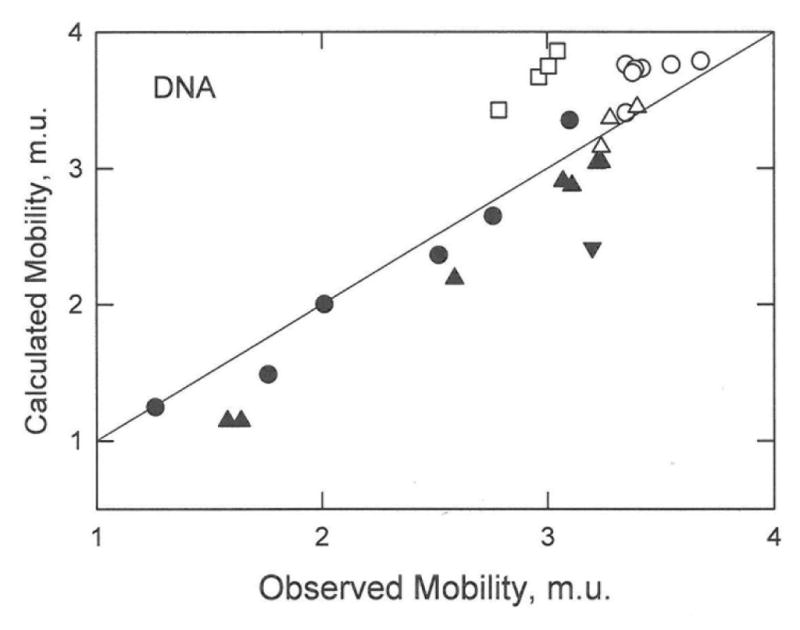
Comparison of the observed mobilities of ss- and dsDNA charge variants with the mobilities calculated from the Manning electrophoresis equation. The symbols correspond to: (●), ssDNA-16; (▲), ssDNA-20,23; (▼), ssDNA-8; (△), dsDNA-20,23; (o), dsDNA-118; and (□), dsDNA-99. The drawn line denotes a 1:1 correspondence between the observed and calculated mobilities.
Linear Charge Density vs. Surface Charge Density
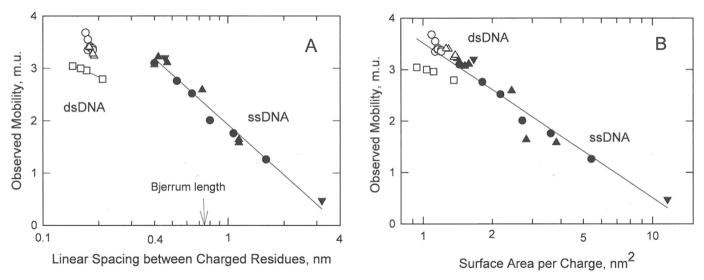
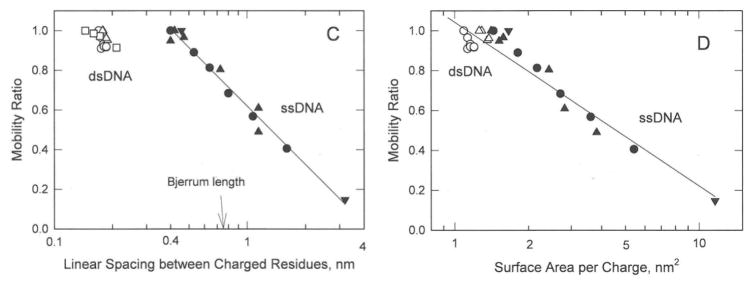
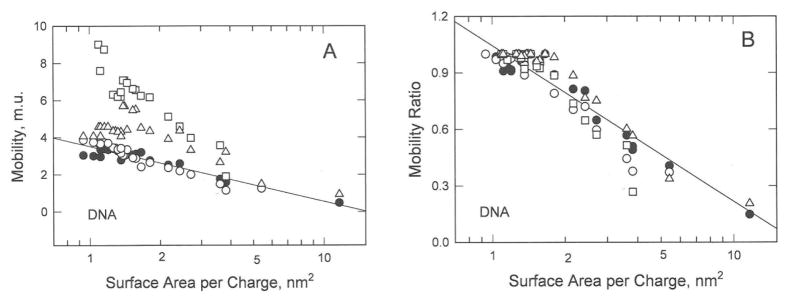
The reasonably good agreement between the observed DNA mobilities and those calculated from Manning electrophoresis equation (Figure 6) suggests that DNA charge density is well described by the linear distance between charged residues, b. Hence, Figure 1 suggests the observed mobilities of the DNA charge variants should be directly related to the logarithm of b as well as the logarithm of the fractional charge. However, the observed mobilities of the ss- and dsDNA charge variants do not exhibit a common dependence on log b, as shown in Figure 7A. The same results are observed for the mobility ratios, as shown in Figure 7C. In addition, the mobilities and mobility ratios observed for the ssDNA charge variants are independent of the Bjerrum length, the distance at which electrostatic interactions between two elementary charges become comparable to thermal energy (0.714 nm for monovalent ions in water at 20°C). Since counterion condensation is predicted to occur whenever the linear charge separation is less than the Bjerrum length,22 the mobilities and mobility ratios observed for the ssDNA oligomers would be expected to exhibit a discontinuity at or near the Bjerrum length. The results therefore suggest that the mobilities of the DNA charge variants might be more closely related to the surface area per charge, as assumed in zeta potential theories,1,2,30–34 than to the linear distance between charged residues. As shown in Figures 7B and 7D, the observed mobilities and mobility ratios of the ss- and dsDNA charge variants exhibit a common dependence on the logarithm of the surface area per charge. Hence, the surface area per charge appears to the variable controlling the electrophoretic mobilities of both ss- and dsDNA charge variants.
Figure 7.
Dependence of the mobilities and mobility ratios observed for the DNA charge variants on: (A) and (C), the logarithm of the linear spacing between charged residues; and (B) and (D), the logarithm of the surface area per charge. The symbols are the same as in Figure 1. The vertical arrows in (A) and (C) correspond to the Bjerrum length, 0.714 nm in water at 20°C. The lines were drawn by linear regression; r2 = 0.973 and 0.979 for ssDNA in (A) and (C), respectively, and 0.902 and 0.918 for all DNAs in (B) and (D), respectively.
Dependence of Observed and Calculated DNA Mobilities on Surface Area per Charge
The mobilities observed for the DNA charge variants are plotted as a function of the logarithm of the surface area per charge in Figure 8A, and compared with the mobilities calculated from the Manning electrophoresis equation28 and zeta potential theories for rods.23,24 DNA surface areas were estimated from the length of each oligomer, calculated as described above, assuming a radius of 10Å for dsDNA39 and 5Å for ssDNA.40 As expected from Figure 6, the mobilities calculated from the Manning equation (open circles) in Figure 8A are very close to the observed mobilities (solid circles). However, the mobilities calculated for the DNA charge variants from zeta potential theories for rods (open triangles and squares) are significantly larger than the observed mobilities, in part because relaxation effects are not included in the theories.23,24 To minimize such purely solvent effects, mobility ratios were calculated for each of the DNA charge variants by dividing the calculated mobility of a given charge variant by the calculated mobility of the most highly charged DNA in that data set. The observed and calculated mobility ratios are plotted in Figure 8B. The calculated mobility ratios are reasonably close to the observed mobility ratios, indicating that both the Manning equation and zeta potential theories correctly describe the dependence of the observed mobility on the logarithm of the surface area per charge.
Figure 8.
Dependence of the observed and calculated mobilities of the DNA charge variants on the logarithm of the surface area per charge. (A), Observed and calculated mobilities; (B), observed and calculated mobility ratios. The solid circles in (A) and (B) correspond to the observed mobilities or mobility ratios; the open symbols correspond to mobilities or mobility ratios calculated from: (o), the Manning equation;28 (□),van der Drift et al.;23 and (△),Gonzales-Tovar et al.24 The drawn line in (A) corresponds to the observed mobilities (r2 = 0.918); the drawn line in (B) describes the calculated and observed mobility ratios (r2 = 0.917).
Small Aromatic Polyions
Mobility ratios were calculated for the benzene and naphthalene charge variants from the Manning electrophoresis equation. The surface areas of the benzene and naphthalene charge variants were estimated by assuming they were approximately globular in shape with radii similar to the average values observed in the crystal structures of pyromellitic acid (benzene-1,2,4,5-tetracarboxylic acid)41 and 2,6-naphthalenecarboxylic acid,42 respectively. The calculated mobility ratios are larger than the observed mobility ratios and exhibit a weaker dependence on the logarithm of the surface area per charge, as shown in Figure 9. The discordant results can be attributed in part to variations in the shape of the small polyions with the number of appended charged groups and in part to the fact that the Manning equation was derived for long rigid rods, not small polyions approximately globular in shape.
Figure 9.
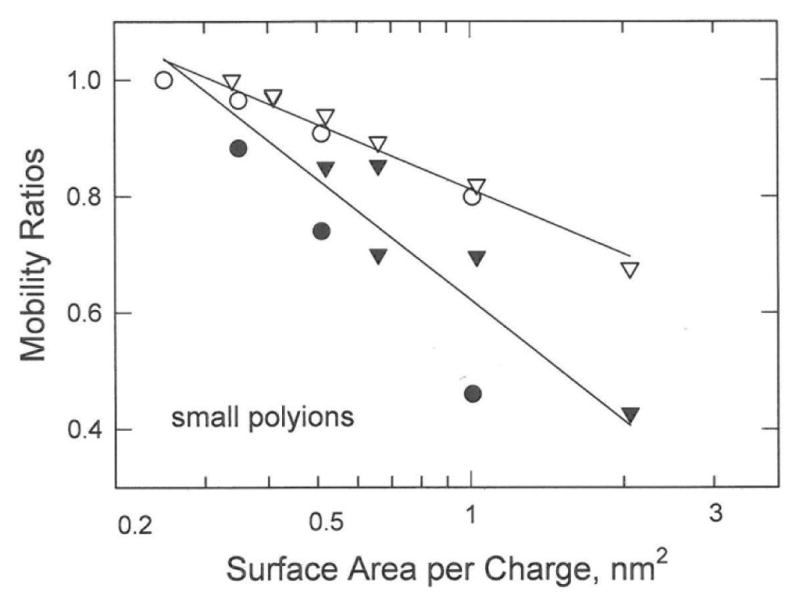
Comparison of the observed and calculated mobility ratios of small aromatic polyions. The open symbols correspond to mobility ratios calculated from the Manning electrophoresis equation; the solid symbols correspond to the observed mobility ratios. The symbols refer to: (●,o), benzene charge variants; and (▼,▽), naphthalene charge variants.
BCA Charge Ladder
The mobility ratios observed for the BCA charge variants21 are compared with the mobility ratios calculated from the Manning electrophoresis equation28 and zeta potential theories for spheres1,2 in Figure 10. The BCA charge variants were approximated as spheres with radii of 25 nm, close to the average value observed in the crystal structures of BCA I and BCA II isozymes.38 The mobility ratios calculated from the zeta potential theories are somewhat lower than the observed mobility ratios but exhibit a similar dependence on the logarithm of the surface area per charge. By contrast, the mobility ratios calculated from the Manning electrophoresis equation exhibit a different dependence on the logarithm of the surface area per charge. Since BCA is approximately globular in shape,38 it is not surprising that zeta potential theories derived for spheres describe the mobility ratios more accurately than the Manning electrophoresis theory, which was derived for long rod-like DNA molecules.
Figure 10.
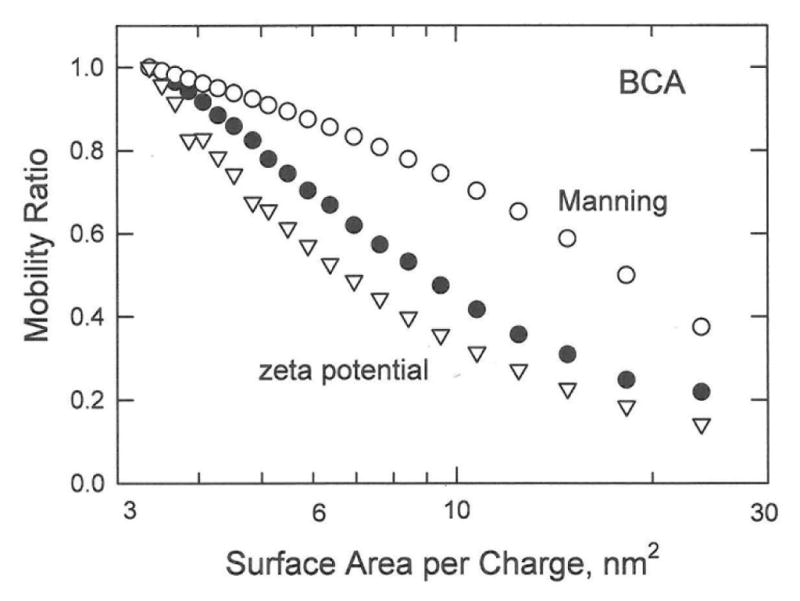
Dependence of the observed and calculated mobility ratios of the BCA charge variants on the logarithm of the surface area per charge. The symbols correspond to: (●), observed mobility ratios; (o), mobility ratios calculated from the Manning electrophoresis equation28; and (▽), mobility ratios calculated from zeta potential theories for spheres.1,2
Synthetic Copolymers
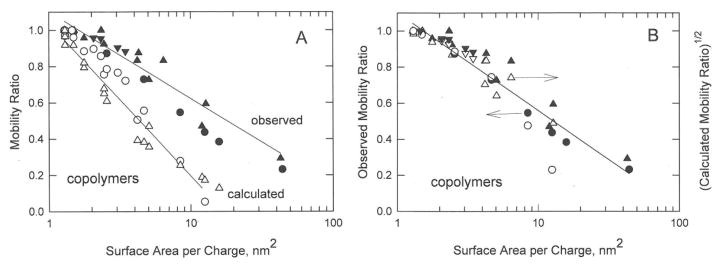
The mobility ratios observed for the acrylamide/Amps16,18 and acrylamide/acrylic acid15 copolymers are plotted in Figure 11A (solid symbols) as a function of the logarithm of the surface area per charge. The copolymers were assumed to be rod-like in shape with average lengths calculated from the molar mass or degree of polymerization given by the authors, using an average spacing of 2.55 Å/monomer.16 The mobility ratios calculated for the copolymers from the Manning electrophoresis equation28 and zeta potential theories for rods23,24 are shown as the open symbols in Figure 11A. The calculated and observed mobility ratios decrease linearly with the logarithm of the surface area per charge, as expected. However, the slopes of the two lines differ significantly; the observed mobility ratios decrease more slowly with increasing surface area per charge than the calculated mobility ratios.
Figure 11.
Comparison of the observed (solid symbols) and calculated (open symbols) mobility ratios of copolymer charge variants. (A), Observed and calculated mobility ratios. (B), Observed mobility ratios (left axis) and the square root of the calculated mobility ratios (right axis). In both (A) and (B), the solid symbols correspond to the mobility ratios observed for: (●), acrylamide/acrylic acid copolymers; (▲), acrylamide/Amps copolymers; and (▼), polystyrene sulfonates. The open symbols correspond to mobility ratios calculated from: (o), the Manning electrophoresis equation;28 or (△), zeta potential theories for rods.23,24 In (B), the left axis corresponds to the observed mobility ratios; the right axis corresponds to the square root of the mobility ratios calculated from the Manning electrophoresis equation.28 The solid lines were drawn by linear regression. In (A), r2 = 0.922 for the observed mobility ratios and 0.958 for the calculated mobility ratios; in (B), r2 = 0.903.
From the discussion of Figure 5, it seems likely that the synthetic copolymers can be approximated as freely jointed chains with end-to-end lengths dependent on the square root of the number of monomers. If so, the observed mobility ratios might be related to the square root of the mobility ratios calculated from electrophoresis theories, rather than the mobility ratios themselves. To test this hypothesis, the observed mobility ratios of the synthetic copolymers are compared with the square root of the mobility ratios calculated from the Manning electrophoresis equation in Figure 11B. The observed and calculated mobility ratios can now be described by the same straight line.
Conclusions
Several important conclusions can be drawn from this work. (1) If the electrophoretic mobilities of polyions that vary only in the number of covalently attached charged groups are electrophoresed under a constant set of experimental conditions, the results can be compared by dividing the mobility of each charge variant by the mobility of the most highly charged polyion in that data set (Figures 1 – 4). Normalizing the mobilities in this manner minimizes the dependence of the mobility on the size of the analyte and the physical properties of the BGE because the frictional coefficients of the polyions and the viscosities and dielectric constants of the solvent cancel out in the mobility ratios.20 The analysis depends only on the assumption that the frictional coefficients of the charge variants of a given polyion are approximately constant.
(2) The electrophoretic mobilities of charge variants of ss- and dsDNA oligomers increase linearly with the logarithm of the fractional charge, not the first power of the charge as expected from the traditional Debye-Hückel-Onsager theory. Since the ss- and dsDNA charge variants exhibit the same dependence on the logarithm of the fractional charge (Figure 1), the single-stranded charge variants must be highly stretched in the BGEs used for electrophoresis. In addition, the mobilities and mobility ratios of the single-stranded charge variants are not dependent on whether the linear spacing between charged residues is greater or less than the Bjerrum length (Figures 7A and 7C). The results therefore suggest either that counterion condensation22 does not occur for such small oligomers or that the condensed counterions are not located within the shear surface of the DNA. 1–3,6–8,10,35
(3) The mobility ratios observed for the charge variants of many types of polyions, including ss- and dsDNA oligomers,19 small aromatic polyions,11,12 adenosine nucleotides,26 small positively charged peptides,14 and proteins containing different numbers of charge-modified amino acids21,43 exhibit a common dependence on the logarithm of fractional charge, while the mobility ratios observed for the charge variants of synthetic copolymers exhibit a weaker dependence on this variable (Figure 5A). Hence, there appears to be a fundamental difference between the mobilities and mobility ratios observed for the copolymers and other polyion charge variants as a function of charge density. It seems likely that the disparate results are due to the statistical coiling of the copolymer backbone chains, which compact the conformation and decrease the interaction of their charged residues with the solvent. As a result, the effective charge of the copolymers appears to be related to the logarithm of the square root of the fractional charge rather than the logarithm of the fractional charge itself (Figure 5B).
(4) The Manning electrophoresis equation28 provides an excellent description of the mobilities observed for ss- and dsDNA charge variants in a variety of BGEs, using no adjustable parameters (Figure 6). Hence, the Manning equation incorporates most of the relaxation and retardation effects that affect the mobility. The mobilities of DNA charge variants calculated from zeta potential theories for rods are too high, in part because relaxation effects have not been included in these theories.23,24
(5) The mobilities and mobility ratios observed for the DNA charge variants decrease linearly with the logarithm of b, the linear separation between charged residues (Figures 7A and 7C), as expected from the Manning electrophoresis equation.28 However, the ss- and dsDNA data sets do not overlap, as might be expected from Figure 1. The data sets do overlap when the mobilities and mobility ratios are plotted as a function of the logarithm of the surface area per charge (Figures 7B and 7D), suggesting that the surface area per charge is the controlling variable in DNA electrophoresis. Zeta potential theories also suggest that electrophoretic mobilities of polyions are related to their surface charge densities1–3,6–8,10
(6) Zeta potential theories for spheres1–3 predict the mobility ratios observed for BCA charge variants more accurately than the Manning electrophoresis equation (Figure 10). This result is not surprising since the Manning equation was derived for long rod-like DNA molecules, not small approximately spherical polyions.
Acknowledgments
Useful discussions with Earle Stellwagen are gratefully acknowledged. Partial financial support from NSF (Grant CHE0748271) and NIH (Grant GM061009) is also acknowledged.
References
- 1.Wiersema PH, Loeb AL, Overbeek JTG. Calculation of the Electrophoretic Mobility of a Spherical Colloid Particle. J Colloid Interface Sci. 1966;22:78–99. [Google Scholar]
- 2.O’Brien R, White LR. Electrophoretic Mobility of a Spherical Colloidal Particle. J Chem Soc Faraday 1. 1978;74:1607–1626. [Google Scholar]
- 3.Viovy JL. Electrophoresis of DNA and Other Polyelectrolytes: Physical Mechanisms. Rev Mod Phys. 2000;72:813–872. [Google Scholar]
- 4.Bockris JO’M, Reddy AKN. Modern Electrochemistry, Vol. 1, Ionics. 2. Plenum Press; New York: 1998. [Google Scholar]
- 5.Gonzáles-Tovar E, Lozada-Sassou M. The Spherical Double Layer: A Hypernetted Chain Mean Spherical Approximation Calculation for a Model Spherical Colloid Particle. J Phys Chem. 1989;93:3761–3768. [Google Scholar]
- 6.Ohshima H, Healy TW, White LR. Accurate Analytic Expressions for the Surface Charge Density/Surface Potential Relationship and Double-Layer Potential Distribution for a Spherical Colloidal Particle. J Colloid Interface Sci. 1982;90:17–26. [Google Scholar]
- 7.Lyklema J. Fundamentals of Interface and Colloid Science, Vol. II, Solid-Liquid Interfaces. Academic Press; San Diego: 1995. [Google Scholar]
- 8.Grahame DC. The Electrical Double Layer and the Theory of Electrocapillarity. Chem Rev. 1947;41:441–501. doi: 10.1021/cr60130a002. [DOI] [PubMed] [Google Scholar]
- 9.Stellwagen E, Stellwagen NC. Probing the Electrostatic Shielding of DNA with Capillary Electrophoresis. Biophys J. 2003;84:1855–1866. doi: 10.1016/S0006-3495(03)74993-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Khair AS, Squires TM. The Influence of Hydrodynamic Slip on the Electrophoretic Mobility of a Spherical Colloidal Particle. Phys Fluids. 2009;21:042001. [Google Scholar]
- 11.Friedl W, Reijenga JC, Kenndler E. Ionic Strength and Charge Number Correction for Mobilities of Multivalent Organic Anions in Capillary Electrophoresis. J Chromatogr A. 1995;709:163–170. [Google Scholar]
- 12.Cottet H, Gareil P. From Small Charged Molecules to Oligomers: A Semiempirical Approach to the Modeling of Actual Mobility in Free Solution. Electrophoresis. 2000;21:1492–1504. doi: 10.1002/(SICI)1522-2683(20000501)21:8<1493::AID-ELPS1493>3.0.CO;2-E. [DOI] [PubMed] [Google Scholar]
- 13.Dong Q, Stellwagen E, Dagle JM, Stellwagen NC. Free Solution Mobility of Small Single-Stranded Oligonucleotides with Variable Charge Densities. Electrophoresis. 2003;24:3323–3329. doi: 10.1002/elps.200305589. [DOI] [PubMed] [Google Scholar]
- 14.Grossman PD, Colburn JC, Lauer HH. A Semiempirical Model for the Electrophoretic Mobilities of Peptides in Free-Solution Capillary Electrophoresis. Anal Biochem. 1989;179:28–33. doi: 10.1016/0003-2697(89)90195-4. [DOI] [PubMed] [Google Scholar]
- 15.Whitlock LR. In: New Directions in Electrophoretic Methods. Jorgenson JW, Phillips M, editors. Chapter 15. American Chemical Society; Washington DC: 1987. pp. 222–245. [Google Scholar]
- 16.Gao JY, Dubin PL, Sato T, Morishima Y. Separation of Polyelectrolytes of Variable Compositions by Free-Zone Capillary Electrophoresis. J Chromatogr A. 1997;766:233–236. [Google Scholar]
- 17.Cottet H, Gareil P, Theodoly O, Williams CE. A Semi-empirical Approach to the Modeling of the Electrophoretic Mobility in Free Solution: Application to Polystyrenesulfonates of Various Sulfonation Rates. Electrophoresis. 2000;21:3529–3540. doi: 10.1002/1522-2683(200011)21:17<3529::AID-ELPS3529>3.0.CO;2-2. [DOI] [PubMed] [Google Scholar]
- 18.Anik N, Airiau M, Labeau MP, Vuong CT, Reboul J, Lacroix-Desmazes P, Gérardin C, Cottet H. Determination of Polymer Effective Charge by Indirect UV Detection in Capillary Electrophoresis: Toward the Characterization of Macromolecular Architectures. Macromolecules. 2009;42:2767–2774. [Google Scholar]
- 19.Stellwagen NC, Peters JP, Dong Q, Maher LJ, III, Stellwagen E. The Free Solution Mobility of DNA and Other Analytes Varies as the Logarithm of the Fractional Negative Charge. Electrophoresis. 2014;35:1855–1863. doi: 10.1002/elps.201400040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Stellwagen E, Renze A, Stellwagen NC. Capillary Electrophoresis Is a Sensitive Monitor of the Hairpin-Random Coil Transition in DNA Oligomers. Anal Biochem. 2007;365:103–110. doi: 10.1016/j.ab.2007.03.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Carbeck JD, Negin RS. Measuring the Size and Charge of Proteins Using Protein Charge Ladders, Capillary Electrophoresis and Electrokinetic Models of Colloids. J Am Chem Soc. 2001;123:1252–1253. doi: 10.1021/ja005740m. [DOI] [PubMed] [Google Scholar]
- 22.Manning GS. The Molecular Theory of Polyelectrolyte Solutions with Applications to the Electrostatic Properties of Polynucleotides. Q Rev Biophys. 1978;11:170–246. doi: 10.1017/s0033583500002031. [DOI] [PubMed] [Google Scholar]
- 23.Van der Drift WPJT, de Keizer A, Overbeek JTG. Electrophoretic mobility of a Cylinder with High Surface Charge Density. J Colloid Interface Sci. 1979;71:67–78. [Google Scholar]
- 24.Gonzales-Tovar E, Lozada-Cassou M, Henderson D. Hypernetted Chain Approximation for the Distribution of Ions around a Cylindrical Electrode. II. Numerical Solution for a Model Cylindrical Polyelectrolyte. J Chem Phys. 1985;83:361–372. [Google Scholar]
- 25.Stellwagen NC, Magnusdótter S, Dagle JM, Gelfi C, Righetti PG. Free Solution Mobility of DNA Molecules Containing Variable Numbers of Cationic Phosphoramidate Internucleoside Linkages. J Chromatogr A. 2000;883:267–275. doi: 10.1016/s0021-9673(00)00415-5. [DOI] [PubMed] [Google Scholar]
- 26.Stellwagen E, Stellwagen NC. Quantitative Analysis of Cation Binding to the Adenosine Nucleotides Using the Variable Ionic Strength Method: Validation of the Debye-Hückel-Onsager Theory of Electrophoresis in the Absence of Counterion Binding. Electrophoresis. 2007;28:1053–1062. doi: 10.1002/elps.200600487. [DOI] [PubMed] [Google Scholar]
- 27.Stellwagen E, Lu YJ, Stellwagen NC. Unified Description of Electrophoresis and Diffusion for DNA and Other Polyions. Biochemistry. 2003;42:11745–11750. doi: 10.1021/bi035203p. [DOI] [PubMed] [Google Scholar]
- 28.Manning GS. Limiting Laws and Counterion Condensation in Polyelectrolyte Solutions. 7. Electrophoretic Mobility and Conductance. J Phys Chem. 1981;85:1508–1515. [Google Scholar]
- 29.Record MT, Jr, Anderson CF, Lohman TM. Thermodynamic Analysis of Ion Effects on the Binding and Conformational Equilibria of Proteins Nucleic Acids: The Roles of Ion Association or Release, Screening, and Ion Effects on Water Activity. Q Rev Biophys. 1978;11:103–178. doi: 10.1017/s003358350000202x. [DOI] [PubMed] [Google Scholar]
- 30.O’Brien RW, Hunter RJ. The Electrophoretic Mobility of Large Colloidal Particles. Can J Chem. 1981;59:1878–1887. [Google Scholar]
- 31.Ohshima H. Electrophoretic Mobility of a Spherical Colloidal Particle in a Salt-Free Medium. J Colloid Interface Sci. 2002;248:499–503. doi: 10.1006/jcis.2002.8232. [DOI] [PubMed] [Google Scholar]
- 32.Huang QR, Dubin PL, Moorefield CN, Newkome GR. Counterion Binding on Charged Spheres: Effect of pH and Ionic Strength on the Mobility of Carboxyl-Terminated Dendrimers. J Phys Chem B. 2000;104:898–904. [Google Scholar]
- 33.Patra CN, Bhuiyan LB. The Effect of Ionic Size on Polyion-Small Ion Distributions in a Cylindrical Double Layer. Condens Matter Phys. 2005;8:425–446. [Google Scholar]
- 34.Makino K, Ohshima H. Electrophoretic Mobility of a Colloidal Particle with Surface Charge Density. Langmuir. 2010;26:18016–18019. doi: 10.1021/la1035745. [DOI] [PubMed] [Google Scholar]
- 35.Schellman JA, Stigter D. Electrical Double Layer, Zera Potential, and Electrophoretic Charge of Double-Stranded DNA. Biopolymers. 1977;16:1415–1434. doi: 10.1002/bip.1977.360160704. [DOI] [PubMed] [Google Scholar]
- 36.Chatterji A, Horbach J. Electrophoretic Properties of Highly Charged Colloids: A Hybrid Molecular Dynamics/Lattice Boltzmann Simulation Study. J Chem Phys. 2007;126:064907. doi: 10.1063/1.2431174. [DOI] [PubMed] [Google Scholar]
- 37.Das RK, Ruff KM, Pappu RV. Relating Sequence Encoded Information to Form and Function of Intrinsically Disordered Proteins. Curr Opin Struct Biol. 2015;32:102–112. doi: 10.1016/j.sbi.2015.03.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Lindskog S. Structure and Mechanism of Carbonic Anhydrase. Pharmacol Ther. 1997;74:1–20. doi: 10.1016/s0163-7258(96)00198-2. [DOI] [PubMed] [Google Scholar]
- 39.Garcia de la Torre J, Navarro S, Lopez Martinez MC. Hydrodynamic Properties of a Double-Helical Model for DNA. Biophys J. 1994;66:1573–1579. doi: 10.1016/S0006-3495(94)80949-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Mathe J, Aksimentiev A, Nelson DR, Schulten K, Meller A. Orientation Discrimination of Single-Stranded DNA Inside the α-Hemolysin Membrane Channel. Proc Natl Acad Sci USA. 2005;102:12377–12382. doi: 10.1073/pnas.0502947102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Takusagawa F, Hirotsu K, Shimada A. The Crystal and Molecular Structure of Pyromellitic Acid Dihydrate (Benzene-1,2,4,5-tetracarboxylic Acid Dihydrate) Bull Chem Soc Japan. 1971;44:1274–1278. [Google Scholar]
- 42.Kaduk JA, Golab JT. Structures of 2,6-Disubstituted Naphthalenes. Acta Cryst. 1999;B55:85–94. doi: 10.1107/s0108768198008945. [DOI] [PubMed] [Google Scholar]
- 43.Carbeck JD, Colton IJ, Anderson JR, Deutch JM, Whitesides GM. Correlations Between the Charge of Proteins and the Number of Ionizable Groups They Incorporate: Studies Using Protein Charge Ladders, Capillary Electrophoresis, and Debye-Hückel Theory. J Am Chem Soc. 1999;46:10671–10679. [Google Scholar]