Comparison of Two Detailed Models of Aedes aegypti Population Dynamics

Abstract

The success of control programs for mosquito borne diseases can be enhanced by crucial information provided by models of the mosquito populations. Models, however, can differ in their structure, complexity and biological assumptions, and these differences impact their predictions. Unfortunately, it is typically difficult to determine why two complex models make different predictions because we lack structured side-by-side comparisons of models using comparable parameterization. Here we present a detailed comparison of two complex, spatially-explicit, stochastic models of the population dynamics of Aedes aegypti, the main vector of dengue, yellow fever, chikungunya and Zika viruses. Both models describe the mosquito's biological and ecological characteristics, but differ in complexity and specific assumptions. We compare the predictions of these models in two selected climatic settings, a tropical and weakly seasonal climate in Iquitos, Peru, and a temperate and strongly seasonal climate in Buenos Aires, Argentina. Both models were calibrated to operate at identical average densities in unperturbed conditions in both settings, by adjusting parameters regulating densities in each model (number of larval development sites and amount of nutritional resources). We show that the models differ in their sensitivity to environmental conditions (temperature and rainfall), and trace differences to specific model assumptions. Temporal dynamics of the Ae. aegypti populations predicted by the two models differ more markedly under strongly seasonal Buenos Aires conditions. We use both models to simulate killing of larvae and/or adults with insecticides in selected areas. We show that predictions of population recovery by the models differ substantially, an effect likely related to model assumptions regarding larval development and (direct or delayed) density dependence. Our methodical comparison provides important guidance for model improvement by identifying key areas of Ae. aegypti ecology that substantially affect model predictions, and revealing the impact of model assumptions on population dynamics predictions in unperturbed and perturbed conditions.

Introduction

Mosquito-borne pathogens, such as dengue viruses and the malarial protozoans, have major impacts on human health. Some of these pathogens have undergone significant expansion in their range, such as dengue and chikungunya viruses over recent decades (Gubler et al. 1995, Gubler 1998, WHO 2009) or Zika virus in the past year (Musso et al. 2015). Additionally, there is concern that climate change could cause further expansions. New control methods (WHO 2012), including new vaccines against dengue (Webster et al. 2009, Sabchareon et al. 2012, Capeding et al. 2014, Hadinegoro et al. 2015, Villar et al. 2015) and transgenic mosquitoes (Sinkins and Gould 2006, McGraw and O'Neill 2013), are being developed as an alternative or supplement to traditional vector control methods such as insecticide application or source reduction (Ekpereonne et al. 2010, Achee et al. 2015). Modelers of these diseases are being called upon by policy makers to assess the likely impacts of both climate change and novel control measures, and hence to inform control policy and resource allocation decisions. As a result, ever increasingly detailed questions are being asked of mathematical models. In many instances, the ability to answer these questions (for instance, the relative effectiveness of insecticide treatments targeted at different mosquito life stages, or the impact of a given increase in temperature) requires the use of models that include considerable biological detail, raising issues of appropriate levels of model complexity. In order for model predictions to be useful in informing policy decisions, the modelers should have confidence in the robustness of their predictions, or at least to have a clear idea of the limitations of their model's ability to make trustworthy predictions.

The dynamics of mosquito-borne infections are particularly impacted by climatic conditions because the population dynamics of mosquito populations are sensitive to temperature and rainfall and the dynamics of the pathogen within the mosquito are temperature-dependent. Mosquito population dynamics also depend strongly on the local ecology, not least because of density-dependent regulation of mosquito numbers in a given locale. Given the public health significance of these mosquitoes and the potentially large impact that density dependence could have on the success of mosquito control measures, surprisingly little is known about density dependence in these species under natural conditions. Although laboratory studies have provided insight into temperature and resource dependent growth and development of immature mosquitoes (Gilpin and McCleland 1979, Rueda et al. 1990, Arrivillaga et al. 2004), translating these into descriptions of natural environments is challenging (Walsh et al. 2013). For instance, it is unclear how levels of nutrients used in lab experiments compare to those present in reality, or how development of immatures differs between constant and variable temperature settings. Thus, the modeler is not only faced with the question of how much complexity to include in their model but also with the question of how to include incompletely characterized biological processes.

In an ideal world, performance of a model would be evaluated by comparing its predictions to field data. In the case of mosquito population dynamics, few time series of sufficient quality exist to allow such comparisons to be made. Beyond this, when such data do exist they are usually employed to help parameterize the model, tailoring it to the locale of interest, complicating its use for model validation. Sensitivity and uncertainty analyses have been proposed as methods to better understand the limitations on the predictive ability of a model (Xu et al. 2010, Ellis et al. 2011). To assess the importance of parametric uncertainty (i.e. uncertainty concerning the appropriate values of the parameters that appear within a given model), uncertainty analysis considers the range of model outcomes that result when parameter values are drawn from specified distributions. Decomposition of the variation in model outputs in terms of variation in parameters allows for the identification of those parameters (and hence the processes) that most impact model dynamics. Unfortunately, it is typical for such analyses to focus on the dynamics of a single model and hence they fail to account for uncertainty concerning the structure of the model itself.

In this study, we explore the impact of complexity and descriptions of the complexity by comparing the predictions made by two detailed models of the population dynamics of Aedes aegypti, the major vector of dengue, chikungunya and Zika viruses. We aim to identify model assumptions and components that are most explanatory of any observed discrepancies. Given that vector control is currently the major way of controlling arboviral diseases, notably dengue, and that the success of this approach is an important question that models are being asked to address, we pay particular attention to the impact of vector control measures. Although transmission of infection is the ultimate endpoint of interest, in this study, we restrict our attention to mosquito population dynamics.

This paper is organized as follows: we first present Background Information on Ae. aegypti and the broad structure of the two models. In the Methods section, we provide details of the models that are particularly relevant to this study (more comprehensive descriptions of both models can be found in previously published papers) and the methodologies used to compare their behavior. Following the Results section, we conclude with a Discussion that summarizes our findings and the lessons learned from this study.

Background

The mosquito Aedes aegypti is the primary vector of several arboviral diseases, including dengue, the most significant mosquito-borne viral disease of humans with as many as 390 million cases per year (Bhatt et al. 2013). This mosquito is highly anthropophilic: water containers associated with human habitation form the principal larval habitat for Ae. aegypti, and humans are its preferred host. Larval competition impacts the duration of larval development, the probability that a larva will successfully complete its development and the size of the adult that then emerges. This competition is believed to be the major factor regulating the population density of Ae. aegypti, so a description of this process is a key component of population dynamic models for the species (Dye 1984). Unfortunately, larval competition is poorly characterized, both in terms of its mechanistic basis (e.g. the nature of food being consumed and the feeding habits of larvae) and in terms of its outcome (e.g. a description of how larval survival and/or development depends on the number of larvae present) (Walsh et al. 2013). Dynamics of immature stages of Ae. aegypti are subject to environmental impacts, for instance hatching of eggs is promoted by rainfall events and developmental rates of larvae are temperature-dependent (Southwood et al. 1972, Gilpin and McClelland 1979, Rueda et al. 1990).

In this paper we compare two models—Skeeter Buster and AedesBA—that describe the population dynamics of Ae. aegypti. The Skeeter Buster model (Magori et al. 2009), developed at NC State University, is an extension of the earlier CIMSiM model (Focks et al. 1993; 1993a) and its parameterization and performance has been most intensively studied for the geographic setting of Iquitos, Peru (Legros et al. 2011). The AedesBA model (Otero et al. 2006; 2008), developed at the University of Buenos Aires, Argentina, is primarily intended to describe the Buenos Aires setting. These two geographic settings provide an interesting contrast: Iquitos, Peru, has an equatorial climate with year-round frequent rainfall, high humidity and temperature. In contrast, Buenos Aires has a temperate climate with marked seasonality. These models are described in detail elsewhere (Magori et al. 2009, Xu et al. 2010, Legros et al. 2011, Otero et al. 2006; 2008), so here we only describe specific model features that are relevant to the current study.

The two models describe larval development and competition in quite different ways. Skeeter Buster models individual larval habitats (“containers”) and their food resources, with larval growth and development depending on the availability of resources. The food resource of a habitat is depleted by larval growth but replenished over time by accumulation processes (e.g. as vegetative matter falls into a container and microbial growth increases). On the other hand, AedesBA employs a phenomenological description of larval competition at the level of a city block, incorporating a logistic-like larval death term for which per-capita larval mortality increases linearly with larval density. The coefficient of this linear increase effectively sets the larval carrying capacity.

Both models assume temperature-dependent rates drawn mostly from the earlier CIMSiM model (Focks et al. 1993; 1993a), which itself is based upon earlier work of Sharpe and DeMichele (Sharpe et al. 1977). It is assumed that temperature impacts developmental rates of all mosquito life stages, i.e. eggs, larvae, pupae and adults, via factors that reflect the temperature scaling of rates of enzyme kinetics reactions. In Skeeter Buster, it is assumed that mortality takes a nominal value within a window of optimal temperatures, but increases outside the window, reaching 100% daily mortality at specified minimum and maximum temperatures. It should be pointed out that in a given environment, temperatures may always lie within the “ideal” temperature window (this is the case for Iquitos). AedesBA assumes that mortalities of eggs and adults do not depend on temperature while those of larvae and pupae follow a specified functional form (Horsfall 1955; Bar-Zeev 1958; Rueda et al. 1990). Rainfall affects egg hatching in both models: Skeeter Buster explicitly models the water level in individual containers and the heights at which eggs were laid, with egg development and hatching rates being dependent on whether eggs are submerged. In AedesBA, egg hatching is promoted by rainfall events of over 7.5mm, although there is a background rate of egg hatching in the absence of rain.

Both models are spatially explicit, although model space is typically defined at different scales. Skeeter Buster was primarily designed to model individual houses and the containers found at each, while AedesBA usually operates at the city block scale. In Skeeter Buster, adults can move between neighboring houses on a daily basis, leading to a lifetime dispersal kernel that allows movement over a local neighborhood. In addition, rarer longer distance adult movement events are possible. In AedesBA, a subset of adult females (“flyers”) undergoes dispersal in search of oviposition sites; these dispersal events occur to neighboring blocks.

This broad overview of the two models shows that they share many similarities but have important differences. Before exploring how these impact the dynamics of the predicted populations, we discuss specific structural details of the models in more detail.

Methods

Model description: Skeeter Buster

Skeeter Buster (Magori et al. 2009) models the development of immature stages of Ae. aegypti (eggs, larvae and pupae) in individually simulated water-holding containers, as well as adult stages in individual dwellings. Physiological development of cohorts of immatures is tracked in a temperature-dependent fashion described above. Transition to the next immature stage can only occur if development has reached a predetermined threshold age and weight, and additional requirements can be imposed for specific life stages. For example, developed eggs hatch into larvae with different probabilities depending on whether they are submerged in water, and on the temperature of the water. The water level inside each container is determined based on predicted water input (from rainfall and/or manual input) and evaporation (Focks et al. 1993).

The weight of larvae is modeled by explicitly tracking the amount of nutritional resources present in a given container on any given day. When food is limiting, the increase in weight of a larval cohort is slowed down, resulting in a longer development time. Starving larvae are also subject to an additional mortality. This competition for food results in density-dependent larval development time and survival. Food is randomly added to every container at a given average daily rate, and decays at a fixed rate. If food is depleted from larval consumption within a given container, it can take several days to reach this maximum again, potentially resulting in delayed density dependence (i.e. the presence of larval cohorts in a container can render it less suitable for subsequent cohorts).

Stochasticity in these developmental processes means that there is some variation in the emergence time for a cohort of larvae that hatched on a given day. Both the average and standard deviation of emergence times depend on environmental and nutritional conditions. In one representative set of simulations, the coefficient of variation (i.e. standard deviation of emergence time divided by the average emergence time) was equal to 0.18 (Kenichi Okamoto, personal communication).

Adults are initially assigned to the site where the container from which they emerge is located. In the simplest form of the model (as employed in this study), individual sites are laid out on a regular rectangular lattice, and adults move every day to one of the four immediately neighboring sites (von Neumann neighborhood) with a probability of 30% (direction chosen at random). Additional rare events of long range dispersal can be simulated, in which an adult can migrate to any site (with equal probability) located no further than a given maximum distance (here, 15 steps) with a daily probability of 2%.

Females are assumed to mate only once (Craig 1967), and unmated females have the opportunity to mate every day if males are present in the same location. Female fecundity is proportional to weight (Naksathit et al. 1998), which is determined by the weight at pupation of the larval cohort from which a given female originates (and therefore depends on the nutritional contents of the container in which this cohort has developed). We remark that, unlike many other population dynamic models of Ae. aegypti (including its CIMSiM parent), Skeeter Buster explicitly tracks male mosquitoes (because one of its intended uses is to explore transgenic control strategies), although this aspect of the model is not of major concern for this study.

Model description: AedesBA

The model that was developed at the University of Buenos Aires, nicknamed AedesBA, is a continuous time stochastic compartmental model where the sub-populations progress according to jumps with distributions described by a Kolmogorov forward equation (Feller 1940). The AedesBA model presented in Otero et al. 2006 and Otero et al. 2008 describes Ae. aegypti populations based on the life cycle of the mosquito and its dispersal. It considers six different sub-populations: eggs, larvae, pupae and three kind of females: adult females in their first gonotrophic cycle (A1 females), females in subsequent gonotrophic cycles (A2 females), and flyers (F), which are the adult females who have already finished a gonotrophic cycle and fly in order to deposit their eggs. The model assumes that mosquito dispersal is negligible during the gonotrophic cycle, and once the gonotrophic cycle ends, the female begins to fly, becoming a Flyer in search of oviposition sites. After egg laying she returns to being a gonotrophic female.

The population of adult male mosquitoes is not taken into account explicitly and it is assumed that (on average) one half of the emerging adults are females. The availability of food, mates, and humans was not incorporated into the model because these variables are not believed to be limiting factors in a temperate city such as Buenos Aires.

AedesBA is a spatially explicit model, in which the region of interest is represented by a collection of patches arranged on a grid. Dynamics within a patch are assumed to be homogeneous, while adults may disperse between patches, described by population dispersal coefficients.

The evolution of the six sub-populations in each patch is affected by twelve different possible local events: egg maturation and hatching, pupation, adult emergence, completion of gonotrophic cycles of adults A1 and A2, oviposition by flyers, and six death events, each one corresponding to each sub-population. Events occur at rates that depend on population values and on temperature. Given that temperature changes over the course of the year, this introduces a time dependence in the event rates (Otero et al. 2006).

The AedesBA model used for this work is an improved version of the model presented in Otero et al. 2008. The modifications correspond to the incorporation of the rain as the main event triggering the hatching of mature eggs. The population and events taken into account in the model are presented in Appendix S1: Fig. S1.

Immature eggs mature at a temperature-dependent rate (Otero et al. 2006). Then, the mature eggs can hatch following two different paths: “normal hatching” is induced by a single rainfall event of at least 7.5mm, the second process, “abnormal hatching”, is independent of rainfall and simulates several other possible mechanisms such as human action (watering of containers), spontaneous hatching, eggs laid on top of the water and other mechanisms that do not depend on rain (Appendix S1: Fig. S1). About 80% of the eggs mature following the normal path when rains are frequent. The hatching rate depends on the temperature in the same form as the egg maturation rate and the absolute value of hatching rate at 27°C is 0.583 day⁻¹, corresponding to the values reported by Southwood et al. 1972.

Simulated environments: Iquitos and Buenos Aires

We carried out simulations in two distinct environments: a tropical setting Iquitos, Peru (3°44′S 73°15′W) and a temperate setting Buenos Aires, Argentina (34°36′12″S 58°22′54″W). The models were set up by defining for each situation (i) a set of climatic data representative of the simulated location, and (ii) a spatial grid of individual sites. Because both models typically operate at different spatial scales, part of this set-up task involves selecting a common spatial scale, i.e. defining each individual site in the models as a specific unit area in the city, with containers assigned to each site in Skeeter Buster, and a specific density of breeding sites assigned in AedesBA.

Location-specific climatic data was obtained from the Climate Data Online database of the National Climatic Data Center (NCDC) at weather stations situated in Iquitos (5 years, January 1st 1999 to December 31st 2003) and Buenos Aires (5 years, July 1st 2005 to July 1st 2010). Data collected included daily temperatures (minimal, maximal and average), amount of precipitation and relative humidity. The daily mean temperature and daily rainfall of Iquitos and Buenos Aires in the periods studied are shown in Appendix S1: Figs. S2 and S3, respectively.

In Skeeter Buster, the simulation grid was defined in both cases (unless specified otherwise) as a set of 400 sites arranged on a 20×20 square. Each site was assigned 10 identical containers, i.e. a total of 4,000 containers in the simulated area. Container characteristics differed between the Iquitos and Buenos Aires setups in two ways. First, the daily nutritional inputs into each container were defined in a location-specific fashion to reflect differences in population density between these two cities (see Calibration of simulated population densities). Second, the filling methods for each container (used by Skeeter Buster to calculate and track water level within containers) differed between locations. In Iquitos, containers were set to only receive water from passively collected rainfall, since this type of habitat accounts for a large majority of pupal production in this population (Morrison et al. 2004). In Buenos Aires, on the other hand, it was found necessary to set a fraction of the containers in each site (1, 3 or 5 out of 10) to be manually-filled, i.e. receive water daily irrespective of rainfall. Without these manually-filled containers, the Buenos Aires population would go extinct during the winter in all simulations.

In AedesBA the simulation grid was defined in both cases (unless specified otherwise) as a grid of 400 sites arranged on a 20×20 square, each of which was assumed to have the same density of breeding sites. Breeding site density differed between Iquitos and Buenos Aires simulations and was defined in each location as described in the following section.

Calibration of simulated population densities

For proper model comparison, the average mosquito densities per unit area in both models were set to identical values. In Skeeter Buster, this was done by adjusting the daily input of food in each container in the simulated grid. We ran simulations with food input values ranging between 0.2 and 2.0 mg.day⁻¹ (increment of 0.1) in Iquitos, and between 1.0 and 4.6 mg.day⁻¹ (increment of 0.4) in Buenos Aires. In AedesBA this procedure was carried out by adjusting the breeding site density in the simulated grid. We ran simulations with breeding site densities ranging between 1 and 25 (increment of 1) in Iquitos, and between 1 and 50 (increment of 5) in Buenos Aires.

In both settings, both models were run for a one-year burn-in period and then the average number of adult females in the simulated area was calculated by averaging over the next four whole years in the Iquitos case and across four productive seasons (defined as the December 1st to June 30th time span) in the Buenos Aires case. For each combination of model and geographic setting, a linear fit was produced to describe the relationship between this average number of females and the daily food input value (Skeeter Buster) or breeding site density (AedesBA). The calibrated food input value or breeding site density was then derived from this linear relationship according to the desired average density (identical in both models for a given geographic setting). All subsequent simulations were then carried out using this food input value or breeding site density.

Artificial environmental inputs

In order to investigate the sensitivity of each model to temperature and rainfall data from the location of interest, artificial weather inputs were created for each of the environments simulated in this study (Iquitos and Buenos Aires). In these artificial inputs, daily temperature θ(t) was either kept constant (using the average α of daily values collected across one year) or followed a sinusoidal curve fitted using non-linear regression (Equation 1) to the observed daily values:

$$\theta \left(t\right)=\alpha +\beta \cos \left(\frac{2\pi t}{\gamma }+\delta \right)$$ (1)

Here β is the seasonal amplitude of temperature variations, γ = 365 days is the period and δ is the phase. For Iquitos, this fit yielded values of α_Iq = 25.8 °C and β_Iq = 0.6 °C, whereas in Buenos Aires we obtained α_BA = 17.9 °C and β_BA = 6.2 °C.

Daily rainfall amounts ρ(t) were calculated by partitioning the total amount of rain observed in a given year, P, using a fixed period τ (equal to 1, 2, 4, 6, 8 or 10 days) between rainfall events (Equation 2):

$$\rho \left(t\right)=\{\begin{array}{cc}\frac{P\tau }{365}\hfill & \text{if}t\mathrm{mod}\tau =0\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}$$ (2)

Simulated control

Vector control interventions were simulated in both models in order to investigate the dynamics of population depletion and subsequent recovery from such interventions. We modeled four types of control: (i) a larvicidal control, in which all larvae were removed from each container present in the targeted area; (ii) an adulticidal control, where adults of both sexes were removed across the targeted area; (iii) a combination of the above larvicidal and adulticidal controls; and (iv) a comprehensive control where individuals of all stages (eggs, larvae, pupae and adults) were removed from the targeted area.

In each case, control was applied for one week either to the entire simulated area, or restricted to a set of sites situated in the center of this area (e.g., a 10×10 target square at the center of a 20×20 grid for cases (i), (ii) and (iii) or a 30×30 target square at the center of a 45×45 grid for case (iv)). Note that, in Skeeter Buster, the dynamics of containers was not otherwise affected by control, i.e. water level dynamics and food accumulation was modeled normally.

We recognize that we are modeling highly idealized control regimes. In reality, control measures will not be this effective: it will typically be impossible for a control team to gain access to every single property or to achieve complete coverage in those properties that are visited. However, the use of these extremes was seen as helpful in comparing the models.

Results

As described above, simulations were carried out for both tropical (Iquitos) and temperate (Buenos Aires) environments. Because there were many similarities between these two sets of results, we shall focus on the results obtained in the Iquitos setting, presenting the majority of the results from the simulated Buenos Aires environment in Appendix S1. Unless stated otherwise, all the results shown correspond to averages taken over 20 simulation runs.

Model Calibration

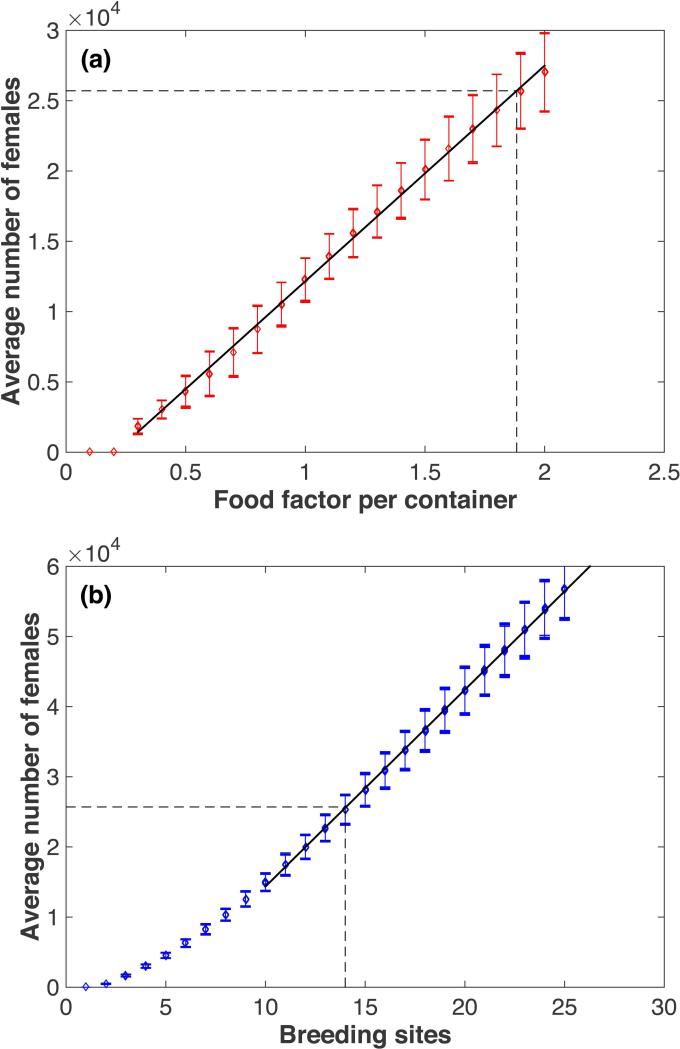
For calibration purposes, simulation results were obtained using temperature and rainfall data from Iquitos for the period 1999 through 2003, as described above. Figure 1 shows the average number of adult females, calculated over the last four simulated years, as a function of the daily food input values for Skeeter Buster, and of the number of breeding sites for AedesBA. The linear fit constructed for both models (Fig. 1) gives us a direct relationship between these two parameters. Since both models were originally designed to operate at different spatial scales, as described in the Methods (Skeeter Buster at the level of individual houses, AedesBA at the level of city blocks), we first had to select the specific spatial scale at which both models would be set up throughout this study. We elected to operate at a baseline density of about 60 females per individual site in each model (i.e. about 25,000 adult females in the whole population), a density representative of those observed in the field in one city block in Iquitos, assuming each block represents approximately 30 houses. Therefore, in both models, and for the purposes of this study, each individual spatial location is designed to represent such a city block.

Figure 1.

Calibration of simulated population densities. (a) Top panel: Skeeter Buster model. The average total number of female adults (Nf) in the population is plotted against the value of the food factor per container (FF). The black line shows the linear regression (excluding values where the population is extinct) with the following equation: Nf = −3161 + 15327*FF. (b) Bottom panel: AedesBA model. The average total number of female adults in the population is plotted against the number of breeding sites per grid cell (Nbs). The black line shows the linear regression (restricted to values of Nbs>10) with the following equation: Nf = −13690 + 2805*Nbs. The dashed lines mark the selected values for the population of Iquitos (corresponding to Nf = 25704).

This calibration process gave us default values of 1.88 mg.day⁻¹ food input per container in Skeeter Buster and 14 breeding sites per block in AedesBA. All subsequent simulations regarding Iquitos were carried out using these values. We chose not to carry out a detailed calibration of the dispersal parameters between the two models as visual inspection suggested that the default parameters gave reasonably similar dispersal patterns.

Artificial weather

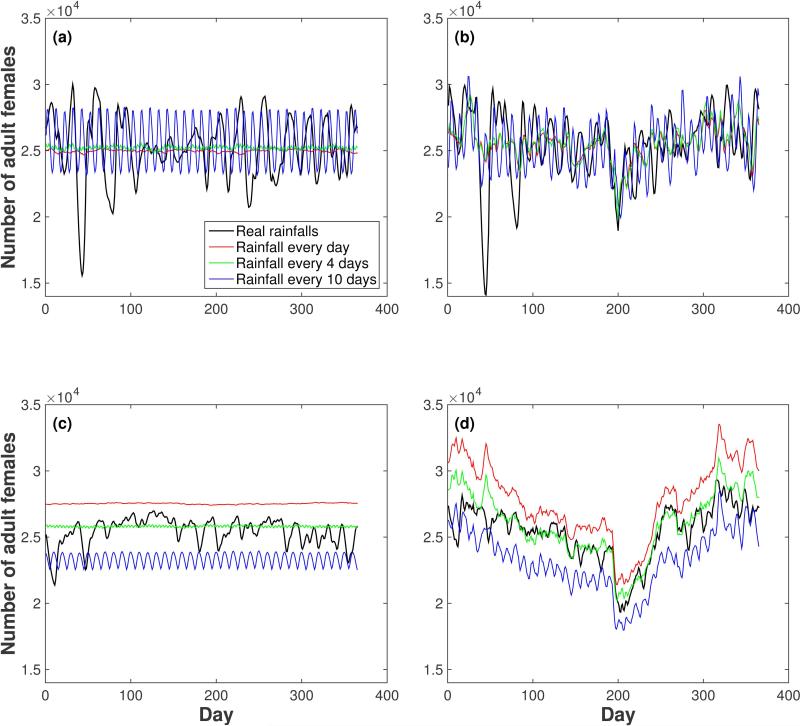
The results of the average of 20 runs using artificial weather inputs in the Iquitos setting are presented in Figs. 2 and 3. While the calibration process ensures that the time series from both models have the same average numbers of mosquitoes when real weather data is used, the variation around this average is more pronounced in Skeeter Buster than in AedesBA (Fig. 2(a) and (c)). Unsurprisingly, when all variation in daily temperatures and rainfall is removed, the time series from both models are virtually constant, albeit at different values (around 25,000 adult females in Skeeter Buster and 27,500 adult females in AedesBA). In AedesBA, the average number of females across the year decreases with increases in the interval between rainfalls (this pattern is best seen when daily temperatures are kept constant (Fig. 2(c)), but still holds with real temperature values (Fig. 2(d))) or with sinusoidal temperature time series, when only seasonal variation is maintained (see Appendix S1: Fig. S4). This pattern of sensitivity of average mosquito density to rainfall frequency is absent from Skeeter Buster (Fig. 2(a), (b) and Appendix S1: Fig S4, panel (a)), where the average number of adult females remains constant across rainfall regimens.

Figure 2.

Effect of artificial weather inputs on the number of adult females in the Iquitos setting. (a) Skeeter Buster model, constant daily temperatures, (b) Skeeter Buster model, actual daily temperatures, (c) AedesBA model, constant daily temperatures, (d) AedesBA model, actual daily temperatures. Each curve corresponds to the time course of the number of adult females for different rainfall regimes: real rainfalls (black) and periodic rainfalls (according to equation (2)) with a period of 1 day (red), 4 days (green) or 10 days (blue). All results shown are averages over 20 simulation runs.

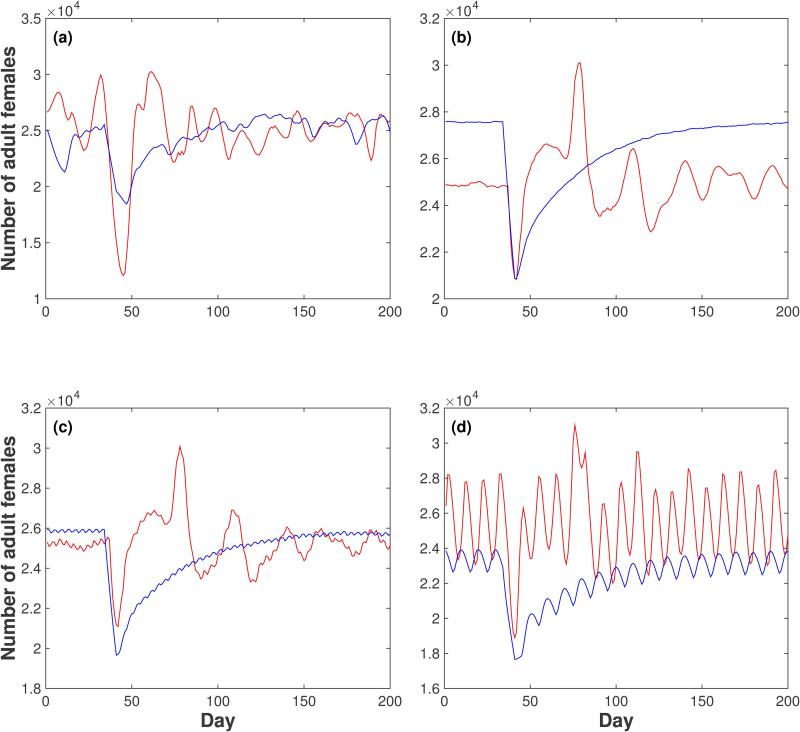
Figure 3.

Effect of a one-week drop in temperature on the number of adult females. A sudden drop in temperature from 25.8 °C (the annual average) to 20 °C is simulated between days 35 and 41 inclusive, under various rainfall regimes: (a) actual daily rainfall, (b) rainfall every day, (c) rainfall every 4 days and (d) rainfall every 10 days. The amount of daily rainfall is adjusted in the periodic regimes so that the annual total is the same across all 4 regimes. Plotted curves correspond to the time course of the number of adult females according to the Skeeter Buster model (red curves) and the AedesBA model (blue curves). All results shown are averages over 20 simulation runs.

When a sudden 7-day drop in temperature of 5.8 °C is simulated in Iquitos (Fig. 3), both models respond as expected with a drop in the overall number of females (as well as in other life stages, not shown here). After this one-week period of low temperatures, however, the models both predict a return to the previous density, but differ in the timing of this return. In AedesBA the numbers gradually increase to reach the pre-perturbation value in about 100 days, whereas Skeeter Buster predicts a faster recovery in under 20 days. Skeeter Buster also exhibits a temporary “rebound” above the pre-perturbation value, occurring approximately 40 days after the return to default temperatures (a time which corresponds to one generation in these conditions in the model), resulting from the lowered competition in breeding sites as a result of the colder conditions.

Simulated control

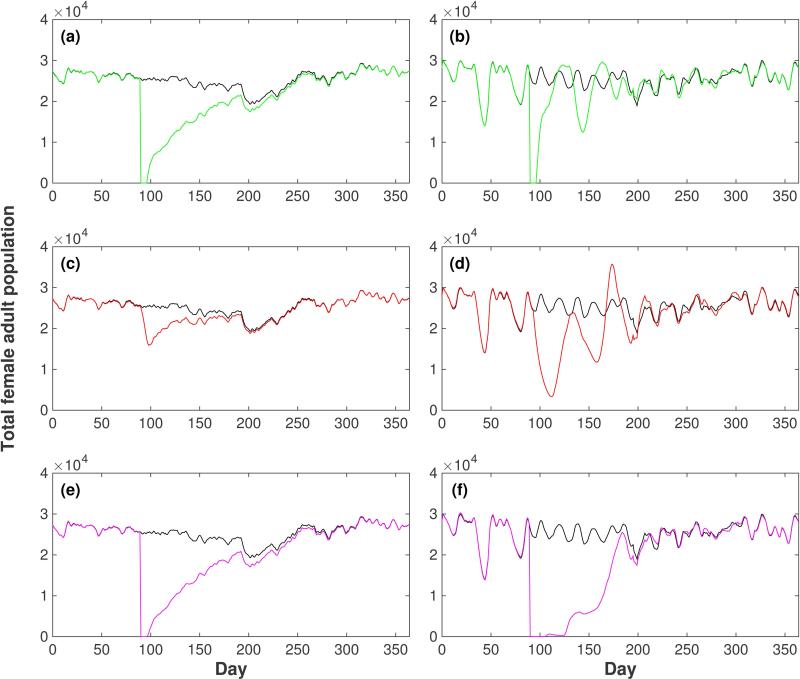
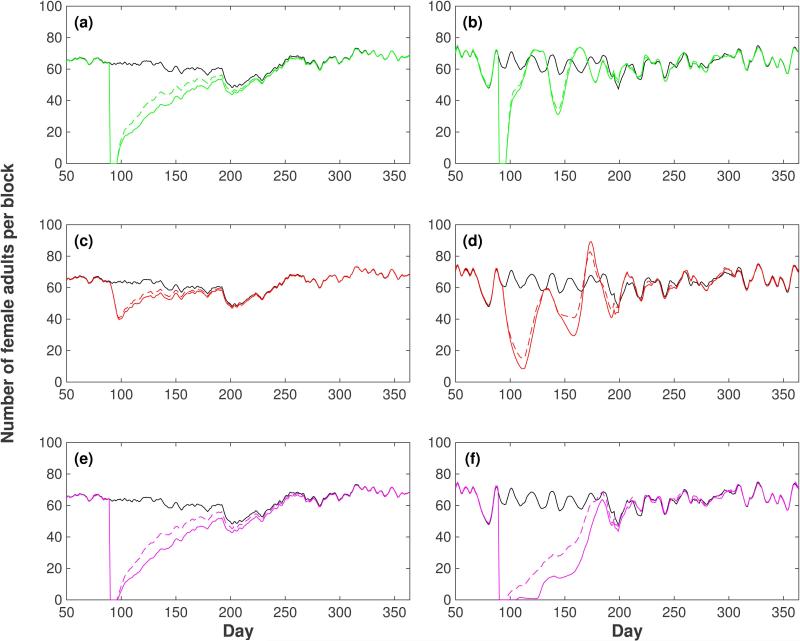
We first studied the effect on the female adult population of three idealized vector control interventions in Iquitos. These interventions consisted of the complete elimination of adults, larvae and both populations simultaneously for one week (days 90 – 96). As explained in the Methods section these strategies correspond to the application of adulticides, larvicides and both simultaneously. Figure 4 compares the time course of the total female population in the 20×20 block grid in both populations under the three different interventions: adulticidal control (Fig. 4(a) and Fig. 4(b)), larvicidal control (Fig. 4(c) and Fig. 4(d)) and both controls simultaneously (Fig. 4(e) and Fig. 4(f)).

Figure 4.

Effect of control strategies on the female adult population in Iquitos. Three different strategies were simulated: use of adulticides (first row: panels (a) and (b), green line), use of larvicides (second row: panels (c) and (d), red line) and use of adulticides and larvicides simultaneously (third row: panels (e) and (f), magenta line). The control strategies were carried out for one week (days 90 to 96) with 100 % efficiency. Left column (panels (a), (c) and (e)): AedesBA model. Right column (panels (b), (d) and (f)): Skeeter Buster model. The time series of the total female population in the grid without intervention (black line) is shown in each panel. All results shown are averages over 20 simulation runs.

In the case of the AedesBA model we observed that adulticidal control is more efficient than larvicidal control (Fig. 4(a) vs Fig. 4(c)). When adults are controlled there is a much larger reduction of the adult population and there is a longer time for the controlled population to return to the trajectory of the uncontrolled population (longer than 100 days compared to less than 100 days). The recovery of the population after the intervention is smooth, slow and without oscillations. The use of the combined strategy of adulticidal and larvicidal control (Fig. 4(e)) does not show any significant advantage compared to the adulticidal control.

In the case of the Skeeter Buster model (Fig. 4(b), (d) and (f)) we observed damped oscillations of the populations after the interventions in agreement with the presence of delayed density dependence. During these oscillations the population size transiently increases beyond its pre-intervention size. Interestingly, the time taken for the recovering population to return to dynamics comparable to the uncontrolled population is fairly similar (roughly 100 days) to that seen for the AedesBA model, even though the manner of the return is quite different. The use of the combined strategy of adulticidal and larvicidal control (Fig. 4(f)) seems to be more efficient than the individual controls and in this case the population does not show any significant oscillation.

In order to study the effect of adult dispersal on the recovery of the populations we performed interventions in only a small part of the 20×20 block grid. In this case the control was performed in a square area of 100 blocks in the center of the 20×20 grid. Again, the three control strategies—use of adulticides, larvicides and both simultaneously—were carried out for one week (days 90-96 of the second year of simulation). The time courses of the female population densities (population per block under control) for both models without interventions and for the three control strategies in the 20×20 grid and in the 10×10 grid are shown in Fig. 5.

Figure 5.

Effect of control strategies on the female adult population in Iquitos, with the control performed in the whole area (20×20 block grid) as well as in a smaller area of 10×10 blocks in the center of the 20×20 grid. Three different strategies were simulated: use of adulticides (first row: panels (a) and (b), green lines), use of larvicides (second row: panels (c) and (d), red lines) and use of adulticides and larvicides simultaneously (third row: panels (e) and (f), magenta lines). Solid lines represent control in the whole 20×20 grid, dashed lines represent control in the central 10×10 square only. The control strategies were carried out for one week (days 90 to 96) with 100 % efficiency in their respective target areas. Left column (panels (a), (c) and (e)): AedesBA model. Right column (panels (b), (d) and (f)): Skeeter Buster model. The average number of female adults in each block that is under control (and only in those blocks) is plotted for each type of control, along with the corresponding time series in a population with no intervention (black line). All results shown are averages over 20 simulation runs

For the AedesBA model the recovery is slightly faster in the case of the control in the 10×10 grid compared to control in the entire 20×20 grid. This is also the case for the Skeeter Buster model for each of the three controls, however in the case of simultaneous adulticidal and larvicidal control we observed a bigger difference between the intervention in the 20×20 grid and in the 10×10 grid.

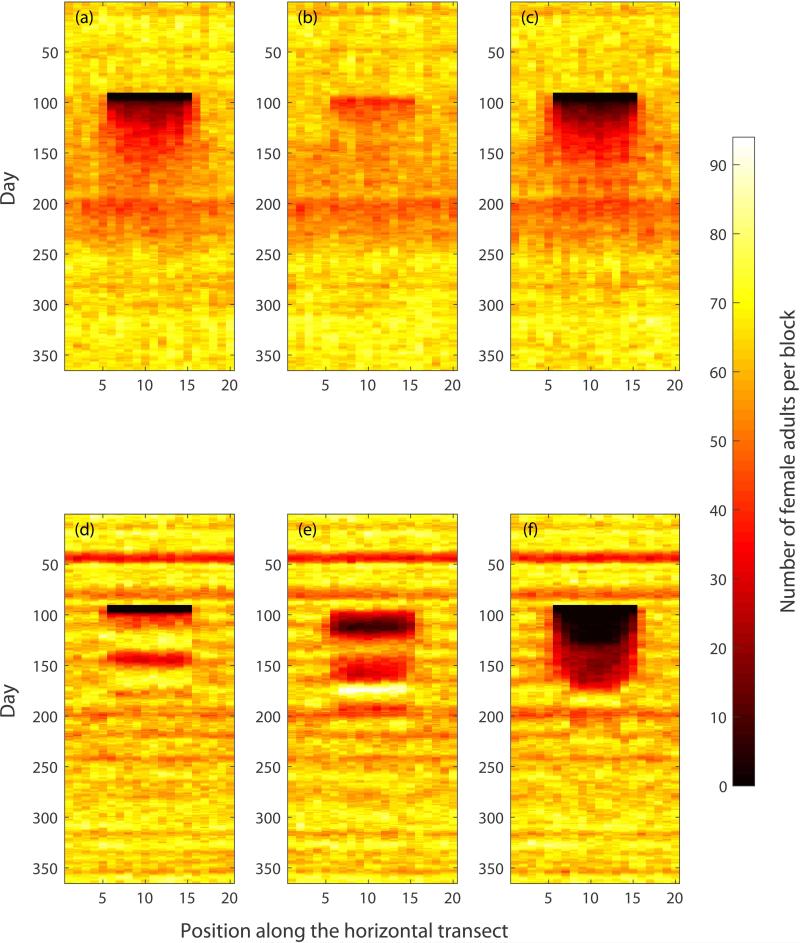
To illustrate the spatial aspects of population recovery, Fig. 6 depicts the evolution of the female adult population along a 20 block transect bisecting the grid. The horizontal axis corresponds to block position along the 20 block transect and the vertical axis corresponds to time. Figure 6 (a), (b) and (c) correspond to adulticidal control, larvicidal control and both controls for the AedesBA model, and Fig. 6 (d), (e) and (f) correspond to adulticidal control, larvicidal control and both controls for the Skeeter Buster model. For both models we can see that the recovery of the population is faster in the borders of the 10×10 grid compared to the recovery in the center, compatible with adult dispersal from the untreated region of the grid to the zone under intervention. This effect is particularly noticeable in situations where population suppression is effective and recovery is largely monotonic (i.e. for AedesBA when adulticide is deployed and Skeeter Buster when both adulticide and larvicide are used), as witnessed by the “D-shaped” pattern in the corresponding spatiotemporal plots (Figs. 6 (a), (c) and (f)).

Figure 6.

Evolution of the female adult population along a 20 block transect taken through the center of the grid under various control interventions. The horizontal axis corresponds to the block position along the 20 block transect, the vertical axis corresponds to time. The color corresponds to the number of female adults in a given block according to the color bar on the right. First row (panels (a), (b) and (c)): AedesBA model. Second row (panels (d), (e) and (f)): Skeeter Buster model. First column (panels (a) and (d)): use of adulticide. Second column (panels (b) and (e)): use of larvicide. Third column (panels (c) and (f)): simultaneous use of adulticide and larvicide. Each control strategy was simulated with 100% efficiency during days 90 through 96 in a 10×10 grid in the center of the 20×20 simulation arena. Note that this 7-day window is visible as a black rectangle in panels (a), (c), (d) and (f), where the use of adulticide removes every female adult from the targeted area. All results shown are averages over 5 simulation runs.

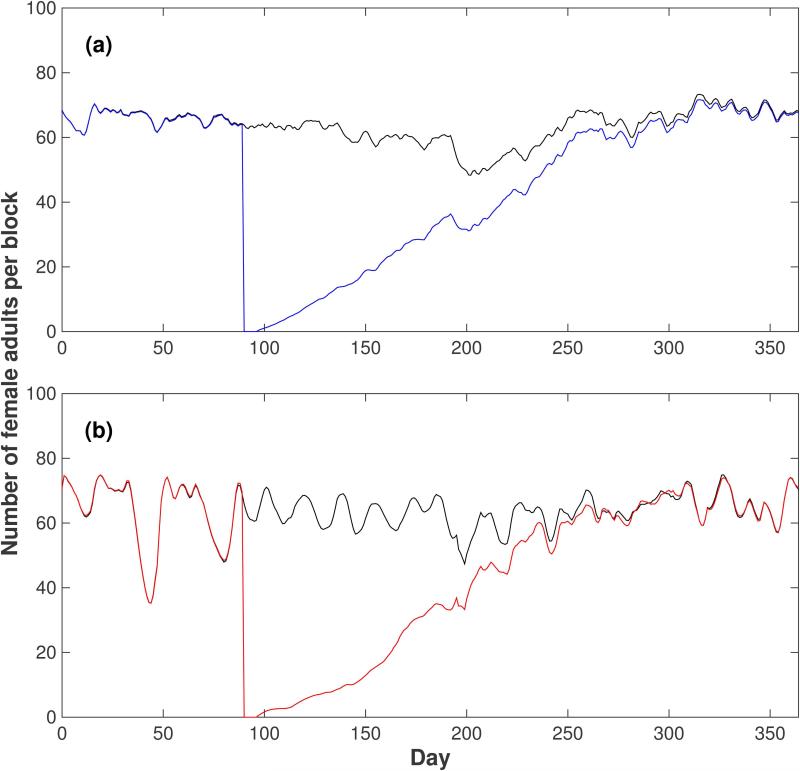
We studied another control intervention consisting of a comprehensive control where individuals of all stages (eggs, larvae, pupae and adults) were removed from the target area. The grid considered was a square grid of 45×45 blocks and the target area consisted of the central 900 block (i.e. a 30×30 grid in the center of the 45×45 grid). In this case the recovery of the population in the central grid is initially due to mosquito dispersal, i.e. involves a recolonization process. Figure 7 shows the effect of this control on the evolution of the female adult population in Iquitos. A similar time course of the female adult population density is observed for both models. The spatiotemporal dynamics following this control measure are shown in Fig. 8.

Figure 7.

Effect of targeted elimination of all mosquito stages on the evolution of the female adult population in Iquitos. (a) Top panel (blue line): AedesBA model. (b) Bottom panel (red line): Skeeter Buster model. The control strategy was simulated with 100% efficiency on all life stages (eggs, larvae, pupae and adults of both sexes) in a 30×30 grid in the center of a 45×45 grid for one week (days 90 to 96). The time course of the female adult population density is shown in each panel, along with the corresponding time series in a population without intervention (black line). All results shown are averages over 20 simulation runs.

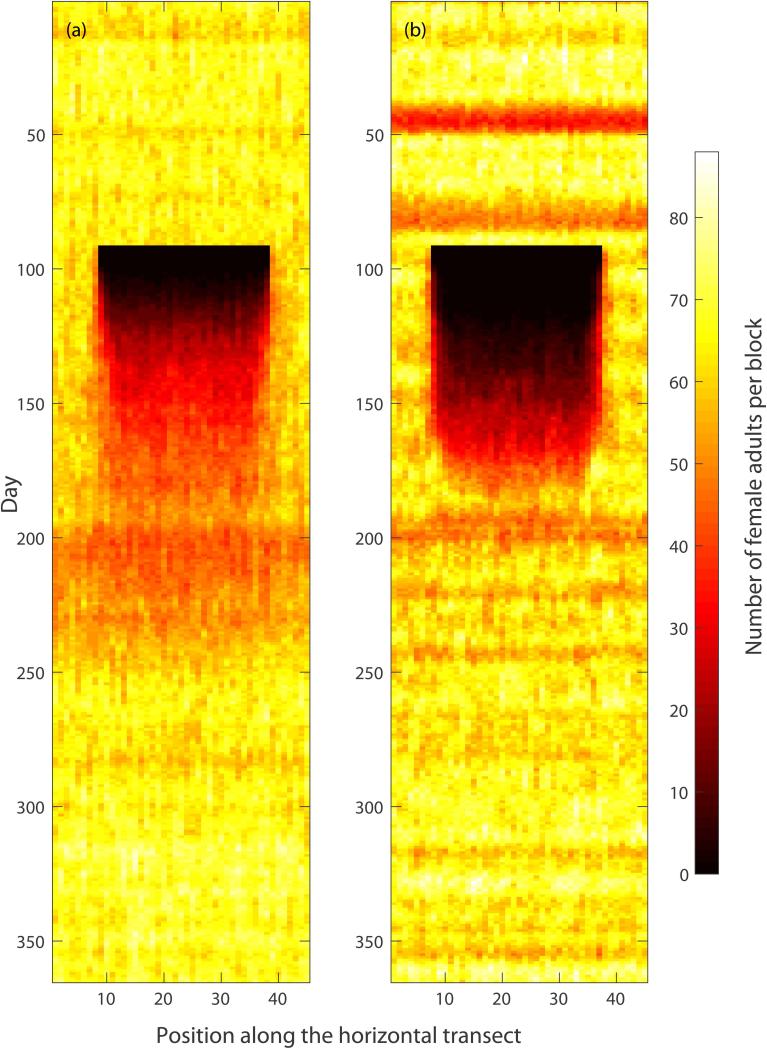
Figure 8.

Evolution of the female adult population along a 45 block transect taken through the center of the grid, with targeted elimination of all mosquito stages in the central area. The horizontal axis corresponds to the block position along the 45 block transect, the vertical axis corresponds to time. The color corresponds to the number of female adults in a given block according to the color bar on the right. Panel (a): AedesBA model. Panel (b): Skeeter Buster model. Control was simulated during days 90 through 96 in a 30×30 grid in the center of the 45×45 simulation arena, and was assumed to eliminate all mosquito stages (eggs, larvae, pupae and adults of both sexes) with 100% efficiency in each targeted block. All results shown are averages over 5 simulation runs.

Discussion and Conclusions

This study considered the behavior of two models for the population dynamics of the Aedes aegypti mosquito under both unperturbed and perturbed (i.e. in the presence of mosquito control measures) conditions. The two models differ in their complexities, specifically the level of biological detail used to describe the system, having several major differences in their underlying biological assumptions while still sharing several others.

Both models have been confronted to some extent with observed field dynamics (Legros et al. 2011, Otero et al. 2008), but when dealing with this type of biologically-detailed spatial model, this approach is associated with several challenges. First, the amount of entomological field data available for comparison with model predictions is often limited, as collection of entomological data at the spatial scale characteristic of these models is extremely challenging and resource-consuming. Additionally, when available, such data is typically obtained in an unperturbed mosquito population, and there is little field data available to test model predictions after a well-characterized perturbation. Finally, it should be noted that location-specific entomological data is needed to calibrate these models to a location of interest, as illustrated in this study. This process substantially limits the ability to use the same data to assess model predictions.

Consequently, we elected to compare the behavior of the two models against each other in diverse environmental settings, including when populations are subjected to a variety of perturbation scenarios. With this approach we aimed to determine which biological assumptions led to important differences in predicted dynamics and hence to uncover those biological processes that deserve closer experimental study in order to improve the predictive ability of these (and other) models for Ae. aegypti population dynamics.

The population dynamics of Ae. aegypti are known to be impacted by weather (temperature, humidity and rainfall) and are generally believed to be regulated by density-dependent processes acting on immature life stages. The two models differed in the way they modeled these features and notable differences in dynamics were observed as a consequence. Patterns of rainfall had a larger impact on dynamics in AedesBA than in Skeeter Buster: significant rainfall events (>7.5mm of rain in a day) are assumed to trigger hatching of eggs in AedesBA, while Skeeter Buster tracks the level of water in containers, tending to smooth out the impact of daily differences in rainfall. Concentration of precipitation in such rainfall events leads to a decrease in the overall predicted density of mosquitoes in AedesBA compared to when the same total amount of precipitation falls more evenly over time; this effect is not seen in Skeeter Buster. In the Buenos Aires setting, Skeeter Buster required the presence of containers that were manually filled with water in order to allow persistence of the mosquito population in the model.

AedesBA assumes that larval populations obey logistic-type growth, with per-capita larval death rates that increase linearly with the current larval population density. In contrast, Skeeter Buster employs a resource-driven description of larval density dependence, tracking food input and utilization within individual containers and with food-dependent larval development and mortality rates. There is a fundamental difference between density dependence in the two models: in AedesBA, density dependence is a function of the current larval density whereas in Skeeter Buster it is a function of the (recent) history of a container. This distinction is commonly characterized as direct versus delayed density dependence and has a marked impact on the response to control predicted by the two models. In Skeeter Buster, suppression of the immature mosquito population (whether directly by larvicide or indirectly by suppression of the egg-laying adult female population) leads to an accumulation of food in containers, providing an abundance of resources for immatures present following the cessation of control. Oscillatory “boom and bust” dynamics then ensue: the immature population can grow and develop rapidly, causing the adult population to exceed that seen in the uncontrolled setting before resource depletion causes it to decrease (see Figs. 4(b) and (d), for example, but not in Fig. 4(f)). In contrast, in the AedesBA model, the population returns to its pre-control state in a predominantly monotonic fashion (e.g. Fig. 4 (a), (c) and (e)). Cohort effects in the development of immatures also play into the dynamics predicted by Skeeter Buster, although they are most noticeable in delaying the appearance of adults following the combined adulticide/larvicide control (Fig. 4(f), when adults are visible after about day 110). No such delay is seen in AedesBA because its first order kinetics assumption for immature development allows the rapid development of a fraction of immatures, enabling the adult population to begin recovery almost immediately after the cessation of control (Fig. 4(e)).

Despite the large number of differences between both models, most of the differences in performance can be tracked to the subsystems corresponding to the relations between food, competition and development. This fact should not be a surprise. The description of the life budget of the mosquito has been taken from the same sources and under the same “physiological assumption” meaning that the physiological characteristics of the species determine its development (opposite views would give relevance to local strains and environmental interactions). The relation to the environment and the ecological factors (such as intra-specific competition) are among the lesser known parts of Ae. aegypti biology. It is also at this point where the models of the mosquito must be detached from the rest of the universe to make them possible. Both facts combined imply that the models run on conjectures and compromises about biology at this point. The consequences of such conjectures and compromises do not show up under standard conditions but rather in the face of exceptional circumstances such as control methods or severe weather fluctuations (e.g. droughts). We must keep in mind that both models had been previously compared to data such as egg-trap counts in Buenos Aires city and both were able to reproduce the data (Legros et al. 2011, Otero et al. 2008). In the standard language of modeling, both models had been validated, yet they would suggest different control strategies. The observation puts validation in perspective: successful reproduction of behavior seen under one circumstance is no guarantee that a model will perform satisfactorily in other situations.

From the viewpoint of a model user, and for decision makers who want to rely on models of Ae. aegypti population dynamics, the present comparison exercise highlights several important lessons that should be kept in mind when using models in such a context. First and foremost, this emphasizes the fact that model outcomes are inherently dependent on model features, structure and underlying assumptions, sometimes in a complex fashion and, importantly, in ways that cannot always be anticipated by a priori knowledge about a given model. For example, if the regular parameters used for Skeeter Buster to describe mosquito populations in Iquitos are used in Buenos Aires (changing the climatological data) the prediction would be the extinction of the population. This stems from Skeeter Buster's assumptions on handling water levels and filling methods of larval breeding sites, and has consequences on population dynamics that (i) can be drastic, and (ii) are strongly dependent on weather patterns, specifically seasonality of precipitation. Similarly, the smooth recovery of mosquito populations after a complete intervention predicted by AedesBA is more likely than not to be the result of modeling decisions. Because of its design in terms of a few compartments (sub-populations), the modeled mosquito population in AedesBA does not exhibit strong cohort effects: the coefficient of variation (CV) for development times is in the range 0.86 to 0.70, while field data reported in Southwood et al. 1972 is associated with a CV of 0.33 and laboratory data in Rueda et al. 1990 report values of 0.07. (Follow-up explorations prompted by the current study led to the assertion that the CV is a function of the environmental conditions (abundance of food, see Romeo Aznar et al. 2015)).

Beyond these observations, the most important lessons from this comparison study relate to the use of models for decision-making, and, by extension, to the choice of models for such purposes. Generally speaking, our results illustrate the complex fashion in which model outputs and model assumptions are related. In this study, this was revealed by the many (and sometimes unexpected) differences in model output and the process undertaken to trace these differences back to specific model components. This complexity makes it very difficult to define what features a model should include, or to choose a specific model from a set of available models, even within the framework of a specific scientific question of interest. For example, in this study, we show that the simulation of localized vector control is sensitive to model assumptions about mosquito life history, weather patterns, breeding site distribution and human-mediated manual filling of containers. While some of these aspects might have been considered a priori, others are far less trivial. For this reason, we choose to refrain from making recommendations about which model to use for any specific question of interest, and we generally argue that this is a difficult question to answer, across all fields of ecological modeling.

Instead, we emphasize two important lessons from this study. First, the observed complexity of the relationship between model features and model outputs reminds model creators to take great care when making decisions about including specific features or making specific assumptions in model development. This entails a thorough examination of the consequences of such an addition on model outcomes, informed by (but not limited to) the specific output metrics that are anticipated to be of highest interest to model end-users. Second, for model users, this study illustrates the difficulty of interpreting the results of a specific model, and correspondingly the difficulty of choosing a given model when several options are available. In simple terms, we emphasize here that it will often be beneficial to use several models to gain a better understanding of the implications of the underlying assumptions on observed model results, and that in any case, model results cannot be fully understood (and therefore trusted) without a deep knowledge about the intricacies of the generating model.

In the end, the model comparisons carried out in this study helped to produce “surprises” that triggered further scientific inquiries. We argue therefore that this type of exercise in model comparison and careful examination is extremely beneficial to modelers and model users alike, and should be more widespread in many fields of ecological and biological research. We learned from Peirce: “Every inquiry whatsoever takes its rise in the observation... of some surprising phenomenon, some experience which either disappoints an expectation, or breaks in upon some habit of expectation...” (Peirce quoted by Burke, 1946) and the inquiries are followed by retroduction (often called abduction): Retroduction is the provisional adoption of a hypothesis, because every possible consequence of it is capable of experimental verification, so that the persevering application of the same method may be expected to reveal its disagreement with facts, if it does so disagree. (Peirce, 1931). According to Peirce (see Burke, 1946), abduction is the only creative step in the scientific inquiry.

In summary, the present experience indicates that:

• The structure of the models in part determines the outcomes and is not neutral.

• Biological assumptions incorporated in models are not always explicit: there are often hidden assumptions that may be difficult to detect.

• Since empirical observations are always isolated, some sort of theory or belief is the main fabric of models (theories themselves).

• The predictions of the models must be further analyzed in terms of the confidence we have in the determining factors, and this confidence must be honestly challenged before we accept the prediction.

Models must be taken for what they are: theories, fallible pieces in our search for truth.

The comparison between modeling approaches was useful for the teams developing the models: with each point of disagreement between predictions, revisions that were needed for one or both models. The AedesBA model has been revised twice as a consequence of this work. In the first round, the representation of the process of hatching was revised and a dynamic for food was incorporated (Romeo Aznar et al. 2013), eliminating the effective mortality. This redesign, with the improvement of one subsystem of the model, however showed the inadequacy of other subsystems. A new round of critical thinking, supported by new experiments, suggested by the model, brought about a new vision of development in which the environment plays a greater role than was previously believed (Romeo Aznar et al. 2015) and that challenged the long held confidence put in the Gilpin model (Gilpin and McClelland 1979). For the Skeeter Buster group, the results of this comparison led to the design and execution of experiments to collect data on the dynamics of mosquito populations subject to the kinds of control measures described here. These field experiments in Iquitos are still ongoing but promise to be highly informative in assessing the ability of Skeeter Buster, AedesBA, and other models of Ae. aegypti population dynamics, to describe the response of mosquito populations to vector control measures and to help us better understand the nature and impact of density dependence on this response. Ultimately, the choice between multiple models—assuming that their predictions differ for the question at hand— must be informed by empirical data.