SC3 - consensus clustering of single-cell RNA-Seq data

Abstract

Single-cell RNA-seq (scRNA-seq) enables a quantitative cell-type characterisation based on global transcriptome profiles. We present Single-Cell Consensus Clustering (SC3), a user-friendly tool for unsupervised clustering which achieves high accuracy and robustness by combining multiple clustering solutions through a consensus approach. We demonstrate that SC3 is capable of identifying subclones based on the transcriptomes from neoplastic cells collected from patients.

One of the key applications of scRNA-seq is determining cell types based on transcriptome profiles alone through unsupervised clustering^1–3. A full characterisation of the transcriptional landscape of individual cells holds an enormous potential, both for basic biology and clinical applications. SC3 is an interactive and user-friendly R-package for clustering and its integration with Bioconductor⁴ and scater⁵ makes it easy to incorporate into existing bioinformatic workflows.

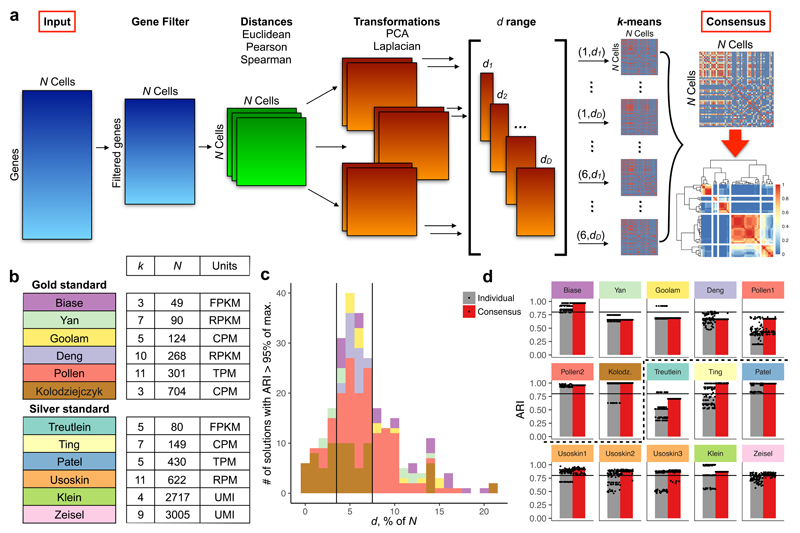
The SC3 pipeline is presented in Fig. 1a, Methods. Each of the steps requires the specification of a number of parameters. Choosing optimal parameter values is difficult and time-consuming. To avoid this problem, SC3 utilizes a parallelisation approach, whereby a significant subset of the parameter space is evaluated simultaneously to obtain a set of clusterings. SC3 then combines all the different clustering outcomes into a consensus matrix that summarises how often each pair of cells is located in the same cluster. The final result provided by SC3 is determined by complete-linkage hierarchical clustering of the consensus matrix into k groups.

Figure 1. The SC3 framework for consensus clustering.

(a) Overview of clustering with SC3 framework (see Methods). The consensus step is exemplified using the Treutlein data. (b) Published datasets used to set SC3 parameters. N is the number of cells in a dataset; k is the number of clusters originally identified by the authors; Units: RPKM is Reads Per Kilobase of transcript per Million mapped reads, RPM is Reads Per Million mapped reads, FPKM is Fragments Per Kilobase of transcript per Million mapped reads, TPM is Transcripts Per Million mapped reads. (c) Histogram of the d values where ARI>.95 is achieved for the gold standard datasets. The black vertical lines indicate the interval d = 4-7% of the total number of cells N, showing high accuracy in the classification. (d) 100 realizations of the SC3 clustering of the datasets shown in (b). Dots represent individual clustering runs. Bars correspond to the median of the dots. Red and grey colours correspond to clustering with and without consensus step. The black line corresponds to ARI=0.8. The dashed black line separates gold and silver standard datasets.

To constrain the parameter values of the SC3 pipeline, we first considered six publicly available scRNA-Seq datasets^* (Fig. 1b). The datasets were selected on the basis that one can be highly confident in the cell-labels as they represent cells from different stages, conditions or lines, and thus we consider them as ‘gold standard’. To quantify the similarity between the reference labels and the clusters obtained by SC3, we used the Adjusted Rand Index (ARI, see Methods) which ranges from 1, when the clusterings are identical, to 0 when the similarity is what one would expect by chance. For the gold standard datasets, we found that the quality of the outcome as measured by the ARI was sensitive to the number of eigenvectors, d, retained after the spectral transformation (Fig. S1, S2). For all six datasets we find that the best clusterings were achieved when d is between 4-7% of the number of cells, N (Fig. 1c, S3a, Methods). The robustness of the 4-7% region was supported by a simulation experiment where the reads from the six gold standard datasets were downsampled by a factor of ten (Methods and Fig. S3a). We further tested the SC3 pipeline on six other published datasets, where the cell labels can only be considered ‘silver standard’ since they were assigned using computational methods and the authors’ knowledge of the underlying biology. Again, we find that SC3 performs well when using d in the 4-7% of N interval (Fig. S3b). The final step, consensus clustering, improves both the accuracy and the stability of the solution. k-means based methods will typically provide different outcomes depending on the initial conditions. We find that this variability is significantly reduced with the consensus approach (Fig. 1d).

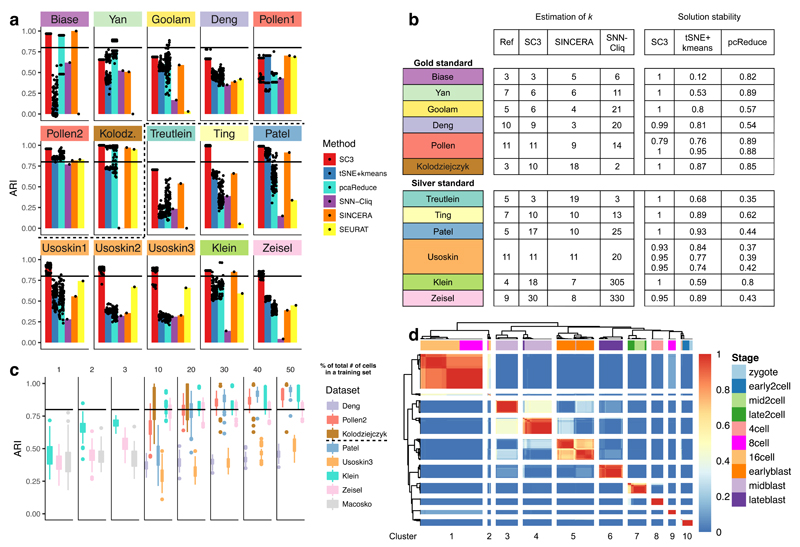
To benchmark SC3, we considered five other methods: tSNE⁶ followed by k-means clustering (a method similar to the one used by Grün et al¹), pcaReduce⁷, SNN-Cliq⁸, SINCERA⁹ and SEURAT¹⁰. As Fig. 2a shows, SC3 performs better than the five tested methods across all datasets (Wilcoxon signed-rank test p-value < 0.01), with only a few exceptions. In addition to considering accuracy, we also compared the stability of SC3 with other stochastic methods (pcaReduce and tSNE+kmeans, but not SEURAT) by running them 100 times (Fig. 2b, Methods, black dots in Fig. 2a). In contrast to the other methods that rely on different initializations, SC3 is highly stable.

Figure 2. Benchmarking of SC3 against existing methods.

(a) SC3, tSNE+kmeans and pcaReduce were applied 100 times to each dataset. SNN-Cliq and SINCERA are deterministic and were run only once. SEURAT was also run once, however was optimised over different values of the density parameter G (Methods). Each panel shows the ARI (black dots, Methods) between the inferred clusterings and the reference labels. Bars correspond to the median of the dots. For the Pollen and Usoskin datasets all different hierarchies were considered (Data Avaialbility). The black line indicates ARI = 0.8. The dashed black line separates gold and silver standard datasets. (b) Number of clusters $\widehat{k}$ predicted by SC3, SINCERA and SNN-Cliq for all datasets. Ref is the reference clustering reported by the authors. (c) The performance of the hybrid SC3 (Methods). Dots represent outliers higher (lower) than the highest (lowest) value within 1.5 x IQR, where IQR is the interquartile range. The black line indicates ARI = 0.8. The dashed black line in the legend separates gold and silver standard datasets. (d) The consensus matrix as generated by SC3 for the Deng dataset (Methods). The matrix indicates how often each pair of cells was assigned to the same cluster by the different parameter combinations as indicated by the colorbar (1 - always, 0 - never). SC3 finds a clustering with k = 10 clusters, separated by the white lines as visual guides. The colors at the top represent the reference labels, corresponding to different stages of development (see colour guide).

Although SC3’s consensus strategy provides a high accuracy, it comes at a moderate computational cost: the run time for N = 2,000 is ~20 mins (Fig. S4a). The main bottleneck is the k-means clustering and by reducing how many different runs are considered it is possible to cluster 5,000 cells in ~20 mins with only a slight reduction in accuracy (Fig. S4b). To apply SC3 to even larger datasets, we have implemented a hybrid approach that combines unsupervised and supervised methodologies. SC3 selects a subset of 5,000 cells uniformly at random, and obtains clusters from this subset as described above. Subsequently, the inferred labels are used to train a support vector machine (SVM, Methods), which is employed to assign labels to the remaining cells. Our result shows that the use of an SVM to predict cell labels works well (Fig. 2c, S4c and Methods). Using the hybrid approach, we were able to analyse a large Drop-Seq dataset with N = 44,808 cells and k = 39 clusters¹⁰ and our results were again in good agreement with the original authors’ (Supplementary Results, Methods, Fig. S5, Table S1). The main drawback of the sampling strategy is that one may fail to identify rare cell-types, and when N>>5,000 there is a substantial risk that the sampled distribution will differ significantly from the full distribution (Methods). If the user is trying to identify a rare subpopulation (e.g. cancer stem cells), then methods specifically designed to identify rare cell-types such as RaceID¹ or GiniClust¹¹ may be more appropriate.

To help the user identify a good choice of k, we have implemented a method based on Random Matrix Theory (RMT)^12,13 for determining the number of clusters (Methods). Overall, we find good agreement between these estimates, $\widehat{k}$, and the numbers suggested by the original authors (Fig. 2b). Additionally, in the interactive SC3 session the user can explore different choices of k in real time, by either assessing the consensus matrix (Fig. 2d), the silhouette index¹⁴ (a measure of how tightly grouped the cells in the clusters are), or the expression matrix.

To help the user interpret the clustering result SC3 can identify differentially expressed genes, marker genes, and outlier cells (Fig. S6, Methods, Table S2). Marker genes are particularly useful since they can be used to uniquely identify a cluster. To illustrate these features, we analysed the Deng¹⁵ dataset tracing embryonic developmental stages. The most stable result for k = 10 is shown in Fig. 2d, and our clusters largely agree with the known sampling timepoints. In total, we identified ~3000 marker genes (Table S3), many of which had been previously reported as specific to the different developmental stages^16,17. Furthermore, the analysis reveals several genes specific to each developmental stage which had previously not been reported (Table S3). Importantly, when using the reference labels reported by the authors¹⁵, nine cells have high outlier scores (purple cells in Fig. S6c). As it turns out, these were prepared using the Smart-Seq2 protocol instead of the Smart-Seq protocol^8,15.

Finally, we investigated the ability of SC3 to identify subclones based on transcriptomes. Myeloproliferative neoplasms, a group of diseases characterised by the overproduction of terminally differentiated cells of the myeloid lineage, reflect an early stage of tumorigenesis where multiple subclones are known to coexist in the same patient¹⁸. From exome sequencing data, we previously identified TET2 and JAK2V61F as the only driver mutations in a large patient cohort¹⁹. Haematopoietic stem cells (HSCs) are thought to be the cell of origin in myeloproliferative neoplasms. To gain further insight into the transcriptional landscape of patient derived HSCs, we obtained scRNA-seq data from the two patients (Figs. S7a-b, S8, Methods, Table S4). For patient 1 (N = 51), both the silhouette index of SC3 and our RMT method suggested that k = 3, provides the best clustering, revealing three clusters of similar size (Fig. S9). For patient 2 (N = 89) SC3 indicated k=1 (Fig. S10), in agreement with the RMT algorithm, suggesting that one single cluster might best reflect the underlying transcriptional changes.

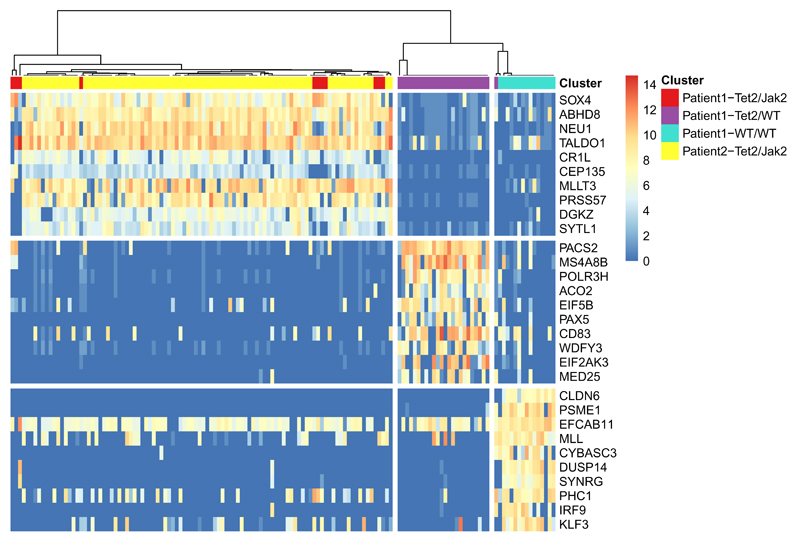
Since known driver mutations in these patients are the TET2 and JAK2V617F loci²⁰ we hypothesized that the different clusters correspond to different combinations of mutations within different clones. The genotype composition for each HSC clone was determined by growing individual haematopoietic stem cells into granulocyte/macrophage colonies, followed by Sanger sequencing of the TET2 and JAK2V617F loci (Fig. S7b-c). In agreement with the clustering defined by SC3, patient 1 (k=3) was found to harbor three different subclones: (i) cells with both TET2 and JAK2V617F mutations, (ii) cells with a TET2 mutation and (iii) wild-type cells (Fig. S7c). Strikingly, the SC3-clusters contain 22%, 29% and 49% of the cells, in excellent agreement with the proportions of each genotype found in the patient, namely 20%, 30% and 50% (Fig. S7c). Thus, we hypothesize that cluster 1 corresponds to the double mutant, cluster 2 corresponds to cells with only a TET2 mutation, and cluster 3 corresponds to wild-type cells. The HSC compartment of patient 2 was 100% mutant for TET2 and JAK2V617F (Fig. S7c), which again was consistent with clustering of k=1 suggested by SC3 (Fig. S10). We then analysed the pooled cells from patient 1 and 2. SC3 clustering again suggested k=3 (Figs. 3, S11), in agreement with the RMT algorithm. Most importantly, all of the putative double mutant cells from patient 1 were grouped with the double mutant cells from patient 2. SC3 reported 33 marker genes for the putative TET2 mutant and 202 marker genes for the putative double mutant clone (Fig. 3, Table S5). Together with additional evidence (Supplementary Results, Fig. S12), we conclude that SC3 is able to identify subclones across patients.

Figure 3. Using SC3 to define subclones from two patients with myeloproliferative neoplasm.

Marker gene expression matrix (after Gene Filter and Log-transformation, Methods) of the combined dataset (patient 1 + patient 2). Clusters (separated by white vertical lines) correspond to k = 3 (Methods). Only the top 10 marker genes are shown for each cluster.

Methods

SC3 clustering

SC3 takes as input an expression matrix M where columns correspond to cells and rows correspond to genes/transcripts. Each element of M corresponds to the expression of a gene/transcript in a given cell. By default SC3 does not carry out any form of normalization or correction for batch effects. SC3 is based on five elementary steps. The parameters in each of these steps can be easily adjusted by the user, but are set to sensible default values, determined via the gold standard datasets (see text).

1. Gene filter

The gene filter removes genes/transcripts that are either expressed (expression value is more than 2) in less than X% of cells (rare genes/transcripts) or expressed (expression value is more than 0) in at least (100-X)% of cells (ubiquitous genes/transcripts). By default X is 6. The motivation for the gene filter is that ubiquitous and rare genes are most often not informative for the clustering. We also explored all three parameters defined in the gene filter (expression thresholds of rare and ubiquitous genes/transcripts and the percentage X) and found that in general the gene filter did not affect the accuracy of clustering (Fig. S3c). However, the gene filter significantly reduced the dimensionality of the data, thereby speeding up the method.

For further analysis the filtered expression matrix M is log-transformed after adding a pseudo-count of 1: M’ = log2(M + 1).

2. Distance calculations

Distance between the cells, i.e. columns, in M’ are calculated using the Euclidean, Pearson and Spearman metrics to construct distance matrices.

We investigated the impact of dropouts on distance calculations by considering a modified distance metric that ignores dropouts. This was done by excluding genes that were not expressed in at least one cell from the distance calculation. We found that this did not improve the performance (Fig. S3d).

3. Transformations

All distance matrices are then transformed using either principal component analysis (PCA) or by calculating the eigenvectors of the associated graph Laplacian (L = I - D^-1/2AD^-1/2, where I is the identity matrix, A is a similarity matrix (A = exp(-A’/max(A’))), where A’ is a distance matrix) and D is the degree matrix of A, a diagonal matrix which contains the row-sums of A on the diagonal (D_ii = ∑_j A_ij). The columns of the resulting matrices are then sorted in ascending order by their corresponding eigenvalues.

4. k-means

k-means clustering is performed on the first d eigenvectors of the transformed distance matrices (Fig. 1a) by using the default kmeans() R function with the Hartigan and Wong algorithm²¹. By default, the maximum number of iterations is set to 10⁹ and the number of starts is set to 1,000.

5. Consensus clustering

SC3 computes a consensus matrix using the Cluster-based Similarity Partitioning Algorithm (CSPA)²². For each individual clustering result a binary similarity matrix is constructed from the corresponding cell labels: if two cells belong to the same cluster, their similarity is 1, otherwise the similarity is 0 (Fig. 1a). A consensus matrix is calculated by averaging all similarity matrices of individual clusterings. To reduce computational time, if the length of the d range (D on Fig. 1a) is more than 15, a random subset of 15 values selected uniformly from the d range is used.

The resulting consensus matrix is clustered using hierarchical clustering with complete agglomeration and the clusters are inferred at the k level of hierarchy, where k is defined by a user (Fig. 1a). In principle, the k used for the hierarchical clustering need not be the same as the k used in step 5. However, for simplicity in SC3 the two parameters are constrained to have the same value.

Fig. 1d shows how the quality and the stability of clustering improves after consensus clustering.

Adjusted Rand Index

If cell-labels are available (e.g. from a published dataset) the Adjusted Rand Index (ARI)²³ can be used to calculate similarity between the SC3 clustering and the published clustering. ARI is defined as follows. Given a set of n elements, and two clusterings of these elements the overlap between the two clusterings can be summarised in a contingency table, where each entry denotes the number of objects in common between the two clusterings. The ARI can then be calculated as:

$$ARI=\frac{{\displaystyle {\sum }_{ij}\left(\begin{array}{c}{n}_{ij}\\ 2\end{array}\right)-\left[{\displaystyle {\sum }_i\left(\begin{array}{c}{a}_i\\ 2\end{array}\right){\displaystyle {\sum }_j\left(\begin{array}{c}{b}_j\\ 2\end{array}\right)}}\right]}/\left(\begin{array}{c}n\\ 2\end{array}\right)}{\frac{1}{2}\left[{\displaystyle {\sum }_i\left(\begin{array}{c}{a}_i\\ 2\end{array}\right)+{\displaystyle {\sum }_j\left(\begin{array}{c}{b}_j\\ 2\end{array}\right)}}\right]-\left[{\displaystyle {\sum }_i\left(\begin{array}{c}{a}_i\\ 2\end{array}\right){\displaystyle {\sum }_j\left(\begin{array}{c}{b}_j\\ 2\end{array}\right)}}\right]/\left(\begin{array}{c}n\\ 2\end{array}\right)}$$

where n_ij are values from the contingency table, a_i is the sum of the i^th row of the contingency table, b_j is the sum of the j^th column of the contingency table and ( ) denotes a binomial coefficient.

Since the reference labels are known for all published datasets, ARI is used for all comparisons throughout the paper.

Downsampling of the gold standard datasets

For each gene i and each cell j, the downsampled expression value was generated by drawing from a binomial distribution with parameters p = .1 and n = round(M_ij).

Additional validation of SC3 pipeline

Additionally, we investigated the impact of dropouts by considering a modified distance metric that ignores dropouts, but we found that this did not improve the performance (Fig. S3d, Methods).

Identification of a suitable number of groups $\widehat{k}$

Matrix Z is obtained from M’ by subtracting the mean and dividing by the standard deviation for each column (z-score). Next, the eigenvalues of X =Z^T*Z are calculated. The number of clusters $\widehat{k}$ is determined by the number of eigenvalues that are significantly different with a p-value <.001 from the Tracy-Widom distribution^24,25 with mean ${(\sqrt{n-1}+\sqrt{p})}^2$ and standard deviation $(\sqrt{n-1}+\sqrt{p})\cdot {(\frac{1}{\sqrt{n-1}}+\frac{1}{\sqrt{p}})}^{\frac{1}{3}},$ where n is the number of genes/transcripts and p is the number of cells.

Benchmarking

For each dataset we used the expression units provided by the authors (Fig. 1b). The gene filter was applied to all the datasets. For tSNE+k-means, SNN-Cliq and pcaReduce the same log-transformation as in SC3 (M’ = log2(M + 1)) was applied. For SINCERA we used the original z-score normalisation²⁶ instead of the log-transformation. For tSNE the Rtsne R package was used with the default parameters. For SEURAT we used the original Seurat R package (version 1.3): we performed tSNE embedding with the default parameters once (following the authors’ tutorial at http://www.satijalab.org/clustertutorial1.html) and then clustered the data using DBSCAN algorithm multiple times, where we varied the density parameter G in the range 10^-3-10³ to find a maximal ARI (this ARI is presented in Fig. 2a). SEURAT was not able to find more than one cluster for the smallest datasets (Biase, Yan, Goolam, Treutlein and Ting) leading to very small ARI scores. For all methods we supplied the k used by the original authors.

Cluster stability

We calculated stability of clustering solutions by running each method 100 times and finding the most frequent solution and the number of times (N_c) it appeared. The stability measure shown in Fig. 2b is then calculated as N_c/100.

Support Vector Machines (SVM)

When using SVM a specific fraction of the cells is selected at random with uniform probability. Next, a support vector machine²⁷ model with a linear kernel is constructed based on the obtained clustering. We used the svm function of the e1071 R-package with default parameters. The cluster IDs for the remaining cells are then predicted by the SVM model.

Identification of rare cell-types

To specifically evaluate the sensitivity of SC3 for identifying rare cell-types, we carried out a synthetic experiment, whereby cells from one cell-type were removed iteratively from the Kolodziejczyk and Pollen datasets. For the Pollen dataset, all but 1-7 of the cells in one of the 11 clusters were removed. The limit of 7 cells corresponds to the size of the smallest cluster in the original data. Subsequently, SC3 was run using k=11, and we asked whether or not the cells of the rare cell-type were located in a separate cluster. This was repeated 100 times for each cell-type and Fig. S4d reports the percentage of runs when the rare cells were found together in a cluster with no other cells. Note that the ARI is a poor indicator of the ability to identify rare cells since this measure is relatively insensitive to the behavior of a small fraction of the cells. For the Kolodziejczyk dataset, we used a similar strategy, but we allowed for 1-101 cells in the rare group. For the Pollen dataset, SC3 can detect clusters containing ~1% of the cells, whereas for the Kolodziejczyk dataset ~10% of the cells are required (Fig. S4d). We hypothesize that the ability to identify rare cells reflects the origins of the two datasets; the Pollen data is more diverse as it represents 11 different cell lines while the Kolodziejczyk data comes from one cell-type grown in three different conditions.

For the hybrid SC3 approach with 30% of cells used to train the SVM we were able to calculate the probability of including the rare cell-types in the training set analytically by multiplying the data from Fig. S4d by the probability of all rare cells to be included in the drawn sample (30% of all cells). This probability was calculated using the hypergeometric distribution R function: phyper(n.rare.cells - 1, n.rare.cells, n.other.cells, 0.3*(n.other.cells + n.rare.cells), lower.tail=F), where n.rare.cells is the number of rare cells and n.other.cells is the number of other cells in the dataset (Fig. S4e).

Biological insights

SC3 can identify differentially expressed genes as genes that vary between two or more clusters. Accordingly, marker genes are identified as genes that are highly expressed in only one of the clusters and are able to distinguish one cluster from all the remaining ones (Fig. S6a). Cell outliers are identified through the calculation of a score for each cell using the Minimum Covariance Determinant²⁸. Cells that fit well into their clusters receive an outlier score of 0, whereas high values indicate that the cell should be considered an outlier.

Identification of differential expression

Differential expression is calculated using the non-parametric Kruskal-Wallis test, an extension of the Mann-Whitney test for the scenario when there are more than two groups. The Kruskal-Wallis test has the advantage of being non-parametric, but as a consequence, it is not well suited for situations where many genes have the same expression value. A significant p-value indicates that gene expression in at least one cluster stochastically dominates one other cluster. SC3 provides a list of all differentially expressed genes with p-values<0.01, corrected for multiple testing (using the default “holm” method of p.adjust() R function) and plots gene expression profiles of the 50 most significant differentially expressed genes. Note that the calculation of differential expression after clustering can introduce a bias in the distribution of p-values, and thus we advise to use the p-values for ranking the genes only.

Identification of marker genes

For each gene a binary classifier is constructed based on the mean cluster expression values. The area under the receiver operating characteristic (ROC) curve is used to quantify the accuracy of the prediction. A p-value is assigned to each gene by using the Wilcoxon signed rank test comparing gene ranks in the cluster with the highest mean expression with all others (p-values are adjusted by using the default “holm” method of p.adjust() R function). The genes with the area under the ROC curve (AUROC) >0.85 and with the p-value<0.01 are defined as marker genes. The AUROC threshold corresponds to the 99% quantile of the AUROC distributions obtained from 100 random permutations of cluster labels for all datasets (Table S2 and Fig. S6b). SC3 provides a visualization of the gene expression profiles for the top 10 marker genes of each obtained cluster.

Cell outlier detection

Outlier cells are detected by first taking an expression matrix of each individual cluster (all cells with the same labels) and reducing its dimensionality using the robust method for PCA (ROBPCA)²⁹. This method outputs a matrix with N rows (number of cells in the cluster) and P columns (retained number of principal components after running ROBPCA). SC3 then uses p=min(P, 3) first principal components for further analysis. If ROBPCA fails to perform or P=0, SC3 shows a warning message. We found (results not shown) that this usually happens when the distribution of gene expression in cells is too skewed towards 0. Second, robust distances (Mahalanobis) between the cells in each cluster are calculated from the reduced expression matrix using the minimum covariance determinant (MCD)²⁸. We then used a threshold based on the Q% quantile of the chi-squared distribution (with p degrees of freedom) to define outliers. By default Q=99.99, but it can be manually adjusted by a user. Finally, we define an outlier score as the difference between the square root of the robust distance and the square root of the Q% quantile of the chi-squared distribution (with p degrees of freedom). The outlier score is plotted as a barplot (Fig. S6c).

Gene and Pathway enrichment analysis

We utilized g:Profiler web tool³⁰ to perform gene and pathway enrichment analysis in all obtained sets of genes.

Analysis of the Macosko dataset

To analyze the Drop-Seq dataset we followed the procedure used by Macosko et al and selected the 11,040 cells where more than 900 genes were expressed. Moreover, due to the low read depth, the gene filter was removed. We then sampled 5,000 cells and clustered using SC3, including the SVM step, 100 times. All 100 solutions were consistent between each other resulting in an average ARI of 0.58 and they were sufficiently accurate compared to the reference authors’ clustering yielding an average ARI of 0.54 (Fig. S5a). Since each of the 100 solutions were different, we added an additional consensus clustering step using the “best of k” consensus algorithm³¹. This approach provided a single solution based on the 100 different solutions and it was as accurate as the individual solutions with an ARI of 0.52 (the actual labels are presented in Table S1). The SC3 consensus solution splits the large original cluster (cluster 24 with 29,400 cells) hierarchically into 2 clusters of smaller sizes (18105 + 10558 = 28663 cells, clusters 4 and 8 in Fig. S5b). Additional gene and pathway enrichment analysis for the differentially expressed genes between the two clusters is presented in Table S1. If more than 75% of the cells from the reference cluster are shared with the SC3 cluster we defined these two clusters as matched. In total 31 reference clusters were matched to the SC3 clusters.

Patients

Both patients provided written informed consent. Diagnoses were made in accordance with the guidelines of the British Committee for Standards in Haematology.

Isolation of haematopoietic stem and progenitor cells

Cell populations were derived from peripheral blood enriched for haematopoietic stem and progenitor cells (CD34+, CD38-, CD45RA-, CD90+), hereafter referred to as HSCs. For single cell cultures, individual HSCs were sorted into 96-well plates (Fig. S7a-b) and grown in a cytokine cocktail designed to promote progenitor expansion as previously described³². For scRNA-seq studies, single HSCs were directly sorted into lysis buffer as described in Picelli et al³³.

Determination of mutation load

Colonies of granulocyte/macrophage composition were picked and DNA isolated for Sanger sequencing for JAK2V617F and TET2 mutations as previously described by Ortmann et al³⁴.

Single cell RNA-Sequencing

Single HSCs were sorted into 96-well plates and cDNA generated as described previously³³. The Nextera XT library making kit was used for library generation as described by Picelli et al³³.

Processing of scRNA-seq data from HSCs

96 single cell samples per patient with 2 sequencing lanes per sample were sequenced yielding a variable number of reads (mean = 2,180,357, std dev = 1,342,541). FastQC³⁵ was used to assess the sequence quality. Foreign sequences from the Nextera Transposase agent were discovered and subsequently removed with Trimmomatic³⁶ using the parameters HEADCROP:19 ILLUMINACLIP:NexteraPE-PE.fa:2:30:10 TRAILING:28 CROP:90 MINLEN:60 to trim the reads to 90 bases before being mapped with TopHat³⁷ to the Ensembl reference genome version GRCh38.77 augmented with the spike-in controls downloaded from the ERCC consortium. Counts of uniquely mapped reads in each protein coding gene and each ERCC spike-in were calculated using SeqMonk (http://www.bioinformatics.bbsrc.ac.uk/projects/seqmonk) and were used for further downstream analysis. Quality control of the cells contained two steps: 1. filtering of cells based on the number of expressed genes; 2. filtering of cells based on the ratio of the total number of ERCC spike-in reads to the total number of reads in protein coding genes. Filtering threshold were manually chosen by visual exploration of the quality control features (Fig. S8). After filtering, 51 and 89 cells were retained from patient 1 and patient 2, correspondingly. The expression values in each dataset were then normalised by first using a size-factor normalisation (from DESeq2 package³⁸) to account for sequencing depth variability. Secondly, to account for technical variability, a normalisation based on ERCC spike-ins was performed using the RUVSeq package³⁹ (RUVg() function with parameter k=1). For combined patient data, normalisation steps were performed after pooling the cells. The resulting filtered and normalised datasets were clustered by SC3. Potential biases of cell filtering on the proportions of cells in the clusters of patient 1 are considered in the Supplementary Data 1. It shows that the cluster of lower cell quality is separated from the other biologically meaningful clusters of patient 1 and it does not change the total proportion of the biologically meaningful clusters. Supplementary Data 2 shows that SC3 results of clustering of patient 1 do not depend on the normalization procedure.

Clustering of patient scRNA-seq data by SC3

We clustered scRNA-seq data from patient 1 and patient 2 separately as well as a combined dataset containing data from patient 1 + patient 2. For patient 1, in agreement with the RMT algorithm, the best clustering was achieved for k=3 (Fig. S9). Data from patient 2 was homogeneous and SC3 was unable to identify more than one meaningful cluster (Fig. S10), again in agreement with the RMT algorithm. For the combined dataset for patient 1 + patient 2 the best values of the silhouette index were obtained when k was 2 or 3 (Fig. S11). In both cases all of the cells from cluster 1 in patient 1 were grouped with the cells from patient 2. For k=3 clusters 1 and 3 of patient 1 were also resolved. The RMT algorithm also provided k=3 for the merged patient 1 + patient 2 dataset.

Comparison of clustering of patient 1 scRNA-seq data

Results of the clustering of the patient 1 data by other methods and their comparison to SC3 is presented in the Supplementary Data 3 and 4.

Identification of differentially expressed genes from microarray data

The microarray data of patient 1 was obtained from Array Express accession number E-MTAB-3086³⁴. One replicate (2B) was identified as an outlier and removed. The limma R package⁴⁰ was used to identify 932 differentially expressed genes between WT and TET2/JAK2V617F double mutant using an adjusted (by false discovery rate) p-value threshold of 0.1.

Marker genes analysis for patients

For both patients, to increase the number of marker genes, the AUROC threshold was set to 0.7 instead of the default value of 0.85 and the 0.1 p-value threshold was chosen.