Reliability of the depth-dependent high-resolution BOLD hemodynamic response in human visual cortex and vicinity

Abstract

Functional magnetic resonance imaging (fMRI) often relies on a hemodynamic response function (HRF), the stereotypical blood oxygen level dependent (BOLD) response elicited by a brief (<4 seconds) stimulus. Early measurements of the HRF used coarse spatial resolutions (≥3 mm voxels) that would generally include contributions from white matter, gray matter, and the extra-pial compartment (the space between the pial surface and skull including pial blood vessels) within each voxel. To resolve these contributions, high-resolution fMRI (0.9-mm voxels) was performed at 3T in early visual cortex and its apposed white-matter and extra-pial compartments. The results characterized the depth dependence of the HRF and its reliability during nine fMRI sessions. Significant HRFs were observed in white-matter and extra-pial compartments as well as in gray matter. White-matter HRFs were faster and weaker than in the gray matter, while extra-pial HRFs were comparatively slower and stronger. Depth trends of the HRF peak amplitude were stable throughout a broad depth range that included all three compartments for each session. Across sessions, however, the depth trend of HRF peak amplitudes was stable only in the white matter and deep-intermediate gray matter, while there were strong session-to-session variations in the superficial gray matter and the extra-pial compartment. Thus, high-resolution fMRI can resolve significant and dynamically distinct HRFs in gray matter, white matter, and extra-pial compartments.

1. Introduction

Blood oxygen-level dependent (BOLD) functional magnetic resonance imaging (fMRI) is a powerful non-invasive technique widely used to infer the spatiotemporal structure of brain activity. The BOLD signal is caused by local changes in MR susceptibility within and around blood vessels due to transient changes in deoxyhemoglobin concentration evoked by local neural activity. The BOLD signal generated by brief neural activity is called the hemodynamic response function (HRF), and typically consists of a sequence of three temporal periods: initial latency with little signal or possible signal decrease, then a peak that likely corresponds to a transient period of intravascular hyper-oxygenation, followed by an undershoot [1, 2]. The HRF can be used to quantify brain activation based on the assumption of a linear relationship with corresponding brain responses. Therefore, a detailed understanding of the spatiotemporal characteristics of the HRF is essential.

Human BOLD fMRI studies with relatively large voxel sampling size (~3—6 mm) can blur data over a range of white matter (WM), gray matter (GM) and pial vasculature [3, 4]. This is of particular concern in the convoluted human cerebral cortex, which has a thickness in the range of 1.5—4.5 mm, with the thinnest GM typically found in the depths of the sulci [5–7]. The pial vessels that supply and drain cortical blood are expected to have their own dynamics of coupling with the HRF in the parenchyma [8, 9] and white matter also has its own BOLD signal [10–13]. Furthermore, a partial sampling between adjacent sides of a sulcus can further confuse matters by mixing contributions from disparate portions of the cortical surface. A historically conventional fMRI voxel (≥3mm, commonly used over two decades of research), may therefore contain significant fractions of undesirable signals, so called partial volume effects, which have the potential to alter the HRF considerably from that found in a localized region of GM where neuronal activity occurs.

There are a few recent studies that examined the variation in the hemodynamic response through the depth of cortex using fMRI at 7T field strength. Using 1-mm sampling and a blocked stimulus protocol, Polimeni et al. noted that signal amplitude increases monotonically from the GM/WM interface to the pial surface, while the spatial variability of these signals increases with distance above the underlying WM [14]. More recent studies examined the HRF itself [15, 16]. They confirmed that signal amplitudes increase from deep to superficial GM, and also noted faster time-to-peak, and narrower full-width-half-maximum (FWHM) for deep as compared to superficial GM in human visual and motor cortices. Using high spatial but very limited temporal resolution, Koopmans et al. also found that the BOLD response amplitude is greater in superficial and intermediate layers than in deeper layers of human visual cortex at 3T [17]. Using a blocked stimulus protocol, we previously observed that laminar profiles of hemodynamic activity exhibit peak signal amplitudes in the superficial GM [7].

However, there are three aspects that have not yet been fully addressed for the depth-dependent HRF. First, the variability of the depth-dependent HRF peak amplitudes have not been clearly characterized. Previous studies demonstrated that the variability for the peak amplitude increased from deep to superficial GM [14–16]. However, it was not clear what causes this variability. Second, there has been no depth-dependent characterization of the reliability of temporal HRF parameters, e.g., time-to-peak and FWHM. Finally, there have been limited efforts to address BOLD signals outside of the GM. Hall et al characterized amplitude and temporal HRF parameters in WM, GM, and pial vasculature, but it was conducted in only one subject with relatively coarse resolution [9]. Although task-related WM BOLD signal have been measured in various brain structures such as corpus callosum [18–20], internal capsule [21–23] and optic radiations [24, 25], only a few studies have shown the existence of the HRF in the WM [26–29]. Moreover, it is not clear how the HRF observed in the WM is related to stimulus-evoked activity in apposed active GM. It has often been assumed that such signals are either weak or unrelated to stimulus-evoked activity in the GM, and therefore, most previous studies have attempted to examine the HRF only in the GM [14–17, 30, 31]. However, because of the limited spatial resolution of fMRI studies, partial volume effects will inevitably mix potential signals from WM and the pial vasculature with GM signals. To understand such partial volume effects, it is necessary to characterize the HRFs in WM and the pial vasculature, including their variability and reliability using fMRI with high spatial resolution.

Here, we offer a detailed assessment of the depth-dependence of the HRF in human early visual cortex (areas V1—3) and apposed WM and pial vasculature at 3T using high-resolution fMRI (0.9-mm voxels) and a 3D depth-mapping approach. We had three aims. First, we tested the hypothesis that stimulation will evoke distinct HRFs not only in GM, but also in apposed WM and pial vasculature. Second, we measured depth profiles of HRF parameters to test previous work indicating that both peak amplitude and temporal parameters of the HRF should increase monotonically from deep to superficial gray matter, and extended these results into adjacent WM and pial vasculature. Third, we examined how the reliability of the HRF and its parameters varied with respect to depth, to better understand previous results that indicated spatial reliability decreases from deep to superficial GM, and again extended these results into apposed WM and pial vasculature.

2. Material and Methods

Imaging experiments were performed on a 3T GE Signa HD12 scanner. Six male subjects, ages 20—56, participated in the experiments. Repeat sessions were performed on three subjects to improve statistical power; all gave informed consent under procedures reviewed and authorized by the UT Austin Institutional Review Board.

2. 1 Structural measurements

We obtained 0.7-mm isovoxel volume anatomies for all subjects using an inversion-prepared fast RF-spoiled gradient-recalled echo (fSPGR) sequence with an 8-channel GE-product head-coil. The FreeSurfer software suite was used to initially segment the WM and GM at 1-mm sampling, which was then upsampled to 0.7-mm. The WM segmentation was then edited manually across early visual cortex to improve accuracy and reduce errors.

Our surface-based analysis utilized an inner (GM/WM) and outer (pial) surface of the cortex. We produced a GM/WM interface mesh on the white-matter volume by isosurface contour extraction followed by mesh refinement using a volume-preserving deformable-mesh algorithm [6, 32]. For the pial surface, we used the mesh produced from the FreeSurfer segmentation, edited manually by visual inspection to correct occasional errors in early visual cortex.

We constructed a self-reciprocal coordinate system using a signed-distance function [6]. This approach created unique depth trajectories that provided one-to-one correspondence between vertices on the GM/WM interface and the pial surface. Let S_gw be the signed distance above the GM/WM interface (positive outside the surface, negative within) and S_p be the signed distance above the pial surface. The distance magnitudes were obtained by calculating point-to-triangle distances for each point in the volume and signs were then assigned based on the segmentations (e.g., for S_gw, negative in the WM, positive elsewhere). We then defined a normalized depth parameter w based on:

$$(1-w)S_{\mathit{\text{gw}}}+w{S}_p=0$$ (1)

In most regions, the above equation was solved explicitly: w = S_gw/(S_gw − S_p) except where the denominator was close to zero. In these regions, eqn. (1) was solved directly using a root-solving algorithm [33]. This approach is similar to our previously published work [6], but offers two advantages. First, it avoids the computational intensity of the deformable surface evolution by substituting the much simpler algebraic solution of eqn. (1). Second, it utilizes a direct computation of signed distance function that is based upon the segmentation, rather than the topology of the surface representations. This avoided the pitfalls of occasional topological defects that often occur in the pial surfaces.

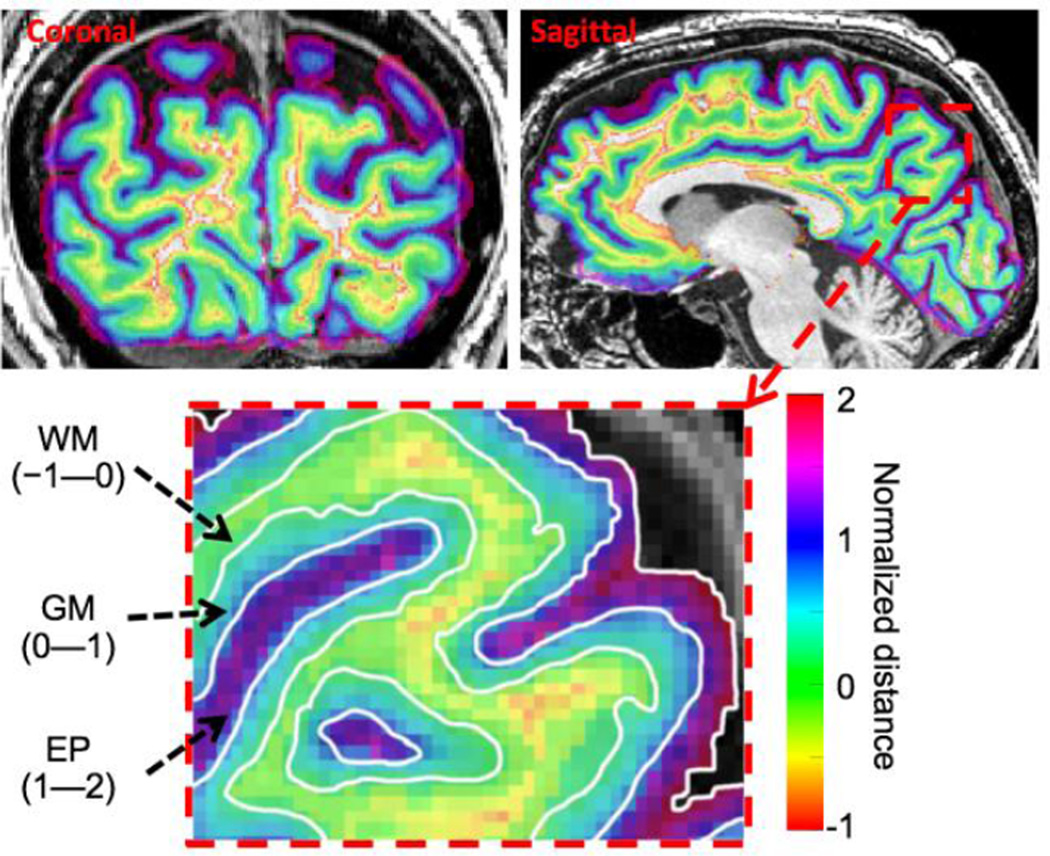
The normalized depth w was zero on the GM/WM interface, went to unity at the pial surface, and formed a self-reciprocal depth coordinate in the vicinity of the GM that was normalized by the local GM thickness (Fig. 1). We used the term “extra-pial” (EP) compartment for the space between the pial surface and skull, values of w > 1, which included the highly vascular sub-arachnoid space [34].

Figure 1.

Example of normalized depth map on coronal and sagittal slices for a subject. Coronal slice locations are in posterior occipital lobe close to the functional slice prescription. Sagittal slices are near the mid-sagittal plane to clearly show the calcarine sulcus. Right: enlargement of sagittal slice showing normalized depth coordinate ranges for WM, GM, and EP compartments.

2. 2 FMRI acquisition

Functional data was acquired using a custom 7-channel surface coil array (ScanMed, Omaha NE) fabricated on a flexible former so that it could be worn closely against the head. We used a three-shot (TR = 500 ms, TE= 25 ms) spiral acquisition (acquisition time 27 ms, bandwidth 125 kHz) [7, 35] with a linear field-map correction and a shot-by-shot self-navigation correction to remove mean phase shifts between the shots. We acquired eight 0.9-mm-thick slices (FOV: 90 mm² with 128 × 128 base resolution) to cover portions of early visual areas (V1—3) and their adjacent WM and EP compartments every 1.5 s. A long (9-ms) sinc excitation enabled the acquisition of such thin slices.

A set of T1-weighted structural images was obtained with good gray-white contrast on the same prescription of functional data at the end of the session using a 3D RF-spoiled GRASS (SPGR) sequence (15° flip angles, TI = 450 ms, 0.7-mm isometric voxel size, 12 slices). These images were used to align the functional data to the segmented high-resolution structural reference volume described in section 2.1 with a robust, intensity based registration algorithm [36].

2. 3 Stimulus and HRF measurements

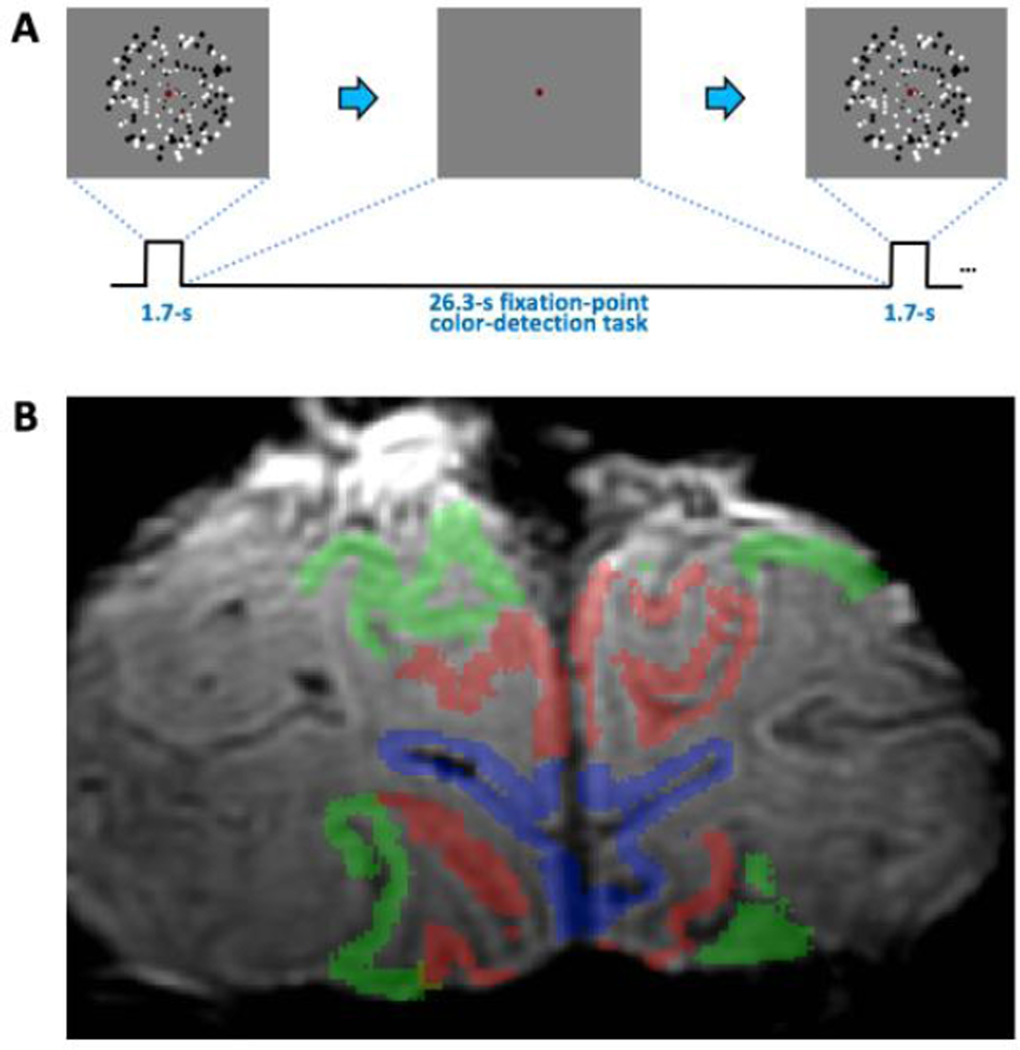
Subjects fixated on central dot throughout each run. A 1.7-s duration stimulus of 4-Hz flickering randomly positioned dots was presented to the subject to induce a hemodynamic response. Variably sized (scaled with eccentricity to match visual acuity) black/white dots (n =150) were presented in a 22°-diameter of visual angle on a gray background. This was followed by a 26.3-s blank inter-stimulus interval (ISI) period to record the subsequent HRF (Fig. 2A). To control visual attention and encourage stable fixation during this period, subjects performed a fixation point task. The fixation dot changed color every 0.5 second among a set of 12 colors randomly chosen across an HSV space. Subjects were required to detect a specific target color and push a button within 0.5 second. This 28-s duration trial was repeated 18 times in each run. To improve temporal resolution, the stimulus onset was randomly jittered (delayed) by 0, 0.5, or 1 second for every trial, and the analysis accounts for this jittering (see below section 2. 4). Each scan typically consisted of 5 such runs. We discarded the first 28-s-duration HRF for each run to avoid various onset-transient effects, which provided a total of 85 HRFs in early visual cortex.

Figure 2.

Experimental methods. A) Stimulus was a brief display of 4-Hz flickering dots, followed by a long blank period to allow the HRF to evolve and subside. B) T2* weighted image with color overlays delineating ROIs, blue: V1, red: V2, green: V3.

2. 4 ROI definitions

Visual-area boundaries were estimated using population receptive-field mapping methods [37] obtained for each subject in separate session. The data were analyzed in the portion of the prescription that sampled both in area V1 (blue, Fig. 2B), and in the combination of areas V2 and V3 (V23) to sample extrastriate tissue (red and green). We averaged our signals across two ROIs in the GM, and corresponding WM and EP compartments to yield 18 distinct compartmental HRFs and depth profiles of their corresponding parameters.

2. 5 fMRI data preprocessing

Our data were acquired using a sequential slice-acquisition order, so motion correction was performed first using a robust intensity-based registration approach [36] applied to the temporally smoothed version of the data. The smoothing is necessary because of the low SNR of our high-resolution data. We chose 5-frame boxcar smoothing to avoid noisy motion estimates, and thereby remove only slow changes in head motion. Our highly experienced subjects generally moved very little (total motion typically ≤1 mm) over the course of each run. We then performed a slice-acquisition timing correction. Next, data were transformed into the volume anatomy coordinates, using the same intensity-based registration method, and then corrected for stimulus-onset jittering to improve temporal resolution.

2. 6 HRF parameters

We obtained four parameters from the HRFs. The peak amplitude was identified as the global maximum of signal amplitude; the time-to-peak was the time at this peak. Full-width-at-half maximum (FWHM) was the time span over which the signal exceeded half of the peak amplitude. The time-to-offset was defined as the time at half maximum after the hyperoxic peak. To improve the precision of these measurements, we first upsampled the HRF time series to Δt = 0.1 s using cubic-spline interpolation.

2. 7 Analysis of HRFs in white-matter, gray-matter and extra-pial compartments

We needed to identify voxels in the WM and EP compartments that were in the vicinity of the gray-matter ROI. However, to minimize partial volume effects, we chose voxels within the WM and EP compartments that were spatially distinct from the GM. For our primary analysis in the WM, we selected voxels whose centers were located 0.9 mm to 1.8 mm from GM/WM interface so that the selected voxels were separated from the GM with at least half of a voxel distance. As a test, we also selected voxels with a larger separation, depth range 1.6—2.5 mm from the GM/WM interface. The WM voxels in this depth range were identified by computationally tracking ∇⃗w from voxels of each gray-matter ROI. Similarly, we used the same two depth ranges from the pial surface for the extra-pial compartment.

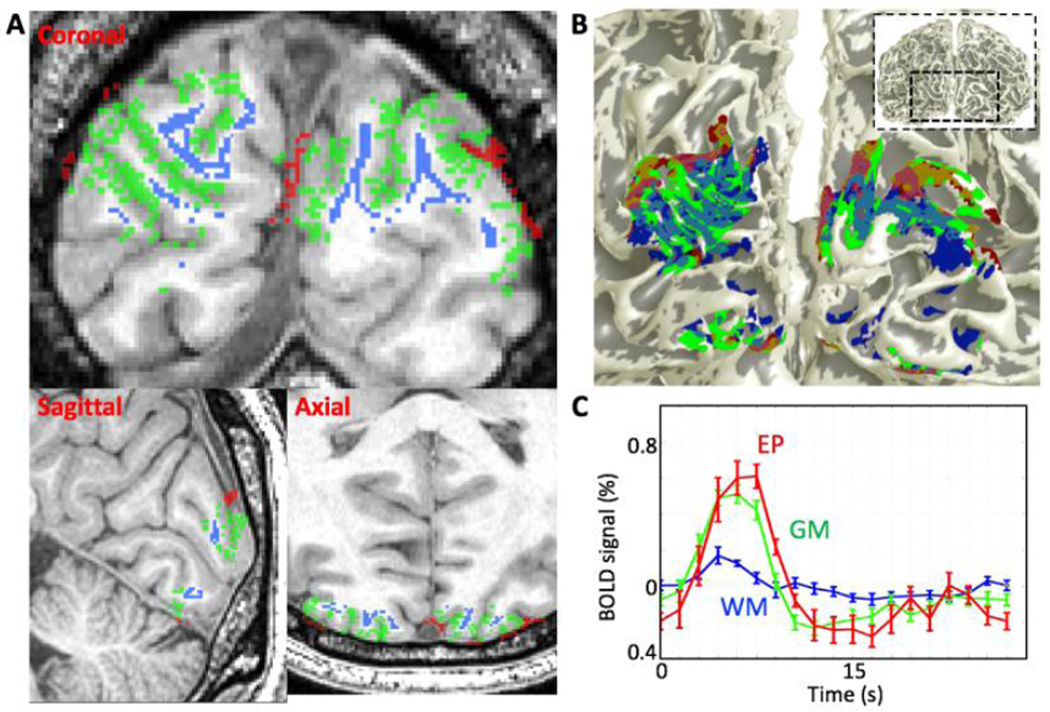
We selected strong responses without regard to the depth of their maximum response in each compartment. We ranked the responses by a depth-averaged contrast-to-noise ratio metric. First, the time-series data was averaged throughout the selected voxels in each compartment [6, 7]. We then calculated a contrast-to-noise ratio (CNR) by treating each HRF event time series as a vector. The mean HRF vector across events was computed, then the dot product was taken of each event with the mean to generate a univariate “contrast” value for each event [38]. The CNR was next estimated as the ratio of the mean contrast to its standard deviation. Based on the CNR values, we then chose the top 50% of the responses of the selected voxels in each WM (blue, Fig. 3A—B) and EP (red) compartment. The HRFs were obtained by spatially averaging the responses in this set of voxels in each compartment, and temporally averaging over the many stimulus events.

Figure 3.

A) Example of the region for top 50% of strong response voxels in each compartment on coronal, sagittal and axial slices: WM (blue), GM (green), EP compartments (red). To avoid partial volume effects, the voxels in the WM and EP compartments are separated by at least 0.9 mm from GM/WM interface and pial surface respectively. B) Overlaid selected voxels in each compartment onto 3D GM/WM interface. C) Mean time series of the selected region in each compartment. Error bars are 68% confidence intervals obtained using a bootstrapping scheme.

The GM HRFs were calculated in an analogous fashion. First, responses were depth averaged over a normalized depth range (0.2 ≤ w ≤ 0.8) to minimize partial volume effects. Then, we again selected the top 50% voxels based on CNR (Fig. 3A–B, green).

To permit comparison of responses in the WM and EP compartments to responses in the GM compartment regardless of sessions, session-to-session variations needed to be excluded. We therefore, normalized each WM and EP HRF parameters by dividing by its corresponding GM HRF parameters in each session.

To test how WM and EP HRFs vary with GM HRFs, we obtained linear correlation coefficients, R, of peak amplitude and time-to-offset between the GM compartment and the WM and EP compartments. Positive correlations provided evidence that similar hemodynamic mechanisms underlay HRFs in WM and EP compartments.

2. 8 Depth analysis of HRFs

We examined HRF variations as a continuous function of normalized depth. First, we selected voxels that encompass the top 50% response within the GM (0.2 ≤ w ≤ 0.8) to obtain a depth-averaged ROI. All voxels within this ROI were extended throughout the GM (depth range 0—1), and into apposed WM (depth −0.5—0) and EP (depth 1—1.5) compartments by tracking ∇⃗w. Normalized depth bins of width 0.25 (one quarter of local gray-matter depth, mean thickness 0.58 mm) were defined on the normalized depth range of −0.5 to 1.5 at increments of 0.1 to generate depth profiles of HRF parameters.

2. 9 Variability and reliability of the HRF

The noise in fMRI data is known to have a non-Gaussian distribution [39, 40]. We therefore used bootstrapping to estimate the statistical distributions for ROI data obtained in each session [41, 42]. Time-series from the many trials (n = 85) within a session were resampled with replacement, and then averaged together. This procedure was repeated 2,000 times to estimate the distribution of amplitude values at each time point of the HRF. A similar procedure was used to estimate the distributions for each of the HRF parameters. We then measured 68% confidence intervals (equivalent to a single standard deviation) for each parameter from their corresponding distributions. Note that this scheme implicitly accounted for multiple comparisons because it obtained the distribution upon the entire sample set. We defined the mean difference between the upper and lower confidence intervals and the signal as the “variability,” equivalent to the standard-error-of-the-mean for normally distributed data. We also defined the “reliability” as a ratio of the mean parameter value to its variability, a generalized form of signal-to-noise ratio; reliability >2 thus corresponds to the usual definition of statistical significance, equivalent to p < 0.05. We used these metrics to quantify depth variations in parameter reliability.

2. 10 Linear fit

Linear fits of the parameters as a function of normalized depth were performed to identify trends within the GM. Statistics were again estimated by bootstrapping, performing a least-square fit to each resampled average of the data. We reported the mean slopes and utilized p-values to determine statistical significant of linear trends. A p-value corresponded to the null hypothesis that the sign of the slope was not the same as the mean slope.

2. 11 Normalization across sessions

Absolute values of the HRFs and their parameters varied substantially across sessions. To permit averaging across sessions, we normalized the HRF parameters from each session by dividing by the parameter’s mean through the gray-matter depth range of 0.2—0.8. After averaging across sessions, we “denormalized” by multiplying the result by the mean depth-averaged parameter in GM across sessions, thus returning the data to physically meaningful units.

3. Results

3. 1 HRFs in white matter and extra-pial compartments

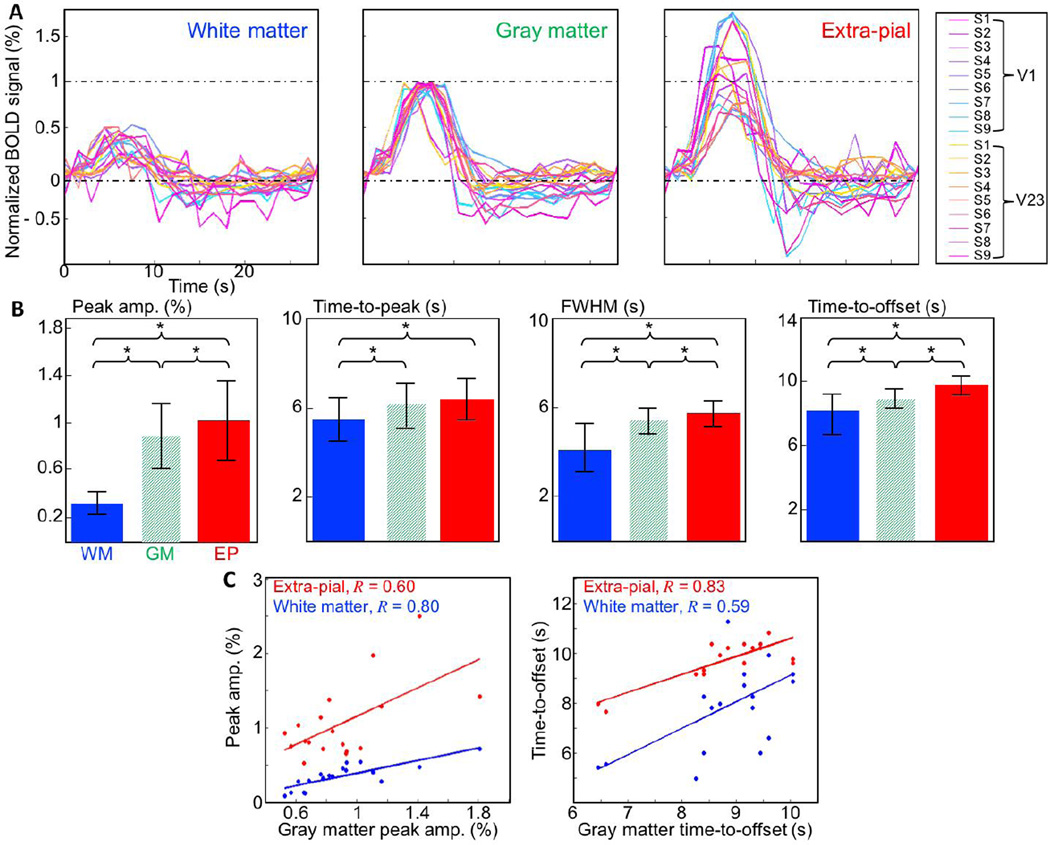
The top 50% of strong HRF voxel responses in each compartment were shown in three anatomical planes for one session (Fig. 3A, blue: WM, green: GM, and red: EP compartments). The WM and EP response regions were located clearly outside of the GM. We projected these three regions onto the 3D GM/WM interface (Fig 3B). We found approximate spatial registration between both WM (Fig. 3B, blue) and EP (red) response regions, and the GM response region (green). Reliable HRFs existed in the WM and EP compartments, even after mitigation of partial volume contamination from the GM (Fig. 3C).

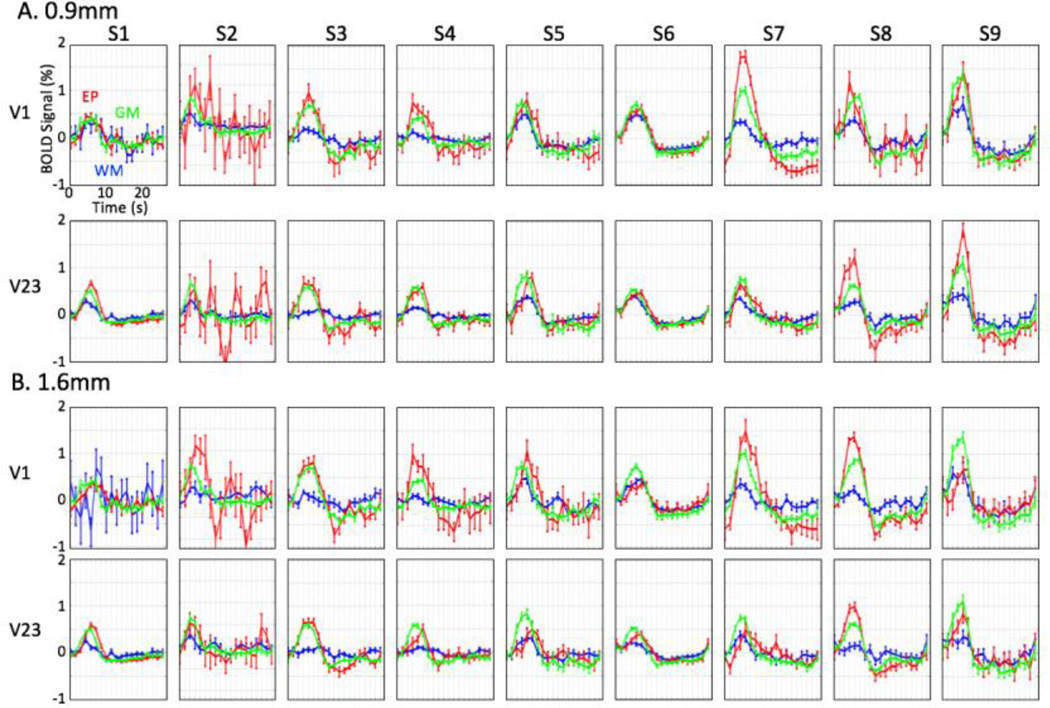
Results for all sessions confirmed the existence of reliable HRFs in the WM (blue lines), and EP (red) compartments. These HRFs exhibited reliable hyperoxic peak amplitudes for across ROIs and sessions (Fig. 4A). To further reduce the possibility of partial volume effects, we repeated our analysis by generating depth-averaged HRFs in the WM and EP compartments over a larger separation range, 1.6—2.5 mm from the GM (Fig. 4B): corresponding to separation of the corners of 0.9-mm voxels. Results were very similar, with significant peak amplitudes in WM and EP compartments across ROIs and sessions.

Figure 4.

mean HRFs of each compartment for two ROIs in nine sessions: WM (blue), GM (green), and EP (red) compartments; error bars show 68% confidence intervals. Voxels within depth range of A) 0.9—1.8mm, and B) 1.6—2.5mm from GM are selected for the HRFs in WM and EP compartments.

The HRF in each compartment showed the stereotypical initial delay and hyperoxic peak, but their amplitude and temporal characteristics were noticeably different among the compartments; 68% confidence intervals were marked to show time-series variability. HRFs for each compartment showed their considerable variability across ROIs and sessions (Fig 4).

We normalized these HRFs by the peak amplitude of the corresponding GM HRF and showed 18 individual relative mean HRFs in each compartment (Fig. 5A). Bar graphs show mean and standard deviation of various HRF parameters in each compartment (Fig. 5B). In the GM, peak amplitude was 0.9±0.3%, time-to-peak 6.1±1.1 s, FWHM 5.4±0.6 s, and time-to-offset 8.9±1 s. Peak amplitude increased monotonically from WM through GM to EP compartments. Relative hyperoxic peak amplitudes in the WM were significantly weaker than in the GM (p < 0.01) but still very reliable (0.35±0.1%). The relative peak amplitudes of EP HRFs were 20% stronger but much more variable (1.08±0.35%) than those of the GM HRFs (Fig 5B).

Figure 5.

A) 15 HRFs in each compartment. The each HRF in the WM (left) and EP (right) compartments is normalized by the peak amplitude of the corresponding GM HRFs for direct comparison between compartments. B) HRF parameters averaged across ROIs and sessions for each compartment. Error bar show a standard deviation. The ‘*’ denotes significant difference between the two compartments (p < 0.05). C) Plots of raw (unnormalized) peak amplitudes (left) and time-to-offset (right) for EP (red) and WM (blue) HRFs show strong and significant correlations (p ≤ 0.01).

The GM HRFs, after amplitude normalization, showed much greater temporal stability across ROIs and sessions. However, the HRFs in all compartments show much greater variability at later times after the hyperoxic peak. All temporal HRF parameters tended to increase from the WM to EP compartments. Time-to-peak went from 5.5±1 s in the WM, to 6.1 s in the gray matter, and 6.4±0.9 s in the EP compartment. Time-to-peak in the WM differed significantly from that observed in both GM (p = 0.01) and EP (p < 0.01) compartments. Time-to-peak in the EP compartment showed only a trend to be slower than in the GM (p = 0.25). FWHM was 4.1±1.1 s in the WM, 5.4 s in the GM, and 6.4±0.9 s in the EP compartment. FWHM increased significantly both from WM to GM (p < 0.01) and from GM to EP (p = 0.03). The time-to-offset was the most reliable and distinctive temporal HRF parameter between the compartments. It increased from 7.9±1.4 s in the WM, to 8.9 s in the GM, and 9.8±0.9 s in the EP compartment. Differences are significant between all three compartments (p ≤ 0.01).

We examined correlations of theses HRF parameters among compartments before normalization. For the peak amplitudes (Fig. 5C, left), there were strong and significant (p ≤ 0.01) correlations between both WM and GM compartments (R = 0.80, blue line) and EP and GM compartments (R= 0.60, red line). Similarly, time-to-offset (Fig. 5C, right) showed strong and significant (p ≤ 0.01) correlations between both EP and GM compartments (R= 0.83, red line) and WM and GM compartments (R= 0.59, blue line).

3. 2 Linear fits of HRF parameters within the gray matter

We quantified linear trends of the HRF parameters within the GM. We found significant linear trends of the peak amplitude; mean and standard deviation of slope was 0.57±0.32% per cortical thickness that is, peak amplitude changed across the whole of the GM thickness (0 ≤ w ≤ 1) in both ROIs for all sessions (18/18). Temporal HRF parameters showed less reliable results for depth-dependent linear trends: time-to-peak (9/18), FWHM (7/18), and time-to-offset (15/18, 1.1±0.6 s per cortical thickness).

3. 3 Depth-dependent analysis of the HRF parameters

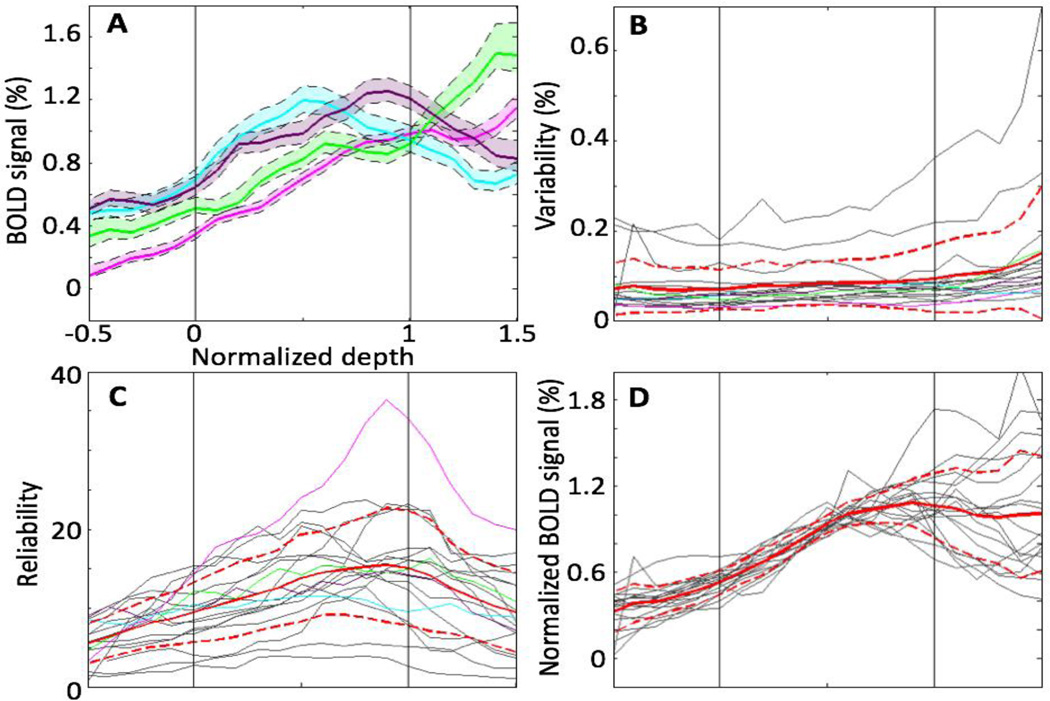
Fig. 6 presents a continuous depth analysis of the peak amplitude from the WM to EP compartments (−0.5 ≤ w ≤ 1.5). Depth profiles from individual sessions were highly reliable throughout this depth range. Example depth profiles of peak amplitude (Fig. 6A) increased strongly from the WM through the GM, and reached a peak within the superficial GM (cyan & magenta) or in the EP compartment (green & gray). Peak values varied somewhat across ROIs and sessions, but were in the range of 0.5—1.6%. Generally, peak amplitudes had small and consistent confidence intervals across most of the depth range. We termed the width of these confidence intervals as variability, plotted in Fig. 6B for each session and ROI. Variability was generally very low in the WM and GM: mean of variability across sessions and ROIs (solid red line) was less than 0.08%. Variability was somewhat larger in the EP compartment, but still less than 0.13%. Thus, variability was generally much less than the peak amplitude, reflecting the strong reliability of the measurements.

Figure 6.

Depth analysis of the peak amplitude for ROIs and sessions. A) Examples (colored lines) of variation of depth profiles. Shaded regions show 68% confidence interval. B) Variability for examples (colored lines) as well as all individual depth profiles (gray lines). C) Mean and standard deviation of the reliability, which is to ratio of the BOLD signal to variability: gray line shows individual reliability. D) Depth profiles (gray lines) normalized by mean of corresponding peak amplitude in the GM: mean (red) and standard deviation (dashed red) across ROIs and sessions.

We defined the ratio of peak amplitude to the variability as reliability (Fig. 6C). For all data, reliability had a stereotypical pattern, rising strongly from the WM through the GM to reach a maximum near the pial surface, and then dropping through the extra-pial compartment. Nevertheless, the mean reliabilities of depth profiles across ROIs and sessions were >5 throughout the given depth range (−0.5 ≤ w ≤ 1.5), again reflecting the high quality of the depth-profile measurements.

Although each depth had very small confidence intervals (Fig 6A, colored shaded regions), there were substantial session-to-session depth variations of normalized peak amplitude in the EP compartment, Fig. 6D. Profiles were tightly clustered with similar slopes through the WM and deep GM, than strongly diverge in the superficial GM and EP compartment. This behavior was quantified by the standard deviation of the peak-amplitude reliability across depth profiles (red-dashed lines in Fig. 6D).

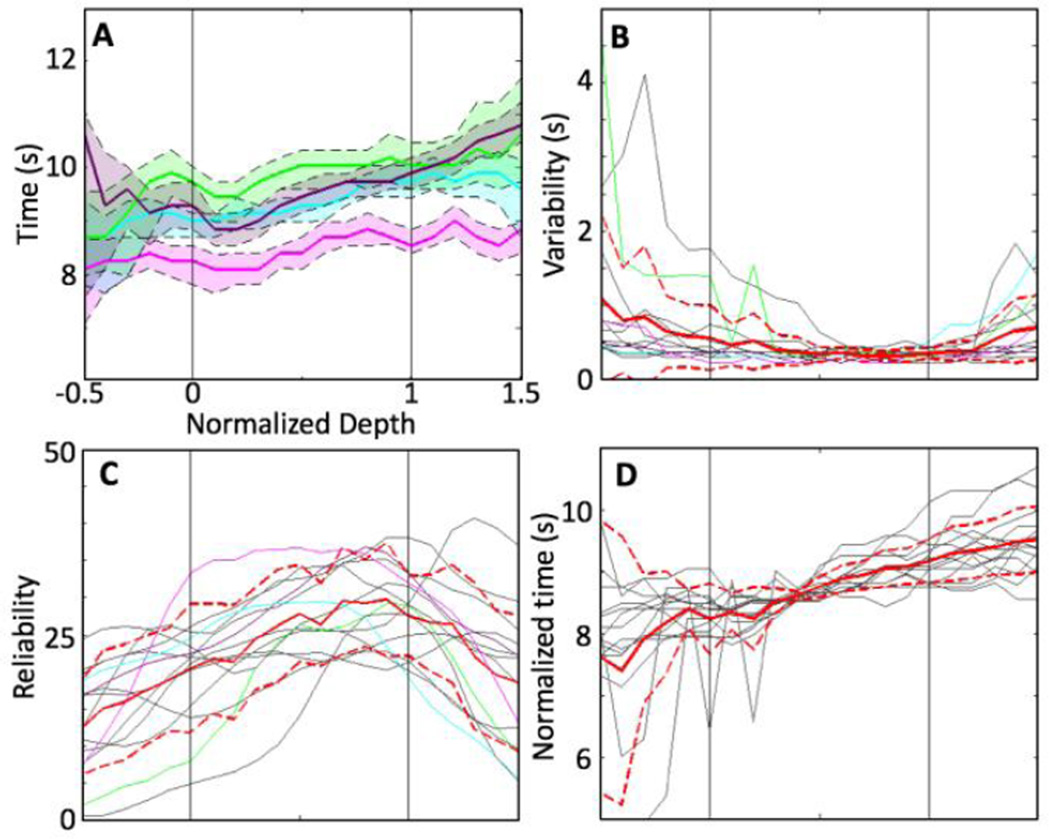
Depth profiles of time-to-offset, the most reliable temporal HRF parameter, are shown in Fig. 7. Example profiles exhibited a monotonic increase from deep to superficial GM (Fig. 7A). Variability of the timing (Fig. 7B, colored lines) was lowest within the GM, particularly in the superficial GM and the nearby EP. Variability was larger in the deeper GM, WM, and EP compartments. Timing reliability (Fig. 7C) also increased monotonically from deep to superficial GM, because of the linear increase in time-to-offset, with relatively small and consistent variability throughout the GM. Reliability was lower in the WM and EP compartments than in the GM because of their relatively larger variability.

Figure 7.

Depth analysis of the time-to-offset. 15 depth profiles that have significant linear trends within the GM are used. A) Examples (colored lines) of variation of depth profiles. Shaded regions show 68% confidence interval within each example. B) Variability of the examples (colored lines) as well as all individual depth profiles (gray). C) Mean (red) and standard deviation (dashed red) of the reliability across ROIs and sessions. D) Depth profiles (gray) normalized by mean of the corresponding time-to-offset in the GM: mean (red) and standard deviation (dashed red) across ROIs and sessions.

Individual depth-profiles of time-to-offset varied somewhat in magnitude. The normalization procedure enabled the examination of depth trends that exclude session-to-session variations (Fig. 7D). The slopes of the depth trends were consistent only in the GM compartment, and become particularly variable in the WM.

4. Discussion

High-resolution fMRI, aligned with a carefully segmented high-resolution structural reference volume, was used to quantify depth-dependent variations in the HRF at 3T. Our simple but effective visual stimulus evoked reliable HRFs in early visual cortex and apposed white-matter and extra-pial compartments. Our analysis of the HRF from the WM to EP compartments enabled a detailed characterization of the HRF in the vicinity of activated human early visual cortex.

4. 1 HRFs in white-matter, gray-matter and extra-pial compartments

We observed strong, very reliable HRFs in the GM. This result was consistent with many other studies. However, the reliability of our measurements was higher than reported in other studies. This likely reflects our use of high spatial resolution to reduce partial-volume effects, and the use of a fixation-point task to reduce cognitive noise during the ISI.

The HRFs in the WM and EP compartments have not been well characterized in most previous studies [14–17, 30, 31]. In fact, signals from these regions were commonly assumed to be caused by either partial volume effects, or as nuisance effects created by vascular functions that were unrelated to a given task or stimulus. Therefore, most depth-dependent HRF studies have not examined the signals outside of the GM [14–17]. Here, we showed the existence of distinct HRFs in the WM and EP compartments by careful analysis. First, we used high-resolution (0.9-mm) fMRI. Although we averaged signals from many voxels to obtain meaningful HRFs in each compartment, the high-resolution fMRI data still provided good depth resolution, enabling the separation of the signals in the WM and EP compartments from the GM. To obtain HRFs in WM and EP compartments, we only selected voxels at least 0.9-mm (our voxel resolution) away from GM/WM interface and pial surface to reduce partial volume. Similar results were also obtained at a larger separation (1.6 mm), Fig. 4. Second, we used a self-reciprocal, single-valued coordinate system that enabled identification of apposed WM and EP compartments that corresponded to a given ROI in the GM. Within the folded complexity of the GM, spatial relationships can be obscure, so the establishment of a self-reciprocal coordinate system is critical [6, 43, 44]. The use of such a depth metric should provide better correspondence of vascular responses in the WM and EP compartments to stimulus-evoked activity in the GM. The projections of strong response regions in all three compartments onto 3-D GM/WM interface (Fig. 3B) confirmed their spatial registration.

Qualitatively, the WM HRF showed early temporal behavior (up to the hyperoxic peak) that was similar to that seen in the GM HRF, which indicated that the WM may be driven by the same stimulus-evoked blood flow dynamics as the apposed GM. This finding was consistent with previous WM HRF measurements performed at relative low resolution, >3 mm voxel [9]. However, the HRF was weaker in the WM (Fig 5B): peak amplitude ~39% of that observed in the GM, but normalized peak amplitudes were still reliable (0.35±0.1%). The weaker peak amplitudes may reflect the much lower vascular density of the WM [10, 34, 45], or that blood flow to the WM was less sensitive to neural activity in the apposed GM. However, the strong peak amplitude correlation for each session between WM and GM (5C, left, blue line) indicated that the WM HRF was tightly coupled with the GM HRF. HRF responses also exhibited slightly faster temporal delay parameters (time-to-peak and time-to-offset) in the WM than in the GM (Fig. 5B). The time-to-offset between GM and WM also showed strong correlation (5C, right, blue line). Thus, there was a significant HRF in the WM with distinct temporal dynamics.

Many studies have observed task-evoked BOLD signals in deep white-matter regions such as corpus callosum and internal capsule [12, 18, 20, 23, 29, 46–48]. The existence of a deep WM BOLD signal was also supported by measurements showing correlations between glucose concentration and corpus callosum activation by intracortical electrostimulation in the rat [49]. In contrast, our results focused on the existence of a task-evoked BOLD signal in white matter apposed to activated GM. With our methods, we obtained more reliable task-related WM BOLD signals than those observed in the deep white matter fMRI studies. Note that we could not measure any deep white matter signals because of our relatively narrow prescription necessary to acquire high spatiotemporal resolution.

The topic of white-matter BOLD activation is still controversial [50–53]. Our observed white-matter HRF could correspond to "vascular spill-over" from the gray matter. A small fraction of penetrating arterioles pass through the gray matter without branching and vascularize the white matter, often with glomerular loop formations [34]. These vessels are mostly linked to the larger pial arterioles that also supply blood to the gray matter where neural activity mainly occurs. Accordingly, the white-matter HRF can be driven by similar blood flow dynamics. Alternatively, the blood flow dynamics in the WM could be determined from its own metabolism evoked by neural activity. Previously, cerebral metabolic rate of glucose in WM was shown to correlate to electrical fiber activity in rat corpus callosum[49], suggesting that our observed WM HRF could have been independently evoked by local metabolic demand. In our data, we observed that the WM HRF rose more quickly to a peak than in the GM. The early period of the HRF corresponds primarily to a competition between inflowing oxygenated blood and local cerebral metabolic rate of oxygen (CMRO₂) [54–57]. Because WM is more distant from vascular sources at the pial surface, convective flow delays should be similar or even longer, suggesting that local metabolism in the WM is lower than in GM, arguing against a metabolic-demand linkage for the observed WM HRF. On the other hand, the FWHM of the hyperoxic peak was also smaller in the WM than the GM, possibly invalidating this simple logic. Detailed modeling of these laminar and compartmental differences will be necessary to further assess these possibilities.

We cannot, however, rule out the possibility that the observed white-matter signals were the consequence of spatial blurring in the fMRI data. Such blurring would have to correspond to “long-range tails” to the fMRI point-spread functions. Our ideal spiral reconstructions showed no evidence for long tails. Relaxometry of cortical gray matter typically shows only a single exponential decay component with T2* ~ 50 ms, so blurring from transverse decay should be very small given our 27-ms acquisition time. Moreover, the HRF observed in the WM had different temporal features than that observed in the GM, while pure spatial blurring would make the WM HRF temporally identical to the GM HRF. Thus, we tentatively conclude that white matter apposed to early visual cortex has a weak and qualitatively unique HRF.

The HRF peak amplitude was stronger and more variable in the EP compartment than the GM. Our results were thus consistent with analyses that emphasized the confounding effects of BOLD responses from these superficial vascular structures [8, 17]. The substantial spatial variation of the pial vascular density along the cortical surface may contribute to the large variation of the peak amplitude in the EP compartment [34]. Nevertheless, there were strong correlations between peak amplitudes in the GM and EP compartments (Fig. 5C left, red line). HRF temporal delay parameters (time-to-peak and time-to-offset) in the EP compartment were relatively reliable and the timings were slightly slower than the GM (Fig. 5B), which is consistent with previous measurements outside the GM [9]. Moreover, there was a strong correlation of time-to-offset between the GM and EP compartments (5C, right, red line). These results indicated that the HRF in the EP compartment was linked with neural activity in the gray-matter parenchyma. Draining veins and sinuses are likely to be major sources of the signal in the EP compartment. The combination of their strong variability, spatial separation from the neural activity in the GM, yet good temporal synchronization with the GM signals indicated that these EP-compartment signals will both degrade and confound fMRI experiments carried out at conventional spatial resolutions.

4. 2 Depth-dependent parameters and their variability and reliability

We performed continuous depth analysis throughout the WM, GM and EP compartments (−0.5 ≤ w ≤ 1.5). For the peak amplitude, we observed significant monotonic depth trends from deep to superficial GM, which is consistent with previous studies [15–17].

The reliability of individual sessions was remarkably high (>5) throughout this depth range. Consider that each session collected a sample of a portion of active visual cortex gray matter, and apposing WM and EP compartment activity. The reliability of the peak amplitude (Fig. 6C) mostly followed the depth trend of peak amplitude (Fig. 6D) because of the low and consistent variability within each depth-profile. We showed that HRFs were reliably evoked throughout this depth range (Fig. 6B) by our stimulus. The shapes of the depth profiles of the deeper activity, from superficial WM to central GM, were notably consistent across ROIs and sessions.

However, there were substantial session-to-session variations for the peak amplitude in the superficial GM and EP compartment (Fig. 6C, dashed red lines). Thus, the results indicated that session-to-session variation among depth profiles was much larger than the within-session variability, producing large depth-trend variations in the superficial GM and EP compartments. The reliability in the deep GM and the large variation in the superficial GM were consistent with the depth-dependent variations in spatial reliability reported by Polimeni et al [14]. There are at least two possible sources for these variations. First, there can be substantial spatial variation across sessions in how each slice prescription samples the superficial pial vascular density [34]. This could cause the EP-compartment variations, and impact the superficial GM HRF through partial-volume effects. Another source of variation between sessions concerns the in-out nature of the vascular sources for the BOLD responses. Deeper GM, and possibly the WM, receive blood flow only from superficial sources, while superficial GM- and EP-compartment activity correspond to both direct superficial sources as well as venous return from deeper gray matter. The specific mixing of these laminar sources is probably also spatially variable along the cortical surface and could further contribute to the observed session variations.

To better characterize the later period of the HRF (after the hyperoxic peak), we utilized a time-to-offset metric, in addition to the time-to-peak and FWHM parameters studied previously [15, 58, 59]. We found that all temporal parameters tended to exhibit a monotonic increase from deep to superficial GM, which is consistent with previous studies [15, 16]. This monotonic increase suggested an initial neurovascular response in the deep GM followed by responses in more superficial GM. However, our results showed that time-to-offset was the most reliable temporal parameter, with a significant monotonic increase from deep to superficial GM (15/18). The greater reliability in this trailing edge of the hyperoxic peak may be the consequence of its more purely vascular character. The leading edge of the hyperoxic peak is likely affected by both blood flow and oxygen metabolism [60–62], but most models of the BOLD HRF would postulate a more purely vascular mechanism for the trailing edge of the response [54, 56, 57, 63, 64]. The weaker depth trends for time-to-peak and FWHM may be a consequence of the nonlinear competition between oxygen demand (CMRO₂ response) and blood supply (CBF response) that occurs early in the HRF [56, 57].

Although there were some variations of absolute timing for time-to-offset, normalized depth profiles confirmed significant linear trends across sessions and ROIs (1.12±0.63 s/cortical thickness). The variability within each session was lowest in the central to superficial GM resulting in the largest temporal reliability. This depth range usually has high vascular density [34, 45, 65], which may suggest particularly tight, regional neurometabolic and neurovascular coupling in the central-superficial GM. Alternatively, consider the spatiotemporal character of the venous blood flow in neocortex, which dominates the BOLD response. Venous outflow on the deepest layers reflects only local inflow, while venous outflow on the superficial layers reflects an aggregation of blood flow responses both locally and from all deeper layers. This pooling of flow response could serve to stabilize the timing of hyperoxic peak, increasing its reliability. However, this timing reliability may come at the cost of temporal blurring of the responses from the individual layers of cortex. This aggregation hypothesis is also consistent with the monotonic depth trend toward increasing FWHM of the hyperoxic peak from deep to superficial compartments.

In the WM, we observed relatively larger variability of time-to-offset both within each session (Fig. 7B, dashed red line) and across sessions (7D, dashed red line). Within individual session, temporal instability after the hyperoxic peak reflected the weaker HRF in the WM; amplitude noise reduced the reliability of the timing measurements. However, session-to-session variations again reduced the overall stability of the HRF timing in the WM. The observed variability may reflect greater heterogeneity in vascular sources to the WM, some of which may not be directly evoked by the stimulus.

Our work demonstrated task-evoked HRFs in all WM, GM and EP compartments as well as depth trends of their parameters in the GM with our simple stimulus. We performed repeated sessions for three subjects to increase statistical power. However, we could not report session-to-session variability within each subject because of our small dataset. We also characterized only small portion of early visual cortex. Future work should endeavor to more fully characterize the HRF, including spatial variations across the brain, across subjects, and its long-term temporal stability. This would enable clinical applications in which the HRF is used to evaluate brain health by discerning the effects of pathology on neurovascular coupling. High-resolution fMRI methods, such as those described here, could then further illuminate the mechanisms of such pathology on blood flow and neural metabolism.

5. Conclusions

We used high-resolution fMRI to measure depth-dependent HRFs and observed distinct differences between HRF parameters and their reliability in the WM, GM and EP compartments. HRF peak amplitudes in the WM and EP compartments were statistically significant, and both amplitude and timing parameters were tightly coupled with corresponding GM HRF parameters, suggesting that HRFs in all compartments were stimulus evoked. WM HRFs were weaker and faster than in the GM. EP compartment HRFs were stronger and slower than in the GM, but showed strong variations across sessions. Within the GM, depth profiles showed a significant monotonic increase from deep to superficial for amplitude and temporal parameters of the HRF. Time-to-offset was the most reliable temporal parameter of the HRF.

The variability of the peak amplitude within each session was low both in the GM, and apposed WM and EP compartments. Reliability of the peak amplitude was highest in the superficial GM, because its HRFs were large in amplitude and exhibited small within-session variability. However, we also found large variations across ROIs and sessions in the superficial GM and EP compartments. The combination of strong amplitudes and large variations across ROIs and sessions exacerbate the confounding effects of extra-pial compartment signals.

Altogether, our data demonstrated and quantified BOLD fMRI HRFs not only in the GM, but also in apposed WM and EP compartments. High-resolution fMRI thus can separate BOLD signals for each compartment, revealing distinct hemodynamics processes that affect the interpretation of fMRI data.