Universal modal radiation laws for all thermal emitters

Significance

Radiation laws must relate the fraction of incident radiation absorbed by an object and the amount of radiation emitted when it is hot so that objects can come to the same temperature just by exchanging electromagnetic radiation. Such laws are fundamentally important and set limits to practical applications such as in the conversion of light to electricity and in heat and thermal management generally. Kirchhoff’s classic results work well in many situations, but fail in others (specifically for “nonreciprocal” materials), and were derived using simplified models that do not apply to modern nanotechnology and light beams. We derive revised versions of laws that avoid these problems and discover additional and unexpected radiation laws that substantially expand the fundamental relations between optical absorption and emission.

Abstract

We derive four laws relating the absorptivity and emissivity of thermal emitters. Unlike the original Kirchhoff radiation law derivations, these derivations include diffraction, and so are valid also for small objects, and can also cover nonreciprocal objects. The proofs exploit two recent approaches. First, we express all fields in terms of the mode-converter basis sets of beams; these sets, which can be uniquely established for any linear optical object, give orthogonal input beams that are coupled one-by-one to orthogonal output beams. Second, we consider thought experiments using universal linear optical machines, which allow us to couple appropriate beams and black bodies. Two of these laws can be regarded as rigorous extensions of previously known laws: One gives a modal version of a radiation law for reciprocal objects—the absorptivity of any input beam equals the emissivity into the “backward” (i.e., phase-conjugated) version of that beam; another gives the overall equality of the sums of the emissivities and the absorptivities for any object, including nonreciprocal ones. The other two laws, valid for reciprocal and nonreciprocal objects, are quite different from previous relations. One shows universal equivalence of the absorptivity of each mode-converter input beam and the emissivity into its corresponding scattered output beam. The other gives unexpected equivalences of absorptivity and emissivity for broad classes of beams. Additionally, we prove these orthogonal mode-converter sets of input and output beams are the ones that maximize absorptivities and emissivities, respectively, giving these beams surprising additional physical meaning.

Radiation laws relating the absorptivity and emissivity of an object are at the core of the thermal physics of radiation and are particularly interesting for understanding limits to efficiency of solar energy conversion (e.g., refs. 1 and 2), for example. The core relation is Kirchhoff’s radiation law (3–6), which equates the absorptivity and emissivity of a surface. This law is often extended to a “directional” version, which equates the absorptivity of a given direction of input beam and the emissivity into the opposite or “reversed” direction. Typical textbook approaches (5, 6) to the directional law trace back to Planck’s rederivation (4) of Kirchhoff’s approach (3). Both Kirchhoff’s and Planck’s treatments explicitly make two assumptions: (i) The optical properties of the object are reciprocal (e.g., excluding Faraday rotation); (ii) diffraction is neglected, presuming objects much larger than a wavelength and using ray rather than wave optics. It is, however, now known that such a directional radiation law is not correct for nonreciprocal systems (1, 7), and nanophotonic structures for the control of thermal radiation (8–22) can have feature sizes much smaller than the wavelength. Given the fundamental thermodynamic importance and the technological relevance of radiation laws, we need to understand just what are the valid laws that cover nonreciprocal behavior and subwavelength structures and whether there are some deeper universal laws for all linear optical systems. Fundamental constraints on nonreciprocal thermal radiation are specifically important in determining the limit of thermal energy conversion. For example, it is known that the Landsberg limit for conversion of thermal radiation (such as solar radiation) to electricity (23), which represents the upper thermodynamic limit in terms of efficiency for such conversion, can be achieved only in systems where the reciprocity is broken (24, 25).

Here, we take an approach using orthogonal beams or “modes” to describe the radiation, thus automatically including diffraction. We derive three related and general laws, valid for reciprocal and nonreciprocal linear optical objects. These give equivalences of absorptivities and emissivities of broad classes of modes, beyond anything anticipated from the previous Kirchhoff laws. Then, adding reciprocity, we prove a fourth law—a rigorous “modal” version of the directional Kirchhoff law for reciprocal systems, showing that the absorptivity from any mode or beam is equal to the emissivity into its “backward” (strictly, phase-conjugated) version.

Approach

Our approach uses two recently proposed concepts in constructing our proofs. First, we use the “mode-converter” basis sets to describe the fields (26). These sets, which can be derived for any linear optical object, give a complete set of orthogonal input fields or modes that couple one by one, through interaction with the object, to a corresponding complete set of orthogonal output fields or modes. These specific modes, which implicitly obey all diffraction phenomena, are essential here: we use them in constructing the proofs, two of the related general laws we derive have to be stated in terms of them, and the discussion here gives an additional physical meaning to them in terms of absorption and emission. Second, we use a universal linear optical component or machine (27) that allows us to construct useful thought experiments.

As in the original Kirchhoff derivation (3), we presume we are working at or near one (angular) frequency $\omega$ of radiation so all of the functions we use below are then essentially only spatial functions (with also vector polarization character). For mathematical convenience, we use complex fields; as usual, at the end we can return to real fields by taking the real part. We can consider all such spatial functions to be multiplied by a monochromatic time-varying function $\exp \left(i\omega t\right).$ More physically, we can presume we are considering a very small bandwidth around such a center frequency and a time duration of interest that is long enough to consider equilibrium but short enough that we do not notice any phase differences between frequencies within this bandwidth over the time of interest. In what follows, we presume we have corresponding frequency filters, which pass this narrow bandwidth perfectly and reflect all other wavelengths, in front of all black bodies we use in our arguments.

Modes, Basis Sets, and Singular-Value Decomposition.

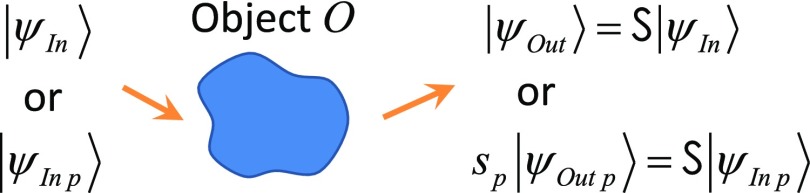
To start, we consider how a linear optical object O takes an incident input field $|{\psi }_{In}\rangle$ and turns it into an output field of the form $|{\psi }_{Out}\rangle$ (Fig. 1) as a result of a linear interaction that we represent with a linear operator or “object” matrix S (Terminology for the Matrix S). (This interaction does not include thermal emission from the object, which we add later.) So, mathematically,

$$|{\psi }_{Out}\rangle =\text{S}|{\psi }_{In}\rangle$$ [1]

(Note we use Dirac bra-ket linear algebra notation here—Dirac “Bra-Ket” Notation for its standard definitions and properties. This means we can avoid explicit statements of vector or polarization properties, although such properties are implicitly covered. This generality means our analysis also covers other linear fields, such as acoustic waves.)

Fig. 1.

Shining an input wave $|{\psi }_{In}\rangle$ on the linear optical object O leads to an output wave $|{\psi }_{Out}\rangle$ as a result of the linear interaction described by the operator or matrix S. If we shine one of the orthogonal input mode-converter basis function waves, such as the pth such (normalized) input mode $|{\psi }_{In\hspace{0.17em}p}\rangle ,$ then the resulting output wave is the corresponding pth orthogonal (normalized) output mode-converter basis function wave $|{\psi }_{Out\hspace{0.17em}p}\rangle$ but with (complex) amplitude s_p, where s_p is the corresponding pth singular value of S.

For any such matrix S, it is always possible to perform the singular value decomposition (SVD) (26, 28). One statement of such a decomposition is

$$\text{S}={\text{V}}_S{\text{D}}_{diag}{\text{U}}_S,$$ [2]

where U_S and V_S are unitary matrices and D_diag is a diagonal matrix. We can also rewrite this as

$$\text{S}={\displaystyle \sum _p{s}_p|{\psi }_{Out\hspace{0.17em}p}\rangle }\langle {\psi }_{In\hspace{0.17em}p}|.$$ [3]

Formally, the singular values s_p are the diagonal elements of D_diag, $\langle {\psi }_{In\hspace{0.17em}p}|$ are the rows of U_S, and $|{\psi }_{Out\hspace{0.17em}p}\rangle$ are the columns of V_S. The set of orthogonal input functions or “mode-converter input modes” $\left\{|{\psi }_{In\hspace{0.17em}n}\rangle \right\}$ constitutes the so-called right singular vectors of $\text{S}$ and can be deduced as the eigenfunctions of ${\text{S}}^{†}\text{S};$ that is, the solutions of

$${\text{S}}^{†}\text{S}|{\psi }_{In\hspace{0.17em}p}\rangle ={\left|s_p\right|}^2|{\psi }_{In\hspace{0.17em}p}\rangle$$ [4]

and similarly the set of orthogonal output functions or “mode-converter output modes” $\left\{|{\psi }_{Out\hspace{0.17em}n}\rangle \right\}$ constitute the left singular vectors of S and are the eigenfunctions of $\text{S}{\text{S}}^{†},$ as in

$$\text{S}{\text{S}}^{†}|{\psi }_{Out\hspace{0.17em}p}\rangle ={\left|s_p\right|}^2|{\psi }_{Out\hspace{0.17em}p}\rangle .$$ [5]

The specific elements in the two sets are related by

$$\text{S}|{\psi }_{In\hspace{0.17em}p}\rangle =s_p|{\psi }_{Out\hspace{0.17em}p}\rangle$$ [6]

and

$${\text{S}}^{†}|{\psi }_{Out\hspace{0.17em}p}\rangle =s_p^{\ast }|{\psi }_{In\hspace{0.17em}p}\rangle .$$ [7]

These SVD function sets $\left\{|{\psi }_{In\hspace{0.17em}n}\rangle \right\}$ and $\left\{|{\psi }_{Out\hspace{0.17em}p}\rangle \right\}$ have an important physical meaning: When one of the orthogonal input beams or functions $|{\psi }_{In\hspace{0.17em}p}\rangle$ interacts with the object, it leads to one and only one of the orthogonal output beams or functions $|{\psi }_{Out\hspace{0.17em}p}\rangle ,$ with a complex amplitude coupling strength $s_p$ (Fig. 1). Equivalently, each such orthogonal input mode $|{\psi }_{In\hspace{0.17em}p}\rangle$ is mapped or “converted” by the object to give an amplitude only in the corresponding orthogonal output mode $|{\psi }_{Out\hspace{0.17em}p}\rangle ,$ thus defining a set of orthogonal “channels” “through” the object. Hence every such linear optical device can be described as a mode converter (26). Other than the usual arbitrariness of linear combinations of any possible degenerate eigensolutions, these sets of functions are unique and complete; no other complete set of orthogonal input functions generates orthogonal output functions, and these orthogonal “mode-converter pairs” $|{\psi }_{In\hspace{0.17em}p}\rangle$ and $|{\psi }_{Out\hspace{0.17em}p}\rangle$ always exist and can be used as basis sets to describe any possible linear relation from input to output. In contrast to plane wave basis descriptions, these beams can be straightforwardly normalized to represent beams of unit power. With unit input power in $|{\psi }_{In\hspace{0.17em}p}\rangle ,$ from Eq. 6 the resulting amplitude in the output beam of form $|{\psi }_{Out\hspace{0.17em}p}\rangle$ is s_p and the power in that beam is ${\left|s_p\right|}^2.$

A Mode-Separating Machine.

For our thought experiments and proofs here, we work with “single-mode” black bodies Such a black body allows only one optical mode (at a given frequency and polarization state) to propagate in and out of it. (Existence and Required Properties of Black Bodies for an extended discussion). For example, we could imagine this black body is connected to the external world only through a single-mode optical fiber that also allows only one polarization state to propagate.

We want to take the output from such a single-mode black body and losslessly construct from it any desired input wave $|{\psi }_I\rangle$ to shine on the object O. We also want simultaneously to be able losslessly to collect any wave in any desired output beam mode $|{\psi }_O\rangle$ and route it as the input back into such a single-mode black body. In this way, we can consider thermal equilibrium between the object O and such black bodies.

In our thought experiments, we consider multiple single-mode black bodies and multiple orthogonal input fields to object O and orthogonal output fields from object O that are connected losslessly in and out of these black bodies. Because all of these various input and output fields may be overlapping in space, the question arises whether we can make an optical machine that can losslessly perform all of the necessary transformations and combinations. Fortunately, recent work (27) shows it is possible, at least in principle, to design and make such a universal lossless linear optical machine.

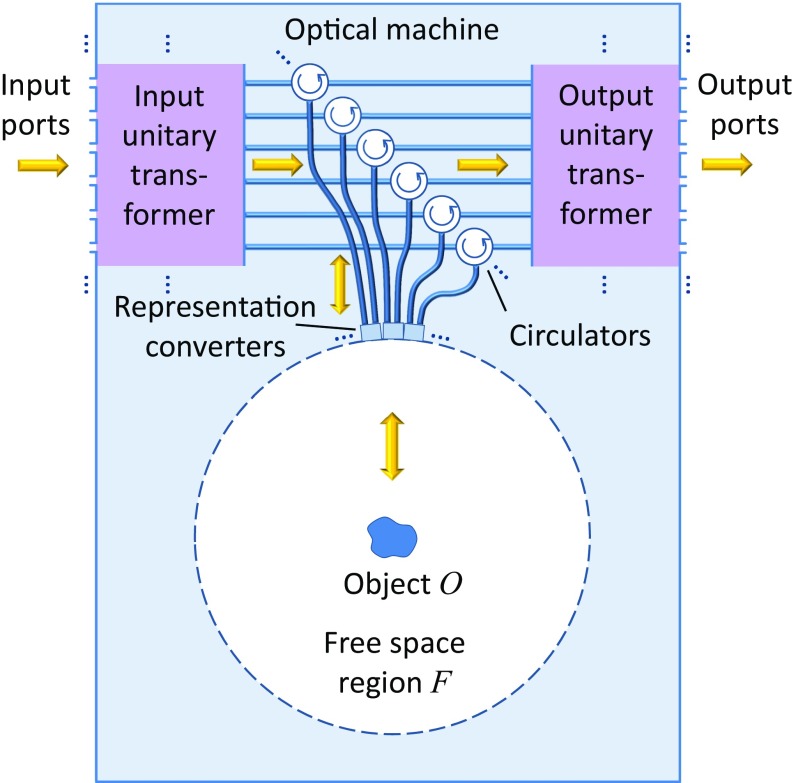
Here, we presume we can in principle make such an optical machine. The function of this optical machine is, first, to take light in specific single-mode input ports and map each such input into a specific desired input wave incident on the object O inside a free-space region F. The resulting waves on the object can be chosen to be any orthogonal set, and specifically these waves can be completely overlapping in space. Second, the machine can collect light in any specific orthogonal set of waves from the object, including waves that can be completely overlapping, and map each such orthogonal output wave to a different specific output port on the right of the machine (Internal Structure of a Universal Lossless Linear Optical Machine and Fig. S1 for an extended discussion).

Fig. S1.

Sketch of an optical machine for losslessly mapping field amplitudes in each single-mode input port to any desired orthogonal incident waves (modes) on the object and collecting from any desired orthogonal output modes from the object and mapping those to corresponding single-mode output ports. The representation converters convert, forward and backward, between two waveguide amplitudes in the same polarization and a plane-wave patch of arbitrary desired polarization at the edge of the free space region F. Only a few such converters and waveguides are shown, but a large number of these are presumed to cover the entire spherical shell bounding F, with the waveguides connected through the circulators to the unitary transformers. The radius of F is presumed to be very large, with the object O approximately at the center of F. The unitary transformers can each implement any desired linear mapping (or matrix) between the amplitudes in their single-mode input ports or waveguides on their left to their single-mode output ports on their right.

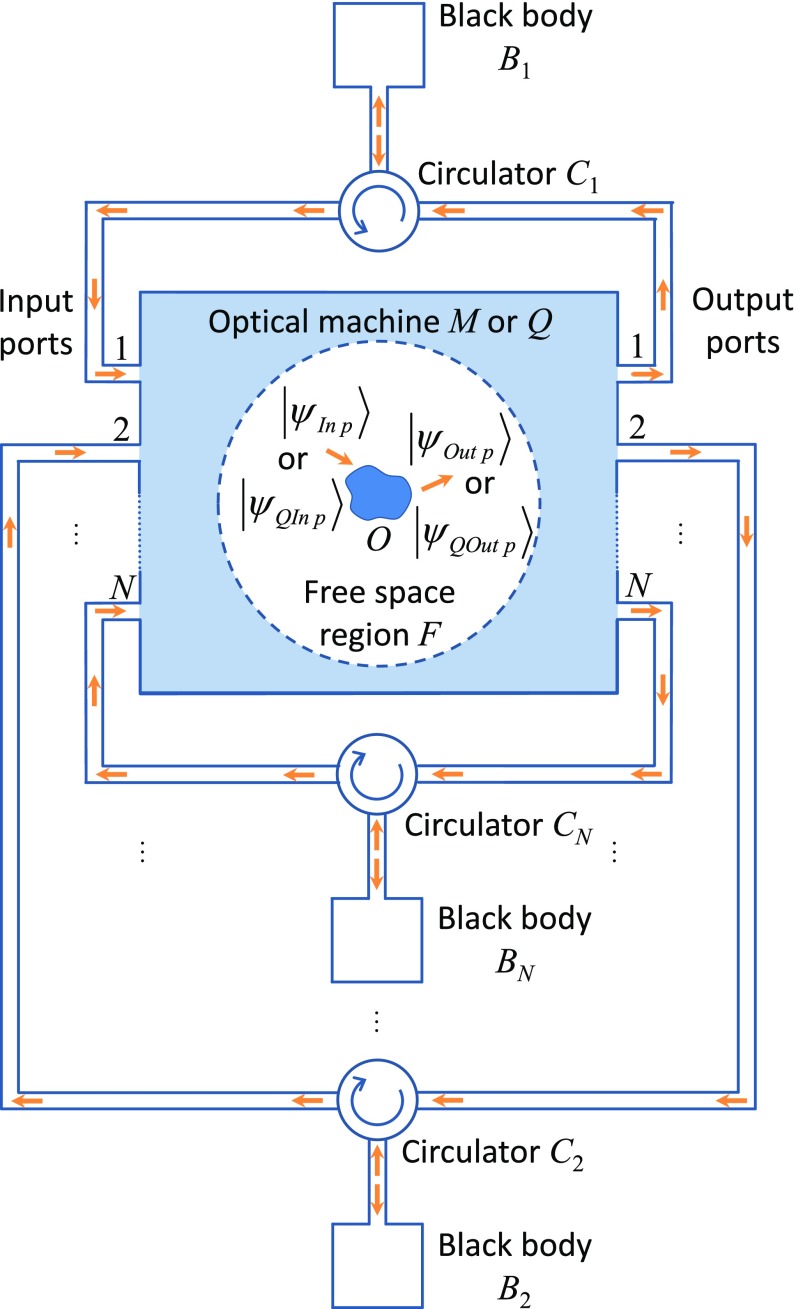
Here we use the specific arrangement in Fig. 2. Now we have added single-mode black bodies together with some external single-mode waveguide optics and circulators. We explicitly consider two different versions of the machine, labeled M and Q, respectively. Both presume we have some large number N of input and output ports and black bodies.

Fig. 2.

Object O in free space region F is surrounded by one of two different linear optical machines, M or Q. For machine M, radiation in input port p is converted to the mode-converter input function $|{\psi }_{In\hspace{0.17em}p}\rangle ,$ which is then incident on O. Radiation scattered or emitted from O into the mode-converter output function $|{\psi }_{Out\hspace{0.17em}p}\rangle$ is collected by the machine M and coupled to output port p. In machine Q, input port p is coupled to some other input wave $|{\psi }_{QIn\hspace{0.17em}p}\rangle$ and radiation in some other output wave $|{\psi }_{QOut\hspace{0.17em}p}\rangle$ is coupled to output p. The sets of functions $\left\{|{\psi }_{QIn\hspace{0.17em}n}\rangle \right\}$ and $\left\{|{\psi }_{QOut\hspace{0.17em}n}\rangle \right\}$ are each orthogonal and complete for describing input and output radiation for O but are in general different from the mode-converter sets $\left\{|{\psi }_{In\hspace{0.17em}n}\rangle \right\}$ and $\left\{|{\psi }_{Out\hspace{0.17em}n}\rangle \right\}.$ Each circulator C_p routes the radiation from output port p and shines it into black body B_p and routes the output radiation from B_p to input port p.

We presume that, knowing the object O physically, we can perform the SVD and deduce the mode-converter basis sets $\left\{|{\psi }_{In\hspace{0.17em}n}\rangle \right\}$ and $\left\{|{\psi }_{Out\hspace{0.17em}n}\rangle \right\}$ and the corresponding set of singular values $\left\{s_n\right\}.$ For definiteness, we can presume that we consider the N elements in the mode-converter basis sets $\left\{|{\psi }_{In\hspace{0.17em}n}\rangle \right\}$ and $\left\{|{\psi }_{Out\hspace{0.17em}n}\rangle \right\}$ corresponding to the N smallest singular values. (Small singular values mean strong absorption, as is clarified below.) We presume we have chosen N large enough that these sets describe all of the waves of interest to a sufficient degree of approximation.

Machine M has N input ports and output ports that we can think of as single-mode waveguides. Because of the machine’s design, we have waves only entering the input ports and exiting the output ports; we never have waves in the other directions in these ports. (The machine itself, because it separates forward and backward waves, is nonreciprocal, although that nonreciprocity does not mean we are restricting object O to be either reciprocal or nonreciprocal.) A unit amplitude in input port p is converted by the machine M to unit amplitude in the input mode-converter basis wave $|{\psi }_{In\hspace{0.17em}p}\rangle$ inside the machine, which is then incident on object O. Similarly, a unit amplitude of wave in the mode-converter output function $|{\psi }_{Out\hspace{0.17em}p}\rangle$ is converted by the machine M into unit amplitude in output port p. The circulator C_p routes the output light from port p to be the input light to black body B_p and routes the output light from B_p to input port p. In what follows, we can think of black body B_p as being B₁ at the top of Fig. 2, but any one of the black bodies can be chosen.

Terminology for the Matrix S

In choosing a terminology for the matrix S, most obviously, we might call it a scattering matrix, and that would be technically correct from a mathematical point of view. There are, however, two reasons not to do so. First, in the way we set up this problem, some specific incident light beam $|{\psi }_{In\hspace{0.17em}q}\rangle$ that nearly or completely misses the object, and hence is not in any real physical sense strongly scattered by it, would have essentially the largest possible value of the “scattering amplitude” s_q, namely $\left|s_q\right|\cong 1,$ passing all its power to the corresponding output beam $|{\psi }_{Out\hspace{0.17em}q}\rangle .$ Second, it is common (although not essential, mathematically or physically) in discussing scattering matrices to use backward (phase-conjugated) versions of the input beams or modes as the basis for representing the output beams. (Such a choice is one of the ways in which a reciprocal object has a symmetric S matrix, for example.) Here, however, we do not want to start by presuming any such output basis; indeed, because we want to cover the nonreciprocal case, we may not even be justified in choosing such a backward (phase-conjugated) basis for the output beams; at least, we would need to go through some additional arguments to justify that. In our mathematics, we do not need to constrain the output basis in this way, so we avoid doing so. Indeed, it may be best to think of the matrix S as scattering from the input mode-converter basis functions to the output mode-converter basis functions, regardless of what those are.

In the paper introducing the idea of mode-converter basis functions (26), the corresponding matrix was referred to as the “device matrix.” We could use that terminology here, but because we may not be considering a device here, the broader term “object matrix” may be more appropriate.

Derivation of Modal Radiation Laws

Absorptivity and Emissivity of a Mode-Converter Pair.

Now, using machine M of Fig. 2, we derive a relation between the absorptivity of a given mode-converter input wave $|{\psi }_{In\hspace{0.17em}p}\rangle$ and the emissivity into the corresponding scattered mode-converter output wave $|{\psi }_{Out\hspace{0.17em}p}\rangle .$ Because of our use of the mode-converter basis sets in machine M, black body B_p receives only power that is scattered (into output mode $|{\psi }_{Out\hspace{0.17em}p}\rangle$) from the input mode $|{\psi }_{In\hspace{0.17em}p}\rangle$—power that itself comes only from the black body B_p output power—plus any power that is emitted into this output mode $|{\psi }_{Out\hspace{0.17em}p}\rangle$ from the object O. Here we are using the mode-converter basis sets precisely because we want to avoid considering any scattering from other input modes into the output mode of interest and any emitted power in other output modes; none of the output power from any of the other black bodies is scattered back into the black body B_p.

All power in the input wave $|{\psi }_{In\hspace{0.17em}p}\rangle$ comes from the output of black body B_p. For an incident power $P_{in}$ in a wave of the form $|{\psi }_{In\hspace{0.17em}p}\rangle ,$ from Eq. 6 the scattered output power $P_{scat}$ (which is all in the output wave of form $|{\psi }_{Out\hspace{0.17em}p}\rangle$) is

$$P_{scat}={\left|s_p\right|}^2{P}_{in}.$$ [8]

All of the power not scattered is absorbed by the lossy object O. So the absorbed power is $P_{abs}=\left(1-{\left|s_p\right|}^2\right)P_{in}.$ So the fraction of the incident power absorbed is, by definition, the absorptivity

$${\alpha }_{Mp}=\frac{P_{abs}}{P_{in}}=1-{\left|s_p\right|}^2.$$ [9]

Now, because we presume the object O to be at some nonzero temperature T_eq, it is emitting radiation. By definition of the emissivity ${\epsilon }_{Mp}$ for this mode, the emitted thermal power into mode $|{\psi }_{Out\hspace{0.17em}p}\rangle$ (at the frequency ω or in the narrow frequency range of interest around it) is $P_{therm}={\epsilon }_{Mp}{P}_B,$ where $P_B$ is the power that a black body at this same temperature T_eq would emit into a single mode at this frequency or in the narrow frequency range of interest.

The total power going back into black body B_p is the sum of this thermal emitted power in mode $|{\psi }_{Out\hspace{0.17em}p}\rangle$ and the power scattered into mode $|{\psi }_{Out\hspace{0.17em}p}\rangle .$ Using Eq. 8 with $P_{in}=P_B,$ the total power going back into black body B_p is therefore

$$P_{B\hspace{0.17em}in}={\epsilon }_{Mp}{P}_B+{\left|s_p\right|}^2{P}_B.$$ [10]

But if the black body B_p is to be in thermal equilibrium with the object O at this temperature T_eq, this input power $P_{B\hspace{0.17em}in}$ to the black body must equal its output power, which is $P_B;$ i.e., $P_{B\hspace{0.17em}in}=P_B$ in thermal equilibrium. So, from Eq. 10 and dividing both sides by $P_B$ and rearranging,

$${\epsilon }_{Mp}=1-{\left|s_p\right|}^2.$$ [11]

But comparing this to Eq. 9, we see that

$${\epsilon }_{Mp}={\alpha }_{Mp}.$$ [12]

This gives an important first result that is different from Kirchhoff's results.

Law 1.

For an object O with mode-converter input and output mode sets $\left\{|{\psi }_{In\hspace{0.17em}n}\rangle \right\}$ and $\left\{|{\psi }_{Out\hspace{0.17em}n}\rangle \right\},$ respectively, the absorptivity ${\alpha }_{Mp}$ from any such input mode $|{\psi }_{In\hspace{0.17em}p}\rangle$ equals the emissivity ${\epsilon }_{Mp}$ into the corresponding output mode $|{\psi }_{Out\hspace{0.17em}p}\rangle .$

We can also prove the converse of this statement (Proof of the Converse to the First Law and Fig. S2).

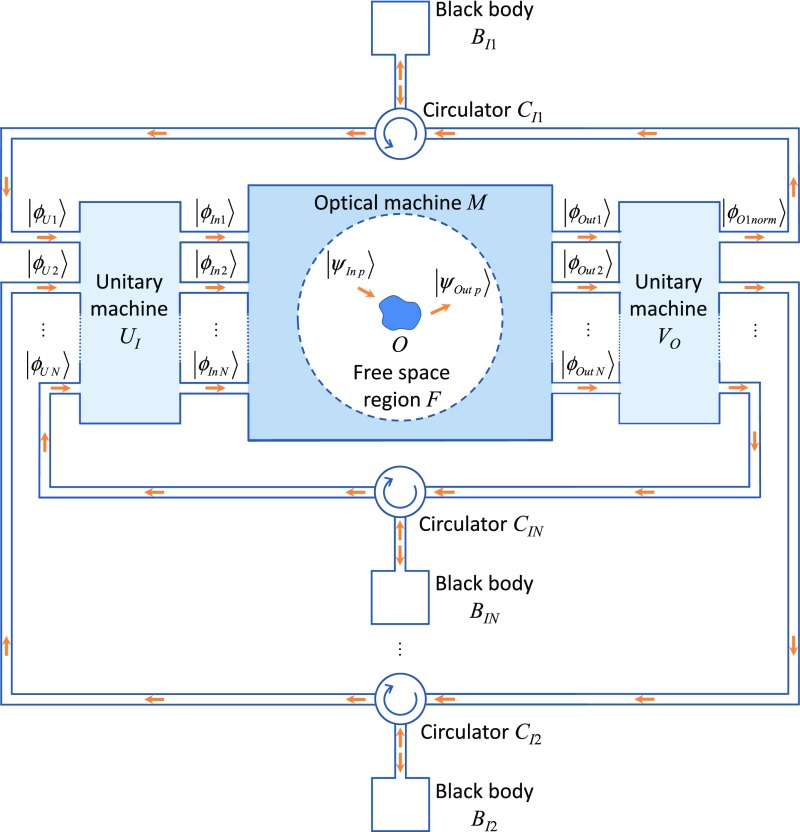
Fig. S2.

Optical arrangement for considering the converse of Law 1. An arbitrary unitary machine U_I at the input to machine M allows black body $B_{I1}$ to deliver power to an arbitrary superposition of input modes at the input to the optical machine M. Radiation from that particular input is scattered from the object O to give power in some output mode $|{\psi }_{O1\hspace{0.17em}norm}\rangle .$ Any power scattered or emitted into that mode $|{\psi }_{O1norm}\rangle$ is collected by the output unitary machine $V_O$ (into the single-mode waveguide mode $|{\varphi }_{O1\hspace{0.17em}norm}\rangle$) and routed to the input to black body $B_{U1}.$ Other radiation scattered into or emitted from output modes orthogonal to $|{\psi }_{O1\hspace{0.17em}norm}\rangle$ is collected and routed to other black bodies $B_{I2}$ to $B_{IN},$ whose output power is fed into the remaining input modes $|{\varphi }_{U2}\rangle$ to $|{\varphi }_{UN}\rangle .$

If the absorptivity ${\alpha }_{Mp}$ from an input mode equals the emissivity ${\epsilon }_{Mp}$ into the corresponding scattered output mode, then these input and output modes are a mode-converter pair.

Note that Law 1 and, mathematically, Eq. 12 are not the conventional statement of Kirchhoff’s directional radiation law; that refers to the absorptivity from one mode and the emissivity into the backward (i.e., the phase-conjugated) version of the same mode. The equality in our Law 1 here is between the absorptivity of the mode-converter input mode and the emissivity into the corresponding mode-converter output mode—that is, the output mode into which the input mode scatters.

This approach makes no assumptions about the scattering object other than that it is linear. Specifically, that object can also be nonreciprocal, so we have derived a condition for absorptivity and emissivity of nonreciprocal as well as reciprocal objects.

Universal Modal Radiation Law.

Now consider that we change to machine Q that maps the input ports one by one to some possibly different set of orthogonal input functions $\left\{|{\psi }_{QI\hspace{0.17em}n}\rangle \right\}$ and maps some possibly different set of orthogonal output functions $\left\{|{\psi }_{QO\hspace{0.17em}n}\rangle \right\}$ one by one to the corresponding output ports. Formally, we can regard these new functions as being related by arbitrary unitary transforms $\text{U}$ and $\text{V}$ to the mode-converter basis functions, i.e., $|{\psi }_{QI\hspace{0.17em}p}\rangle =\text{U}|{\psi }_{In\hspace{0.17em}p}\rangle ,$ $|{\psi }_{QO\hspace{0.17em}p}\rangle =\text{V}|{\psi }_{Out\hspace{0.17em}p}\rangle ,$ and we can consider these sets to span the same spaces as the sets $\left\{|{\psi }_{In\hspace{0.17em}n}\rangle \right\}$ and $\left\{|{\psi }_{Out\hspace{0.17em}n}\rangle \right\}.$

In general, if we had a unit input power in a wave $|{\psi }_{QI\hspace{0.17em}p}\rangle$ from a given black body $B_{Ip},$ we would have a scattered output vector $|{\psi }_O\rangle =\text{S}|{\psi }_{QI\hspace{0.17em}p}\rangle$ with power $\langle {\psi }_O|{\psi }_O\rangle =\langle {\psi }_{QI\hspace{0.17em}p}|{\text{S}}^{†}\text{S}|{\psi }_{QI\hspace{0.17em}p}\rangle .$ So the fraction of this unit input power that is absorbed is

$${\alpha }_{Qp}=1-\langle {\psi }_{QI\hspace{0.17em}p}|{\text{S}}^{†}\text{S}|{\psi }_{QI\hspace{0.17em}p}\rangle ,$$ [13]

which by definition is the absorptivity for this input mode $|{\psi }_{QI\hspace{0.17em}p}\rangle .$

At this point, we can usefully define a matrix $\text{A},$

$$\text{A}={\text{I}}_I-{\text{S}}^{†}\text{S},$$ [14]

where ${\text{I}}_I$ is the identity matrix in the input space. Then Eq. 13 can be written ${\alpha }_{Qp}=\langle {\psi }_{QI\hspace{0.17em}p}|\text{A}|{\psi }_{QI\hspace{0.17em}p}\rangle .$ Because the choice of the actual input mode onto the object here is arbitrary (because $\text{U}$ is arbitrary), we can write for any input mode $|i\rangle$ on the object that the corresponding absorptivity is

$${\alpha }_i=\langle i|\text{A}|i\rangle$$ [15]

and for this reason we can call $\text{A}$ the “absorptivity” matrix.

Now, in the situation in Fig. 2 with machine Q, the absorbed power in black body $B_p$ consists of the emission of the object O to it, as well as the parts of the emitted power from all of the other bodies that get scattered by object O into $B_p.$ In thermal equilibrium of all of the black bodies with the object O at some temperature T_eq, that absorbed power into $B_p$ must balance the emitted power $P_B$ from $B_p.$ By definition of the object matrix S, for unit amplitude in an input port n, the amplitude that is scattered to an output port m is the corresponding matrix element $\langle {\psi }_{QO\hspace{0.17em}m}|\text{S}|{\psi }_{QI\hspace{0.17em}n}\rangle \equiv S_{mn}.$ Hence, the fraction of the power from black body $B_n$ that is scattered to black body $B_m$ is ${\left|S_{mn}\right|}^2$ and so a scattered power of $P_B{\left|S_{mn}\right|}^2.$ Because all of these output modes $\left\{|{\psi }_{QO\hspace{0.17em}n}\rangle \right\}$ are by choice orthogonal, the total scattered power from all of the other black bodies to black body $B_m$ is the sum of these powers over all of the output modes; that is,

$$P_B{\displaystyle \sum _n{\left|S_{mn}\right|}^2}\equiv P_B{\displaystyle \sum _n\langle {\psi }_{QO\hspace{0.17em}m}|\text{S}|{\psi }_{QI\hspace{0.17em}n}\rangle \langle {\psi }_{QI\hspace{0.17em}n}|{\text{S}}^{†}|{\psi }_{QO\hspace{0.17em}m}\rangle }\hspace{0.17em}\equiv P_B\langle {\psi }_{QO\hspace{0.17em}m}|\text{S}{\text{S}}^{†}|{\psi }_{QO\hspace{0.17em}m}\rangle ,$$ [16]

where we have used the equivalence ${\displaystyle \sum _n|{\psi }_{QI\hspace{0.17em}n}\rangle \langle {\psi }_{QI\hspace{0.17em}n}|}\hspace{0.17em}\equiv {\text{I}}_I$ (i.e., the identity operator for the input space). By definition of the emissivity ${\epsilon }_{Qm},$ the emitted power into the output mode $|{\psi }_{QOm}\rangle$ is ${\epsilon }_{Qm}{P}_B,$ so the equilibrium power balance in black body $B_m$ requires

$$P_B={\epsilon }_{Qm}{P}_B+P_B{\displaystyle \sum _n{\left|S_{mn}\right|}^2}.$$ [17]

Equivalently, if we define a matrix $\text{E},$

$$\text{E}={\text{I}}_O-\text{S}{\text{S}}^{†},$$ [18]

where ${\text{I}}_O$ is the identity matrix in the output space, then dividing Eq. 17 by $P_B$ and rearranging gives ${\epsilon }_{Qm}=\langle {\psi }_{QO\hspace{0.17em}m}|\text{E}|{\psi }_{QO\hspace{0.17em}m}\rangle .$ Again, the choice of the output mode from the object that corresponds to $|{\psi }_{QOm}\rangle$ is arbitrary because $\text{V}$ is arbitrary, so for any (normalized) output mode $|f\rangle$ from the object

$${\epsilon }_f=\langle f|\text{E}|f\rangle ,$$ [19]

and for this reason we can call $\text{E}$ the “emissivity” matrix.

Now, consider a specific arbitrary normalized input mode $|i\rangle ,$ which can be expanded on the mode-converter input basis functions as

$$|i\rangle ={\displaystyle \sum _m{c}_m|{\psi }_{In\hspace{0.17em}m}\rangle }.$$ [20]

From Eq. 15 and using Eqs. 4 and 9, we have

$$\begin{array}{c}{\alpha }_i={\displaystyle \sum _{n,m}{c}_n^{\ast }{c}_m}\langle {\psi }_{In\hspace{0.17em}n}|{\text{I}}_I-{\text{S}}^{†}\text{S}|{\psi }_{In\hspace{0.17em}m}\rangle \\ ={\displaystyle \sum _{n,m}{c}_n^{\ast }{c}_m}\left(1-{\left|s_m\right|}^2\right)\langle {\psi }_{In\hspace{0.17em}n}|{\psi }_{In\hspace{0.17em}m}\rangle \\ ={\displaystyle \sum _{n,m}{c}_n^{\ast }{c}_m}\left(1-{\left|s_m\right|}^2\right){\delta }_{nm}={\displaystyle \sum _m{\left|c_m\right|}^2\left(1-{\left|s_m\right|}^2\right)}\\ ={\displaystyle \sum _m{\left|c_m\right|}^2{\alpha }_{Mm}}.\end{array}$$ [21]

Let us also construct a (normalized) output mode $|f\rangle$ expanded on the mode-converter output basis functions

$$|f\rangle ={\displaystyle \sum _m{c}_m\exp \left(i{\theta }_m\right)|{\psi }_{Out\hspace{0.17em}m}\rangle }.$$ [22]

Explicitly now we allow additional arbitrary phase factors $\exp \left(i{\theta }_m\right);$ the ${\theta }_m$ are arbitrary (real) phases associated with each expansion coefficient c_m. This means that, although we are constructing this output mode of interest with expansion coefficients that have the same magnitudes as the expansion coefficients for the input mode $|i\rangle ,$ we are allowing these output mode expansion coefficients to have arbitrary phases. From Eqs. 19 and 22, using Eqs. 5 and 11,

$$\begin{array}{c}{\epsilon }_f={\displaystyle \sum _{n,m}{c}_n^{\ast }\exp \left(-i{\theta }_n\right)c_m\exp \left(i{\theta }_m\right)\langle {\psi }_{Out\hspace{0.17em}n}|{\text{I}}_O-\text{S}{\text{S}}^{†}|{\psi }_{Out\hspace{0.17em}m}\rangle }\\ ={\displaystyle \sum _{n,m}{c}_n^{\ast }\exp \left(-i{\theta }_n\right)c_m\exp \left(i{\theta }_m\right)\left(1-{\left|s_m\right|}^2\right){\delta }_{nm}=}{\displaystyle \sum _m{\left|c_m\right|}^2{\epsilon }_{Mm}}.\end{array}$$ [23]

So, finally, using our Law 1 (and as stated in Eq. 12) [or, equivalently, noting the same $(1-|s_m{|}^2)$ factors in the sums in both Eqs. 21 and 23],

$${\epsilon }_f={\alpha }_i,$$ [24]

which is the second result of our paper. Note here that the phases ${\theta }_m$ do not matter; all that does matter is that for our input mode $|i\rangle$ of interest, its power splitting between the input mode-converter modes is the same as the power splitting between the output mode-converter modes in our output mode $|f\rangle$ of interest. Hence entire broad sets of input modes have emissivities equal to an entire broad set of output modes. We can state this law as follows.

Law 2.

For an output beam whose power is split in given fractions among the mode-converter output modes, its emissivity is the same as the absorptivity of an input beam whose power is split in the same fractions among the corresponding mode-converter input modes.

Law 2 is not anticipated in the original Kirchhoff approach, and it is valid for reciprocal and nonreciprocal objects.

We can also draw two corollaries from this argument, which are immediately apparent from Eqs. 21 and 23, respectively, and both follow simply from Law 2.

Law 2, corollary 1.

All input beams whose power is split in the same fractions among the mode-converter input modes have the same absorptivity.

Law 2, corollary 2.

All output beams whose power is split in the same fractions among the mode-converter output modes have the same emissivity.

Incidentally, our Law 1 above (also Eq. 12), can now be seen to be a special case of this Law 2 for the case where one of the ${\left|c_m\right|}^2=1$ and all of the others are therefore zero.

Alternative Interpretation of Mode-Converter Input and Output Modes.

Note that the output mode-converter basis functions are also eigenfunctions of E and the input mode-converter basis functions are also eigenfunctions of A. Explicitly, from Eqs. 4 and 5

$$\text{A}|{\psi }_{In\hspace{0.17em}p}\rangle =\left({\text{I}}_I-{\text{S}}^{†}\text{S}\right)|{\psi }_{In\hspace{0.17em}p}\rangle =\left(1-{\left|s_p\right|}^2\right)|{\psi }_{In\hspace{0.17em}p}\rangle$$ [25]

$$\text{E}|{\psi }_{Out\hspace{0.17em}p}\rangle =\left({\text{I}}_O-\text{S}{\text{S}}^{†}\right)|{\psi }_{Out\hspace{0.17em}p}\rangle =\left(1-{\left|s_p\right|}^2\right)|{\psi }_{Out\hspace{0.17em}p}\rangle .$$ [26]

By the maximization properties of eigenvalues for Hermitian operators, this means that the input mode-converter basis functions $\left\{|{\psi }_{In\hspace{0.17em}n}\rangle \right\}$ are the orthogonal functions that correspond to the maximum absorptivities, and the corresponding output mode-converter basis functions $\left\{|{\psi }_{Out\hspace{0.17em}p}\rangle \right\}$ are the orthogonal functions that correspond to the maximum emissivities. In principle, these sets of functions could be found in a set of experiments designed to find the orthogonal beams with the maximum absorptivities and emissivities, which gives an alternative physical meaning to these sets of beams. For example, we could empirically and iteratively first find the beam with the largest absorptivity, then the beam orthogonal to that with the next largest absorptivity, and so on, which would physically construct the set $\left\{|{\psi }_{In\hspace{0.17em}n}\rangle \right\}.$ We could follow a similar procedure with emissivities to construct $\left\{|{\psi }_{Out\hspace{0.17em}p}\rangle \right\}.$ Note this conceptual approach works for both reciprocal and nonreciprocal objects, in contrast to one other physical method for iteratively establishing these mode-converter functions that may work only for reciprocal objects (29).

An Integrated Radiation Law.

Note from [25] that

$$\text{Tr}\left(\text{A}\right)\equiv {\displaystyle \sum _p\langle {\psi }_{In\hspace{0.17em}p}|\text{A}|{\psi }_{In\hspace{0.17em}p}\rangle }={\displaystyle \sum _p{\alpha }_{Mp}}={\displaystyle \sum _p\langle {\psi }_{In\hspace{0.17em}p}|\left(1-{\left|s_p\right|}^2\right)|{\psi }_{In\hspace{0.17em}p}\rangle }={\displaystyle \sum _p\left(1-{\left|s_p\right|}^2\right)}$$ [27]

and from [26] that

$$\text{Tr}\left(\text{E}\right)\equiv {\displaystyle \sum _p\langle {\psi }_{Out\hspace{0.17em}p}|\text{E}|{\psi }_{Out\hspace{0.17em}p}\rangle }={\displaystyle \sum _p{\epsilon }_{Mp}}={\displaystyle \sum _p\langle {\psi }_{Out\hspace{0.17em}p}|\left(1-{\left|s_p\right|}^2\right)|{\psi }_{Out\hspace{0.17em}p}\rangle }={\displaystyle \sum _p\left(1-{\left|s_p\right|}^2\right)},$$ [28]

where by “Tr” we mean the trace of the operator (i.e., the sum of its diagonal elements). Hence, the sum of the absorptivities of the mode-converter input modes and the sum of the emissivities of the mode-converter output modes are equal. More generally, though, because the trace of an operator is independent of the (complete) basis set used to represent it, and because, as in [15] and [19], the absorptivities and emissivities on any basis sets of input and output modes, respectively, are given just by the diagonal elements on those basis sets, then from [27] and [28]

$$\text{Tr}\left(\text{A}\right)=\text{Tr}\left(\text{E}\right)$$ [29]

so we can state an integrated radiation law, valid for both reciprocal and nonreciprocal objects:

Law 3.

For an arbitrary linear object, the sum of the absorptivities of any complete set of input modes is equal to the sum of the emissivities of any complete set of output modes.

A Modal Radiation Law for Reciprocal Systems.

For Law 4, we first define reciprocity; we do this directly, rather than by appeal to other laws of physics (such as Maxwell’s equations), although such other laws can clarify what systems show reciprocity. If we shine a normalized input field $|{\psi }_I\rangle$ on a linear scattering object, then we can write the resulting scattered field as a complex amplitude $s$ of a normalized function $|{\psi }_O\rangle ,$ i.e., a field $s|{\psi }_O\rangle .$ Then we define reciprocity for this object as follows:

Given that an arbitrary input field $|i\rangle$ gives rise to a scattered field $s|f\rangle =\text{S}|i\rangle$ from an object O ($|i\rangle$ and $|f\rangle$ both being normalized), then object O is reciprocal if and only if input field ${|f\rangle }^{\ast },$ which is the phase conjugate of $|f\rangle ,$ gives rise to a scattered field $s{|i\rangle }^{\ast }=\text{S}{|f\rangle }^{\ast },$ where ${|i\rangle }^{\ast }$ is the phase conjugate of $|i\rangle .$

By “phase conjugate” here we mean that, for a complex field, we take the complex conjugate of the spatial part of the field, although not the temporal part. So, for example, the phase conjugate of a “right-going” plane wave $\exp \left[i(\omega t-kz)\right]$ is the “left-going” plane wave $\exp \left[i(\omega t+kz)\right]$ and the phase conjugate of a beam expanding to the “right” from a beam waist would converge from the right back onto the original waist (30). [Note, incidentally, that such phase conjugation is not necessarily or generally the same as time reversal (30, 31).]

For a reciprocal electromagnetic system as described by symmetric permittivity and permeability tensors, its scattering matrix, expressed on (real) input and output mode basis sets that satisfy $|i\rangle ={|i\rangle }^{\ast }$ and $|f\rangle ={|f\rangle }^{\ast },$ is symmetric (31). Our reciprocity definition is the equivalent to the standard description of the scattering matrix of a reciprocal system and is more appropriate in the present situation because we do not assume the modal basis to be real.

Note that the constant $s$ is the same in both the “forward” and backward (phase-conjugated) versions, which means that the backward version is attenuated by the same real factor as the forward version in such scatterings and that the phase delay in the forward scattering is the same as the phase delay in the backward scattering.

For a reciprocal scatterer, because the reciprocity conditions apply for any input field, they must apply to the mode-converter basis functions. In particular, from Eq. 6 and our reciprocity definition,

$$\text{S}{|{\psi }_{Out\hspace{0.17em}p}\rangle }^{\ast }=s_p{|{\psi }_{In\hspace{0.17em}p}\rangle }^{\ast }.$$ [30]

(Note we do not use the complex conjugate of $s_p$ in Eq. 30; as stated above, both the phase delay and the magnitude of the scattering must be the same for the forward and backward versions of the scattering by a reciprocal scatterer.)

These resulting sets of functions $\left\{{|{\psi }_{Out\hspace{0.17em}n}\rangle }^{\ast }\right\}$ and $\left\{{|{\psi }_{In\hspace{0.17em}n}\rangle }^{\ast }\right\}$ are necessarily complete sets for describing input and output functions, respectively; they are orthonormal because the sets $\left\{|{\psi }_{In\hspace{0.17em}n}\rangle \right\}$ and $\left\{|{\psi }_{Out\hspace{0.17em}n}\rangle \right\}$ are, and they have the same number of elements, with the same singular values. Hence, for this reciprocal case, they form equally good sets of mode-converter pairs and have the same kinds of mathematical properties as those original sets. (The reason we have some choice about how we write these sets is because each eigenvalue ${\left|s_p\right|}^2$ in [4] and in [5] is necessarily twofold degenerate in this reciprocal case; both the input function $|{\psi }_{In\hspace{0.17em}p}\rangle$ and the input function ${|{\psi }_{Out\hspace{0.17em}p}\rangle }^{\ast }$ have the same ${\left|s_p\right|}^2,$ as do the output functions $|{\psi }_{Out\hspace{0.17em}p}\rangle$ and ${|{\psi }_{In\hspace{0.17em}p}\rangle }^{\ast }.$) Hence, as in Eq. 7, we can write

$${\text{S}}^{†}{|{\psi }_{In\hspace{0.17em}p}\rangle }^{\ast }=s_p^{\ast }{|{\psi }_{Out\hspace{0.17em}p}\rangle }^{\ast }.$$ [31]

Hence for some input mode $|i\rangle$ as in Eq. 20, with absorptivity ${\alpha }_i$ as in Eq. 21, the emissivity of ${|i\rangle }^{\ast }$ can be calculated using Eqs. 9, 19, and 31 as

$${\epsilon }_{i\ast }=1-\left({\langle \iota |}^{\ast }\right)\text{S}{\text{S}}^{†}{|\iota \rangle }^{\ast }={\displaystyle \sum _m{\left|c_m\right|}^2}\left(1-{\left|s_m\right|}^2\right)={\alpha }_i.$$ [32]

Hence, for a reciprocal object, not only have we now proved the standard statement of the directional version of Kirchhoff’s radiation law, that the absorptivity for any given direction of beam is equal to the emissivity back into that direction, but also we have proved a more general version, valid for any form of input beam.

Law 4.

For any given input beam $|i\rangle$ at a given frequency incident on a reciprocal object, the absorptivity is equal to the emissivity into the phase-conjugated version ${|i\rangle }^{\ast }$ of that beam.

This is therefore a fully modal statement of a radiation law for reciprocal thermal emitters and absorbers; it applies for any input beam and the corresponding reversed beam, not just for plane waves, and it is derived with all diffractive effects fully included. We also note that as indicated by Law 2, ${|i\rangle }^{\ast }$ is only one of the many possible modes to which the emissivity is equal to the absorptivity of the input mode $|i\rangle .$ Thus, our result, Law 2, generalizes the standard Kirchhoff’s law even in the reciprocal case.

Proof of the Converse to the First Law

We can ask, what are the necessary criteria for any input wave if it is to result in the absorptivity of that wave being equal to the emissivity into the resulting scattered wave? Specifically, we have proved (Law 1 of the main text) that the absorptivity of a mode-converter input mode equals the emissivity into the corresponding output mode. Now we examine whether the same equivalence holds for the absorptivity of an arbitrary input field and the emissivity into the resulting scattered field, and we show that it does not; in fact, these input and output modes have to be mode-converter pairs for this relation to hold. So this property is one that we can reliably deduce only for the mode-converter pairs of input and output functions.

We imagine a machine as in Fig. S2. We have inserted a unitary optical machine $U_I$ between a set of single-mode inputs $\left\{|{\varphi }_{U\hspace{0.17em}n}\rangle \right\}$ into this machine and the set of single-mode inputs $\left\{|{\varphi }_{In\hspace{0.17em}n}\rangle \right\}$ of our existing machine M. We presume that a set of N single-mode black bodies $B_{Iq}$ is connected through circulators to give input powers into these single-mode inputs $\left\{|{\varphi }_{U\hspace{0.17em}n}\rangle \right\}.$ An input into a specific port j of this machine will generate a wave

$$|{\psi }_{Ij}\rangle ={\displaystyle \sum _p{U}_{Ipj}|{\psi }_{In\hspace{0.17em}p}\rangle }$$ [S1]

incident on the object O, where the $U_{Ipj}$ are the matrix elements of the matrix ${\text{U}}_I$ that describes the machine $U_I.$ This resulting function $|{\psi }_{Ij}\rangle$ is formally a linear superposition of input mode-converter basis functions, as described by Eq. S1.

We are specifically interested in the response to radiation into one specific input, which we can choose, without loss of generality, to be the top left input, with single-mode input function $|{\varphi }_{U1}\rangle .$ A normalized (i.e., unit power) wave into that input will generate an input function onto the object O of $|{\psi }_{I1}\rangle ,$ which will in turn generate a scattered output from object O given by

$$|{\psi }_{O1}\rangle =\text{S}|{\psi }_{I1}\rangle .$$ [S2]

We are interested in a normalized version $|{\psi }_{O1\hspace{0.17em}norm}\rangle$ of this scattered wave function because we want to compute the amount of power that will be scattered into this particular scattered output mode as a result of output power from all of the black bodies $B_{Iq}.$ Formally, we can define a coefficient $b_{11}$ and define its magnitude by examining the total power in the scattered beam $|{\psi }_{O1}\rangle ,$ giving

$${\left|b_{11}\right|}^2=\langle {\psi }_{O1}|{\psi }_{O1}\rangle =\langle {\psi }_{I1}|{\text{S}}^{†}\text{S}|{\psi }_{I1}\rangle$$ [S3]

so that

$$|{\psi }_{O1norm}\rangle \equiv \frac{1}{b_{11}}|{\psi }_{O1}\rangle$$ [S4]

is a function with unit power. Equivalently, we can now write instead of Eq. S2

$$\text{S}|{\psi }_{I1}\rangle =b_{11}|{\psi }_{O1norm}\rangle .$$ [S5]

Now we can consider all of the power from all of the black bodies $B_{Iq}$ that is scattered into this output mode function $|{\psi }_{O1\hspace{0.17em}norm}\rangle .$ For unit power in an input q to the unitary machine $U_I,$ the resulting scattered wave from the object is

$$|{\psi }_{Oq}\rangle =\text{S}|{\psi }_{Iq}\rangle .$$ [S6]

Note now that these output functions $|{\psi }_{Oq}\rangle$ for different q are not necessarily orthogonal to one another because the various input functions $|{\psi }_{Ij}\rangle ,$ although they are orthogonal because they result from a unitary transform from orthogonal inputs, do not necessarily correspond to the mode-converter input basis functions, and these output scattered functions do not necessarily correspond to the mode-converter output basis functions. So in general some power from one or more of the other black bodies $B_{Iq}$ can be scattered into the mode $|{\psi }_{O1norm}\rangle .$ Specifically, we expect an amplitude in the output mode $|{\psi }_{O1norm}\rangle$ as a result of unit power in input q of the machine $U_I$ of

$$b_{1q}=\langle {\psi }_{O1norm}|\text{S}|{\psi }_{Iq}\rangle .$$ [S7]

We note that, mathematically,

$$b_{1q}^{\ast }\equiv b_{1q}^{†}\equiv {\left[\langle {\psi }_{O1norm}|\text{S}|{\psi }_{Iq}\rangle \right]}^{†}=\langle {\psi }_{Iq}|{\text{S}}^{†}|{\psi }_{O1norm}\rangle .$$ [S8]

If we presume that we have the black body single-mode power of $P_B$ emerging from each of the black bodies, then the power from any black body $B_{Iq}$ that is scattered into mode $|{\psi }_{O1norm}\rangle$ is

$$P_{s1q}=P_B{b}_{1q}{b}_{1q}^{\ast }.$$ [S9]

So, the total power from all of the black bodies that is scattered into the output mode $|{\psi }_{O1norm}\rangle$ is

$$P_{Tot\hspace{0.17em}scatt}=P_B{\displaystyle \sum _q{P}_{s1q}=}{P}_B{\displaystyle \sum _q{b}_{1q}{b}_{1q}^{\ast }}=P_B{\displaystyle \sum _q\langle {\psi }_{O1norm}|\text{S}|{\psi }_{Iq}\rangle \langle {\psi }_{Iq}|{\text{S}}^{†}|{\psi }_{O1norm}\rangle }.$$ [S10]

Now, the power absorbed by the object O from the input from black body $B_{I1}$ is the power that is not scattered into the output mode; that is,

$$P_{abs1}=P_B-P_{s11}.$$ [S11]

So, the absorptivity of this input mode $|{\psi }_{I1}\rangle$ is, by definition,

$${\alpha }_{U1}=1-\frac{P_{s11}}{P_B}$$ [S12]

and so, using Eq. S9,

$${\alpha }_{U1}=1-b_{11}{b}_{11}^{\ast }.$$ [S13]

Now, we presume that we use another unitary optical machine $V_O$ at the output of our machine M. This machine specifically extracts the output mode $|{\psi }_{O1norm}\rangle ,$ presents it as the function $|{\varphi }_{O1norm}\rangle$ at an output single-mode guide, and passes it back to the input of black body $B_{I1}$ through the circulator. This machine $V_O$ also takes all of the power in all functions orthogonal to $|{\psi }_{O1norm}\rangle$ and passes it losslessly back to the inputs to the other black bodies, $B_{Iq}$ (with $q\ne 1$) in a fashion whose details otherwise do not matter for the present argument.

With this optical arrangement, we can now examine the overall thermal equilibrium between the object O and the black body $B_{I1}.$ That body is emitting a power $P_B$ as usual. To have the total input power to that black body equal to this emitted power, as required for thermal equilibrium between black body $B_{I1}$ and the object O, we must have an emitted power $P_{em1}$ from the object O into mode $|{\psi }_{O1norm}\rangle$ such that

$$P_B=P_{em1}+P_{Tot\hspace{0.17em}scatt}$$ [S14]

so

$$P_{em1}=P_B-P_{Tot\hspace{0.17em}scatt}.$$ [S15]

That is, dividing throughout by $P_B,$ which gives the definition of the emissivity ${\epsilon }_{U1}$ into mode $|{\psi }_{O1norm}\rangle ,$

$${\epsilon }_{U1}=1-\frac{P_{Tot\hspace{0.17em}scatt}}{P_B}=1-{\displaystyle \sum _q{b}_{1q}{b}_{1q}^{\ast }}.$$ [S16]

So the absorptivity ${\alpha }_{U1}$ of mode $|{\psi }_{I1}\rangle ,$ given by Eq. S13, equals the emissivity into the scattered mode $|{\psi }_{O1norm}\rangle ,$ given by Eq. S16, if and only if

$$b_{11}{b}_{11}^{\ast }={\displaystyle \sum _q{b}_{1q}{b}_{1q}^{\ast }}.$$ [S17]

But each such product $b_{1q}{b}_{1q}^{\ast }\ge 0.$ Hence, we conclude that the absorptivity and emissivity are equal for an input mode only if $b_{1q}=0$ for all $q\ne 1,$ which we can write as

$$b_{1q}=\langle {\psi }_{O1norm}|\text{S}|{\psi }_{Iq}\rangle =0\hspace{1em}\text{for all}\hspace{1em}q\ne 1$$ [S18]

or equivalently

$$b_{1q}^{\ast }=\langle {\psi }_{Iq}|{\text{S}}^{†}|{\psi }_{O1norm}\rangle =0\hspace{1em}\text{for all}\hspace{1em}q\ne 1.$$ [S19]

That means that all of the scattered waves from the other orthogonal input modes $|{\psi }_{Iq}\rangle$ ($q\ne 1$) have to be orthogonal to the scattering from the mode $|{\psi }_{I1}\rangle ,$ which means physically that $|{\psi }_{I1}\rangle$ is one of the input mode-converter modes and $|{\psi }_{O1norm}\rangle$ is the corresponding mode-converter output mode, for object O. Mathematically, we already know from Eq. S5 that $\left(1/b_{11}\right)\text{S}|{\psi }_{I1}\rangle =|{\psi }_{O1norm}\rangle ,$ so substituting in Eq. S19 gives

$$b_{11}{b}_{1q}^{\ast }=\langle {\psi }_{Iq}|{\text{S}}^{†}\text{S}|{\psi }_{I1}\rangle =0\hspace{1em}\text{for all}\hspace{1em}q\ne 1,$$ [S20]

which means that ${\text{S}}^{†}\text{S}|{\psi }_{I1}\rangle \propto |{\psi }_{I1}\rangle ,$ and specifically

$${\text{S}}^{†}\text{S}|{\psi }_{I1}\rangle ={\left|b_{11}\right|}^2|{\psi }_{I1}\rangle ,$$ [S21]

which means that $|{\psi }_{I1}\rangle$ is one of the right singular vectors of $\text{S}.$ From Eq. S5, we see that $|{\psi }_{O1norm}\rangle$ is the corresponding left singular vector. Hence, we have proved that, for the absorptivity of an input mode to be equal to the emissivity of the corresponding scattered mode, these input and output modes must be mode-converter basis function pairs.

Our labeling of the mode in this argument as mode “1” was arbitrary. So we conclude quite generally that the absorptivity $\alpha$ of a given input mode is equal to the emissivity $\epsilon$ of the corresponding scattered output mode only if these two modes are mode-converter basis function pairs.

Conclusions

Here we have derived four laws for thermal radiation. These give general laws for the absorptivity and emissivity of modes of electromagnetic radiation for linear optical objects, with Laws 1, 2, and 3 applying for both reciprocal and nonreciprocal objects. Law 4 generalizes the directional Kirchhoff radiation law for reciprocal optical objects, equating the absorptivity of any input beam with the emissivity into the backward (phase-conjugated) version of that beam. We have constructed these laws using the mathematical and physical properties of the mode-converter input and output basis function pairs that exist for any linear optical object and that can be deduced by singular-value decomposition. We have also shown that these mode-converter input and output functions are the orthogonal functions with the largest absorptivities and emissivities, respectively, which allows a different way of physically interpreting and establishing what they are. Because of the generality of the approach here, these results could apply to other kinds of waves, such as thermal equilibration by acoustic waves, for example. We expect these laws will provide a clearer and expanded foundation for discussion of thermal emission and absorption generally and for solar energy conversion in particular and give us additional tools to analyze and describe thermal emitters in a rigorous modal basis.

Dirac “Bra-Ket” Notation

In Dirac “bra-ket” notation (e.g., ref. 32), $|\psi \rangle ,$ known as a “ket” vector, is used to represent a function and can be considered as a “column” vector of complex amplitudes that describe the function; the vector elements could be the amplitudes of the function at a sufficiently large number of points or the expansion coefficients on some basis (which here would be some valid complete set of propagating electromagnetic modes within the free-space region). We use nonitalic uppercase letters, such as $\text{A},$ to represent linear operators, which we can think of as matrices.

The operation indicated by a superscript “dagger” $†$ means we are taking the Hermitian adjoint; that corresponds first to reflecting about the leading diagonal of a matrix (i.e., first taking the transpose of the matrix) and then taking the complex conjugate of all matrix elements. The notation $\langle \psi |,$ known as a “bra” vector, refers to the same function as $|\psi \rangle ,$ but writes it as a row vector with elements that are the complex conjugates of the corresponding column elements of $|\psi \rangle .$ Formally, ${\left(|\psi \rangle \right)}^{†}=\langle \psi |$ and ${\left(\langle \psi |\right)}^{†}=|\psi \rangle .$ The written contents (here $\psi$) of the bra and ket vectors are just labels or names and have no other algebraic significance unless we separately give them such meaning (such as a number for some state). The fact that we are using this notation does not mean that we are necessarily considering quantum mechanical functions; we are simply using Dirac notation as a convenient way to write down linear algebra in situations where we may also be dealing with complex functions.

The notation $\{\dots \}$ means we are considering an entire set of such functions or modes rather than a specific one.

We presume that we are defining fields in such a way that for any specific propagating field $|\psi \rangle$ the “inner product” $\langle \psi |\psi \rangle$ (which is an algebraic shorthand for the “row-vector” and “column-vector” product $\langle \psi ||\psi \rangle$) gives the propagating power in the field. Basis sets of modes used here will generally be normalized so that they have unit power.

In the Dirac notation, we note that, for some space for which a set of functions $\left\{|{\varphi }_n\rangle \right\}$ is complete, the identity operator I (written here an uppercase “I”) can be written $\text{I}\equiv {\displaystyle \sum _p|{\varphi }_p\rangle }\langle {\varphi }_p|,$ which is an algebraic equivalence we use in our proofs.

Existence and Required Properties of Black Bodies

In the proofs in this paper, we make use of the idea of black bodies. Those were, however, defined by the original Kirchhoff paper (3), so in deriving radiation laws anew here, we could conceivably be assuming what we are trying to prove. To avoid this, we can separately define such black bodies and their necessary properties for the present proof. This argument uses standard approaches, but we construct it here for completeness anyway.

We presume we can construct a body with only a single-mode input port, such as a single-mode optical fiber operating in only one polarization, and with no other way for electromagnetic radiation to enter or leave the body. (We could, for example, cover the rest of the outside of the body with a very good reflector.) We also presume that such a body can be constructed so that it absorbs essentially all of the light incident in this particular mode, and we call any such perfectly absorbing body a (single-mode) black body; empirically, we believe this is possible at least in principle, such as by constructing the inside of the black body with internal walls that are at least partially absorbing. The electromagnetic radiation entering the body will bounce around inside the black body until it is absorbed; because the inside of the black body is presumed very large, the possibility of this radiation leaking back out of the input port before it is absorbed is presumed to be arbitrarily small.

Now we imagine we construct a second black body, similar in that it also is connected only by such a single-mode port. The details of the design of this second black body do not matter as long as it also has the characteristic that it absorbs essentially all of the incident electromagnetic radiation in this single mode.

Next, presume that these two black bodies are initially at the same temperature and are connected to one another through this single-mode fiber connection and have no external connection to any other heat source or sink. Then the power emitted by these two bodies into the single-mode fiber must be the same; otherwise, because each black body absorbs all of the power it receives from the other, one black body could heat up the other, thereby violating the second law of thermodynamics.

Hence, for any specific temperature and choice of emission frequency or frequency bandwidth, any such black body that absorbs and/or emits in only one single mode, independent of the details of its design, must emit some specific power P_B into this mode. This is the property we need for such black bodies so that we can proceed with the rest of our arguments here.

Of course, the actual calculation of what that power P_B is requires additional physics, which was solved by Planck with his proposal of the quantization of the emission of electromagnetic radiation, but we do not need that specific value here for our arguments.

Internal Structure of a Universal Lossless Linear Optical Machine

To construct a universal lossless linear optical machine as in Fig. 2 of the main text, based on the principles in ref. 27, we need two aspects: (i) to be able to transform losslessly from continuous fields of arbitrary shapes in arbitrary polarization states into field amplitudes in a specific polarization state distributed across some appropriately large number of single-mode waveguides and vice versa from such waveguides into continuous fields—we can view this aspect as a “representation conversion”; (ii) to be able to perform an arbitrary lossless (i.e., unitary) linear transformation between the field amplitudes in an “input” set of single-mode waveguides and field amplitudes in an output set of single-mode waveguides—we can call the device that accomplishes this a “unitary transformer”.

One concept for a representation converter element would be some square, flat surface “patch” that would take plane wave radiation incident normally on the surface in an arbitrary polarization state and convert this losslessly into field amplitudes in the same polarization state (such as a “horizontal” polarization) in two waveguides. An example of such an element would be a polarization-splitting grating coupler (33). Although practically making such an element with arbitrarily low loss would be hard, we presume such an element is possible in principle for our thought experiments.

Conceptually, we imagine covering the inside of a large spherical surface in free space with a large number of such surface elements in patches, as sketched in Fig. S1. With sufficiently many such small patches, such covering would be possible to any arbitrary degree of completeness. In the middle of the sphere we would place the object O. Because the radius of the sphere is assumed to be very large, any radiation emitted or scattered from object O arriving from the free space region at any given patch would be essentially plane and normal to the patch’s surface and so could be efficiently collected into the two waveguides emerging from that patch. In this way, all of the light emitted or scattered from O could be collected as field amplitudes, all in the same polarization, in a set of single-mode guides. Similarly, appropriate field amplitudes in the waveguides shining into such representation converters could generate a patch of plane-wave field of arbitrary desired polarization emerging into the free space region to give arbitrary input waves on the object.

In the optical machine in Fig. S1, circulators separate input and output waves; as drawn, light incident on the left port appears as an output at the bottom port, and light incident “upward” in the bottom port appears as an output at the right port. Circulators, which are nonreciprocal elements, can be made in various ways, such as using Faraday isolators.

It is now well understood how to design arbitrary unitary transformers, using lossless meshes (27, 34–37) of two-beam (e.g., Mach–Zehnder) interferometers that can implement any unitary matrix mapping between input amplitudes (all in the same polarization) in a set of input waveguides and output amplitudes in a corresponding set of output waveguides. (Such transformers can even design themselves or be trained for their function.) When these outputs drive the representation converters, any desired overlapping orthogonal set of waves can be launched in the free space region starting from corresponding amplitudes in the individual input ports. Similarly, wave amplitudes in any overlapping orthogonal set of modes leaving the free space region can be coupled one by one to the individual output ports on the right, using the output unitary transformer. Changing from machine M to machine Q in the main text corresponds to changing the input and output unitary transformers in Fig. S1.

Such an optical machine as in Fig. 2 allows us therefore to map input ports losslessly to desired incident waves on the object O and to collect any emitted or scattered light in any arbitrary output modal basis, mapping each such modal amplitude to individual output ports. Of course, this is only a “thought” apparatus; it might possibly have to be quite large, in size and in number of patches and/or ports, to handle any given object O sufficiently, and is not necessarily currently practical. Such a machine is physically possible in principle, however, which is sufficient for our thought experiments.