Variations in crowding, saccadic precision, and spatial localization reveal the shared topology of spatial vision

Significance

Our ability to see, localize, and interact with stimuli varies depending on their location in the visual field. Here we consider the source of these variations for several aspects of spatial vision: crowding (the disruption of object recognition in clutter), spatial localization, and saccadic eye movements. We observe a range of variations across both individuals and the visual field with strong correlations between all tasks. However, a number of dissociations exclude the possibility that these correlations arise from the same spatial representation of the visual field. Rather, we propose a “topology of spatial vision,” whereby idiosyncratic variations in spatial precision are established early in the visual system and inherited up to the highest levels of object recognition and motor planning.

Abstract

Visual sensitivity varies across the visual field in several characteristic ways. For example, sensitivity declines sharply in peripheral (vs. foveal) vision and is typically worse in the upper (vs. lower) visual field. These variations can affect processes ranging from acuity and crowding (the deleterious effect of clutter on object recognition) to the precision of saccadic eye movements. Here we examine whether these variations can be attributed to a common source within the visual system. We first compared the size of crowding zones with the precision of saccades using an oriented clock target and two adjacent flanker elements. We report that both saccade precision and crowded-target reports vary idiosyncratically across the visual field with a strong correlation across tasks for all participants. Nevertheless, both group-level and trial-by-trial analyses reveal dissociations that exclude a common representation for the two processes. We therefore compared crowding with two measures of spatial localization: Landolt-C gap resolution and three-dot bisection. Here we observe similar idiosyncratic variations with strong interparticipant correlations across tasks despite considerably finer precision. Hierarchical regression analyses further show that variations in spatial precision account for much of the variation in crowding, including the correlation between crowding and saccades. Altogether, we demonstrate that crowding, spatial localization, and saccadic precision show clear dissociations, indicative of independent spatial representations, whilst nonetheless sharing idiosyncratic variations in spatial topology. We propose that these topological idiosyncrasies are established early in the visual system and inherited throughout later stages to affect a range of higher-level representations.

Our sensitivity to visual stimuli varies substantially across the visual field with characteristic patterns that are evident across a wide range of tasks. Most notably, our ability to see fine detail decreases sharply as objects move into peripheral vision (1). These abilities are further disrupted by crowding, the impairment of object recognition in clutter, which also increases with eccentricity (2, 3). Both of these effects have been attributed to an overrepresentation of the fovea at the expense of peripheral vision, known as “cortical magnification” (4, 5), which has been observed in a range of retinotopically organized areas of the brain (6, 7). Here we ask whether other variations in visual sensitivity can similarly be attributed to topological principles within the visual system and consider whether these variations might share a common source.

Variations across the visual field are particularly apparent with crowding, a process that presents the fundamental limitation on object recognition in peripheral vision (8). Crowding disrupts the recognition of a target object when flanker objects fall within a surrounding “interference zone.” As well as increasing in size with eccentricity, these zones show an elliptical shape whereby flankers along the radial axis from fixation cause crowding over a greater extent than those along the tangential/iso-eccentric axis (9, 10). These variations may similarly reflect cortical magnification, given the greater rate of change along the radial axis than along the tangential axis (11), although perhaps at a cortical locus beyond V1 (12). Crowded interference zones are also larger along the vertical than along the horizontal meridian (10, 13, 14) and in the upper rather than the lower visual field (10, 15), with considerable variation between individuals (9, 10).

Similar patterns are evident across a range of processes in spatial vision, consistent with a common source for these topological variations. As noted above, an increase in stimulus eccentricity impairs performance for acuity (1) and grating resolution (4). Both the decline in eccentricity and radial/tangential anisotropy have also been found for the discrimination of phase (16) and orientation (17) and for localization tasks such as Vernier acuity and bisection (5, 18, 19). Eye movements are similarly affected — both the distribution of landing errors for saccadic eye movements (20) and the detection of position shifts in saccadic targets (21) show these characteristics. Additionally, as with crowding, performance is worse in the upper than in the lower visual field for gap resolution and Vernier acuity (22, 23), along with a range of other spatial identification measures (24, 25) that similarly show worse performance along the vertical than the horizontal meridian.

The simplest explanation for these common patterns of variation would be that they arise from the same retinotopic map of the visual field. For the diverse range of spatial tasks listed above, this seems unlikely. For example, although performance on Vernier tasks has clear links with cortical area V1 (26), as do variations in grating resolution (27), both can also be linked with retinal variations (5). Crowding also shows neural correlates in area V1 (28–30), although stronger links have been proposed with cortical area V2 (31), and neural modulations have been found as high as area V4 (32) and beyond (33). Distinct neural correlates are perhaps more clear in the case of saccadic eye movements, which likely rely on a distinct retino-collicular pathway to the cortex, unlike the geniculo-striate route taken by signals for perceptual localization (34).

The common pattern of variations across the visual field may instead be due to shared topological properties in the spatial maps that underlie these processes. Given the hierarchical structure of the visual system, with inherited receptive field properties at each stage (35), variations in this topological representation could arise early in the visual system, with patterns specific to each individual that are inherited throughout later stages. Alternatively, these similarities may simply reflect common organizational principles (e.g., 36) that arise independently within distinct regions. To establish a direct relationship between specific processes, we therefore need to move beyond these general similarities to examine intertask correlations in sensitivity across individuals. The aim of the present study was to examine the nature of these variations for several tasks.

We began by measuring the covariations between crowding and the precision of saccadic eye movements. Recent studies suggest that there may be a particularly strong link between these processes (37–39), despite the more general dissociation between perceptual and saccadic localization (40–43) and their apparently distinct cortical routes (34). Our first aim was therefore to examine whether saccadic precision and crowding covary across the visual field by measuring the size of crowded interference zones and the precision of saccade landing positions (“saccade error zones”) for the same stimuli in a range of visual-field locations. Our results demonstrate a strong correlation between the spatial zones measured in the two tasks. To examine whether these processes rely on a shared representation of the visual field (with the same representation of the target location), we also examined trial-by-trial variations in the two judgments. If both processes rely on the same target-location estimate, trials with crowded response errors should show large saccade errors and vice versa; two processes with distinct spatial maps (and independent target-location estimates) should not show this correlation. We do not find this correlation, suggesting that the two are not inextricably linked. To consider the origin of the relationship between crowding and saccades, we conducted a second experiment to compare crowding with two “lower-level” measures of spatial localization: gap resolution and bisection thresholds. We observe strong correlations between these spatial-localization measures and crowding, consistent with a shared source of topological variations. Hierarchical regression analyses further reveal that these lower-level correlations account for much of the shared variance between crowding and saccadic precision. Altogether, our results are consistent with these spatial tasks resulting from dissociable processes that nonetheless inherit their topological variations from a common source.

Results

Experiment 1.

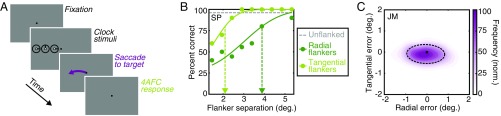
We first compared the precision of saccades with the spatial extent of crowding in a dual-task paradigm. Participants were required to saccade to the center of a crowded clock target and subsequently identify the orientation of its stroke (Fig. 1A). Twelve participants were tested with stimuli at two eccentricities (4° and 8°) in each of the four cardinal directions from fixation.

Fig. 1.

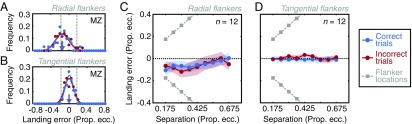
Procedures and sample data from experiment 1. (A) The time course of a sample trial. After a variable fixation period (0.2–1.4 s), three clock stimuli (not to scale) appeared in one of eight locations for 300 ms (flankers are depicted along the radial axis). Participants were required to fixate throughout the stimulus duration, to saccade to the white dot of the central target clock immediately after its offset, and to then indicate the orientation of the central target stroke. (B) Sample behavioral data from participant SP at 8° in the left visual field. Uncrowded performance is shown as the dashed gray line, and dark-green and light-green dots depict crowded performance with flankers on the radial and tangential dimensions, respectively. Cumulative Gaussian functions are fitted to crowded conditions; the dashed vertical arrow shows the critical spacing at which performance reaches 80% correct—values that defined the “crowding zone.” (C) An example 2D frequency distribution of saccade landing positions for participant JM at 4° in the left visual field. The cross shows the target location with the normalized frequency of saccade landing positions shown via the color-saturation scale. The saccade error zone was defined as an ellipse containing 80% of all saccade-landing errors, shown with the dashed black line.

To compute the interference zones for crowding, here referred to as “crowding zones,” the proportion of correct responses in the clock-orientation task was plotted as a function of the center-to-center separation between target and flanker elements (Fig. 1B). In all cases, uncrowded performance was close to ceiling. Under crowded conditions, performance was poor when flankers were close to the target and improved at larger separations. Radial flankers disrupted performance over a wider range of separations than tangential flankers. Psychometric functions were fitted to the data to determine the target-flanker separation at which performance reached 80% correct (dashed arrows in Fig. 1B), which we take as the dimensions of the crowding zone.

We also computed frequency distributions for the landing positions of the saccade on each trial to the target stimulus. Fig. 1C shows an example normalized frequency distribution of saccades, where landing errors are clearly greater along the radial than along the tangential axis. To characterize this pattern and compare it with that of crowding zones, we fitted 2D Gaussian functions to the landing errors and defined an ellipse with major and minor axes that captured 80% of the landing positions (shown with a black dashed line in Fig. 1C). The major and minor axes of this ellipse were taken as the radial and tangential dimensions of the “saccade error zone.”

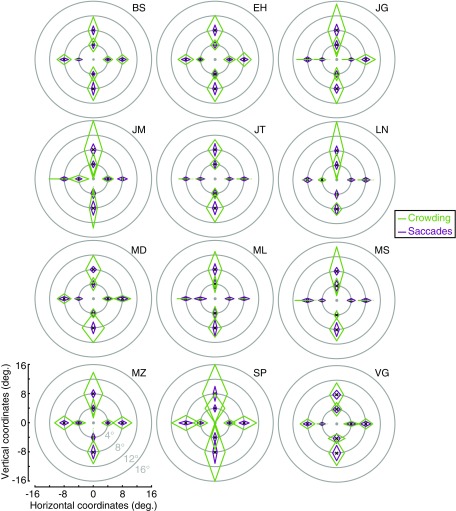
The dimensions of both crowding and saccade zones were computed in each visual-field location for each participant (Fig. S1 and SI Materials and Methods). For crowding, these values indicate the center-to-center separation at which crowding becomes negligible. For saccades, they indicate the boundary at which landing errors become unlikely. When averaged across all conditions, the half-width of saccade error zones was 0.91° ± 0.03° (mean ± SEM). The average half-width of crowding zones was twice this size at 1.85° ± 0.11°. Mean values are shown in Fig. 2A for each visual-field location and separately for the radial and tangential dimensions. Note that saccade error zones tend to be smaller than crowding zones, but that there is also covariation between the two. For example, crowding zones were larger on the vertical than on the horizontal meridian, which is also true for saccade error zones.

Fig. S1.

Individual data from experiment 1. Crowding (green) and saccade error (purple) zones for each participant, shown across the visual field. The fovea is shown as a gray dot with each zone plotted around the location of the central target during trials (black crosses). For each of the eight locations tested across the visual field, the size of the crowding and saccade error zones is shown for radial and tangential dimensions. Axes are shown in the Lower Left panel.

Fig. 2.

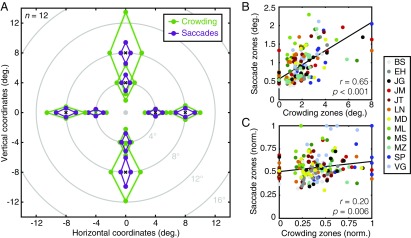
Crowding and saccade error zones from experiment 1. (A) Average crowding (green) and saccade error (purple) zones across participants (n = 12), shown across the visual field. The fovea is indicated as a gray dot with each zone plotted around the location of the target during trials (black crosses). For each location, the size of crowding and saccade error zones is shown for radial and tangential dimensions with light shaded regions indicating the (comparatively small) SEM across participants. (B) Crowding zones plotted against saccade error zones (both in degrees of visual angle) with individual data shown in different colors (see legend). The black line shows the best-fitting linear regression. (C) The correlation between normalized crowding and saccade error zones (where data are independent of eccentricity and the radial-tangential anisotropy), plotted as in B.

For both crowding and saccades, we conducted four-way mixed-effects ANOVAs with eccentricity, direction, and axis as fixed effects and participants as a random effect. For crowding, there were significant main effects of flanker axis with radial flankers disrupting recognition over greater distances than tangential flankers (F_1,33 = 73.80, P < 0.001) and eccentricity (F_1,33 = 133.56, P < 0.001) with more crowding at 8° than at 4°. The main effect of visual-field direction was also significant (F_3,33 = 33.77, P < 0.001), with planned comparisons showing that this was due to larger crowding zones along the vertical meridian than along the horizontal (t₉₅ = −8.42, P < 0.001) and greater crowding in the upper than the lower visual field (t₄₇ = 3.89, P < 0.001). Crowding did not differ significantly between the left and right visual fields (t₄₇ = 0.54, P = 0.59). The main effect for participants was not significant (F_11,33 = 2.04, P = 0.13). Two-way interactions between eccentricity and direction (F_3,33 = 17.41, P < 0.001), axis and eccentricity (F_1,33 = 26.67, P < 0.001), and direction and axis (F_3,33 = 5.36, P = 0.004) were all significant, as were the three-way interactions between the fixed effects (F_3,33 = 7.93, P < 0.001) and between axis, direction, and participants (F_33,33 = 2.23, P = 0.01). All other interactions with participants were nonsignificant (all Fs < 2).

Saccade errors show a similar pattern. There were significant main effects of the axis of saccade error, with greater errors along the radial than the tangential axis (F_1,33 = 179.17, P < 0.001), and of eccentricity (F_1,33 = 72.32, P < 0.001), with less precise saccades at 8° than 4°. The main effect of visual-field direction was again significant (F_3,33 = 20.56, P < 0.001) due to saccades being significantly less precise along the vertical than the horizontal meridian (t₉₅ = −6.05, P < 0.001) and less precise in the lower than in the upper visual field (t₄₇ = −3.49, P = 0.001). Saccades did not differ to the left or right of fixation (t₄₇ = 1.21, P = 0.23). The main effect of participants was again nonsignificant (F_11,33 = 1.09, P = 0.47). Two-way interactions between eccentricity and direction (F_3,33 = 7.32, P < 0.001), eccentricity and axis (F_1,33 = 24.29, P < 0.001), and direction and axis (F_3,33 = 9.45, P < 0.001) were all significant, although all two-way interactions with participants were nonsignificant (all Fs < 1). The three-way interaction between the fixed effects was significant (F_3,33 = 7.61, P < 0.001), as were the interactions between eccentricity, axis, and participants (F_11,33 = 3.03, P = 0.007) and between axis, direction, and participants (F_33,33 = 2.03, P = 0.02).

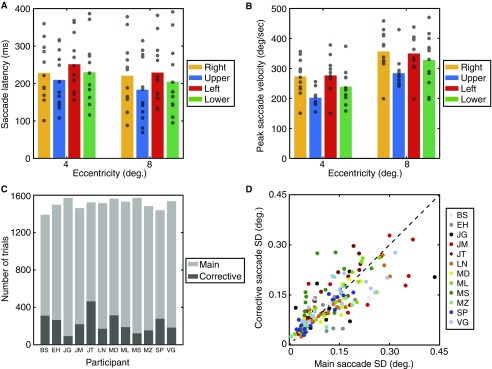
Altogether, variations in crowding and saccades share many similarities. Consistent with prior studies on crowding (2, 9, 10, 13, 14) and saccadic landing errors (20) in isolation, we find that error zones for both crowding and saccades increase with eccentricity and that both are larger along the radial than the tangential dimension. Both crowding and saccades show larger error zones along the vertical than the horizontal meridian with no difference between left and right visual fields. Similar interactions are also evident with both visual-field anisotropies and a radial-tangential anisotropy that increase with eccentricity. However, there are also clear dissimilarities. In matched locations of the visual field, the scale of crowding zones is over twice the size of saccade zones. Additionally, although crowding is greater in the upper visual field, saccade error is greater in the lower visual field. A similar performance decrement in the lower visual field is also apparent for saccadic latency (Fig. S2), consistent with prior observations (44).

Fig. S2.

Saccade metrics from experiment 1. (A) Saccade latency values for each of the eight visual-field locations tested. Latencies are plotted by eccentricity on the x axis with the colored bars separating values for the four directions in the visual field (see legend). Mean values are shown as bars with individuals as gray points. (B) Peak saccade velocities for each of the eight visual-field locations, plotted as in A. (C) Frequency of corrective saccades on trials with an accurate main saccade. For each participant (indicated on the x axis), the number of trials with accurately recorded main saccades is shown as a light-gray bar and the number of these trials containing additional corrective saccades shown as a dark-gray bar. (D) Saccade precision for main saccades vs. corrective saccades. The SD of landing error values is plotted for main saccades on the x axis against corrective saccades on the y axis, both in degrees of visual angle. Individuals are color-coded (see legend) with unity values shown as a black dashed line.

We next examined correlations between the size of crowding and saccade error zones across participants and locations, as plotted in Fig. 2B. As can be seen, there was a highly significant correlation between the two (r₁₉₀ = 0.65, P < 0.001). That is, when crowding disrupted identification over a large spatial extent, saccade errors were large. There are, however, several factors contributing to this correlation. As outlined in the Introduction, both the increase in error with eccentricity (5, 6) and the radial-tangential anisotropy (11, 36) may simply reflect the pattern of cortical magnification that occurs in all retinotopically organized cortical regions. This common “map topology” could affect both crowding and saccades even if their underlying processes did not operate on the same spatial representation (e.g., if these properties were to arise independently within distinct cortical regions). Any test of such a link should therefore look beyond these shared organizational principles.

To determine whether crowding and saccade error zones are correlated irrespective of these well-established factors, we normalized each dataset. To remove the effects of eccentricity, crowding and saccade error zones were divided by the eccentricity at which they were measured. To remove the radial-tangential anisotropy, we divided the radial and tangential zone sizes by the maximum size in each condition. This gave values between 0 and 1 for both datasets (Fig. 2C) with a reduced correlation across participants and locations that nonetheless remained highly significant (r₁₉₀ = 0.20, P = 0.006). In other words, an individual with a larger crowding zone at a particular location would also tend to have greater saccade error at that location, independently of the common effects of eccentricity and the radial-tangential anisotropy.

The correlation between crowding and saccade errors suggests either that both rely on a common spatial representation of the visual field or that they rely on distinct spatial maps with common topological properties inherited from earlier processing stages. Our dual-task paradigm (with the requirement to saccade to the target and to identify its orientation) allowed us to distinguish these possibilities via trial-by-trial variations in the two measures. If both processes use the same estimate of the target location, trials with crowded identification errors should show large saccade errors and vice versa. Conversely, if the two processes rely on distinct spatial maps, there should be either no difference in saccade error for incorrect vs. correct trials or the opposite pattern if participants were to trade their precision in one task against the other due to capacity limitations (45).

We began these analyses by separating crowded trials in which identification responses were determined as correct vs. incorrect, separately for each participant and location. Here, the average saccade error zone for correct trials (0.92° ± 0.03°) was larger than the zone for incorrect trials (0.76° ± 0.03°, t₁₉₁ = 8.36, P < 0.001). That is, saccadic precision was worse when participants correctly identified the target clock and vice versa. This runs counter to the prediction for two inextricably linked processes of localization. It seems rather that participants trade their precision in one task over the other—the hallmark of a dual task trade-off.

Another way to assess the interrelatedness of crowding and saccades is through the accuracy of saccades (i.e., their location relative to the target), rather than their precision (their dispersion across trials). That is, participants may have incorrectly identified the target because they identified the wrong element (as in mislocalization theories of crowding) (46). If the two processes were inextricably linked in their localization, participants should also saccade to the wrong element in these cases. To examine this, we separated landing positions on correct vs. incorrect trials and separately for radial and tangential flankers. Because this includes data at two eccentricities (4° and 8°), we divided saccade error values by the target eccentricity. For radial-flanker conditions, we examined saccade error only in the radial dimension and likewise for tangential-flanker conditions. Fig. 3A plots a frequency histogram of the saccadic error for one participant under the most closely spaced conditions at each eccentricity (0.175 × target eccentricity). If saccade-landing positions were to change between correct and incorrect trials, there should be multiple peaks in the landing positions, clustered around either the target or one of the flankers. This is clearly not the case: both datasets are well described by unimodal Gaussian functions. Furthermore, although there is a wide dispersion of saccade errors, which overlaps with the flanker locations, both correct and incorrect distributions are highly similar in both their mean location and width. This is also apparent for saccade errors in the tangential dimension on trials in which flankers were arranged tangentially (Fig. 3B). Here, the error rarely overlaps with the flanker locations with distributions for correct and incorrect trials again overlapping substantially.

Fig. 3.

Saccadic landing errors plotted as a function of target identification. (A) Frequency histograms for radial saccade landing positions on crowded trials with correct (blue) and incorrect (red) target identification at the closest target-flanker radial separation for participant MZ. Landing positions are plotted as a proportion of the target eccentricity. Gray dashed lines show flanker locations. (B) Frequency histograms for tangential saccadic landing error with the smallest tangential target-flanker separation, plotted as in A. (C) Mean saccade landing errors across all participants in the radial dimension as a function of the separation of radial flankers, depicted separately for correct and incorrect trials. Flanker locations are indicated with gray squares. Shaded regions show the SEM across participants. (D) Mean landing errors in the tangential dimension as a function of the separation of tangential flankers, plotted as in C.

These distributions of radial saccadic error in radial flanker conditions were computed for each participant and target-flanker separation. We then fitted Gaussian functions and took the mean in each case. As shown in Fig. 3C, saccades with radial flankers at the closest separation undershot the target by 10.6% of the target eccentricity on correct trials and 6.6% on incorrect trials. The undershoot magnitude decreased with increasing target-flanker separation to near-zero values at the largest separations. Note that this decrease in the mean landing error with increasing target-flanker separation is in the opposite direction to the change in flanker locations (gray squares in Fig. 3C).

These values were submitted to a three-way mixed effects ANOVA with target-flanker separation and identification correctness as fixed effects and participants as a random effect. For radial saccade error with radial flankers, this gave significant main effects of separation (F_8,215 = 4.43, P < 0.001) and participants (F_11,215 = 20.34, P < 0.001), but both the main effect of correctness (F_1,215 = 0.05, P = 0.80) and the interaction (F_8,215 = 0.90, P = 0.50) were nonsignificant. In other words, undershoot errors occurred at the closest separations and decreased as the target-flanker separation increased, but this did not differ between correct and incorrect trials. There was similarly no effect with tangential flankers (Fig. 3D) with saccades landing close to the target regardless of the target-flanker separation or performance in the identification task (for the same three-way mixed effects ANOVA, all P > 0.05). Thus, the probability that participants made a saccade to either of the flankers does not change in trials in which they correctly or incorrectly identified the target.

We attribute the changes that we do observe in the magnitude of saccadic undershoot errors to the “global effect” (47) whereby distractor elements bias saccades away from the target toward intermediate locations. Given the effects of cortical magnification discussed earlier, the inner flanker would be effectively closer to the target than the outer flanker, thus having a greater “pull” for the saccades. As flanker distance increases, this effect diminishes because the increasing separation decreases the overlap in activation within saccadic planning maps. Crucially for our purposes, however, this effect is not modulated by whether participants were correct or incorrect on the identification task. There is a clear dissociation between perceptual identification and saccade localization in this sense.

Altogether, although both tasks show similar patterns of variation with a significant correlation, clear differences are also present (e.g., crowding is greater in the upper than the lower visual field whereas saccades show the opposite pattern). Participants were also able to make a trade-off in performance between the tasks, with flankers able to bias saccade landing positions independently of performance on the identification task. Our results therefore do not suggest the tight linkage between crowding and saccades that would arise from a shared target localization. Rather, they suggest that crowding and saccade planning rely on two interrelated but dissociable spatial representations. If these similarities were to arise due to an inheritance of a common topology from earlier stages of the visual system, we would expect to see similar patterns of variations in tasks that derive from lower-level processes. This was the aim of experiment 2.

Experiment 2.

We next compared crowding (measured with our clock stimuli; Fig. 4A) with two estimates of spatial resolution and precision. The first was a gap-resolution task (Fig. 4B) where participants indicated the orientation of a Landolt-C element (as a measure of the highest spatial scale at which stimulus differences are visible). The second was a three-dot bisection judgment (18), included as a measure of spatial precision (the ability of participants to localize spatially extended stimuli). Here, participants were required to indicate the offset of a target dot from the midpoint defined by two reference dots (Fig. 4C). The collinearity of the dots in bisection tasks avoids the orientation cues of Vernier tasks (48) with “spatial filter” cues of this nature further minimized through large interdot separations (49). Performance on both of these tasks has been attributed to the earliest stages of visual processing, perhaps as early as the retina (5, 26). If the correlation between crowding and saccades arises from a common spatial representation, specific only to these two tasks, we should not see a correlation between crowding and either gap resolution or bisection. If instead there is some inheritance of topological variations throughout the visual system, then all of these tasks may be correlated.

Fig. 4.

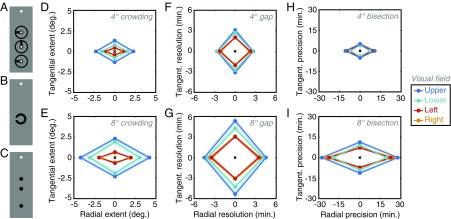
Stimuli and results from experiment 2. (A) Clock stimuli from the crowding task, shown with the white fixation circle. (B) Landolt-C stimuli used in the gap-resolution task. (C) Three-dot stimuli used in the bisection task. (D) Mean crowding zone sizes for all participants (n = 10) for both radial and tangential dimensions at 4° eccentricity for all visual-field locations (see color legend). Shaded regions show SEM across participants. (E) Mean crowding zones at 8°, plotted as in D. (F) Mean gap-resolution thresholds at 4°, plotted in minutes of arc, following the conventions of D (although note the scale difference). (G) Mean gap-resolution thresholds at 8°. (H) Mean bisection thresholds at 4°, plotted in minutes of arc (note again the scale difference). (I) Mean bisection thresholds at 8°.

Crowding, gap resolution, and bisection were thus tested across the eight locations of the visual field. Across all locations, axes, and participants, the average gap-resolution threshold for the Landolt-C task was 3.18′ ± 0.11′ of arc, whereas bisection thresholds averaged 11.43′ ± 0.69′. An order of magnitude larger again, the average crowding zone size was 1.59° ± 0.10°, slightly reduced from the values of experiment 1.

Because of the considerable scale differences between these tasks, we plot the zones from each dataset separately to show their variation across the visual field. For crowding, the mean radial/tangential zones are presented in Fig. 4D for 4° eccentricity and in Fig. 4E for 8°. A four-way mixed-effects ANOVA gave significant main effects of eccentricity (F_1,27 = 98.22, P < 0.001), with more crowding at 8° than at 4°, and flanker axis, with radial flankers again producing crowding over greater distances than tangential flankers (F_1,27 = 77.74, P < 0.001). The main effect of visual-field direction was again significant (F_3,27 = 36.04, P < 0.001) with contrasts showing this to be due to larger crowding zones on the vertical meridian than on the horizontal (t₇₉ = 10.58, P < 0.001) and greater crowding in the upper than in the lower visual field (t₃₉ = 4.92, P < 0.001). Crowding did not differ between the left and right visual fields (t₃₉ = −1.85, P = 0.07). The main effect of participants was also significant (F_9,27 = 3.76, P = 0.006), as was the two-way interaction between visual-field direction and participants (F_27,27 = 2.28, P = 0.04). All other two-way interactions with participants were nonsignificant (all Fs < 2). Two-way interactions between eccentricity and direction (F_3,27 = 28.10, P < 0.001) and axis and eccentricity (F_1,27 = 44.49, P < 0.001) were both significant, although the interaction between direction and axis was not (F_3,27 = 1.93, P = 0.15). The three-way fixed-effects interaction was nonsignificant (F_3,27 = 1.08, P = 0.37), as were the interactions between eccentricity, axis, and participants and between eccentricity, direction, and participants (F < 1), although the three-way interaction between axis, direction, and participants was significant (F_27,27 = 2.39, P = 0.01). Overall, we replicate the results of experiment 1.

This pattern differs slightly for the two position tasks. Gap resolution thresholds are shown in Fig. 4 F and G for 4° and 8° eccentricity. For this task, there was no main effect of the axis of judgment (F_1,27 = 0.85, P = 0.38), indicating that left/right judgments of gap location were equivalent with up/down judgments. There was nonetheless a main effect of eccentricity (F_1,27 = 128.67, P < 0.001) with gap resolution worse at 8° than 4° and a main effect for visual-field direction (F_3,27 = 33.27, P < 0.001). As with crowding, this is due to higher thresholds along the vertical than the horizontal meridian (t₇₉ = 8.74, P < 0.001), and higher thresholds in the upper vs. the lower visual field (t₃₉ = 4.06, P < 0.001) with no difference in thresholds between the left and right visual fields (t₃₉ = 0.14, P = 0.89). The main effect of participants was again significant (F_9,27 = 13.45, P = 0.009), although all two-way interactions with participants were not (all Fs < 1). The two-way interaction between eccentricity and direction was significant (F_3,27 = 11.68, P < 0.001), as was the interaction between direction and axis (F_3,27 = 2.10, P = 0.016), although the interaction between axis and eccentricity was not significant (F_1,27 = 0.03, P = 0.73). The three-way interaction between axis, direction, and participants was significant (F_27,27 = 4.42, P < 0.0001), although interactions between the fixed effects (F_3,27 = 2.49, P = 0.08) and the remaining interactions were all nonsignificant (all Fs < 2).

Bisection thresholds are shown in Fig. 4 H and I for each eccentricity. Here there was a main effect of the axis of judgments with radial thresholds significantly higher than tangential thresholds (F_1,27 = 85.46, P < 0.001). There was also a main effect of eccentricity (F_1,27 = 107.97, P < 0.001) with higher thresholds at 8° than 4° and a main effect of visual-field direction (F_3,27 = 6.95, P = 0.001) with higher thresholds in the upper than in the lower visual field (t₃₉ = 4.83, P < 0.001) and no difference between the left and right visual fields (t₃₉ = 0.95, P = 0.35). Unlike the other two tasks, there was no difference between thresholds along the vertical and horizontal meridians (t₇₉ = 1.30, P = 0.20). The main effect of participants was nonsignificant (F_9,27 = 1.37, P = 0.32), as were all two-way interactions with participants (all Fs < 2). The two-way interaction between eccentricity and direction was significant (F_3,27 = 11.68, P < 0.001), as was the interaction between axis and eccentricity (F_1,27 = 55.15, P < 0.001), although the interaction between direction and axis was not (F_1,27 = 42.66, P = 0.07). The three-way interaction between the fixed effects was not significant (F_3,27 = 0.66, P = 0.58), nor were any three-way interactions with participants (all Fs < 2).

To summarize, performance in all three tasks degrades with eccentricity and varies across the visual field with worse performance in the upper than in the lower visual field. All three tasks also show an interaction such that the visual-field anisotropy grows with eccentricity. However, although crowding and gap resolution are worse along the vertical than the horizontal meridian, this is not true for bisection. Additionally, although bisection and crowding are worse along the radial than the tangential dimension, this is not true for gap-resolution thresholds as a main effect. There is also a considerable scale difference between the tasks: crowding zones are 30 times larger than gap-resolution thresholds and 8 times larger than bisection thresholds.

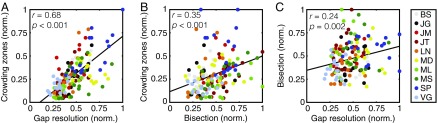
We next examined the intertask correlations. Using raw values, crowding zone sizes were strongly correlated with both gap-resolution thresholds (r₁₅₈ = 0.64, P < 0.001) and bisection thresholds (r₁₅₈ = 0.60, P < 0.001). Gap-resolution thresholds were also correlated with bisection thresholds (r₁₅₈ = 0.44, P < 0.001). As in experiment 1, however, these correlations include both the effects of eccentricity and the radial-tangential anisotropy that may reflect common topological properties for all retinotopically organized cortical maps. We thus normalized each dataset as before. The comparison between normalized crowding zones and gap-resolution thresholds is shown in Fig. 5A. This gives a highly significant correlation (r₁₅₈ = 0.68, P < 0.001) demonstrating that, when crowding zones are large, gap-resolution thresholds are also large. Fig. 5B shows a similar relationship between crowding zones and bisection zones. This again yields a highly significant correlation (r₁₅₈ = 0.35, P < 0.001). Finally, Fig. 5C shows the strong relationship between gap-resolution and bisection thresholds (r₁₅₈ = 0.24, P = 0.002). Altogether, the relationship between crowding and saccades is clearly not unique: similar relationships exist between crowding, gap-resolution, and bisection thresholds.

Fig. 5.

Correlations between crowding, gap-resolution, and bisection thresholds. (A) The correlation between normalized gap-resolution thresholds and the normalized spatial extent of crowding. Participants are denoted by color (see color legend). (B) The correlation between normalized bisection thresholds and the normalized spatial extent of crowding, plotted as in A. (C) The correlation between normalized gap-resolution thresholds and normalized bisection thresholds.

Combined Analysis.

Our results thus far are consistent with variations in each of these tasks deriving from a common source. To examine the relationship between these tasks more directly, we conducted a hierarchical regression analysis using data from all four tasks. Because crowding was measured in both experiments, we first needed to reduce these estimates to a single value. Given the strong correlation between crowding zones in the two experiments (Fig. S3), we took their average (for each location and participant) so as not to bias our analyses toward one experiment over the other. We then conducted a hierarchical linear regression analysis. Because our aim was ultimately to understand the source(s) of variation in the size of the crowding zone, we included crowding as the dependent variable and the three remaining tasks as predictors. As before, we sought to remove the universal map topology from each dataset by normalizing all values by both eccentricity and axis. Only data from the 10 participants who completed both experiments was included. The hierarchical regression analysis consisted of two models with distinct predictor variables entered simultaneously in each case. In the first model, the size of the saccade zones was the sole predictor variable for the sizes of the crowding zones (with resulting values shown in Table 1). As in experiment 1, this correlation was highly significant (F_1,159 = 9.69, P = 0.002) with a standardized β-value of 0.240 and an r² of 0.058, indicating that normalized saccade precision can explain ∼5.8% of the variance in the normalized spatial extent of crowding.

Fig. S3.

Correlations between interference zones for crowding in experiment 1 (x axis) and experiment 2 (y axis). Data are plotted in degrees of visual angle. Participants are denoted by color, each tested in eight locations and with flankers on two axes (see color legend).

Table 1.

Results from a hierarchical linear regression with two models that each predict variation in the size of crowding zones

Model	R2	Task	β	r2	t	P
1	0.058	Saccades	0.240	0.058	3.113	0.002
2	0.429	Saccades	0.114	0.020	1.797	0.074
		Gap resolution	0.531	0.298	8.132	<0.001
		Bisection	0.222	0.073	3.517	0.001

Model 1 includes only saccade precision as a predictor (listed under ‘”Task”); model 2 includes all three comparison tasks as predictor variables, all added simultaneously into the model. For each variable, we report the total R² for each model, as well as standardized β, partial r², t, and P values for each predictor. Predictors that were significant at the P < 0.05 level are shown in boldface type.

The second model added the lower-level predictors of gap resolution and bisection. This model is also highly significant (F_3,159 = 39.02, P < 0.001) with a larger R² value of 0.429 in total. All three predictors thus account for a greater proportion of the variance in crowding than saccades alone. However, when we consider the unique variance explained by each predictor, both gap resolution and bisection emerge as significant predictors with standardized β-values of 0.531 and 0.222, explaining 29.8% and 7.3% of the variance, respectively. The inclusion of both predictors is significant. In contrast, saccades are no longer a significant predictor of the variance in crowding zones. That is, although saccade precision is a significant predictor of the size of crowding zones on its own, it fails as a predictor when included with lower-level performance measures. The correlation between crowding and saccades is therefore likely to arise because both processes correlate with the lower-level processes of gap resolution and bisection. In contrast, these two predictors—gap-resolution and bisection thresholds—explain significant amounts of the variation in crowding zones, despite also correlating with each other.

SI Materials and Methods

Individual Patterns of Variation in Saccadic Precision and Crowding.

In experiment 1 we measured crowding and saccadic error zones in eight locations across the visual field. In addition to the averaged values for these zones (plotted in Fig. 2A), Fig. S1 plots data from each of our 12 participants individually. As with the averaged zone values, crowding zones are typically far larger than saccade error zones. However, there is also covariation between the two. For example, note the square-shaped zones for both crowding and saccades in participant VG (lower right in Fig. S1), compared with the considerably larger and more elongated zones for participant SP. Note also the general tendency for both saccade and crowding zones to be larger along the vertical meridian than the horizontal meridian. In addition to these commonalities, however, the dissociations that we observe at the group level can also be seen here. For example, saccade error zones at 8° eccentricity tend to be larger in the lower visual field (particularly visible in participant MZ) whereas for crowding the reverse is true (particularly for participant LN). Thus, as with the group data, here we observe for individuals that there are both similarities in the pattern of variation for crowding and saccadic errors (including the horizontal–vertical anisotropy) and dissociations (including differences in the upper vs. lower visual field).

Additional Saccade Metrics.

In addition to the measurements of saccadic precision in experiment 1, we also examined a range of additional saccade parameters. We first examined saccade latency values, measured as the time taken to initiate a saccade following stimulus offset (the cue to make a saccade). Saccades were detected using the analyses outlined in Materials and Methods. Fig. S2A shows the mean saccade latency across individuals for each visual-field location (at two eccentricities and in four directions from fixation). Here it can be seen that saccades occur more rapidly toward the upper than the lower visual field and more rapidly toward the vertical than the horizontal meridian.

These values were submitted to a three-way mixed effects ANOVA with eccentricity and visual-field direction as fixed effects and participants as a random effect. The main effect of eccentricity was significant (F_1,95 = 15.79, P = 0.002) with shorter latencies to 8° eccentricity than to 4°. The main effect of visual-field direction was also significant (F_3,95 = 4.93, P = 0.006) with significantly shorter saccadic latencies toward the upper than the lower visual field (t₂₃ = −2.61, P = 0.016) and no significant difference between left and right saccades (t₂₃ = −1.77, P = 0.09). The main effect of participants was also significant (F_11,95 = 27.40, P < 0.001), as was the interaction between visual-field direction and participants (F_33,95 = 3.60, P = 0.002). Interactions between both eccentricity and visual-field direction (F_3,95 = 1.01, P = 0.40) and eccentricity and participant (F_11,95 = 1.40, P = 0.22) were nonsignificant.

We therefore replicate prior reports (44) that saccades are initiated more rapidly toward objects in the upper than in the lower visual field. As with our findings for saccadic precision reported in the main text, this effect goes in the opposite direction to effects for crowding. Although we are not aware of any specific measurements of reaction times for crowding across the visual field, visual search times have been found to be significantly slower for elements in the upper than in the lower visual field (76), again in the opposite direction to saccadic latencies. This is not to say that saccadic latency bears no relation to visual input at all; saccadic latencies have been shown to decrease as stimulus luminance increases (77), for example. We therefore interpret the dissociation between saccadic latency and crowding as further evidence that these specific processes operate on separate representations of the visual field. As discussed in the main text, and consistent with prior proposals (34), the distinct cortical route for saccades may involve the superior colliculus where the representation of the upper visual field is more finely detailed than that of the lower visual field (50). Here we suggest that this representation may allow for both more precise and more rapid saccades to the upper visual field.

In addition to saccadic latencies, we also examined the peak velocity for saccades to each of the eight locations in the visual field. These values were measured in the period between the onset and offset of the main saccade sequence (as outlined in Materials and Methods). As plotted in Fig. S2B, these values also show a range of anisotropies. When submitted to a three-way mixed effects ANOVA, as above, there was a significant main effect of eccentricity (F_1,95 = 121.99, P < 0.001) with more rapid saccades to 8° eccentricity than to 4°. The main effect of visual-field direction was also significant (F_3,95 = 9.30, P = 0.001) with significantly slower saccade velocities toward the upper than the lower visual field (t₂₃ = −3.01, P = 0.005) and no significant difference between left and right saccades (t₂₃ = −0.18, P = 0.86). The main effect of participants was also significant (F_11,95 = 4.75, P = 0.002), as were the interactions between visual-field direction and participants (F_33,95 = 6.44, P < 0.001) and between eccentricity and participant (F_11,95 = 2.91, P = 0.009). The interaction between eccentricity and visual-field direction was nonsignificant (F_3,95 = 0.55, P = 0.65).

In conjunction with our estimates of saccadic precision, these values of saccadic velocity conform to the frequently observed speed–accuracy trade-off (78, 79), which is likely to be a consistent property of the main sequence in saccadic eye movements. In particular, saccades move more slowly to the upper visual field, where they are more precise, and more rapidly to the lower field, where they are less precise. Note that this is unlikely to be a decisional speed–accuracy trade-off whereby participants would be increasing their saccadic precision by taking more time to prepare the saccade. A decisional process would manifest as a trade-off between saccadic latency and precision. As above, we observe that latency and precision covary across the visual field.

Finally, our analyses in the main text concern the characteristics of the first saccade made during each trial. As described in Materials and Methods, these saccades were defined as having a latency greater than 100 ms but below 500 ms, an amplitude above 1°, and a landing position that fell within a virtual circle centered on the target with a radius equal to the target eccentricity. However, it is possible that participants may have initiated corrective saccades after this initial main sequence to bring their final landing position closer to the desired goal (80). We therefore examined the characteristics of these corrective saccades in our experiment by examining trials in which a main saccade was detected (as above) and then examining subsequent eye movements within the trial. As with the main saccade sequence, corrective saccades were detected in the first instance using the velocity distribution (73), with saccade onset and offset detected when the velocity of a moving average, taken across 20 eye-position samples, exceeded 3 SDs from the mean. On trials where a main saccade was detected, subsequent eye movements were recorded as a corrective saccade if their latency was within 300 ms from the main saccade. This criterion was used because longer durations are likely to indicate subsequent saccades to other locations (e.g., back to fixation) rather than a corrective saccade (80). Corrective saccades were also required to have a minimum amplitude of 0.1° and a direction of movement within ±90° of the main saccade (again to exclude trials where return-to-fixation saccades were recorded).

The frequency of corrective saccades is plotted for each participant in Fig. S2C, shown within the total frequency of main saccades recorded across the whole experiment. Corrective saccades occurred on 15.4% of trials on average (range: 5.9–30.5%). With so few trials per location in the visual field it was not possible to run the same analyses as in the main experiment where frequency distributions were fitted with ellipses to determine the major and minor axes of the error zone—fits would be poorly constrained with too little data. We consequently examined the SD of landing positions as an analog of these measurements. Overall, there was no significant difference between the SD of landing positions for the main sequence of saccades vs. the subsequent corrective saccades on the same trials (t₁₉₂ = −0.243, P = 0.81). These values are plotted in Fig. S2D. Here it can be further seen that the number of data points that fall above the unity line (indicating greater precision for main vs. corrective saccades) is roughly equal to the number of data points below the line (indicating greater precision for corrective saccades). Indeed, corrective saccades were more precise (i.e., their SD values were lower) for only 42.6% of visual-field locations, and larger on the remainder. This is quite close to chance, suggesting no benefit for these corrective saccades. We suggest that this is due to the saccade target being extinguished before saccade execution in our experiment; corrective saccades are frequently initiated by visual feedback from a still-present fixation target (80). It is therefore unlikely that the incorporation of corrective saccades to our dataset would increase the observed values of saccadic precision substantially.

The Consistency of Interference Zones for Crowding.

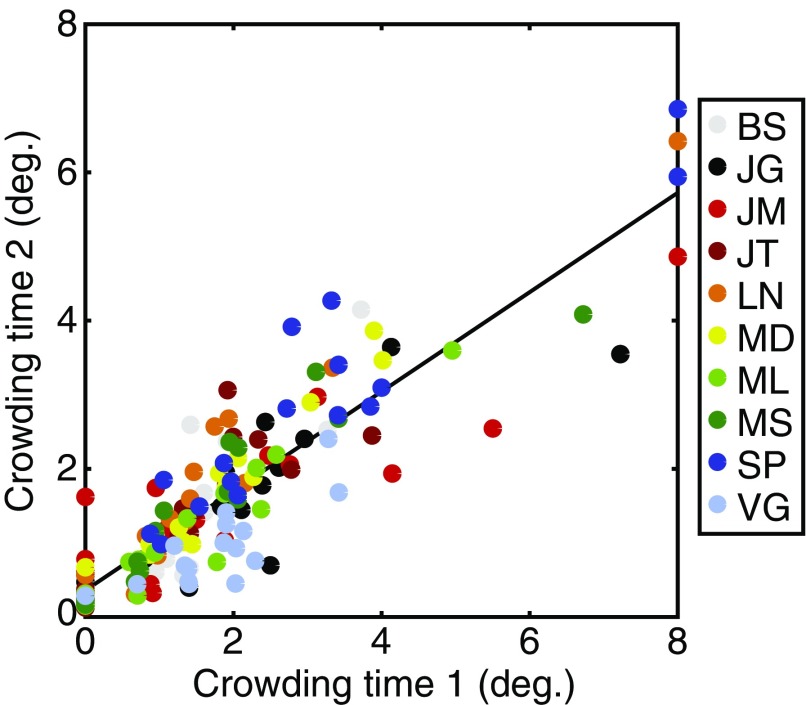
Because crowding was measured in both experiments, we were able to examine the reliability of our estimates of the crowding zone. Ten participants completed both experiments, for whom we examined the correlation between the crowding zones measured at these time points. As shown in Fig. S3, these zone sizes were indeed highly correlated (r₁₅₈ = 0.89, P < 0.001). This correlation remained even after normalizing the crowding zones (r₁₅₈ = 0.80, P < 0.001). We can thus conclude that the variation in crowding zones is highly consistent over time (9–12 mo separated the two measurements for each participant), procedure (constant stimuli vs. QUEST) (Materials and Methods), and attentional load (two tasks in experiment 1 and one in experiment 2). The strong correlation between these measurements suggests that these idiosyncratic variations in crowding are likely to be stable traits for each individual, rather than moment-to-moment fluctuations in performance.

Discussion

Our results demonstrate a pattern of shared variations across a range of measures in spatial vision: crowding, gap resolution, bisection, and the precision of saccadic eye movements. The zones of interference for crowding increase in size with eccentricity, show a pronounced radial-tangential anisotropy, are larger in the upper (vs. lower) visual field and along the vertical (vs. horizontal) meridian with a precise pattern that varies between participants. Similar variations occur for gap resolution, bisection, and saccades, albeit with an exception for saccade error zones, which are smaller in the upper than the lower field. All three processes also show strong correlations with crowding, even when normalized to remove the effects of eccentricity and the radial-tangential anisotropy. However, our hierarchical linear regression analysis suggests that it is the lower-level spatial vision measures—gap resolution and bisection—that explain most of the variance in crowding. In other words, the correlation between crowding and saccades is likely to arise indirectly because both tasks correlate with lower-level processes. We explain these findings by proposing that idiosyncratic variations in our spatial representation of the visual field arise in the earliest stages of the visual system of each individual and that they are then inherited throughout later stages. This “topology of spatial vision” gives a signature pattern of correlated variations across a range of processes, including those with apparent dissociations like crowding and saccades.

A key assumption with this proposal is that our tasks do in fact rely on separable processes with distinct spatial representations of the visual field. Contrary to recent suggestions that crowding and saccades are closely linked (37–39), four aspects of our data lead us to reject an inextricable linkage between these processes. First, although crowding and saccades show similar patterns of variation, saccadic precision is worse in the lower visual field than in the upper—the opposite pattern not only to crowding, but also to a wide range of perceptual tasks (24, 25). Second, our participants were clearly able to trade their precision between the two processes; saccadic precision was highest in trials where crowded identification was incorrect and vice versa. Third, our trial-by-trial variations revealed biases in saccadic landing positions (with a tendency to undershoot the target) that were not linked with performance on the crowded identification task. Finally, the correlation between saccades and crowding was the weakest of all of the intertask correlations, dropping out of the hierarchical analysis when gap resolution and bisection were included as copredictors. This dissociation between crowding and saccades is consistent with the more general dissociation between perceptual and saccadic localization observed previously (40–43). Note, however, that where previous studies have used trial-by-trial dissociations in speed perception and smooth pursuit to argue for distinct noise sources within a common processing stage (41, 42), we argue based on the further dissociations above that distinct spatial representations are more likely, at least for processes of spatial localization. These dissociations may reflect the greater reliance of saccadic localization on the retino-collicular neural pathway than on the geniculo-striate pathway used for perceptual localization (34). Accordingly, recent work demonstrates that collicular receptive fields are smallest in the lower field (50), matching our measures of saccadic precision.

Gap resolution and bisection can similarly be dissociated from crowding by the large difference in scale between the tasks: gap resolution and bisection take place over minutes of arc; crowding in the same locations covers several degrees. Additionally, as outlined in the Introduction, resolution and bisection have clear links with both retinal variations and cortical area V1 (5, 26, 27). It is difficult in this sense to dissociate gap resolution and bisection from one another; although they measure distinct aspects of localization (the resolution of fine details and the localization of spatially separated elements, respectively), their overlapping loci make their separation difficult to determine. The physiological basis of crowding can nonetheless be separated from these localization processes, given its stronger links with higher-order regions including cortical areas V2, V4, and beyond (31–33). A range of behavioral studies also support a later-stage locus for visual crowding (3, 13, 51–53). Furthermore, although acuity and crowding are correlated in the “normal” periphery (as in our gap-resolution data) and within-group for cases of amblyopia (54, 55), between-group comparisons reveal a clear acuity-crowding dissociation (56, 57). It may be that low-level spatial precision sets the precedence for crowding in development, but that disruptions to the visual system through additional factors such as a loss of binocularity (54) can dissociate these two factors. This potential for dissociation is further support that these processes rely on distinct cortical representations.

It is in the context of the dissociations between these tasks—spatial localization, crowding, and saccades—that their correlated pattern of variations across the visual field is particularly surprising. We explain this by suggesting that idiosyncratic variations in our spatial representation of the visual field arise in the earliest stages of the visual system. Given that the receptive fields at each stage in the visual system are likely built via the summation of inputs from preceding stages (e.g., 58), idiosyncrasies in early retinotopic maps (e.g., variations in cell density or receptive field size) would be propagated throughout the system and magnified as one moved up the cortical hierarchy. Prior studies have linked variations in both acuity (26) and perceived object size (59) with idiosyncrasies in visual cortical regions as early as V1. However, signatures of these variations are present as early as the photoreceptors of the retina, which show a clear decline in density with eccentricity (60), and the retinal ganglion cells, which show radially elongated receptive fields (61, 62). This “topological seed” may then propagate throughout the visual system, eventually scaling up to the level seen for the size of crowding zones, by far the largest spatial variations measured in our experiments. Distinct processes with separate spatial maps, as with crowding and saccadic eye movements, would nonetheless show some similarities due to this shared inheritance. Given that variations have been observed across the visual field for processes ranging from the perception of binocular disparity (63) to the perceived age and gender of faces (64), we would expect to see similar dependencies for a range of tasks throughout the visual system.

In linking these disparate tasks, we suggest that idiosyncrasies in spatial precision can have wide-reaching consequences, even altering processes of identification, as in crowding. This bears some similarity with mislocalization theories of crowding, which propose that these disruptions arise from uncertainty about the gross target location (46). However, the vast difference in scale between our measures of spatial precision and crowding is in fact inconsistent with this idea: there are target-flanker separations where interelement separations are clear (being well above bisection thresholds), yet crowding remains (because the separation is within the interference zone). Our dual-task analyses are also inconsistent with mislocalizations of this nature (Fig. 3). Accordingly, prior studies report that mislocalization errors are far less frequent than mislocalization models predict (65–67). Rather than the mislocalization of entire objects, we propose that the mislocalization of object features causes crowding and that this occurs within higher processing stages over a spatial region determined by the pooling of inputs from earlier stages. This aligns with pooling models of crowding, where target and flanker elements are combined to alter the target appearance (65–68). Here the role of spatial precision is somewhat implicit: the veridical target and flanker signals are present in the visual system, as their values serve as inputs to the pooling mechanism, but a pooled value is perceived because some detectors respond to both elements. Theories based on attentional resolution could be interpreted in a similar fashion (51). In this sense, we link the topological seed with variations in receptive field size and sampling density and suggest that variations in these factors can produce both the observed variations in spatial precision (at early stages of the visual system) and variations in our ability to identify objects (through the pooling of these inputs that leads to crowding). Through this inherited pattern of topology, variations in our spatial representation of the visual field can have wide-reaching effects on our ability to identify, localize, and interact with objects in the world.

Materials and Methods

Participants.

Twelve participants were tested in experiment 1: three of the authors (B.S., J.A.G., and M.S.) and nine naive participants. Five were female, eight were right-eye dominant (tested with the Crider ring test) (69), with ages from 22 to 37 y. All had normal or corrected-to-normal acuity. Ten of these participants also completed experiment 2, including the three authors. Informed consent was obtained before participation, with protocols approved by the Université Paris Descartes Review Board.

Apparatus.

Experiments were programmed in Matlab (Mathworks, Inc.) on an Apple iMac using the PsychToolbox (70, 71). In experiment 1, stimuli were presented binocularly and viewed from a distance of 55 cm on a 20-inch Compaq P1220 monitor with 1,024- × 768-pixel resolution and a 120-Hz refresh rate. The monitor was calibrated using a Minolta photometer and linearized in software to give a mean and maximum luminance of 45.4 cd/m² and 90.9 cd/m², respectively. Gaze position was measured for the dominant eye of each participant using a desktop-mounted SR Research EyeLink 1000, calibrated before each block of trials and whenever necessary thereafter. Gaze position was recorded using the Eyelink toolbox (72). This configuration allowed the measurement of gaze position with a resolution below 0.25° at a sampling rate of 1,000 Hz. In experiment 2, stimuli were presented on a 30-inch Apple cinema display with 2,560- × 1,600-pixel resolution and a 60-Hz refresh rate. The monitor was similarly calibrated to give luminance values between 1 cd/m² and 372 cd/m². Stimuli were presented binocularly and viewed from 100 cm for the acuity and bisection tasks and from 50 cm for the crowding task. In both experiments, head movements were minimized using chin and forehead rests, with responses to the identification tasks made via keyboard, and no feedback during trials.

Experiment 1: Stimuli and Procedures.

Because participants were required to both identify and make a saccade to a specified target, it was important that stimuli had both clearly defined features (for identification) and a clearly defined center (to direct saccades toward); saccades driven by identity alone (e.g., “saccade to the vertical stimulus”) would make it difficult to separate identification errors from localization errors (39). Our clock stimuli, depicted in Fig. 1A, allowed us to instruct participants to saccade toward the central white dot of the target (after stimulus offset) and to then make a four-alternative forced-choice (4AFC) decision regarding the orientation of the target-clock stroke (up, down, left, or right). Failures of identification here would not preclude saccadic precision; indeed, participants reported that the central dot of the target element was visible even when crowding occurred.

Stimuli were presented at two eccentricities (4° and 8°) in four directions from fixation (up, down, left, and right). Clocks had a total diameter of 0.7° or 1.4° at 4° and 8° eccentricity, respectively. The width of the outer circle outline was 0.05° or 0.11°, as was the outline around the central white point. The width of the internal “hand” stroke was 0.11° or 0.21°, and its length was the radius of the clock. The inner white dot of the clocks was either 0.11° or 0.21° in diameter. Stimuli were presented at 100% contrast with black and white luminance values of 0.16 cd/m² and 90.9 cd/m². At each visual field location, the target clock was presented either in isolation or flanked by two additional clocks. When crowded, flankers were placed on one of two axes: radially aligned with fixation or on the tangential dimension. Flankers were separated from the target by one of nine center-to-center separations between 0.175× and 0.675× the target eccentricity. At 4° this gave values from 0.7° to 2.7° in steps of 0.25°. At 8° values were from 1.4° to 5.4° in steps of 0.5°. The orientation of the target stroke was randomly selected in each trial, as was the orientation of the flanker clocks. Both flankers shared the same orientation, and matched target-flanker orientations were allowed.

The time course of a sample trial is shown in Fig. 1A. Participants began by fixating on a black circle (0.42° diameter) near the screen center with a location that was jittered with a radial shift between 0° and 0.5° in a random direction on each trial. Stimuli were presented relative to fixation to minimize the likelihood of stereotyped saccades (e.g., if the monitor boundaries were used as a cue for the saccade). If the measured gaze position was within 1.5° of fixation, then the trial began. Participants kept their gaze on the central circle during a fixation period (between 0.2 s and 1.4 s) and during the stimulus presentation (0.3 s). After stimulus offset, participants made a saccade toward the central white dot of the target clock and reported the clock-stroke orientation at the end of the trial. If a saccade was made before the offset of the clock stimuli (i.e., eye gaze was detected online as more than 1.5° from the fixation dot), the trial was canceled and repeated at the end of the block to maintain equal trial numbers under each condition before offline analyses.

In total, there were 2 eccentricity conditions, 4 directions from fixation, 2 flanker axis conditions, and 10 separation conditions (including an uncrowded single-clock condition). Each block of trials contained two repetitions for each condition to give 320 trials per block. Each participant completed five blocks, as well as an initial 160-trial practice block, to give 1,760 trials per participant.

Psychometric functions were fitted to behavioral data using a cumulative Gaussian with three parameters (midpoint, slope, and lapse rate). The critical spacing for each axis was taken as the target-flanker separation at which performance reached 80% correct (a value that was well above chance yet still attainable by all participants). To avoid impossible values, critical spacing values larger than the target eccentricity tested were recorded as either 4° or 8°, and those below zero (when performance was at ceiling for all separations) were given zero values. Zero and maximum values were assigned to 26 and 5 data points of 192, respectively. Note that zero values do not imply the absence of crowding, but rather that our stimulus sizes precluded the measurement of crowding in these locations.

Saccades were detected offline based on their velocity distribution (73). Saccade onset and offset were detected when the velocity of a moving average, taken across 20 eye-position samples, exceeded 3 SDs from the mean. We excluded trials in which saccade latency was either below 100 ms or greater than 500 ms, as well as trials in which the saccade amplitude was below 1° or where saccade landing coordinates diverged excessively from the central target-clock location (defined by a virtual circle centered on the target with a radius equal to the eccentricity). Trials were also excluded when blinks were detected during stimulus presentation. In total, 6.1% of trials were rejected with these criteria, which left an average of 1,507 trials per participant (range: 1,391–1,572). Saccadic landing positions were corrected for eye drift by subtracting the difference between the fixation target position and the gaze position at the saccade onset. From this we computed normalized frequency histograms for the region of space surrounding the target element. An example of a histogram where data has been smoothed by a 2D Gaussian filter with a SD of 0.25° is shown in Fig. 1C. For saccade landing errors in each visual-field location, we fitted 2D Gaussian functions to the data with five parameters (x/y SDs, orientation, and x/y peak location) and computed the saccade error zone as the major and minor axes of an ellipse fitted to the data such that 80% of saccade errors fell within the boundary of the ellipse.

Experiment 2: Stimuli and Procedures.

Three tasks were tested in this experiment. In each case, stimuli were presented in the eight locations of the visual field described above. To reduce testing time, performance in each task was assessed using an adaptive QUEST procedure (74). Stimuli in the crowding task were largely the same as in experiment 1 (Fig. 4A) with Weber contrast reduced to 50%. As before, participants were required to identify the orientation of the strokes of the target clock (up, down, left, or right), although here without the concurrent saccade task. On each trial, a target clock was presented with two flankers, both positioned along either the radial or the tangential axis with respect to fixation. The QUEST procedure varied the center-to-center separation between target and flankers (separately at each location and for each flanker dimension), converging on the separation that gave 80% correct performance (as taken in experiment 1 to define the crowding zone). Staircases were constrained such that the minimum possible separation had the target and flanker stimuli abutting (0.7° and 1.4° at the two eccentricities) and a maximum separation of 3.65° and 7.3°, respectively.

For the gap-resolution task, participants identified the orientation of a single Landolt-C element (Fig. 4B). Stimuli were at 50% Weber contrast, dark against the midgray background, with a stroke width equal to one-fifth the stimulus diameter. On each trial, a Landolt-C target was presented randomly in one of the eight possible locations for 0.3 s. Participants were required to indicate the direction of the “gap” in the Landolt-C. Judgements of the gap location were separated into two distinct two-alternative forced choice (2AFC) tasks tested in separate blocks: horizontal (left/right) and vertical gap judgments (top/bottom). This allowed direct comparison with the radial and tangential dimensions of the other tasks. We assume in doing so that the resolution of a Landolt-C gap relies on the dimension that is orthogonal to the axis of judgment. That is, to resolve a horizontally located gap (e.g., on the left, as in Fig. 4B), the crucial variation is along the vertical axis, where the black tips of the C must be differentiated from the midgray gap. We thus classed the 2AFC judgments along the vertical stimulus dimension as “horizontal” judgments and vice versa. Each was then grouped according to its location in the visual field to be radial or tangential with respect to fixation. Stimulus sizes were determined on each trial by a QUEST staircase set to converge on 75% correct performance (midway between chance and ceiling).

For the bisection task, stimuli consisted of three dots (Fig. 4C), each at 50% Weber contrast with a diameter of 14′ (at 4° eccentricity) or 26′ (at 8°). Dots were aligned either vertically or horizontally with participants required to indicate whether the central target dot was left or right of the midpoint defined by the outer reference dots (for horizontal conditions) or above/below the midpoint (for vertical conditions) in separate blocks. Reference dots were presented with a separation of either 2° or 4° at each of the two eccentricities, respectively (equivalent to the critical spacing values for crowding observed in experiment 1). In each trial, the three dots were presented randomly for 0.3 s in one of the eight locations. The target dot was displaced from the midpoint by an offset determined by a QUEST staircase set to converge at 75% correct. The maximum allowed offset was 0.8° and 1.6° for each eccentricity.

In each of the three tasks, staircases for the eight locations were interleaved in a single block with each staircase running for 45 trials to give 360 trials per block. The two axes of judgment (for gap-resolution and bisection tasks) were run in separate blocks, as was the axis of the flankers in the crowding task. Participants repeated each block three times, randomly interleaved, to give a total of 6,480 trials per participant. For each task, the three threshold estimates under each condition were averaged to a single value, separately for each participant.