Bayesian Total-Evidence Dating Reveals the Recent Crown Radiation of Penguins

Abstract

The total-evidence approach to divergence time dating uses molecular and morphological data from extant and fossil species to infer phylogenetic relationships, species divergence times, and macroevolutionary parameters in a single coherent framework. Current model-based implementations of this approach lack an appropriate model for the tree describing the diversification and fossilization process and can produce estimates that lead to erroneous conclusions. We address this shortcoming by providing a total-evidence method implemented in a Bayesian framework. This approach uses a mechanistic tree prior to describe the underlying diversification process that generated the tree of extant and fossil taxa. Previous attempts to apply the total-evidence approach have used tree priors that do not account for the possibility that fossil samples may be direct ancestors of other samples, that is, ancestors of fossil or extant species or of clades. The fossilized birth–death (FBD) process explicitly models the diversification, fossilization, and sampling processes and naturally allows for sampled ancestors. This model was recently applied to estimate divergence times based on molecular data and fossil occurrence dates. We incorporate the FBD model and a model of morphological trait evolution into a Bayesian total-evidence approach to dating species phylogenies. We apply this method to extant and fossil penguins and show that the modern penguins radiated much more recently than has been previously estimated, with the basal divergence in the crown clade occurring at Ma and most splits leading to extant species occurring in the last 2 myr. Our results demonstrate that including stem-fossil diversity can greatly improve the estimates of the divergence times of crown taxa. The method is available in BEAST2 (version 2.4) software www.beast2.org with packages SA (version at least 1.1.4) and morph-models (version at least 1.0.4) installed. [Birth–death process; calibration; divergence times; MCMC; phylogenetics.]

Establishing the timing of evolutionary events is a major challenge in biology. Advances in molecular biology and computer science have enabled increasingly sophisticated methods for inferring phylogenetic trees. While the molecular data used to build these phylogenies are rich in information about the topological aspects of trees, these data only inform the relative timing of events in units of expected numbers of substitutions per site. The fossil record is frequently used to convert the timescale of inferred phylogenies to absolute time (Zuckerkandl and Pauling 1962; 1965). Exactly how to incorporate information from the fossil record into a phylogenetic analysis remains an active area of research.

Bayesian Markov chain Monte Carlo (MCMC) methods are now the major tool in phylogenetic inference (Yang and Rannala 1997; Mau et al. 1999; Huelsenbeck and Ronquist 2001) and are implemented in several widely used software packages (Lartillot et al. 2009; Drummond et al. 2012; Ronquist et al. 2012b; Bouckaert et al. 2014). To date species divergences on an absolute time scale, Bayesian approaches must include three important components to decouple the confounded rate and time parameters: (i) a model describing how substitution rates are distributed across lineages; (ii) a tree prior characterizing the distribution of speciation events over time and the tree topology; and (iii) a way to incorporate information from the fossil or geological record to scale the relative times and rates to absolute values. Relaxed molecular clock models act as prior distributions on lineage-specific substitution rates and their introduction has greatly improved divergence dating methods (Thorne et al. 1998; Drummond et al. 2006; Rannala and Yang 2007; Drummond and Suchard 2010; Heath et al. 2012; Li and Drummond 2012). These models do not assume a strict molecular clock, instead they allow each branch in the tree to have its own rate of molecular evolution drawn from a prior distribution of rates across branches. Stochastic branching models describing the diversification process that generated the tree are typically used as prior distributions for the tree topology and branching times (Yule 1924; Kendall 1948; Nee et al. 1994; Rannala and Yang 1996; Yang and Rannala 1997; Gernhard 2008; Stadler 2009). When diversification models and relaxed-clock models are combined in a Bayesian analysis, it is possible to estimate divergence times on a relative time scale. External evidence, however, is needed to estimate absolute node ages.

Various approaches have been developed to incorporate information from the fossil record or biogeographical dates into a Bayesian framework to calibrate divergence time estimates (Rannala and Yang 2003; Thorne and Kishino 2005; Yang and Rannala 2006; Ho and Phillips 2009; Heath 2012; Heled and Drummond 2012, 2015; Parham et al. 2012; Silvestro et al. 2014). Calibration methods (also called “node dating”) are the most widely used approaches for dating trees (Ho and Phillips 2009) where absolute branch times are estimated using prior densities for the ages of a subset of divergences in the tree. The placement of fossil-based calibration priors in the tree is ideally determined from prior phylogenetic analyses that include fossil and extant species, which could be based on analysis of morphological data alone, analysis of morphological data incorporating a backbone constraint topology based on molecular trees, or simultaneous analysis of combined morphological and molecular data-sets. In practice, however, fossil calibrations are often based on identifications of apomorphies in fossil material or simple morphological similarity.

Node calibration using fossil constraints has two main drawbacks. First, having identified fossils as belonging to a clade, a researcher needs to specify a prior distribution on the age of the common ancestor of the clade. Typically the oldest fossil in the clade is chosen as the minimum clade age but there is no agreed upon method of specifying the prior density beyond that. One way to specify a prior calibration density is through using the fossil sampling rate that can be estimated from fossil occurrence data (Foote and Raup 1996). However, this approach must be executed with caution and attention to the quality of the fossil record for the clade of interest, as posterior estimates of divergence times are very sensitive to prior calibration densities of selected nodes (Warnock et al. 2012, 2015; Dos Reis and Yang 2013; Zhu et al. 2015) meaning that erroneous calibrations lead to erroneous results (Heads 2012).

The second major concern about node calibration is that the fossilization process is modeled only indirectly and in isolation from other forms of data. A typical node-dating analysis is sequential: it first uses morphological data from fossil and extant species to identify the topological location of the fossils within a given extant species tree topology, then uses fossil ages to construct calibration densities, and finally uses molecular data to estimate the dated phylogeny. Treating the different types of data in this sequential manner implies an independence between the processes that produce the different types of data, which is statistically inaccurate and errors at any step can propagate to subsequent analyses. Furthermore, at the last step in the sequential analysis, multiple different prior distributions are applied to estimate the dated phylogeny: a tree prior distribution and calibration distributions. Since these distributions all apply to the same object, they interact and careful consideration must be given to their specification so as to encode only the intended prior information (Heled and Drummond 2012; Warnock et al. 2015). There is currently no efficient general method available to coherently specify standard tree priors jointly with calibration distributions (Heled and Drummond 2015).

In the total-evidence approach to dating (Lee et al. 2009; Pyron 2011; Ronquist et al. 2012a), one specifies a probabilistic model that encompasses the fossil data, molecular data and morphological data and then jointly estimates parameters of that model, including a dated phylogeny, in a single analysis using all available data. It builds on previously described methods for combining molecular and morphological data to infer phylogenies (Nylander et al. 2004) using a probabilistic model of trait evolution (the Mk model of Lewis 2001). The total-evidence approach to dating can be applied by employing a clock model and a tree prior distribution to calibrate the divergence times. The tree prior distribution describes the diversification process where fossil and extant species are treated as samples from this process. The placement of fossils and absolute branch times are determined in one joint inference rather than in separate analyses. The combination of clock models and substitution models for molecular and morphological data and a model of the process that generates dated phylogenetic trees with fossils comprises a full probabilistic model that generates all data used in the analysis.

This approach can utilize all available fossils as individual data points. In contrast, the node calibration method only directly incorporates the age of the oldest fossil of a given clade, typically as a hard minimum for the clade age. The overall fossil record of the clade can be indirectly incorporated as the basis for choosing a hard or soft maximum or to justify the shape of a prior distribution, however, individual fossils aside from the oldest will not contribute directly (except perhaps if they are used to generate a confidence interval).

Although total-evidence dating overcomes limitations of other methods that use fossil evidence to date phylogenies, some aspects of the method still need to be improved (Arcila et al. 2015). One improvement is using better tree prior models. Previous attempts at total-evidence dating analyses have used uniform, Yule, or birth–death tree priors that do not model the fossil sampling process and do not allow direct ancestors among the sample (e.g., Pyron 2011; Ronquist et al. 2012a; Wood et al. 2013). However, the probability of ancestor–descendant pairs among fossil and extant samples is not negligible (Foote 1996). Moreover, ancestor–descendant pairs need to be considered when incomplete and nonidentified specimens are included in the analyses because such specimens might belong to the same single lineages as other better preserved fossils.

A good choice of the tree prior model is important for dating methods due to the limited amount of fossil data. Dos Reis and Yang (2013) and Zhu et al. (2015) showed that calibration methods are not statistically consistent, that is, increasing the amount of sequence data with a fixed number of calibration points does not decrease the uncertainty in divergence time estimates. Zhu et al. (2015) conjectured that total-evidence approaches are not statistically consistent, implying that the speciation process assumptions play a significant role in dating phylogenies.

The fossilized birth–death (FBD) model (Stadler 2010; Didiera et al. 2012; Stadler et al. 2013) explicitly models the fossilization process together with the diversification process and accounts for the possibility of sampled direct ancestors. Heath et al. (2014) used this model to estimate divergence times in a Bayesian framework from molecular data and fossil occurrence dates on a fixed tree topology. A comparison of different divergence dating methods showed that total-evidence analyses with simple tree prior models estimated significantly older divergence ages than analyses of molecular data and fossil occurrence dates with the FBD model (Arcila et al. 2015).

Until recently, combining the FBD model with a total-evidence dating approach was complicated by the fact that existing implementations of the MCMC algorithm over tree space did not allow trees with sampled ancestors. Gavryushkina et al. (2014) addressed this problem and enabled full Bayesian inference using FBD model in the BEAST2 software (Bouckaert et al. 2014) with the SA package (https://github.com/CompEvol/sampled-ancestors). This extended the Heath et al. (2014) method by allowing uncertainty in the tree topology of the extant species and placement of fossil taxa. Additionally, Zhang et al. (2016) implemented a variant of the FBD process that accounts for diversified taxon sampling and applied this to a total-evidence dating analysis of Hymenoptera (Ronquist et al. 2012a). This study demonstrated the importance of modeling the sampling of extant taxa when considering species-rich groups (Hohna et al. 2011).

Here we implement total-evidence dating with the FBD model by including morphological data to jointly estimate divergence times and the topological relationships of fossil and living taxa. We applied this method to a fossil-rich data set of extant and fossil penguins, comprising both molecular and morphological character data (Ksepka et al. 2012). Our analyses yield dated phylogenies of living and fossil taxa in which most of the extinct species diversified before the origin of crown penguins, congruent with previous estimates of penguin relationships based on parsimony analyses (Ksepka et al. 2012). Furthermore, our analyses uncover a significantly younger age for the most recent common ancestor (MRCA) of living penguins than previously estimated (Baker et al. 2006; Brown et al. 2008; Subramanian et al. 2013; Jarvis et al. 2014; Li et al. 2014).

Materials and Methods

MCMC Approach

We developed a Bayesian MCMC framework for analysis of morphological and molecular data to infer divergence dates and macroevolutionary parameters. The MCMC algorithm takes molecular sequence data from extant species, morphological data from extant and fossil species and fossil occurrence dates (or fossil occurrence intervals) as input data and simultaneously estimates dated species phylogenies (tree topology and divergence times), macroevolutionary parameters, and substitution and clock model parameters. We assume here that the gene phylogeny coincides with the species phylogeny. The state space of the Markov chain is a dated species phylogeny, 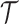, substitution and clock model parameters, , and tree prior parameters, . The posterior distribution is

$$\begin{array}{rrr}& & f(\mathcal{T},\overline{\theta },\overline{\eta }|D,\overline{\tau })\propto f(D,\overline{\tau }|\mathcal{T},\overline{\theta },\overline{\eta })f(\mathcal{T},\overline{\theta },\overline{\eta })\hfill \\ & & \hspace{0.17em}=f(D|\mathcal{T},\overline{\theta })f(\overline{\tau }|\mathcal{T})f(\mathcal{T}|\overline{\eta })f(\overline{\eta })f(\overline{\theta }),\hfill \end{array}$$

where is a matrix of molecular and morphological data and is a vector of time intervals assigned to fossil samples. On the right-hand side of the equation, there is a tree likelihood function, , a tree prior probability density, 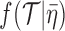, prior probability densities for the parameters, and a probability density, , of obtaining stratigraphic ranges , given 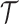(remember, that defines the exact fossilization dates). The tree prior density 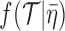is defined by equation (2) or (7) in Gavryushkina et al. (2014).

The full model describes the tree branching process, morphological and molecular evolution along the tree, fossilization events, and assignment of the stratigraphic ranges to fossil samples, since we do not directly observe when a fossilization event happened. Thus, the stratigraphic ranges for the fossils are considered as data. We do not explicitly model the process of the age range assignment but assume that for a fossilization event that happened at time the probability of assigning ranges does not depend on (as a function) if and is zero otherwise. This implies that is a constant whenever the sampling times are within intervals and zero otherwise and we get:

$$f(\mathcal{T},\overline{\theta },\overline{\eta }|D,\overline{\tau })\propto f(D|\mathcal{T},\overline{\theta })\delta (\mathcal{T}\in T_{\overline{\tau }})f(\mathcal{T}|\overline{\eta })f(\overline{\eta })f(\overline{\theta }),$$ (1)

where 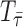is a set of phylogenies with sampled nodes within corresponding intervals.

Modeling the Speciation Process

We describe the speciation process with the FBD model conditioning on sampling at least one extant individual (equation (2) in Gavryushkina et al. 2014). This model assumes a constant rate birth–death process with birth rate 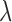and death rate where fossils are sampled through time according to a Poisson process with a constant sampling rate and extant species are sampled at present with probability . The process starts at some time in the past–-the time of origin, where time is measured as a distance from the present. This process produces species trees with sampled two-degree nodes which we call sampled ancestors (following Gavryushkina et al. 2013; 2014). Such nodes represent fossil samples and lie directly on branches in the tree. They are direct ancestors to at least one of the other fossils or extant taxa that has been sampled.

We need to clarify what we mean by sampling. We have two types of sampling: fossil sampling and extant sampling. Suppose an individual from a population represented by a branch in the full species tree fossilized at some time in the past. Then this fossil was discovered, coded for characters and included in the analysis. This would correspond to a fossil sampling event. Further, if an individual from one of the extant species was sequenced or recorded for morphological characters and these data are included to the analysis we say that an extant species is sampled. Suppose one sampled fossil belongs to a lineage that gave rise to a lineage from which another fossil or extant species was sampled. In such a case we obtain a sampled ancestor, that is, the former fossil is a sampled ancestor and the species to which it belongs is ancestral to the species from which the other fossil or extant species was sampled. If two fossils from the same taxon with different age estimates are included in an analysis, the older fossil has the potential to be recovered as a direct ancestor and would be considered a sampled ancestor under our model.

In most cases, we re-parameterize the FBD model with where

$$\begin{array}{rr}d=\lambda -\mu \hfill & \text{net diversification rate}\hfill \\ \nu =\frac{\mu }{\lambda }\hfill & \text{turnover rate}\hfill \\ s=\frac{\psi }{\mu +\psi }\hfill & \text{fossil sampling proportion}.\hfill \end{array}$$ (2)

These parameters are commonly used to describe diversification processes. We also use the standard parameterization assuming in some analyses. Note, that the time of origin is a model parameter as opposed to the previous application of the FBD model (Heath et al. 2014) where instead, the process was conditioned on the age of the MRCA, that is, the oldest bifurcation node leading to the extant species, and all fossils were assumed to be descendants of that node. Here, we allow the oldest fossil to be the direct ancestor or sister lineage to all other samples because there is no prior evidence ruling those scenarios out.

Bayes Factors

To assess whether there is a signal in the data for particular fossils to be sampled ancestors we calculated Bayes factors for each fossil. By definition a Bayes factor is:

$$\mathrm{B}\mathrm{F}=\frac{P(D,\overline{\tau }|H_1,M)}{P(D,\overline{\tau }|H_2,M)}=\frac{P(H_1|D,\overline{\tau },M)P(H_2|M)}{P(H_2|D,\overline{\tau },M)P(H_1|M)},$$

where is the hypothesis that a fossil is a sampled ancestor, 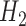is the hypothesis that it is a terminal node, and is the combined model of speciation and morphological and molecular evolution. Thus, is the posterior probability that a fossil is a sampled ancestor and is a terminal node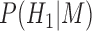, and and are the corresponding prior probabilities.

The Bayes factor reflects the evidence contained in the data for identifying a fossil as a sampled ancestor and compares the prior probability to be a sampled ancestor to the posterior probability. However, we could not calculate the probabilities and , so instead we looked at the evidence added by the morphological data toward identifying a fossil as a sampled ancestor to the evidence contained in the temporal data. That is, we replaced prior probabilities with posterior probabilities given that we sampled 19 extant species and 36 fossils and assigned age ranges to fossils, , and calculated analogues of the Bayes factors:

$$\widehat{\mathrm{B}\mathrm{F}}=\frac{P(H_1|D,\overline{\tau },M)P(H_2|\overline{\tau },M)}{P(H_2|D,\overline{\tau },M)P(H_1|\overline{\tau },M)}.$$

To approximate , we sampled from the distribution:

$$f(\mathcal{T},\overline{\eta }|\overline{\tau })\propto \delta (\mathcal{T}\in T_{\overline{\tau }})f(\mathcal{T}|\overline{\eta })f(\overline{\eta })$$ (3)

using MCMC. Having a sample from the posterior distribution (1) and a sample from the conditioned prior distribution (3) we calculate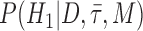d and 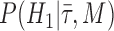as fractions of sampled trees in which the fossil appears as a sampled ancestor in corresponding MCMC samples. Similarly, we calculated and 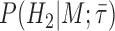using trees in which the fossil is a terminal node.

Data

We analyzed a data set from Ksepka et al. (2012) consisting of morphological data from fossil and living penguin species and molecular data from living penguins. The morphological data matrix used here samples 36 fossil species (we excluded Anthropornis sp. UCMP 321023 due to absence of the formal description for this specimen) and 19 extant species (we treated the Northern, Southern, and Eastern Rockhopper penguins as three distinct species for purpose of the analysis). The original matrix contained 245 characters. We excluded outgroup taxa (Procellariiformes and Gaviiformes) because including them would violate the model assumptions: a uniform sampling of extant species is assumed, whereas the matrix sampled all extant penguins but only a small proportion of outgroup species and also did not sample any fossil taxa from these outgroups. We excluded characters that became constant after excluding outgroup taxa, resulting in a matrix of 202 characters. The morphological characters included in the matrix ranged from two- to seven-state characters. The majority of these characters (95%) have fewer than four states. Further, 48 of the binary characters were coded as present/absent. The molecular alignment comprises the nuclear recombination-activating gene 1 (RAG-1), and the mitochondrial 12S, 16S, cytochrome oxidase 1 (CO1), and cytochrome b genes. Each region is represented by more than 1000 sites with 8145 sites in total. Some regions are missing for a few taxa.

The morphological data-set was originally developed to resolve the phylogenetic placement of fossil and extant penguins in a parsimony framework. Thus, efforts were focused on parsimony-informative characters. Though some apomorphic character states that are observed only in a single taxon are included in the data-set, no effort was made to document every possible autapomorphy. Thus, such characters can be expected to be undersampled. As with essentially all morphological phylogenetic data-sets, invariant characters were not scored.

We updated the fossil stratigraphic ages—previously summarized in Ksepka and Clarke (2010)—to introduce time intervals for fossil samples as presented in online Supplementary Material (SM), Table 1 available on dryad at http://dx.doi.org/10.5061/dryad.44pf8). For fossil species known from a single specimen, fossil stratigraphic ages represent the uncertainty related to the dating of the layer in which the fossil was found. For fossils known from multiple specimens, the ages were derived from the ages of the oldest and youngest specimens.

Table 1.

The posterior probability of a fossil’s placement in the crown (only for fossils with non-zero probability)

Fossil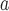	Probability
Spheniscus megaramphus	0.9992
Spheniscus urbinai	0.9991
Pygoscelis grandis	0.9928
Spheniscus muizoni	0.9201
Madrynornis mirandus	0.9007
Marplesornis novaezealandiae	0.1652
Palaeospheniscus bergi	0.0001
Palaeospheniscus biloculata	0.0001
Palaeospheniscus patagonicus	0.0001
Eretiscus tonnii	0.0001

The six fossils with probabilities greater than 0.05 were used for the total-evidence analysis without stem fossils.

Morphological Evolution and Model Comparison

We apply a simple substitution model for morphological character evolution—the Lewis Mk model (Lewis 2001), which assumes a character can take states and the transition rates from one state to another are equal for all states. We do not model ordered characters and treated 34 characters that were ordered in the Ksepka et al. (2012) matrix as unordered.

Evolution of morphological characters has a different nature from evolution of DNA sequences and, therefore, requires different assumptions. In contrast to molecular evolution models, we do not know the number of states each character can take and the number of states is not constant for different characters. We consider two ways to approach this problem. First, we can assume that the number of possible states for a character is equal to the number of different observed states. Typically, one would count the number of different states in the data matrix for the character. Here, we obtained the number of observed states from the larger data matrix used in Ksepka et al. (2012) containing 13 outgroup species. Having the number of observed characters for each character, we partition the morphological data matrix in groups of characters having the same number of states and apply a distinct substitution model of the corresponding dimension to each partition. Another approach is to treat all the characters as evolving under the same model. The model dimension in this case is the maximum of the numbers of states observed for characters in the matrix. We refer to the first case as “partitioned mode” and to the second case as “unpartitioned model”. Another difference comes from the fact that typically only variable characters are recorded. Thus, the second adjustment to the model accounts for the fact that constant characters are never coded. This model is called the Mkv model (Lewis 2001). We compared a model which assumed no variation in substitution rates of different morphological characters with a model using gamma distributed rates with a shared shape parameter for all partitions. We also compared a strict clock model and an uncorrelated relaxed clock model (Drummond et al. 2006) with a shared clock rate across partitions. To assess the impact of different parameterizations of the FBD model that induce slightly different prior distributions of trees we also considered two parameterizations (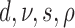–parameterization vs. 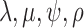–parameterization).

We completed a model selection analysis comparing different combinations of the assumptions for the Lewis Mk model, morphological substitution rates, and FBD model assumptions by running eight analyses of morphological data with different model settings. We then estimated the marginal likelihood of the model in each analysis using a path sampling algorithm (Baele et al. 2012), with 20 steps and 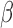-powers derived as quantiles of the Beta distribution with 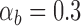and . 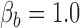The traditional model selection tool is a Bayes factor, which is the ratio of the marginal likelihoods of two models: 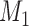and 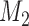. A Bayes factor greater than one indicates that model 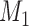is preferred over model 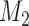. Following this logic, the model that provides the best fit is the model with the largest marginal likelihood. The model combinations with marginal likelihoods are described in Table 2.

Table 2.

The tree prior parameterization, clock, and substitution models used for eight analyses of penguin morphological data with marginal likelihoods for model testing

#	Partitions	Gamma	Lewis model	Clock	Parameterization from two runs	Marginal log-likelihood
1			Mk	Strict		,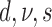
2		G	Mk	Strict		,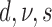
3	P		Mk	Strict		,
4	P	G	Mk	Strict		,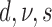
5	P		Mk	Strict	()	,
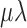6	P		Mkv	Strict		,
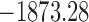7	P	G	Mkv	Strict		,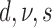
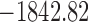8	P	G	Mkv	Relaxed		,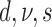

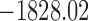
The analysis under model 8 has the largest marginal log-likelihood and was thus the model best supported by the data when evaluated using Bayes factors.

Posterior Predictive Analysis

For most of the bifurcation events in trees from the posterior samples of the penguin analyses only one lineage survives, whereas another lineage goes extinct. This suggests a non-neutrality in the evolution of the populations. To assess whether the FBD model, which assumes all lineages in the tree develop independently, fits the data analyzed here, we performed the posterior predictive analysis following (Drummond and Suchard 2008) under model 8 in Table 2. The idea of such an analysis is to compare the posterior distribution of trees to the posterior predictive distribution (Gelman et al. 2013) and this type of Bayesian model checking has been recently developed for a range of phylogenetic approaches (Bollback 2002; Rodrigue et al. 2009; Brown 2014; Lewis et al. 2014). The posterior predictive distribution can be approximated by the sample of trees simulated under parameter combinations drawn from the original posterior distribution. Out of computational convenience and similar to calculating for the Bayes factors, we conditioned the posterior predictive distribution on having sampled fossils within ranges, , used in the original analysis.

A way to compare posterior and posterior predictive distributions is to consider various tree statistics and calculate the tail-area probabilities by calculating the 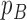probability, which is simply the proportion of times when a given test statistic for the simulated tree exceeds the same statistic for the tree from the posterior distribution corresponding to the same parameters. Extreme values of , that is, values that are less than 0.05 or greater than 0.95, would indicate the data favor a non-neutral scenario. For this analysis, we considered tree statistics which can be grouped into two categories: statistics that describe the branch length distribution and the tree shape. The test statistics and corresponding 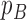-values are summarized in Table 3.

Table 3.

The posterior predictive analysis of the penguin data for branch length and tree-shape statistics indicating no significant difference in the posterior and posterior predictive tree distributions for model 2 (in Table 2)

Description	Notation	-value
Branch length distribution statistics
The total length of all branches in the tree		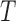0.83
The ratio of the length of the subtree induced by extant taxa and the total tree length		0.33
Genealogical Fu and Li’s calculated as the normalized difference between external branch length in the tree with suppressed sampled ancestor nodes and total tree length.		0.5
The time of the MRCA of all taxa		0.57
The time of the MRCA of all extant taxa		0.46
Tree shape statistics
The maximum number of bifurcation nodes between a bifurcation node and the leaves summed over all bifurcation nodes except for the root		0.75
Coless’s tree imbalance index calculated as the difference between the numbers of leaves on two sides of a node summed over all internal bifurcation nodes and divided by the total number of leaves		0.28
The number of cherries (two terminal nodes forming a monophyletic clade, sampled ancestors are suppressed)		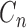0.54
The number of sampled ancestors	SA	0.26

A value is the proportion of times a given test statistic for the simulated tree exceeds the value of that statistic for the tree from the posterior distribution.

All values are within [0.05, 0.95].

Total-Evidence Analysis of Penguins

For the total-evidence analysis of the penguin data set, we chose the substitution and clock models for morphological character evolution with the largest marginal likelihood from the model comparison analysis (analysis 8 in Table 2). This model suggests that the data are partitioned in groups of characters with respect to the number of observed states. Each partition evolves under the Lewis Mkv model and the substitution rate varies across characters according to a Gamma distribution shared by all partitions. The morphological clock is modeled with an uncorrelated relaxed clock model with log-normal distributed rates. For molecular data we assume a general-time reversible model with gamma-distributed rate heterogeneity among sites (GTR+) for each of the five loci with separate rate, frequency, and gamma shape parameters for each partition. A separate log-normal uncorrelated relaxed clock model is assumed for the molecular data alignment. Each branch is assigned a total clock rate drawn from a log-normal distribution and this rate is scaled by a relative clock rate for each gene so that relative clock rates for five partitions sum up to one. We also ran the same analysis under the strict molecular clock. We assumed the FBD model as a prior distribution for time trees with uniform prior distributions for turnover rate and fossil sampling proportion, log-normal prior distribution for net diversification rate with 95% highest probability density (HPD) interval covering estimated in (Jetz et al. 2012) and sampling at present probability fixed to one since all modern penguins were included in the analyses. We also analyzed this data set under the birth–death model without sampled ancestors (Stadler 2010).

In addition to analyzing the full data set, we performed a separate analysis of only living penguins and the crown fossils, to examine the effect of ignoring the diversification of fossil taxa along the stem lineage. Crown fossils were selected if the fossil lineage was a descendant of the MRCA of all extant species with a posterior probability greater than 0.05 in the full analysis (i.e., the analysis with stem and crown fossils). Thus, this analysis includes six fossils (listed in Table 1) and all living penguins. For this analysis we did not condition on recording only variable characters (i.e., we used the Mk model) because after removing a large proportion of stem fossils, some characters become constant.

Summarizing Trees

First, we summarized the posterior distribution of full trees using summary methods from (Heled and Bouckaert 2013). As a summary tree we used the maximum sampled-ancestor clade credibility tree (MSACC tree). An MSACC tree is a tree from the posterior sample that maximizes the product of posterior clade probabilities. Here, a clade denotes two types of objects. The first type is a monophyletic set of taxa with a bifurcation node as the MRCA. Such clades are completely defined by a set of taxon labels meaning that we do not distinguish between clades with the same taxon set but different topologies. The second type is a monophyletic set of taxa with a two-degree sampled node as the MRCA. This can happen when one of the taxa in the group is a sampled ancestor and it is ancestral to all the others in the clade. Then this taxon will be the MRCA of the whole group assuming it is an ancestor to itself. These clades are defined by the pair 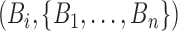where 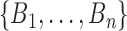are taxon labels and , , is the taxon that is ancestral to all taxa in the clade.

Second, we removed all fossil lineages from the posterior trees thereby suppressing two-degree nodes and then summarized the resulting trees (which are strictly bifurcating) with a maximum clade credibility tree with common ancestor ages. To assign a common ancestor age to a clade, we consider a set of taxa contained in the clade and find the age of the MRCAs of these taxa in every posterior tree (including the trees where these taxa are not monophyletic) and take the mean of these ages.

Results and Discussion

Model Comparison

For each of the eight analyses listed in Table 2, we plotted the probability of each fossil to be a sampled ancestor (Figure 1). This shows that assumptions about the clock and substitution models as well as the tree prior model contribute to identifying a fossil as a sampled ancestor. The comparison of the marginal likelihoods for different assumptions about the clock and substitution models shows that the substitution model where characters are partitioned in groups with the same number of states and with gamma variation in the substitution rate across characters is the best model for this data-set.

Figure 1.

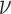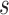Posterior probabilities of fossils to be sampled ancestors for eight models summarized in Table 2. In the legend, P stands for the partitioned model, G for gamma variation across characters, Mkv for conditioning on variable characters, R for relaxed clock model, dns for , , and tree prior parameterization, lmp for 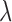, , and tree prior parameterization, and the numbers correspond to analyses in Table 2.

Posterior Predictive Analysis

The posterior predictive analysis did not reject the FBD process, where lineages evolve independently of each other, as an adequate model for describing the speciation–extinction–fossilization sampling process for these data. The values for all nine statistics were within the interval (Table 3). The plots of the posterior and posterior predictive distributions for several statistics (Fig. 2) show that there is no obvious discrepancy in these distributions. Thus, there is no signal in the data to reject a neutral diversification of penguins.

Figure 2.

The posterior and posterior predictive distributions for the tree length, 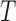, and genealogical statistics on the left and tree imbalance statistic and Colless’s tree imbalance index, 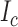, on the right for model 8 in Table 2. The plots do not show obvious discrepancy in the posterior and posterior predictive distributions of these statistics. The posterior predictive distribution for the branch length related statistics ( and ) is more diffuse than the posterior distribution although both distributions concentrate around the same area. The distributions of the tree imbalance statistics almost coincide.

In this analysis, we conditioned the posterior predictive distribution to have the given age ranges. To assess the overall fit of the FBD model, one needs to perform a posterior predictive analysis where the posterior predictive distribution is not conditioned on the age ranges nor on the number of sampled nodes. We have not performed such an analysis.

Penguin Phylogeny

The MSACC tree (Fig. 3) shows that most of the penguin fossils do not belong to the crown clade and that the crown clade Spheniscidae originated only 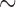12.7 Ma ago. The posterior probabilities of most clades including fossils are low, reflecting the large uncertainty in the topological placement of the fossil taxa, whereas many clades uniting extant taxa receive substantially higher posterior probabilities.

Figure 3.

An MSACC tree for the total-evidence analysis. The numbers at the bases of clades show the posterior probabilities of the clades. The filled circles represent sampled ancestors. Fossils with positive evidence of being sampled ancestors are shown in red (gray in printed version). Fossils Paraptenodytes antarcticus and Palaeospheniscus patagonicus both appear around the same time and have the same prior probabilities of 0.42 of being sampled ancestors but the morphological data provides positive evidence for the former to belong to a terminal lineage and for the latter to be a sampled ancestor. Penguin reconstructions used with permission from the artists: fossil species by Stephanie Abramowicz and extant penguin species by Barbara Harmon.

We calculated Bayes factors for all fossils to be sampled ancestors assuming the prior probability that a fossil is a sampled ancestor is defined by the tree prior model conditioned on the number of sampled extant and fossil species and assigned sampling intervals. Adding comparative (morphological and molecular) data to the sample size and sampling intervals provides positive evidence that the fossil taxa representing the species Palaeospheniscus patagonicus and Icadyptes salasi are sampled ancestors. Eretiscus tonnii, Marplesornis novaezealandiae, Paraptenodytes antarcticus, and Pygoscelis grandis show positive evidence to be terminal samples (Fig. 4).

Figure 4.

The evidence for fossils to be sampled ancestors. The samples above the shaded area (i.e., with log Bayes Factors greater than 1) have positive evidence to be sampled ancestors and below the shaded area (log Bayes factors lower than 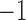) have positive evidence to be terminal nodes.

Due to the large uncertainty in the topological placement of fossil taxa, the relationships displayed in the summary tree are not the only ones supported by the posterior distribution. Thus, in some cases an alternate topology cannot be statistically rejected and a careful review of the entire population of sampled trees is required to fully account for this. Below, we summarize the features of the MSACC topology that differ from previous estimates of penguin phylogeny, keeping this uncertainty in mind.

The relationships within each genus are similar to those reported in previous parsimony analyses of the data-set (Ksepka et al. 2012), with some exceptions within the crested penguin genus Eudyptes. These agree with the results of Baker et al. (2006) based on Bayesian analysis of the same molecular loci (without morphological data), though it should be noted that our Bayesian analysis shows a degree of uncertainty in the resolution of the Eudyptes clade. The summary tree obtained after removing fossil taxa displays a different set of relationships within Eudyptes with high posterior probabilities (Fig. 5).

Figure 5.

The maximum clade credibility tree of extant penguins with common ancestor ages. The bars are the 95% HPD intervals for the divergence times. The mean estimates and 95% HPD intervals are summarized in Supplementary Table 4 available on dryad. The numbers at the bases of clades show the posterior probabilities of the clades (after removing fossil samples).

Allowing fossils to represent ancestors yields several interesting results. Although there is no evidence in comparative data to support an ancestral position for Spheniscus muizoni (Fig. 4) the combined comparative and temporal data yields the posterior probability of 0.61 that it is an ancestor of the extant Spheniscus radiation (i.e., in 61% of the posterior trees, this taxon is a direct ancestor of the four extant Spheniscus species and possibly some other species as well). The ancestral position is consistent with the morphological data set: S. muizoni preserves a mix of derived character states that support placement within the Spheniscus clade and primitive characters which suggests it falls outside the clade formed by the four extant Spheniscus species. Furthermore, at least for the discrete characters sampled, it does not exhibit apomorphies providing direct evidence against ancestral status.

Madrynornis mirandus is recovered as ancestor to the Eudyptes + Megadyptes clade, though this placement receives low posterior probability (0.15). This fossil taxon was inferred as the sister taxon to Eudyptes by several previous studies (Hospitaleche et al. 2007; Ksepka and Clarke 2010; Ksepka et al. 2012); though see (Chavez Hoffmeister et al. 2014), and so had been recommended as a calibration point for the Eudyptes–Megadyptes divergence (Ksepka and Clarke 2010) and used as such (Subramanian et al. 2013). In our analysis, a Megadyptes + Eudyptes clade excluding Madrynornis is present in all posterior trees, that is, the results reject the possibility that this taxon is the sister taxon to Eudyptes and its use as a calibration point is in need of further scrutiny. Our results indicate a 0.9 posterior probability that M. mirandus belongs in the crown, but do not provide solid support for the precise placement of this fossil taxon. Presumably the position of M. mirandus outside of Eudyptes + Megadyptes clade is at least partially attributable to the temporal data—its age means a more basal position is more consistent with the rest of the data.

Most of the clades along the stem receive very low posterior probabilities, which is not unexpected given that some stem penguin taxa remain poorly known, with many morphological characters unscorable. These clades correspond to the large polytomies from Ksepka et al. (2012) (polytomies are not allowed in the summary method we used here). Of particular note is the placement of Palaeospheniscus bergi and Palaeospheniscus biloculata on a branch along the backbone of the tree leading to all modern penguin species. Palaeospheniscus penguins share many synapomorphies with crown penguins and only a single feature in the matrix (presence of only the lateral proximal vascular foramen of the tarsometatarsus) contradicts this possibility (and supports their forming a clade with E. tonnii in the strict consensus of Ksepka et al. 2012). The posterior distribution of our analysis supports a clade containing the three Palaeospheniscus species and E. tonnii with probability 0.06, and so this relationship cannot be ruled out.

Overall, the estimated clades with large posterior probabilities (greater than 0.5) agree with those clades previously estimated from the same data set using parsimony methods (Ksepka et al. 2012). Low posterior probability values are due to the sparse morphological data (and complete lack of molecular data) for many early stem taxa. Several species such as Palaeeudyptes antarcticus are based on very incomplete fossils, in some cases a single element, and so we view the relationships estimated for deep stem penguins as incompletely established for the time being. Despite the high degree of uncertainty in the phylogenetic relationships of fossil species, the overall support for the general scenario placing most fossil penguins along the stem with a recent appearance of crown penguins is strong. To better describe, measure, and visualize the topological uncertainty of total-evidence analyses, methods similar to Billera et al. (2001), Owen and Provan (2011), and Gavryushkin and Drummond (2016) should be developed for serially sampled trees with sampled ancestors.

Divergence Dates

We estimated the divergence dates for extant penguins (Fig. 5 and Table 4 Supplementary available on dryad). In general, the estimates are younger than those reported in previous studies: (Baker et al. 2006; Brown et al. 2008; Subramanian et al. 2013; Jarvis et al. 2014; Li et al. 2014). Baker et al. (2006) used the penalized-likelihood approach (Sanderson 2002) with secondary calibrations, and estimated the origin of crown penguins to be 40.5 Ma (95% confidence interval: 34.2–47.6 Ma). Brown et al. (2008; Fig. 4) estimated this age at 50 Ma using a Bayesian approach with uncorrelated rates and 20 calibrations distributed through Aves, including the stem penguin Waimanu manneringi. Subramanian et al. (2013) estimated a much younger crown age by using a Bayesian analysis with node calibration densities based on four fossil penguin taxa: W. manneringi, M. mirandus, S. muizoni, and P. grandis. Their estimate of the age of the MRCA of the extant penguins was 20.4 Ma (95% HPD interval: 17–23.8 Ma) (Subramanian et al. 2013). Most recently, (Jarvis et al. 2014; Li et al. 2014) estimated the age of the crown penguins at 23 Ma (95% confidence interval: 6.9–42.8 Ma) using a Bayesian method in MCMCTree (Dos Reis and Yang 2011) based on genomes from two penguin species (Aptenodytes forsteri and Pygoscelis adeliae) and calibrations for higher avian clades including W. manneringi. Notably, this last date can be considered applicable to the crown only if Aptenodytes or Pygoscelis is the sister taxon to all other penguins, otherwise this date applies to a more nested node, implying an older age for the crown.

Our total-evidence analysis under the FBD model suggests that the MRCA is younger than any of these previous estimates at 12.7 Ma (95% HPD interval [9.9, 15.7]; see Fig. 5 and Table 4 Supplementary available on dryad). We assert that this is the best constrained estimate of the age of the penguin crown clade to date, because it avoids potential pitfalls related to the use of secondary calibrations, samples all extant species, and most importantly includes all reasonably complete fossil taxa directly as terminals or sampled ancestors. This final point is crucial, not only because including fossils as terminals has been shown influence phylogenetic accuracy under many conditions (e.g., Hermsen and Hendricks 2008; Grande 2010; Hsiang et al. 2015), but also because at least one fossil taxon—previously used as a node calibration—was recovered at a more basal position in our results. The small gap between our 12.7 Ma estimate for the MRCA of extant penguins and the oldest identified crown fossil at 10 Ma is consistent with the fossil record of penguins as a whole, which includes a dense sampling of stem species from 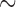60 to 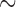10 Ma, and only crown fossils from 10 Ma onwards. Moreover, our results suggest many extant penguin species are the product of recent divergence events, with 13 of 19 sampled species splitting from their sister taxon in the last 2 myr. Penguins have a relatively dense fossil record compared to other avian clades, with thousands of specimens known from four continents and spanning nearly the entirety of their modern day geographical range. If crown penguins originated at 20–50 Ma as implied by previous studies, it would require major ghost lineages (Clarke et al. 2007; Clarke and Boyd 2014), and thus a modest to extreme fossilization bias favoring the preservation of stem penguin fossils and disfavoring the preservation of crown penguin fossils. Such a bias is difficult to envision, as both stem and crown penguins share a dense bone structure and preference for marine habitats that would suggest similar fossilization potential.

Inclusion of stem fossil diversity has a profound impact on the inferred age of the penguin crown clade. To demonstrate this effect, we performed a total-evidence analysis including only living penguins and crown fossils (i.e., fossil taxa identified as crown penguins in our primarily analysis). Both the age estimate and the inferred uncertainty in the MRCA age of crown penguins increased substantially with the MRCA age shifting to 22.8 Ma (95% HPD interval: 14.2–33.6 Ma; Fig. 5). This shows that including the stem-fossil diversity allows for a better estimate of the crown age of penguins—one that is more consistent with the fossil record. Furthermore, these additional data points contribute to better estimates of diversification parameters.

For the complete analysis of stem and crown taxa, the mean estimate of the net diversification rate, , was 0.039 with [0.002, 0.089] HPD interval although this estimate is sensitive to the prior distribution (Supplementary Fig. 2 available on dryad), the turnover rate, , was 0.88 ([0.72, 1]) and the sampling proportion, 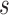, was 0.23 ([0.06, 0.43]).

The posterior distribution for the scale parameter of the log-normal distribution in the uncorrelated relaxed clock model for the molecular alignment was bimodal with a mode around 0.4 and a mode around zero. This suggested a strict molecular clock model might fit the data. The additional analysis of this data set under the strict molecular clock slightly shifted the estimates of the time of the MRCA of crown penguins toward the past although the posterior intervals largely overlap (Fig. 6).

Figure 6.

The ages of the MRCAs of the extant penguin taxa for the eight analyses (Table 2) of morphological data, total-evidence analysis with all fossils under relaxed (8DNA R) and strict (8DNA S) molecular clocks, total-evidence analysis under the birth–death model without sampled ancestors (8BDDNA R), and total-evidence analysis with crown fossils only. Abbreviations in the names of analyses are the same as in Figure 1.

Using the birth–death sampling model without sampled ancestors (Stadler 2010) instead of the FBD model shifted the estimated divergence times toward the past (Fig. 6 and Supplementary Fig. 1 available on dryad). Gavryushkina et al. (2014) showed in simulation studies that ignoring sampled ancestors results in an increase in the diversification rate. We can observe the same trend here: the mean of the net diversification rate for the analysis under the birth–death model without sampled ancestors was 0.092 (95% HPD: [0.007, 0192]) compared to 0.039 ([0.002, 0.089]) for the FBD model. Although we would expect a decrease in the diversification rate in older trees on the same number of extant tips, in the birth–death model without sampled ancestors, a sampling event causes an extinction of the lineage. Thus, the diversification rate (here, modeled as the difference in the birth and death rates) does not account for the extinction “by sampling”. The mean estimate for 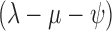, which better describes the diversification rate in the birth–death model without sampled ancestors, was 0.019 ([0.061, 0.099]).

Implications for Crown Penguin Evolution

With many extant penguin species inhabiting extreme polar environments, penguin evolution is often considered through the lens of global climate change. The fossil record has revealed that, despite their celebrated success in modern polar environments, penguins originated during a warm period in Earth’s history, and the first Antarctic penguins were stem taxa that were distantly related to extant Antarctica species and arrived on that landmass prior to the formation of permanent polar ice sheets (Ksepka et al. 2006). However, our divergence estimates are consistent with global cooling having a profound impact on later stages of crown penguin radiation. The Middle Miocene Transition at 14 Ma marks the onset of a steady decline in sea surface temperature, heralding the onset of full-scale ice sheets in Antarctica (Zachos et al. 2001; Hansen et al. 2013; Knorr and Lohmann 2014). Expansion of Antarctic ice sheets may have opened a new environment for Aptenodytes and Pygoscelis, the most polar-adapted penguin taxa (including four of the five species that breed in continental Antarctica). Previous studies have placed Aptenodytes and Pygoscelis on basal branches of the penguin crown, leading to the hypothesis that crown penguins originated in Antarctica and spread to lower latitudes as climate cooled (Baker et al. 2006). However, the geographical distribution of stem fossils suggests instead that Aptenodytes and Pygoscelis secondarily invaded Antarctica, taking advantage of a novel environment (Ksepka et al. 2006). Our analysis provides additional support for this secondary colonization hypothesis by uniting Aptenodytes and Pygoscelis as a clade and revealing a very recent age for this Antarctic group at 9.8 Ma (Fig. 5), indicating they did not radiate until well after permanent ice sheets were established.

Morphological Clock

We assume that clock models can be applied to morphological data. A recent study by Lee et al. (2014a) confirms that younger taxa undergo more morphological evolutionary change. Most previous total-evidence or morphological analyses used relaxed clock models for morphology evolution (Pyron 2011; Ronquist et al. 2012a; Lee et al. 2014a, 2014b; Dembo et al. 2015; Zhang et al. 2016). In many studies (Beck and Lee 2014; Lee et al. 2014a; Dembo et al. 2015), including this study, model comparison analyses favored a relaxed morphological clock over a strict morphological clock.

The estimated coefficient of variation for the log-normal distribution of the morphological clock rates in the penguin analysis was 1.15 indicating a high rate variation among the branches. However, in our analysis, the choice of the morphological clock model did not influence much the estimate of the parameter of the primary interest—the age of the crown radiation. Using the relaxed clock model as opposed to the strict clock model only slightly shifted the age toward the past and inflated the 95% HPD interval (Fig. 6, analyses 7 and 8).

Many total-evidence analyses inferred implausibly old divergence dates (Ronquist et al. 2012a; Slater 2013; Wood et al. 2013; Beck and Lee 2014). Beck and Lee (2014) suggested that oversimplified modeling of morphological evolution and a relaxed morphological clock may result in overestimated divergence times. Our analysis did not show this and we, on the contrary, estimated a much younger age of the crown penguin radiation than had been previously estimated. This could be attributed to the large number of stem fossils in our analysis, given that excluding these fossils leads to a much older estimate. The overestimated ages can also be explained by sampling biases (Zhang et al. 2016) or using inappropriate tree prior models. Using a birth–death model without sampled ancestors in our analysis slightly shifted the ages of the crown divergences toward the past (Fig. 6 and Supplementary Fig. 1 available on dryad).

Sampled Ancestors

We examined the total posterior probability of a fossil species to be a sampled ancestor, that is, a direct ancestor to other sampled fossil or extant species. If an ancestor–descendant pair is in question, one can also estimate the posterior probability of one species to be an ancestor to another species or a group of species as we calculated in the case of the probability of the S. muizoni representing an ancestor of extant Spheniscus radiation.

The evidence for ancestry comes from morphological data, fossil occurrence times and prior distributions for the parameters of the FBD model and morphological evolution model. Here, we used uniform prior distributions except for the net diversification rate and morphological evolution rate.

The analysis of the penguin data set shows a large number of potential sampled ancestors. The Bayes factors calculated here showed the ancestry evidence contained in the morphological data. The evidence coming from the occurrence times or from all data together remains to be assessed. We hypothesize that the large number of sampled ancestors is due to the temporal pattern of the penguin fossils. We additionally analyzed dinosaur (Lee et al. 2014b), trilobite (Congreve and Lieberman 2011), and Lissamphibia (Pyron 2011) data-sets with large proportions of missing characters where we only detected up to four sampled ancestors (out of 40–120 fossils; data not shown). An analysis by Zhang et al. (2016) of Hymenoptera also did not show many sampled ancestors. Thus, the abundance of sampled ancestors in the penguin phylogeny is not likely to be due to the paucity of the morphological data.

Further Improvements

Here we used the FBD model, which is an improvement over previously used uniform, Yule, or birth–death models for describing the speciation process. However, other more sophisticated models may improve the inference or fit better for other data sets. The skyline variant of the FBD model (Stadler et al. 2013; Gavryushkina et al. 2014; Zhang et al. 2016) allows for stepwise changes in rates (i.e., diversification, turnover, and fossil sampling) over time. Accounting for the possibility of changes in fossil sampling rate, 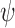, over time might be important for analyses considering groups of deeply diverged organisms where poor fossil preservation may result in underestimates of divergence times if the sampling rate is considered constant. Furthermore, models that allow age-dependent (Lambert 2010; Hagen et al. 2015) or lineage-dependent (Maddison et al. 2007; Alfaro et al. 2009; Alexander et al. 2016) speciation and extinction rates while appropriately modeling fossil sampling may also improve divergence dating and estimation of macroevolutionary parameters.

Another direction of method development is modeling morphological character evolution—a topic that has sparked numerous debates (e.g., Goloboff 2003; Spencer and Wilberg 2013). A recent study by Wright and Hillis (2014) showed that Bayesian methods for estimating tree topologies using morphological data—even under a simple probabilistic Lewis Mk model—outperform parsimony methods, partly because rate variation is modeled. Here, we considered two schemes to assign a number of possible states to a character. The model comparison analysis favored the model where the number of possible states is equal to the number of observed states in a character. A more accurate modeling would be to consider each character and assign the number of states on the basis of the character description (e.g., characters for traits that are either present or absent will be assigned two states) or use model averaging within an MCMC analysis where each character is assigned different number of states during the MCMC run. Moreover, it may also be important to appropriately model ascertainment bias when using the Lewis Mk model. These extensions include accounting for the absence of invariant and parsimony uninformative characters in the morphological data matrix (Koch and Holder 2012). Importantly, more biologically appropriate models of phenotypic characters are needed to advance phylogenetic methods for incorporating fossil data (e.g., Felsenstein 2005; Revell 2014). The total-evidence method with FBD can also be used to estimate the past evolutionary relationship between extinct species where only morphological data is available (Lee et al. 2014a).

We assigned age ranges to different fossils in differing ways. Some of the fossil species are known from only one fossil specimen and in this case, we assigned the age range based on the uncertainty related to the dating of the layer in which the fossil was found. For other species, there are a number of fossils found in different localities. In this case, we derived the age interval from probable ages of all specimens. In order to strictly follow the sampling process assumed by the FBD model, it would be necessary to treat every known fossil specimen individually and include all such specimens into an analysis. Unfortunately, this would lead to enormous data sets with thousands of taxa, most with very high proportions of missing data. However, in cases where a large number of fossils are known from the same locality and are thus very close in age and potentially belong to the same population, this group of fossils may be treated as just one sample from the relevant species at that time horizon. Such improved modeling would require devoting considerable effort to differentiating fossils and recording characters for particular specimens, rather than merging morphological data from different fossil specimens believed to belong to the same species. This could, however, lead to more accurate inference and better understanding of the past diversity.

Finally, our analysis focused on a matrix sampling all fossil penguins represented by reasonably complete specimens. Many poorly known fossil taxa have also been reported, along with thousands of isolated bones. Finding a balance between incorporating the maximum number of fossils, which inform sampling rate and time, and the computational concerns with adding large numbers of taxa with low proportions of informative characters will represent an important challenge for analyses targeting penguins and other groups with extensive fossil records.

We advocate the use of the total-evidence approach with models that allow sampled ancestors when estimating divergence times. This approach may offer advantages not only over node calibration methods that rely on first analyzing morphological data to identify calibration points and then calibrating phylogenies with ad hoc prior densities, but also over total-evidence methods that do not account for fossils that are sampled ancestors. Many recent applications of total-evidence dating have yielded substantially older estimates than node calibration methods (e.g., Ronquist et al. 2012a; Slater 2013; Wood et al. 2013; Beck and Lee 2014; Arcila et al. 2015). Among other explanations (Beck and Lee 2014; Zhang et al. 2016), using tree priors that do not account for sampled ancestors could have contributed to the ancient dates.

Supplementary Material

Data available from the Dryad Digital Repository: http://dx.doi.org/10.5061/dryad.44pf8.

Funding

This work was partially supported by Marsden grant UOA1324 from the Royal Society of NZ [U0A1324 to A.G., D.W., and A.J.D.]; a Rutherford Discovery Fellowship from the Royal Society of New Zealand [to A.J.D.]; the European Research Council under the Seventh Framework Program of the European Commission [PhyPD: grant agreement number 335529 to T.S., in part]; and a US National Science Foundation grant [DEB-1556615 to T.A.H. and D.T.K.].