Predictive Models of Spatial Transcriptional Response to High Salinity^,

Organ transcriptional response to high salinity is regulated by a core set of pCREs.

Abstract

Plants are exposed to a variety of environmental conditions, and their ability to respond to environmental variation depends on the proper regulation of gene expression in an organ-, tissue-, and cell type-specific manner. Although our knowledge of how stress responses are regulated is accumulating, a genome-wide model of how plant transcription factors (TFs) and cis-regulatory elements control spatially specific stress response has yet to emerge. Using Arabidopsis (Arabidopsis thaliana) as a model, we identified a set of 1,894 putative cis-regulatory elements (pCREs) that are associated with high-salinity (salt) up-regulated genes in the root or the shoot. We used these pCREs to develop computational models that can better predict salt up-regulated genes in the root and shoot compared with models based on known TF binding motifs. In addition, we incorporated TF binding sites identified via large-scale in vitro assays, chromatin accessibility, evolutionary conservation, and pCRE combinatorial relationships in machine learning models and found that only consideration of pCRE combinations led to better performance in salt up-regulation prediction in the root and shoot. Our results suggest that the plant organ transcriptional response to high salinity is regulated by a core set of pCREs and provide a genome-wide view of the cis-regulatory code of plant spatial transcriptional responses to environmental stress.

Plants are equipped with a wide range of mechanisms to respond to environmental stresses such as excess heat, salinity, drought, and pathogen attack (Bostock et al., 2014; Rasheed et al., 2016). These stress response mechanisms are indispensable for plant survival and have a significant spatial component whereby organs and tissues respond differently to environmental changes (Cramer et al., 2011; Gargallo-Garriga et al., 2014; Pierik and Testerink, 2014). In the case of high-salinity stress (referred to as salt stress), after perceiving an increase in soil salt concentration, the primary physiological response of the root is to exclude sodium from the xylem and to send hormonal signals of stress to the shoot, while the shoot must respond to the effects of ion toxicity and water limitation (Munns, 2002; Munns and Tester, 2008). In addition to physiological changes that are spatially specific, it is well documented that differential gene expression under stress conditions can be regulated in a highly organ- and tissue-specific manner (Kreps et al., 2002; Kilian et al., 2007; Dinneny et al., 2008; Geng et al., 2013), which ultimately impacts plant development and physiology.

Spatially and conditionally specific gene expression is expected to be subject to the control of transcriptional regulatory machineries, including transcription factors (TFs) and their associated cis-regulatory elements (CREs). Currently, TFs and their corresponding CREs regulating the stress response have received considerable attention (Seki et al., 2002; Haberer et al., 2011; Qin et al., 2011), but our knowledge of the spatial regulation of the stress response is limited. CREs can be identified based on coexpression (Beer and Tavazoie, 2004; Priest et al., 2009; Wang et al., 2009; Zou et al., 2011; Austin et al., 2016) and/or through in vitro and in vivo TF binding experiments (Harbison et al., 2004; Franco-Zorrilla et al., 2014; Weirauch et al., 2014; O’Malley et al., 2016). The coexpression approach has been used successfully to identify putative cis-regulatory elements (pCREs) regulating stress-responsive gene expression in yeast (Saccharomyces cerevisiae; Beer and Tavazoie, 2004) and in Arabidopsis (Arabidopsis thaliana; Zou et al., 2011). In addition, pCREs are overrepresented in the 1-kb regions upstream of tissue- and cell type-specifically expressed genes (Jiao et al., 2009). Although some of these pCREs are similar to the binding sequences of TFs known to regulate stress-responsive genes (Jiao et al., 2009), it remains unclear how they may be relevant to spatial stress response regulation.

One computational approach for assessing the relevance of pCREs is to ask how well they can be used to establish a computational model predictive of the transcriptional response to stress (Zou et al., 2011; Yáñez-Cuna et al., 2013). Such a model is referred to as the cis-regulatory code (CRC), which is defined as the sets of CREs involved in gene regulation in a particular environment, location, or time (Zou et al., 2011; Yáñez-Cuna et al., 2013). One major conclusion from CRC studies is that TFs frequently regulate gene expression patterns in combination. For example, in yeast, the identification of CREs through TF binding data uncovered a complex regulatory code involving combinations of multiple CREs (Harbison et al., 2004). In humans, genes expressed in specific tissues are regulated by particular combinations of TFs and CREs (Hu and Gallo, 2010). In Arabidopsis, CRCs based on pCRE combinations resulted in more precise predictions of salt stress up-regulated genes (Zou et al., 2011) than using individual CREs. CRCs can potentially be further improved by knowledge of TF binding. For example, computational models considering in vitro TF binding site information, sequence conservation, DNA structure, and/or chromatin accessibility were shown to be predictive of in vivo TF binding in mouse (Zhong et al., 2013) and in yeast (Tsai et al., 2015). Tissue-specific TF binding also was predicted using information about binding motifs and histone modifications (McLeay et al., 2011). These examples highlight the relevance and utility of CRCs and the integration of multiple relevant data sets for understanding the mechanisms underlying the genome-wide spatial transcriptional response to stress. However, such a spatial response CRC is not available.

The goal in this study was to uncover the CRCs underlying the spatially specific transcriptional response to stress using plants as a model. Specifically, we focused on the CREs relevant to salt stress response in the aboveground (shoot) and the belowground (root) parts of Arabidopsis. Salt stress was chosen because it is well studied both physiologically (Munns, 2002; Munns and Tester, 2008) and molecularly (Zhu, 2002; Golldack et al., 2011) and because there are documented differences in the transcriptional response to salt in the root and shoot (Kreps et al., 2002; Kilian et al., 2007). Additionally, there are known TFs and CREs for salt stress (Golldack et al., 2011; Matiolli et al., 2011; Mizoi et al., 2012; Nakashima et al., 2012) that could be used to verify our results. To assess the transcriptional changes in response to salt stress across different organs in Arabidopsis, we first asked how the functional annotations of salt up-regulated genes in roots and shoots differed. Next, to determine how well current knowledge of TF binding sites in Arabidopsis can explain spatial salt up-regulation, we used motifs and binding sites identified through two large-scale in vitro studies (Weirauch et al., 2014; O’Malley et al., 2016) to generate models of root and shoot salt up-regulation. We then identified additional pCREs using a coexpression approach to assess if these newly identified pCREs allowed better predictions of the spatial response to salt stress. We tested pCREs to see if they could be used individually to establish a cis-regulatory model explaining spatial patterns of up-regulation during salt stress. To evaluate whether we could further improve spatial salt stress response prediction, we filtered pCRE sites according to information about in vitro TF binding (Weirauch et al., 2014; O’Malley et al., 2016), chromatin accessibility, and conserved noncoding regions (Haudry et al., 2013). Lastly, we built prediction models using combinations of pCREs.

RESULTS AND DISCUSSION

Transcriptional Responses to Stress Have a Strong Spatial Component

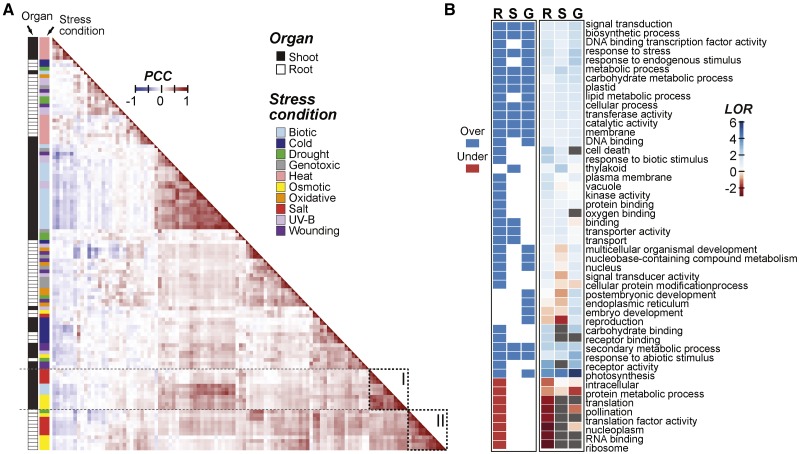
Earlier global gene expression studies have demonstrated that different plant organs have distinct transcriptional responses to stress (Kreps et al., 2002; Kilian et al., 2007; Dinneny et al., 2008; Geng et al., 2013). To assess the extent to which organs have unique expression patterns under different stress conditions and to determine the similarities between organ (root versus shoot) stress responses, we determined the correlations between the levels of differential expression across multiple conditions and time points using two types of existing data sets: (1) root and shoot samples under abiotic stress (Kilian et al., 2007) and (2) shoot samples under biotic stress (see “Materials and Methods”). There were several patterns worth noting. First, samples for related stress conditions tended to cluster together, and these stress condition clusters tended to have root and shoot subclusters (Fig. 1A). For example, osmotic and salt stress samples formed a cluster with subclusters composed of shoot and root samples (dotted rectangles I and II, respectively, in Fig. 1A).

Figure 1.

Arabidopsis gene expression correlation across stress data sets and Gene Ontology (GO) terms enriched in salt-responsive genes. A, Between-sample Pearson’s correlation coefficient (PCC) calculated based on log₂ fold change (log₂[stress treatment/control]) of genes in shoot and root samples under each stress condition/treatment duration combination. The orders of rows and columns are the same, and they are sorted based on hierarchical clustering of the pairwise PCC values. Dotted rectangles I and II highlight osmotic and salt stress clusters, respectively. B, Heat map indicating GO slim terms significantly overrepresented (blue) or underrepresented (red) in genes that are differentially up-regulated during salt stress after 3 h in root only (R), shoot only (S), or globally in both organs (G; log₂ fold change > 1, P ≤ 0.05). The heat map at right summarizes the log₂ odds ratio (LOR) from the enrichment test (gray, LOR cannot be calculated).

The median PCC for the log₂ fold-change values between samples from the same organ but different stress conditions (median PCC = 0.17) was significantly lower than between samples from the same stress condition but different organs (median PCC = 0.31; Mann-Whitney, P < 2.2e-16). Thus, the stress condition has much more of an impact on overall expression pattern than organ identity. Nonetheless, under some stress conditions, there were stronger organ-specific effects. For example, the salt stress response correlations between organs (median PCC = 0.24) were significantly lower those between samples from the same organ (median PCC = 0.69; Mann-Whitney, P < 2.2e-16). Taken together, our findings are consistent with earlier studies (Kreps et al., 2002; Dinneny et al., 2008; Geng et al., 2013) that found that, while there is a specific transcriptional response to each stress, this response is further influenced by the organ where genes are expressed. In the following sections, we focus on the spatial response to high-salinity (salt) stress.

Given that the stress response is influenced by spatial considerations, we next assessed what types of genes based on GO terms tend to be differentially up-regulated in the root and shoot during salt stress using enrichment analysis (see “Materials and Methods”). Three sets of significantly salt up-regulated genes were defined: (1) global, 246 genes up-regulated in both the root and the shoot; (2) root specific, 1,854 genes up-regulated only in the root; and (3) shoot specific, 276 genes up-regulated only in the shoot. There were 48 GO terms significantly overrepresented/underrepresented in one or more of the gene sets defined above (Fig. 1B). For example, thylakoid and plastid terms were overrepresented among shoot-specifically up-regulated genes, consistent with an earlier finding that photosynthesis is significantly impacted by salt stress (Chaves et al., 2009). Among the GO terms, signal transduction and response to stress were overrepresented in all three gene sets (Fig. 1B). Since these three gene sets are mutually exclusive, this result suggests that, in the root and the shoot, unique signaling pathway genes are up-regulated, as are pathways that are globally necessary for the stress response. This result is supported by work on the SOS pathway, which involves components that are common to both organs as well as those specific to the root and shoot (Zhu, 2002; Ji et al., 2013). Interestingly, DNA binding TF activity and DNA binding were enriched only among the root-specifically and globally up-regulated genes. This suggests that there is a set of global TFs and another set specific to the root. In addition, genes up-regulated in the root may be regulated by both a global and a root-specific set of TFs, whereas genes up-regulated in the shoot may be regulated primarily by a global TF set. This possibility is explored further below.

To summarize, a variety of functional categories were found to be enriched in genes up-regulated by salt stress. In some instances, root-specifically, shoot-specifically, and globally up-regulated genes had the same enriched functional categories. These common enriched terms suggest that roots and shoots up-regulate similar types of genes. However, there are also genes up-regulated in an organ-specific manner that may be regulated by distinct sets of up-regulated TFs. The TFs that are specifically up-regulated in roots may help to explain the differences in expression pattern that we observe between the roots and shoots under salt stress. For example, the root-specifically up-regulated genes may be controlled by the root-specific TFs. Because TFs may differ in the CREs they bind, and because there are substantial amounts of in vitro TF-DNA interaction data in Arabidopsis (Weirauch et al., 2014; O’Malley et al., 2016), we next examined whether known TF binding data are associated with organ-specific, salt-induced gene expression.

A Model Incorporating Known TF Binding Motifs Performs Better Than a Random Model in Predicting Salt Up-Regulation

Because TFs exert their regulatory roles by binding to CREs, we expected that the global and organ-specific activities of TFs would be reflected in the types of CREs that are found in the regulatory regions of global, root-specific, and shoot-specific salt up-regulated genes. We hypothesized that each organ had a different set of CREs regulating salt stress up-regulated genes and that these CREs could be used to construct CRCs that are models for predicting stress-responsive gene expression (Zou et al., 2011). To test these hypotheses, we collected Arabidopsis TF binding data from two large-scale in vitro studies, Catalog of Inferred Sequence Binding Preferences (CIS-BP; Weirauch et al., 2014) and DNA Affinity Purification Sequencing (DAP-seq; O’Malley et al., 2016), that evaluated the binding sites of 758 TFs (Supplemental Table S1). Given the extensive coverage of TFs, we expected that these data sets would cover a significant number of cis-regulatory sequences relevant for controlling root and/or shoot up-regulated genes. Here, the root up-regulated genes were defined as the union of the root-specifically and globally (in both root and shoot) up-regulated genes under high-salinity treatment. Similarly, the shoot up-regulated genes were the union of the shoot-specifically and globally up-regulated genes.

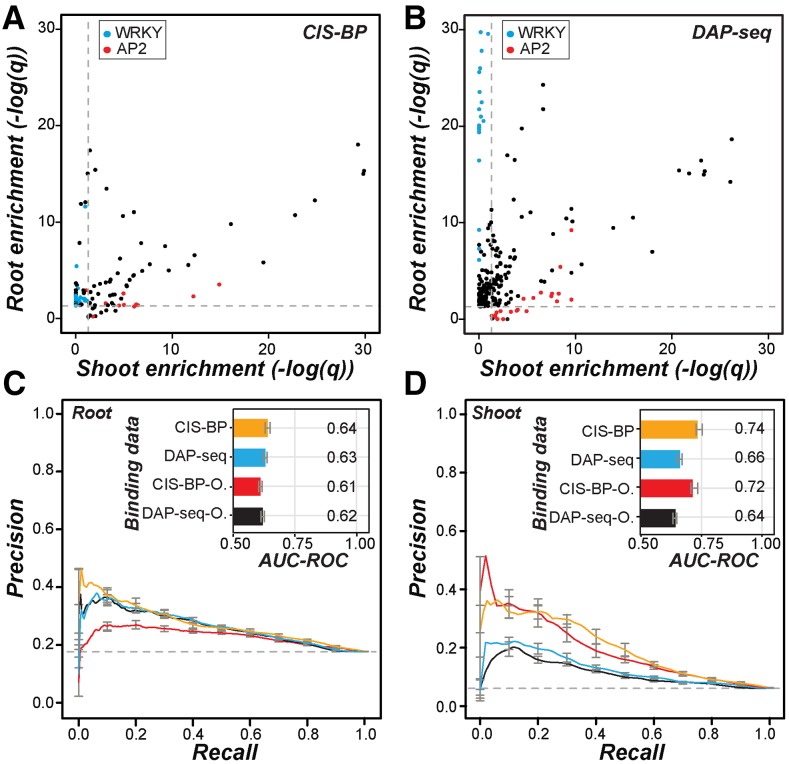
We first asked if the TF binding sites predicted based on the CIS-BP data and the binding sites inferred from DAP-seq peaks were significantly overrepresented in the putative promoter regions, within 1 kb upstream of transcriptional start sites (TSS), of root and shoot up-regulated genes. Among binding site information for 758 TFs, we found that the binding sites of 262 and 397 TFs were significantly overrepresented in the putative promoters of root and shoot up-regulated genes, respectively, compared with nonresponsive genes. Overall, we found that if the CIS-BP TF binding sites were enriched in the promoter regions of root up-regulated genes, the same sites also tended to be enriched among shoot up-regulated genes (enrichment score PCC = 0.88, P = 9.20e-42; Fig. 2A). This also was the case when DAP-seq data were used, but to a much lesser degree (PCC = 0.25, P = 2.27e-04; Fig. 2B). This finding suggests that some cis-regulatory sites are common between root and shoot up-regulated genes. Nonetheless, the correlations were not perfect, suggesting that some CIS-BP TF and DAP-seq binding sites are differentially enriched between up-regulated genes in root and shoot. Consistent with this notion, the binding sites of some TF families were enriched in an organ-specific manner. For example, WRKY binding sites were overrepresented only in root up-regulated genes, and AP2 sites were overrepresented mostly in shoot up-regulated genes (Fig. 2, A and B). Next, to assess the extent to which known TF binding data explain the organ-specific response, we established CRCs with machine learning methods to predict whether a gene is up-regulated or nonresponsive to salt stress in the root or shoot based on the presence and absence of CIS-BP transcription factor binding motifs (TFBMs) or DAP-seq sites in the putative promoter regions (see “Materials and Methods”).

Figure 2.

Overrepresentation of known TF binding sites in organ salt up-regulated genes and performance of in vitro TF binding data in predicting salt up-regulation. A, Scatterplot of the enrichment score [–log(q)] of CIS-BP TFBM sites in the promoters of root (y axis) and shoot (x axis) up-regulated genes compared with nonresponsive genes. Each point is for one TFBM. Blue, WRKY family TFs; red, AP2 family TFs. Dotted lines indicate the q value threshold at 0.05. B, As in A but using DAP-seq data. Each point is for one TF. C, Precision-recall curves and AUC-ROCs (inset) of CRCs predicting root up-regulated genes using CIS-BP TFs (orange) or DAP-seq TFs (blue). O, CIS-BP and DAP-seq sites overrepresented among root up-regulated genes indicated in red and black, respectively. The colors of the precision-recall curves correspond to the colors for binding data subsets in the AUC-ROC bar chart. Error bars correspond to the se from 10-fold cross-validation for each model. D, As in C but for shoot up-regulated genes.

We used two approaches to evaluate CRC model performance. The first is area under curve-receiver operating characteristic (AUC-ROC), where a perfect model would have AUC-ROC = 1 and random predictions would lead to AUC-ROC = 0.5. The second approach is the precision-recall curve, where precision is the proportion of correctly predicted genes that are up-regulated in an organ and recall is the proportion of truly up-regulated genes in an organ that are correctly predicted. Better models would have precision-recall curves tending more toward the top right corner of the graph, and random predictions would be no better than the background (dotted lines in Fig. 2, C and D). The model built with all CIS-BP or DAP-seq binding site data made better predictions than randomly expected in the root and in shoot (Fig. 2, C and D), indicating that, as expected, these TF binding data contain relevant regulatory information for root and shoot salt up-regulation. Consistent with the expectation that only a subset of TFs would be involved in the organ-specific up-regulation, models using binding data of TFs with overrepresented numbers of binding sites in salt up-regulated genes resulted in similar performance to models using data for all TFs with binding sites overrepresented in either the root or shoot (Fig. 2, C and D). In addition, models based on binding sites of TFs that were not overrepresented performed poorly (AUC-ROC = 0.54–0.56).

Although the in vitro TF binding data sets are extensive, binding information is available only for ∼38% of the known Arabidopsis TFs (Weirauch et al., 2014; Barah et al., 2016; O’Malley et al., 2016); thus, some relevant CREs might not be included in the models. In addition, it is worth noting that the performance of models for root salt up-regulated genes is not as good as that of models for shoot salt up-regulated genes (Fig. 2, C and D). Thus, to improve our understanding of what CREs are associated with salt up-regulation and how these CREs may influence salt up-regulation in the root and shoot, we next identified putative CREs based on coexpression and assessed how the regulatory logic differs between the root and shoot salt up-regulation.

pCREs Derived from Coexpression Clusters Are Similar, But Not Identical, to Known TFBMs

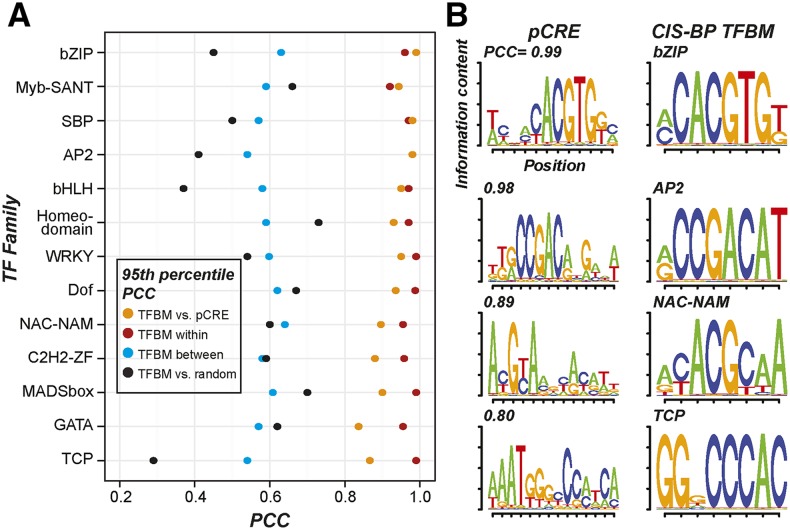
We hypothesized that motifs identified through coexpression clustering would provide additional spatial response regulatory information compared to the large-scale TF in vitro binding data (Weirauch et al., 2014; O’Malley et al., 2016). To test this, we identified 1,894 pCREs overrepresented in the putative promoters of root and/or shoot salt up-regulated genes found in coexpression clusters defined based on the stress fold-change data (see “Materials and Methods”; Supplemental Table S2). Next, we asked if the pCREs identified based on coexpression were similar to CIS-BP and DAP-seq TFBMs (Weirauch et al., 2014; O’Malley et al., 2016). We calculated the PCC values of the position weight matrices (PWMs) of all pCRE and TFBM motif pairs to find the best matching pCRE-TFBM pairs, where lower PCC values indicate diminishing similarity (Fig. 3A). Three criteria were used to determine whether a pCRE-TFBM pair had significant similarity. First, we identified pCREs that are identical to TFBMs. Only two pCREs were identical (PCC = 1) to experimentally determined binding motifs: ATBZIP63, which is involved in abscisic acid (ABA) biosynthesis (Matiolli et al., 2011), and ABF3, which is involved in ABA signaling (Kang et al., 2002), consistent with their roles in the salt stress response. Second, given that PCC = 1 is highly stringent, we designated a pCRE-TFBM pair as having significant similarity if its PCC is significantly higher (at the 5% level) than PCCs of TF pairs from the same family (red circles in Fig. 3A). Based on this second criterion, 4% of the pCREs were significantly similar to TFBMs. Third, we designated a pCRE-TFBM pair as having significant similarity if its PCC is significantly higher (at the 5% level) than PCCs of TF pairs from different families (blue circles in Fig. 3A). This is reasonable because the TFBM PCC values tend to be higher within families than between families (Supplemental Fig. S1). In addition, the third criterion allowed us to identify the families of TFs that may bind the pCREs. Based on the third criterion, 25% and 33% of the pCREs can be assigned to TF families in CIS-BP and DAP-seq, respectively (Supplemental Table S2). Considering both large-scale in vitro TF binding studies, 38% of pCREs have a significant TFBM match. Example TFBMs and their best-matching pCREs are shown in Figure 3B.

Figure 3.

Similarity of the pCREs to CIS-BP TFBMs. A, The 95th percentile PCC values between TFBMs, pCREs, and/or random motifs. The y axis shows TF families, and the x axis shows PCC values. Orange, PCCs between TFBMs from a family and pCREs with their best matches in the same family (TFBM vs. pCRE); red, PCCs between TFBMs from a TF family (TFBM within); blue, PCCs between TFBMs in one family and their best matching TFBMs in other families (TFBM between); black, PCCs between TFBM from a family and random motifs (TFBM vs. random). B, Sequence logos of and PCCs between the example pCREs (left) and their best matching TFBMs (right) in the bZIP, AP2, NAC-NAM, and TCP TF families.

Although 38% of the organ pCREs enriched among salt up-regulated genes are significantly similar to one or more TFBMs, what should be made of the remaining 62% of pCREs? One possibility is that these pCREs are bound by TFs in families with representative TFs in in vitro binding studies, such that the binding preference of the representatives is too divergent from the TFs recognizing the pCREs. To test this, we asked if the pCREs are more similar to a known TFBM than to sequences drawn randomly from the genome (black circles in Fig. 3A) and found that PCC values between pCREs and their best matching TFBMs are all higher than the 95th percentile value in the pCRE random sequence PCC distribution (Fig. 3A). Thus, all pCREs are more significantly similar to known TFBMs than random sequences. These findings suggest that the pCREs are not simply random, meaningless sequences pulled from the genome. In addition, the coexpression-based analysis contributed to an expanded set of CREs that are relevant for organ salt up-regulation, considering that the majority of pCREs do not resemble known TFBMs.

The pCRE Set Further Improves the Prediction of Salt Up-Regulation in a Spatially Specific Manner

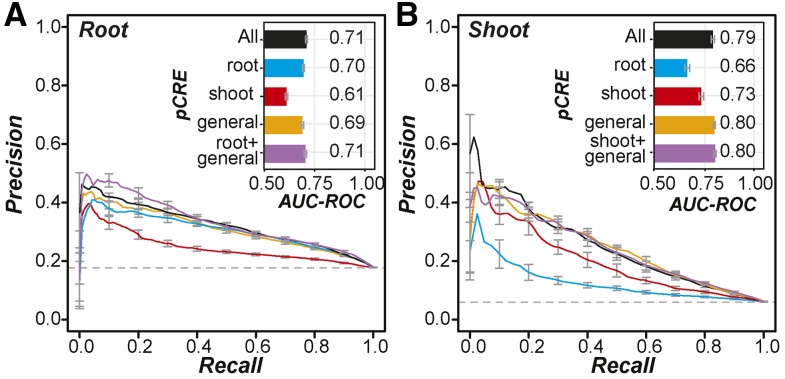
To determine if the pCRE set predicts salt up-regulation better than known in vitro TF binding sites (Weirauch et al., 2014; O’Malley et al., 2016), we used the pCRE set to model salt up-regulated expression (see “Materials and Methods”; Fig. 4). Salt up-regulation prediction models based on pCREs had better prediction performance for both root up-regulated genes (AUC-ROC = 0.71; red in Fig. 4A) and shoot up-regulated genes (AUC-ROC = 0.79; red in Fig. 4B) than models based on CIS-BP and DAP-seq data (root AUC-ROC = 0.64 and shoot AUC-ROC = 0.74; Fig. 2, C and D). This improvement indicates that using motifs discovered from coexpression clusters containing root and/or shoot up-regulated genes led to better prediction models of organ salt up-regulation. We should emphasize that the pCREs uncovered from coexpression clusters and the CIS-BP and DAP-seq TFBMs used to build these models were enriched in salt up-regulated genes and were mapped with the same threshold P value (see “Materials and Methods”). Thus, our finding indicates that motif finding based on coexpression can be highly complementary to large-scale in vitro binding studies in improving our knowledge of cis-regulation.

Figure 4.

Performance of salt up-regulation prediction models using pCREs identified from coexpression clusters. A, Precision-recall curves for models predicting root salt up-regulated genes using all pCREs (black), root pCREs (blue), shoot pCREs (red), general pCREs (orange), and root + general pCREs (purple). The bar plot in the inset indicates the corresponding AUC-ROC values of the models. Error bars represent the se of precision values or AUC-ROCs from 10-fold cross-validation. B, Precision-recall curves and AUC-ROC values for models predicting shoot up-regulated genes using all pCREs (black), root pCREs (blue), shoot pCREs (red), general pCREs (orange), and shoot + general pCREs (purple).

Next, we classified 1,894 organ pCREs into three subsets that were overrepresented in the promoters of genes up-regulated by salt in the root (759 root pCREs), in the shoot (237 shoot pCREs), and in both the root and shoot (898 general pCREs). The rationale for defining these pCRE subsets was that the root and shoot subsets might be more critical to controlling expression for the root-specifically and shoot-specifically up-regulated genes, respectively, while the general pCREs might be critical for globally up-regulated genes. To test this hypothesis, salt up-regulation prediction models were established using root, shoot, and general pCREs where each pCRE was treated as an independent predictor. To predict root up-regulated genes (including genes up-regulated globally and in the root specifically), we found that a model based on root pCREs (AUC-ROC = 0.7) was much better than a model based on shoot pCREs (AUC-ROC = 0.61; Fig. 4A). Similarly, a model based on shoot pCREs better predicted shoot salt up-regulated genes (AUC-ROC = 0.73) than a model based on root pCREs (AUC-ROC = 0.66; Fig. 4B).

Thus, the root and shoot pCRE sets are better at predicting up-regulated genes in the organs with which they are associated, demonstrating that they are relevant to spatially specific up-regulated genes. In addition, root pCREs alone or the combination of the general and the root pCRE sets resulted in models that performed as well as the model using the all-pCRE set (AUC-ROC = 0.71; Fig. 4A). This suggests that, surprisingly, shoot pCREs provide no additional information for predicting root up-regulated genes. In contrast, although the model based only on shoot pCREs performed reasonably well in predicting shoot up-regulated genes (AUC-ROC = 0.73), it did not perform as well as the model based only on the general pCREs (AUC-ROC = 0.80; Fig. 4B). This further supports the notion that shoot up-regulated genes may be regulated by a global set of TFs (Fig. 1B) that bind to the set of general pCREs. Another surprise was that, for root up-regulated gene prediction, the models based on the root pCREs, the general pCREs, and the union of the general and the root pCREs performed similarly (Fig. 4A). One potential explanation is that each model captured a distinct subset of the organ up-regulated genes. To assess the extent to which the models predicted similar sets of genes, we examined how genes were classified when different pCRE subsets were used (see “Materials and Methods”). We found that more root-specifically up-regulated genes were predicted with the root pCRE-based models (24%) compared with models using general pCREs (9%; Supplemental Fig. S2).

Taken together, these results demonstrate that the identification of pCREs using stress expression data can lead to improvements in modeling gene expression over known in vitro TF binding sites. This supports our hypothesis that coexpression-based approaches would improve CRE discovery. We also found that salt stress up-regulated genes in the root and the shoot may be regulated by different subsets of motifs in the pCRE set. Genes up-regulated by salt stress in the root can be best predicted with a model considering both the root and the general pCRE sets without considering shoot pCREs. However, the shoot up-regulated genes likely are regulated primarily by general pCREs, as seen in the equivalent performance of the general pCRE model and the full pCRE model in predicting shoot up-regulated genes.

Filtering pCREs Based on TF Binding, DNase I Hypersensitivity, and Conservation

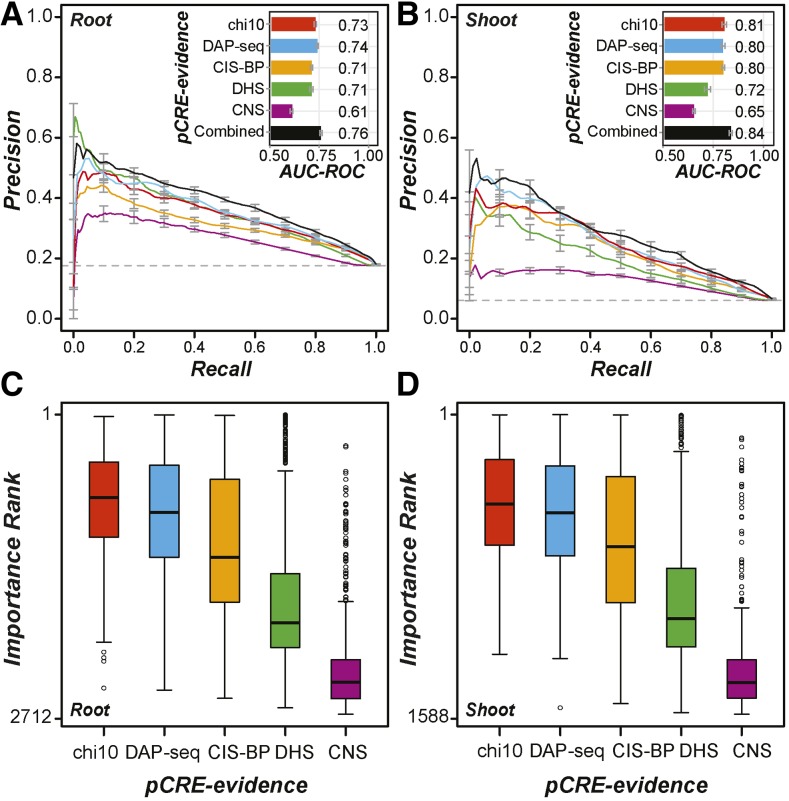
We have demonstrated that the pCREs identified in this study can predict organ salt up-regulation. However, the large number of pCREs identified (1,894) raises the question of whether some motifs are redundant or not particularly informative and could be filtered out. To reduce redundancy, we first removed highly similar pCRE pairs (see “Materials and Methods”). Next, we used feature selection algorithms to identify the pCREs that perform best in predicting root up-regulated genes (Fig. 4A) and shoot up-regulated genes (Fig. 4B). Among the feature selection algorithms used, the χ² statistic-based approach performed best (see “Materials and Methods”; Supplemental Fig. S3). With a threshold χ² ≥ 10, 678 (41%) and 397 (35%) pCREs (referred to as chi10-selected pCREs) were regarded as informative and could better predict root (AUC-ROC = 0.73; Fig. 5A) and shoot (AUC-ROC = 0.81; Fig. 5B) salt up-regulation, respectively, compared with the full set of pCREs (Fig. 4).

Figure 5.

Performance of salt up-regulation prediction models using filtered pCRE sets. A, Precision-recall curves for models predicting root salt up-regulated genes using six sets of pCRE sites. Red, All sites of pCREs selected with the χ² test feature selection method with a threshold χ² statistic ≥ 10 (chi10; Supplemental Fig. S3, E and F); blue, chi10-selected pCRE sites overlapping with DAP-seq peaks; orange, chi10 pCRE sites overlapping with CIS-BP TFBM sites; green, chi10 pCRE sites overlapping with DHS peaks; purple, chi10 pCRE sites overlapping with CNS; black, all the above information combined. The bar plot in the inset indicates the corresponding AUC-ROC values of the models. B, Precision-recall curves and AUC-ROCs for models predicting shoot salt up-regulated genes using the six sets of pCRE sites as in A. C, Distribution of importance ranks of all chi10-selected pCREs (chi10) and chi10 pCREs filtered based on DAP-seq, CIS-BP, DHS, or CNS data. The ranks were obtained from the model built with the combined data set in A for root. D, As in C but based on the model built with the combined data set in B for shoot.

To further improve predictions of organ salt gene up-regulation, we took advantage of additional regulatory information, including the in vitro TF binding data (CIS-BP and DAP-seq), chromatin accessibility measured according to DNase I hypersensitivity (DHS) experiments (Sullivan et al., 2014), as well as conserved noncoding sequences (CNS) among Brassicaceae species (Haudry et al., 2013). Although root and shoot up-regulated gene promoters were overrepresented with DHS regions (Fisher’s exact test [FET], all P < 5e-13) and with CNS (FET, all P < 1e-12), compared with nonresponsive genes, the performance of models based on only DHS or CNS was the same as random guesses (AUC-ROC ∼ 0.5), suggesting that additional regulatory sequence information is needed. Thus, we hypothesized that a pCRE site would be more informative in predicting gene expression if it overlapped with a potential TF binding site, a chromatin-accessible region, and/or CNS.

Models based on DAP-seq-filtered pCREs had similar performance to models using the original unfiltered pCREs in predicting organ salt up-regulation (AUC-ROC = 0.73–0.74 and 0.80–0.81; Fig. 5, A and B). Because the model performance remained the same, and 9% to 14% of the pCRE sites were removed, it is likely that filtering based on DAP-seq data eliminated some false-positive pCRE sites but also true-positive sites. This is also true for pCRE sites filtered based on CIS-BP data (Fig. 5A). On the other hand, filtering pCRE sites based on DHS information further decreased the performance for shoot up-regulation prediction but did not impact prediction in the root (Fig. 5B). Thus, pCRE sites informative for predicting shoot salt up-regulation were likely removed, potentially because chromatin accessibility can only partially predict gene expression (Liu et al., 2015) and/or because the DHS data used are for conditions other than high-salinity stress (Sullivan et al., 2014). One surprising finding was that models based on pCRE sites overlapping with CNS had the worst performance in predicting both root and shoot up-regulated genes. This is likely because the CNS were identified with stringent criteria and filtering eliminated a substantial number of true cis-regulatory sites. In addition, this finding suggests that there are cis-regulatory sites that are important in organ salt up-regulation but that are not highly conserved.

Taken together, using pCRE information alone yields models with the best performance in predicting organ salt up-regulation. Additional TF binding information, DHS, and CNS either did not improve or worsened the model performance. We should emphasize that this result is not simply a ranking of how useful a given type of data are for predicting salt-responsive expression but provides an assessment of how they can be useful for improving the model. In future modeling studies, it will be important to assess how additional regulatory information should be represented to optimize prediction, to generate and utilize condition-specific data sets, and to reduce the stringency for calling conserved sequences.

The Most Informative pCREs and Their Properties

To identify the minimal set of pCREs needed for salt up-regulation predictions, we ranked all chi10-selected pCREs as well as those with DAP, CIS-BP, DHS, and/or CNS evidence according to importance scores generated during machine learning runs (see “Materials and Methods”). Each chi10-selected pCRE was examined five times by either applying no filter to the sites the pCRE mapped to or by filtering based on four types of evidence (DAP, CIS-BP, DHS, or CNS; Fig. 5). Thus, for each chi10-selected pCRE, five possible pCRE-evidence pairs (with no, DAP, CIS-BP, DHS, or CNS filter) were evaluated for how informative they were in predicting organ salt up-regulation. Consistent with the finding that models with CNS filtering have the lowest performance in predicting organ salt up-regulation, we found that CNS features were the least important in predictions (Fig. 5, C and D). With the machine learning results, we next ranked root and shoot pCRE-evidence pairs and identified the top 100 and 10 pCREs for root or shoot up-regulation.

The models based on the top 100 pCRE-evidence pairs yielded AUC-ROC values of 0.72 and 0.8 for predicting root and shoot up-regulation, respectively, and these models are comparable to the models based on all chi10-selected pCREs (red in Fig. 5, A and B). However, using only the top 10 pCRE-evidence pairs, the prediction performance was significantly worse (AUC-ROC = 0.66 and 0.72 for root and shoot predictions, respectively). This result suggests that the most important 100 pCRE-evidence pairs, including 39 and 40 pCREs for root and shoot, respectively, are as informative for predicting organ salt up-regulated genes as the entire pCRE set. Among the pCREs in this minimal set, 10 are common between the root and shoot subsets. This minimal set includes three ABRE and ABRE-core-like pCREs (Supplemental Table S3), consistent with the roles of this element in abiotic stress-responsive gene expression (Narusaka et al., 2003). Another known salt-responsive element is the DRE (Narusaka et al., 2003). Although the DRE is not included in this minimal set, it is among the full set of pCREs identified (kkrCCGACrNgmNw; Supplemental Table S2). We should note that the rest do not resemble known salt-responsive cis-elements.

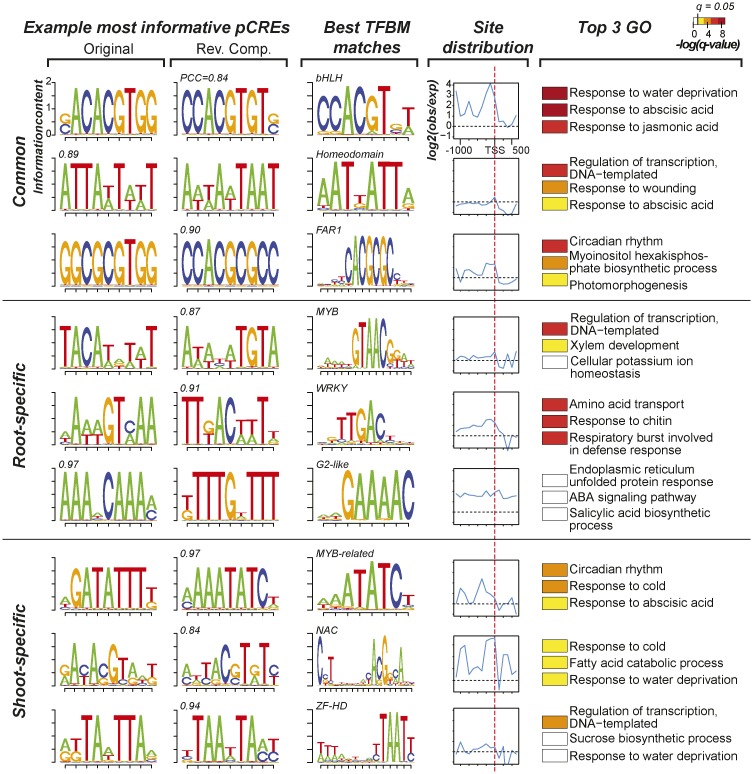
In addition to similarities to known TFBMs, we explored the observed frequencies of pCRE sites in 100-bp bins of regions flanking the TSS and compared them with the numbers of sites in random sequences. We found that, in general, the most informative pCRE sites are in proximal promoter regions upstream of the TSS (Supplemental Fig. S4), consistent with other studies (Zou et al., 2011; Yu et al., 2016). Nonetheless, depending on the individual pCRE, the distribution pattern varies (example pCREs in Fig. 6). For example, the sACACGTGG pCRE, which is important for both root and shoot salt up-regulation, is enriched over the entire length of the putative promoter, particularly in regions immediately upstream of the TSS, and is likely bound by bHLH TFs (the first motif in Fig. 6). In contrast, the ATTAwTwwT pCRE was not enriched in the promoter region but contributes significantly to salt up-regulation prediction (the second pCRE in Fig. 6). This motif is not the TATA box, which is highly enriched in the first 50 bp upstream of TSS (Bernard et al., 2010). Its importance in salt up-regulation and the lack of enrichment may suggest that ATTAwTwwT binding is controlled mostly through chromatin accessibility, a hypothesis that needs to be further tested. We also found that, among the most informative pCREs, 31% (12) of root and 40% (16) of shoot CREs have a significant TFBM match (Supplemental Table S3). For the most informative pCREs with no clear resemblance to known TFBMs, it remains to be determined if they tend to be pCREs that require cooperative binding; this cannot be assessed with existing in vitro binding data.

Figure 6.

Characteristics of pCREs important in predicting organ salt up-regulation. Example pCREs from the most important 39 root and 40 shoot pCREs are shown. The top, middle, and bottom rows contain three common, three root-specific, and three shoot-specific pCREs, respectively. The first and second columns show sequence logo representations of the pCREs and their corresponding reverse complement (Rev. Comp.) motifs, respectively. The PCC value between a pCRE and its best matching TFBM is shown above the sequence logo. The third column contains sequence logos and the TF family of the best matching TFBMs for the pCREs listed. The fourth column shows the degrees of pCRE site enrichment (log₂[observed number of pCRE sites/randomly expected number]) from 1 kb upstream of the TSS (dotted red line) to 500 bp downstream. The fifth column shows the top three enriched GO Biological Process categories containing genes with sites of the pCRE in question. For the color bar at top [-log(q-value)], the q value is derived from the P value of FET after multiple testing correction; white indicates values below the 5% significance level.

In addition to the locations of pCREs and the TFs that likely bind to these pCREs, we asked what types of genes (based on GO Biological Process annotation) tend to be associated with (i.e. have sites of) the most important pCREs (Supplemental Table S4). We found that the most important pCRE sites tend to be in the promoters of genes that, as expected, have roles in the regulation of transcription as well as responses to water deprivation, cold, wounding, ABA, jasmonic acid, and ethylene (Fig. 6; Supplemental Table S4). Interestingly, five pCREs tend to be found in genes involved in circadian regulation (Supplemental Table S4), including GGCGCGTGG and aGATATTTk (Fig. 6). Given that it is well known that the stress response is frequently gated by the circadian clock (Greenham and McClung, 2015), our findings further suggest that such gated responses may have a strong spatial component regulated by the pCREs we have identified. Taken together, the fact that only 39 root and 40 shoot pCREs are necessary to predict organ salt up-regulation implies that the remaining 1,854 pCREs we have identified are not as important. Alternatively, it is possible that the importance of some of these seemingly uninformative pCREs may be revealed only in combination, as demonstrated in previous studies of the regulation of gene expression under stress conditions (Harbison et al., 2004; Zou et al., 2011) and tissue-specific expression (Yu et al., 2006; Hu and Gallo, 2010).

pCREs Work Best in Combination

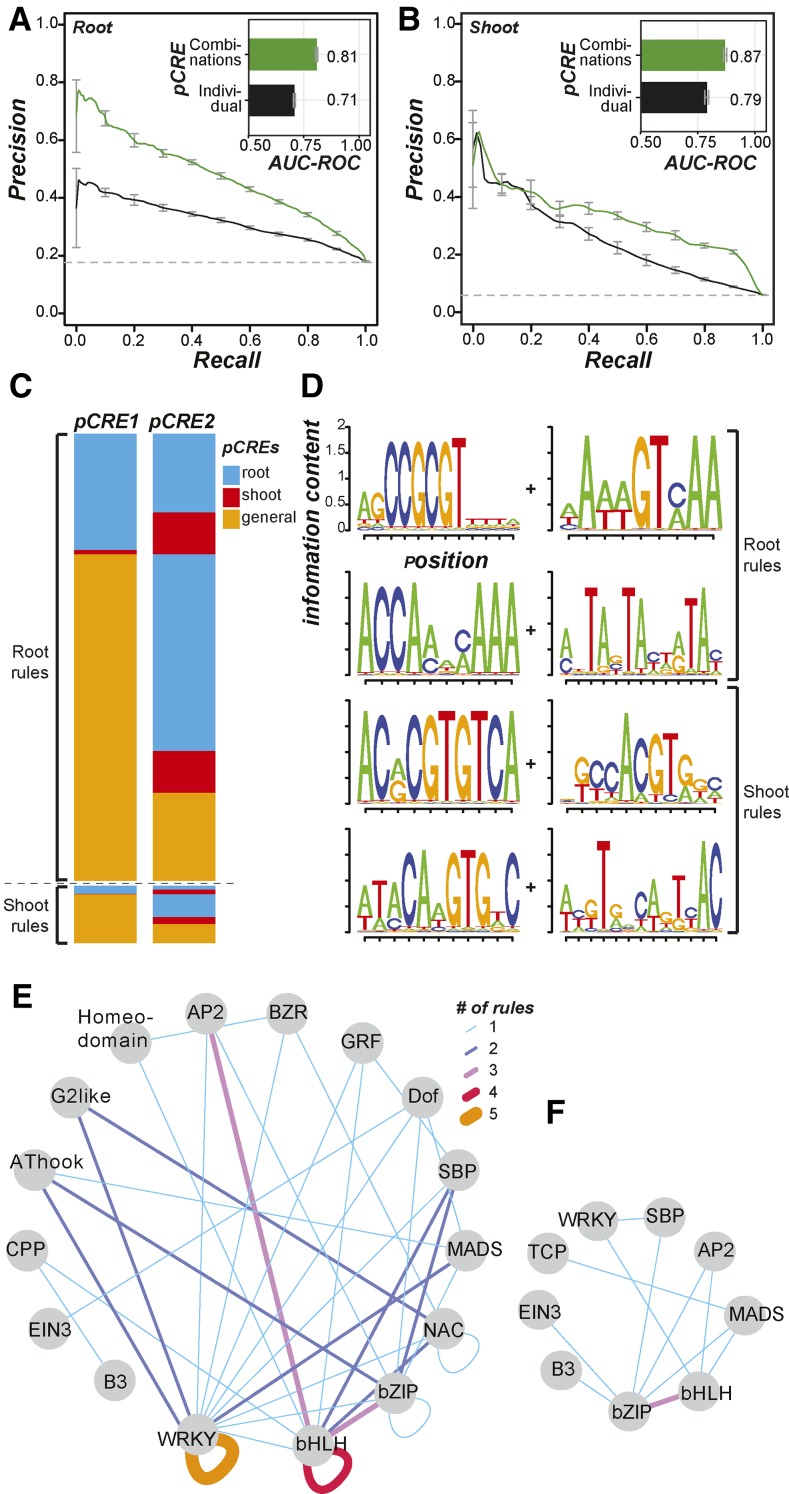
So far, the salt up-regulation prediction models that we have described considered many pCREs collectively but treated each individual pCRE as an independent predictor. Therefore, we asked: (1) whether pCRE combinations are important for predicting salt up-regulated genes in the root and/or the shoot, (2) what these important pCRE combinations are, (3) what types of pCREs work in combination, and (4) if combinatorial rules important in predicting root expression also are important for shoot expression, or vice versa. To identify pCRE combinations relevant to the up-regulation of genes under salt stress, we used the classification by association (CBA) method (see “Materials and Methods”). Due to computational complexity, we restricted our analysis to binary combinatorial rules where the presence of two pCREs predicts up-regulation (pCRE A + pCRE B → up-regulation in the organ of interest). Rule sets were generated for both the root and the shoot salt up-regulated genes. As some pCREs may only be informative in combination, we included all 1,894 pCREs without any filtering to identify combinatorial rules. This also enabled us to compare the pCREs involved in rules with the individual pCREs found to be most informative. We identified 2,826 and 351 combinatorial rules for root and shoot up-regulation, respectively (Supplemental Table S5). A total of 1,086 pCREs were present in combinatorial rules that were predictive of root up-regulation (root rules), but only 389 were also chi10-selected pCREs that were informative for predicting up-regulation when considered individually. Similarly, only 136 out of 427 pCREs in the shoot rules were chi10 selected. Thus, a substantial number of pCREs are informative for predicting root and shoot salt up-regulation only when considered in combination.

We also found that only 12 root rules (among 2,826) had the same pCRE combinations as the shoot rules, suggesting that the great majority of the rules for one organ were specific to that organ. Most importantly, models based on only the combinatorial rule sets improved predictions for both root (AUC-ROC = 0.81; Fig. 7A) and shoot (AUC-ROC = 0.87; Fig. 7B) up-regulated genes compared with the models based on the presence/absence of single pCREs (AUC-ROC = 0.71 and 0.79 for root and shoot, respectively; Fig. 4). These results indicate the involvement of pCRE combinations in salt up-regulation. In addition, they demonstrate that the rules capture the physical interaction between two presumed TFs binding to a pair of pCREs. Nonetheless, we found that the sites of a pair of pCREs in a rule are not significantly closer together in salt up-regulated genes compared with nonresponsive genes (Supplemental Fig. S5, A and B). This is consistent with the finding that the distance distribution of the binding sites of interacting human TFs was not significantly different from the random expectation (Yu et al., 2006). Thus, pCRE sites important for combinatorial regulation may not be constrained by distance.

Figure 7.

Summary of root and shoot combinatorial pCRE rules and model performance. A, Precision-recall curves and AUC-ROCs of root salt up-regulation models based on combinatorial rules (green) and the full pCRE set (black). B, Precision-recall curves and AUC-ROCs of shoot salt up-regulation models based on combinatorial rules (green) and the full pCRE (black). C, Heat maps summarizing the types of pCREs (blue, root specific; red, shoot specific; and orange, general) involved in root or shoot salt up-regulation rules. D, Sequence logos of pCRE involved in top root and shoot rules. E, Inference of TF interactions based on root combinatorial rules. Node, A TF family with one or more TFs with significant similarity to a pCRE involved in root rules; edge, inferred based on pCRE combinations with thickness/color indicating the number of times that a pair of TFs from various families interact based on the pCRE combinatorial rules. F, Same as in E but for shoot pCRE combinatorial rules.

We next examined if the combinatorial rules tend to be composed of a general pCRE and an organ (root or shoot) pCRE, two general pCREs, or two organ pCREs (Fig. 7C). We found that there was a significant difference in the distribution of these three categories of combinatorial rules for the shoot rules (χ² test, P = 6e-06). In particular, there were more general-general pCRE combinations than expected (odds ratio = 1.5) and fewer organ-organ pCRE rules than expected (odds ratio = 0.52). This aligns with the notion that the general pCREs are more important for the regulation of shoot up-regulated genes. The root rules also had a significantly different distribution of rule types (χ² test, P = 0.01), but the effect sizes were generally low (odds ratio range = 0.89–1.1). Thus, it does not appear that rules for root up-regulated genes are composed of both a general pCRE and a pCRE from one of the organ sets. Example combinatorial rules are shown in Figure 7D. To further assess the biological significance of the combinatorial rules, we first determined how frequently each combinatorial rule mapped to the putative promoters of salt up-regulated genes. We found that even the most abundant rules were present in only 2% to 3% of the salt up-regulated genes (median = 1.3% and 0.7% for root and shoot, respectively). Although these rules are very specific, collectively, they lead to models that can better predict salt up-regulated genes than models based on the presence/absence of individual pCREs. This finding highlights the complexity of the regulatory logic: a large number of regulatory sequences and combinatorial rules where each explains the expression pattern of only a small number of genes.

Next, we examined the relationships between the TFs that likely bind to the pCREs in the combinatorial rules (Fig. 7, E and F). We found that, in root rules, within-family pairs including WRKY-WRKY and bHLH-bHLH were most common, found in five and four of the 35 rules that have TFBM annotations, respectively. In addition, WRKY was the most abundant TF family in root rules (19%; Fig. 7E), consistent with the finding that WRKY TF binding sites from CIS-BP and DAP-seq were overrepresented in root up-regulated gene promoters (Fig. 2A). This finding also suggests the involvement of WRKY homodimers or heterodimers in root salt up-regulation. In shoot rules, the bHLH-bZIP combination was most abundant, and 27% of the pCREs in the shoot rules were similar to bZIP TFBMs (Fig. 7F). Finally, we assessed the functions of genes containing both pCRE sites in a combinatorial rule and found that these genes are involved predominantly in the responses to ABA and water deprivation (Supplemental Table S6). These categories are common for genes that have root and shoot rules and suggest that the combinatorial rules we have identified are likely important in the ABA-dependent signaling component of the abiotic stress response (Yoshida et al., 2014). It is interesting that translational elongation also was enriched, indicating a potential link between stress transcriptional and translational control.

Taken together, our findings suggest that the organ pCREs work best in combination. The greater importance of combinatorial rules aligns well with what is already known in mammals, where individual CREs are important for expression in multiple tissues but CRE combinations are more relevant in controlling tissue-specific expression (Priest et al., 2009; Austin et al., 2016). Both root rules and shoot rules incorporate pCREs from the full set of organ pCREs, but there is little overlap (0.4%–3%) in the two sets of rules. This suggests that pCREs need to be considered in combination to better predict salt up-regulation. While some of the rules have motif pairs that are closer together than we would expect by chance, most of the rules do not have a significantly shorter distance between motifs. This may indicate that rules without a strong constraint on the distance between pCREs may still be important for spatial salt stress up-regulation.

CONCLUSION

In this study, we identified a set of 1,894 pCREs from coexpression clusters that were relevant to the up-regulation of transcript abundance under salt stress in the root and shoot of Arabidopsis. Among these pCREs, 38% are similar to the known binding motifs of TFs from multiple families. Machine learning models for predicting salt up-regulation based on the pCRE set had significantly better performance than those based on in vitro binding data from two large-scale studies (Weirauch et al., 2014; O’Malley et al., 2016). Thus, the pCREs identified likely contain cis-regulatory information for the spatial response to salt. We also found that salt up-regulation in the root requires both a general pCRE set that is relevant to up-regulation in both the root and shoot as well as a root pCRE set associated primarily with root-specifically salt up-regulated genes. In contrast, the regulation of shoot salt up-regulated genes relies primarily on a general pCRE set. Considering that substantially more genes were up-regulated in the root (2,100) compared with the shoot (524), this difference in the composition of relevant pCREs may reflect differences in regulatory complexity and the fact that root is the primary organ exposed to high-salinity treatment. Filtering pCREs based on in vitro TF binding data, chromatin accessibility, and conservation, we found that ∼40 pCREs could predict organ salt up-regulation with the same performance as the model using all pCREs (39 root and 40 shoot pCREs, with 10 pCREs in common; Supplemental Table S3). Nonetheless, the organ salt up-regulation models considering combinations of pCREs had significantly improved performance over the models considering pCREs collectively but treating each pCRE as an independent predictor. Most importantly, most pCREs in the combinatorial rules were not considered important when they were treated as independent predictors and would have been false negatives in common motif-finding practices.

One limitation of our study is that the pCREs were identified based on the expression data alone without knowledge of whether the sites mapped by these pCREs were bound by TFs. To alleviate this limitation, we incorporated in vitro binding that led to models with the same performance as those considering only pCREs. Nonetheless, we found that the pCREs identified are complementary to in vitro-derived TF binding information. Because the in vitro TF binding provides an assessment of what kinds of sequences could be bound and not where the in vivo binding sites are in the genome, the binding data alone were not expected to predict condition-specific expression well. By combining the pCREs identified using condition-specific information and the in vitro binding data, condition-specific regulators and regulatory sequences could be pinpointed. In addition to in vitro TF binding data, chromatin accessibility data (DHS) were incorporated into prediction models but led to reduced or identical model performance compared with the model using pCREs only. This is likely because the DHS data we used were generated for different developmental stages of Arabidopsis under conditions not related to salt stress (see “Materials and Methods”). Finally, CNS were incorporated to filter pCRE sites but yielded models with the lowest prediction performance. One explanation is that stress response pCREs may have higher evolutionary rates and are not well conserved. Another possible reason is that CNS are defined in a stringent fashion. Although some pCRE sites relevant to organ salt up-regulation are under selection, they are beyond the limit of detection. These possibilities can be tested by incorporating conserved site information defined using multiple thresholds and methods detecting selection that do not rely only on sequence comparisons.

Another limitation of our study is that our model could only predict salt up-regulation with reasonable performance. Although we identified pCREs from coexpression clusters overrepresented with salt down-regulated genes, the performance of predictive models using these pCREs was no better than random guesses (AUC-ROC = ∼0.5). One potential reason is that predictions of salt down-regulation (or down-regulation of the stress response in general) require additional levels of information beyond cis-regulatory sequences, such as microRNAs and RNA turnover. Related to this, other areas of future interest include the identification of pCRE sites outside of the putative promoter regions. We currently focused only on 1 kb upstream of the TSS, and we have missed CRE sites located in introns and/or coding regions. For example, one study showed that at least 21 introns are involved in enhancing gene expression in Arabidopsis (Rose et al., 2008). It also has been shown that putative cis-regulatory sites in exonic regions have significantly reduced nucleosome occupancy, which is correlated with gene expression levels (Liu et al., 2015). Another important factor that we did not consider in our models is pCRE copy number, which has been shown to play an important regulatory role. For example, cis-elements such as ABREs drive gene expression when present in multiple copies (Narusaka et al., 2003). Our earlier attempt to consider copy number information (in an additive fashion) to predict overall salt up-regulation was not successful (Zou et al., 2011). It is likely necessary to consider pCRE copy number nonadditively (i.e. to model the effect of copy number by considering cooperativity between sites). However, this will introduce more parameters and require more expression data (e.g. time series) to prevent model overfitting. Thus, there remain substantial challenges that must be overcome in future studies.

Finally, we also need to improve the resolution of spatial response from the organ to the cell type level. The next logical step is to identify pCREs that can be used to predict the differential expression of genes in a cell type-specific manner. Our results show that coexpression-based CRE identification in conjunction with machine learning-based modeling is a promising method for globally assessing spatial gene regulation in the context of stress. In addition to providing a genome-wide view of potential cis-regulatory mechanisms, this approach may have possible applications in engineering plants that can respond to stresses. The use of native, tissue-specific inducible promoters to engineer plants is promising, but it is limited by the promoters that are available already in nature (Potenza et al., 2004). The methods we used here may help to identify individual and/or combinations of cis-regulatory sequences that can be used in synthetic promoters to drive tissue-specific expression in the context of stress.

MATERIALS AND METHODS

Expression Data Processing and Analysis

Arabidopsis (Arabidopsis thaliana) abiotic stress expression data for the root and shoot (Kilian et al., 2007) and biotic stress data for the shoot were downloaded from the AtGenExpress Web site (http://www.weigelworld.org/resources/microarray/AtGenExpress/). The data came preprocessed and normalized. We calculated the log₂ fold change and associated P values for each stress condition and its corresponding control at each time point and each organ using limma (Ritchie et al., 2015) in the R environment (R Core Team, 2012). The P values were adjusted (Benjamini and Hochberg, 1995) to control for the false discovery rate. Genes were considered up-regulated at log₂ fold change ≥ 1 and adjusted P ≤ 0.05. Genes up-regulated after salt treatment for 3 h in the root and shoot were referred to as root and shoot up-regulated genes, respectively. Genes were considered nonresponsive if they were not significantly differentially expressed (up- or down-regulated) under any stress condition at any time point in the root or the shoot. Each organ had its own set of nonresponsive genes (root nonresponsive and shoot nonresponsive). This stringent definition of nonresponsive genes was chosen because cis-regulatory sequences may be relevant to regulating responses not only to salt but also to other stress conditions.

To assess the relationship between the degree of differential expression in the root and shoot under different stress conditions, PCCs of log₂ fold-change values were calculated for all conditions and organ combinations. A heat map of the PCC values (Fig. 1) was generated using the gplots package in R (Warnes et al., 2015). To identify the functional categories enriched in salt up-regulated genes (3 h) in the root, in the shoot, or in both root and shoot, each plant GO slim category (http://www.geneontology.org/ontology/subsets/goslim_plant.obo) was tested to determine if it contained an overrepresented/underrepresented number of genes up-regulated in the root, shoot, or both organs with FET implemented in SciPy (http://www.scipy.org/). The P values were adjusted for multiple testing (Storey, 2003).

In Vitro TF Binding, DNase I Hypersensitivity, and Conserved Noncoding Data Sets

Two sets of in vitro binding data were used. The first set included position frequency matrices (PFMs) obtained from the CIS-BP database Web site (Weirauch et al., 2014). These PFMs are based on either protein-binding microarray data or TRANSFAC motifs (Weirauch et al., 2014). The PFMs were converted to PWMs adjusted for the background AT (0.33) and CG (0.17) contents of the Arabidopsis genome using the TAMO package (Gordon et al., 2005). This resulted in a final set of 355 PWMs (referred to as TFBMs). To map the TFBMs, first the 1-kb sequences upstream of TSS of all genes in Arabidopsis were downloaded from The Arabidopsis Information Resource (ftp://ftp.arabidopsis.org/). The TFBMs from CIS-BP were mapped to the putative promoter sequences using Motility (http://cartwheel.caltech.edu) with a threshold of P < 1e-06. The second set of in vitro binding data included 344 DAP-seq experiments testing in vitro binding to naked genomic DNA of 598 TFs from the Plant Cistrome Database (O’Malley et al., 2016). A DAP-seq peak (∼200 bp long) contains the TF binding site, and only peaks with the fraction of reads in peaks of 5% or greater were considered further. We identified TFBM sites and DAP-seq peaks that were overrepresented in the promoters of the root up-regulated and shoot up-regulated genes by performing FET against the root-nonresponsive and shoot-nonresponsive genes, respectively.

DHS data (Sullivan et al., 2014) were obtained from the Gene Expression Omnibus (GSE53322 and GSE53324) in the form of peaks in bed format. The DHS data sets were derived from multiple developmental stages and tissues including 7-d-old dark-grown Arabidopsis Columbia-0 seedlings, roots, root hair cells, root nonhair cells, and seed coats. In our study, each DHS data set was treated as a distinct feature for predicting salt up-regulation. Arabidopsis-based coordinates of ∼90,000 CNS among Brassicaceae species were obtained (http://mustang.biol.mcgill.ca:8885; Haudry et al., 2013) to assess whether CNS may be informative for predicting salt up-regulation. In addition, both DHS and CNS regions were used to filter pCRE sites to see if sites with different degrees of chromatin accessibility and conservation contribute differently to salt up-regulation prediction.

Salt Up-Regulation pCRE Identification

To identify pCREs associated with salt up-regulated genes in the root and shoot, we used a published pipeline with modifications (Zou et al., 2011). The stress expression data set in the form of a log₂ fold-change expression matrix was used to identify coexpression clusters using iterated rounds of k-means clustering such that all clusters contained 60 genes or less, while clusters smaller than 10 genes were excluded. Clusters enriched in salt up-regulated genes in any time point in either roots or shoots were used to identify 6- to 18-bp motifs in the putative promoter regions of genes in each cluster. Six motif-finding programs were used: AlignACE (Roth et al., 1998), MDScan (Liu et al., 2002), MEME (Bailey and Elkan, 1994), Motif Sampler (Thijs et al., 2001), Weeder (Pavesi et al., 2006), and YMF (Sinha and Tompa, 2000). In the initial motif-finding step, ∼300,000 motifs were identified, many of which were redundant. Two rounds of pCRE merging/enrichment testing were performed. In the first round, the ∼300,000 motifs were merged if their consensus sequences shared the same International Union of Pure and Applied Chemistry codes and/or if they were highly similar to each other (in the same cluster) based on clusters defined using Kullback-Leibler distance (Zou et al., 2011). In the enrichment step, these merged pCREs were mapped to the 1-kb promoter regions of genes in Arabidopsis using Motility (http://cartwheel.caltech.edu), and we kept those motifs that mapped with P < 1e-06. The pCREs were analyzed further if their mapped sites were significantly overrepresented (FET, adjusted P ≤ 0.05) in the promoters of salt up-regulated genes.

In the second round, we further merged enriched motifs based on PCC distance of the motif PWMs. Using the PCC distance matrix, motifs were clustered hierarchically, and distinct clusters were demarcated with a PCC distance threshold of 0.1, which was found previously to be the first percentile of PCC distances for nonredundant motifs in the JASPER CORE data set (Zou et al., 2011). Within each cluster, a single motif was chosen based on having the most significant degree of enrichment for genes up-regulated under salt stress in roots and/or shoots. The motifs identified from all clusters were collectively referred to as pCREs. To identify pCREs particularly relevant to root, shoot, or general salt up-regulation, a final round of FET was done to identify motifs that were significantly overrepresented (P < 0.05) only in root salt up-regulated genes (root pCREs), only in shoot salt up-regulated genes (shoot pCREs), and among genes up-regulated in both organs (general pCREs). In the end, 1,894 shoot, root, and general pCREs were identified. The log-odds matrices and sequence logos of these pCREs are provided in TAMO format in Supplemental Data S1.

Comparison of pCREs and TFBMs

To assess the similarity between the pCREs identified here and the known TFBMs from CIS-BP (Weirauch et al., 2014) and DAP-seq (O’Malley et al., 2016), the PCCs between the PWMs of all pCRE-TFBM, all pCRE, and all TFBM combinations were calculated. For each motif pair, the PWM of the shorter motif was compared against the PWM of the longer one in a moving window with a step size of one position, and a PCC value was calculated. To account for the orientation difference between a pair of motifs, the reverse-complement PWM of one motif also was compared against the other (original orientation). The maximum PCC value of a motif pair (considering all windows in both orientations) was used as the representative value of motif similarity. For each pCRE, the pCRE-TFBM combination with highest PCC was analyzed further. To assess the statistical significance of the correlation between a pCRE-TFBM pair, a within-TF family PCC distribution was established using TFBMs from each TF family. This allowed us to test whether a pCRE was more similar to a TFBM of a particular family than those between TFBMs within that same family. The PCC distribution of each TFBM family was fitted with normal or β-distribution functions based on maximum likelihood using the MASS package (Venables and Ripley, 2002) in R. Every PCC between a pCRE and a TFBM from a family was compared with the cumulative density function of the fitted within-family distribution to get a P value. All P values from the pairwise comparisons were adjusted for multiple testing within the same family (Storey, 2003).

To further assess which TF families pCREs might bind to, between-family TFBM PCC distributions were generated and fitted as described above. We compared the PCC for each pCRE-TFBM pair with the between-family distributions to generate a P value, which was adjusted for multiple testing (Storey, 2003). We set a q value of 0.05 as the threshold to say that a pCRE may be bound by the same family as the TFBM. Because the TFBMs for some families were more divergent than others (there was a wide range of median PCCs for the within-family distribution; Supplemental Fig. S1), the false-negative rate (failure to assign a pCRE to certain families) varied. To assess if pCREs were more similar to TFBMs than to random genomic sequences, 1,894 random PWMs with the same length distribution as the pCREs were generated. For a random PWM of length k, 15 k-mers were generated randomly using the background distribution of AT-GC in Arabidopsis and consolidated into a PWM using the MotifTools.Motif_from_counts function in TAMO (Gordon et al., 2005). The random PWMs were then compared with TFBMs to establish the distribution of PCC to randomized PWMs.

Prediction of Salt Up-Regulation Using Machine Learning and Feature Selection

Our goal was to model the salt up-regulation of genes in each organ as a classification problem involving two classes: salt up-regulated genes in an organ and genes that are not responsive under any stress condition. The Support Vector Machine (SVM; Cortes and Vapnik, 1995) and Random Forest (RF; Breiman, 2001) algorithms were used for the classification implemented in the Waikato Environment for Knowledge Analysis (Weka; Frank et al., 2004). To get the importance scores of each feature, RF from the scikit-learn package in Python (Pedregosa et al., 2011) also was used. Every model in this article had two components: (1) a set of genes, each of which is classified as up-regulated or nonresponsive (expression class), and (2) a set of cis-regulatory sites (CIS-BP TFBMs, DAP-seq peaks, or pCREs) and their presence/absence on the putative promoter of each gene (promoter features). We established machine learning models using five sets of pCRE sites: all mapped pCRE sites as well as pCRE sites that overlapped with CIS-BP TFBM sites, DAP-seq peaks, DHS regions, and CNS. In this setup, the models predict the genes from the two expression classes using the presence or absence of the promoter features. Grid searches were used to find the best combination of the following three parameters in SVM: (1) the ratio of nonresponsive to up-regulated genes; (2) the parameter of the soft margin; and (3) the γ-parameter of the Radial Basis Function kernel. The latter two parameters are part of the SVM method itself. Similarly, grid searches were used for RF predictions, including (1) the ratio of nonresponsive to up-regulated genes and (2) the number of attributes. The ratio of negative to positive examples was achieved using the Weka class weka.filters.supervised.instance.SpreadSubsample, which subsamples the nonresponsive genes to achieve the desired ratio of up-regulated to nonresponsive genes. We used 10-fold cross validation as implemented in Weka, and the average AUC-ROC from all 10 cross validation runs was calculated using the ROCR package (Sing et al., 2005). RF model results were reported in that study, as the performances of SVM and RF models were correlated, and RF was easier to scale up to large data sets. The parameter combination with the maximum average AUC-ROC was taken as the best parameter for each model, and this maximum AUC-ROC is what we report for each model. Precision-recall curves were plotted using the output from the model with the maximum AUC-ROCs.

To eliminate redundant motifs, we used three univariate feature selection methods: (1) the Caret R Package, which is PCC based; (2) Correlation Feature Selection in Weka, where correlation is based on a minimum description length, symmetrical uncertainty, and relief (Hall, 1999); and (3) χ² tests on the pCRE sets in Weka. For the PCC-based method, we calculated the PCC between each pairwise feature (pCRE sites). For the pairs of features that have PCC > 0.5, only one feature was kept. This is an arbitrary threshold; however, removing 15% to 20% of pCREs did not change the AUC-ROC values of the prediction models. For the Correlation Feature Selection method, we kept the default settings in Weka. The χ² test in Weka yields ranks for each pCRE based on the χ² statistic. We used the χ² statistics of 10 and 20 as thresholds for keeping high-ranked pCREs.

Biological Characteristics of the Most Informative pCRE Set

We selected the minimal set of pCREs (39 root and 40 shoot pCREs) based on the top 100 pCRE-evidence pairs identified with a feature selection algorithm (described in the previous section) and the importance scores for predicting organ salt up-regulation. To determine where these pCREs tend to be located, we mapped pCREs to the organ up-regulated genes as well as randomized sequences. The mapped region included 1 kb upstream and 500 bp downstream of the TSS of the salt up-regulated genes, which were divided into 15 100-bp bins. For comparison, we randomized the 100-bp sequences from the up-regulated gene (while preserving the nucleotide compositions) and mapped the pCREs to these random sequences as well. To identify the functional categories enriched in genes that have pCRE sites in their promoters, Arabidopsis GO slim categories were used. FET was used to assess the statistical significance of enrichment, and the P values were adjusted for multiple testing (Storey, 2003).

Binary Prediction of Root and Shoot Up-Regulated Genes

Although the AUC-ROC is a good measure of the overall performance of machine learning models, it does not indicate how well individual genes are predicted. Thus, it is possible that two models with similar levels of performance as measured by AUC-ROC correctly predict different sets of genes. To assess which genes were predicted by models based on different pCRE sets, and to see if different models correctly predict different sets of genes, the Weka program CrossValidationAddPredictions was used to identify whether a gene was correctly predicted as up-regulated or nonresponsive during salt stress. This program makes a model as described above, but it keeps track of the prediction for each gene. We used the best parameter combination identified from the original grid search as the basis for the binary prediction run. We chose the parameter combinations with the maximum average AUC-ROC. For that given run, maximum F-measure (harmonic mean of precision and recall, calculated using ROCR) was used as the threshold to create binary predictions for each gene. We also assessed the overlap of correctly predicted up-regulated genes (true positives) based on models using different pCRE sets by looking at the percentage of the up-regulated genes correctly predicted by two different models.

Combinatorial Motif Rule Discovery

To test if the combinations of specific pCREs were predictive of salt up-regulation in the root or shoot, the CBA (Ma, 1998) method was used to identify combinatorial rules in the form pCRE A + pCRE B → up-regulation. This method is useful for identifying rules where some combinations of features are associated with a class. The features in our case were the presence or absence of pCRE pairs in a gene promoter, and the class was root or shoot up-regulation. The root or shoot up-regulated and nonresponsive genes were broken up into different subsamples. Each of these subsamples was run through CBA using multiple values for minimum confidence (percentage of genes where pCRE A + pCRE B → up-regulation out of all the instances of pCRE A + pCRE B) and support (percentage of genes with the rule pCRE A + pCRE B → up-regulation). Rules for shoot up-regulated genes were discovered using a minimum support of 0.5% and a minimum confidence of 60%, with a nonresponsive-to-up-regulated ratio of 2:1. We went through several rounds of CBA to discover root rules using different values of support, confidence, and nonresponsive-to-up-regulated ratios. We ended up using a minimum support of 0.1%, a minimum confidence of 60%, and subsamples with 976 nonresponsive genes to 488 responsive genes, which were the same numbers of genes used to generate the shoot rules. These parameters were chosen because the rules generated gave an appreciable gain in the AUC-ROC when performing predictions. Due to the limitation of using the graphical user interface of CBA, we were not able to do an extensive exploration of the best CBA parameter values. Thus, it is possible that there is a more optimal parameter set that will yield a greater performance gain.

To determine if there was a bias in which pCRE subsets were involved in the rules, we categorized each rule as general pCRE + general pCRE, organ pCRE + general pCRE, and organ pCRE + organ pCRE. We performed a χ² test for each rule set, comparing the observed numbers of each rule category with what would be expected if the pCREs were randomly paired together as a rule. The distance between pairs of pCREs in a rule was calculated for all instances of the rules in the putative promoters. The minimal distance between the closest ends of two pCREs was determined. To determine if the minimal distances were significantly different from random expectations, background distributions of pCREs were generated by modeling the frequency of distances between two random pCREs of the same lengths as the pCREs in the rule pair based on an earlier approach (Yu et al., 2006). The only difference in our method was that we compared the observed distance distributions with the background distribution using a Mann-Whitney test instead of a Kolmogorov-Smirnov test, as the Mann-Whitney test can more directly test whether one distribution has higher or lower distances than the other distribution.

Supplemental Data

The following supplemental materials are available.

• Supplemental Figure S1. Distributions of PCCs between TFBMs within and between example TF families.

• Supplemental Figure S2. Contribution of general, root, and shoot pCREs to the prediction of true-positive genes that are globally, root-specifically, and shoot-specifically up-regulated.

• Supplemental Figure S3. Feature selection of pCREs and performance of RF models using selected pCREs.

• Supplemental Figure S4. Distribution of pCRE sites.

• Supplemental Figure S5. Summary of the distance between pairs of motifs in combinatorial rules.

• Supplemental Table S1. CIS-BP and DAP-seq TFBMs used in this study.

• Supplemental Table S2. pCREs identified and their properties.

• Supplemental Table S3. Minimal list of pCREs and their TFBM matches.

• Supplemental Table S4. GO Biological Processes enriched among genes that have the most informative pCRE sites.

• Supplemental Table S5. Combinatorial rules and their TFBM matches.

• Supplemental Table S6. GO Biological Processes enriched among genes that have pCRE combinatorial rules.

• Supplemental Data S1. Log-odds matrix for motif.

Glossary

TF

transcription factor

CRE

cis-regulatory element

pCRE

putative cis-regulatory element

CRC

cis-regulatory code

PCC

Pearson’s correlation coefficient

GO

Gene Ontology

CIS-BP

Catalog of Inferred Sequence Binding Preferences

DAP-seq

DNA Affinity Purification Sequencing

TSS

transcriptional start sites

TFBM

transcription factor binding motif

AUC-ROC

area under curve-receiver operating characteristic

PWM

position weight matrix

ABA

abscisic acid

DHS

DNase I hypersensitivity

CNS

conserved noncoding sequences

FET

Fisher’s exact test

CBA

classification by association

PFMs

position frequency matrices

SVM

Support Vector Machine

RF

Random Forest

Weka

Waikato Environment for Knowledge Analysis