Variable Mesophyll Conductance among Soybean Cultivars Sets a Tradeoff between Photosynthesis and Water-Use-Efficiency^,

Genetic variance for mesophyll conductance among cultivars in both chambers and the field indicate photosynthesis, but not water use efficiency, would be improved by enhancing mesophyll conductance.

Abstract

Photosynthetic efficiency is a critical determinant of crop yield potential, although it remains below the theoretical optimum in modern crop varieties. Enhancing mesophyll conductance (i.e. the rate of carbon dioxide diffusion from substomatal cavities to the sites of carboxylation) may increase photosynthetic and water use efficiencies. To improve water use efficiency, mesophyll conductance should be increased without concomitantly increasing stomatal conductance. Here, we partition the variance in mesophyll conductance to within- and among-cultivar components across soybean (Glycine max) grown under both controlled and field conditions and examine the covariation of mesophyll conductance with photosynthetic rate, stomatal conductance, water use efficiency, and leaf mass per area. We demonstrate that mesophyll conductance varies more than 2-fold and that 38% of this variation is due to cultivar identity. As expected, mesophyll conductance is positively correlated with photosynthetic rates. However, a strong positive correlation between mesophyll and stomatal conductance among cultivars apparently impedes positive scaling between mesophyll conductance and water use efficiency in soybean. Contrary to expectations, photosynthetic rates and mesophyll conductance both increased with increasing leaf mass per area. The presence of genetic variation for mesophyll conductance suggests that there is potential to increase photosynthesis and mesophyll conductance by selecting for greater leaf mass per area. Increasing water use efficiency, though, is unlikely unless there is simultaneous stabilizing selection on stomatal conductance.

Historical increases in crop productivity are attributable primarily to the optimization of two out of the four parameters contributing to yield potential. Yield potentials are a function of incoming solar radiation, the interception efficiency of that radiation by the canopy, the efficiency of converting intercepted radiation into biomass, and the proportion of biomass partitioned to harvestable product (i.e. harvest index; Monteith, 1977). Beginning with the green revolution, major advances in crop yield potential have been realized through maximizing canopy radiation interception efficiency (Evans, 1993) and harvest indices (Hay, 1995). In soybean (Glycine max), interception efficiency has increased through a combination of later maturation leading to longer growing seasons and a decreased susceptibility to lodging (Koester et al., 2014). Likewise, the harvest index is optimized in many modern crops, including soybean, and regularly accounts for 50% or more of aboveground biomass (Hay, 1995). The optimization of harvest indices and interception efficiencies in many of the most widely cultivated crops is nearing its upper limit (Zhu et al., 2010). However, we can improve upon the remaining determinant of yield potential: the efficiency of converting absorbed light to biomass (Beadle and Long, 1985; Slattery et al., 2013; Koester et al., 2014, 2016; Slattery and Ort, 2015).

Because photosynthesis is the primary determinant of conversion efficiency, several routes to improving crop photosynthetic rates have been identified (for review, see Long et al., 2006; von Caemmerer and Evans, 2010; Zhu et al., 2010; Evans, 2013; Ort et al., 2015). Some strategies rely on biological engineering of photosynthetic enzymes: for example, altering Rubisco to reduce photorespiration or to increase carboxylation (Whitney et al., 2011; Betti et al., 2016; Prins et al., 2016) or up-regulating other rate-limiting Calvin cycle enzymes (Lefebvre et al., 2005; Zhu et al., 2007). Another even more ambitious approach aims to reengineer the entire photosynthetic pathway by introducing C₄-type carbon-concentrating mechanisms into C₃ crops (Mitchell and Sheehy, 2006; Sage and Sage, 2009; Sage and Zhu, 2011). An alternative, and potentially more readily achievable, strategy that could improve photosynthetic rates, and possibly water use efficiency (WUE), is to enhance the mesophyll conductance to CO₂ (g_m; Flexas et al., 2013a). Several analyses show that g_m can limit photosynthetic rates at magnitudes similar to stomatal conductance (g_s; Grassi and Magnani, 2005; Galmés et al., 2013; Tomás et al., 2013), and simulations indicate that a doubling of g_m in C₃ crops would result in a nearly 20% boost to photosynthetic rates (Zhu et al., 2010). g_m alters the CO₂ concentration gradient from the substomatal cavity (C_i) to the chloroplast stroma (C_c) and is presumed to be independent of water loss from the leaf. Therefore, an additional advantage of improving photosynthesis through enhancing g_m is the potential for concurrent improvement of WUE.

The expectation that increasing g_m will improve intrinsic WUE (steady-state assimilation [A_N]/g_s) must be tempered by the possibility of a correlation between g_m and g_s (Flexas et al., 2016). A positive relationship between g_m and g_s has been reported in several studies (Barbour et al., 2010; Gu et al., 2012; Flexas et al., 2013a, 2013b), although two studies in wheat (Triticum aestivum) detected no relationship between g_m and g_s (Jahan et al., 2014; Barbour et al., 2016). It is not yet clear if the coordination between g_m and g_s is associated with the independent scaling of both diffusional conductances with the overall physiological activity of leaves or if there is an underlying mechanistic relationship we have yet to appreciate (e.g. reliance on the same aquaporins in both the diffusion path of CO₂ and the outside-xylem portion of hydraulic flow; Flexas et al., 2013b). Given the potential for coordination between g_m and g_s, the absolute value of g_m may be less of a determinant to improving WUE than is the relative value of g_m to g_s (i.e. the ratio g_m/g_s). However, few studies have investigated intraspecific variation in g_m, and fewer still have resolved how g_m and g_s covary.

While theory demonstrates that improving g_m will result in greater photosynthetic rates, the available empirical data on g_m to this point has focused primarily on cross-species comparisons. Surprisingly, less attention has been paid to intraspecific comparisons, where genetic variation in g_m, should it exist, would provide both the genetic material and a guide to select for a reduced diffusional limitation. Across species, g_m varies at least 24-fold in seed plants (Tomás et al., 2013), with the lowest values observed in evergreen trees and shrubs and upper values seen in grasses and herbaceous dicots (Flexas et al., 2008). From the reports currently available, it appears that g_m varies within genera and species, although most attention has focused on grasses. In studies of barley (Hordeum vulgare) and rice (Oryza sativa), where only four cultivars of each were compared, g_m varied among them by ∼30% (Barbour et al., 2010; Adachi et al., 2013). Another study in rice found nearly 60% variation among 11 inbred lines (Gu et al., 2012). In wheat, 2-fold variation was found among 10 genotypes (Jahan et al., 2014) and 3-fold variation among 150 mapping population lines (Barbour et al., 2016). Clearly, genetic variation for g_m exists in the monocots, although in 2014, half of the world’s 10 most planted (as total area) crops were eudicots (FAOSTAT 2016; http://faostat3.fao.org/download/Q/QC/E). Tomato (Solanum lycopersicum) and grape (Vitis vinifera) are the only eudicot food crops for which g_m has been studied at the intrageneric (Muir et al., 2014, 2017) or intraspecific (Galmés et al., 2011; Tomás et al., 2014) level, and estimates of genetic variation for g_m in these and other eudicot crops are lacking, revealing a substantial knowledge gap.

g_m is an emergent trait influenced by many independent leaf properties, with contributions from both structural and biochemical traits (Flexas et al., 2012). Anatomically, higher g_m is associated with thinner cell walls and greater mesophyll cell surface area exposed to intercellular air spaces per unit of leaf area (S_MES; Evans et al., 2009; Terashima et al., 2011). Cell wall thickness does influence the resistance of CO₂ diffusion into cells, but the small variance in cell wall thickness expected among genotypes of short-lived crop leaves developing under uniform conditions should exert little influence on the variance of g_m (Giuliani et al., 2013). However, S_MES partially determines the number of parallel diffusion paths for CO₂ into mesophyll cells and differs among species within genera (Giuliani et al., 2013) and genotypes within species (Galmés et al., 2013), providing a key trait underlying variation in g_m. Leaf density (L_D) and leaf thickness (L_T) combine to determine leaf mass per area (LMA). Across species, the relationship between g_m and LMA is negative (Hassiotou et al., 2009; Niinemets et al., 2009), because species with higher LMA have thicker cell walls and greater cell densities leading to reduced S_MES. Within species, particularly those with relatively thin leaves such as soybean, only the upper limit of g_m seems controlled by LMA (Flexas et al., 2008), which may reflect an altered LMA-S_MES relationship at lower values of LMA (Milla-Moreno et al., 2016). For species with low LMA leaves, at the intraspecific level, the components of LMA (i.e. L_D and L_T) or LMA itself may provide meaningful predictors of g_m as proxies for S_MES.

We used soybean as a model eudicot crop to assess how g_m varied across cultivars and covaried with leaf physiological and structural traits associated with photosynthesis (Table I). We addressed several questions. (1) Does A_N scale with g_m as strongly across cultivars of soybean, a thin-leafed eudicot, as reported for other crops and cross-species comparisons? (2) If g_m does scale with A_N, then does genetic variation exist for this trait? (3) Is WUE greater in cultivars with greater g_m, or (4) is scaling between g_m and WUE precluded by coordination between g_m and g_s? And (5) is LMA, or are its components, predictive of g_m? We hypothesized that (1) the role of g_m on carbon supply would lead to coordination with A_N, (2) any correlation between g_m and g_s would result in no detectable relationship between WUE and g_m, and (3) leaves with greater LMA, thickness, and density would exhibit lower g_m. These hypotheses were tested on 12 cultivars of edamame soybean grown under controlled conditions and then examined further in eight of those cultivars at three growth stages under field conditions. Analyses in two environments and across three growth stages gave us a robust design with which to assess the variation and covariation of g_m among cultivars, providing confidence in results that were consistent across these groups.

Table I. List of all traits estimated in this study, the symbols used throughout the text, and their units.

Category and Trait	Symbol	Units
Leaf function
Apparent photorespiratory CO2 compensation point	Ci*	Pa
Mitochondrial respiration in the light	Rd	µmol CO2 m−2 s−1
Absorptance at 470 and 665 nm	α	unitless
Chlorophyll content	SPAD	unitless
Net assimilation rate	AN	µmol CO2 m−2 s−1
Maximum light- and CO2-saturated assimilation rate	Amax	µmol CO2 m−2 s−1
Stomatal conductance to water vapor	gs	mol water m−2 s−1
Stomatal conductance to CO2	gs-co2	mol CO2 m−2 s−1
Mesophyll conductance	gm	µmol CO2 m−2 s−1 Pa−1
Ratio of mesophyll to stomatal conductance	gm/gs-co2	mol CO2 mol−1 CO2
Intrinsic WUE	AN/gs	µmol CO2 mol−1 water
Integrated WUE, the ratio of 13C to 12C of leaf tissue	δ13C	‰
Calibrated linear electron transport rate	Jcal	µmol electrons m−2 s−1
CO2 concentration gradient between intercellular air spaces and chloroplast stroma	Ci-Cc	µmol CO2 mol−1 air
Nitrogen concentration	Nmass	% (w/w)
Nitrogen concentration per area	Narea	mg N m−2 leaf
Leaf structure
Leaf thickness	LT	mm
Leaf density	LD	g cm−3
Leaf mass per area	LMA	g m−2
Leaf dry matter content	LDMC	g dry weight g−1 fresh weight

RESULTS

Parameters Used to Estimate g_m

To improve the accuracy of our variable-J estimates of g_m, we determined the apparent photorespiratory CO₂ compensation point (C_i*) and day respiration rate (R_d) for all soybean cultivars. C_i* and R_d were estimated from Laisk curves on chamber-grown plants (n = 5–8 and n = 72). Mean C_i* was 4.08 ± 0.058 (se) Pa CO₂, and mean R_d was 0.937 ± 0.036 µmol CO₂ m⁻² s⁻¹. Both C_i* and R_d differed among cultivars (P < 0.05; Table II; Supplemental Fig. S1), although only cultivar-specific R_d vales were used, under the presumption that the true photorespiratory compensation point (Γ*) should not vary across such closely related plants. A sensitivity analysis examining how variable Γ* alters estimates of genetic variance for g_m among cultivars revealed that g_m does depend on Γ*, but the effects of Γ* on genetic variance in g_m were minimal (Supplemental Fig. S2). The mean C_i* here falls between the value of Γ* from tobacco (Nicotiana tabacum; Bernacchi et al., 2002) commonly used for soybean (Bernacchi et al., 2005; Rosenthal et al., 2014; Köhler et al., 2017) and a value calculated from soybean Rubisco kinetic properties (Gallé et al., 2013), and it further matches exactly the C_i* estimated for soybean with similar methodology (Walker and Ort, 2015). Thus, the mean C_i* value was used as a proxy for Γ* in all calculations. Cultivar-specific R_d values were used here and ranged from 0.63 to 1.32 µmol CO₂ m⁻² s⁻¹ (Supplemental Fig. S1). Since these R_d values were estimated from plants grown in a controlled environment only, we performed a sensitivity analysis to assess how variation in R_d would alter estimates of genetic variance for g_m from field-grown plants (Supplemental Fig. S3) by recalculating g_m for all field measurements using an unvarying R_d for all cultivars ranging from 0.5 to 1.5 µmol m⁻² s⁻¹. Estimates of genetic variance in g_m were nearly unresponsive to this magnitude variation in R_d (Supplemental Fig. S3).

Table II. Variance partitioning within and between cultivars for traits measured as part of the controlled environment experiment and those used for both experiments (i.e. C_i* and R_d).

Variance attributed to cultivar provides an upper limit estimate of the contribution of genetics to observed trait variability. Trait abbreviations are as in Table II. Min and Max are the minimum and maximum trait values. The variance components were estimated by partitioning variance within and between cultivars with restricted maximum likelihood (REML).

Trait	Range		Variance Components		Variance Attributed to Cultivar
	Min	Max	Cultivar	Residual
					%
Ci*	3.07	5.60	4.172 × 10−2	0.20434	17.00
Rd	0.327	1.57	1.904 × 10−2	7.773 × 10−2	19.68
α	0.843	0.917	8.876 × 10−5	1.965 × 10−4	31.12
SPAD	28.0	41.5	1.909	5.341	26.33
AN	15.9	27.8	2.905	4.772	37.84
Amax	19.5	38.9	6.113	20.415	23.04
gs	0.155	0.421	6.174 × 10−4	3.1206 × 10−3	16.52
gs-co2	0.0966	0.263
gm	1.22	2.71	4.224 × 10−2	6.66 × 10−2	38.81
gm/gs-co2	0.410	1.21	0	0.5102	0
Ci-Cc	90.2	144	18.33	97.64	15.81
AN/gs	55.1	109	0	170.4	0
Jcal	135	219	127.2	283.4	31.00
LT	0.163	0.285	1.025 × 10−4	6.704 × 10−4	13.26
LD	0.0771	0.181	1.035 × 10−4	5.356 × 10−4	16.19
LMA	20.1	39.1	1.113 × 10−16	27.14	0
LDMC	0.163	0.241	4.402 × 10−5	2.963 × 10−4	12.93

Leaf absorptance at 470 and 665 nm (α; Table I) was measured on all plants to constrain the calibration of electron transport rates used in the estimation of g_m. Absorptance averaged 0.89 (range, 0.82–0.96; Tables II and III; Supplemental Fig. S4). Under both controlled and field conditions, cultivar identity was a significant source of variation in absorptance (P < 0.01) primarily attributable to one cultivar that also had consistently greater relative chlorophyll content, as assessed with a clamp-on chlorophyll meter. Absorptance increased with plant growth stage in the field (P < 0.001) and overall was greater for field-grown plants than for those grown in chambers. Relative chlorophyll content differed among cultivars under both field and controlled environment conditions (P < 0.01). Nitrogen concentrations were determined for the field-grown plants; these did not differ among cultivars on a leaf-area or leaf-mass (w/w) basis. Nitrogen content per leaf area increased with growth stage in the field (Table III; P < 0.001), while nitrogen per leaf mass peaked at the early reproductive growth stage (P < 0.001).

Table III. ANOVA statistics from linear mixed-effects models for traits measured in the field experiment.

For each trait, the growth stage of measurement was treated as a fixed effect, and cultivar identity was treated as a random effect to partition phenotypic variance to within and between cultivars. Trait abbreviations are as in Table II. Min and Max are the minimum and maximum trait values. Model degrees of freedom are type III Satterthwaite approximates. Variance components were estimated by partitioning variance within and between cultivars with REML. Significance levels are as follows: n.s., P > 0.05, and ***, P < 0.001 after adjusting for multiple comparisons. Effects were not estimated for g_s-co2, since it is a direct transformation of g_s.

Trait	Range		Growth Stage, Fixed Effect		Variance Component		Variance Attributed to Cultivar
	Min	Max	F2,78-86	P	Cultivar	Residual
							%
α	0.815	0.955	59.5	***	8.007 × 10−5	3.445 × 10−4	18.86
SPAD	25	54.8	129.1	***	4.291	11.848	26.59
AN	7.8	33.4	3.0	n.s.	4.84	18.08	21.12
gs	0.0988	0.585	35.2	***	8.88 × 10−4	7.29 × 10−3	10.86
gs-co2	0.0618	0.365
gm	0.39	2.42	8.7	***	0.0178	0.1357	11.60
gm/gs-co2	0.445	1.389	33.4	***	0.00	2.186 × 10−2	0.00
Ci-Cc	62.0	229.8	14.0	***	76.91	553.91	12.19
AN/gs	41.5	114.0	67.1	***	0.00	116	0.00
δ13C	−31.31	−26.2	107.8	***	0.1842	0.3746	32.96
Jcal	95.0	300.4	1.1	n.s.	346.7	2164.3	13.81
Narea	0.380	3.163	55.5	***	9.855 × 10−3	0.1702	5.47
Nmass	1.937	5.891	19.9	***	0.00	0.4463	0.00
LT	0.145	0.3025	39.8	***	1.602 × 10−5	6.741 × 10−4	2.32
LD	0.105	0.281	184.2	***	1.355 × 10−4	5.387 × 10−4	20.10
LMA	19.6	80.8	147.4	***	5.001	67.21	6.93
LDMC	0.172	0.374	244.6	***	1.308 × 10−4	5.5574 × 10−4	19.01

Physiological and Structural Trait Variations among Cultivars

When grown in controlled environment chambers, phenotypic variance in leaf structure and physiology varied to similar extents across the 12 cultivars studied. Among cultivars, variance was greater for physiological than for structural traits (Table II). Calibrated electron transport rate (J_cal) ranged 1.6-fold with cultivar, explaining 31% of the variance. Cultivar identity contributed little to the 2.7-fold variance in g_s, while g_m ranged 2.2-fold, with 38.8% of total phenotypic variance in g_m found among cultivars. Differences in g_m led to variation in the CO₂ concentration gradient between C_i and C_c (C_i-C_c), where 15.8% of the variance was explained by cultivar. A 1.7-fold range in A_N was observed, with 37.8% of the variance among cultivars. Little of the phenotypic variance in structural traits was explained by cultivar (Table II).

Eight of the 12 cultivars also were grown in the field and measured at three growth stages that corresponded to late vegetative (V4 and V5), early reproductive (R2–R4), and late reproductive (R6) periods. Cultivar identity and growth stage both affected phenotypic trait variation in the field (Table III). Cultivar tended to have a greater effect on physiological traits, while growth stage tended to have stronger effects on structural traits (Table III). For instance, among cultivars, variance was 13.8% for J_cal and 21.1% for A_N; neither trait differed by growth stage (Table III; Supplemental Fig. S5, A and D). g_s was highest during vegetative growth in July at 425 ± 18 mmol m⁻² s⁻¹ (mean ± se), then declined through reproductive growth to a low of 236 ± 18.3 mmol m⁻² s⁻¹ during the late reproductive stage in September (Supplemental Fig. S5B), seemingly tracking precipitation (Supplemental Fig. S6). g_m (Supplemental Fig. S5C) and C_i-C_c (data not shown) behaved similarly; both g_m and C_i-C_c were indistinguishable between vegetative and early reproductive growth, then g_m declined at the late reproductive stage, resulting in an increase of C_i-C_c (Table III). Phenotypic variance attributed to cultivar for g_s, g_m, and C_i-C_c, was lower in the field than in the controlled environment (compare Tables II and III). Intrinsic (A_N/g_s) and integrated (δ¹³C) WUE tracked g_s throughout the season (i.e. A_N/g_s increased steadily while δ¹³C became less negative from late vegetative to late reproductive growth). None of the variance in A_N/g_s was contributed by cultivar identity, while one-third of the variance in δ¹³C was among cultivars (Table III).

Leaf structural traits differed among cultivars and more strongly between growth stages. Although the youngest fully expanded top-canopy leaves were always sampled, the leaves sampled at the late reproductive stage were clearly older and more robust than those sampled earlier in the season. L_T differed negligibly among cultivars, but it did increase at the late vegetative growth stage (Table III). Among cultivars, variance explained some variation in L_D and leaf dry matter content (LDMC), although again, the largest differences were observed at the late reproductive growth stage (R6). Environmental variance and development dominated variation in LMA, which increased slightly between vegetative and early reproductive growth and 1.8-fold in the late reproductive stage, with no detectable among-cultivar contribution (Table III).

Trait Correlations with g_m

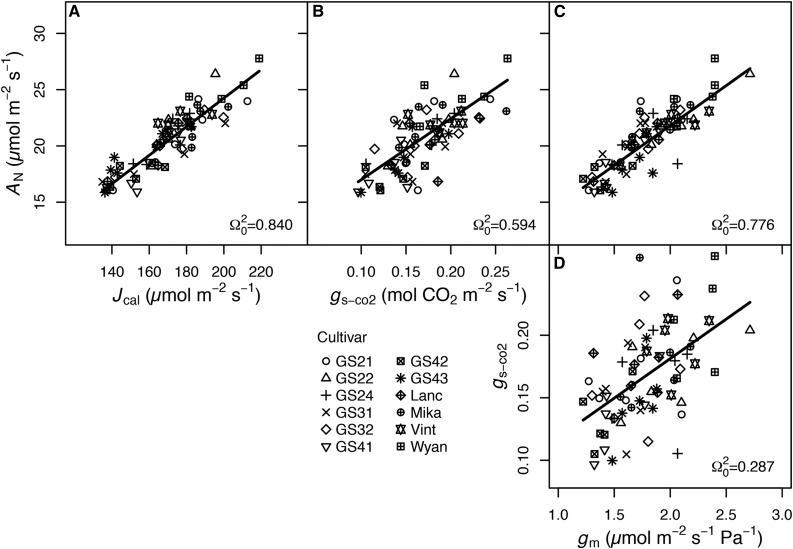
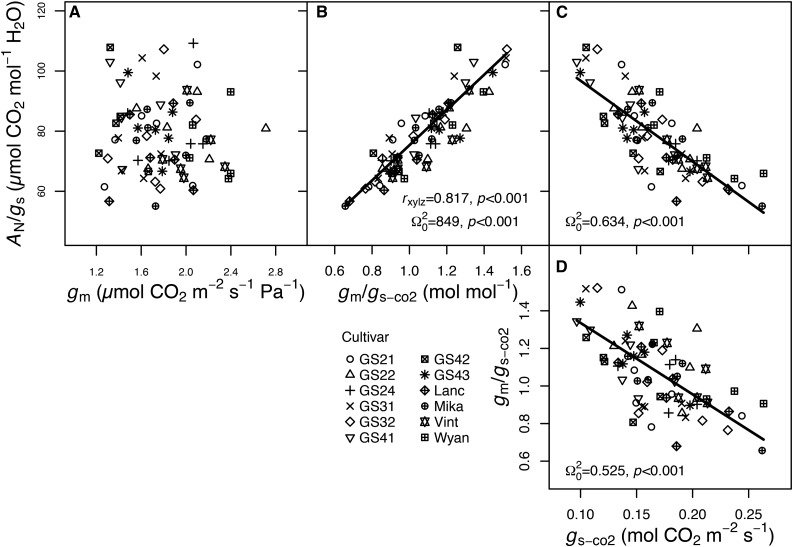
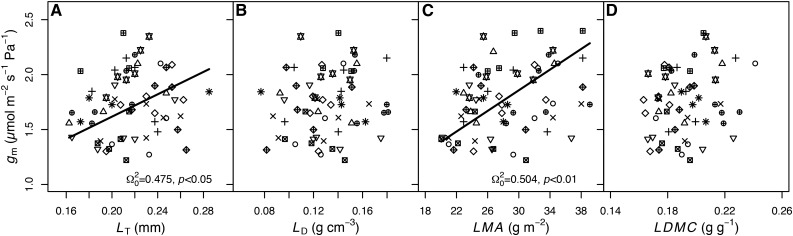
In the controlled environment, most physiological traits were correlated with one another, and cultivar identity often explained modest amounts of variance in these relationships (Table IV). Steady-state photosynthetic rate was closely coupled with J_cal (coefficient of determination [Ω²₀] = 0.84, P < 0.001), g_s-co2 (Ω²₀ = 0.594, P < 0.001), and g_m (Ω²₀ = 0.776, P < 0.001; Fig. 1, A–C), with 14.5%, 11.3%, and 10.4%, respectively, of the variance in these relationships found among cultivars. The two diffusional conductances to CO₂, g_m and g_s-co2, were correlated (Ω²₀ = 0.287, P < 0.001; Fig. 1D), and cultivar identity was responsible for 23.3% of the variation in this relationship. No relationship between intrinsic WUE (A_N/g_s) and g_m was detected (P > 0.1; Fig. 2A). We separated the effects of g_m on A_N/g_s without the confounding correlation of g_m with g_s-co2 by analyzing the relationship between the ratio of g_m/g_s-co2 and A_N/g_s. There was a strong positive relationship between g_m/g_s-co2 and A_N/g_s (Ω²₀ = 0.849, P < 0.001; Fig. 2B), with 19.7% of the variance among cultivars. The correlation between g_m/g_s-co2 and A_N/g_s may be spurious, because g_s is in the denominator of both terms (i.e. both A_N/g_s and g_m/g_s-co2 declined with increasing g_s or g_s-co2; Fig. 2, C and D). However, when controlling for g_s, the partial correlation of A_N/g_s and g_m/g_s-co2 was still significant (r_xy|z = 0.817, P < 0.001). g_m was positively correlated with LMA (Ω²₀ = 0.504, P < 0.01; Fig. 3C) and not correlated with LDMC. Of the components of LMA, L_T, and L_D, only L_T was significantly associated with g_m (Ω²₀ = 0.475, P < 0.05; Fig. 3A).

Table IV. Estimates of cultivar effect on bivariate relationships for the controlled environment and field experiments.

Variance components were estimated with REML. Significance of the cultivar effect was determined with likelihood ratio tests, and P values were adjusted for multiple testing. Significance levels are as follows: n.s., P > 0.05; *, P < 0.05; and **, P < 0.01. Abbreviations are as in Table II.

Experiment	Trait 1	Trait 2	Variance Explained by Cultivar	P
			%
Controlled environment	AN	gs	11.3	n.s.
	AN	gm	10.4	n.s.
	AN	Jcal	14.5	*
	gm	gsco2	23.3	*
	gm	Jcal	24.5	**
	AN/gs	gm	0	n.s.
	AN/gs	Ci-Cc	0	n.s.
	AN	LMA	33.6	**
	gm	LT	41.1	**
	gm	LD	32.8	**
	gm	LMA	36.1	**
	gm	LDMC	33.4	**
Field	AN	gs	13.6	n.s.
	AN	gm	1.97	n.s.
	AN	Jcal	0	n.s.
	gm	gsco2	0	n.s.
	gm	Jcal	0	n.s.
	AN/gs	gm	1.11	n.s.
	δ13C	gm	27.3	**
	δ13C	Ci/Ca	41.3	**
	AN/gs	Ci-Cc	0	n.s.
	AN	LMA	11.2	n.s.
	gm	LT	9.20	n.s.
	gm	LD	6.33	n.s.
	gm	LMA	6.91	n.s.
	gm	LDMC	11.6	n.s.

Figure 1.

Relationships between light-saturated A_N and total J_cal (A), g_s-co2 (B), and g_m (C) and between g_s-co2 and g_m (D) for the 12 soybean cultivars grown in the controlled environment experiment. Symbols for the different cultivars are indicated (n = 5–6 replicates). Regression lines and Ω²₀ are from linear mixed-effects models (in all cases, P < 0.01).

Figure 2.

Relationships between A_N/g_s and g_m (A), g_m/g_s-co2 (B), and g_s-co2 (C) and between g_m/g_s-co2 and g_s-co2 (D) for the 12 soybean cultivars in the controlled environment experiment. Different symbols represent the different cultivars as indicated (n = 5–6 replicates). Regression lines, Ω²₀, and P values are from linear mixed-effects models. In B, the partial correlation (r_xy|z) of A_N/g_s with g_m/g_s-co2 after accounting for g_s also is presented.

Figure 3.

Relationships between g_m and leaf structural traits, LMA (A), L_T (B), L_D (C), and LDMC (D), for chamber-grown soybean from the controlled environment experiment. Different symbols indicate different cultivars as indicated in Figures 1 and 2 (n = 5–6 replicates). Regression lines, Ω²₀, and P values are from linear mixed-effects models with cultivar as a random effect.

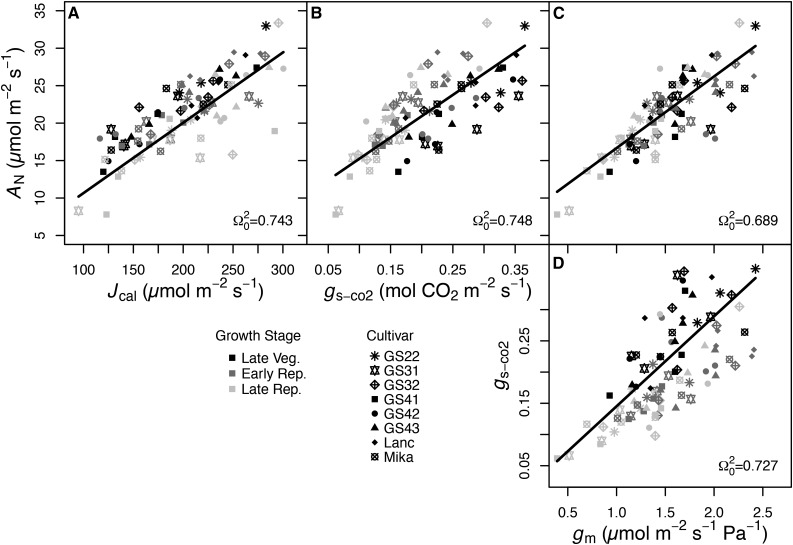
In the field, correlations among physiological traits were generally strong and often modified across growth stages. To examine the effects of among-cultivar trait variation independent of growth stage, linear mixed-effects models were fit treating both the predictor trait and growth stage as fixed effects and cultivar identity as a random effect. Steady-state assimilation was coordinated with CO₂ supply as g_s-co2 (Ω²₀ = 0.748, P < 0.001), g_m (Ω²₀ = 0.689, P < 0.001), or total CO₂ conductance (Ω²₀ = 0.795; data not shown), and with reductant supply as J_cal (Ω²₀ = 0.743, P < 0.001; Fig. 4, A–C). Bivariate relationships of g_s-co2 and J_cal with A_N differed among growth stages (P < 0.001 for each), and the relationship between A_N and g_m was not modified by growth stage. g_m and g_s-co2 were correlated (Ω²₀ = 0.611, P < 0.001) and differed by growth stage (P < 0.001; Fig. 4D). Intrinsic WUE was not significantly related to g_m, but δ¹³C was negatively correlated with g_m (Ω²₀ = 0.780, P < 0.05; Fig. 5, A and C), and 27% of the variance in this relationship was among cultivars (Table IV). The ratio of intercellular to ambient [CO₂] (C_i/C_a) was negatively correlated with A_N/g_s (P < 0.001), but not δ¹³C (Fig. 5, B and C), although, in both cases, growth stage modified the relationships (P < 0.001). A strong positive relationship existed between A_N/g_s and g_m/g_s-co2 (Ω²₀ = 0.762, P < 0.001; Supplemental Fig. S7A). As in the controlled environment, this is due partly to spurious correlation with g_s in both denominators (Supplemental Fig. S7, B and C). After controlling for spurious correlation with a partial correlation analysis, the effect size was reduced, but the positive A_N/g_s-g_m/g_s-co2 relationship did remain significant (r_xy|z = 0.605, P < 0.001).

Figure 4.

Relationships between steady-state A_N and total J_cal (A), A_N and g_s-co2 (B), A_N and g_m (C), and g_s-co2 and g_m (D). Data are from the eight soybean cultivars in the field experiment and measured at the late vegetative (V5 and V6; black symbols), early reproductive (R2–R4; dark gray symbols), and late reproductive (R6; light gray symbols) growth stages. Different symbols represent different cultivars as indicated, with n = 4 replicates for each cultivar-growth stage combination except GS22, where n = 3. Ω²₀ and regression lines are from linear mixed-effects models with the x variable and growth stage as predictors and cultivar treated as a random effect (P < 0.001 for all).

Figure 5.

Relationships between A_N/g_s and g_m (A), A_N/g_s and C_i/C_a (B), δ¹³C and g_m (C), and δ¹³C and C_i/C_a (D) from the field experiment. Different symbols represent different cultivars (see Fig. 4 legend) with n = 4 replicates, and shading represents late vegetative (V4 and V5; black symbols), early reproductive (R2–R4; dark gray symbols), and late reproductive (R6; light gray symbols) growth stages. The dashed line is marginally significant (P < 0.1), while the solid lines are significant (P < 0.05), according to linear mixed-effects models with growth stage and the variable on the x axis as fixed effect predictors and cultivar identity as a random effect. In all cases, growth stage was a significant predictor (P < 0.001). Cultivar identity significantly improved model fit in C and D (P < 0.001).

Covariation between structural and physiological traits was generally low, resulting from the substantially higher LMA and L_D at the late reproductive stage. Within the late vegetative and early reproductive growth stages, positive relationships were observed between g_m and LMA or L_D (Supplemental Fig. S8), leading to marginally significant (P < 0.1) relationships for g_m versus LMA and g_m versus L_D across all stages after correcting for multiple comparisons. g_m was not associated with L_T or LDMC (Supplemental Fig. S8). Development had a strong effect on all these relationships: that is, without accounting for growth stage, the correlation of g_m with these structural traits becomes negative (positive above) because of a significant decrease in g_m and increase in LMA, L_T, and L_D observed at the late reproductive (R6) stage. As expected, across all three growth stages, L_T, L_D, and LMA were each positively correlated with A_N (P < 0.01; data not shown).

Trait Correlations Were Consistent between Experiments

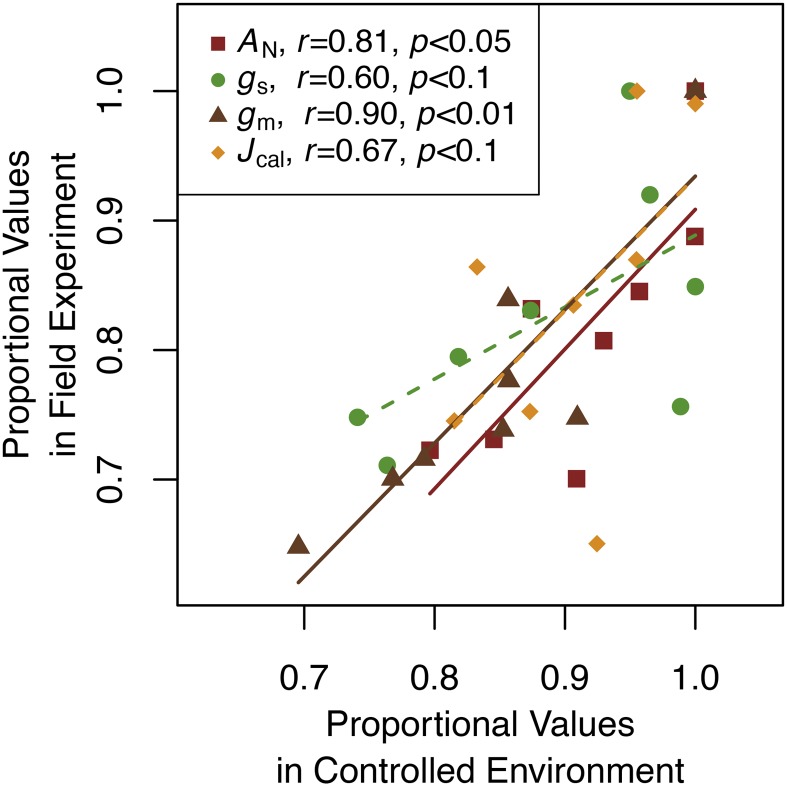
To test the consistency of key trait rankings between the controlled environment and field experiments, we compared standardized (see “Materials and Methods”) cultivar-mean A_N, J_cal, g_m, and g_s from the late vegetative growth stage from the field with those measured in the controlled environment (all chamber plants were measured at the late vegetative stage). Using Spearman’s rank correlations, A_N (r = 0.81) and g_m (r = 0.9) were consistent between experiments (after adjusting for multiple comparisons; P < 0.05 for both; Fig. 6). Electron transport (r = 0.67) and g_s (r = 0.6) were somewhat consistent between chambers and field environments (P < 0.1; Fig. 6). Regression slopes also were tested for consistency across both environments and growth stages using standardized major axis regression (Supplemental Table S1). Of the 42 possible comparisons, slopes differed in just nine cases, all of which were comparisons of slopes from chamber-grown plants with field-grown plants (Supplemental Table S1), indicating that trait correlations were similar between environments and were especially stable among growth stages in the field.

Figure 6.

Consistency among estimates of A_N, g_s, g_m, and J_cal for late vegetative (V2–V4) growth stage soybean plants grown in a controlled environment or in the field. Symbols are cultivar-mean values standardized as a proportion of maximum cultivar-mean trait values. Correlations and P values are Spearman-rank correlations adjusted for multiple comparisons. Solid lines indicate significant relationships (P < 0.05), and the dashed line is marginally significant (P < 0.1).

Trait Coordination

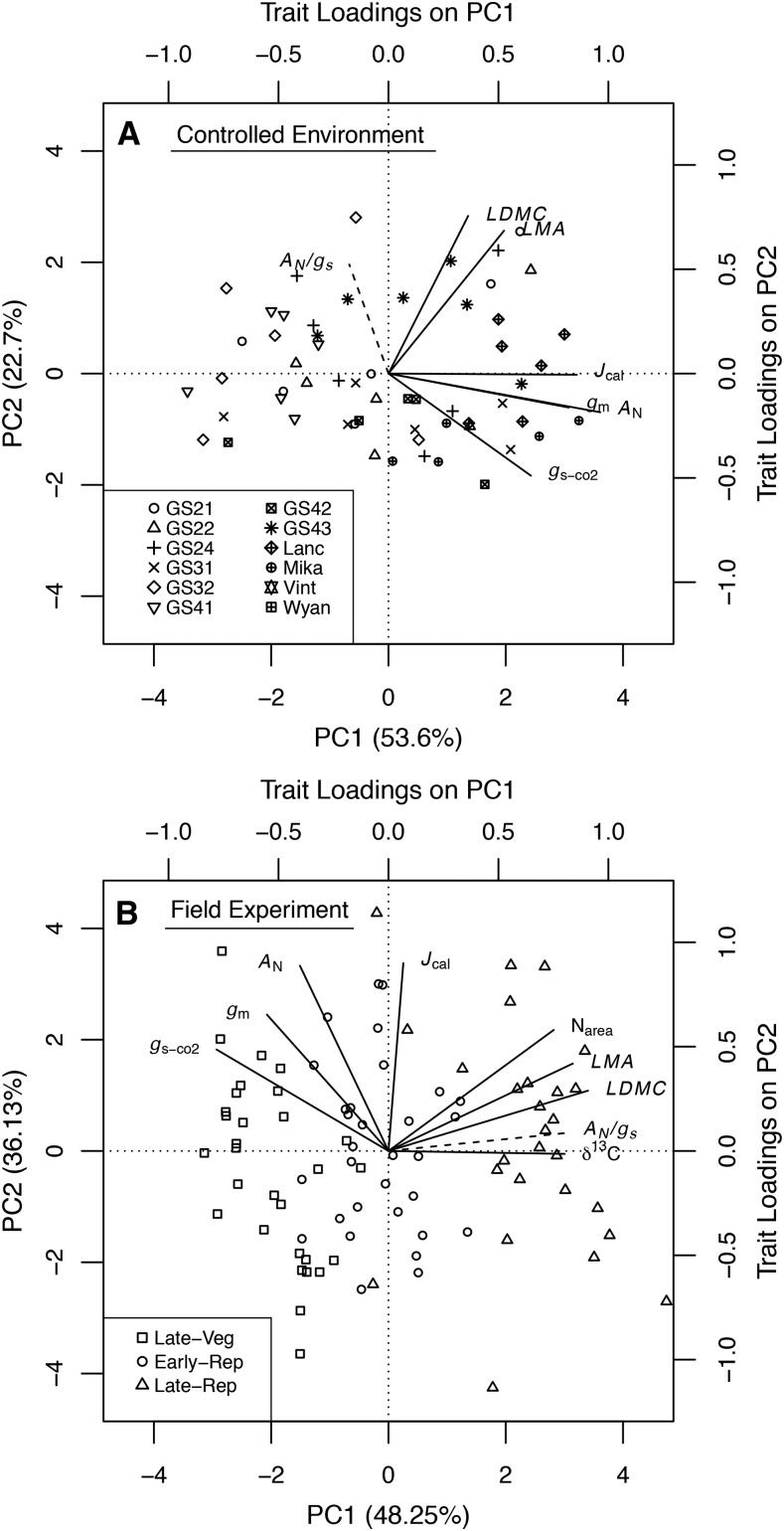
To better understand multivariate trait coordination, we performed principal component analyses with all major traits for both controlled environment and field experiments. Of particular interest were the relationships of intrinsic (A_N/g_s) and integrated (δ¹³C) WUE with g_s-co2, g_m, and A_N as well as the relationships between physiological and structural traits. For the controlled environment experiment, the first two principal components cumulatively explained 76.3% of the variance (53.6% and 22.7%, respectively). Physiological traits loaded most heavily with the first principal component (PC1) and structural traits with the second principal component (PC2; Fig. 7A). All traits loaded positively with PC1, indicating coordination between greater photosynthetic activity and more structurally robust leaves. On PC2, the structural traits loaded positively while A_N, g_m, and especially g_s-co2 had slightly negative loadings, suggesting a tradeoff in the positive scaling of structure and physiology. Because A_N/g_s is a direct combination of other traits, it was not used in fitting the principal component analysis but was mapped after fitting (see “Materials and Methods”). When mapped, A_N/g_s plotted nearly orthogonal to the g_s-co2 loading in the trait space of the first two principal components (Fig. 7A), indicating a CO₂ supply-water loss tradeoff and that, under chamber conditions, intrinsic WUE was primarily influenced by g_s.

Figure 7.

Principal component analyses for the main traits investigated here from the controlled environment experiment on 12 cultivars of soybean (A) and the field experiment on eight of the same cultivars (B). A_N, g_s-co2, g_m, J_cal, LMA, and LDMC were used in the fitting in A and B. Additionally, in B, N_area and δ¹³C were used in the fitting. A_N/g_s (dashed lines) was mapped in the trait space in both A and B. In A, different symbols indicate different cultivars, while in B, they indicate different soybean growth stages.

In the field experiment, the first two principal components accounted for 84.4% of the variation (48.3% and 36.1%, respectively). A tradeoff between CO₂ supply (g_s-co2 and g_m) and leaf structural robustness and water loss was present on PC1, where structural traits (LMA, LDMC, and nitrogen content per leaf area [N_area]) and δ¹³C loaded positively while A_N, g_m, and especially g_s-co2 loaded negatively (Fig. 7B). Leaves with greater LMA and higher LDMC had lower g_s-co2 and, in turn, greater δ¹³C. There was positive coordination among all traits except δ¹³C along PC2. Intrinsic (A_N/g_s) WUE mapped to nearly the same location as δ¹³C, and both were inversely located relative to A_N, g_m, and especially g_s-co2 on PC1. Individual observations within each growth stage were scattered widely across PC2. A clear pattern was apparent along PC1, with late vegetative observations clustering on the negative end (i.e. with greater physiological trait values), early reproductive observations clustering around zero, and late reproductive observations clustering on the positive end with greater leaf structural robustness.

Important similarities in trait coordination and tradeoffs emerged under both controlled and field environments. Physiological traits associated with carbon uptake (i.e. A_N and J_cal) loaded heavily on one principal component and structural traits or WUE traits with the other principal component. In both cases, g_s and g_m had the same directionality of loadings on the first two principal components, but g_s-co2 loaded more strongly along the second principal component, indicating some variance in g_s-co2 independent of g_m (Fig. 7). For both experiments, A_N and g_m were more closely associated with one another than either was with g_s-co2, and mapping of A_N/g_s was to a greater extent in opposition to g_s-co2 than in accordance with A_N. Thus, in both chamber- and field-grown plants, there was some coordination and some tradeoff between leaf structure (as LMA or LDMC) and the physiological traits A_N and g_m.

DISCUSSION

Enhancing g_m can improve carbon assimilation and may improve intrinsic WUE (Flexas et al., 2013a, 2016) and yield potential in C₃ crops (Slattery et al., 2013). Consistent with some recent studies (Barbour et al., 2010, 2016; Galmés et al., 2011; Gu et al., 2012; Giuliani et al., 2013; Jahan et al., 2014), we found strong support for the relationship between A_N and g_m. g_m is reported to respond to environmental stimuli and stress at time scales ranging from seconds to seasons (Bernacchi et al., 2002; Grassi and Magnani, 2005; Galmés et al., 2007; von Caemmerer and Evans, 2015; Sorrentino et al., 2016). Here, the relationship between A_N and g_m among 12 soybean cultivars spanning five maturity groups is consistent between growth chamber and field experiments and across developmental stages (Figs. 1 and 4). The consistent relative rankings of cultivars for g_m and A_N indicates that there is genetic differentiation for g_m in soybean. The degree to which g_m is genetically determined remains to be fully quantified (Barbour et al., 2016), but our results indicate that there is potential for selection on g_m to improve carbon assimilation.

Our second hypothesis was partially supported. We found no significant relationship between A_N/g_s and g_m (Figs. 2A and 5A); this is consistent with results in rice (Giuliani et al., 2013) and wheat (Jahan et al., 2014), while a negative correlation was found in well-watered and water-stressed tomato (see Supplemental Table S1 in Galmés et al., 2011). The disparity between the prevailing assumption that enhancing g_m will improve A_N/g_s (Flexas et al., 2013a, 2016) and data inconsistent with this idea stems from the correlation between g_m and g_s reported here (Figs. 1 and 4) and elsewhere (Barbour et al., 2010; Galmés et al., 2011; Gu et al., 2012; Giuliani et al., 2013). The similarity of responses of g_m and g_s to water stress, salt stress, light, and CO₂ led to the hypothesis that g_m and g_s are inextricably coregulated (Flexas et al., 2008; Vrábl et al., 2009; Sorrentino et al., 2016). Yet, g_m and g_s can vary independently. Tazoe et al. (2011) elegantly demonstrated that g_m was unchanged while g_s differed in wild-type compared with ost1 Arabidopsis (Arabidopsis thaliana) mutants with stomata unresponsive to abscisic acid (ABA) or drought (Mustilli et al., 2002). Likewise, Vrábl et al. (2009) concluded that the link between g_m and g_s in wheat is flexible, since g_s but not g_m declined after ABA treatment, although others have observed that g_s and g_m decline in unison following ABA treatment (Sorrentino et al., 2016). g_s also is highly sensitive to the leaf-to-air vapor pressure deficit (VPD), and Warren (2008) reported that g_s could be altered by varying VPD without affecting g_m. Outside of two studies in wheat (Jahan et al., 2014; Barbour et al., 2016), either no relationship, or a negative relationship, has been found between g_m and A_N/g_s. The extent of coordination between g_m and g_s seems to vary within and among species and even between the cultivars measured here (Supplemental Fig. S5, B and C). And given the potential for g_s to respond to environmental stimuli independent of g_m, we speculate that inconsistencies in the A_N/g_s versus g_m relationship among studies may arise simply from variation in measurement conditions or may indicate that these relationships are species or genotype specific (Perez-Martin et al., 2009). Finally, the tendency for a negative A_N/g_s versus g_m relationship also was apparent among aquaporin transformants expressing altered g_m (Flexas et al., 2016), raising the possibility that variation in aquaporin expression (Perez-Martin et al., 2014) might explain genotypic, environmental, or developmental differences in g_m reported here and in the literature.

Do dynamic tradeoffs between g_m and A_N/g_s affect WUE throughout the growing season? Seasonally integrated WUE can be estimated from leaf carbon isotope ratios (δ¹³C; Farquhar et al., 1989). When stomata close, A_N/g_s increases and substomatal [CO₂] (C_i) decreases relative to atmospheric [CO₂] (C_a). Consistently lowered C_i leads to lower discrimination (Δ) against ¹³C by Rubisco. Therefore, Δ is proportional to the C_i/C_a ratio, and δ¹³C in leaf dry matter is interpreted as resulting from the mean leaf lifetime C_i/C_a ratio, which can be related to A_N/g_s. Larger values of δ¹³C can be interpreted as higher integrated WUE as long as the leaf-to-air VPD does not vary among samples (Farquhar et al., 1989). From our gas exchange, we see that g_m and g_s-co2 were correlated (Fig. 4); thus, we observed both greater C_i and C_c with greater g_m, allowing Rubisco to discriminate against ¹³CO₂ to a greater extent, yielding more negative δ¹³C values. Since the δ¹³C of leaves from the field-grown plants was inversely associated with g_m (Fig. 5C), we conclude that cultivars with higher g_m had lower integrated WUE. The only other study measuring δ¹³C and g_m in an intraspecific crop comparison (Giuliani et al., 2013) found a nonsignificant, but also negative, relationship between the traits. We recognize that g_m itself alters carbon isotope fractionation, since it partly determines C_c. No direct relationship was seen between C_i/C_a and δ¹³C, indicating that some variation in δ¹³C was unrelated to WUE and likely was a result of variation in g_m (Seibt et al., 2008).

Can we simultaneously increase assimilation and water efficiency in soybean? Optimizing both WUE and A_N will require selection for a greater g_m-to-g_s-co2 ratio and not g_m in isolation (Flexas et al., 2013a). We did find a consistent positive relationship between A_N/g_s and g_m/g_s-co2 and, in the field, a positive relationship between δ¹³C and g_m/g_s-co2. Similar positive intraspecific scaling of A_N/g_s and g_m/g_s has been found in tomato (Galmés et al., 2011), rice (Giuliani et al., 2013), and grape (Tomás et al., 2014). Together, these results indicate that WUE could be improved by increasing g_m, but only at a common g_s. After controlling for g_s in the denominator of both A_N/g_s and g_m/g_s-co2 using partial correlations, the strength of these relationships was greatly reduced but still significant (Fig. 2; Supplemental Fig. S7). Corroborating evidence from the principal component analyses indicates that the variation in A_N/g_s was driven more by variation in g_s than in A_N. While the A_N/g_s-g_m/g_s correlation is clearly significant with meaningful effects in other studies (Flexas et al., 2013a), the spurious nature of the relationship in our data set indicates that care should be taken when interpreting this relationship in future studies. Ultimately, our data support a framework of enhancing A_N through selection for increased cultivar-mean g_m but not simultaneous improvements in A_N/g_s.

Despite the increased environmental heterogeneity, the reduction in the number of cultivars, and the inclusion of multiple developmental stages, the results from the field experiment were consistent with the chamber study. With the sole exception of g_m/g_s-co2, trait values had a smaller minimum and a greater maximum in the field relative to controlled chambers. The increase in phenotypic variance in the field systematically reduced among-cultivar variance for physiological traits (compare Tables II and III), which is consistent with theory and previous reports (Conner et al., 2003). If trait variance is partitioned for the controlled environment experiment including only the cultivars grown in the field, the among-cultivar variance for g_m drops from 38.8% to 25.7% and that for A_N drops from 37.8% to 25.6%, values closer to those from the field experiment (11.6% and 21.1%, respectively). Despite low power for detection, cultivar-mean A_N and g_m rankings were consistent between controlled environment and field growth conditions (Fig. 6). Bivariate trait relationships also were quite consistent across experiments. All significant relationships observed in the controlled environment, with the exception of the g_m-L_T, also were found in the field. Further evidence of bivariate consistency is provided by the abundance of overlap in the slopes of bivariate trait relationships between environments and across growth stages (Supplemental Table S1). These consistencies highlight the role of genetic control over these traits.

Traits potentially contributing to the variation of g_m are generally time consuming and complex to quantify (e.g. anatomical leaf traits). This recognition provides incentive to find strong correlates of g_m that are more tractable and that can be used as proxies for g_m itself. Because g_m is an emergent trait, we quantified LMA, L_T, L_D, and LDMC to test if these traits would provide predictive power to detect variance in g_m across cultivars. These traits varied little across cultivars grown in chambers, with only L_T and LMA significantly related to g_m, or A_N for that matter, and the variance in g_m explained by LMA was modest (Ω²₀ = 0.5). This result held in measurements of field-grown plants, although with a much-reduced share of the variance in g_m explained (Supplemental Fig. S8). To our knowledge, the g_m-LMA relationship across crop genotypes has only been reported in two other studies, and both report a negative correlation among genotypes (Galmés et al., 2011; Gu et al., 2012). If the effect of growth stage had not been accounted for in our analysis of the field data set, the g_m-LMA relationship also would be interpreted as negative, while the true relationship among cultivars in our study was always positive.

When is the g_m-LMA relationship positive? Light gradients may explain the positive relationship between these two traits in forest canopies, where, for example, LMA in beech (Fagus sylvatica) trees scaled positively with both g_m and photosynthetic capacity (Montpied et al., 2009). A positive association of g_m with LMA also was observed in populations of Populus balsamifera trees (Soolanayakanahally et al., 2009). Milla-Moreno et al. (2016) extended this work on P. balsamifera, revealing a positive relationship between LMA and the thickness of the palisade mesophyll layer. The surface area of mesophyll cells exposed to intercellular air space, known to scale with g_m, increased with palisade thickness, providing a mechanistic link between g_m and LMA (Milla-Moreno et al., 2016). Whether the positive scaling in soybean presented here can be explained by a similar mechanism is an open question worth exploring. The reported negative correlation of LMA and g_m reported by Galmés et al. (2011) was likely due to differences between watering treatments, where stressed plants had higher LMA and lower g_m, rather than to inherent differences among genotypes. The contrast between our positive g_m-LMA relationship and that found by Gu et al. (2012) is harder to explain, since they saw a negative relationship between LMA and g_m in rice regardless of plant water status. A recent study in tomato and tomato wild relatives, bridging the gap between these intraspecific studies and broad taxonomic surveys where the g_m-LMA relationship is consistently negative, demonstrates that, at finer taxonomic scales, this relationship is more labile, resulting from low coordination between LMA and leaf physiological activity (Muir et al., 2017). In any event, if the observed scaling of g_m with LMA holds, it suggests an appealing trait for preliminary selection of candidate soybean genotypes with fast photosynthetic physiologies.

CONCLUSION

To artificially select and improve agronomically relevant traits, genotypic variation must exist for those traits and that variation must be heritable (Falconer and Mackay, 1996). In this study, we show that there is genetic variation for g_m and that variation is highly coordinated with leaf photosynthetic physiology and, to a lesser extent, with coarse leaf structure across soybean cultivars. Genetic variation for g_m (Jahan et al., 2014) and the recent detection of the only known quantitative trait locus associated with g_m hints at the genetic basis for g_m in wheat (Barbour et al., 2016). Whether that quantitative trait locus can be identified in other taxa remains to be seen. Indeed, the genetic basis, magnitude, and nature of genetic variation in g_m must continue to be evaluated in wheat and other taxa, as well as in variable environments, to fully grasp its potential to improve crop productivity. However, in soybean, unlike in wheat (Barbour et al., 2016), the coupling of g_m and g_s may interfere with the potential to improve WUE through selection on g_m.

MATERIALS AND METHODS

Controlled Environment Experiment

Twelve cultivars of soybean (Glycine max) with varying maturity group status were obtained from a number of sources (Supplemental Table S2) and grown under controlled conditions in growth chambers. Seeds were sown directly in 3.75-L pots containing Pro-Mix HP medium (Premier Tech Horticulture). Plants were maintained at 25°C/21°C in a 16/8-h light/dark cycle with an irradiance of approximately 550 µmol m⁻² s⁻¹ at the top of the canopy. All plants were well watered and fertilized weekly with a solution of Plantex (Plant Products). Pots were rotated within chambers every 4th day and between chambers weekly. Gas exchange was measured before flowering on the middle leaflet of the fourth or fifth trifoliate, whichever was the youngest and fully expanded. The relative chlorophyll content of leaves was estimated with a SPAD chlorophyll meter (SPAD 502 Plus; Spectrum Technologies) prior to measurement, and an effort was made to only select leaves within a range of 30 to 40 relative chlorophyll units. Three leaves were below 30, and one was above 40. Chamber-grown plants were used for A_N-C_i curves to estimate g_m and for Laisk curves to estimate biochemical properties.

Field Experiment

Two plants of each cultivar from the controlled environment experiment were transferred to a glasshouse and grown for seed collection. Plants were well watered, fertilized weekly, and allowed to grow until they naturally senesced. Adequate seed was collected from eight cultivars to allow planting in the field the following summer (Table I). The field plot consisted of 13 10-m-long rows. Cultivars were planted within rows in 1-m-long groupings with 30 cm between groups and eight groups per row. The eight cultivars of edamame soybean were confined to four rows, interspersed among the remaining nine rows that were planted with soybean from other experiments. Seeds were sown to a depth of 3 cm and separated by 7.5 cm on June 4, 2015. The plot is located in a river flood plain and is underlain by Haymond silt loam soil of alluvial origin (Hay1AO; U.S. Department of Agriculture Natural Resources Conservation Service). Total precipitation throughout the growing season (June through September) was 432 mm, the mean daily temperature was 21.7°C, and absolute minimum/maximum temperatures were 7°C/33°C (Supplemental Fig. S6). Precipitation immediately preceding and during seed sowing was low (Supplemental Fig. S6). To improve germination and seedling establishment, we irrigated the field three times during the week after planting. The field was rainfed thereafter. Gas exchange was measured on plants at three times throughout the season (see next paragraph). Precipitation was high preceding the first gas-exchange campaign and relatively lower preceding the second and third campaigns (Supplemental Figs. S6).

Leaves were collected for gas-exchange measurements in the laboratory at three developmental stages: late vegetative (plants at V4 and V5), early reproductive (R2–R4), and late reproductive (R6). As is common with soybean (Bernacchi et al., 2005; Ainsworth et al., 2007), the youngest completely expanded trifoliates were excised predawn in the field and stored in the dark with petioles in water until they could be recut under water in the laboratory. Leaves were removed from the dark 25 min before measurement and allowed to acclimate under a light-emitting diode panel at approximately 1,650 µmol m⁻² s⁻¹. A_N-C_i curves were measured on all leaves.

Gas-Exchange Measurements

Determination of R_d and C_i*

So-called Laisk curves were measured on plants from growth chambers to calculate the apparent C_i* and R_d of each cultivar (Laisk, 1977; Brooks and Farquhar, 1985). Leaves were acclimated at 25°C, a CO₂ concentration of 400 µmol mol⁻¹, a photosynthetic photon flux density (PPFD) of 1,200 µmol m⁻² s⁻¹, and a VPD of less than 1.5 with an open gas-exchange system (LI-6400; LiCor) and a 2- × 3-cm broadleaf chamber (LI-6400-02B). Subambient CO₂-response curves (CO₂ set points of 90, 75, 55, and 42 µmol mol⁻¹) were measured at three subsaturating PPFDs (235, 175, and 125 µmol m⁻² s⁻¹). Leaves were reacclimated at ambient conditions between curves. To control for the large differential in CO₂ concentrations between the ambient air and the leaf chamber and the low fluxes at subambient [CO₂], the entire chamber head was loosely sealed in a plastic bag immediately before and during the response curves, allowing the exhaust air from the leaf chamber to surround the outside of the chamber. The first CO₂ set point was not used in the analyses, since it took nearly that length of time for the air in the bag to turn over completely at the low flow rate (250 µmol s⁻¹) used for Laisk curves. Laisk curves were measured on five to eight replicates of each cultivar.

C_i* and R_d were calculated by the modified slope-intercept method of Walker and Ort (2015). For each cultivar, a linear regression was performed on the aggregated CO₂-response curves for a given PPFD. The slopes and intercepts from the three regressions were extracted. A second linear regression was performed with the slopes from the first regressions as the x values and intercepts as the y values. C_i* was taken as the absolute value of the slope from the second regression, while R_d was taken as the y intercept. We found no differences between C_i* and R_d calculated by the slope-intercept method of Walker and Ort (2015) and the traditional common-slope method (paired Student’s t tests, P > 0.1 for both) or the sd values of these estimates. The procedure followed here for measuring Laisk curves, though, did follow several of the recommended procedures of Walker and Ort (2015). Measuring only four subambient CO₂ partial pressures ensured that curves at each irradiance were completed rapidly and minimized the deactivation of Rubisco. Maximum CO₂ partial pressures used in the fittings also were consistently below 10 Pa. Note that Walker and Ort (2015) further recommend the use of at least four irradiances, and additional recommendations have since been proposed (Hanson et al., 2016).

A_N-C_i Curves

Combined CO₂-response and fluorescence curves were measured on five to six replicates of each cultivar for the controlled environment experiment and on one plant from each row-by-cultivar combination from the field experiment, providing four replicates of each cultivar per growth stage (with the exception of one cultivar that had only three replicates per stage due to poor germination). Leaves were clamped into the 6400-40 fluorescence head cuvette and allowed to acclimate to ambient conditions for at least 30 min. Ambient conditions for A_N-C_i curves were equivalent to those for Laisk curves except that a flow rate of 300 µmol s⁻¹ was used, and for leaves from the field the PPFD was set to 1,800 µmol m⁻² s⁻¹. Once steady-state conditions were reached, a point was logged and the [CO₂] was iteratively changed in the sequence 400, 325, 250, 175, 100, 50, 400, 400, 500, 650, 950, 1,250, 1,600, and 2,000 µmol mol⁻¹. At each CO₂ set point, gas-exchange parameters and steady state fluorescence (F_s) were logged, and a multiphase flash chlorophyll fluorescence routine was executed following the recommended procedures of Loriaux et al. (2013) to determine the maximum fluorescence (F_m′). Following this response curve, the leaf was allowed to reacclimate to ambient conditions until net assimilation and g_s returned to steady-state conditions. The air stream supplied to the leaf was then switched to a humidified tank of N₂ with 1% oxygen, and a second CO₂-response curve was executed with only subambient CO₂ concentrations (400, 325, 250, 175, 100, and 50 µmol mol⁻¹). Again, F_s and F_m′ were estimated with the multiphase flash routine at each set point.

Diffusional leaks during CO₂-response curves resulting from the large differentials in [CO₂] between the inside of the leaf chamber and the ambient air can cause substantial error in leaf flux rates (Flexas et al., 2007; Rodeghiero et al., 2007). We estimated diffusional leaks by measuring identical curves on heat-inactivated leaves (n = 12) according to Flexas et al. (2007). The apparent photosynthetic rate of heat-inactivated leaves was subtracted from the photosynthetic rate of experimental leaves, followed by correction of C_i following the equations used by the LI-6400 (Flexas et al., 2007, 2012).

Variable-J g_m Calculation

Several methods exist to estimate g_m, and their relative strengths and weaknesses are reviewed elsewhere (Pons et al., 2009; Gu and Sun, 2014). Here, we employed methods and protocols to minimize errors that can arise using the variable-J method (Pons et al., 2009). g_m was estimated with the variable-J equation of Harley et al. (1992):

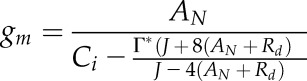(1)

where A_N and C_i were the leak-corrected gas-exchange values from the LI-6400, R_d values were cultivar-specific values taken from Laisk curves, and Γ* was approximated by the mean of all C_i* values also obtained from Laisk curves (see above or below). The electron transport rate (J) was estimated as follows. First the quantum yield of PSII (Φ_PSII) and the quantum yield of CO₂ fixation (Φ_CO2) were quantified as:

(2)

(3)

where α was the leaf absorptance measured at 470 ± 5 and 665 ± 5 nm (the peak wavelengths emitted by the 6400-40 light source) immediately following gas exchange using a spectroradiometer and leaf-clamp integrating sphere (Jaz Spectroclip; Ocean Optics). Absorptance at the two wavelengths was weighted to account for the gas-exchange measurement light being 10% blue and 90% red. The average of three measures of absorptance made across the leaf blade, avoiding major veins, was used in the calculations. Using the CO₂-response curve measured at 1% oxygen, a linear regression of Φ_PSII on Φ_CO2 was performed, and the regression coefficients were then used to calibrate the Φ_PSII values at 21% oxygen (Valentini et al., 1995; Long and Bernacchi, 2003) as:

(4)

(5)

A J_cal was then calculated as:

(6)

and used in the variable-J equation for estimating g_m. CO₂-response curves were measured at 1% oxygen, and the above electron transport rate corrections were performed, for all plants except the field sampling at the early reproductive stage. In order to facilitate more rapid sampling at this stage, thus standardizing maturity as much as was possible, the 1% oxygen curves on these plants were omitted. The mean slope and intercept values from Equation 4 resulting from measurements at the late vegetative stage were used in this instance to correct the electron transport rate following Equations 5 and 6, with the addition of PPFD being corrected with measured α values.

Values of g_m reported throughout this article are those calculated from measurements where the ambient [CO₂] (C_a) in the reference air stream was 325 µmol mol⁻¹. Estimating g_m with a C_a of 250, 325, and 400 µmol mol⁻¹ resulted in an inverse relationship between g_m and C_a. The correlation of g_m calculated at each of these three C_a values was high (r > 0.9, P < 0.001), and the mean of the three estimates was not significantly different from the value calculated at C_a = 325 µmol mol⁻¹. These values were ultimately used, as we assume a larger drop in [CO₂] across the boundary layer of leaves outside the well-mixed gas-exchange chamber; therefore, the g_m estimates at C_s = 325 µmol mol⁻¹ are likely more representative of the average values under growth conditions.

The CO₂ concentration in the chloroplast (C_c) was calculated with the estimated g_m values according to Fick’s first law:

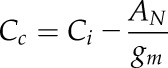(7)

and used to calculate the C_i-C_c and the ratios C_i/C_a and C_c/C_i.

Leaf Morphology

After gas-exchange and absorptance measurements, seven 1-cm-diameter punches were taken from the leaf lamina avoiding primary veins. Lamina thickness was measured on four punches with digital calipers and averaged to determine L_T. The punches were then weighed for fresh mass, dried for more than 72 h at 65°C, and weighed again for dry mass. LMA was calculated from dry mass and the cumulative area of the punches. Dividing LMA by L_T yielded L_D. Then, LDMC was calculated as the ratio of dry mass to fresh mass. After massing, the dry leaf tissue from plants in the field experiment was ground to a fine powder and analyzed for carbon, nitrogen, and ¹³C content (δ¹³C) at the University of Illinois.

Statistical Analysis

All analyses and visualizations were performed in R version 3.3.0 (R Core Team, 2015). To estimate the influence of genetics on cultivar trait differentiation, variation among cultivars for traits of interest from the controlled environment experiment was assessed by partitioning total phenotypic variance within and among cultivars with REML. For field-grown plants, all cultivars were replicated in four blocks within a larger soybean field. Cultivar and block were treated as random effects with growth stage as a fixed effect using the lmer function of the lme4 package (Bates et al., 2015). Then, the genetic component of phenotypic variance was partitioned using REML. Bivariate trait relationships were analyzed with linear mixed-effects models where one of the traits was treated as a fixed effect predictor and block and cultivar were treated as random effects, also with lmer. For mixed-effects models, the significance of fixed effects was determined with Student’s t tests using Satterthwaite-approximated degrees of freedom. The significance of random effects was determined with likelihood ratio tests comparing models with and without the random effect. Effect sizes for bivariate relationships are reported as Ω²₀ values, a mixed-model analog to r² calculated as 1 minus the variance in residuals divided by the variance in the fitted response variable (Xu, 2003). The significance level of all tests was adjusted to reflect multiple testing on nonindependent observation by controlling for the false discovery rate and adjusting P values accordingly (Benjamini and Hochberg, 1995).

To test for univariate cultivar trait consistencies across experiments, we compared the values of key traits (A_N, g_s, g_m, and J_cal) as measured in the controlled environment (measured during vegetative growth) with the late vegetative stage from the field experiment for all cultivars measured in both experiments. We divided cultivar-mean trait values by the maximum cultivar-mean value in each experiment to produce standardized proportional rankings. Then, Spearman’s rank correlations were performed on the standardized traits between experiments using a one-tailed test to determine if the relative rankings of cultivars were consistent in chamber- and field-grown plants. To examine if bivariate relationships were consistent across experiments, we compared the slopes of the primary relationships from the controlled environment experiment and all three growth stages from the field experiment with standardized major-axis regression using the smatr package (Warton et al., 2012). Slopes were considered different at α = 0.05 after correcting for multiple comparisons.

Multivariate trait coordination was assessed with principal component analysis. Of all the traits measured in the controlled environment experiment, we included A_N, g_s-co2, g_m, J_cal, LMA, and LDMC as primary variables in fitting the analysis. Since the calculation of A_N/g_s is a linear combination of other variables, it was included as a supplementary variable that was mapped in the principal component trait space but not used in the fitting. For the field experiment, we included A_N, g_s-co2, g_m, J_cal, N_area, δ¹³C, LMA, and LDMC. In addition to again mapping A_N/g_s as a supplementary continuous variable, growth stage was included as a supplementary factor variable to investigate any seasonal shifts in the positioning of observations. Principal component analyses were fit with the FactoMineR package (Lê et al., 2008).

All data for reproducing the figures and analyses in this article are available from the Dryad Digital Repository (http://dx.doi.org/10.5061/dryad.2gd3b).

Supplemental Data

The following supplemental materials are available.

• Supplemental Figure S1. Mean ± se cultivar R_d and C_i* as determined from Laisk curves on five to eight chamber-grown plants.

• Supplemental Figure S2. The reliance of g_m estimates on the value of Γ*.

• Supplemental Figure S3. Comparisons of g_m calculated using cultivar-specific and a range of unvarying R_d estimates for the late vegetative, early reproductive, and late reproductive growth stages of field-grown soybean cultivars indicated along the x axis.

• Supplemental Figure S4. Mean ± se α at 470 and 665 nm for each cultivar from the controlled environment experiment and the field experiment.

• Supplemental Figure S5. Mean A_N, g_s, g_m, and J_cal for cultivars grown in the field.

• Supplemental Figure S6. Daily precipitation, 15-d cumulative precipitation, and mean temperature across the growing season from a meteorological tower located ∼200 m from the field experiment.

• Supplemental Figure S7. Relationships between A_N/g_s to g_m/g_s-co2, A_N/g_s to g_s-co2, and g_m/g_s-co2 to g_s-co2.

• Supplemental Figure S8. Relationships between g_m and LMA, L_T, L_D, and LDMC from the field experiment.

• Supplemental Table S1. Comparisons of standardized major axis regression slopes from primary bivariate relationships presented for all possible comparisons of the three growth stages.

• Supplemental Table S2. Cultivars used in this study along with their maturity group status and the source of seeds.

Glossary

WUE

water use efficiency

LMA

leaf mass per area

LDMC

leaf dry matter content

PC1

first principal component

PC2

second principal component

ABA

abscisic acid

VPD

vapor pressure deficit

PPFD

photosynthetic photon flux density

REML

restricted maximum likelihood