Gravity dependence of the effect of optokinetic stimulation on the subjective visual vertical

Applying a rotating optokinetic stimulus while recording the subjective visual vertical in different whole body roll angles, we noted the optokinetic-induced bias to correlate with the roll angle. These findings allow the hypothesis that the established optimal weighting of single-sensory cues depending on their reliability to estimate direction of gravity could be extended to a bias caused by visual self-motion stimuli.

Abstract

Accurate and precise estimates of direction of gravity are essential for spatial orientation. According to Bayesian theory, multisensory vestibular, visual, and proprioceptive input is centrally integrated in a weighted fashion based on the reliability of the component sensory signals. For otolithic input, a decreasing signal-to-noise ratio was demonstrated with increasing roll angle. We hypothesized that the weights of vestibular (otolithic) and extravestibular (visual/proprioceptive) sensors are roll-angle dependent and predicted an increased weight of extravestibular cues with increasing roll angle, potentially following the Bayesian hypothesis. To probe this concept, the subjective visual vertical (SVV) was assessed in different roll positions (≤ ± 120°, steps = 30°, n = 10) with/without presenting an optokinetic stimulus (velocity = ± 60°/s). The optokinetic stimulus biased the SVV toward the direction of stimulus rotation for roll angles ≥ ± 30° (P < 0.005). Offsets grew from 3.9 ± 1.8° (upright) to 22.1 ± 11.8° (±120° roll tilt, P < 0.001). Trial-to-trial variability increased with roll angle, demonstrating a nonsignificant increase when providing optokinetic stimulation. Variability and optokinetic bias were correlated (R² = 0.71, slope = 0.71, 95% confidence interval = 0.57–0.86). An optimal-observer model combining an optokinetic bias with vestibular input reproduced measured errors closely. These findings support the hypothesis of a weighted multisensory integration when estimating direction of gravity with optokinetic stimulation. Visual input was weighted more when vestibular input became less reliable, i.e., at larger roll-tilt angles. However, according to Bayesian theory, the variability of combined cues is always lower than the variability of each source cue. If the observed increase in variability, although nonsignificant, is true, either it must depend on an additional source of variability, added after SVV computation, or it would conflict with the Bayesian hypothesis.

NEW & NOTEWORTHY Applying a rotating optokinetic stimulus while recording the subjective visual vertical in different whole body roll angles, we noted the optokinetic-induced bias to correlate with the roll angle. These findings allow the hypothesis that the established optimal weighting of single-sensory cues depending on their reliability to estimate direction of gravity could be extended to a bias caused by visual self-motion stimuli.

to allow one to accurately and precisely orient and navigate in space, the brain must monitor and adjust body position relative to gravity. This requires continuous internal estimates for the direction of gravity and has been assessed behaviorally by paradigms such as the subjective visual vertical (SVV) (Howard 1982) or the subjective haptic vertical (Schuler et al. 2010). Current theories of how the brain accomplishes this task propose that both vestibular and extravestibular (visual, proprioceptive) signals are integrated in a weighted fashion (Angelaki et al. 2009; Borah et al. 1988; Karmali et al. 2014; Vingerhoets et al. 2009). Bayesian observer theory predicts that the brain weighs these sensory cues according to their relative reliabilities (and prior likelihood) to estimate the body’s most likely roll position (Körding and Wolpert 2004; Laurens and Droulez 2007; MacNeilage et al. 2007). Among vestibular sensors, the otolith organs (utriculus and sacculus) detect linear acceleration and therefore also directly sense the direction of gravity (Schoene 1964). In a near upright position, otolith afferents provide an accurate and precise estimate of the direction of gravity; however, the signal-to-noise ratio decreases with increasing roll, resulting in an overall m-shaped curve of SVV trial-to-trial variability in the roll plane (De Vrijer et al. 2009, 2008; Tarnutzer et al. 2009b). This roll-angle dependency has been linked to the mechanical properties of the peripheral otolith organs (e.g., nonlinearities of the tuning functions and the particular distribution of preferred stimulation directions) and to central computational mechanisms that are not optimally tuned for roll angles distant from upright (Tarnutzer et al. 2009b).

Although the role of visual input for spatial orientation in general (Asch and Witkin 1948a, 1948b; Brandt et al. 2014; Cousins et al. 2014; Mergner et al. 1995) and in the SVV task specifically has been widely studied (Corbett and Enns 2006; Morgan et al. 2015; Pavlou et al. 2011; Spinelli et al. 1995), little is known on the role of dynamic visual stimuli. Previously it has been observed that, when upright, a rotating optokinetic stimulus shifts the perceived orientation of a visual line and postural upright, consistent with a shift in the internal representation of the gravity vector (Dichgans et al. 1972). With increasing roll angle and consecutively decreasing reliability of otolith sensory input, we predict that other (extravestibular) sensory inputs are weighed more heavily when generating an internal estimate of the direction of gravity. This hypothesis accords with preliminary observations in three healthy human subjects for head-on-trunk roll angles of up to 60°, which suggested a roll-angle dependency of the optokinetic-induced bias (Dichgans et al. 1974). The primary aim of the present study was to confirm these early observations in a larger study population and over a greater range of roll angles using a rotating optokinetic stimulus similar to the one previously described (Bronstein et al. 1996; Dichgans et al. 1972, 1974). Along with the prediction that the rotating optokinetic stimulus introduces a sensory conflict between the vestibular and the visual system and that it will bias the internal estimate of the direction of gravity, the secondary aim of this study is to assess whether trial-to-trial variability will be unaffected by the superimposed optokinetic stimulus compared with the classic SVV paradigm (obtained in darkness) because the optokinetic stimulus will induce the same dynamic visual cue at all angles. In line with the previously discussed evidence that multisensory fusion could be interpreted as a Bayesian optimal-observer model, we speculated that our two aims together could provide new evidence supporting or opposing the use of this theoretical framework to describe the integration of bias caused by visual self-motion stimuli in the perception of verticality.

MATERIALS AND METHODS

Ten healthy right-handed human subjects (3 females; aged 18-48 yr; mean age ± 1 SD: 30.6 ± 8.7 yr) were included. One additional subject was excluded because of complete disorientation and resulting mostly random adjustments when presenting the optokinetic stimulus. Written, informed consent of all subjects was obtained after a full explanation of the experimental procedure and after screening for potential vestibular dysfunction by use of a questionnaire. The protocol was approved by the Cantonal ethics committee Zurich (KEK-ZH-2013-0026) and was in accordance with the ethical standards laid down in the 2013 Declaration of Helsinki for research involving human subjects.

Experimental setting.

All recordings were performed on a three-axis motor-driven turntable (Acutronic, Jona, Switzerland). Subjects were secured with a four-point safety belt with the head restrained in natural straight-ahead position with a thermoplastic mask. SVV measurements were obtained in nine different whole body roll orientations (upright, ± 30°, ± 60°, ± 90°, ± 120°). A video projector attached to the turntable was used to present the rotating optokinetic stimulus onto a sphere 1.5 m in front of the subject, covering the central 100° of the binocular visual field. A special lens was placed in front of the standard projector lens to compensate for the short project-to-sphere distance and curvature of the viewing surface. The optokinetic stimulus consisted of a random distribution of white dots of various size presented on a black background (Fig. 1) and was generated using the Psychophysics Toolbox (Brainard 1997; Pelli 1997) and GNU Octave (version 3.2.3). To be consistent with previous work (Dichgans et al. 1974), rotational velocity of the optokinetic stimulus was set to 60°/s, and the stimulus was rotated in either the clockwise (CW) or counterclockwise (CCW) direction. This results in three different trial conditions (optokinetic off, optokinetic CW, and optokinetic CCW). A mechanical shutter was closed in between trials and during trials without the optokinetic stimulus, which prevented residual light from the projector from providing any room illumination. The order of trials [27 different trial-types (3 visual stimulus conditions × 9 turntable roll positions)] was random. Turntable positions were reached by turntable movements with 10°/s² constant acceleration and deceleration. We chose this acceleration value as a compromise between minimizing the repositioning time while maximizing comfort of the subject. These acceleration and deceleration values are well above both the detection threshold of the semicircular canals (SCC) [0.05 °/s² (Diamond and Markham 1983; Shimazu and Precht 1965)] and perceptual thresholds (Lewis et al. 2011). Therefore, the motion stimulates the SCCs and can affect a subject’s SVV adjustments (Jaggi-Schwarz and Hess 2003; Pavlou et al. 2003). To minimize effects of SCC stimulation, trials were delayed by 5 s after turntable movements. Previously we have demonstrated that for static SVV adjustments with a 5-s delay postrotatory torsional ocular drift at the time subjects confirm arrow adjustments was small (0.10 ± 0.06°/s), suggesting a minor or absent contribution of SCC stimulation to the SVV (Tarnutzer et al. 2009a). A remote control box allowed the subjects both to rotate an arrow (covering the central 9.5° of the binocular visual field) projected by a laser on the sphere and to confirm adjustments. For trials with the optokinetic stimulus, the arrow was projected on top of the visual stimulus, but the line was always clearly visible because it was much brighter (e.g., the line was not obscured by the dots). The optokinetic stimulus and arrow were concurrently switched on at the beginning of the trial and were extinguished together at the end of the trial.

Fig. 1.

Graphical illustration of the experimental setup. All measurements were obtained on a motorized 3-axis turntable (for visualization purposes shown here as regular chair). Visual stimuli were projected from the turntable on a sphere 1.5 m away from the subject. This included both the red arrow used to indicate perceived direction of vertical and the rotatory optokinetic stimulus. This visual stimulus consisted of white dots of various sizes, randomly distributed on the inner surface of a sphere, with a dark background. The dots rotated at ± 60 °/s. On each trial, a new distribution of dots was randomly created.

Experimental paradigm.

All participants completed one session, lasting ~120 min in total. All trials were collected in complete darkness (except for the luminous arrow used to indicate perceived vertical and the optokinetic stimulus). The starting roll orientation of the arrow was random within the entire 360° roll plane. Subjects were instructed to move the arrow along the shortest path possible to align with the perceived direction of gravity. Adjustment time for single SVV trials was limited to 5 s. This time limit to complete the task ensured that subjects spent about equal time on the task in all conditions, which reduced potential time-dependent differences in arrow adjustment variability (Tarnutzer et al. 2012). Subjects confirmed completion of single trials by pushing a button. Before data collection, 5-10 training trials were provided for each subject to become familiar with the paradigm. For each condition and roll orientation, 12 trials were collected, resulting in 108 trials per condition and 324 trials in total. Recordings were split in four blocks. Subjects were brought upright and provided short breaks between blocks. During these breaks, the room lights were briefly turned on.

Definition of terms frequently used.

CW shifts relative to the earth-vertical axis and CW rotations of the optokinetic stimulus (as seen by the participant) have positive signs and CCW shifts, and optokinetic rotations have negative signs. The term trial-to-trial variability is used to refer to the within-subject SD of SVV adjustments. In relation to trial-to-trial variability, the term precision reflects the inverse, i.e., the degree of reproducibility. Accuracy, on the other hand, is defined as the magnitude of the mean adjustment error.

Data analysis.

We defined the normal range of SVV values according to previous publications, i.e., SVV within ± 2.5° of true earth-vertical when sitting or standing upright (Brandt et al. 1994; Pérennou et al. 2008). As our data was normally distributed (using the Jarque-Bera hypothesis test of composite normality, jbtest.m, Matlab 7.0), mean (± 1 SD), values were provided when pooling individual data points. Statistical analysis was performed using SPSS 23 (IBM, Armonk, NY). We applied a generalized linear model for all statistical analyses if not specified otherwise. Main effects included the trial condition (n = 3; optokinetic off vs. optokinetic CW vs. optokinetic CCW), the direction of rotation of the SVV arrow (n = 2; CW vs. CCW), and turntable position (n = 9). Turntable, optokinetic stimulus, and line orientation signals were processed with interactive programs written in Matlab (MathWorks, Natick, MA). The level of significance was kept at P = 0.05, and Fisher's least significant difference method was used to correct for multiple comparisons. Linear regression analysis using robustfit.m (Matlab 7.0) was applied when analyzing correlations between dependent and independent variables. Principal component analysis (PCA) was chosen to evaluate correlations between dependent variables. This procedure is equivalent to orthogonal linear regression or total least squares, which minimizes the perpendicular distances from the data points to the fitted model (Van Huffel and Vandewalle 1991). Multiple least square linear regression differs from PCA in that it implies that one variable (i.e., the independent variable) is known without error. Conversely, PCA appropriately adjusts for errors along all axes. As a measure of the goodness of fit, we provide the R² value. To estimate the sampling distribution of the slope of the fit obtained by PCA, we used bootstrapping to construct 1,000 resamples and calculated the 95% confidence interval (CI). A correlation between the two dependent variables was considered significant whenever the 95% CI of the slope did not include zero.

Data modeling.

A Bayesian optimal-observer model has been shown to be a good descriptor of the multisensory fusion process determining SVV adjustments (Clemens et al. 2011). We investigated whether such a model can also explain the way optokinetic input influences SVV adjustments (SVV_okn). According to the optimal-observer theory, the final SVV estimate is obtained by summing all sensory cues, weighting them by their reliability, as determined by the variability of each cue. Mathematically, the final estimate is independent of the order in which the inputs are summed. Therefore, we considered only two inputs, one representing the optokinetic bias and the other representing the optimally weighted sum of all other inputs available to the subjects [including both sensory inputs and prior knowledge (Clemens et al. 2011; De Vrijer et al. 2009, 2008)]. This approach is convenient, as it allowed us to use the mean of the SVV adjustments without optokinetic stimulation and its corresponding trial-to-trial variability as input variables for the model. The model prediction of the SVV adjustment with optokinetic stimulation is represented by the following equation:

$$\overline{SVV\_okn}=\frac{{\sigma }_{svv}^2}{{\sigma }_o^2+{\sigma }_{svv}^2}O+\frac{{\sigma }_o^2}{{\sigma }_o^2+{\sigma }_{svv}^2}SVV$$ (1)

SVV is the mean of the SVV adjustments in our data set without optokinetic stimulation (i.e., the optimally weighted sum of all other cues available to the subject), while σ_svv is the trial-to-trial variability (standard deviation) associated with SVV (estimated from SVV trials without optokinetic stimulation). O (not estimated and therefore a free parameter) is the central value of the bias caused by the optokinetic stimulus, and σ_o (not estimated and therefore a free parameter) quantifies its variability. Accordingly, the SVV variability observed in the trials with optokinetic stimulation could be estimated as the following equation:

$$\overline{{\sigma }_{svv\_okn}}=\sqrt{\frac{{\sigma }_{svv}^2{\sigma }_o^2}{{\sigma }_o^2+{\sigma }_{svv}^2}}$$ (2)

The Matlab function “lsqcurvefit” was used to find the two parameters O and σ_o generating $\overline{SVV\_okn}$ and $\overline{{\sigma }_{svv\_okn}}$ that better fit the mean SVV adjustments observed during the trials with optokinetic stimulation (SVV_okn) and its associated trial-to-trial variability (σ_{svv_okn}) for all roll angles. Because it is reasonable to assume that the roll-tilt sensation caused by the optokinetic input does not change across roll angles, we considered O as constant. Regarding the variability of the optokinetic input, we tested two hypotheses. First, we considered a basic condition where σ_o is constant and independent of the roll-tilt angle, using the following equation:

$${\sigma }_o={\sigma }_{o\_offset}$$ (3)

Second, we considered a condition that assumes σ_o increases with the roll-angle mimicking the variability hypothesized for the otolith signal (Tarnutzer et al. 2009b) with the following equation:

$${\sigma }_o=\left|\frac{\theta }{7}\right|+{\sigma }_{o\_offset}$$ (4)

where σ_{o_offset} is a positive value to be optimized by our fitting algorithm and $\theta$ is the roll-tilt angle. As discussed above, the value of SVV was obtained from the mean of SVV adjustments without optokinetic stimulation across all subjects, while σ_svv corresponded to the mean trial-to-trial variability for each roll angle (see previous section).

The quality of fit was assessed by computing the root mean squared error (RMSE) and the R² value for both the mean $\overline{SVV\_okn}$ and $\overline{{\sigma }_{svv\_okn}}$.

RESULTS

Individual mean adjustment errors (± 1 SD) were calculated for the different trial conditions in all subjects. On average, 2.0% of trials were missed (6.4 ± 3.5 trials per session). None of the subjects reported motion sickness during the recordings.

Adjustment errors: optokinetic vs. nonoptokinetic conditions.

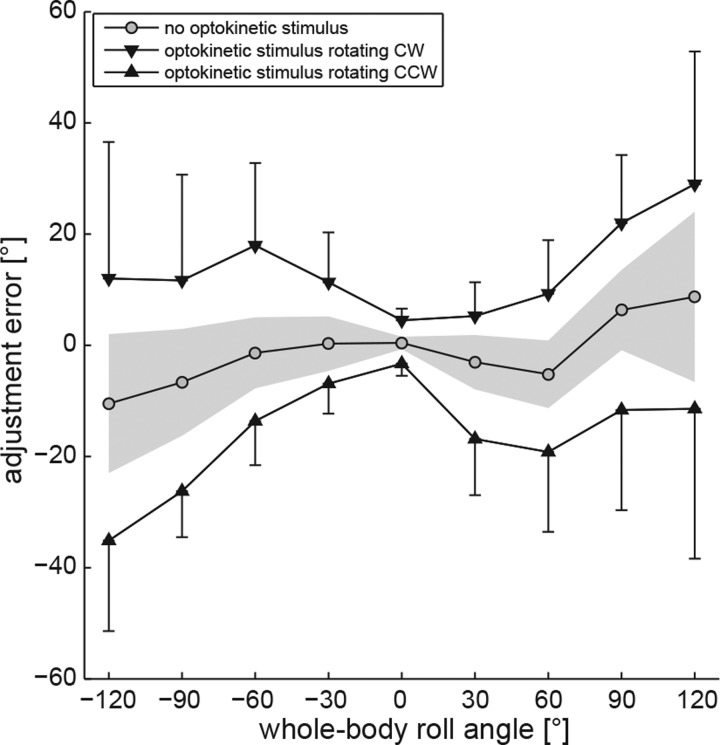
Providing the optokinetic stimulus resulted in a roll-angle-dependent shift in perceived vertical in the direction of rotation of the visual stimulus. The group averages are shown in Fig. 2. Although adjustments for the nonoptokinetic (control) condition (gray circles connected with a black line) were accurate when upright (0.4 ± 0.7°), adjustments showed systematic errors both at small angles [overcompensating whole body roll for angles up to 60° right ear down (Mueller 1916)] and at larger angles [undercompensating whole body roll for angles larger than 60° on both sides (Aubert 1861)]. For the optokinetic (test) conditions, shifts when upright were in the direction of rotation and averaged 4.5 ± 2.1° (optokinetic CW) and −3.3 ± 2.2° (optokinetic CCW), respectively. With increasing whole body roll angle, deviations relative to the control condition increased. Statistical analysis (generalized linear model) confirmed a main effect for the condition (df = 2, χ² = 417.03, P < 0.001) and the turntable position (df = 8, χ² = 97.51, P < 0.001), whereas the direction of arrow rotation had no influence (df = 1, χ² = 0.04, P = 0.840). There was a significant interaction between the turntable position and the condition (df = 16, χ² = 63.68, P < 0.001). Pairwise comparisons of adjustment errors for a given roll angle and the different test conditions (optokinetic CW vs. optokinetic CCW) demonstrated significances for all roll-tilted conditions (P ≤ 0.005), except while in upright position where only a trend was observed (P = 0.063). Pairwise comparisons between the test conditions and the control condition yielded significant differences (P ≤ 0.001) for all roll-tilted conditions except at 30° left ear down for optokinetic CCW vs. optokinetic off (P = 0.081) and at 30° right ear down for optokinetic CW vs. optokinetic off (P = 0.056). Differences when upright also did not reach significance.

Fig. 2.

Overall mean adjustment errors and interindividual variability (expressed as ± 1 SD) plotted against whole body roll orientation including all 10 subjects studied. Circles are control condition without optokinetic stimulus; accompanying gray shaded area reflects ± 1 SD. Inverted triangles are condition with optokinetic stimulus rotating clockwise (CW). Triangles are condition with optokinetic stimulus rotating counterclockwise (CCW). Error bars indicate 1 SD.

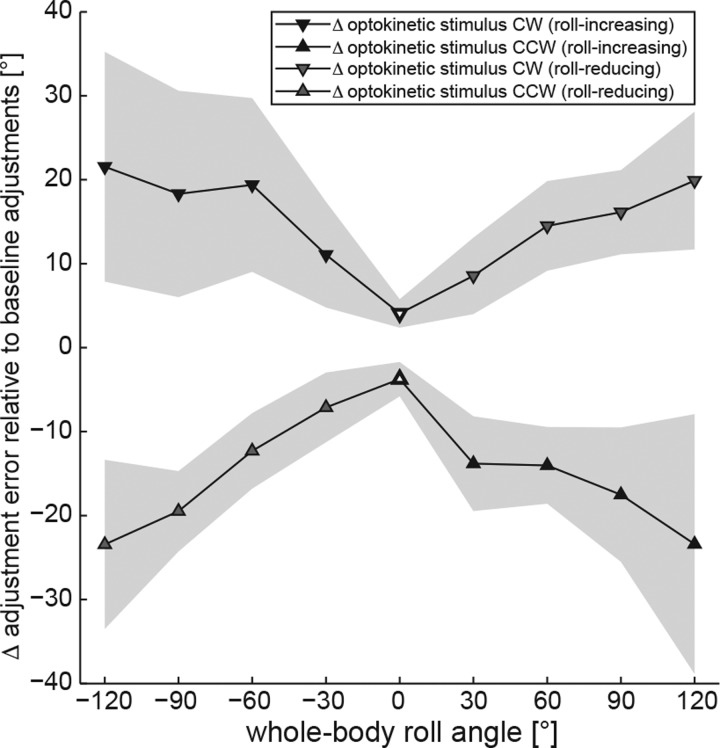
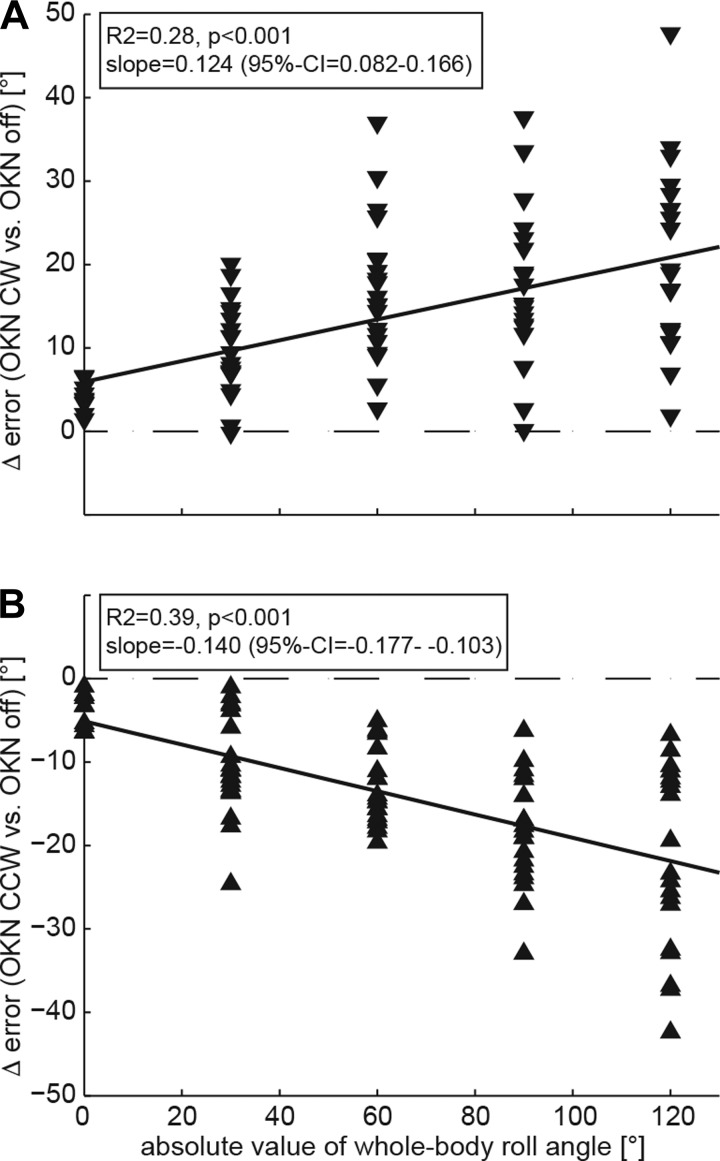
By subtracting adjustment errors in the control condition from those in the test conditions in individual subjects, Δ adjustment error for both optokinetic CW and optokinetic CCW was calculated. When Δ adjustment error was plotted against roll angle, a v-shaped pattern emerged, with Δ error increasing with whole body roll angle (Fig. 3). This was further confirmed by use of linear regression analysis (robustfit.m), which showed a significant correlation between Δ adjustment error and the whole body roll angle for both optokinetic CW (Fig. 4A) and optokinetic CCW (Fig. 4B) test conditions. Because a previous report indicated marked asymmetry in the optokinetic SVV effect based on the stimulus direction (Dichgans et al. 1974), we compared absolute values of Δ error for optokinetic CW and optokinetic CCW (generalized linear model) test conditions. This allowed us to compare conditions resulting in a reduced perception of roll (i.e., increased roll undercompensation; gray filled symbols, Fig. 3) with those resulting in an increased perception of roll (i.e., decreased roll undercompensation or even shift to roll overcompensation; black filled symbols, Fig. 3). Overall, only a trend toward a significant interaction was observed (df = 1, χ² = 15.30, P = 0.054). Pairwise comparisons for all nine roll angles tested indicated that this trend mainly emerged from significant differences in Δ error at small roll angles for tilt-reducing and tilt-increasing conditions (60° left ear down, P = 0.029 and at 30° right ear-down, P = 0.036), reflecting larger Δ error for roll tilt-increasing conditions. To study the effect of direction of stimulus rotation, we compared the magnitude of Δ error for a given roll tilt angle (left ear down vs. right ear down) using a generalized linear model. A significant difference in Δ error was noted only for ± 30° roll when the optokinetic stimulus was rotating CCW (P = 0.018), whereas, in all other comparisons for the CCW rotating stimulus and in all comparisons for the CW rotating stimulus, no significant differences were found.

Fig. 3.

Overall mean differences (Δ) in adjustment errors and interindividual variability (expressed as ± 1 SD) in the test conditions (inverted triangles are optokinetic stimulus rotating CW; triangles are optokinetic stimulus rotating CCW) compared with the control condition (i.e., without a rotating visual stimulus) including all 10 subjects are plotted against whole body roll orientation. The gray shaded areas indicate ± 1 SD of Δ. For better comparison with the calculations provided by De Vrijer (2009), conditions resulting in a reduction of perceived roll tilt (i.e., an increase in roll undercompensation or the A-effect, gray filled symbols) or increase of perceived roll tilt [i.e., a reduction in roll undercompensation and/or a shift to roll overcompensation (E-effect), back-filled symbols] are shown separately.

Fig. 4.

Linear regression analysis plotting the difference in subjective visual vertical (SVV) adjustments for the control condition and the test conditions with the optokinetic stimulus (OKN) rotating either CW (A) or CCW (B) for individual subjects and conditions against the absolute whole body roll angle (i.e., pooling trials with identical whole body roll angle but opposite sides such as 90° right ear down and 90° left ear down roll tilt). Inset: provides the goodness of fit (R² value) along with its P value and the slope (including the 95% confidence interval, CI).

Trial-to-trial variability.

Trial-to-trial variability in individual subjects is plotted against the whole body roll angle for the control and test conditions in Fig. 5. Both the test conditions and the control condition demonstrated increasing variability values with increasing roll angle. Although statistical analysis (generalized linear model) confirmed a main effect for turntable position (df = 8, χ² = 174.85, P < 0.001), no main effect for the condition was observed (df = 2, χ² = 4.02, P = 0.134). Furthermore, no significant interactions were found.

Fig. 5.

Overall trial-to-trial variability including interindividual SD plotted against whole body roll orientation including all 10 subjects studied. For explanation of symbols see legend of Fig. 1.

To evaluate the link between precision of SVV estimates and the impact of the optokinetic stimulus, we correlated individual SVV variability values with Δ error for optokinetic CW and optokinetic CCW conditions. Because both parameters (variability and Δ error) were dependent variables, i.e., contained noise, PCA was used (see materials and methods section). Pooling values for optokinetic CW and optokinetic CCW, a high correlation (R² = 0.71) with a slope significantly different from zero (slope = 0.71, 95% CI = 0.57–0.86) was found, as shown in Fig. 6.

Fig. 6.

Principal component analysis correlating individual SVV variability values and differences (Δ) in adjustment errors. Trials with different whole body roll orientations and trials with CW and CCW rotation of the optokinetic stimulus were pooled.

Trial-adjustment time.

On average, trial adjustments were confirmed after 3.14 ± 0.47 s. Statistical analysis revealed a small but significant main effect for trial duration between the three conditions (df = 2, χ² = 16.07, P < 0.001), with trial duration slightly larger for trials with a CW (3.23 ± 0.47) and CCW (3.14 ± 0.48) optokinetic stimulus compared with no optokinetic stimulus (3.05 ± 0.46 s). We then correlated Δ error with adjustment time to evaluate for possible influences of the duration of presentation of the rotating optokinetic stimulus before confirming the SVV adjustment. With the use of PCA, no significant correlation between time and Δ error was found (R² = 0.17, slope = 0.03, 95% CI = −0.03 to 0.04).

Model fit results.

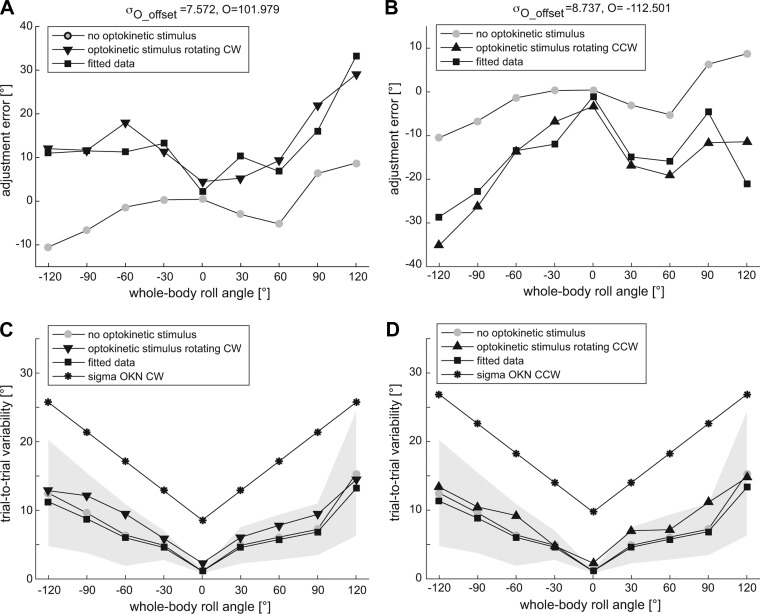
The values for the optimized parameters for optokinetic bias (O) and its associated variability (σ_{o_offset}) that best fit the adjustment errors recorded with the optokinetic stimulus were found for both assumptions of variability (σ_o) tested (see Eqs. 3 and 4). Assuming a constant value for σ_o (i.e., σ_o = σ_{o_offset}), the optimal values were O = 39.8° and σ_{o_offset} = 10.6° for CW optokinetic stimulus and O = −41.5° and σ_{o_offset} = 10.6° for the CCW optokinetic stimulus. The associated R² values were $R^2\left(\overline{SV{V}_{okn}}\right)=0.63$ for CW and $R^2\left(\overline{SV{V}_{okn}}\right)=0.55$ for CCW, respectively, while the $R^2\left(\overline{{\sigma }_{sv{v}_{okn}}}\right)$ were lower than 0.5 for both stimulus directions. The associated RMSE were $\text{RMSE}\left(\overline{SV{V}_{okn}}\right)=4.53$ and $\text{RMSE}\left(\overline{{\sigma }_{sv{v}_{okn}}}\right)=3.67$ for CW and $\text{RMSE}\left(\overline{SV{V}_{okn}}\right)=6.20$ and $\text{RMSE}\left(\overline{{\sigma }_{sv{v}_{okn}}}\right)=3.66$ for CCW. The data and the simulated curve corresponding to the best fitting parameters assuming that σ_o is constant are shown in Fig. 7.

Fig. 7.

Comparison of model fits with experimental data assuming that σ_o (indicated by asterisks in C and D) is constant (Eq. 3). The lines with squares represent the model simulation of the adjustment errors with the optokinetic stimulation (A and C: CW stimulus rotation; B and D: CCW stimulus rotation) obtained on the basis of Eq. 1 (top) and Eq. 2 (bottom), using the parameters that best fit the actual adjustment errors recorded in with the optokinetic stimulation (line with triangles/inverted triangles, top). The fit uses the adjustment errors recorded without optokinetic stimulation (lines with gray circles, top) as input value. The trial-to-trial variability recorded without optokinetic stimulation (lines with circles, bottom) is also plotted for comparison, but it was not used in the fit procedure.

With σ_o that varied with the roll angle (i.e., ${\sigma }_o=\left|\frac{\theta }{7}\right|+{\sigma }_{o\_offset}$), the optimal values were O = 102.0° and σ_{o_offset} = 6.7° for CW optokinetic stimulus and O = −112.5° and σ_{o_offset} = 8.7° for the CCW optokinetic stimulus. R² values ($R^2\left(\overline{SV{V}_{okn}}\right)=0.73$ and $R^2\left(\overline{{\sigma }_{sv{v}_{okn}}}\right)=0.63$ for CW and $R^2\left(\overline{SV{V}_{okn}}\right)=0.69$ and $R^2\left(\overline{{\sigma }_{sv{v}_{okn}}}\right)=0.64$ for CCW) and RMSE ($\text{RMSE}\left(\overline{SV{V}_{okn}}\right)=3.90$ and $\text{RMSE}\left(\overline{{\sigma }_{sv{v}_{okn}}}\right)=2.21$ for CW and $\text{RMSE}\left(\overline{SV{V}_{okn}}\right)=5.16$ and $\text{RMSE}\left(\overline{{\sigma }_{sv{v}_{okn}}}\right)=2.26$ for CCW), indicating high goodness of fit as demonstrated graphically by the overlapping of observed and fitted data (Fig. 8).

Fig. 8.

Comparison of model fits with experimental data assuming that σ_o (indicated by black stars in C and D) is roll angle dependent (Eq. 4). The lines with squares represent the model simulation of the adjustment errors with the optokinetic stimulation (A and C: CW stimulus rotation; B and D: CCW stimulus rotation) obtained on the basis of Eq. 1 (top) and Eq. 2 (bottom), using the parameters that best fit the actual adjustment errors recorded in with the optokinetic stimulation (line with triangles/inverted triangles, top). The lines with gray circles refer to the adjustment errors (A and B) and the trial-to-trial variability (C and D) recorded without optokinetic stimulation.

DISCUSSION

The aim of this study was to investigate how distinct visual and vestibular sensory cues are centrally integrated and weighted to generate an internal estimate of direction of gravity. To probe this parieto-temporal multisensory vestibular cortical network (Dieterich and Brandt 2015; Kahane et al. 2003; Lopez and Blanke 2011), we used a rotating optokinetic stimulus to bias verticality perception. The individuals’ estimates of perceived visual vertical were significantly shifted in the direction of optokinetic rotation and correlated with the whole body roll-tilt angle. This correlation indicates integration of both visual and vestibular input. Although the bias induced by optokinetic stimulation was 3.9° when upright, it grew to 22.1° at ± 120° roll tilt, reflecting a more than fivefold increase and suggesting a larger weight for the optokinetic stimulus at higher roll angles. The trial-to-trial variability increased with increasing roll angle, but, interestingly, this variability was independent of the optokinetic stimulus. Supporting these findings, previous SVV modeling that accounted for the physiological properties of the otolith organs (nonlinear discharge rates, nonuniform distribution of afferents in the roll plane) indicated that SVV variability estimates are closely linked to the noise in the otolith organs while also being subject to central modulation (Tarnutzer et al. 2009b).

The growing optokinetic-induced bias likely reflects this increased weight the brain applies to visual input with increasing roll angles because of the concurrent reduced weight applied to vestibular (otolithic) input. Reweighting of sensory cues when estimating the direction of gravity is consistent with Bayesian optimal observer analysis in which the brain weights distinct sensory input signals depending on their reliability using internal models (Angelaki et al. 2009; Borah et al. 1988; Wolpert et al. 1995). This hypothesis is supported in this study by the significant correlation (R² = 0.71) between SVV variability and the optokinetic-related bias in SVV adjustments (Fig. 6). The similarity of the trial-to-trial variability between the control and the test conditions indicates that the reliability of the optokinetic input is small compared with the reliability of the other cues contributing to the SVV assessments. The increased weight of visual input with roll angles therefore likely reflects only relative reweighting attributable to the well-described decrease of otolith reliability with increasing roll angle.

To further illustrate our hypothesis, we used a simplified Bayesian optimal observer model. The absence of a direct measurement of the bias and variability of the optokinetic cue alone prevents a reasonable evaluation of the model. With the use of a hypothetical space-fixed, large roll-tilt cue with high variability (i.e., with low reliability) generated by the optokinetic stimulation though, the pros and cons of this approach can be seen. The existence of a similar optokinetic-driven bias has been hypothesized previously as a byproduct of the tilt-translation discrimination mechanism. As otolith sensors alone, as any accelerometer, do not allow distinguishing roll tilts from translation [Einstein’s equivalence principle (Einstein 1907)], our brain combines angular velocity input with a frequency segregation mechanism of the otolith input (Bos and Bles 2002). Such a computation, when a constant velocity optokinetic stimulus is present, has a stable solution suggesting that the actual gravity vector is roll tilted away from the otolith output by a value θ = ωτ, where ω is the angular velocity of the optokinetic stimulus and τ is the cutoff frequency of the frequency segregation mechanism (range: 5–10 s) (Bos and Bles 2002). With consideration that, in our experiment ω =  ± 60°/s, the resulting θ (i.e., the optokinetic bias O in our model) is predicted to be a very large value. An optimal observer model combining the SVV adjustments without the optokinetic stimulus and this hypothetical optokinetic effect fit the data well.

The model also indicates that the bias induced by the optokinetic stimulus must be considered unreliable by the optimal observer (i.e., its variance is high), justifying the relatively limited effect if compared with the size of the cue. This is not surprising, as O derives from a byproduct of a visual motion cue, which, at the time of SVV measurements, is not yet even relevant at the perceptual level (subjects completed the task before the onset of circular vection). Beside this major conclusion, it is worth emphasizing that the basic assumption of a constant variability σ_o across roll angle generates a fit that, although adequate, fails to match a qualitatively important feature of the data (Fig. 7). Specifically, when assuming that σ_o is constant, the experimentally observed bias in the SVV assessments when the subject is upright is absent in the model output. This suggested that a more complex function should be used to describe either the bias O or σ_o. If we consider O to be the byproduct of the tilt-translation discrimination mechanism (Bos and Bles 2002), it is obvious to consider it roll angle independent, as it will always be referenced to the actual direction of gravity. Its variability, however, should be related to the variability of the otolith sensors. A model using σ_o increasing linearly with the roll-tilt angle, i.e., mimicking the variability of the otolith sensors (Tarnutzer et al. 2009b), indeed resulted in an improved fit of the data including the pattern observed when upright.

In summary, the model supports the hypothesis that exposure to an optokinetic stimulus immediately results in a large bias of perceived direction of gravity that follows the pattern of variability of the otolith organs. This observation could provide an intriguing explanation of our data and would extend the concept of optimal sensory fusion to cues derived from visual self-motion perception. An aspect of the data that cannot be explained by the model, however, is the small increase of variability in SVV assessments performed during the optokinetic stimulation compared with those trials without it (Figs. 2, 7, and 8). Because, according to the Bayesian theory, the variability of combined cues is always lower than the variability of each source cue, if the observed increase in variability, although not significant here, is true, then either it must depend on an additional source of variability, added after the computation of the SVV, or it would conflict with the Bayesian hypothesis. We can hypothesize that this source of variability originates from increased noise in the data collection. Some of our subjects spontaneously reported that the task with the optokinetic stimulation was “more difficult” because accurate positioning of the arrow was challenged by background motion, causing an illusion of relative motion of the stationary arrow. Such uncertainty would justify an increase of the trial-to-trial variability independently from the variability of the actual SVV estimate. However, as neither our data, nor that of any other experiment of which we are aware, could provide a direct measurement of the bias and variability of the optokinetic stimulation alone or of such additional noise, a full assessment of the Bayesian hypothesis presently is not possible.

Comparison of our findings with previous studies.

The pattern of increasing optokinetic bias with increasing whole body roll tilt found here confirms preliminary observations by Dichgans in upright (Dichgans et al. 1972) and roll-tilted positions up to 60° (Dichgans et al. 1974) in a larger group of subjects and extends observations to roll angles as large as 120°. Similarly, Bronstein and colleagues (1996) also described a larger shift in SVV by a optokinetic stimulus when roll tilted right ear down by 90°. More recently, as part of her doctoral thesis, De Vrijer studied visual-vestibular interactions for roll angles up to 120° in eight human subjects and reported roll-angle-dependent changes in SVV adjustments when presenting an optokinetic stimulus (De Vrijer 2009), findings that are consistent with ours. Compared with the experimental setup used here, however, the paradigm applied by De Vrijer differs in several important aspects. First, in the thesis by De Vrijer, before a series of three SVV adjustments was obtained at a given roll angle, the optokinetic stimulus (35°/s constant rotation, covering 90° of the subject’s visual field, with central 23° spared to avoid interaction with the luminous line) was presented for 30 s to allow perceptual saturation. Previously, average delay to saturation of circular vection has been reported to occur 18 s after stimulus onset (Dichgans et al. 1972).

The overall mean (± 1 SD) adjustment errors (after correcting for roll-tilt-dependent shifts of SVV in darkness) from the different studies discussed here are compared in Fig. 9.

Fig. 9.

Comparison of overall mean differences (Δ) in adjustment errors and interindividual variability (expressed as ± 1 SD) for the rotating optokinetic stimulus vs. the static condition between the present study (inverted black triangles: CW rotation of optokinetic stimulus; black triangles: CCW rotation of optokinetic stimulus) and previous publications from Dichgans and coworkers (Dichgans et al. 1974) (gray circles: stimulus rotating CW; gray squares: CCW rotation of optokinetic stimulus), De Vrijer and coworkers (De Vrijer 2009) (black stars: CW rotation of optokinetic stimulus; black diamonds: CCW rotation of optokinetic stimulus), and Bronstein and coworkers (Bronstein et al. 1996) (gray triangles pointing to the left: CW rotation of stimulus; gray triangles pointing to the right: CCW rotation of optokinetic stimulus). Data from the previous publications were retrieved from published figures or tables. Note that both the roll angles studied and the angular velocity of the optokinetic stimulus varied among studies. Furthermore, the delay of trial onset after presenting the optokinetic stimulus varied between 0 and 30 s, while it was not reported in another study (Bronstein et al. 1996). In analogy with previous publications, we distinguished between conditions that resulted in an increase of perceived roll tilt and a decrease of perceived roll tilt.

Previous studies have distinguished between trial conditions in which the direction of the optokinetic stimulus and head roll were in the same or opposite directions. Although the latter condition resulted in an increase of the estimated roll tilt (reflected by a decrease in roll undercompensation), the first condition resulted in a decrease of the estimated roll angle (reflected by an increase in roll undercompensation) (De Vrijer 2009; Dichgans et al. 1974). De Vrijer reported shifts in SVV adjustments larger than 50° at 120° whole body roll for roll-tilt-increasing conditions, which is about twice as large as observed in our paradigm (De Vrijer 2009). For roll-tilt-decreasing conditions, on the other hand, shifts were in a comparable range (up to 25° at ± 120° roll) to our study. These discrepancies may be explained by differences in the paradigm. Two phenomena may contribute to SVV shifts when the optokinetic stimulus is presented for 30 s before the subject adjusts the line: 1) the rotating visual background inducing an optokinetic nystagmus (Cheung and Howard 1991; Laurens et al. 2011), and 2) circular vection [i.e., a sensation of illusionary self-rotation when indeed the visual surroundings are moving (Cheung and Howard 1991)] building up over time (Mergner et al. 1995). In a study by Thilo and Gresty (2002), roll circular vection was perceived on average 8.9 s after onset of the optokinetic stimulus (albeit in combination with sinusoidal roll oscillations up to 25° and 0.05 Hz). Held and colleagues (1975) have shown that the optokinetic-induced shift in SVV grows with stimulus duration, increasing from <5° after 5 s to >10° after 30 s when upright. In our paradigm, adjustments were limited to 5 s after onset of the optokinetic stimulus, and average trial duration was 3 s. As a result, circular vection is expected to be marginal/absent. When asked to report on circular vection, 9 out of 10 participants did not notice any circular vection, whereas one subject described an emerging sense of self-motion at the largest (>90°) roll angles. The visual velocity, however, is already computed and available to sensory fusion, as confirmed by the short delay of optokinetic nystagmus (Cheung and Howard 1991; Laurens et al. 2011). A similar pattern was observed in studies by Dichgans et al. (1974) and Bronstein et al. (1996), again showing relatively larger shifts for roll-tilt-increasing conditions and similar shifts for the roll-tilt-decreasing conditions. However, in the study by Dichgans, no information was given about the latency of trial onset from the presentation of the optokinetic stimulus, leaving the impact of circular vection unclear. Conclusions based on the study by Bronstein and colleagues are limited because only two whole body roll positions (upright and lying on the right side) were assessed.

In the paradigm by De Vrijer, time limits for each SVV adjustment were much broader, allowing a subject up to 30 s for single adjustments. Previously, we have shown that the accuracy of a subject’s adjustment in the SVV task correlates with the time spent for each adjustment (Tarnutzer et al. 2012), potentially biasing results by varying trial duration. Likewise, keeping subjects in a static roll-tilted position for repetitive measurements over several minutes as done by De Vrijer may introduce drifts in SVV estimates attributable to adaptation (Tarnutzer et al. 2013). Such adaptation bears the risk of over-/underestimating the optokinetic-induced bias depending on the relative direction of the optokinetic stimulus relative to adaptation.

Previously, optokinetic-induced shifts in the SVV have been reported to be asymmetric, depending on the direction of body roll tilt (De Vrijer 2009; Dichgans et al. 1974), with larger shifts when the optokinetic rotation was opposite to head roll. In this condition, undercompensation of body roll increases, i.e., perceived roll tilt decreases (termed roll-tilt-decreasing condition), whereas, in cases with the direction of optokinetic rotation and the direction of head roll going in parallel, head roll is overcompensated, i.e., perceived roll-tilt increases (termed roll-tilt-increasing condition). In our data set, however, we observed asymmetric shifts in two out of nine roll positions only. Of note, the optokinetic bias in the roll-tilt-decreasing condition in the De Vrijers paradigm closely matched the SVV bias observed here (for both conditions with the optokinetic stimulus and head roll going into the same or into opposite directions). These discrepancies may also be related to differences in the experimental paradigm as described above, especially the amount of circular vection induced, as these asymmetries have been related to the direction of optokinetic roll. Dichgans (1974) hypothesized that, although rotation opposite to the side of whole body roll tilt will support a postural uprighting process, rotations toward the side of roll tilt will antagonize it, resulting in a smaller optokinetic bias and therefore possibly less circular vection.

Compared with previous studies, the experimental setup used here resembles the setup used by De Vrijer (2009) in parts. However, there were several significant modifications that reduced potential bias (e.g., drift in perceived vertical by prolonged static roll), allowed us to study effects of the rotating optokinetic stimulus independently from circular vection, and linked the precision of estimates with their accuracy. Specifically, by collecting a larger number of trials in each position and condition compared with De Vrijer (2009), we were able to determine the trial-to-trial variability as well, which is a significant extension of existing studies. This data corroborated that the optokinetic bias likely has a consistent (i.e., roll angle independent) value, which both increases its weight relative to other sensory cues as other sensory signals become less reliable and does not affect the overall variability of SVV estimates.

Possible mechanisms for the optokinetic-induced bias.

Because both for the SVV and for subjective body tilt an increasing optokinetic effect with roll angle has been reported (Dichgans et al. 1974; Young et al. 1975), De Vrijer (2009) hypothesized that the shift in SVV may reflect an alteration in subjective body roll. However, over a range of ± 120° roll, the optokinetic-induced bias was distinct for the SVV and the subjective body roll task in two ways: first, the effect size for the SVV task was about twice as large as for the subjective body roll task and second, the difference in effect size for roll-tilt-increasing conditions vs. roll-tilt-decreasing conditions reported for the SVV was lacking in the subjective body roll task. Therefore, this hypothesis was refuted by de Vrijer to explain their observations. Static head roll induces reflexive compensatory torsional eye movements with a gain of 0.05–0.25, termed ocular counterroll [OCR (Collewijn et al. 1985; Diamond and Markham 1983)]. Roll overcompensation (E-effect) in subjective visual horizontal adjustments has been linked to OCR (Wade and Curthoys 1997); however, because the amount of OCR mainly depends on otolith input (Fernandez et al. 1972), no differences in the control and test conditions are expected. With a roll optokinetic stimulus of similar field size (~50°) and velocity [~40°/s; i.e., above the saturation level of optokinetic stimulation (Held et al. 1975)] as in our experiment, a torsional optokinetic nystagmus with a gain of 0.05–0.06 (or 3–3.5°/s) will be generated (Farooq et al. 2004). Such torsional eye movements may influence vision-based assessments of the perceived direction of gravity (such as the SVV). Whether torsional eye movements may explain (at least partially) the roll-angle dependency of the SVV adjustment bias while presenting the optokinetic stimulus has not been assessed. Theoretically, the amount of torsional nystagmus should decrease when the eyes are already counterrolled and an optokinetic stimulus in the direction of the induced torsion is applied; however, as discussed further below, when the direction of head roll and rotating optokinetic stimulus are opposite, this tends to result in larger rather than (as predicted) smaller shifts of the SVV (De Vrijer 2009; Dichgans et al. 1974).

By asking subjects to adjust a luminous line along the body-longitudinal axis (subjective line body task, SLB) while presenting an optokinetic stimulus, De Vrijer (2009) addressed the hypothesis that the optokinetic SVV bias is the sum of the shift in subjective body roll and the shift related to torsional eye movements. Although the SLB-related optokinetic bias reduced the difference between the SVV and the subjective body roll-tilt-related optokinetic bias sufficiently to explain the pattern found for the roll-tilt-decreasing conditions, its effect size was too small to fill the gap for the roll-tilt-increasing condition (De Vrijer 2009).

Taken together, it is most likely a combination of different effects that contribute to these roll-angle-dependent shifts in SVV when presenting an optokinetic stimulus. While based on its presence for distinct paradigms [SVV, subjective body roll, postural vertical (Brandt et al. 1973; De Vrijer 2009; Dichgans et al. 1974)], a shift in the internal estimate of direction of gravity (independent from the specific paradigm used) is proposed, and the experimental setup will affect the magnitude of the optokinetic shift as well. Therefore, circular vection seems to affect both the magnitude and directional asymmetries (direction of rotation of optokinetic stimulus and direction of head roll) of the optokinetic-induced bias on the SVV (De Vrijer 2009), as shown in our study with shifts of smaller size and lack of asymmetry in shifts. The contribution of ocular torsion, however, remains unclear, and previous studies suggest rather a minor role (De Vrijer 2009).

Conclusions.

Our results confirm a close interaction between visual and vestibular sensory input when the brain generates internal estimates of the direction of gravity, providing insights into the mechanisms of graviception. Adding an optokinetic bias did not change SVV trial-to-trial variability, confirming the key role of otolith input for the precise estimate of the direction of gravity. By limiting the duration of the optokinetic stimulus presentation and static whole body roll position, we were able to minimize several potential confounders, including the perception of roll circular vection and adaptation to static roll tilt. Nonetheless, the roll-angle-dependent shift in SVV by the optokinetic stimulus was preserved, suggesting that the mere presence of a rotatory visual background shifts the perception of earth vertical. These experimental findings were supported by an optimal observer model and further support the concept of weighted multisensory integration when estimating the direction of gravity with visual input gaining influence when otolith input becomes less reliable.

GRANTS

This work was supported by Swiss National Science Foundation (grant no. 32003B_130163/1), Berne, Switzerland; the Betty and David Koetser Foundation for Brain Research, Zurich, Switzerland; the Center of Integrative Human Physiology, University of Zurich, Switzerland; Bonizzi-Theler-Foundation, Zurich, Switzerland; Dr. Dabbous Foundation, University of Zurich, Switzerland.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

B.K.W. performed experiments; B.K.W., C.J.B., N.C., G.B., and A.A.T. interpreted results of experiments; B.K.W., C.J.B., N.C., G.B., and A.A.T. edited and revised manuscript; B.K.W., C.J.B., N.C., G.B., and A.A.T. approved final version of manuscript; N.C. and A.A.T. analyzed data; A.A.T. prepared figures; A.A.T. drafted manuscript.