Detection of superior genotype of fatty acid synthase in Korean native cattle by an environment-adjusted statistical model

Abstract

Objective

This study examines the genetic factors influencing the phenotypes (four economic traits:oleic acid [C18:1], monounsaturated fatty acids, carcass weight, and marbling score) of Hanwoo.

Methods

To enhance the accuracy of the genetic analysis, the study proposes a new statistical model that excludes environmental factors. A statistically adjusted, analysis of covariance model of environmental and genetic factors was developed, and estimated environmental effects (covariate effects of age and effects of calving farms) were excluded from the model.

Results

The accuracy was compared before and after adjustment. The accuracy of the best single nucleotide polymorphism (SNP) in C18:1 increased from 60.16% to 74.26%, and that of the two-factor interaction increased from 58.69% to 87.19%. Also, superior SNPs and SNP interactions were identified using the multifactor dimensionality reduction method in Table 1 to 4. Finally, high- and low-risk genotypes were compared based on their mean scores for each trait.

Conclusion

The proposed method significantly improved the analysis accuracy and identified superior gene-gene interactions and genotypes for each of the four economic traits of Hanwoo.

INTRODUCTION

Beef quality depends on fatty acid composition (FAC) and the degree of marbling. Beef’s delicious flavor comes from its carcass fat with small amounts of saturated fatty acids (SFAs) and large amounts of monounsaturated fatty acids (MUFAs) [1–3]. The MUFA:SFA ratio is an indirect factor determining the taste of beef [4]. Oleic acid (C18:1), a major MUFA in beef fat, is considered a vital ingredient in the aroma of cooked beef [1,5]. For high-quality beef, it is important to improve its FAC, particularly its C18:1. According to the livestock-rating system of the Korea Institute for Animal Products Quality Evaluation, carcass weight (CWT) and marbling score (MS) are major indicators of beef quality in carcass traits.

In particular, fatty acid synthase (FASN), which is abundantly expressed in adipose tissue, is a complex homodimeric enzyme that regulates the biosynthesis of long-chain fatty acids [6]. We recently examined the genetic relationships between the FAC of beef and multiple nucleotide sequence variants in the gene encoding FASN [7]. We found that five single-nucleotide polymorphism (SNP) variants, namely g.12870 T>C, g.13126 T>C, g.15532 C>A, g.16907 T>C, and g.17924 G>A in exon regions 23, 24, 34, 37, and 39, respectively, were associated with the composition of unsaturated fatty acids and MUFAs in the adipose tissue of Japanese Black cattle and Korean native cattle (p<0.05). In addition, the g.17250–17251 AT Indel, g.16907 T>C, g.15532 C>A, g.15603 G>A, and g.17924 G>A variants have been found to be associated with the myristic acid content of adipose tissue in the beef cattle crossbred between Jersey and Limousin (p<0.05) [8]. Another crossbred between Japanese Black cattle and Limousin has been found to show the association between FAC and g.16024 A>G and g.16039 T>C (p<0.05) [9]. In addition, g.17924 G>A and g.18663 T>C have been found to be associated with the oleic acid content of adipose tissue in Japanese Black cattle (p<0.05) [10]. Based on these findings, the FASN gene, which is closely related to C18:1 as an important factor influencing the beef flavor, may play an important role in improving beef quality.

This study identifies the SNPs in exons of the FASN gene influencing C18:1, MUFAs, CWT, and MS in Hanwoo (Korean native cattle). The FASN gene is significantly related to FAC and carcass traits [7,11]. The first important point is that most traits of economic importance in livestock are multifactorial in nature, and are thus influenced by multiple genes and their interactions with environmental factors. Enhancing the accuracy of genetic analysis necessitates a statistical model that excludes environmental effects. Therefore, this study proposes an analysis of covariance (ANCOVA) model that includes environmental and genetic factors influencing the phenotype of Hanwoo and uses a new adjusted model that eliminates the estimated values of environmental factors. In addition, the study employs the multifactor dimensionality reduction (MDR) method to test the main and interaction effects of multiple SNPs on the meat quality of Hanwoo and compares the analysis accuracy between the adjusted and unadjusted models. Finally, the study explores superior genotype groups based on interactions between SNPs in exons of the FASN gene.

MATERIALS AND METHODS

Phenotypes and SNP genotyping

A total of 513 Hanwoo cattle were bred at 17 farms in Gyeongsangbuk-do, Korea and fed according to each farmer’s feeding program. In general, they were weaned and castrated at 6 months of age, fed with growth stage feed for 18 months, and then fed a highly concentrated diet for their last 6 months. All steers were slaughtered at 941±72 days of age with an average CWT of 427.25 ±43.281 kg. The MS was measured 24 h after slaughter. First, the carcasses were dissected at the last rib and the first lumber vertebra according to the Animal Product Grading System of Korea. MS ranged from 1 to 9, where a higher score indicates more abundant intramuscular fat. FAC was analyzed using gas-chromatography (PerkinElmer, Inc., Waltham, MA, USA) [7,12,13]. The composition of the fatty acids, MS, and CWT were used to establish phenotypes for the genetic association analysis of Hanwoo.

Total genomic DNA was extracted from the longissimus muscle by using the LaboPass TM Tissue Mini kit (Cosmo Genetech, Seoul, Korea). Five polymorphic exonic SNPs of the FASN gene in GenBank (Accession no. AF285607) were genotyped, according to our previous study [7]. We previously examined the genetic relationships between the FAC of beef and multiple nucleotide sequence variants in the FASN gene, and five variants, namely g.12870 T>C, g.13126 T>C, g.15532 C>A, g.16907 T>C, and g.17924 G>A in exon regions 23, 24, 34, 37, and 39, respectively, were found to be associated with the composition of unsaturated fatty acids [7].

A statistical ANCOVA model of the economic traits of Hanwoo

The economic traits of Hanwoo are affected by individual SNPs, calving farms, age, etc. In this study, we used C18:1, MUFAs, MS, and CWT as economic traits and SNPs in exons of the FASN gene, calving farms and age as factors. The relationship between economic traits and factors can be expressed as the following ANCOVA model:

$$\begin{array}{l}{Y}_k=\mu +{\alpha }_0(A_k-\overline{A})+{\alpha }_1{F}_{1k}+\cdots +{\alpha }_{l-1}{F}_{l-1,k}+{\beta }_1{G}_{1k}+\cdots +{\beta }_m{G}_{mk}+{\varepsilon }_k\\ i=1,2,\cdots ,l;\hspace{0.17em}j=1,2,\cdots ,m;\hspace{0.17em}k=1,2,\cdots ,n,\end{array}$$

where Y_k indicates the economic traits of Hanwoo k, μ is the overall mean, A_k the covariate for age in days at slaughter, Ā the mean of A_k, α₀ the covariate effect, F_ik an indicator variable for calving farm i (17 classes), α_i the fixed effect of F_ik, G_jk the genotype j, β_j the fixed effect of G_jk, and ε_k a random residual assumed to have an independent and identical normal distribution. In a statistical model, if a qualitative (categorical) variable has more than two classes (17 calving farms), we require additional indicator variables in the model [14]. Since the calving farm variable has 17 classes, we require 16 indicator variables.

Define the binary F_ik as follows:

$$F_{ik}=\{\begin{array}{ll}1,\hfill & if\hspace{0.17em}the\hspace{0.17em}farm\hspace{0.17em}of\hspace{0.17em}the\hspace{0.17em}kth\hspace{0.17em}Hanwoo\hspace{0.17em}is\hspace{0.17em}ith,\hfill \\ 0,\hfill & otherwise.\hfill \end{array}(i=1,2,\cdots ,l-1)$$

The above model can be briefly expressed as follows:

$$Y=\mu +E\alpha +G\beta +\varepsilon$$

The economic traits of Hanwoo can be treated as the Y matrix, and environmental and genetic factors, as the E and G matrices, respectively:

$$\begin{array}{l}\mathit{E}\mathit{\alpha }=\left(\begin{array}{ccccc}{A}_1^{\prime }& F_{11}& F_{21}& \cdots & F_{l-1,1}\\ A_2^{\prime }& F_{12}& F_{22}& \cdots & F_{l-1,2}\\ A_3^{\prime }& F_{13}& F_{23}& \cdots & F_{l-1,3}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ A_n^{\prime }& F_{1n}& F_{2n}& \cdots & F_{l-1,n}\end{array}\right){({\alpha }_0{\alpha }_1{\alpha }_2\cdots {\alpha }_{l-1})}^{\prime },\\ \mathit{G}\mathit{\beta }=\left(\begin{array}{cccc}{G}_{11}& G_{21}& \cdots & G_{m1}\\ G_{12}& G_{22}& \cdots & G_{m2}\\ G_{13}& G_{23}& \cdots & G_{m3}\\ ⋮& ⋮& \ddots & ⋮\\ G_{1n}& G_{2n}& \cdots & G_{mn}\end{array}\right){({\beta }_1{\beta }_2{\beta }_3\cdots {\beta }_m)}^{\prime },\\ A^{\prime }=A_k-\overline{A},i=1,2,\cdots ,l;j=1,2,\cdots ,m;k=1,2,\cdots ,n,\end{array}$$

where the age in days at slaughter and the calving farm are environmental factors and SNPs are genetic factors.

Here environmental factors were excluded from the ANCOVA model because a statistical model was required only for genetic factors. Statistical analysis was conducted using SPSS v22.0 (SPSS Inc., Chicago, IL, USA):

$$\mathit{Z}=\mathit{Y}=\mathit{E}\widehat{\mathit{\alpha }},$$

where Z, Y, α̂ are

$$\mathit{Z}=\left(\begin{array}{c}adj(Y_1)\\ adj(Y_2)\\ adj(Y_3)\\ ⋮\\ adj(Y_n)\end{array}\right),\mathit{Y}=\left(\begin{array}{c}{Y}_1\\ Y_2\\ Y_3\\ ⋮\\ Y_n\end{array}\right),\widehat{\mathit{\alpha }}=\left(\begin{array}{c}{\widehat{\alpha }}_0\\ {\widehat{\alpha }}_1\\ {\widehat{\alpha }}_2\\ ⋮\\ {\widehat{\alpha }}_{l-1}\end{array}\right).$$

The above model can be defined as an “adjusted model” that excludes environmental factors. Superior SNPs and SNP-SNP interactions influencing economic traits were identified by applying the MDR method to adjusted data (Z).

Multifactor dimensionality reduction analysis

The MDR method is nonparametric and model-free and has been implemented in case-control studies [15]. For application to continuous data, each phenotype was divided into the case group (Y = 1) and the control group (Y = 0) by using the k-means clustering method. The MDR method classifies the phenotypes into two groups: high and low. Each individual is assigned to a cell (e.g., if there are two SNPs with three genotypes per SNP, then there are nine possible cells), and each cell is defined as a high- or low-risk group.

Then the error is

$$Error=\frac{{}^N(Y=0|high){}^{-N}(Y=1|low)}{N_{total}}.$$

The MDR steps were conducted according to the procedure we have previously reported [7]. The procedure is described here briefly as follows:

• Step 1. Data were randomly divided into 10 equal parts: one testing set and nine training sets as part of the cross-validation procedure.

• Step 2. A set of n SNPs was selected from the pool of all SNPs.

• Step 3. Based on the observed level of each n, steers were partitioned into classes referred to as cells. If n = 2, then a set of two SNPs was selected, and because one SNP had three genotypes, there were 3² = 9 possible cells. Case-control ratios were calculated for each cell.

• Step 4. The case-control ratio of total data was used as the threshold such that a cell with a higher case-control ratio than the threshold was labeled as high and the remainder, as low.

• Step 5. The MDR model with the smallest test data error was chosen among all two-factor combinations.

• Step 6. To evaluate the predictive ability of the model, the test data error was estimated using a 10-fold cross-validation method.

These six steps were repeated for each possible combination of given n. The model with the minimum test data error was selected as the best model. However, statistical significance was not determined by the test data error for the selected best model. Therefore, t-tests were conducted, and Cohen’s d was calculated to determine empirical significance thresholds by applying the same MDR method.

Effect size

The p-value is commonly used to describe test results. The weakness of the power of a statistical test is that the p-value is influenced by sample size. Therefore, the null hypothesis can be rejected in most cases if the sample is very large, even when the real difference is negligible. To overcome this weakness, effect size can be used in the statistical analysis. Effect size can be defined as the “standardized measure of the size of the mean difference of the relationship among the study groups”. In this regard, Cohen’s d was used for effect size to indicate standardized differences for a comparison of two independent means [16,17]:

$$Cohen’s\hspace{0.17em}d=\frac{({\mu }_{high}-{\mu }_{low})}{\sqrt{\frac{{\sigma }_{high}^2+{\sigma }_{low}^2}{2}}},$$

where the bigger the difference between two independent means, the bigger the effect size.

RESULTS

In this study, the used genetic factors were five individual SNPs (g.12870 T>C, g.13126 T>C, g.15532 C>A, g.16907 T>C, and g.17924 G>A) in the exon of the FASN gene that were associated with FAC of Korean cattle and not deviated from the Hardy-Weinberg equilibrium [7].

Tables 1 to 4 summarize the accuracy of gene-gene interaction models for the four economic traits. This accuracy was determined before and after environmental factors were adjusted for. According to the results, the higher-order interaction model was significantly more accurate than the SNP model, and adjusted data were more accurate than raw data.

Table 1.

The best SNP in five-factor interactions of the C18:1 base in the MDR method for Korean native cattle

Adjustment	Model	Training acc.1)	Test acc.2)	CVC3)
Before	g.13126 T>C	0.6016	0.6016	10/10
	g.13126 T>C, g.15532 C>A	0.6235	0.5869	9/10
	g.13126 T>C, g.15532 C>A, g.16907 T>C	0.6407	0.6176	10/10
	g.12870 T>C, g.13126 T>C, g.15532 C>A, g.16907 T>C	0.6517	0.6300	10/10
	g.12870 T>C, g.13126 T>C, g.15532 C>A, g.16907 T>C, g.17921 G>A	0.6565	0.6317	10/10
After	g.13126 T>C	0.7426	0.7426	10/10
	g.13126 T>C, g.15532 C>A	0.8719	0.8719	10/10
	g.13126 T>C, g.15532 C>A, g.17924 G>A	0.9886	0.9829	8/10
	g.12870 T>C, g.13126 T>C, g.15532 C>A, g.17924 G>A	1.0000	0.9956	10/10
	g.12870 T>C, g.13126 T>C, g.15532 C>A, g.16907 T>C, g.17924 G>A	1.0000	0.9846	10/10

SNP, single nucleotide polymorphism; MDR, multifactor dimensionality reduction.

¹⁾Training-balanced accuracy.

²⁾Test-balanced accuracy.

³⁾Cross-validation consistency.

Table 4.

The best SNP in five-factor interactions of the CWT base in the MDR method for Korean native cattle

Adjustment	Model	Training acc.1)	Test acc.2)	CVC3)
Before	g.15532 C>A	0.5212	0.4442	5/10
	g.12870 T>C, g.15532 C>A	0.5441	0.4479	8/10
	g.13126 T>C, g.15532 C>A, g.17924 G>A	0.5664	0.4829	7/10
	g.13126 T>C, g.15532 C>A, g.16907 T>C, g.17924 G>A	0.5781	0.4847	6/10
	g.12870 T>C, g.13126 T>C, g.15532 C>A, g.16907 T>C, g.17924 G>A	0.5865	0.4770	10/10
After	g.12870 T>C	0.8440	0.8440	10/10
	g.12870 T>C, g.17924 G>A	0.9177	0.9054	8/10
	g.12870 T>C, g.16907 T>C, g.17924 G>A	0.9484	0.9351	9/10
	g.12870 T>C, g.13126 T>C, g.15532 C>A, g.17924 G>A	0.9651	0.9612	10/10
	g.12870 T>C, g.13126 T>C, g.15532 C>A, g.16907 T>C, g.17924 G>A	1.0000	0.9922	10/10

SNP, single nucleotide polymorphism; CWT, carcass weight; MDR, multifactor dimensionality reduction.

¹⁾Training-balanced accuracy.

²⁾Test-balanced accuracy.

³⁾Cross-validation consistency.

First, the accuracy was compared before and after adjustment. The accuracy of the best SNP in C18:1 increased from 60.16% to 74.26%, and that of the two-factor interaction increased from 58.69% to 87.19%. In addition, the accuracy of MUFAs, MS, and CWT increased by 16.78%p, 28.98%p, and 39.98%p, respectively, in the best SNP and by 27.73%p, 43.53%p, and 45.75%p in the two-factor interaction. Therefore, adjusted data were used to identify gene-gene interaction effects.

Second, superior SNPs and SNP interactions were identified using the MDR method. In the case of C18:1 (Table 1) and MUFAs (Table 2), g.13126 T>C had the highest score for both training- and test-balanced accuracy (74.26% for C18:1 and 74.61% for MUFAs). In terms of the two-factor interaction, g.13126 T>C and g.15532 C>A had the highest training-and test-balanced accuracy (87.19% for C18:1 and 88.10% for MUFA), with a cross-validation consistency of 10 out of 10. For MS, the SNP g.12870 T>C showed the highest accuracy at 80.75%, and the two-factor interaction model g.12870 T>C and g.15532 C>A showed the highest testing-balanced accuracy at 97.12% (Table 3). The best SNP for CWT was g.12870 T>C at 84.4% accuracy, and the two-factor interaction between g.12870 T>C and g.17924 G>A showed the highest accuracy at 90.54% (Table 4).

Table 2.

The best SNP in five-factor interactions of the MUFA base in the MDR method for Korean native cattle

Adjustment	Model	Training acc.1)	Test acc.2)	CVC3)
Before	g.13126 T>C	0.5871	0.5783	10/10
	g.13126 T>C, g.15532 C>A	0.6127	0.6037	10/10
	g.13126 T>C, g.15532 C>A, g.16907 T>C	0.6221	0.5633	6/10
	g.12870 T>C, g.13126 T>C, g.15532 C>A, g.16907 T>C	0.6296	0.5715	8/10
	g.12870 T>C, g.13126 T>C, g.15532 C>A, g.16907 T>C, g.17921 G>A	0.6337	0.5660	10/10
After	g.13126 T>C	0.7461	0.7461	10/10
	g.13126 T>C, g.15532 C>A	0.8810	0.8810	10/10
	g.13126 T>C, g.15532 C>A, g.17924 G>A	0.9957	0.9935	10/10
	g.12870 T>C, g.13126 T>C, g.15532 C>A, g.17924 G>A	1.0000	0.9957	10/10
	g.12870 T>C, g.13126 T>C, g.15532 C>A, g.16907 T>C, g.17924 G>A	1.0000	0.9848	10/10

SNP, single nucleotide polymorphism; MUFA, monounsaturated fatty acid; MDR, multifactor dimensionality reduction.

¹⁾Training-balanced accuracy.

²⁾Test-balanced accuracy.

³⁾Cross-validation consistency.

Table 3.

The best SNP in five-factor interactions of the MS base in the MDR method for Korean native cattle

Adjustment	Model	Training acc.1)	Test acc.2)	CVC3)
Before	g.15532 C>A	0.5459	0.5177	10/10
	g.12870 T>C, g.15532 C>A	0.5689	0.5359	8/10
	g.12870 T>C, g.15532 C>A, g.16907 T>C	0.5836	0.5092	7/10
	g.12870 T>C, g.13126 T>C, g.15532 C>A, g.16907 T>C	0.5957	0.5205	10/10
	g.12870 T>C, g.13126 T>C, g.15532 C>A, g.16907 T>C, g.17924 G>A	0.6019	0.5278	10/10
After	g.12870 T>C	0.8075	0.8075	10/10
	g.12870 T>C, g.15532 C>A	0.9712	0.9712	10/10
	g.12870 T>C, g.13126 T>C, g.15532 C>A	0.9915	0.9858	10/10
	g.12870 T>C, g.13126 T>C, g.15532 C>A, g.16907 T>C	1.0000	0.9886	10/10
	g.12870 T>C, g.13126 T>C, g.15532 C>A, g.16907 T>C, g.17924 G>A	1.0000	0.9744	10/10

SNP, single nucleotide polymorphism; MS, marbling score; MDR, multifactor dimensionality reduction.

¹⁾Training-balanced accuracy.

²⁾Test-balanced accuracy.

³⁾Cross-validation consistency.

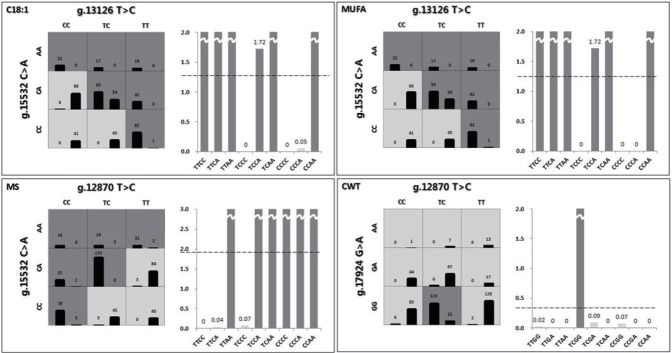
Third, gene-gene interactions of C18:1, MUFAs, MS, and CWT were investigated using a detailed MDR interaction model, and the two-factor interaction was selected as the best for each economic trait (Figure 1). Each genotype was divided into a high- or low-risk group in the selected two-factor interaction. If the case-control ratio for each genotype was higher than the threshold, then the genotype was identified as a high-risk group. In addition, mean scores between high- and low-risk groups were compared (Table 5). The thresholds of C18:1 and MUFAs were 1.2599 and 1.2208, respectively. Each case-control ratio for TTCC, TTCA, TTAA, TCCA, TCAA, and CCAA for the interaction between g.13126 T>C and g.15532 C>A was above the respective threshold; these six genotypes were therefore classified as the high-risk group and the others as the low-risk group. According to the threshold (1.9148) of MS, TTAA, TCCA, TCAA, CCCC, CCCA, and CCAA, the interaction between g.12870 T>C and g.15532 C>A was classified as the high-risk group. In the case of CWT, the threshold was 0.3359, and therefore the TCGA of the g.12870 T>C and g.17924 G>A interaction was identified as the high-risk group.

Figure 1.

The best two-factor interaction for four traits based on the multifactor dimensionality reduction (MDR) method for Korean native cattle. The high-risk group is indicated by dark grey, and the low-risk group, by grey. The left bar of a cell represents case frequency, and the right bar, control frequency.

Table 5.

Comparison of mean scores between high- and low-risk groups of Korean native cattle

Traits	SNP	Genotype	N	Mean	SD	t-test p-value	Cohen’s d
C18:1	g.13126 T>C	TT	141	44.832	0.929	6.982 (<0.001)	1.681
		TC, CC	372	43.155	1.061
	g.15532 C>A	AA	65	45.123	0.966	4.840 (<0.001)	1.620
		CA, AA	448	43.397	1.156
	g.13126 T>C, g.15532 C>A	TTCC, TTCA, TTAA, TCCA, TCAA, CCAA	337	44.238	0.896	20.866 (<0.001)	1.905
		Others	176	42.425	1.005
MUFA	g.13126 T>C	TT	141	53.799	0.902	6.528 (<0.001)	1.783
		TC, CC	372	52.023	1.083
	g.15532 C>A	AA	65	54.107	0.985	4.747 (<0.001)	1.684
		CA, CC	448	52.279	1.177
	g.13126 T>C, g.15532 C>A	TTCC, TTCA, TTAA, TCCA, TCAA, CCAA	337	53.162	0.911	21.600 (<0.001)	1.977
		Others	176	51.265	1.005
MS	g.12870 T>C	TT, TC	353	5.749	0.397	9.829 (<0.001)	0.980
		CC	160	5.300	0.511
	g.15532 C>A	CA, AA	344	5.765	0.359	10.287 (<0.001)	1.029
		CC	169	5.291	0.544
	g.12870 T>C, g.15532 C>A	TTAA,TCCA,TCAA, CCCC, CCCA,CCAA,	338	5.846	0.300	18.843 (<0.001)	1.852
		Others	175	5.151	0.437
CWT	g.12870 T>C	TC	217	429.997	5.802	7.528 (<0.001)	0.688
		TT, CC	296	425.227	7.902
	g.17924 G>A	GG	358	429.327	6.656	10.590 (<0.001)	1.007
		GA, AA	155	422.436	7.021
	g.12870 T>C, g.17924 G>A	TCGA	137	432.251	3.787	13.394 (<0.001)	1.132
		Others	376	425.421	7.643

SNP, single nucleotide polymorphism; SD, standard deviation; MUFA, monounsaturated fatty acid; MS, marbling score; CWT, carcass weight.

Finally, high- and low-risk genotypes were compared based on their mean scores for each trait (Table 5). Table 5 compares individual SNP and interaction effects. The t-test was significant (p<0.001), and the effect size of the genotype of the SNP interaction was larger than that of the individual SNP.

DISCUSSION

To determine the interaction effect of Hanwoo, we used five SNPs which are known as the factors affecting the flavor and quality of beef [18]. Phenotypes are influenced by environmental and genetic factors. To enhance the accuracy of the genetic effect analysis, the study proposes a new statistical model that excludes environmental factors based on an ANCOVA model. The statistical model has qualitative independent variable which has more than two classes (17 farms). Then, we tried additional indicator variables in the model [14]. The results verify a significant increase in analysis accuracy.

Data from 513 Hanwoo steer from 17 farms in Gyengsangbuk-do were employed to construct an ANCOVA model of how economic traits are influenced by five SNPs and environmental factors. Here economic traits were C18:1, MUFAs, MS, and CWT and five SNPs (g.12870 T>C, g.13126 T>C, g.15532 C>A, g.16907 T>C, and g.17924 G>A), which we previously found to influence the flavor and quality of beef [7]. Some of these SNPs might change their functions by producing missense codons. The g.13126 T<C changes an amino acid from tyrosine to histidine. The g.15532 C<A or g.17924 G<A changes an amino acid from leucine to isoleucine or from alanine to threonine. Although the other SNPs are synonymous, we could not rule out the possibility that they might change splicing regulatory sequences, or that such genetic associations might be spuriously produced with their linked loci within each block [18].

Then, we constructed an adjusted statistical model using an ANCOVA model and calculated adj (Y) values. The MDR method was used for individual SNPs and five-factor interactions for each economic trait (C18:1, MUFAs, MS, and CWT). According to the results, the accuracy of SNP interactions was much higher than that of individual SNPs. The most significant two-factor interaction was g.13126 T>C*g.15532 C>A for C18:1 and MUFAs. In addition, the g.12870 T>C*g.15532 C>A interaction showed the highest accuracy in MS, and the g.12870 T>C*g.17924 G>A interaction showed the highest accuracy in CWT. The three SNPs in exons 34 (g.15532 C<A), 37 (g.16907 T<C), and 39 (g.17924 G<A) were all associated with myristic acid in a crossbred of Limousin and Jersey (p<0.05) but not with C18:1 [8]. The g.17924 was associated also with oleic acid in American Angus cattle (p<0.05) [10] and Korean cattle (p<0.05) [19]. This implies that these two-factor interactions had the greatest impact on economic traits influencing the flavor and quality of beef. The selected interaction for CWT changed before adjustment because CWT was heavily influenced by environmental factors. Figure 1 shows the contingency tables of the best two-factor interactions for each economic trait. The chi-square test of interactions was conducted to validate the results, and all tests were significant. In the figure, three factors and their possible multifactor classes or cells are represented in a three-dimensional space [20]. The left bar of the cell refers to case frequency, and the right bar, to control frequency. Dark grey cells and grey cells indicate “high-risk” and “low-risk” groups, respectively, depending on whether the case-control ratio was above a certain threshold. The threshold was determined based on the case-control ratio for the whole data. Because the data were passed through the k-means clustering method for each trait, they had three different case-control ratios. Therefore, cells were classified based on the threshold for each trait. The high- and low-risk groups are shown in the graphs. The threshold was 1.2599 in C18:1. Nine genotypes of the two-factor interaction were divided into two groups by comparing their case-control ratios and thresholds. TTCC, TTCA, TTAA, TCCA, TCAA, and CCAA were labeled as the high-risk group and the others as the low-risk group. In MUFAs, MS, and CWT, the thresholds were 1.2208, 1.9148, and 0.3359, respectively. Similarly, each genotype was determined by comparing its ratio and threshold. TTCC, TTCA, TTAA, TCCA, TCAA, and CCAA for MUFAs; TTAA, TCCA, TCAA, CCCC, CCCA, and CCAA for MS; and TCGA for CWT were classified as the high-risk group. There was a significant difference between the high- and low-risk groups (Table 5), indicating that high-risk genotypes were superior. In particular, two-factor interactions showed clear differences between the high- and low-risk groups. According to the results, the gene-gene interaction effect was superior to the individual SNP effect. As shown in Table 5, individual and interaction effects of SNPs were examined and compared for C18:1, MUFAs, MS, and CWT. The superior genotype groups, which were all and significant, were 44.238 (standard deviation [SD] = 0.896, p<0.001, Cohen’s d = 1.905) for C18:1, 53.162 (SD = 0.911, p<0.001, Cohen’s d = 1.977) for MUFAs, 5.846 (SD = 0.3, p<0.001, Cohen’s d = 1.852) for MS, and 432.251 (SD = 3.787, p<0.001, Cohen’s d = 1.132) for CWT (Table 5). The interaction effect of SNPs was greater than the individual effect for C18:1, MUFAs, MS, and CWT.

The results verify that the proposed MDR nonparametric statistical method for detecting gene interactions is suitable for small samples and can be used to perform an exhaustive search of all n-locus models by collapsing multi-locus genotypes into high- and low-risk groups [20]. The MDR method may be used for the genetic assessment of quantitative traits after further development. Finally, these genotypes of individual SNPs and their combinations may be useful genetic markers for improving beef quality, which is one of the most important goals of the Korean beef cattle industry [21].