Mechanics of human voice production and control

Abstract

As the primary means of communication, voice plays an important role in daily life. Voice also conveys personal information such as social status, personal traits, and the emotional state of the speaker. Mechanically, voice production involves complex fluid-structure interaction within the glottis and its control by laryngeal muscle activation. An important goal of voice research is to establish a causal theory linking voice physiology and biomechanics to how speakers use and control voice to communicate meaning and personal information. Establishing such a causal theory has important implications for clinical voice management, voice training, and many speech technology applications. This paper provides a review of voice physiology and biomechanics, the physics of vocal fold vibration and sound production, and laryngeal muscular control of the fundamental frequency of voice, vocal intensity, and voice quality. Current efforts to develop mechanical and computational models of voice production are also critically reviewed. Finally, issues and future challenges in developing a causal theory of voice production and perception are discussed.

I. INTRODUCTION

In the broad sense, voice refers to the sound we produce to communicate meaning, ideas, opinions, etc. In the narrow sense, voice, as in this review, refers to sounds produced by vocal fold vibration, or voiced sounds. This is in contrast to unvoiced sounds which are produced without vocal fold vibration, e.g., fricatives which are produced by airflow through constrictions in the vocal tract, plosives produced by sudden release of a complete closure of the vocal tract, or other sound producing mechanisms such as whispering. For voiced sound production, vocal fold vibration modulates airflow through the glottis and produces sound (the voice source), which propagates through the vocal tract and is selectively amplified or attenuated at different frequencies. This selective modification of the voice source spectrum produces perceptible contrasts, which are used to convey different linguistic sounds and meaning. Although this selective modification is an important component of voice production, this review focuses on the voice source and its control within the larynx.

For effective communication of meaning, the voice source, as a carrier for the selective spectral modification by the vocal tract, contains harmonic energy across a large range of frequencies that spans at least the first few acoustic resonances of the vocal tract. In order to be heard over noise, such harmonic energy also has to be reasonably above the noise level within this frequency range, unless a breathy voice quality is desired. The voice source also contains important information of the pitch, loudness, prosody, and voice quality, which convey meaning (see Kreiman and Sidtis, 2011, Chap. 8 for a review), biological information (e.g., size), and paralinguistic information (e.g., the speaker's social status, personal traits, and emotional state; Sundberg, 1987; Kreiman and Sidtis, 2011). For example, the same vowel may sound different when spoken by different people. Sometimes a simple “hello” is all it takes to recognize a familiar voice on the phone. People tend to use different voices to different speakers on different occasions, and it is often possible to tell if someone is happy or sad from the tone of their voice.

One of the important goals of voice research is to understand how the vocal system produces voice of different source characteristics and how people associate percepts to these characteristics. Establishing a cause-effect relationship between voice physiology and voice acoustics and perception will allow us to answer two essential questions in voice science and effective clinical care (Kreiman et al., 2014): when the output voice changes, what physiological alteration caused this change; if a change to voice physiology occurs, what change in perceived voice quality can be expected? Clinically, such knowledge would lead to the development of a physically based theory of voice production that is capable of better predicting voice outcomes of clinical management of voice disorders, thus improving both diagnosis and treatment. More generally, an understanding of this relationship could lead to a better understanding of the laryngeal adjustments that we use to change voice quality, adopt different speaking or singing styles, or convey personal information such as social status and emotion. Such understanding may also lead to the development of improved computer programs for synthesis of naturally sounding, speaker-specific speech of varying emotional percepts.

Understanding such cause-effect relationship between voice physiology and production necessarily requires a multi-disciplinary effort. While voice production results from a complex fluid-structure-acoustic interaction process, which again depends on the geometry and material properties of the lungs, larynx, and the vocal tract, the end interest of voice is its acoustics and perception. Changes in voice physiology or physics that cannot be heard are not that interesting. On the other hand, the physiology and physics may impose constraints on the co-variations among fundamental frequency (F0), vocal intensity, and voice quality, and thus the way we use and control our voice. Thus, understanding voice production and voice control requires an integrated approach, in which physiology, vocal fold vibration, and acoustics are considered as a whole instead of disconnected components. Traditionally, the multi-disciplinary nature of voice production has led to a clear divide between research activities in voice production, voice perception, and their clinical or speech applications, with few studies attempting to link them together. Although much advancement has been made in understanding the physics of phonation, some misconceptions still exist in textbooks in otolaryngology and speech pathology. For example, the Bernoulli effect, which has been shown to play a minor role in phonation, is still considered an important factor in initiating and sustaining phonation in many textbooks and reviews. Tension and stiffness are often used interchangeably despite that they have different physical meanings. The role of the thyroarytenoid muscle in regulating medial compression of the membranous vocal folds is often understated. On the other hand, research on voice production often focuses on the glottal flow and vocal fold vibration, but can benefit from a broader consideration of the acoustics of the produced voice and their implications for voice communication.

This paper provides a review on our current understanding of the cause-effect relation between voice physiology, voice production, and voice perception, with the hope that it will help better bridge research efforts in different aspects of voice studies. An overview of vocal fold physiology is presented in Sec. II, with an emphasis on laryngeal regulation of the geometry, mechanical properties, and position of the vocal folds. The physical mechanisms of self-sustained vocal fold vibration and sound generation are discussed in Sec. III, with a focus on the roles of various physical components and features in initiating phonation and affecting the produced acoustics. Some misconceptions of the voice production physics are also clarified. Section IV discusses the physiologic control of F0, vocal intensity, and voice quality. Section V reviews past and current efforts in developing mechanical and computational models of voice production. Issues and future challenges in establishing a causal theory of voice production and perception are discussed in Sec. VI.

II. VOCAL FOLD PHYSIOLOGY AND BIOMECHANICS

A. Vocal fold anatomy and biomechanics

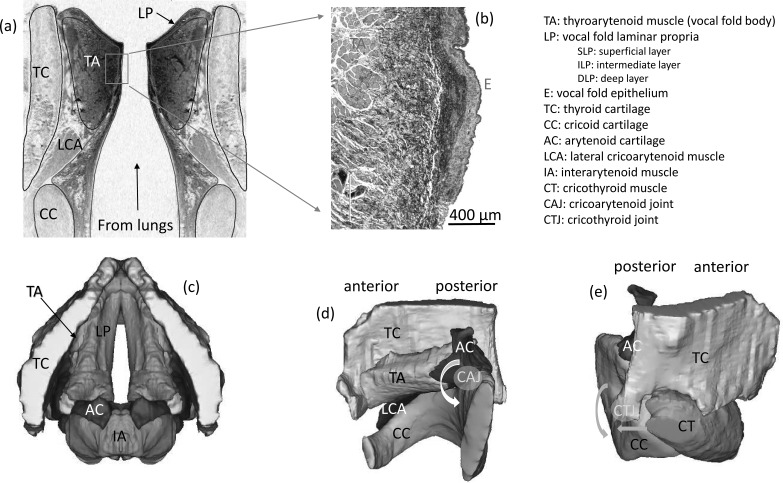
The human vocal system includes the lungs and the lower airway that function to supply air pressure and airflow (a review of the mechanics of the subglottal system can be found in Hixon, 1987), the vocal folds whose vibration modulates the airflow and produces voice source, and the vocal tract that modifies the voice source and thus creates specific output sounds. The vocal folds are located in the larynx and form a constriction to the airway [Fig. 1(a)]. Each vocal fold is about 11–15 mm long in adult women and 17–21 mm in men, and stretches across the larynx along the anterior-posterior direction, attaching anteriorly to the thyroid cartilage and posteriorly to the anterolateral surface of the arytenoid cartilages [Fig. 1(c)]. Both the arytenoid [Fig. 1(d)] and thyroid [Fig. 1(e)] cartilages sit on top of the cricoid cartilage and interact with it through the cricoarytenoid joint and cricothyroid joint, respectively. The relative movement of these cartilages thus provides a means to adjust the geometry, mechanical properties, and position of the vocal folds, as further discussed below. The three-dimensional airspace between the two opposing vocal folds is the glottis. The glottis can be divided into a membranous portion, which includes the anterior portion of the glottis and extends from the anterior commissure to the vocal process of the arytenoid, and a cartilaginous portion, which is the posterior space between the arytenoid cartilages.

FIG. 1.

(Color online) (a) Coronal view of the vocal folds and the airway; (b) histological structure of the vocal fold lamina propria in the coronal plane (image provided by Dr. Jennifer Long of UCLA); (c) superior view of the vocal folds, cartilaginous framework, and laryngeal muscles; (d) medial view of the cricoarytenoid joint formed between the arytenoid and cricoid cartilages; (e) posterolateral view of the cricothyroid joint formed by the thyroid and the cricoid cartilages. The arrows in (d) and (e) indicate direction of possible motions of the arytenoid and cricoid cartilages due to LCA and CT muscle activation, respectively.

The vocal folds are layered structures, consisting of an inner muscular layer (the thyroarytenoid muscle) with muscle fibers aligned primarily along the anterior-posterior direction, a soft tissue layer of the lamina propria, and an outmost epithelium layer [Figs. 1(a) and 1(b)]. The thyroarytenoid (TA) muscle is sometimes divided into a medial and a lateral bundle, with each bundle responsible for a certain vocal fold posturing function. However, such functional division is still a topic of debate (Zemlin, 1997). The lamina propria consists of the extracellular matrix (ECM) and interstitial substances. The two primary ECM proteins are the collagen and elastin fibers, which are aligned mostly along the length of the vocal folds in the anterior-posterior direction (Gray et al., 2000). Based on the density of the collagen and elastin fibers [Fig. 1(b)], the lamina propria can be divided into a superficial layer with limited and loose elastin and collagen fibers, an intermediate layer of dominantly elastin fibers, and a deep layer of mostly dense collagen fibers (Hirano and Kakita, 1985; Kutty and Webb, 2009). In comparison, the lamina propria (about 1 mm thick) is much thinner than the TA muscle.

Conceptually, the vocal fold is often simplified into a two-layer body-cover structure (Hirano, 1974; Hirano and Kakita, 1985). The body layer includes the muscular layer and the deep layer of the lamina propria, and the cover layer includes the intermediate and superficial lamina propria and the epithelium layer. This body-cover concept of vocal fold structure will be adopted in the discussions below. Another grouping scheme divides the vocal fold into three layers. In addition to a body and a cover layer, the intermediate and deep layers of the lamina propria are grouped into a vocal ligament layer (Hirano, 1975). It is hypothesized that this layered structure plays a functional role in phonation, with different combinations of mechanical properties in different layers leading to production of different voice source characteristics (Hirano, 1974). However, because of lack of data of the mechanical properties in each vocal fold layer and how they vary at different conditions of laryngeal muscle activation, a definite understanding of the functional roles of each vocal fold layer is still missing.

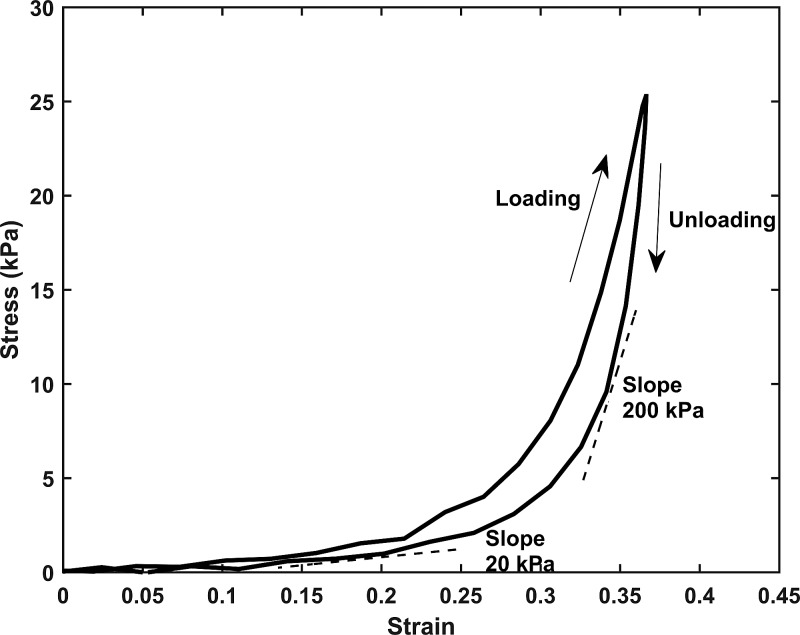
The mechanical properties of the vocal folds have been quantified using various methods, including tensile tests (Hirano and Kakita, 1985; Zhang et al., 2006b; Kelleher et al., 2013a), shear rheometry (Chan and Titze, 1999; Chan and Rodriguez, 2008; Miri et al., 2012), indentation (Haji et al., 1992a,b; Tran et al., 1993; Chhetri et al., 2011), and a surface wave method (Kazemirad et al., 2014). These studies showed that the vocal folds exhibit a nonlinear, anisotropic, viscoelastic behavior. A typical stress-strain curve of the vocal folds under anterior-posterior tensile test is shown in Fig. 2. The slope of the curve, or stiffness, quantifies the extent to which the vocal folds resist deformation in response to an applied force. In general, after an initial linear range, the slope of the stress-strain curve (stiffness) increases gradually with further increase in the strain (Fig. 2), presumably due to the gradual engagement of the collagen fibers. Such nonlinear mechanical behavior provides a means to regulate vocal fold stiffness and tension through vocal fold elongation or shortening, which plays an important role in the control of the F0 or pitch of voice production. Typically, the stress is higher during loading than unloading, indicating a viscous behavior of the vocal folds. Due to the presence of the AP-aligned collagen, elastin, and muscle fibers, the vocal folds also exhibit anisotropic mechanical properties, stiffer along the AP direction than in the transverse plane. Experiments (Hirano and Kakita, 1985; Alipour and Vigmostad, 2012; Miri et al., 2012; Kelleher et al., 2013a) showed that the Young's modulus along the AP direction in the cover layer is more than 10 times (as high as 80 times in Kelleher et al., 2013a) larger than in the transverse plane. Stiffness anisotropy has been shown to facilitate medial-lateral motion of the vocal folds (Zhang, 2014) and complete glottal closure during phonation (Xuan and Zhang, 2014).

FIG. 2.

Typical tensile stress-strain curve of the vocal fold along the anterior-posterior direction during loading and unloading at 1 Hz. The slope of the tangent line (dashed lines) to the stress-strain curve quantifies the tangent stiffness. The stress is typically higher during loading than unloading due to the viscous behavior of the vocal folds. The curve was obtained by averaging data over 30 cycles after a 10-cycle preconditioning.

Accurate measurement of vocal fold mechanical properties at typical phonation conditions is challenging, due to both the small size of the vocal folds and the relatively high frequency of phonation. Although tensile tests and shear rheometry allow direct measurement of material modules, the small sample size often leads to difficulties in mounting tissue samples to the testing equipment, thus creating concerns of accuracy. These two methods also require dissecting tissue samples from the vocal folds and the laryngeal framework, making it impossible for in vivo measurement. The indentation method is ideal for in vivo measurement and, because of the small size of indenters used, allows characterization of the spatial variation of mechanical properties of the vocal folds. However, it is limited for measurement of mechanical properties at conditions of small deformation. Although large indentation depths can be used, data interpretation becomes difficult and thus it is not suitable for assessment of the nonlinear mechanical properties of the vocal folds.

There has been some recent work toward understanding the contribution of individual ECM components to the macro-mechanical properties of the vocal folds and developing a structurally based constitutive model of the vocal folds (e.g., Chan et al., 2001; Kelleher et al., 2013b; Miri et al., 2013). The contribution of interstitial fluid to the viscoelastic properties of the vocal folds and vocal fold stress during vocal fold vibration and collision has also been investigated using a biphasic model of the vocal folds in which the vocal fold was modeled as a solid phase interacting with an interstitial fluid phase (Zhang et al., 2008; Tao et al., 2009, Tao et al., 2010; Bhattacharya and Siegmund, 2013). This structurally based approach has the potential to predict vocal fold mechanical properties from the distribution of collagen and elastin fibers and interstitial fluids, which may provide new insights toward the differential mechanical properties between different vocal fold layers at different physiologic conditions.

B. Vocal fold posturing

Voice communication requires fine control and adjustment of pitch, loudness, and voice quality. Physiologically, such adjustments are made through laryngeal muscle activation, which stiffens, deforms, or repositions the vocal folds, thus controlling the geometry and mechanical properties of the vocal folds and glottal configuration.

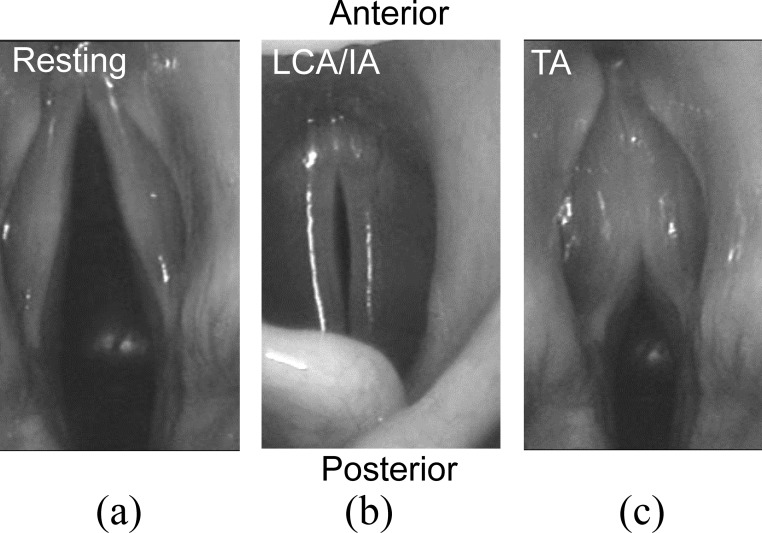
One important posturing is adduction/abduction of the vocal folds, which is primarily achieved through motion of the arytenoid cartilages. Anatomical analysis and numerical simulations have shown that the cricoarytenoid joint allows the arytenoid cartilages to slide along and rotate about the long axis of the cricoid cartilage, but constrains arytenoid rotation about the short axis of the cricoid cartilage (Selbie et al., 1998; Hunter et al., 2004; Yin and Zhang, 2014). Activation of the lateral cricoarytenoid (LCA) muscles, which attach anteriorly to the cricoid cartilage and posteriorly to the arytenoid cartilages, induce mainly an inward rotation motion of the arytenoid about the cricoid cartilages in the coronal plane, and moves the posterior portion of the vocal folds toward the glottal midline. Activation of the interarytenoid (IA) muscles, which connect the posterior surfaces of the two arytenoids, slides and approximates the arytenoid cartilages [Fig. 1(c)], thus closing the cartilaginous glottis. Because both muscles act on the posterior portion of the vocal folds, combined action of the two muscles is able to completely close the posterior portion of the glottis, but is less effective in closing the mid-membranous glottis (Fig. 3; Choi et al., 1993; Chhetri et al., 2012; Yin and Zhang, 2014). Because of this inefficiency in mid-membranous approximation, LCA/IA muscle activation is unable to produce medial compression between the two vocal folds in the membranous portion, contrary to current understandings (Klatt and Klatt, 1990; Hixon et al., 2008). Complete closure and medial compression of the mid-membranous glottis requires the activation of the TA muscle (Choi et al., 1993; Chhetri et al., 2012). The TA muscle forms the bulk of the vocal folds and stretches from the thyroid prominence to the anterolateral surface of the arytenoid cartilages (Fig. 1). Activation of the TA muscle produces a whole-body rotation of the vocal folds in the horizontal plane about the point of its anterior attachment to the thyroid cartilage toward the glottal midline (Yin and Zhang, 2014). This rotational motion is able to completely close the membranous glottis but often leaves a gap posteriorly (Fig. 3). Complete closure of both the membranous and cartilaginous glottis thus requires combined activation of the LCA/IA and TA muscles. The posterior cricoarytenoid (PCA) muscles are primarily responsible for opening the glottis but may also play a role in voice production of very high pitches, as discussed below.

FIG. 3.

Activation of the LCA/IA muscles completely closes the posterior glottis but leaves a small gap in the membranous glottis, whereas TA activation completely closes the anterior glottis but leaves a gap at the posterior glottis. From unpublished stroboscopic recordings from the in vivo canine larynx experiments in Choi et al. (1993).

Vocal fold tension is regulated by elongating or shortening the vocal folds. Because of the nonlinear material properties of the vocal folds, changing vocal fold length also leads to changes in vocal fold stiffness, which otherwise would stay constant for linear materials. The two laryngeal muscles involved in regulating vocal fold length are the cricothyroid (CT) muscle and the TA muscle. The CT muscle consists of two bundles. The vertically oriented bundle, the pars recta, connects the anterior surface of the cricoid cartilage and the lower border of the thyroid lamina. Its contraction approximates the thyroid and cricoid cartilages anteriorly through a rotation about the cricothyroid joint. The other bundle, the pars oblique, is oriented upward and backward, connecting the anterior surface of the cricoid cartilage to the inferior cornu of the thyroid cartilage. Its contraction displaces the cricoid and arytenoid cartilages backwards (Stone and Nuttall, 1974), although the thyroid cartilage may also move forward slightly. Contraction of both bundles thus elongates the vocal folds and increases the stiffness and tension in both the body and cover layers of the vocal folds. In contrast, activation of the TA muscle, which forms the body layer of the vocal folds, increase the stiffness and tension in the body layer. Activation of the TA muscle, in addition to an initial effect of mid-membranous vocal fold approximation, also shortens the vocal folds, which decreases both the stiffness and tension in the cover layer (Hirano and Kakita, 1985; Yin and Zhang, 2013). One exception is when the tension in the vocal fold cover is already negative (i.e., under compression), in which case shortening the vocal folds further through TA activation decreases tension (i.e., increased compression force) but may increase stiffness in the cover layer. Activation of the LCA/IA muscles generally does not change the vocal fold length much and thus has only a slight effect on vocal fold stiffness and tension (Chhetri et al., 2009; Yin and Zhang, 2014). However, activation of the LCA/IA muscles (and also the PCA muscles) does stabilize the arytenoid cartilage and prevent it from moving forward when the cricoid cartilage is pulled backward due to the effect of CT muscle activation, thus facilitating extreme vocal fold elongation, particularly for high-pitch voice production. As noted above, due to the lack of reliable measurement methods, our understanding of how vocal fold stiffness and tension vary at different muscular activation conditions is limited.

Activation of the CT and TA muscles also changes the medial surface shape of the vocal folds and the glottal channel geometry. Specifically, TA muscle activation causes the inferior part of the medial surface to bulge out toward the glottal midline (Hirano and Kakita, 1985; Hirano, 1988; Vahabzadeh-Hagh et al., 2016), thus increasing the vertical thickness of the medial surface. In contrast, CT activation reduces this vertical thickness of the medial surface. Although many studies have investigated the prephonatory glottal shape (convergent, straight, or divergent) on phonation (Titze, 1988a; Titze et al., 1995), a recent study showed that the glottal channel geometry remains largely straight under most conditions of laryngeal muscle activation (Vahabzadeh-Hagh et al., 2016).

III. PHYSICS OF VOICE PRODUCTION

A. Sound sources of voice production

The phonation process starts from the adduction of the vocal folds, which approximates the vocal folds to reduce or close the glottis. Contraction of the lungs initiates airflow and establishes pressure buildup below the glottis. When the subglottal pressure exceeds a certain threshold pressure, the vocal folds are excited into a self-sustained vibration. Vocal fold vibration in turn modulates the glottal airflow into a pulsating jet flow, which eventually develops into turbulent flow into the vocal tract.

In general, three major sound production mechanisms are involved in this process (McGowan, 1988; Hofmans, 1998; Zhao et al., 2002; Zhang et al., 2002a), including a monopole sound source due to volume of air displaced by vocal fold vibration, a dipole sound source due to the fluctuating force applied by the vocal folds to the airflow, and a quadrupole sound source due to turbulence developed immediately downstream of the glottal exit. When the false vocal folds are tightly adducted, an additional dipole source may arise as the glottal jet impinges onto the false vocal folds (Zhang et al., 2002b). The monopole sound source is generally small considering that the vocal folds are nearly incompressible and thus the net volume flow displacement is small. The dipole source is generally considered as the dominant sound source and is responsible for the harmonic component of the produced sound. The quadrupole sound source is generally much weaker than the dipole source in magnitude, but it is responsible for broadband sound production at high frequencies.

For the harmonic component of the voice source, an equivalent monopole sound source can be defined at a plane just downstream of the region of major sound sources, with the source strength equal to the instantaneous pulsating glottal volume flow rate. In the source-filter theory of phonation (Fant, 1970), this monopole sound source is the input signal to the vocal tract, which acts as a filter and shapes the sound source spectrum into different sounds before they are radiated from the mouth to the open as the voice we hear. Because of radiation from the mouth, the sound source is proportional to the time derivative of the glottal flow. Thus, in the voice literature, the time derivate of the glottal flow, instead of the glottal flow, is considered as the voice source.

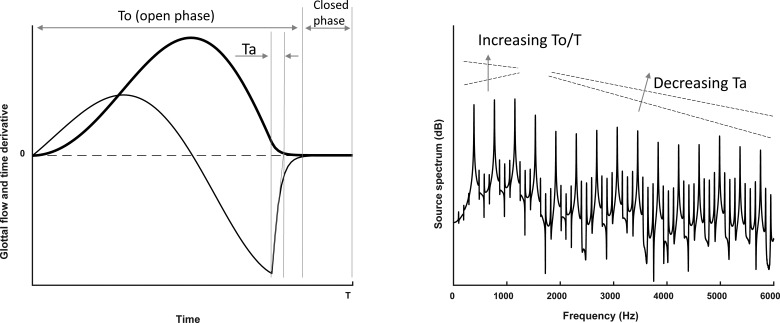
The phonation cycle is often divided into an open phase, in which the glottis opens (the opening phase) and closes (the closing phase), and a closed phase, in which the glottis is closed or remains a minimum opening area when the glottal closure is incomplete. The glottal flow increases and decreases in the open phase, and remains zero during the closed phase or minimum for incomplete glottal closure (Fig. 4). Compared to the glottal area waveform, the glottal flow waveform reaches its peak at a later time in the cycle so that the glottal flow waveform is more skewed to the right. This skewing in the glottal flow waveform to the right is due to the acoustic mass in the glottis and the vocal tract (when the F0 is lower than a nearby vocal tract resonance frequency), which causes a delay in the increase in the glottal flow during the opening phase, and a faster decay in the glottal flow during the closing phase (Rothenberg, 1981; Fant, 1982). Because of this waveform skewing to the right, the negative peak of the time derivative of the glottal flow in the closing phase is often much more dominant than the positive peak in the opening phase. The instant of the most negative peak is thus considered the point of main excitation of the vocal tract and the corresponding negative peak, also referred to as the maximum flow declination rate (MFDR), is a major determinant of the peak amplitude of the produced voice. After the negative peak, the time derivative of the glottal flow waveform returns to zero as phonation enters the closed phase.

FIG. 4.

(Color online) Typical glottal flow waveform and its time derivative (left) and their correspondence to the spectral slopes of the low-frequency and high-frequency portions of the voice source spectrum (right).

Much work has been done to directly link features of the glottal flow waveform to voice acoustics and potentially voice quality (e.g., Fant, 1979, 1982; Fant et al., 1985; Gobl and Chasaide, 2010). These studies showed that the low-frequency spectral shape (the first few harmonics) of the voice source is primarily determined by the relative duration of the open phase with respect to the oscillation period (To/T in Fig. 4, also referred to as the open quotient). A longer open phase often leads to a more dominant first harmonic (H1) in the low-frequency portion of the resulting voice source spectrum. For a given oscillation period, shortening the open phrase causes most of the glottal flow change to occur within a duration (To) that is increasingly shorter than the period T. This leads to an energy boost in the low-frequency portion of the source spectrum that peaks around a frequency of 1/To. For a glottal flow waveform of a very short open phase, the second harmonic (H2) or even the fourth harmonic (H4) may become the most dominant harmonic. Voice source with a weak H1 relative to H2 or H4 is often associated with a pressed voice quality.

The spectral slope in the high-frequency range is primarily related to the degree of discontinuity in the time derivative of the glottal flow waveform. Due to the waveform skewing discussed earlier, the most dominant source of discontinuity often occurs around the instant of main excitation when the time derivative of the glottal flow waveform returns from the negative peak to zero within a time scale of Ta (Fig. 4). For an abrupt glottal flow cutoff (Ta = 0), the time derivative of the glottal flow waveform has a strong discontinuity at the point of main excitation, which causes the voice source spectrum to decay asymptotically at a roll-off rate of −6 dB per octave toward high frequencies. Increasing Ta from zero leads to a gradual return from the negative peak to zero. When approximated by an exponential function, this gradual return functions as a lower-pass filter, with a cutoff frequency around 1/Ta, and reduces the excitation of harmonics above the cutoff frequency 1/Ta. Thus, in the frequency range concerning voice perception, increasing Ta often leads to reduced higher-order harmonic excitation. In the extreme case when there is minimal vocal fold contact, the time derivative of the glottal flow waveform is so smooth that the voice source spectrum only has a few lower-order harmonics. Perceptually, strong excitation of higher-order harmonics is often associated with a bright output sound quality, whereas voice source with limited excitation of higher-order harmonics is often perceived to be weak.

Also of perceptual importance is the turbulence noise produced immediately downstream of the glottis. Although small in amplitude, the noise component plays an important role in voice quality perception, particularly for female voice in which aspiration noise is more persistent than in male voice. While the noise component of voice is often modeled as white noise, its spectrum often is not flat and may exhibit different spectral shapes, depending on the glottal opening and flow rate as well as the vocal tract shape. Interaction between the spectral shape and relative levels of harmonic and noise energy in the voice source has been shown to influence the perception of voice quality (Kreiman and Gerratt, 2012).

It is worth noting that many of the source parameters are not independent from each other and often co-vary. How they co-vary at different voicing conditions, which is essential to natural speech synthesis, remains to be the focus of many studies (e.g., Sundberg and Hogset, 2001; Gobl and Chasaide, 2003; Patel et al., 2011).

B. Mechanisms of self-sustained vocal fold vibration

That vocal fold vibration results from a complex airflow-vocal fold interaction within the glottis rather than repetitive nerve stimulation of the larynx was first recognized by van den Berg (1958). According to his myoelastic-aerodynamic theory of voice production, phonation starts from complete adduction of the vocal folds to close the glottis, which allows a buildup of the subglottal pressure. The vocal folds remain closed until the subglottal pressure is sufficiently high to push them apart, allowing air to escape and producing a negative (with respect to atmospheric pressure) intraglottal pressure due to the Bernoulli effect. This negative Bernoulli pressure and the elastic recoil pull the vocal folds back and close the glottis. The cycle then repeats, which leads to sustained vibration of the vocal folds.

While the myoelastic-aerodynamic theory correctly identifies the interaction between the vocal folds and airflow as the underlying mechanism of self-sustained vocal fold vibration, it does not explain how energy is transferred from airflow into the vocal folds to sustain this vibration. Traditionally, the negative intraglottal pressure is considered to play an important role in closing the glottis and sustaining vocal fold vibration. However, it is now understood that a negative intraglottal pressure is not a critical requirement for achieving self-sustained vocal fold vibration. Similarly, an alternatingly convergent-divergent glottal channel geometry during phonation has been considered a necessary condition that leads to net energy transfer from airflow into the vocal folds. We will show below that an alternatingly convergent-divergent glottal channel geometry does not always guarantee energy transfer or self-sustained vocal fold vibration.

For flow conditions typical of human phonation, the glottal flow can be reasonably described by Bernoulli's equation up to the point when airflow separates from the glottal wall, often at the glottal exit at which the airway suddenly expands. According to Bernoulli's equation, the flow pressure p at a location within the glottal channel with a time-varying cross-sectional area A is

$$p=P_{\mathit{sup}}+\left(P_{\mathit{s}\mathit{u}\mathit{b}}-P_{\mathit{sup}}\right)\left(1-\frac{{A_{\mathit{s}\mathit{e}\mathit{p}}}^2}{A^2}\right),$$ (1)

where P_sub and P_sup are the subglottal and supraglottal pressure, respectively, and A_sep is the time-varying glottal area at the flow separation location. For simplicity, we assume that the flow separates at the upper margin of the medial surface. To achieve a net energy transfer from airflow to the vocal folds over one cycle, the air pressure on the vocal fold surface has to be at least partially in-phase with vocal fold velocity. Specifically, the intraglottal pressure needs to be higher in the opening phase than in the closing phase of vocal fold vibration so that the airflow does more work on the vocal folds in the opening phase than the work the vocal folds do back to the airflow in the closing phase.

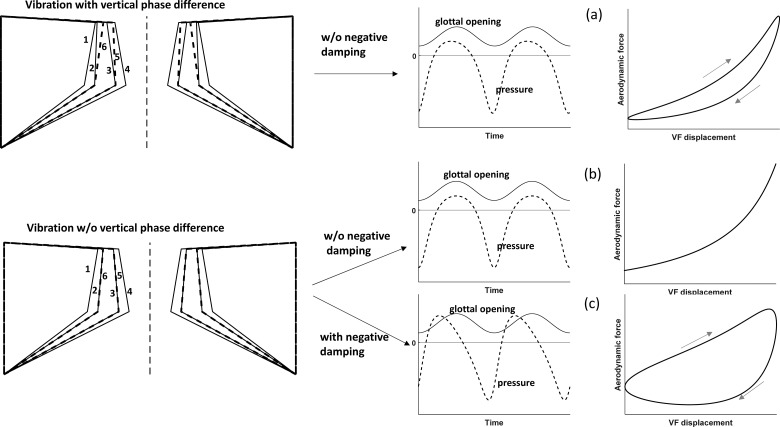
Theoretical analysis of the energy transfer between airflow and vocal folds (Ishizaka and Matsudaira, 1972; Titze, 1988a) showed that this pressure asymmetry can be achieved by a vertical phase difference in vocal fold surface motion (also referred to as a mucosal wave), i.e., different portions of the vocal fold surface do not necessarily move inward and outward together as a whole. This mechanism is illustrated in Fig. 5, the upper left of which shows vocal fold surface shape in the coronal plane for six consecutive, equally spaced instants during one vibration cycle in the presence of a vertical phase difference. Instants 2 and 3 in solid lines are in the closing phase whereas 5 and 6 in dashed lines are in the opening phase. Consider for an example energy transfer at the lower margin of the medial surface. Because of the vertical phase difference, the glottal channel has a different shape in the opening phase (dashed lines 5 and 6) from that in the closing (solid lines 3 and 2) when the lower margin of the medial surface crosses the same locations. Particularly, when the lower margin of the medial surface leads the upper margin in phase, the glottal channel during opening (e.g., instant 6) is always more convergent [thus a smaller A_sep/A in Eq. (1)] or less divergent than that in the closing (e.g., instant 2) for the same location of the lower margin, resulting in an air pressure [Eq. (1)] that is higher in the opening phase than the closing phase (Fig. 5, top row). As a result, energy is transferred from airflow into the vocal folds over one cycle, as indicated by a non-zero area enclosed by the aerodynamic force-vocal fold displacement curve in Fig. 5 (top right). The existence of a vertical phase difference in vocal fold surface motion is generally considered as the primary mechanism of phonation onset.

FIG. 5.

Two energy transfer mechanisms. Top row: the presence of a vertical phase difference leads to different medial surface shapes between glottal opening (dashed lines 5 and 6; upper left panel) and closing (solid lines 2 and 3) when the lower margin of the medial surface crosses the same locations, which leads to higher air pressure during glottal opening than closing and net energy transfer from airflow into vocal folds at the lower margin of the medial surface. Middle row: without a vertical phase difference, vocal fold vibration produces an alternatingly convergent-divergent but identical glottal channel geometry between glottal opening and closing (bottom left panel), thus zero energy transfer (middle row). Bottom row: without a vertical phase difference, air pressure asymmetry can be imposed by a negative damping mechanism.

In contrast, without a vertical phase difference, the vocal fold surface during opening (Fig. 5, bottom left; dashed lines 5 and 6) and closing (solid lines 3 and 2) would be identical when the lower margin crosses the same positions, for which Bernoulli's equation would predict symmetric flow pressure between the opening and closing phases, and zero net energy transfer over one cycle (Fig. 5, middle row). Under this condition, the pressure asymmetry between the opening and closing phases has to be provided by an external mechanism that directly imposes a phase difference between the intraglottal pressure and vocal fold movement. In the presence of such an external mechanism, the intraglottal pressure is no longer the same between opening and closing even when the glottal channel has the same shape as the vocal fold crosses the same locations, resulting in a net energy transfer over one cycle from airflow to the vocal folds (Fig. 5, bottom row). This energy transfer mechanism is often referred to as negative damping, because the intraglottal pressure depends on vocal fold velocity and appears in the system equations of vocal fold motion in a form similar to a damping force, except that energy is transferred to the vocal folds instead of being dissipated. Negative damping is the only energy transfer mechanism in a single degree-of-freedom system or when the entire medial surface moves in phase as a whole.

In humans, a negative damping can be provided by an inertive vocal tract (Flanagan and Landgraf, 1968; Ishizaka and Matsudaira, 1972; Ishizaka and Flanagan, 1972) or a compliant subglottal system (Zhang et al., 2006a). Because the negative damping associated with acoustic loading is significant only for frequencies close to an acoustic resonance, phonation sustained by such negative damping alone always occurs at a frequency close to that acoustic resonance (Flanagan and Landgraf, 1968; Zhang et al., 2006a). Although there is no direct evidence of phonation sustained dominantly by acoustic loading in humans, instabilities in voice production (or voice breaks) have been reported when the fundamental frequency of vocal fold vibration approaches one of the vocal tract resonances (e.g., Titze et al., 2008). On the other hand, this entrainment of phonation frequency to the acoustic resonance limits the degree of independent control of the voice source and the spectral modification by the vocal tract, and is less desirable for effective speech communication. Considering that humans are capable of producing a large variety of voice types independent of vocal tract shapes, negative damping due to acoustic coupling to the sub- or supra-glottal acoustics is unlikely the primary mechanism of energy transfer in voice production. Indeed, excised larynges are able to vibrate without a vocal tract. On the other hand, experiments have shown that in humans the vocal folds vibrate at a frequency close to an in vacuo vocal fold resonance (Kaneko et al., 1986; Ishizaka, 1988; Svec et al., 2000) instead of the acoustic resonances of the sub- and supra-glottal tracts, suggesting that phonation is essentially a resonance phenomenon of the vocal folds.

A negative damping can be also provided by glottal aerodynamics. For example, glottal flow acceleration and deceleration may cause the flow to separate at different locations between opening and closing even when the glottis has identical geometry. This is particularly the case for a divergent glottal channel geometry, which often results in asymmetric flow separation and pressure asymmetry between the glottal opening and closing phases (Park and Mongeau, 2007; Alipour and Scherer, 2004). The effect of this negative damping mechanism is expected to be small at phonation onset at which the vocal fold vibration amplitude and thus flow unsteadiness is small and the glottal channel is less likely to be divergent. However, its contribution to energy transfer may increase with increasing vocal fold vibration amplitude and flow unsteadiness (Howe and McGowan, 2010). It is important to differentiate this asymmetric flow separation between glottal opening and closing due to unsteady flow effects from a quasi-steady asymmetric flow separation that is caused by asymmetry in the glottal channel geometry between opening and closing. In the latter case, because flow separation may occur at a more upstream location for a divergent glottal channel than a convergent glottal channel, an asymmetric glottal channel geometry (e.g., a glottis opening convergent and closing divergent) may lead to asymmetric flow separation between glottal opening and closing. Compared to conditions of a fixed flow separation (i.e., flow separates at the same location during the entire cycle, as in Fig. 5), such geometry-induced asymmetric flow separation actually reduces pressure asymmetry between glottal opening and closing [this can be shown using Eq. (1)] and thus weakens net energy transfer. In reality, these two types of asymmetric flow separation mechanisms (due to unsteady effects or changes in glottal channel geometry) interact and can result in very complex flow separation patterns (Alipour and Scherer, 2004; Sciamarella and Le Quere, 2008; Sidlof et al., 2011), which may or may not enhance energy transfer.

From the discussion above it is clear that a negative Bernoulli pressure is not a critical requirement in either one of the two mechanisms. Being proportional to vocal fold displacement, the negative Bernoulli pressure is not a negative damping and does not directly provide the required pressure asymmetry between glottal opening and closing. On the other hand, the existence of a vertical phase difference in vocal fold vibration is determined primarily by vocal fold properties (as discussed below), rather than whether the intraglottal pressure is positive or negative during a certain phase of the oscillation cycle.

Although a vertical phase difference in vocal fold vibration leads to a time-varying glottal channel geometry, an alternatingly convergent-divergent glottal channel geometry does not guarantee self-sustained vocal fold vibration. For example, although the in-phase vocal fold motion in the bottom left of Fig. 5 (the entire medial surface moves in and out together) leads to an alternatingly convergent-divergent glottal geometry, the glottal geometry is identical between glottal opening and closing and thus this motion is unable to produce net energy transfer into the vocal folds without a negative damping mechanism (Fig. 5, middle row). In other words, an alternatingly convergent-divergent glottal geometry is an effect, not cause, of self-sustained vocal fold vibration. Theoretically, the glottis can maintain a convergent or divergent shape during the entire oscillation cycle and yet still self-oscillate, as observed in experiments using physical vocal fold models which had a divergent shape during most portions of the oscillation cycle (Zhang et al., 2006a).

C. Eigenmode synchronization and nonlinear dynamics

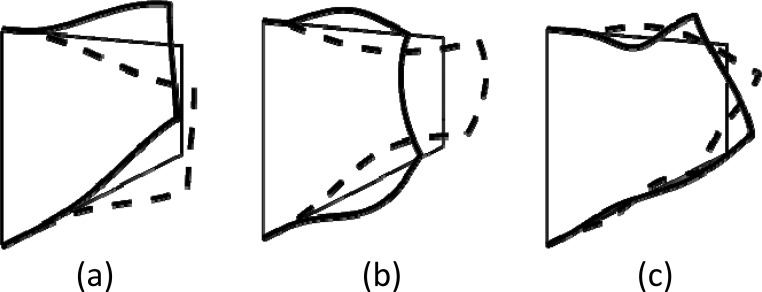
The above shows that net energy transfer from airflow into the vocal folds is possible in the presence of a vertical phase difference. But how is this vertical phase difference established, and what determines the vertical phase difference and the vocal fold vibration pattern? In voice production, vocal fold vibration with a vertical phase difference results from a process of eigenmode synchronization, in which two or more in vacuo eigenmodes of the vocal folds are synchronized to vibrate at the same frequency but with a phase difference (Ishizaka and Matsudaira, 1972; Ishizaka, 1981; Horacek and Svec, 2002; Zhang et al., 2007), in the same way as a travelling wave formed by superposition of two standing waves. An eigenmode or resonance is a pattern of motion of the system that is allowed by physical laws and boundary constraints to the system. In general, for each mode, the vibration pattern is such that all parts of the system move either in-phase or 180° out of phase, similar to a standing wave. Each eigenmode has an inherently distinct eigenfrequency (or resonance frequency) at which the eigenmode can be maximally excited. An example of eigenmodes that is often encountered in speech science is formants, which are peaks in the output voice spectra due to excitation of acoustic resonances of the vocal tract, with the formant frequency dependent on vocal tract geometry. Figure 6 shows three typical eigenmodes of the vocal fold in the coronal plane. In Fig. 6, the thin line indicates the resting vocal fold surface shape, whereas the solid and dashed lines indicate extreme positions of the vocal fold when vibrating at the corresponding eigenmode, spaced 180° apart in a vibratory cycle. The first eigenmode shows an up and down motion in the vertical direction, which does not modulate glottal airflow much. The second eigenmode has a dominantly in-phase medial-lateral motion along the medial surface, which does modulate airflow. The third eigenmode also exhibits dominantly medial-lateral motion, but the upper portion of the medial surface vibrates 180° out of phase with the lower portion of the medial surface. Such out-of-phase motion as in the third eigenmode is essential to achieving vocal fold vibration with a large vertical phase difference, e.g., when synchronized with an in-phase eigenmode as in Fig. 6(b).

FIG. 6.

Typical vocal fold eigenmodes exhibiting (a) a dominantly superior-inferior motion, (b) a medial-lateral in-phase motion, and (c) a medial-lateral out-of-phase motion along the medial surface.

In the absence of airflow, the vocal fold in vacuo eigenmodes are generally neutral or damped, meaning that when excited they will gradually decay in amplitude with time. When the vocal folds are subject to airflow, however, the vocal fold-airflow coupling modifies the eigenmodes and, in some conditions, synchronizes two eigenmodes to the same frequency (Fig. 7). Although vibration in each eigenmode by itself does not produce net energy transfer (Fig. 5, middle row), when two modes are synchronized at the same frequency but with a phase difference in time, the vibration velocity associated with one eigenmode [e.g., the eigenmode in Fig. 6(b)] will be at least partially in-phase with the pressure induced by the other eigenmode [e.g., the eigenmode in Fig. 6(c)], and this cross-model pressure-velocity interaction will produce net energy transfer into the vocal folds (Ishizaka and Matsudaira, 1972; Zhang et al., 2007).

FIG. 7.

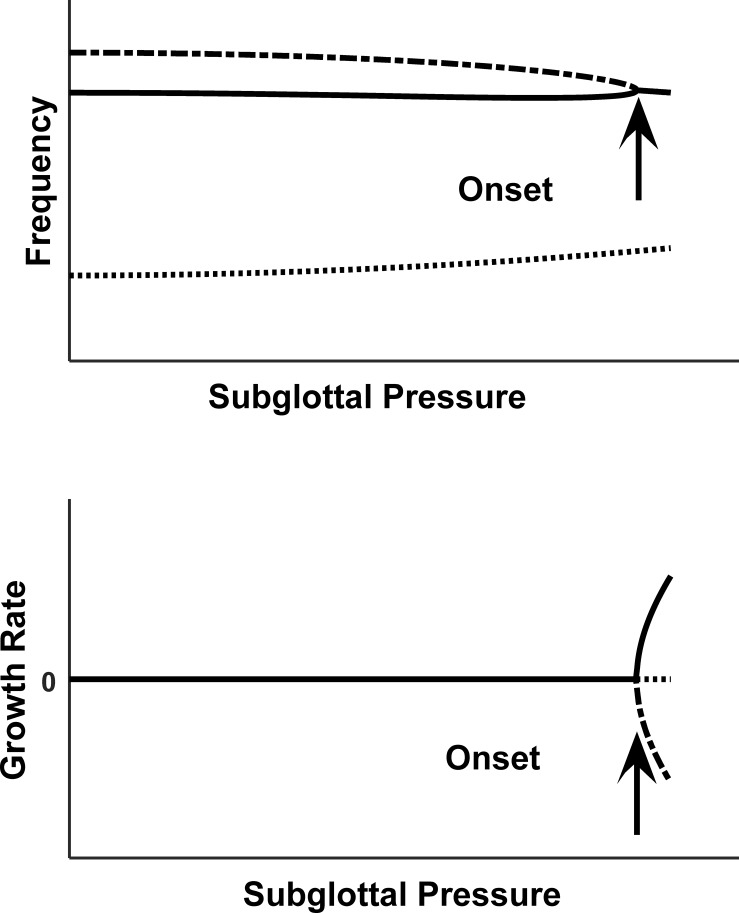
A typical eigenmode synchronization pattern. The evolution of the first three eigenmodes is shown as a function of the subglottal pressure. As the subglottal pressure increases, the frequencies (top) of the second and third vocal fold eigenmodes gradually approach each other and, at a threshold subglottal pressure, synchronize to the same frequency. At the same time, the growth rate (bottom) of the second mode becomes positive, indicating the coupled airflow-vocal fold system becomes linearly unstable and phonation starts.

The minimum subglottal pressure required to synchronize two eigenmodes and initiate net energy transfer, or the phonation threshold pressure, is proportional to the frequency spacing between the two eigenmodes being synchronized and the coupling strength between the two eigenmodes (Zhang, 2010):

$$P_{\mathit{t}\mathit{h}}=\frac{{{\omega }_{0,2}}^2-{{\omega }_{0,1}}^2}{\beta },$$ (2)

where ω_0,1 and ω_0,2 are the eigenfrequencies of the two in vacuo eigenmodes participating in the synchronization process and β is the coupling strength between the two eigenmodes. Thus, the closer the two eigenmodes are to each other in frequency or the more strongly they are coupled, the less pressure is required to synchronize them. This is particularly the case in an anisotropic material such as the vocal folds in which the AP stiffness is much larger than the stiffness in the transverse plane. Under such anisotropic stiffness conditions, the first few in vacuo vocal fold eigenfrequencies tend to cluster together and are much closer to each other compared to isotropic stiffness conditions (Titze and Strong, 1975; Berry, 2001). Such clustering of eigenmodes makes it possible to initiate vocal fold vibration at very low subglottal pressures.

The coupling strength β between the two eigenmodes in Eq. (2) depends on the prephonatory glottal opening, with the coupling strength increasing with decreasing glottal opening (thus lowered phonation threshold pressure). In addition, the coupling strength also depends on the spatial similarity between the air pressure distribution over the vocal fold surface induced by one eigenmode and vocal fold surface velocity of the other eigenmode (Zhang, 2010). In other words, the coupling strength β quantifies the cross-mode energy transfer efficiency between the eigenmodes that are being synchronized. The higher the degree of cross-mode pressure-velocity similarity, the better the two eigenmodes are coupled, and the less subglottal pressure is required to synchronize them.

In reality, the vocal folds have an infinite number of eigenmodes. Which eigenmodes are synchronized and eventually excited depends on the frequency spacing and relative coupling strength among different eigenmodes. Because vocal fold vibration depends on the eigenmodes that are eventually excited, changes in the eigenmode synchronization pattern often lead to changes in the F0, vocal fold vibration pattern, and the resulting voice quality. Previous studies have shown that a slight change in vocal fold properties such as stiffness or medial surface shape may cause phonation to occur at a different eigenmode, leading to a qualitatively different vocal fold vibration pattern and abrupt changes in F0 (Tokuda et al., 2007; Zhang, 2009). Eigenmode synchronization is not limited to two vocal fold eigenmodes, either. It may also occur between a vocal fold eigenmode and an eigenmode of the subglottal or supraglottal system. In this sense, the negative damping due to subglottal or supraglottal acoustic loading can be viewed as the result of synchronization between one of the vocal fold modes and one of the acoustic resonances.

Eigenmode synchronization discussed above corresponds to a 1:1 temporal synchronization of two eigenmodes. For a certain range of vocal fold conditions, e.g., when asymmetry (left-right or anterior-posterior) exists in the vocal system or when the vocal folds are strongly coupled with the sub- or supra-glottal acoustics, synchronization may occur so that the two eigenmodes are synchronized not toward the same frequency, but at a frequency ratio of 1:2, 1:3, etc., leading to subharmonics or biphonation (Ishizaka and Isshiki, 1976; Herzel, 1993; Herzel et al., 1994; Neubauer et al., 2001; Berry et al., 1994; Berry et al., 2006; Titze, 2008; Lucero et al., 2015). Temporal desynchronization of eigenmodes often leads to irregular or chaotic vocal fold vibration (Herzel et al., 1991; Berry et al., 1994; Berry et al., 2006; Steinecke and Herzel, 1995). Transition between different synchronization patterns, or bifurcation, often leads to a sudden change in the vocal fold vibration pattern and voice quality.

These studies show that the nonlinear interaction between vocal fold eigenmodes is a central feature of the phonation process, with different synchronization or desynchronization patterns producing a large variety of voice types. Thus, by changing the geometrical and biomechanical properties of the vocal folds, either through laryngeal muscle activation or mechanical modification as in phonosurgery, we can select eigenmodes and eigenmode synchronization pattern to control or modify our voice, in the same way as we control speech formants by moving articulators in the vocal tract to modify vocal tract acoustic resonances.

The concept of eigenmode and eigenmode synchronization is also useful for phonation modeling, because eigenmodes can be used as building blocks to construct more complex motion of the system. Often, only the first few eigenmodes are required for adequate reconstruction of complex vocal fold vibrations (both regular and irregular; Herzel et al., 1994; Berry et al., 1994; Berry et al., 2006), which would significantly reduce the degrees of freedom required in computational models of phonation.

D. Biomechanical requirements of glottal closure during phonation

An important feature of normal phonation is the complete closure of the membranous glottis during vibration, which is essential to the production of high-frequency harmonics. Incomplete closure of the membranous glottis, as often observed in pathological conditions, often leads to voice production of a weak and/or breathy quality.

It is generally assumed that approximation of the vocal folds through arytenoid adduction is sufficient to achieve glottal closure during phonation, with the duration of glottal closure or the closed quotient increasing with increasing degree of vocal fold approximation. While a certain degree of vocal fold approximation is obviously required for glottal closure, there is evidence suggesting that other factors also are in play. For example, excised larynx experiments have shown that some larynges would vibrate with incomplete glottal closure despite that the arytenoids are tightly sutured together (Isshiki, 1989; Zhang, 2011). Similar incomplete glottal closure is also observed in experiments using physical vocal fold models with isotropic material properties (Thomson et al., 2005; Zhang et al., 2006a). In these experiments, increasing the subglottal pressure increased the vocal fold vibration amplitude but often did not lead to improvement in the glottal closure pattern (Xuan and Zhang, 2014). These studies show that addition stiffness or geometry conditions are required to achieve complete membranous glottal closure.

Recent studies have started to provide some insight toward these additional biomechanical conditions. Xuan and Zhang (2014) showed that embedding fibers along the anterior-posterior direction in otherwise isotropic models is able to improve glottal closure (Xuan and Zhang, 2014). With an additional thin stiffer outmost layer simulating the epithelium, these physical models are able to vibrate with a considerably long closed period. It is interesting that this improvement in the glottal closure pattern occurred only when the fibers were embedded to a location close to the vocal fold surface in the cover layer. Embedding fibers in the body layer did not improve the closure pattern at all. This suggests a possible functional role of collagen and elastin fibers in the intermediate and deep layers of the lamina propria in facilitating glottal closure during vibration.

The difference in the glottal closure pattern between isotropic and anisotropic vocal folds could be due to many reasons. Compared to isotropic vocal folds, anisotropic vocal folds (or fiber-embedded models) are better able to maintain their adductory position against the subglottal pressure and are less likely to be pushed apart by air pressure (Zhang, 2011). In addition, embedding fibers along the AP direction may also enhance the medial-lateral motion, further facilitating glottal closure. Zhang (2014) showed that the first few in vacuo eigenmodes of isotropic vocal folds exhibit similar in-phase, up-and-down swing-like motion, with the medial-lateral and superior-inferior motions locked in a similar phase relationship. Synchronization of modes of similar vibration patterns necessarily leads to qualitatively the same vibration patterns, in this case an up-and-down swing-like motion, with vocal fold vibration dominantly along the superior-inferior direction, as observed in recent physical model experiments (Thomson et al., 2005; Zhang et al., 2006a). In contrast, for vocal folds with the AP stiffness much higher than the transverse stiffness, the first few in vacuo modes exhibit qualitatively distinct vibration patterns, and the medial-lateral motion and the superior-inferior motion are no longer locked in a similar phase in the first few in vacuo eigenmodes. This makes it possible to strongly excite large medial-lateral motion without proportional excitation of the superior-inferior motion. As a result, anisotropic models exhibit large medial-lateral motion with a vertical phase difference along the medial surface. The improved capability to maintain adductory position against the subglottal pressure and to vibrate with large medial-lateral motion may contribute to the improved glottal closure pattern observed in the experiment of Xuan and Zhang (2014).

Geometrically, a thin vocal fold has been shown to be easily pushed apart by the subglottal pressure (Zhang, 2016a). Although a thin anisotropic vocal fold vibrates with a dominantly medial-lateral motion, this is insufficient to overcome its inability to maintain position against the subglottal pressure. As a result, the glottis never completely closes during vibration, which leads to a relatively smooth glottal flow waveform and weak excitation of higher-order harmonics in the radiated output voice spectrum (van den Berg, 1968; Zhang, 2016a). Increasing vertical thickness of the medial surface allows the vocal fold to better resist the glottis-opening effect of the subglottal pressure, thus maintaining the adductory position and achieving complete glottal closure.

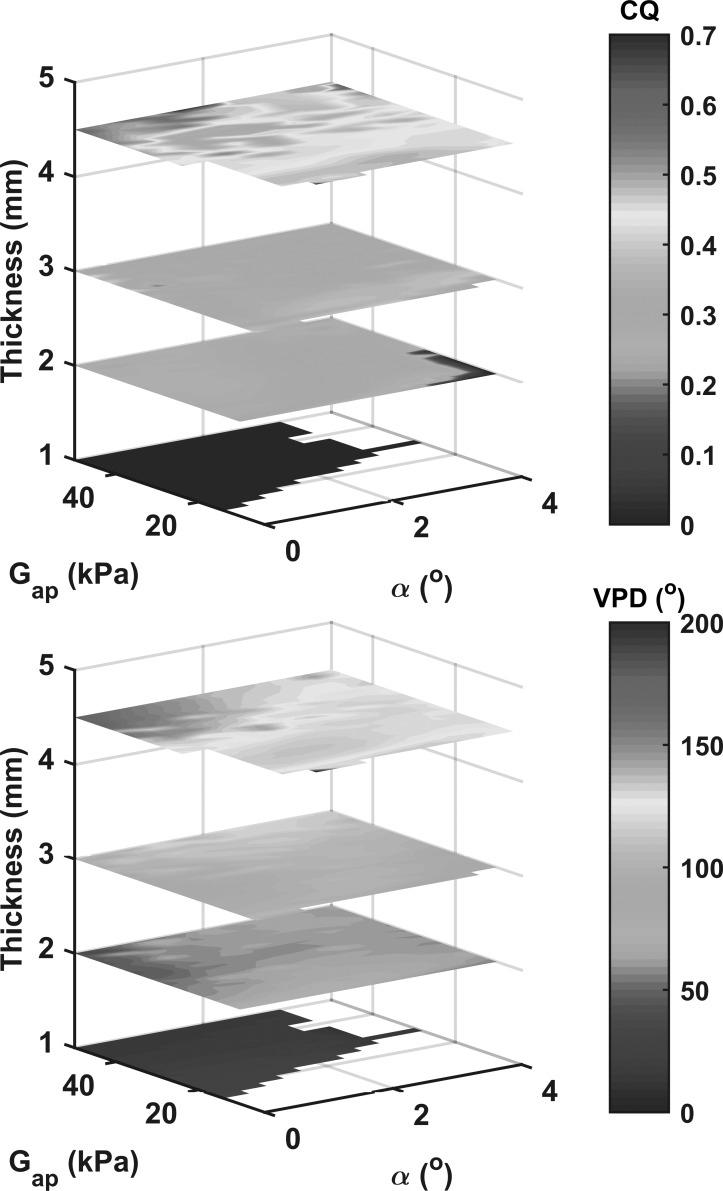
Once these additional stiffness and geometric conditions (i.e., certain degree of stiffness anisotropy and not-too-small vertical vocal fold thickness) are met, the duration of glottal closure can be regulated by varying the vertical phase difference in vocal fold motion along the medial surface. A non-zero vertical phase difference means that, when the lower margins of the medial surfaces start to open, the glottis would continue to remain closed until the upper margins start to open. One important parameter affecting the vertical phase difference is the vertical thickness of the medial surface or the degree of medial bulging in the inferior portion of the medial surface. Given the same condition of vocal fold stiffness and vocal fold approximation, the vertical phase difference during vocal fold vibration increases with increasing vertical medial surface thickness (Fig. 8). Thus, the thicker the medial surface, the larger the vertical phase difference, and the longer the closed phase (Fig. 8; van den Berg, 1968; Alipour and Scherer, 2000; Zhang, 2016a). Similarly, the vertical phase difference and thus the duration of glottal closure can be also increased by reducing the elastic surface wave speed in the superior-inferior direction (Ishizaka and Flanagan, 1972; Story and Titze, 1995), which depends primarily on the stiffness in the transverse plane and to a lesser degree on the AP stiffness, or increasing the body-cover stiffness ratio (Story and Titze, 1995; Zhang, 2009).

FIG. 8.

(Color online) The closed quotient CQ and vertical phase difference VPD as a function of the medial surface thickness, the AP stiffness (G_ap), and the resting glottal angle (α). Reprinted with permission of ASA from Zhang (2016a).

Theoretically, the duration of glottal closure can be controlled by changing the ratio between the vocal fold equilibrium position (or the mean glottal opening) and the vocal fold vibration amplitude. Both stiffening the vocal folds and tightening vocal fold approximation are able to move the vocal fold equilibrium position toward glottal midline. However, such manipulations often simultaneously reduce the vibration amplitude. As a result, the overall effect on the duration of glottal closure is unclear. Zhang (2016a) showed that stiffening the vocal folds or increasing vocal fold approximation did not have much effect on the duration of glottal closure except around onset when these manipulations led to significant improvement in vocal fold contact.

E. Role of flow instabilities

Although a Bernoulli-based flow description is often used for phonation models, the realistic glottal flow is highly three-dimensional and much more complex. The intraglottal pressure distribution is shown to be affected by the three-dimensionality of the glottal channel geometry (Scherer et al., 2001; Scherer et al., 2010; Mihaescu et al., 2010; Li et al., 2012). As the airflow separates from the glottal wall as it exits the glottis, a jet forms downstream of the flow separation point, which leads to the development of shear layer instabilities, vortex roll-up, and eventually vortex shedding from the jet and transition into turbulence. The vortical structures would in turn induce disturbances upstream, which may lead to oscillating flow separation point, jet attachment to one side of the glottal wall instead of going straight, and possibly alternating jet flapping (Pelorson et al., 1994; Shinwari et al., 2003; Triep et al., 2005; Kucinschi et al., 2006; Erath and Plesniak, 2006; Neubauer et al., 2007; Zheng et al., 2009). Recent experiments and simulations also showed that for a highly divergent glottis, airflow may separate inside the glottis, which leads to the formation and convection of intraglottal vortices (Mihaescu et al., 2010; Khosla et al., 2014; Oren et al., 2014).

Some of these flow features have been incorporated in phonation models (e.g., Liljencrants, 1991; Pelorson et al., 1994; Kaburagi and Tanabe, 2009; Erath et al., 2011; Howe and McGowan, 2013). Resolving other features, particularly the jet instability, vortices, and turbulence downstream of the glottis, demands significantly increased computational costs so that simulation of a few cycles of vocal fold vibration often takes days or months. On the other hand, the acoustic and perceptual relevance of these intraglottal and supraglottal flow structures has not been established. From the sound production point of view, these complex flow structures in the downstream glottal flow field are sound sources of quadrupole type (dipole type when obstacles are present in the pathway of airflow, e.g., tightly adducted false vocal folds). Due to the small length scales associated with the flow structures, these sound sources are broadband in nature and mostly at high frequencies (generally above 2 kHz), with an amplitude much smaller than the harmonic component of the voice source. Therefore, if the high-frequency component of voice is of interest, these flow features have to be accurately modeled, although the degree of accuracy required to achieve perceptual sufficiency has yet to be determined.

It has been postulated that the vortical structures may directly affect the near-field glottal fluid-structure interaction and thus vocal fold vibration and the harmonic component of the voice source. Once separated from the vocal fold walls, the glottal jet starts to develop jet instabilities and is therefore susceptible to downstream disturbances, especially when the glottis takes on a divergent shape. In this way, the unsteady supraglottal flow structures may interact with the boundary layer at the glottal exit and affect the flow separation point within the glottal channel (Hirschberg et al., 1996). Similarly, it has been hypothesized that intraglottal vortices can induce a local negative pressure on the medial surface of the vocal folds as the intraglottal vortices are convected downstream and thus may facilitate rapid glottal closure during voice production (Khosla et al., 2014; Oren et al., 2014).

While there is no doubt that these complex flow features affect vocal fold vibration, the question remains concerning how large an influence these vortical structures have on vocal fold vibration and the produced acoustics. For the flow conditions typical of voice production, many of the flow features or instabilities have time scales much different from that of vocal fold vibration. For example, vortex shedding at typical voice conditions occurs generally at frequencies above 1000 Hz (Zhang et al., 2004; Kucinschi et al., 2006). Considering that phonation is essentially a resonance phenomenon of the vocal folds (Sec. III B) and the mismatch between vocal fold resonance and typical frequency scales of the vortical structures, it is questionable that compared to vocal fold inertia and elastic recoil, the pressure perturbations on vocal fold surface due to intraglottal or supraglottal vortical structures are strong enough or last for a long enough period to have a significant effect on voice production. Given a longitudinal shear modulus of the vocal fold of about 10 kPa and a shear strain of 0.2, the elastic recoil stress of the vocal fold is approximately 2000 Pa. The pressure perturbations induced by intraglottal or supraglottal vortices are expected to be much smaller than the subglottal pressure. Assuming an upper limit of about 20% of the subglottal pressure for the pressure perturbations (as induced by intraglottal vortices, Oren et al., 2014; in reality this number is expected to be much smaller at normal loudness conditions and even smaller for supraglottal vortices) and a subglottal pressure of 800 Pa (typical of normal speech production), the pressure perturbation on vocal fold surface is about 160 Pa, which is much smaller than the elastic recoil stress. Specifically to the intraglottal vortices, while a highly divergent glottal geometry is required to create intraglottal vortices, the presence of intraglottal vortices induces a negative suction force applied mainly on the superior portion of the medial surface and, if the vortices are strong enough, would reduce the divergence of the glottal channel. In other words, while intraglottal vortices are unable to create the necessary divergence conditions required for their creation, their existence tends to eliminate such conditions.

There have been some recent studies toward quantifying the degree of the influence of the vortical structures on phonation. In an excised larynx experiment without a vocal tract, it has been observed that the produced sound does not change much when sticking a finger very close to the glottal exit, which presumably would have significantly disturbed the supraglottal flow field. A more rigorous experiment was designed in Zhang and Neubauer (2010) in which they placed an anterior-posteriorly aligned cylinder in the supraglottal flow field and traversed it in the flow direction at different left-right locations and observed the acoustics consequences. The hypothesis was that, if these supraglottal flow structures had a significant effect on vocal fold vibration and acoustics, disturbing these flow structures would lead to noticeable changes in the produced sound. However, their experiment found no significant changes in the sound except when the cylinder was positioned within the glottal channel.

The potential impact of intraglottal vortices on phonation has also been numerically investigated (Farahani and Zhang, 2014; Kettlewell, 2015). Because of the difficulty in removing intraglottal vortices without affecting other aspects of the glottal flow, the effect of the intraglottal vortices was modeled as a negative pressure superimposed on the flow pressure predicted by a base glottal flow model. In this way, the effect of the intraglottal vortices can be selectively activated or deactivated independently of the base flow so that its contribution to phonation can be investigated. These studies showed that intraglottal vortices only have small effects on vocal fold vibration and the glottal flow. Kettlewell (2015) further showed that the vortices are either not strong enough to induce significant pressure perturbation on vocal fold surfaces or, if they are strong enough, the vortices advect rapidly into the supraglottal region and the induced pressure perturbations would be too brief to have any impact to overcome the inertia of the vocal fold tissue.

Although phonation models using simplified flow models neglecting flow vortical structures are widely used and appear to qualitatively compare well with experiments (Pelorson et al., 1994; Zhang et al., 2002a; Ruty et al., 2007; Kaburagi and Tanabe, 2009), more systematic investigations are required to reach a definite conclusion regarding the relative importance of these flow structures to phonation and voice perception. This may be achieved by conducting parametric studies in a large range of conditions over which the relative strength of these vortical structures are known to vary significantly and observing their consequences on voice production. Such an improved understanding would facilitate the development of computationally efficient reduced-order models of phonation.

IV. BIOMECHANICS OF VOICE CONTROL

A. Fundamental frequency

In the discussion of F0 control, an analogy is often made between phonation and vibration in strings in the voice literature (e.g., Colton et al., 2011). The vibration frequency of a string is determined by its length, tension, and mass. By analogy, the F0 of voice production is also determined by its length, tension, and mass, with the mass interpreted as the mass of the vocal folds that is set into vibration. Specifically, F0 increases with increasing tension, decreasing mass, and decreasing vocal fold length. While the string analogy is conceptually simple and heuristically useful, some important features of the vocal folds are missing. Other than the vague definition of an effective mass, the string model, which implicitly assumes cross-section dimension much smaller than length, completely neglects the contribution of vocal fold stiffness in F0 control. Although stiffness and tension are often not differentiated in the voice literature, they have different physical meanings and represent two different mechanisms that resist deformation (Fig. 2). Stiffness is a property of the vocal fold and represents the elastic restoring force in response to deformation, whereas tension or stress describes the mechanical state of the vocal folds. The string analogy also neglects the effect of vocal fold contact, which introduces additional stiffening effect.

Because phonation is essentially a resonance phenomenon of the vocal folds, the F0 is primarily determined by the frequency of the vocal fold eigenmodes that are excited. In general, vocal fold eigenfrequencies depend on both vocal fold geometry, including length, depth, and thickness, and the stiffness and stress conditions of the vocal folds. Shorter vocal folds tend to have high eigenfrequencies. Thus, because of the small vocal fold size, children tend to have the highest F0, followed by female and then male. Vocal fold eigenfrequencies also increase with increasing stiffness or stress (tension), both of which provide a restoring force to resist vocal fold deformation. Thus, stiffening or tensioning the vocal folds would increase the F0 of the voice. In general, the effect of stiffness on vocal fold eigenfrequencies is more dominant than tension when the vocal fold is slightly elongated or shortened, at which the tension is small or even negative and the string model would underestimate F0 or fail to provide a prediction. As the vocal fold gets further elongated and tension increases, the stiffness and tension become equally important in affecting vocal fold eigenfrequencies (Titze and Hunter, 2004; Yin and Zhang, 2013).

When vocal fold contact occurs during vibration, the vocal fold collision force appears as an additional restoring force (Ishizaka and Flanagan, 1972). Depending on the extent, depth of influence, and duration of vocal fold collision, this additional force can significantly increase the effective stiffness of the vocal folds and thus F0. Because the vocal fold contact pattern depends on the degree of vocal fold approximation, subglottal pressure, and vocal fold stiffness and geometry, changes in any of these parameters may have an effect on F0 by affecting vocal fold contact (van den Berg and Tran, 1959; Zhang, 2016a).

In humans, F0 can be increased by increasing either vocal fold eigenfrequencies or the extent and duration of vocal fold contact. Control of vocal fold eigenfrequencies is largely achieved by varying the stiffness and tension along the AP direction. Due to the nonlinear material properties of the vocal folds, both the AP stiffness and tension can be controlled by elongating or shortening the vocal folds, through activation of the CT muscle. Although elongation also increases vocal fold length which lowers F0, the effect of the increase in stiffness and tension on F0 appears to dominate that of increasing length.

The effect of TA muscle activation on F0 control is a little more complex. In addition to shortening vocal fold length, TA activation tensions and stiffens the body layer, decreases tension in the cover layer, but may decrease or increase the cover stiffness (Yin and Zhang, 2013). Titze et al. (1988) showed that depending on the depth of the body layer involved in vibration, increasing TA activation can either increase or decrease vocal fold eigenfrequencies. On the other hand, Yin and Zhang (2013) showed that for an elongated vocal fold, as is often the case in phonation, the overall effect of TA activation is to reduce vocal fold eigenfrequencies. Only for conditions of a slightly elongated or shortened vocal folds, TA activation may increase vocal fold eigenfrequencies. In addition to the effect on vocal fold eigenfrequencies, TA activation increases vertical thickness of the vocal folds and produces medial compression between the two folds, both of which increase the extent and duration of vocal tract contact and would lead to an increased F0 (Hirano et al., 1969). Because of these opposite effects on vocal fold eigenfrequencies and vocal fold contact, the overall effect of TA activation on F0 would vary depending on the specific vocal fold conditions.

Increasing subglottal pressure or activation of the LCA/IA muscles by themselves do not have much effect on vocal fold eigenfrequencies (Hirano and Kakita, 1985; Chhetri et al., 2009; Yin and Zhang, 2014). However, they often increase the extent and duration of vocal fold contact during vibration, particularly with increasing subglottal pressure, and thus lead to increased F0 (Hirano et al., 1969; Ishizaka and Flanagan, 1972; Zhang, 2016a). Due to nonlinearity in vocal fold material properties, increased vibration amplitude at high subglottal pressures may lead to increased effective stiffness and tension, which may also increase F0 (van den Berg and Tan, 1959; Ishizaka and Flanagan, 1972; Titze, 1989). Ishizaka and Flanagan (1972) showed in their two-mass model that vocal fold contact and material nonlinearity combined can lead to an increase of about 40 Hz in F0 when the subglottal pressure is increased from about 200 to 800 Pa. In the continuum model of Zhang (2016a), which includes the effect of vocal fold contact but not vocal fold material nonlinearity, increasing subglottal pressure alone can increase the F0 by as large as 20 Hz/kPa.

B. Vocal intensity

Because voice is produced at the glottis, filtered by the vocal tract, and radiated from the mouth, an increase in vocal intensity can be achieved by either increasing the source intensity or enhancing the radiation efficiency. The source intensity is controlled primarily by the subglottal pressure, which increases the vibration amplitude and the negative peak or MFDR of the time derivative of the glottal flow. The subglottal pressure depends primarily on the alveolar pressure in the lungs, which is controlled by the respiratory muscles and the lung volume. In general, conditions of the laryngeal system have little effect on the establishment of the alveolar pressure and subglottal pressure (Hixon, 1987; Finnegan et al., 2000). However, an open glottis often results in a small glottal resistance and thus a considerable pressure drop in the lower airway and a reduced subglottal pressure. An open glottis also leads to a large glottal flow rate and a rapid decline in the lung volume, thus reducing the duration of speech between breaths and increasing the respiratory effort required in order to maintain a target subglottal pressure (Zhang, 2016b).

In the absence of a vocal tract, laryngeal adjustments, which control vocal fold stiffness, geometry, and position, do not have much effect on the source intensity, as shown in many studies using laryngeal, physical, or computational models of phonation (Tanaka and Tanabe, 1986; Titze, 1988b; Zhang, 2016a). In the experiment by Tanaka and Tanabe (1986), for a constant subglottal pressure, stimulation of the CT and LCA muscles had almost no effects on vocal intensity whereas stimulation of the TA muscle slightly decreased vocal intensity. In an excised larynx experiment, Titze (1988b) found no dependence of vocal intensity on the glottal width. Similar secondary effects of laryngeal adjustments have also been observed in a recent computational study (Zhang, 2016a). Zhang (2016a) also showed that the effect of laryngeal adjustments may be important at subglottal pressures slightly above onset, in which case an increase in either AP stiffness or vocal fold approximation may lead to improved vocal fold contact and glottal closure, which significantly increased the MFDR and thus vocal intensity. However, these effects became less efficient with increasing vocal intensity.

The effect of laryngeal adjustments on vocal intensity becomes a little more complicated in the presence of the vocal tract. Changing vocal tract shape by itself does not amplify the produced sound intensity because sound propagation in the vocal tract is a passive process. However, changes in vocal tract shape may provide a better impedance match between the glottis and the free space outside the mouth and thus improve efficiency of sound radiation from the mouth (Titze and Sundberg, 1992). This is particularly the case for harmonics close to a formant, which are often amplified more than the first harmonic and may become the most energetic harmonic in the spectrum of the output voice. Thus, vocal intensity can be increased through laryngeal adjustments that increase excitation of harmonics close to the first formant of the vocal tract (Fant, 1982; Sundberg, 1987) or by adjusting vocal tract shape to match one of the formants with one of the dominant harmonics in the source spectrum.

In humans, all three strategies (respiratory, laryngeal, and articulatory) are used to increase vocal intensity. When asked to produce an intensity sweep from soft to loud voice, one generally starts with a slightly breathy voice with a relatively open glottis, which requires the least laryngeal effort but is inefficient in voice production. From this starting position, vocal intensity can be increased by increasing either the subglottal pressure, which increases vibration amplitude, or vocal fold adduction (approximation and/or thickening). For a soft voice with minimal vocal fold contact and minimal higher-order harmonic excitation, increasing vocal fold adduction is particularly efficient because it may significantly improve vocal fold contact, in both spatial extent and duration, thus significantly boosting the excitation of harmonics close to the first formant. In humans, for low to medium vocal intensity conditions, vocal intensity increase is often accompanied by simultaneous increases in the subglottal pressure and the glottal resistance (Isshiki, 1964; Holmberg et al., 1988; Stathopoulos and Sapienza, 1993). Because the pitch level did not change much in these experiments, the increase in glottal resistance was most likely due to tighter vocal fold approximation through LCA/IA activation. The duration of the closed phase is often observed to increase with increasing vocal intensity (Henrich et al., 2005), indicating increased vocal fold thickening or medial compression, which are primarily controlled by the TA muscle. Thus, it seems that both the LCA/IA/TA muscles and subglottal pressure increase play a role in vocal intensity increase at low to medium intensity conditions. For high vocal intensity conditions, when further increase in vocal fold adduction becomes less effective (Hirano et al., 1969), vocal intensity increase appears to rely dominantly on the subglottal pressure increase.

On the vocal tract side, Titze (2002) showed that the vocal intensity can be increased by matching a wide epilarynx with lower glottal resistance or a narrow epilarynx with higher glottal resistance. Tuning the first formant (e.g., by opening mouth wider) to match the F0 is often used in soprano singing to maximize vocal output (Joliveau et al., 2004). Because radiation efficiency can be improved through adjustments in either the vocal folds or the vocal tract, this makes it possible to improve radiation efficiency yet still maintain desired pitch or articulation, whichever one wishes to achieve.

C. Voice quality

Voice quality generally refers to aspects of the voice other than pitch and loudness. Due to the subjective nature of voice quality perception, many different descriptions are used and authors often disagree with the meanings of these descriptions (Gerratt and Kreiman, 2001; Kreiman and Sidtis, 2011). This lack of a clear and consistent definition of voice quality makes it difficult for studies of voice quality and identifying its physiological correlates and controls. Acoustically, voice quality is associated with the spectral amplitude and shape of the harmonic and noise components of the voice source, and their temporal variations. In the following we focus on physiological factors that are known to have an impact on the voice spectra and thus are potentially perceptually important.

One of the first systematic investigations of the physiological controls of voice quality was conducted by Isshiki (1989, 1998) using excised larynges, in which regions of normal, breathy, and rough voice qualities were mapped out in the three-dimensional parameter space of the subglottal pressure, vocal fold stiffness, and prephonatory glottal opening area (Fig. 9). He showed that for a given vocal fold stiffness and prephonatory glottal opening area, increasing subglottal pressure led to voice production of a rough quality. This effect of the subglottal pressure can be counterbalanced by increasing vocal fold stiffness, which increased the region of normal voice in the parameter space of Fig. 9. Unfortunately, the details of this study, including the definition and manipulation of vocal fold stiffness and perceptual evaluation of different voice qualities, are not fully available. The importance of the coordination between the subglottal pressure and laryngeal conditions was also demonstrated in van den Berg and Tan (1959), which showed that although different vocal registers were observed, each register occurred in a certain range of laryngeal conditions and subglottal pressures. For example, for conditions of low longitudinal tension, a chest-like phonation was possible only for small airflow rates. At large values of the subglottal pressure, “it was impossible to obtain good sound production. The vocal folds were blown too wide apart…. The shape of the glottis became irregularly curved and this curving was propagated along the glottis.” Good voice production at large flow rates was possible only with thyroid cartilage compression which imitates the effect of TA muscle activation. Irregular vocal fold vibration at high subglottal pressures has also been observed in physical model experiments (e.g., Xuan and Zhang, 2014). Irregular or chaotic vocal fold vibration at conditions of pressure-stiffness mismatch has also been reported in the numerical simulation of Berry et al. (1994), which showed that while regular vocal fold vibration was observed for typical vocal fold stiffness conditions, irregular vocal fold vibration (e.g., subharmonic or chaotic vibration) was observed when the cover layer stiffness was significantly reduced while maintaining the same subglottal pressure.

FIG. 9.

A three-dimensional map of normal (N), breathy (B), and rough (R) phonation in the parameter space of the prephonatory glottal area (Ag0), subglottal pressure (Ps), vocal fold stiffness (k). Reprinted with permission of Springer from Isshiki (1989).

The experiments of van den Berg and Tan (1959) and Isshiki (1989) also showed that weakly adducted vocal folds (weak LCA/IA/TA activation) often lead to vocal fold vibration with incomplete glottal closure during phonation. When the airflow is sufficiently high, the persistent glottal gap would lead to increased turbulent noise production and thus phonation of a breathy quality (Fig. 9). The incomplete glottal closure may occur in the membranous or the cartilaginous portion of the glottis. When the incomplete glottal closure is limited to the cartilaginous glottis, the resulting voice is breathy but may still have strong harmonics at high frequencies. When the incomplete glottal closure occurs in the membranous glottis, the reduced or slowed vocal fold contact would also reduce excitation of higher-order harmonics, resulting in a breathy and weak quality of the produced voice. When the vocal folds are sufficiently separated, the coupling between the two vocal folds may be weakened enough so that each vocal fold can vibrate at a different F0. This would lead to biphonation or voice containing two distinct fundamental frequencies, resulting in a perception similar to that of the beat frequency phenomenon.

Compared to a breathy voice, a pressed voice is presumably produced with tight vocal fold approximation or even some degree of medial compression in the membranous portion between the two folds. A pressed voice is often characterized by a second harmonic that is stronger than the first harmonic, or a negative H1-H2, with a long period of glottal closure during vibration. Although a certain degree of vocal fold approximation and stiffness anisotropy is required to achieve vocal fold contact during phonation, the duration of glottal closure has been shown to be primarily determined by the vertical thickness of the vocal fold medial surface (van den Berg, 1968; Zhang, 2016a). Thus, although it is generally assumed that a pressed voice can be produced with tight arytenoid adduction through LCA/IA muscle activation, activation of the LCA/IA muscles alone is unable to achieve prephonatory medial compression in the membranous glottis or change the vertical thickness of the medial surface. Activation of the TA muscle appears to be essential in producing a voice change from a breathy to a pressed voice quality. A weakened TA muscle, as in aging or muscle atrophy, would lead to difficulties in producing a pressed voice or even sufficient glottal closure during phonation. On the other hand, strong TA muscle activation, as in for example, spasmodic dysphonia, may lead to too tight a closure of the glottis and a rough voice quality (Isshiki, 1989).

In humans, vocal fold stiffness, vocal fold approximation, and geometry are regulated by the same set of laryngeal muscles and thus often co-vary, which has long been considered as one possible origin of vocal registers and their transitions (van den Berg, 1968). Specifically, it has been hypothesized that changes in F0 are often accompanied by changes in the vertical thickness of the vocal fold medial surface, which lead to changes in the spectral characteristics of the produced voice. The medial surface thickness is primarily controlled by the CT and TA muscles, which also regulate vocal fold stiffness and vocal fold approximation. Activation of the CT muscle reduces the medial surface thickness, but also increases vocal fold stiffness and tension, and in some conditions increases the resting glottal opening (van den Berg and Tan, 1959; van den Berg, 1968; Hirano and Kakita, 1985). Because the LCA/IA/TA muscles are innervated by the same nerve and often activated together, an increase in the medial surface thickness through TA muscle activation is often accompanied by increased vocal fold approximation (Hirano and Kakita, 1985) and contact. Thus, if one attempts to increase F0 primarily by activation of the LCA/IA/TA muscles, the vocal folds are likely to have a large medial surface thickness and probably low AP stiffness, which will lead to a chest-like voice production, with large vertical phase difference along the medial surface, long closure of the glottis, small flow rate, and strong harmonic excitation. In the extreme case of strong TA activation and minimum CT activation and very low subglottal pressure, the glottis can remain closed for most of the cycle, leading to a vocal fry-like voice production. In contrast, if one attempts to increase F0 by increasing CT activation alone, the vocal folds, with a small medial surface thickness, are likely to produce a falsetto-like voice production, with incomplete glottal closure and a nearly sinusoidal flow waveform, very high F0, and a limited number of harmonics.

V. MECHANICAL AND COMPUTER MODELS FOR VOICE APPLICATIONS

Voice applications generally fall into two major categories. In the clinic, simulation of voice production has the potential to predict outcomes of clinical management of voice disorders, including surgery and voice therapy. For such applications, accurate representation of vocal fold geometry and material properties to the degree that matches actual clinical treatment is desired, and for this reason continuum models of the vocal folds are preferred over lumped-element models. Computational cost is not necessarily a concern in such applications but still has to be practical. In contrast, for some other applications, particularly in speech technology applications, the primary goal is to reproduce speech acoustics or at least perceptually relevant features of speech acoustics. Real-time capability is desired in these applications, whereas realistic representation of the underlying physics involved is often not necessary. In fact, most of the current speech synthesis systems consider speech purely as an acoustic signal and do not model the physics of speech production at all. However, models that take into consideration the underlying physics, at least to some degree, may hold the most promise in speech synthesis of natural-sounding, speaker-specific quality.

A. Mechanical vocal fold models

Early efforts on artificial speech production, dating back to as early as the 18th century, focused on mechanically reproducing the speech production system. A detailed review can be found in Flanagan (1972). The focus of these early efforts was generally on articulation in the vocal tract rather than the voice source, which is understandable considering that meaning is primarily conveyed through changes in articulation and the lack of understanding of the voice production process. The vibrating element in these mechanical models, either a vibrating reed or a slotted rubber sheet stretched over an opening, is only a rough approximation of the human vocal folds.

More sophisticated mechanical models have been developed more recently to better reproduce the three-dimensional layered structure of the vocal folds. A membrane (cover)-cushion (body) two-layer rubber vocal fold model was first developed by Smith (1956). Similar mechanical models were later developed and used in voice production research (e.g., Isogai et al., 1988; Kakita, 1988; Titze et al., 1995; Thomson et al., 2005; Ruty et al., 2007; Drechsel and Thomson, 2008), using silicone or rubber materials or liquid-filled membranes. Recent studies (Murray and Thomson, 2012; Xuan and Zhang, 2014) have also started to embed fibers into these models to simulate the anisotropic material properties due to the presence of collagen and elastin fibers in the vocal folds. A similar layered vocal fold model has been incorporated into a mechanical talking robot system (Fukui et al., 2005; Fukui et al., 2007; Fukui et al., 2008). The most recent version of the talking robot, Waseda Talker, includes mechanisms for the control of pitch and resting glottal opening, and is able to produce voice of modal, creaky, or breathy quality. Nevertheless, although a mechanical voice production system may find application in voice prosthesis or humanoid robotic systems in the future, current mechanical models are still a long way from reproducing or even approaching humans' capability and flexibility in producing and controlling voice.

B. Formant synthesis and parametric voice source models

Compared to mechanically reproducing the physical process involved in speech production, it is easier to reproduce speech as an acoustic signal. This is particularly the case for speech synthesis. One approach adopted in most of the current speech synthesis systems is to concatenate segments of pre-recorded natural voice into new speech phrases or sentences. While relatively easy to implement, in order to achieve natural-sounding speech, this approach requires a large database of words spoken in different contexts, which makes it difficult to apply to personalized speech synthesis of varying emotional percepts.

Another approach is to reproduce only perceptually relevant acoustic features of speech, as in formant synthesis. The target acoustic features to be reproduced generally include the F0, sound amplitude, and formant frequencies and bandwidths. This approach gained popularity with the development of electrical synthesizers and later computer simulations which allow flexible and accurate control of these acoustic features. Early formant-based synthesizers used simple sound sources, often a filtered impulse train as the sound source for voiced sounds and white noise for unvoiced sounds. Research on the voice sources (e.g., Fant, 1979; Fant et al., 1985; Rothenberg et al., 1971; Titze and Talkin, 1979) has led to the development of parametric voice source models in the time domain, which are capable of producing voice source waveforms of varying F0, amplitude, open quotient, and degree of abruptness of the glottal flow shutoff, and thus synthesis of different voice qualities.

While parametric voice source models provide flexibility in source variations, synthetic speech generated by the formant synthesis still suffers limited naturalness. This limited naturalness may result from the primitive rules used in specifying dynamic controls of the voice source models (Klatt, 1987). Also, the source model control parameters are not independent from each other and often co-vary during phonation. A challenge in formant synthesis is thus to specify voice source parameter combinations and their time variation patterns that may occur in realistic voice production of different voice qualities by different speakers. It is also possible that some perceptually important features are missing from time-domain voice source models (Klatt, 1987). Human perception of voice characteristics is better described in the frequency domain as the auditory system performs an approximation to Fourier analysis of the voice and sound in general. While time-domain models have better correspondence to the physical events occurring during phonation (e.g., glottal opening and closing, and the closed phase), it is possible some spectral details of perceptual importance are not captured in the simple time-domain voice source models. For example, spectral details in the low and middle frequencies have been shown to be of considerable importance to naturalness judgment, but are difficult to be represented in a time-domain source model (Klatt, 1987). A recent study (Kreiman et al., 2015) showed that spectral-domain voice source models are able to create significantly better matches to natural voices than time-domain voice source models. Furthermore, because of the independence between the voice source and the sub- and supra-glottal systems in formant synthesis, interactions and co-variations between vocal folds and the sub- and supra-glottal systems are by design not accounted for. All these factors may contribute to the limited naturalness of the formant synthesized speech.

C. Physically based computer models

An alternative approach to natural speech synthesis is to computationally model the voice production process based on physical principles. The control parameters would be geometry and material properties of the vocal system or, in a more realistic way, respiratory and laryngeal muscle activation. This approach avoids the need to specify consistent characteristics of either the voice source or the formants, thus allowing synthesis and modification of natural voice in a way intuitively similar to human voice production and control.

The first such computer model of voice production is the one-mass model by Flanagan and Landgraf (1968), in which the vocal fold is modeled as a horizontally moving single-degree of freedom mass-spring-damper system. This model is able to vibrate in a restricted range of conditions when the natural frequency of the mass-spring system is close to one of the acoustic resonances of the subglottal or supraglottal tracts. Ishizaka and Flanagan (1972) extended this model to a two-mass model in which the upper and lower parts of the vocal fold are modeled as two separate masses connected by an additional spring along the vertical direction. The two-mass model is able to vibrate with a vertical phase difference between the two masses, and thus able to vibrate independently of the acoustics of the sub- and supra-glottal tracts. Many variants of the two-mass model have since been developed. Titze (1973) developed a 16-mass model to better represent vocal fold motion along the anterior-posterior direction. To better represent the body-cover layered structure of the vocal folds, Story and Titze (1995) extended the two-mass model to a three-mass model, adding an additional lateral mass representing the inner muscular layer. Empirical rules have also been developed to relate control parameters of the three-mass model to laryngeal muscle activation levels (Titze and Story, 2002) so that voice production can be simulated with laryngeal muscle activity as input. Designed originally for speech synthesis purpose, these lumped-element models of voice production are generally fast in computational time and ideal for real-time speech synthesis.

A drawback of the lumped-element models of phonation is that the model control parameters cannot be directly measured or easily related to the anatomical structure or material properties of the vocal folds. Thus, these models are not as useful in applications in which a realistic representation of voice physiology is required, as, for example, in the clinical management of voice disorders. To better understand the voice source and its control under different voicing conditions, more sophisticated computational models of the vocal folds based on continuum mechanics have been developed to understand laryngeal muscle control of vocal fold geometry, stiffness, and tension, and how changes in these vocal fold properties affect the glottal fluid-structure interaction and the produced voice. One of the first such models is the finite-difference model by Titze and Talkin (1979), which coupled a three-dimensional vocal fold model of linear elasticity with the one-dimensional glottal flow model of Ishizaka and Flanagan (1972). In the past two decades more refined phonation models using a two-dimensional or three-dimensional Navier-Stokes description of the glottal flow have been developed (e.g., Alipour et al., 2000; Zhao et al., 2002; Tao et al., 2007; Luo et al., 2009; Zheng et al., 2009; Bhattacharya and Siegmund, 2013; Xue et al., 2012, 2014). Continuum models of laryngeal muscle activation have also been developed to model vocal fold posturing (Hunter et al., 2004; Gommel et al., 2007; Yin and Zhang, 2013, 2014). By directly modeling the voice production process, continuum models with realistic geometry and material properties ideally hold the most promise in reproducing natural human voice production. However, because the phonation process is highly nonlinear and involves large displacement and deformation of the vocal folds and complex glottal flow patterns, modeling this process in three dimensions is computationally very challenging and time-consuming. As a result, these computational studies are often limited to one or two specific aspects instead of the entire voice production process, and the acoustics of the produced voice, other than F0 and vocal intensity, are often not investigated. For practical applications, real-time or not, reduced-order models with significantly improved computational efficiency are required. Some reduced-order continuum models, with simplifications in both the glottal flow and vocal fold dynamics, have been developed and used in large-scale parametric studies of voice production (e.g., Titze and Talkin, 1979; Zhang, 2016a), which appear to produce qualitatively reasonable predictions. However, these simplifications have yet to be rigorously validated by experiment.

VI. FUTURE CHALLENGES

We currently have a general understanding of the physical principles of voice production. Toward establishing a cause-effect theory of voice production, much is to be learned about voice physiology and biomechanics. This includes the geometry and mechanical properties of the vocal folds and their variability across subject, sex, and age, and how they vary across different voicing conditions under laryngeal muscle activation. Even less is known about changes in vocal fold geometry and material properties in pathologic conditions. The surface conditions of the vocal folds and their mechanical properties have been shown to affect vocal fold vibration (Dollinger et al., 2014; Bhattacharya and Siegmund, 2015; Tse et al., 2015), and thus need to be better quantified. While in vivo animal or human larynx models (Moore and Berke, 1988; Chhetri et al., 2012; Berke et al., 2013) could provide such information, more reliable measurement methods are required to better quantify the viscoelastic properties of the vocal fold, vocal fold tension, and the geometry and movement of the inner vocal fold layers. While macro-mechanical properties are of interest, development of vocal fold constitutive laws based on ECM distribution and interstitial fluids within the vocal folds would allow us to better understand how vocal fold mechanical properties change with prolonged vocal use, vocal fold injury, and wound healing, which otherwise is difficult to quantify.

While oversimplification of the vocal folds to mass and tension is of limited practical use, the other extreme is not appealing, either. With improved characterization and understanding of vocal fold properties, establishing a cause-effect relationship between voice physiology and production thus requires identifying which of these physiologic features are actually perceptually relevant and under what conditions, through systematic parametric investigations. Such investigations will also facilitate the development of reduced-order computational models of phonation in which perceptually relevant physiologic features are sufficiently represented and features of minimum perceptual relevance are simplified. We discussed earlier that many of the complex supraglottal flow phenomena have questionable perceptual relevance. Similar relevance questions can be asked with regard to the geometry and mechanical properties of the vocal folds. For example, while the vocal folds exhibit complex viscoelastic properties, what are the main material properties that are definitely required in order to reasonably predict vocal fold vibration and voice quality? Does each of the vocal fold layers, in particular, the different layers of the lamina propria, have a functional role in determining the voice output or preventing vocal injury? Current vocal fold models often use a simplified vocal fold geometry. Could some geometric features of a realistic vocal fold that are not included in current models have an important role in affecting voice efficiency and voice quality? Because voice communication spans a large range of voice conditions (e.g., pitch, loudness, and voice quality), the perceptual relevance and adequacy of specific features (i.e., do changes in specific features lead to perceivable changes in voice?) should be investigated across a large number of voice conditions rather than a few selected conditions. While physiologic models of phonation allow better reproduction of realistic vocal fold conditions, computational models are more suitable for such systematic parametric investigations. Unfortunately, due to the high computational cost, current studies using continuum models are often limited to a few conditions. Thus, the establishment of cause-effect relationship and the development of reduced-order models are likely to be iterative processes, in which the models are gradually refined to include more physiologic details to be considered in the cause-effect relationship.

A causal theory of voice production would allow us to map out regions in the physiological parameter space that produce distinct vocal fold vibration patterns and voice qualities of interest (e.g., normal, breathy, rough voices for clinical applications; different vocal registers for singing training), similar to that described by Isshiki (1989; also Fig. 9). Although the voice production system is quite complex, control of voice should be both stable and simple, which is required for voice to be a robust and easily controlled means of communication. Understanding voice production in the framework of nonlinear dynamics and eigenmode interactions and relating it to voice quality may facilitate toward this goal. Toward practical clinical applications, such a voice map would help us understand what physiologic alteration caused a given voice change (the inverse problem), and what can be done to restore the voice to normal. Development of efficient and reliable tools addressing the inverse problem has important applications in the clinical diagnosis of voice disorders. Some methods already exist that solve the inverse problem in lumped-element models (e.g., Dollinger et al., 2002; Hadwin et al., 2016), and these can be extended to physiologically more realistic continuum models.

Solving the inverse problem would also provide an indirect approach toward understanding the physiologic states that lead to percepts of different emotional states or communication of other personal traits, which are otherwise difficult to measure directly in live human beings. When extended to continuous speech production, this approach may also provide insights into the dynamic physiologic control of voice in running speech (e.g., time contours of the respiratory and laryngeal adjustments). Such information would facilitate the development of computer programs capable of natural-sounding, conversational speech synthesis, in which the time contours of control parameters may change with context, speaking style, or emotional state of the speaker.