Tension-activated channels in the mechanism of osmotic fitness in Pseudomonas aeruginosa

Pseudomonas aeruginosa is resistant to drastic osmotic changes because of its ability to quickly jettison small osmolytes through osmotic release channels. Çetiner et al. reveal that it uses one MscL-like and at least two types of MscS-like channels during its osmotic response.

Abstract

Pseudomonas aeruginosa (PA) is an opportunistic pathogen with an exceptional ability to adapt to a range of environments. Part of its adaptive potential is the ability to survive drastic osmolarity changes. Upon a sudden dilution of external medium, such as during exposure to rain, bacteria evade mechanical rupture by engaging tension-activated channels that act as osmolyte release valves. In this study, we compare fast osmotic permeability responses in suspensions of wild-type PA and Escherichia coli (EC) strains in stopped-flow experiments and provide electrophysiological descriptions of osmotic-release channels in PA. Using osmotic dilution experiments, we first show that PA tolerates a broader range of shocks than EC. We record the kinetics of cell equilibration reported by light scattering responses to osmotic up- and down-shocks. PA exhibits a lower water permeability and faster osmolyte release rates during large osmotic dilutions than EC, which correlates with better survival. To directly characterize the PA tension-activated channels, we generate giant spheroplasts from this microorganism and record current responses in excised patches. Unlike EC, which relies primarily on two types of channels, EcMscS and EcMscL, to generate a distinctive two-wave pressure ramp response, PA exhibits a more gradual response that is dominated by MscL-type channels. Genome analysis, cloning, and expression reveal that PA possesses one MscL-type (PaMscL) and two MscS-type (PaMscS-1 and 2) proteins. In EC spheroplasts, both PaMscS channels exhibit a slightly earlier activation by pressure compared with EcMscS. Unitary currents reveal that PaMscS-2 has a smaller conductance, higher anionic preference, stronger inactivation, and slower recovery compared with PaMscS-1. We conclude that PA relies on MscL as the major valve defining a high rate of osmolyte release sufficient to curb osmotic swelling under extreme shocks, but it still requires MscS-type channels with a strong propensity to inactivation to properly terminate massive permeability response.

Introduction

Powerful adaptive mechanisms to environmental changes are characteristic of all commensal or pathogenic microorganisms that propagate between hosts through soil or fresh water. Unlike enteric species such as Escherichia coli (EC), dwelling primarily in guts, Pseudomonas aeruginosa (PA) is an opportunistic pathogen adaptable to a broader range of habitats, including soil, freshwater (Mena and Gerba, 2009), medical equipment (Hall-Stoodley et al., 2004), the urinary tract (Mittal et al., 2009), and tissues and airways of immunocompromised and cystic fibrosis patients (Agger and Mardan, 1995; Hogardt and Heesemann, 2010). Part of its adaptive potential derives from the ability to quickly adjust its turgor pressure under conditions of drastically varied osmolarity. Adaptation of PA to higher osmolarity, as in most bacteria (Wood et al., 2001), involves accumulation of common compatible osmolytes such as glycine betaine and more specifically N-acetylglutaminylglutamine amide (D’Souza-Ault et al., 1993). A steady PA growth at high osmolarity alters transcription levels of at least 66 genes coding for a variety of functions, including osmoprotectant synthesis enzymes, hydrophilins, type III secretion systems, and associated cytotoxins, as well as two-component signaling systems (Aspedon et al., 2006). The organism also survives large osmolarity downshifts; a hypotonic shock from standard LB into distilled water was used in several studies to release periplasmic proteins from PA (Hoshino, 1979; Glick and Garber, 1983). It was noted that cytoplasmic proteins did not appear in the shock fluid, and cell viability did not suffer as a result of this procedure. Apart from that, the PA response to hypoosmotic shock has not been studied in any detail.

EC served as the first bacterial model for studies of osmoregulation (Epstein, 1986; Csonka, 1989; Wood, 2006) and hypoosmotic responses (Kung et al., 2010; Naismith and Booth, 2012). In 1962, Britten and McClure (Britten and McClure, 1962) reported that during abrupt osmotic down-shock, bacteria can release ∼95% of their total amino acid pool and remain completely viable. They assumed that the metabolites are released when “the cell passes through a transient state in which the structures (e.g. the cytoplasmic membrane and/or the cell wall) are distended.” When patch-clamp traces of giant EC spheroplasts (Martinac et al., 1987) and liposome-reconstituted inner membrane proteins (Sukharev et al., 1993) were recorded, the notion of stretch-activated channels acting as possible turgor pressure regulators then replaced this early hypothesis. Identification and cloning of the two most represented inner membrane mechanosensitive (MS) channels, MscL (Sukharev et al., 1994) and MscS (Levina et al., 1999), and preparation of the double knockout (mscL-, mscS-) strain has since demonstrated that these two channels fulfill the function of osmolyte release valves rescuing cells from abrupt osmotic down-shock (Levina et al., 1999). Expression of either MscL or MscS extends the tolerated range of down-shocks from 300 mOsm (in the double null mutant) to 900–1,000 mOsm (Levina et al., 1999). Under strong osmotic down-shocks, fast osmolyte exchange in living cells may take as little as 50–100 ms (Boer et al., 2011).

The low-threshold MscS channel (Levina et al., 1999), which exhibits adaptive behavior (Akitake et al., 2005; Belyy et al., 2010), and the high-threshold MscL (Sukharev et al., 1997) were recognized as major contributors to the graded tension-driven permeability responses in EC (Perozo and Rees, 2003; Steinbacher et al., 2007; Booth and Blount, 2012). Further efforts identified five additional MscS-related proteins in EC, which form low-abundance MS channels (Schumann et al., 2010; Edwards et al., 2012) capable of alleviating moderate and gradually imposed osmotic downshifts (Bialecka-Fornal et al., 2015). The studies emphasized the importance of two parameters: channel density in the membrane (Bialecka-Fornal et al., 2012; Booth and Blount, 2012) and the rate of osmotic downshift in defining the lytic threshold and survival range for bacteria (Bialecka-Fornal et al., 2015).

The osmotic survival data obtained in MS channel knockout strains (Levina et al., 1999; Reuter et al., 2014; Bialecka-Fornal et al., 2015) have indicated that the peptidoglycan layer alone cannot restrain cell swelling to prevent lysis at strong shocks. As the magnitude of osmotic shock increases, water influx must stretch the peptidoglycan, generating tension in the membrane that can activate MS channels, which then start dissipating the osmotic gradient. This sequence suggests a simple kinetic criterion for the effective channel-mediated rescuing mechanism: the cell will remain mechanically stable in the range of osmotic gradients as long as the efflux of small intracellular osmolytes can outpace the osmotic influx of water and thus limit cell volume increase and membrane stretching. Before one can propose a quantitative model of this process and predict in what situations the cell will be rescued or ruptured, we need a detailed multilevel phenomenological description of the system that takes into account the whole-cell osmotic behavior as well as molecular components and events in the membrane. A comparative approach that takes into consideration two distantly related gram-negative bacterial species may point to critical parameters.

In the present work, we perform initial osmotic viability tests on early logarithmic cultures of PA and find that it can tolerate stronger shocks than EC. We continued with stopped-flow measurements of water and osmolyte exchange in the two strains and found that PA has an overall kinetic advantage in both processes in terms of curbing water influx. We devised a procedure for giant spheroplast preparation and performed a patch-clamp characterization of MS channels in the native membrane of PA, which reveals a different structure of the channel population compared with EC. We cloned and characterized two MscS-like and one MscL-like channel species from PA, which are substantially distinct from their EC orthologues. The data provide us with the first experimental ground to relate the whole-cell osmoprotective responses in bacteria with the densities and electrophysiological properties of MS channel components in their native membranes contributing to osmotic resistance.

Materials and methods

Strains and media

We chose Frag1, a WT EC strain that was previously used in studies of potassium transport (Rhoads et al., 1976) and is a parental strain for a collection of MS channel deletion strains (Levina et al., 1999; Edwards et al., 2012). For heterologous expression of PA MS channels, we used the MJF641 (aka Δ7) strain derived from Frag-1 devoid of seven endogenous MS channel genes (Δ mscL, mscS, mscK, ybdG, ynaI, ybiO, and yjeP; Edwards et al., 2012). Both EC strains were gifts from I. Booth (University of Aberdeen, Aberdeen, Scotland, UK). In addition, we used PB104 (Δ mscL; Blount et al., 1996) and PB113 (Δ mscS, mscK; Li et al., 2002) strains to characterize individual cloned PA MS channels in the presence of EC counterparts. The WT PA-14 strain of PA was provided by V. Lee (University of Maryland, College Park, MD).

Osmotic survival assays

Only early logarithmic cultures (OD₆₀₀ ∼0.25) were used in all experiments because the cells are larger (Sezonov et al., 2007) and more sensitive to osmotic conditions. From standard overnight cultures, cells were transferred to the high-osmotic LB medium (HiLB) adjusted to 1,200 mOsm by adding 413 mM (24 g/liter) NaCl to a standard LB medium. With a small inoculum (1:700), cells were allowed to go through five or six duplications; in HiLB, it took 3–4 h to reach an OD₆₀₀ of 0.25. This OD marks a true early logarithmic stage for PA and EC because both strains are able to grow to an OD of 2.5–2.7 under these conditions (Fig. S1). 100-µl culture aliquots were abruptly diluted into 5 ml media of lower osmolarity. After a 15-min incubation at room temperature, shocked bacteria were sequentially diluted 1:25 in the same shock medium twice, and 75-µl aliquots were plated in triplicate. Because WT bacteria were completely tolerant to low and intermediate shocks, a standard set of shock media included 400 mOsm LB, 250 mOsm MLB, 125 mOsm MLB/2, 50 mOsm MLB/5, and 0 mOsm deionized water. Colonies were manually counted the next morning. The colony number divided by the number in the unshocked control (diluted into HiLB) in each particular experiment was taken as the survival fraction. Independent shock experiments were repeated at least six times.

Stopped-flow experiments

Cells were grown in either 250 mOsm MLB or 1,200 mOsm HiLB for the up- or down-shock experiments, respectively. Cells harvested at OD₆₀₀ of 0.25 were concentrated with a brief centrifugation and brought to OD₆₀₀ of 2.2. Dilutions of HiLB with sterile deionized water produced down-shock media of 900 (3/4), 800 (2/3), 720 (3/5), 600 (1/2), 450 (3/8), 300 (1/4), and 150 (1/8) mOsm.

A Bio-Logic SFM-2000 stopped flow machine equipped with two independent motorized syringes, a 21-µl optical mixing chamber, modular spectrophotometer, and a computer for protocol programming and data acquisition was used in experiments. The small-angle scattering from the suspension upon rapid (∼8 ms) mixing was measured with a PMT tube covered with a special insert masking the straight incident light in the center within the 5° angle (custom engineered at Bio-Logic Science Instruments). The light was collected in the range between 5 and 12 degrees. Because we used noncollimated light entering the chamber from the light guide, we observed a substantial amount of “stray” light captured by the PMT. The fraction of signal attributable to scattering from cells was extracted by subtracting stray light contribution obtained in mixing controls with pure HiLB supernatant without cells. The mixing ratio in shock experiments was always 1:10 (176 µl cell suspension + 1,760 µl dilution medium) delivered into the optical cell at the total rate of 8.5 ml/s. The scattering kinetics were collected for 4 s, and five to seven sequential trials were averaged. Changes of scattering reflecting the fast processes of water or solute equilibration typically completed within 0.5–1 s.

In Rayleigh–Gans approximation (Koch et al., 1996), the intensity of the forward scattered light measured at a given density of cell suspension grows monotonously with the cell volume and refractive index difference between the cell (n_cell) and the medium (n_m). The refractive index of the cell, in turn, depends on the total concentration of solutes inside. Although the exact theoretical expression for the small-angle scatter is rather complex (see Supplemental text), two specific cases may yield easily tractable scaling relationships. For up-shocked cells undergoing moderate osmotic shrinkage (water leaves while all osmolytes remain inside), the intensity of scattering can be well approximated by the volume to the power of −(2/3), i.e., inverse of the cell surface area (Koch, 1961). The same dependence takes place for the initial stage of osmotic swelling under hypoosmotic shock before the osmolyte release has started. However, after the bacteria expand longitudinally (Rojas et al., 2014) and reach their maximum size (the volume can increase by up to 23%; Baldwin et al., 1988; Buda et al., 2016), further changes in cell dimensions and shape are relatively small and apparently curbed by both peptidoglycan rigidity and ensuing osmolyte dissipation. When membrane tension reaches activation threshold for the channels and osmolyte release begins, the subsequent changes in the scattering are mainly caused by the changes of cellular refractive index, which reflects the concentration of all solutes inside. At this stage, scattering is roughly proportional to the square of solute mass inside the cell. Under the assumption that the release of osmolytes is an exponential process with characteristic time of τ, the time courses of light scattering were fitted with the following equation:

$$I=I_0+S{\left(m_i+m_{p0}{e}^{\frac{t_0-t}{\tau }}\right)}^2,$$ (1)

where I₀ is the constant offset accounting for stray light, m_i and m_p are the fractions (masses) of impermeable and permeable osmolytes, respectively, S is the scaling constant, and t₀ designates the start of the fitting interval. Derivation of Eq. 1 can be found in the Supplemental text. The fitting of the scattering traces 0.5-s long with Eq. 1 was performed in MATLAB, typically in the range between the point of steepest negative slope (maximal rate designated by the minimum of the first derivative) and the end of the trace, as shown in Figs. S3 and S4.

To determine water permeability rates, we performed osmotic up-shock experiments on cells grown in MLB. The kinetics of light scattering increase caused by cell shrinkage in a hypertonic medium were recorded at different osmotic gradients, and rate constants were determined from monoexponential fits. The osmotic water permeability coefficient, P_f, was calculated according to van Heeswijk and van Os (1986):

$$P_f=\frac{k}{\begin{array}{c}\left(\frac{S}{\begin{array}{c}{V}_0\end{array}}\right)V_w\mathrm{\Delta }C\end{array}},$$ (2)

where k is the rate constant of scattering signal change (s⁻¹) calculated from monoexponential fit, S/V₀ is the initial surface area to volume (SA:V) ratio, V_w is the partial molar volume of water (18 cm³/mol), and ΔC is the difference of osmolality between inside and outside. The sizes of PA and EC cells in early logarithmic cultures were measured microscopically under 60× differential interference contrast objective as in Baldwin and Bankston (1988). Histograms of length and width distributions were generated from manual measurements on 300–400 cells of each type. Surface areas and volumes of cells were calculated in the approximation of a cylindrical shape capped with hemispheres: SA = 4πr² + 2πrl and V = 4/3πr³ + πr²l.

Preparation of giant spheroplasts and patch clamp

The standard procedure of giant spheroplast preparation from EC (Martinac et al., 1987) begins with growth in the presence of 0.06 mg/ml cephalexin, which blocks cell septation. Within 1.5–2 h, the growing but not dividing bacteria form 100–250-µm-long filaments. The filaments are transferred into a hypertonic buffer (1 M sucrose) and treated with 0.2 mg/ml lysozyme in the presence of 5 mM EDTA, which degrades the peptidoglycan layer within 5–10 min. As a result, filaments collapse into spheres 3–7 µm in diameter. The reaction is stopped by excess Mg²⁺ that terminates the effect of EDTA and activates DNase. Sedimentation through a one-step sucrose gradient separates the spheroplasts from the rest of the reaction mixture.

The procedure of PA giant spheroplast preparation was similar, but with two modifications. Instead of cephalexin, the PA filaments were grown in the presence of 0.2 mg/ml carbenicillin (1.5–2 h). Filaments were collected by low-speed centrifugation, resuspended in 1 M sucrose, and subjected to the “plasting” reaction in the presence of 10 mM EDTA and 0.6 mg/ml lysozyme for 15–20 min. Spheroplasts were separated from the debris by centrifugation through a one-step sucrose gradient, aliquoted, and stored at −80°C.

Borosilicate glass (Drummond 2-000-100) pipets 1–1.3 µm in diameter were used to form tight seals with the inner membrane. All recordings were done in excised inside-out patches in symmetrical 200 mM KCl, 10 mM CaCl₂, 90 mM MgCl₂ solution buffered by 10 mM HEPES, pH 7.2. Currents were recorded in voltage-clamp mode under preprogrammed mechanical stimuli combined from steps or ramps of negative pressure (suction) delivered from a modified HSPC-1 pressure clamp apparatus (ALA Scientific Instruments).

Cloning of MS channel genes from PA

EC MscS and MscL protein sequences were used to search the PA14 genome using the BLAST tool in the NCBI database. A single homologue of MscL and six proteins of different length with detectable homology to MscS were found. The alignments identified two MscS homologues of similar length (278–283 amino acids). Using primers complementary to the flanking sequences, the three open reading frames were PCR-amplified and subcloned into the pB10d vector (Okada et al., 2002) as BglII–HindIII fragments. The identity of inserts to the reference sequences in the PA14 genomic database was confirmed by automated sequencing. PaMscL (PA14_61050), PaMscS-1 (PA14_57110), and PaMscS-2 (PA14_65040) were expressed in MJF641 EC cells, and giant spheroplasts were generated, enabling patch-clamp examination of these individual channel species.

Online supplemental material

The supplemental text outlines the theory of light scattering measurements on bacterial suspensions and derivation of Eq. 1. Fig. S1 shows the growth curves for PA and EC in MLB and HiLB. Fig. S2 presents raw scattering traces. Figs. S3 and S4 show examples of fitting. Fig. S5 describes the variability of ramp responses in EC and PA excised patches. Fig. S6 presents sequence alignments. Fig. S7 shows Boltzmann fitting of PaMscS-1 and 2 activation curves to help extract the spatial and energy parameters of opening. Table S1 presents bioinformatics data on MS channel homologues in EC and PA.

Results

PA versus EC: Osmotic survival and kinetics of osmolyte and water exchange

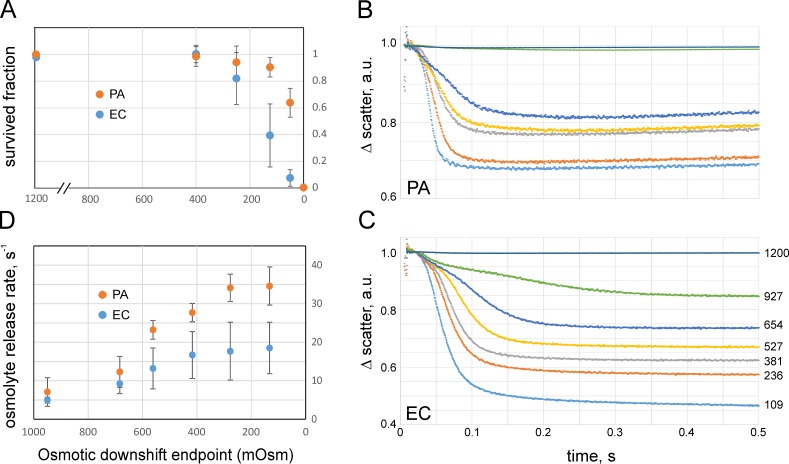
Cells grown in 1,200 mOsm HiLB were diluted into media of different osmolality, incubated for 15 min, additionally diluted in the same final shock medium to an optimal plating density, and plated. This initial high-osmotic condition, while permitting cell growth, allowed for downshifts strong enough to reduce cell survival rates down to 0.5–1%. Fig. 1 A depicts the results of colony counts, which shows that both WT PA and EC strains, carrying a full complement of MS channels, are completely resistant to osmotic downshifts of up to 800 mOsm in magnitude (downshift endpoint of 400 mOsm). At shocks higher than 950 mOsm, the viability of both strains starts declining, with a more pronounced loss in EC. PA shows a marked decline only at 1,050 mOsm downshift. This indicates that cells preadapted to higher osmolarity (i.e., having accumulated high concentrations of osmolytes) become vulnerable to osmotic down-shock. As seen in Fig. 1 A, the range of osmotic shocks tolerated by EC (grown in HiLB) is narrower than that for PA. Apparently, under such conditions, the accumulated osmolytes cannot be ejected fast enough, and the influx of water leads to a critical surge of turgor pressure that damages the cell. The fact that PA survives drastic shocks better may suggest that the overall osmolyte handling system in PA is more efficient. In the following sections, we will address the questions of timing of cell equilibration and the nature of changes of membrane permeability for this organism.

Figure 1.

Osmotic survival correlates with osmolyte exchange rates. (A) Fractions of WT PA (PA14) and EC (Frag1) surviving osmotic down-shock as assayed by plate counts. The symbols and bars represent mean and standard deviation (n = 6). The x axis represents the end osmolarity upon a downshift from the initial 1,200 mOsm. (B and C) Stopped-flow recordings of small-angle light scattering changes upon mixing of suspensions of PA (B) and EC (C) with a 10-fold excess of low-osmolarity media (means of five sequential trials). The numbers by curves denote the osmolarity at the end of downshift from 1,200 mOsm (downshift endpoint). The 1,200 mOsm medium (HiLB) was standard LB supplemented with 413 mM NaCl. The scattering traces reflect the kinetics of dissipation of osmolytes contributing to the refractive index of the cytoplasm. The fitting of the scattering traces was done with nonexponential Eq. 1 (see Materials and methods) starting from the point of steepest downfall (see Fig. S3 and S4). a.u., arbitrary units. (D) The osmolyte release rates (1/τ) extracted from fits. The shock magnitude axis is aligned with A. Error bars represent standard deviation (n = 4). The osmolyte release rates are nearly equal at moderate shocks; however, at high shocks, specifically in PA, the rate sharply increases, which correlates with higher survival. For all experiments, the cultures were taken in early logarithmic phase (OD₆₀₀ of 0.25).

Note that both cultures were largely “wiped out” in distilled water, showing only 0.1–0.4% survival. When shocked into distilled water not from HiLB, but from standard LB (400 mOsm), PA and EC survival rates are 13 ± 7% and 46 ± 9% (n = 4), respectively. The magnitude of shock in this instance is relatively small (400 mOsm), and the experiments above showed that bacteria easily tolerate an 800 (1,200 → 400) mOsm downshift (Fig. 1 A). The cells apparently suffer more from ion depletion in deionized water than from osmotic rupture, and EC cells are more tolerant to this type of perturbation.

To observe the osmolyte release in real time, we measured the kinetics of forward light scattering from HiLB-adapted EC and PA cells to abrupt dilutions into media of different osmolarity using the stopped-flow technique. Fig. 1 (B and C) shows a series of scaled light scattering traces recorded on PA and EC, respectively, obtained at different magnitudes of shock. The set of initial traces is presented in Fig. S2, but for the ease of comparison, the traces shown in Fig.1 (B and C) are normalized such that the maximal scattering level immediately after mixing (t = 10 ms) was equated to unity and the curves represent fractional scattering decrease in the course of swelling and osmolyte release. In EC, the fast kinetics of scattering decrease was usually completed by 0.3 s, with amplitudes ranging from 15% at the mild shocks to 55% at the strongest shocks relative to the initial scattering level attributable to the presence of cells (after subtraction of stray light signal). For PA, the fast processes at all shocks completed by 150 ms with practically no scattering change at mild downshift (∼2%) and an ∼35% signal decrease at the strongest shock.

According to Rayleigh–Gans approximation for bacterial turbidity (Koch et al., 1996), the small-angle scattering grows monotonously with the difference in refractive indexes inside and outside the cell. The refractive index inside is roughly proportional to the nonaqueous content of the cytoplasm, the light scattering signal caused by osmolyte loss in hypoosmotic medium is proportional to the square of cellular anhydrous mass (dry weight), and the decrease of scattering reflects the combined effect of all permeable osmolyte loss. In the case of severe shocks, the scattering from EC suspension drops by half (Fig. 1 C), suggesting that cells lose ∼30% of their internal nonaqueous components. Assuming that macromolecules stay inside, the cells likely release the major part of their small molecules (Britten and McClure, 1962). From the amplitude of the scattering signal (35%; Fig. 1 B), one may conclude that PA loses ∼19% of its internal light-refracting content at the most severe shocks, which is less than EC.

From Fig. 1 (B and C) and Figs. S2, S3, and S4, one may see that each curve begins with a noisy part representing the turbulent mixing period (∼8 ms) followed by a low-slope region (lag phase) reflecting cell swelling. The swelling period shortens as the shock magnitude increases. The nature of this initial period will be further investigated, but currently, we presume that during this time, the turgor pressure and tension build up until reaching a critical level that activates the MS channels, which then start dissipating osmolytes. At this moment, the scattering curve bends down. During the falling phase, which becomes steeper as the shock magnitude increases, different fractions of the channel population open and release osmolytes at different rates, whereas the continuing water influx maintains an above-threshold tension in the inner membrane. Finally, when the osmotic gradient is sufficiently dissipated, tension drops to a subthreshold level, the channels close, and the signal flattens.

The general trend is that with the increasing shock magnitude, the swelling period shortens and the release phase becomes faster. This also generates a larger overall scattering drop caused by an increase in the amount of solutes ejected from cells. Fits of experimental traces to Eq. 1 (presented in Figs. S3 and S4) describe the fast falling phase of osmolyte release in both PA and EC reasonably well. EC traces (Fig. S4), however, reveal a slower process leading to a slight deviation of the fit from the actual traces toward the end of 0.5 s. Note that the scattering signal is proportional to the square of the cellular refractive index (or dry weight), and thus the time course is not exponential but rather represents a squared exponent (Eq. 1), which visually exaggerates the rate of the release process.

Fig. 1 D shows the dependencies of the release rate on the magnitude of osmotic downshift. The x axis of this graph is aligned with the viability graph on Fig. 1 A. Up to a shock magnitude of 800 mOsm (end point of 400 mOsm), viabilities of both EC and PA are uncompromised, and the release rates from both types of cells are similar. Viabilities start declining at stronger shocks, precisely when the release rates approach saturation. In EC, the release system seems to have reached its capacity earlier, which correlates with the onset of EC viability decline. At those shock magnitudes, the release rate in PA keeps increasing and saturates only at stronger shocks (270 and 150 mOsm endpoints in Fig. 1 D). Again, the loss of PA viability is observed after the release rate flattens. It appears that the PA release system is able to absorb stronger shocks by working faster.

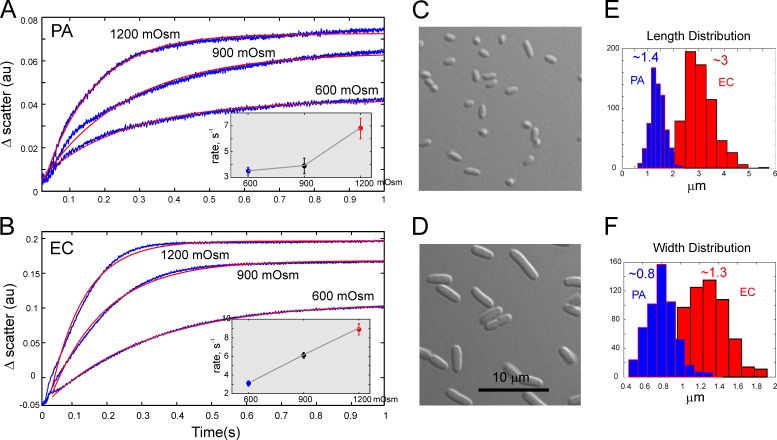
Because the initial swelling rate depends primarily on water permeability through the cell envelope and the osmotic gradient, we performed opposite up-shock experiments measuring cell shrinkage that reflects water efflux rates (Fig. 2). From monoexponential fits of the scattering traces, we obtained the rates of cytoplasmic volume change as a function of shock magnitude for PA and EC, respectively (Fig. 2, A and B, insets). The results indicate that the rate of cytoplasm condensation in EC is a nearly linear function of the shock magnitude. In PA, however, this rate had a hyperlinear dependence on shock magnitude.

Figure 2.

The up-schock experiments record the rates of cell shrinkage and permit estimations of water permeability. (A and B) Stopped-flow recordings of small-angle light scattering upon mixing of suspensions of PA (A) or EC (B) grown in MLB (250 mOsm) with 10-fold excess of higher-osmolarity media (indicated by the traces). Experimental traces (blue) are overlaid with monoexponential fits (red). The insets show shrinkge rates as functions of shock magnitude. The error bars reperesent standard deviations (n = 4). Increased concentration of intracellular solutes and the accompanying increase of refractive index produce an increase in scattering. (C and D) Both cultures were grown to OD₆₀₀ of 0.25 and imaged under DIC. (E and F) Histograms of length (E) and width (F) distributions were generated from microscopic measurements on 300–400 cells of each type. The mean sizes of PA and EC cells were 1.4 × 0.8 µm and 3.0 × 1.3 µm (length × width). The assumption that cells are cylinders with spherical ends produces surface areas of 3.5 µm² and 11.3 µm² and cell volumes of 0.57 µm³ and 2.94 µm³, respectively. The SA:V ratios are 6.18 µm⁻¹ and 3.85 µm⁻¹ for PA and EC, respectively.

Following van Heeswijk and van Os (1986) and Maurel et al. (1997), we estimated the water permeability coefficient (P_f) by using the parameter of SA:V ratio for the osmotically active compartment. Under the assumption that cells are cylinders with spherical caps at each end, with mean dimensions presented in Fig. 2, the corresponding SA:V ratios are 3.8 ± 0.1 and 6.2 ± 0.8 µm⁻¹ for EC and PA, respectively. For the rate constants of scattering signal of 3.5 ± 0.3 and 3.2 ± 0.2 s⁻¹ measured at 600 mOsm shock, P_f values were (2.0 ± 0.7) × 10⁻² cm/s for PA and (3.1 ± 0.9) × 10⁻² cm/s for EC, with uncertainties estimated using the error propagation rules taking contributions from all parameters (Eq. 2). We found that at higher shocks, the calculated P_f values become considerably lower. Larger volume perturbation potentially invokes other factors that may resist compaction such as macromolecular crowding (Cayley and Record, 2003). Because the cells in this case may not behave like ideal osmometers, we favor the P_f values obtained with the lowest degree of osmotic and mechanical perturbation. From these measurements, we conclude that smaller PA cells have a lower water permeability, which in the event of abrupt osmotic swelling buys more time for osmolyte release.

EC and PA spheroplast preparation and patch-clamp channel activation in situ

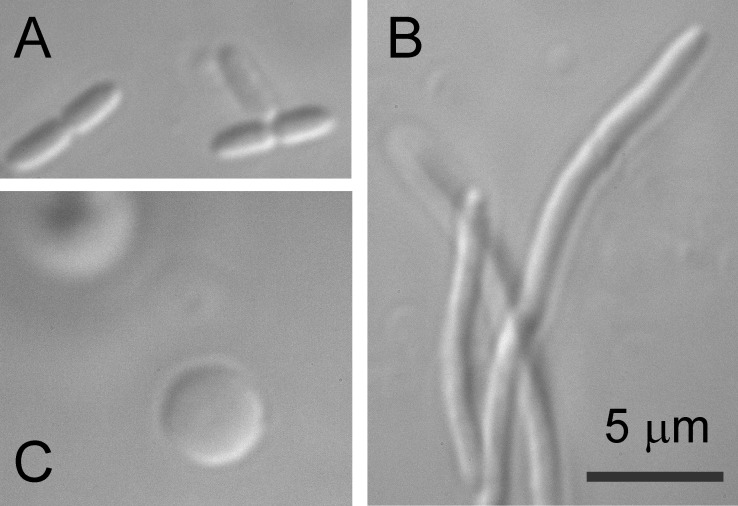
To obtain a “microscopic” picture of osmotic permeability increase and characterize channel activities in native membranes, giant spheroplasts of both Frag-1 and PA-14 strains were prepared. Frag-1 formed filaments in the presence of a standard concentration of 0.06 mg/ml cephalexin. These filaments were then converted into 3–6-µm spheres with lysozyme in the presence of EDTA within 5–10 min. We attempted the same procedure on PA only to find that the PA14 strain is completely insensitive to cephalexin. However, following earlier work by Hubert (Hubert et al., 1971), we were able to effectively induce filamentous growth of PA in the presence of 0.2–0.3 mg/ml carbenicillin (Fig. 3). PA filaments were sensitive to lysozyme, but the plasting reaction required double amounts of lysozyme and EDTA and an extended reaction time (15–20 min) compared with EC.

Figure 3.

Steps in the giant spheroplast preparation as viewed by DIC microscopy. (A) Intact PA (PA14) cells. (B and C) Filamentous forms induced by carbenicillin (B) and giant spheroplasts after lysozyme digestion (C).

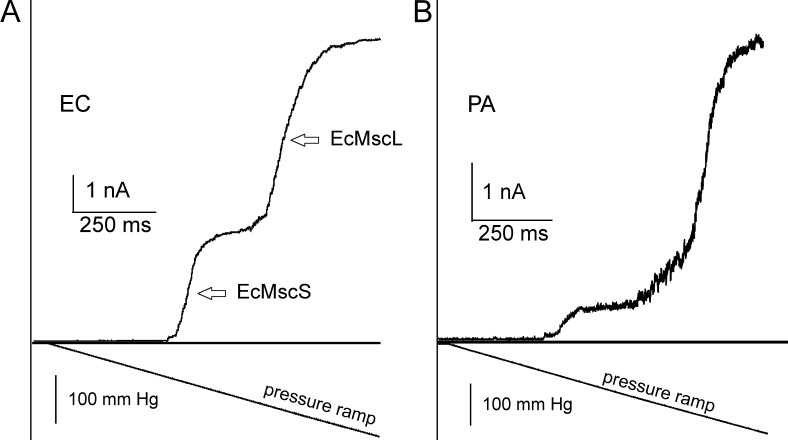
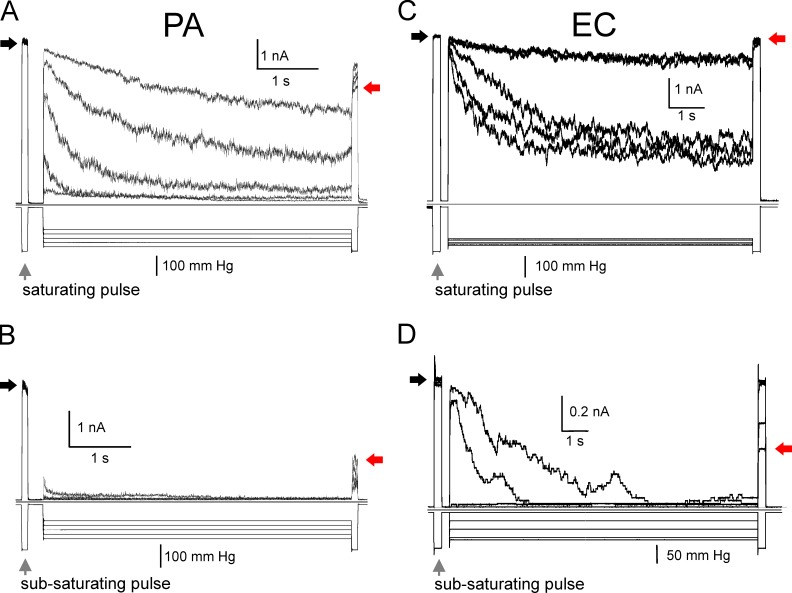
Formation of a gigaohm seal with borosilicate glass pipettes (tip diameter of 1–1.3 µm) took a mean of 5–10 min at constant 15–30 mmHg suction. Patch excision was achieved by gently tapping the micromanipulator (no air exposure). Typical pressure ramp responses recorded in EC and spheroplasts are shown in Fig. 4. Pipette pressure was linearly increased within 1 s from 0 mm Hg to saturating pressure (∼250 mm Hg), at which point all active channels are found in the open state (P_o ∼1). Recordings from native patches reveal that the cytoplasmic membranes of both organisms harbor MS channels at comparable densities. In EC, two distinct waves result from early activating MscS family channels and the late-acting MscL population (Fig. 4 A). The PA membrane displays a much smaller wave attributable to MscS-like channels. Half of the patches do not show a characteristic two-wave response (Fig. S4). The less clear separation between the PaMscS and PaMscL waves suggests that PA might have a different structure of channel population; a larger variety of channels with different gating tensions and conductances may give rise to some overlap of their activities in ramp responses.

Figure 4.

The composition of MS channel populations in EC and PA as revealed by pressure ramp experiments. (A and B) Pressure ramps applied to excised patches of native MS channel populations in EC (A) and PA (B) produce comparable conductance responses. The characteristic double-wave pattern is observed in EC patches. The channel population in EC patch contains ∼60 MscS and 50 MscL channels. PA always shows a smaller proportion of low-threshold MscS-like channels compared with a more dominant MscL-like channel population (∼80 per patch; see Table 2 and Fig. S5). The symmetric recording buffer contained 200 KCl, 90 mM MgCl₂, 10 mM CaCl₂, and 10 mM HEPES, pH 7.2.

Ramp responses recorded from multiple patches provided us with single-channel conductances and sufficient statistics of channel numbers per patch (Fig. S5 and Table 1). Under the assumption that the tension midpoint for activating high-threshold MscL channels is the same and equal to 12 mN/m, we calculated the radius of patch curvature in each experiment. Again, assuming that under the tension of 12 mN/m the patch is a hemisphere, we estimated patch area and channel densities. From the numbers, it is evident that PA has its MscL at a higher density and apparently relies more on this type of channel.

Table 1. Numbers and densities of channels in native inside-out patches from ramp traces recorded from PE (PA14) and EC (Frag1) giant spheroplasts.

Cell type	No. of MscS per patch	No. of MscL per patch	Midpoint ratio pMscS/pMscL	MscL midpoint	Patch radius	Patch area	MscS/µm2	MscL/µm2	n
				mmHg	µm	µm2
Frag1	62 ± 6 (1 nS)	47 ± 3 (3 nS)	0.58 ± 0.02	156 ± 4	1.3 ± 0.1	11 ± 1	6 ± 1	4.4 ± 0.3	12
PA14	13 ± 4 (0.97 nS)	78 ± 10 (2.1 nS)	0.54 ± 0.02	162 ± 13	1.4 ± 0.2	13 ± 3	1.2 ± 0.4	7 ± 1	8

A ±15% uncertainty in the absolute values of midpoint tensions for EC and PA MscL may result in an ∼30% error in patch area and a similar error in channel density estimation.

In the next experiments, we tested how repeatable are population currents depending on preconditioning tension. The purpose of these trials was to determine the fraction of the population that may adapt or inactivate. We adjusted the amplitude of stimuli to probe either the entire population (low- and high-threshold) or only the low-threshold population. The data presented in Fig. 5 reveal that specifically the low-threshold populations in both organisms are prone to tension-dependent inactivation. A pulse-step-pulse protocol was used in two different modes to visualize inactivation. In the “saturating” mode (Fig. 5, A and C), we used the first pulse at saturating amplitude to reveal the entire active population of channels in the patch. The test pulse was followed with a lower-amplitude conditioning step (usually near half-saturating pressure), during which part of the population could redistribute between the open, closed, and inactivated states. The same saturating test pulse applied at the end reveals the fraction of noninactivated channels available for opening. As seen in Fig. 5 A, the entire active PA channel population may lose up to 30% of the current after being subjected to a 6-s subsaturating conditioning step (indicated by black and red arrows). When subjected to subsaturating steps, the entire EC population loses less activity (Fig. 5 C). However, when we scaled down the amplitudes of mechanical stimuli to probe only the low-threshold fraction of channels, we see a larger fractional reduction of the current at the end, indicative of a massive channel outflow into the inactivated state. The experiment illustrates that similar to EC and Vibrio cholerae (Rowe et al., 2013), the low-threshold PA population is prone to strong tension-dependent inactivation (Fig. 5 B). As was suggested before (Akitake et al., 2007; Boer et al., 2011), the physiological purpose of channel “disengagement” at moderate prolonged stimuli is to avoid flickering between open and closed states and prevent dissipation of metabolites at nonthreatening tensions.

Figure 5.

The puse-step-pulse protocol reveals adaptable fractions of channel populations in PA and EC. (A–D) The low- and high-threshold subpopulations of native channels in PA (A and B) and EC (C and D) exhibit distinctive adaptive behaviors. Exposure of excised patches to prolonged moderate tension produces massive inactivation of the native low-threshold channel population. (A) The first 0.1-s pressure pulse invokes ∼50% of total patch conductance, engaging the low-threshold population. The following 10-s step of variable amplitude conditions the low-threshold population, and the last pulse, equal in amplitude to the first, reveals the much smaller population that remains active after the conditioning step. When the same protocol utilizes saturating pulses (engaging the entire channel population) and a broader range of conditioning steps, a larger fraction of the population remains active. The experiment shows that the low-threshold population in PA is especially prone to inactivation. Red arrows indicate current levels produced by the remaining channel population at the end compared with the amplitude of response to the initial pulse (black arrows).

Genomic databases predict one MscL and two MscS-like channels in PA

Searching the PA14 gene and protein databases with EC MscL and MscS sequences revealed one MscL-like protein, PA14_61050 (PaMscL), with 64% amino acid identity to EcMscL and two MscS-like proteins, PA14_57110 (PaMscS-1) and PA14_65040 (PaMscS-2), with 36% and 29% identity to EcMscS, respectively. Four additional proteins belonging to the MscS family, but with lower overall homology, were also found (Table S1).

Based on the amino acid sequence alignments (Fig. S6), PaMscL is predicted to have a more hydrophobic gate than EC MscL (V23→I substitution; 10), a possibly lower conductance, a different pattern of charges in the N-terminal and periplasmic domains, and increased flexibility in the TM2 helix (A95→G). An additional two prolines in the TM2-S3 linker suggest that there must be a lower probability of helix formation in this generally disordered segment (Steinbacher et al., 2007).

Alignments of MscS homologues (Fig. S6) reveal a highly conserved organization and preservation of interdomain contacts. There are several substitutions in critical domains, which may change the conductance, activation thresholds, and propensity to inactivation. For instance, the double glycine motifs in the “hinge 1” locus of both PaMsc-1 and PaMscS-2 (corresponds to single G121 in EcMscS) predict that these channels may have a less stable open state and potentially be more prone to inactivation or may exhibit a slow recovery (see Fig. 8 and accompanying text).

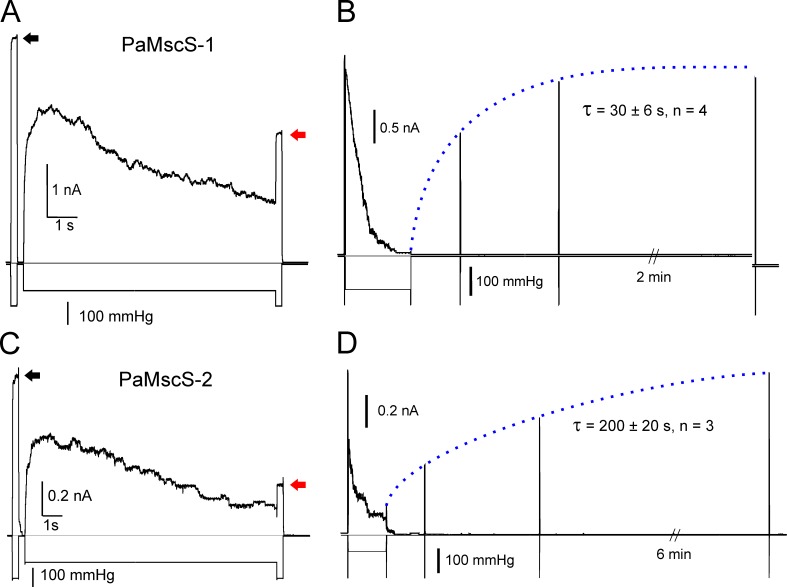
Figure 8.

The inactivation and recovery of PaMscS-1 and PaMscS-2. (A and C) Pulse-step-pulse protocols show that both MscS-like homologues from PA inactivate. The degree of inactivation is determined as the ratio of current at the end (red arrows) to the initial test pulse response of full population (black arrows). PaMscS-2 displays ∼60% inactivation, which is more than PaMscS-1 and about twice what is seen in its EC counterpart. (B and D) The recovery from inactivation shows that PaMscS-2 recovers much more slowly than PaMscS-1, indicating a more stable inactivated state.

Properties of single channels from PA: Conductances and ionic selectivity

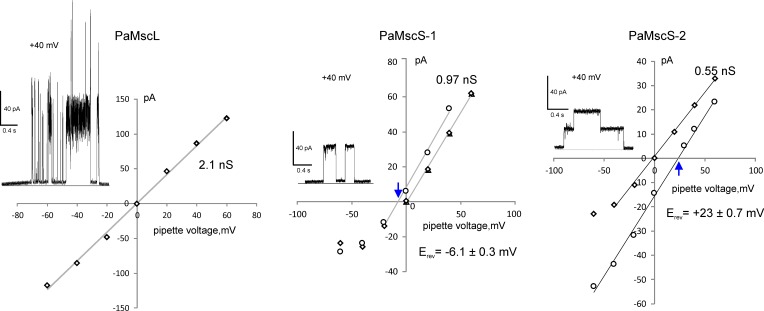
Open reading frames coding for PaMscL, PaMscS-1, and PaMscS-2 were PCR-amplified and cloned into the pB10d expression vector. Each of the three proteins were expressed in MJF641 EC spheroplasts. I-V curves of the cloned PA channels were obtained under both symmetric and asymmetric ionic conditions to determine single channel conductance and selectivity, respectively (Fig. 6). The slope of the I-V curve under symmetric conditions (200 mM KCI, bath/pipette) revealed PaMscL has a conductance of 2.1 nS, which was 30% less than EcMscL. Under asymmetric conditions (100:500 mM KCl), no shift of I-V curve was observed, indicating that PaMscL is nonselective (unpublished data). PaMscS-1 has a conductance of ∼1 nS, which is similar to its single EC orthologue, EcMscS. On the other hand, PaMscS-2 has a relatively low conductance of 0.55 nS. In an asymmetric solution containing 5:1 gradient of KCI, the reversal potentials of both PaMscS channels shifted toward the equilibrium potential for CI⁻, indicating that PaMscS-1 and PaMscS-2 favor anions over cations with P_CI/P_K ∼1.5 and 4.4, respectively.

Figure 6.

Current to voltage relationships for unitary currents measured for PaMscL, PaMscS-1, and PsMscS-2. The examples of single-channel currents are shown as insets in each panel. Based on the Goldman equation, the E_rev shift for PaMscS-1 in response to 1:5 (pipette/bath) gradient of KCl (relative to symmetric conditions) of −6.1 mV predicts the permeability ratio P_CI/P_K of 1.5. For PaMscS-2, the E_rev shift of 23 mV (5:1 pipette/bath gradient) predicts P_CI/P_K of 4.4. Reversal potentials are indicated by blue arrows. The three MS channels were expressed in EC MJF 641 cells and recorded under symmetric and asymmetric ionic conditions. In the experiment with PaMscS-2, the gradient was inverted (5:1) because, for yet unknown reasons, no channel activity was observed in the opposite configuration.

Determination of tension sensitivities for PA MscS-like channels and their spatial and energetic parameters for activation

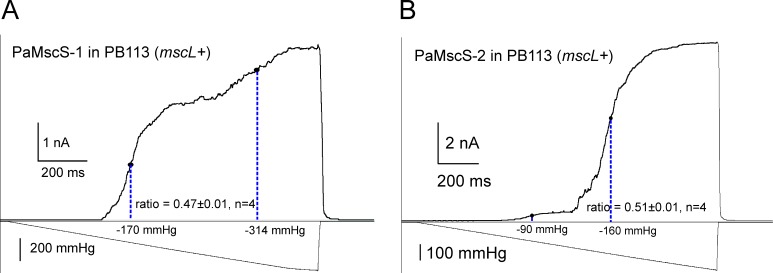
Without the ability to visualize small spheroplast patches, we used EcMscL present in the PB113 EC strain to gauge tension midpoints for heterologously expressed PaMscS-1 and 2. Having a well-characterized MS channel as an internal standard in the same patch helps to convert the pressure into tension scale. At a constant patch curvature, ratios of midpoint tensions and pressures (γ_0.5/ΔP_0.5) should stay constant for any channel. Subjected to pressure ramps, PaMscS channels activate first, forming the first wave of current, which is followed by a second wave of MscL (Fig. 7) known to half-activate at 12 mN/m. Based on p_MscS/p_MscL ratios of 0.47 and 0.51, the tension midpoints for PaMscS-1 and PaMscS-2 in this particular setting were determined to be 5.6 and 6.1 mN/m. The activating tension for PaMsc-1, therefore, is slightly lower than that for EC MscS previously estimated between 6.5 (Sukharev, 2002) and 7.8 (Belyy et al., 2010) mN/m. Likewise, the midpoint of PaMscL was gauged against EcMscS in PB103 mscL⁻ strain carrying a native copy of MscS. The p_EcMscS/p_PaMscL ratio in this experiment was 0.54 ± 0.01 (n = 3), which is exactly the ratio measured in WT EC spheroplasts (traces not depicted). Thus, PaMscL has the same tension midpoint as EcMscL (i.e., ∼12 mN/m; Sukharev et al., 1999; Moe and Blount, 2005).

Figure 7.

Midpoint determination of PA MscS-like channels using MscL as an intrinsic tension gauge. (A and B) The homologues PaMscS-1 (A) and PaMscS-2 (B) were expressed in PB113 EC cells carrying native MscL. Each of these channels generates a “wave” of current with its own midpoint. The p_MscS/p_MscL midpoint ratios for both MscS homologues (∼0.5) are slightly lower than that of EC MscS (∼0.6), indicating that these channels open at lower tension. PaMscS-2 is expressed at a much lower level despite full induction.

Having midpoint tensions determined for each channel, the pressure scale on the activation curves was converted to tension. The open probability of the channel can then be fitted to the two-state Boltzmann function P_o = 1/(1 + exp((ΔE − γΔA)/kT)) to extract the free energy difference between open–closed state (ΔE) in the absence of tension and the in-plane expansion of the channel (ΔA) associated with opening (Fig. S7). The estimated spatial and energetic parameters for PaMscS-1 and 2 based on multiple independent patches were very similar. The free energy difference and the in-plane expansion of the closed to open state transition were determined to be 17.1 ± 0.5 kT, 11.0 ± 0.5 nm² for PaMscS-1 (n = 16) and 15 ± 2 kT, 10.0 ± 1 nm² for PaMscS-2 (n = 4), which are comparable with the gating parameters earlier reported for EC MscS (Akitake et al., 2005; Boer et al., 2011). See Table 2 for a summary.

Table 2. The summary of experimentally determined parameters for the two PaMscS channels in comparison to EC MscS.

Channel	ΔE	ΔA	P0.5MscS/P0.5MscL	Conductance	Selectivity PCI/PK	Inactivation	Recovery time
	kT	nm2		nS		%	s
EC MscS	∼20–28 (Akitake et al., 2005)	∼12–14 (Akitake et al., 2005; Boer et al., 2011)	0.58 ± 0.02 (n = 12)	∼1–1.1 (Sukharev, 2002)	∼1.5 (Sukharev, 2002)	36 ± 5 (n = 15)	1.5–3 (Akitake et al., 2005)
PaMscS-1	17.1 ± 0.5 (n = 16)	11.0 ± 0.5 (n = 16)	0.47 ± 0.01 (n = 4)	0.96 ± 0.02 (n = 3)	∼1.5 (n = 3)	40 ± 8 (n = 10)	30 ± 6 (n = 4)
PaMscS-2	15 ± 2 (n = 3)	10 ± 1 (n = 3)	0.51 ± 0.01 (n = 4)	0.55 ± 0.02 (n = 3)	∼4.4 (n = 3)	64 ± 3 (n = 7)	200 ± 70 (n = 3)

The degree of inactivation was measured at saturating pressure after a 10-s conditioning pressure step of amplitude around p_0.5.

PaMscS-1 and 2 channels exhibit inactivation and slow recovery

In Fig. 5, we present traces recorded in native patches that illustrate partial inactivation of the low-threshold PA channel population. This low-threshold population must include both PaMscS-1 and 2, which were individually tested for inactivation in MJF641 spheroplasts (Fig. 8, A and B). As previously, the amount of inactivation for Pa MS channels was probed by a pulse-step-pulse protocol (Akitake et al., 2005, 2007; Belyy et al., 2010). After a 10-s conditioning step (at p_1/2), PaMscS-1 displayed 30 ± 5% inactivation, whereas PaMscS-2 showed 60 ± 3% inactivation, which is about twice what was observed in EC MscS (Kamaraju et al., 2011). In the recovery protocol, after the population was partially inactivated, the conditioning pressure was dropped to zero and the recovery process was monitored with a train of short test pulses over time (Fig. 8, C and D). The characteristic times (τ) of recovery were 30 ± 6 s for PaMscS-1 and 200 ± 60 s for PaMscS-2 (0.5 and 3.4 min, respectively). The time required for full recovery after complete inactivation of PaMscS-1 was ∼5 min, whereas full recovery of PaMscS-2 took over 10 min.

The relative ability of PA channels to rescue EC MJF641 from osmotic down-shock

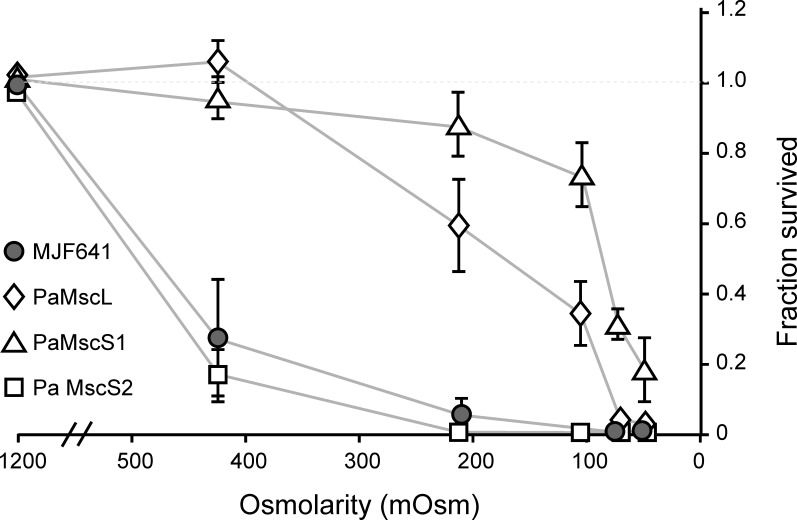
The electrophysiological characterization of the PA channels revealed broad variations in terms of conductivity, inactivation, and time needed for full recovery from the inactivated state. This prompted us to investigate the functional requirements that a MS channel should have to be a good emergency valve. We heterologously expressed PaMscL and PaMscS-1 and 2 in the channel-free MJF641 strain and monitored their individual contribution to osmotic survival. As long as the osmotic down-shock is <1,000 mOsm, both PaMscL and PaMscS-1 were able to rescue the unprotected strain (Fig. 9). Notably, PaMscS-2 was unable to save MJF641 cells from osmotic down-shock regardless of its magnitude.

Figure 9.

Relative ability of PA MS channels to rescue EC MJF641 from osmotic down-shock. At moderate osmotic down-shocks, PaMscL and PaMscS-1 were good at rescuing the MJF641. Surprisingly, PaMscS-2 did not serve as a good emergency valve, and the cells displayed poor survival statistically indistinguishable from channel-free MJF641. The plate counts are shown as means with standard deviations (n = 8).

Discussion

In this paper, we present the first multifaceted phenomenological study of the emergency osmolyte release system in WT PA in comparison with EC. The data reveal the overall kinetics of cell equilibration with the hypoosmotic environment and some information on the molecular components mediating fast permeability response, such as predominant channel types, their densities, conductances, propensities to inactivation, and rates of recovery. At the same time, the work outlines several unknowns that will be needed for a quantitative model of the MS channel–mediated rescuing mechanism.

A better osmotic survival of PA compared with EC under severe down-shocks correlates with a faster osmolyte release process recorded with a stopped-flow technique. The scattering traces (Fig. 1) reveal the initial swelling period followed by a falling phase reflecting the process of osmolyte release, which is well fitted with a squared exponential equation (Eq. 1) as shown in supplemental Figs. S3 and S4. The swelling period shortens and the rates of release monotonously grow with the magnitude of down-shock in both cultures. Because PA cells are considerably smaller (Fig. 2) and have a higher SA:V ratio, both swelling and release processes in PA are expected to be faster. Indeed they are, but not dramatically. One of the reasons is likely to be lower water permeability of the PA envelope estimated from the up-shock experiments (Fig. 2). PA has a phospholipid composition somewhat different from EC (Benamara et al., 2011), which may explain the difference; both species contain aquaporin and glyceroporin genes, but the contributions of these facilitators to the swelling speed are unknown. In any event, lower water permeability is beneficial as it reduces the water influx, allowing more time for osmolyte release.

The osmotic rescuing mechanism implies that the overall permeability of the tension-activated release system is sufficient to counteract the water influx driven by an abrupt osmotic downshift. As tension builds up, the MscS and MscL channels open gradually and, if water keeps coming in, more channels open and start dissipating the concentration and pressure gradients faster, thus acting in a negative feedback manner. At high shocks, when all channels are engaged (release rate approaches saturation; Fig. 1 D), water influx may overwhelm the “sieving” capacity of the channels, and a pressure surge above the limit of the envelope’s mechanical stability would damage the cell. As suggested by traces in Fig. 1 (B and C), the slope and duration of scattering decrease reflect the fraction of channels that are open. Not only does the rate of release increase with the magnitude of shock, but the fraction of released osmolytes also increases, as seen from the total amplitude of the scattering signal as compared with its level at the end. Based on the amplitude of the scattering signal change under the strongest shocks (Fig. 1, B and C), PA and EC lose ∼20% and 30% of their dry weight with characteristic times of 28 and 50 ms, respectively. In PA, the release rate steadily increases and saturates only at the highest shocks (Fig. 1 D). In EC, in contrast, we observe an earlier saturation of the release rate in that region, suggesting that the total permeability of channel population has reached its capacity, which correlates with the earlier onset of viability decline (Fig. 1 A).

To dissect the osmolyte release system in finer detail, we devised a procedure for PA giant spheroplast preparation and patch-clamp recording in situ. The traces recorded with linear pressure ramps reveal more gradual conductance increase in PA (Fig. 4 and Fig. S5) with a much smaller fraction of low-threshold MscS-like component compared with EC. Table 1 indicates that the relative contributions of MscS and MscL populations are different in EC and PA. Although EC uses MscS and MscL in comparable densities, PA relies primarily on its own MscL, which is one third less conductive than EcMscL. The smaller size of PA cells should also be factored into the rescuing mechanism. It has been noted previously that surface to volume ratio does play a role in metabolic activity and environmental survival of bacteria (Roszak and Colwell, 1987). With a larger surface to volume ratio, smaller cells may undergo faster swelling, leaving less time for osmolyte ejection and thus making them more vulnerable. On the other hand, by the same token, a smaller volume can be cleared from permeable substances faster. The smaller cells, because of higher curvature, also have a “Laplacian” advantage of sustaining lower membrane tension at a given pressure gradient. The scaling of swelling and release rates with area and volume still need to be measured and compared with theoretical predictions.

The analysis of the PA14 genome identified one MscL-like and two MscS-like proteins. Four more putative proteins from the MscS family, homologous to EC MscK, YbdG, YbiO, and YjeP were identified, but no obvious homologue of YnaI was found (Table S1). We cloned PaMscL and the two closest MscS homologues designated as PaMscS-1 and 2. As predicted, PaMscL had a lower unitary conductance (2.1 nS) compared with EcMscL (3.1 nS), possibly because of bulkier side chains lining its hydrophobic gate. PaMscS-1 was very close to its EC orthologue (36% identity) in terms of conductance, selectivity, and inactivation; however, it exhibited longer recovery. PaMscS-2 was characterized as having half the conductance of its EC orthologue, considerably stronger anionic selectivity, a strong propensity to inactivation, and a very long (5–6 min) recovery. In EC spheroplasts, PaMscS-2 was functionally expressed at lower levels and in osmotic experiments was unable to rescue MJF641 cells.

According to thermodynamic analysis of activation curves (Fig. S7), PaMscS-1 and 2 expand by ∼12 nm² in the course of opening transition (Table 1). Both channels have a more flexible TM3 helix because of a regular glycine hinge in position 113 and a double-glycine hinge in position 121 (see alignment in Fig. S6). The mechanism likely proceeds through buckling of the TM3 helix at G121, which leads to adaptive closure and then, if tension still persists, subsequent kinking at G113, resulting in complete inactivation (Akitake et al., 2007). This stronger propensity to inactivation in the low-threshold MscS-like channels in PA does not seem to be an accident. The PA cells are characterized by smaller volume and larger surface to volume ratio. If the channels were noninactivating, moderate near-threshold tensions would prompt these channels to flicker between closed and open states, washing away vital osmolytes. The inactivation mechanism, which disengages the channels at persisting moderate tension, minimizes futile dissipation of vital gradients (Boer et al., 2011). We must note that the dominant high-threshold PaMscL does not inactivate. From the relative densities of MscS and MscL channels (Table 1), we may conclude that PA relies primarily on its MscL, which activates at strong shocks and serves as the main permeation path for osmolytes. MscL opening will release osmolytes and water, thus driving tension down to the MscL threshold. The system obviously requires the low-threshold MscS channels to further reduce membrane tension to levels considerably below the threshold for MscL to prevent its futile flickering. Although present at low density, MscS channels are able to “disarm” MscL and upon reaching their own tension threshold, they are able to inactivate, which appears to be the proper way to terminate the massive permeability response.

What do we need to know to be able to come up with a quantitative model that would produce the time course of tension in the inner membrane as a function of osmotic shock and predict whether the shocked cell will be rescued or damaged? There are many parameters that are still unknown. The amount of peptidoglycan layer prestretch and the surplus of inner membrane area under constitutive turgor pressure are unknown. The changes of cell geometry during osmotic cell swelling have been recently described for relatively slow changes of osmolarity (Rojas et al., 2014; Buda et al., 2016), but not for millisecond rates. Although it is known that many compatible osmolytes and other small molecules leave the cell in the course of osmotic permeability response (Wood et al., 2001), the permeabilities of MscS and MscL to specific osmolytes have not been reported. It is not clear whether the densities of channels assayed by patch clamp in giant spheroplasts (Rowe et al., 2013) precisely reflect the densities in unperturbed actively growing cells (Bialecka-Fornal et al., 2012). Nevertheless, the presented results have moved us one step closer to a better mechanistic understanding of physiological permeability response to osmotic down-shock and have given some explanation to the higher osmotic stability of highly adaptable PA as compared with enteric EC.