A comparative evaluation of models to predict human intestinal metabolism from nonclinical data

Abstract

Extensive gut metabolism is often associated with the risk of low and variable bioavailability. The prediction of the fraction of drug escaping gut wall metabolism as well as transporter‐mediated secretion (F _g) has been challenged by the lack of appropriate preclinical models. The purpose of this study is to compare the performance of models that are widely employed in the pharmaceutical industry today to estimate F _g and, based on the outcome, to provide recommendations for the prediction of human F _g during drug discovery and early drug development. The use of in vitro intrinsic clearance from human liver microsomes (HLM) in three mechanistic models – the ADAM, Q _gut and Competing Rates – was evaluated for drugs whose metabolism is dominated by CYP450s, assuming that the effect of transporters is negligible. The utility of rat as a model for human F _g was also explored. The ADAM, Q _gut and Competing Rates models had comparable prediction success (70%, 74%, 69%, respectively) and bias (AFE = 1.26, 0.74 and 0.81, respectively). However, the ADAM model showed better accuracy compared with the Q _gut and Competing Rates models (RMSE =0.20 vs 0.30 and 0.25, respectively). Rat is not a good model (prediction success =32%, RMSE =0.48 and AFE = 0.44) as it seems systematically to under‐predict human F _g. Hence, we would recommend the use of rat to identify the need for F _g assessment, followed by the use of HLM in simple models to predict human F _g. © 2017 Merck KGaA. Biopharmaceutics & Drug Disposition Published by John Wiley & Sons, Ltd.

Introduction

The oral route is the most common route of drug administration due to its convenience and lower medical cost compared with other routes. Furthermore, oral dosing tends to enhance patient compliance. Following oral administration, the drug should be dissolved in the gastrointestinal (GI) fluid and then pass through the intestinal wall and the liver to enter the systemic circulation. Oral bioavailability (F) is thus defined as:

$$F=F_a\bullet F_g\bullet F_h$$ (1)

Where F _a is the fraction of oral dose absorbed from the intestinal lumen; F _g is the fraction of drug that escaped both intestinal first‐pass metabolism (biotransformation in the gut and/or in the intestinal wall) and transporter‐mediated secretion to become available in the hepatic portal blood; and F _h is the fraction of drug escaping hepatic first‐pass elimination (biotransformation and/or biliary secretion). Low bioavailability drugs are associated with higher patient variability 1, require large doses that cause difficulties for patients to swallow, need expensive formulations and may increase the body burden, thus impacting the benefit–risk profile for patients. Candidate drugs with poor bioavailability are therefore undesirable as they tend to fail in the clinical developmental phase. Poor solubility or permeability and high first‐pass metabolism from intestine and liver are the major reasons for low bioavailability. While optimization efforts to maximize solubility and permeability and to minimize hepatic first‐pass metabolism have been very successful 2, it has been difficult to assess the need to optimize a lead series with respect to intestinal first‐pass metabolism.

The intestine is the most important extrahepatic site for drug biotransformation with numerous pathways of metabolism involving both phase I and phase II reaction enzymes. An analysis of 309 drugs with intravenous (i.v.) and oral clinical pharmacokinetics (PK) noted that around 30% of the drugs studied had an intestinal extraction greater than 20% 3. A majority of these drugs are metabolized by the Phase I enzyme, CYP3A, which has a dominant role in the enterocytes, accounting for 82% of the total intestinal CYP450 enzymes 4. CYP2C9 and CYP2C19 are also expressed in the small intestine but to a lower extent (14% and 2%, respectively). The intestine is the first organ encountered by a drug following oral dosing. In addition, the intestinal transit time is long (i.e. up to 24 h in human) and pre‐systemic metabolism is not limited by plasma protein binding or blood perfusion rates, but by permeability across enterocytes 5. Hence, a high concentration of drug in the enterocytes during absorption may lead to a high metabolic extraction before the drug enters the liver. Additionally, P‐glycoprotein (P‐gp) is highly expressed in intestinal epithelial cells and may reduce drug absorption. However, the effect of P‐gp on drug absorption is not quantitatively important, especially for highly permeable compounds 6, 7, 8. Furthermore, soluble drugs given at higher doses may saturate efflux transporters, which may explain the limited effects on F _g 9. Kadono et al. suggested that the effects of P‐gp on the fraction of drug absorbed and the intestinal availability are substantially minor for highly permeable compounds 10.

Many in vitro and in vivo models for estimating the human intestinal first‐pass metabolism have been reported in the literature. A detailed review of the different approaches is beyond the scope of this article, but can be found elsewhere 11. In vitro systems that have been proposed for the estimation of intestinal extraction include human intestinal microsomes (HIMs), human intestinal S9 fractions, recombinant systems expressing P450 enzymes and human liver microsomes (HLMs), amongst others. Intestinal subcellular fractions (S9 homogenates or HIM) have been established to quantitatively characterize and extrapolate intestinal metabolism 12, 13, 14, 15, 16. However, there is a lack of standardized methodology and consensus for the optimal isolation of subcellular fractions in the intestine and preparation of enterocytes. Furthermore, prediction using these systems requires the use of expensive co‐factors for optimal enzyme activity, but only limited information is currently available on the physiological concentrations of these cofactors in the intestine. Another limitation is that fractions do not contain a full complement of metabolic enzymes, especially of phase II metabolism and lack uptake and efflux transporters. The lack of experimentally defined enzyme abundance and enzyme activity scaling factors further limits the utility of in vitro systems for the estimation of intestinal metabolism. Accordingly, in vitro intrinsic clearance (CL _int) obtained in HLM can be used to predict intestinal metabolism when differences in enzyme abundance between liver and intestine are taken into account. Indeed, the rate of enzyme activity of the hepatic and intestinal CYP3A enzymes are considered similar 17, 18 and reasonable approximations of intestinal intrinsic clearances may be extrapolated from values obtained using recombinant enzyme or HLM 14, 15. In addition, recombinant P450, as well as liver microsomes and hepatocytes, have the advantage of being used routinely for predicting the hepatic clearance.

In vitro scaling and modeling methods with varying levels of mechanistic complexity were developed in order to predict in vivo human F _g 19, 20, 21. The Q _gut model was proposed by Yang et al. to determine F _g 14, 15. The intestine is viewed as a single tissue compartment which includes a flow term (Q _gut) accounting for both permeability through the enterocyte membrane and the villus blood flow as factors that influence the exposure to the metabolic enzyme. This simple approach requires only in vitro CL _int and cell permeability data to investigate intestinal metabolism. In their Competing Rates model, Benet et al. viewed the gut extraction ratio as being a function of the rate constant for gut metabolism divided by the sum of the rate constants for the competing processes of metabolism and absorption in the enterocyte 22. Both the Q _gut and the Competing Rates models fail to consider transporter‐mediated secretion that could impact the gut extraction of substrates of transporter proteins. Sophisticated physiology‐based models of first‐pass intestinal drug metabolism have been elaborated by Pang et al. with the implementation of the Segregated Flow Model (SFM) and the Segmental Segregated Flow Model (SSFM) 23, 24, 25. The SFM takes tissue layers and distributions in blood supply into account in describing the intestinal absorption where the drug flows to a non‐absorbing layer and absorbing enterocyte layer. Built on the SFM, the SSFM divides the intestine into three segments of equal lengths and flows, describing heterogeneity in segmental transporter and metabolic functions. However, the immediate value of such models in predicting F _g is limited by their complexity and the difficulty in determining many parameters defining the kinetics of active transport in the absence of information on the absolute abundance of uptake and efflux transporter proteins. Nevertheless, major features of the SSFM are present in the Advanced Dissolution Absorption and Metabolism (ADAM) module of the Simcyp Population‐Based Simulator® which has a user‐friendly interface and is widely available in academia and industry 26, 27, 28. The ADAM model is based on the Compartmental and Transit (CAT) model 29. It is a multi‐compartmental physiologically based pharmacokinetic (PBPK) model that incorporates both physiological and compound‐specific parameters. It divides the human GI tract into nine segments, from stomach to colon, which are different in terms of size, abundance of enzymes and transporter, transit time, pH and bile salt concentration. The ADAM model also takes into account inter‐individual variability in the physiological parameters 27, 30. In this review, we focus on the ADAM, Q _gut and Competing Rates models that are commonly available for predicting F _g in an industrial context, and assume negligible contributions to F _g from transporter‐mediated secretion and reabsorption. The characteristics of the three models are described in Table 1.

Table 1.

Comparison of models for intestinal metabolism investigated in this study 11, 13

	ADAM	Q gut	Competing Rates
Equations	Schematic representation of the Simcyp's ADAM model in which drug absorption from each segment is described as a function of release from the formulation, dissolution, precipitation, luminal degradation, permeability, metabolism, transport and transit from one segment to another	$Q_{\mathit{gut}}=\frac{Q_{\mathit{\text{villi}}}\bullet {\mathit{CL}}_{\mathit{\text{perm}}}}{Q_{\mathit{\text{villi}}}+{\mathit{CL}}_{\mathit{\text{perm}}}}$ $F_g=\frac{Q_{\mathit{gut}}}{Q_{\mathit{gut}}+f_{u,g}\bullet {\mathit{CLu}}_{\mathit{int},g}}$	Simplified Q gut $F_g=\frac{{\mathit{CL}}_{\mathit{\text{perm}}}}{{\mathit{CL}}_{\mathit{\text{perm}}}+{\mathit{CLu}}_{\mathit{int},g}}$
Assumptions	– Same CYP enzyme activity in the liver and in the intestine, corrected for difference in enzyme abundance	Same CYP enzyme activity in the liver and in the intestine, adjustment for abundance – f u,g = 1	– Same CYP enzyme activity in the liver and in the intestine, adjustment for abundance – High blood flow or low permeability or low metabolism
Strengths	– Integrate permeability, solubility data and physiological parameters – Regional differences and individual variability can be accommodated	– Simple, easily accessible – Villus blood flow and cellular permeability drive prediction of F g	– Simple – F g estimated by combining the rate constants for absorption (CL perm) and gut wall metabolism (CL int)
Limitations	– Validity of assumptions difficult to establish for all compounds – Poor quality of input data could undermine the value of the complex model	– Valid for CYP3A compounds – Inaccuracy for high intestinal extraction drugs	– Valid for CYP3A compounds – Inaccuracy for high intestinal extraction drugs

During preclinical development, animal models such as mice, rats, dogs and non‐human primates are employed to understand the PK characteristics of new candidate drugs. Compared with in vitro models, in vivo models integrate the physiologic architecture of the small intestine and physiologically relevant expression profiles of enzymes, cofactors and transporter proteins. Among the preclinical species, the rat provides a good indication of the human oral absorption for small molecules 8, 31. Due to species differences in the isoform, regional abundances and activities of drug metabolizing enzymes and transporters 32, the rat may not be a good preclinical model for predicting human intestinal loss 33. However, for a high permeability drug, intestinal extraction is not limited by intrinsic clearance of the drug in the enterocytes but rather by permeability. Consequently, differences in enzyme isoforms and their activity may have little impact on intestinal extraction and the rat may serve as a good model for human F _g, at least for high permeability compounds. A previous study has shown a fairly good correlation between rat and human F _g derived from the in vivo profiles of CYP3A substrates, and between rat and human F _g derived from intestinal microsomes for drugs predominantly metabolized by CYP3A 12, 13.

The objective of this work is to compare the performance of three mechanistic models – the ADAM model implemented within Simcyp®, the Q _gut model and the Competing Rates model – for predicting human F _g assuming that the effect of P‐gp in epithelial cells is negligible. CL _int derived from both in vitro data and in vivo PK was employed in the three mechanistic models to predict F _g for drugs cleared predominantly by CYP 450 s in order to recommend the best in vitro system and mechanistic model to implement during drug discovery and early development. The utility of rat as a model for human F _g has also been explored.

Material and Methods

Compound selection for studying intestinal metabolism

Compound selection was based on previous literature studies indicating intestinal metabolism. The human bioavailability databases published by Lombardo et al. (2013) 34, Musther et al. (2014) 35, Bueters et al. (2013) 33 and Varma et al. (2010) 3 were used for this purpose. An inclusion criterion in this study was the availability of i.v. and oral single dose PK data in humans and rats to enable the deconvolution of F _g. When i.v. and oral PK data were available for multiple doses, only those that resulted in similar systemic concentrations were selected. Prodrug compounds were excluded due to difficulties in assessing the extent of conversion to the active drug by hydrolysis. Drugs whose elimination is well known to involve non‐CYP enzymes and transporters were also excluded. After reviewing the original data and references, drugs undergoing UGT‐mediated biotransformation (>10%) were excluded so that the selected drugs are predominantly metabolized by CYPs.

Experimental methods

Rat plasma protein binding

The protein binding of test compounds was determined by ultrafiltration using serum from rat. The test items (final concentration 5 μm) were incubated in triplicate with three different serum dilutions (1:2, 1:5 and 1:10) for 30 min at 37°C using slight agitation. After the incubation, the 96‐well filter plates were centrifuged for 45 min at 3500 rpm and 37°C; 25 μl portions of filtrate samples were treated with 50 μl of ethanol and 50 μl of internal standard solution and analysed by LC–MS/MS. The fraction unbound was calculated from the drug concentrations in the filtrate samples.

Intrinsic metabolic clearance determined in human liver microsomes

Human liver microsomes were purchased from Xenotech‐Sekisui and constituted a pool of samples from more than 200 individuals. Microsomes (final concentration 0.5 mg/ml), 50 mm phosphate buffer pH 7.4, and compound (final concentration 1 μm) were added to the assay plate and allowed to pre‐incubate for 5 min at 37°C. The reaction was initiated by the addition of NADPH (final concentration 1.5 mm) and the plate was shaken at 800 rpm at 37°C. After 0, 5, 10, 20 and 30 min, aliquots were taken, and the reaction was stopped using cold acetonitrile. The samples were centrifuged at 4000 rpm for 30 min at 4°C and analysed by LC–MS/MS. Four test compounds were pooled for analysis. The in vitro CL _int was calculated from the rate of compound disappearance. Nonspecific binding of drugs to microsomal protein (fu_inc) was predicted using the following equation 36:

$${\mathit{fu}}_{\mathit{inc}}=\frac{1}{1+C\bullet {10}^{0.072\bullet \mathit{\text{logP}}/D2+0.067\bullet \mathit{\text{logP}}/D-1.126}}$$ (2)

Where C is the microsomal protein concentration reported in the in vitro studies, logP represents the logarithm of the ratio of the concentration of unionized drug partitioned between octanol and water and logD represents the logarithm of the ratio of the concentration of all drug species (ionized and unionized drugs) distributed between octanol and water at pH 7.4. The unbound microsomal intrinsic clearance (CL _int,u) was obtained by dividing the measured CL _int by the fu_inc.

Solubility in fasted state simulated intestinal fluid (FaSSIF)

A 2 ml solution of drug concentration 1 mg/ml in FaSSIF (pH 6.5) was prepared and transferred to a 5 ml Whatman Uniprep Syringeless Filter. The resulting suspension was shaken for 24 h and 450 rpm at 37°C. After 24 h, the suspension samples were filtered and quantified by LC‐DAD. The pH was checked at the end of the experiment.

In vitro permeability

The Caco‐2 cells (TC7 clone) were maintained in DMEM in an atmosphere of 8.5% CO₂. For transport experiments, 0.125 × 10⁶ cells/well were seeded on polycarbonate filter inserts and allowed to grow and differentiate for 10–14 days before the cell monolayers were used for experiments. Drug transport experiments were carried out using a cocktail approach with cyclosporine A (10 μm) as a transporter inhibitor in order to obtain an estimate of the passive permeability. Up to five test items and reference compounds were dissolved in Hank's balanced salt solution (HBSS) at pH 7.4 to yield a final concentration of 1 μm. The assays were performed in HBSS containing 25 mm HEPES (pH 7.4) in an atmosphere of 5% CO₂ at 37°C. Prior to the study, the monolayers were washed in pre‐warmed HBSS. At the start of the experiments, pre‐warmed HBSS containing the test items was added to the donor side of the monolayer and HBSS without test items was added to the receiver side. The plates were shaken at 150 rpm at 37°C during the experiment. After 2 h, the Transwell® insert containing the monolayer was carefully removed and placed in a new plate, and aliquots of both the receiver and donor sides were taken and diluted with an equal volume of ACN containing the internal standard. The mixture was centrifuged and the supernatant analysed by LC–MS/MS. The apparent permeability coefficients (Papp) were calculated using the formula Papp = (Vrec/A × C ₀donor) × dCrec/dt × 10⁶ with dCrec/dt being the change in concentration in the receiver compartment with time, Vrec the volume of the sample in the receiver compartment, C ₀donor the concentration in the donor compartment at time 0, and A the area of the compartment with the cells.

Prediction of permeability from physicochemical properties

Predicted effective permeability (P _eff) values were estimated using the following equation 37:

$$log{P}_{\mathit{eff}}=-3.061+0.19\bullet ClogP-0.01\bullet \mathit{PSA}-0.245\bullet \mathit{HBD}$$ (3)

Where ClogP is the calculated octanol–water partitioning coefficient, PSA is the polar surface area, and HBD is the number of hydrogen bonds donors. ClogP, PSA and HBD were collected from literature (references are provided in Supplemental Table S1) for all compounds investigated.

Estimation of human in vivo F_g using human in vivo PK data

In‐house PBPK model

A generic whole body PBPK model built in Matlab® (MathWorks Inc., Natick, MA, USA) and previously described 38, 39 has been used to simulate the PK profiles. This model has 14 organs represented as compartments and linked together by the arterial and venous blood compartments.

Fraction absorbed F_a

Using the in‐house PBPK model, the fraction absorbed was estimated for a range of hypothetical in vitro solubility and permeability values (from lowest to highest values). The predicted absorbed fractions were used as a guiding tool to select the method for determining human F _g. The indirect method was applied for drugs whose permeability and solubility would lead to a fraction absorbed greater than 0.9, and the PBPK modeling was used for drugs which are likely to have absorption issues defined as F _a < 0.9.

Estimation of human in vivo F_g using the indirect method

The indirect method of determining gut extraction relies on the plasma concentration–time profiles after i.v. and oral administration of the drug. Knowing the total clearance (CL) and the renal clearance (CL _r), the metabolic clearance (CL _m) can be calculated:

$$\mathit{CL}=\frac{{\mathit{\text{Dose}}}_{\mathit{iv}}}{{\mathit{AUC}}_{\mathit{iv}}}$$ (4)

$${\mathit{CL}}_m=\mathit{CL}-{\mathit{CL}}_r$$ (5)

Assuming negligible metabolism in enterocytes following i.v. administration, the metabolic clearance of a drug after i.v. dose reflects only hepatic clearance (CL _h) in the absence of biliary clearance:

$${\mathit{CL}}_h=\mathit{CL}-{\mathit{CL}}_r$$ (6)

The F _h can then be calculated from the hepatic extraction (E _h) or the hepatic clearance and the liver blood flow (Q _h).

$$F_h=1-E_h=1-\frac{{\mathit{CL}}_h}{Q_h}$$ (7)

To estimate F _g, F _a is assumed to be 1 in Equation (1).

The human liver blood flow was taken to be 21 ml/min/kg for human 40. If the calculated F _g value exceeded 1, it was set to 1 indicating no intestinal metabolism.

Estimation of human in vivo F_g using the in‐house PBPK model

The estimation of F _g of a compound from its in vivo i.v. and oral concentration–time profiles using the in‐house PBPK model was described by Peters 38 and by Karlsson 12. The i.v. and oral plasma profiles were digitized from the graphs using a script originally written by Tushar Bhangale (Bioengineering Department, University of Washington, Seattle, USA) in Matlab®. The i.v. perfusion data were corrected to an i.v. bolus by subtracting the data during perfusion time in order to have a better fit for the absorption phase.

Estimation of human F _g using in vivo PK‐derived CL _int in the ADAM, Q _gut and Competing Rates models

In order to compare the models that estimate F _g using CL _int as input, it is important to eliminate the uncertainty arising from in vivo relevance of in vitro data. Therefore, hepatic CL _int derived from in vivo human clearance were used.

The ADAM model within Simcyp®

Simulations were performed using the Simcyp Simulator (Version 15, Simcyp Ltd, Sheffield, UK). Files with physicochemical parameters (molecular weight, logP _o:w, acid/base status, and pKa), permeability, fraction unbound in plasma and blood/plasma ratio (Tables 2 and 3) were created for each compound. The human jejunal effective permeability (P _eff) was predicted from Equation (3). The default approach used is that jejunal P _eff is assumed to apply in each of the seven segments of the small intestine although the user is free to modify regional P _eff if required. This approach also applied the same P _eff value in the stomach and in the colon. In order to compare the impact of different measures of permeability, the Caco‐2 permeability was also used. Compounds were considered as immediate release solid formulation and FaSSIF or aqueous solubility at pH 7.4 were used. Drug distribution is modeled with a minimal PBPK model and using values of volume of distribution at steady state (Vss) that were collected from the literature (Table 3). The CL _int values were calculated from human in vivo clearance using the retrograde calculator within Simcyp®. The percentage contribution of CYP isoforms (Figure 1) in the hepatic metabolic clearance were used to predict the CL _int for recombinant CYP isoforms. Total clearance data were obtained from the literature and used to estimate renal clearance. CL _r was calculated as the product of the total clearance and the fraction excreted unchanged in the urine (f _e) collected from the literature. A clinical trial was designed for each compound based on 10 virtual subjects of the Simcyp Healthy Volunteers population with the same oral dose from the study. Each clinical study was simulated 10 times.

Table 2.

Physicochemical properties and measured in vitro data

		Molecular weight Da	Solubility (Biorelevant media or Buffer, pH 7.4) mg/ml	Acid pKa	Base pKa	PSA	HBD	ClogP	log D	Calculated P eff from physicochemical properties 37 10−4 cm/s	Measured P‐Caco2 10−6 cm/s	Calculated P eff from P‐Caco2 10−4 cm/s	Measured human liver microsomes CL int μl/min/mg protein	Predicted fuinc 36	BDDCS class
1	Alprazolam	308.8	40	–	–	33.3	0	2.56	1.26	12.4	38.6	4.3	< 10	0.92	1
2	Alprenolol	249.4	0.55	–	9.7	46.2	2	2.65	1.34	3.1	31.5	3.9	128	0.43	1
3	Chlorpromazine	318.9	0.814 (FaSSIF)	–	9.7	1.8	0	5.3	2.82	84.8			47	0.08	1
4	Clozapine	326.8	0.35 (FaSSIF)	–	7.5	25.6	1	3.71	2.99	13.9	28.4	3.7	33	0.54	2
5	Cyclosporine	1202.6	0.027	–	–	290.1	5	14.36	2.92	0.3				0.62	2
6	Diltiazem	414.5	0.47	–	8.1	56.5	0	3.65	2.22	11.7			35	0.67	1
7	Domperidone	425.9	0.135 (FaSSIF)	–	7.9	66.8	2	4.27	3.33	3.9	38.6	4.3	166	0.33	2
8	Erythromycin	733.9	2	–	8.9	203.3	5	1.61	1.16	0.01				0.94	3
9	Felodipine	384.3	0.04 (FaSSIF)	5.1	–	68.7	1	5.3	4.76	10.3	4.3	1.5	210	0.72	2
10	Flumazenil	303.3	0.13	–	–	57.0	0	1.29	0.87	4.1			39	0.95	1
11	Itraconazole	705.6	0.006 (FaHIF)	3.7	–	84.7	0	5.99	3.27	17.0				0.48	2
12	Lidocaine	234.3	4.1	–	7.9	33.7	1	1.95	1.88	5.3	42.2	4.5	15	0.81	1
13	Metoprolol	267.4	299.8 (FaHIF)	–	9.7	55.0	2	1.49	0.16	1.5			19	0.82	1
14	Midazolam	325.8	0.024	–	5.6	20.1	0	3.42	1.53	24.4			392	0.89	1
15	Mirtazapine	265.4	0.002	–	7.7	12.3	0	2.81	0.28	22.4	33.2	4.0	11	0.72	1
16	Nalbuphine	357.4	35.5	8.7	10.0	78.3	3	1.39	0.81	0.5	29.8	3.8	< 10	0.96	1
17	Nicardipine	479.5	0.227 (FaSSIF)	–	7.3	114.0	1	5.23	‐0.42	3.5				0.07	1
18	Nifedipine	346.3	0.041 (FaHIF)	–	–	112.9	1	3.13	2.80	1.4			141	0.65	2
19	Nimodipine	418.4	0.024	–	–	121.6	1	4	2.86	1.7	22.2	3.3	> 1000	0.63	2
20	Nisoldipine	388.4	0.006	–	–	110.5	1	3.26	4.96	0.4	56.7	5.2	> 1000	0.52	2
21	Nitrendipine	360.4	0.008 (FaSSIF)	–	–	112.9	1	3.73	3.81	1.9				0.38	2
22	Omeprazole	345.4	0.035	–	–	71.0	1	2.57	2.23	3.0			< 10	0.79	1
23	Saquinavir	670.8	2.22	–	7.7	178.8	5	4.73	5.05	0.07	5.0	1.6	> 1000	0.13	2
24	Sildenafil	474.6	3.5	–	6.0	105.2	1	1.98	2.45	1.0	28.6	3.7	98	0.95	1
25	Tacrolimus	804.0	0.008		9.3	185.9	3	5.78	3.96	0.3				0.03	2
26	Tolterodine	325.5	12	–	10.7	24.1	1	5.24	2.38	28.1	26.2	3.6	115	0.07	1
27	Triazolam	343.2	0.005	–	–	33.3	0	2.62	1.63	12.7				0.88	1
28	Venlafaxine	277.4	572	–	9.3	32.8	1	3.27	0.76	9.7	33.2	4.0	< 10	0.57	1
29	Verapamil	454.6	0.005	–	8.9	56.3	0	4.47	0.89	16.8			171	0.18	1
30	Zolmitriptan	287.4	20	–	9.5	56.8	2	1.29	‐1.47	1.3				0.96	1
31	Zolpidem	307.4	23	6.3	–	30.0	0	3.03	2.35	16.4			< 10	0.89	1

FaSSIF, fasted simulated small intestinal fluid are obtained in‐house, and FaHIF, fasted human intestinal fluid from literature 19, 46.

References for solubility, pKa, PSA, HBD, ClogP, logD, BDDCS are provided in Supplemental Table S1.

Table 3.

Pharmacokinetic data in humans and rats

		Humans								Rats
		i.v. dose mg	oral dose mg	F	CL l/h	Vss l/kg	f up	R b	Urinary excretion (f e) % of dose	i.v. dose mg	oral dose mg	F	CL ml/min/kg	f up	R b
1	Alprazolam	1	1	0.96	3.11	0.72	0.29	0.78	20	0.48	2.67	0.28	133	0.35	0.81
2	Alprenolol	7.25	100	0.06	65.90	2.99	0.18	0.76	0.5	0.5	2.5	0.04	79		1.71
3	Chlorpromazine	10	50	0.31	76.6	8.88	0.06	1.2	< 1	2.5	2.5	0.02	52	0.01	1.48
4	Clozapine	25	200	0.86	13.02	1.6	0.06	0.86	< 1	0.96	3.84	0.05	77.5	0.1	**
5	Cyclosporine	111.45	371.5	0.39	16.50	1.1	0.07	1.36	< 1	1.18	1.18	0.2	2	0.06	1.28
6	Diltiazem	20	120	0.47	48.3	5.2	0.18	1.00	3	1.43	4.28	0.06	42	0.18	0.93
7	Domperidone	10	10	0.39	42.06	5.71	0.08	0.74	< 1	0.63	0.63	0.5	39.2	0.09	1.3
8	Erythromycin	500	500	0.21	18.73	0.60	0.1	0.91	12	0.58	5.63	0.14	105	0.48	**
9	Felodipine	2.5	27.5	0.25	49.4	4.4	0.004	0.7	< 1	0.03	0.74	0.1	61	0.001	0.68
10	Flumazenil	2	30	0.22	72.06	0.97	0.58	1	0.5	0.56	5.63	0.28	147	0.14	**
11	Itraconazole	100	100	0.76	22.86	7.4	0.002	*	< 1	3	3	0.35	9.1	0.009	**
12	Lidocaine	200	300	0.42	42	1.34	0.33	0.87	8	4.25	21.25	0.02	31.8	0.38	1.27
13	Metoprolol	5	5	0.36	65.34	5.18	0.88	1.1	10	0.23	0.23	0.23	65.2	0.80	1.5
14	Midazolam	10.5	20	0.7	19.38	0.74	0.02	0.75	< 1	2.75	4.13	0.25	46	0.06	0.81
15	Mirtazapine	3.5	15	0.4	38.3	3.52	0.15	0.67	4	0.55	2.75	0.07	29.4	0.11	**
16	Nalbuphine	20	60	0.12	90	4.63	0.5	*	7	0.66	6	0.01	63	0.25	**
17	Nicardipine	15	30	0.45	34.57	0.76	0.01	0.71	0	1.14	3.42	0.22	115	0.01	**
18	Nifedipine	1.46	20	0.47	36	1.67	0.04	0.67	0	0.25	0.75	0.46	8.7	0.004	**
19	Nimodipine	2.1	60	0.33	58.8	0.94	0.02	*	< 0.1	0.86	3.42	0.22	1.5	0.03	**
20	Nisoldipine	0.37	20	0.04	50.82	4.1	0.003	*	< 1	0.2	0.2	0.03	45.8	0.009	**
21	Nitrendipine	2	20	0.39	78.89	5.39	0.01	1.46	< 1	1	1	0.12	16.5	0.04	1.46
22	Omeprazole	10	10	0.32	39.48	0.24	0.05	0.59	0	1.33	5.3	0.09	39.2	0.13	0.66
23	Saquinavir	12	600	0.01	60.6	3.63	0.03	0.74	1	2.35	11.75	0.07	88.5	0.05	0.82
24	Sildenafil	50	50	0.41	40.08	1.4	0.04	0.64	0	2.85	2.85	0.06	38.5	0.05	0.56
25	Tacrolimus	1.55	3.88	0.21	78.75	1.74	0.01	35	< 1	0.43	2.13	0.11	16.5	**	1.4
26	Tolterodine	1.28	3.2	0.72	27.72	1.4	0.04	*	1	0.13	3	0.02	166.7	0.15	**
27	Triazolam	0.25	0.25	0.8	12.72	0.58	0.1	0.62	2	0.64	1.28	0.16	51.4	0.28	1.5
28	Venlafaxine	10	50	0.37	60.35	4.4	0.73	1.0	4.6	7.26	7.26	0.13	64.5	0.59	**
29	Verapamil	10	120	0.39	49.7	4	0.09	0.89	< 3	0.13	1.25	0.06	29.3	0.05	0.85
30	Zolmitriptan	3.5	10	0.7	43.06	1.8	0.75	*	8	0.13	0.13	0.41	29.4		**
31	Zolpidem	5	5	0.78	18.85	0.68	0.08	0.66	< 1	0.25	0.25	0.27	15	0.13	0.86

^* When no data were available, a value of R _b of 0.55 should be considered if the drug is an acid, or a value of R _b of 1 if the drug is basic or neutral 56.

^** When rat values were not available, human values were considered.

References for f _up, R _b and urinary excretion are found in Supplemental Table S1.

References for i.v. and oral dose, F, CL, Vss are found in Supplemental Table S2.

Note: Rat Vss values were not needed and human urinary excretion values were used for rat.

Figure 1.

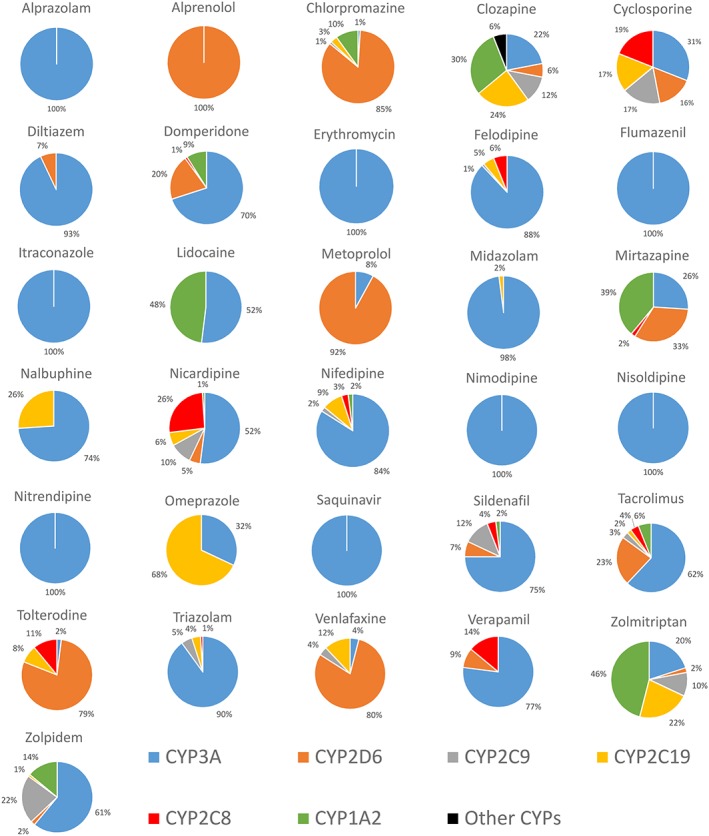
Human hepatic CYP450 pie for the dataset of drugs. The percentage contributions of individual CYP450 enzymes were calculated from CYP450 reaction phenotyping (CRP), inhibition studies, total immunoquantified CYP450 based on published data (references in Supplemental Table S3)

Q_gut model and the model of competing rates

The Q _gut approach does not account for the regional differences in enzyme and transporter expression and activities and resembles the well‐stirred liver model 41:

$$F_g=\frac{Q_{\mathit{gut}}}{Q_{\mathit{gut}}+f_{u,g}\bullet {\mathit{CLu}}_{\mathit{int},g}}$$ (8)

where f _u,g is the fraction of unbound drug in the enterocytes and CLu_int,g is the intrinsic metabolic clearance in the gut. The model relies on the fact that a high permeability through the enterocyte membrane will decrease the exposure to the metabolic enzyme as well as a high villus blood flow transporting the drug away from the enterocyte.

$$Q_{\mathit{gut}}=\frac{Q_{\mathit{\text{villi}}}\bullet {\mathit{CL}}_{\mathit{\text{perm}}}}{Q_{\mathit{\text{villi}}}+{\mathit{CL}}_{\mathit{\text{perm}}}}$$ (9)

Q _villi is the human blood flow entering the villi with a value of 18 l/h 14. CL _perm is the permeability through the enterocytes and is calculated using P _eff and the calculated human small intestinal cylindrical surface area, A, of 0.66 m² 14:

$${\mathit{CL}}_{\mathit{\text{perm}}}=P_{\mathit{eff}}\bullet A$$ (10)

P _eff can be evaluated using the measured Caco‐2 permeability (P _{Caco‐2,pH 7.4}, expressed in 10⁻⁶ cm/s):

$$P_{\mathrm{eff}}={10}^{0.4926log\left(P_{\mathit{\text{Caco}}-2,\mathit{pH}7.4}\right)}$$ (11)

The Q _gut model has been shown to provide the best prediction with f _u,g = 1 [14]. Therefore, the effective free fraction (f _u,g) is assumed to be 1 and Equation (8) can be rearranged to:

$$F_g=\frac{{\mathit{CL}}_{\mathit{\text{perm}}}}{{\mathit{CL}}_{\mathit{\text{perm}}}+{\mathit{CLu}}_{\mathit{int},g}+\frac{{\mathit{CL}}_{\mathit{\text{perm}}}\bullet {\mathit{CLu}}_{\mathit{int},g}}{Q_{\mathit{\text{villi}}}}}$$ (12)

If the product of CL _perm · CLu_int,g is small compared with Q _villi, the Q _gut model reduces to the model of Competing Rates 12, 22:

$$F_g=\frac{{\mathit{CL}}_{\mathit{\text{perm}}}}{{\mathit{CL}}_{\mathit{\text{perm}}}+{\mathit{CLu}}_{\mathit{int},g}}$$ (13)

Equation (13) suggests that the fraction escaping gut metabolism is a ratio of the permeability to the competing rates of permeability and gut metabolism.

The intrinsic hepatic clearance (CLu_int,h) was calculated from the i.v. systemic plasma clearance (CL _h) using the well‐stirred model 41 and where f _up is the fraction of drug unbound in plasma:

$${\mathit{CLu}}_{\mathit{int},h}=\frac{{\mathit{CL}}_h\bullet Q_h}{f_{\mathit{up}}\bullet \left(Q_h-{\mathit{CL}}_{h,\mathit{\text{blood}}}\right)}$$ (14)

The hepatic plasma clearance (CL _h) was estimated by subtracting renal clearance from the total systemic clearance when necessary. The hepatic blood clearance (CL _h,blood) is the hepatic plasma clearance adjusted by the blood/plasma ratio (R _b):

$${\mathit{CL}}_{h,\mathit{\text{blood}}}=\frac{{\mathit{CL}}_h}{R_b}$$ (15)

The calculations were based on a liver blood flow of 21 ml/min/kg for a ‘reference individual’ (70 kg and 1.7 m). HLM CL _int was calculated assuming a liver weight (LW) of 1718.4 g (Simcyp's mean value for the healthy volunteer population) and a microsomal protein per gram of liver (MPPGL) of 40 mg/g 42:

$$\mathit{HLM}{\mathit{CL}}_{\mathit{int}}=\frac{{\mathit{CLu}}_{\mathit{int},h}}{\mathit{LW}\bullet \mathit{\text{MPPGL}}}$$ (16)

HLM CL _int values were transformed into intestinal intrinsic clearances CLu_int,g using scalars, assuming that the substrates are mainly metabolized by CYP3A, 2C9 and 2C19 in the intestine and taking account of their contribution in the hepatic metabolism:

$${\mathit{CLu}}_{\mathit{int},g,j}=\frac{\mathit{HLM}{\mathit{CL}}_{\mathit{int}}}{A_{\mathit{CYP}\mathit{\text{liver}},j}}\bullet A_{\mathit{CYP}\mathit{\text{intestine}},j}\bullet {\%}_{\mathit{CYP}\mathit{\text{liver}},j}$$ (17)

Where CLu_int,g,j is the intrinsic clearance for a particular j CYP isoform, A _{CYP liver,j} is the liver abundance of a particular isoform, A _{CYP intestine, j} is the small intestine content of a particular isoform. The value is corrected by the percentage contribution of a particular isoform in the liver (%_{CYP liver,j}) (Figure 1). An average CYP3A, 2C9 and 2C19 hepatic abundance of 155, 12.2 and 1.5 pmol/mg protein and a combined intestinal CYP3A, 2C9 and 2C19 abundance of 70.5, 73 and 14 nmol/mg protein 4, 14, 43 were used to convert hepatic intrinsic clearance to intestinal intrinsic clearance. The total intestinal intrinsic clearance (CLu_int,g) was the sum of the individual calculated CLu_int,g,j of these three enzymes.

Estimation of human F_g using in vitro HLM CL_int in the ADAM, Q_gut, and competing rates models

The ADAM model within Simcyp®

The method described in the previous section was applied to estimate F _g using ADAM, except that experimental unbound HLM CL _int was used instead of CL _int derived from human in vivo PK data. The intrinsic clearance for a particular CYP isoform was calculated by accounting for the percentage contribution of that isoform in the liver.

$${\mathit{HLM}\mathit{CL}}_{\mathit{int},j}={\mathit{HLM}\mathit{CL}}_{\mathit{int}}\bullet {\%}_{\mathit{CYP}\mathit{\text{liver}},j}$$ (18)

Where HLM CL _int,j is the intrinsic clearance for a particular j^th CYP isoform and HLM CL _int is the total unbound intrinsic clearance in human liver microsomes. Experimental HLM CL _int values of <10 or >1000, were set to their respective limits.

Q_gut model and the model of Competing Rates

The method described in the previous section was applied to estimate F _g using Q _gut and Competing Rates models, except that experimental unbound HLM CL _int was used instead of CL _int derived from human in vivo PK data.

Rat F_g as a model for human F_g

Rat F _g is obtained from rat in vivo PK data using in‐house PBPK model or indirect approach in the same way as described for human. An average hepatic blood flow value is taken as 80 ml/min/kg in rat.

Data analysis

Prediction success of the models evaluated was defined as the percentage of drugs falling into the right categories described by low F _g (< 0.33), medium F _g (0.33–0.66) or high F _g (> 0.66).

The prediction accuracy of evaluated models was assessed with the root mean squared error (RMSE) (Eq. (19)), where greater accuracy was represented by a lower RMSE 44.

$$\mathit{\text{RMSE}}=\sqrt{\frac{\sum {\left(\mathit{\text{predicted}}{F}_g-\mathit{\text{observed}}{F}_g\right)}^2}{\mathit{\text{number of predictions}}\left(N\right)}}$$ (19)

Where predicted F _g refers to F _g derived from ADAM, Q _gut, Competing Rates models or from rat model and observed F _g refers to F _g extracted by PBPK or indirect approaches from human in vivo profiles.

The bias associated with the models evaluated was assessed by the average fold error (AFE) (Eq. (20)). Models with AFE values close to 1 have low bias. An AFE value of less than or greater than 1 indicates an overall under‐ or over‐prediction, respectively 45.

$$\mathit{AFE}={10}^{\frac{1}{n}\sum \mathit{log}\left(\frac{\mathit{\text{predicted}}{F}_g}{\mathit{\text{observed}}{F}_g}\right)}$$ (20)

Parameters were considered comparable when differences were less than a 10% deviation.

Results

Compound selection and characterization

A set of 31 drugs that satisfied the selection criteria and represented a broad chemical and metabolic spectrum was identified. Many of these drugs were predominantly metabolized by CYP3A (Figure 1). The physicochemical properties as well as in vitro data measured in‐house for the 31 drugs are summarized in Table 2. Values of P _eff estimated from either Caco‐2 data or physicochemical properties are also listed in Table 2. HLM CL _int measured for 23 drugs covered three orders of magnitude ranging from <10 to >1000 μl/min/mg protein. Calculated values for non‐specific binding to microsomal protein are listed in Table 2. Drugs analysed were classified according to the Biopharmaceutics Drug Disposition System (BDCCS) classification. Most of the 31 drugs belonged to Class 1 (highly soluble/highly metabolized: 61%) and fewer to Class 2 (poorly soluble/highly metabolized: 36%) or Class 3 (highly soluble/poorly metabolized: 3%). The PK data in human and rat collected from literature for the 31 drugs are shown in Table 3.

Estimation of human in vivo F_g using human in vivo PK data

Six out of seven drugs with low solubility and/or permeability were identified as being limited (F _a < 0.9) by solubility and/or permeability using the in‐house PBPK model (Table 4). For these six drugs, human F _g values were estimated through deconvolution of in vivo i.v. and oral PK data using the in‐house PBPK model. For all other compounds, the indirect method was employed for deconvolution assuming F _a = 1. These human in vivo F _g data from either of the two methods were employed in the evaluation of the various prediction models in this study and are presented in Table 5. Table 5 also lists the human in vivo F _g values from literature sources for comparison with human in vivo F _g values estimated in this work.

Table 4.

Values of human fraction absorbed (F _a) using in‐house PBPK or ADAM model within Simcyp® and based on permeability derived from physicochemical properties

	Predicted human F a
	In‐house PBPK	ADAM model within Simcyp®
Alprazolam	1	1
Alprenolol	1	1
Chlorpromazine	1	1
Clozapine	1	1
Cyclosporine	0.09	0.39
Diltiazem	1	1
Domperidone	1	1
Erythromycin	0.04	0.02
Felodipine	1	1
Flumazenil	1	1
Itraconazole	1	0.97
Lidocaine	1	1
Metoprolol	1	0.96
Midazolam	1	1
Mirtazapine	1	1
Nalbuphine	0.73	0.67
Nicardipine	1	1
Nifedipine	1	0.89
Nimodipine	1	0.72
Nisoldipine	0.21	0.36
Nitrendipine	1	0.67
Omeprazole	1	1
Saquinavir	0.2	0.18
Sildenafil	0.93	0.91
Tacrolimus	0.49	0.52
Tolterodine	1	1
Triazolam	1	1
Venlafaxine	1	1
Verapamil	1	1
Zolmitriptan	1	0.96
Zolpidem	1	1

Table 5.

Summary of human in vivo F _g values estimated by indirect or PBPK approaches and from literature

		Human in vivo F g (PBPK or indirect approaches)	F g (Karlsson) 12	F g (Gertz) 15	F g (Yang) 14	F g (Gertz) 57
1	Alprazolam	0.91	0.94	0.94	0.86	0.89*
2	Alprenolol	1
3	Chlorpromazine	0.38
4	Clozapine	0.31
5	Cyclosporine	0.82	0.6	0.44	0.62*	0.65*
6	Diltiazem	0.94
7	Domperidone	0.45
8	Erythromycin	0.30	0.23
9	Felodipine	0.65	0.38	0.45	0.58*	0.53*
10	Flumazenil	1
11	Itraconazole	0.72
12	Lidocaine	0.82
13	Metoprolol	1
14	Midazolam	0.69	0.52	0.51	0.57**	0.57*
15	Mirtazapine	1
16	Nalbuphine	1
17	Nicardipine	0.78
18	Nifedipine	0.87	0.47	0.74	0.68*	0.62*
19	Nimodipine	0.22
20	Nisoldipine	0.15		0.11
21	Nitrendipine	0.58
22	Omeprazole	1
23	Saquinavir	0.12	0.47	0.18	0.67*	0.54*
24	Sildenafil	0.83	0.7	0.54		0.82*
25	Tacrolimus	0.39	0.36	0.14	0.26
26	Tolterodine	0.60
27	Triazolam	0.64	0.63	0.75	0.67*	0.4*
28	Venlafaxine	1
29	Verapamil	0.51	0.4	0.65		0.71*
30	Zolmitriptan	0.54
31	Zolpidem	0.92		0.79

^* Determined from an interaction study using grapefruit juice as enzyme inhibitor.

^** Determined in anhepatic patients after intraduodenal drug administration.

Estimation of human F_g using in vivo PK‐derived CL_int in the ADAM, Q_gut, and competing rates models

Simulation with the ADAM model in Simcyp® indicated permeability‐ and/or solubility‐limited absorption for nine drugs (cyclosporine, erythromycin, nalbuphine, nifedipine, nimodipine, nisoldipine, nitrendipine, saquinavir, tacrolimus in Table 4). The impact of differences in P _eff derived from Caco‐2 or physicochemical properties on the predicted F _g using either the Q _gut or the ADAM models appears to be minimal (R ² = 0.99 and 0.93 respectively, Figure 2). And the use of the fraction of drug unbound in plasma or blood as an alternative to f _u,g = 1 resulted in the complete loss of prediction success and values of F _g approaching 1 for almost all drugs investigated (data not shown).

Figure 2.

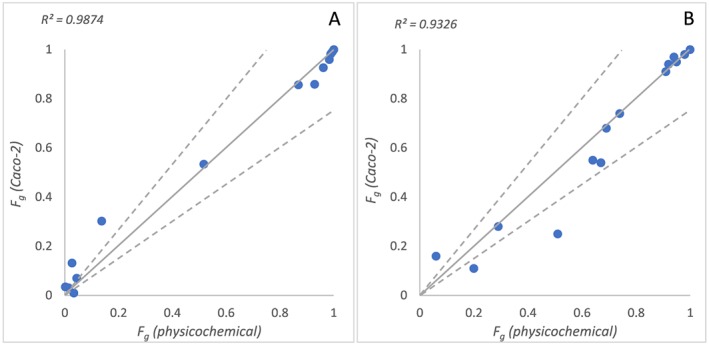
Relationship between predicted F _g using permeability data based on physicochemical properties and Caco‐2 data with human in vivo clearance in Q _gut (A) or ADAM (B) models. Solid line represents line of unity, and dashed lines represent 1.5‐fold deviation from unity

Table 6 summarizes the F _g predicted by ADAM, Q _gut or Competing Rates models using CL _int derived from human in vivo clearance. Correlations between human F _g predicted using the three models and human in vivo F _g are shown in Figure 3. Table 7 shows the qualitative binning of drugs into low/medium/high F _g.

Table 6.

Summary of human F _g values predicted by ADAM, Q _gut, Competing Rates models using CL _int derived from human in vivo clearance

		F g (ADAM, in vivo CL int)	F g (Q gut, in vivo CL int)	F g (Competing Rates, in vivo CL int)
1	Alprazolam	1	0.99	1
2	Alprenolol	0.69	1	1
3	Chlorpromazine	0.72	0.97	1
4	Clozapine	0.94	0.96	0.99
5	Cyclosporine	0.96	0.52	0.54
6	Diltiazem	0.82	0.76	0.89
7	Domperidone	0.74	0.52	0.62
8	Erythromycin	0.95	0.02	0.02
9	Felodipine	0.06	0.03	0.07
10	Flumazenil	0.82	0.64	0.73
11	Itraconazole	0.22	0.12	0.30
12	Lidocaine	0.95	0.87	0.92
13	Metoprolol	0.99	0.97	0.97
14	Midazolam	0.67	0.45	0.77
15	Mirtazapine	0.92	0.93	0.98
16	Nalbuphine	0.67	0.03	0.03
17	Nicardipine	0.43	0.16	0.22
18	Nifedipine	0.70	0.21	0.24
19	Nimodipine	0.29	0.04	0.05
20	Nisoldipine	0.20	0.01	0.02
21	Nitrendipine	0.24	0.03	0.03
22	Omeprazole	0.68	0.42	0.50
23	Saquinavir	0.51	0.00	0.00
24	Sildenafil	0.64	0.14	0.15
25	Tacrolimus	0.59	0.02	0.02
26	Tolterodine	0.91	0.98	1
27	Triazolam	0.94	0.93	0.97
28	Venlafaxine	0.98	0.99	1
29	Verapamil	0.72	0.64	0.85
30	Zolmitriptan	0.99	0.97	0.97
31	Zolpidem	0.90	0.90	0.97

Figure 3.

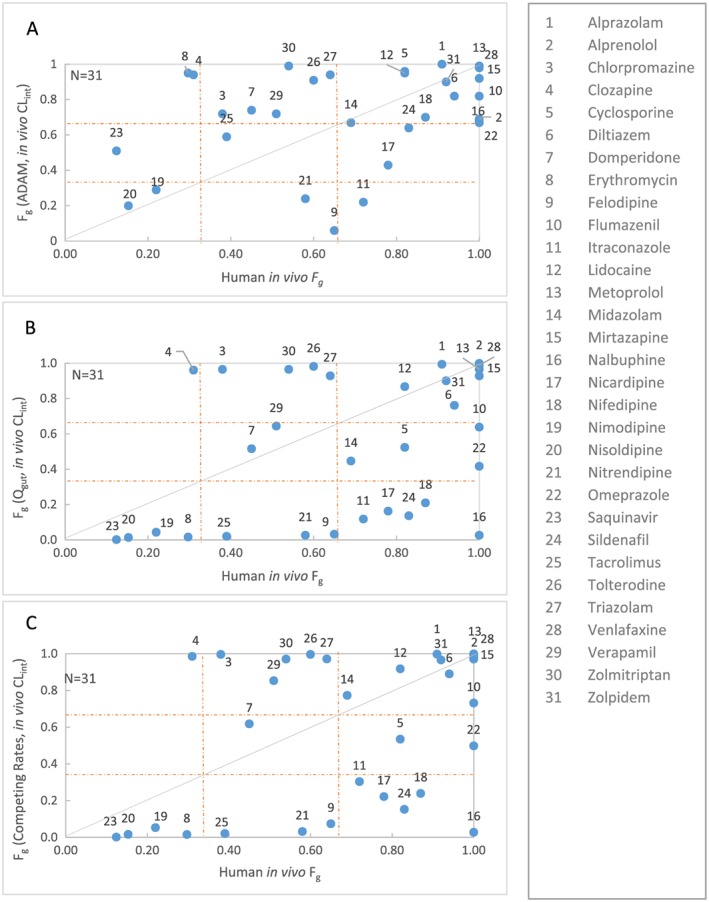
Comparison of human in vivo F _g extracted from PBPK/indirect approaches vs predicted F _g using CL _int derived from human in vivo clearance in ADAM (A), Q _gut (B) or Competing Rates (C) models. Solid line represents line of unity. The dotted lines at 0.33 and 0.66 represent cut‐off values for categorization of low, medium and high F _g

Table 7.

Performance of ADAM, Q _gut or Competing Rates models using CL _int derived from human in vivo clearance vs human in vivo F _g estimated from PBPK or indirect approaches. Percentage of low, medium or high F _g drugs that were predicted in different bins. Percentage of drugs that were correctly predicted are shown in bold

ADAM	n = 31		Human in vivo F g from PBPK/indirect approaches
			Low (< 0.33)	Medium (0.33–0.66)	High (> 0.66)
	F g (ADAM, in vivo CL int)	Low	6%	6%	3%
		Medium	3%	3%	6%
		High	6%	19%	45%
	Prediction success =54% RMSE =0.31 AFE = 1.02
Q gut	n = 31		Human in vivo F gfrom PBPK/indirect approaches
			Low (< 0.33)	Medium (0.33–0.66)	High (> 0.66)
	F g (Q gut, in vivo CL int)	Low	13%	13%	16%
		Medium	0%	6%	13%
		High	3%	10%	26%
	Prediction success =45% RMSE =0.42 AFE = 0.39
Competing Rates	n = 31		Human in vivo F g from PBPK/indirect approaches
			Low (< 0.33)	Medium (0.33–0.66)	High (> 0.66)
	F g (Competing Rates, in vivo CL int)	Low	13%	10%	16%
		Medium	0%	3%	6%
		High	3%	16%	32%
	Prediction success =48% RMSE =0.40 AFE = 0.46

Prediction success for the ADAM, Q _gut and Competing Rates models were 54%, 45% and 48%, respectively. The prediction accuracy for the ADAM model is better compared with Q _gut and Competing Rates models (RMSE =0.31, 0.42 and 0.40 respectively). The Q _gut and Competing Rates models tend to underestimate F _g compared with ADAM (AFE = 0.39 and 0.46 vs 1.02; Figure 3).

Estimation of human F_g using in vitro HLM CL_int in the ADAM, Q_gut, and competing rates models

Table 8 summarizes the F _g predicted by ADAM, Q _gut or Competing Rates models using HLM CL _int. Correlations between human F _g derived from in vitro models using the three models and human in vivo F _g are shown in Figure 4. Table 9 shows the qualitative binning of drugs into low/medium/high for F _g predicted by ADAM, Q _gut or Competing Rates models using HLM CL _int. The prediction success for the ADAM, Q _gut and Competing Rates models were 70%, 74% and 69%, respectively. A better prediction success for the low F _g category was observed using Q _gut and Competing Rates models compared with the ADAM model (13% and 13% vs 0%). Prediction accuracy for the ADAM is slightly better compared with Q _gut and Competing Rates models (RMSE =0.20 vs 0.30 and 0.25, respectively). All three models have comparable bias (AFE = 1.26 vs 0.74 and 0.81; Figure 4).

Table 8.

Summary of F _g values predicted by ADAM, Q _gut, Competing Rates models using in vitro HLM CL _int and in vivo rat F _g values estimated by indirect or PBPK approaches

		F g (ADAM, in vitro CL int)	F g (Q gut, in vitro CL int)	F g (Competing Rates, in vitro CL int)	Rat in vivo F g
1	Alprazolam	0.98	0.97	0.99	1
2	Alprenolol	0.92	1	1	0.09
3	Chlorpromazine	0.82	0.98	1	0.04
4	Clozapine	0.96	0.96	0.98	1
5	Cyclosporine				0.37
6	Diltiazem	0.92	0.89	0.95	0.13
7	Domperidone	0.66	0.39	0.49	0.80
8	Erythromycin				0.28
9	Felodipine	0.71	0.59	0.77	0.42
10	Flumazenil	0.94	0.85	0.90	1
11	Itraconazole				0.39
12	Lidocaine	0.97	0.97	0.98	0.03
13	Metoprolol	0.99	0.98	0.99	0.49
14	Midazolam	0.64	0.54	0.83	0.86
15	Mirtazapine	0.99	0.99	1	0.15
16	Nalbuphine	0.99	0.82	0.83	0.01
17	Nicardipine				1
18	Nifedipine	0.83	0.36	0.40	0.55
19	Nimodipine	0.38	0.07	0.09	0.23
20	Nisoldipine	0.40	0.06	0.07	0.06
21	Nitrendipine				0.14
22	Omeprazole	0.99	0.97	0.98	0.35
23	Saquinavir	0.48	0.00	0.00	0.13
24	Sildenafil	0.92	0.49	0.53	0.36
25	Tacrolimus				0.16
26	Tolterodine	0.63	0.89	0.97	1
27	Triazolam				0.28
28	Venlafaxine	0.99	1	1	0.65
29	Verapamil	0.49	0.39	0.67	0.1
30	Zolmitriptan				0.65
31	Zolpidem	0.99	0.98	0.99	0.35

Figure 4.

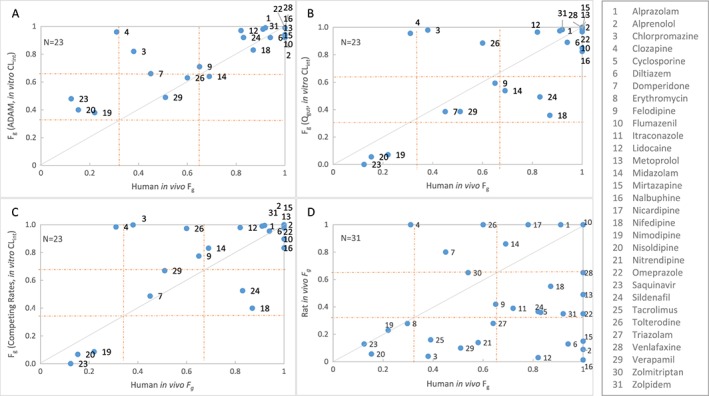
Comparison of human in vivo F _g vs predicted F _g using in vitro HLM CL _int in ADAM (A), Q _gut (B) or Competing Rates (C) models and Rat model (D). Solid line represents line of unity. The dotted lines at 0.33 and 0.66 represent cut‐off values for categorization of low, medium and high F _g

Table 9.

Performance of in vitro and in vivo models available during discovery phases and early drug development (ADAM, Q _gut or Competing Rates models using in vitro HLM CL _int and rat model). Percentage of low, medium or high F _g drugs that were predicted in different bins. Percentage of drugs that were correctly predicted are shown in bold

ADAM	n = 23		Human in vivo F g
			Low (< 0.33)	Medium (0.33–0.66)	High (> 0.66)
	F g (ADAM, in vitro CL int)	Low	0%	0%	0%
		Medium	13%	13%	4%
		High	4%	9%	57%
	Prediction success =70% RMSE =0.20 AFE = 1.26
Q gut	n = 23		Human in vivo F g
			Low (< 0.33)	Medium (0.33–0.66)	High (> 0.66)
	F g (Q gut, in vitro CL int)	Low	13%	0%	0%
		Medium	0%	13%	13%
		High	4%	9%	48%
	Prediction success =74% RMSE =0.30 AFE = 0.74
Competing Rates	n = 23		Human in vivo F g
			Low (< 0.33)	Medium (0.33–0.66)	High (> 0.66)
	F g (Competing Rates, in vitro CL int)	Low	13%	0%	0%
		Medium	0%	4%	9%
		High	4%	17%	52%
	Prediction success =69% RMSE =0.25 AFE = 0.81
Rat	n = 31		Human in vivo F g
			Low (< 0.33)	Medium (0.33–0.66)	High (> 0.66)
	Rat in vivo F g	Low	13%	16%	16%
		Medium	0%	6%	26%
		High	3%	6%	13%
	Prediction success =32% RMSE =0.48 AFE = 0.44

Rat F_g as a model for human F_g

Table 8 presents the F _g derived from rat in vivo PK used for the model evaluation. Correlation between human in vivo F _g and rat in vivo F _g are shown in Figure 4. Table 9 shows the qualitative binning of drugs into low/medium/high for F _g derived from rat. Prediction success is only 32% for rat model and prediction accuracy is low (RMSE =0.48). The rat has a high tendency to under‐predict human F _g (AFE = 0.44), especially the higher human F _g values.

Figure 5 illustrates the fold‐error for F _g predictions of the four evaluated models, namely the use of HLM in the three mechanistic models and the rat model, all of which are readily available in drug discovery and early development.

Figure 5.

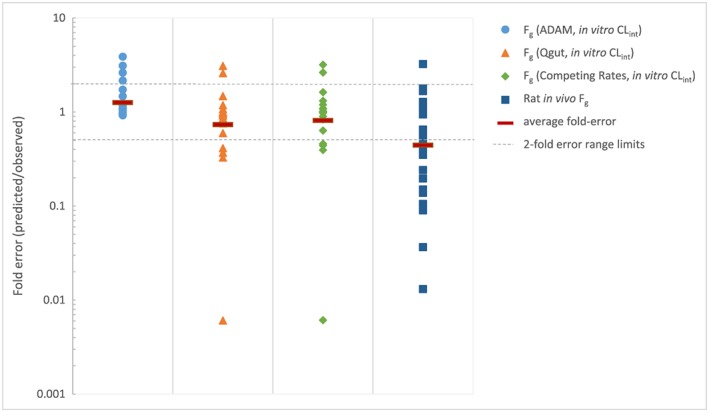
Comparison of the fold‐error in predicted F _g of evaluated models (ADAM, Q _gut, Competing Rates and Rat models)

Discussion

A total of 31 drugs met all the pre‐defined selection criteria. The size of the dataset was limited by the lack of i.v. PK in human, as i.v. dosing is not often performed during drug development. Selection was not restricted to compounds metabolized by CYP3A alone but to all CYP450 isoenzymes to take into account the possibility that drugs which are not metabolized by CYP3A in the liver may still be extracted by this enzyme in the gut in the absence of other competing enzymes. Despite contradictory reports in the literature 13, 15, our work demonstrates that estimates of F _g using P _eff from either physicochemical properties or Caco‐2 data were similar. Therefore, P _eff from physicochemical properties was used for the estimation of F _g in all models evaluated. This allowed the expansion of the dataset from 14 to 31 drugs since Caco‐2 data were not available for 17 drugs. In our work, the Q _gut model provided the best prediction with f _u,g = 1 which is consistent with the results reported by Yang et al. 17 and may be justified by a higher intestinal extraction in the mucosal to serosal direction than in the opposite direction under sink conditions.

Human in vivo F _g estimated through deconvolution using in vivo i.v. and oral PK data with either indirect method or the in‐house PBPK model were comparable to those reported in the literature (Table 5). Apart from the F _g data derived from anhepatic patients and grapefruit juice method, all other human in vivo F _g data in the literature also rely on the deconvolution of oral PK data. The quality of F _g obtained through deconvolution will be adversely impacted by uncertainty in the estimation of F _a, unknown clinical relevance of intestinal efflux, high variability associated with low bioavailability, as well as by auto‐inhibition or saturation of hepatic drug metabolizing enzymes in the oral route, leading to over‐estimation of F _h when using i.v. clearance. Uncertainty in the estimation of F _a might be due to unknown formulation effects in vivo or due to the absence of in vitro–in vivo correlation with respect to solubility, dissolution and permeability. At least six drugs selected in this study have solubility‐ or permeability‐limited absorption (drugs with F _a < 0.9 in Table 4), which is consistent with their BDDCS classification. In vitro aqueous solubility tends to under‐predict the intestinal solubilizing capacity for many lipophilic drugs and drug candidates 46. In our study, solubility in biorelevant media (e.g. simulated intestinal fluids) was not available for all of the drugs whose F _a is likely to be impacted by poor solubility (nisoldipine, saquinavir, tacrolimus). In addition to physiological factors specific to the subjects and physicochemical properties of the drug, absorption can also be affected by biopharmaceutical properties 47, 48. In our study, we do not consider the effects of formulation‐specific dissolution of a drug on its absorption and intestinal availability. Although a quantitative method to predict intestinal absorption of P‐gp and/or CYP3A substrates based on in vitro assays has been reported 49, in the interest of simplicity, we have not considered intestinal efflux in the deconvolution of F _g from i.v. and oral PK profiles. Negligence of efflux is perhaps justified for high permeability/high solubility drugs, that are likely to have high intestinal concentrations following oral administration 9. However, for efflux substrates whose therapeutic doses are low (domperidone, metoprolol, nicardipine, nifedipine, nisoldipine, tacrolimus), neglect of efflux for P‐gp substrates 50 may have the consequence of over‐estimating gut metabolism. Finally, the assumption of linear pharmacokinetics in the dose range covering i.v. and oral doses, may not be valid if liver inlet concentrations during hepatic first‐pass far exceed those from i.v. dose. Saturation or inhibition of hepatic clearance during hepatic first‐pass of an oral drug results in the over‐estimation of F _g. There is a 10‐fold or more difference in the i.v. and oral doses for alprenolol, felodipine, flumazenil, nifedipine, nisoldipine, saquinavir, verapamil (Table 3). In addition to the above, human in vivo F _g values can be quite variable depending on the source of the in vivo PK data. This is reflected in the large range of F _g values generated in this study through either the indirect method or in‐house PBPK model and those reported in the literature 12, 14, 15 (see Table 5). A higher incidence of inter‐individual variability for low bioavailability drugs 1 propagates into the estimation of human in vivo F _g estimates from different studies. Values of F _g derived from the grapefruit juice method are not impacted by the uncertainties in F _a and F _h but are still a composite measure of intestinal loss by both P‐gp efflux and CYP3A‐mediated metabolism.

A comparative evaluation of ADAM, Q _gut and Competing Rates models employing in vivo CL _int showed only a modest prediction success of around 50% for all three models. The more mechanistic ADAM model showed a slightly higher prediction success. This suggests that apart from correcting for differences in the abundance of CYPs between the liver and the gut, other factors such as differences in the activity of the enzymes in the two organs may also need to be considered when using hepatic CL _int 51. In addition to CYP3A, the abundance of CYP2C isoforms were also taken into account in this study since they are also present in the intestine 4. The Q _gut model and the simpler Competing Rates model have similar prediction success (45% and 48%, respectively), prediction accuracy (RMSE =0.42 and 0.40 respectively) and bias (AFE = 0.39 and 0.46, respectively), which confirms the literature report that there is little risk of losing accuracy by employing the model of Competing Rates to estimate F _g 12. The assumptions, strengths and limitations of the ADAM, Q _gut and Competing Rates models are summarized in Table 1. The ADAM model accounts for regional variations in enzyme abundance within the GI tract and considers individual phenotypic variations in the key metabolizing enzymes 20. This approach also applies the same P _eff value in the stomach and in the colon. Even though this may lead to an over‐estimation of P _eff in the colon, the overall impact on F _a is negligible for drugs that are mostly absorbed in the small intestine 28. Although the ADAM model is mechanistically sophisticated, high quality input such as absolute abundances of transporters and enzymes in the gut as well as reliable scaling factors are required in order to obtain better confidence in its predictions of F _g.

In vitro systems for the study of intestinal metabolism include Ussing chamber preparations, enterocyte preparations and intestinal microsomes amongst others (Table 10). Although intestinal subcellular fractions could be used for predicting intestinal extraction, the use of HLM assays is a much more attractive option in terms of speed, capacity, cost and availability. Gertz et al. 15 have shown that differences in unbound intrinsic clearances from human intestinal microsomes and HLM after normalizing for CYP3A abundances in intestine and liver are not significant. Similar results have been observed with human jejunal microsomes 19. In our study, in vitro HLM CL _int were available only for 23 drugs. Among the drugs that were left out due to lack of HLM data are cyclosporine, tacrolimus and triazolam, drugs that are generally studied for intestinal metabolism. The application of in vitro HLM CL _int into mechanistic models allows the quantification of human gut wall metabolism. The use of in vitro CL _int in the two frequently available models in drug development, ADAM and Q _gut, showed similar prediction success and bias. However, the ADAM model was associated with the lowest RMSE.

Table 10.

Comparison of common methods for estimating human intestinal metabolism during drug discovery 11, 13, 58

		Assumptions	Strengths	Limitations
In vitro systems	Recombinant P450 and human liver microsomes (HLMs)	– Same CYP isoform activity in the intestine and the liver	– Easy to use – High throughput – Well characterized	– No phase II or cytosolic enzymes – Uncertainty in the scaling factors in intestine
	Human intestinal microsomes (HIMs) and S9 fraction	– Same CYP isoform activity in the intestine and the liver	– High throughput – Intestinal S9 contain membrane‐bound enzymes and cytosolic enzymes	– Physiological scaling factors not well characterized – Lacking standardized methodology – Expensive co‐factors not at physiological concentrations – Large inter‐individual variability
	Ussing Chamber preparations	– Scalability to whole organ	– Closest resemblance to in vivo	– Limited tissue viability – Scaling up to whole intestine undefined
In vivo	Rat model	– In the absence of data, total clearance is assumed to be hepatic clearance – No saturation or auto‐inhibition during hepatic first‐pass of orally administered drug	– Native architecture of small intestine and physiologically relevant expression profiles of enzymes, co‐factors and transporters	– Similar issues as indirect approach in human – Additional CYP isoforms and other enzymes – Difficult to separate F a and F g – Uncertainty in liver blood flow – Oral dose not administered at site of absorption

Irrespective of the method of estimation (using in vitro or in vivo CL _int in the three mechanistic models), the F _g values of chlorpromazine, clozapine and tolterodine seem to be over‐predicted. For chlorpromazine, given the limited share of the intestinal CYPs in the metabolism of this compound, in vivo F _g should be close to 1, but this is not the case. This suggests that either the CYP phenotyping is inaccurate or there are alternative routes of intestinal loss that were not captured in our analysis. It has been reported that clozapine could be N‐glucuronidated 52 and this could explain the low human in vivo F _g with the use of liver microsomes compared with the predicted F _g. A similar explanation may be valid for tolterodine which has a phenolic structural motif. For compounds mainly metabolized by CYP2D6, and lacking non‐CYP metabolic pathways, intestinal metabolism does not seem to play a role as for example, alprenolol, metoprolol and venlafaxine.

In general, the Q _gut model predicts lower values of F _g compared with the ADAM model (Tables 6 and 8). This is especially true for compounds with low permeability (P _eff < 0.5) such as cyclosporine, erythromycin, nalbuphine, saquinavir and tacrolimus. This rationale can also be extended to compounds with P _eff < 1.5 such as nifedipine and sildenafil. Furthermore, compounds that are highly bound to proteins (f _up < 0.005) such as felodipine, itraconazole and nisoldipine are likely to have underestimated values of F _g.

The better prediction outcomes for in vitro rather than for in vivo data were unexpected and difficult to explain. However, while the in vitro data represent only CYP‐mediated metabolism, the in vivo clearance incorporates extra‐hepatic metabolism which may not be sufficiently accounted for in deriving hepatic clearance.

An earlier report suggested that the rat could be a good model for predicting human intestinal metabolism 12. However in this study, we observed that the intestinal loss of many drugs were systematically over‐predicted in rat compared with human, which confirms the conclusion from another literature study 33. Notable among the exceptions are clozapine, domperidone and tolterodine. Clozapine and tolterodine are likely to have glucuronidation in the gut in human, even though it is not a predominant pathway in the liver. It is generally accepted that glucuronidation can vary widely across species 53. A number of underlying assumptions were made in calculating intestinal loss in rat. Extra‐hepatic and non‐renal routes were neglected in the estimation of hepatic blood clearance from i.v. rat PK. When no information on renal clearance in rat was available, human renal excretion was used. But as renal excretion was relatively low or non‐existing for most of the drugs, the use of total systemic clearance rather than hepatic systemic clearance may not lead to significant discrepancies. The rat liver blood flow employed in this study is 80 ml/min/kg. However, several values have appeared in the literature ranging from 55 to 161 ml/min/kg 54, 55. Three drugs (alprazolam, flumazenil, tolterodine) showed blood clearance values exceeding maximum liver blood flow value used in this study, which makes the estimation of F _h and therefore estimation of rat in vivo F _g prone to error. The higher intestinal loss in the rat compared with humans is perhaps attributable to clinical formulations that are designed for optimal absorption. In addition, physiological differences, as well as the greater variety and abundance of CYP isoforms in the GI tract of rat 32 could explain the higher intestinal loss in rat. Since rat seems to always over‐predict intestinal metabolism, it can serve as an initial filter to identify compounds that can potentially undergo CYP‐mediated gut metabolism in human and therefore requiring further quantitative assessment of F _g. Absence of intestinal extraction in the rat could signal lack of CYP‐mediated gut metabolism in human.

Conclusions

All three mechanistic models investigated had comparable overall performance for CYP‐mediated intestinal metabolism in this study, reflecting the fact that uncertainties associated with deconvolution and correction for differences in the enzyme abundances in the metabolizing organs outweigh the benefits of complex mechanistic considerations. In comparison with the ADAM model that requires a number of high‐quality data for a reliable prediction of F _g, simpler models such as the Q _gut and Competing Rates requiring very little input should be preferred in discovery and early development. The ADAM model should be preferred once clinical data become available and metabolic pathways in human are better characterized.

Despite all the assumptions and limitations, it is encouraging to note that HLM CL _int, corrected for differences in enzyme abundances between the liver and intestine, appears to be reasonably good for assessing the risk for human intestinal metabolism. However, it is noteworthy that F _g of compounds with low permeability or high protein binding is likely to be under‐predicted. Since the rat systematically over‐predicts human intestinal extraction, it can serve as an initial screen, while simple models such as the Q _gut or even the more parsimonious Competing Rates model with human in vitro HLM CL _int could be used to predict human intestinal extraction. All mechanistic models require in vitro systems that closely mimic the in vivo situation. Therefore, generating high‐quality in vitro data will be crucial for successful prediction of intestinal metabolism.

Conflict of Interest

The authors have no conflict of interest to declare.

Supporting information

Table S1. Summary of drug related parameters for 31 drugs investigated.

Table S2. Literature source for human and rat pharmacokinetic data.

Table S3. Compounds CYP contribution in liver (pie).

Yau, E. , Petersson, C. , Dolgos, H. , and Peters, S. A. (2017) A comparative evaluation of models to predict human intestinal metabolism from nonclinical data. Biopharm. Drug Dispos., 38: 163–186. doi: 10.1002/bdd.2068.