Joint Estimation of Precision Matrices in Heterogeneous Populations

Abstract

We introduce a general framework for estimation of inverse covariance, or precision, matrices from heterogeneous populations. The proposed framework uses a Laplacian shrinkage penalty to encourage similarity among estimates from disparate, but related, subpopulations, while allowing for differences among matrices. We propose an efficient alternating direction method of multipliers (ADMM) algorithm for parameter estimation, as well as its extension for faster computation in high dimensions by thresholding the empirical covariance matrix to identify the joint block diagonal structure in the estimated precision matrices. We establish both variable selection and norm consistency of the proposed estimator for distributions with exponential or polynomial tails. Further, to extend the applicability of the method to the settings with unknown populations structure, we propose a Laplacian penalty based on hierarchical clustering, and discuss conditions under which this data-driven choice results in consistent estimation of precision matrices in heterogenous populations. Extensive numerical studies and applications to gene expression data from subtypes of cancer with distinct clinical outcomes indicate the potential advantages of the proposed method over existing approaches.

1. Introduction

Estimation of large inverse covariance, or precision, matrices has received considerable attention in recent years. This interest is in part driven by the advent of high-dimensional data in many scientific areas, including high throughput omics measurements, functional magnetic resonance images (fMRI), and applications in finance and industry. Applications of various statistical methods in such settings require an estimate of the (inverse) covariance matrix. Examples include dimension reduction using principal component analysis (PCA), classification using linear or quadratic discriminant analysis (LDA/QDA), and discovering conditional independence relations in Gaussian graphical models (GGM).

In high-dimensional settings, where the data dimension p is often comparable or larger than the sample size n, regularized estimation procedures often result in more reliable estimates. Of particular interest is the use of sparsity inducing penalties, specifically the ℓ₁ or lasso penalty [30], which encourages sparsity in off-diagonal elements of the precision matrix [7, 8, 33, 34]. Theoretical properties of ℓ₁-penalized precision matrix estimation have been studied under both multivariate normality, as well as some relaxations of this assumption [4, 19, 25, 26].

Sparse estimation is particularly relevant in the setting of GGMs, where conditional independencies among variables correspond to zero off-diagonal elements of the precision matrix [14]. The majority of existing approaches for estimation of high-dimensional precision matrices, including those cited in the previous paragraph, assume that the observations are identically distributed, and correspond to a single population. However, data sets in many application areas include observations from several distinct subpopulations. For instance, gene expression measurements are often collected for both healthy subjects, as well as patients diagnosed with different subtypes of cancer. Despite increasing evidence for differences among genetic networks of cancer and healthy subjects [11, 27], the networks are also expected to share many common edges. Separate estimation of graphical models for each of the subpopulations would ignore the common structure of the precision matrices, and may thus be inefficient; this inefficiency can be particularly significant in high-dimensional low sample settings, where p ≫ n.

To address the need for estimation of graphical models in related subpopulations, few methods have been recently proposed for joint estimation of K precision matrices ${\mathrm{\Omega }}^{(k)}={({\omega }_{ij}^{(k)})}_{i,j=1}^p\in {ℝ}^{p\times p}$, k = 1, …, K [6, 9]. These methods extend the penalized maximum likelihood approach by combining the Gaussian likelihoods for the K subpopulations

$${\ell }_n(\mathrm{\Omega })=\frac{1}{n}\sum _{k=1}^K{n}_k(\text{log det }({\mathrm{\Omega }}^{(k)})-\text{tr }({\hat{\mathrm{\Sigma }}}_n^{(k)}{\mathrm{\Omega }}^{(k)}\left)\right).$$ (1)

Here, n_k and ${\hat{\mathrm{\Sigma }}}_n^{(k)}$ are the number of observations and the sample covariance matrix for the kth subpopulation, respectively, $n={\sum }_{k=1}^K{n}_k$ is the total sample size and tr(·) and det(·) denote matrix trace and determinant.

To encourage similarity among estimated precision matrices, Guo et al. [9] modeled the (i, j)-element of Ω^(k) as product of a common factor θ_ij and group-specific parameters ${\gamma }_{ij}^{(k)}$, i.e. ${\omega }_{ij}^{(k)}={\delta }_{ij}{\gamma }_{ij}^{(k)}$. Identifiability of the estimates is ensured by assuming δ_ij ≥ 0. A zero common factor δ_ij = 0 induces sparsity across all subpopulations, whereas ${\gamma }_{ij}^{(k)}=0$ results in condition-specific sparsity for ${\omega }_{ij}^{(k)}$. This reparametrization results in a non-convex optimization problem based on the Gaussian likelihood with ℓ₁-penalties ∑_i≠j δ_ij and ${\sum }_{i\ne j}{\sum }_{k=1}^K|{\gamma }_{ij}^{(k)}|$. Danaher et al. [6] proposed two alternative estimators by adding an additional convex penalty to the graphical lasso objective function: either a fused lasso penalty ${\sum }_{i\ne j}{\sum }_{k\ne k\prime }|{\omega }_{ij}^{(k)}-{\omega }_{ij}^{k\prime }|$ (FGL), or a group lasso penalty ${\sum }_{i\ne j}\sqrt{{\sum }_{k=1}^K{({\omega }_{ij}^{(k)})}^2}$ (GGL). The fused lasso penalty has also been used by Kolar et al. [13], for joint estimation of multiple graphical models in multiple time points. The fused lasso penalty strongly encourages the values of ${\omega }_{ij}^{(k)}$ to be similar across all subpopulations, both in values as well as sparsity patterns. On the other hand, the group lasso penalty results in similar estimates by shrinking all ${\omega }_{ij}^{(k)}$ across subpopulations to zero if ${\sum }_{k=1}^K{({\omega }_{ij}^{(k)})}^2$ is small.

Despite their differences, methods of Guo et al. [9] and Danaher et al. [6] inherently assume that precision matrices in K subpopulations are equally similar to each other, in that they encourage ${\omega }_{ij}^{(k)}$ and ${\omega }_{ij}^{(k\prime )}$ and ${\omega }_{ij}^{(k)}$ and ${\omega }_{ij}^{(k″)}$ to be equally similar. However, when K > 2, some subpopulations are expected to be more similar to each other than others. For instance, it is expected that genetic networks of two subtypes of cancer be more similar to each other than to the network of normal cells. Similarly, differences among genetic networks of various strains of a virus or bacterium are expected to correspond to the evolutionary lineages of their phylogenetic trees. Unfortunately, existing methods for joint estimation of multiple graphical models ignore this heterogeneity in multiple subpopulations. Furthermore, existing methods assume subpopulation memberships are known, which limits their applicability in settings with complex but unknown population structures; an important example is estimation of genetic networks of cancer cells with unknown subtypes.

In this paper, we propose a general framework for joint estimation of multiple precision matrices by capturing the heterogeneity among subpopulations. In this framework, similarities among disparate subpopulations are presented using a subpopulation networkG(V, E, W), a weighted graph whose node set V is the set of subpopulations. The edges in E and the weights W_kk′ for (k, k′) ∈ E represent the degree of similarity between any two subpopulations k, k′. In the special case where W_kk′ = 1 for all k, k′, the subpopulation similarities are only captured by the structure of the graph G. An example of such a subpopulation network is the line graph corresponding to observations over multiple time points, which is used in estimation of time-varying graphical models [13]. As we will show in Section 2.3, other existing methods for joint estimation of multiple graphical models, e.g. proposals of Danaher et al. [6], can also be seen as special cases of this general framework.

Our proposed estimator is the solution to a convex optimization problem based on the Gaussian likelihood with both ℓ₁ and graph Laplacian [15] penalties. The graph Laplacian has been used in other applications for incorporating a priori knowledge in classification [24], for principal component analysis on network data [28], and for penalized linear regression with correlated covariates [10, 15, 17, 18, 32, 37]. The Laplacian penalty encourages similarity among estimated precision matrices according to the subpopulation network G. The ℓ₁-penalty, on the other hand, encourages sparsity in the estimated precision matrices. Together, these two penalties capture both unique patterns specific to each subpopulation, as well as common patterns shared among different subpopulations.

We first discuss the setting where G(V, E, W) is known from external information, e.g. known phylogenetic trees (Section 2), and later discuss the estimation of the subpopulation memberships and similarities using hierarchical clustering (Section 4). We propose an alternating methods of multipliers (ADMM) algorithm [3] for parameter estimation, as well as its extension for efficient computation in high dimensions by decomposing the problem into block-diagonal matrices. Although we use the Gaussian likelihood, our theoretical results also hold for non-Gaussian distributions. We establish model selection and norm consistency of the proposed estimator under different model assumptions (Section 3), with improved rates of convergence over existing methods based on penalized likelihood. We also establish the consistency of the proposed algorithm for the estimation of multiple precision matrices, in settings where the subpopulation network G or subpopulation memberships are unknown. To achieve this, we establish the consistency of hierarchical clustering in high dimensions, by generalizing recent results of Borysov et al. [1] to the setting of arbitrary covariance matrices, which is of independent interest.

The rest of the paper is organized as follows. In Section 2 we describe the formal setup of the problem and present our estimator. Theoretical properties of the proposed estimator are studied in Section 3, and Section 4 discusses the extension of the method to the setting where the subpopulation network is unknown. The ADMM algorithm for parameter estimation and its extension for efficient computation in high dimensions are presented in Section 5. Results of the numerical studies, using both simulated and real data examples, are presented in Section 6. Section 7 concludes the paper with a discussion. Technical proofs are collected in the Appendix.

2. Model and Estimator

2.1. Problem Setup

Consider K subpopulations with distributions ℘^(k), k = 1, …, K. Let X^(k) = (X^(k),1, …, X^(k),p)^T ∈ ℝ^p be a random vector from the kth subpopulation with mean μ_k and the covariance matrix ${\mathrm{\Sigma }}_0^{(k)}={({\sigma }_{ij}^{(k)})}_{i,j=1}^p$. Suppose that an observation comes from the kth subpopulation with probability π_k > 0.

Our goal is to estimate the precision matrices ${\mathrm{\Omega }}_0^{(k)}\equiv {({\mathrm{\Sigma }}_0^{(k)})}^{-1}\equiv {({\omega }_{ij}^{(k)})}_{i,j=1}^p$, k = 1, …, K. To this end, we use the Gaussian log-likelihood based on the correlation matrix (see Rothman et al. [26]) as a working model for estimation of true ${\mathrm{\Omega }}_0^{(k)}$, k = 1, …, K. Let $X_i^{(k)}$, i = 1, …, n_k, be independent and identically distributed (i.i.d.) copies from ℘^(k), k = 1, …, K. We denote the correlation matrices and their inverse by ${\mathrm{\Theta }}^{(k)}={({\theta }_{ij}^{(k)})}_{i,j=1}^p$, and ${\mathrm{\Psi }}^{(k)}={({\psi }_{ij}^{(k)})}_{i,j=1}^p$, k = 1, …, K, respectively. The Gaussian log-likelihood based on the correlation matrix can then be written as

$${\tilde{\ell }}_n(\mathrm{\Theta })=\frac{1}{n}\sum _{k=1}^K{n}_k(\text{log det }({\mathrm{\Theta }}^{(k)})-\text{tr }({\mathrm{\Psi }}_n^{(k)}{\mathrm{\Theta }}^{(k)}\left)\right),$$ (2)

where ${\mathrm{\Psi }}_n^{(k)}$, k = 1, …, K is the sample correlation matrix for subpopulation k.

Examining the derivative of (2), which consists of ${\mathrm{\Psi }}_0^{(k)}-{\mathrm{\Psi }}_n^{(k)}$, k = 1, …, K, justifies its use as a working model for non-Gaussian data: the stationary points of (2) is ${\mathrm{\Psi }}_n^{(k)}$, which gives a consistent estimate of ${\mathrm{\Psi }}_0^{(k)}$. Thus we do not, in general, need to assume multivariate normality. However, in certain applications, for instance LDA/QDA and GGM, the resulting estimate is useful only if the data follows a multivariate normal distribution.

2.2. The Laplacian Shrinkage Estimator

Let Θ = (Θ⁽¹⁾, …, Θ^(K)) and write ${\mathrm{\Theta }}_{ij}={({\theta }_{ij}^{(1)},\dots ,{\theta }_{ij}^{(K)})}^T\in {ℝ}^K$, i, j = 1, …, p for a vector of (i, j)-elements across subpopulations. Our proposed estimator, Laplacian Shrinkage for Inverse Covariance matrices from Heterogeneous populations (LASICH), first estimates the inverse of the correlation matrices for each of the K subpopulations, and then transforms them into the estimator of inverse covariance matrices, as in Rothman et al. [26]. In particular, we first obtain the estimate Θ̂ of the true inverse correlation matrix by solving the following optimization problem

$${\hat{\mathrm{\Theta }}}_{{\rho }_n}\equiv \underset{\mathrm{\Theta }={\mathrm{\Theta }}^T,\mathrm{\Theta }\succ 0}{\text{arg min}}-{\tilde{\ell }}_n(\mathrm{\Theta })+{\rho }_n{\Vert \mathrm{\Theta }\Vert }_1+{\rho }_n{\rho }_2{\Vert \mathrm{\Theta }\Vert }_L\equiv \underset{\mathrm{\Theta }={\mathrm{\Theta }}^T,\mathrm{\Theta }\succ 0}{\text{arg min}}-{\tilde{\ell }}_n(\mathrm{\Theta })+{\rho }_n\sum _{k=1}^K\sum _{i\ne j}\left|{\mathrm{\Theta }}_{ij}^{(k)}\right|+{\rho }_n{\rho }_2\sum _{i\ne j}{\Vert {\mathrm{\Theta }}_{ij}\Vert }_L,$$ (3)

where Θ = Θ^T enforces the symmetry of individual inverse correlation matrices, i.e. Θ^(k) = (Θ^(k))^T, and Θ ≻ 0 requires that Θ^(k) is positive definite for k = 1, …, K. The ℓ₁-penalty ${\Vert \mathrm{\Theta }\Vert }_1={\sum }_{k=1}^K{\Vert {\mathrm{\Theta }}^{(k)}\Vert }_1$ in (3) encourages sparsity in estimated inverse correlation matrices. The graph Laplacian penalty, on the other hand, exploits the information in the subpopulation network G to encourage similarity among values of ${\theta }_{ij}^{(k)}$ and ${\theta }_{ij}^{(k\prime )}$. The tuning parameters ρ_n and ρ_nρ₂ control the size of each penalty term.

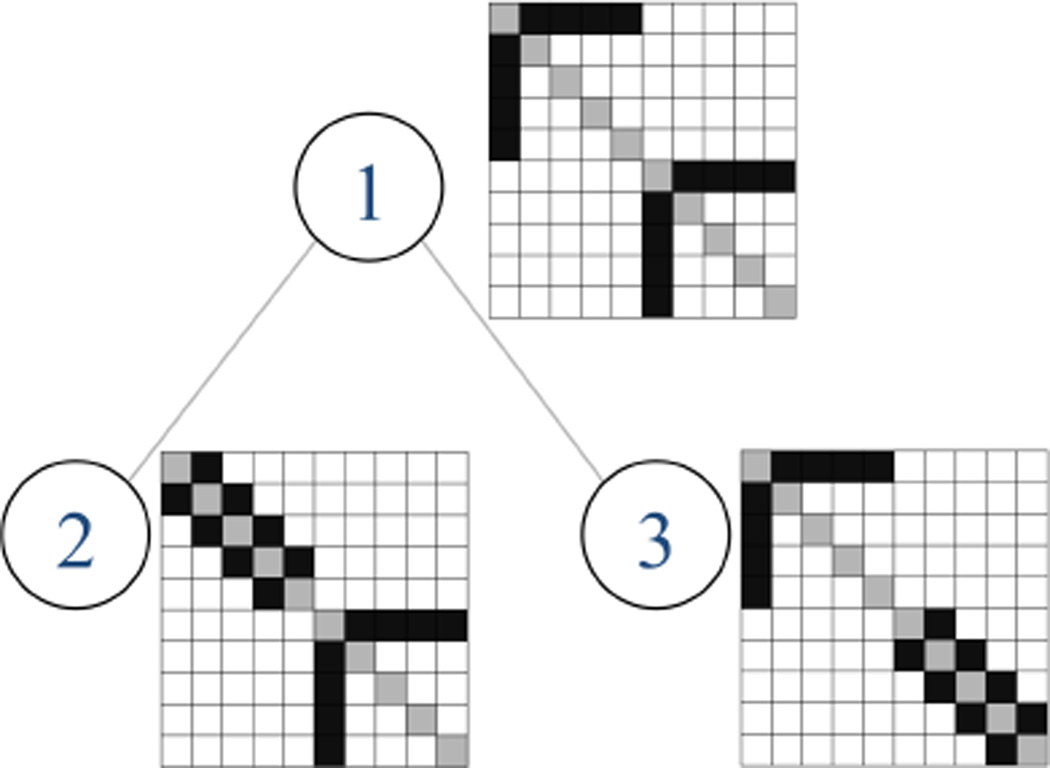
Figure 1 illustrates the motivation for the graph Laplacian penalty ‖Θ_ij‖_L in (3). The gray-scale images in the figure show the hypothetical sparsity patterns of precision matrices Θ⁽¹⁾, Θ⁽²⁾, Θ⁽³⁾ for three related subpopulations. Here, Θ⁽¹⁾ consists of two blocks with one “hub” node in each block; in Θ⁽²⁾ and Θ⁽³⁾ one of the blocks is changed into a “banded” structure. It can be seen that one of the two blocks in both Θ⁽²⁾ and Θ⁽³⁾ have a similar sparsity pattern as Θ⁽¹⁾. However, Θ⁽²⁾ and Θ⁽³⁾ are not similar. The subpopulation network G in this figure captures the relationship among precision matrices of the three subpopulations. Such complex relationships cannot be captured using the existing approaches, e.g. Danaher et al. [6], Guo et al. [9], which encourage all precision matrices to be equally similar to each other. More generally, G can be a weighted graph, G(V, E, W), whose nodes represent the subpopulations 1, …, K. The edge weights W : E → ℝ₊ represent the similarity among pairs of subpopulations, with larger values of W_kk′ ≡ W (k, k′) > 0 corresponding to more similarity between precision matrices of subpopulations k and k′.

Fig 1.

Illustration of similarities in the sparsity patterns of precision matrices Ω⁽¹⁾, Ω⁽²⁾ and Ω⁽³⁾. Nonzero and zero off-diagonal entries are colored in black and white, respectively, while diagonal entires are colored in gray. The associated subpopulation network G reflects the similarities between precision matrices of subpopulations 1 and 2 and 1 and 3. The simulation experiments in Section 6.1 use a similar subpopulation network in a high-dimensional setting.

In this section, we assume that the weighted graph G is externally available, and defer the discussion of data-driven choices of G, based on hierarchical clustering, to Section 4. Given G, the (unnormalized) graph Laplacian penalty ‖Θ_ij‖_L is defined as

$${\Vert {\mathrm{\Theta }}_{ij}\Vert }_L={\left\{\sum _{k,k\prime =1}^K{W}_{kk\prime }{({\theta }_{ij}^{(k)}-{\theta }_{ij}^{(k\prime )})}^2\right\}}^{1/2}$$ (4)

where W_kk′ = 0 if k and k′ are not connected. The Laplacian shrinkage penalty can be alternatively written as ${\Vert {\mathrm{\Theta }}_{ij}\Vert }_L={\mathrm{\Theta }}_{ij}^{T}L{\mathrm{\Theta }}_{ij}$, where $L={\left(l_{kk\prime }\right)}_{k,k\prime =1}^K\in {ℝ}^{K\times K}$ is the Laplacian matrix [5] of the subpopulation network G defined as

$$l_{kk\prime }=\{\begin{array}{cc}{d}_k-W_{kk},\hfill & k=k\prime ,d_k\ne 0,\hfill \\ -W_{kk\prime },\hfill & k\ne k\prime ,\hfill \\ 0,\hfill & \text{otherwise},\hfill \end{array}$$

where d_k = ∑_k′≠kW_kk′ is the degree of node k in G with W_kk′ = 0 if k and k′ are not connected. The Laplacian shrinkage penalty can also be defined in terms of the normalized graph Laplacian, I − D^−1/2W D^−1/2, where D = diag(d₁, …, d_K) is the diagonal degree matrix. The normalized Laplacian penalty,

$${\Vert {\mathrm{\Theta }}_{ij}\Vert }_L={\left\{\sum _{k,k\prime =1}^K{W}_{kk\prime }{(\frac{{\theta }_{ij}^{(k)}}{\sqrt{d_k}}-\frac{{\theta }_{ij}^{(k\prime )}}{\sqrt{d_{k\prime }}})}^2\right\}}^{1/2},$$

which we also denote as ‖Θ_ij‖_L, imposes smaller shrinkage on coefficients associated with highly connected subpopulations. We henceforth primarily focus on the normalized penalty.

Given estimates of the inverse correlation matrices Θ̂⁽¹⁾, …, Θ̂^(K) from (3), we obtain estimates of precision matrices Ω^(k) by noting that Ω^(k) = Ξ^(k)Θ^(k)Ξ^(k), where Ξ^(k) is the diagonal matrix of reciprocals of the standard deviations ${\mathrm{\Xi }}^{(k)}=\text{diag}({\{{\sigma }_{11}^{(k)}\}}^{-1/2},\dots ,{\{{\sigma }_{pp}^{(k)}\}}^{-1/2})$. Our estimator ${\hat{\mathrm{\Omega }}}_{{\rho }_n}=({\hat{\mathrm{\Omega }}}_{{\rho }_n}^{(1)},\dots ,{\hat{\mathrm{\Omega }}}_{{\rho }_n}^{(K)})$ of precision matrices Ω is thus defined as

$${\hat{\mathrm{\Omega }}}_{{\rho }_n}^{(k)}={\{{\hat{\mathrm{\Xi }}}^{(k)}\}}^{-1}{\hat{\mathrm{\Theta }}}_{{\rho }_n}^{(k)}{\{{\hat{\mathrm{\Xi }}}^{(k)}\}}^{-1},k=1,\dots ,K,$$

where ${\hat{\mathrm{\Xi }}}^{(k)}=\text{diag}(1/{\{{\hat{\sigma }}_{11}^{(k)}\}}^{1/2},\dots ,1/{\{{\hat{\sigma }}_{pp}^{(k)}\}}^{1/2})$ with sample variance ${\hat{\sigma }}_{ii}^{(k)}$ for the ith element in the kth subpopulation.

A number of alternative strategies can be used instead of the graph Laplacian penalty in (3). First, similarity among coefficients of precision matrices can also be imposed using a ridge-type penalty, ${\Vert {\mathrm{\Theta }}_{ij}\Vert }_L^2$. The main difference is that our penalty ‖Θ_ij‖_L discourages the inclusion of edges ${\theta }_{ij}^{(1)},\dots ,{\theta }_{ij}^{(K)}$ if they are very different across the K subpopulations. Another option is to use the graph trend filtering [31], which impose a fused lasso penalty over the subpopulation graph G. Finally, ignoring the weights W_kk′ in (4), the Laplacian shrinkage penalty resembles the Markov random field (MRF) prior used in Bayesian variable selection with structured covariates [16]. While our paper was under review, we became aware of the recent work by Peterson et al. [23], who utilize an MRF prior to develop a Bayesian framework for estimation of multiple Gaussian graphical models. This method assumes that edges between pairs of random variable are formed independently, and is hence more suited for Erdős-Rényi networks. Our penalized estimation framework can be seen as an alternative to using an MRF prior to estimate the precision matrices in a mixture of Gaussian distributions.

2.3. Connections to Other Estimators

To connect our proposed estimator to existing methods for joint estimation of multiple graphical models, we first give an alternative interpretation of the graph Laplacian penalty ${\Vert {\mathrm{\Theta }}_{ij}\Vert }_L={({\mathrm{\Theta }}_{ij}^{T}L{\mathrm{\Theta }}_{ij})}^{1/2}$ as a norm for a transformed version of ${\mathrm{\theta }}_{ij}^{(k)}\mathrm{s}$. More specifically, consider the mapping g_G : ℝ^K → ℝ^K defined based on the Laplacian matrix for graph G

$$g_G({\mathrm{\Theta }}_{ij})=\{\begin{array}{cc}0,\hfill & k=k\prime ,\hfill \\ \sqrt{W_{kk\prime }}(\frac{{\theta }_{ij}^{(k)}}{\sqrt{2d_k}}-\frac{{\theta }_{ij}^{(k\prime )}}{\sqrt{2d_{k\prime }}}),\hfill & k\ne k\prime ,\hfill \end{array}$$

if G has at least one edge. For a graph with no edges, define g_G(Θ_ij) = I_K⊗Θ_ij = diag(Θ_ij), where I_K is the K-identity matrix, and ⊗ denotes the Kronecker product. It can then be seen that the graph Laplacian penalty can be rewritten as

$${\Vert {\mathrm{\Theta }}_{ij}\Vert }_L={\Vert g_G({\mathrm{\Theta }}_{ij})\Vert }_F.$$

where ‖·‖_F is the Frobenius norm.

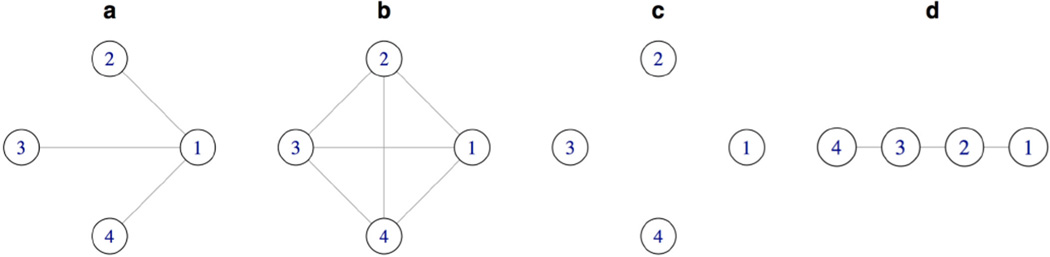
Using the above interpretation, other methods for joint estimation of multiple graphical models can be seen as penalties on transformations g_G(Θ_ij) corresponding to different graphs G. We illustrate this connection using the hypothetical subpopulation network shown in Figure 2a.

Fig 2.

Comparison of subpopulation networks used in the penalty for different methods for joint estimation of multiple precision matrices: a) the true network, modeled by LASICH; b) FGL; c) GGL & Guo et al; and d) estimation of time-varying networks (Kolar & Xing, 2009); see Section 2.3 for details.

Consider first the FGL penalty of Danaher et al. [6], applied to elements of the inverse correlation matrix $|{\theta }_{ij}^{(k)}-{\theta }_{ij}^{(k\prime )}|$. Let G_C be a complete unweighted graph (W_kk′ = 1 ∀k ≠ k′), in which all $\left(\begin{array}{c}\hfill K\hfill \\ \hfill 2\hfill \end{array}\right)$ node-pairs are connected to each other (Figure 2b). It is then easy to see that

$$\sum _{k\ne l}|{\theta }_{ij}^{(k)}-{\theta }_{ij}^{(l)}|=\sqrt{2(K-1)}{\Vert g_{G_C}({\mathrm{\Theta }}_{ij})\Vert }_1,$$

where the factor of $\sqrt{2(K-1)}$ can be absorbed into the tuning parameter for the FGL penalty. A similar argument can also be applied to the GGL penalty of Danaher et al. [6], ‖Θ_ij‖, by considering instead an empty graph G_e with no edges between nodes (Figure 2c). In this case, the mapping g_G would give a diagonal matrix with elements ${\mathrm{\theta }}_{ij}^{(k)}$, and hence ‖Θ_ij‖ = ‖g_Ge(Θ_ij)‖_F.

Unlike proposals of Danaher et al. [6], the estimator of Guo et al. [9] is based on a non-convex penalty, and does not naturally fit into the above framework. However, Lemma 2 in Guo et al. [9] establishes a connection between the optimal solutions of the original optimization problem, with those obtained by considering a single penalty of the form ${\{{\sum }_{k=1}^K|{\theta }_{ij}^{(k)}|\}}^{1/2}\equiv {\Vert {\mathrm{\Theta }}_{ij}\Vert }_{1,2}$. Similar to GGL, the connection with the method of Guo et al. [9] can be build based on the above alternative formulation, by considering again the empty graph G_e (Figure 2c), but instead the ‖·‖_1,2 penalty, which is a member of the CAP family of penalties [36]. More specifically,

$${\{\sum _{k=1}^K|{\omega }_{ij}^{(k)}|\}}^{1/2}={\Vert g_{G_e}({\mathrm{\Theta }}_{ij})\Vert }_{1,2}.$$

Using the above framework, it is also easy to see the connection between our proposed estimator and the proposal of Kolar et al. [13]: the total variation penalty in Kolar et al. [13] is closely related to FGL, with summation over differences in consecutive time points. It is therefore clear that the penalty of Kolar et al. [13] (up to constant multipliers) can be obtained by applying the graph Laplacian penalty defined for a line graph connecting the time points (Figure 2d).

The above discussion highlights the generality of the proposed estimator, and its connection to existing methods. In particular, while FGL and GGL/Guo et al. [9] consider extreme cases with isolated, or fully connected nodes, one can obtain more flexibility in estimation of multiple precision matrices by defining the penalty based on the known subpopulation network, e.g. based on phylogenetic trees or spatio-temporal similarities between fMRI samples. The clustering-based approach of Section 4 further extends the applicability of the proposed estimator to the settings where the subpopulation network in not known a priori. The simulation results in Section 6 show that the additional flexibility of the proposed estimator can result in significant improvements in estimation of multiple precision matrices, when K > 2. The above discussion also suggests that other variants of the proposed estimator can be defined, by considering other norms. We leave such extensions to future work.

3. Theoretical Properties

In this section, we establish norm and model selection consistency of the LASICH estimator. We consider a high-dimensional setting p ≫ n_k, k = 1, …, K, where both n and p go to infinity. As mentioned in the Introduction, the normality assumption is not required for establishing these results. We instead require conditions on tails of random vectors X^(k) for each k = 1, …, K. We consider two cases, exponential tails and polynomial tails, which both allow for distributions other than multivariate normal.

Condition 1 (Exponential Tails)

There exists a constant c₁ ∈ (0, ∞) such that

$$𝔼\left[\text{exp }\right\{t(X_j^{(k)}-{\mu }_j^{(k)})/{({\sigma }_{jj}^{(k)})}^{1/2}\left\}\right]\le e^{c_1^2{t}^2/2},\forall t\in ℝ,k=1,\dots ,K,j=1,\dots ,p.$$

Condition 2 (Polynomial Tails)

There exist constants c₂, c₃ > 0 and c₄such that

$$𝔼\left[{\{X_j^{(k)}/{({\sigma }_{jj}^{(k)})}^{1/2}\}}^{4(c_2+c_3+1)}\right]\le c_4,k=1,\dots ,K,j=1,\dots ,p.$$

Since we adopt the correlation-based Gaussian log-likelihood, we require the boundedness of the true variances to control the error between true and sample correlation matrices.

Condition 3 (Bounded variance)

There exist constants c₅ > 0 andc₆ < ∞ such that $c_5\le {\text{min}}_{k,j}{\sigma }_{jj}^{(k)}$and ${\text{max}}_{k,j}{\sigma }_{jj}^{(k)}\le c_6$.

Condition 4 (Sample size)

Let ${\lambda }_{\mathrm{\Theta }}\equiv {\text{max}}_k{\Vert {\mathrm{\Theta }}_0^{(k)}\Vert }_2$. Let

$$C_1\equiv {\{2c_5^{-2}+c_5+c_6^{-3/2}+2c_5^{-5/2}{c}_6+{(c_5^{-4}+2c_5^{-5}{c}_6)}^{1/2}\}}^{-1}.$$

1. (Exponential tails). It holds that

   $$n\ge \text{max }\{\frac{12}{{\text{min}}_k{\pi }_k},2^{18}{3}^3{C}_1^2{(1+4c_1^2)}^2{c}_6^2{\lambda }_{\mathrm{\Theta }}^4{(1+{\Vert L\Vert }_2^{1/2})}^{2}s\}\text{ log }p,$$

   and log p/n → 0.
2. (Polynomial tails). Let $C_2={\text{sup}}_n\{{\rho }_n\sqrt{n/\text{log }p}\}=O(1)$where ρ_nis given in Lemma 1 in theAppendixand c₇ > 0 be some constant. It holds that

   $$n\ge \text{max }\{\frac{p^{1/c_2}}{c_7^{1/c_2}},2^7{3}^2{C}_1^2{C}_2^{2}K\underset{k}{\text{ min }}{\pi }_k{\lambda }_{\mathrm{\Theta }}^4{(1+{\Vert L\Vert }_2^{1/2})}^{2}s\text{ log }p\}.$$

Condition 4 determines the sufficient sample size n = Σ_k for consistent estimation of precision matrices Θ⁽¹⁾, …, Θ^(K) in relation to, among other quantities, the number of variables p, the sparsity pattern s and the spectral norm of the Laplacian matrix ‖L‖₂ of the subpopulation network G. While a general characterization of ‖L‖₂ is difficult, investigating its value in special cases provides insight into the effect of the underlying population structure on the required sample size. Consider, for instance, two extreme cases: for a fully connected graph G associated with K subpopulations, ‖L‖₂ = 1/(K − 1); for a minimally connected “line” graph, corresponding to e.g. multiple time points, ‖L‖₂ = 2: with K = 5, 30% more samples are needed for the line graph, compared to a fully connected network. The above calculations match our intuition that fewer samples are needed to consistently estimate precision matrices of K subpopulations that share greater similarities. This, of course, makes sense, as information can be better shared when estimating parameters of similar subpopulations. Note that, here L represents the Laplacian matrix of the true subpopulation network capturing the underlying population structure. The above conditions thus do not provide any insight into the effect of misspecifying the relationship between subpopulations, i.e., when an incorrect L is used. This is indeed an important issue that garners additional investigation; see Zhao and Shojaie [37] for some insight in the context of inference for high dimensional regression. In Section 4, we will discuss a data-driven choice of L that results in consistent estimation of precision matrices.

Before presenting the asymptotic results, we introduce some additional notations. For a matrix $A={(a_{ij})}_{i,j=1}^p\in {ℝ}^{p\times p}$, we denote the spectral norm ‖A‖₂ = max_{x∈ℝ^p,‖x‖=1}‖Ax‖, and the element-wise ℓ_∞-norm ‖A‖_∞ = max_i,j |a_i,j| where ‖x‖ is the Euclidean norm for a vector x. We also write the induced ℓ_∞-norm ‖A‖_∞/∞ = sup_‖x‖∞=1‖Ax‖_∞ where ‖x‖_∞ = max_i |x_i| for x = (x₁, …, x_p). For the ease of presentation, the results in this section are presented in asymptotic form; non-asymptotic results and proofs are deferred to the Appendix.

3.1. Consistency in Spectral Norm

Let $s\equiv ⧣\{(i,j):{\omega }_{0,ij}^{(k)}\ne 0,i,j=1,\dots ,p,i\ne j,k=1,\dots ,K\}$, and $d={\text{max}}_{k,i}⧣\{(i,j):{\omega }_{0,ij}^{(k)}\ne 0,j=1,\dots ,p,i\ne j\}$. The following theorem establishes the rate of convergence of the LASICH estimator, in spectral norm, under either exponential or polynomial tail conditions (Condition 1 or 2). Convergence rates for LASICH in ℓ_∞-and Frobenius norm are discussed in Section 3.3.

Theorem 1

Suppose Conditions 3 and 4 hold. Under Condition 1 or 2,

$$\sum _{k=1}^K{\Vert {\hat{\mathrm{\Omega }}}_{{\rho }_n}^{(k)}-{\mathrm{\Omega }}_0^{(k)}\Vert }_2=O_P\left(\sqrt{\frac{{\lambda }_{\mathrm{\Theta }}^4(s+1)\text{ log }p}{n}}\right),$$

as n, p → ∞ where ρ_nis given in Lemma 1 in theAppendixwith γ = min_k π_k/2.

Theorem 1 is proved in the Appendix. The proof builds on tools from Negahban et al. [20]. However, our estimation procedure does not match their general framework: First, we do not penalize the diagonal elements of the inverse correlation matrices; our penalty is thus not a norm. Second, the Laplacian matrix is nonpositive definite. Thus, the Laplacian shrinkage penalty is not strictly convex. The results from Negahban et al. [20] are thus not directly applicable to our problem. To establish the estimation consistency, we first show, in Lemma 3, that the function r(·) = ‖·‖₁ + ρ₂‖·‖_L is a seminorm, and is, moreover, convex and decomposable. We also characterize the subdifferential of this seminorm in Lemma 6, based on the spectral decomposition of the graph Laplacian L. The rest of the proof uses tools from Negahban et al. [20], Rothman et al. [26] and Ravikumar et al. [25], as well as new inequalities and concentration bounds. In particular, in Lemma 4 we establish a new ℓ_∞ bound for the empirical covariance matrix for random variables with polynomial tails, which is used to established the consistency in the spectral norm under Condition 2.

The convergence rate in Theorem 1 compares favorably to several other methods based on penalized likelihood. Few results are currently available for estimation of multiple precision matrices. An exception is Guo et al. [9], who obtained a slower rate of convergence O_p({(s + p) log p/n}^1/2) under the normality assumption and based on a bound on the Frobenius norm. Our rates of convergence are comparable to the results of Rothman et al. [26] for spectral norm convergence of a single precision matrix, obtained under the normality assumption. Ravikumar et al. [25], on the other hand, assumed the irrepresentability condition to obtain the rate O_p({min{s + p, d²} log p/n}^1/2) and O_p({min{s + p, d²}p^{τ/(c₂+c₃+1)}/n}^1/2), under exponential and polynomial tail conditions, respectively, where τ > 2 is some scalar. The rate in Theorem 1 is obtained without assuming the irrepresentability condition. In fact, our rates of convergence are faster than those of Ravikumar et al. [25] given the irrepresentability condition 5 (see Corollary 1). Cai et al. [4] obtained improved rates of convergence under both tail conditions for an estimator that is not found by minimizing the penalized likelihood objective function, and may be nonpositive definite. Finally, note that the results in [4, 25, 26] are for separate estimation of precision matrices and hold for the minimum sample size across subpopulations, min_kn_k, whereas our results hold for the total samples size Σ_kn_k.

3.2. Model Selection Consistency

Let $S^{(k)}=\{(i,j):{\omega }_{0,ij}^{(k)}\ne 0,i,j=1,\dots ,p\}$ be the support of ${\mathrm{\Omega }}_0^{(k)}$, and denote by d the maximum number of nonzero elements in any rows of ${\mathrm{\Omega }}_0^{(k)}$, k = 1, …, K. Define the event

$$ℳ({\hat{\mathrm{\Omega }}}_{{\rho }_n},{\mathrm{\Omega }}_0)\equiv \{\text{sign}({\hat{\omega }}_{{\rho }_n,ij}^{(k)})=\text{sign}({\omega }_{0,ij}^{(k)}),i,j=1,\dots ,p,k=1,\dots ,K\},$$ (5)

where sign(a) is 1 if a > 0, 0 if a = 0 and −1 if a < 0. We say that an estimator Ω̂_ρn of Ω₀ is model-selection consistent if $P\left\{ℳ\right({\hat{\mathrm{\Omega }}}_{{\rho }_n},{\mathrm{\Omega }}_0\left)\right\}\to 1$.

We begin by discussing an irrepresentability condition for estimation of multiple graphical models. This restrictive condition is commonly assumed to establish model selection consistency of lasso-type estimators, and is known to be almost necessary [19, 35]. For the graphical lasso, Ravikumar et al. [25] showed that the irrepresentability condition amounts to a constraint on the correlation between entries of the Hessian matrix Γ = Ω⁻¹ ⊗ Ω⁻¹ in the set S corresponding to nonzero elements of Ω, and those outside this set. Our irrepresentability condition is motivated by that in Ravikumar et al. [25], however, we adjust the index set S to also account for covariances of “non-edge variables” that are correlated with each other. More specifically, the description of irrepresentability condition in Ravikumar et al. [25] involves Γ_SS consisting only of elements σ_ijσ_kl with (i, j) ∈ S and (k, l) ∈ S. However, σ_ij ≠ 0 for (i, j) ∉ S is not taken into account by this definition. We thus adjust the index set S so that Γ_SS also includes elements σ_ijσ_kl if (i, k) ∈ S and (j, l) ∈ S. This definition is based on the crucial observations that Γ = Σ ⊗ Σ involves the covariance matrix Σ instead of the precision matrix Ω, and that some variables are correlated (i.e., σ_ij ≠ 0) even though they may be conditionally independent (i.e., ω_ij = 0). Defining S^(k) for k = 1, …, K as above, we assume the following condition.

Condition 5 (Irrepresentability condition)

The inverse ${\mathrm{\Theta }}_0^{(k)}$of the correlation matrix ${\mathrm{\Psi }}_0^{(k)}$satisfies the irrepresentability condition for S^(k)with parameter α: (a) ${({\mathrm{\Theta }}_0^{(k)}\otimes {\mathrm{\Theta }}_0^{(k)})}_{S^{(k)}{S}^{(k)}}$and ${({\mathrm{\Psi }}_0^{(k)}\otimes {\mathrm{\Psi }}_0^{(k)})}_{S^{(k)}{S}^{(k)}}$are invertible, and (b) there exists some α ∈ (0, 1] such that

$$\underset{(i,j)\in {(S^{(k)})}^c}{\text{max}}{\Vert {\mathrm{\Gamma }}_{\{(i,j)\}\times S^{(k)}}^{(k)}{\{{\mathrm{\Gamma }}_{S^{(k)}{S}^{(k)}}^{(k)}\}}^{-1}\Vert }_1\le 1-\alpha ,$$ (6)

for k = 1, …, K where ${\mathrm{\Gamma }}^{(k)}\equiv {\mathrm{\Psi }}_0^{(k)}\otimes {\mathrm{\Psi }}_0^{(k)}$.

In addition to the irrepresentability condition, we require bounds on the magnitude of ${\theta }_{ij}^{(k)}\ne 0$ and their normalized difference.

Condition 6 (Lower bounds for the inverse correlation matrices)

There exists a constant c₈ ∈ ℝ such that

$${\theta }_{\text{min}}\equiv \underset{k=1,\dots ,K,i\ne j}{\text{min}}|{\theta }_{0,ij}^{(k)}|\ge c_8>0.$$

Moreover, for Ω_0,ij ≠ 0, LΩ_0,ij ≠ 0 and there exists a constant c₉ > 0 such that

$$\underset{l_{kk\prime }\ne 0,\frac{{\omega }_{0,ij}^{(k)}}{\sqrt{d_k}}-\frac{{\omega }_{0,ij}^{(k\prime )}}{\sqrt{d_{k\prime }}}\ne 0}{\text{min}}|\frac{{\theta }_{0,ij}^{(k)}}{\sqrt{d_k}}-\frac{{\theta }_{0,ij}^{(k\prime )}}{\sqrt{d_{k\prime }}}|\ge c_9.$$

The first lower bound in Condition 6 is the usual “min-beta” condition for model selection consistency of lasso-type estimators. The second lower bound, which is represented here for the normalized Laplacian penalty, is a mild condition which ensures estimates based on inverse correlation matrices can be mapped to precision matrices. For any pair of subpopulations k and k′ connected in G it requires that if the difference in (normalized) entries of the entires of the precision matrices are nonzero, the difference in (normalized) entries of inverse correlation matrices are bounded away from zero. In other words, the bound guarantees that Θ_0,ij is not in the null space of L, whenever Ω_0,ij is outside of the null space. This bound can be relaxed if we use a positive definite matrix L_ε = L + εI for ε > 0 small.

Our last condition for establishing the model selection consistency concerns the minimum sample size and the tuning parameter for the graph Laplacian penalty. This condition is necessary to control the ℓ_∞-bound of the error Θ̂_ρn − Θ₀, as in Ravikumar et al. [25]. Our minimum sample size requirement is related to the irrepresentability condition. Let κ_Γ be the maximum of the absolute column sums of the matrices {(Γ^(k))⁻¹}_S^(k)S^(k), k = 1, …, K, and κ_Ψ be the maximum of the absolute column sums of the matrices ${\mathrm{\Psi }}_0^{(k)}$, k = 1, …, K. The minimum sample size in Ravikumar et al. [25] is also a function of the irrepresentability constant, in particular, their κ_Γ involves ${\{({\mathrm{\Gamma }}_{S^{(k)}{S}^{(k)}}^{(k)})\}}^{-1}$. There is, therefore, a subtle difference between our definition and theirs: in our definition, the matrix is first inverted and then partitioned, while in Ravikumar et al. [25], the matrix is first partitioned and then inverted. Corollary 2 establishes the model selection consistency under a weaker sample size requirement, by exploiting instead the control of the spectral norm in Theorem 1.

Condition 7 (Sample size and regularization parameters)

Let

$$C_3=\text{max }\left\{\frac{2^6{3}^4{\kappa }_{\mathrm{\Psi }}^2{\kappa }_{\mathrm{\Gamma }}^2}{{\text{min}}_k{\pi }_k^2}\text{max }\right\{1,\frac{2^6{7}^2{\kappa }_{\mathrm{\Psi }}^4{\kappa }_{\mathrm{\Gamma }}^2}{{\alpha }^2{\text{ min}}_k{\pi }_k^2}\},\frac{36}{c_8^2},\frac{2^4{3}^2}{c_9^2{\text{ min}}_k{d}_k}\}$$

1. (Exponential tails). It holds

   $$n>\frac{12\text{ log }p}{{\text{min}}_k{\pi }_k}\text{max }\{1,2^6{3}^2{C}_1^2{(1+c_1^2)}^2{c}_6^2{C}_3{d}^2\}$$

2. (Polynomial tails). It holds $n>\text{max}\{p^{1/c_2}{c}_7^{-1/c_2},C_1^2{C}_2^2{C}_3{d}^2\text{ log }p\}$.

3. It holds that ${\rho }_2\le {\alpha }^2/\{4{\Vert L\Vert }_2^{1/2}(2-\alpha )\}$.

With these condition, we obtain

Theorem 2

Suppose that Conditions 3, 5, 6 and 7 hold. Under Condition 1 or 2, P(ℳ(Ω̂_ρn, Ω₀)) → 1 as n, p → ∞ where ρ_nis given in Lemma 1 in theAppendixwith γ = min_k π_k/2.

3.3. Additional Results

In this section, we establish norm and variable selection consistency of LASICH under alternative assumptions. Our first result gives better rates of convergence for consistency in the ℓ_∞-, spectral and Frobenius norms, under the condition for model selection consistency. Our rates in Corollary 1 improve the previous results by Ravikumar et al. [25], and are comparable to that of Cai et al. [4] in the ℓ_∞- and spectral norms under both tail conditions.

Corollary 1

Suppose the conditions in Theorem 2 hold. Then, under Condition 1 or 2,

$$\sum _{k=1}^K{\Vert {\hat{\mathrm{\Omega }}}_{{\rho }_n}^{(k)}-{\mathrm{\Omega }}_0^{(k)}\Vert }_F=O_P\left(\sqrt{\frac{\text{min}\{{\lambda }_{\mathrm{\Theta }}^{4}p(s+1),{\kappa }_{\mathrm{\Gamma }}^2(s+p)\}\text{ log }p}{n}}\right),$$

$$\sum _{k=1}^K{\Vert {\hat{\mathrm{\Omega }}}_{{\rho }_n}^{(k)}-{\mathrm{\Omega }}_0^{(k)}\Vert }_2=O_P\left(\sqrt{\frac{\text{min}\{{\lambda }_{\mathrm{\Theta }}^4(s+1),{\kappa }_{\mathrm{\Gamma }}^2{d}^2\}\text{ log }p}{n}}\right),$$

$$\sum _{k=1}^K{\Vert {\hat{\mathrm{\Omega }}}_{{\rho }_n}^{(k)}-{\mathrm{\Omega }}_0^{(k)}\Vert }_{\infty }=O_P\left(\sqrt{\frac{{\kappa }_{\mathrm{\Gamma }}^2\text{ log }p}{n}}\right).$$

Our next result in Corollary 2 establishes the model selection consistency under a weaker version of the irrepresentability condition (Condition 6). Aside from the difference in the index sets S^(k), the form of the Condition 6 and the assumption of invertibility of ${({\mathrm{\Psi }}_0^{(k)}\otimes {\mathrm{\Psi }}_0^{(k)})}_{S^{(k)}{S}^{(k)}}$ are similar to those in Ravikumar et al. [25]. On the other hand, Ravikumar et al. [25] do not require invertibility of ${({\mathrm{\Theta }}_0^{(k)}\otimes {\mathrm{\Theta }}_0^{(k)})}_{S^{(k)}{S}^{(k)}}$. However, their proof is based on an application of Brouwer’s fixed point theorem, which does not hold for the corresponding function (Eq. (70) in page 973) since it involves a matrix inverse, and is hence not continuous on its range. The additional inevitability assumption in Condition 6 is used to address this issue in Lemma 11. The condition can be relaxed if we assume an alternative scaling of the sample size stated in Condition 8 below instead of Condition 7.

Condition 8

Let ${\lambda }_{\mathrm{\Psi }}={\text{max}}_k\Vert {\mathrm{\Psi }}_0^{(k)}\Vert$. Suppose ${\rho }_2\le {\alpha }^2/\{4{\Vert L\Vert }_2^{1/2}(2-\alpha )\}$and

1. (Exponential tails)

   $$n>2^{19}{3}^3{\{\underset{k}{\text{min }}{\pi }_k\}}^{-3}{C}_1^2{(1+4c_1^2)}^2{c}_6^2{\lambda }_{\mathrm{\Theta }}^4{(1+{\rho }_2{\Vert L\Vert }_2^{1/2})}^{2}s\text{ log }p\text{ max}\{{\lambda }_{\mathrm{\Psi }},4{\lambda }_{\mathrm{\Theta }}^4{\alpha }^{-1}\},$$

   or
2. (Polynomial tails)

   $$n>2^{12}{3}^3{\{\underset{k}{\text{min }}{\pi }_k\}}^{-2}{K}^2{C}_1^2{C}_2^2{\lambda }_{\mathrm{\Theta }}^4{(1+{\rho }_2{\Vert L\Vert }_2^{1/2})}^{2}s\text{ log }p\text{ max}\{{\lambda }_{\mathrm{\Psi }},4{\lambda }_{\mathrm{\Theta }}^4{\alpha }^{-1}\}.$$

Corollary 2

Suppose that Conditions 3, 6 and 8 hold. Suppose also that Condition 5 holds without requiring the invertibility of ${({\mathrm{\Theta }}_0^{(k)}\otimes {\mathrm{\Theta }}_0^{(k)})}_{S^{(k)}{S}^{(k)}}$. Then, under Condition 1 or 2, P(ℳ(Ω̂_ρn, Ω₀)) → 1 as n, p → ∞ where ρ_nis given in Lemma 1 in theAppendix with γ = min_k π_k/2.

4. Laplacian Shrinkage based on Hierarchical Clustering

Our proposed LASICH approach utilizes the information in the subpopulation network G. In practice, however, similarity between subpopulations may be difficult to ascertain or quantify. In this section, we present a modified LASICH framework, called HC-LASICH, which utilizes hierarchical clustering to learn the relationships among subpopulations. The information from hierarchical clustering is then used to define the weighted subpopulation network. Importantly, HC-LASICH can even be used in settings where the subpopulation membership is unavailable, for instance, to learn the genetic network of cancer patients, where cancer subtypes may be unknown.

We use hierarchical clustering with a complete, single or average linkage to estimate both the subpopulation memberships and the weighted subpopulation network G. Specifically, the length of a path between two subpopulations in the dendrogram is used as a measure of dissimilarity between two subpopulations; the weights for the subpopulation networks are simply defined by taking the inverse of these lengths. Throughout this section, we assume that the number of subpopulations K is known. While a number of methods have been proposed for estimating the number of subpopulations in hierarchical clustering (see e.g. Borysov et al. [1] and the references therein), the problem is beyond the scope of this paper.

Let I = (I⁽¹⁾, …, I^(K)) be the subpopulation membership indicator such that I follows the multinomial distribution Mult_K (1, (π₁, …, π_K)) with parameter 1 and subpopulation membership probabilities (π₁, …, π_K) ∈ (0, 1)^K. Note that I is missing and is to be estimated. Let I_i, i = 1, …, n be i.i.d. copies of I and ${\hat{I}}_i=({\hat{I}}_i^1,\dots ,{\hat{I}}_i^K)$ be an estimated subpopulation indicator for the ith observation via hierarchical clustering. Based on the estimated subpopulation membership and subpopulation network Ĝ, we apply our method to obtain the estimator, HC-LASICH, ${\hat{\mathrm{\Omega }}}_{HC,{\rho }_n}=({\hat{\mathrm{\Omega }}}_{HC,{\rho }_n}^{(1)},\dots ,{\hat{\mathrm{\Omega }}}_{HC,{\rho }_n}^{(K)})$. Interestingly, HC-LASICH enjoys the same theoretical properties as LASICH, under the normality assumption. To show this, we first establish the consistency of hierarchical clustering in high dimensions, which is of independent interest. Our result is motivated by the recent work of [1], who study the consistency of hierarchical clustering for independent normal variables X^(k) ~ N(μ^(k), σ^(k)I); we establish similar results for multivariate normal distributions with arbitrary covariance structures. We make the following assumption.

Condition 9

For k, k′ = 1, …, K, let

$${\overline{\lambda }}^{(k)}=p^{-1}\sum _{j=1}^p{\lambda }^{(k),j},$$

$${\mu }^{(k,k\prime )}=p^{-1}{\Vert {\mathrm{\Lambda }}_{k,k\prime }^{1/2}{Q}_{k,k\prime }^T{[{\mathrm{\Sigma }}^{(k)}+{\mathrm{\Sigma }}^{(k\prime )}]}^{1/2}[{\mu }^{(k)}-{\mu }^{(k\prime )}]\Vert }^2,$$

where λ^(k),jis the eigenvalues of Σ^(k)with λ^(k),1 ≤ λ^(k),2 ≤ … ≤ λ^(k),p, and the spectral decomposition of Σ^(k) + Σ^(k′)is ${\mathrm{\Sigma }}^{(k)}+{\mathrm{\Sigma }}^{(k\prime )}=Q_{k,k\prime }{\mathrm{\Lambda }}_{k,k\prime }{Q}_{k,k\prime }^T$. It holds that

$${\mu }^{(k,k\prime )}>2\text{ min }\{{\overline{\lambda }}^{(k)},{\overline{\lambda }}^{(k\prime )}\}-{\lambda }^{(k),p}-{\lambda }^{(k\prime ),p},k\ne k\prime ,k,k\prime =1,\dots ,K,$$

$$0<c_{10}\le {\lambda }^{(k),j}\le c_{11}<\infty ,\Vert {\mu }^{(k)}\Vert \le c_{11},k=1,\dots ,K,j=1,\dots ,p.$$

for constants m and M.

Under the normality assumption, the following results shows that the probability of successful clustering converges to 1, as p, n → ∞.

Theorem 3

Suppose that that X^(k), k = 1, …, K, is normally distributed. Under Condition 9,

$$P({\hat{I}}_i=I_i,i=1,\dots ,n)\to 1,$$ (7)

as n, p → ∞.

To proof of Theorem 3 generalizes recent results of Borysov et al. [1] to the case of arbitrary covariance structures. A key component of the proof is a new bound on the ℓ₂ norm of a multivariate normal random variable with arbitrary mean and covariance matrix established in Lemma 14. The proof of the lemma uses new concentration inequalities for high-dimensional problems in [2], and may be of independent interest.

Note that the consistent estimation of subpopulation memberships (7) implies that the estimated hierarchy among clusters also matches the true hierarchy. Thus, with successful clustering established in Theorem 3, theoretical properties of Ω̂_{HC, ρn} naturally follow.

Theorem 4

Suppose that X^(k), k = 1, …, K, is normally distributed and that Condition 9 holds. (i) Under the conditions of Theorem 1,

$$\sum _{k=1}^K{\Vert {\hat{\mathrm{\Omega }}}_{HC,{\rho }_n}^{(k)}-{\mathrm{\Omega }}_0^{(k)}\Vert }_2=O_P\left(\sqrt{\frac{{\lambda }_{\mathrm{\Theta }}^4(s+1)\text{ log }p}{n}}\right).$$

Suppose, moreover, that the conditions of Theorem 2 holds. Then

$$\sum _{k=1}^K{\Vert {\hat{\mathrm{\Omega }}}_{HC,{\rho }_n}^{(k)}-{\mathrm{\Omega }}_0^{(k)}\Vert }_F=O_P\left(\sqrt{\frac{\text{min}\{{\lambda }_{\mathrm{\Theta }}^{4}p(s+1),{\kappa }_{\mathrm{\Gamma }}^2(s+p)\}\text{ log }p}{n}}\right),$$

$$\sum _{k=1}^K{\Vert {\hat{\mathrm{\Omega }}}_{HC,{\rho }_n}^{(k)}-{\mathrm{\Omega }}_0^{(k)}\Vert }_2=O_P\left(\sqrt{\frac{\text{min}\{{\lambda }_{\mathrm{\Theta }}^4(s+1),{\kappa }_{\mathrm{\Gamma }}^2{d}^2\}\text{ log }p}{n}}\right),$$

$$\sum _{k=1}^K{\Vert {\hat{\mathrm{\Omega }}}_{HC,{\rho }_n}^{(k)}-{\mathrm{\Omega }}_0^{(k)}\Vert }_{\infty }=O_P\left(\sqrt{\frac{{\kappa }_{\mathrm{\Gamma }}^2\text{ log }p}{n}}\right).$$

(ii) Under the conditions of Theorem 2,

$$P(ℳ({\hat{\mathrm{\Omega }}}_{HC,{\rho }_n},{\mathrm{\Omega }}_0))\to 1,\mathit{\text{ as }}n,p\to \infty .$$

5. Algorithms

We develop an alternating directions method of multipliers (ADMM) to efficiently solve the convex optimization problem (3).

Let $A^{(k)}={(a_{ij}^{(k)})}_{i,j=1}^p\in {ℝ}^{p\times p},B^{(k)}={(b_{ij}^{(k)})}_{i,j=1}^p\in {ℝ}^{p\times p},C^{(k)}={(c_{ij}^{(k)})}_{i,j=1}^p\in {ℝ}^{p\times p},D^{(k)}={(d_{ij}^{(k)})}_{i,j=1}^p\in {ℝ}^{p\times p}$, k = 1, … K. Define A = (A⁽¹⁾, …, A^(K)), B = (B⁽¹⁾, …, B^(K)), C = (C⁽¹⁾, …, C^(K)), D = (D⁽¹⁾, …, D^(K)), and $c_{ij}\equiv {(c_{ij}^{(1)},\dots ,c_{ij}^{(K)})}^T\in {ℝ}^K,d_{ij}\equiv {(d_{ij}^{(1)},\dots ,d_{ij}^{(K)})}^T\in {ℝ}^K,e_{C,ij}\equiv {(e_{C,ij}^{(1)},\dots ,e_{C,ij}^{(K)})}^T\in {ℝ}^K$ where $E_C^{(k)}={(e_{C,ij}^{(k)})}_{i,j=1}^p$.

To facilitate the computation, we consider instead a perturbed graph Laplacian L_ε = L + εI, where I is the identity matrix and ε > 0 is a small perturbation. The difference between solutions to the original and modified optimization problem is largely negligible for small ε; however, the positive definiteness of L_ε results in more efficient computation. A similar idea was used in Guo et al. [9] and Rothman et al. [26] to avoid dividision by zero. The optimization problem (3) with L replaced by L_ε can then be written as

$$\text{minimize}\sum _{k=1}^K\frac{n_k}{n}\left(\text{tr }\right({\mathrm{\Psi }}_n^{(k)}{A}^{(k)})-\text{log det}(A^{(k)}))+{\rho }_n\sum _{k=1}^K{\Vert B^{(k)}\Vert }_1+{\rho }_n{\rho }_2\sum _{i\ne j}{(c_{ij}^T{L}_{\epsilon }{c}_{ij})}^{1/2}$$ (8)

$$\mathrm{s}.\mathrm{t}.A^{(k)}=D^{(k)},B^{(k)}=D^{(k)},L_{\epsilon }{c}_{ij}=L_{\epsilon }{d}_{ij}k=1,\dots ,K,i,j=1,\dots ,p.$$

Using Lagrange multipliers E = (E_A, E_B, E_C)^T, with $E_A=(E_A^{(1)},\dots ,E_A^{(K)})$ with $E_A^{(k)}\in {ℝ}^{p\times p}$, k = 1, …, K, $E_B=(E_B^{(1)},\dots ,E_B^{(K)})$ with $E_B^{(k)}\in {ℝ}^{p\times p}$, k = 1, …, K, and $E_C=(E_C^{(1)},\dots ,E_C^{(K)})$ with $E_C^{(k)}\in {ℝ}^{p\times p}$, k = 1, …, K, the augmented Lagrangian in scaled form is given by

$$L_{\varrho }(A,B,C,D,E)\equiv n^{-1}\sum _{k=1}^K{n}_k\left(\text{tr }\right({\mathrm{\Psi }}_n^{(k)}{A}^{(k)})-\text{log det}(A^{(k)}))+{\rho }_n\sum _{k=1}^K{\Vert B^{(k)}\Vert }_1+{\rho }_n{\rho }_2\sum _{i\ne j}{(c_{ij}^T{L}_{\epsilon }{c}_{ij})}^{1/2}+\frac{\varrho }{2}\sum _{k=1}^K{\Vert A^{(k)}-D^{(k)}+E_A^{(k)}\Vert }_F^2+\frac{\varrho }{2}\sum _{k=1}^K{\Vert B^{(k)}-D^{(k)}+E_B^{(k)}\Vert }_F^2+\frac{\varrho }{2}\sum _{i,j}{\Vert L_{\epsilon }^{1/2}{c}_{ij}-L_{\epsilon }^{1/2}{d}_{ij}+e_{C,ij}\Vert }_F^2.$$

Here ϱ > 0 is a regularization parameter and $L_{\epsilon }^{1/2}$ is the square root of L_ε with $L_{\epsilon }={(L_{\epsilon }^{1/2})}^T{L}_{\epsilon }^{1/2}$.

The proposed ADMM algorithm is as follows.

• Step 0. Initialize A^(k) = A^(k),0, B^(k) = B^(k),0, C^(k) = C^(k),0, D^(k) = D^(k),0, $E_A^{(k)}=E_A^{(k),0},E_B^{(k)}=E_B^{(k),0},E_C^{(k)}=E_C^{(k),0}$ and choose ϱ > 0. Select a scalar ϱ > 0.

• Step m. Given the (m − 1)th estimates,

  • –
    (Update A^(k)) Find A^m minimizing $-{\ell }_n(A)-(\varrho /2){\sum }_{k=1}^K\Vert A^{(k)}-D^{(k),m-1}-E_A^{(k),m-1}\Vert$ (see pages 46–47 of Boyd et al. [3] for details).
  • –
    (Update B^(k)) Compute $B_{ij}^{(k),m}=S_{{\rho }_n/\varrho }(D_{ij}^{(k),m-1}-E_{B,ij}^{(k),m-1})$, where S_y(x) is x − y if x > y, is 0 if |x| ≤ y, and is x + y if x < −y.
  • –
    (Update C^(k)) For (x)₊ = max{x, 0}, compute

    $$c_{ij}^m={(1-\frac{{\rho }_n{\rho }_2}{\varrho \Vert L_{\epsilon }^{1/2}{d}_{ij}^{m-1}-e_{C,ij}^{m-1}\Vert })}_{+}(d_{ij}^{m-1}-L_{\epsilon }^{-1/2}{e}_{C,ij}^{m-1}).$$
  • –
    (Update D^(k)) Compute

    $$d_{ij}^m={(2I+L_{\epsilon })}^{-1}\{a_{ij}^m+e_{A,ij}^{m-1}+b_{ij}^m+e_{B,ij}^{m-1}+L_{\epsilon }{c}_{ij}^m+{(L_{\epsilon }^{1/2})}^T{e}_{C,ij}^{m-1}\}.$$
  • –
    (Update E_A) Compute $E_A^{(k),m}=E_A^{(k)}+A^{(k),m}-D^{(k),m}$.
  • –
    (Update E_B) Compute $E_B^{(k),m}=E_B^{(k)}+B^{(k),m}-D^{(k),m}$,
  • –
    (Update E_C) Compute $e_{C,ij}^{(k),m}=e_{C,ij}^{(k)}+L^{1/2}(c_{ij}^{(k),m}-d_{ij}^{(k),m})$.

• Repeat the iteration until the maximum of the errors $r_A^{(k)}=A^{(k)}-D^{(k)},r_B^{(k),m}=B^{(k),m}-D^{(k),m},r_C^{(k),m}=C^{(k),m}-D^{(k),m}$, s^(k),m = ϱ(D^(k),m − D^(k),m−1) in the Frobenius norm is less than a specified tolerance level.

The proposed ADMM algorithm facilitates the estimation of parameters of moderately large problems. However, parameter estimation in high dimensions can be computationally challenging. We next present a result that determines whether the solution to the optimization problem (3), for given values of tuning parameters ρ_n, ρ₂, is block diagonal. (Note that this result is an exact statement about the solution to (3), and does not assume block sparsity of the true precision matrices; see Theorems 1 and 2 of Danaher et al. [6] for similar results.) More specifically, the condition in Proposition 1 provides a very fast check, based on the entries of the empirical correlation matrices ${\mathrm{\Psi }}_n^{(k)}$, k = 1, …, K, to identify the block sparsity pattern in ${\hat{\mathrm{\Omega }}}_{{\rho }_n}^{(k)}$, k = 1, …, K after some permutation of the features.

Let U_L = [u₁ … u_K] ∈ ℝ^K×K where u₁, …, u_K’s are eigenvectors of L corresponding to 0, λ_L,2, …, λ_L,K. Define ${\mathrm{\Lambda }}_L^{-1/2}$ as the diagonal matrix with diagonal elements 0, ${\lambda }_{L,2}^{-1/2},\dots ,{\lambda }_{L,K}^{-1/2}$.

Proposition 1

The solution ${\hat{\mathrm{\Omega }}}_{{\rho }_n}^{(k)}$, k = 1, …, Kto the optimization problem(3)consists of the block diagonal matrices with the same block structure diag(Ω₁, …, Ω_B) among all groups if and only if for ${\mathrm{\Psi }}_{n,ij}={({\psi }_{n,ij}^{(1)},\dots ,{\psi }_{n,ij}^{(K)})}^T$

$$\underset{\upsilon \in {[-1,1]}^K}{\text{min}}\Vert {\mathrm{\Lambda }}_L^{-1/2}{U}_L(\frac{n_k}{n}{\mathrm{\Psi }}_{n,ij}-{\rho }_n\upsilon )\Vert \le {\rho }_n{\rho }_2,$$ (9)

and for all i, j such that the (i, j) element is outside the blocks.

The proof of the Proposition is similar to Theorems 1 of Danaher et al. [6] and is hence omitted. Condition 9 can be easily verified by applying quadratic programming to the left hand side of the inequality. The solution to (3) can then be equivalently found by solving the optimization problem separately for each of the blocks; this can result in significant computational advantages for moderate to large values of ρ_nρ₂.

6. Numerical Results

6.1. Simulation Experiments

We compare our method with four existing methods, graphical lasso, the method of Guo et al. [9], FGL and GGL of Danaher et al. [6]. For graphical lasso, estimation was carried out separately for each group with the same regularization parameter.

Our simulation setting is motivated by estimation of gene networks for healthy subjects and patients with two similar diseases caused by inactivation of certain biological pathways. We consider K = 3 groups with sample sizes n = (50, 100, 50) and dimension p = 100. Data are generated from multivariate normal distributions $N({\mu }^{(k)},{({\mathrm{\Omega }}_0^{(k)})}^{-1})$, k = 1, 2, 3; all precision matrices ${\mathrm{\Omega }}_0^{(k)}$ are block diagonal with 4 blocks of equal size.

To create the precision matrices, we first generated a graph with 4 components of equal size, each as either an Erdős-Rényi or scale free graphs with 95 total edges. We randomly assigned Unif((−7, −5) ∪ (.5, .7)) values to nonzero entries of the corresponding adjacency matrix A and obtained a matrix Ã. We then added 0.1 to the diagonal of à to obtain a positive definite matrix ${\mathrm{\Omega }}_0^{(1)}$. For each of subpopulations 2 and 3, we removed one of the components of the graph by setting the off diagonal entries of à to zero, and added a perturbation from Unif(−2, .2) to nonzero entries in Ã. Positive definite matrices ${\mathrm{\Omega }}_0^{(2)}$ and ${\mathrm{\Omega }}_0^{(3)}$ were obtained by adding 0.1 to the diagonal elements. All partial correlations ranges from .28 to .54 in the absolute values. A similar setting was considered in in Danaher et al. [6], where the graph included more components, but no perturbation was added. We consider two simulation settings, with known and unknown subpopulation network G.

6.1.1. Known subpopulation network G

In this case, we set μ^(k) = 0, k = 1, 2, 3 and use the graph in Figure 1 as the subpopulation network.

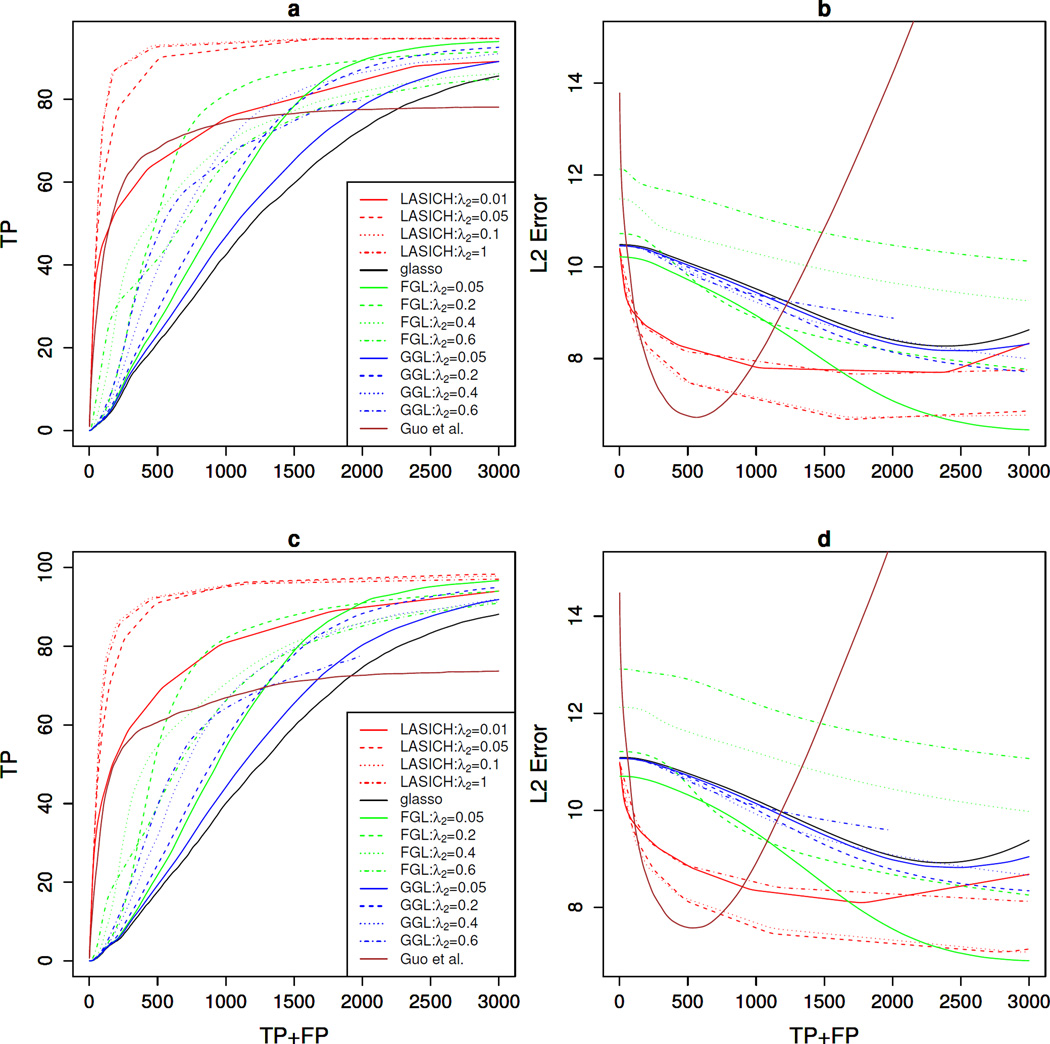
Figures 3a,c show the average number of true positive edges versus the average number of detected edges over 50 simulated data sets. Results for multiple choices of the second tuning parameter are presented for FGL, GGL and LASICH. It can be seen that in both cases, LASICH outperforms other methods, when using relatively large values of ρ₂. Smaller values of ρ₂, on the other hand, give similar results as other methods of joint estimation of multiple graphical models. These results indicate that, when the available subpopulation network is informative, the Laplacian shrinkage constraint can result in significant improvement in estimation of the underlying network.

Fig 3.

Simulation results for joint estimation of multiple precision matrices with known subpopulation memberships. Results show the average number of true positive edges (a & c) and estimation error, in Frobenius norm (b & d) over 50 data sets with n = 200 multivariate normal observations generated from a graphical model with p = 100 features; results in top row (a & b) are for an Erdős-Rényi graph and those in bottom row (c & d) are for a scale free (power-law) graph.

Figures 3b,d show the estimation error, in Frobenius norm, versus the number of detected edges. LASICH has larger errors when the estimated graphs have very few edges, but, its error decreases as the number of detected edges increase, eventually yielding smaller errors than other methods. The non-convex penalty of Guo et al. [9] performs well in terms of estimation error, although determining the appropriate range of tuning parameter for this method may be difficult.

6.1.2. Unknown subpopulation network G

In this case, the subpopulation memberships and the subpopulation network G are estimated based on hierarchical clustering. We randomly generated μ⁽¹⁾ from a multivariate normal distribution with a covariance matrix σ²I. For subpopulations 2 and 3, the elements of μ⁽¹⁾ corresponding to the empty components of the graph were set to zero to obtain μ⁽²⁾ and μ⁽³⁾. Hierarchical clustering with complete linkage was applied to data to obtain the dendrogram; we took inverse of distances in the dendrogram to obtain similarity weights used in the graph Laplacian.

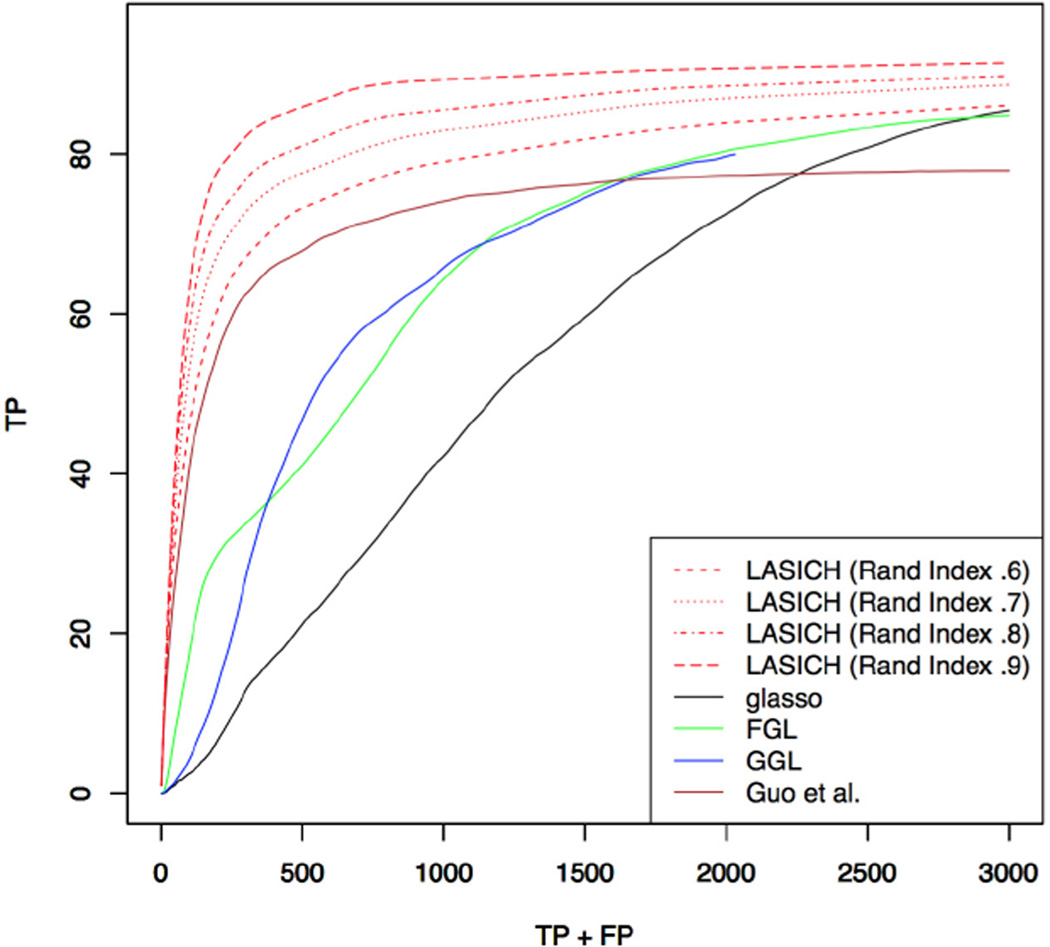
Figures 4 compares the performance of HC-LASICH, in terms of support recovery, to competing methods, in the setting where the subpopulation memberships and network are estimated from data (Section 4). Here the differences in subpopulation means μ^(k,k′) are set up to evaluate the effect of clustering accuracy. The four settings considered correspond to average Rand indices of .6 .7, .8 and .9 across 50 data sets, respectively. Here the second tuning parameter for HC-LASICH, GGL and FGL is chosen according to the best performing model in Figure 3. As expected, changing the mean structure, and correspondingly the Rand index, does not affect the performance of other methods. The results indicate that, as long as features can be clustered in a meaningful way, HC-LASICH can result in improved support recovery. Data-adaptive choices of the tuning parameter corresponding to the Laplacian shrinkage penalty may result in further improvements in the performance of the HC-LASICH. However, we do not pursue such choices here.

Fig 4.

Simulation results for joint estimation of multiple precision matrices with unknown subpopulation memberships. Results show the average number of true positive edges over 50 data sets with n = 200 multivariate normal observations generated from a graphical model with over an Erdős-Rényi graph with p = 100 features. Results for HC-LASICH and FGL/GGL correspond to the best choice of the second tuning parameter among those in Figure 3a. The Rand indices for HC-LASICH are averages over 50 generated data sets.

6.2. Genetic Networks of Cancer Subtypes

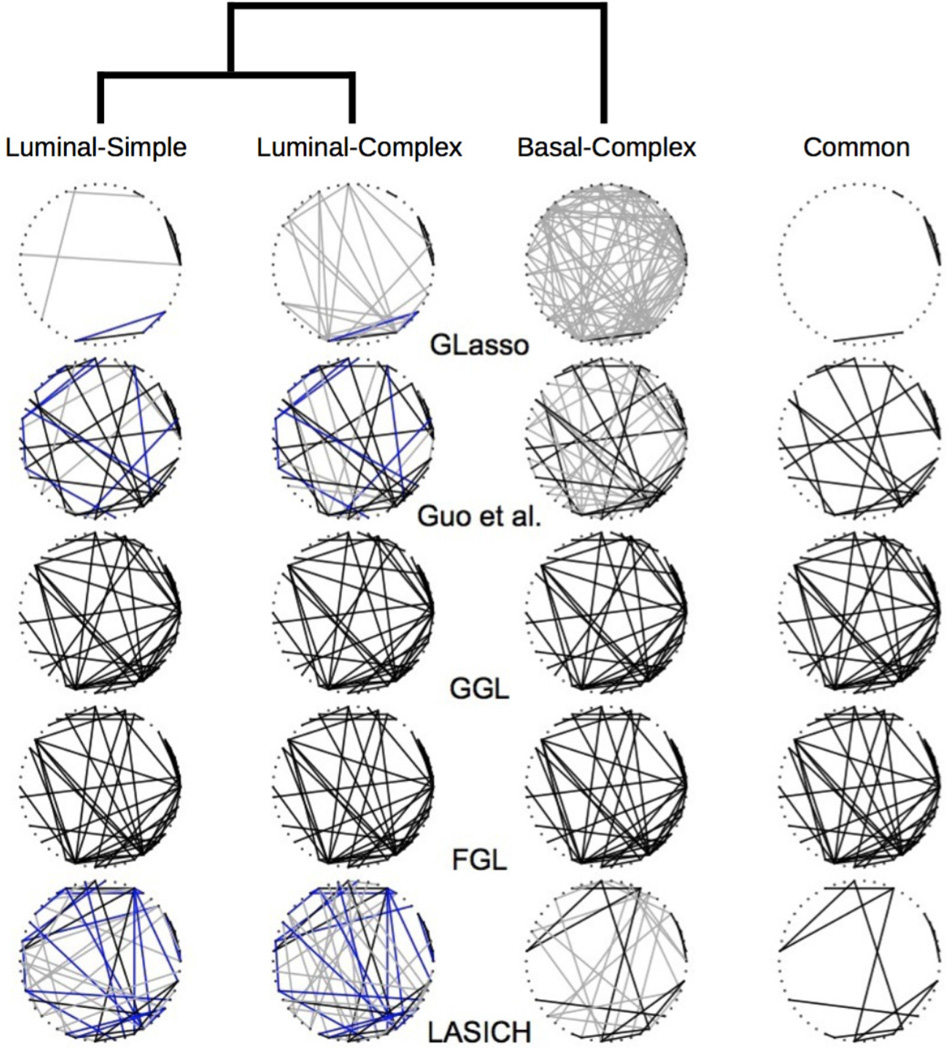
Breast cancer is heterogenous with multiple clinically verified subtypes [22]. Jönsson et al. [12] used copy number variation and gene expression measurements to identify new subtypes of breast cancer and showed that the identified subtypes have distinct clinical outcomes. The genetic networks of these different subtypes are expected to share similarities, but to also have unique features. Moreover, the similarities among the networks are expected to corroborate with the clustering of the subtypes based on their molecular profiles. We applied network estimation methods of Section 6.1 to a subset of the microarray gene expression data from Jönsson et al. [12], containing data for 218 patients classified into three previously known subtypes of breast cancer: 46 Luminal-simple, 105 Luminal-complex and 67 Basal-complex samples. For ease of presentation, we focused on 50 genes with largest variances. The hierarchical clustering results of Jönsson et al. [12], reproduced in Figure 5 for the above three subtypes, were used to identify the subpopulation membership; reciprocals of distances in the dendrogram were used to define similarities among subtypes used in the graph Laplacian penalty.

Fig 5.

Dendrogram of hierarchical clustering of three subtypes of breast cancer from Jönsson et al. (2010) along with estimated gene networks using graphical lasso (Glasso), method of Guo et al., FGL and GGL of Daneher et al. (2014) and LASICH. Blue edges are common to Luminal subtypes and black edges are shared by all three subtypes; condition specific edges are drawn in gray.

To facilitate the comparison, tuning parameters were selected such that the estimated networks of the three subtypes using each method contained a total of 150 edges. For methods with two tuning parameters, pairs of tuning parameters were determined using the Bayesian information criterion (BIC), as described in Guo et al. [9]. Estimated genetic networks of the three cancer subtypes are shown in Figure 5. For each method, edges common in all three subtypes, those common in Luminal subtypes and subtype specific edges are distinguished.

In this example, separate graphical lasso estimates and FGL/GGL estimates are two extremes. Estimated network topologies from graphical lasso vary from subtype to subtype, and common structures are obscured; this variability may be because similarities among subtypes are not incorporated in the estimation. In contrast, FGL and GGL give identical networks for all subtypes, perhaps because both methods encourage the estimated networks of all subtypes to be equally similar. Intermediate results are obtained using LASICH and the method of Guo et al. [9]. The main difference between these two methods is that Guo et al. [9] finds more edges common to all three subtypes, whereas LASICH finds more edges common to the Luminal subtypes. This difference is likely because LASICH prioritizes the similarity between the Luminal subtypes via graph Laplacian while the method of Guo et al. [9] does not distinguish between the three subtypes. The above example highlights the potential advantages of LASICH in providing network estimates that better corroborate with the known hierarchy of subpopulations.

7. Discussion

We introduced a flexible method for joint estimation of multiple precision matrices, called LASICH, which is particularly suited for settings where observations belong to three or more subpopulations. In the proposed method, the relationships among heterogenous subpopulations is captured by a weighted network, whose nodes correspond to subpopulations, and whose edges capture their similarities. As a result, LASICH can model complex relationships among subpopulations, defined, for example, based on hierarchical clustering of samples.

We established asymptotic properties of the proposed estimator in the setting where the relationship among subpopulations is externally defined. We also extended the method to the setting of unknown relationships among subpopulations, by showing that clusters estimated from the data can accurately capture the true relationships. The proposed method generalizes existing convex penalties for joint estimation of graphical models, and can be particularly advantageous in settings with multiple subpopulations.

A particularly appealing feature of the proposed extension of LASICH is that it can also be applied in settings where the subpopulation memberships are unknown. The latter setting is closely related to estimation of precision matrices for mixture of Gaussian distributions. Both approaches have limitations and drawbacks: on the one hand, the extension of LASICH to unknown subpopulation memberships requires certain assumptions on differences of population means (Section 4). On the other hand, estimation of precision matrices for mixture of Gaussians is computationally challenging, and known rates of convergence of parameter estimation in mixture distributions (e.g. in Städler et al. [29]) are considerably slower.

Throughout this paper we assumed that the number of subpopulations is known. Extensions of this method to estimation of graphical models in populations with an unknown number of subpopulations would be particularly interesting for analysis of genetic networks associated with heterogeneity in cancer samples, and are left for future research.

Appendix

8. Appendix: Proofs and Technical Detials

We denote true inverse correlation matrices as ${\mathrm{\Theta }}_0=({\mathrm{\Theta }}_0^{(1)},\dots ,{\mathrm{\Theta }}_0^{(K)})$ and true correlation matrices as ${\mathrm{\Psi }}_0=({\mathrm{\Psi }}_0^{(1)},\dots ,{\mathrm{\Psi }}_0^{(K)})$, where ${\mathrm{\Theta }}_0^{(k)}\equiv {({\mathrm{\Psi }}_0^{(k)})}^{-1}\equiv {({\theta }_{0,ij}^{(k)})}_{i,j=1}^p$, and ${\mathrm{\Psi }}_0^{(k)}={({\psi }_{0,ij}^{(k)})}_{i,j=1}^p$. The estimates of the population parameters are dented as ${\hat{\mathrm{\Sigma }}}_n^{(k)}={({\hat{\sigma }}_{ij})}_{i,j=1}^p,{\mathrm{\Psi }}_n^{(k)}={({\psi }_{n,ij})}_{i,j=1}^p$, and ${\hat{\mathrm{\Theta }}}_{{\rho }_n}^{(k)}={({\hat{\theta }}_{{\rho }_n,ij}^{(k)})}_{i,j=1}^p$. For a vector x = (x₁, …, x_p)^T and J ⊂ {1, …, p}, we denote x_J = (x_j, j ∈ J)^T. For a matrix A, λ_k(A) is the kth smallest eigenvalue and A⃗ is the vectorization of A. For J ⊂ {(i, j) : i, j = 1, …, p} and A ∈ ℝ^p×p, A⃗_J is a vector in ℝ^|J| obtained by removing elements corresponding to (i, j) ∉ J from A⃗. A zero-filled matrix A_J ∈ ℝ^p×p is obtained from A by replacing a_ij by 0 for (i, j) ∉ J.

8.1. Consistency in Matrix Norms

Theorem 1 is a direct consequence of the following result.

Lemma 1

1. Suppose that Condition 1 holds. Let γ ∈ (0, min_k π_k) be arbitrary. For

   $$n\ge \text{max }\{\frac{6}{\gamma }\text{log }p,\frac{2^{15}{3}^3{C}_1^2}{{\gamma }^3}{(1+4c_1^2)}^2\underset{k,i}{\text{max}}{\{{\sigma }_{ii}^{(k)}\}}^2{\lambda }_{\mathrm{\Theta }}^4{(1+{\rho }_2{\Vert L\Vert }_2^{1/2})}^{2}s\text{ log }p\}$$

   and ${\rho }_n=2^3\sqrt{6}{C}_1(1+4c_1^2){\gamma }^{-1/2}{\text{ max}}_{k,i}{\sigma }_{ii}^{(k)}\sqrt{\text{log }p/n}$, we have with probability (1 − 2K/p)(1 − 2K exp(−2n(min_k π_k − γ)²)) that

   $$\sum _{k=1}^K{\Vert {\hat{\mathrm{\Theta }}}_{{\rho }_n}^{(k)}-{\mathrm{\Theta }}_0^{(k)}\Vert }_F\le \frac{2^{15/2}{3}^{3/2}{C}_1}{{\gamma }^{3/2}}(1+4c_1^2)\underset{k,i}{\text{max}}{\sigma }_{ii}^{(k)}{\lambda }_{\mathrm{\Theta }}^2(1+{\rho }_2{\Vert L\Vert }_2^{1/2})\sqrt{\frac{s\text{ log }p}{n}}.$$
2. Suppose that Condition 2 holds with p ≤ c₇n^c₂, c₂, c₃, c₇ > 0. For ρ_n = C₁Kδ_nsatisfying

   $$2^4{3}^2{C}_1{\rho }_n^2{\gamma }^{-2}s{(1+{\rho }_2{\Vert L\Vert }_2^{1/2})}^2{\lambda }_{\mathrm{\Theta }}^4\le 1/4$$

   and $\tau >(2^7+2^3\sqrt{1+2^4{3}^2{c}_4{\text{ max}}_{k,i}{\{{\sigma }_{ii}^{(k)}\}}^2})/(9c_4{\text{ max}}_{k,i}{\{{\sigma }_{ii}^{(k)}\}}^2)$we have with probability (1 − 2K exp(−2n(min_k π_k − γ)²))ν _nthat

   $$\sum _{k=1}^K{\Vert {\hat{\mathrm{\Theta }}}_{{\rho }_n}^{(k)}-{\mathrm{\Theta }}_0^{(k)}\Vert }_F\le 2^4{3}^{3/2}{C}_1{\gamma }^{-2}K(1+{\rho }_2{\Vert L\Vert }_2^{1/2}){\lambda }_{\mathrm{\Theta }}^2{s}^{1/2}{\delta }_n,$$

   where

   $${\delta }_n\equiv \underset{k,i}{\text{max}}{\{{\sigma }_{ii}^{(k)}\}}^2{c}_4(4+\tau ){\gamma }^{-1}\frac{\text{log }p}{n}+(1+2\underset{k,i}{\text{max}}|{\mu }^{(k),i}|)\sqrt{\underset{k,i}{\text{max}}{\{{\sigma }_{ii}^{(k)}\}}^2{c}_4(4+\tau ){\gamma }^{-1}\frac{\text{log }p}{n}}+2\underset{k,i,j}{\text{max}}𝔼|X^{(k),i}{X}^{(k),j}|I(|X^{(k),i}{X}^{(k),j}|\ge \sqrt{\frac{\gamma n}{\text{log }p}})+4{\{\underset{k,i}{\text{max}}𝔼|X^{(k),i}|I(|X^{(k),i}|\ge \sqrt{\frac{\gamma n}{\text{log }p}}\left)\right\}}^2+2(1+2\underset{k,i}{\text{max}}|{\mu }^{(k),i}|)\underset{k,i}{\text{max}}𝔼|X^{(k),i}|I(|X^{(k),i}|\ge \sqrt{\frac{\gamma n}{\text{log }p}})=O\left(\sqrt{\frac{\text{log }p}{n}}\right),$$

   and

   $${\nu }_n\equiv \frac{3c_7{c}_4{\text{ max}}_{k,i}{\{{\sigma }_{ii}^{(k)}\}}^2{(\text{log }p)}^{c_2+c_3+1}}{{\gamma }^{c_3}{n}^{c_3}}+\frac{c_7{c}_4{\text{ max}}_{k,i}{\sigma }_{ii}^{(k)}{(\text{log }p)}^{2(c_2+c_3+1)}}{n^{c_2+c_3+1}}+8p^2\text{ exp }(-\frac{{\text{max}}_{k,i}{\sigma }_{ii}^{(k)}{c}_4(4+\gamma )\text{ log }p}{2{\text{ max}}_{k,i}{\sigma }_{ii}^{(k)}{c}_4+\sqrt{{\text{max}}_{k,i}{\{{\sigma }_{ii}^{(k)}\}}^2{c}_4(64+16\tau )}/3})=o(1).$$

Our proofs adopt several tools from Negahban et al. [20]. Note however that our penalty does not penalize the diagonal elements, and is hence a seminorm; thus, their results do not apply to our case. We first introduce several notations. To treat multiple precision matrices in a unified way, our parameter space is defined to be the set ℝ̃^(pK)×(pK) of (pK) × (pK) symmetric block diagonal matrices, where the kth diagonal block is a p × p matrix corresponding to the precision matrix of subpopulation k. We write A ∈ ℝ̃^(pK)×(pK) for a K-tuple ${(A^{(k)})}_{k=1}^K$ of diagonal blocks A^(k) ∈ ℝ^p×p. Note that for A, B ∈ ℝ̃^(pK)×(pK), ${\langle A,B\rangle }_{pK}={\sum }_{k=1}^K{\langle A^{(k)},B^{(k)}\rangle }_p$ where 〈·, ·〉_p is the trace inner product on ℝ^p×p. In this parameter space, we evaluate the following map from ℝ̃^(pK)×(pK) to ℝ given by

$$f(\mathrm{\Delta })=-{\tilde{\ell }}_n({\mathrm{\Theta }}_0+\mathrm{\Delta })+{\tilde{\ell }}_n({\mathrm{\Theta }}_0)+{\rho }_n\{r({\mathrm{\Theta }}_0+\mathrm{\Delta })-r({\mathrm{\Theta }}_0)\},$$

where r : ℝ̃^(pK)×(pK) ↦ ℝ is given by r(Θ) = ‖Θ‖₁+ ρ₂‖Θ‖_L. This map provides information on the behavior of our criterion function in the neighborhood of Θ₀. A similar map with a different penalty was studied in Rothman et al. [26]. A key observation is that f(0) = 0 and f(Δ̂_n) ≤ 0 where Δ̂_n = Θ̂_ρn − Θ₀.

The following lemma provides a non-asymptotic bound on the Frobenius norm of Δ (see Lemma 4 in Negahban et al. [21] for a similar lemma in a different context). Let $S={\cup }_{k=1}^K{S}^{(k)}$ be the union of the supports of ${\mathrm{\Omega }}_0^{(k)}$. Define a model subspace $ℳ=\{\mathrm{\Omega }\in {\widetilde{ℝ}}^{(pK)\times (pK)}:{\omega }_{ij}^{(k)}=0,(i,j)\notin S,k=1,\dots ,K\}$ and its orthocomplement ${ℳ}^{\perp }=\{\mathrm{\Omega }\in {\widetilde{ℝ}}^{(pK)\times (pK)}:{\omega }_{ij}^{(k)}=0,(i,j)\in S,k=1,\dots K\}$ under the trace inner product in ℝ̃^(pK)×(pK). For $A={(a_{ij})}_{i,j=1}^{pK}\in {\widetilde{ℝ}}^{(pK)\times (pK)}$, we write A = A_ℳ + A_ℳ^⊥ where A_ℳ and A_ℳ^⊥ are the projection of A into ℳ and _ℳ^⊥, in the Frobenius norm, respectively. In other words, the (i, j)-element of A_ℳ is a_ij if (i, j) ∈ S and zero otherwise, and the (i, j)-element of A_ℳ^⊥ is a_ij if (i, j) ∉ S and zero otherwise. Note that Θ₀ ∈ ℳ. Define the set 𝒞 = {Δ ∈ ℝ̃^(pK)×(pK) : r(Δ_ℳ^⊥) ≤ 3r(Δ_ℳ)}.

Lemma 2

Let ε > 0 be arbitrary. Suppose ${\rho }_n\ge 2{\text{ max}}_{1\le k\le K}{\Vert {\hat{\mathrm{\Psi }}}_n^{(k)}-{\mathrm{\Psi }}_0^{(k)}\Vert }_{\infty }$. Iff (Δ) > 0 for all elements Δ ∈ 𝒞 ⋂ {Δ ∈ ℝ̃^(pK)×(pK) : ‖Δ‖_F = ε} then ‖Δ̂_n‖_F ≤ ε.

Proof

We first show that Δ̂_n ∈ 𝒞. We have by the convexity of −ℓ̃_n(Θ) that

$$-{\tilde{\ell }}_n({\mathrm{\Theta }}_0+{\hat{\mathrm{\Delta }}}_n)+{\tilde{\ell }}_n({\mathrm{\Theta }}_0)\ge -|\langle -\nabla {\tilde{\ell }}_n({\mathrm{\Theta }}_0),{\hat{\mathrm{\Delta }}}_n\rangle |.$$

It follows from Lemma 3(iv) with our choice ρ_n that the right hand side of the inequality is further bounded below by −2⁻¹ ρ_n (r(Δ̂_n,ℳ) + r(Δ̂_n,ℳ^⊥)). Applying Lemma 3(iii), we obtain

$$0\ge f({\hat{\mathrm{\Delta }}}_n)=-{\tilde{\ell }}_n({\mathrm{\Theta }}_0+{\hat{\mathrm{\Delta }}}_n)+{\tilde{\ell }}_n({\mathrm{\Theta }}_0)+r({\mathrm{\Theta }}_0+{\hat{\mathrm{\Delta }}}_n)-r({\mathrm{\Theta }}_0)\ge \frac{{\rho }_n}{2}r({\hat{\mathrm{\Delta }}}_{n,{ℳ}^{\perp }})-\frac{3{\rho }_n}{2}r({\hat{\mathrm{\Delta }}}_{n,ℳ}),$$

or r(Δ̂_n,ℳ^⊥) ≤ 3r(Δ̂_n,ℳ). This verifies Δ̂_n ∈ 𝒞. Note that f, as a function of Δ is sum of two convex functions ℓ_n and r, and is hence convex. Thus, the rest of the proof follows exactly as Lemma 4 in Negahban et al. [21].

Lemma 3

Let Δ ∈ ℝ̃^(pK)×(pK).

1. The gradient of ℓ̃_n(Θ₀) is a block diagonal matrix given by

   $$\nabla {\tilde{\ell }}_n({\mathrm{\Theta }}_0)=n^{-1}\text{ diag}\{n_1({\mathrm{\Psi }}_0^{(1)}-{\hat{\mathrm{\Psi }}}_n^{(1)}),\dots ,n_K({\mathrm{\Psi }}_0^{(K)}-{\hat{\mathrm{\Psi }}}_n^{(K)})\}.$$ (10)
2. Let c > 0 be a constant. For ‖Δ‖_F ≤ c and n_k/n ≥ γ > 0 for all k and n,

   $$-{\tilde{\ell }}_n({\mathrm{\Theta }}_0+\mathrm{\Delta })+{\tilde{\ell }}_n({\mathrm{\Theta }}_0)+\langle \nabla {\tilde{\ell }}_n({\mathrm{\Theta }}_0),\mathrm{\Delta }\rangle \ge \frac{\gamma }{2{\{{\lambda }_{\mathrm{\Theta }}+c\}}^2}{\Vert \mathrm{\Delta }\Vert }_F^2\equiv {\kappa }_{{\ell }_n,c}{\Vert \mathrm{\Delta }\Vert }_F^2.$$ (11)
3. The map r is a seminorm, convex, and decomposable with respect to (ℳ, ℳ^⊥) in the sense that r(Θ₁ + Θ₂) = r(Θ₁) + r(Θ₂) for every Θ₁ ∈ ℳ and Θ₂ ∈ ℳ^⊥. Moreover,

   $$r({\mathrm{\Theta }}_0+\mathrm{\Delta })-r({\mathrm{\Theta }}_0)\ge r({\mathrm{\Delta }}_{{ℳ}^{\perp }})-r({\mathrm{\Delta }}_{ℳ}).$$
4. For Δ ∈ ℝ̃^(pK)×(pK),

   $$|\langle \nabla {\tilde{\ell }}_n({\mathrm{\Theta }}_0),\mathrm{\Delta }\rangle |\le r(\mathrm{\Delta })\underset{1\le k\le K}{\text{max}}{\Vert {\hat{\mathrm{\Psi }}}_n^{(k)}-{\mathrm{\Psi }}_0^{(k)}\Vert }_{\infty }.$$ (12)
5. For Θ ∈ ℝ̃^(pK)×(pK),

   $$r({\mathrm{\Theta }}_{ℳ})\le {(s+1)}^{1/2}(1+{\rho }_2{\Vert L\Vert }_2^{1/2}){\Vert {\mathrm{\Theta }}_{ℳ}\Vert }_F.$$

Proof

1. The result follows by taking derivatives blockwise.

2. Rothman et al. [26] (page 500–502) showed that

   $$-{\tilde{\ell }}_n({\mathrm{\Theta }}_0+\mathrm{\Delta })+{\tilde{\ell }}_n({\mathrm{\Theta }}_0)-\langle -\nabla {\tilde{\ell }}_n({\mathrm{\Theta }}_0),\mathrm{\Delta }\rangle =\sum _{k=1}^K\frac{n_k}{n}(-\text{log det}({\mathrm{\Theta }}_0^{(k)}+{\mathrm{\Delta }}^{(k)})+\text{log det}({\mathrm{\Theta }}_0^{(k)})+\langle {\mathrm{\Psi }}_0^{(k)},{\mathrm{\Delta }}^{(k)}\rangle )\ge \sum _{k=1}^K\frac{n_k}{n}\frac{{\Vert {\mathrm{\Delta }}^{(k)}\Vert }_F^2}{2{\text{ min}}_{0\le \upsilon \le 1}{\{{\Vert {\mathrm{\Theta }}_0^{(k)}\Vert }_2+\upsilon {\Vert {\mathrm{\Delta }}^{(k)}\Vert }_2\}}^2}.$$
   Since ‖A‖₂ ≤ ‖A‖_F, n_k/n ≥ γ and ‖Δ‖_F ≤ c, this is further bounded below by

   $$\sum _{k=1}^K\frac{\gamma }{2}\frac{{\Vert {\mathrm{\Delta }}^{(k)}\Vert }_F^2}{{\{{\Vert {\mathrm{\Theta }}_0^{(k)}\Vert }_2+{\Vert {\mathrm{\Delta }}^{(k)}\Vert }_F\}}^2}\ge {\kappa }_{{\ell }_n,c}{\Vert \mathrm{\Delta }\Vert }_F^2.$$
3. Because the graph Laplacian L is a positive semidefinite matrix, the triangle inequality r(Θ₁ + Θ₂) ≤ r(Θ₁) + r(Θ₂) holds. To see this let L = L̃L̃^T be any Cholesky decomposition of L. Then

   $${\{{(x+y)}^{T}L(x+y)\}}^{1/2}=\Vert {\tilde{L}}^T(x+y)\Vert \le \Vert {\tilde{L}}^{T}x\Vert +\Vert {\tilde{L}}_y\Vert ={\{x^{T}Lx\}}^{1/2}+{\{y^{T}Ly\}}^{1/2}.$$
   It is clear that r(cΘ) = cr(Θ) for any constant c. Thus, given that r does not penalize the diagonal elements, it is a seminorm. The decomposability follows from the definition of r. The convexity follows from the same argument for the triangle inequality. Since Θ₀ + Δ = Θ₀ + Δ_ℳ + Δ_ℳ^⊥, the triangle inequality and the decomposability of r yield

   $$r({\mathrm{\Theta }}_0+\mathrm{\Delta })-r({\mathrm{\Theta }}_0)\ge r({\mathrm{\Theta }}_0+{\mathrm{\Delta }}_{{ℳ}^{\perp }})-r({\mathrm{\Delta }}_{ℳ})-r({\mathrm{\Theta }}_0)=r({\mathrm{\Delta }}_{{ℳ}^{\perp }})-r({\mathrm{\Delta }}_{ℳ}).$$
4. We show that, for A, B ∈ ℝ̃^(pK)×(pK) with diag(B) = 0, 〈A, B〉 ≤ r(A)‖B‖_∞. If A is a diagonal matrix (or if A = 0), the inequality trivially holds since 〈A, B〉 = 0. If not, r(A) ≠ 0 so that

   $$\frac{\langle A,B\rangle }{r(A)}\le \frac{{\Vert A\Vert }_1{\Vert B\Vert }_{\infty }}{{\Vert A\Vert }_1}={\Vert B\Vert }_{\infty }.$$

   Since the diagonal elements of ∇ℓ̃_n(Θ₀) are all zero, the result follows.

5. For s ≠ 0, we have

   $$\frac{r({\mathrm{\Theta }}_{ℳ})}{{\Vert {\mathrm{\Theta }}_{ℳ}\Vert }_F}\le \underset{\mathrm{\Theta }\in ℳ}{\text{sup}}\frac{{\sum }_{k=1}^K{\Vert {\mathrm{\Theta }}^{(k)}\Vert }_1}{{\Vert \mathrm{\Theta }-\text{diag}(\mathrm{\Theta })\Vert }_F}+\underset{\mathrm{\Theta }\in ℳ}{\text{sup}}\frac{{\rho }_2{\sum }_{i\ne j}\sqrt{{\theta }_{ij}^{T}L{\theta }_{ij}}}{{\Vert \mathrm{\Theta }\Vert }_F}\le s^{1/2}+{\rho }_2\underset{\mathrm{\Theta }\in ℳ}{\text{sup}}\frac{{\sum }_{i\ne j}\sqrt{{\Vert L\Vert }_2{\Vert {\theta }_{ij}\Vert }_F^2}}{{\Vert \mathrm{\Theta }\Vert }_F}\le s^{1/2}(1+{\rho }_2{\Vert L\Vert }_2^{1/2}).$$

   In the last inequality we used that $\sqrt{{\sum }_{j=1}^J{\sum }_{i=1}^I{a}_{ij}^2}\ge J^{-1/2}{\sum }_{j=1}^J\sqrt{{\sum }_{i=1}^I{a}_{ij}^2}$, which follows by the concavity of the square root function. For s = 0, we trivially have $0=r({\mathrm{\Theta }}_{ℳ})\le s^{1/2}\{1+{\rho }_2{\Vert L\Vert }_2^{1/2}\}{\Vert {\mathrm{\Theta }}_{ℳ}\Vert }_F$. Combining these two cases yields the desired result.

Next, we obtain an upper bound for ${\text{max}}_{1\le k\le K}{\Vert {\hat{\mathrm{\Psi }}}_n^{(k)}-{\mathrm{\Psi }}_0^{(k)}\Vert }_{\infty }$, which holds with high-probability assuming the tail conditions of the random vectors.

Lemma 4

Suppose that n_k/n ≥ γ > 0 for all k and n.

1. Suppose that Condition 1 holds. Then for n ≥ 6γ⁻¹ log p we have

   $$P({\Vert {\hat{\mathrm{\Sigma }}}_n-{\mathrm{\Sigma }}_0\Vert }_{\infty }\ge 2^3\sqrt{6}{(1+4c_1^2)}^2{\gamma }^{-1/2}\underset{k,i}{\text{max}}{\sigma }_{ii}^{(k)}\sqrt{\frac{\text{log }p}{\gamma n}})\le 2K/p.$$ (13)
2. Suppose that Condition 2 holds with c₂, c₃ > 0 and p ≤ c₇n^c₂. Then we have for $\tau >{\text{max}}_k(2^7+2^3\sqrt{1+2^4{3}^2{c}_4{\text{ max}}_{k,i}{\{{\sigma }_{ii}^{(k)}\}}^2})/(9c_4{\text{ max}}_{k,i}{\{{\sigma }_{ii}^{(k)}\}}^2)$

   $$P({\Vert {\hat{\mathrm{\Sigma }}}_n-{\mathrm{\Sigma }}_0\Vert }_{\infty }\ge \sum _{k=1}^K{\delta }_n^{(k)})\le K{\nu }_n$$ (14)

   where

   $${\delta }_n^{(k)}\equiv (1+2\underset{i}{\text{max}}|{\mu }^{(k),i}|)(2{\delta }_{n,1}^{(k)}+{\delta }_{n,2}^{(k)})+{({\delta }_{n,1}^{(k)})}^2+{({\delta }_{n,2}^{(k)})}^2+2{\delta }_{n,3}^{(k)},$$

   with

   $${\delta }_{n,1}^{(k)}\equiv \underset{i,j}{\text{max}}𝔼|X_l^{(k),i}{X}_l^{(k),j}|I(|X_l^{(k),i}{X}_l^{(k),j}|\ge n_k^{1/2}{(\text{log }p)}^{-1/2}),$$

   $${\delta }_{n,2}^{(k)}\equiv {\{c_4\underset{k,i}{\text{max}}{\left\{{\sigma }_{ii}^{(k)}\right\}}^2(4+\tau )\text{ log }p/n_k\}}^{1/2},$$

   $${\delta }_{n,3}^{(k)}\equiv \underset{i}{\text{max}}𝔼|X_l^{(k),i}|I(|X_l^{(k),i}|\ge n_k^{1/2}{(\text{log }p)}^{-1/2}).$$

3. Suppose that Condition 3 holds and that P(‖Σ̂_n − Σ₀‖_∞ ≥ b_n) = o(1) and b_n = o(1) as n → ∞. Then P(‖Ψ̂_n − Ψ₀‖_∞ ≥ C₁b_n) = o(1).

Proof

1. This was proved by Ravikumar et al. [25].

2. Note that

   $${\hat{\mathrm{\Sigma }}}_n^{(k)}-{\mathrm{\Sigma }}^{(k)}=n_k^{-1}\sum _{l=1}^{n_k}{(X_l^{(k)})}^{\otimes 2}-𝔼{(X^{(k)})}^{\otimes 2}-{({\overline{X}}^{(k)}-{\mu }^{(k)})}^{\otimes 2}-{\mu }^{(k)}{({\overline{X}}^{(k)}-{\mu }^{(k)})}^T-({\overline{X}}^{(k)}-{\mu }^{(k)}){({\mu }^{(k)})}^T.$$
   We first evaluate the probability in (14) for $n_k^{-1}{\sum }_{l=1}^{n_k}{(X_l^{(k)})}^{\otimes 2}-𝔼{(X^{(k)})}^{\otimes 2}$. Let

   $$Y_l^{(k),ij}\equiv X_l^{(k),i}{X}_l^{(k),j}-𝔼X_l^{(k),i}{X}_l^{(k),j},$$

   $${Ȳ}_l^{(k),ij}\equiv X_l^{(k),i}{X}_l^{(k),j}I\left(\right|X_l^{(k),i}{X}_l^{(k),j}|\le \sqrt{\frac{n_k}{\text{log }p}})-𝔼X_l^{(k),i}{X}_l^{(k),j}I\left(\right|X_l^{(k),i}{X}_l^{(k),j}|\le \sqrt{\frac{n_k}{\text{log }p}}),$$

   $${Ỹ}_l^{(k),ij}\equiv Y_l^{(k),ij}-{Ȳ}_l^{(k),ij}.$$
   We have

   $$P\left(\underset{i,j}{\text{max}}\right|\sum _{l=1}^{n_k}{Ỹ}_l^{(k),ij}|\ge 2n_k{\delta }_{n,1}^{(k)})\le P\left(\underset{i,j}{\text{max}}\right|\sum _{l=1}^{n_k}{X}_l^{(k),i}{X}_l^{(k),j}I\left(\right|X_l^{(k),i}{X}_l^{(k),j}|\ge \sqrt{\frac{n_k}{\text{log }p}})|\ge n_k{\delta }_{n,1}^{(k)})\le P(\underset{l,i}{\text{max}}{(X_l^{(k),i})}^2\ge n_k^{1/2}{(\text{log }p)}^{-1/2})(xy\le \text{max}\{x^2,y^2\})\le p{n}_k\frac{𝔼X_{0i}^{4(c_2+c_3+1)}{(\text{log }p)}^{c_2+c_3+1}}{n_k^{c_2+c_3+1}}(\text{Markov}’\mathrm{s}\text{ inequality})\le \frac{c_7{c}_4{\text{max}}_{k,i}{\{{\sigma }_{ii}^{(k)}\}}^2{(\text{log }p)}^{c_2+c_3+1}}{n_k^{c_3}}(p\le c_7{n}^{c_2})\le \frac{c_7{c}_4{\text{max}}_{k,i}{\{{\sigma }_{ii}^{(k)}\}}^2{(\text{log }p)}^{c_2+c_3+1}}{{\gamma }^{c_3}{n}^{c_3}}\equiv {\nu }_{n,1},$$ (15)

   where the first inequality follows from the triangle inequality. Note that

   $$𝔼{\left({Ȳ}_l^{(k),ij}\right)}^2\le 𝔼{\left[X_l^{(k),i}{X}_l^{(k),j}I\right(|X_l^{(k),i}{X}_l^{(k),j}|\le \sqrt{\frac{n_k}{\text{log }p}})]}^2\le 𝔼{|X_l^{(k),i}{X}_l^{(k),j}|}^2\le 2^{-1}(𝔼{\left(X_l^{(k),i}\right)}^4+𝔼{\left(X_l^{(k),j}\right)}^4)\le c_4\underset{k,i}{\text{max}}{\left\{{\sigma }_{ii}^{(k)}\right\}}^2.$$
   It follows from Bernstein’s inequality that

   $$P\left(\underset{i,j}{\text{max}}\right|\sum _{l=1}^{n_k}{Ȳ}_l^{(k),ij}|\ge n_k{\delta }_{n,2}^{(k)})\le 2p^2\text{ exp }(-\frac{c_4{\text{max}}_{k,i}{\{{\sigma }_{ii}^{(k)}\}}^2(4+\tau )\text{ log }p}{2c_4{\text{max}}_{k,i}{\{{\sigma }_{ii}^{(k)}\}}^2+2\sqrt{c_4{\text{max}}_{k,i}{\{{\sigma }_{ii}^{(k)}\}}^2(64+16\tau )}/3})\equiv {\nu }_{n,2}.$$ (16)
   Now, for $\tau >(2^7+2^3\sqrt{1+2^4{3}^2{c}_4{\text{ max}}_{k,i}{\{{\sigma }_{ii}^{(k)}\}}^2})/(9c_4{\text{ max}}_{k,i}{\{{\sigma }_{ii}^{(k)}\}}^2)$, ν_n,2 → 0 as p → ∞. Note that for this to hold it suffices to have

   $$\frac{3c_4{\text{max}}_{k,i}{\{{\sigma }_{ii}^{(k)}\}}^2(4+\tau )}{6c_4{\text{max}}_{k,i}{\{{\sigma }_{ii}^{(k)}\}}^2+8\sqrt{c_4{\text{max}}_{k,i}{\{{\sigma }_{ii}^{(k)}\}}^2(4+\tau )}}>2,$$

   so that the power in the exponent is negative. This inequality reduces to

   $$3c_4\underset{k,i}{\text{max}}{\{{\sigma }_{ii}^{(k)}\}}^2\tau >16\sqrt{c_4\underset{k,i}{\text{max}}{\{{\sigma }_{ii}^{(k)}\}}^2(4+\tau )}.$$
   We can solve this by changing a quadratic equation for τ, since τ of our interest is positive. Combining (15) and (16) yields

   $$P({\Vert \frac{1}{n_k}\sum _{i=1}^{n_k}{(X_l^{(k)})}^{\otimes 2}-𝔼{(X^{(k)})}^{\otimes 2}\Vert }_{\infty }\ge 2{\delta }_{n,1}^{(k)}+{\delta }_{n,2}^{(k)})\le {\nu }_{n,1}+{\nu }_{n,2}.$$ (17)
   Let

   $$Z_l^{(k),i}\equiv X_l^{(k),i}-𝔼X_l^{(k),i},$$

   $${\overline{Z}}_l^{(k),i}\equiv X_l^{(k),i}I(|X_l^{(k),i}|\le n_k^{1/2}{(\text{log }p)}^{-1/2})-𝔼X_l^{(k),i}I(|X_l^{(k),i}|\le n_k^{1/2}{(\text{log }p)}^{-1/2}),$$

   $${\tilde{Z}}_l^{(k),i}\equiv U_l^{(k),i}-{\overline{Z}}_l^{(k),i}.$$
   Proceeding as for $Y_l^{(k),ij}$’s, we have

   $$P\left(\underset{i}{\text{max}}\right|\sum _{l=1}^{n_k}{\tilde{Z}}_l^{(k),i}|\ge 2n_k{\delta }_{n,3}^{(k)})\le \frac{c_7{c}_4{\text{ max}}_{k,i}{\{{\sigma }_{ii}^{(k)}\}}^2{(\text{log }p)}^{2(c_2+c_3+1)}}{{\gamma }^{c_2+c_3+1}{n}^{c_2+c_3+1}}\equiv {\nu }_{n,3},$$

   and

   $$P\left(\underset{i}{\text{max}}\right|\sum _{k=1}^n{\overline{Z}}_l^{(k),i}|\ge n_k{\delta }_{n,2}^{(k)})\le {\nu }_{n,2}.$$
   Thus, we have

   $$P({\Vert {({\overline{X}}^{(k)}-{\mu }^{(k)})}^{\otimes 2}\Vert }_{\infty }\ge {({\delta }_{n,2}^{(k)})}^2+{(2{\delta }_{n,3}^{(k)})}^2)\le P(\underset{i}{\text{max}}|{\overline{X}}^{(k),i}-{\mu }^{(k),i}|\ge \sqrt{{({\delta }_{n,1}^{(k)})}^2+{({\delta }_{n,2}^{(k)})}^2})\le P\left(\underset{i}{\text{max}}\right|\sum _{k=1}^n{\overline{Z}}_l^{(k),i}|\ge n_k{\delta }_{n,2}^{(k)})+P\left(\underset{i}{\text{max}}\right|\sum _{l=1}^{n_k}{\tilde{Z}}_l^{(k),i}|\ge 2n_k{\delta }_{n,3}^{(k)})\le {\nu }_{n,2}+{\nu }_{n,3},$$ (18)

   and

   $$P({\Vert ({\overline{X}}^{(k)}-{\mu }^{(k)}){({\mu }^{(k)})}^T\Vert }_{\infty }\ge \underset{i}{\text{max}}|{\mu }^{(k),i}|(2{\delta }_{n,1}^{(k)}+{\delta }_{n,2}^{(k)}))\le P(\underset{i}{\text{max}}|{\overline{X}}^{(k),i}-{\mu }^{(k),i}|\ge 2{\delta }_{n,1}^{(k)}+{\delta }_{n,2}^{(k)})\le {\nu }_{n,1}+{\nu }_{n,2}.$$ (19)
   Combining (17)–(19) yields

   $$P({\Vert {\hat{\mathrm{\Sigma }}}_n^{(k)}-{\mathrm{\Sigma }}^{(k)}\Vert }_{\infty }\ge (1+2\underset{i}{\text{ max}}|{\mu }^{(k),i}|)(2{\delta }_{n,1}^{(k)}+{\delta }_{n,2}^{(k)})+{({\delta }_{n,2}^{(k)})}^2+{(2{\delta }_{n,3}^{(k)})}^2)\le 3{\nu }_{n,1}+4{\nu }_{n,2}+{\nu }_{n,3}={\nu }_n.$$

   Note that ${\delta }_{n,1}^{(k)},{\delta }_{n,2}^{(k)},{\delta }_{n,3}^{(k)}$, ν_n,1, ν_n,2, ν_n,3 → 0 as n, p → ∞ if log p/n → 0. Note also that ${\delta }_{n,1}^{(k)},{\delta }_{n,2}^{(k)}$ and ${({\delta }_{n,3}^{(k)})}^2$ are $O\left(\sqrt{\text{log }p/n}\right)$ on the set where n_k/n ≥ γ.

   For example, we have by Jensen’s inequality that

   $$\sqrt{\frac{n}{\text{log }p}}{({\delta }_{n,3}^{(k)})}^2=\sqrt{\frac{n}{\text{log }p}}\underset{i}{\text{max}}{\{𝔼|X^{(k),i}|I\{|X^{(k),i}|\ge n_k^{1/2}{(\text{log }p)}^{-1/2}\}\}}^2\le \underset{i}{\text{max}}𝔼\frac{n}{n_k}\sqrt{\frac{n_k}{\text{log }p}}{|X^{(k),i}|}^{2}I\{|X^{(k),i}|\ge n_k^{1/2}{(\text{log }p)}^{-1/2}\}\le {\gamma }^{-1}\underset{i}{\text{max}}𝔼{|X^{(k),i}|}^{3}I\{|X^{(k),i}|\ge n_k^{1/2}{(\text{log }p)}^{-1/2}\}\le c_4{\gamma }^{-1}\underset{i}{\text{max}}{\{{\sigma }_{ii}^{(k)}\}}^2.$$
3. Given that $|{\sigma }_{0,ij}^{(k)}|\le \sqrt{{\sigma }_{0,ii}^{(k)}{\sigma }_{0,jj}^{(k)}},$

   $$|{\psi }_{n,ij}^{(k)}-{\psi }_{0,ij}^{(k)}|=|\frac{{\hat{\sigma }}_{n,ij}^{(k)}}{\sqrt{{\hat{\sigma }}_{n,ii}^{(k)}{\hat{\sigma }}_{n,jj}^{(k)}}}-\frac{{\sigma }_{0,ij}^{(k)}}{\sqrt{{\sigma }_{0,ii}^{(k)}{\sigma }_{0,jj}^{(k)}}}|=\frac{|\sqrt{{\sigma }_{0,ii}^{(k)}{\sigma }_{0,jj}^{(k)}}({\hat{\sigma }}_{n,ij}^{(k)}-{\sigma }_{0,ij}^{(k)})+{\sigma }_{0,ij}^{(k)}(\sqrt{{\sigma }_{0,ii}^{(k)}{\sigma }_{0,jj}^{(k)}}-\sqrt{{\hat{\sigma }}_{n,ii}^{(k)}{\hat{\sigma }}_{n,jj}^{(k)}}\left)\right|}{\sqrt{{\hat{\sigma }}_{n,ii}^{(k)}{\hat{\sigma }}_{n,jj}^{(k)}{\sigma }_{0,ii}^{(k)}{\sigma }_{0,jj}^{(k)}}}\le \frac{\sqrt{{\sigma }_{0,ii}^{(k)}{\sigma }_{0,jj}^{(k)}}}{\sqrt{{\hat{\sigma }}_{n,ii}^{(k)}{\hat{\sigma }}_{n,jj}^{(k)}{\sigma }_{0,ii}^{(k)}{\sigma }_{0,jj}^{(k)}}}\left\{\right|{\hat{\sigma }}_{n,ij}^{(k)}-{\sigma }_{0,ij}^{(k)}|+|\sqrt{{\sigma }_{0,ii}^{(k)}{\sigma }_{0,jj}^{(k)}}-\sqrt{{\hat{\sigma }}_{n,ii}^{(k)}{\hat{\sigma }}_{n,jj}^{(k)}}\left|\right\},$$

   wherein

   $$\sqrt{{\sigma }_{0,ii}^{(k)}{\sigma }_{0,jj}^{(k)}}-\sqrt{{\hat{\sigma }}_{n,ii}^{(k)}{\hat{\sigma }}_{n,jj}^{(k)}}=\frac{\sqrt{{\sigma }_{0,jj}^{(k)}}}{\sqrt{{\sigma }_{0,ii}^{(k)}}+\sqrt{{\hat{\sigma }}_{n,ii}^{(k)}}}({\sigma }_{0,ii}^{(k)}-{\hat{\sigma }}_{n,ii}^{(k)})+\frac{\sqrt{{\hat{\sigma }}_{n,ii}^{(k)}}}{\sqrt{{\sigma }_{0,jj}^{(k)}}+\sqrt{{\hat{\sigma }}_{n,jj}^{(k)}}}({\sigma }_{0,jj}^{(k)}-{\hat{\sigma }}_{n,jj}^{(k)}).$$
   Since b_n → 0, b_n ≤ c₅/2 for n sufficiently large by Condition 3. On the event ‖Σ̂_n − Σ₀‖_∞ ≤ b_n with n large, $0<c_5/2\le {\sigma }_{0,ii}^{(k)}-c_5/2\le {\hat{\sigma }}_{n,ii}^{(k)}\le {\sigma }_{0,ii}^{(k)}+c_5/2\le c_6+c_5/2$. Thus,

   $$\frac{\sqrt{{\sigma }_{0,ii}^{(k)}{\sigma }_{0,jj}^{(k)}}}{\sqrt{{\hat{\sigma }}_{n,ii}^{(k)}{\hat{\sigma }}_{n,jj}^{(k)}{\sigma }_{0,ii}^{(k)}{\sigma }_{0,jj}^{(k)}}}\le \frac{2(c_5+2c_6)}{c_5^2}$$

   $$\frac{\sqrt{{\sigma }_{0,jj}^{(k)}}}{\sqrt{{\sigma }_{0,ii}^{(k)}}+\sqrt{{\hat{\sigma }}_{n,ii}^{(k)}}}\le \frac{\sqrt{c_6}}{2\sqrt{c_5}}$$

   $$\frac{\sqrt{{\hat{\sigma }}_{n,ii}^{(k)}}}{\sqrt{{\sigma }_{0,jj}^{(k)}}+\sqrt{{\hat{\sigma }}_{n,jj}^{(k)}}}\le \frac{\sqrt{c_5+2c_6}}{2\sqrt{c_5}}.$$
   It follows that

   $$|{\psi }_{n,ij}^{(k)}-{\psi }_{0,ij}^{(k)}|\le \{2c_5^{-2}+c_5+c_6^{-3/2}+2c_5^{-5/2}{c}_6+{(c_5^{-4}+2c_5^{-5}{c}_6)}^{1/2}\}\underset{k,i,j}{\text{max}}|{\hat{\sigma }}_{n,ij}^{(k)}-{\sigma }_{0,ij}^{(k)}|.$$
   Thus, we have

   $$P({\Vert {\hat{\mathrm{\Psi }}}_n-{\mathrm{\Psi }}_0\Vert }_{\infty }\ge C_1{b}_n)\le P({\Vert {\hat{\mathrm{\Psi }}}_n-{\mathrm{\Psi }}_0\Vert }_{\infty }\ge C_1{b}_n,{\Vert {\hat{\mathrm{\Sigma }}}_n-{\mathrm{\Sigma }}_0\Vert }_{\infty }<b_n)+P({\Vert {\hat{\mathrm{\Sigma }}}_n-{\mathrm{\Sigma }}_0\Vert }_{\infty }\ge b_n)\le 2P({\Vert {\hat{\mathrm{\Sigma }}}_n-{\mathrm{\Sigma }}_0\Vert }_{\infty }\ge b_n)\to 0.$$

So far we have assumed n_k/n ≥ γ in lemmas. We evaluate the probability of this event noting that n_k ~ Binom(n, π_k).

Lemma 5

Let ε > 0 such that γ ≡ min_k π_k − ε > 0. Then

$$P(\underset{k}{\text{min}}{n}_k/n\le \underset{k}{\text{min}}{\pi }_k-\epsilon )\le 2K\text{ exp}(-2n{\epsilon }^2).$$ (20)

Proof

We have by Hoeffding’s inequality that

$$P(\underset{k}{\text{min}}{n}_k/n\le \underset{k}{\text{min}}{\pi }_k-\epsilon )\le P(\exists k,n_k/n\le \underset{k}{\text{min}}{\pi }_k-\epsilon )\le P(\exists k,n_k/n\le {\pi }_k-\epsilon )\le P(\exists k,|n_k/n-{\pi }_k|\ge \epsilon )\le \sum _{k=1}^{K}P(|n_k/n-{\pi }_k|\ge \epsilon )\le 2K\text{ exp}(-2n{\epsilon }^2).$$

Proof of Lemma 1

We apply Lemma 2 to obtain the non-asymptotic error bounds.

We first compute a lower bound for f(Δ). Suppose ε ≤ c. For Δ ∈ 𝒞 ∩ {Δ ∈ ℝ̃^(pK)×(pK) : ‖Δ‖_F = ε}, we have by Lemma 3(ii) and (iii) that

$$f(\mathrm{\Delta })\ge -\langle {\tilde{\ell }}_n({\mathrm{\Theta }}_0),\mathrm{\Delta }\rangle +{\kappa }_{{\ell }_n,c}{\Vert \mathrm{\Delta }\Vert }_F^2+{\rho }_n\{r({\mathrm{\Delta }}_{{ℳ}^{\perp }})-r({\mathrm{\Delta }}_{ℳ})\}.$$

The assumption on ρ_n and Lemma 3(iii) and (iv) then yield

$$|\langle {\tilde{\ell }}_n({\mathrm{\Theta }}_0),\mathrm{\Delta }\rangle |\le \frac{{\rho }_n}{2}\{r({\mathrm{\Delta }}_{ℳ})+r({\mathrm{\Delta }}_{{ℳ}^{\perp }})\}.$$

From this inequality and Lemma 3(v) we have

$$f(\mathrm{\Delta })\ge {\kappa }_{{\ell }_n,c}{\Vert \mathrm{\Delta }\Vert }_F^2-\frac{3{\rho }_n}{2}r({\mathrm{\Delta }}_{ℳ})\ge {\kappa }_{{\ell }_n,c}{\Vert \mathrm{\Delta }\Vert }_F^2-\frac{3{\rho }_n}{2}{(s+1)}^{1/2}(1+{\rho }_2{\Vert L\Vert }_2^{1/2}){\Vert \mathrm{\Delta }\Vert }_F.$$

Viewing the right hand side of the above inequality as a quadratic equation in ‖Δ‖_F, we have f(Δ) > 0 if

$${\Vert \mathrm{\Delta }\Vert }_F\ge \frac{3{\rho }_n}{{\kappa }_{{\ell }_n,c}}{(s+1)}^{1/2}(1+{\rho }_2{\Vert L\Vert }_2^{1/2})\equiv {\epsilon }_c>0.$$

Thus, if we show that there exists a c₀ > 0 such that ε_c0 ≤ c₀, Lemma 2 yields that ‖Θ̂_ρn − Θ₀‖_F ≤ ε_c0.

Consider the inequality (x + y)²z^1/2 ≤ y where x, y, z ≥ 0. This inequality holds for (x, y, z) such that x = y and xz^1/2 = 1/4. We apply the inequality above with x = λ_Θ, y = c, $z=2^4{3}^2{\rho }_n^2{\gamma }^{-2}s{(1+{\rho }_2{\Vert L\Vert }_2^{1/2})}^2$ and solve xz ≤ 1/4 for n. (i) For ${\rho }_n=2^3\sqrt{6}{C}_1{(1+4c_1^2)}^2{\gamma }^{-1/2}{\text{ max}}_{k,i}{\sigma }_{ii}^{(k)}\sqrt{\text{log }p/n}$, xz ≤ 1/4 yields

$$n\ge \text{max }\{\frac{6\text{ log }p}{\gamma },\frac{2^{15}{3}^3{C}_1^2{(1+4c_1^2)}^2}{{\gamma }^3}\underset{k,i}{\text{max}}{\{{\sigma }_{ii}^{(k)}\}}^2{\lambda }_{\mathrm{\Theta }}^4{(1+{\rho }_2{\Vert L\Vert }_2^{1/2})}^{2}s\text{ log }p\},$$

and (x + y)⁴z becomes

$${\epsilon }_{{\text{max}}_k\{{\Vert {\mathrm{\Theta }}_0^{(k)}\Vert }_2\}}^2\le 2^{15}{3}^3{(1+c_1^2)}^2\underset{k,i}{\text{max}}{({\sigma }_{ii}^{(k)})}^2{(1+{\rho }_2{\Vert L\Vert }_2^{1/2})}^2{\gamma }^{-3}{\lambda }_{\mathrm{\Theta }}^4\frac{s\text{ log }p}{n}.$$

(ii) For ρ_n = C₁Kδ_n, there is no closed form solution for n. Note that δ_n → 0 if log p/n → 0 so that xz ≤ 1/4 holds for n sufficiently large, given that ${\sum }_{k=1}^K{\delta }_n^{(k)}\le K{\delta }_n$.

Computing appropriate probabilities using Lemmas 4 and 5 completes the proof.

Proof of Theorem 1

The estimation error ${\Vert {\hat{\mathrm{\Omega }}}_{{\rho }_n}^{(k)}-{\mathrm{\Omega }}_0\Vert }_2^{(2)}$ in the spectral norm can be bounded and evaluated in the same way as in the proof of Theorem 2 of Rothman et al. [26] together with Lemma 1.

8.2. Model Selection Consistency

Our proof is based on the primal-dual witness approach of Ravikumar et al. [25], with some modifications to overcome a difficulty in their proof when applying the fixed point theorem to a discontinuous function. First, we define the oracle estimator ${\check{\mathrm{\Theta }}}_{{\rho }_n}=({\check{\mathrm{\Theta }}}_{{\rho }_n}^{(1)},\dots ,{\check{\mathrm{\Theta }}}_{{\rho }_n}^{(K)})$ by

$${\check{\mathrm{\Theta }}}_{{\rho }_n}=\underset{{\mathrm{\Theta }}^{(k)}>0,{\mathrm{\Theta }}^{(k)}={({\mathrm{\Theta }}^{(k)})}^T,{\mathrm{\Theta }}_{{\left(s^{(k)}\right)}^c}^{(k)}=0}{\text{arg min}}{n}^{-1}\sum _{k=1}^K{n}_k\left(\text{tr }\right({\mathrm{\Psi }}_n^{(k)}{\mathrm{\Theta }}^{(k)})-\text{log det}({\mathrm{\Theta }}^{(k)}))+{\rho }_n\sum _{k=1}^K{\Vert {\mathrm{\Theta }}^{(k)}\Vert }_1+{\rho }_n{\rho }_2\sum _{i,j}\sqrt{{\mathrm{\Theta }}_{ij}^{T}L{\mathrm{\Theta }}_{ij}},$$ (21)

where ${\mathrm{\Theta }}_{{(S^{(k)})}^c}^{(k)}=0$ indicates that ${\mathrm{\Theta }}_{(i,j)}^{(k)}=0$ for (i, j) ∉ S^(k).

Lemma 6

1. Let A ∈ ℝ^p×pbe a positive semidefinite matrix with eigenvalues 0 ≤ λ₁ ≤ λ₂ ≤ ⋯ ≤ λ_pand corresponding eigenvectors u_i satisfying u_i ⊥ u_j, i ≠ j and ‖u_i‖ = 1. The subdifferential $\partial \sqrt{x^{T}Ax}$of $f(x)=\sqrt{x^{T}Ax}$is

   $$\partial \sqrt{x^{T}Ax}=\{\begin{array}{cc}Ax/\sqrt{x^{T}Ax},\hfill & Ax\ne 0,\hfill \\ \{U{\mathrm{\Lambda }}^{1/2}y:\Vert y\Vert \le 1\},\hfill & Ax=0.\hfill \end{array}$$

   where U ∈ ℝ^p×phas u_i as the ith columns and Λ^1/2is the diagonal matrix with ${\lambda }_i^{1/2}$, i = 1, …, p, as diagonal elements. Furthermore, the subgradients are bounded above, i.e.

   $${\Vert \nabla f(x)\Vert }_{\infty }\le {\Vert A\Vert }_2^{1/2},\mathit{\text{ for all }}\nabla f(x)\in \partial \sqrt{x^{T}Ax}.$$
2. Let A ∈ ℝ^p×pbe a positive semidefinite matrix and S = {S_i} ⊂ {1, …, p}. Suppose A_SS has eigenvalues 0 ≤ λ_1,S ≤ λ_2,S ≤ ⋯ ≤ λ_|S|,Sand corresponding eigenvectors u_i,S satisfying u_i,S ⊥ u_j,S, i ≠ j and ‖u_i,S‖ = 1. Let g_S : ℝ^|S| → ℝ^pbe a map defined by g_S(x) = y where y_i = x_Sj for i = S_j for and y_i = 0 for i ∉ S. The subdifferential $h_{A,S}(x)=\sqrt{g_S{(x)}^{T}A{g}_S(x)}$equals to the subdifferential of $\sqrt{x^T{A}_{SS}x}$given by

   $$\partial \sqrt{x^T{A}_{SS}x}=\{\begin{array}{cc}{A}_{SS}x/\sqrt{x^T{A}_{SS}x},\hfill & A_{SS}x\ne 0,\hfill \\ U_S{\mathrm{\Lambda }}_S^{1/2}\{y:\Vert y\Vert \le 1\},\hfill & A_{SS}x=0.\hfill \end{array}$$

   where U_S ∈ ℝ^|S|×|S|has u_i,S as the ith columns and ${\mathrm{\Lambda }}_S^{1/2}$is the diagonal matrix with ${\lambda }_{i,S}^{1/2}$, i = 1, …, |S|, as diagonal elements. For x with A_SSx ≠ 0, there is a relationship between $\partial \sqrt{x^T{A}_{SS}x}$and $\partial \sqrt{y^{T}Ay}$at y = g_S(x) given by

   $${\left\{\frac{Ay}{\sqrt{y^{T}Ay}}\right\}}_S=\frac{A_{SS}x}{\sqrt{x^T{A}_{SS}x}},$$

   $${\left\{\frac{Ay}{\sqrt{y^{T}Ay}}\right\}}_{S^c}=\frac{A_{S^{c}S}x}{\sqrt{x^T{A}_{SS}x}}.$$
   Subgradients are bounded above:

   $${\Vert \nabla h_{A,S}(x)\Vert }_{\infty }\le {\Vert A_{SS}\Vert }_2^{1/2}\le {\Vert A\Vert }_2^{1/2},\forall \nabla f_{A,S}(x)\in \partial \sqrt{x^T{A}_{SS}x}.$$

Proof

1. For x with Ax ≠ 0, f(x) is differentiable and the subgradient of f at x is simply the matrix derivative. By definition, for x with Ax = 0, the subgradient υ of f at x satisfies the following inequality

   $$\sqrt{y^{T}Ay}\ge \langle y-x,\upsilon \rangle ,$$ (22)

   for all y. Choosing y = 2x and y = 0 yield 0 ≥ 〈x, υ〉 and 0 ≥ − 〈x, υ〉, implying 〈x, υ〉 = 0. The inequality (22) reduces to $\sqrt{y^{T}Ay}\ge \langle y,\upsilon \rangle$, for any y. If Ay = 0, a similar argument implies that 〈y, υ〉 = 0. Hence υ ⊥ y for every y with Ay = 0.
   Let j₀ be the smallest index such that λ_j0 > 0. Because u_j ’s form an orthonormal basis, any arbitrary vector y can be written as $y={\sum }_{j=1}^p{\beta }_j{u}_j$. Moreover, the null space of A is the span of u₁, …, u_j0−1. Thus, the subgradient υ can be written as $\upsilon ={\sum }_{j=j_0}^p{\alpha }_j{u}_j$. Thus, using the spectral decomposition of A as $A={\sum }_{j=j_0}^p{\lambda }_j{u}_j{u}_j^T$, we can write $f(y)={\{{\sum }_{j=j_0}^p{\lambda }_j{\beta }_j^2\}}^{1/2}$. On the other hand, $\langle y,\upsilon \rangle ={\sum }_{j=j_0}^p{\alpha }_j{\beta }_j$. Thus, the inequality (22) further reduces to

   $${\left\{\sum _{j=j_0}^p{\lambda }_j{\beta }_j^2\right\}}^{1/2}\ge \sum _{j=j_0}^p{\alpha }_j{\beta }_j,\forall {\beta }_j\in ℝ.$$
   It follows from the Cauchy-Schwartz inequality that the left hand side of the inequality is bounded from above;

   $$\sum _{j=j_0}^p{\alpha }_j{\beta }_j=\sum _{j=j_0}^p\frac{{\alpha }_j}{{\lambda }_j^{1/2}}{\lambda }_j^{1/2}{\beta }_j\le {\left\{\sum _{j=j_0}^p\frac{{\alpha }_j^2}{{\lambda }_j}\right\}}^{1/2}{\left\{\sum _{j=j_0}^p{\lambda }_j{\beta }_j^2\right\}}^{1/2}.$$
   Thus,

   $$\partial f(x)=\{\upsilon :\upsilon =\sum _{j=j_0}^p{\alpha }_j{\upsilon }_j,\sum _{j=j_0}^p\frac{{\alpha }_j^2}{{\lambda }_j}\le 1,{\alpha }_j\in ℝ\}.$$

   It is easy to see that this set is the image of the map UΛ^1/2 on the closed ball of radius 1.

   Given that ‖x‖_∞ ≤ ‖x‖, to establish the bound in the ℓ_∞-norm, we compute the bound in the Euclidean norm. We use the same notation as in (i). For x with Ax ≠ 0,

   $$\Vert \frac{Ax}{\sqrt{x^{T}Ax}}\Vert =\frac{\Vert U{\mathrm{\Lambda }}^{1/2}{\mathrm{\Lambda }}^{1/2}{U}^{T}x\Vert }{\Vert {\mathrm{\Lambda }}^{1/2}{U}^{T}x\Vert }\le {\Vert U{\mathrm{\Lambda }}^{1/2}\Vert }_2.$$

   But ${\Vert U{\mathrm{\Lambda }}^{1/2}\Vert }_2={\text{sup}}_{\Vert x\Vert =1}\Vert U{\mathrm{\Lambda }}^{1/2}x\Vert ={\text{sup}}_{x\in {ℝ}^K}\Vert U{\mathrm{\Lambda }}^{1/2}(U^{T}x)\Vert /\Vert U^{T}x\Vert ={\Vert A\Vert }_2^{1/2}$, because ‖U^T x‖ = ‖x‖. For x with Ax = 0, $\Vert {\mathrm{\Lambda }}^{1/2}y/\Vert y\Vert \Vert \le {\Vert A\Vert }_2^{1/2}$ for every y. Because of the form of the subdifferential and the fact that ‖U x‖ = ‖x‖, the result follows.

2. Let B_S be a product of elementary matrices for row and column exchange such that B_Sg_S(x) = (x, 0). Notice that $B_S=B_S^{-1}$ and that $B_S=B_S^T$ since B_S only rearranges elements of vectors and exchanges rows by multiplication from the left. Note also that ‖B_S‖₂ ≤ ‖B_S‖_∞/∞ = 1, since ‖C‖₂ ≤ ‖C‖_∞/∞ for C = C^T and each row of B_S has only one element with value 1. Because

   $${\{h_{A,S}(x)\}}^2=g_S{(x)}^{T}A{g}_S(x)={(B_S{g}_S(x))}^T(B_{S}A{B}_S)(B_S{g}_S(x))=x^T{A}_{SS}x,$$

   the subdifferential of h_A,S(x) follows from (ii). For x with A_SSx ≠ x and y = g_S(x), $Ay=B_{S}A{B}_S{(x,0)}^T=B_S{(A_{SS}x,A_{S^{c}S}^{T}x)}^T\ne 0$ because of invertibility of B_S. The relationship holds since

   $$\left[\begin{array}{c}\hfill {(Ay/\sqrt{y^{T}Ay})}_S\hfill \\ \hfill {(Ay/\sqrt{y^{T}Ay})}_{S^c}\hfill \end{array}\right]=B_S\frac{Ay}{\sqrt{y^{T}Ay}}=\frac{1}{\sqrt{x^T{A}_{SS}x}}\left[\begin{array}{c}\hfill A_{SS}x\hfill \\ \hfill A_{S^{c}S}x\hfill \end{array}\right]$$

   An ℓ_∞-bound follows from (i) and the fact that ${\Vert A_{SS}\Vert }_2\le {\Vert B_S\Vert }_2^2{\Vert A\Vert }_2={\Vert A\Vert }_2$.

Lemma 7

For sample correlation matrices ${\hat{\mathrm{\Psi }}}_n=({\hat{\mathrm{\Psi }}}_n^{(1)},\dots ,{\hat{\mathrm{\Psi }}}_n^{(K)})$and any ρ_n > 0, the convex problem(3)has a unique solution ${\hat{\mathrm{\Theta }}}_{{\rho }_n}=({\hat{\mathrm{\Theta }}}_{{\rho }_n}^{(1)},\dots ,{\hat{\mathrm{\Theta }}}_{{\rho }_n}^{(K)})$ with ${\hat{\mathrm{\Theta }}}_{{\rho }_n}^{(k)}>0$, k = 1, …, K, characterized by

$$n^{-1}{n}_k({\psi }_{n,ij}^{(k)}-{[{\{{\hat{\mathrm{\Theta }}}_{{\rho }_n}^{(k)}\}}^{-1}]}_{ij})+{\rho }_n{Û}_{1,ij}^{(k)}+{\rho }_n{\rho }_2{Û}_{2,ij}^{(k)}=0,$$ (23)

with ${Û}_{1,ij}^{(k)}\in \partial |{\hat{\theta }}_{{\rho }_n,ij}^{(k)}|$and ${({Û}_{2,ij}^{(1)},\dots ,{Û}_{2,ij}^{(K)})}^T\in \partial \sqrt{{\hat{\mathrm{\Theta }}}_{{\rho }_n,ij}^{T}L{\hat{\mathrm{\Theta }}}_{{\rho }_n,ij}}$for every i ≠ j and k = 1, …, K. Moreover,

$$n^{-1}{n}_k({\psi }_{n,ii}^{(k)}-{[{\{{\hat{\mathrm{\Theta }}}_{{\rho }_n}^{(k)}\}}^{-1}]}_{ii})+{\rho }_n{Û}_{1,ij}^{(k)}+{\rho }_n{\rho }_2{Û}_{2,ij}^{(k)}=0,$$ (24)

with ${Û}_{1,ij}^{(k)}={Û}_{2,ij}^{(k)}=0$for every i = 1, …, p, andk = 1, …, K.

For each (i, j) ∈ S, let $S_{ij}=\{k:{\mathrm{\Theta }}_{0,ij}^{(k)}\ne 0\}$. The convex problem(21)has a unique solution ${\check{\mathrm{\Theta }}}_{{\rho }_n}=({\check{\mathrm{\Theta }}}_{{\rho }_n}^{(1)},\dots ,{\check{\mathrm{\Theta }}}_{{\rho }_n}^{(K)})$with ${\check{\mathrm{\Theta }}}_{{\rho }_n}^{(k)}>0$characterized by

$$n^{-1}{n}_k({\psi }_{n,ij}^{(k)}-{[{\{{\check{\mathrm{\Theta }}}_{{\rho }_n}^{(k)}\}}^{-1}]}_{ij})+{\rho }_n{Ǔ}_{1,ij}^{(k)}+{\rho }_n{\rho }_2{Ǔ}_{2,ij}^{(k)}=0,$$ (25)

with ${Ǔ}_{1,ij}^{(k)}\in \partial |{\check{\theta }}_{{\rho }_n,ij}^{(k)}|$ and ${Ǔ}_{2,ij}^{(k)}\in \partial \sqrt{{\{{\check{\mathrm{\Theta }}}_{{\rho }_n,ij}\}}_{S_{ij}}^T{L}_{S_{ij}{S}_{ij}}{\{{\check{\mathrm{\Theta }}}_{{\rho }_n,ij}\}}_{S_{ij}}}$for every i ≠ j and k = 1, …, K. Moreover,

$$n^{-1}{n}_k({\psi }_{n,ii}^{(k)}-{[{\{{\check{\mathrm{\Theta }}}_{{\rho }_n}^{(k)}\}}^{-1}]}_{ii})+{\rho }_n{Ǔ}_{1,ij}^{(k)}+{\rho }_n{\rho }_2{Ǔ}_{2,ij}^{(k)}=0,$$ (26)

with ${Ǔ}_{1,ij}^{(k)}={Ǔ}_{2,ij}^{(k)}=0$for every i = 1, …, p, and k = 1, …, K.

Proof

A proof for the uniqueness of the solution is similar to the proof of Lemma 3 of Ravikumar et al. [25]. The rest is the KKT condition using Lemma 6.

We choose a pair Ũ = (Ũ₁, Ũ₂) of the subgradients of the first and second regularization terms evaluated at Θ̌_ρn. For each (i, j) with Ω_0,ij = 0 or with LΘ̌_ρn,ij = 0, set

$${Ũ}_{1,ij}^{(k)}={\rho }_n^{-1}{n}^{-1}{n}_k(-{\psi }_{n,ij}^{(k)}+{[{\{{\check{\mathrm{\Theta }}}_{{\rho }_n}^{(k)}\}}^{-1}]}_{ij}),{Ũ}_{2,ij}^{(k)}=0,k=1,\dots ,K.$$

For (i, j) with ${\omega }_{0,ij}^{(k)}\ne 0$, for all k = 1, …, K, set

$${Ũ}_{1,ij}^{(k)}={Ǔ}_{1,ij}^{(k)},{Ũ}_{2,ij}^{(k)}={Ǔ}_{2,ij}^{(k)},k=1,\dots ,K.$$

For (i, j) with LΘ̌_ρn,ij ≠ 0, Ω_0,ij ≠ 0 but ${\omega }_{0,ij}^{(k\prime )}=0$ for some k′, set

$${Ũ}_{1,ij}^{(k)}={\rho }_n^{-1}{n}^{-1}{n}_k(-{\psi }_{n,ij}^{(k)}+{[{\{{\check{\mathrm{\Theta }}}_{{\rho }_n}^{(k)}\}}^{-1}]}_{ij})-{\rho }_2\frac{l_k{\check{\mathrm{\Theta }}}_{{\rho }_n,ij}}{\sqrt{{\check{\mathrm{\Theta }}}_{{\rho }_n,ij}^{T}L{\check{\mathrm{\Theta }}}_{{\rho }_n,ij}}},$$

and

$${Ũ}_{2,ij}^{(k)}=\frac{l_k^T{\check{\mathrm{\Theta }}}_{{\rho }_n,ij}}{\sqrt{{\check{\mathrm{\Theta }}}_{{\rho }_n,ij}^{T}L{\check{\mathrm{\Theta }}}_{{\rho }_n,ij}}},$$

if ${\omega }_{0,ij}^{(k)}=0$. Otherwise, let

$${Ũ}_{1,ij}^{(k)}={Ǔ}_{1,ij}^{(k)},{Ũ}_{2,ij}^{(k)}=\frac{l_k^T{\check{\mathrm{\Theta }}}_{{\rho }_n,ij}}{\sqrt{{\check{\mathrm{\Theta }}}_{{\rho }_n,ij}^{T}L{\check{\mathrm{\Theta }}}_{{\rho }_n,ij}}}.$$

Here, l_k is the kth row of L.

The main idea of the proof is to show that (Θ̌_ρn, Ũ) satisfies the optimality conditions of the original problem with probability tending to 1. In particular, we show the following equation, which holds by construction of Ũ₁ and Ũ₂, is in fact the KKT condition of the original problem (3):

$$n^{-1}{n}_k({\hat{\mathrm{\Psi }}}_n^{(k)}-{\{{\check{\mathrm{\Theta }}}_{{\rho }_n}^{(k)}\}}^{-1})+{\rho }_n{Ũ}_1^{(k)}+{\rho }_n{\rho }_2{Ũ}_2^{(k)}=0.$$ (27)

To this end, we show that Ũ₁ and Ũ₂ are both subgradients of the original problem. We can then conclude that the oracle estimator in the restricted problem (21) is the solution to the original problem (3). Then it follows from the uniqueness of the solution that Θ̌_ρn = Θ̂_ρn.

Let ${\mathrm{\Xi }}^{(k)}={\hat{\mathrm{\Psi }}}_n^{(k)}-{\mathrm{\Psi }}_0^{(k)},R^{(k)}({\mathrm{\Delta }}^{(k)})={\{{\check{\mathrm{\Theta }}}_{{\rho }_n}^{(k)}\}}^{-1}-{\mathrm{\Psi }}_0^{(k)}+{\mathrm{\Psi }}_0^{(k)}{\mathrm{\Delta }}^{(k)}{\mathrm{\Psi }}_0^{(k)}$, and ${\check{\mathrm{\Delta }}}^{(k)}={\check{\mathrm{\Theta }}}_{{\rho }_n}^{(k)}-{\mathrm{\Theta }}_0^{(k)}$.

Lemma 8

Suppose that max{‖Ξ^(k)‖_∞, R^(k)(Δ̌^(k))‖_∞} ≤ αρ_n/8, and ${\rho }_2\le {\alpha }^2/\{4{\Vert L\Vert }_2^{1/2}(2-\alpha )\}$. Suppose moreover thatLΘ̌_ρn,ij ≠ 0 for (i, j) ∈ S. Then $|{Ũ}_{1,ij}^{(k)}|<1$for (i, j) ∈ (S^(k))^c.

Proof

We rewrite (27) to obtain

$$\frac{n_k}{n}{\mathrm{\Psi }}_0^{(k)}{\check{\mathrm{\Delta }}}^{(k)}{\mathrm{\Psi }}_0^{(k)}+\frac{n_k}{n}{\mathrm{\Xi }}^{(k)}-\frac{n_k}{n}{R}^{(k)}({\check{\mathrm{\Delta }}}^{(k)})+{\rho }_n{Ũ}_1^{(k)}+{\rho }_n{\rho }_2{Ũ}_2^{(k)}=0.$$

We further rewrite the above equation via vectorization;

$$\frac{n_k}{n}({\mathrm{\Psi }}_0^{(k)}\otimes {\mathrm{\Psi }}_0^{(k)}){\overrightarrow{\check{\mathrm{\Delta }}}}^{(k)}+\frac{n_k}{n}{\overrightarrow{\mathrm{\Xi }}}^{(k)}-\frac{n_k}{n}{\overrightarrow{R}}^{(k)}({\check{\mathrm{\Delta }}}^{(k)})+{\rho }_n{\overrightarrow{Ũ}}_1^{(k)}+{\rho }_n{\rho }_2{\overrightarrow{Ũ}}_2^{(k)}=0.$$

We separate this equation into two equations depending on S^(k);

$$\frac{n_k}{n}{\mathrm{\Gamma }}_{S^{(k)}{S}^{(k)}}^{(k)}{\overrightarrow{\check{\mathrm{\Delta }}}}_{S^{(k)}}^{(k)}+\frac{n_k}{n}{\overrightarrow{\mathrm{\Xi }}}_{S^{(k)}}^{(k)}-\frac{n_k}{n}{\overrightarrow{R}}_{S^{(k)}}^{(k)}({\check{\mathrm{\Delta }}}^{(k)})+{\rho }_n{\overrightarrow{Ũ}}_{1,S^{(k)}}^{(k)}+{\rho }_n{\rho }_2{\overrightarrow{Ũ}}_{2,S^{(k)}}^{(k)}=0,$$

$$\frac{n_k}{n}{\mathrm{\Gamma }}_{{(S^{(k)})}^c{S}^{(k)}}^{(k)}{\overrightarrow{\check{\mathrm{\Delta }}}}_{S^{(k)}}^{(k)}+\frac{n_k}{n}{\overrightarrow{\mathrm{\Xi }}}_{{(S^{(k)})}^c}^{(k)}-\frac{n_k}{n}{\overrightarrow{R}}_{{(S^{(k)})}^c}^{(k)}\left({\check{\mathrm{\Delta }}}^{(k)}\right)+{\rho }_n{\overrightarrow{Ũ}}_{1,{(S^{(k)})}^c}^{(k)}+{\rho }_n{\rho }_2{\overrightarrow{Ũ}}_{2,{(S^{(k)})}^c}^{(k)}=0.$$ (28)

where (Ũ⃗_l)_J ≡ Ũ⃗_k,J, l = 1, 2. Here we used ${\check{\mathrm{\Delta }}}_{{(S^{(k)})}^c}^{(k)}=0$. Since ${\mathrm{\Gamma }}_{S^{(k)}{S}^{(k)}}^{(k)}$ is invertible, we solve the first equation to obtain

$$\frac{n_k}{n}{\overrightarrow{\check{\mathrm{\Delta }}}}_{S^{(k)}}^{(k)}={({\mathrm{\Gamma }}_{S^{(k)}{S}^{(k)}}^{(k)})}^{-1}\{-\frac{n_k}{n}{\overrightarrow{\mathrm{\Xi }}}_{S^{(k)}}^{(k)}+\frac{n_k}{n}{\overrightarrow{R}}_{S^{(k)}}^{(k)}({\check{\mathrm{\Delta }}}^{(k)})-{\rho }_n{\overrightarrow{Ũ}}_{1,S^{(k)}}^{(k)}-{\rho }_n{\rho }_2{\overrightarrow{Ũ}}_{2,S^{(k)}}^{(k)}\}.$$

Substituting this expression into (28) yields

$${\overrightarrow{Ũ}}_{1,{(S^{(k)})}^c}^{(k)}={\rho }_n^{-1}{\mathrm{\Gamma }}_{{(S^{(k)})}^c{S}^{(k)}}^{(k)}{({\mathrm{\Gamma }}_{S^{(k)}{S}^{(k)}}^{(k)})}^{-1}(\frac{n_k}{n}{\overrightarrow{\mathrm{\Xi }}}_{S^{(k)}}^{(k)}-\frac{n_k}{n}{\overrightarrow{R}}_{S^{(k)}}^{(k)}({\check{\mathrm{\Delta }}}^{(k)}))+{\mathrm{\Gamma }}_{{(S^{(k)})}^c{S}^{(k)}}^{(k)}{({\mathrm{\Gamma }}_{S^{(k)}{S}^{(k)}}^{(k)})}^{-1}{\overrightarrow{Ũ}}_{1,S^{(k)}}^{(k)}+{\rho }_2{\mathrm{\Gamma }}_{{(S^{(k)})}^c{S}^{(k)}}^{(k)}{({\mathrm{\Gamma }}_{S^{(k)}{S}^{(k)}}^{(k)})}^{-1}{\overrightarrow{Ũ}}_{2,S^{(k)}}^{(k)}-{\rho }_n^{-1}(\frac{n_k}{n}{\overrightarrow{\mathrm{\Xi }}}_{{(S^{(k)})}^c}^{(k)}-\frac{n_k}{n}{\overrightarrow{R}}_{{(S^{(k)})}^c}^{(k)}({\check{\mathrm{\Delta }}}^{(k)}))-{\rho }_2{\overrightarrow{Ũ}}_{2,{(S^{(k)})}^c}^{(k)}.$$

Taking the ℓ_∞-norm yields

$${\Vert {\overrightarrow{Ũ}}_{1,{(S^{(k)})}^c}^{(k)}\Vert }_{\infty }\le {\rho }_n^{-1}{\Vert {\mathrm{\Gamma }}_{{(S^{(k)})}^c{S}^{(k)}}^{(k)}{({\mathrm{\Gamma }}_{S^{(k)}{S}^{(k)}}^{(k)})}^{-1}\Vert }_{\infty /\infty }({\Vert {\overrightarrow{\mathrm{\Xi }}}_{S^{(k)}}^{(k)}\Vert }_{\infty }+{\Vert {\overrightarrow{R}}_{S^{(k)}}^{(k)}({\check{\mathrm{\Delta }}}^{(k)})\Vert }_{\infty })+{\Vert {\mathrm{\Gamma }}_{{(S^{(k)})}^c{S}^{(k)}}^{(k)}{({\mathrm{\Gamma }}_{S^{(k)}{S}^{(k)}}^{(k)})}^{-1}\Vert }_{\infty /\infty }({\Vert {\overrightarrow{Ũ}}_{1,S^{(k)}}^{(k)}\Vert }_{\infty }+{\rho }_2{\Vert {\overrightarrow{Ũ}}_{2,S^{(k)}}^{(k)}\Vert }_{\infty })+{\rho }_n^{-1}({\Vert {\overrightarrow{\mathrm{\Xi }}}_{{(S^{(k)})}^c}^{(k)}\Vert }_{\infty }+{\Vert {\overrightarrow{R}}_{{(S^{(k)})}^c}^{(k)}({\check{\mathrm{\Delta }}}^{(k)})\Vert }_{\infty })+{\rho }_2{\Vert {\overrightarrow{Ũ}}_{2,{(S^{(k)})}^c}^{(k)}\Vert }_{\infty }\le \frac{2-\alpha }{{\rho }_n}({\Vert {\overrightarrow{\mathrm{\Xi }}}_{{(S^{(k)})}^c}^{(k)}\Vert }_{\infty }+{\Vert {\overrightarrow{R}}_{{(S^{(k)})}^c}^{(k)}({\check{\mathrm{\Delta }}}^{(k)})\Vert }_{\infty })+1-\alpha +(2-\alpha ){\rho }_2{\Vert L\Vert }_2^{1/2}.$$

Here we used that ‖A_x‖_∞ ≤ ‖A‖_∞/∞ ≤ ‖A‖_∞ and ${\Vert {\mathrm{\Gamma }}_{{(S^{(k)})}^c{S}^{(k)}}^{(k)}{({\mathrm{\Gamma }}_{S^{(k)}{S}^{(k)}}^{(k)})}^{-1}\Vert }_{\infty /\infty }\le 1-\alpha$, and applied Lemma 6 to bound ‖Ũ⃗_{2, (S^(k))^c}‖_∞ and ‖Ũ⃗_{2, (S^(k))}‖_∞ by ${\Vert L\Vert }_2^{1/2}$. We also used ${\Vert {\overrightarrow{Ũ}}_{1,S^{(k)}}^{(k)}\Vert }_{\infty }={\Vert {\overrightarrow{Ǔ}}_{1,S^{(k)}}^{(k)}\Vert }_{\infty }\le 1$ by construction of Ũ₁ and the assumption that ${\check{\mathrm{\Theta }}}_{{\rho }_n}^{(k)}\ne 0$. It follows by the assumption of the lemma that

$${\Vert {Ũ}_{{(S^{(k)})}^c}^{(k)}\Vert }_{\infty }\le \frac{2-\alpha }{{\rho }_n}\frac{\alpha {\rho }_n}{4}+(1-\alpha )+(2-\alpha ){\rho }_2{\Vert L\Vert }_2^{1/2}\le 1-\frac{\alpha }{2}-\frac{{\alpha }^2}{4}+\frac{{\alpha }^2}{4}<1.$$

Lemma 9 (Lemma 5 of Ravikumar et al. [25])

Suppose that ‖Δ‖_∞ ≤ 1/(3κ_Ψd) with

$${({\mathrm{\Delta }}^{(k)})}_{(S^{(k)}\cup \{(i,i):i=1,\dots ,p]\}{)}^c}=0.$$

Then ‖H^(k)‖_∞/∞ ≤ 3/2 where $H^{(k)}\equiv {\sum }_{j=1}^{\infty }{(-1)}^j{({\mathrm{\Psi }}_0^{(k)}{\mathrm{\Delta }}^{(k)})}^j$, k = 1, …, K, andR^(k)(Δ^(k)) has representation $R^{(k)}({\mathrm{\Delta }}^{(k)})={\mathrm{\Psi }}_0^{(k)}{\mathrm{\Delta }}^{(k)}{\mathrm{\Psi }}_0\mathrm{\Delta }{H}^{(k)}{\mathrm{\Psi }}_0^{(k)}$with ${\Vert R^{(k)}({\mathrm{\Delta }}^{(k)})\Vert }_{\infty }\le (3/2)d{\Vert {\mathrm{\Delta }}^{(k)}\Vert }_{\infty }^2{({\kappa }_{\mathrm{\Psi }})}^3$.

Lemma 10

Suppose ${\Vert \mathrm{\Delta }\Vert }_2\le 1/(2{\text{ max}}_k{\Vert {\mathrm{\Psi }}_0^{(k)}\Vert }_2)$with ${\mathrm{\Delta }}_{{(S^{(k)}\cup \{{(i,i)}_{i=1}^p]\})}^c}^{(k)}=0$. Then ‖H^(k)‖_∞/∞ ≤ 2 where $H^{(k)}\equiv {\sum }_{t=1}^{\infty }{(-1)}^t{({\mathrm{\Psi }}_0^{(k)}{\mathrm{\Delta }}^{(k)})}^t$, k = 1, …, K, andR^(k)(Δ^(k)) has representation $R^{(k)}({\mathrm{\Delta }}^{(k)})={\mathrm{\Psi }}_0^{(k)}{\mathrm{\Delta }}^{(k)}{\mathrm{\Psi }}_0\mathrm{\Delta }{H}^{(k)}{\mathrm{\Psi }}_0^{(k)}$with ${\Vert R^{(k)}({\mathrm{\Delta }}^{(k)})\Vert }_{\infty }\le 2{\lambda }_{\mathrm{\Theta }}^3{\Vert {\mathrm{\Delta }}^{(k)}\Vert }_2^2$.

Proof

Note that the Neumann series for a matrix (I − A)⁻¹ converges if the operator norm of A is strictly less than 1, and that the ℓ_∞-norm is bounded by the operator norm. A proof is similar to that of Lemma 5 of Ravikumar et al. [25] with the induced infinity norm ‖·‖_∞/∞ replaced by the operator norm in appropriate inequalities.

The following lemma is similar to the statement of Lemma 6 of Ravikumar et al. [25].

Lemma 11

Suppose that

$$r\equiv \frac{4}{{\text{min}}_k{\pi }_k}{\kappa }_{\mathrm{\Gamma }}(\underset{k}{\text{max}}{\Vert {\mathrm{\Xi }}^{(k)}\Vert }_{\infty }+{\rho }_n+{\rho }_n{\rho }_2{\Vert L\Vert }_2^{1/2})<\frac{1}{6d\text{ max }\{{\kappa }_{\mathrm{\Psi }},{\kappa }_{\mathrm{\Psi }}^3{\kappa }_{\mathrm{\Gamma }}\}},$$

for k = 1, …, K. Suppose moreover that ${({\mathrm{\Theta }}_0^{(k)}\otimes {\mathrm{\Theta }}_0^{(k)})}_{S^{(k)}{S}^{(k)}}$are invertible for k = 1, …, K. Then with probability $1-2K\text{ exp}(-n{\text{ min}}_k{\pi }_k^2/2)$,

$$\underset{k}{\text{max}}{\Vert {\tilde{\mathrm{\Theta }}}_{{\rho }_n}^{(k)}-{\mathrm{\Theta }}_0^{(k)}\Vert }_{\infty }\le (3/2)r.$$

Proof

We apply Shauder’s fixed point theorem on the event min_k π_k/2 ≤ n_k/n, which holds with probability $1-2K\text{ exp}(-n{\text{ min}}_k{\pi }_k^2/2)$ by Lemma 5 with ε = min_k π_k/2. We first define the function f_k and its domain 𝒟_k to which the fixed point theorem applies. Let S̅^(k) = S^(k) ∪ {(i, i) : 1 ≤ i ≤ p}, and define

$${𝒟}_k=\{A\in {𝕊}^{p\times p}:x^T(A+{\mathrm{\Theta }}_0^{(k)})x\ge 0,{\forall }_x\in {ℝ}^p,{\Vert A_{{\overline{S}}^{(k)}}\Vert }_{\infty }\le r,A_{{({\overline{S}}^{(k)})}^c}=0\},$$

where 𝕊^p×p is the space of symmetric p × p matrices. Then 𝒟_k is a convex, compact subset of the set of 𝕊^p×p.

Let ${Ǔ}_l^{(k)}\in {ℝ}^{p\times p}$, l = 1, 2, be zero-filled matrices whose (i, j)-element is ${Ǔ}_{l,ij}^{(k)}$ in Lemma 7 if (i, j) ∈ S^(k) and zero otherwise. Define the map g_k on the set of invertible matrices in ℝ^p×p by $g_k(B)=(n_k/n)(B^{-1}-{\hat{\mathrm{\Psi }}}_n^{(k)})-{\rho }_n{Ǔ}_1^{(k)}-{\rho }_n{\rho }_2{Ǔ}_2^{(k)}$. Note that ${\{g_k({\check{\mathrm{\Theta }}}_{{\rho }_n}^{(k)})\}}_{S^{(k)}}=0$ is the KKT condition for the restricted problem (21). Let δ > 0 be a constant such that δ < min{1/2, 1/{10(4dr + 1)}}r and $\delta +r\le 1/\{6d\text{ max}\{{\kappa }_{\mathrm{\Psi }},{\kappa }_{\mathrm{\Psi }}^3{\kappa }_{\mathrm{\Gamma }}\}$. Define a continuous function f_k : 𝒟_k ↦ 𝒟_k as

$$({f_k(A))}_{ij}=\{\begin{array}{cc}{A}_{ij}\hfill & i=j,\hfill \\ {\{h_k(A){\mathrm{\Theta }}_0^{(k)}{g}_k(A+{\mathrm{\Theta }}_0^{(k)}+\delta I){\mathrm{\Theta }}_0^{(k)}+A\}}_{ij},\hfill & i\ne j,(i,j)\in S^{(k)}\hfill \\ 0,\hfill & \text{otherwise},\hfill \end{array}$$

where

$$h_k(A)\equiv \frac{2^{-1}\text{ min}\{{\lambda }_1(A+{\mathrm{\Theta }}_0^{(k)}),2^{-1}\}+2^{-1}}{\text{max}\{|{\lambda }_1({\{{\mathrm{\Theta }}_0^{(k)}{g}_k(A+{\mathrm{\Theta }}_0^{(k)}+\delta I){\mathrm{\Theta }}_0^{(k)}\}}_{S^{(k)}}-I)|,1\}}.$$

Let ${\tilde{f}}_k(A)=h_k(A){\mathrm{\Theta }}_0^{(k)}{g}_k(A+{\mathrm{\Theta }}_0^{(k)}+\delta I){\mathrm{\Theta }}_0^{(k)}$. Then f_k(A) = (f̃_k(A))_S^(k) + A for A ∈ 𝒟_k.

We now verify the conditions of Shauder’s fixed point theorem below. Once these conditions are established, the theorem yields that f_k(A) = A. Since (f_k(A))_(S̅^(k))^c = A for any A ∈ 𝒟_k, and h_k(A) > 0, the solution A to f_k(A) = A is determined by ${({\mathrm{\Theta }}_0^{(k)}{g}_k(A+{\mathrm{\Theta }}_0^{(k)}+\delta I){\mathrm{\Theta }}_0^{(k)})}_{S^{(k)}}=0$. Vectorizing this equation to obtain ${({\mathrm{\Theta }}_0^{(k)}\otimes {\mathrm{\Theta }}_0^{(k)})}_{S^{(k)}{S}^{(k)}}{\{g_k(A+{\mathrm{\Theta }}_0^{(k)}+\delta I)\}}_{S^{(k)}}=0$, it follows from the invertibility of ${({\mathrm{\Theta }}_0^{(k)}\otimes {\mathrm{\Theta }}_0^{(k)})}_{S^{(k)}{S}^{(k)}}$ that ${\{g_k(A+{\mathrm{\Theta }}_0^{(k)}+\delta I)\}}_{S^{(k)}}=0$. By the uniqueness of the KKT condition, the solution is $A={\check{\mathrm{\Theta }}}_{{\rho }_n}^{(k)}-{\mathrm{\Theta }}_0^{(k)}-\delta I$. Since A ∈ 𝒟_k, and δ < r/2, we conclude ${\Vert {\check{\mathrm{\Theta }}}_{{\rho }_n}^{(k)}-{\mathrm{\Theta }}_0^{(k)}\Vert }_{\infty }\le (3/2)r$.

In the following, we write A⃗ = vec(A) for a matrix A for notational convenience. For J ⊂ {(i, j) : i, j = 1, …, p}, vec(A)_J should be understood as A⃗_J.

The function f_k is continuous on 𝒟_k. To see this, note first that $A+{\mathrm{\Theta }}_0^{(k)}+\delta I$ is positive definite for every A ∈ 𝒟_k so that the inversion is continuous. Note also that all elements in the matrices involved with eigenvalues in h_k(A) are uniformly bounded in 𝒟_k, and hence the eigenvalues are also uniformly bounded.

To show that f_k(A) ∈ 𝒟_k, first we show that $f_k(A)+{\mathrm{\Theta }}_0^{(k)}$ is positive semidefinite. This follows because for any x ∈ ℝ^p

$$x^T(f_k(A)+{\mathrm{\Theta }}_0^{(k)})x=x^T\{{({\tilde{f}}_k(A))}_{S^{(k)}}-I\}x+x^T(A+{\mathrm{\Theta }}_0^{(k)})x+x^{T}x\ge h_k(A){\lambda }_1({\{{\mathrm{\Theta }}_0^{(k)}{g}_k(A+{\mathrm{\Theta }}_0^{(k)}+\delta I){\mathrm{\Theta }}_0^{(k)}\}}_{S^{(k)}}-I){\Vert x\Vert }^2+{\lambda }_1(A+{\mathrm{\Theta }}_0^{(k)}){\Vert x\Vert }^2+{\Vert x\Vert }^2\ge 0.$$

To see this, note that if ${\lambda }_A\equiv {\lambda }_1({\{{\mathrm{\Theta }}_0^{(k)}{g}_k(A+{\mathrm{\Theta }}_0^{(k)}+\delta I){\mathrm{\Theta }}_0^{(k)}\}}_{S^{(k)}}-I)$ is positive, then the inequality easily follows. On the other hand, if λ_A < −1, we have

$$h_k(A){\lambda }_A{\Vert x\Vert }^2\ge -2^{-1}\text{ min}\{{\lambda }_1(A+{\mathrm{\Theta }}_0^{(k)}),2^{-1}\}{\Vert x\Vert }^2-2^{-1}{\Vert x\Vert }^2\ge -({\lambda }_1(A+{\mathrm{\Theta }}_0^{(k)})/2+1/2){\Vert x\Vert }^2.$$

Lastly, if −1 ≤ λ_A < 0, we have

$$h_k(A){\lambda }_A{\Vert x\Vert }^2\ge -|{\lambda }_A|[2^{-1}\text{ min}\{{\lambda }_1(A+{\mathrm{\Theta }}_0^{(k)}),2^{-1}\}+1/2]{\Vert x\Vert }^2\ge -|{\lambda }_A|({\lambda }_1(A+{\mathrm{\Theta }}_0^{(k)})/2+1/2){\Vert x\Vert }^2.$$

Next, we show that ‖f_k(A)_S̅^(k)‖_∞ ≤ r. Because diag(f_k(A)) = diag(A), it suffices to show ‖f_k(A)_S^(k)‖_∞ ≤ r. Since $\delta +r\le 1/\{6d\text{ max}\{{\kappa }_{\mathrm{\Psi }},{\kappa }_{\mathrm{\Psi }}^3{\kappa }_{\mathrm{\Gamma }}\}$,

$${\Vert {\mathrm{\Psi }}_0^{(k)}(A+\delta I)\Vert }_{\infty /\infty }\le {\kappa }_{\mathrm{\Psi }}d{\Vert A+\delta I\Vert }_{\infty }\le {\kappa }_{\mathrm{\Psi }}d(r+\delta )\le 1/3.$$

It then follows from Lemma 9 that

$$R(A+\delta I)={(A+\delta I+{\mathrm{\Theta }}_0^{(k)})}^{-1}-{\mathrm{\Psi }}_0^{(k)}+{\mathrm{\Psi }}_0^{(k)}(A+\delta I){\mathrm{\Psi }}_0^{(k)}={\{{\mathrm{\Psi }}_0^{(k)}(A+\delta I)\}}^2{H}^{(k)}{\mathrm{\Psi }}_0^{(k)}.$$

Thus, adding and subtracting ${\mathrm{\Psi }}_0^{(k)}$ yields

$${\tilde{f}}_k(A)+A=h_k(A){\mathrm{\Theta }}_0^{(k)}((n_k/n){\{{\mathrm{\Psi }}_0^{(k)}(A+\delta I)\}}^2{H}^{(k)}{\mathrm{\Psi }}_0^{(k)}-(n_k/n){\mathrm{\Xi }}^{(k)}-{\rho }_n{Ǔ}_1^{(k)}-{\rho }_n{\rho }_2{Ǔ}_2^{(k)}){\mathrm{\Theta }}_0^{(k)}+(1-(n_k/n)h_k(A))A-(n_k/n)\delta h_k(A)I.$$

Vectorization and restriction on S^(k) gives

$${\Vert \text{vec}{(f_k(A))}_{S^{(k)}}\Vert }_{\infty }={\Vert \text{vec}{({\tilde{f}}_k(A)+A)}_{S^{(k)}}\Vert }_{\infty }\le (n_k/n)h_k(A){\Vert {\{{({\mathrm{\Gamma }}^{(k)})}^{-1}\}}_{S^{(k)}{S}^{(k)}}\text{vec}{({\{{\mathrm{\Psi }}_0^{(k)}(A+\delta I)\}}^2{H}^{(k)}{\mathrm{\Psi }}_0^{(k)})}_{S^{(k)}}\Vert }_{\infty }+(1-(n_k/n)h_k(A)){\Vert \text{vec}{(A)}_{S^{(k)}}\Vert }_{\infty }+(n_k/n)\delta +h_k(A){\Vert {\{{({\mathrm{\Gamma }}^{(k)})}^{-1}\}}_{S^{(k)}{S}^{(k)}}\{\text{vec}{((n_k/n){\mathrm{\Xi }}^{(k)})}_{S^{(k)}}+{\rho }_n\text{vec}{({Ǔ}_1^{(k)})}_{S^{(k)}}+{\rho }_n{\rho }_2\text{vec}{({Ǔ}_2^{(k)})}_{S^{(k)}}\}\Vert }_{\infty },$$ (29)

where ${\{{({\mathrm{\Gamma }}^{(k)})}^{-1}\}}_{S^{(k)}{S}^{(k)}}={({\mathrm{\Theta }}^{(k)}\otimes {\mathrm{\Theta }}_0^{(k)})}_{S^{(k)}{S}^{(k)}}$. Here we used h_k(A) ≤ (1/4 + 1/2)/1 = 3/4. For the first term of the upper bound in (29), it follows by the inequality ‖Ax‖_∞ ≤ ‖A‖_∞/∞‖x‖_∞ for A ∈ ℝ^p×p and x ∈ ℝ^p, Lemma 9 and the choice of δ satisfying $\delta +r\le 1/\{6d\text{ max}\{{\kappa }_{\mathrm{\Psi }},{\kappa }_{\mathrm{\Psi }}^3{\kappa }_{\mathrm{\Gamma }}\}$ that

$${\Vert {\{{({\mathrm{\Gamma }}^{(k)})}^{-1}\}}_{S^{(k)}{S}^{(k)}}\text{vec}{({\{{\mathrm{\Psi }}_0^{(k)}(A+\delta I)\}}^2{H}^{(k)}{\mathrm{\Psi }}_0^{(k)})}_{S^{(k)}}\Vert }_{\infty }\le {\kappa }_{\mathrm{\Gamma }}{\Vert R^{(k)}(A+\delta I)\Vert }_{\infty }\le {\kappa }_{\mathrm{\Gamma }}\frac{3}{2}d{\Vert A+\delta I\Vert }_{\infty }^2{\kappa }_{\mathrm{\Psi }}^3\le {\kappa }_{\mathrm{\Gamma }}\frac{3}{2}d{\Vert A+\delta I\Vert }_{\infty }(r+\delta ){\kappa }_{\mathrm{\Psi }}^3\le (r+\delta )/4.$$

For the second term, it follows by the assumption, the inequality that ‖Ax‖_∞ ≤ ‖A‖_∞/∞‖x‖_∞ for A ∈ ℝ^p×p and x ∈ ℝ^p, and Lemma 6 that

$${\Vert {\{{({\mathrm{\Gamma }}^{(k)})}^{-1}\}}_{S^{(k)}{S}^{(k)}}\{\frac{n_k}{n}\text{vec}{({\mathrm{\Xi }}^{(k)})}_{S^{(k)}}+{\rho }_n\text{vec}{({Ǔ}_1^{(k)})}_{S^{(k)}}+{\rho }_n{\rho }_2\text{vec}{({Ǔ}_2^{(k)})}_{S^{(k)}}\}\Vert }_{\infty }\le {\kappa }_{\mathrm{\Gamma }}(\Vert {\mathrm{\Xi }}^{(k)}+{\rho }_n+{\rho }_n{\rho }_2{\Vert L\Vert }_2^{1/2})=(\underset{k}{\text{min }}{\pi }_k)r/4\le (n_k/n)r/2.$$

Thus, we can further bound ‖vec((f̃_k(A) + A)_S^(k))‖_∞ by

$$\frac{n_k}{n}{h}_k(A)\frac{r+\delta }{4}+\frac{n_k}{n}{h}_k(A)\frac{r}{2}+(1-\frac{n_k}{n}{h}_k(A))r+\frac{n_k}{n}\delta =r\{1-\frac{n_k}{n}\frac{h_k(A)}{4}\}+\frac{n_k}{n}\{1+\frac{h_k(A)}{4}\}\delta .$$ (30)

Since

$${\Vert {({\mathrm{\Theta }}_0^{(k)}{g}_k(A+{\mathrm{\Theta }}_0^{(k)}+\delta I){\mathrm{\Theta }}_0^{(k)})}_{S^{(k)}}\Vert }_{\infty }\le {\Vert A_{S^{(k)}}\Vert }_{\infty }+{\Vert {\mathrm{\Theta }}_0^{(k)}{g}_k(A+{\mathrm{\Theta }}_0^{(k)}+\delta I){\mathrm{\Theta }}_0^{(k)}+A{)}_{S^{(k)}}\Vert }_{\infty },$$

and δ ≤ r/2, a similar reasoning shows that

$$\begin{gathered} {\Vert {\left({\mathrm{\Theta }}_0^{(k)}{g}_k\right(A+{\mathrm{\Theta }}_0^{(k)}+\delta I\left){\mathrm{\Theta }}_0^{(k)}\right)}_{S^{(k)}}\Vert }_{\infty } \\ \le (n_k/n){\Vert {\left\{{({\mathrm{\Gamma }}^{(k)})}^{-1}\right\}}_{S^{(k)}{S}^{(k)}}\text{ vec }{\left({\{{\mathrm{\Psi }}_0^{(k)}(A+\delta I)\}}^2{H}^{(k)}{\mathrm{\Psi }}_0^{(k)}\right)}_{S^{(k)}}\Vert }_{\infty } \\ +(2-(n_k/n)){\Vert \text{vec}{(A)}_{S^{(k)}}\Vert }_{\infty }+(n_k/n)\delta \\ +{\Vert {\left\{{({\mathrm{\Gamma }}^{(k)})}^{-1}\right\}}_{S^{(k)}{S}^{(k)}}\{(n_k/n)\text{vec}{({\mathrm{\Xi }}^{(k)})}_{S^{(k)}} \\ +{\rho }_n\text{vec}{({Ǔ}_1^{(k)})}_{S^{(k)}} \\ +{\rho }_n{\rho }_2\text{vec }({({Ǔ}_2^{(k)})}_{S^{(k)}}\left)\right\}\Vert }_{\infty } \\ \le \frac{r+\delta }{4}+\frac{r}{2}+2r+\delta \le 4r. \end{gathered}$$

Thus, the inequality ‖B‖₂ ≤ ‖B‖_∞/∞ for B = B^T implies that

$$|{\lambda }_1({\{{\mathrm{\Theta }}_0^{(k)}{g}_k(A+{\mathrm{\Theta }}_0^{(k)}+\delta I){\mathrm{\Theta }}_0^{(k)}\}}_{S^{(k)}}-I)|\le {\Vert {\lambda }_1({\{{\mathrm{\Theta }}_0^{(k)}{g}_k(A+{\mathrm{\Theta }}_0^{(k)}+\delta I){\mathrm{\Theta }}_0^{(k)}\}}_{S^{(k)}})\Vert }_2+1\le {\Vert {\lambda }_1({\{{\mathrm{\Theta }}_0^{(k)}{g}_k(A+{\mathrm{\Theta }}_0^{(k)}+\delta I){\mathrm{\Theta }}_0^{(k)}\}}_{S^{(k)}})\Vert }_{\infty /\infty }+1\le 4dr+1.$$

Hence h_k(A) ≥ 1/(8dr + 2) for every A ∈ 𝒟_k.

Now (30) is further bounded by r:

$$r\{1-\frac{n_k}{n}\frac{h_k(A)}{4}\}+\frac{n_k}{n}\{1+\frac{h_k(A)}{4}\}\delta \le r\{1-\frac{n_k}{n}\frac{h_k(A)}{4}\}+\frac{n_k}{n}\{1+\frac{h_k(A)}{4}\}\frac{r}{10(4dr+1)}\le r\{1-\frac{n_k}{n}\frac{h_k(A)}{4}\}+\frac{n_k}{n}\{1+\frac{h_k(A)}{4}\}\frac{h_k(A)r}{5}\le r-\frac{n_k}{n}\frac{h_k(A)-h_k^2(A)}{20}r\le r.$$

Here we used the fact that δ ≤ r/{10(4dr + 1)} and 1/(8dr + 2) ≤ h_k(A) < 1. Thus, ‖(f_k(A))_S^(k)‖_∞ ≤ r.

Since (f_k(A))_(S^(k))^c = 0 by definition, all the conditions for the fixed point theorem are established. This completes the proof.

We are now ready to prove Theorem 2. Note that Condition 7 implies that

$${\rho }_n<\text{min }\left\{\frac{{\text{min}}_k{\pi }_k}{72d{\kappa }_{\mathrm{\Gamma }}}\text{min }\right\{\frac{1}{{\kappa }_{\mathrm{\Psi }}},\frac{1}{{\kappa }_{\mathrm{\Psi }}^3{\kappa }_{\mathrm{\Gamma }}},\frac{{\text{min}}_k{\pi }_k}{56{\kappa }_{\mathrm{\Psi }}^3{\kappa }_{\mathrm{\Gamma }}}\alpha \},\frac{c_8}{6},\frac{c_9{\text{min}}_k\sqrt{d_k}}{12}\}.$$

Proof of Theorem 2

We prove that the oracle estimator Θ̌_ρn satisfies (I) the model selection consistency and (II) the KKT conditions of the original problem (3) with (Θ̌_ρn, Ũ₁, Ũ₂). The model selection consistency of Θ̂_ρn = Θ̌_ρn then follows by the uniqueness of the solution to the original problem. The following discussion is on the event that min_k π_k/2 ≤ n_k/n, k = 1, …, K, and max_k‖Ξ^(k)‖_∞ ≤ α/8. Note that this event has probability approaching 1 by Lemmas 4 and 5.

First we obtain an ℓ_∞-bound of the error of the oracle estimator. Note that by Condition 7 and the fact that α ∈ [0, 1)

$$\frac{\alpha }{8}+1+{\rho }_2{\Vert L\Vert }_2^{1/2}\le \frac{\alpha }{8}+1+\frac{{\alpha }^2}{4(2-\alpha )}\le 3.$$

Thus, it follows from Condition 7 that

$$\frac{4}{{\text{min}}_k{\pi }_k}{\kappa }_{\mathrm{\Gamma }}({\Vert {\mathrm{\Xi }}^{(k)}\Vert }_{\infty }+{\rho }_n+{\rho }_n{\rho }_2{\Vert L\Vert }_2^{1/2})<\frac{12{\kappa }_{\mathrm{\Gamma }}}{{\text{min}}_k{\pi }_k}\frac{{\text{min}}_k{\pi }_k}{72d{\kappa }_{\mathrm{\Gamma }}}\text{min }\{\frac{1}{{\kappa }_{\mathrm{\Psi }}},\frac{1}{{\kappa }_{\mathrm{\Psi }}^3{\kappa }_{\mathrm{\Gamma }}}\}=\frac{1}{6d\text{ max}\{{\kappa }_{\mathrm{\Psi }},{\kappa }_{\mathrm{\Psi }}^3{\kappa }_{\mathrm{\Gamma }}\}}.$$

Because ${({\mathrm{\Theta }}_0^{(k)}\otimes {\mathrm{\Theta }}_0^{(k)})}_{S^{(k)}{S}^{(k)}}$ is invertible by Condition 5, we can apply Lemma 11 to obtain ${\Vert {\check{\mathrm{\Theta }}}_{{\rho }_n}^{(k)}-{\mathrm{\Theta }}_0^{(k)}\Vert }_{\infty }\le (6/{\text{min}}_k{\pi }_k){\kappa }_{\mathrm{\Gamma }}({\Vert {\mathrm{\Xi }}^{(k)}\Vert }_{\infty }+{\rho }_n+{\rho }_n{\rho }_2{\Vert L\Vert }_2^{1/2})$ with probability approaching 1.

As a consequence of the ℓ_∞-bound, Θ̌_ρn,ij ≠ 0 for (i, j) ∈ S, because ${\Vert {\check{\mathrm{\Theta }}}_{{\rho }_n}^{(k)}-{\mathrm{\Theta }}_0^{(k)}\Vert }_{\infty }\le 3{\rho }_n\le c_8/2<{\text{min}}_{k=1,\dots ,K,i\ne j}|{\theta }_{0,ij}^{(k)}|$ by Conditions 6 and 7. This establishes the model selection consistency of the oracle estimator.

Next, we show that the Oracle estimator satisfies the KKT condition of the original problem (3). As the first step, we prove ${Ũ}_{1,ij}^{(k)}\in \partial {\check{\mathrm{\Theta }}}_{{\rho }_n}^{(k)}$ for every i, j, k with probability approaching 1. Since Θ̌_ρn,ij ≠ 0 for (i, j) ∈ S with probability approaching 1, ${Ũ}_{1,ij}^{(k)}={Ǔ}_{1,ij}^{(k)}$ for (i, j) ∈ S^(k) by construction. For (i, j) ∈ (S^(k))^c, we need to prove $|{Ũ}_{1,ij}^{(k)}|<1$ for every i, j, k. To this end, it suffices to verify that ${\Vert R^{(k)}({\check{\mathrm{\Theta }}}_{{\rho }_n}^{(k)}-{\mathrm{\Theta }}_0^{(k)})\Vert }_{\infty }\le \alpha /8$ and apply Lemma 8. Applying Lemma 9 with ${\Vert {\check{\mathrm{\Theta }}}_{{\rho }_n}^{(k)}-{\mathrm{\Theta }}_0^{(k)}\Vert }_{\infty }\le (6/{\text{min}}_k{\pi }_k){\kappa }_{\mathrm{\Gamma }}({\Vert {\mathrm{\Xi }}^{(k)}\Vert }_{\infty }+{\rho }_n+{\rho }_n{\rho }_2{\Vert L\Vert }_2^{1/2})$ and Condition 7 gives

$${\Vert R^{(k)}({\check{\mathrm{\Theta }}}_{{\rho }_n}^{(k)}-{\mathrm{\Theta }}_0^{(k)})\Vert }_{\infty }\le \frac{3}{2}d{\kappa }_{\mathrm{\Psi }}^3{\Vert {\check{\mathrm{\Theta }}}_{{\rho }_n}^{(k)}-{\mathrm{\Theta }}_0^{(k)}\Vert }_{\infty }^2\le \frac{3}{2}d{\kappa }_{\mathrm{\Psi }}^3\frac{324{\kappa }_{\mathrm{\Gamma }}^2}{{\text{min}}_k{\pi }_k^2}{\rho }_n^2\le \frac{486d{\kappa }_{\mathrm{\Psi }}^3{\kappa }_{\mathrm{\Gamma }}^2}{{\text{min}}_k{\pi }_k^2}\left\{\frac{{\text{min}}_k{\pi }_k}{72d{\kappa }_{\mathrm{\Gamma }}}\frac{{\text{min}}_k{\pi }_k}{56{\kappa }_{\mathrm{\Psi }}^3{\kappa }_{\mathrm{\Gamma }}}\alpha \right\}{\rho }_n\le \frac{\alpha }{8}\alpha .$$

Next, we prove that ${Ũ}_{2,ij}\in \partial \sqrt{{\check{\mathrm{\Theta }}}_{{\rho }_n,ij}L{\check{\mathrm{\Theta }}}_{{\rho }_n,ij}}$ for every (i, j). For (i, j) with ${\omega }_{0,ij}^{(k)}\ne 0$ for all k = 1, …, K, ${Ũ}_{2,ij}={Ǔ}_{{\rho }_n}\in \partial \sqrt{{\check{\mathrm{\Theta }}}_{{\rho }_n,ij}L{\check{\mathrm{\Theta }}}_{{\rho }_n,ij}}$. For (i, j) with Ω_0,ij = 0, ${Ũ}_{2,ij}=0\in \partial \sqrt{{\check{\mathrm{\Theta }}}_{{\rho }_n,ij}L{\check{\mathrm{\Theta }}}_{{\rho }_n,ij}}$ by Lemma 6. For (i, j) with Ω_0,ij ≠ 0 and ${\omega }_{0,ij}^{(k\prime )}=0$ for some k′,

$${Ũ}_{2,ij}=L{\check{\mathrm{\Theta }}}_{{\rho }_n,ij}/\sqrt{{\check{\mathrm{\Theta }}}_{{\rho }_n,ij}L{\check{\mathrm{\Theta }}}_{{\rho }_n,ij}}\in \partial \sqrt{{\check{\mathrm{\Theta }}}_{{\rho }_n,ij}L{\check{\mathrm{\Theta }}}_{{\rho }_n,ij}}$$

if LΘ̌_ρn,ij ≠ 0. To see LΘ̌_ρn,ij ≠ 0 holds with probability approaching 1, let (k, k′) ∈ S with k ≠ k′ such that ${\mathrm{\Theta }}_{0,ij}^{(k)}/\sqrt{d_k}-{\mathrm{\Theta }}_{0,ij}^{(k\prime )}/\sqrt{d_{k\prime }}\ne 0$. This pair (k, k′) exists by Condition 6 and the assumption LΘ_0,ij ≠ 0. We assume without loss of generality ${\theta }_{0,ij}^{(k)}/\sqrt{d_k}-{\theta }_{0,ij}^{(k\prime )}/\sqrt{d_{k\prime }}>0$. Since ${\Vert {\check{\mathrm{\Theta }}}_{{\rho }_n}^{(k)}-{\mathrm{\Theta }}_0^{(k)}\Vert }_{\infty }\le 3{\rho }_n\le c_9{\text{min}}_k\sqrt{d_k}/12$, it follows from Condition 7 that

$$\frac{{\check{\theta }}_{{\rho }_n,ij}^{(k)}}{\sqrt{d_k}}-\frac{{\check{\theta }}_{{\rho }_n,ij}^{(k\prime )}}{\sqrt{d_{k\prime }}}\ge \frac{{\theta }_{0,ij}^{(k)}}{\sqrt{d_k}}-\frac{{\theta }_{0,ij}^{(k\prime )}}{\sqrt{d_{k\prime }}}-3{\rho }_n(\frac{1}{\sqrt{d_k}}+\frac{1}{\sqrt{d_{k\prime }}})\ge c_9-3{\rho }_n(\underset{W_{k,k\prime }\ne 0}{\text{max}}\frac{1}{\sqrt{d_k}}+\frac{1}{\sqrt{d_{k\prime }}})\ge \frac{1}{2}{c}_9.$$

Hence, ${\check{\mathrm{\Theta }}}_{{\rho }_n,ij}^{T}L{\check{\mathrm{\Theta }}}_{{\rho }_n,ij}\ge W_{kk\prime }{c}_9^2/4>0$ or LΘ̌_ρn,ij ≠ 0.

Finally, we show that Equation (27) for the KKT condition holds. For the (i, j)-element of the equation with Ω_{0, ij} = 0, this equation hold by construction for every k = 1, …, K. For the (i, j)-element with ${\omega }_{0,ij}^{(k)}\ne 0$ for every k = 1, …, K, the equation holds for every k = 1, …, K, because it is the equation for the KKT condition of the corresponding element in a restricted problem (21). For (i, j)-element with Ω_{0, ij} ≠ 0 and ${\omega }_{0,ij}^{(k\prime )}=0$ for some k′, note that Θ̌_ρn,ij ≠ 0 with probability approaching 1 and that the rearrangement in Θ_ij and corresponding exchange of rows and columns of L for each i, j does not change the original and restricted optimization problems (3) and (21). Thus, with the appropriate rearrangement of elements and exchange of rows and columns, ${Ũ}_{2,ij}^{(k)}$ with ${\omega }_{0,ij}^{(k)}\ne 0$ is in fact ${Ǔ}_{2,ij}^{(k)}$. Thus for such k the equation holds because of the corresponding KKT condition in the restricted problem (21). For other k, the equation holds by construction. We thus conclude the oracle estimator satisfies the KKT condition of the original problem (3). This completes the proof.

Proof of Corollary 1

In the proof of Theorem 2, the ℓ_∞-bound of the error yields

$${\Vert {\hat{\mathrm{\Theta }}}_{{\rho }_n}^{(k)}-{\mathrm{\Theta }}_0^{(k)}\Vert }_{\infty }=O_P({\kappa }_{\mathrm{\Gamma }}{\rho }_n).$$

Note that if one of two matrices A and B is diagonal, ‖AB‖_∞ ≤ ‖A‖_∞‖B‖_∞. Thus, we can proceed in the same way as in the proof of Theorem 2 of Rothman et al. [26] to conclude that

$${\Vert {\hat{\mathrm{\Omega }}}_n^{(k)}-{\mathrm{\Omega }}_0^{(k)}\Vert }_{\infty }=O_P({\kappa }_{\mathrm{\Gamma }}{\rho }_n).$$

The result follows from a similar argument to the proof of Corollary 3 in Ravikumar et al. [25].

Proof of Corollary 2

It follows from Condition 8 and Lemma 1 applied to Θ̌_ρn that ${\Vert {\check{\mathrm{\Theta }}}_{{\rho }_n}^{(k)}-{\mathrm{\Theta }}_0^{(k)})\Vert }_2\le 1/(2{\lambda }_{\mathrm{\Theta }})$. Then we can apply Lemma 10 instead of Lemma 9. The rest is similar to the proof of Theorem 2.

Hierarchical Clustering

For simplicity, we prove Theorem 3 for the case of K = 2; the proof can be easily generalized to K > 2. Let X and Y be the random variable from the first and subpopulation, respectively. Suppose that X = (X₁, …, X_p)^T ~ N(μ_X, Σ_X) with μ_X = (μ_1,X, …, μ_p,X) and the spectral decomposition ${\mathrm{\Sigma }}_X=Q_X{\mathrm{\Lambda }}_X{Q}_X^T$ of Σ_X where λ_1,X, …, λ_p,X are the eigenvalues of Σ_X and that Y ~ N(μY, Σ_Y) with μ_Y = (μ_1,Y, …, μ_p,Y) and the spectral decomposition ${\mathrm{\Sigma }}_Y=Q_Y{\mathrm{\Lambda }}_Y{Q}_Y^T$ of Σ_Y where λ_1,Y, …, λ_p,Y are the eigenvalues of Σ_Y. Define Z = (X − Y) = (Z₁, …, Z_p)^T ~ N(μ_Z, Σ_Z) with μ_Z = (μ_1,Z, …, μ_p,Z) and the spectral decomposition ${\mathrm{\Sigma }}_Z=Q_Z{\mathrm{\Lambda }}_Z{Q}_Z^T$ of Σ_Z where λ_1,Z, …, λ_{p, Z} are the eigenvalues of Σ_Z. Let $\tilde{X}={({\tilde{X}}_1,\dots ,\tilde{X})}^T={\mathrm{\Lambda }}_X^{1/2}{Q}_X^T{\mathrm{\Sigma }}_X^{-1/2}X,Ỹ={({Ỹ}_1,\dots ,Ỹ)}^T={\mathrm{\Lambda }}_Y^{1/2}{Q}_Y^T{\mathrm{\Sigma }}_Y^{-1/2}Y$ and $\tilde{Z}={({\tilde{Z}}_1,\dots ,\tilde{Z})}^T={\mathrm{\Lambda }}_Z^{1/2}{Q}_Z^T{\mathrm{\Sigma }}_Z^{-1/2}Z$. Then X̃ ~ N(μ̃_X, Λ_X), Ỹ ~ N(μ̃_Y, Λ_Y) and Z̃ ~ N(μ̃_Z, Λ_Z), where

$${\tilde{\mu }}_X={({\tilde{\mu }}_{1,X},\dots ,{\tilde{\mu }}_{p,X})}^T\equiv {\mathrm{\Lambda }}_X^{1/2}{Q}_X^T{\mathrm{\Sigma }}_X^{-1/2}{\mu }_X,$$

$${\tilde{\mu }}_Y={({\tilde{\mu }}_{1,Y},\dots ,{\tilde{\mu }}_{p,Y})}^T\equiv {\mathrm{\Lambda }}_Y^{1/2}{Q}_Y^T{\mathrm{\Sigma }}_Y^{-1/2}{\mu }_Y,$$

$${\tilde{\mu }}_Z={({\tilde{\mu }}_{1,Z},\dots ,{\tilde{\mu }}_{p,Z})}^T\equiv {\mathrm{\Lambda }}_Z^{1/2}{Q}_Z^T{\mathrm{\Sigma }}_Z^{-1/2}{\mu }_Z.$$

Let also

$${\mu }_{\tilde{X}}^2=\Vert {\tilde{\mu }}_X^2\Vert /p,{\mu }_{Ỹ}^2=\Vert {\tilde{\mu }}_Y^2\Vert /p,{\mu }_{\tilde{Z}}^2=\Vert {\tilde{\mu }}_Z^2\Vert /p,$$

$${\overline{\lambda }}_X=\sum _{k=1}^p{\lambda }_{k,X}/p,{\overline{\lambda }}_Y=\sum _{k=1}^p{\lambda }_{k,Y}/p,{\overline{\lambda }}_Z=\sum _{k=1}^p{\lambda }_{k,Z}/p.$$

Lemma 12 (Lemma 1 of Borysov et al. [1])

Let W₁, …, W_p be independent non-negative random variables with finite second moments. Let $S={\sum }_{j=1}^p(W_j-𝔼W_j)$and $\upsilon ={\sum }_{j=1}^p𝔼W_j^2$. Then for any t > 0 P(S ≤ −t) ≤ exp(−t²/(2υ)).

The following lemma is an extension of Lemma 2 in Borysov et al. [1].

Lemma 13

Let $0<a<{\mu }_{\tilde{X}}^2+{\overline{\lambda }}_X$. Then

$$P({\Vert X\Vert }^2<ap)\le \text{exp }(-\frac{p^2{({\mu }_{\tilde{X}}^2+{\overline{\lambda }}_X-a)}^2}{2{\sum }_{j=1}^p({\tilde{\mu }}_{j,X}^4+6{\tilde{\mu }}_{k,X}^2{\lambda }_{j,X}+3{\lambda }_{j,X}^2)}).$$

Proof

Note that elements of X̃ are independent and that X̃_j ~ N(μ̃_j,X, λ_j,X). Thus, we have

$$𝔼{\tilde{X}}_j^2={\tilde{\mu }}_{j,X}^2+{\lambda }_{j,X},\text{ Var}({\tilde{X}}_j^2)=2({\lambda }_{j,X}^2+2{\tilde{\mu }}_{j,X}^2{\lambda }_{j,X}),$$

$$𝔼{\tilde{X}}_j^4={\tilde{\mu }}_{j,X}^4+6{\tilde{\mu }}_{j,X}^2{\lambda }_{j,X}+3{\lambda }_{j,X}^2.$$

Applying Lemma 12 with $W_i={\tilde{X}}_i^2$, since P (‖X‖² < ap) = P (‖X̃‖² < ap), we get

$$P({\Vert X\Vert }^2<ap)=P[\sum _{j=1}^p({\tilde{X}}_j^2-{\tilde{\mu }}_{j,X}^2-{\lambda }_{j,X})<-p({\mu }_{\tilde{X}}^2+{\overline{\lambda }}_X-a)]\le \text{exp }(-\frac{p^2{({\mu }_{\tilde{X}}^2+{\overline{\lambda }}_X-a)}^2}{2{\sum }_{j=1}^p({\tilde{\mu }}_{j,X}^4+6{\tilde{\mu }}_{j,X}^2{\lambda }_{j,X}+3{\lambda }_{j,X}^2)}).$$

The following is an extension of Lemma 3 in Borysov et al. [1].

Lemma 14

Let $a>{\overline{\lambda }}_X+{\mu }_{\tilde{X}}^2$. Then

$$P({\Vert X\Vert }^2>ap)\le \text{exp }(-\frac{1}{2}(p+\sum _{j=1}^p\frac{a}{{\lambda }_{j,X}}-\sum _{j=1}^p\sqrt{1+2\frac{a}{{\lambda }_{j,X}}}\left)\right).$$

Proof

By Markov’s inequality, for $t>{\sum }_{j=1}^p{\lambda }_{j,X}+{\tilde{\mu }}_{j,X}^2$, we get

$$P(\sum _{j=1}^p{X}_j^2\ge t)=P(\sum _{j=1}^p{\tilde{X}}_j^2\ge t)=P\left[\text{exp }\right(\sum _{j=1}^p\gamma {\tilde{X}}_j^2-\gamma {\lambda }_{j,X}-\gamma {\tilde{\mu }}_{j,X}^2)\ge \text{exp }(\gamma t-\gamma \sum _{j=1}^p({\lambda }_{j,x}+{\tilde{\mu }}_{j,X}^2)\left)\right]\le \text{exp }(-\gamma (t-\sum _{j=1}^p({\tilde{\mu }}_{j,X}^2+{\lambda }_{j,X})\left)\right)\prod _{j=1}^p𝔼\text{ exp}((\gamma {\lambda }_{j,X}){\tilde{X}}_j^2/{\lambda }_{j,x})=\text{exp }(-\gamma (t-\sum _{j=1}^p{\tilde{\mu }}_{j,X}^2\left)\right)\prod _{j=1}^p\text{exp }(-\gamma {\lambda }_{j,X}-\frac{1}{2}\text{ log}(1-2\gamma {\lambda }_{j,X}))\times \text{exp }\left(\frac{\gamma {\tilde{\mu }}_{j,X}^2}{1-2\gamma {\lambda }_{j,X}}\right).$$

Since for all u ∈ (0, 1), −log(1 − u) − u ≤ u²/{2(1 − u)} (see page 28 of Boucheron et al. [2]), the above display is bounded above by

$$\text{exp }(-\gamma (t-\sum _{i=1}^p{\tilde{\mu }}_{i,X}^2\left)\right)\prod _{i=1}^p\text{exp }\left(\frac{{\gamma }^2{\lambda }_{i,X}^2}{1-2\gamma {\lambda }_{i,X}}\right)\text{ exp }\left(\frac{\gamma {\tilde{\mu }}_{i,X}^2}{1-2\gamma {\lambda }_{i,X}}\right).$$

Using the following result from Boucheron et al. [2]

$$\underset{\gamma \in (0,1/c)}{\text{inf}}\frac{\upsilon {\gamma }^2}{2(1-c\gamma )}-t\gamma =-\frac{\upsilon }{c^2}h\left(\frac{ct}{\upsilon }\right).$$

wherein $h(u)=1+u-\sqrt{1+2u}$, u > 0, we further obtain the upper bound

$$\text{exp }\left(\gamma \sum _{i=1}^p{\tilde{\mu }}_{i,X}^2\right)\prod _{i=1}^p\text{exp }(-\frac{1}{2}(1+\frac{t}{{\lambda }_{i,X}p}-\sqrt{1+\frac{2t}{{\lambda }_{i,X}p}}\left)\right)\text{ exp }\left(\frac{\gamma {\tilde{\mu }}_{i,X}^2}{1-2\gamma {\lambda }_{i,X}}\right).$$

Taking γ ↓ 0, the upper bound becomes

$$\text{exp }(-\frac{1}{2}(p+\sum _{i=1}^p\frac{t}{{\lambda }_{i,X}p}-\sum _{i=1}^p\sqrt{1+\frac{2t}{{\lambda }_{i,X}p}}\left)\right).$$

Choosing t = ap, we have

$$P(\sum _{i=1}^p{\tilde{X}}_i^2\ge ap)\le \text{exp }(-\frac{1}{2}(p+\sum _{i=1}^p\frac{a}{{\lambda }_{i,X}}-\sum _{i=1}^p\sqrt{1+2\frac{a}{{\lambda }_{i,X}}}\left)\right).$$

Note that f(u) = (1 + 2u)^1/2 ≤ u for u ≥ 0 because f′(0) = 1 and f′ is decreasing for u > 0. Thus, $P({\sum }_{i=1}^p{\tilde{X}}_i^2\ge ap)\to 0$ as p → ∞.

Proof of Theorem 3

For simplicity, we present the proof for the case of K = 2; the proof can be easily generalized to K > 2. Let n₁ and n₂ be the sample sizes for the first and second subpopulations, respectively. Define

$$E_1=\{\underset{i,j}{\text{max}}\Vert X_i-X_j\Vert <\underset{k,l}{\text{min}}\Vert X_k-Y_l\Vert \},E_3=\{\underset{i,j}{\text{max}}{\Vert X_i-X_j\Vert }^2<ap\},$$

$$E_2=\{\underset{i,j}{\text{max}}\Vert Y_i-Y_j\Vert <\underset{k,l}{\text{min}}\Vert X_k-Y_l\Vert \},E_4=\{\underset{i,j}{\text{max}}{\Vert Y_i-Y_j\Vert }^2<ap\},$$

$$E_5=\{\underset{k,l}{\text{max}}{\Vert X_k-Y_l\Vert }^2>ap\},$$

for a fixed a > 0 satisfying the assumption. The intersection E₁ ∩ E₂ is contained in the event that the clustering performs in the way that two subpopulations are joined in the last step. The intersection E₃ ∩ E₄ ∩ E₅ is also contained in E₁ ∩ E₂, or in other words, $P({(E_1\cap E_2)}^c)\le P(E_3^c)+P(E_4^c)+P(E_5^c)$. Thus, it suffices to show that $P(E_3^c)+P(E_4^c)+P(E_5^c)\to 0$ as n, p → ∞.

For $E_3^c$ and $E_4^c$ we have by Lemma 14 that

$$P(E_3^c)\le \sum _{i,j}^{n}P({\Vert X_i-X_j\Vert }^2>ap)=\frac{n_1(n_1-1)}{2}P({\Vert X_1-X_2\Vert }^2>ap)\le \frac{n_1(n_1-1)}{2}\text{ exp }(-\frac{1}{2}(p+\sum _{l=1}^p\frac{a}{2{\lambda }_{l,X}}-\sum _{l=1}^p\sqrt{1+\frac{a}{{\lambda }_{l,X}}}\left)\right)\le \text{exp}(-\frac{1}{2}(p+\sum _{l=1}^p\frac{a}{2{\lambda }_{l,X}}-\sum _{l=1}^p\sqrt{1+\frac{a}{{\lambda }_{l,X}}})+2\text{ log }{n}_1)=\text{ exp }(-\frac{p}{2}(1+\frac{1}{p}\sum _{l=1}^p\frac{a}{2{\lambda }_{l,X}}-\frac{1}{p}\sum _{l=1}^p\sqrt{1+\frac{a}{{\lambda }_{l,X}}}+4\frac{\text{ log }{n}_1}{p}\left)\right)$$

and that

$$P(E_4^c)\le \text{exp }(-\frac{p}{2}(1+\frac{1}{p}\sum _{l=1}^p\frac{a}{2{\lambda }_{l,Y}}-\frac{1}{p}\sum _{l=1}^p\sqrt{1+\frac{a}{{\lambda }_{l,Y}}}+4\frac{\text{log }{n}_2}{p}\left)\right).$$

for a satisfying a > 2 max{λ̄_X, λ̄_Y}.

Note that log n_k/p → 0, k = 1, 2 as n₁, n₂, p → ∞. Moreover $x-\sqrt{1+2x}\ge 0$ for x > 0. Thus, $P(E_3^c)\to 0$ and $P(E_4^c)\to 0$ as n₁, n₂, p → ∞. For $E_5^c$, we have by Lemma 13 that

$$P(E_5^c)\le \sum _{i,j}P({\Vert X_i-Y_j\Vert }^2<ap)\le n_1{n}_{2}P({\Vert X_1-Y_1\Vert }^2<ap)\le \text{exp}(-\frac{p^2{({\mu }_{\tilde{Z}}^2+{\overline{\lambda }}_Z-a)}^2}{2{\sum }_{l=1}^p({\tilde{\mu }}_{i,Z}^4+6{\tilde{\mu }}_{l,Z}^2{\lambda }_{l,Z}+3{\lambda }_{l,Z}^2)}+\text{log }{n}_1{n}_2)$$

for $a<{\mu }_{\tilde{Z}}^2+{\overline{\lambda }}_Z$. Given the assumption c₁₀ ≤ λ_j,X ≤ c₁₁, c₁₀ ≤ λ_j,Y ≤ c₁₁, max{|μ_j,X|, |μ_j,Y|} ≤ c₁₁, j = 1, 2, …. Thus, we get $P(E_5^c)\to 0$ as n₁, n₂, p → 1.

Since 2λ̄_X − λ_p,X − λ_p,Y ≥ 2λ̄_X − λ̄_Z, and 2λ̄_Y − λ_p,X − λ_p,Y ≥ 2λ̄_Y − λ̄_Z, the assumption that ${\mu }_{\tilde{Z}}^2>2\text{ min}\{{\overline{\lambda }}_X,{\overline{\lambda }}_Y\}-{\lambda }_{p,X}-{\lambda }_{p,Y}$ implies that there exists a such that a < μ̄_Z̃ + λ̄_Z and a > 2 max{λ̄_X, λ̄_Y}. This completes the proof.