Abstract
Ventricular assist devices (VADs) have already helped many patients with heart failure but have the potential to assist more patients if current problems with blood damage (hemolysis, platelet activation, thrombosis and emboli, and destruction of the von Willebrand factor (vWf)) can be eliminated. A step towards this goal is better understanding of the relationships between shear stress, exposure time, and blood damage and, from there, the development of numerical models for the different types of blood damage to enable the design of improved VADs.
In this study, computational fluid dynamics (CFD) was used to calculate the hemodynamics in three clinical VADs and two investigational VADs and the shear stress, residence time, and hemolysis were investigated. A new scalar transport model for hemolysis was developed. The results were compared with in vitro measurements of the pressure head in each VAD and the hemolysis index in two VADs. A comparative analysis of the blood damage related fluid dynamic parameters and hemolysis index was performed among the VADs.
Compared to the centrifugal VADs, the axial VADs had: higher mean scalar shear stress (sss); a wider range of sss, with larger maxima and larger percentage volumes at both low and high sss; and longer residence times at very high sss. The hemolysis predictions were in agreement with the experiments and showed that the axial VADs had a higher hemolysis index.
The increased hemolysis in axial VADs compared to centrifugal VADs is a direct result of their higher shear stresses and longer residence times. Since platelet activation and destruction of the vWf also require high shear stresses, the flow conditions inside axial VADs are likely to result in more of these types of blood damage compared with centrifugal VADs.
Keywords: computational fluid dynamics (CFD), hemodynamics, ventricular assist device (VAD), artificial organs, hemolysis, thrombosis, platelet activation, von Willebrand factor (vWf)
Introduction
Globally, cardiovascular disease is the leading cause of mortality. [1]. Among the various forms of cardiovascular disease, heart failure (HF) affects 5.8 × 106 patients in the United States [2]. Despite optimal medical treatment, some patients still do not improve and the available therapies fail to control their symptoms; for them, cardiac transplantation may be the only option. However, only around 2200 transplants are performed in the U.S. each year [2]; in other words, only about 6% of the estimated 35,000 U.S. patients who would benefit actually receive a heart [3,4]. To address the need to support the circulation in patients with end-stage HF, a wide variety of mechanical circulatory support devices (MCSDs) have been developed over the past four decades.
Ventricular assist devices (VADs), one class of MCSDs, are pumps designed to augment or replace the function of one or more chambers of the failing heart. Positive displacement pulsatile pumps maintain the physiological pulsatility of the flow but typically experience problems with mechanical failure of diaphragms and valves [5]. The advantages of rotary continuous flow VADs are their simpler designs, involving fewer moving parts, their smaller size, and lower power consumption [6].
While VADs have already benefitted many patients, they have the potential to help many more if blood damage problems can be eliminated [7,8]. Blood damage includes hemolysis, platelet activation, alteration of the coagulation cascade, thrombosis and emboli, reduced functionality of the white blood cells, and destruction of von Willebrand factor (vWf).
Hemolysis is damage to the red blood cells, resulting in the release of hemoglobin into the blood plasma. This trauma manifests as morphological changes, shortened life span, biochemical alterations, and complete rupture. Mechanical shear stress causes hemolysis either by exerting sufficient stress to rupture the red blood cell (RBC) membrane or through the formation of pores in the membrane when a critical stress or strain is exceeded. In addition to the magnitude of the shear stress, hemolysis is also caused by increasing the duration of exposure to an elevated shear stress [9]. Shear stress below a critical magnitude and exposure time results in elastic deformation of the cells, however, above that threshold, hemoglobin leaks into the plasma [10]. The amount of hemolysis has been found to be a power law function of shear stress magnitude and exposure time [11].
Platelets are the prominent cells involved in both physiological hemostasis and pathological thrombosis with platelet hyper-reactivity and circulating activated platelets associated with many cardiovascular, infectious, metabolic, and autoimmune disorders [12,13]. Platelets become activated when exposed to chemical agonists, such as ADP, thrombin, thromboxane A2, and serotonin, and under mechanical shear stress [14]. There are two main theories for the precise mechanism by which mechanical shearing activates platelets: either shear stress affects platelets directly via vWf binding to the platelet GPIbα receptor, or shear stress causes mechanical lysis of stored agonists from platelets and RBCs, which then activate the platelets. Hellums [15] showed that the locus of points on the shear stress-exposure time plane at which the platelets become activated, follow a consistent curve over a wide range of conditions (see Fig. 1, with data from Refs. [15–20]).
Fig. 1.
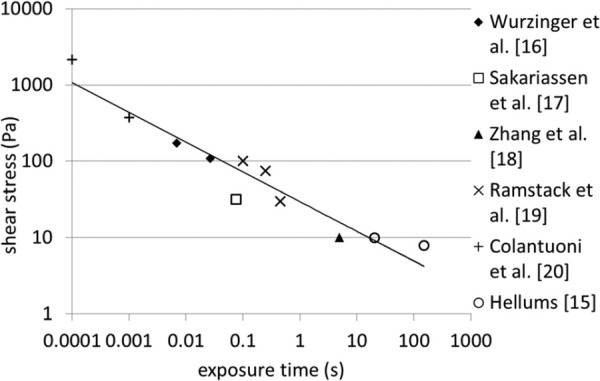
Hellums' shear stress-exposure time threshold required to activate platelets, with some additional data
Ventricular assist devices have significant infection rates and it has been suggested that shear stress on the white blood cells (WBCs) is hindering their ability to fight off infection [21]. The limited data on the effects of shear stress on WBCs suggest that with an exposure time around 0.1 s, a shear stress of 13 Pa reduces phagocytosis, and shear stresses above that produce more impairment [21].
vWf is crucial to platelet deposition and aggregation and, therefore, to normal hemostasis. It is secreted by endothelial cells as a very large polymer which is converted in the plasma to a series of multimers via proteolysis [22]. It is thought that shear stress in the circulation changes the conformation of the vWf in a way that enhances its susceptibility to proteolysis. This could be by exposing the cleavage site [22]. This process is occurring in the normal circulation, with wall shear stress in the range of 0–5 Pa. However, it is thought to be accelerated in patients with acquired von Willebrand disease due to aortic stenosis [23] or VADs [24]. It is thought that the higher shear stress in these patients may increase the cleavage effect beyond the normal situation. Table 1 gives results of shear stress effects on vWf from the literature [22, 23, 25].
Table 1.
vWf response to shear stress
The development of computational models of blood damage will assist in the design of better VADs and potentially other MCSDs. A crucial step to developing models of blood damage for use with VADs is to understand, in detail, the nature of the flow conditions experienced by the blood within these types of devices. Analytical estimates of the maximum shear stress in VADs, based on the impeller radius, speed, and clearance gap [26] are between 20 and 500 Pa. However, these assume a linear velocity gradient between the blade tip and outer housing; in reality, the gradient is steeper at the wall [27]. The analysis also neglects the complicated nature of the real flow field, with backward flows, vortices, and helical flows. Optical techniques, such as particle image velocimetry (PIV) and laser Doppler velocimetry, have been used to measure shear stress in several VADs, including a centrifugal VAD in which the maximum shear stress was around 44 Pa [28]. Oil drops on the impeller surface have been used to give a relative assessment of the wall shear stress [29]. These experimental studies are limited by the area of the flow field which can be viewed and often use two dimensional techniques. Computational fluid dynamics (CFD) enables a fully three dimensional analysis of the whole VAD and has been used in the design and development of VADs since the early 1990 s [26,30,31], along with other blood contacting devices (for examples, see Refs. [32,33,34]). There are a number of studies using CFD to investigate localized shear stress in different regions of VADs, particularly for design analysis or improvement [35–39]. However, there are fewer studies in which the authors have analyzed the whole VAD to obtain the volumetric parameters. Nishida et al. [40] used CFD, validated against particle tracking velocimetry, to analyze shear stress throughout the volume of their centrifugal VAD and found the volumetric mean varied with the operating speed from 161 to 358 Pa, however, the maximum was much higher. Chua et al. [41] found that 75% of the volume of their pump had a shear stress below 250 Pa and the maximum shear stress was between 2500 and 2750 Pa.
The objectives of this work were to investigate the flow fields within VADs and to determine the range of shear stresses and residence times experienced by the blood inside them and to evaluate their contribution to blood damage. To that end, CFD was used to calculate the flow fields in five rotary VADs with different characteristics and, from the flow fields, shear stress and residence time parameters were calculated. A scalar transport model for hemolysis was then used to compare hemolysis indices for the five VADs.
Methods
Devices.
Five different rotary continuous flow VADs were analyzed and the details of their design features are given in Table 2.
Table 2.
Details of VADs analyzed
| Type | Bearing | Impeller radius (mm) | Impeller clearance gap (mm) | Target point | Population | |
|---|---|---|---|---|---|---|
| AxVAD1 | Axial | Pin | 6.98 | 0.11895 | 10 k rpm, 4 l/min | Adult |
| AxVAD2 | Axial | Hydrodynamic | 6.10 | 0.1 | 10 k rpm, 5 l/min | Adult |
| AxVAD3 | Axial | Conical | 5.79 | 0.1016 | 12 k rpm, 2 l/min | Child |
| CentVAD1 | Centrifugal | Magnetic levitation | 21.2 | 1.5 a | 3 k rpm, 5 l/minc | Adult |
| CentVAD2 | Centrifugal | Magnetic levitation | 9.0 | 0.5 b | 7 k rpm, 3 l/min | Adult and child |
Approximate since the impeller position varies with operating condition.
Gap between magnet housing and outer case (smaller than impeller-case gap).
In circulatory support.
Geometry.
The geometries of the five devices were obtained from their computer aided drawing (CAD) files or constructed by measuring the actual device components. A precision laser scan (QC Group Inc., Minnetonka, MN) of an AxVAD1 impeller taken from an explanted clinical pump was used to obtain the geometry of that part. Commercial software (Ansys) was used to construct models of the blood flow domains. The flow domain was constructed by filling the volume between the impeller and the outer casing using Ansys DesignModeler.
For the axial VADs the blade, diffuser, and straightener (where applicable) regions were separately constructed using BladeModeler. This involved importing the surfaces from the CAD files to obtain the blade shapes in terms of the meridional profile, angle, and thickness. The blade geometry represented this way was over-laid on the original blade geometry to ensure this step did not make any alterations. Care was also taken to ensure that the hub and shroud of the different regions were in exact alignment.
The two centrifugal VADs in the study both had magnetically levitated impellers. The axial position of these impellers is determined by the balance of lift and magnetic forces. The design of the CentVAD2 impeller results in very small lift forces (<0.5 N) and, therefore, it moves a maximum of 0.3 mm (8% of the total possible range of motion) from the zero speed position. Thus, the CentVAD2 impeller was placed in the zero speed position before extracting the flow domain geometry. However, the lift forces on the CentVAD1 impeller are much larger (2–9 N) and the magnetic bearing is not stiff enough to prevent the impeller from lifting up, which results in a range of axial positions (1–3 mm) above the base of the casing (a range which is 34% of the total possible range of axial positions). The position of the impeller has been shown to affect calculations of pressure, shear stress, and hemolysis in the CentVAD1 [42]. The position of the impeller was measured using the following procedure. The impeller was mechanically displaced in the axial direction in measured increments by means of direct pressure (downwards) or stacked shims (upwards). At each impeller displacement, the resulting magnetic flux signal strength was measured by sensors in the motor and recorded. From this data, a calibration curve was produced. The magnetic flux signals were then recorded with the pump working under the actual operating conditions and later calibrated using the curve to reveal the actual impeller positions.
Two of the VADs in this study have been analyzed by our group before [39,43], however, the models and calculations presented were all redone to ensure consistency between the devices.
Meshing.
The VADs were meshed using a combination of hexahedral, tetrahedral, and prism elements. TurboGrid was used to mesh the blade, diffuser, and straightener passages of the axial VADs using hexahedral elements with o-grids to ensure a high concentration of elements near the blades. The remaining regions of the axial VADs, along with the centrifugal VADs, were meshed using Ansys Meshing. Certain regions, including the inlet and outlet tubes and the region around the magnetic rotor in the centrifugal VAD, were meshed using hexahedral elements. The remainder of the domain was meshed using tetrahedral elements with prism layers. There were nonconformal interfaces between the different types of mesh in the axial VADs but the meshes on either side had similar element sizes. Details of the meshes are given in Fig. 2 and Table 3.
Fig. 2.
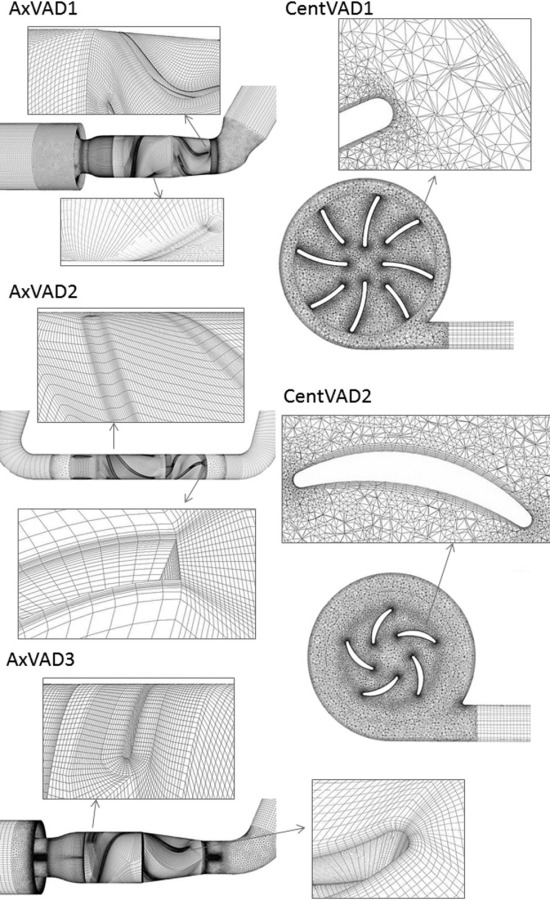
Meshes used for the VAD calculations
Table 3.
Details of meshes. Very high sss volume is the volume with sss > 150 Pa.
|
AxVAD1 |
AXVAD2 |
AxVAD3 |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cells (×106) | Mesh error (%) | Mean sss (Pa) | Very high sss volume(%) | Cells (× 106) | Mesh error (%) | Mean sss (Pa) | Very high sss volume (%) | Cells (× 106) | Mesh error (%) | Mean sss (Pa) | Very high sss volume (%) | |
| Coarse | 2.6 | 22 | 10.3 | 0.801 | 1.2 | 30 | 9.64 | 0.383 | 2.6 | 29 | 10.6 | 1.23 |
| Middle | 5.2 | 16 | 10.3 | 0.862 | 1.9 | 15 | 9.84 | 0.448 | 5.1 | 22 | 10.8 | 1.25 |
| Fine | 7.5 | 15 | 10.4 | 0.812 | 4.3 | 5 | 9.86 | 0.513 | 7.0 | 20 | 9.14 | 1.03 |
| CentVAD1 | CentVAD2 | |||||||||||
| Cells (× 106) | Mesh error (%) | Mean sss (Pa) | Very high sss volume(%) | Cells (× 106) | Mesh error (%) | Mean sss (Pa) | Very high sss volume (%) | |||||
| Coarse | 2.3 | 9.5 | 7.98 | 0.112 | 2.7 | 50 | 8.73 | 0.220 | ||||
| Middle | 3.0 | 5.5 | 8.15 | 0.116 | 3.8 | 32 | 8.89 | 0.222 | ||||
| Fine | 4.3 | 1.9 | 8.31 | 0.132 | 5.0 | 20 | 9.09 | 0.245 | ||||
In addition to these meshes, a finer mesh and a coarser mesh were produced for each VAD. These had the same structure as the original (middle) meshes and were produced by multiplying each mesh dimensional parameter by a factor of 0.8 (finer mesh) or 1.25 (coarser mesh) to yield a set of three meshes. The actual refinement ratio (r) was calculated as (number of mesh elements in finer mesh/number of mesh elements in coarser mesh)1/3. The calculations for the operating condition at the center of the operating range were repeated with the fine and coarse meshes. The discretization errors for the velocity magnitude were then analyzed according to the principles outlined by Roache [44] and the shear stress parameters were calculated for all three meshes.
Computational Fluid Dynamics.
The blood flow was calculated using the commercial finite volume software Fluent 13.0 (Ansys Inc.). The motion of the impellers was incorporated using the multiple reference frame (MRF) approach: a steady state approximation of the actual flow. The impeller was enclosed in a region with axial symmetry. For the axial VADs, this extended radially as far as the shroud (outer housing) and axially from a plane before the impeller blades to a plane between the impeller and diffuser blades. The outlets of the centrifugal VADs result in a nonaxially symmetric geometry and, therefore, the volume was divided into a cylindrical region surrounding the impeller and a second region outside of that region. In the MRF method, the flow in the region surrounding the impeller is calculated in a frame of reference moving with the same velocity as the impeller. Flow in the other region is calculated in a stationary reference frame. At the interface between the two regions, a local transformation is performed to enable the flow variables in one zone to be used for calculating fluxes at the boundary of the adjacent zone.
The Reynolds numbers (Re) for the flow at the inlet to the VADs range from 374 up to 4985 (Table 4), meaning the flow regime ranges from laminar through transitional to low Re turbulent. The impeller Re is in the range of 18,704–84,717, which means that the flow should be laminar, since a transition should occur at 106. However, with the complex flow fields which occur in these VADs, we believe that the flow is most likely to be in the low Re turbulent regime. Because of the range of Re there is no universally accepted method for calculating the turbulent flow through VADs [26]. For the VADs in this work the shear stress transport (SST)-kω turbulence model [45] was used since it was found to give accurate predictions of the pressure head in the VADs. Additionally in our calculations of flow through a simplified medical device, which we compared with published PIV results [46], it produced accurate velocity fields.
Table 4.
VAD fluid dynamic and simulation parameters
| VAD | Simulation flow range (l/min) | Simulation speed range (k rpm) | Inlet Re range | Impeller Re range |
|---|---|---|---|---|
| AxVAD1 | 2–4 | 8–12 | 817–1634 | 24,490–36,734 |
| AxVAD2 | 3–7 | 8–12 | 1061–2476 | 18,704–28,056 |
| AxVAD3 | 1–3 | 10–14 | 374–1122 | 21,071–29,499 |
| CentVAD1 | 3–7 | 3–5 | 2136–4985 | 84,717–14,120 |
| CentVAD2 | 1–5 | 5–9 | 884–4420 | 25,447–45,804 |
Note: Inlet Re = vdρ/μ, impeller Re = 2r2ωρ/μ, where v is the mean inlet velocity, d is the inlet diameter, μ is the viscosity, ρ is the density, r is the impeller radius, and ω is the rotational speed in rad s −1.
Steady state solutions were calculated with second order discretization used for all the equations and the semi-implicit method for pressure-linked equations scheme used for pressure-velocity coupling. Convergence was assessed using the velocity and turbulence residuals, which were below 10 × 3, the pressure head, which was stable, and the mass balance error, which was less than 0.03% of the mass flow rate.
Blood was treated as an incompressible Newtonian fluid with a viscosity of 3.5 × 10−3 kg/ms and a density of 1050 kg/m3. It is well known that blood is a shear thinning fluid, however, because the shear rates found in VADs are high (>100 s −1) it was treated as Newtonian.
For each device calculations were performed at the optimum operating condition and eight other conditions spanning the range of typical usage. The inlet boundary condition was a parabolic velocity profile, which was positioned far enough upstream of the VAD to ensure a fully developed velocity profile proximal to the VAD inlet. The outlet boundary condition was uniform pressure which, again, was positioned far enough from the VAD to achieve a fully developed flow. Turbulence at the boundaries was specified with the turbulence intensity (calculated using intensity = 0.16 Re−1/8 [47]) and the hydraulic diameter (which equaled the tube diameter since the inlets/outlets were cylindrical).
The calculations were performed on a PC workstation with two Intel Xeon quad core 2.83 GHz processors and 64 GB RAM. Each calculation was run in parallel on four of the processors and took around 12 h to converge.
Scalar Shear Stress.
The scalar shear stress sss (σ) was calculated from the shear stress components σij using the following equation [48] which was implemented with a user defined function
| (1) |
Histograms of the sss for the entire volume of the VAD were produced and used to calculate the mean sss, the maximum sss, and volumes with specific sss thresholds.
Hemolysis.
Hemolysis was calculated using an Eulerian scalar transport approach. Here, hb′ was defined as a scalar variable equal to hb1/α, where hb is the plasma free hemoglobin as a percentage of the total blood hemoglobin [49]. The scalar transport equation was then expressed as
| (2) |
where S is the source term defined as S = ρ(HB · C · σβ)1/ α , with HB as the total blood hemoglobin concentration; here, 10 g/dL was used. The equation was implemented as a user defined scalar. The hemolysis index (HI) in percent was then calculated from the mass-weighted average of hb at the outlet of the device divided by HB. This method has been tested [49] with sets of constants empirically derived by different authors [11,50,51]. While a reasonable correlation was found between the experimental results and those calculated using constants from Heuser and Opitz [50], which were also used by Song et al. [52], the calculations considerably overpredicted. For this work, a gradient descent algorithm was used to fit the calculations to the experimental results and obtain a new set of power law constants. Four operating conditions from each of two of the VADs, one centrifugal (CentVAD1) and one axial (AxVAD1), were used for the fitting to ensure that the different conditions present in these two types of device were all present (see Table 5). For validation, hemolysis was measured in the same two VADs at different operating conditions (shown in Table 5).
Table 5.
Operating conditions used for fitting and validation of the power law based scalar transport hemolysis model
| Speed (rpm) | Flow (l/min) | |
|---|---|---|
| Operating conditions used for fitting | ||
| CentVAD1 | 2000 | 3.0 |
| 3000 | 1.0 | |
| 3000 | 7.0 | |
| 5000 | 3.0 | |
| AxVAD1 | 8000 | 3.0 |
| 10,000 | 1.0 | |
| 10,000 | 4.5 | |
| 12,000 | 3.0 | |
| Operating conditions used for validation | ||
| CentVAD1 | 3000 | 3.0 |
| 3000 | 5.0 | |
| 4000 | 3.0 | |
| 4000 | 5.0 | |
| 4000 | 7.0 | |
| 5000 | 5.0 | |
| 5000 | 7.0 | |
| AxVAD1 | 10,000 | 3.0 |
The measurements of plasma hemoglobin in the two VADs were carried out with ovine blood (30% hematocrit) over a 3 h period using a recirculating flow loop, according to the recommended practice for the assessment of hemolysis in continuous flow pumps specified by the American Society of Testing and Materials (ASTM F1841-97) [53]. Details of blood preparation and checking can be found in Ref. [51]. The following equation was used to find the single pass hemolysis index (HI) from the change in plasma free hemoglobin over multiple passes
| (3) |
Here, Q is the flow rate, T is the length of time the blood has been recirculating, and V is the volume of the flow loop.
Results
Mesh.
Mesh discretization errors are given in Table 3 and ranged between 5.5 and 32% for the middle meshes, which were used for the final calculations. While 32% is a large error, there was only a small difference in the sss parameters between the middle and fine meshes (a 9% difference in the very high sss volume for that case), showing that the calculations are still of acceptable precision for this study.
Validation.
The calculations were validated by comparing the simulated pressure head with that measured in an experimental flow loop (see Fig. 3). Mean differences between the calculated and experimental pressure head were AxVAD1: 17 mmHg; AxVAD2: 7.4 mmHg; AxVAD3: 9.3 mmHg; CentVAD1: 15 mm Hg; and CentVAD2: 19 mmHg. The largest percentage differences occurred in AxVAD1 and AxVAD3 and were likely due to the very high spatial velocity gradients and the interaction between the impeller and diffuser blades, which created particularly complicated flow patterns in these VADs. Despite optimizing the mesh and modeling schemes it was not possible to reduce these differences.
Fig. 3.
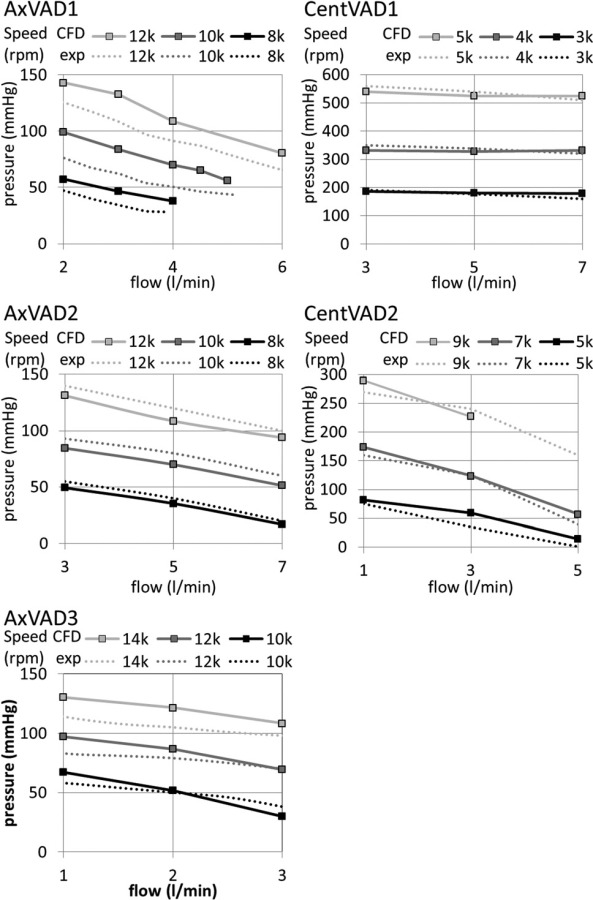
Comparison of the experimental and numerical pressure head in each VAD
Flow Fields.
Velocity fields for the VADs are shown in Fig. 4 for representative operating conditions. Extensive information on the flow fields was obtained from the simulations. Summaries of these flow fields are given below and more details are given in the supplementary material [54].
Fig. 4.

Flow field in each VAD at the optimal operating condition represented as path lines and contours of velocity magnitude
AxVAD1.
The flow entered the pump through the tripod pin and at most operating conditions smoothly followed the shape of the impeller blades. An exception to this was at 12 k rpm and 3 l/ min, when some recirculation zones occurred near the hub. Turbulent disturbances, including helical flow and recirculation zones, developed in the downstream half of the diffuser blades. The helical flow usually persisted into the outlet where there was also a recirculation zone caused by the bend there.
AxVAD2.
The inlet bend created a recirculation zone which was minimized by the presence of the flow straightener. At the higher speed and lower flow rates there was some preswirl before the impeller. The flow through the impeller itself was smooth for all operating conditions. Disturbances developed in the diffuser blade passages and the helical flow was enhanced by the bend in the outlet.
AxVAD3.
Flow entered the pump through the tripod conical bearing and at most operating conditions smoothly followed the shape of the impeller blades. However, at the lower speeds and higher flow rates there were small recirculation zones at the tips of the impeller blades. Disturbances, including helical flow and large recirculation zones, developed in the diffuser blade passages. There was a small recirculation zone following the bend in the outlet tube.
CentVAD1.
Flow entered from the inlet in the center of the VAD from where it was circumferentially and radially spun and exited through the outlet. Some blood took the secondary flow path outside the rotating magnet. There is a recirculation zone in the outlet.
CentVAD2.
Depending upon the operating condition, there were either recirculation zones or helical flow in the inlet. The flow entered the VAD through the central hole and was circumferentially spun. Some blood took the secondary flow path outside the rotating magnet. At some operating conditions, there was helical flow in the volute and/or a recirculation zone or helical flow in the outlet.
Shear Stress.
The scalar shear stress (sss) in the VADs was analyzed using contour plots, iso-surfaces, and volume histograms. Depending upon the VAD, operating condition, and location, the sss ranged from 0 to 3060 Pa. For all VADs the bulk of the volume (that is, more than half the VAD) had an sss of less than 5 Pa (see Fig. 5 and supplementary material [54]). The volumetric mean sss ranged from 4 to 13 Pa (see Fig. 6). The different VADs are designed for different purposes: for example, adult versus pediatric support, or circulatory support versus the possibility of extracorporeal membrane oxygenation. Therefore, they have very different rotational speeds and have different shapes and sizes. For comparative purposes, the shear stress parameters were analyzed at their calculated pressure head and for a fixed flow rate of 3 l/min. It could be argued that this is fair, since it enables comparison at the same clinical conditions, or that it is unfair, since some of the devices are operating off their design point (see the section titled “Limitations”). Shear stresses of less than about 1 Pa have been linked with thrombosis [55], therefore, the volume in that sss range was calculated (low sss volume). The CentVAD1, which has the largest total volume, clearly had the largest low sss volume, which decreased from 5 cm3 at 100 mmHg to 1 cm3 at 550 mmHg. However, the low sss percentage (low sss volume as a percentage of the total VAD volume) was largest for the three axial VADs, 25–30%, which compares with 5–15% for the two centrifugal VADs (see Fig. 6).
Fig. 5.
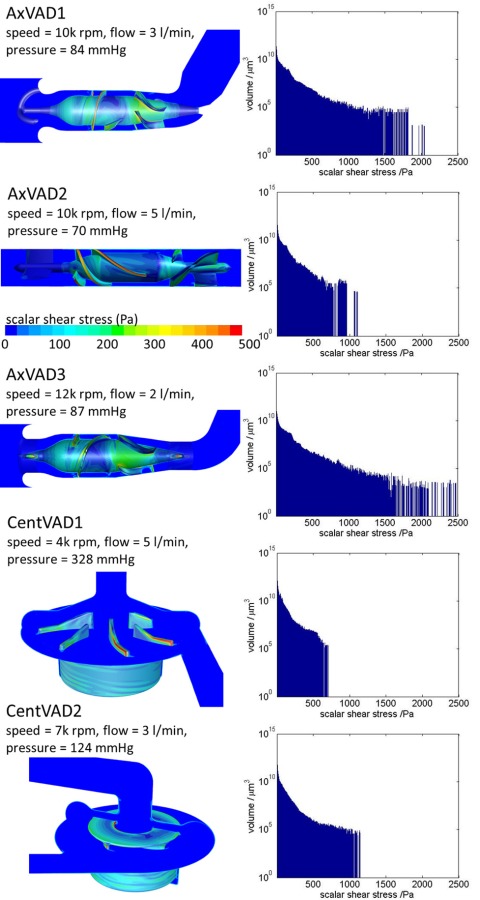
Contours of the sss and volumetric sss histogram for each VAD at the optimal operating condition
Fig. 6.

Plots of sss parameters with a flow rate = 3 l/min. Low sss volume 5 volume with sss < 1 Pa. High sss volume = volume with sss > 9 Pa. Higher sss volume = volume with sss > 50 Pa. Very high sss volume = volume with sss > 150 Pa.
There is limited data on the level of shear stress required to break the vWf multimer (Table 1). For this study, a threshold of 9 Pa was used as an indicator of the potential to break the vWf at a higher rate than in the normal vasculature and regions with sss greater than 9 Pa were called high sss regions. The high sss volume generally increases with the pressure head and is similar for the AxVAD1, AxVAD2, and CentVAD2, ranging from around 17% at 50 mmHg to around 25% at 150 mmHg (see Fig. 6). The high sss volume is smaller for CentVAD1 (12–24%). The high sss volume decreases with increasing pressure for AxVAD3 because this VAD does not function well at 3 l/min and 10 k rpm and there is a lot of flow disturbance which creates additional shearing.
Transit times for blood through the VADs are of the order of 0.1 s and, therefore, a threshold of 50 Pa was used as an indicator of potential platelet activation (see Ref. [15] and Fig. 1). Regions with sss greater than 50 Pa are called higher sss regions. Higher sss volume increases with the pressure head and the VADs are in the following order of increasing higher sss volume: CentVAD1 <CentVAD2 < AxVAD2 < AxVAD1 < AxVAD3 (see Fig. 6). The volume for the CentVAD1 ranges from 0.4% at 74 mmHg to 4.2% at 541 mmHg, whereas the volume for AxVAD3 ranges from 5.5 at 27 mmHg to 5.8% at 101 mmHg.
Shear stresses above 150 Pa have been associated with hemolysis [56] and regions with a sss above 150 Pa were termed very high sss. In the AxVAD1 these were located along the impeller and diffuser blades (see Fig. 5 and the supplementary material [54]) and, as the speed was increased, large patches of the hub and shroud surfaces also became very high sss regions. At 12 k rpm the whole gap between the impeller blades and the shroud exceeded 150 Pa. The very high sss regions in the AxVAD2 and AxVAD3 were similar. In the AxVAD3 there were additional very high sss regions at the tips of the tripod bearings. In the CentVAD1 the very high sss regions were located on the trailing edge and the top of the high pressure side of the blades. The size of the regions increased as the flow rate increased from 3 to 7 l/min. As the speed increased from 3 k rpm to 5 k rpm, large very high sss regions appeared in the secondary flow path around the rotating magnet. The very high sss regions were similarly located in the CentVAD2 but with the addition of regions on the outer housing at the highest speed (9 k rpm). All five VADs had regions of very high sss at all the operating conditions investigated. The total volumes of these ranged from about 1 to 100 mm3 and were largest, both in absolute and percentage terms, for the three axial VADs, followed by the CentVAD2 and then the CentVAD1 (see Fig. 6). The AxVAD3 had the largest maximum sss, which ranged from 2200 to 3060 Pa.
Residence Time.
The mean residence time was the longest for the CentVAD1, decreasing from 1.81 to 0.25 s in the flow range of 3 to 7 l/min. The CentVAD2 and AxVAD2 had almost identical residence times (0.17 s at 3 l/min) because they have the same volume. The next shortest times were for the AxVAD1 (0.12 s at 3 l/ min) and the AxVAD3 had the shortest time (0.09 s at 3 l/min).
The residence time for each mesh element, or “elemental residence time” te, is given by te = ve/qe where ve and qe are the volume of the element and flow rate through it, respectively. The flow weighted elemental residence time is then
| (4) |
where Q is the flow rate through the VAD. Then the flow weighted residence time for each shear stress level was calculated from the total volume at that shear stress level and the VAD flow rate. Histograms were plotted for the residence time over the full range of sss (see the supplementary material [54]). To fairly compare the residence times for different VADs, the results for different rotational speeds were linearly interpolated to give the residence times for shear stress thresholds at an operating condition which would give a pressure head of 100 mmHg. The low sss residence time (time at sss < 1 Pa) is the longest for the CentVAD1, which has the largest volume, with a time of 0.085 s at 3 l/min, and was the shortest in the CentVAD2 and AxVAD3 (0.02 s) (see Fig. 7). The residence time at high sss (>9 Pa) is the longest for the CentVAD1 (0.08 s at 3 l/min) but close for the other four VADs (0.02–0.04 s at 3 l/min) (data not shown). At higher sss (>50 Pa), all five VADs have a similar residence time (0.004–0.007 s at 3 l/min). However, for the residence time above 150 Pa there is a clear difference between the trends for the axial and centrifugal VADs. At 3 l/min the axial VADs have a residence time of around 0.0014 s, whereas the centrifugal VADs are around 0.0003 s. Note that, although in most cases the residence time decreases as the flow rate increases, this is not always true: for the CentVAD2 the residence time above 150 Pa increases with the flow rate. This is because, in interpolating the results for different rotational speeds at a fixed pressure head of 100 mmHg, the equivalent rotational speed increases with flow rate. Faster speeds result in time at larger shear stresses, which counteracts the trend for shorter times. This interplay between the increased flow rate and rotational speed depends on the shape of the pressure-flow curves (see Fig. 3): the CentVAD2 has the steepest curves.
Fig. 7.
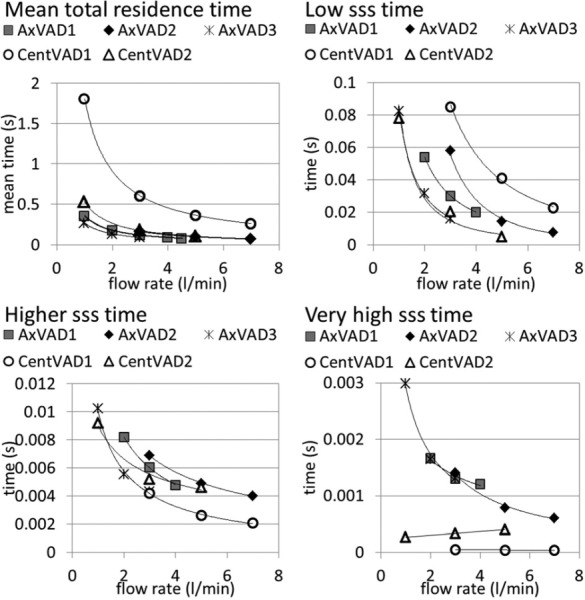
Plots of residence time parameters at pressure = 100 mmHg. Low sss volume = volume with sss < 1 Pa. Higher sss volume = volume with sss > 50 Pa. Very high sss volume = volume with sss > 150 Pa.
Hemolysis.
The scalar transport hemolysis models currently available in the literature have been found to accurately predict relative comparisons of hemolysis at different operating conditions and in different devices. However, their predictions tend to be greater than the actual absolute hemolysis measurements [49]. In this work, the computational predictions were fit to the experimental measurements of HI (%) in two of the VADs: the CentVAD1 and the AxVAD1. In this way, new constants for the power law equation were found and these were: a = 1.963, b = 7.762 × 10 −1, and c = 1.745 × 10 −6. The RMS error of the fitted results compared to the experimental measurements was 1.27 × 10 −6, and their correlation coefficient was 0.85, with the trend line having a gradient of 0.92. These can be compared to the results with the original constants (from Heuser and Opitz [50] and used by Song et al. [52]) which had an RMS error = 2.15 × 10 −6, a correlation coefficient of 0.85, and a trend line gradient = 1.16. The new constants were then tested by a comparison of the hemolysis predictions with experimental measurements in the same devices but at different operating conditions. The RMS error for the eight conditions in the CentVAD1 was 8.06 × 10 −5 and the error for the one condition in the AxVAD1 was 3.01 × 10 −5.
The contour plots of the normalized HI show where plasma free hemoglobin is expected to accumulate (see Fig. 8). In the axial VADs the hub and shroud from just upstream of the impeller blades down to the diffuser blades have a high HI. These VADs also have regions upstream of the impeller blades extending into the flow passage, which are due to the tip leakage flow, which has a high HI, mixing with the incoming flow which has a very low HI. In the centrifugal VADs the HI is highest in the secondary flow path, around the base of the magnet, due to the slow flow in that region.
Fig. 8.
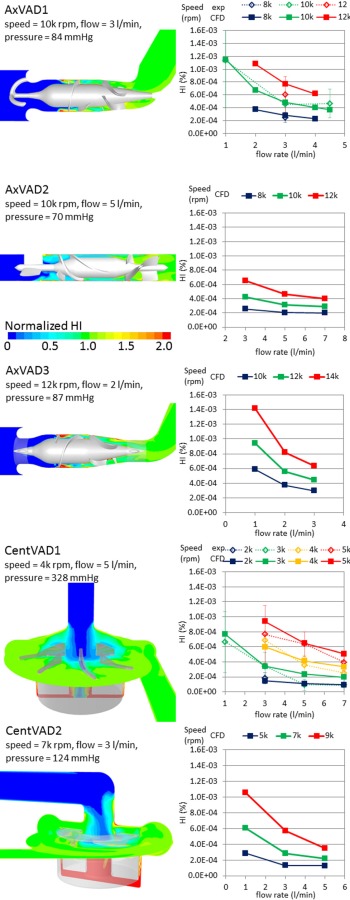
Left: contour plots of HI normalized to the outlet value to show the special variation in each VAD. Right: variation in the HI with the operating condition in each VAD and a comparison with the experimental data in the CentVAD1 and AxVAD1.
For each VAD the HI decreases as the flow rate increases and increases as the rotational speed is increased (see Fig. 8). After accounting for the flow rate, the AxVAD1 and AxVAD2 both have similar HIs at the same speeds. For example, at 3 l/min the HI range for the AxVAD1 is 2.8 × 10 −4–7.7 × 10 −4%, whereas it is 2.6 × 10 −4–6.5 × 10 −4% in the AxVAD2. The AxVAD3 also has an HI similar to those two, albeit at the higher speeds at which it operates (3 l/min: 3.0 × 10−4–6.3 × 10 −4%).The two centrifugal VADs also seem to have fairly similar ranges of the HI for a given flow rate, although the range for the CentVAD1 is wider and that for the CentVAD2 is shifted to lower HI values (at 3 l/min, CentVAD1: 1.5 × 10−4–9.4 × 10−4%, CentVAD2: 1.3 × 10 × 4–5.7 × 10 × 4%). To account for the different rotational speeds req uired to produce a given pressure, and thereby compare the different VADs at the same flow rate and pressure head, the HI values were linearly interpolated to find the HI at a flow rate = 3 l/min and pressure = 100 mmHg (see Fig. 9). The HI for the axial VADs is between 1.7 and 3.4 times that in the centrifugal VADs. The higher maximum shear stresses, larger volumes, and longer residence times at very high shear stress (sss > 150 Pa) resulted in larger HIs. The CentVAD2 experiences a larger maximum sss, larger volumes at high shear stress, and longer residence times at high shear stress as compared with the CentVAD1, which explains the higher HI compared to that VAD. However, the order of the HI values for the axial VADs (AxVAD2 < AxVAD1 < AxVAD3) while being the same as the order for the volumetric sss parameters (mean, maximum, and all high sss volumes), is not predicted by the residence times at high, higher, or very high sss. The residence time for higher sss thresholds (for example: sss > 200 Pa) (data not shown) predict the HI values for all VADs in the same order as the volumetric sss parameters.
Fig. 9.
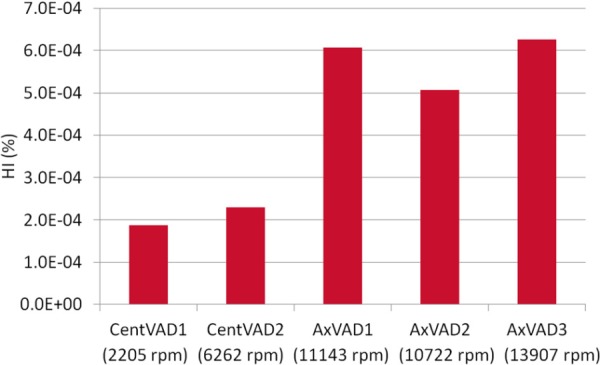
Comparison of the HI between VADs with each VAD operating at a flow = 3 l/min and pressure = 100 mmHg. The speeds required to produce those conditions are also shown.
Discussion
Flow fields in the five different VADs were calculated, using CFD at operating conditions spanning their range of uses and shear stresses, and residence times were investigated. Additionally, a scalar transport model was used to compare hemolysis in the different VADs. The calculations of the pressure head and hemolysis were in satisfactory agreement with experimental values, and the mesh study gave small differences in the sss parameters, showing that the calculations were acceptable for the proposed analysis, given the limitations which are outlined in the following text.
The shear stress in the three axial VADs spanned a wider range than in the two centrifugal VADs, resulting in larger mean, larger maximum sss, and larger percentage volumes experiencing high (>9 Pa) higher (>50 Pa) and very high (>150 Pa) sss. Interestingly the percentage volume at low sss (<1 Pa) was also larger in the axial VADs. The smaller low and high shear regions in the centrifugal VADs imply that their volumes are more concentrated between 1 and 9 Pa. The mean total residence time in one centrifugal VAD was much longer than the other VADs due to its larger size and this additional time was mostly concentrated at sss between 1 and 9 Pa, but also resulted in longer times with both sss < 1 Pa and sss > 9 Pa. There was a considerable difference in the residence time at very high sss (>150 Pa) between the axial and centrifugal VADs, with blood in the axial VADs being exposed to very high sss for around 5 times longer than blood in the centrifugal VADs at a flow rate of 3 l/min.
At the same level of support (flow = 3 l/min and pressure = 100 mmHg) the axial VADs had around three times the HI of the CentVAD1 and around twice the HI of the CentVAD2. Both the shear stress magnitude and exposure time contribute to hemolysis. While the mean total residence time within the axial VADs was either shorter than (CentVAD1) or comparable to (CentVAD2) the residence time in the centrifugal VADs, the residence time at shear stresses which may result in hemolysis was much higher in the axial VADs. The axial VADs also had a higher maximum sss, which could hemolyze the red blood cells very quickly [51].
While hemolysis is an issue with VADs [57], it is not the most common problem [8]. However, the HI levels reported in this work are symptomatic of other types of blood damage which result from the flow conditions in axial VADs and are found clinically, including: platelet activation [58], thrombosis and emboli [59], and destruction of the von Willebrand factor [24]. From Hellums' [15] plot of the shear stress versus exposure time threshold for platelet activation, we decided on an approximate value of 50 Pa (“higher sss”) for the threshold in these VADs, which have transit times on the order of 0.1 s. The percentage volumes at higher sss were in the order of CentVAD1 < CentVAD2 < AxVAD2 < AxVAD1 < AxVAD3, suggesting that the platelet activation levels may also be in that order. However, the residence time results were contradictory: the higher sss times were in the order of CentVAD1 < AxVAD3 < CentVAD2 < AxVAD1 < AxVAD2. This is likely because this simplistic single threshold fails to account for the fast activation at the very high sss levels. If the residence time is calculated with a high enough threshold (sss > 200 Pa), the VADs are put into the same order given by the higher sss volumes. The conditions for thrombosis to occur have, for a long time, been known to involve three aspects: the nature of the surface, the condition of the blood, and the local flow conditions. The first two aspects are present: the VADs in the study use different materials but all are artificial and allow clotting to some degree; the platelets are exposed to nonphysiological shear stresses and will be activated to some degree. The third aspect is the local flow conditions which will promote thrombosis if there is stagnant or slow flow, recirculation, and low shear stresses [34]. All of the VADs contain some regions of slow flow and recirculation (see Fig. 4 and the supplementary material [54]). The percentage volumes at low sss were larger for the axial VADs than for the centrifugal VADs, which may suggest that these VADs are more likely to allow the activated platelets to produce blood clots. There is limited data on the shear stress conditions required to break down the vWf multimers but since the process occurs normally at arterial shear stress levels, it is likely that all the VADs will accelerate it.
Limitations.
The majority of the analyses were conducted for a flow rate of 3 l/min and/or pressure head of 100 mmHg. This was to enable the comparison of the VADs at the same use condition and the value was chosen since it is achievable by all of the VADs; 3 l/min is the optimum flow rate for one VAD (CentVAD2), but is lower than optimum for three VADS (AxVAD1, AxVAD2, and CentVAD1) and is higher for the AxVAD3. A rotary flow pump operates less efficiently off the design point with additional vortices and turbulence generated, which would be expected to increase the shear stresses. The volumetric sss parameters were also compared at the optimum conditions (see the supplementary material [54]) and while the difference, as compared to the analysis at 3 l/min, was small, there were some noticeable changes: a slightly smaller volumetric mean and maximum sss at optimum flow rates; the low sss volume increased for the AxVAD3; the slope for the high sss volume in the AxVAD3 was positive at the optimum flow rate, rather than negative as noted earlier; the higher sss volume for the AxVAD3 decreased. A similar comparison of the time parameters at optimum rotational speed showed that operating the AxVAD2 and AxVAD3 at their intended rotational speeds reduced the very high sss residence time, due to increased efficiency, whereas the time for the two centrifugal VADs increased because the optimum rotational speed is larger than that required to produce 100 mmHg.
Our model for hemolysis was adapted from other scalar transport power-law models [49], with the constants obtained by fitting the results to the experimental data. The power law constants were fitted to four experimental conditions from two different VADs (one axial and one centrifugal) and then the model was validated by a comparison with more data from the same VADs. Ideally, data from different VADs would have been used for the validation.
The blood model was a single phase Newtonian fluid. In reality, we know that blood has two main phases, RBCs and plasma, and has a shear thinning viscosity. Only very small regions have a shear rate less than 100 s −1 (0.35 Pa); for example, the CentVAD1 at 3 k rpm and 3 l/min has just 1.8% of the volume with sss < 0.35 Pa. The viscosity of blood used here (0.0035 Pa s) is based on the high shear limit for blood. The increased viscosity at a low shear rate is expected to increase the shear stress in those regions and, therefore, slightly reduce the size of the low sss volumes.
The single phase nature of the blood model used is an important limitation on the blood damage results. There is some evidence that, under the high shear rates found in VADs, the RBCs may be pushed away from the walls, resulting in a reduced apparent viscosity for blood [60], an effect which could be similar to the reduced viscosity in small capillary tubes (the Fahraeus Lindqvist effect [61]). There is also data showing that red blood cells may be excluded from the blade tip clearance gaps when these are made small enough [62]. If the RBCs are moved away from the VAD walls and out of the tip gaps there will be fewer of them experiencing the highest shear stresses. Thus, although our hemolysis model correctly predicts hemolysis because it was fitted to do so, it may be giving the right results for the wrong reasons. These kinds of effects will be different for different VADs and, in future work, the hemolysis model should be tested in more VADs. While the RBCs may be excluded from the highest shear regions, the effect will be the opposite for the platelets: since they inhabit the plasma portion of blood more of them could be exposed to the highest shear stresses, increasing the number that become activated.
The flow conditions assumed in this work have been simplified. Steady flow was assumed whereas, in reality, the flow through VADs has a pulsatile component due to the beating heart. This pulsatile component is likely to increase the flow disturbances and reduce the amount of streamlined flow during the deceleration phase [63]. Flow to the inlets of the CentVAD1 and CentVAD2 was through a straight cylindrical tube, mimicking either the cannulae used in vivo or the tubes of an experimental flow loop. The inlet for the AxVAD2 was taken from the VAD geometry and consists of a gently converging tube with a bend upstream of the pump. However, the AxVAD1 and AxVAD3 fit directly into the left ventricle (LV), a situation which was not mimicked by the computational geometry at the inlet for which a straight tube, which fit over the outer diameter of the VAD, was used instead. A straight tube was used rather than an LV geometry because of the variation in LV shapes and for a comparison with the experimental pressure head and hemolysis results. The motion of the LV in vivo is likely to reduce the size of the low sss regions on the inlet side of the VAD.
In this work, the MRF method was used to account for the rotation of the impeller. The MRF method is an approximation which cannot account for transient effects or conditions other than steady state [26]. In reality, as the impeller blades pass the outlet (centrifugal VADs) or interact with the diffusers (axial VADs), there is a fluctuation in the pressure head [64] and the flow field and, hence, the shear stress field changes.
Conclusion
Shear stress, residence time, and hemolysis were calculated in the five different VADs. Several major differences were found between the axial and centrifugal VADs: the axial VADs had a higher mean scalar shear stress (sss); the axial VADs had a wider range of sss, with larger maxima and larger percentage volumes at both low and high sss; the axial VADs had longer residence times at very high sss; and the axial VADs had higher hemolysis indices. Although hemolysis in VADs is not currently a major issue, these results suggest that axial VADs may also have higher rates of other types of blood damage such as platelet activation, thrombosis, and destruction of the vWf.
Acknowledgment
This work was funded by the National Institutes of Health (Grant No. R01HL088100).
References
- [1]. WHO, 2007, “Fact Sheet No. 317.”
- [2]. Lloyd-Jones, D. , Adams, R. J. , Brown, T. M. , Carnethon, M. , and Dai, S. , 2010, “Heart Disease and Stroke Statisitics 2010 Update: A Report From the American Heart Association,” Circulation, 121, pp. e46–e215. 10.1161/CIRCULATIONAHA.109.192667 [DOI] [PubMed] [Google Scholar]
- [3]. Warrell, D. A. , Cox, T. M. , Firth, J. D. , and Benz, E. J. , 2005, Oxford Textbook of Medicine, 4th ed., Oxford University Press, Oxford. [Google Scholar]
- [4]. Health Resources and Services Administration, U. S. Department of Health and Human Services, 2009, “Organ Procurement and Transplant Network.”
- [5]. Allen, G. S. , Murray, K. D. , and Olsen, D. B. , 1997, “The Importance of Pulsa-tile and Nonpulsatile Flow in the Design of Blood Pumps,” Artif. Organs, 21, pp. 922–928. [DOI] [PubMed] [Google Scholar]
- [6]. Song, X. , Throckmorton, A. L. , Untaroiu, A. , Patel, S. , Allaire, P. E. , Wood, H. G. , and Olsen, D. B. , 2003, “Axial Flow Blood Pumps,” ASAIO J., 49, pp. 355–364. [PubMed] [Google Scholar]
- [7]. Thompson, L. O. , Loebe, M. , and Noon, G. P. , 2003, “What Price Support? Ventricular Assist Device Induced Systemic Response,” ASAIO J., 49(5), pp. 518–526. 10.1097/01.MAT.0000085672.42122.49 [DOI] [PubMed] [Google Scholar]
- [8]. Genovese, E. A. , Dew, M. A. , Teuteberg, J. J. , Simon, M. A. , Kay, J. S. M. P. , Bhama, J. K. , Bermudez, C. A. , Lockard, K. L. , Winowich, S. , and Kormos, R. L. , 2009, “Incidence and Patterns of Adverse Event Onset During the First 60 Days After Ventricular Assist Device Implantation,” Ann. Thorac. Surg., 88(4), pp. 1162–1170. 10.1016/j.athoracsur.2009.06.028 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9]. Leverett, L. B. , Hellums, J. D. , Alfrey, C. P. , and Lynch, E. C. , 1972, “Red Blood Cell Damage by Shear Stress,” Biophys. J., 12(3), pp. 257–272. 10.1016/S0006-3495(72)86085-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10]. Kuypers, F. A. , 1998, “Red Cell Membrane Damage,” J. Heart Valve Dis., 7, pp. 387–395. [PubMed] [Google Scholar]
- [11]. Giersiepen, M. , Wurzinger, L. J. , Opitz, R. , and Reul, H. , 1990, “Estimation of Shear Stress-Related Blood Damage in Heart Valve Prosthesis—in vitro Comparison of 25 Aortic Valves,” Int. J. Artif. Organs, 13, pp. 300–306. [PubMed] [Google Scholar]
- [12]. Stassen, J. M. , Arnout, J. , and Deckmyn, H. , 2004, “The Hemostatic System,” Curr. Med. Chem., 11(17), pp. 2245–2260. Available at: http://www.ingentaconnect.com/content/ben/cmc/2004/00000011/00000017/art00002 [DOI] [PubMed] [Google Scholar]
- [13]. Varga-Szabo, D. , Pleines, I. , and Nieswandt, B. , 2008, “Cell Adhesion Mechanisms in Platelets,” Arterioscler., Thromb., Vasc. Biol., 28(3), pp. 403–412. 10.1161/ATVBAHA.107.150474 [DOI] [PubMed] [Google Scholar]
- [14]. Sorensen, E. N. , Burgreen, G. W. , Wagner, W. R. , and Antaki, J. F. , 1999, “Computational Simulation of Platelet Deposition and Activation: I. Model Developement and Properties,” Ann. Biomed. Eng., 27(4), pp. 436–448. 10.1114/1.200 [DOI] [PubMed] [Google Scholar]
- [15]. Hellums, J. D. , 1994, “1993 Whitaker Lecture: Biorheology in Thrombosis Research,” Ann. Biomed. Eng., 22(5), pp. 445–455. 10.1007/BF02367081 [DOI] [PubMed] [Google Scholar]
- [16]. Wurzinger, L. J. , Opitz, R. , Blasberg, P. , and Schmid-Schonbein, H. , 1985, “Platelet and Coagulation Parameters Following Millisecond Exposure to Laminar Shear Stress,” Thromb. Haemostasis, 54, pp. 381–386. [PubMed] [Google Scholar]
- [17]. Sakariassen, K. S. , Holme, P. A. , Orvin, U. , Barstad, R. M. , Solum, N. O. , and Brosstad, F. R. , 1998, “Shear-Induced Platelet Activation and Platelet Micro-particle Formation in Native Human Blood,” Thromb. Res., 92(6), pp. S33–S41. 10.1016/S0049-3848(98)00158-3 [DOI] [PubMed] [Google Scholar]
- [18]. Zhang, J.-N. , Bergeron, A. L. , Yu, Q. , Sun, C. , McBride, L. , Bray, P. F. , and Dong, J. F. , 2003, “Duration of Exposure to High Fluid Shear Stress is Critical in Shear-Induced Platelet Activation-Aggregation,” Thromb. Haemostasis, 90, pp. 672–678. [DOI] [PubMed] [Google Scholar]
- [19]. Ramstack, J. M. , Zuckerman, L. , and Mockros, L. F. , 1979, “Shear-Induced Activation of Platelets,” J. Biomech., 12(2), pp. 113–125. 10.1016/0021-9290(79)90150-7 [DOI] [PubMed] [Google Scholar]
- [20]. Colantuoni, G. , Hellums, J. D. , Moake, J. L. , and Alfrey, C. P., Jr. , 1977, “The Response of Human Platelets to Shear Stress at Short Exposure Times,” Trans. Am. Soc. Artif. Intern. Organs, 23(1), pp. 626–630. 10.1097/00002480-197700230-00169 [DOI] [PubMed] [Google Scholar]
- [21]. Carter, J. , Hristova, K. , Harasaki, H. , and Smith, W. A. , 2003, “Short Exposure Time Sensitivity of White Cells to Shear Stress,” ASAIO J., 49(6), pp. 687–691. 10.1097/01.MAT.0000094194.93742.A7 [DOI] [PubMed] [Google Scholar]
- [22]. Tsai, H.-M. , Sussman, I. I. , and Nagel, R. L. , 1994, “Shear Stress Enhances the Proteolysis of von Willebrand Factor in Normal Plasma,” Blood, 83, pp. 2171–2179. [PubMed] [Google Scholar]
- [23]. Vincentelli, A. , Susen, S. , Le Tourneau, T. , Six, I. , Fabre, O. , Juthier, F. , Bauters, A. , Decoene, C. , Goudemand, J. , Prat, A. , and Jude, B. , 2003, “Acquired von Willebrand Syndrome in Aortic Stenosis,” New Engl. J. Med., 349(4), pp. 343–349. 10.1056/NEJMoa022831 [DOI] [PubMed] [Google Scholar]
- [24]. Uriel, N. , Pak, S.-W. , Jorde, U. P. , Jude, B. , Susen, S. , Vincentelli, A. , Ennezat, P. V. , Cappleman, S. , Naka, Y. , and Mancini, D. , 2010, “Acquired von Wille-brand Syndrome After Continuous-Flow Mechanical Device Support Contributes to a High Prevalence of Bleeding During Long-Term Support and at the Time of Transplantation,” J. Am. Coll. Cardiol., 56(15), pp. 1207–1213. 10.1016/j.jacc.2010.05.016 [DOI] [PubMed] [Google Scholar]
- [25]. Di Stasio, E. and De Cristofaro, R. , 2010, “The Effect of Shear Stress on Protein Conformation Physical Forces Operating on Biochemical Systems: The Case of von Willebrand Factor,” Biophys. Chem., 153(1), pp. 1–8. 10.1016/j.bpc.2010.07.002 [DOI] [PubMed] [Google Scholar]
- [26]. Fraser, K. H. , Taskin, M. E. , Griffith, B. P. , and Wu, Z. J. , 2011, “The Use of Computational Fluid Dynamics in the Development of Ventricular Assist Devices,” Med. Eng. Phys., 33(3), pp. 263–280. 10.1016/j.medengphy.2010.10.014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27]. Day, S. W. , McDaniel, J. C. , Wood, H. G. , Allaire, P. E. , Landrot, N. , and Curtas, A. , 2001, “Particle Image Velocimetry Measurements of Blood Velocity in a Continuous Flow Ventricular Assist Device,” ASAIO J., 47(4), pp. 406–411. 10.1097/00002480-200107000-00021 [DOI] [PubMed] [Google Scholar]
- [28]. Chua, L. P. , Ong, K. S. , Yu, C. M. S. , and Zhou, T. , 2004, “Leakage Flow Rate and Wall Shear Stress Distributions in a Biocentrifugal Ventricular Assist Device,” ASAIO J., 50(6), pp. 530–536. 10.1097/01.MAT.0000144363.92963.CB [DOI] [PubMed] [Google Scholar]
- [29]. Wu, Z. J. , Gottlieb, R. K. , Burgreen, G. W. , Holmes, J. A. , Borzelleca, D. C. , Kameneva, M. V. , Griffith, B. P. , and Antaki, J. F. , 2001, “Investigation of Fluid Dynamics Within a Miniature Mixed Flow Blood Pump,” Exp. Fluids, 31(6), pp. 615–629. 10.1007/s003480100308 [DOI] [Google Scholar]
- [30]. Sukumar, R. , Ahavale, M. M. , Makhijani, V. B. , and Przekwas, A. J. , 1996, “Application of Computational Fluid Dynamics Techniques to Blood Pumps,” Artif. Organs, 20(5), pp. 529–533. 10.1111/j.1525-1594.1996.tb04475.x [DOI] [PubMed] [Google Scholar]
- [31]. Antaki, J. F. , Ghattas, O. , Burgreen, G. W. , He, B. , 1995, “Computational Flow Optimization of Rotary Blood Pump Components,” Artif. Organs, 19(7), pp. 608–615. 10.1111/j.1525-1594.1995.tb02389.x [DOI] [PubMed] [Google Scholar]
- [32]. Wu, Z. J. , Taskin, M. E. , Zhang, T. , Fraser, K. H. , and Griffith, B. P. , 2012, “Computational Model-Based Design of a Wearable Artificial Pump-Lung for Cardiopulmonary/Respiratory Support,” Artif. Organs, 36(4), pp. 387–399. 10.1111/j.1525-1594.2011.01369.x [DOI] [PubMed] [Google Scholar]
- [33]. Frank, A. O. , Walsh, P. W. , and Moore, J. E., Jr ., 2002, “Computational Fluid Dynamics and Stent Design,” Artif. Organs, 26(7), pp. 614–621. 10.1046/j.1525-1594.2002.07084.x [DOI] [PubMed] [Google Scholar]
- [34]. Fraser, K. H. , Zhang, T. , Taskin, M. E. , Griffith, B. P. , and Wu, Z. J. , 2010, “Computational Fluid Dynamics Analysis of Thrombosis Potential in Ventricular Assist Device Drainage Cannulae,” ASAIO J., 56(3), pp. 157–163. 10.1097/MAT.0b013e3181d861f1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35]. Kido, K. , Hoshi, H. , Watanabe, N. , Kataoka, H. , Ohuchi, K. , Asama, J. , Shinshi, T. , Yoshikawa, M. , and Takatani, S. , 2006, “Computational Fluid Dynamics Analysis of the Pediatric Tiny Centrifugal Blood Pump (TinyPump),” Artif. Organs, 30(5), pp. 392–399. 10.1111/j.1525-1594.2006.00231.x [DOI] [PubMed] [Google Scholar]
- [36]. Legendre, D. , Antunes, P. , Bock, E. , Andrade, A. , Biscegli, J. F. , and Ortiz, J. P. , 2008, “Computational Fluid Dynamics Investigation of a Centrifugal Blood Pump,” Artif. Organs, 32(4), pp. 342–348. 10.1111/j.1525-1594.2008.00552.x [DOI] [PubMed] [Google Scholar]
- [37]. Untaroiu, A. , Throckmorton, A. L. , Patel, S. M. , Wood, H. G. , Allaire, P. E. , and Olse, D. B. , 2005, “Numerical and Experimental Analysis of an Axial Flow Left Ventricular Assist Device: The Influence of the Diffuser on Overall Pump Performance,” Artif. Organs, 29(7), pp. 581–591. 10.1111/j.1525-1594.2005.29095.x [DOI] [PubMed] [Google Scholar]
- [38]. Wu, J. , Paden, B. E. , Borovetz, H. S. , and Antaki, J. F. , 2010, “Computational Fluid Dynamics Analysis of Blade Tip Clearances on Hemodynamic Performance and Blood Damage in a Centrifugal Ventricular Assist Device,” Artif. Organs, 34, pp. 402–411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39]. Taskin, M. E. , Fraser, K. H. , Zhang, T. , Gellman, B. , Fleischli, A. , Dasse, K. A. , Griffith, B. P. , and Wu Z. J., 2011, “Computational Characterization of Flow and Hemolytic Performance of the UltraMag Blood Pump for Circulatory Support,” Artif. Organs, 34, pp. 1099–1113. [DOI] [PubMed] [Google Scholar]
- [40]. Nishida, M. , Maruyama, O. , Kosaka, R. , Yamane, T. , Kogure, H. , Kawamura, H. , Yamamoto, Y. , Kuwana, K. , Sankai, Y. , and Tsutsui, T. , 2009, “Hemocompatibility Evaluation With Experimental and Computational Fluid Dynamic Analyses for a Monopivot Circulatory Assist Pump,” Artif. Organs, 33(4), pp. 378–386. 10.1111/j.1525-1594.2009.00730.x [DOI] [PubMed] [Google Scholar]
- [41]. Chua, L. P. , Su, B. , Tau, M. L. , and Zhou, T. , 2007, “Numerical Simulation of an Axial Blood Pump,” Artif. Organs, 31(7), pp. 560–570. 10.1111/j.1525-1594.2007.00422.x [DOI] [PubMed] [Google Scholar]
- [42]. Fraser, K. H. , Taskin, M. E. , Zhang, T. , Richardson, J. S. , Gellman, B. , Dasse, K. , Griffith, B. P. , and Wu, Z. J. , 2010, “Effect of Impeller Position on CFD Calculations of Blood Flow in Magnetically Levitated Centrifugal Blood Pumps,” Proceedings of the ASME 2010 Summer Bioengineering Conference (SBC2010), Naples, FL. [Google Scholar]
- [43]. Zhang, J. , Gellman, B. , Koert, A. , Dasse, K. A. , Gilbert, R. J. , Griffith, B. P. , and Wu, Z. J. , 2006, “Computational and Experimental Evaluation of the Fluid Dynamics and Hemocompatability of the Centrimag Blood Pump,” Artif. Organs, 30(3), pp. 168–177. 10.1111/j.1525-1594.2006.00203.x [DOI] [PubMed] [Google Scholar]
- [44]. Roache, P. J. , 1997, “Quantification of Uncertainty in Computational Fluid Dynamics,” Ann. Rev. Fluid Mech., 29(1), pp. 123–160. 10.1146/annurev.fluid.29.1.123 [DOI] [Google Scholar]
- [45]. Menter, F. R. , 1994, “Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications,” AIAA J., 32(8), pp. 1598–1605. 10.2514/3.12149 [DOI] [Google Scholar]
- [46]. Hariharan, P. , Giarra, M. , Reddy, V. Day, S. W. , Manning, K. B. , Deutsch, S. , Stewart, S. F. , Myers, M. R. , Berman, M. R. , Burgreen, G. W. , Paterson, E. G. , and Malinauskas, R. A. , 2011, “Multilaboratory Particle Image Velocimetry Analysis of the Benchmark Nozzle Model to Support Validation of Computational Fluid Dynamics Simulations,” ASME J. Biomech. Eng., 133, p. 041002. [DOI] [PubMed] [Google Scholar]
- [47]. Ansys Inc.: Fluent Theory Guide.
- [48]. Bludszuweit, C. , 1995, “Model for a General Mechanical Blood Damage Prediction,” Artif. Organs, 19(7), pp. 583–598. 10.1111/j.1525-1594.1995.tb02385.x [DOI] [PubMed] [Google Scholar]
- [49]. Taskin, M. E. , Fraser, K. H. , Zhang, T. , Wu, C. , Griffith, B. P. , and Wu, Z. J. , 2012, “Evaluation of Eulerian and Lagrangian Models for Hemolysis,” ASAIO J. 58 (4)pp. 363–372. 10.1097/MAT.0b013e318254833b [DOI] [PubMed] [Google Scholar]
- [50]. Heuser, G. , and Opitz, R. , 1980, “A Couette Viscometer for Short Time Shearing of Blood,” Biorheology, 17, pp. 17–24. [DOI] [PubMed] [Google Scholar]
- [51]. Zhang, T. , Taskin, M. E. , Fang, H. B. , Pampori, A. , Jarvik, R. , Griffith, B. P. , and Wu Z. J., 2011, “Study of Flow-Induced Hemolysis Using Novel Couette-Type Blood Shearing Devices,” Artif. Organs, 35(12), pp. 1180–1186. 10.1111/j.1525-1594.2011.01243.x [DOI] [PubMed] [Google Scholar]
- [52]. Song, X. , Throckmorton, A. L. , Wood, H. G. , Antaki, J. F. , and Olsen, D. B. , 2003, “Computational Fluid Dynamics Prediction of Blood Damage In a Centrifugal Pump,” Artif. Organs, 27(10), pp. 938–941. 10.1046/j.1525-1594.2003.00026.x [DOI] [PubMed] [Google Scholar]
- [53]. American Society for Testing and Materials, 1998, “Standard Practice for Assessment of Hemolysis in Continuous Flow Blood Pumps,” Annual Book of ASTM Standards, West Conshohocken, PA, Vol. 13.01. [Google Scholar]
- [54]. See supplementary material at http://medschool.umaryland.edu/artificial_organs/pubs.asp for: additional mesh study results; detailed descriptions of the flow fields and shear stress histograms for each operating condition; images showing the locations of high shear stress regions; histograms for residence time; and comparative sss and time results at optimum VAD conditions.
- [55]. Hochareon, P. , Manning, K. B. , Fontaine, A. A. , Tarbell, J. M. , and Deutsch, S. , 2004, “Correlation of in vivo Clot Deposition With the Flow Characteristics in the 50 cc Penn State Artificial Heart: A Preliminary Study,” ASAIO J., 50(6), pp. 537–542. 10.1097/01.MAT.0000145694.40637.A0 [DOI] [PubMed] [Google Scholar]
- [56]. Alemu, Y. and Bluestein, D. , 2007, “Flow Induced Platelet Activation and Damage Accumulation in a Mechanical Heart Valve: Numerical Studies,” Artif. Organs, 31(9), pp. 677–688. 10.1111/j.1525-1594.2007.00446.x [DOI] [PubMed] [Google Scholar]
- [57]. Loffler, C. , Straub, A. , Bassler, N. , Pernice, K. , Beyersdorf, F. , Bode, C. , Siegenthaler, M. P. , and Peter, K. , 2009, “Evaluation of Platelet Activation in Patients Supported by the Jarvik 2000 High-Rotational Speed Impeller Ventricular Assist Device,” J. Thorac. Cardiovasc. Surg., 137(3), pp. 736–741. 10.1016/j.jtcvs.2008.09.019 [DOI] [PubMed] [Google Scholar]
- [58]. Steinlechner, B. , Dworschak, M. , Birkenberg, B. , Duris, M. , Zeidler, P. , Fischer, H. , Milosevic, L. , Wieselthaler, G. , Wolner, E. , Quehenberger, P. , and Jilma, B. , 2009, “Platelet Dysfunction in Outpatients With Left Ventricular Assist Devices,” Ann. Thorac. Surg., 87(1), pp. 131–138. 10.1016/j.athoracsur.2008.10.027 [DOI] [PubMed] [Google Scholar]
- [59]. Schmid, C. , Tjan, T. D. T. , Etz, C. , Schmidt, C. , Wenzelburger, F. , Wilhelm, M. , Rothenburger, M. , Drees, G. , and Scheld, H. H. , 2005, “First Clinical Experience With the Incor Left Ventricular Assist Device,” J. Heart Lung Transplant, 24(9), pp. 1188–1194. 10.1016/j.healun.2004.08.024 [DOI] [PubMed] [Google Scholar]
- [60]. Vidakovic, S. , Ayre, P. , Woodard, J. , Lingard, N. , Tansley, G. , and Reizes, J. , 2000, “Paradoxical Effects of Viscosity on the VentrAssist Rotary Blood Pump,” Artif. Organs, 24(6), pp. 478–482. 10.1046/j.1525-1594.2000.06600.x [DOI] [PubMed] [Google Scholar]
- [61]. Fahraeus, R. and Lindqvist, T. , 1931, “The Viscosity of the Blood in Narrow Capillary Tubes,” Am. J. Physiol., 96, pp. 562–568. Available at: http://ajplegacy.physiology.org/content/96/3/562 [Google Scholar]
- [62]. Antaki, J. F. , Diao, C.-G. , Shu, F.-J. , Wu, J.-C. , Zhao, R. , and Kameneva, M. V. , 2008, “Microhaemodynamics Within the Blade Tip Clearance of a Centrifugal Turbodynamic Blood Pump,” Proc. Inst. Mech. Eng., Part H: J. Eng. Med., 222(4), pp. 573–581. 10.1243/09544119JEIM352 [DOI] [PubMed] [Google Scholar]
- [63]. Shu, F. , Vandenberghe, S. , and Antaki, J. F. , 2009, “The Importance of dQ/dt on the Flow Field in a Turbodynamic Pump With Pulsatile Flow,” Artif. Organs, 33(9), pp. 757–762. 10.1111/j.1525-1594.2009.00849.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- [64]. Song, X. , Throckmorton, A. L. , Wood, H. G. , Allaire, P. E. , and Olsen, D. B. , 2004, “Transient and Quasi-Steady Computational Fluid Dynamics Study of a Left Ventricular Assist Device,” ASAIO J., 50(5), pp. 410–417. 10.1097/01.MAT.0000136507.57707.0F [DOI] [PubMed] [Google Scholar]


