A Fluid Dynamics Study in a 50 cc Pulsatile Ventricular Assist Device: Influence of Heart Rate Variability

Abstract

Although left ventricular assist devices (LVADs) have had success in supporting severe heart failure patients, thrombus formation within these devices still limits their long term use. Research has shown that thrombosis in the Penn State pulsatile LVAD, on a polyurethane blood sac, is largely a function of the underlying fluid mechanics and may be correlated to wall shear rates below 500 s⁻¹. Given the large range of heart rate and systolic durations employed, in vivo it is useful to study the fluid mechanics of pulsatile LVADs under these conditions. Particle image velocimetry (PIV) was used to capture planar flow in the pump body of a Penn State 50 cubic centimeters (cc) LVAD for heart rates of 75–150 bpm and respective systolic durations of 38–50%. Shear rates were calculated along the lower device wall with attention given to the uncertainty of the shear rate measurement as a function of pixel magnification. Spatial and temporal shear rate changes associated with data collection frequency were also investigated. The accuracy of the shear rate calculation improved by approximately 40% as the resolution increased from 35 to 12 μm/pixel. In addition, data collection in 10 ms, rather than 50 ms, intervals was found to be preferable. Increasing heart rate and systolic duration showed little change in wall shear rate patterns, with wall shear rate magnitude scaling by approximately the kinematic viscosity divided by the square of the average inlet velocity, which is essentially half the friction coefficient. Changes in in vivo operating conditions strongly influence wall shear rates within our device, and likely play a significant role in thrombus deposition. Refinement of PIV techniques at higher magnifications can be useful in moving towards better prediction of thrombosis in LVADs. [DOI: 10.1115/1.4005001]

1. Introduction

It has been estimated that nearly 81 × 10⁶ Americans are affected by some form of cardiovascular disease, with greater than 5 × 10⁶ diagnosed with heart failure (HF) [1]. The American Heart Association/American College of Cardiology has classified the progression of HF into four stages (A–D) of increasing severity which has led to guidelines for diagnosis and treatment. In instances of stage D HF, commonly referred to as end-stage HF, indications of advanced structural heart disease and refractory symptoms of HF are present and require intervention. Heart transplantation remains the gold-standard for treatment of stage D HF; however, due to the limited number of donor hearts, it is estimated that nearly 5–10 patients are in waiting for every transplant recipient in the United States [2]. In these situations, alternative therapy options are necessary and treatment often results in temporary or permanent (destination) ventricular assist device (VAD) use for cardiac support.

The success of VADs as a means of long-term support has been previously demonstrated in the Randomized Evaluation of Mechanical Assistance for the Treatment of Congestive Heart Failure (REMATCH) study. The REMATCH trial strengthened arguments for left ventricular assist device (LVAD) use over previously debated intravenous inotropic therapy (IIT) as a means of improving cardiac support. Patients implanted with LVADs reported one year survival rates of 57% compared to 40% for those treated with IIT [3]. The findings of the REMATCH study not only illustrated the survival advantage of VADs for patients with diminished heart function, but it realized their potential as an option for destination therapy. Since the time of the REMATCH trial, gains in VAD technology have increased 1 year survival for U.S. patients implanted with them from 52% [4] to nearly 78% by 2010 in a given study [5].

The improved quality of life for patients with LVADs has justified their use as a means of HF treatment; however, thrombosis remains a significant complication limiting their long-term practicality. It has been shown that the potential for thrombus formation in LVADs is associated with the blood material interface, the surface topography, and the fluid mechanics within the device [6]. Over the past four decades, Penn State has sought to understand these phenomena through the development of pneumatic and pusher plate driven pulsatile LVADs.

Since the first 100 cubic centimeters (cc) LVAD implantation at Hershey Medical Center in 1976 [7], Penn State, with Arrow International Inc., developed a fully implantable 70 cc Lion-Heart device that reached clinical trials by 2001 [8]. While LionHeart implants showed little clot deposition, their size was only suitable for patients with large circulation volume. In order to accommodate smaller patients in need of a LVAD, a 50 cc device (model V-0) was created by 2000 [9]. Building upon, extensive efforts have gone into characterizing the level of thrombus formation within this device.

A 30 day in vivo study of the 50 cc LVAD, performed by Yamanaka et al., demonstrated that the majority of clots were attached to the back of the device's polyurethane diaphragm and along its bottom wall [10]. To more fully understand the reason for clot deposition at these sites, flow studies focused on areas within the pump that displayed recirculation, high blood residence time, and wall shear rates below 500 s⁻¹, as Hubbell and McIntire suggest that shear rates below this promote thrombus growth and platelet adhesion on polyurethane [11].

The first in vitro study of 50 cc thrombolytic regions was conducted by Hochareon et al. with the use of particle image velocimetry (PIV), the LVAD, and a mock circulatory loop simulating the native cardiovascular system [9,12]. These results showed low wall shear rates, on the order of 250 s⁻¹, along the bottom portion of the diaphragm for over 300 ms of the cardiac cycle. These low wall shear zones correlated to regions of reported clot deposition by Yamanaka et al. [10].

To improve the wall washing in these regions, Kreider et al., considered the effects of mitral valve orientation on the development of the flow, particularly the initial formation of the diastolic jet, within the 50 cc V-0 device [13]. They showed that rotating the mitral valve through four orientations in the housing altered the flow penetration to the bottom wall where thrombosis is thought to occur. Kreider et al. concluded that the 30° and 45° rotations towards the fluid region and away from the pusher plate not only produced the highest velocities in thrombus-prone regions, but also increased the duration of wall washing compared to other valve angles [13].

While the higher valve angles produced better flow characteristics within the LVAD, the potential for clotting, based on the wall shear rate, was still possible. In order to minimize the level of thrombus formation within the device, the model was modified by rounding the back edge of the model, lengthening the chamber depth, and angling the inlet and outlet ports towards the perimeter walls of the chamber. These modifications were made with the intent of further directing flow toward the walls to wash regions of the pump previously susceptible to thrombosis. The newer design led to less than desirable flow patterns within the device and poor wall washing [14]. Nanna et al. provided an analysis of three further device iterations [15]. Due to the uniformity of rotational flow and extended wall washing in a newer version of the 50 cc (V-2), this device was chosen as the best model to consider here.

While substantial effort has gone into characterizing flow and wall shear in the 50 cc device, most of this work has been performed under ideal operating conditions that are physiologic for an adult patient. Animal (calf) studies, however, have shown large fluctuations in heart rate and systolic/diastolic duration over the course of the implant study. Since these animal trials are used as models in predicting thrombosis in human implants, fluid mechanic analyses of these operating conditions are important.

Oley et al. explored the effects of off-design operation of the 50 cc V-0 model, primarily focusing on the fluid dynamic changes within the device under altered heart rate and the resulting potential for thrombus formation [16]. Studies were performed at heart rates of 60, 75, and 90 beats per minute (bpm) at 35% systolic duration and 75 bpm at 50% systolic duration. The higher heart rate (90 bpm) yielded higher velocities in the diastolic jet and further penetration towards the bottom chamber wall. Increased systolic durations had a similar effect as the decrease in pump filling time increased washing along the bottom wall of the device. While increasing heart rate and decreasing diastolic duration likely reduced the level of flow stasis and clot formation in the bottom region of the pump, separation along the inlet wall was of particular concern. Geometric changes within the 50 cc V-2 model were made to lessen this flow separation.

While previous investigations have observed flow changes within older 50 cc designs under varying operating situations, little has been done to explore these effects in the V-2 device. Animal testing of this pump has shown that animal heart rates range between 90 and 180 bpm with corresponding systolic durations of 38%–50%. The objectives of this study are to mimic low and high flow conditions in an in vitro setting and characterize the overall flow patterns and wall shear rates with PIV. Attention is given to the accuracy of the shear rate calculation, to the necessary frequency of data collection with high magnification PIV, and to the scaling of the shear rate distribution with heart rate.

2. Materials and Methods

In order to study the effects of varying heart rates and systolic durations on the flow within the 50 cc device, an in vitro model, geometrically identical to the clinical device was machined out of optically clear acrylic with an index of refraction of 1.49. The model does not maintain the implantable device's polyurethane blood sac, but rather incorporates a modified polyurethane diaphragm to allow for optical PIV measurements to be made. Two Bjork-Shiley Monostrut tilting disk valves were used to maintain unidirectional flow through the device's inlet and outlet. The inlet and outlet valve orientations were rotated 30° and 0° from the horizontal axis of the device, respectively. These valve angles, shown in Fig. 1, were chosen based on their promotion of the strong wall-washing characteristics identified by Kreider et al. [13].

Fig. 1.

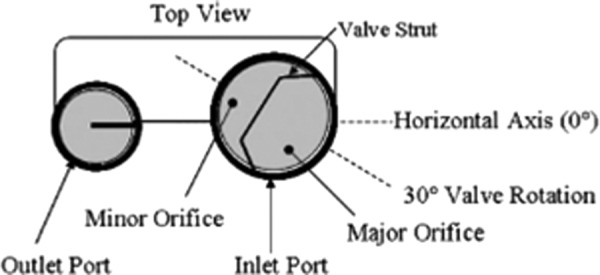
The 50 cc inlet and outlet valve orientations[13]

A Superpump, positive displacement piston system (StarFish Medical, Victoria, BC) was used to drive the overall flow within the device. The pulsatile nature of flow was established through the reciprocating motion of a polyvinyl chloride pusher plate attached to a piston shaft and aligned to contact the polyurethane diaphragm. The diaphragm is not attached to the pusher plate during operation to more closely approximate the sac motion in vivo [17]. In vitro sac motion was tracked through a linear variable displacement transducer (Solartron Metrology, West Sussex, UK). The Superpump's software controlled heart rate, systolic duration, and stroke length in order to simulate settings observed in vivo.

Clinical physiologic parameters were further mimicked with a mock circulatory loop designed to simulate fundamental elements of the native cardiovascular system. The mock loop was made up of a venous reservoir, atrial and arterial compliance chambers, and a resistance plate [18], all connected with Tygon tubing and incorporated with the acrylic model. Flow was measured at the inlet and outlet of the device with ultrasonic flow meters (Tran-sonic Systems, Inc., Ithaca, NY) and pressure transducers (Argon Medical Devices, Athens, TX) at the arterial and atrial compliance chambers monitored pressures throughout the cardiac cycle. The mock loop was filled with a blood analog composed of glycerin, xanthan gum, water, and NaI to match the viscoelastic nature of 40% hematocrit blood and the index of refraction of the acrylic model. The fluid was seeded with 10 μm glass particles for PIV measurement.

PIV has been used extensively in previous Penn State fluid mechanic investigations of the 50 cc device [6,9,12,13,15,16]. For this study, an Nd:YAG laser, part of a Gemini PIV 15 system (New Wave Research, Inc., Fremont, CA) directed two 532 nm polarized lasers, capable of delivering 120 mJ laser pulsations with a 5–10 ns pulse width, to an attenuator to regulate energy exiting the laser shutter. Upon emission from the laser head, the 6 mm circular laser beam was directed to cylindrical and spherical lenses to condition the light into a 250 μm thick light sheet. The acrylic 50 cc model was positioned within the light sheet waist for optimal PIV imaging. The light sheet position, relative to the model, was controlled by mounting the optics on a linear stage (Newport Corporation, Irvine, CA) to adjust its location to within 10 μm.

A two megapixel CCD camera (Model 630057 PowerView Plus, TSI, Inc., Shoreview, MN) with a 50 mm F1.8 lens (Nikon Corporation, Tokyo, Japan) was mounted on three traverses for positioning. The lens edge was aligned parallel to the light sheet. Laser pulsing and image capture were coordinated through a LaserPulse Synchronizer (TSI, Inc., Shoreview, MN). The synchronizer was triggered during specific phases of the cardiac cycle by setting a delay from a threshold level on the rising portion of the inflow waveform. The synchronization of camera exposure and laser emission for a set of images was controlled through Insight^TM 3 G software (TSI, Inc., Shoreview, MN).

After all images were collected, an Insight^TM 3 G processing algorithm separated each image pair into smaller interrogation regions (IR) of 32 pixels × 32 pixels. The displacement of the tracer particles, within each window, was analyzed with a cross correlation method to observe changes in particle patterns from one image to the next. Using a fast Fourier transform correlation engine, Gaussian peak detection algorithm, and a recursive Nyquist grid, displacement vectors were determined and subsequently divided by the laser pulse separation to obtain fluid velocities within each IR. Not all IRs, however, produced valid correlations. The pulsatile and three dimensional flow of the device, along with boundary layer velocity gradients, low particle displacements, and minimal particle counts made high magnification PIV challenging along thrombus prone regions of the device wall. PIV techniques were employed to realize accurate velocity measurements with laser pulse separation time strictly controlled between 25 and 1000 μs to optimize particle displacements. In instances where IRs contained invalid correlations, a vector conditioner was applied to replace invalid vectors with the median value of neighboring IR velocities. Flow fluctuations caused by beat-to-beat variability were minimized by averaging valid velocities in each IR for a minimum of 50 image pairs. The resulting velocities for each image pair were applied to the fluid centroid of the IRs and were then factored into a first-order wall shear rate algorithm, previously described by Hochareon et al. [19]. The accuracy of the wall shear rate calculation is dependent upon the error of both the measured IR velocity and its orthogonal distance to the device wall. The error associated with these parameters was investigated by low (35 μm/pixel) and high (12 μm/pixel) magnification PIV data collection within the 50 cc V-2 model at a heart rate of 86 bpm and 37% systolic duration. Flow studies for this investigation were conducted at a cross body plane 5 mm from the front wall of the device [Fig. 2(a)] in regions shown in Fig. 2(b). The 5 mm plane was selected for analysis as prior 50 cc device studies by Hochareon et al. [9] showed that areas of low wall shear rates were present at the base of the pump. These pump regions correlated well to in vivo clot deposition [12].

Fig. 2.

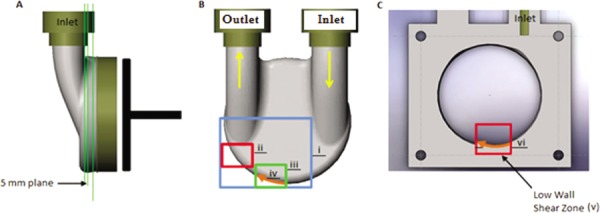
(a) 5 mm measurement plane for PIV studies. (b) Schematic of pump body displaying areas of PIV data collection. The (i) blue box indicates the low PIV magnification and the (ii) red and (iii) green boxes the high PIV magnification areas of study. Wall shear rates are calculated along a 16 mm portion of the wall in the direction of the (iv) orange line. (c) 5 mm plane sectional cut exposing the (v) low wall shear zone with (vi) 16 mm orange line representing the region for the 10 and 50 ms wall shear rate comparison.

In establishing confidence in our high magnification PIV measurement, the amount of data required to characterize flow within the device increased substantially. Efforts to optimize the amount of data collection were desirable, and the unsteadiness of V-2 raised questions about the appropriate frequency of data collection. For this reason, further data was collected at every 10 ms in the cycle at a heart rate of 86 bpm and 37% systolic duration for 200 image pairs. Shear rate comparisons for 10 and 50 ms intervals were made along the base of the 5 mm plane, as shown in Fig. 2(c), where thrombosis was probable. Spatial and temporal wall shear rate analyses were considered to resolve issues with the necessary time intervals for PIV data collection.

Finally, an extensive shear rate study was conducted at 12 μm/ pixel to resolve flow features along the lower device wall. Heart rates of 75, 115, and 150 bpm and corresponding systolic durations of 38%, 45%, and 50% were considered in this analysis. In order to directly compare wall shear rate measurements at the same instant in the cardiac cycle for multiple heart rates, the data collection frequency was scaled on both diastolic and systolic cycle times. For all heart rates, 200 image pairs were collected approximately every 7% of diastole and every 7% of systole. Comparisons between this in vitro data and in vivo experiments will be used to strengthen the prediction of thrombus formation in the 50 cc device.

3. Results and Discussion

In order to investigate the accuracy of the wall shear rate calculation under low and high PIV magnifications, near wall velocity vector measurements and their orthogonal distance to the device wall were considered within low shear regions of the 50 cc V2 model [Fig. 2(b)]. PIV velocity maps within these regions, illustrating average flow at a given time step in the cardiac cycle, were collected every 50 ms for 350 ms of the cardiac cycle when the inlet jet was dominant. A sample flow map, 300 ms from the onset of diastole, is shown in Fig. 3. Flow magnitude is indicated by a contour map with arrows corresponding to the direction of flow. The consistency of data at both magnifications is shown through highly similar flow characteristics and velocities for sections i, ii, and iii of Fig. 2(b).

Fig. 3.

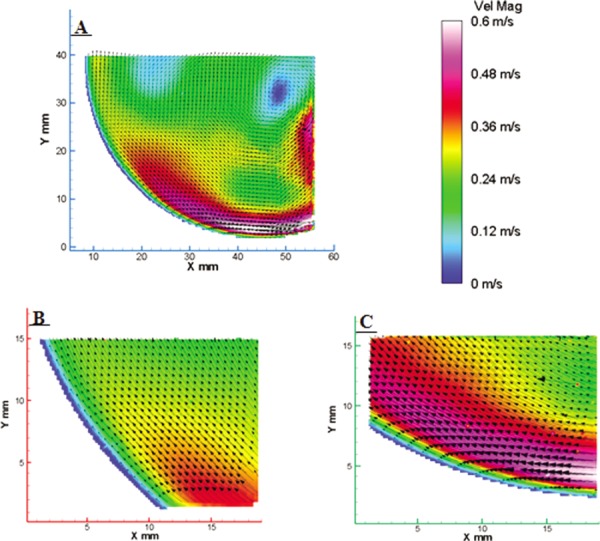
Flow maps corresponding to the locations defined in Fig. 2(b). The low PIV magnification results are represented by the (a) blue box, and the high PIV magnification results by the (b) red and (c) green boxes. Flow similarities at the two different PIV magnifications exist for flow 300 ms from the onset of diastole.

Wall shear rates were calculated along the 18 mm section iv of Fig. 2(b) and are presented as contour maps for both magnifications in Fig. 4. Wall shear rates within the 50 ms intervals were interpolated between neighboring time steps for visual clarity. Positive shear is defined by flow in the clockwise direction and is shown as the yellow to red hues on the color map. Shear values are normalized by 500 s⁻¹ such that values between −1 and 1 are of concern because they have potential for thrombus formation. The x-axis indicates the position along the wall for a defined region, and the y-axis displays the cardiac cycle time.

Fig. 4.

Contour plots displaying wall shear rate calculations along the (iv) orange line of Fig. 2(b) for the (a) low and (b) high PIV magnifications. Positive shear is a result of flow in the clockwise direction, with negative shear caused by flow in the counterclockwise direction. The shear rate was normalized over 500 s⁻¹ to observe areas between −1 and 1 that are prone to thrombus deposition.

The shear rate distributions at both magnifications appear similar in both magnitude and direction. These shear rates, however, were calculated from IR velocity vectors and their corresponding orthogonal distance to the device wall. Both of these measurements were dependent on PIV magnification and IR size. In order to consider only the effect of PIV magnification on the wall shear rate calculation, an IR spatial resolution of 32 pixels × 32 pixels was maintained for both magnifications.

At the low magnification, velocities used in the shear rate calculation were generally larger than those at the high magnification. This was a result of the IRs extending further into the fluid volume at 35 μm/pixel magnification resulting in fluid flow that was less influenced by the no slip boundary condition at the wall. Similarly, projected distances of these vectors to the device wall were larger at the low magnification due to velocity vectors being located further from the wall. Shear rate calculations for 200, 350, and 500 ms time steps, relative to wall distance, are shown in Fig. 5 for both magnifications. These points in the cycle were chosen as they display low, mid, and high regions of shear.

Fig. 5.

Shear rate calculations for 200, 350, and 500 ms of the cardiac cycle from Fig. 4 Dashed and solid lines represent results for the low and high PIV magnifications, respectively

The shear rates are similar in magnitude for all three time steps with deviations seen only at the peak shear rates occurring at 350 ms. While it may seem that the added collection time required by high magnification PIV has little benefit, the accuracy of the calculation must be considered. Raffel et al. have shown that for data that is not pixel locked, minimum velocities with PIV can be resolved to approximately 0.2 times the spatial resolution divided by the pulse separation [20]. Pixel locking was examined by plotting histograms of sub-pixel particle displacements. There were no indications of pixel locking in the regions considered. The minimum pulse separations at low and high magnifications were 300 μs and 150 μs, respectively. This leads to velocity resolutions of 0.023 m/s at low, and 0.016 m/s at high magnifications.

Average velocities for all three examined time steps were greater than this, implying accurate velocity measurement.

In order to directly compare the accuracy of the wall shear rate calculation at both magnifications, velocity vectors located 325 μm (within 2 IRs) radially outward from the device wall were considered. At this distance, a velocity value of 0.163 m/s produces a shear rate of approximately 500 s⁻¹. The error associated with this velocity measurement is plus or minus the velocity resolution defined above. Previous studies, examining wall location definition, have shown the ability to locate the wall to within a half a pixel and a thorough error analysis was carried out as was detailed in Ref. [21]. From this, the error in the projected vector-to-wall distance is ± 17.5 μm at the low magnification, and ± 6 μm at the high magnification. Considering both velocity measurement and vector orthogonal distance, the error in the wall shear rate calculation is approximately 100 s⁻¹ at the low magnification, and 60 s⁻¹ at the high magnification. Thus, increasing the magnification by about a factor of 3 leads to a 40% reduction in the shear rate error. This improved confidence at higher magnifications was used as a basis for the remaining shear rate studies.

While increases in magnification led to improved shear rate accuracy, additional data collection was required as smaller sections of the 50 cc wall were analyzed. Furthermore, efforts to resolve shear rates closer to the wall exposed large ranges of velocity gradients within the boundary layer. Rapidly changing flow in these regions caused by pump pulsatility led to questions about the necessary frequency of data collection. To test this, images were acquired at 10 and 50 ms intervals in areas of low flow at the bottom wall of the 5 mm body plane (v), as shown in Fig. 2(c).

Data was collected from 50–600 ms of the cardiac cycle for this region. The orange arrow (vi), representing a 16 mm section of the wall, was sequenced in the clockwise direction resulting in negative shear rates being calculated. Shear rate plots at 10 and 50 ms data collection times for this phase are displayed in Fig. 6.

Fig. 6.

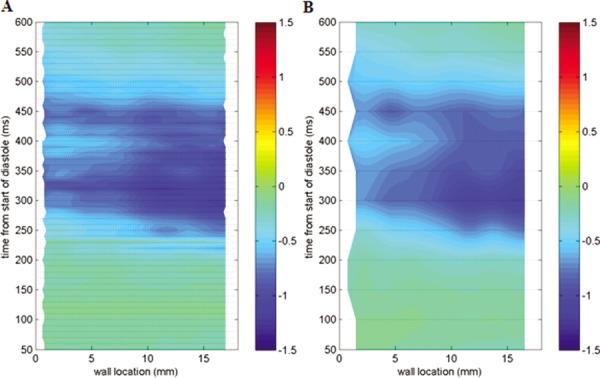
Contour plots displaying wall shear rate calculations along the orange line in Fig. 2(c) at the high PIV magnification. Data was collected every 10 ms in Fig. 6(a), and every 50 ms in Fig. 6(b).

The contour map, as a whole, displays shear rates with similar magnitude and direction for both 10 and 50 ms incremented data. A substantial portion of this region displays shear rates along the bottom wall that are less than 500 s⁻¹. These results are consistent with those observed by Hochareon et al. at neighboring planes in the 50 cc V-0 device [12]. Raw shear values were plotted along the wall in 10 ms increments for 50 ms periods of relative low and high negative shear. The low shear region is shown in Fig. 7(a) for 500–550 ms of the cardiac cycle and the high shear region in Fig. 7(b) for 300–350 ms. These areas were explored to observe differences in spatial shear rate changes for both low and high shear zones.

Fig. 7.

Spatial plots of wall shear rates along the (vi) orange line of Fig. 2(c), corresponding to regions of relative (a) low flow, 500–550 ms, and (b) high flow, 300–350 ms, into the cardiac cycle. Wall shear rates are shown every 10 ms for both time periods.

The shear rates increase in a stepwise manner from 500–550 ms of the cycle for 10 ms increments, although cross over is present at multiple locations for several time bands. The 520 ms interval intersects 3 of the 5 neighboring line plots. Flow maps at this interval show no evidence of rapid changes in velocity magnitude and direction, nor do vector counts show the low valid counts in these regions that could lead to fluctuations in orthogonal vector to wall distances. Lines with such oscillations are suggestive of beat-to-beat variability. The overall shear rate for this portion of the cycle is well under 500 s⁻¹, suggesting that this section of the wall is susceptible to thrombosis.

Shear rate plots at the time steps displaying greater shear rates were more sensitive to data collection intervals. Several cross over points exist between adjacent time bands. The 320 ms plot lies completely below that of all other bands for about 12 mm of the wall. The 300 and 350 ms intervals are closer in magnitude than all neighboring time steps at a distance of about 4.5 mm. Perhaps more importantly, locations further along the wall (∼7.5–9.5 mm) reach 500 s⁻¹ thresholds that would likely be missed by data interpolation over 50 ms. These regions lie on the edge of shear rate values that may be sufficient for thrombus washing. Spatial plots within this portion of the cardiac cycle suggest that 50 ms time increments are not sufficient for data collection in higher shear regions. Temporal plots at 3, 6, 9, 12, and 15 mm locations along the wall further examine shear rate variability.

Figure 8(a) examines temporal shear rates in 10 ms increments, while Fig. 8(b) does the same for 50 ms increments. These plots once again show similarities in shear rate patterns as a whole, although fluctuations in wall shear magnitude exist in 10 ms periods. Fifty millisecond contour plots tend to smooth out these resolvable gradients, missing time steps where flow may have an impact on thrombosis. For example, the 320 ms cycle time of Fig. 8(a) gives three locations along the wall where shear rates exceed 500 s⁻¹. Figure 8(b) only shows two locations reaching this level.

Fig. 8.

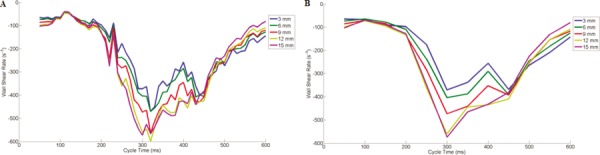
Temporal plots of wall shear rates along the (vi) orange line of Fig. 2(c), corresponding to PIV data collection in (a) 10 ms intervals and (b) 50 ms intervals

While only two spatial and temporal plots are shown here, data were examined for the remaining portions of the cardiac cycle. The results show significant variations in wall shear rates, irrespective of cycle time, between the 10 and 50 ms data collection times, with periods of over- and under-prediction being frequent in the low wall shear zone of Fig. 2(c). From these results, we recommend that data be collected in 10 ms intervals so as not to miss important shear information. It is useful to note, however, that the 10 ms data collection interval concentrated only on a heart rate of 86 bpm with a systolic duration of 37%. Under these conditions, a 10 ms interval corresponds to data collection every 2.3% and 3.9% of diastole and systole, respectively, while a 50 ms interval results in image capture every 11.4% of diastole and 19.4% of systole. In vivo animal studies, however, have shown varying physiological heart rates of 75, 115, and 150 bpm with systolic durations of 38%, 45%, and 50%, respectively, requiring the data collection interval to be considered as a percentage of both diastole and systole for direct wall shear rate comparison. For PIV studies at these conditions, images were acquired in 7% increments for both diastole and systole. This percentage was chosen as a compromise between data collection time and temporal and spatial shear rate resolution.

The relationship between heart rate and systolic duration changes on shear rate development within the 50 cc device was investigated with high magnification PIV along the lower half of the device wall. An approximate 6 mm section, beginning 29.2 mm from the center of the inlet port and along the circumference of the device is considered here. This wall segment was sequenced in a counterclockwise direction primarily against the direction of flow. The results of the shear rate calculation for this region are explored in detail with the line plot shown in Fig. 9, at a location 3 mm along the 6 mm section. Peak shear rates at this position are 1436 (75 bpm), 3003 (115 bpm), and 4632 s⁻¹ (150 bpm). Heart rates of 115 and 150 bpm display shear rates largely above the 500 s⁻¹ threshold throughout most of diastole. At 75 bpm, shear rates do not reach this level until 50% into diastole and remain above it until 85% into diastole. For most of systole for all heart rates at these locations, the boundary is likely susceptible to clot deposition as sub 500 s⁻¹ shear rates exist. The consistency of data collection, for all heart rates, is demonstrated by the fact that end systole shear rates are within approximately 50 (75 bpm), 75 (115 bpm), and 180 s⁻¹ (150 bpm) of those at the onset of diastole.

Fig. 9.

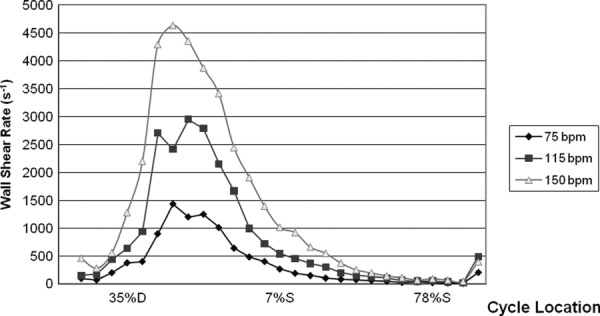
Wall shear rates, at the 5 mm plane, for 75, 115, and 150 bpm for a 6 mm section, 29.2 mm from the center of the inlet port and along the circumference of the device

The shear rates for all heart rates and systolic durations follow a similar distribution throughout the cycle. The scalability of these parameters was investigated with changes in the average inlet velocities. These velocities were calculated for all heart rates by dividing the average volumetric flow rates by the device inlet area (5.38 × 10⁻⁴ m²), resulting in average inlet velocities of 0.11, 0.16, and 0.21 m/s for 75, 115, and 150 bpm heart rates, respectively.

Shear contour plots along the 6 mm wall length show that increases in heart rate approximately scale with the kinematic viscosity divided by the square of the average inlet velocity, as shown in Fig. 10. This is effectively the same as half the friction coefficient. There is an overall similar pattern of shear rate for most of the cardiac cycle, suggesting that changes in operating conditions primarily strengthen the flow field leaving flow pattern and direction nearly unchanged. Normalized shear rates at the 3 mm location are plotted over time, along the dashed lines of Fig. 10, in Fig. 11. This plot reveals the usefulness of the scaling by showing near identical patterns of shear rate. Notable differences are present for all heart rates at the larger shear rate magnitudes. This may be due to transitional flow changes in the boundary layer. In general, regions of highest shear rates tend to deviate further from the normalization when contrasted with lower shear rates. The beginning of these differences occurs around 42% of diastole, with the largest difference at 50% of diastole. Percent differences for these locations are 25.1% and 32.3%, respectively. While the reason behind these discrepancies remains unknown, shear rates at the higher heart rates are substantially above 500 s⁻¹ for more of the cardiac cycle compared to 75 bpm. As the 50 cc pump has been shown to experience all 3 studied heart rates during animal trials, we suspect that any regions reaching 500 s⁻¹, at any point during the implant, will not show thrombosis.

Fig. 10.

Contour plots displaying wall shear rate calculations for the 6 mm section, referenced in Fig. 9, at the high magnification. Shear rate distributions for (a) 75, (b) 115, and (c) 150 bpm, respectively. All images of wall shear rates are normalized with kinematic viscosity over the square of the average inlet velocity. The contour scale applies to this normalization. Dashed lines correspond to the normalized wall shear rate plots of Fig. 11.

Fig. 11.

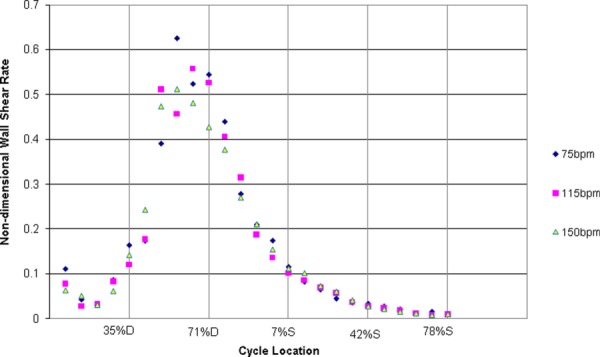
Normalized wall shear rates for 75, 115, and 150 bpm along the dashed lines of Fig. 10

4. Conclusions

Extensive effort has gone into the development of a pulsatile Penn State 50 cc LVAD for cardiac support of patients with limited chest cavity size. Thirty day animal studies were used to test the performance of the device in vivo. Results of this work, by researchers at Hershey Medical Center, showed thrombus deposition favoring regions of the lower wall, a result not seen in larger devices. An important aspect of thrombogenicity is the local fluid flow. Animal experiments are characterized by large variations in pump heart rate and systolic duration, which are not easy to model in the laboratory. To better understand this relationship, PIV was used to characterize shear rates, along the device wall, for varying heart rates and systolic durations under 12 and 35 μm/pixel magnifications. We determined that increasing the PIV magnification from 35 to 12 μm/pixel resulted in better resolution of near wall velocities and improved confidence in wall identification, both of which improve the shear rate calculation. From these experiments, the error associated with a first order shear rate approximation decreased by approximately 40% with the change in magnification.

We then explored the frequency of PIV data collection along regions of the lower device wall. Data was collected in both 10 and 50 ms intervals for a heart rate of 86 bpm and systolic duration of 37%. Ten millisecond intervals showed significant shear rate variability in near wall locations that a 50 ms collection time missed. For areas along the wall, 50 ms increments both over- and under-predicted shear rates around the 500 s⁻¹ threshold. We concluded that data collection should ideally be done in 10 ms intervals for this heart rate and systolic duration.

Finally, shear rates were calculated along the lower device wall at the 12 μm/pixel PIV magnification. Data was collected in 7% increments for all heart rates and systolic durations to permit comparisons at the same points in the cardiac cycle. Shear line plots showed substantial regions of low shear rates, under 500 s⁻¹, present for a large percentage of diastole at 75 bpm, and for several time steps for all heart rates in systole. Changes in shear rate magnitude for a 6 mm wall section were examined through normalized shear contour plots. Shear rates were shown to reasonably scale with the kinematic viscosity over the square of the average inlet velocity. This normalization was most appropriate for lower shear rates, with larger deviations in higher shear regions present for some locations within the pump. This normalization can be useful when predicting the potential for thrombus formation for varying operating conditions. It is important to note, however, that the amount of thrombus observed on explanted animal trial blood sacs is likely a function of the range of heart rates and systolic durations seen in vivo. While lower heart rates may result in pump regions exposed to shear rates less than 500 s⁻¹, minor increases will produce shear rates above this threshold at the same locations. These changes may have consequential effects on thrombosis within our pulsatile device.