Abstract
The success of total knee arthroplasty depends, in part, on the ability of the surgeon to properly manage the soft tissues surrounding the joint, but an objective definition as to what constitutes acceptable postoperative joint stability does not exist. Such a definition may not exist due to lack of suitable instrumentation, as joint stability is currently assessed by visual inspection while the surgeon manipulates the joint. Having the ability to accurately and precisely measure knee stability at the time of surgery represents a key requirement in the process of objectively defining acceptable joint stability. Therefore, we created a novel sterilizable device to allow surgeons to measure varus-valgus, internal-external, or anterior-posterior stability of the knee during a total knee arthroplasty. The device can be quickly adjusted between 0 deg and 90 deg of knee flexion. The device interfaces with a custom surgical navigation system, which records the resultant rotations or translations of the knee while the surgeon applies known loads to a patient's limb with a handle instrumented with a load cell. We validated the performance of the device by having volunteers use it to apply loads to a mechanical linkage that simulated a knee joint; we then compared the joint moments calculated by our stability device against those recorded by a load cell in the simulated knee joint. Validation of the device showed low mean errors (less than 0.21 ± 1.38 Nm and 0.98 ± 3.93 N) and low RMS errors (less than 1.5 Nm and 5 N). Preliminary studies from total knee arthroplasties performed on ten cadaveric specimens also demonstrate the utility of our new device. Eventually, the use of this device may help determine how intra-operative knee stability relates to postoperative function and could lead to an objective definition of knee stability and more efficacious surgical techniques.
Introduction
While the success of total knee arthroplasty (TKA) depends on many factors, including patient selection, prosthesis design, component alignment, the preoperative condition of the joint, and postoperative rehabilitation, adequately managing the soft tissues surrounding the knee is a key factor in achieving a successful operation [1]. Improper intra-operative management of soft tissues due to surgical inaccuracy or prosthesis selection [2] can lead to postoperative complications. Postoperative malalignment of the collateral ligaments can lead to early loosening of the prosthetic joint, and leaving the knee too tight, may cause stiffness and limited motion [3–5]. The severity and location of wear patterns on the polyethylene insert are also associated with knee stability from ligament management [6]. Instability, tightness, and wear that result from improper soft tissue management typically necessitate revision surgery [4,7] or result in reduced patient satisfaction.
Despite its importance to the success of the operation, debate exists regarding the appropriate amount of knee stability. In general, surgeons believe that the knee should not be too tight and that a little varus-valgus laxity should be achieved postoperatively, with the ideal knee believed to be looser in flexion than in extension and looser laterally (i.e., under varus stress) than medially [8]. However, no objective data quantifies “loose” or “tight” or defines how much “looseness” or “tightness” is needed for superior post-operative outcomes. While many surgeons have become skilled in developing a qualitative “feel” for knee laxity or stiffness, establishing appropriate forces in the collateral ligaments remains a challenge that is not always achieved [9], and an objective definition as to what constitutes acceptable postoperative stability does not exist. Replacing a subjective feel of laxity or stiffness with an objective definition for knee stability is an important step toward improving surgical reconstructions.
In contrast to the subjective feel used by surgeons to evaluate knee stability during total knee arthroplasty, biomechanical researchers have defined knee stability as the rotation or translation of the joint that occurs as the result of an applied moment or force, respectively. By knowing the displacement profile that results from a given applied load profile, knee stability can be categorized by two distinct parameters—laxity and stiffness [10]. Researchers who have characterized knee stability in cadavers have threaded a stud through the femur and tibia [10,11] or potted the proximal end of the femur [12] to rigidly attach the femur to ground and provide a rigid attachment for a hand-held force transducer. Clearly, potting the femur is not an option in vivo, and threading a stud to secure the femur or tibia is also not appropriate for measurements of knee stability inside of an operating room due to the unacceptable risk of weakening the bones. For in vivo investigations, researchers have used relatively large mechanisms with straps and pads to restrict the motion of the thigh [13–16], mechanisms with flat plates [17] or brackets [15] to restrict and apply loads to the foot, and other mechanisms that have used counterweights to support the thigh and eliminate gravity induced shear force at the knee [17]. However, such devices cannot be sterilized, and their size and complexity preclude their use inside of an operating room or in a simulated surgical theater.
Having the ability to characterize intra-operative laxity and stiffness represents a key requirement in the process of objectively defining acceptable joint stability and would mark a substantial improvement over the subjective measurements currently made by surgeons. Previous studies have shown that it is possible to accurately measure joint displacements using surgical navigation tools [1,18,19], but applying known forces and moments to the knee during a TKA remains a challenge to characterizing laxity and stiffness. To address that challenge, we created a novel device to allow surgeons to quantify varus-valgus, internal-external, and anterior-posterior laxity and stiffness of the knee during a total knee arthroplasty. This manuscript focuses the design and development of that device and has three objectives. First, we will describe the components of the new knee stability measurement device. Second, we will describe the theoretical development and governing equations for the device. Third, we will describe how we determined its systematic error, precision, intra-observer repeatability, and inter-observer reproducibility in applying known forces and moments to the knee.
Methods
The custom device enables calculations of knee stability, both laxity and stiffness, by recording the magnitude and direction of loads applied to the leg and the motions of the knee that result from those loads. The device interfaces with a custom surgical navigation system, which records the resultant rotations or translations of the knee while the surgeon applies known loads to a patient's limb with a handle instrumented with a load cell. The device can be adjusted between 0 deg and 90 deg of knee flexion, is fully sterilizable, and is size and weight appropriate for use in an operating room or a simulated surgical theater. The device has several main components (Fig. 1), which will be described in the following paragraphs.
Fig. 1.
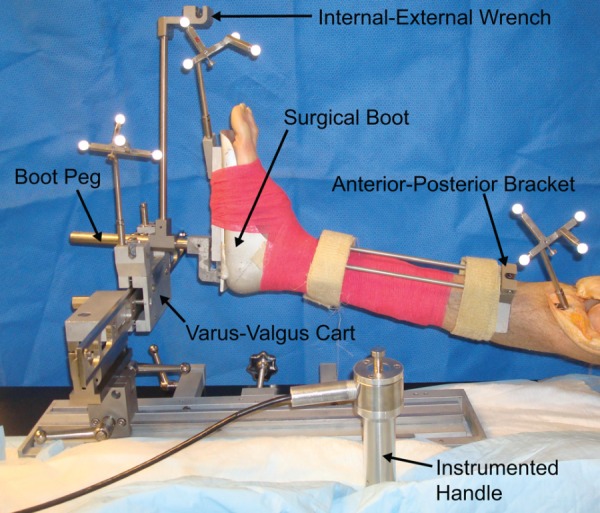
Device overview showing the surgical boot, boot peg, instrumented handle, varus-valgus cart, internal-external wrench, and anterior-posterior bracket
Device Description.
A combination of a modified surgical boot and a rotating fork maintain knee flexion angle while allowing uncoupled axial rotation of the tibia [13,14,20] when the knee is in full extension. The surgical boot maintains ankle angle and provides surfaces onto which other mechanical components can be attached. The boot used in the current design is a modified aluminum Alvarado boot (Zimmer, Warsaw, IN), which is frequently used to stabilize the limb during TKA, but includes a 1.5875 cm (5/8 in.) diameter boot peg that extends 15.25 cm perpendicular from the sole of the boot. The location of the boot peg can be adjusted within a slot along the long axis of the boot to better align it with the tibia's mechanical axis [21] in the sagittal plane so that varus-valgus and internal-external moments can be applied about their correct axes and minimize off-axis loading. This peg sits in a fork that maintains flexion angle by posteriorly supporting the distal leg, while allowing the leg and boot to translate proximally/distally and rotate freely in all other directions at a given knee flexion angle.
Forces for all three stability tests are applied using a stainless steel handle that is instrumented with a 445 N (100 lb) tension/compression load cell (Sensotec, Morristown, NJ). Such a handle is advantageous for assessing joint stability during TKA for several reasons. First and most importantly, the surgeon's hands are being used as the device actuator. In current surgical practice, surgeons manually manipulate the limb to establish their qualitative feel for knee laxity or stiffness. Even though we modify this practice with our device, the surgeon is still pushing and pulling on the limb with the handle and is always in control of the measurement process. Therefore, unlike the large mechanisms that assess knee stability in a laboratory setting (e.g., Refs. [15,20,22].), the surgeon is always in direct control of the loads that are applied to the patient and can ensure that those loads are consistent with current practice and will not cause injury due to excessive loading. Any testing can be immediately stopped if the surgeon believes that loading the joint beyond a certain point would be unsafe and potentially pose a risk of injury to the patient. Second, the load cell is a single piece of welded stainless steel, making it well-suited for repeated sterilization, and 0.3175 cm drainage holes along the handle allow sterilization fluid to easily flow in and out of the inside cavities of the handle. Third, the handle is able to protect the tension-compression load cell from unwanted, off-axis loads that could cause damage. A set of stainless steel linear bearings in the handle ensure that nonaxial loads are absorbed by the handle and not applied to the load cell. These bearings surround a stainless steel rod that is threaded into the load cell and the back of the housing of the handle. Lastly, the handle easily engages various components of the device for the varus-valgus, internal-external, and anterior-posterior stability tests. A rigid engagement is created by a cylindrical head and neck on the front end of the handle, which slides into matched slots on components of the device. An M8 ball spring plunger (McMaster-Carr, Elmhurst, IL) along these slots provides downward force on the handle's cylindrical neck when engaged and securely engages the handle in the slot.
Varus-valgus moments are applied to the leg by pushing and pulling a cart along a low friction track that is oriented medial-lateral to the leg with the instrumented handle (Fig. 2). Using this cart and track combination ensures that forces are applied in a repeatable direction by constraining the position of the instrumented handle and ensures that loads that are not being applied normal to the leg are instead dissipated to the track. The cart features radial ball bearings, which allow it to slide with negligible friction along the track. The peg that extends from the distal end of the boot engages with a fork on the cart. The fork is able to rotate freely about an axis that is perpendicular to the path of the cart, and a stack of three radial bearings on the medial and lateral sides of the fork hold the boot peg in the fork. Therefore, since the boot peg simply rests on a surface that permits proximal-distal translation, the cart fork-to-boot peg interface does not restrict the motion of the foot and allows for freedom of coupled motions (translations and rotations) while the knee is held at a given flexion angle during testing.
Fig. 2.
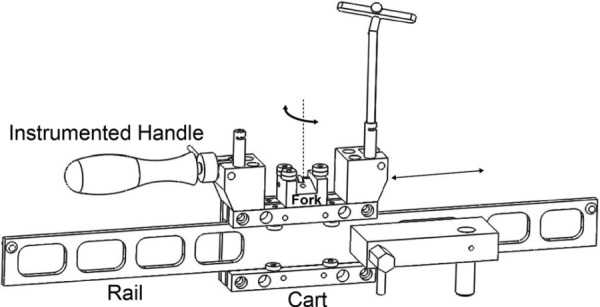
The varus-valgus low friction slide, which is shown disconnected from the support frame for clarity. The surgeon applies loads to the cart with the instrumented handle, causing it to translate on the rail. As the cart translates, the bearings on the fork interact with the peg of the boot that is resting on the fork, driving the leg into varus or valgus. Blocks at both ends of the cart have attachment points for the instrumented handle, allowing the stability test to be performed from both the medial and lateral sides of the patient. The fork is allowed to rotate with respect to the cart.
Internal-external moments are applied to the leg by attaching a 30.48 cm (12 in.) lever arm, or wrench, to the boot peg and then applying a force to the far end of this wrench with the instrumented handle (Fig. 3). The handle can connect to both the medial and lateral sides of the wrench, allowing this stability test to be performed from both sides of the patient.
Fig. 3.
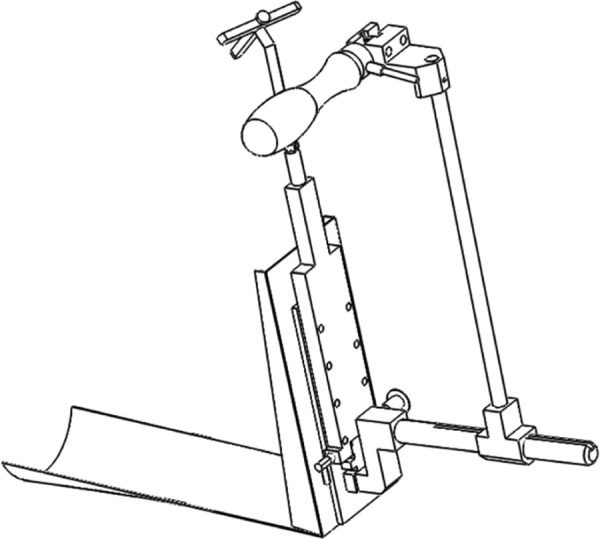
Internal-external stability test wrench with a 12.0 in. (30.48 cm) lever arm. Rotation between the wrench and the boot peg is constrained by a 4 mm (5/32 in.) wide rectangular channel running along the anterior surface of the boot peg and a rectangular key. During testing, the handle of the wrench is located directly anterior to the fork to prevent the application of unwanted varus-valgus moments during tests of internal-external stability.
Anterior-posterior forces are applied to the leg through the instrumented handle via a V-shaped bracket that is based on the design of the KT-1000 Arthrometer. The bracket attaches on the anterior side of the tibia and rests against the bone using two pads, located at the proximal and distal end of the bracket. Velcro™ strips that can be sterilized in an autoclave are attached to the proximal and distal pads with screws and are used to hold the bracket to the leg.
A frame rigidly attaches the device to an operating room table, while adjustable clamps in the frame allow for adjustment between different flexion angles without having to move the patient on the operating table. A plate on the table forms the base of the frame and can be placed on top of the sterile surgical drapings. The base of the frame is clamped in a pan and rigidly clamps to a table, thereby securely fastening the device to the table.
When the surgery and stability tests are finished, the device can be disassembled into manageable parts for cleaning, sterilization, and transport. Stainless steel was used for components close to the knee and components that needed extra strength such as the varus-valgus rail. Aluminum was used for the remaining components to minimize weight. All components are designed to be sterilized in an autoclave except the instrumented handle, which is sterilized in a disinfecting bath.
Calculations of Knee Stability.
A custom surgical navigation system [19] records the motions of femur, tibia, boot, and varus-valgus slide cart and the applied loads through the instrumented force handle and uses that data to calculate resultant kinematics and the moment or force that is applied to the patient. By knowing resultant displacements and applied loads, we can then calculate rotational knee stability in terms of degrees of rotation for a given applied moment and anterior-posterior stability in terms of millimeters of translations for a given applied force. The navigation system features a Polaris Optical Tracking System (Northern Digital, Toronto, ON, Canada) to record the position and orientation of passive optical reference frames that are attached to the femur, tibia, boot, and varus-valgus slide cart.
Similar to the way navigation systems establish anatomical coordinate systems that relate the position and orientation of the optical reference frames to the underlying bony anatomy [23], surgeons who use the stability device have to establish coordinate systems that relate the position and orientation of the optical reference frames to the geometry of the femur, tibia, boot, and varus-valgus cart. Anatomical coordinate systems for the femur and the tibia are established using a procedure described previously [19]. To briefly summarize that convention, the z-axis of the femoral anatomical coordinate system coincides with the femoral mechanical axis and defines the superior-inferior axis; the y-axis defines the anterior-posterior axis, and the x-axis defines the medial-lateral axis. The directions of the x,y,z axes are similar on the tibia, with the z-axis coinciding with the tibial mechanical axis.
To establish the boot and slide cart coordinate systems, “locator” points, or small bores, are located on these parts for accurate and repeatable placement of the stylus tip. The physical anterior-posterior position of the boot peg in the boot is positioned such that the boot peg is approximately aligned with the tibia's mechanical axis before the boot coordinate system is determined. Once the boot peg is locked into place, the boot coordinate system is established by digitizing proximal and distal points on the boot peg and an anterior point on the boot's sole (Fig. 4). The slide cart coordinate system is established by digitizing three points on the distal side of the slide cart and one point on the fork (Fig. 5). The origin is defined as a point located 1 cm anterior to the point located on the fork, which is the distance from the locator point to the center of the boot peg. This point represents the location along the fork axis-of-rotation, which is also located at the center of the boot peg's cross section. Forces applied to the boot peg from the fork's medial and lateral radial bearings intersect this point.
Fig. 4.
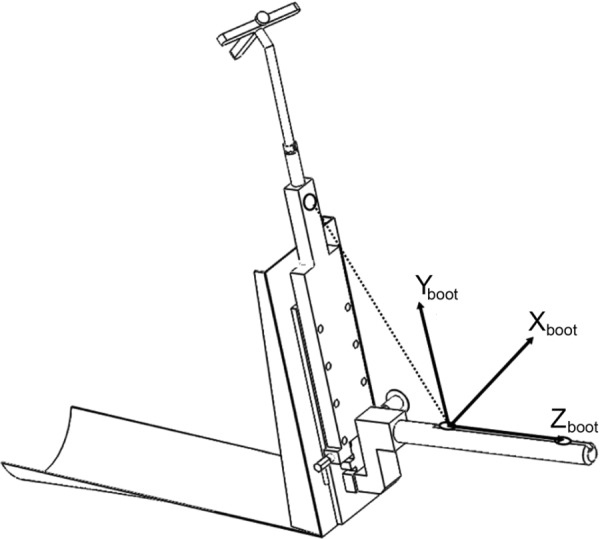
Boot coordinate system is found by identifying locator points (shown circled). The position of the peg is first adjusted so that it is collinear with the mechanical axis of the tibia. The vector connecting the two points on the boot peg forms the superior-inferior axis or the z-axis, corresponding to the tibial mechanical axis. The cross product of a vector connecting the proximal boot peg point and the anterior point with the z-axis forms the medial-lateral axis or x-axis. Finally, the cross product of the z-axis with the x-axis forms the y-axis. The origin of the boot coordinate system is unimportant for later calculations but is arbitrarily set as the proximal boot peg point.
Fig. 5.
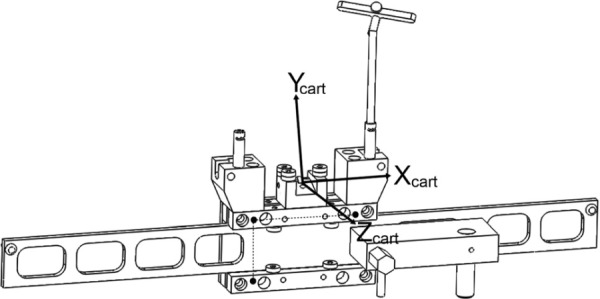
The slide cart coordinate system is found by identifying three locator points on the cart and one point on the fork (shown as solid circles and connected by the dotted lines). A vector connecting the anterior-medial and anterior-lateral points on the distal side of the slide cart form the medial-lateral or x-axis. The cross product of the x-axis with the vector connecting the anterior-medial and posterior-medial points forms the superior/inferior axis or z-axis. The cross product of the z-axis with the x-axis forms the y-axis.
Anterior-posterior stability is defined as the anterior-posterior displacement of the femur with respect to the tibia for a given force, recorded directly from the load cell. The anterior-posterior displacement of the knee is defined as the anterior-posterior position of the origin of the femoral anatomic coordinate system described within the tibial anatomic coordinate system [19]. Anterior-posterior force is assumed to be exactly the measured load cell reading. No further calculations are performed.
The internal-external rotational stability is the calculated internal-external rotation of the tibia relative to the femur when subjected to the axial moment, which is defined as the force measured by the load cell and applied to the wrench multiplied by the moment arm of the wrench (12 in., 30.48 cm). This applied internal-external moment is created about the boot peg or boot's z-axis. Since the boot's z-axis and tibia's z-axis (the mechanical axis) are rarely exactly aligned, the fraction of the moment, which is coincident with the tibia's z-axis, is calculated.
The varus-valgus moment is created by the reaction forces between the boot peg and the slide cart's fork. When a force is applied to the cart using the handle, the knee experiences a combined medial-lateral force and varus-valgus moment, and the line of action of the force applied via the handle acts through the origin of the slide cart's coordinate system. The lever arm of the varus-valgus moment is defined as the vector from the origin of the tibial anatomic coordinate system to the origin of the slide cart's coordinate system, and this calculation is facilitated by the coordinate systems that were previously defined for these segments. However, the force applied to the slide cart's medial-lateral (x-axis) will not be normal to the leg as the boot peg rotates in the fork relative to the slide cart. Given the transformation matrix of the boot's coordinate system with respect to the slide cart's coordinate system, it is possible to determine the component of the applied force that is being applied in the medial-lateral direction to the leg. This component of force, multiplied by the moment arm, creates the varus-valgus moment about the knee.
Device Validation on a Mechanical Limb.
We validated the performance of the new measurement device with a mechanical lower extremity, consisting of a rigid metal thigh and shank links connected with a hinge to represent the knee. This hinge could be manipulated into a desired flexion and varus-valgus position and then locked into place for isometric application of forces and moments. A six degree-of freedom load cell (Model 2667, R.A. Denton Inc., Rochester, NY) was built into the proximal section of the shank link, with its center located 11.7 cm distal to the knee hinge. This distance allowed for a connection between the knee hinge and the load cell. This load cell was used to determine “ground truth” for the loads applied to the mechanical limb.
We assessed the intra-observer and inter-observer repeatability of the device in a series of experiments involving six observers. Each observer made four sets of measurements five times each on our simulated lower extremity with the “knee” at 0 deg and 90 deg of flexion: varus-valgus stability with the knee at 0 deg of varus-valgus alignment, varus-valgus stability with the knee at 10 deg of varus alignment, internal-external stability, and anterior-posterior stability. One observer repeated the entire set of measurements five additional times. A large range of loads have previously been applied to the limb to assess knee stability [10,13,20,24], and the ideal loads that should be used during a TKA remains unknown. Based on those previous values reported in the literature and initial testing with cadaveric specimens as surrogates for anesthetized patients, we chose maximum loads that experienced surgeons felt they could use on a patient during TKA. Specifically, in all trials, the observers applied ± 20 Nm of varus-valgus moment, ±20Nm of axial moment, and ±100 N of anterior-posterior load at 0 deg of knee flexion and ±20 Nm of varus-valgus moment, ±15 Nm of axial moment, and ±100 N of anterior-posterior load at 90 deg of knee flexion. While such loads may not be appropriate for every TKA, the principal advantage of our device is that the surgeons can stop testing if they believe a certain load is injurious to a given patient. At all loading conditions, the position of the mechanical limb and the magnitude of the applied load in the instrumented handle were measured with the navigation system while the ground truth resultant load was recorded with the six degree-of freedom load cell in the mechanical limb. Since the ability of our navigation system to determine the position and orientation of the knee has already been established [19], the validation of the device was solely focused on the ability of our system to apply the desired moments and forces to the knee while the mechanical limb was held constant at a prescribed position and orientation.
The measurement error was considered to be the difference between the moment/force calculated by the new device and navigation system based on the load cell in the instrumented handle and the moment/force recorded by the load cell within the mechanical limb. With this convention, a positive number indicated that the value calculated by the device and navigation system was greater than the value recorded by the load cell.
The inter- and intra-observer errors were analyzed in three ways. First, we calculated the mean and standard deviation of the error during the experiments. Second, we calculated the root mean squared (RMS) error. Finally, we plotted the relationship between the moment/force calculated by the new device and navigation system on a y-axis against the ground truth moment/force recorded by the load cell within the mechanical limb (x-axis) and used the coefficient of determination (R2) and the slope and y-intercept of the best fit line of the data to assess performance. With this approach, a “perfect” device would have a y-intercept of 0 and a slope and R2 that both equal 1.
Preliminary Studies on Cadaveric Specimens.
In further preparation for our goal of making intra-operative measurements of knee stability, we have, to date, successfully used this device on ten cadaveric specimens undergoing a total knee arthroplasty in our laboratory (Fig. 6). After making an initial incision, a fellowship-trained orthopedic surgeon (Beal) attached optical reference frames to the femur, tibia, and device and established local coordinate systems on the leg [19] and device as we have described previously. The surgeon then applied the same loads to the specimens that were used to validate the device with the mechanical lower limb and used the navigation system to record resultant rotations and displacements of the leg with the knee in full extension and at 90 deg of flexion. Each set of loading conditions (e.g., from 0 applied load to 20 Nm varus to 20 Nm valgus and then back to 0 load) was repeated three times each. He then performed a PCL-retaining TKA with implants from the Zimmer Natural Knee II product line (Zimmer Inc., Warsaw, IN) and repeated the stability measurements after installing the prosthetic components. Stability data from one representative specimen with the knee in full extension are presented here.
Fig. 6.

Use of the device to collect varus-valgus (a), internal-external (b), and anterior-posterior (c) stability data on a cadaver specimen with the knee in full extension in our laboratory
Results
Results from Validation Experiments.
Our experiments suggest that the device has a low systematic error and is precise (low standard deviation of the error) (Tables 1 and 2). Mean errors for our device across all trials were –0.11 ± 0.73 Nm for varus-valgus loading, 0.21 ± 1.38 Nm for internal-external loading, and 0.98 ± 3.93 N for anterior-posterior loading. Both intra-observer and inter-observer RMS errors for varus-valgus and internal-external moments were less than 1.5 Nm, and the RMS errors for anterior-posterior forces were less than 5 N. High coefficients of determination and best-fit lines with slopes no worse than 0.0333 away from unity and y-intercept values no worse than 1 N and –0.25 Nm illustrate the ability of our device and navigation system to accurately calculate the applied moment/force (Tables 3 and 4).
Table 1.
Inter-observer errors for applying loads
| Description of Test | Mean ± Standard Deviation | RMSE ± Standard Deviation |
|---|---|---|
| Varus-valgus, 0 deg varus, 0 deg flexion | –0.26 ± 1.38 Nm | 1.27 ± 0.78 Nm |
| Varus-valgus, 0 deg varus, 90 deg flexion | –0.18 ± 0.96 Nm | 0.96 ± 0.32 Nm |
| Varus-valgus, 10 deg varus, 0 deg, flexion | –0.28 ± 1.30 Nm | 0.74 ± 0.15 Nm |
| Varus-valgus, 10 deg varus, 90 deg flexion | –0.15 ± 0.78 Nm | 0.80 ± 0.16 Nm |
| Internal-external, 0 deg flexion | –0.21 ± 1.38 Nm | 1.19 ± 0.57 Nm |
| Internal-external, 90 deg flexion | 0.06 ± 0.97 Nm | 0.95 ± 0.21 Nm |
| Anterior-posterior, 0 deg flexion | 0.98 ± 3.93 N | 4.05 ± 0.46 N |
| Anterior-posterior, 90 deg flexion | –0.09 ± 3.42 N | 3.35 ± 0.89 N |
Table 2.
Intra-observer errors for applying loads
| Description of Test | Mean ± Standard Deviation | RMSE ± Standard Deviation |
|---|---|---|
| Varus-valgus, 0 deg varus, 0 deg flexion | –0.25 ± 0.93 Nm | 0.95 ± 0.15 Nm |
| Varus-valgus, 0 deg varus, 90 deg flexion | –0.24 ± 0.71 Nm | 0.75 ± 0.12 Nm |
| Varus-valgus, 10 deg varus, 0 deg flexion | –0.11 ± 0.73 Nm | 0.74 ± 0.15 Nm |
| Varus-valgus, 10 deg varus, 90 deg flexion | –0.12 ± 0.65 Nm | 0.66 ± 0.04 Nm |
| Internal-external, 0 deg flexion | 0.04 ± 1.40 Nm | 1.35 ± 0.42 Nm |
| Internal-external, 90 deg flexion | 0.17 ± 0.88 Nm | 0.88 ± 0.07 Nm |
| Anterior-posterior, 0 deg flexion | 0.77 ± 5.43 N | 4.89 ± 2.31 N |
| Anterior-posterior, 9 deg flexion | 0.45 ± 2.43 N | 2.47 ± 0.42 N |
Table 3.
Linear best-fit approximations for inter-observer validation data
| Description of Test | Slope | Intercept | R2 |
|---|---|---|---|
| Varus-valgus, 0 deg varus, 0 deg flexion | 0.9873 | –0.2507 | 0.9984 |
| Varus-valgus, 0 deg varus, 90 deg flexion | 1.0221 | –0.1733 | 0.9659 |
| Varus-valgus, 10 deg varus, 0 deg flexion | 0.9882 | –0.2746 | 0.9971 |
| Varus-valgus, 10 deg varus, 90 deg flexion | 1.0215 | –0.1699 | 0.9932 |
| Internal-external, 0 deg flexion | 1.0695 | –0.1112 | 0.9888 |
| Internal-external, 90 deg flexion | 1.0845 | 0.0759 | 0.9919 |
| Anterior-posterior, 0 deg flexion | 1.0043 | 0.9343 | 0.9944 |
| Anterior-posterior, 90 deg flexion | 1.0142 | –0.2278 | 0.9967 |
Table 4.
Linear best-fit approximations for intra-observer validation data
| Description of Test | Slope | Intercept | R2 |
|---|---|---|---|
| Varus-valgus, 0 deg varus, 0 deg flexion | 0.9977 | –0.2493 | 0.9894 |
| Varus-valgus, 0 deg varus, 90 deg flexion | 1.0252 | –0.2344 | 0.9923 |
| Varus-valgus, 10 deg varus, 0 deg flexion | 1.0036 | –0.1099 | 0.9945 |
| Varus-valgus, 10 deg varus, 90 deg flexion | 1.0126 | –0.1332 | 0.9940 |
| Internal-external, 0 deg flexion | 1.0878 | 0.1673 | 0.9889 |
| Internal-external, 90 deg flexion | 1.0892 | 0.1646 | 0.9919 |
| Anterior-posterior, 0 deg flexion | 0.9667 | 1.0098 | 0.9903 |
| Anterior-posterior, 90 deg flexion | 1.0145 | 0.2731 | 0.9980 |
Results From Preliminary Studies on Cadaveric Specimens.
We were able to successfully record data that elucidated differences in joint stability before and after a TKA (Fig. 7). In general, our results showed that TKA increased the laxity and decreased the stiffness of the native knee in all three testing directions. The relatively small standard deviations of our data on the cadaveric specimens were similar to low standard deviations displayed with the use of the mechanical limb and demonstrated the repeatability of our device with human knees.
Fig. 7.
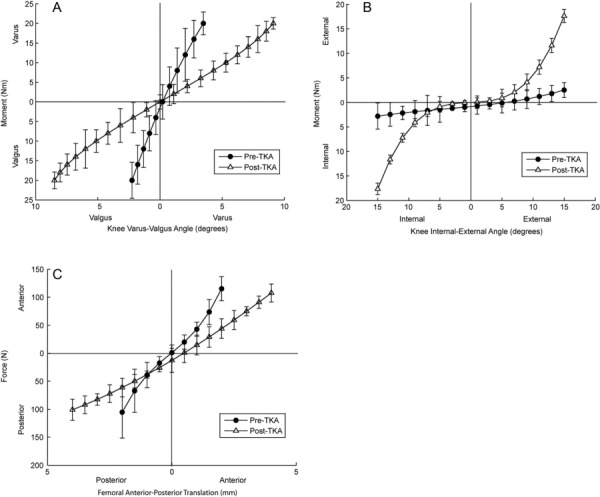
Representative varus-valgus (a), internal-external (b), and anterior-posterior (c) stability data from one representative cadaver specimen with the knee in full extension. Mean values from three cycles of testing are plotted along with ± one standard deviation. The novel device is able to collect repeatable data that is able to elucidate differences in stability before and after a total knee arthroplasty.
Discussion
We have created a novel device that leverages the capabilities of our custom navigation system to quantify knee stability during a total knee arthroplasty and demonstrated its performance with a mechanical lower extremity and cadaveric specimens. Our RMS errors for varus-valgus and internal-external rotational moments from our study with a mechanical lower extremity were both less than 1.5 Nm, and our RMS errors for anterior-posterior stability was less than 5.0 N. The small magnitude of these errors, along with the similarities between the intra-observer and inter-observer errors suggest that the device can be used by a wide variety of surgeons as a valuable tool to characterize knee stability.
The performance of our device is better than or equal to previous approaches of measuring knee stability. Previous stability devices have primarily reported errors regarding measuring the position of the limb that can be as small as 1 deg [22] and as large as 7 deg [20]. Our custom navigation system has a worst case angular accuracy of 1.25 deg in the transverse plane [25] (internal-external rotation), although we are currently working to improve the measurement accuracy in that plane. In some investigations into knee stability [11,14,24], the accuracy of the measurement equipment was not reported, and detailed evaluations of a device's error or bias when applying loads, as we have reported here, are also unknown. Therefore, we are unable to compare the performance of our approach in those cases. Clinically, the original version of the Knee Society Scoring system deducted points for greater than 5 mm or 6 deg of knee laxity [26]. Since our device can discriminate values significantly much smaller than that, we believe it has great clinical utility. We recognize that it is possible that the moments and forces experienced by a real human knee might be slightly different than the ones experiences by our mechanical linkage due to the extra degrees of freedom and laxity of the human knee. However, our validation against an objective ground truth (i.e., readings from the six degree-of-freedom load cell in the mechanical limb) gives us confidence in the results of all subsequent studies that are performed with this device.
Even though postoperative stability may be different from what can be recorded intra-operatively [8], an objective definition of joint stability that can be established with this device is needed because some early evidence suggests that it is possible to predict postoperative function from intra-operative measurements of joint stability. Wasielewski et al. [27] used a custom pressure transducer to record tibiofemoral pressure data intra-operatively as a surrogate measure of joint stability. They discovered that abnormal intra-operative compartment pressures and distributions were correlated with condylar liftoff and abnormal femoral translation while performing deep-knee bends post-operatively. Additionally, knee instability has been shown to correlate with muscle co-contractions in patients with osteoarthritis [28], but whether a similar relationship exists between joint stability seen at the time of surgery and muscle activation patterns following a TKA remains unknown. With the more accurate measurements that are afforded with our device, it is our hope to establish the relationship between intra-operative measurements of knee stability and postoperative function in future studies.
Our very positive experiences with the device on the cadaveric specimens give us additional confidence that we will eventually be able to use it inside of an operating room. The surgeon and the associated support staff all approved of the device, commenting on how the instrumented handle ensures patient safety and also how the entire device is assembled of components that are commonly used inside of the operating room at our institution (e.g., Alvarado boot, pins, navigation system, etc.). The surgeon also noted that the device was intuitive and easy to use and that the stability measurements could be made in a relatively short period of time.
Despite these positive experiences, the device is not without limitations. First, it is a somewhat large piece of equipment that is not currently used during TKAs. The size and weight of this initial prototype would need to decrease in order for it to be more widely used by community surgeons. Second, measurement errors mostly occurred when the end of the instrumented handle slipped out of a mating slot on the device or when there was movement between the boot and the leg. While greater care can be used to ensure that the handle is fully seated before applying a load, some slippage between the boot and the leg is inherent to the design of the device because we are not using a direct and rigid attachment, such as a threaded rod, to apply loads to the limb. However, our results suggest that this error is minimal. Finally, the device is designed to apply loads a fixed knee flexion angle. While these loads correspond to clinical assessments, we are unable to apply coupled loads, such as combined varus-valgus and internal-external moments or apply loads while we dynamically flex the knee. Such capabilities can be considered in future versions of the device.
In conclusion, we have met our design criteria by leveraging the measurement capabilities of our custom navigation system to create a novel and effective device for the assessment of knee stability during a total knee arthroplasty. The device has measurement errors that are equal to or better than larger systems that have measured knee stability in a laboratory setting and has been used inside a simulated surgical theater with cadaveric limbs to ensure that it meets the design requirements for an operating room. In the future, the use of this device inside of an operating room should aid in the process of establishing an objective definition for knee stability and in creating objective criteria that may standardize surgical technique for total knee arthroplasty.
Acknowledgment
This project was partially supported by Award Number R01AR056700 from the National Institute of Arthritis and Musculoskeletal and Skin Diseases. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institute of Arthritis and Musculoskeletal and Skin Diseases or the National Institutes of Health.
Contributor Information
Robert A. Siston, Department of Mechanical and Aerospace Engineering, , Department of Orthopaedics, , The Ohio State University, , Columbus, OH 43210 , e-mail: siston.1@osu.edu.
Erin E. Hutter, Department of Mechanical and Aerospace Engineering, , The Ohio State University, , Columbus, OH 43210
Matthew D. Beal, Department of Orthopaedics, , The Ohio State University, , Columbus, OH 43210
Ajit M. W. Chaudhari, Department of Mechanical and Aerospace Engineering, , Department of Orthopaedics, , The Ohio State University, , Columbus, OH 43210
References
- [1]. Siston, R. A. , Goodman, S. B. , Delp, S. L. , and Giori, N. J. , 2007, “Coronal Plane Stability Before and After Total Knee Arthroplasty,” Clin. Orthop. Relat. Res., 463, pp. 43–49. [DOI] [PubMed] [Google Scholar]
- [2]. Yercan, H. S. , Ait Si Selmi, T. , Sugun, T. S. , and Neyret, P. , 2005, “Tibiofemoral Instability in Primary Total Knee Replacement: A Review, Part 1: Basic Principles and Classification,” The Knee, 12(4), pp. 257–266. 10.1016/j.knee.2005.01.004 [DOI] [PubMed] [Google Scholar]
- [3]. Fehring, T. K. , and Valadie, A. L. , 1994, “Knee Instability after Total Knee Arthroplasty,” Clin. Orthop. Relat. Res., 299, pp. 157–162. [PubMed] [Google Scholar]
- [4]. Keeney, J. A. , Clohisy, J. C. , Curry, M. , and Maloney, W. J. , 2005, “Revision Total Knee Arthroplasty for Restricted Motion,” Clin. Orthop. Relat. Res., 440, pp. 135–140. 10.1097/01.blo.0000185312.43955.c8 [DOI] [PubMed] [Google Scholar]
- [5]. Insall, J. N. , Binazzi, R. , Soudry, M. , and Mestriner, L. A. , 1985, “Total Knee Arthroplasty,” Clin. Orthop. Relat. Res., 192, pp. 13–22. [PubMed] [Google Scholar]
- [6]. Wasielewski, R. C. , Galante, J. O. , Leighty, R. M. , Natarajan, R. N. , and Rosenberg, A. G. , 1994, “Wear Patterns on Retrieved Polyethylene Tibial Inserts and Their Relationship to Technical Considerations During Total Knee Arthroplasty,” Clin. Orthop. Relat. Res., 299, pp. 31–43. [PubMed] [Google Scholar]
- [7]. Mulhall, K. J. , Ghomrawi, H. M. , Scully, S. , Callaghan, J. J. , and Saleh, K. J. , 2006, “Current Etiologies and Modes of Failure in Total Knee Arthroplasty Revision,” Clin. Orthop. Relat. Res., 446, pp. 45–50. 10.1097/01.blo.0000214421.21712.62 [DOI] [PubMed] [Google Scholar]
- [8]. Bellemans, J. , D'hooghe, P. , Vandenneucker, H. , Van Damme, G. , and Victor, J. , 2006, “Soft Tissue Balance in Total Knee Arthroplasty: Does Stress Relaxation Occur Perioperatively?,” Clin. Orthop. Relat. Res., 452, pp. 49–52. 10.1097/01.blo.0000238790.29102.95 [DOI] [PubMed] [Google Scholar]
- [9]. Griffin, F. M. , Insall, J. N. , and Scuderi, G. R. , 2000, “Accuracy of Soft Tissue Balancing in Total Knee Arthroplasty,” J. Arthroplasty, 15(8), pp. 970–973. 10.1054/arth.2000.6503 [DOI] [PubMed] [Google Scholar]
- [10]. Markolf, K. L. , Mensch, J. S. , and Amstutz, H. C. , 1976, “Stiffness and Laxity of the Knee–the Contributions of the Supporting Structures. A Quantitative in Vitro Study,” J. Bone Jt. Surg. Am., 58(5), pp. 583–594. 10.2106/00004623-197658050-00001 [DOI] [PubMed] [Google Scholar]
- [11]. Van Damme, G. , Defoort, K. , Ducoulombier, Y. , Van Glabbeek, F. , Bellemans, J. , and Victor, J. , 2005, “What Should the Surgeon Aim for When Performing Computer-Assisted Total Knee Arthroplasty?,” J. Bone Jt. Surg. Am., 87(Suppl 2), pp. 52–58. [DOI] [PubMed] [Google Scholar]
- [12]. Fukubayashi, T. , Torzilli, P. A. , Sherman, M. F. , and Warren, R. F. , 1982, “An in Vitro Biomechanical Evaluation of Anterior-Posterior Motion of the Knee. Tibial Displacement, Rotation, and Torque,” J. Bone Jt. Surg. Am., 64(2), pp. 258–264. 10.2106/00004623-198264020-00018 [DOI] [PubMed] [Google Scholar]
- [13]. Mills, O. S. , and Hull, M. L. , 1991, “Rotational Flexibility of the Human Knee Due to Varus/Valgus and Axial Moments in Vivo,” J. Biomech., 24(8), pp. 673–690. 10.1016/0021-9290(91)90332-H [DOI] [PubMed] [Google Scholar]
- [14]. Markolf, K. L. , Graff-Radford, A. , and Amstutz, H. C. , 1978, “In Vivo Knee Stability. A Quantitative Assessment Using an Instrumented Clinical Testing Apparatus,” J Bone Jt. Surg Am., 60(5), pp. 664–674. 10.2106/00004623-197860050-00014 [DOI] [PubMed] [Google Scholar]
- [15]. Fleming, B. C. , Brattbakk, B. , Peura, G. D. , Badger, G. J. , and Beynnon, B. D. , 2002, “Measurement of Anterior-Posterior Knee Laxity: A Comparison of Three Techniques,” J. Orthop. Res., 20(3), pp. 421–426. 10.1016/S0736-0266(01)00134-6 [DOI] [PubMed] [Google Scholar]
- [16]. Van Der Esch, M. , Steultjens, M. , Ostelo, R. W. , Harlaar, J. , and Dekker, J. , 2006, “Reproducibility of Instrumented Knee Joint Laxity Measurement in Healthy Subjects,” Rheumatology, 45(5), pp. 595–599. 10.1093/rheumatology/kei243 [DOI] [PubMed] [Google Scholar]
- [17]. Shultz, S. J. , and Nguyen, A. D. , 2007, “Bilateral Asymmetries in Clinical Measures of Lower-Extremity Anatomic Characteristics,” Clin. J. Sport Med., 17(5), pp. 357–361. 10.1097/JSM.0b013e31811df950 [DOI] [PubMed] [Google Scholar]
- [18]. Cromie, M. J. , Siston, R. A. , Giori, N. J. , and Delp, S. L. , 2008, “Posterior Cruciate Ligament Removal Contributes to Abnormal Knee Motion During Posterior Stabilized Total Knee Arthroplasty,” J. Orthop. Res., 26(11), pp. 1494–1499. 10.1002/jor.20664 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19]. Siston, R. A. , Giori, N. J. , Goodman, S. B. , and Delp, S. L. , 2006, “Intraoperative Passive Kinematics of Osteoarthritic Knees before and After Total Knee Arthroplasty,” J. Orthop. Res., 24(8), pp. 1607–1614. 10.1002/jor.20163 [DOI] [PubMed] [Google Scholar]
- [20]. Shultz, S. J. , Shimokochi, Y. , Nguyen, A. D. , Schmitz, R. J. , Beynnon, B. D. , and Perrin, D. H. , 2007, “Measurement of Varus-Valgus and Internal-External Rotational Knee Laxities in Vivo–Part I: Assessment of Measurement Reliability and Bilateral Asymmetry,” J. Orthop. Res., 25(8), pp. 981–988. 10.1002/jor.20397 [DOI] [PubMed] [Google Scholar]
- [21]. Yoshioka, Y. , Siu, D. W. , Scudamore, R. A. , and Cooke, T. D. , 1989, “Tibial Anatomy and Functional Axes,” J. Orthop. Res., 7(1), pp. 132–137. 10.1002/jor.1100070118 [DOI] [PubMed] [Google Scholar]
- [22]. Mills, O. S. , and Hull, M. L. , 1991, “Apparatus to Obtain Rotational Flexibility of the Human Knee Under Moment Loads in Vivo,” J. Biomech., 24(6), pp. 351–369. 10.1016/0021-9290(91)90025-I [DOI] [PubMed] [Google Scholar]
- [23]. Siston, R. A. , Giori, N. J. , Goodman, S. B. , and Delp, S. L. , 2007, “Surgical Navigation for Total Knee Arthroplasty: A Perspective,” J. Biomech., 40(4), pp. 728–735. 10.1016/j.jbiomech.2007.01.006 [DOI] [PubMed] [Google Scholar]
- [24]. Sharma, L. , Lou, C. , Felson, D. T. , Dunlop, D. D. , Kirwan-Mellis, G. , Hayes, K. W. , Weinrach, D. , and Buchanan, T. S. , 1999, “Laxity in Healthy and Osteoarthritic Knees,” Arthritis Rheum., 42(5), pp. 861–870. [DOI] [PubMed] [Google Scholar]
- [25]. Siston, R. A. , Patel, J. J. , Goodman, S. B. , Delp, S. L. , and Giori, N. J. , 2005, “The Variability of Femoral Rotational Alignment in Total Knee Arthroplasty,” J. Bone Jt. Surg. Am., 87(10), pp. 2276–2280. [DOI] [PubMed] [Google Scholar]
- [26]. Insall, J. N. , Dorr, L. D. , Scott, R. D. , and Scott, W. N. , 1989, “Rationale of the Knee Society Clinical Rating System,” Clin. Orthop. Relat. Res., 248, pp. 13–14. [PubMed] [Google Scholar]
- [27]. Wasielewski, R. C. , Galat, D. D. , and Komistek, R. D. , 2005, “Correlation of Compartment Pressure Data From an Intraoperative Sensing Device With Postoperative Fluoroscopic Kinematic Results in TKA Patients,” J. Biomech., 38(2), pp. 333–339. 10.1016/j.jbiomech.2004.02.040 [DOI] [PubMed] [Google Scholar]
- [28]. Schmitt, L. C. , and Rudolph, K. S. , 2008, “Muscle Stabilization Strategies in People With Medial Knee Osteoarthritis: The Effect of Instability,” J. Orthop. Res., 26(9), pp. 1180–1185. 10.1002/jor.20619 [DOI] [PMC free article] [PubMed] [Google Scholar]


