Abstract
The mechanical characterization of soft anisotropic materials is a fundamental challenge because of difficulties in applying mechanical loads to soft matter and the need to combine information from multiple tests. A method to characterize the linear elastic properties of transversely isotropic soft materials is proposed, based on the combination of dynamic shear testing (DST) and asymmetric indentation. The procedure was demonstrated by characterizing a nearly incompressible transversely isotropic soft material. A soft gel with controlled anisotropy was obtained by polymerizing a mixture of fibrinogen and thrombin solutions in a high field magnet (B = 11.7 T); fibrils in the resulting gel were predominantly aligned parallel to the magnetic field. Aligned fibrin gels were subject to dynamic (20–40 Hz) shear deformation in two orthogonal directions. The shear storage modulus was 1.08 ± 0. 42 kPa (mean ± std. dev.) for shear in a plane parallel to the dominant fiber direction, and 0.58 ± 0.21 kPa for shear in the plane of isotropy. Gels were indented by a rectangular tip of a large aspect ratio, aligned either parallel or perpendicular to the normal to the plane of transverse isotropy. Aligned fibrin gels appeared stiffer when indented with the long axis of a rectangular tip perpendicular to the dominant fiber direction. Three-dimensional numerical simulations of asymmetric indentation were used to determine the relationship between direction-dependent differences in indentation stiffness and material parameters. This approach enables the estimation of a complete set of parameters for an incompressible, transversely isotropic, linear elastic material.
1. Introduction
Mechanical anisotropy is a feature of many soft tissues [1–5]. The dependence of the mechanical response on the direction of loading arises from microstructural features such as collagen fiber bundles [6–9]. The mechanical characterization of anisotropic materials is a fundamental challenge because of the requirement that the responses to multiple loadings must be combined to develop even a linear elastic material characterization (see, e.g., Ref. [10]).
Our specific interest is brain tissue, which presents additional experimental challenges because it is delicate and highly compliant (moduli lie in the 0.1–1 kPa range) [1,11,12]. Brain tissue contains both white matter (myelinated axonal fibers), which is structurally anisotropic, and gray matter, which has no apparent structural anisotropy [6,13]. Brain tissue mechanics are central to mathematical models of brain biomechanics and might be an important determinant of injury susceptibility [14]. Such models would ideally include the complete characterization of the anisotropic mechanics and structure-function relationships in brain tissue. However, techniques involving stretching, such as biaxial stretch plus indentation [15], are not feasible for brain tissue, because of the difficulty of gripping specimens. Cyanoacrylate adhesives have been used to hold samples in tension [11], however, the use of adhesives preclude testing a single sample in more than one direction. (The requirement for multiple loading scenarios to characterize anisotropic materials restricts test procedures to those that do not permanently alter the mechanics of a specimen.) Furthermore, fibrous anisotropic materials may exhibit different properties when loaded in tension and compression, because fibers stretch in tension, but may buckle in compression.
A long-term objective of this work is the identification of an appropriate form and all of the parameters for an anisotropic constitutive model of brain tissue. Proposed models include the hyperelastic white matter constitutive model of Meaney [16] or the nonlinear transversely isotropic viscoelastic model of Ning et al. [17]. In hyperelastic models of a transversely isotropic material, the strain energy is a function of the invariants (I1, I2, I3) of a finite deformation strain tensor, and also of the “pseudoinvariants” (I4, I5) that are invariant to rotation about the normal to the plane of isotropy [18]. As an example, the model of Ning et al. accounted for anisotropy due to fiber stretch (using the I4 pseudoinvariant), however, did not account for anisotropy due to other fiber-matrix interactions (captured by the I5 pseudoinvariant). As a first step towards this long-term objective, we develop and demonstrate a procedure for finding the complete set of parameters of a transversely isotropic linear elastic model for a soft gel undergoing small strain.
The proposed procedure involves the combination of dynamic shear and asymmetric indentation tests, which are promising methods for probing mechanical anisotropy in brain tissue because they require only simple fixtures to hold the sample, and they are nondestructive at small strains. We show that the combination of these two tests can be used to determine all of the parameters of an incompressible transversely isotropic linear elastic material. Shear tests, performed in the plane of isotropy and in a plane perpendicular to the plane of isotropy, uniquely identify two distinct shear moduli. Indentation with a rectangular tip, as proposed by Bischoff [19], applies different stresses to the material in directions parallel and perpendicular to the long axis of the tip. Thus, a different force-displacement curve will be obtained depending on whether the long axis is aligned with the predominant fiber direction.
Several groups have measured the mechanical properties of brain tissue either by symmetric indentation [20] or by dynamic shear testing (DST) alone [1,21]. Dynamic shear testing can characterize anisotropy in a shear modulus, if the plane in which the shear is applied is either parallel or normal to the dominant fiber direction. It is very difficult, however, to use DST to illuminate the contribution of fiber stretch to the mechanical response. Studies using symmetric indentation or unconfined compression [20,22,23] alone do not detect anisotropy. Cox et al. [24] used an inverse algorithm to extract anisotropic hyperelastic parameters using both the force-displacement curve from symmetric indentation and the principal stretches (determined by viewing the material under the tip with an optical microscope) combined with a computational model. However, the principal stretches are difficult to determine reliably, and require significant additional instrumentation. In contrast, the proposed asymmetric indentation method requires only the force-displacement curves, interpreted in the context of corresponding numerical simulations.
In this paper, we demonstrate the combined shear-indentation approach by applying it to characterize the linear elastic properties of an anisotropic fibrin gel. Fibrin gel can be made anisotropic by allowing the gel to polymerize in a high magnetic field, which leads to a network with a preferred fiber axis aligned with the magnetic field [25,26]. The mechanical properties of this network depend on fiber bending and rotation; hence, they are related to the orientation of fibrils [27].
The following sections describe the theory and methods behind the use of combined shear-indentation procedures to measure the mechanical parameters of soft transversely isotropic materials.
2. Methods
2.1. Theory: Mathematical Model and Numerical Simulation.
2.1.1. Linear Elastic, Transversely Isotropic Constitutive Material Model.
Transversely isotropic materials are symmetric about an axis perpendicular to the plane of isotropy. For a compressible, transversely isotropic, linear elastic material the strain energy function Wc can be written as a function of invariants of infinitesimal strain tensor ε and the unit vector normal to the plane of isotropy a [28]. We assume a is known, and the reference coordinate system is aligned with the e1 axis parallel to a
| (1) |
The five independent material parameters λ, α, β, μ1, and μ2 completely describe the mechanical behavior of a transversely isotropic elastic material with the strain energy function Wc.
The stress-strain relationship for the compressible material is derived from the partial derivatives of Wc in Eq. (1) with respect to the strain tensor ε
| (2) |
In this equation, the 6 × 6 matrix Ec is the elasticity or stiffness matrix. The compliance matrix can also be used to describe this transversely isotropic material. The subscript 1 refers to the direction perpendicular to the plane of isotropy (a = e1) and the subscript 2 refers to the plane of isotropy (spanned by e2 and e3).
For an incompressible material, tr (ε) is zero and the strain energy function WI can be written with only three of the terms in Eq. (1), plus −p tr(ε) as an additional term where p acts as a Lagrange multiplier [28]. The number of independent material parameters reduces from five to three: μ1, μ2, and β
| (3) |
Since a unique stiffness matrix cannot be defined for an incompressible material, we derive a compliance matrix SI by inverting the stiffness matrix for the compressible material (Eq. (2)), and then satisfy the incompressibility constraint tr(ε) = 0 by letting the parameter λ become infinitely large. For an incompressible, linearly elastic, transversely isotropic material with the strain energy function of Eq. (3), we find
| (4) |
The 6 × 6 matrix that relates strain to stress in the preceding equation is the compliance matrix SI.
For an incompressible transversely isotropic material, the two shear moduli can be uniquely determined by two shear tests: one in which shear is applied in the plane of isotropy (to find μ2), and one in which shear is applied to a perpendicular plane (to find μ1). Only one other test is required to determine β. We propose an asymmetric indentation test to extract β using a model based method to analyze the force-displacement data.
2.1.2. 3-D Finite Element Model of Asymmetric Indentation.
The simulation of the response of a transversely isotropic material to asymmetric indentation provides the necessary relationships between experimental data (stiffness measurements) and intrinsic material parameters (moduli). Yang and Cheng [29] developed a semianalytical solution of a flat indenter indenting an isotropic, elastic half-plane, which establishes a linear relationship between the indentation stiffness and elastic modulus. The idealizations of the indenter shape, isotropy, plane strain, and an infinite sample width precludes the use of this solution to obtain numerical estimates of transversely isotropic elastic moduli directly from the experimental indentation data.
A 3-D finite element (FE) model of an asymmetric rigid tip indenting a transversely isotropic elastic layer of material (see Fig. 1) was analyzed using commercial software (Abaqus 6.10.1, Simulia Corp.). The FE model geometry consisted of a layer of elastic material 3.0 mm in thickness and 18.0 mm in diameter (the gel), indented with a rectangular indenter with a cross-sectional area of 1.6 mm × 19.0 mm. The corners of the rectangular indenter were rounded; hence, the initial contact width was 1.0 mm and the initial contact area between the indenter and gel was 18.0 mm2. The model included geometric nonlinearity. To reduce the number of elements required, only one quarter of the gel was modeled and symmetry boundary conditions were applied to the straight edges of the quarter gel model (Fig. 1(b)). The mesh was graded in the ex and ez directions to increase the number of elements in the indented region. The element size under and near the indenter was reduced until the reaction force changed by less than 1% in successive mesh refinements. The smallest elements under the edge of the indenter were approximately 0.02 × 0.09 × 0.04 mm3. The quarter gel model contained 103,925 eight node brick elements (C3D8) and the rigid rectangular indenter was discretized into 1686 rigid elements (R3D3). Contact between the indenter and the gel was approximated as frictionless sliding. The displacement uz of all nodes on was set to zero to approximate frictionless contact between the gel and rigid substrate. All other surfaces had traction-free boundary conditions.
Fig. 1.
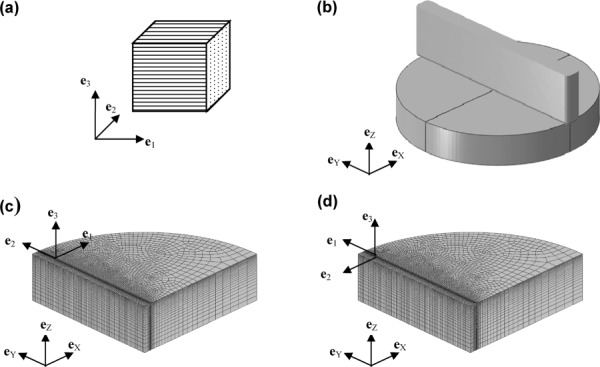
(a) An element of a transversely isotropic material. The plane of isotropy is the 2–3 plane, and the vector normal to the plane of isotropy a is aligned with the e1 unit vector. (b) A 3-D finite element (FE) model of indentation of an elastic material with a rectangular tip. Only one quarter of the circular gel is modeled. (c) The material coordinate system is aligned with the global model (eX, eY, eZ) coordinate system so that the predominant fiber direction is perpendicular to the long axis of the indenter. (d) The material coordinate system is rotated 90 deg about eZ so that predominant fiber direction is parallel to the long axis of the indenter.
The engineering constants required by the Abaqus finite element software can be written in terms of β, λ, α, μ1, and μ2. As shown in the Appendix, limiting values of the moduli and Poisson's ratios as λ/μ2 becomes very large can be written in terms of the reduced set of parameters β, μ1, and μ2. To generate the values for different combinations of the strain energy parameters, the ratios μ1/μ2 and β/μ2 were varied while the ratio λ/μ2 was fixed at 200, resulting in a bulk modulus of approximately 200μ2.
Indentation simulations were performed with the axis of trans-verse isotropy oriented perpendicular to the long axis of the indenter (e1 = eX). To model indentation with the fibers aligned with the long axis of the indenter, the local co-ordinate system of the material section was rotated by 90 deg without changing the orientation of the indenter (e1 = eY).
A quasi-static displacement boundary condition for uz was prescribed for the indenter in increments of −0.05 mm and the equations were solved with the Abaqus/Standard implicit solver. The maximum prescribed displacement of the indenter was uz = −0.3 mm, which is 10% of the simulated gel thickness.
2.1.2.1. Sensitivity of force-displacement curves to transversely isotropic material parameters.
Force-displacement curves were obtained in both material orientations from FE simulations by varying the ratio of β/μ2 or μ1/μ2 as follows: the ratio β/μ2 was set at 0, 5, 10, 15, or 20 while μ1/μ2 was set at 1, 2, 4, or 8 and μ2 was fixed at 500 Pa. This resulted in 20 combinations of β/μ2 and μ1/μ2. The ranges for the ratios μ1/μ2 and β/μ2 were chosen to span the ranges observed in the experiments. The value of μ2 was set to 500, 1000, and 2000 Pa with μ1 /μ2 = 2 and β = 0 constant to verify the linearity of the solutions with respect to μ2. The model predicted force-displacement curves for indentation depths of 0 to 0.2 mm were fitted to a straight line and the slope was used to estimate the indentation stiffness. The stiffness values obtained with the long axis of the indenter parallel to and perpendicular to the fiber direction are denoted k∥ and k⊥, respectively. We obtained the empirical correlations k∥ = f (μ2) and k⊥ = k∥ = g(μ1/μ2, β1/μ2) in terms of the transversely isotropic strain energy function parameters. From the parametric FE simulations, f and g were chosen as functions of the material parameters. The choice for the specific form of functions f and g is discussed in Sec. 3.1
| (5) |
| (6) |
The values of the unknown coefficients ao, bo, and co were obtained by linear least squares fits. The coefficient ao was fit using k∥ and the coefficients bo and co were fit using values of k⊥ = k∥ over the ranges of μ1/μ2 and β/μ2 in the parametric simulations.
2.2. Experimental Methods.
2.2.1. Magnetically Aligned Fibrin Gels.
Fibrin gel samples were fabricated in a two-step process: (a) the preparation of separate fibrinogen and thrombin solutions, and (b) mixing the two solutions and pouring the mixture into circular dishes. Aligned gels were created by immediately placing the filled dishes in a high field strength magnet during gelation.
2.2.1.1. Fibrin gel preparation.
Human plasminogen-free fibrinogen (EMD Biosciences, La Jolla, CA, Product No. 341578) was dissolved in tris-buffered saline (TBS) (33 mM Tris, 8 g/L NaCl, 0.2 g/L KCl, pH 7.4) for 4 h at 37 ° C, transferred to dialysis tubing (Thermo Scientific, Rockford, IL, Product No. 68700, 8000 MWCO) and dialyzed in 4 L TBS overnight. The fibrinogen solution was then filtered with a 5 μm and, subsequently, 0.2 μm filter, and the concentration was determined by measuring the absorbance at 280 nm with a spectrophotometer. The fibrinogen solution was diluted with TBS to a final concentration of 10 mg/mL. Thrombin (Sigma-Aldrich, St. Louis, MO, Product No. T4648) was diluted to 0.4 NIH units/mL with TBS and 50 mM Ca++. The solutions were allowed to cool in ice at 0° C before being transported to the magnet.
2.2.1.2. Magnetic alignment.
Two 35 mm diameter Petri dishes with fibrin and thrombin solutions were placed in a custom built thermal chamber filled with ice at 0° C and placed at the center of the bore of an 11.7 T MRI scanner (Varian, Inc., Palo Alto, CA). After 30 min, the temperature increase in the chamber was less than 2° C and subsequently, the temperature was gradually increased to 22° C in 15 min and left in the magnet for an additional 45 min at 22° C. The direction of the magnetic field during polymerization, denoted by the unit vector e1, was recorded and marked on each sample. Matching control samples were polymerized in an adjacent room outside the 5 G perimeter with similar temperature control.
2.2.2. Dynamic Shear Testing.
Circular samples were cut using an 11.6 mm inner diameter circular punch from the first 35 mm dish with the direction of alignment marked on each aligned fibrin gel sample. The approximate thickness and weight w of each sample were measured before testing. The samples were placed on a custom-built dynamic shear testing system (see Fig. 2), which was previously described [30]. The lower surface of the sample underwent small amplitude (∼0.03 mm) horizontal oscillations created by a voice coil driving a flexure. The horizontal displacement of the flexure ux was measured with a capacitance probe (Lion Precision) and the shear force on the stationary upper surface Fs was measured with two piezoelectric force transducers (PCB Piezotronics, Depew, NY).
Fig. 2.
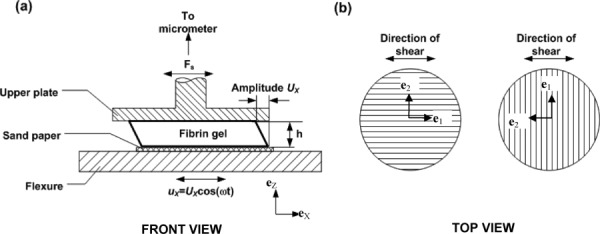
(a) Schematic diagram of the dynamic shear testing (DST). The sample is deformed in simple shear by the harmonic displacement of the base, while the force on the stationary upper surface is measured. (b) Fibrin gel orientation for the DST. The vertical and horizontal lines indicate the dominant fiber directions of the aligned gel. When the imposed displacement is parallel to the dominant fiber axis, shear is imposed in a plane normal to the plane of isotropy. When displacement is perpendicular to the dominant fiber axis, the plane of isotropy undergoes shear deformation.
Aligned fibrin gel samples were placed on the tester with the fiber direction either parallel (e1 = eX) or perpendicular (e1 = eY) to the direction of flexure oscillations (see Fig. 2(b)). Control gels were also tested in two orientations by rotating the sample 90 deg after the first test. Contact was determined by lowering the top plate using a digital micrometer until oscillatory forces were observed in both the left and right force transducers [30]. The voice coil was excited using a “chirp,” which swept through frequencies from 0 to 200 Hz in 15 s. A data acquisition and control system (Siglab 20–22, Spectral Dynamics, San Jose, CA) averaged data from three successive chirps and converted the measured displacement and shear force data to a complex transfer function. The thickness of the gel was computed based on the gap height when contact was established, and a second set of data was acquired with the gel compressed by 5% of its thickness. The gel was then rotated 90 deg about the eZ axis and another set of data was acquired in the new orientation. The sample was weighed again at the conclusion of the test to measure fluid loss during testing.
2.2.2.1. Data analysis.
The average shear stress τ is calculated from the shear force Fs divided by the area of the gel sample A. The mass of the sample m and the gap measured at contact h were used to calculate A = m/ρh. For an oscillatory shear displacement, the nominal shear strain is γ = ux/h = Ux cos(ωt)/h, where ω is the angular frequency of excitation. The relationship between the shear strain and shear stress is used to calculate the apparent complex shear modulus μ* as a function of the excitation frequency
| (7) |
where the storage (or elastic) component of the shear modulus is denoted as μ′, and the loss (or viscous) component is denoted as μ″. The magnitude of the apparent shear modulus |μ*| and phase angle δ are and δ = arctan(μ′/μ″).
The displacement of the lower plate can induce shear waves in the sample due to sample inertia if the sample thickness approaches the shear wave length λ equal to the shear wave speed c divided by the wave frequency f. For an elastic material . Based on the approximate shear modulus |μ* | of 0.5 to 1.0 kPa and gel density of ρ = 1000 kg = m3, the expected shear wave length at 40 Hz is 18 mm to 25 mm, or 6 to 8 times the sample thickness of 3 mm. Thus, the inertial effects for frequencies below 40 Hz were assumed to be small. The effect of sample inertia at higher frequencies can be accounted for by a more detailed analysis [30].
2.2.3. Asymmetric Indentation.
Each fibrin gel sample was cut with a 17.5 mm diameter punch from the second 35 mm dish, weighed and placed at the bottom of a glass Petri dish. An asymmetric rectangular stainless steel indenter tip with the dimensions of 19.1 mm × 1.6 mm was used to indent the gel. The bottom edges of the indenter were rounded with a 0.3 mm radius. The top of the indenter tip assembly was connected to a load cell (Honey-well Sensotec, Model 31, 150 g), which was connected in turn to an actuator (Model M-227.25, Mercury DC-Motor Controller, Polytech π, Auburn, MA) mounted on a stainless steel frame. The absolute movement of the actuator tip was recorded with a non-contact proximity probe (Model 10001-5MM, Metrix Instrument, TX). The thickness of the gel sample was separately measured. Voltage signals from the load cell and proximity probe were sampled at 1000 Hz using an analog-to-digital data acquisition card (Model USB-9162, National Instruments). The system actuator was controlled by custom written software (Matlab v2009, The Mathworks, Natick, MA).
The gel surface contact was measured by moving the indenter tip downwards in approximately 14 μm increments until the force change between successive increments was at least 0.2 mN. Subsequently, the gel was submerged in phosphate-buffered saline (PBS) and allowed to equilibrate for 10 min. The actuator was moved approximately 10 μm further downwards and the force was recorded. This was considered the nominal contact point of the sample surface in water and the gap between the indenter and bottom of the dish was defined as the gel thickness. The indentation protocol was a three step displacement controlled stress relaxation test (see Fig. 3(c)). Each displacement step (0.2 mm) was completed in 0.33 s. After each step, the indenter was held stationary for 240 s to allow the sample to relax. The actuator was then retracted and the gel was rotated approximately 90 deg with respect to the long axis of the asymmetric tip. The tip was then moved down to its previous contact position, and the multistep indentation test was repeated. The sample was weighed at the end of the test.
Fig. 3.
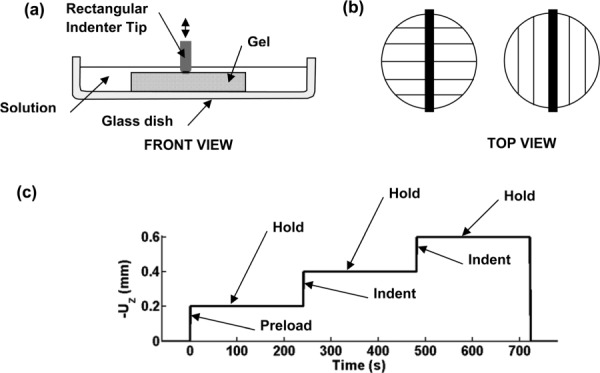
Experiment setup for asymmetric indentation of aligned fibrin gels. (a) Schematic diagram of disk-shaped gel sample (diameter: 18 mm; thickness: 3.0 mm) and an indenter with a rounded rectangular tip 19.1 mm in length and 1.0 mm to 1.6 mm in width. The gel is submerged in a PBS solution and rests on the bottom of a glass dish. (b) Top view of indentation with fibers aligned perpendicular or parallel to the long axis of the indenter. Lines indicate the direction of the magnetic alignment. (c) The indentation protocol consisting of a series of imposed displacements during which force and displacement are measured. A preload and hold (force-relaxation) step is followed by the actual indentation step which was used for data analysis. A third displacement step is performed to observe the relaxation behavior of the fibrin gel.
The analysis was performed as follows: (a) Displacement and force signals were measured relative to the first recorded values and converted to μm and mN respectively. (b) Each loading and relaxation step was identified and a linear fit to the force-displacement curve of each loading step in the indentation test was used to estimate the indentation stiffness. The indentation stiffness from the second displacement step was used for parameter estimation. In some cases the indentation force did not increase until the second displacement step, indicating a lack of contact. In these cases, the stiffness from the third displacement step was used for parameter estimation.
2.3. Estimation of Material Parameters.
The experimental stiffness values were combined with the results of the parametric finite element studies to obtain the material parameters. For each indentation test, the unknown parameters μ1, μ2, and β were determined from the experimental stiffnesses and as follows: (i) The shear modulus in the isotropy plane μ2 was calculated from and the numerically-estimated coefficient ao. (ii) The shear modulus perpendicular to the plane of isotropy μ1 was calculated by multiplying the shear moduli ratio μ1/μ2 measured by DST by μ2. (iii) The anisotropic parameter ratio β/μ2 was determined from the ratio of the measured indentation stiffnesses , the ratio of the shear moduli μ1/μ2, and the numerically-estimated coefficients bo and co in Eq. (6).
3. Results
3.1. Numerical Simulations
3.1.1. Parametric Plots—Dependence of Indentation Stiffness on Material Parameters.
Converged solutions were obtained from the parametric FE simulations for indentation up to depths of 0.25 mm for the parameter ranges studied. The force-displacement curves for the two indenter orientations are shown in Fig. 4, for an indentation depth of 0.2 mm. The curves appear nearly linear, with a small increase in slope with indentation depth, due primarily to the greater contact area between the indenter and gel. The linear stiffness values k∥ and k⊥ were estimated from the two simulations for each parameter set.
Fig. 4.
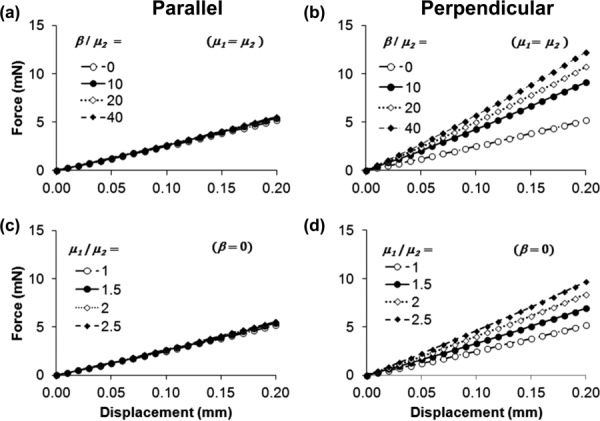
Force-displacement curves illustrating the effects of transversely isotropic material parameter ratios μ1/μ2 and β/μ2: (a) and (b) β/μ2 = 0, 10, 20, or 40; μ1 = μ2 = 0.5 kPa; (c) and (d) μ1/μ2 = 1, 1.5, 2, or 2.5, μ2 = 0.5 kPa and β = 0. The left column ((a) and (c)) shows results obtained with the dominant fiber direction parallel to the long axis of the indenter tip (see Fig. 1(c)) and the right column ((b) and (d)) shows the result obtained with the dominant fiber axis perpendicular to the long axis of the indenter tip (see Fig. 1(d)). The force-displacement curves for each set of parameters are approximately linear and the slopes of the force-displacement curves represent indentation stiffness with the dominant fiber axis parallel (k∥) and perpendicular (k⊥) to the long axis of the indenter.
In general, k∥ and k⊥ depend on the structural parameters along with the material parameters. These structural parameters include the ratio of the indentation depth to the sample thickness and the ratio of the indenter width to the sample diameter. In our parametric studies, we fixed the values of the structural parameters, therefore, the differences in indentation force and stress patterns can be attributed to differences in material parameters.
The three normal stress components are shown in Fig. 5 at an indentation depth of 0.2 mm for an isotropic material (μ = 0.5 kPa) and for a transversely anisotropic material (μ1 = 1 kPa, μ2 = 0.5 kPa, β = 5 kPa) indented with the fibers parallel to the indenter and perpendicular to the indenter. Compressive strains (not shown) under the indenter were similar for isotropic and transversely isotropic materials, with the largest magnitude occurring near the edge of the indenter (ε33 ≈ 0:15 for an indentation depth of 0.2 mm).
Fig. 5.
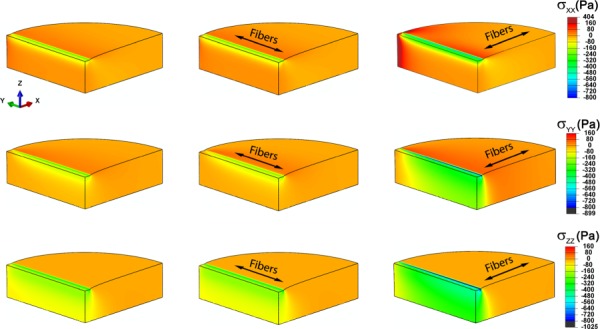
Normal stress components in the global coordinate system (eX, eY, eZ) for asymmetric indentation to a depth of 0.2 mm. (a), (d), (g) Stresses for isotropic material (μ, E, ν) = (0.5, 1.498, 0.4975). (b), (e), (h) Stresses for a transversely isotropic elastic material with parameters (μ1, μ2, β) = (0.5, 1.0, 5.0) or, equivalently (E1, E2, ν12, ν2) = (8.4975, 1.881, 0.4975, 0.881), indented with the fibers parallel to the long axis of the indenter (eY). (c), (f), (i) Stresses for the same transversely isotropic material indented with the fibers perpendicular to the long axis of the indenter. All moduli are stated in kPa; Poisson's ratios are dimensionless.
When the fibers are parallel to the indenter, shear deformation is primarily in the plane of isotropy, and fiber stretch is minimized; therefore, the stiffness and overall response of the aligned gel are similar to those of the isotropic material. When the fibers are perpendicular to the indenter, tensile stresses develop in the fiber direction and significantly more shear is imposed in planes normal to the plane of isotropy. These effects cause the deformations and stresses to be less local, and make the sample appear stiffer in this orientation.
As β/μ2 or μ1/μ2 increased, the stiffness k⊥ increased, but k∥ changed only slightly, increasing only 10% over the range of parameter ratios studied (consistent with the observations in the previous paragraph). Thus, the parallel indentation stiffness k∥ is roughly proportional to μ2 (see Eq. (5)) with the proportionality constant a = 56.2 (mN/mm)/kPa. The ratio k⊥/ k∥ is described by a linear function of the parameter ratios μ1/μ2 and (see Eq. (6)). The values of all 20 parametric pairs were used to obtain the best-fit constants bo = 0.448 and co = 0.187 (R2 = 0.99).
3.2. Experimental Measurements.
3.2.1. Dynamic Shear Testing.
The complex shear modulus μ*(ω) of the fibrin gels was calculated using Eq. (7) for samples precompressed by 5% (this prestrain satisfies small-strain conditions, but provides consistent contact and traction). For aligned gels, the storage and loss components of the shear modulus μ′, measured with fibers parallel to the excitation direction for aligned gels is denoted by and and the shear modulus components measured with fibers perpendicular to the excitation direction are denoted by and . For control gels, the shear modulus components for the first test are denoted by and and for the components for the second test by and .
The components of μ*(ω) are shown as a function of frequency f from 20 Hz to 40 Hz for a representative control and aligned gels (see Figs. 6(a) and 6(b)). The values of μ′ and μ″ averaged over the frequency range from 20 to 40 Hz were used to characterize each fibrin gel sample (see Figs. 6(c), 6(d), and Table 2). The order of the tests for aligned gels was varied as described in the following text. Differences between and and between and are statistically significant for aligned gels (p < 0.001, paired Student's t-test), however, differences between and and between and (control gels) were not. It is clear that the elastic and viscous properties of fibrin gel are direction-dependent in shear for aligned gels but not for control gels. For both types of gels, the elastic component μ′ is the dominant term in μ*(ω) and is approximately 4 to 5 times greater than the viscous component μ″.
Fig. 6.
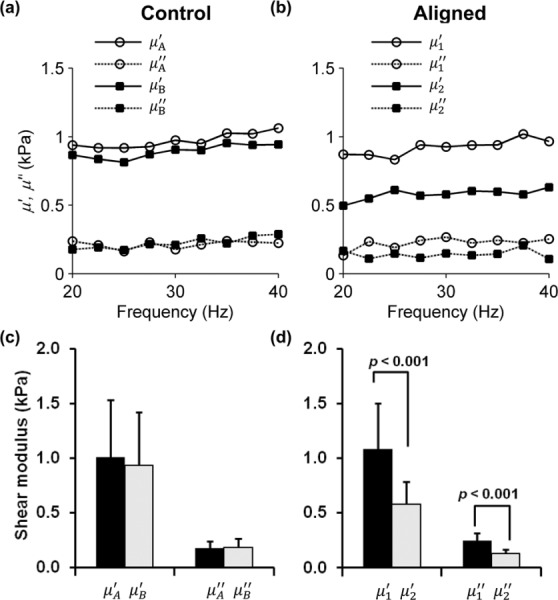
Storage (elastic) and loss (viscous) components of the complex shear modulus μ* = μʹ + iμʺ measured using the DST for (a) a representative control gel tested in one orientation (μA) and then rotated about the vertical axis by 90 deg (μB), and (b) a representative aligned gel tested with shear loading applied in a plane parallel to the dominant fiber axis (μ1), or in a plane normal to the dominant fiber axis (μ2). Data are shown over the frequency range of 20–40 Hz. Samples were tested at 0%, and 5% precompression; data is shown only for 5% precompression. Comparison of the components of the complex shear modulus of the (c) control gels (n = 5), and (d) aligned gels (n = 13) samples, estimated by the DST over the range of 20–40 Hz. Differences between the storage moduli (μ′ 1 and μ′ 2) and between the loss moduli (μ″ 1 and μ″ 2) for the aligned gels were statistically significant (p values as shown; Student's t-test), indicating material anisotropy. Error bars show one standard deviation.
To account for any effect of the testing order on the DST results, aligned gels were divided into groups where the shear plane was parallel to the fiber direction (n = 7) or perpendicular to the fiber direction (n = 6) for the first of the two tests. The ratio was calculated for each gel. There were no significant differences between the ratios computed for the gels in the two groups.
3.2.2. Asymmetric Indentation.
The force-displacement curves for representative control and aligned fibrin gels are shown in Figs. 7(a) and 7(b) for the two indenter orientations. Force-time curves during the hold period show the stress-relaxation response of the gels (see Figs. 7(c) and 7(d)). In the control gel, the indentation loading response is independent of the tip orientation, however, in the aligned gel the forces are larger when indenting with the fibers perpendicular to the indenter. The force relaxation curves for the two tests of the control gel are similar, while the force relaxation curves of the aligned gels differ initially but eventually reach similar small force values. The control gel appears to have a faster relaxation response between 0 s and 10 s, compared to the aligned gel.
Fig. 7.
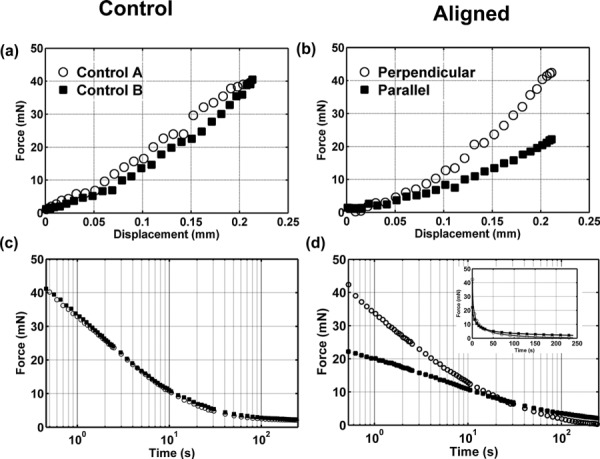
(a) and (b) Force-displacement measurements during indentation of (a) control (nonaligned) fibrin gels (open circles, first test; closed squares, second test) and (b) aligned fibrin gels (open circles, indenter perpendicular to dominant fiber direction; closed squares, indenter aligned with dominant fiber direction). The indentation loading ramp duration was 0.33 s. (c) and (d) Force relaxation for 240 s after indentation of control fibrin gels and aligned fibrin gels. Relaxation time is plotted on a logarithmic scale. Both control and aligned fibrin gels lose more than 90% of their peak indentation force after 240 s. Inset in panel (d) shows force relaxation for aligned gels on a linear time scale.
The loading portion of the force-displacement curves selected for each of the two orientations was fit with a straight line to obtain the stiffness values and . The R2 value was greater than 0.9 for all of the linear fits. The stiffness when indenting with fibers perpendicular to the indenter was greater than the perpendicular stiffness in all indentation tests of aligned gels.
The values of and were significantly different (paired Student's t-test, p = 0.013, n = 8) for the aligned gels (see Fig. 8(a)). For control gels, the mean value of the indentation stiffness measured in the second test was 7% lower than in the first test, and the decrease was significant (paired Student's t-test, p = 0.04, n = 6). The stiffness ratio was significantly greater for the aligned gels than the control gels, however, the differences in the normalized equilibrium stiffness ratio in aligned gels and control gels in the two directions were not significant (see Fig. 8(b)).
Fig. 8.
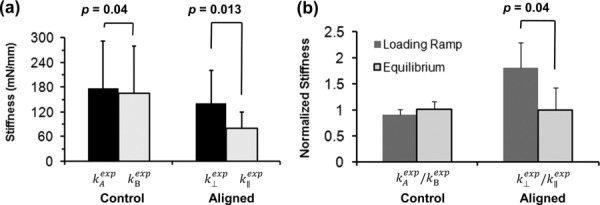
(a) The stiffness of fibrin gel samples is the slope of the indentation force-displacement loading curve (Figs. 7(a) and 7(b)). The perpendicular stiffness and the parallel stiffness were significantly different for the aligned gels (n = 8, paired Student's t-test, p = 0.013). The indentation stiffness of control gels was slightly but significantly higher for the first test than the second test (n = 6, paired Student's t-test, p = 0.04). (b) Normalized stiffness during the loading ramp and at equilibrium (after relaxation) in the aligned and control gels. The normalized stiffness during loading was significantly different from the normalized stiffness at equilibrium for the aligned gels (n = 8, paired Student's t-test, p = 0.04), but not for the control gels.
3.3. Transversely Isotropic Material Parameters of Fibrin Gels.
For control gels, the shear modulus of each gel was calculated using Eq. (5): , where ao = 56.5 (mN/mm)/kPa. For aligned gels, the shear modulus in the plane of isotropy was estimated with Eq. (5): .Since the samples for the DST and asymmetric indentation were from the same batch, the ratio of the two shear moduli measured from the DST was used when both measurements were made (5 of 8 gels). For three aligned gels, the DST measurements from the same batch were not available, and the mean value of was used. Using the shear modulus ratio and the experimentally measured indentation stiffness ratio, Eq. (6) was solved for β /μ2 (see Table 1). The corresponding elastic moduli E1 and E2 and Poisson's ratios were determined using expressions (A8)–(A12) and are shown in Table 1.
Table 1.
Summary of experimental results and associated material parameters for the DST and indentation tests
| Aligned | ||||||
|---|---|---|---|---|---|---|
| Control | Elastic (storage) component of shear modulus | |||||
| μʹ (kPa) | ||||||
| Mean Range | 1.00 ± 0.52 | 1.08 ± 0.42 | 0.58 ± 0.21 | 1.88 ± 0.33 | ||
| 0.49–1.74 | 0.54–1.87 | 0.26–0.94 | 1.45–2.46 | |||
| Indentation stiffness | ||||||
| kexp (mN/mm) | (mN/mm) | (mN/mm) | ||||
| Mean Range | 177 ± 115 | 79 ± 41 | 141 ± 81 | 1.80 ± 0.48 | ||
| 63–350 | 26–136 | 38–267 | 1.16–2.50 | |||
| Strain energy function parameters | ||||||
| μ (kPa) | μ1 (kPa) | μ2 (kPa) | μ1/ μ2 | |||
| Mean Range | 3.2 ± 2.2 | 2.7 ± 1.4 | 1.4 ± 0.7 | 1.9 ± 0.3 | 2.3 ± 2.4 | |
| 1.2–6.6 | 0.7–4.6 | 0.5–2.4 | 1.5–2.4 | 0–5.63 | ||
| Engineering constants | ||||||
| E (kPa) | E1 (kPa) | E2 (kPa) | E1/E2 | ν21 | ν2 | |
| Mean Range | 9.7 6 ± .6 | 24.1 ± 25.5 | 5.1 ± 2.6 | 4.5 ± 3.5 | 0.17 ± 0.09 | 0.82 ± 0.09 |
| 3.5–19.8 | 3.0–72.4 | 1.6–8.5 | 1.9–9.9 | 0.05–0.26 | 0.73–0.94 | |
4. Discussion
A combined shear-indentation test protocol was developed to measure the mechanical properties of transversely isotropic soft materials. The procedure was demonstrated on soft anisotropic fibrin gels polymerized at a high magnetic field strength. Dynamic shear tests in the frequency range of 20–40 Hz showed significant differences in the storage and loss components of μ*. The values of μ′ and μ″ significantly differed with the fiber orientation in the aligned fibrin gels but not in the control gels. The frequency range from 20–40 Hz was chosen to obtain average estimates of μ′ and μ″ (see Figs. 6(a) and 6(b)), since the values were relatively constant in this frequency range. The amplitude of the shear strain (<1%) is well within the small-deformation regime. For fibrin gels aligned in a strong magnetic field, the ratio of the shear storage moduli measured by the DST was 1.9 ± 0.3, which is consistent with the ratio = 3.2 ± 1.3, estimated by magnetic resonance elastography (MRE) at 400 Hz in our previous study [27]. Details of the gel preparation method and alignment protocols differ slightly between the two studies, which may explain the quantitative differences between the ratios.
A multistep indentation protocol (see Fig. 3(c)) was chosen to identify the equilibrium and instantaneous elastic response of the fibrin gel. The total indentation depth, which was ∼ 20% of the sample thickness, was chosen based on the load cell resolution. The primary focus was to characterize the elastic anisotropy, therefore, only the indentation (loading) portion of the data was analyzed in detail. The loading curves in the asymmetric indentation test (see Figs. 7(a) and 7(b)) were obtained at the fastest possible loading rate (∼ 0.5 mm/s) for this instrument, and the indentation time was much less than the relaxation time constant, therefore we assume that the loading curve was dominated by the elastic response of the fibrin network. During the hold period of 240 s, the indenter force decreased to less than 10% of the maximum forces measured during indentation. Since the equilibrium (long-term) values of the indentation force were on the order of the load cell resolution, definite conclusions cannot be drawn about the apparent lack of anisotropy in the equilibrium elastic response.
Asymmetric indentation tests have been previously proposed [19] and numerical simulations have supported their utility to extract the anisotropic properties of tissues. In the current work, we demonstrate the feasibility of this approach in an aligned fibrin gel, which is a structurally anisotropic soft material. An empirical fitting method is proposed, rather than a computationally-intensive inverse modeling approach.
A linear transversely anisotropic elastic material model is used to explain observed differences in the indentation stiffness of aligned fibrin gels. The model-predicted force-displacement curves are approximately linear for a wide range of material parameters up to an indentation depth of ∼ 6% (see Fig. 4). The five independent elastic parameters of a general (compressible) transversely isotropic elastic material cannot be uniquely obtained from the proposed tests. However, we were able to uniquely determine three independent parameters of an incompressible transversely isotropic strain energy function (see Fig. 4): two shear moduli μ1 and μ2 and an axial anisotropy parameter β. These parameters determine an equivalent set of “engineering constants:” elastic moduli and Poisson's ratios (see the Appendix).
In control gels, the average elastic shear modulus obtained by indentation is higher compared to DST. This may be attributed to the larger strains in indentation (>10%) at the end of the second indentation ramp compared to the maximum shear strains (<1%) in the DST. A similar trend was seen in the aligned gels. We also observed relatively large batch-to-batch differences in fibrin properties, which were reflected in a range of values obtained for the material parameters from the DST and indentation. Nonetheless, consistent trends in the DST and indentation data established that fibrin gels are mechanically anisotropic, with stiffer properties in the direction of primary fiber alignment.
Asymmetric indentation is a promising method for obtaining the anisotropic properties of soft tissues, however, the assumptions made in the computational model will influence the relationship between the indentation stiffness and estimated material parameters. In particular, we assumed that the contact between the indenter and gel and between the gel and the dish were both frictionless. While this assumption seems reasonable based on the high water content of the fibrin gel and the testing conditions, we also ran FE models where the coefficient of friction on the contacting surfaces was set to 1 for both isotropic and transversely isotropic materials, using the parameter values of Fig. 5. When friction is included, the indentation stiffness increased by up to 53% for a given value of μ2; accordingly, if the FE model including friction were used to interpret the experimental data, the estimated value of μ2 would decrease. For transversely isotropic gels, friction increases more than , however, this difference (7%) is relatively modest. A second model assumption is that the fibers are exactly aligned either perpendicular or parallel to the indenter during the experiment. If the fibers were misaligned by 15 deg in the transversely isotropic model, the model predicts that the measured ratio could decrease by up to 10%. Thus, the measured may underestimate the actual value, leading to an underestimation of the parameter β. Finally, we assumed that the preload of 1 mN used to identify the contact point caused a very small indentation into the gels. The magnitude of the preload force was chosen based on the resolution and noise level of the force transducer used in this study; in simulations, this force corresponded to an initial indentation of 3–40μ. This uncertainty in the initial indentation represents a source of error, which would be important in materials that exhibit strongly nonlinear behavior.
Although a linear elastic constitutive model will not fully characterize the viscoelastic or large-strain behavior of soft materials such as fibrin or brain tissue, this study shows that, in fibrin, the strain energy function should include both a term due to fiber stretch (associated with the invariant I4, and the parameter β), and a term due to shear in planes normal to the plane of isotropy (associated with the invariant I5, and the parameter μ1). While the linear material model itself may not apply to larger deformations, the strain energy function W of a more general hyperelastic material model must depend on both I4 and I5 in order to reduce to the appropriate form in the limit of small strains. Thus, the linear models and the associated experiments presented here guide the formulation of appropriate nonlinear constitutive laws.
This approach may be used to improve our understanding of the biomechanics of traumatic brain injury. Axonal injuries induced by head impact and acceleration vary by region in the brain and also by the direction of external loading [31]. Although axonal injury induced by head acceleration likely occurs at strain levels above the infinitesimal strains accessible by the current implementation of our method, accurate data on the spatially-varying, anisotropic mechanical properties of white and gray matter remain illuminating, especially when combined with the numerical analysis. Such data will be useful in understanding the susceptibility of specific tissue regions to the amplified stresses experienced during trauma.
Acknowledgment
The work was funded by NIH Grant Nos. RO1 NS055951 (P.V.B.) and K25 HL079165 (G.G.). The authors thank Fan (Peter) Zhu for help in performing the indentation experiments.
Appendix: Engineering Constants
The compliance matrix S for a transversely isotropic linear elastic solid can be written in terms of the engineering constants
| (A1) |
The seven material parameters in S, E1, E2, μ1, μ2, ν2, ν12, and ν21 are related and only five are mutually independent, since the elastic moduli E1, E2 are related to the Poisson's ratios ν12, ν21 by [32]
| (A2) |
| (A3) |
The compliance matrix S should have real and positive eigenvalues; consequently, for a positive definite matrix S the following condition should be met: E1, E2, μ1, and μ2 are non-negative and Poisson's ratios must satisfy the relationships
| (A4) |
| (A5) |
| (A6) |
| (A7) |
For an incompressible material, the trace of the strain tensor must equal zero for all loadings. For a transversely isotropic material this requires that ν12 = 1/2 and ν21 = 1 ‒ ν2, reducing the number of independent material parameters from five to three.
The strain energy function of Eq. (3) was used to derive the compliance matrix SI of Eq. (4) in terms of three independent parameters β, μ1, and μ2 for the case of λ → ∞. The engineering constants of Eq. (A1) ( E1 , E2 , μ1, μ2, v12, v21, v2) can be written as follows in terms of these three parameters for λ → ∞
| (A8) |
| (A9) |
| (A10) |
| (A11) |
| (A12) |
Contributor Information
R. J. Okamoto, Department of Mechanical Engineering , and Materials Science, , Washington University in St. Louis, , St. Louis, MO 63130
S. E. Sakiyama-Elbert, Department of Biomedical Engineering, , Washington University in St. Louis, , St. Louis, MO 63130
G. M. Genin, Department of Mechanical Engineering , and Materials Science, , Washington University in St. Louis, , St. Louis, MO 63130
P. V. Bayly, Department of Mechanical Engineering , and Materials Science, , Washington University in St. Louis, , St. Louis, MO 63130;; Department of Biomedical Engineering, , Washington University in St. Louis, , St. Louis, MO 63130 , e-mail: baylyp@seas.wustl.edu
References
- [1]. Prange, M. T. , and Margulies, S. S. , 2002, “Regional, Directional, and Age-Dependent Properties of the Brain Undergoing Large Deformation,” ASME J. Biomech. Eng., 124, p. 244. 10.1115/1.1449907 [DOI] [PubMed] [Google Scholar]
- [2]. Billiar, K. L. , and Sacks, M. S. , 2000, “Biaxial Mechanical Properties of the Natural and Glutaraldehyde Treated Aortic Valve Cusp—Part I: Experimental Results,” ASME J. Biomech. Eng., 122, pp. 23–30. 10.1115/1.429624 [DOI] [PubMed] [Google Scholar]
- [3]. Hoffmeister, B. K. , Handley, S. M. , Wickline, S. A. , and Miller, J. G. , 1996, “Ultrasonic Determination of the Anisotropy of Young's Modulus of Fixed Tendon and Fixed Myocardium,” J. Acoust. Soc. Am., 100, pp. 3933–3940. 10.1121/1.417246 [DOI] [PubMed] [Google Scholar]
- [4]. Sinkus, R. , Tanter, M. , Catheline, S. , Lorenzen, J. , Kuhl, C. , Sondermann, E. , and Fink, M. , 2005, “Imaging Anisotropic and Viscous Properties of Breast Tissue by Magnetic Resonance-Elastography,” Magn. Reson. Med., 53, pp. 372–387. 10.1002/mrm.20355 [DOI] [PubMed] [Google Scholar]
- [5]. Wang, C. , 2003, “Optical Determination of Anisotropic Material Properties of Bovine Articular Cartilage in Compression,” J. Biomech., 36, pp. 339–353. 10.1016/S0021-9290(02)00417-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6]. Basser, P. J. , and Pierpaoli, C. , 1996, “Microstructural and Physiological Features of Tissues Elucidated by Quantitative-Diffusion-Tensor MRI,” J. Magn. Reson., Ser. B, 111, pp. 209–219. 10.1006/jmrb.1996.0086 [DOI] [PubMed] [Google Scholar]
- [7]. Fung, Y. C. , 1993, Biomechanics: Mechanical Properties of Living Tissues, Springer-Verlag, New York. [Google Scholar]
- [8]. Tower, T. T. , Neidert, M. R. , and Tranquillo, R. T. , 2002, “Fiber Alignment Imaging During Mechanical Testing of Soft Tissues,” Ann. Biomed. Eng., 30, pp. 1221–1233. 10.1114/1.1527047 [DOI] [PubMed] [Google Scholar]
- [9]. Xia, Y. , and Elder, K. , 2001, “Quantification of the Graphical Details of Collagen Fibrils in Transmission Electron Micrographs,” J. Microsc., 204, pp. 3–16. 10.1046/j.1365-2818.2001.00925.x [DOI] [PubMed] [Google Scholar]
- [10]. Holzapfel, G. A. , and Ogden, R. W. , 2009, “On Planar Biaxial Tests for Anisotropic Nonlinearly Elastic Solids,” Math. Mech. Solids, 14, pp. 474–489. 10.1177/1081286507084411 [DOI] [Google Scholar]
- [11]. Miller, K. , and Chinzei, K. , 2002, “Mechanical Properties of Brain Tissue in Tension,” J. Biomech., 35, pp. 483–490. 10.1016/S0021-9290(01)00234-2 [DOI] [PubMed] [Google Scholar]
- [12]. Velardi, F. , Fraternali, F. , and Angelillo, M. , 2006, “Anisotropic Constitutive Equations and Experimental Tensile Behavior of Brain Tissue,” Biomech. Model. Mechanobiol., 5, pp. 53–61. 10.1007/s10237-005-0007-9 [DOI] [PubMed] [Google Scholar]
- [13]. Le Bihan, D. , Breton, E. , Lallemand, D. , Grenier, P. , Cabanis, E. , and LavalJeantet, M. , 1986, “MR Imaging of Intravoxel Incoherent Motions: Application to Diffusion and Perfusion in Neurologic Disorders,” Radiology, 161, pp. 401–407, Available at: http://radiology.rsna.org/content/161/2/401.long. [DOI] [PubMed] [Google Scholar]
- [14]. Zhang, L. , Yang, K. H. , and King, A. I. , 2004, “A Proposed Injury Threshold for Mild Traumatic Brain Injury,” ASME J. Biomech. Eng., 126, pp. 226–236. 10.1115/1.1691446 [DOI] [PubMed] [Google Scholar]
- [15]. Karduna, A. R. , Halperin, H. R. , and Yin, F. C. , 1997, “Experimental and Numerical Analyses of Indentation in Finite-Sized Isotropic and Anisotropic Rubber-Like Materials,” Ann. Biomed. Eng., 25, pp. 1009–1016. 10.1007/BF02684136 [DOI] [PubMed] [Google Scholar]
- [16]. Meaney, D. F. , 2003, “Relationship Between Structural Modeling and Hyperelastic Material Behavior: Application to CNS White Matter,” Biomech. Model. Mechanobiol., 1, pp. 279–293. 10.1007/s10237-002-0020-1 [DOI] [PubMed] [Google Scholar]
- [17]. Ning, X. , Zhu, Q. , Lanir, Y. , and Margulies, S. S. , 2006, “A Transversely Iso-tropic Viscoelastic Constitutive Equation for Brainstem Undergoing Finite Deformation,” ASME J. Biomech. Eng., 128, pp. 925–933. 10.1115/1.2354208 [DOI] [PubMed] [Google Scholar]
- [18]. Holzapfel, G. A. , Gasser, T. C. , and Ogden, R. W. , 2000, “A New Constitutive Framework for Arterial Wall Mechanics and a Comparative Study of Material Models,” J. Elast., 61, pp. 1–48. 10.1023/A:1010835316564 [DOI] [Google Scholar]
- [19]. Bischoff, J. E. , 2004, “Static Indentation of Anisotropic Biomaterials Using Axially Asymmetric Indenters—A Computational Study,” ASME J. Biomech. Eng., 126, pp. 498–505. 10.1115/1.1785808 [DOI] [PubMed] [Google Scholar]
- [20]. Elkin, B. S. , Azeloglu, E. U. , Costa, K. D. , and Morrison, B. , 2007, “Mechanical Heterogeneity of the Rat Hippocampus Measured by Atomic Force Microscope Indentation,” J. Neurotrauma, 24, pp. 812–822. 10.1089/neu.2006.0169 [DOI] [PubMed] [Google Scholar]
- [21]. Hrapko, M. , Van Dommelen, J. a. W. , Peters, G. W. M. , and Wismans, J. S. H. , 2008, “Characterisation of the Mechanical Behaviour of Brain Tissue in Compression and Shear,” Biorheology, 45, pp. 663–676. [PubMed] [Google Scholar]
- [22]. Cheng, S. , and Bilston, L. E. , 2007, “Unconfined Compression of White Matter,” J. Biomech., 40, pp. 117–124. 10.1016/j.jbiomech.2005.11.004 [DOI] [PubMed] [Google Scholar]
- [23]. Van Dommelen, J. A. , Van Der Sande, T. P. , Hrapko, M. , and Peters, G. W. , 2010, “Mechanical Properties of Brain Tissue by Indentation: Interregional Variation,” J. Mech. Behav. Biomed. Mater., 3, pp. 158–166. 10.1016/j.jmbbm.2009.09.001 [DOI] [PubMed] [Google Scholar]
- [24]. Cox, M. a. J. , Driessen, N. J. B. , Boerboom, R. A. , Bouten, C. V. C. , and Baaijens, F. P. T. , 2008, “Mechanical Characterization of Anisotropic Planar Biological Soft Tissues Using Finite Indentation: Experimental Feasibility,” J. Biomech., 41, pp. 422–429. 10.1016/j.jbiomech.2007.08.006 [DOI] [PubMed] [Google Scholar]
- [25]. Torbet, J. , Freyssinet, J. M. , and Hudry-Clergeon, G. , 1981, “Oriented Fibrin Gels Formed by Polymerization in Strong Magnetic Fields,” Nature (London), 289, pp. 91–93. 10.1038/289091a0 [DOI] [PubMed] [Google Scholar]
- [26]. Yamagishi, A. , Takeuchi, T. , Higashi, T. , and Date, M. , 1990, “Magnetic Field Effect on the Polymerization of Fibrin Fibers,” Physica B, 164, pp. 222–228. 10.1016/0921-4526(90)90080-E [DOI] [Google Scholar]
- [27]. Namani, R. , Wood, M. D. , Sakiyama-Elbert, S. E. , and Bayly, P. V. , 2009, “Anisotropic Mechanical Properties of Magnetically Aligned Fibrin Gels Measured by Magnetic Resonance Elastography,” J. Biomech., 42, pp. 2047–2053. 10.1016/j.jbiomech.2009.06.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28]. Spencer, A. , 1984, Continuum Theory of the Mechanics of Fibre-Reinforced Composites, Springer-Verlag, New York. [Google Scholar]
- [29]. Yang, F. Q. , and Cheng, Y. T. , 2009, “Revisit of the Two-Dimensional Indentation Deformation of an Elastic Half-Space,” J. Mater. Res., 24, pp. 1976–1982. 10.1557/jmr.2009.0257 [DOI] [Google Scholar]
- [30]. Okamoto, R. J. , Clayton, E. H. , and Bayly, P. V. , 2011, “Viscoelastic Properties of Soft Gels: Comparison of Magnetic Resonance Elastography and Dynamic Shear Testing in the Shear Wave Regime,” Phys. Med. Biol., 56, pp. 6379–6400. 10.1088/0031-9155/56/19/014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31]. Zhang, L. , Yang, K. H. , and King, A. I. , 2001, “Biomechanics of Neurotrauma,” Neurol. Res., 23, pp. 144–156. 10.1179/016164101101198488 [DOI] [PubMed] [Google Scholar]
- [32]. Bower, A. F. , 2010, Applied Mechanics of Solids, CRC, Boca Raton, FL. [Google Scholar]


