Evaluation of a Voxelized Model Based on DCE-MRI for Tracer Transport in Tumor

Abstract

Recent advances in the treatment of cancer involving therapeutic agents have shown promising results. However, treatment efficacy can be limited due to inadequate and uneven uptake in solid tumors, thereby making the prediction of drug transport important for developing effective therapeutic strategies. In this study, a patient-specific computational porous media model (voxelized model) was developed for predicting the interstitial flow field and distribution of a systemically delivered magnetic resonance (MR) visible tracer in a tumor. The benefits of a voxel approach include less labor and less computational time (approximately an order of magnitude reduction compared to the traditional computational fluid dynamics (CFD) approach developed earlier by our group). The model results were compared with that obtained from a previous approach based on unstructured meshes along with MR-measured tracer concentration data within tumors, using statistical analysis and qualitative representations. The statistical analysis indicated the similarity between the structured and unstructured models' results with a low root mean square error (RMS) and a high correlation coefficient. The voxelized model captured features of the flow field and tracer distribution such as high interstitial fluid pressure inside the tumor and the heterogeneous distribution of the tracer. Predictions of tracer distribution by the voxelized approach also resulted in low RMS error when compared with MR-measured data over a 1 h time course. The similarity in the voxelized model results with experiment and the nonvoxelized model predictions were maintained across three different tumors. Overall, the voxelized model serves as a reliable and swift alternative to approaches using unstructured meshes in predicting extracellular transport within tumors.

1. Introduction

Although significant advancements have been made in the diagnosis and treatment of cancers, targeted drug delivery to malignant tumors still remains a challenge. The transport of macromolecular therapeutic agents in tumor microvasculature plays a vital role in the treatment of solid tumors [1, 2]. However, a major obstacle to systemic transport in tumors is inadequate and uneven uptake, which is widely attributed to the heterogeneous architecture of the tumor microvasculature [3]. Tumors are known to contain highly tortuous, fenestrated, discontinuous vessels, and large avascular areas [4–8]. The resulting heterogeneous vasculature leads to irregular perfusion [9, 10], which causes heterogeneous extravasation of therapeutic agents into tumor tissue.

Another profound effect of abnormal vascular geometry, combined with a lack of lymphatics [11] in tumors, is thought to be the elevation of interstitial fluid pressure (IFP) [12, 13]. Experiments performed by several researchers have revealed an increased IFP in tumors [14–18]. It has been also observed that IFP is uniform throughout the center of the tumor and drops sharply at its periphery [15–19]. However, recent evidence also suggests a lesser uniform IFP inside the tumors [20]. A study conducted by Hassid and his colleagues showed that the IFP inside ectopic human nonsmall-cell lung cancer increased from the periphery inward, with a high plateau inside the tumors. With the absence of pressure gradients in the center of a tumor, convective transport of drugs is expected to be less than at the periphery where pressure gradients exist.

Convective interstitial fluid flow driven by the IFP gradient also affects drug delivery. Interstitial fluid velocity (IFV) within a human neuroblastoma propagated in the flank of an immune suppressed rat was experimentally found to increase from the center towards the periphery of the tumor [19]. Previous modeling studies also suggest that elevated IFP may cause vascular constriction leading to reduction in tumor blood flow [21]. In addition, the presence of a necrotic core has previously been found to have an adverse effect on the distribution of large, slow-diffusing molecules [22]. On the whole, these characteristics of the tumor micro-environment hinder the systemic delivery of therapeutic agents to tumor cells. Hence, quantification of extravasation and drug distribution is necessary for developing successful treatment strategies.

Many of the previous mathematical models of transport in tumors assume either uniformly distributed or regular patterns of parallel and series blood vessels [13, 23–25] neglecting the vascular heterogeneity. Jain and his colleagues modeled the effects of uniformly distributed leaky blood vessels and minimally functioning lymphatics for the case of a spherical solid tumor and showed how elevated IFP leads to heterogeneous extravasation [26]. Pozrikidis developed a theoretical model to describe the blood flow in which tumor microvasculature was generated by branching capillaries using deterministic and random parameters, thus resulting in a capillary tree [27]. It should be noted that tumor angiogenesis patterns in these previous blood vessel models are theoretical and simulated based on rules to generate network structures.

Recently, computational fluid dynamics (CFD) approaches have been used by our group and others to study the extracellular transport in tumors [28–30]. In particular, studies conducted by Pishko et al. [30] accounted for realistic tumor vasculature by using dynamic contrast enhanced-magnetic resonance imaging (DCEMRI) data to estimate the spatial variation of transport properties (the rate transfer constant between plasma and extracellular space K^trans and porosity ϕ), which were mapped into an unstructured mesh of a CFD model that solves for IFP, IFV, and tracer transport. The results of these studies are encouraging; however, the time-intensive labor involved in the approach motivated us to develop a simpler model for tracer transport in tumors based on a voxelized modeling methodology. In this approach, tissue properties and anatomical boundaries are assigned on a voxelby-voxel basis from MRI data. These properties are then incorporated into a porous media transport model to predict the IFP, IFV, and tracer transport, thereby allowing for quicker building of computational transport models and a rapid estimation of tracer distribution. This voxel method circumvents the laborious geometric reconstruction involved in its nonvoxelized counterpart by directly importing MRI data.

In this study, a voxelized model for the systemic transport of the tracer in a tumor was developed and used to predict the distribution of MR visible tracer (Gd-DTPA) in the hind limb of a mouse inoculated with KHT sarcoma cells. The predicted results were compared with those obtained from a nonvoxelized approach [30]. Earlier, voxel methodology has been used by our group to model interstitial transport in the rat spinal cord and brain during tissue infusion [31, 32]. However, the current problem dealing with tumors is different from the previous one related to the brain for three main reasons: 1) systemic infusion of the tracer in contrast to local infusion in the previous study; 2) heterogeneous tracer transport due to variable leakiness compared to homogeneous and anisotropic distribution in the brain model; and 3) steep pressure drops at the tumor periphery, which did not occur in the previous study. A comparative study was conducted by calculating the error between the Gd-DTPA tissue concentrations predicted using the voxelized model, the nonvoxelized model, and those measured using MRI.

2. Methods

In brief, leakiness maps for the tumors were obtained using DCE-MRI and incorporated into a mathematical model which was solved using a commercial solver for IFP, IFV, and tracer concentration in tissue. Although the methods for obtaining the leakiness maps and mathematical model are identical to that of the nonvoxel model, the novel aspect of this paper lies in the computational method, whose differences from the nonvoxel model are elucidated using the flow chart shown in Fig. 1 and in Sec. 2.3.1. The voxelized model eliminated the need for often laborious 3-D geometric reconstruction due to complex anatomical boundaries as described in the flow chart, thereby reducing the computational time.

Fig. 1.

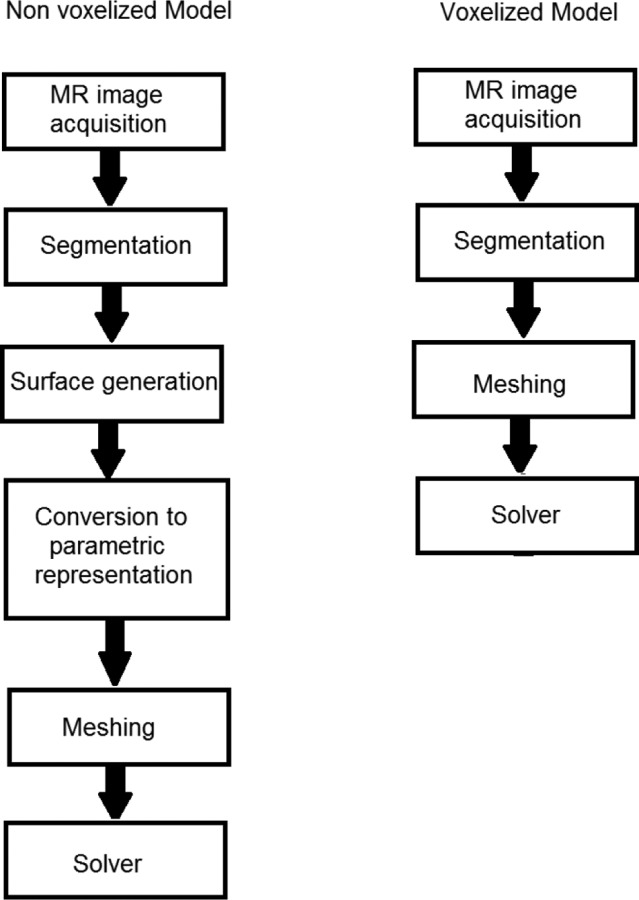
Flow chart comparing the computational methods for voxelized and nonvoxelized modeling

2.1. Estimation of Spatial Variation Maps of Vascular Leakiness.

The experimental data presented in Pishko et al. [30] was used in this study for a comparison between the models. Briefly, an MR visible tracer (Gd-DTPA) was delivered to the hind limb of three C3H female mice inoculated with murine KHT sarcoma cells, through bolus tail vein injection. The MR experiments were performed using a 11.1 T horizontal bore magnet system. Serial DCE-MR images consisting of a T₁ -weighted spin-echo sequence were acquired before and after administration of the tracer. The MRI measured Gd-DTPA concentration in the tissue was then calculated based on the MR signal enhancement due to the contrast agent using the standard spin-echo signal equation [33]. The measured tracer concentration in the tissue at early time points (≈20 min) was fitted to a two-compartment model [34] to obtain the K^trans maps and the ϕ maps. These maps were incorporated into the porous media transport model to predict tracer distribution at later time points.

2.2. Tissue Transport Model.

The mathematical model for fluid flow and transport was the same as that used in the nonvoxel approach. The tissue continuum was modeled as a porous media with spatially varying vascular source terms. Extracellular pressure and velocity fields were computed using the continuity equation and Darcy's law, respectively. Tracer concentration in tissue (C_t) was computed using the convection-diffusion equation with appropriate vascular source terms ensuring mass balance

$$\nabla \cdot \mathit{\nu }=\frac{K^{\text{trans}}}{\overline{K^{\text{trans}}}}{L}_{\mathrm{P}}\frac{S}{V}[p_{\mathrm{v}}-p-{\sigma }_{\mathrm{T}}({\pi }_{\mathrm{v}}-{\pi }_{\mathrm{i}})]-L_{\mathrm{p},\text{ly}}\frac{S_{\mathrm{L}}}{V}(p-p_{\mathrm{L}})$$ (1)

$$\mathit{v}=-K\nabla p$$ (2)

$$\frac{\partial C_{\mathrm{t}}}{\partial t}+\frac{\mathit{\nu }}{\varphi }\cdot \hspace{0.17em}\nabla C_{\mathrm{t}}-D{\nabla }^2{C}_{\mathrm{t}}=K^{\text{trans}}(C_{\mathrm{P}}-\frac{C_{\mathrm{t}}}{\varphi })-L_{\mathrm{p},\text{ly}}\frac{S_{\mathrm{L}}}{V}(p-p_{\mathrm{L}})\frac{C_{\mathrm{t}}}{\varphi }$$ (3)

where v is the IFV, $\overline{K^{\mathit{t}\mathit{r}\mathit{a}\mathit{n}\mathit{s}}}$ is the average value of K^trans over tumor and host tissue voxels, L_p is the hydraulic conductivity of the microvascular wall, S / V is the blood vessel surface area per unit volume, p_v is the vascular fluid pressure, p is the IFP, σ_T is the osmotic reflection coefficient for plasma proteins, π_v and π_i are the osmotic pressures of the plasma and interstitial fluid, respectively, L_p,ly is the lymphatic vessel permeability, S_L / V is the lymphatic vessel surface area per unit volume, which was set to zero in tumor tissue, p_L is pressure in the lymphatic vessels, which was set to zero, K is the tissue hydraulic conductivity, D is the diffusion coefficient for Gd-DTPA and C_p is the tracer concentration in the blood plasma.

Spatial variation of the vascular permeability was implemented to model heterogeneous extravasation of the plasma fluid and tracer transport. The transvascular diffusive flux term in the transport equation was spatially varied by scaling it with K^trans. Similar patterns of leakiness for the tracer and plasma were assumed. With this assumption, normalized values of K^trans, obtained by dividing it with its average value, were used to scale the fluid filtration rate per unit volume in the continuity equation; thus providing the spatial heterogeneity for the plasma fluid source and the convective tracer source in the equations. The parameters/constants used in the governing equations were the same as given in Pishko et al. [30] for comparison.

2.3. Computational Method.

A rectangular volume of size 20 × 10 × 9 mm³ enclosing the tumor was created and meshed using the meshing software (GAMBIT, Fluent, Lebanon, NH). The continuity, momentum, and tracer transport equations for both models were solved using the CFD software package, FLUENT (version 6.3, Fluent, Lebanon, NH). The computations for both voxelized and nonvoxelized models were carried out using a 64-bit Intel 8 core Xeon processor (3.00 GHz) with 4 GB RAM. The governing equations were discretized with a control-volume based technique using FLUENT. Within FLUENT, a user-defined function was used to assign K^trans and ϕ for each voxel in the mesh. For the continuity and tracer transport equations, a user-defined flux macro was used to account for the source terms. A standard pressure interpolation scheme was used to solve for the pressure and a first order upwind method was used to solve for the velocity and the transport equations. The semi-implicit method for pressure-linked equations [35] pressure-velocity coupling method was chosen and the convergence criterion was set to 1 × 10^‒5. A zero fluid pressure condition p = 0 was applied along the cut ends and the remaining outer boundaries of the geometry were assigned as the wall. Initial conditions for tracer transport assumed no initial tracer in the tissue C_t = 0 and the tracer concentration was simulated for t ≤ 1 h with the data compared at discrete time points, t = 5, 30, and 60 min. Mesh independency of the voxel solution was verified by increasing the mesh size by dividing each voxel into eight octants and assigning them with the same transport properties as that of the original voxel. The improved mesh resolution resulted in an approximately 1.4% decrease in the predicted amount of Gd-DTPA in the leg.

2.3.1. Differences.

As previously mentioned, the voxelized model departs from its nonvoxel counterpart in the computational method. The nonvoxelized model necessitated time-consuming geometric construction. The surface generation required a manual geometric smoothing process. The smoothing process was necessary for the proper parametric representation of the host and tumor tissue surfaces using nonuniform rational B-spline surfaces. The host and tumor tissue surfaces were subdivided into multiple patches (≈50–100), which then required manual material property assignment in meshing software. These necessary steps for the nonvoxel method took 8 to 10 h of time, depending on the complexity of the tumor and host tissue geometry. Additionally, the voxelized model used quadrilateral mesh elements (voxels) of a size equal to the MRI resolution (0.104 × 0.104 × 1 mm³⁾, which resulted in approximately 165,000 mesh elements (see Fig. 2(a)) for each of the three mice. In contrast, the nonvoxelized model used an unstructured grid with approximately 2.7, 2.5, and 2.3 × 10⁶ tetrahedral elements for animals I, II, and III, respectively (see Fig. 2(b)), making it computationally intensive. Accordingly, the computational time involved in solving for the flow field and tracer transport by the nonvoxelized model were approximately 1 and 13 h, respectively, while the voxelized model roughly took 20 and 22 min for the same task. It can be observed that the CPU time involved in computing the flow field by both models were comparable; this is due to the fact that the flow simulation is semiautomatic with the hydraulic conductivity gradually increased in steps towards its final value to ensure the stability of the FLUENT solver. Overall, the net computational time was nearly reduced 20-fold with the voxelized model.

Fig. 2.

CFD compatible meshes. (a) Schematic of voxelized (cartesian) mesh (b) Unstructured mesh of reconstructed hindlimb including tumor (light green), skin (green), cut ends (yellow), and a representation of the mid-slice (dark blue). Number of voxels in the figure were reduced by a factor of 16 for more clarity. Horizontal and vertical lines used for plotting the flow field and tracer transport in (c) voxelized and (d) non-voxelized models.

There was one other difference: the impermeability boundary condition along and outside the skin boundary in the voxelized model was achieved by assigning hydraulic conductivity two orders of magnitude lower than the normal tissue to exterior voxels (voxels outside the hind limb, corresponding to the surrounding air), while the nonvoxelized model was directly assigned a wall boundary condition with zero normal flux. The assignment of low hydraulic conductivity in the exterior voxels created a material that was resistant to fluid motion. For the value of hydraulic conductivity chosen for the exterior voxels the mean velocity at the skin boundary was calculated to be close to zero (0.001 μm/s).

2.4. Statistical Analysis.

Quantitative methods to compare the IFP, IFV, and tracer concentration require a one-to-one mapping between both unstructured and Cartesian meshes, which was mathematically cumbersome to derive. Hence, a set of elements common to both of the meshes were identified, based on the location of their cell centers, and used for the analysis. The criteria for matching was that the nonvoxel element should lie within the compared voxel, assuming small variations in the voxel. The preceding criteria resulted in an approximately 97 to 98% match for all animals. The values of the IFP, IFV, and tracer concentration in tissue in these matching elements were compared in analysis. Additionally, a quantitative comparison was conducted between the tracer concentration in tumor tissue predicted by the voxel model and MRI-obtained experimental data at later time points. Different statistical measures were used to ascertain the similarity between model predictions including root mean square (RMS) error, the Pearson product moment correlation coefficient (PPMCC), and error histogram.

2.4.1. Error Histogram.

Error histograms were generated to provide a graphical representation of the frequency distribution of errors in the dependent variables, which was the absolute value of the difference between the compared results. A range for the error was chosen and divided into equal-sized intervals (or bins). The number of occurrences within each range was then calculated for each bin and represented as a bar plot.

3. Results

Tumor flow fields and tracer transport predictions obtained using both computational approaches were compared. In Figs. 3, 4, 5, and 6, contour plots at the tumor mid-slice are supplemented with line plots along the horizontal and vertical bisectors at the mid-slice (see Figs. 2(c) and 2(d)). For a detailed description of the predicted fluid flow and tracer transport in the nonvoxelized tumor model, the reader is referred to Ref. [30]. The voxelized model predicted an elevated IFP inside the tumor where pressure reached a peak value (≈1.62 kPa in animal I, 0.71 kPa in animal II, and 0.87 kPa in animal III) at the tumor core, and rapidly decreased at the tumor boundary. As expected, within the tumor, the predicted pressure gradients were lowest close to the tumor center (≈14.2, 38.5, and 11.2 Pa/mm in animals I, II, and III, respectively) and highest (≈1137, 580, and 764 Pa/mm in animals I, II, and III, respectively) near its periphery. Similar pressure patterns were predicted by the voxelized and nonvoxelized models. However, in the voxelized model the line plots clearly indicated a difference in the magnitude of the predicted pressures between both the models. The magnitude of the peak IFP predicted by the voxelized model was found to be 15% higher than that of its counterpart in animal I, 29% in animal II, and 18% in animal III.

Fig. 3.

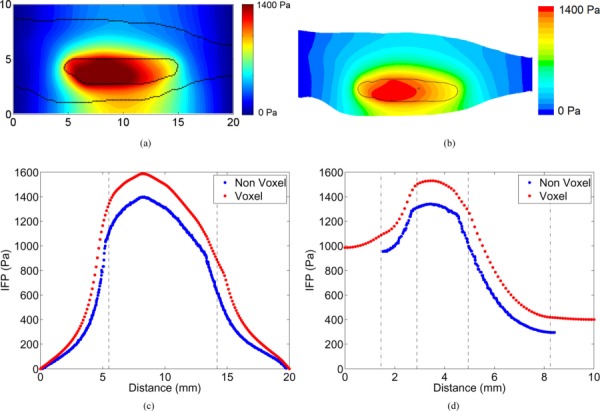
Contours of IFP predicted by (a) voxelized model and (b) non-voxelized models. Tumor and skin boundaries are overlaid on the contours. Line plots compare the predicted IFP by the models along the (c) horizontal and (d) vertical bisectors in the mid-slice. The tumor and skin boundaries are represented by dashed and dash-dot lines, respectively.

Fig. 4.

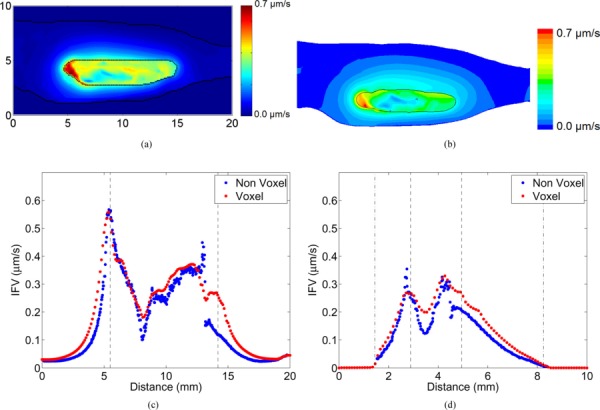
Contours of IFV predicted by (a) voxelized model and (b) non-voxelized models. Tumor and skin boundaries are overlaid on the contours. Line plots compare the predicted IFV by both the models along the (c) horizontal and (d) vertical bisectors in the mid-slice. The tumor and skin boundaries are represented by dashed and dash-dot lines, respectively.

Fig. 5.

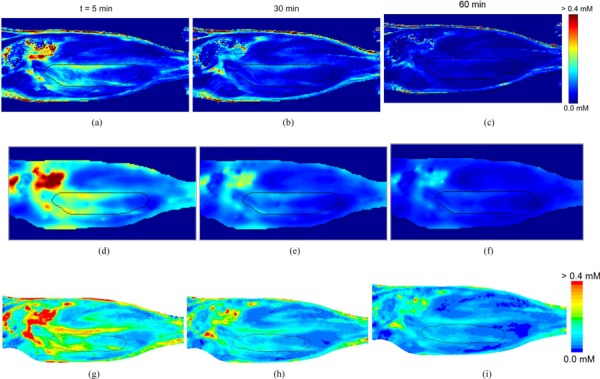
Comparison of tracer concentration contours. MR-derived tissue concentration (top row) compared with voxelized model (middle row) and non-voxelized (bottom row) predictions at t = 5 (a, d & g), 30 (b, e & h), and 60 (c, f & i) min. Tumor and skin boundaries are overlaid on the contours.

Fig. 6.

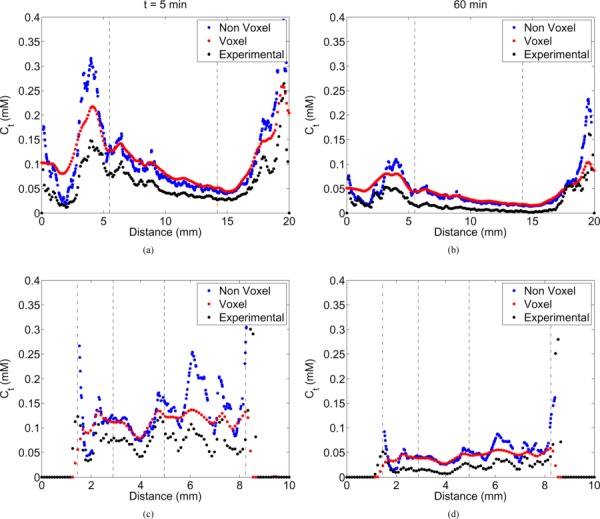
Line plots comparing the predicted tracer concentration in the tissue between the models and experiment along the horizontal (top row) and vertical (bottom row) bisectors of a mid-slice at t = 5 (a & c) and 60 (b & d) mins. The tumor and skin boundaries are represented by dashed and dash-dot lines, respectively.

Despite differences in the predicted IFP between models, the IFV contours and line plots (see Fig. 4) were more similar with the highest velocities (≈0.75, 0.40, and 0.42 μm/s in animals I, II, and III, respectively) occurring along the tumor boundary near the cut ends. The computed IFV values were found to be lower inside the tumor (≈0.03, 0.03, and 0.01 μm/s in animals I, II, and III, respectively).

The interstitial distribution of the Gd-DTPA tracer was simulated at various times (t = 5, 30, and 60 min) after infusion. The predicted tracer distribution of both models and the actual experimental data was heterogeneous with high concentration regions outside the tumor (see Fig. 5). The highest concentrations were approximately 0.4, 0.18, and 0.19 mM in animals I, II, and III, respectively, at t = 5 min in the voxel model. Line plots (shown in Fig. 6) show that the tracer extravasation appears to be less affected by the differences in the flow fields predicted by the models. The accuracy of the voxelized model's prediction with respect to its nonvoxel counterpart was maintained for all of the times simulated. At increasing times, the tracer concentration was reduced and the distribution became more uniform in tissues.

Statistical parameters comparing both model predictions are listed in Table 1. The statistics of the model results appeared similar across all of the animals. The Pearson coefficient for the IFP was high (PPMCC > 0.7), indicating similar patterns in both model predictions. The value of the RMS error reflected the difference in the peak pressures predicted by both models. The low RMS error and the high correlation coefficient (PPMCC > 0.7) in the IFV magnitude and direction showed a reasonable degree of similarity between the model predictions. The RMS error in the tracer concentration was maximum at the initial time points and decreased thereafter with time. However, the correlation coefficients did not change much with time. Error histograms for the flow and tracer transport (see Fig. 7) followed an approximately exponential distribution with the peak close to zero and became steeper with time.

Table 1.

Statistical parameters obtained comparing voxelized and nonvoxelized model results for the baseline simulations in three animals

		Animal I		Animal II		Animal III
Variable	Quantity	RMS error	PPMCC	RMS error	PPMCC	RMS error	PPMCC
IFP	Magnitude	167.09 Pa	0.95	44.45 Pa	0.97	38.72 Pa	0.97
IFV	Magnitude	0.07 μm/s	0.81	0.01 μm/s	0.89	0.02 μm/s	0.92
	Direction	23.10 deg	0.72	25. 64 deg	0.58	16. 44 deg	0.74
Ct	At t = 5 min	0.10 mM	0.79	0.10 mM	0.71	0.08 mM	0.74
	At t = 30 min	0.05 mM	0.79	0.06 mM	0.75	0.04 mM	0.77
	At t = 60 min	0.04 mM	0.78	0.03 mM	0.77	0.03 mM	0.77

Fig. 7.

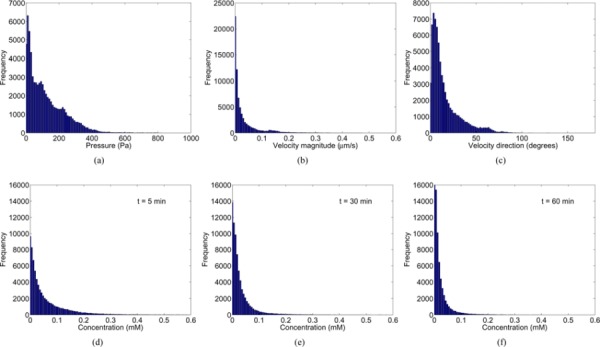
Error histograms for extracellular flow (a, b & c) and tracer transport at t = (d) 5, (e) 30 and (f) 60 mins in baseline simulations for the voxelized model with respect to the nonvoxelized model predictions.

3.1. Validation Study.

Qualitatively, a similar pattern of the Gd-DTPA distribution and washout was observed for the voxelized model, nonvoxelized model, and the experimental data over the course of 1 h (see Fig. 5). High concentration regions were observed outside the tumor and at the edge of the tumor just within the tumor boundary. Washout rates were compared by calculating the volume-averaged Gd-DTPA concentration within the tumor for various time points and fitting the data into a mono-exponential function (see Table 2). The voxelized and nonvoxelized model both compared well with the experimental data. The RMS error was calculated for both models throughout the entire tumor volume along with error frequency histograms (shown in Fig. 8) to illustrate the comparison of the models with the experimental data in space and time. Both the voxelized and nonvoxelized models showed low RMS error, an exponential decay of error with the highest frequency close to zero, and a gradual steepening of error histograms with time. However, for animal III there was a slightly higher RMS error in the voxelized and nonvoxelized model predictions with the experiment, even though the washout rate was very similar to the experimental data (≈12% difference).

Table 2.

Comparison of tracer washout rates and root mean square error within the tumor volume between voxelized and nonvoxelized model results

Animal	Case	Washout rate of volume-averaged Gd-DTPA concentration within tumor volume (min‒1)	RMS error for concentration within tumor volume (mM)
t = 5 min	t = 30 min	t = 60 min
I	Experimental	‒0.031	—	—	—
	Voxelized model	‒0.022	0.072	0.039	0.031
	Nonvoxelized Model	‒0.020	0.120	0.064	0.048
II	Experimental	‒0.020	—	—	—
	Voxelized model	‒0.021	0.070	0.060	0.036
	Nonvoxelized model	‒0.022	0.089	0.062	0.040
III	Experimental	‒0.025	—	—	—
	Voxelized model	‒0.022	0.295	0.258	0.034
	Nonvoxelized Model	‒0.022	0.297	0.259	0.037

Fig. 8.

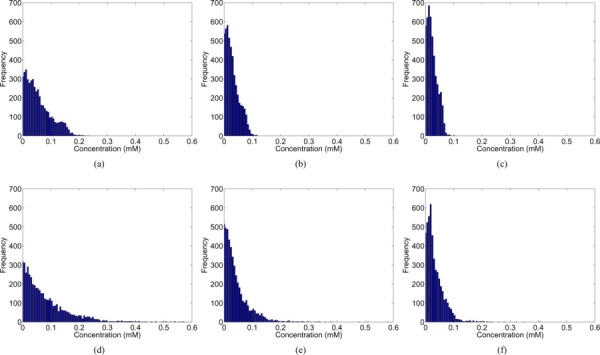
Error histograms for tracer concentration within the tumor for voxel (top row) and non-voxel (bottom row) model results with respect to MR experimental data at t = (a & d) 5, (b & e) 30 and (c & f) 60 min.

4. Discussion and Conclusions

A voxelized modeling approach was used to study the transport of Gd-DTPA following systemic injection in tumors. The benefits of this methodology include easier and more rapid building of computational porous media transport models compared to traditional CFD approaches, which involve complex geometric reconstruction. The voxel model is less labor intensive and potentially simpler to implement. It should also be noted that the voxelized model significantly reduced the computational time by almost an order of magnitude compared to its nonvoxel counterpart. Spatially varying tissue transport properties and anatomical tissue geometries were incorporated into three-dimensional image-based computational porous media models which solved for extracellular flow and transport.

The disparity in the model results is, however, due to the basic differences between both approaches: mesh structure. The voxelized model uses a uniform and rectangular mesh while the nonvoxelized model uses an unstructured mesh. The type of mesh used can affect the solution in two ways: (1) tumor/host tissue volume approximation, and (2) resolution. Using the Cartesian mesh, the voxelized model approximates the tumor and host tissue volumes with rectangular elements, thereby neglecting the curvature at tissue boundaries, while the nonvoxelized model with its variable size elements can account for such boundaries. This results in slight differences in tumor and host tissue volumes which, in turn, affects the solution since the tumor shape and size are important factors determining the interstitial fluid flow [36, 37]. The mesh density also affects the solution since it determines the discretization of the domain with better resolution in finer meshes and vice versa. The mesh size used for the voxelized model was approximately 6–7% of that in the nonvoxel mesh. The low resolution of the voxelized model is due to the limitations of the MRI resolution as this data was directly mapped into the model. It should be noted that the nonvoxel model was used for extensive sensitivity analysis requiring it to capture steep pressure gradients at the tumor boundary; hence, the mesh size was increased to attain numerical convergence. Hence, in this aspect, the voxelized model has much less mesh density compared with its nonvoxelized counterpart, resulting in a lower resolution, as previously mentioned. However, it should be noted that the mesh independency of the voxelized model predictions was verified in the present study. Despite these differences, the voxelized model was still able to capture key features in the flow and transport.

The voxelized model predicted an elevated IFP, conforming with previous experimental observations [14–18] and previous modeling results [13, 22, 28, 30]. However, the IFP predicted by the voxelized model was higher than that predicted by the nonvoxelized model using the same data set. The value of the RMS error reflects this difference since it can be interpreted as the standard deviation between two variables. This discrepancy can be explained by the differences in the tumor volume in both models. The tumor volume approximated by the voxelized model was higher than that of the nonvoxel model (39% higher in animal I, 83% in animal II, and 36% in animal III). This was due to differences in the meshing strategy of the models. The nonvoxelized model used variable-sized elements (unstructured mesh), which likely approximates the tumor volume slightly better than its voxel counterpart, which relies only on fixed-size elements. This effect was particularly more pronounced in animal II, which had the smallest tumor volume. Since the IFP values have been found to be correlated with tumor volume, with a higher IFP for larger tumors [17, 19], the voxelized model with the higher tumor volume was expected to have an IFP higher than the nonvoxelized one. The tumor volumes for animals II and III in the voxelized model were an order of magnitude lower than that in animal I, thus resulting in smaller IFP changes. These differences in the predicted IFP did not have much effect on the predicted extracellular flow, which was driven by the IFP gradient, which was similar between the voxelized and the nonvoxelized model. It should be noted that the correlation coefficient can also be interpreted as the degree of similarity between the slopes of two variables; in other words, a similarity index for the gradients of the variables. From Table 1, it is clear that the correlation coefficient values are high (PPMCC > 0.7) for all three animals, thereby indicating the high degree of similarity in the IFP gradient predicted by both of the models. The approximately exponential error distribution for the IFP with a high frequency near zero error implies the decaying nature of the number of voxels with higher errors.

The IFV predicted by the voxelized model also reflected previous experimental findings [19]. In the experimental study conducted by DiResta and colleagues, the IFV in human neuroblastoma propagated in the flank of an immune suppressed rat was found to increase from the center towards the periphery of the tumor. In this study, the statistical parameters obtained for the IFV indicate a higher degree of similarity between the predictions of the voxelized and nonvoxelized models than for the IFP. As previously mentioned, the IFV which was driven by the IFP gradient was less affected by the changes in the predicted pressure magnitude. This was also reflected in the error histograms, where the error decayed more rapidly than that of the IFP.

The distribution of the Gd-DTPA was heterogeneous, due to spatially varying deposition and limited interstitial transport by diffusion and convection over 1 h. The low tracer concentration measured and predicted inside the tumor was consistent with a reduced fluid filtration and a high IFP. As the tracer was advected through the extracellular space, its correlation coefficient was similar to that obtained for the IFV. A strong peak around zero in the error histograms shows the reliability of the voxelized model in predicting the tracer concentration despite changes in the predicted flow field. It should be noted that, although there were differences between the results obtained through both models, the voxelized model faithfully captured tracer extravasation, which is essential for this drug delivery model.

The validation study revealed that the Gd-DTPA distribution results obtained via nonvoxelized and voxelized models were consistent with the MR experimental observations across a small set of tumors. The error distributions for the predicted tracer concentration within the tumor were comparable for both models over time, thereby exhibiting the similarity in both model predictions. The gradual steepening of the error histograms over time further showed the decay of error over time, which is also reflected in the RMS error values. The slightly high RMS error in animal III could be due to the errors in the estimation of arterial input function parameters, which varies across the tumors and to which the results were found to be sensitive [30]. However, the tracer washout rate was accurately predicted by the voxelized model. This outcome provides further justification for the voxelized porous media tumor models for predicting low molecular weight tracer and drug distribution. It should be noted that matching the tumor modeling results with the experimental values is difficult due to the large number of model parameters which need to be experimentally determined. Additionally, the small velocities encountered in the problem on the order of μm/s make it difficult to experimentally measure the IFV. The experimental measurement of the IFP is beyond the scope of the current study; it should, however, be noted that the computed IFP matches with the previous studies, as described in the preceding paragraphs.

The main aim of this voxelized model study was to gain an overall understanding of the fluid flow and transport in tumors and to provide a reliable alternative to the nonvoxelized approach. Such a model also provides a suitable platform for developing more realistic and widely applicable patient-specific treatment tools. The voxelized model could be extended to study flow and transport in other solid tumors apart from the murine sarcoma considered in this study. For example, in brain tumors diffusion tensor-MRI (DTI) data could be incorporated into the model, accounting for preferential transport along the nerve fibers reported in the literature [38, 39]. With slight modifications to the governing equations to account for an infusion site, the voxelized model can also predict flow and tracer transport following local infusion. Tracer transport in the brain and spinal cord following local infusions has been previously predicted using the voxelized model incorporating the DTI data [31, 32]. Degradation and binding of the solute could also be included by adding a sink term based on a reaction constant in the transport equation.