Near Valve Flows and Potential Blood Damage During Closure of a Bileaflet Mechanical Heart Valve

Abstract

Blood damage and thrombosis are major complications that are commonly seen in patients with implanted mechanical heart valves. For this in vitro study, we isolated the closing phase of a bileaflet mechanical heart valve to study near valve fluid velocities and stresses. By manipulating the valve housing, we gained optical access to a previously inaccessible region of the flow. Laser Doppler velocimetry and particle image velocimetry were used to characterize the flow regime and help to identify the key design characteristics responsible for high shear and rotational flow. Impact of the closing mechanical leaflet with its rigid housing produced the highest fluid stresses observed during the cardiac cycle. Mean velocities as high as 2.4 m/s were observed at the initial valve impact. The velocities measured at the leaflet tip resulted in sustained shear rates in the range of 1500–3500 s−¹, with peak values on the order of 11,000–23,000 s−¹. Using velocity maps, we identified regurgitation zones near the valve tip and through the central orifice of the valve. Entrained flow from the transvalvular jets and flow shed off the leaflet tip during closure combined to generate a dominant vortex posterior to both leaflets after each valve closing cycle. The strength of the peripheral vortex peaked within 2 ms of the initial impact of the leaflet with the housing and rapidly dissipated thereafter, whereas the vortex near the central orifice continued to grow during the rebound phase of the valve. Rebound of the leaflets played a secondary role in sustaining closure-induced vortices.

Introduction

The fluid dynamics of mechanical heart valves have been studied for more than 30 years, and during this time, the general flow characteristics of prosthetic valves have been evaluated to demonstrate safety and efficacy [1]. The need for continual anticoagulation therapy to reduce the risk of thrombosis remains a major disadvantage of mechanical valve prostheses. Furthermore, valve design can greatly impact the likelihood or extent of blood damage [2]. In recent years, there has been a shift in focus of both in vitro experimentation and computation towards interpreting the local flow dynamics near the valve housing of tilting disk and bileaflet valves and around the hinges of bileaflet valves, since hemolysis or platelet activation are more likely to occur in these regions [3].

Red blood cells and platelets are activated, damaged, or lysed by elevated fluid stresses. Prolonged exposure to laminar shear stresses above 1500 dynes/cm² is generally thought to cause hemolysis [4]. Similarly, submerged fluid jets with Reynolds stresses above 4000 dynes/cm² can cause red cell lysis [5]. Fortunately, the elastic nature of a red blood cell membrane enables it to withstand high stresses for short exposure times. Leverett et al. [6] quantified the relationship between exposure time and shear stress with regards to hemolysis. Platelet activation is also a concern with blood-contacting medical devices, mostly during the regurgitation phase [7,8]. Studies have shown that platelets can be activated by much lower shear stresses than is required for hemolysis [9]. Thrombus formation has been documented in and around bileaflet valves in regions of recirculation or flow stagnation, sometimes affecting device functionality [10].

Early work by Yoganathan et al. [11] showed that turbulence downstream flow of mechanical valves contributes to blood cell damage, while Lamson et al. [12] found that backflow through mechanical valves can be as damaging to blood cells as forward flow despite the relatively small affected blood volume (∼2–5% of forward flow). Studies by Baldwin et al. [13], Maymir et al. [14] and Meyer [15] demonstrated, for valve implants and for valves within pulsatile ventricular assist devices, that normal Reynolds stresses caused by regurgitant flow through mechanical prostheses can exceed 20,000 dynes/cm², well above the threshold for hemolysis. Cavitation, which involves the formation and collapse of vaporous bubbles in low pressure regions, is sometimes observed near mechanical mitral valves at closure and is known to cause hemolysis [16,17]. Cavitation potential is dependent on valve design and often coincides with rapid valve deceleration (water hammer) [18], squeeze flow about valve stops [19,20], and vortex motion [21]. Coupled fluid-structure interaction models are also used to predict valve-related blood damage. Cheng et al. [22], for example, computed a maximum wall shear stress exceeding 160,000 dynes/cm² at the tip of a closed bileaflet valve. There has been more recent work using particle image velocimetry and numerical methods to understand the fluid dynamics associated with bileaflet valves focusing on overall hemodynamics and specifically investigating the hinge flow region [23–29].

Recently, our laboratory used three-component laser Doppler velocimetry (LDV) to evaluate flow within the housing gap of a tilting disc mechanical heart valve at closure [30]. To study vortex motion and high-velocity regurgitant jets, we removed a section of the housing along the edge of the occluder and replaced it with an acrylic window. In that environment, we measured fluid velocities of 5.8 m/s, shear rates approaching 100,000 s⁻¹ and fluid accelerations larger than 600 g [30]. Since bileaflet valves often produce less obstruction and more leakage than tilting disc valves, we have investigated the flow field within the housing of a St. Jude Medical bileaflet valve at the instant of closure using similar method.

Methods

Equipment.

Valve replacement is an option for patients with mitral stenosis when the native valve is not suitable for valvotomy. To study flows near a mitral mechanical valve, we first created a 14 mm window in the housing of a 29 mm St. Jude Medical pyrolytic carbon bileaflet valve. The removed portion of the housing was replaced with an optically clear acrylic section of identical dimensions. We did not compromise the structural integrity of the device by altering the housing (Fig. 1). Bulk flow characteristics (i.e. velocity profiles at specific near valve locations) through the modified valve were statistically the same as those captured by LDV through an intact valve of the same size. For all of these experiments, the sewing cuff was removed to provide a rigid mount for LDV quantification. The test chamber was pneumatically driven to simulate mitral valve closure, not the entire cardiac cycle. Even though aortic valve replacement is more common than mitral valve replacement, the large transvalvular pressure gradient makes mitral valves susceptible to stenosis and regurgitation. Mitral valve prostheses are more likely to induce cavitation than aortic mechanical valves due to a rapid drop in pressure. The in vitro test system was previously used for assessing the fluid mechanics associated with tilting disk valve closure and is described in more detail in Manning et al. [30]. The test chamber was comprised primarily of acrylic to permit optical access from multiple vantage points using LDV and particle image velocimetry (PIV). The ventricle housed a pressure catheter three centimeters distal to the valve to monitor the left ventricular pressure throughout the cardiac cycle.

Fig. 1.

A portion of the valve housing was removed to expose the leaflet tip

Test Conditions.

A heart rate of 75 bpm, a systolic duration of 37%, and a peak ventricular pressure of 120 mmHg were used to simulate the cardiac conditions of a patient with a prosthetic mitral valve. For 20 ms leading up to valve closure, we applied a loading rate of 1800 ± 150 mmHg/s on the valve to avoid optical distortion effects associated with cavitation. This loading rate was at the high end of the physiological range of dP/dt's used in Carey et al.'s interlaboratory study of valve closure [31]. At smaller loads, the structure of the vortex did not change drastically; however, its intensity does decrease and the time scale lengthens. The Newtonian blood analog was comprised of sodium iodide, water and glycerin in a weight ratio of 50/30/20. The kinematic viscosity of the fluid was 3.9 cSt. The refractive index of the seeded fluid matched that of the acrylic chamber (n = 1.49).

Flow Visualization.

We used high speed videography to qualitatively assess the size, location and duration of retrograde jets and vortices before conducting the LDV and PIV experiments. A KODAK SR-Ultra Motion Corder was used to record digital images of valve position and potential cavitation at 3000 frames per second. Through flow visualization, we were able to identify flow mechanisms such as vortices shed off the edge of the leaflet tip, flow along the atrial face of the leaflet after closure, retrograde jet flow through the central orifice, fluid rebound, and regurgitation around the periphery (Fig. 2). We also used flow visualization to observe valve closure at smaller dP/dt values in order to verify the presence of similar flow features of lesser strength.

Fig. 2.

High speed images of the near valve closing flow and vortices were taken. (a) The closing volume was observed as streaklines. (b) Vortex initiation and (c) growth were identified. (d) The window in the housing enabled optical access to near valve flows.

LDV Data Acquisition.

Three-component LDV was used to evaluate flows within the gap between the leaflet and housing. A four-Watt argon ion laser (Coherent, Inc., Santa Clara, CA) was coupled to a TSI Fiberlight^TM unit, which separated the laser beam into different detectable wavelengths. A 250 mm focal length lens was coupled to the 50 mm transmitting probe, as shown in Fig. 3. The arrangement produced a nearly spherical measurement volume with diameters of 47, 47, and 50 μm for three-dimensional measurements, and a 47 × 47 × 340 μm ellipsoid for two-dimensional measurements. The measurement volume occurred at the convergence point of the beam pairs. Two-dimensional measurements had an inherent spatial uncertainty of 170 μm in the cross-sectional plane. This spatial uncertainty acted as the primary source of error in the shear rate calculations.

Fig. 3.

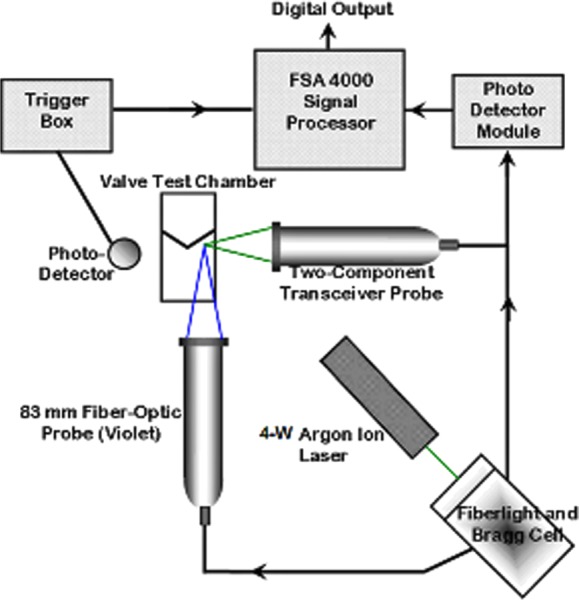
A schematic of the LDV experiments

At each measurement location, 40,000 coincident measurements were acquired over a 55 ms window encompassing valve closure. A gate scale no larger than 200% was used to define valid coincident data capture. The raw signal bursts were sorted into 1 ms time bins, such that each reported velocity was derived from 1800 ± 300 valid individual particle measurements. Data acquisition was triggered during each beat cycle when a laser beam was clipped by the closing leaflet. The optical trigger produced a beat-to-beat temporal error of approximately 250 μs relative to impact. The LDV data acquisition region began at the leaflet tip and extended into the atrium. The size of this region was 2.00 mm × 2.25 mm × 9.00 mm, with measurements taken every 250 to 750 μm. Additional measurements were made along the centerline of the valve, and near-wall measurements were acquired to within 200 μm of the proximal leaflet tip. Leaflet rebound was observed 11.0 ± 1.6 ms after the initial impact.

Mean and fluctuating velocities were calculated by ensemble averaging discrete velocity measurements at each time bin and location. Outliers were removed by an elliptical filtering technique (5σ major axis) developed by Baldwin et al. [32]. The mean velocity for the x-directional component was calculated as follows:

$$U={\left(\frac{\sum _{i=1}^n{u}_i}{n}\right)}_{\mathit{f}\mathit{i}\mathit{l}\mathit{t}\mathit{e}\mathit{r}}$$ (1)

where u_i is a discrete velocity in the direction of U, and n is the total number of measurements acquired. The mean and peak shear rates were determined by the rate change of the velocity vector relative to the nearest surface.

PIV Data Acquisition.

While LDV enabled us to assess near valve flows in great detail, PIV was used to measure the growth and expansion of the regurgitant flow structures in the atrium. Using a dual pulsed Nd:YAG laser (TSI Inc., Shoreview, MN) for illumination, five flow planes normal to the B-datum line were obtained. The B-datum line refers to the centerline of a bileaflet valve where the two leaflets meet in the closed position. Details of the PIV system can be found in Hochareon et al. [33].

Two hundred image pairs were averaged to produce mean vector maps at each time step using interrogation regions of 16 × 16 pixels. Velocity data were collected in 2 ms increments over a 22 ms acquisition period about closure. A recursive Nyquist grid engine was used in combination with a Hart correlation of 16 pixel displacements and a bilinear peak method to track particle displacement and generate vector maps. Kini et al. determined that pixel size resulted in an uncertainty of 0.5% in any given instantaneous flow map [34].

Results

In Vitro Flow Experiments.

As expected, peak axial velocities were found along the centerline of the valve, and the leaflet closing motion generated significant regurgitant flow back in to the atrial chamber. Immediately after leaflet impact, reverse flow was observed in the housing gap. Figure 4 shows the almost instantaneous swing in fluid direction. For reference, complete valve closure occurred roughly 6 deg (or 13 ms) into the RMR cycle of Fig. 4. At this particular location near the leaflet tip (−1.5, 0, 1.1), the peak axial velocity was 2.4 m/s at impact, and the peak U and V velocity components were 0.6 m/s and 0.3 m/s, respectively. Here, the peak fluid deceleration of 1500 m/s² was dictated by valve motion. The primary rebound occurred 11 ms after initial impact and was characterized by a second rapid directional change of the axial (W) velocity. The mean fluid velocity during rebound was 40 ± 5% of that produced during the initial leaflet impact. While the highest velocities were measured in the axial direction, well defined cross-flows were also present.

Fig. 4.

The three velocity components, (a) U, (b) V, and (c) W, were plotted on individual axes to study velocity fluctuations and beat-to-beat variations in a point-wise fashion

The peak axial velocity of 2.4 m/s observed at leaflet impact was more than twice the peak velocity expected through native valves [35]. Figure 5 shows a cross-sectional segment of the mean flow for four distinct time bins, exactly 2.65 mm upstream of the tip of the leaflet. The center of the valve at the leaflet tip was located at (0,0,0), with the valve closing toward the reader. The dominant axial flow (W) is represented by the color contour, while the vectors represent mean U and V cross-flow velocities. Within 2 ms of impact, as shown in Fig. 5(b), the clockwise direction of the vortex completely reversed indicating rebound. The single vortex dissipated within 9 ms of impact, as shown in Fig. 5(d). Flow visualization showed a sister vortex being simultaneously generated proximal to the other leaflet.

Fig. 5.

Three-dimensional reconstructions of the flow taken 2.65 mm upstream of the leaflet tip (a) at impact, (b) 2 ms after impact, (c) 4 ms after impact, and (d) 9 ms after impact

A fluid jet exhibiting three-dimensional, turbulent characteristics was observed near the peripheral orifice. The vector maps in Fig. 6 show the rapid directional change of the flow, which occurred within 4 ms of impact. Here, the reverse flow through the rebounding leaflet was 0.4 m/s, whereas the mean velocity through the closing valve was 1.4 m/s. A vortex did not fully develop until 10 ms after initial impact (Fig. 6(c)), but the fluid energy was largely dissipated by this time. Out-of-plane flow was indicative of a vortex structure. It is believed that 2D computational simulations often underestimate closure-induced fluid stresses and blood damage due to their omission of three-dimensional effects [22].

Fig. 6.

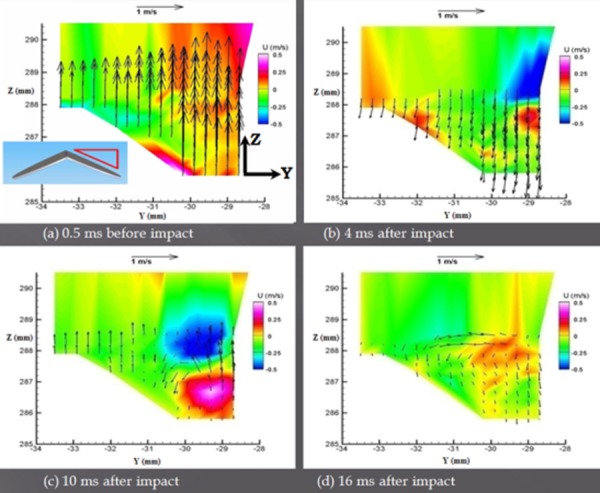
Velocity maps of the centerline plane (a) 0.5 ms before impact, (b) 4 ms after impact, during rebound, (c) 10 ms after impact, and (d) as the flow began to dissipate 16 ms after impact

After compiling near valve LDV profiles, PIV was used to evaluate the growth and movement of the vortex and regurgitant jets in the atrial chamber. Figure 7 shows the PIV flow field along the center plane, an area much larger than that covered by the LDV experiments. Despite the three-dimensional behavior of the flow, we still observed symmetry across the B-datum line when the flow field was deconstructed into one millisecond time bins. Four milliseconds after closure, in Fig. 7(c), the jets dissipated and the vortex became the dominant flow feature. Fluid near the leaflet was drawn back toward the valve due to a sudden deceleration, causing further rotational flow. The valve generated a peak vorticity of 1350 s⁻¹ through the central orifice, and a peak strain rate of 250 s⁻¹ was measured during the rebound stage. A peak vorticity of 600 s⁻¹ was calculated for the dominant vortex formed at the leaflet tip, although the mean vorticity measurements were found to be an order of magnitude lower. Since 200 image pairs were ensemble-averaged to generate a single flow map, the fluid jet and entrained flow appear to be quite symmetrical through central orifice. This symmetric behavior may not be as evident if closing events were studied on an individual basis.

Fig. 7.

Centerline velocity profiles generated using PIV (a) at impact, (b) 2 ms after impact, and (c) 4 ms after impact

Wall Shear Rates.

Shear rates were calculated at locations relative to the valve housing to better understand the relationship between fluid dynamics and blood damage. Mean and peak shear rates at impact are presented in Fig. 8 with their associated uncertainties. The 12% error presented here is attributed primarily to uncertainty associated with the location of the measurement volume relative to the wall. Shear rates were measured from within the flow to the nearest wall, whether that happened to be the adjacent housing or the dynamic leaflet. The peak shear rates of 11,000–23,000 s⁻¹ presented here were approximately 20% of those calculated for a tilting disk valve [30]. Mean wall shear rates ranged from 1500–3500 s⁻¹ across the tip of the leaflet. The near valve shear rates remained above 700 s⁻¹ for the entirety of leaflet closure and rebound. We were justified in using a Newtonian fluid for this study because blood acts as a Newtonian fluid at the high shear rates measured during valve closure, and rheological properties do not appear to have an effect on the closing time or closing volume [36].

Fig. 8.

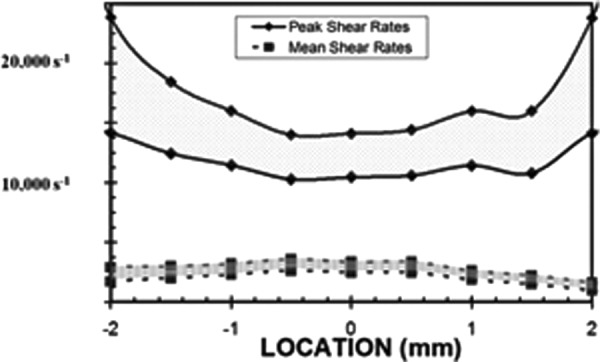
Mean and peak shear rates were computed across the edge of the leaflet

Discussion

Predicting Blood Damage.

The unsteady and sometimes turbulent nature of blood flow through mechanical valves makes it difficult to accurately predict blood damage. The fluid and valve characteristics presented in this paper can be used to validate computational models of bileaflet heart valves. The presence of a strong vortex shed off the leaflet tip, turbulent regurgitant and closing flows, and interactions between the implant and blood can all reduce the lifespan of blood elements. The flow structures and mitral heart valve closing dynamics investigated here were used to validate computational models such as that by Govindarajan et al. [37]. While the valve tip appears to be a major site for blood damage, other locations such as the hinge region are also expected to contribute to hemolysis [3]. When designing bileaflet valves, manufacturers should also carefully consider how the following features will affect fluid stresses: impact location between the leaflet and housing, gap between the housing and the valve in its closed position, the shape/curvature of the leaflet, effective orifice area, and the design of the leaflet tip [38]. These sites are difficult to access through in vitro experimentation [39], and thus are primarily studied using computational simulations.

Leverett et al. [6] studied the relationship between hemolysis, shear stress and exposure time. More recently, Maymir et al. [14] applied a model to LDV data, which combined the effects of shear stress and exposure time. In this study, Reynolds shear stresses as high as 17,500 dynes/cm² were computed, albeit for a short exposure time on the order of 1 ms. Reynolds shear stresses above 1500 dynes/cm² were sustained for much of valve closure and rebound (>40 ms), a period that accounts for more than 5% of the total cardiac cycle. Peak near wall shear stresses as high as 3000 dynes/cm² were calculated for a 5 ms period during each beat cycle. Based on these findings, closure-induced fluid stresses of a bileaflet valve can potentially damage blood cells and activate platelets despite a reduced exposure time. Assuming a constant ejection rate and a beat rate of 75 bpm, the blood volume exposed to fluid stresses above the 1500 dynes/cm² threshold could be as high as 650 mL/min [15]. Furthermore, the volume of blood exposed to leakage flow may range from 125 to 166 mL/min. The local pressure transient on the inflow side of the mitral mechanical valve can act in combination with characteristic flows such as regurgitant jets and vortices to produce blood damage by cavitation [17]. The ensemble-averaged pressure drop measured 1 cm away from the tip of the leaflet was 518 ± 79 mmHg. At a slightly higher, yet still physiologic load of approximately 2500 mmHg/s, cavitation bubbles were observed in approximately 60% of valve closures in a single-shot test chamber. The low pressure regions found in regurgitant jets and vortical structures also increase the likelihood of cavitation and stable bubbles in patients with valve prostheses.

A significant portion of the total blood cell trauma likely occurs on the upstream side of the valve during closure. Regurgitation and vortex formation were two dominant flow features that resulted in fluid stresses high enough to induce hemolysis and platelet activation. During valve closure, the highest fluid stresses were observed in the gap between the leaflet and the valve housing and through the central orifice. Asymmetric valve closure may affect the position and strength of leakage jets, as was the case in these studies.