Micromechanical Anisotropy and Heterogeneity of the Meniscus Extracellular Matrix

Abstract

To understand how the complex biomechanical functions of the meniscus are endowed by the nanostructure of its extracellular matrix (ECM), we studied the anisotropy and heterogeneity in the micromechanical properties of the meniscus ECM. We used atomic force microscopy (AFM) to quantify the time-dependent mechanical properties of juvenile bovine meniscus at deformation length scales corresponding to the diameters of collagen fibrils. At this scale, anisotropy in the elastic modulus of the circumferential fibers, the major ECM structural unit, can be attributed to differences in fibril deformation modes: uncrimping when normal to the fiber axis, and laterally constrained compression when parallel to the fiber axis. Heterogeneity among different structural units is mainly associated with their variations in microscale fiber orientation, while heterogeneity across anatomical zones is due to alterations in collagen fibril diameter and alignment at the nanoscale. Unlike the elastic modulus, the time-dependent properties are more homogeneous and isotropic throughout the ECM. These results enable a detailed understanding of the meniscus structure-mechanics at the nanoscale, and can serve as a benchmark for understanding meniscus biomechanical function, documenting disease progression and designing tissue repair strategies.

1. INTRODUCTION

The meniscus is an essential component of the knee joint, responsible for stability, load transmission and lubrication [1]. To enable efficient transmission of the complex tensile, compressive, and shear stresses, the extracellular matrix (ECM) of meniscus possesses a unique, hierarchically structured framework that is both heterogeneous and anisotropic at multiple length scales [2]. At the macroscale, the outer and middle zones mainly sustain circumferential tensile “hoop” stresses to provide joint stability [3]. In this region, the ECM is dominated by circumferentially aligned type I collagen fiber bundles. By contrast, the inner zone of the meniscus is mostly under compressive loads [4] to reduce cartilage loading [5], and the ECM has less aligned collagen fibers as well as a higher concentration of proteoglycans [6, 7]. At the microscale, the circumferential fibers are encapsulated by a ~ 100–200 μm thick superficial lamellar layer [2] composed of radially oriented fibers. These fibers emanate into the meniscus interior as “radial tie fibers”, and interdigitate throughout the circumferential fibers [8–10]. In between fibers, there exist proteoglycan-rich micro-domains that play a role in local strain transfer and regulate cell mechanotransduction [11]. On top of the superficial lamellar layer, there is a ~ 10 μm thick surface layer of transversely aligned fibrils, a feature similar to the surface of articular cartilage, its loading counterpart [12]. At the nanoscale, adjacent collagen fibers share several individual collagen fibrils, and are interconnected by these fibrils spanning across them (Fig. 1a). This hierarchical, intertwined structure enables the meniscus to sustain a complex array of tensile, compressive and shear loads, and to retain its load bearing capability even in the case of a radial tear that spans 50% across the tissue width [13].

Fig. 1.

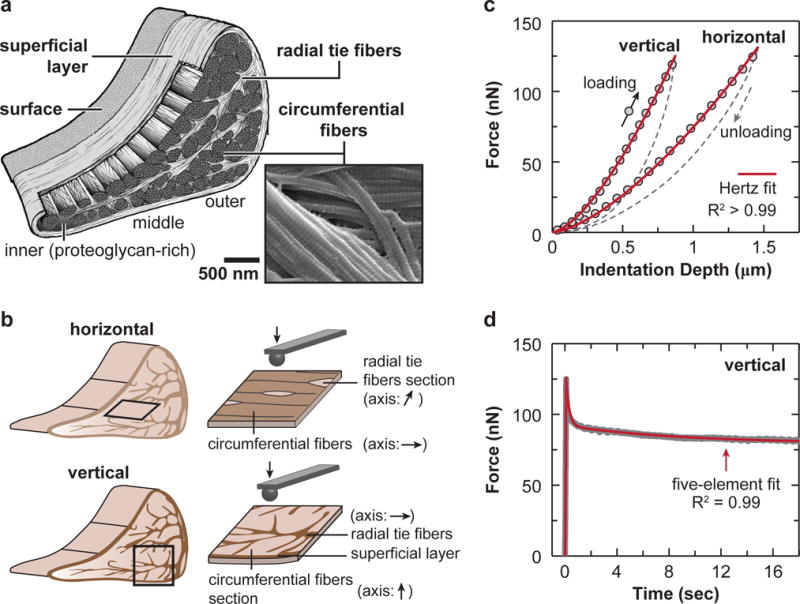
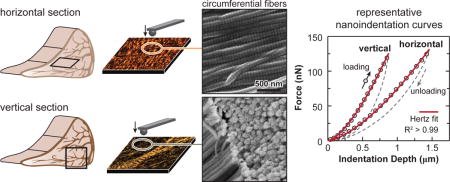
AFM-nanomechanical test set-up. (a) Schematic of the meniscus extracellular matrix (ECM) highlighting the four major structural units: surface, superficial layer, radial tie fibers and circumferential fibers, as well as the zonal variation. Scanning electron microscopy (SEM) image showing that two adjacent circumferential fibers are interconnected by fibrils spanning across them (white arrowhead). (b) Schematics of AFM-nanoindentation test on the horizontal and vertical sections, where the fiber axis orientation within each interior structural unit is shown. (c) Representative indentation force versus depth (F-D) curves measured on both horizontal and vertical sections of outer zone circumferential fibers, and corresponding Hertz model fit (tip radius R ≈ 5 μm, spring constant k ≈ 0.6 N/m, R² > 0.99). (d) Representative relaxation curve of temporal force, F(t), versus time, measured on the vertical section of outer zone circumferential fibers, and corresponding five-element model fit (R² = 0.99).

Meniscal damage is a common cause of joint injury [1], which can lead to the development of post-traumatic osteoarthritis (PTOA) [14], a prevalent form of osteoarthritis (OA) among the younger population [15]. Unfortunately, similar to articular cartilage, the meniscus has limited self-healing capabilities, especially in the avascular, proteoglycan-rich inner zone [16]. To repair damaged meniscus and recover normal joint function, it is necessary not only to replicate the whole tissue morphology of the native meniscus [17], but also to restore its matrix structural heterogeneity at the nano-to-microscale [18], which is critical for the tissue to perform its specialized tissue-level properties [1]. To this end, it is imperative to understand the structure-mechanical function principles of the native meniscus ECM at multiple length scales [19]. However, current mechanical knowledge of the meniscus is mostly limited to the tissue-level, and it is unclear how such complex ECM structure is connected with its mechanical properties [20]. Recently, a few studies started to investigate meniscus mechanics at nm- to-μm scales via instrumented nanoindentation [21, 22] and atomic force microscopy (AFM)-nanoindentation [23–25]. These studies demonstrated the potential of nanomechanical tests in revealing the small scale mechanical characteristics of the meniscus. However, these studies did not intend to focus on the anisotropy or heterogeneity associated with its ECM nanostructure. Without such knowledge, it is challenging to connect the meniscus disease etiology and pathogenesis with its structural complexity [26], or to design biomaterials that can replicate the functions of native tissue [27].

The objective of this study was to quantify the anisotropic and heterogeneous micro mechanics of the meniscus ECM. Inspired by the first, seminal AFM-nanoindentation work on the meniscus [23], we harvested menisci from calf knees, and cryotomed these tissues into micro-sections to expose different structural units of the ECM interior. AFM-based nanoindentation and ramp-and-hold force relaxation were applied to quantify the effective indentation modulus, and time-dependent mechanical properties of different ECM regions. The AFM tests resulted in deformation on the order of 1 μm, reflecting the properties of collagen fibrils at the nano-to-microscale, rather than fibers or fascicles at larger length scales. To connect the biomechanical outcomes with the ECM nanostructure, we analyzed collagen fibril structure at the nanoscale. These results provided new insights into native meniscus ECM biomechanics at multiple scales, further enriching our knowledge of tissue structure-function relationships [28].

2. METHODS

2.1 Sample preparation

Menisci were dissected from juvenile (≤ 3 months old) cows (n = 3) [29]. Multiple animals were used to confirm that the observed micromechanical anisotropy and heterogeneity features were consistent within the population. The outer, middle, and inner zones of the meniscus central body were isolated and embedded in Optimal Cutting Temperature (OCT) media. Each zone was cryo-sectioned transversely and radially onto glass slides to produce ≈ 20 μm thick horizontal and vertical sections, respectively (Fig. 1b). For horizontal sections, samples containing the intact surface, superficial (~ 100 μm from the surface on the tibial side) and deep zones (> 500 μm into the tissue) were taken parallel to the tibial surface. For vertical sections, samples from the central region were taken. Following standard the cryopreservation procedure [23, 24], samples were stored at −20°C in OCT for less than one week until AFM-nanoindentation tests.

2.2 AFM-nanoindentation and ramp-and-hold force relaxation

Prior to testing, sections were thawed and washed in phosphate buffered saline (PBS). On each section, AFM-nanoindentation was performed using microspherical colloidal tips (R ≈ 5 μm, nominal k ≈ 0.6 N/m, HQ:NSC36/Tipless/Cr-Au, cantilever C, NanoAndMore, Watsonville, CA) and a Dimension Icon AFM (BrukerNano, Santa Barbara, CA) at 10 μm/s indentation rate up to a maximum load of ≈ 120 nN (Fig. 1c). For each microstructural region of each section (Fig. 1b,c), indentation was performed on at least 10–15 different locations. For each structural unit, the relationship between the indentation orientation and the collagen fiber axis was summarized in Table 1. At the same location, nanoindentation was repeated three times, where the high repeatability of indentation curves suggested negligible irreversible plastic deformation. During all indentation measurements, tissues were immersed in PBS (0.15 M, pH = 7.4) with protease inhibitors (Pierce) to minimize post-mortem degradation and to maintain physiological-like fluid environment.

Table 1.

Summary of the relationships between indentation orientation and the collagen fiber axis for each structural unit on the horizontal and vertical cross-sections.

structural units	cross-section type
	horizontal	vertical
I. surface	normal (⊥)	–
II. superficial layer	normal (⊥)	normal (⊥)
III. radial tie fibers	oblique (//) or normal (⊥)	normal (⊥)
IV. circumferential fibers	normal (⊥)	parallel (||)

To study the time-dependent micromechanics of the meniscus, a ramp-and-hold force relaxation test was performed via AFM. Immediately following the indentation, the z-piezo was held at a constant position for ≈ 30 seconds, resulting in an approximately constant indentation depth. During this period, both the z-piezo displacement and cantilever bending were recorded as a function of time at 500 Hz sampling rate, from which, the temporal profiles of indentation force, F(t), and depth, D(t) (mostly constant), were extracted.

2.3 Micromechanical data analysis

At each indentation location, indentation force versus depth (F–D) curve was obtained by calibrating the cantilever deflection sensitivity on a mica substrate and spring constant via thermal oscillation [30]. The effective indentation modulus (E_ind) was calculated by fitting the whole loading portion of each F-D curve to the finite thickness-corrected Hertz model [31] via least squares linear regression (Fig. 1c):

$$F=\frac{4}{3}\frac{E_{\mathit{\text{ind}}}}{\left(1-v^2\right)}{R}^{1/2}{D}^{3/2}{C}_{\chi }(F,D,H,R)$$ (1)

where ν is the Poisson’s ratio (≈ 0 for bovine meniscus [32]), R is the tip radius, H is the section thickness, and C_χ is the substrate constraint correction factor that depends on F, D, H and R. Here, E_ind represents the effective resistance to indentation at a finite indentation rate ≈ 10 μm/s, instead of the instantaneous modulus.

For each ramp-and-hold relaxation test, the relaxation segment of indentation force, F(t), was fitted to a five-element spring-dashpot model to extract two time constants, τ₁ and τ₂ (τ₁ < τ₂),

$$F(t)/C_{\chi }=B_0+B_1\mathit{\text{exp}}(-t/{\tau }_1)+B_2\mathit{\text{exp}}(-t/{\tau }_2)$$ (2)

where the correction factor C_χ was applied to account for the substrate effect due to finite specimen thickness. Then, the fitting parameters of B₀, B₁ and B₂ were used to calculate the time-dependent material properties within the Hertzian deformation framework. Following the analysis procedure established by Mattice et al. [33] for relaxation following indentation at a finite ramp rate, we extracted the temporal indentation modulus, E(t),

$$E(t)=E_{\infty }+E_1\text{exp}(-t/{\tau }_1)+E_2\text{exp}(-t/{\tau }_2),$$ (3)

where,

$$E_{\infty }=\frac{B_0(1-v^2)}{D_{\max }^{3/2}(4\sqrt{R}/3)}$$ (4)

and

$$E_k=\frac{B_k(1-v^2)}{(RC{F}_k)D_{max}^{3/2}(4\sqrt{R}/3)},k=1,2.$$ (5)

Here, E_∞ is the equilibrium indentation modulus, E₁ and E₂ are the time-dependent moduli corresponding to the short and long term relaxation mode, respectively. The factor RCF_k, is the “ramp correction factor” that accounts for the finite indentation ramp rate [33, 34],

$$RC{F}_k=\frac{{\tau }_k}{t_R}[\text{exp}(t_R/{\tau }_k)-1],k=1,2.$$ (6)

where t_R is the total rise time of the indentation ramp segment. As a result, this model yielded the equilibrium modulus, E_∞, and the time-dependent properties corresponding to the two relaxation modes, (E₁, τ₁) and (E₂, τ₂). The instantaneous indentation modulus, E₀, was estimated as,

$$E_0=E_{\infty }+E_1+E_2.$$ (7)

We therefore used the ratio of equilibrium versus instantaneous modulus, E_∞/E₀, as an indicator of the degree of elasticity. This method has been used to reveal the time-dependent mechanical properties of costal cartilage [35], the insertional zone of meniscal attachments [36], as well as poly(ethylene glycol) (PEG)-based hydrogels [37]. In this study, the implement of RCF_k resulted in minor changes to E₁ and E₂ (e.g., RCF₁ = 1.30 ± 0.06, RCF₂ = 1.00 ± 0.01, mean ± 95% CI, for the outer zone horizontal section of circumferential fibers), and did not affect the observed trends or conclusions.

2.4 Collagen nanostructure analysis

Since the fiber-level microstructure of the meniscus ECM has been revealed in detail by optical microscopy [9, 10], this study focused on the fibril-level, nanoscale structure of collagen. Immediately after AFM tests, each section was fixed with Karnovsky’s fixative (Electron Microscopy Sciences, Hatfield, PA), dehydrated in a series of graded water-ethanol and ethanol-hexamethyldisilazane (HMDS) mixtures [38], and dried in air to retain the 3D collagen architecture. Scanning electron micrographs (SEM, Zeiss Supra 50VP) were acquired on samples coated with ~ 6 nm thick platinum. In addition, tapping mode AFM images were taken in ambient conditions on uncoated samples using nanosized silicon tips (R ≈ 10 nm, k ≈ 42 N/m, NCHV, BrukerNano) and the Dimension Icon AFM (BrukerNano). For histology, separate deep zone sections were stained with Alcian Blue and Picrosirius Red (PSR) and imaged under polarized light to visualize proteoglycans and collagen fiber bundle organization at the microscale.

For each animal, five SEM images were taken from a 5 μm × 5 μm region of interest (ROI) within each structural unit. The collagen fibril diameter, d_col (in nm), and fibril alignment orientation angle, θ (in rad), were measured from each image by two blinded observers via ImageJ (≈ 100 fibrils per image). To compare fibril diameter among different structural units, values of d_col were pooled from multiple images of the same unit from all three animals. To compare the degree of collagen fibril alignment, we first offset values of θ by their average angle, μ_θ, to ensure μ_θ = 0 within each ROI. Next, we pooled all values from different ROIs of the same structural unit. In addition, since fibril orientation angles are axial data without directions (i.e., θ and θ + π are equivalent), we converted the values of 0 to occupy the whole circular space of [−π π] by multiplying θ by a factor of two [39]. We then fitted the distribution of θ for each structural unit with the von Mises probability density function, which is the analog of normal distribution in the circular space,

$$f(\theta ;{\mu }_{\theta },\kappa )=\frac{1}{2\pi I_0(\kappa )}\text{exp}[\kappa \mathit{\text{cos}}(\theta -{\mu }_{\theta })]$$ (8)

where κ is the concentration parameter (analogous to the inverse of variance), and I₀(κ) is the zeroth order modified Bessel function of the first kind. Here, κ is a measure of how closely the vectors of θ cluster around the average angle μ_θ, and a greater value of κ indicates a higher degree of fibril alignment.

2.5 Statistical analysis

To avoid the assumption of normal distribution of the data, we used nonparametric statistical tests on the micromechanical properties, including E_ind, E_∞, E₁, E₂, E_∞/E₀, τ₁, and τ₂. The Mann-Whitney U test was used to examine the impact of indentation orientation on the same structural unit. The Kruskal-Wallis test followed by the Tukey-Kramer multiple comparison was used to examine the differences among various structural units and anatomical regions, and to examine the zonal variation of each structural unit. For each mechanical parameter, data was pooled from the three animals, as we did not find statistically significant differences between individual animals (e.g., Fig. 2a). For structural data, since ≥ 300 fibrils were measured for each structural unit, according to the central limit theorem, the parametric unpaired two-sample t-test was used to compare d_col of inner versus outer zones for each structural unit, and one-way ANOVA followed by the Tukey-Kramer multiple comparison was used to compare different structural units within each of the inner and outer zone. For fibril orientation data, θ, the Mardia and Jupp test of concentration equality [40] was applied to compare the von Mises concentration parameter κ between inner and outer zones for each structural unit, and to compare κ across structural units within the same zone with the Bonferroni family-wise error correction. In all the tests, a p-value of less than 0.05 was taken as statistically significant.

Fig. 2.

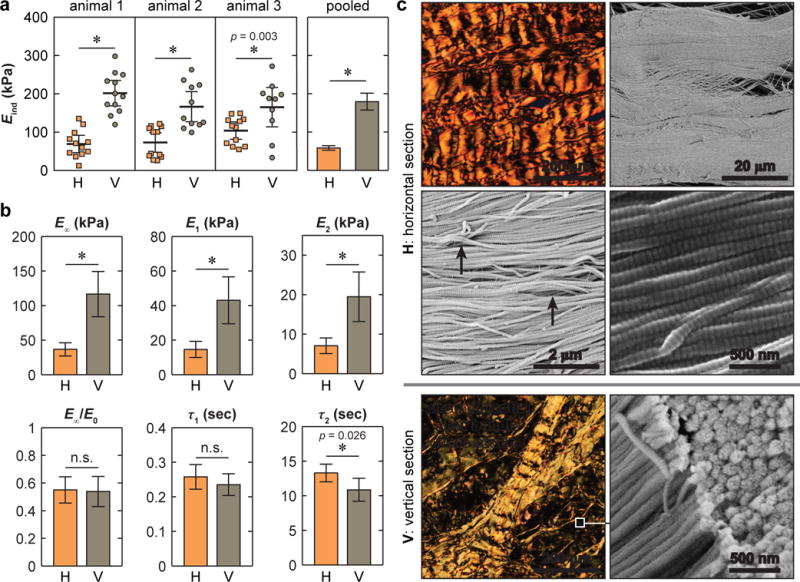
Micromechanical anisotropy of the circumferential fibers. (a) Comparison of effective indentation modulus, E_ind, measured on horizontal versus vertical sections, where comparison of individual locations within each animal and pooled results yield the same significant results (*: p < 0.01 via Mann-Whitney U test, and p < 0.001 if not provided). (b) Comparison of time-dependent micromechanical properties between horizontal and vertical sections: equilibrium modulus (E_∞), degree of elasticity (E_∞/E₀), time coefficients and moduli for short term (E₁, τ₁) and long term (E₂, τ₂) relaxations (mean ± 95% CI of ≥ 20 locations pooled from n = 3 animals, *: p < 0.05 via Mann-Whitney U test, and p < 0.001 if not provided. H: horizontal section, V: vertical section). (c) Polarized light microscopy images of Alcian Blue/Picrosirius Red stained sections showing collagen fiber microstructure, and SEM images showing collagen fibril nanostructure in the deeper zone (white arrowheads: fiber-level crimping with periodicity ~ 30 μm, black arrows: fibril-level crimping with periodicity ~ 1 μm).

3. RESULTS

We detected salient anisotropy in the micromechanical properties of the circumferential fibers, the major structural component of the meniscus ECM (Fig. 2). For all animals, indentation on the vertical section (E_ind = 179 ± 22 kPa, mean ± 95% CI) yielded higher moduli than that on the horizontal section (E_ind = 58.4 ± 5.8 kPa). This trend was the same whether testing individual animals or examining the pooled data from all three animals (Fig. 2a). For time-dependent properties, following the trend of E_ind, the horizontal section also yielded lower equilibrium modulus, E_∞ as well as moduli corresponding to the short term (E₁) and long term (E₂) relaxation, while the degree of elasticity (E_∞/E₀) was similar on both sections (Fig. 2b). The five-element relaxation model fit showed that short term relaxation was a more dominant mode than the long term one for both sections (E₁ > E₂). Meanwhile, for the short term relaxation, both sections had similar τ₁, while for the long term relaxation, the horizontal section showed moderately longer τ₂ (Fig. 2b). On both sections, the alignment and structure of the circumferential fibers were revealed by histology at the microscale and SEM at the nanoscale (Fig. 2c).

We detected significant variations of E_ind amongst various ECM structural units, as shown for the outer zone (Fig. 3). On the vertical section, the circumferential fibers exhibited higher E_ind than other units, while on the horizontal section, a similar E_ind was found across all three units. The intact surface, on the other hand, had the lowest E_ind In addition, heterogeneity of E_ind was also observed between the tension-bearing outer and middle zones versus the compression-bearing inner zone (Fig. 4). For the circumferential fibers, on the vertical section, E_ind of the outer zone was 3.2 ± 0.8 times (mean ± 95% CI) higher than that of the inner zone. On the horizontal section, such difference was much reduced (1.6 ± 0.4 times, Fig. 4a). As a result, the degree of anisotropy was substantially lower in the inner zone, where the ratio of E_ind between vertical versus horizontal section was 2.1 ± 0.7 times in the inner zone, and 3.3 ± 0.7 times in the outer zone (Fig. 4a). Interestingly, unlike the circumferential fibers, the other units, including surface, superficial layer and radial tie fibers, did not exhibit significant zonal variations (Fig. 4b). In addition, since the middle zone had similar E_ind as the outer zone, this study primarily focused on differences between the inner and outer zones.

Fig. 3.

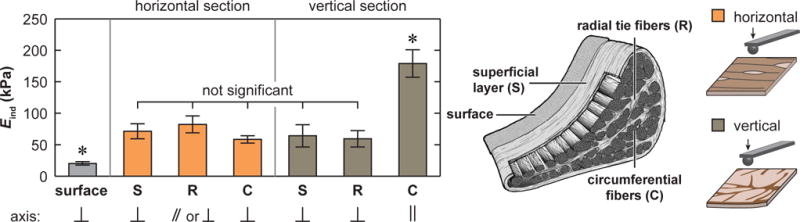
Heterogeneity of the effective indentation modulus, E_ind, across different meniscus ECM structural units of the outer zone (mean ± 95% CI of ≥ 20 locations pooled from n = 3 animals, *: p < 0.0001 from Kruskal-Wallis test followed by Tukey-Kramer multiple comparison).

Fig. 4.

Heterogeneity of the effective indentation modulus, E_ind, across the inner, middle and outer zones of the meniscus ECM. (a) E_ind of circumferential fibers, for each cross-section type, different letters indicate significant difference in E_ind across zones via Kruskal-Wallis test followed by Tukey-Kramer multiple comparison, (*: p < 0.01 between horizontal and vertical sections within each zone via MannWhitney U test). (b) E_ind of other structural units, where no significance was found across zones or between cross-sections (mean ± 95% CI of ≥ 20 locations for each structural unit, pooled from n = 3 animals).

In contrast to the salient heterogeneity in E_ind, the time-dependent mechanical characteristics were more homogeneous (Fig. 5). The modulus values, including E_∞, E₁ and E₂, followed similar trends as E_ind (data are not shown for E₁ and E₂). However, the degree of elasticity (E_∞/E₀) and the relaxation time constants (τ₁ and τ₂) were relatively consistent amongst different structural units (Fig. 5a) and across different zones (Fig. 5b) despite variations in matrix composition and collagen fibril structure. For the circumferential fibers, vertical sections yielded moderately shorter τ₂ only in the outer zone, but had similar τ₁ in comparison to the horizontal section in both outer and inner zones (Figs. 2b, 5b). However, one exception to this finding occurred on the surface, which had similar time constants, but lower E_∞/E₀ and E_∞ compared to all other interior structural units (Fig. 5a).

Fig. 5.

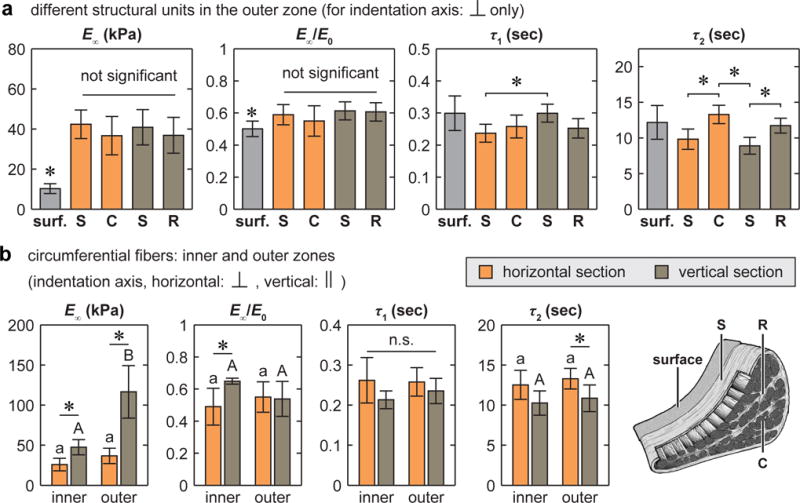
Heterogeneity of time-dependent micromechanical properties of the meniscus ECM: equilibrium modulus, E_∞, degree of elasticity, E_∞/E₀, time constants for short term (τ₁) and long term (τ₂) relaxations (E₁ and E₂ followed the same trend as E_∞, therefore are not shown, where E₁ > E₂). (a) Comparison across different structural units of the outer zone on horizontal and vertical sections, in which the indentation was performed normal to their fiber axes (*: p < 0.05 from Kruskal-Wallis test followed by Tukey-Kramer multiple comparison). (b) Comparison between the inner versus outer zones of the circumferential fibers on horizontal and vertical sections (for each cross-section type, different letters indicate significant difference between inner versus outer zone via Kruskal-Wallis test followed by Tukey-Kramer multiple comparison, *: p < 0.05 between horizontal and vertical sections within each zone via Mann-Whitney U test, all data are shown as mean ± 95% CI of ≥ 20 locations pooled from n = 3 animals).

The ECM collagen fibril nanostructure was revealed by SEM and AFM (Fig. 6a,b). Consistent with previous reports on human [2] and bovine [41] menisci, collagen fibrils on the meniscal surface were oriented randomly within the transverse plane. In the interior, the fibrils were aligned along the fiber axis within each structural unit: circumferentially for circumferential fibers, and radially for superficial layer and radial tie fibers. Quantitative analysis showed that random fibrils on the surface were significantly thinner compared to other regions (p < 0.0001). For all structural units, fibrils in the outer zone are thicker than those in the inner zone (Fig. 7a). In addition, circular analysis using the von Mises model (e.g., Fig. 6c) confirmed the relative randomness of collagen fibril orientation on the surface (κ < 0.5), and high degree of alignment in the interior units (Fig. 7b). In the superficial layer, similar κ was detected between the two regions. In both the radial tie fibers and circumferential fibers, the concentration was higher in the outer zone. Furthermore, in the inner zone, similar κ were observed among the three interior units; in the outer zone, they were significantly different, where radial tie fibers had the highest κ, while superficial layer had the lowest.

Fig. 6.

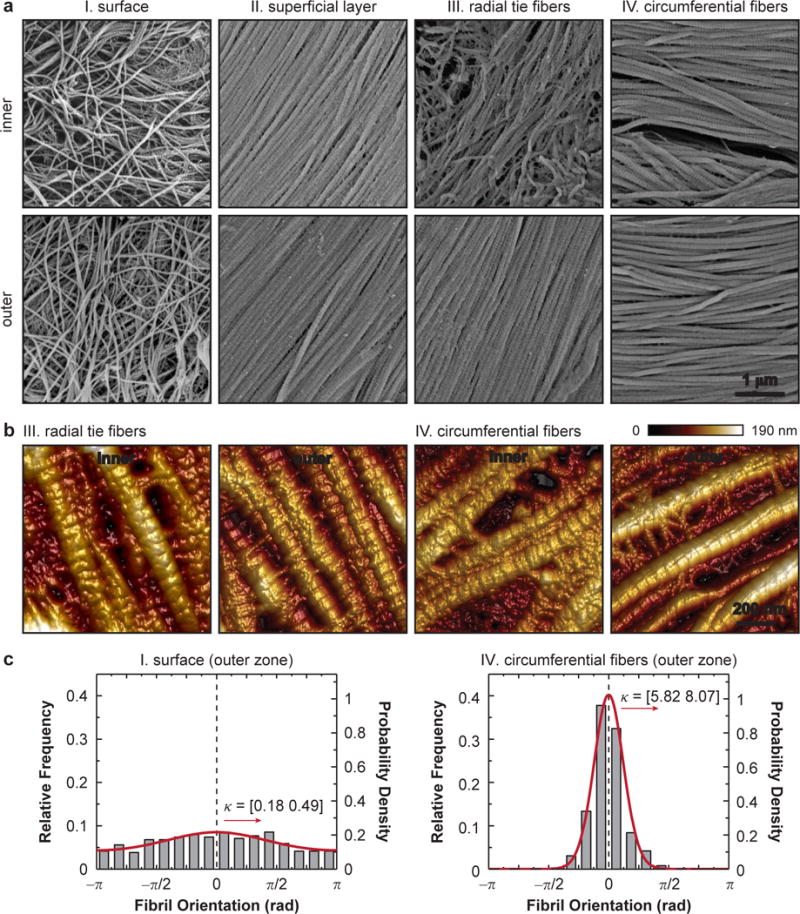
Nanostructure of collagen fibrils in the meniscus ECM. (a) Scanning electron microscopy (SEM) images of each structural unit show the dimension and alignment of collagen fibrils. (b) Higher resolution tapping mode AFM images show the presence of proteoglycans between fibrils. (c) Relative frequency of collagen fibril orientation distribution and corresponding von Mises fit of the intact surface and circumferential fibers in the outer zone. Data are pooled from n = 3 animals for each unit and shown with the 95% CI of κ, the von Mises concentration. The y-axes of the frequency probability mass function (left) and the von Mises probability density function fit (right) are adjusted to account for the interval of each frequency bin, which is π/8.

Fig. 7.

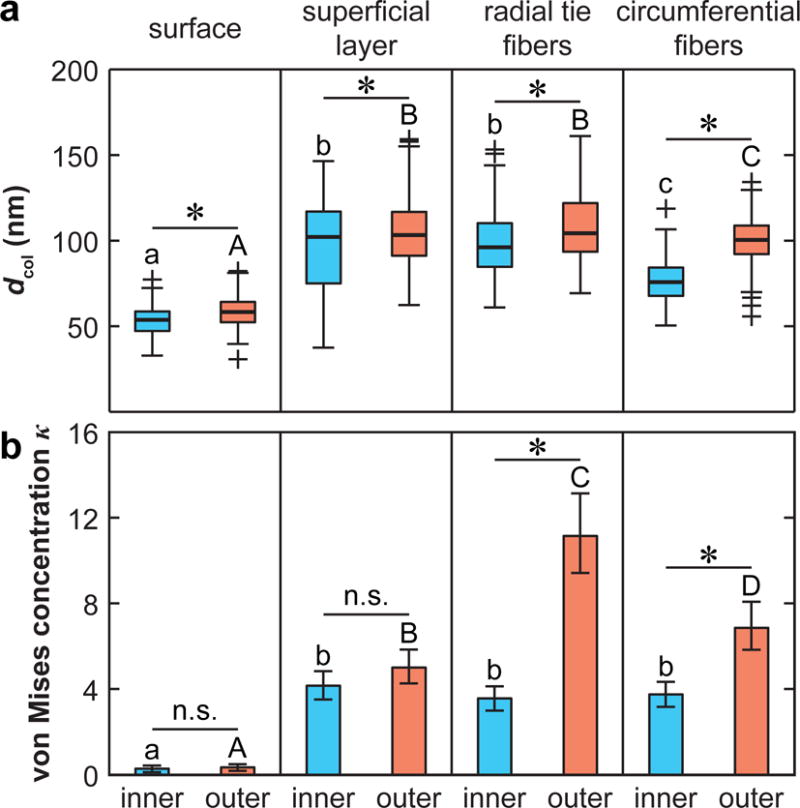
Summary of collagen fibril nanostructure in meniscus ECM inner and outer zones. (a) Box-and-whisker plot of diameter, d_col, distribution (≥ 300 fibrils pooled from n = 3 animals for each unit. Different letters indicate significant difference in d_col across different units within the same zone, and *: p < 0.0001 between inner versus outer zone for the same structural unit via one-way ANOVA followed by Tukey-Kramer multiple comparison). (b) von Mises concentration parameter, κ (mean ± 95% CI, estimated from > 300 fibrils pooled from n = 3 animals for each unit. Different letters indicate significant difference in κ across different units within the same zone, and *: p < 0.01 between inner versus outer zone for the same structural unit via Mardia and Jupp test of equal concentration followed by Bonferroni correction).

4. DISCUSSION

4.1 Anisotropy of the circumferential fibers

The micromechanical anisotropy of circumferential fibers (Fig. 2) is not intuitive. For fibrous tissues, indentation normal to the fiber axis would create long range tensile stress within the fiber plane [42], while indentation parallel to the fiber axis results in fibril compression, bending or buckling [43]. On vertical sections, where indentation was performed parallel to the fiber axis, the measured E_ind was higher than that on horizontal sections, where indentation was performed normal to the fiber axis. This observation seems contradictory to the fact that meniscus is stiffer in tension than in compression [44]. However, this finding can be explained by the hierarchical structure of the meniscus ECM collagen fibers and the fact that deformation takes place locally, i.e., at the microscale. In the ECM, collagen undulation and crimping are present at both the fibril level (nm-scale, black arrows, Fig. 2c) and the fiber level (μm-scale, white arrowheads, Fig. 2c). In accordance, the tensile response of meniscus is highly nonlinear [44]: at small strains (ε << 5%), the stiffness is very low, corresponding to the “toe region” of the stress-strain curve; once the strain reaches a critical uncrimping level (≈ 5–10% [45]), i.e., point at which collagen fibers are fully uncrimped, the stiffness increases drastically, corresponding to the “linear region”. Here, the deformation scale (~ 1 μm) is at least one order lower than the fiber crimping periodicity (~ 30 μm), and similar to the fibril crimping periodicity (~ 1 μm, Fig. 2c). Local strain induced by nanoindentation therefore does not exceed the critical uncrimping level. As a result, fibril uncrimping and sliding, instead of tensile stretching, dominate the indentation response [46, 47]. In fact, on the horizontal section, E_ind is > 10³ × lower than macroscopic linear region tensile moduli of meniscus circumferential fibers (~ 100 MPa) [3], but is consistent with previous nanoindentation results on porcine [23] and human [24] menisci at similar deformation scales. On the other hand, within each fiber, the fibrils are highly aligned and densely packed (Fig. 2c). Due to lateral constraint from interfibrillar contact and fiber bundling, indentation parallel to the fiber axis can result in a continuous multiaxial stress field, leading to an indentation response similar to a material continuum, which is much less compliant than bending or buckling of discrete fibrils [48]. These effects together contribute to the observed anisotropy (Fig. 2a).

It should be noted that the modulus contrast reported here (Fig. 2) does not accurately reflect the intrinsic material anisotropy. Under nanoindentation, the indenter tip introduces a multiaxial stress and strain field, and the modulus estimated by the isotropic Hertz model is an effective measure of the compression resistance governed by the constitutive response of material properties at all axes [49]. As shown for mineralized biological tissues of bone [50] and ganoine [51], such multiaxial loading profile can obscure the intrinsic anisotropy. A more accurate assessment of anisotropy has been achieved by analyzing the shape of indentation residual via an anisotropic mechanics model [50], or by uniaxial compression on focused ion beam-machined micro pillars [52]. For soft tissues such as the meniscus, however, its hydrated nature prevents the use of the residual shape analysis or uniaxial microcompression. A more accurate measure of its intrinsic anisotropy would rely on indenting surfaces prepared by sectioning multiple orientations in combination with anisotropic mechanics models [53].

4.2 Heterogeneity across structural units

The heterogeneity of indentation modulus E_ind among different structural units, as shown for the tension-bearing outer zone (Fig. 3), can be attributed to the complexity of ECM collagen fiber structure. The superficial layer and radial tie fibers are both composed of radially aligned fibers with nano-to-microscale crimping. On the vertical section, when indentation is normal to their fiber axes, they undergo fiber uncrimping and sliding, yielding lower E_ind than circumferential fibers (Fig. 3). On the horizontal section, when indentation is normal to the fiber axes of the circumferential fibers and superficial layer, both units undergo uncrimping and sliding, yielding similar E_ind. For radial tie fibers, the fiber axes bifurcate randomly within the radial plane [10], and horizontal slices thus expose oblique fiber cross-sections, leading to a mixed response of fibril uncrimping and shear, which exhibits similar E_ind as the other two units (Fig. 3). On the other hand, all three units of the interior share a similar nanostructure of densely packed, highly aligned, yet crimped collagen fibrils (Fig. 6a,b). This leads to the similar E_ind when nanoindentation is performed normal to the fiber axis, regardless of the cross-section orientation or structural unit type. Therefore, at least in the tension bearing outer zone, the complexity of meniscus mechanical function appears to be primarily manifested through the organization of different structural units at the micro-to-macro scales, while all the units share similar intrinsic mechanical properties. The ~ 10 μm thick surface layer, however, is an exception. This layer is composed of much thinner, randomly oriented transverse fibrils (Figs. 6,7) with significantly lower E_ind than all other units.

4.3 Heterogeneity across anatomical zones

Between the tension-bearing outer and middle zones [3] and the compression-bearing inner zone [4], the circumferential fibers show marked variations in micromechanical properties (Fig. 4a). The lower E_ind of the inner zone suggests that the decrease in collagen fibril diameter, density and organization (Figs. 6,7) most likely outweighs the effect of increased compression-bearing proteoglycans in the inner zone [6, 7]. Meanwhile, the reduced degree of anisotropy in E_ind in the inner zone can also be attributed to both the decreased alignment of collagen fibers (lower κ, Fig. 7b) and the increase in “amorphous” proteoglycans that are more isotropic in their mechanical contributions.

In contrast to the circumferential fibers, all other structural units do not exhibit such zonal heterogeneity (Fig. 4b). These units do not directly contribute to the tension-compression load bearing functions of the meniscus. Instead, they mainly serve to maintain the integrity of circumferential fibers. Their micromechanical properties are therefore not directly impacted by the zonal variations in meniscus loading conditions. For the surface and the superficial layer, both the collagen orientation and E_ind are similar from inner to outer zones, suggesting similar functions across anatomical regions, possibly including surface load transmission, lubrication and stabilization of the circumferential fibers. For the radial tie fibers, the function of integrating circumferential fibers and sustaining shear stresses is likely less important in the inner zone. However, such changes are manifested through its arborization into smaller sheets and bundles, reduced diameter and alignment within the fiber (Fig. 7) and decreased density from outer to inner zones, instead of the modulus determined by the local fibril nanostructure (Fig. 6).

4.4 Heterogeneity of time-dependent micromechanics

In soft tissues, time-dependent mechanics can be attributed to both poroelasticity that is due to fluid-matrix interactions [54], and intrinsic viscoelasticity that is due to macromolecular friction amongst matrix macromolecules [55]. Given the substantial heterogeneity of the meniscus ECM, it is unlikely for different zones or different structural units to share the same molecular-level time-dependent mechanisms. For example, proteoglycans can be a major player in the hydraulic permeability and intrinsic viscoelasticity of the inner zone, while their contribution to the outer zone mechanics is less important. Therefore, in the presence of heterogeneity of E_ind, the relative homogeneity in E_∞/E₀, τ₁ and τ₂ (Fig. 5a,b) indicates an important mechanical design principle of the meniscus ECM: all the interior structural units, despite their compositional or structural differences, possess similar relative time-dependent mechanical characteristics. This feature can be an effective means to minimize the extent of the redistribution in local stresses and strains, and in the extent of stress concentration at the structural unit boundaries during time-dependent deformation. A similar feature is observed at larger scales, where microindentation (R ≈ 100 μm) detected similar E_∞/E₀ across various anatomical sites of the meniscus surface [21] and the interior horizontal cross-sections [22]. Such self-consistency in time-dependent mechanics is also found for cartilage ECM, where despite variations in proteoglycan content, collagen fibril architecture, hydraulic permeability and modulus, a constant poroelastic time constant was detected throughout cartilage depth [56]. On the other hand, the moderate anisotropy of τ₂ measured on the circumferential fibers in the outer zone (Figs. 2b,5b) highlights that viscoelastic deformation of the collagen fibrils can be different for orientations normal versus parallel to the fiber axis. In contrast, in the inner zone, with less organized collagen fibers and higher “amorphous” proteoglycan content, both τ₁ and τ₂ become isotropic.

To gain further insights into time-dependent mechanisms of the meniscus, we performed scaling analysis [57] to estimate the characteristic poroelastic time constant, τ_p. For the meniscus ECM, the hydraulic permeability is ~ 10⁻¹⁵ m⁴/(N•s) [44], and our nanoindentation results suggest that the aggregate modulus H_A is ~ 0.1 MPa. Under current nanoindentation configuration, we estimate the fluid flow length, L_p ~ R × arccos[(R − D)/R] ≈ 3 μm [57], and thus, τ_p ~ L_p²/(H_Ak)=0.1 sec [58]. In this study, τ₁ is ~ 0.1 sec and τ₂ is ~ 10 sec, it is likely that poroelasticity could be a major factor for the short term relaxation, while the long term relaxation is mostly governed by intrinsic viscoelasticity. This trend is consistent with the time-dependent mechanics of cartilage at the microscale: when L_p is ~ 1 μm, poroelastic deformation is much faster than viscoelasticity [57, 59]. However, this trend is reversed at the macroscale, when L_p is ~ 1 mm [60]. This is because τ_p scales parabolically with L_p [58], τ_p at μm-scale is several orders faster than that at mm-scale [57, 59], while the viscoelastic times remain consistent despite the variation of L_p [61]. Similarly, for hydrogels, a slower τ_p than viscoelastic times is also detected under macroscopic indentation [62]. For this study, however, we did not modulate L_p, and thus, we cannot accurately determine the contribution of poro- versus viscoelasticity. Ongoing studies are applying our custom AFM-nanorheometer [57, 59] to separate the two mechanisms in native meniscus by systemically varying L_p.

4.5 Implications for meniscus tissue function and repair

For meniscus repair, in order to restore the normal meniscus-cartilage contact and loading, it is critical to simulate the shape and bulk tissue-level properties of the meniscus [3, 4, 44, 55]. The direct deterministic benchmarks for successful regeneration are the mechanical properties of native meniscus at the macroscale, rather than at the nano- or microscale [63]. However, the specialized, complex tissue-level biomechanical functions of native meniscus are endowed by the highly complex features of its ECM at smaller lengths. In addition, recent studies suggested that the nanostructure and nanomechanical properties of the meniscus ECM are important factors that regulate cell migration [64] and mechanotransduction [11]. This work can thus provide insights for better mimicking the complex properties of native tissue, and for helping direct meniscus cell behavior in engineered scaffolds.

One limitation of this study is that all the tests were performed at zero tissue-level strain. Given the salient nonlinearity of the meniscus tissue biomechanics [44], the outcomes do not necessarily represent the micromechanical behaviors at higher tissue strains. Currently, studying such behavior is hindered by the technical challenge of applying tensile strain to AFM specimens in fluid. To this day, however, AFM imaging has been performed on thin films in tension [65]. This technique can be modified to enable micromechanical studies of the meniscus under tension and in fluid.

5. CONCLUSIONS

This study connected the anisotropy and heterogeneity in the elastic and time-dependent micromechanical properties of the meniscus ECM with its collagen fibril nanostructure. The anisotropy in modulus is due to differences in collagen fibril deformation modes with regard to its fiber axis. Heterogeneity is associated with the collagen fiber organization among different structural units, while these units share similar nanostructural and micromechanical properties. In contrast to the heterogeneity in modulus, the degree of elasticity and relaxation time constants are more homogeneous and isotropic. These results contribute to a basic understanding of multiscale structure-mechanics relationships of the meniscus ECM, which has the potential to improve the regeneration of meniscus through modulating the local micromechanical environment.

Statement of Significance.

Meniscal damage is a common cause of joint injury, which can lead to the development of posttraumatic osteoarthritis among young adults. Restoration of meniscus function requires repairing its highly heterogeneous and complex extracellular matrix. Employing atomic force microscopy, this study quantifies the anisotropic and heterogeneous features of the meniscus extracellular matrix structure and mechanics. The meniscus micromechanical characteristics are connected with the collagen fibril nanostructure, and its variation with tissue anatomical locations. These results provide a fundamental structure-mechanics knowledge benchmark, against which, repair and regeneration strategies can be developed and evaluated with respect to the specialized structural and functional complexity of the native tissue.