Representation of different exact numbers of prey by a spider-eating predator

Abstract

Our objective was to use expectancy-violation methods for determining whether Portia africana, a salticid spider that specializes in eating other spiders, is proficient at representing exact numbers of prey. In our experiments, we relied on this predator's known capacity to gain access to prey by following pre-planned detours. After Portia first viewed a scene consisting of a particular number of prey items, it could then take a detour during which the scene went out of view. Upon reaching a tower at the end of the detour, Portia could again view a scene, but now the number of prey items might be different. We found that, compared with control trials in which the number was the same as before, Portia's behaviour was significantly different in most instances when we made the following changes in number: 1 versus 2, 1 versus 3, 1 versus 4, 2 versus 3, 2 versus 4 or 2 versus 6. These effects were independent of whether the larger number was seen first or second. No significant effects were evident when the number of prey changed between 3 versus 4 or 3 versus 6. When we changed prey size and arrangement while keeping prey number constant, no significant effects were detected. Our findings suggest that Portia represents 1 and 2 as discrete number categories, but categorizes 3 or more as a single category that we call ‘many’.

1. Introduction

Vertebrates are the usual subjects in numerical-cognition research, but this is unfortunate because there remain important questions concerning how deep into the animal kingdom we can go and still find interesting traces of decisions based on numerical information. For example, to understand the cognitive precursors from which human numerical capacities evolved [1,2], it would be useful to know how widely particular numerical capacities are expressed within the animal kingdom.

Some of the better-known research related to the numerical competence of animals has depended on extensive training of the experimental subjects (e.g. [3,4]) and this might have encouraged thinking that numerical competency is a hard-earned ability that animals adopt only as a last resort [5,6]. However, a shift to a functional perspective (sometimes called an ‘ecological approach’), where the emphasis is on the role that numerical competency plays in the lives of particular animals in their particular natural environments [7–9], has largely supplanted the view that animals attend to number only as a last resort.

The functional perspective has been especially important in our own research (see [10]) on cognitive specialization by jumping spiders (family Salticidae). These spiders are especially convenient experimental subjects because their capacity for seeing fine details related to their prey [11] supports distinctive, and often intricate, vision-based predatory behaviour [12,13].

Our working hypothesis is that situations in which a capacity for numerical cognition might be useful are especially common when predators, including small predatory arthropods, target prey that are similar to themselves in size and are capable of deploying active defence (see [14]). All salticids are predators and most of the species in this large family of almost 6000 described species [15] may feed primarily on insects [16]. However, spiders are the preferred prey of a sizeable minority [17], with species from the genus Portia being the most thoroughly investigated members of this minority [18]. Portia regularly encounters more than one spider at the same time, including spiders capable of killing and eating Portia [19]. For Portia, a well-developed capacity for numerical cognition might often influence survival as well as prey-capture success during predatory sequences. With this hypothesis as our rationale, we decided to use expectancy-violation methods for investigating whether Portia africana can represent the exact number of spiders in a scene.

It has been customary to base expectancy-violation methods on letting a test subject preview a scene that disappears and then, at a later time, comes into view again [20]. For example, a screen might be put between the scene and the test subject and then, during the time when the test subject's view is blocked, a scientist can alter the items in the scene. Data relevant to expectancy violation come from comparing how test subjects respond to altered scenes with how they respond to scenes that stay the same. Instances of the subject gazing at an altered scene for longer than an unaltered scene (i.e. instances of longer ‘looking time’: see [21]) have especially often served as evidence that the subject has detected a mismatch between the current scene and a representation of a scene it had previously loaded into working memory (i.e. this has been a basis for concluding that the individual has experienced expectancy violation).

‘Working memory’ refers to the mechanisms by which priority information is made readily accessible to other cognitive processes [22], including selective attention (e.g. [23]), problem solving (e.g. [24]), making plans (e.g. [25]) and understanding object permanence (e.g. [26]). From experiments, there is evidence of bees relying on working memory when, after training, they successfully complete delayed-matching-to-sample tasks [27,28]. Research on salticids has been different [10,13], as these spiders have been shown, in experiments based on expectancy-violation methods, to rely on working memory without prior training [29].

Expectancy-violation methods are better known from research on pre-verbal infants (e.g. [30]), non-human primates [31] and even parrots [32], and there continues to be a striking scarcity of expectancy-violation methods being used in research on arthropods. Yet Pepperberg & Kozak [32] proposed that, when tailored to the biological characteristics of particular species, expectancy-violation methods should become applicable to a wider range of animals. As an example, we used Portia-specific expectancy-violation methods in experiments designed to determine whether this spider represents specific prey types during predatory sequences [29]. In these experiments, we relied on Portia spontaneously adopting ambushing as a prey-capture method. After seeing a prey item at the beginning of a trial, Portia positioned itself for initiating an attack, but then, before Portia could act, we hid the prey item behind a shutter. When we did this, Portia waited while facing the shutter and then, when we lifted the shutter at a later time, Portia could see prey that was either identical to or different from the type of prey it had seen earlier. The findings from these experiments were as predicted, with significantly fewer Portia individuals following through to make an attack within the allowed time (i.e. Portia hesitated) when the two prey types were different. This suggests that Portia experienced expectancy violation when the representation of the prey type it had loaded into working memory at the beginning of a trial did not match the prey it saw later.

The hypothesis we consider here is that Portia's strategy for using working memory during predatory sequences includes representing the exact number of prey present in a scene. However, our methods here differ from the methods used in the earlier study [29] because, instead of changing the type of prey, we change the number of prey while keeping the type of prey constant. Our methods also differ by being based on Portia's known capacity to undertake detours even when these detours result in losing sight of the prey it is pursing [33–35].

We say ‘number’ because we are interested in whether Portia represents the items in a scene as something countable. By ‘countable’, we mean a correspondence to natural numbers (1, 2 and so forth; see [36]). Our experiments are not designed to determine whether Portia literally counts the number of prey in a scene according to all of the criteria pertaining to ‘true counting’ [37] and we are not proposing that spiders understand numbers as abstract entities [38,39], but we are interested in whether Portia does something more precise than representing countable things as a value of a continuous variable (see [40,41]). Our hypothesis is that Portia relies on representations that correspond to specific cardinal numbers (see [42]).

2. Material and methods

2.1. General

Our test spiders were juveniles (body length, 5.0 mm) of P. africana (hereafter ‘Portia’) that had moulted two weeks earlier and did not moult again for at least two weeks. All test spiders were taken from laboratory cultures (second and third generation) that had been started from specimens collected from our field site (Mbita Point, western Kenya; elevation 1200 m.a.s.l.; latitude 0.4°; longitude 34.2°). As we adopted rearing and general testing procedures that have become standard in our laboratory (e.g. [13]), only essential details are provided here. With our objective being to investigate Portia's innate predisposition to respond to the number of prey in a scene, we standardized rearing, maintenance and testing methods in ways that minimized the risk of prior experience influencing experimental outcomes.

The prey that we used in experiments was an unidentified species of Argyrodes (see [29]) that lives as a kleptoparasitic spider in other spiders' webs (see [43]). Argyrodes is one of Portia's most common prey in our field site and, besides stealing prey from other spiders' webs, Argyrodes preys on other spiders (see [44]), including Portia. As the number of Argyrodes individuals in a single web tends to be highly variable (see [45]), this particular prey might especially often present Portia with situations in which numerical cognition would be relevant.

Instead of using living prey in our experiments, we used lures made from Argyrodes individuals collected as needed from the field. In this way, we could achieve the required tight standardization of the prey we presented to test spiders. As is customary in our research on salticids, we used large sample sizes and we ensured the independence of the data in our experiments by never using any test spider or lure more than once. We also reared each individual test spider in isolation from other conspecific individuals and ensured that no test spiders had any prior experience with the apparatus and procedures used in our experiments, with any species of Argyrodes or with lures of any type.

We carried out all of our experiments between 09.00 and 13.00 (laboratory photoperiod 12 L : 12 D, lights on 08.00). For Portia's maintenance diet in the laboratory, we used juveniles of Leucauge (Tetragnathidae) and Nephilengys (Nephilidae), these being spiders that do not, to human observers, bear especially close resemblance to Argyrodes. Each Portia individual was fed to satiation 3 days per week, with roughly equal numbers of the two prey types being provided. Once per week, we supplemented this maintenance diet by adding male mosquitoes (Anopheles gambiae s.s.) and both sexes of Nilodorum brevibucca (Chironomidae), a non-biting midge species. The mosquitoes came from stock cultures, but we collected the other prey from our field site when needed. As in earlier experiments (e.g. [29]), there was a 7-day pre-trial fast for each test spider, the rationale for the fast being to standardize hunger level and ensure that test spiders were motivated to feed during the trials.

2.2. Lures

For making lures (for details, see [29]), we used three size categories of Argyrodes (small, 2.0 mm; medium, 3.5 mm; large, 5.0 mm). These categories were defined by body length and were accurate to the nearest 0.5 mm. Using CO₂, we immobilized each spider and then placed it in 80% ethanol. On the following day, we removed the spider from the ethanol, put a small drop of sticky gum (Tanglefoot® Pest Barrier) on one side of its abdomen and then positioned it so that the drop of gum held it centred on top of a cork disc. For preservation and for holding the prey spider firmly in place, we sprayed the disc and dead spider with a transparent plastic adhesive (Crystal Clear Lacquer, Atsco Australia Pty). During experiments, the disc was turned on its side so that, from within the apparatus, Portia had a side-on ventral-side-up view of the dead Argyrodes individual. The cork disc was not conspicuous when the lure was viewed side on because Argyrodes' abdomen was wider and higher than the disc's diameter.

2.3. Experimental apparatus

We designed our apparatus (figure 1) based on knowing that Portia will adopt detour routes that require first moving away from prey [46] and from knowing that Portia is reluctant to enter water [35,47]. When explaining our experimental procedures and later when presenting our findings, we will use upper case for the more important parts of the apparatus.

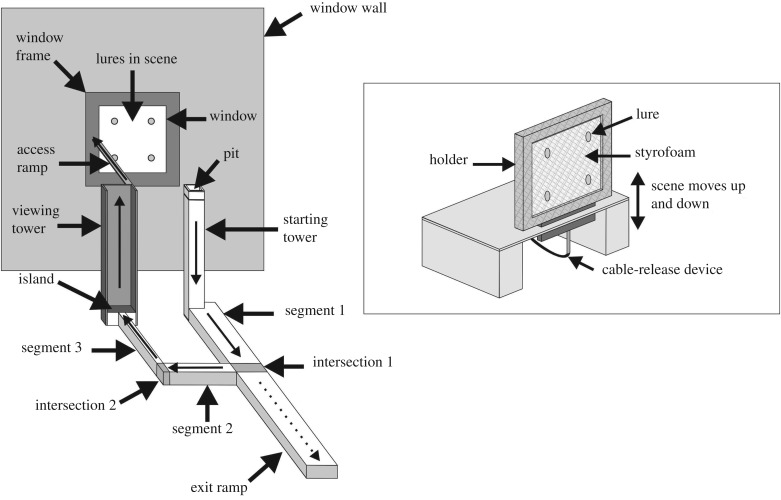
Figure 1.

Apparatus used in expectancy-violation experiments. Not drawn to scale. Side Walls, Front Wall, Ceiling and Pan not shown. Beginning of trial: test spider (Portia africana) walks out of Pit and on to top of Starting Tower. Test spiders complete successful trials by proceeding from Starting Tower along Pathway to top of Viewing Tower. Thin arrows indicate path test spider takes to reach lures; dotted arrow indicates path test spider takes to opt out of completing detour. Inset: example of a Scene with four lures visible to test spider from Starting or Viewing Tower. Cable-release device moves Scene up and down once every 30 s while the test spider is on top of Starting Tower and while test spider is on top of Viewing Tower. When test spider arrives at Island, Scene is removed and then replaced by a different Scene or else the previous Scene is returned.

Each trial began with a test spider on top of a Starting Tower (20 × 20 mm, height 140 mm). From this position, the test spider could view 1–6 lures in a Scene and it could only reach the Scene by walking down from the top of the Starting Tower, across a Pathway and then up to the top of a Viewing Tower (30 × 30 mm, 140 mm high). From the top of the Viewing Tower, which was the same height as the Starting Tower, the test spider could then walk across an Access Ramp that would take it to the Scene.

The Pathway consisted of three Segments, with the Starting Tower rising from one end of Segment 1 and with the Viewing Tower rising from an Island situated at the end of Segment 3. We glued the Pathway (height 20 mm) to the bottom of a Pan (400 × 400 mm) containing distilled water. The water level was 18 mm, which meant that it was 2 mm below the top of the Pathway. A Window Wall and two adjacent Side Walls (400 mm wide × 300 mm high) formed three sides of the Pan. There was a Window (100 × 100 mm) in the Window Wall and the Scene was visible through the Window. Around the Window, there was a Window Frame and, as each of its four sides were 30 mm wide, the outer rim of the Window Frame was 160 × 160 mm.

The Front Wall of the apparatus was 400 mm wide, 150 mm high and parallel to the Window Wall. As the Front Wall was shorter than the other three walls, the experimenter on the other side could easily view the test spider inside the apparatus. There was a Ceiling extending forward from the Window Wall for 250 mm toward the Front Wall. Except for the Holder (see below), the entire apparatus was made of glass and, although all other glass was translucent, the Window Wall and the Viewing Tower were opaque.

The Starting Tower was 100 mm away from the Window Wall, being situated directly across from the right-hand side of the Window with its top being level with the midpoint between the top and bottom of the right-hand side of the Window Frame. We knew from preliminary trials that Portia juveniles of no more than 5 mm in body length rarely attempted and never succeeded in clearing horizontal spans of 100 mm by leaping; as we had stipulated that 5 mm would be the standard test-spider size, we designed the apparatus accordingly. This ensured that the only way Portia could reach the Scene in successful trials was by walking along the Pathway.

After walking down the Starting Tower and crossing Segment 1 (130 mm × 40 mm), the test spider reached Intersection 1 (20 mm × 40 mm) and from there it could then continue on to Segment 2 (100 mm × 20 mm). Alternatively, the test spider could opt out of completing the detour by taking an Exit Ramp (150 mm × 40 mm) to reach the Front Wall of the apparatus, thereby ending the trial and forfeiting its opportunity of reaching the prey.

Test spiders that continued from Segment 2 could next cross Intersection 2 (20 mm × 10 mm) and then continue on to Segment 3 (100 mm × 10 mm). From Segment 3, test spiders could reach the Island (30 mm × 30 mm) and the Viewing Tower that was situated on the Island. The Viewing Tower had three walls, its front wall being the wall closest to the Window Wall. The Tower's two side walls were perpendicular to the Viewing Tower's front wall. These three walls blocked off three sides of the Island, with Segment 3 of the Pathway joining the centre of the wall-less side of the Island. Details pertaining to the apparatus, including the dimensions of segments, were chosen after we tried out numerous prototypes and we were confident they would succeed on the basis of this preliminary work.

The Viewing Tower was opaque and this meant that, on arrival at the Island, a test spider could no longer see the Scene in the Window. We made the side walls of the Viewing Tower slippery by applying mineral oil and this ensured that the test spider's only access to the top of the Viewing Tower was by climbing the inner side of the front wall. This, in turn, ensured that the Scene in the Window came back into view only after the test spider had reached the top of the Viewing Tower. A test spider that reached the top of the Viewing Tower could then get closer to the Scene by walking on to the Access Ramp (100 mm × 10 mm, made from glass) which was situated at the top right-hand corner of the Viewing Tower and extended horizontally to the midpoint between the top and bottom of the Window Frame at the left-hand side of the Window.

Each lure in the Scene was secured by a pin to a square Holder (figure 1, inset). The Holder was a shallow open wooden box (20 mm deep) positioned vertical with the side facing the Window (the ‘front side’) being open. The inner dimensions of the Holder were 110 × 110 mm, and the rim of the box was only 10 mm wide (i.e. the outer dimensions were 130 × 130 mm). Its front side was covered by nylon netting (mesh diameter 2 mm) and a 10-mm thick layer of Styrofoam inside the Holder was pressed against the wooden back. With the Styrofoam in place, the depth of the Holder was 10 mm. There was a metal pin connected to the bottom side of the Holder and this pin was connected to a cable-release mechanism which, when pressed and then released, moved the Holder up and then down 5 mm.

Measured from the nylon netting, the Holder was situated 5 mm behind the Window Wall, with each lure on the side of the netting closest to the Window Wall (distance from bottom of cork disc to netting 2 mm). For one-lure Scenes, we positioned the lure in the centre. For multiple-lure Scenes, we positioned a set of lures in horizontal rows, with 1–3 lures per row. When there was only one lure in a row, it was in the centre. When there were two lures in a row, they straddled the centre. When there were three lures in the row, one lure was in the centre and other two straddled the centre lure. The distance between nearest-neighbour lures, whether they were in the same row or in a different row, was always 30 mm (measured from the centres of the lures).

2.4. Testing procedure

A series of stopwatches was used for timing critical events during trials. There was a square Pit (18 × 18 mm; depth 10 mm) centred in the top of the Starting Tower and, immediately before a trial began, the test spider was resting in the Pit, confined there for 10–15 min by a glass Petri dish (diameter 25 mm) used as a Lid. After removing the Lid, a trial began when the test spider walked spontaneously out and on to the top of the Starting Tower. One of the prerequisites for a successful trial was that the test spider had to remain outside the Pit but on top of the Starting Tower for at least 240 s. Other prerequisites were that the test spider had to fixate its gaze (see [35]) on the Scene at least once and that the sum of the durations of all bouts of fixation on the Scene had to total at least 60 s.

We used a cable-release device for making the Scene move during two 30-s periods, one immediately after the test spider came out of the Pit and the other immediately after the test spider arrived at the top of the Viewing Tower. During these 30-s periods, we moved the Scene up and then down once every 5 s, with each up-down movement taking about 0.5 s. Our rationale for moving the lures was knowing from other work (e.g. [48]) that moving lures were considerably more effective than stationary lures at eliciting detouring.

Trials were considered to be ‘successful’ only if the test spider moved successively from the Starting Tower to Intersection 1, from Intersection 1 to Intersection 2, from Intersection 2 to the Island, and then from the Island to the top of the Viewing Tower, without exceeding the maximum allowed elapse of time (‘latency’) for completing each of the first seven stages in the detour. Maximum allowed latencies were: (i) 300 s for leaving the Starting Tower; (ii) 180 s for leaving Segment 1 by moving on to Intersection 1; (iii) 120 s for leaving Intersection 1 by moving on to Segment 2; (iv) 180 s for leaving Segment 2 by moving on to Intersection 2; (v) 120 s for leaving Intersection 2 by moving on to Segment 3; (vi) 180 s for leaving Segment 3 by moving on to the Island; (vii) 180 s for arriving at the top of the Viewing Tower; (viii) 300 s for moving on to the Access Ramp; (ix) 120 s for arriving at the Window Frame; (x) 120 s for attacking a lure. The maximum allowed latency for each stage was about twice as long as what had been seen during preliminary trials in which the test spider completed the journey from the top of the Starting Tower to the top of the Viewing Tower. ‘Leaving’ is the term we use when the spider advanced to the next part of the apparatus. For example, ‘leaving the Starting Tower’ meant the test spider walked out of the Pit, down from the top of the Starting Tower and on to the surface of Segment 1, with ‘leaving latency’ being the time elapsing between the test spider walking out of the Pit and arriving on Segment 1.

We aborted testing whenever one of the maximum latencies was exceeded and also whenever a test spider doubled back, remained in the Pit for as long as 60 s after the Lid was lifted away from the top of the Starting Tower, left the Starting Tower by leaping, leapt or swam toward a side of the Pan from any part of the apparatus, or left Intersection 1 by moving on to the Exit Ramp. We use the expression ‘doubling back’ for any instance of a test spider moving out of physical contact with the specified part of the apparatus and then returning to that part of the apparatus and remaining there for 30 s. Using these rules, no more than 10% of the trials for any one experiment were ever aborted and the majority of aborted trials were instances of the test spider moving on to the Exit Ramp. Spiders from aborted trials were never used in subsequent trials which meant that, for achieving our predetermined sample size for each experiment, all spiders from aborted trials were replaced by taking other spiders from the laboratory culture. After the test spider completed Stage 7 in a successful trial, it might or might not also complete Stage 8, Stages 8 and 9 or Stages 8–10. When applicable, we also recorded ‘latency to attack a lure’, which was the time elapsing between the spider arriving at the Window Frame and then leaping or lunging on to a lure.

We relied on two specific responses (departure latency and arrival frequency) for evidence of expectancy violation, with both of these responses pertaining to the way the test spider behaved after reaching the top of the Viewing Tower. ‘Departure latency’ was the time elapsing between arriving at the top of the Viewing Tower and stepping on to the Access Ramp. ‘Arrival frequency’ refers to the number of test spiders that, after stepping on to the Access Ramp, continued and reached the Window Frame. We looked for evidence of spiders experiencing expectancy violation by comparing data (i.e. departure latency and arrival frequency) from experimental trials (i.e. trials in which the Scene viewed on the Starting Tower was different from the Scene viewed on the Viewing Tower) with data from control trials (i.e. trials in which the Scene viewed on the Starting Tower was the same as the Scene viewed on the Viewing Tower).

2.5. Experiments

Being interested primarily in whether changing the number of prey individuals in the Scene affected Portia's behaviour, the number of prey we used was kept small, the rationale being to facilitate Portia discerning each prey as an individual object (1 versus 2, 1 versus 3, 1 versus 4, 2 versus 3, 2 versus 4, 2 versus 6, 3 versus 4, 3 versus 6). However, we were aware of how notoriously difficult it can be to manipulate the number of items in an experiment independently of making substantial changes related to potentially relevant non-numerical variables. We also knew that we could not comprehensively rule out all reasonable possibilities of non-numerical variables influencing Portia's behaviour in our experiments; however, we made a start by considering effects of prey size and the directions in which prey individuals faced. Moreover, when three or more prey were in the Scene, we considered whether the way prey were arranged in rows affected experimental outcomes (tables 1 and 2).

Table 1.

Detour-completion latencies of Portia africana (time elapsing between beginning of trial and reaching top of Viewing Tower; Stages 1–7: see the text). Number of prey seen from Viewing Tower the same as seen from Starting Tower. Comparison of control trials (prey arrangement or prey size not changed during trial; Scene 1) with experimental trials (prey arrangement or prey size changed during trial; Scene 2). For each experiment, n for control trials is indicated. For experimental trials, n always 40. Unless otherwise stated, prey were of medium size (see the text). Adjusted alpha for Bonferroni corrections was always 0.01. All comparisons n.s.

question	experiment	no. of prey	Scene 1	Scene 2	n for Control	Mann–Whitney U-test
Does prey arrangement matter?	1a	1 versus 1	1 prey facing right	1 prey facing left	60	Z = 0.53, p = 0.594
	1b		1 prey facing left	1 prey facing right	20	Z = 0.22, p = 0.829
	2a	2 versus 2	2 prey facing each other	2 prey facing away	60	Z = 0.92, p = 0.356
	2b		2 prey facing away	2 prey facing each other	20	Z = 0.58, p = 0.561
	3a	3 versus 3	above: 2 prey facing each other; below: 1 prey facing right	2 prey facing right, 1 prey facing left	60	Z = 0.24, p = 0.807
	3b		2 prey facing right, 1 prey facing left	above: 2 prey facing each other; below: 1 prey facing right	40	Z = 0.81, p = 0.419
	4a	4 versus 4	2 rows of 2 prey facing each other	2 rows of 2 prey facing away	60	Z = 0.16, p = 0.876
	4b		2 rows of 2 prey facing away	2 rows of 2 prey facing each other	20	Z = 0.43, p = 0.665
	5a	6 versus 6	3 rows of 2 prey facing each other	3 rows of 2 prey facing away	60	Z = 0.73, p = 0.467
	5b		3 rows of 2 prey facing away	3 rows of 2 prey facing each other	20	Z = 0.09, p = 0.925
Does prey size matter?	6a	1 versus 1	1 small prey facing right	1 large prey facing right	20	Z = 0.65, p = 0.516
	6b		1 large prey facing right	1 small prey facing right	20	Z = 1.05, p = 0.291
	7a	2 versus 2	2 small prey facing each other	2 large prey facing each other	20	Z = 0.08, p = 0.935
	7b		2 large prey facing each other	2 small prey facing each other	20	Z = 0.89, p = 0.372

Table 2.

Detour-completion latencies of Portia africana (time elapsing between beginning of trial and reaching top of Viewing Tower; Stages 1–7: see the text). Comparison of control trials (number of prey did not change during trial; Scene 1) with experimental trials (number of prey changed during trial; Scene 2). For each experiment, n for control trials is indicated. For experimental trials, n always 40. All prey were of medium size (see the text). Adjusted alpha for Bonferroni corrections was always 0.01. All comparisons NS.

experiment	number of prey	Scene 1	Scene 2	n for Control	Mann–Whitney U-test
8a	1 versus 2	1 prey facing right	2 prey facing each other	60	Z = 0.32, p = 0.747
8b	2 versus 1	2 prey facing each other	1 prey facing right	60	Z = 1.57, p = 0.117
9a	1 versus 3	1 prey facing right	above: 2 prey facing each other; below: 1 prey facing right	60	Z = 0.44, p = 0.661
9b	3 versus 1	above: 2 prey facing each other; below: 1 prey facing right	1 prey facing right	60	Z = 1.04, p = 0.299
10a	1 versus 4	1 prey facing right	2 rows of 2 prey facing each other	60	Z = 0.45, p = 0.653
10b	4 versus 1	2 rows of 2 prey facing each other	1 prey facing right	60	Z = 0.61, p = 0.541
11a	2 versus 3	2 prey facing each other	2 prey facing right, 1 prey facing left	60	Z = 1.01, p = 0.312
11b	3 versus 2	2 prey facing right, 1 prey facing left	2 prey facing each other	40	Z = 1.02, p = 0.308
12a	2 versus 4	2 prey facing each other	2 rows of 2 prey facing each other	60	Z = 1.07, p = 0.284
12b	4 versus 2	2 rows of 2 prey facing each other	2 prey facing each other	60	Z = 0.33, p = 0.739
13a	2 versus 6	2 prey facing each other	3 rows of 2 prey facing each other	60	Z = 1.34, p = 0.179
13b	6 versus 2	3 rows of 2 prey facing each other	2 prey facing each other	60	Z = 0.49, p = 0.621
14a	3 versus 4	above: 2 prey facing each other; below: 1 prey facing right	2 rows of 2 prey facing each other	60	Z = 0.78, p = 0.437
14b	4 versus 3	2 rows of 2 prey facing each other	above: 2 prey facing each other; below: 1 prey facing right	60	Z = 0.32, p = 0.752
15a	3 versus 6	above: 2 prey facing each other; below: 1 prey facing right	3 rows of 2 prey facing each other	60	Z = 1.14, p = 0.252
15b	6 versus 3	3 rows of 2 prey facing each other	above: 2 prey facing each other; below: 1 prey facing right	60	Z = 0.96, p = 0.337

2.6. Data analysis

We first used Mann–Whitney U-tests to compare ‘detour-completion latencies’ (i.e. time elapsing between arriving on the top of the Starting Tower and arriving at the top of the Viewing Tower) in experimental trials with detour-completion latencies in control trials (null hypothesis: latency the same in experimental and control trials). The rest of our data analysis was concerned with the way Portia responded once it was on top of the Viewing Tower. We used χ² tests of independence for comparing frequency data (null hypothesis: arrival frequency the same in experimental and control trials). For comparing the latency data after Portia reached the top of the Viewing Tower, which often failed to meet the assumptions required for parametric data analyses, we used Mann–Whitney U-tests (null hypothesis: departure latency the same in experimental and control trials). As we had made many comparisons using the same datasets, we applied an adjusted alpha of less than or equal to 0.01.

3. Results

Regardless of whether it was prey arrangement, prey size or prey number that changed, there were no significant differences between detour-completion latencies in experimental trials and detour-completion latencies in control trials (tables 1 and 2). On the basis of these non-significant comparisons, we accepted that it was unlikely that detour-completion latency influenced the responses we recorded after test spiders had reached the top of the Viewing Tower.

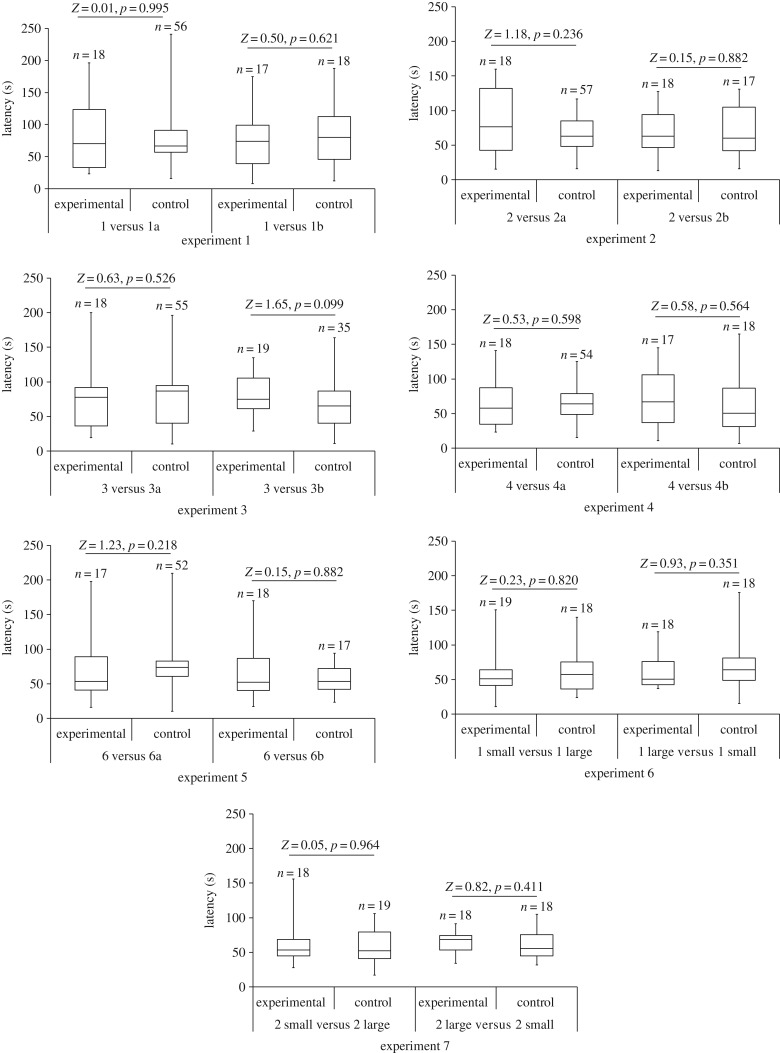
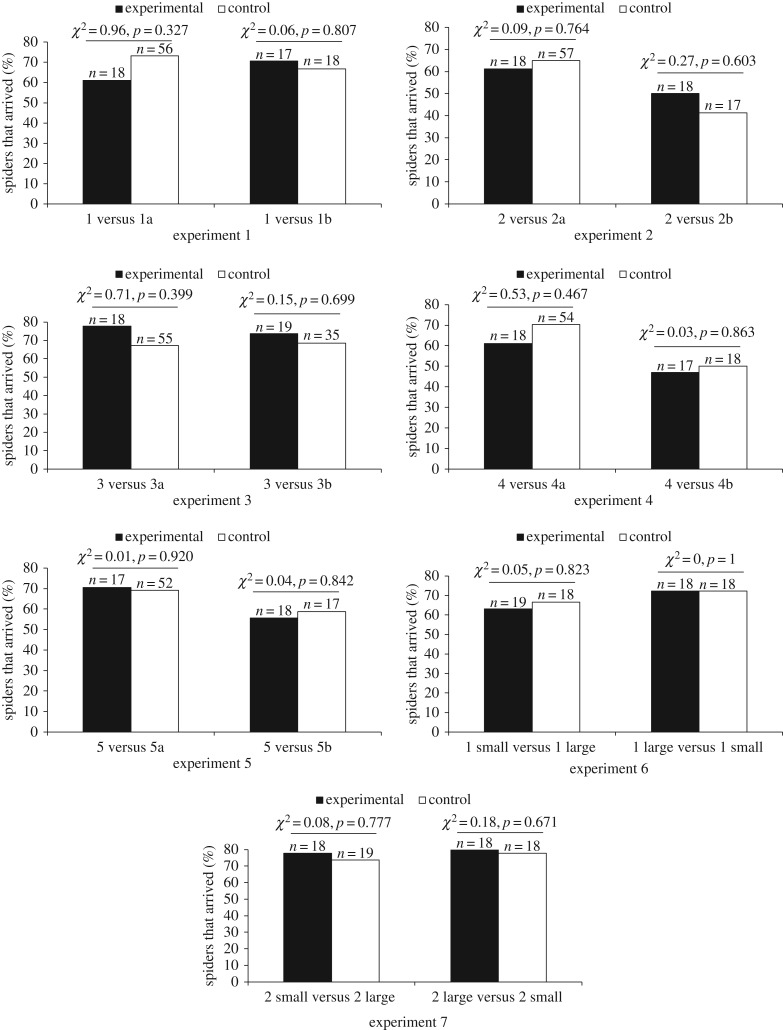
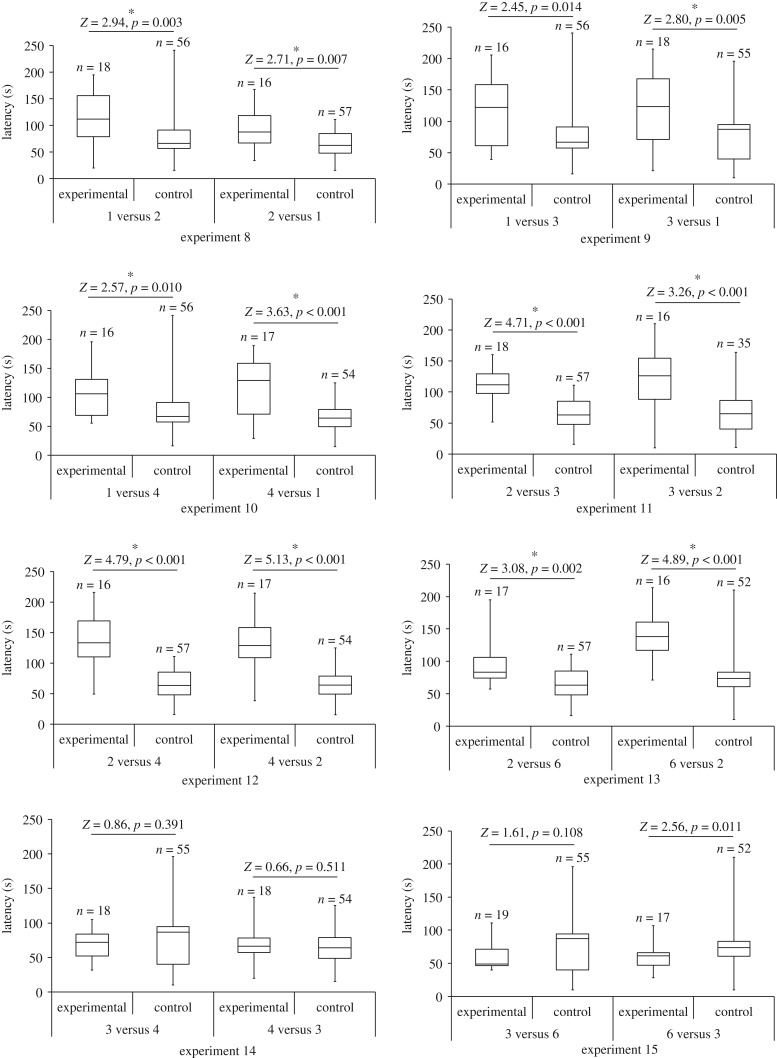
When we changed prey arrangement (experiments 1–5) and prey size (experiments 6–7) while keeping the number of prey in the Scene the same, we found no significant differences in departure latencies (figure 2) or arrival frequencies (figure 3). However, we saw instances of departure latencies (figure 4) and arrival frequencies (figure 5) being consistent with expectancy violation when the number of prey in view from the Viewing Tower was different from the number previously seen by Portia from the Starting Tower.

Figure 2.

Latency (time elapsing between test spider (Portia africana) arriving at the top of the Viewing Tower and crossing the Access Ramp). Experimental: prey arrangement or prey size visible from top of Viewing Tower different from prey arrangement or prey size visible from top of Starting Tower. Control: prey arrangement or prey size visible from top of Viewing Tower same as prey arrangement or prey size visible from top of Starting Tower. In all experiments, prey number was constant. Boxes show medians and upper and lower quartiles, and whiskers show minimum and maximum values. All comparisons n.s. See table 1 for details of each experiment.

Figure 3.

Percentage of test spiders (Portia africana) that arrived at the Window Frame after crossing the Access Ramp. Experimental: prey arrangement or prey size visible from top of Viewing Tower different from prey arrangement or prey size visible from top of Starting Tower. Control: prey arrangement or prey size visible from top of Viewing Tower same as prey arrangement or prey size visible from top of Starting Tower. In all experiments, prey number was constant. All comparisons n.s. See table 1 for details of each experiment.

Figure 4.

Latency (time elapsing between test spider (Portia africana) arriving at the top of the Viewing Tower and crossing the Access Ramp). Experimental: prey number visible from top of Viewing Tower different from prey number visible from top of Starting Tower. Control: prey number visible from top of Viewing Tower same as prey number visible from top of Starting Tower. In all experiments, prey arrangement and prey size was constant. Boxes show medians and upper and lower quartiles, and whiskers show minimum and maximum values. See table 2 for details of each experiment.

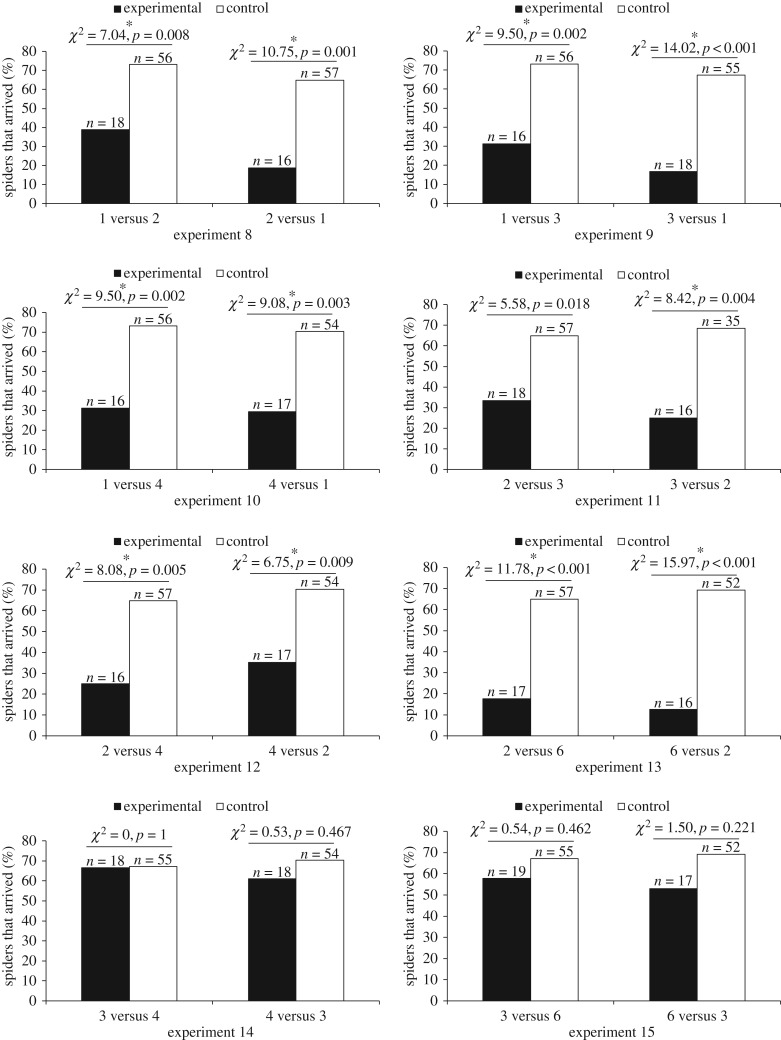
Figure 5.

Percentage of test spiders (Portia africana) that arrived at the Window Frame after crossing the Access Ramp. Experimental: prey number visible from top of Viewing Tower different from prey number visible from top of Starting Tower. Control: prey number visible from top of Viewing Tower same as prey number visible from top of Starting Tower. In all experiments, prey arrangement and prey size was constant. See table 2 for details of each experiment.

Departure latencies were significantly higher and arrival frequencies were significantly lower when the number of prey in the Scene changed from 1 to 2, 2 to 1, 3 to 1, 1 to 4, 4 to 1, 3 to 2, 2 to 4, 4 to 2, 2 to 6 or 6 to 2. When the number of prey changed from 1 to 3 (experiment 9a), arrival frequencies were significantly lower (p = 0.002), but departure latencies were not significantly different after Bonferroni adjustment (p = 0.014; figure 4). When the number of prey changed from 2 to 3 (experiment 11a), departure latencies were significantly longer (p < 0.001), but arrival frequencies were not significantly different after Bonferroni adjustment (p = 0.018; figure 5). No significant experimental-control differences for departure latencies (figure 4) or for arrival frequencies (figure 5) were found when we changed the number of prey in the Scene from 3 to 4, 4 to 3, 3 to 6 or 6 to 3 (experiments 14 and 15).

The number of test spiders that attacked a lure after reaching the Window Frame (Stage 10) was always small (experiments 1–7, 6% of the spiders that reached the Window Frame attacked a lure in experimental trials and 7% attacked a lure in control trials; experiments 8–15, 4% attacked a lure in experimental trials and 6% attacked a lure in control trials) and, accordingly, we carried out no further analysis of these data.

4. Discussion

Test spiders had two opportunities to see a set of prey in a Scene during successful trials, first when they were at the top of the Starting Tower and second when they were at the top of the Viewing Tower. In some instances, there was evidence that the test spider's response while on the Viewing Tower was influenced by whether the number of prey in view was the same as or different from the number seen earlier from the Starting Tower. On this basis, we propose that, while on the Starting Tower, the test spider loaded a representation of prey number into working memory and that, while on the Viewing Tower, it compared the Scene it was viewing with a representation of the Scene acquired while on the Starting Tower.

Using the expression ‘expectancy-violation effect’ for instances in which test-spider response appeared to be influenced by a mismatch in the number of prey viewed from the two locations, we found significant expectancy-violation effects for 1 versus 2, 1 versus 3, 1 versus 4, 2 versus 3, 2 versus 4 and 2 versus 6. In most instances, these effects were independent of directional changes (i.e. the effects were significant regardless of whether the change was from larger to smaller or from smaller to larger) and, in most instances, our evidence of expectancy violation came from both types of data (departure latency and arrival frequency). On the whole, our findings suggest that test spiders were expecting to see a particular exact number of prey items when they arrived at the Viewing Tower and that detecting a mismatch motivated test spiders to spend more time inspecting the Scene for further information. However, details concerning the operating principles of salticid eyes (see below) preclude our methods letting us say precisely what test spiders were doing while on the Viewing Tower.

Two types of data, similar to the types in this study, were also recorded when expectancy-violation methods were used in earlier research on Portia ([29]; also see [35]). Test spiders could see prey of a particular type go out of view and, at a later time, either the same or a different type of prey came into view and the test spider could attack it by leaping. Significantly fewer test spiders initiated predatory attacks when there was a prey-type mismatch than when there was no mismatch, but there were no apparent expectancy-violation effects on attack latency.

When test spiders in our detour-based experiments here arrived at the top of the Tower, their only means of reaching the Scene was by walking along the Access Ramp. The distance was too far to clear by leaping. As an important methodological consequence, requiring walking instead of leaping to reach the prey let us rely on latency, as well as frequency of response, for evidence of expectancy violation. Finding largely consistent trends from two types of data makes us especially confident in our conclusions about Portia's reliance on working memory.

The methods used earlier [29] depended on Portia responding by leaping when prey that had been hidden became visible again at close range. However, in more natural settings, Portia often spends a lot of time moving slowly toward living prey and getting close enough to attack by lunging instead of leaping [18]. We found in our experiments here that, instead of leaping, Portia walked closer to the lures by taking the Access Ramp but then usually failed to attack. Portia's reluctance to attack when close in the experiments here is consistent with findings from other studies which suggest that, when close enough to lunge, Portia is proficient at distinguishing between living prey and lures made from dead prey [11].

Discriminating accurately between 1 and 2, 1 and 3, 1 and 4, 2 and 3, 2 and 4 and 2 and 6, but not 3 and 4 or 3 and 6, appears to be consistent with the range over which vertebrate species have been shown to practise subitizing [49], but the meaning of ‘subitizing’ [50] can be elusive and we are disinclined to use the term ‘subitizing’ for Portia's performance in our experiments. Although subitizing is frequently characterized as an ability to apprehend small numbers rapidly, automatically, pre-attentively and effortlessly, the applicability of ‘automatic’, ‘pre-attentive’ and ‘effortless’ has been disputed [51–55]. However, there appears to be general agreement that subitizing is rapid and, when we consider Portia's behaviour in our experiments, ‘rapid’ in particular appears to be strikingly inapplicable. When discussing subitizing by primates (e.g. [31]), for example, ‘rapid’ normally refers to a response that happens no more than a few seconds after a stimulus is viewed, whereas Portia's departure latency (i.e. time elapsing between arriving at the top of the Viewing Tower and moving on to the Access Ramp) was typically a minute or longer.

Conventional meanings of ‘subitizing’ also appear to be incompatible with our understanding of how salticid eyes work [11]. Salticids have eight eyes, but a large, forward-facing pair, called the ‘principal eyes’, plays the major role in identifying prey. Principal-eye corneal lenses are fixed in place on the spider's carapace but the retinas of these eyes are located at the ends of long, slender eye tubes that extend deep into the salticid's body. When a salticid views an object of interest, it moves these long eye tubes from side to side while simultaneously rotating them alternately clockwise and anticlockwise. Land [56] called these movement patterns ‘scanning’ and he suggested that, while scanning, the salticid carries out an active serial search for salient features in the image. Unfortunately, determining details about Portia's scanning procedure would have required using a highly specialized salticid-specific ophthalmoscope while keeping the salticid tethered in position. This would have been unrealistic during our experiments. However, the proposed process of slow and effortful piece-by-piece rendering of objects [11] seems to be almost the antithesis of the way subitizing is typically described.

Subitizing is sometimes called ‘the object-file system’ but this is ill advised because object files are relevant to more than just subitizing [57], including research on the capacity limits that apply to working memory. That working memory is subject to severe capacity limits is widely accepted and, more specifically, there is considerable evidence of working memory being limited to engaging only three or four object files at one time (see [58]). Although this limit is the same as the limit normally attributed to subitizing, there is also evidence that the proposed working-memory limit at three or four can be exceeded (e.g. [9,59]). Moreover, there are divergent arguments over whether the limits that apply to working memory are best characterized as being based on a limited availability of object files or instead as being based on a limited continuous resource, interference from multiple bindings or some combination of these different factors [60–64]. However, ‘object file system’, but not ‘subitizing’, might be an appropriate expression for Portia's performance in our experiments.

In our experiments, Portia was proficient at distinguishing between numbers of prey in the range of 1–3, but apparently not proficient at making the discriminations 3 versus 4 or 3 versus 6. This may suggest that working memory for Portia is limited to three object files, and yet Portia apparently determined that Scenes containing more than three prey items were different from Scenes containing fewer than three (i.e. 1 versus 4, 2 versus 4 and 2 versus 6 prey). These findings suggest that Portia represents 1 and 2 as discrete number categories and represents 3, 4 and 6 as a single category that we will call ‘many’ (see: [7,65]).

We might propose that, during our experiments, Portia was constrained to use no more than three object files, with a representation of one prey corresponding to only one object file being filled and with a representation of two prey items corresponding to exactly two object files being filled; however, we might also propose that a representation of ‘many’ prey corresponds to all three object files being filled, with this representation not distinguishing between the different numbers of prey equal to or more than three (i.e. 3, 4 and 6). This means that, when we say ‘many’ prey, we are specifying a representation that pertains to something numerical (numerousness) without corresponding to a specific natural number. However, our confidence in this conclusion is not strong because it is currently uncertain whether Portia's failure to discriminate exact numbers in the many-range is truly revealing a capacity limit or whether our findings can instead be explained as instances of Portia not being sufficiently motivated to make these discriminations (see [66,67]).

The numerical competency of spiders has been considered in two previous studies, one on P. africana [68] and the other on Nephila clavipes, an orb-web spider [69]. As with this study, a natural-history perspective was a strong feature in both of these earlier studies.

The experiments using N. clavipes depended on knowing that, instead of feeding immediately after capturing prey, this spider often makes a ‘larder’ by wrapping its prey in silk, fastens the larder to the web's hub and then returns to the stored prey for a meal at a later time [70,71]. In experiments related to numerical cognition, Rodriguez et al. [69] let N. clavipes make larders from specific numbers of mealworms before removing the larders from the web. Nephila clavipes searched for the missing larders and, although orb-web spiders lack the good eyesight for which salticids are known [72], they are proficient at using sensors on their legs for acquiring information from their webs [73]. Rodriguez et al. [69] found that N. clavipes searches longer after the loss of a heavier mealworm from the web than after the loss of a lighter mealworm. They also found that, when total prey weight in the larder was held constant, N. clavipes searched longer after a larder that had been made from a larger number of mealworms was removed from the web.

Portia africana juveniles (body length 3 mm or less) were used in the other earlier study [68], with experiments designed to simulate encounters by P. africana juveniles with Oecobius amboseli, this being a small spider (body length of adults 2–3 mm) that builds small silk nests on stones and on the walls of buildings. The prey-capture routine adopted by P. africana juveniles is to settle beside an occupied oecobiid nest and then, by using their legs for manipulating the nest silk, to make signals to which the resident oecobiid responds by fleeing from its nest. Sometimes, the oecobiid is grabbed and eaten as it leaves the nest. In other instances, a P. africana juvenile makes an ambushing attack when the oecobiid returns and begins to re-enter its nest [74]. Many factors, including whether other P. africana juveniles are already settled at the nest, influence P. africana's initial decision to settle at the nest [75]. The presence of conspecific individuals is relevant because, after one P. africana juvenile captures a single O. amboseli, other P. africana juveniles can feed on the same prey at the same time [74].

In experiments, P. africana juveniles were presented with lures made from dead oecobiids and dead conspecific individuals [68,75] and the sizes and arrangements of the dead prey and conspecific individuals were varied systematically. It was found that P. africana juveniles expressed their strongest predisposition to settle at occupied oecobiid nests when only a single other P. africana juvenile was present beside a nest occupied by an oecobiid. As the P. africana juveniles used in these experiments had no prior experience with oecobiids, oecobiid nests, the apparatus or the testing procedure, these findings pertained specifically to innate predispositions and they suggest that P. africana juveniles make settling decisions by comparing the scene in view with an innate prototype of a preferred scene, with this innate prototype stipulating a single conspecific individual at the nest.

In any experiment related to numerical cognition, it is important to consider potentially confounding non-numerical variables such as the density, cumulative contour lengths and the precise way items are arranged in a scene (see [76,77]) and yet it is notoriously difficult, and perhaps never completely possible, to control for all of the non-numerical variables that might matter [78]. Using lures in this study, as well as in Nelson & Jackson's [68] study, precluded the possibility of prey behaviour or the behaviour of conspecific individuals becoming uncontrolled variables in experiments (see: [79,80]), but ruling out some of the other potentially confounding non-numerical variables can be more difficult.

Rodriguez et al. [69] proposed that N. clavipes remembered the number of separate prey-capture events experienced while making a larder, and then took this memory into account when deciding how much time to put into searching for the missing larder, but they acknowledged another possibility. It might be that N. clavipes remembered the cumulative effort or time taken to make the larder. This would still be interesting in the context of animal cognition, but not so specifically in the context of representing something countable because remembered cumulative effort or time pertains to continuous variables. This limitation on what can be concluded might, in fact, apply widely when proposing that animals represent numbers of events (e.g. see [81]).

In our study, an alternative possibility is that, instead of Portia representing exact numbers of prey, the expectancy-violation effects we observed might have been the consequence of the test spider detecting a mismatch when comparing the effort made while examining the Scene from the Viewing Tower with a representation of the effort that had been made while examining the Scene from the Starting Tower. Evaluating this alternative hypothesis would depend on more precisely specifying what ‘effort’ means and finding a way to manipulate effort while keeping the number of prey in a Scene constant. This alternative hypothesis would also need to address why the limit we detected was precisely three, as it is not clear why a limit so specifically at three would apply if Portia had been representing effort instead of something related more specifically to numbers.

For understanding our experimental findings, returning to the topic of object files might be useful. ‘Object files’ are not literally physical files in an animal's brain, but the theoretical construct known as an ‘object file’ may be useful when trying to understand the individuating of objects and the holding of separate representations in working memory, as well as the process of subitizing. All of these tasks can be relevant to things that are countable [63], with only subitizing implying something rather effortless that happens rapidly and probably by parallel processing.

We propose that the mechanism by which Portia represents exact numbers of prey depends on object files; however, we propose that, instead of relying on subitizing, Portia slowly individuates objects and then holds separate representations of these objects in working memory. We also propose that, instead of using parallel processing (e.g. [82]) for completing the tasks in our experiments, Portia used an effortful serial mechanism [52] for filling a limited number of object files.

Counting is a well-known example of effortful serial processing, but our experiments were not designed for investigating the actual mechanisms by which Portia apprehends and represents numbers of prey. We had a more modest goal of determining whether Portia can represent an exact number of prey. Yet, it would be interesting to consider whether Portia actually does rely on counting or something similar to counting. Gelman & Gallistel [37], in a widely cited review, stipulated that five principles define and govern true counting. The terms they used were ‘one-one’ (usually stated nowadays as ‘one-to-one’, or ‘bijection’), ‘stable-order’ (or ‘ordinality’), ‘cardinal’ (or ‘cardinality’), ‘order-irrelevance’ (or ‘invariance’) and ‘abstraction’ (see [39]).

Whether Portia's behaviour in our experiments corresponds to the first three of these principles is of particular interest because it is these principles that most closely correspond to the mechanics of counting. Bijection, which depends on individuating items or objects (e.g. the individual prey items in our experiments), is achieved when each item in a set is uniquely paired with a single tag (sometimes referred to as a ‘numeron’) from a set of tags. The items and the tags are segregated into two categories; items already counted (i.e. items already assigned a tag) are in one category and items not yet counted and not yet assigned a corresponding tag are in the other category. Ordinality stipulates that there is a specific (‘stable’) order in which tags are serially aligned to the items being counted (i.e. there is a first, a second and so forth). Cardinality becomes relevant after bijection and ordinality have been achieved, with the final ordinal tag specifying, or ‘representing’, the numerical size of the set. In mathematics, this property of a set is specified by a cardinal number, with the corresponding term in cognitive psychology often being ‘numerosity’.

The other two principles, invariance and abstraction, have no clear relevance to Portia's behaviour in our experiments, nor is it easy to identify natural situations in which cognitive capacities inclusive of invariance and abstraction would be adaptively relevant to Portia. With invariance, the cardinal number specifying the size of a set is the same irrespective of the particular item counted first, second and so forth. With abstraction, the process of counting does not depend on the kinds of items being counted. Using the expression ‘true counting’ for instances in which all five principles apply, it would be more accurate to say the relevant question pertains to whether Portia practises ‘proto-counting’ (see [5]).

People use number words as tags for bijection, but Gelman & Gallistel emphasized that words are only one of many possible counting tags. Perhaps, one of their most interesting suggestions was that something they called ‘short-term memory bins' may sometimes be used for tags, especially if these ‘bins’ correspond at least roughly to what are now more often called ‘object files’. This suggests a hypothetical proto-counting procedure that may be applicable to Portia. The bijection method Portia used in our experiments might have been to commit individual object files to individual prey items. That Portia has only three available object files in this context would then explain why Portia's performance was accurate only when the number of prey items was no more than three. Moreover, object-file use might correspond at least roughly to ordinality if Portia fills object files by serial processing and if it has access to the information related to filled versus empty object files. That animals have access to this type of information is already a premise in the literature on subitizing [49]. A representation of the current status of the object files after viewing a collection of prey items might at least roughly correspond to cardinality (i.e. a representation of a Scene consisting of one, two or many prey items, depending on whether one, two or three object files are filled). If this hypothesis is correct, then expectancy violation could have been a consequence of detecting that the number of object files filled while on the Viewing Tower is different from the representation derived by filling object files while on the Starting Tower.

Ethics

All required approvals and permits were included in the authors' visiting scientist contracts with icipe.

Competing interests

There are no competing interests to report.

Funding

Our research was supported by grants from the Royal Society of New Zealand Marsden Fund (UOC1301), the New Zealand Foundation for Research, Science and Technology (UOCX0903), the National Geographic Society (8676–09) and the USA National Institute of Allergy and Infectious Diseases (National Institutes of Health grant no. R01-AI077722).