Abstract.
We tested the agreement of radiologists’ rankings of different reconstructions of breast computed tomography images based on their diagnostic (classification) performance and on their subjective image quality assessments. We used 102 pathology proven cases (62 malignant, 40 benign), and an iterative image reconstruction (IIR) algorithm to obtain 24 reconstructions per case with different image appearances. Using image feature analysis, we selected 3 IIRs and 1 clinical reconstruction and 50 lesions. The reconstructions produced a range of image quality from smooth/low-noise to sharp/high-noise, which had a range in classifier performance corresponding to AUCs of 0.62 to 0.96. Six experienced Mammography Quality Standards Act (MQSA) radiologists rated the likelihood of malignancy for each lesion. We conducted an additional reader study with the same radiologists and a subset of 30 lesions. Radiologists ranked each reconstruction according to their preference. There was disagreement among the six radiologists on which reconstruction produced images with the highest diagnostic content, but they preferred the midsharp/noise image appearance over the others. However, the reconstruction they preferred most did not match with their performance. Due to these disagreements, it may be difficult to develop a single image-based model observer that is representative of a population of radiologists for this particular imaging task.
Keywords: breast cancer, model observers, breast computed tomography, diagnostic performance, reader study
1. Introduction
Computed tomography (CT) is one of the most valuable clinical tools available, because it can provide noninvasive and detailed information of internal organs to visualize disease/injury, enable surgical/treatment planning, and monitor the progress/effectiveness of treatments on patients. Because of these benefits, CT usage has increased dramatically over the last several decades;1 recently, from 2000 to 2013, the number of CT scans performed on parts of the body (other than head) has more than doubled.2 This trend has increased the radiation exposure to the general population in Western Europe,3 as well as in the United States,4 which may increase the cancer risk in some patients. To ensure that the benefits of CT outweigh the risks, reducing radiation dose has been a major focus in establishing new CT protocols. Hence, reducing CT radiation dose is an area of active research in the medical imaging community.
To achieve reduced radiation dose, it is necessary to evaluate and optimize CT image quality to allow radiologists to make the correct diagnosis, while reducing radiation dose to the patient. The standard for evaluating radiologists’ diagnostic performances is an observer study with a large number of radiologists performing a relevant clinical task. However, conducting such a study can be difficult, time-consuming, and expensive. As an alternative, investigators are developing model observers3,5–19 for optimizing imaging devices or software.
Based on the nature of given tasks (e.g., localization, detection, estimation, or classification) and optimization objective [i.e., figure of merit, such as signal-to-noise ratio (SNR) or area under the receiver operating characteristic (ROC) curve (AUC)], and the level of background statistics and signal knowledge (e.g., signal known exactly, background known statistically, etc.), one can develop different types of model observers to optimize imaging devices or software.20 The ideal observer (IO) utilizes the probability density functions (PDF) of signal-present and signal-absent hypotheses to compute the likelihood ratio, and uses the ratio as a decision variable to determine the existence of the desired signal in the image. Hotelling observer (HO) is another type of model observer. HO utilizes the sample mean and variance of given hypotheses (e.g., signal-present or signal-absent hypotheses) to maximize the SNR for a given task. Researchers9,13–15,21 also developed channelized Hotelling observers (CHO) to reduce the dimensionality and computational burden of developing HO or IO by applying various channels to the signal, and using the resulting channel outputs to approximate the performance of regular HO or IO for a given task. Some examples of channels for model observers include: (1) anthropomorphic channels, such as Gabor channels,22 which utilize the characteristics of the human visual system and (2) efficient channels, such as partial least square channels,23 where they are optimized to use as few as possible channels while maintaining the performance of optimal observers.20 These model observers have been applied to various imaging device optimizations, including ultrasound,19 MRI,24 single-photon emission computed tomography (SPECT),11–15 digital breast tomosynthesis,7,16 and CT imaging.10,17,18 Training these model observers involves estimating mean and covariance matrixes of signal and noise/background through simulations using various phantoms or analytical computation from reconstructed images or frequency domain.20
However, most of these model observers have been developed for localization tasks,7–10 detection tasks,11–17 or rather simplified diagnostic tasks18,19 (e.g., determining diseases versus normal or simplified/simulated malignant lesions versus benign lesions). Therefore, developing model observers for classifying real benign and malignant lesions is limited. In addition, the generalizability of these model observers for human observers is not always guaranteed, as they are based on a surrogate population of images.20 In fact, Brankov et al.12–15 developed machine-learning-based CHO, where they trained the CHO using scores from human observers for cardiac perfusion-defect detection using SPECT images. They showed that their CHO estimated the human observer’s performance better than regular CHO for unseen images reconstructed by different algorithms. However, as their studies were based on a phantom and not real clinical images, more research is required to show the generalizability of their CHO for real clinical images.
We, and others, are developing clinical image-based model observers, where quantitative image features are extracted directly from clinical images and are used in a statistical classifier to emulate radiologists’ performances for a given imaging task.25–27 These quantitative image features have been developed for computer-aided detection28 or computer-aided diagnosis,29–31 and they have been carefully crafted to capture the useful characteristics of given images for a given task. Thus, these features are easy to interpret and link how real humans perceive the given images compared to traditional model observers. The imaging task of these previous studies included rankings of radiologists’ perceptual quality of chest radiographs25,26 and radiologists’ rankings of diagnostic performance27 on breast CT (bCT) images. As clinical image-based model observers utilize the features extracted directly from the clinical image, it does not require mathematical or statistical assumptions (e.g., mathematical formulation of a given task and determining statistical characteristics of signal and noise/background components) that traditional model observers require. Thus, we can use clinical image-based model observers to evaluate more clinically difficult tasks, such as classifying benign and malignant breast lesions.
However, to utilize model observers for optimizing CT to answer diagnostic questions, we first need to determine the agreement of radiologists’ diagnostic performances across a range of image qualities. Note that we refer to the diagnostic task in this study as the classification of benign and malignant lesions. Investigating this agreement is critical, since it will determine the feasibility of developing clinical image-based model observers, as well as other model observers for emulating radiologists’ diagnostic tasks. If there are large differences between radiologists’ diagnostic performances across different image qualities, there may be less guidance in developing model observers for clinically relevant tasks.
In this study, we investigated the agreement of radiologists’ diagnostic performances over a spectrum of different breast CT image qualities. To do so, we reconstructed bCT cases with different appearances, or qualities, using iterative and clinical image reconstruction algorithms. We conducted quantitative image feature analysis to select a few reconstruction algorithms and a subset of bCT cases, which cover a wide range of image appearances or qualities that might affect a radiologist’s diagnostic performance. We then conducted a reader study to determine radiologists’ diagnostic performances on selected reconstruction algorithms and bCT cases. In addition, we conducted an additional reader study to determine radiologists’ rankings, in terms of their impression of the best diagnostic information (or simply their preference of one reconstruction algorithm over the others) for the same reconstruction algorithms and bCT cases used for the first reader study.
2. Methods
2.1. Dataset
Under the approval of an Institutional Review Board (IRB), we included a total of 137 pathology proven breast lesions (90 malignant, 47 benign) of 122 noncontrast bCT images of women imaged at the University of California at Davis for this study using a prototype dedicated bCT system developed at the University of California at Davis.32 Table 1 summarizes the detailed characteristics of the dataset, which include patient age, lesion size, breast density, and lesion diagnosis.
Table 1.
Characteristics of bCT dataset.
| Total number of lesions | All |
Selected for train/test the classifier |
Selected for the reader study I |
Selected for the reader study II |
||
|---|---|---|---|---|---|---|
| 137 | 102 | 50 | 30 | |||
| Subject age (years) | Mean [min, max] | 55.6 [35, 82] | 55 [35, 82] | 54.6 [37, 82] | 55.3 [37, 82] | |
| Lesion diameter (mm) | Mean [min, max] | 13.5 [2.3, 35] | 13.4 [2.3, 32.1] | 13.3 [4.3, 29.2] | 13.7 [4.5, 28.5] | |
| Breast density (% among lesions considered) | 1 | 16 (12%) | 11 (11%) | 5 (10%) | 3 (10%) | |
| 2 | 51 (37%) | 36 (35%) | 20 (40%) | 14 (46%) | ||
| 3 | 51 (37%) | 38 (37%) | 17 (34%) | 9 (30%) | ||
| 4 | 19 (14%) | 17 (17%) | 8 (16%) | 4 (14%) | ||
| Diagnosisa | Malignant (% among malignant lesions considered) | IDC | 61 (68%) | 41 (66%) | 18 (72%) | 12 (70%) |
| IMC | 13 (14%) | 10 (16%) | 5 (20%) | 4 (24%) | ||
| ILC | 8 (9%) | 6 (10%) | 1 (4%) | 0 (0%) | ||
| DCIS | 7 (8%) | 5 (8%) | 1 (4%) | 1 (6%) | ||
| Lymphoma | 1 (1%) | 0 (0%) | 0 (0%) | 0 (0%) | ||
| Benign (% among benign lesions considered) | FA | 20 (43%) | 17 (43%) | 11 (44%) | 7 (54%) | |
| FC | 7 (15%) | 4 (10%) | 3 (12%) | 1 (8%) | ||
| FCC | 4 (9%) | 4 (10%) | 1 (4%) | 0 (0%) | ||
| PASH | 2 (4%) | 2 (5%) | 2 (8%) | 0 (0%) | ||
| CAPPS | 2 (4%) | 2 (5%) | 2 (8%) | 1 (8%) | ||
| Other benign lesions such as sclerosing adenosis and cyst | 12 (25%) | 11 (27%) | 6 (24%) | 4 (30%) | ||
IDC, invasive ductal carcinoma; IMC, invasive mammary carcinoma; ILC, invasive lobular carcinoma; DCIS, ductal carcinoma in situ; FA, fibroadenoma; FC, fibrocystic; FCC, fibrocystic changes; PASH, pseudoangiomatous stromal hyperplasia; CAPPS, columnar alteration with prominent apical snouts and secretions.
2.2. Iterative Image Reconstruction Algorithm
To determine radiologists’ diagnostic rankings on different image reconstructions, we used an iterative image reconstruction (IIR) algorithm to obtain CT images with different appearances.33 Reconstructed images () were obtained by using
| (1) |
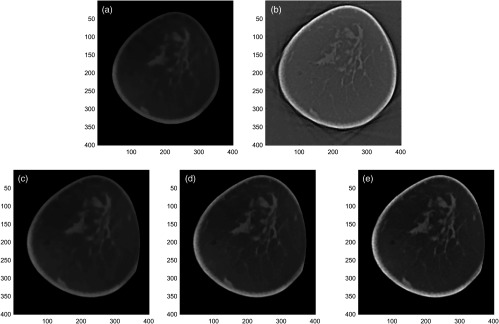
where is reconstructed by minimizing a total-variation (TV) penalized least squares data fidelity, whereas is reconstructed by minimizing a TV-penalized derivative weighted data fidelity. Image reconstruction by maintains the gray-scale information, whereas reconstruction by provides edge information (i.e., high-spatial-frequency image content). Images reconstructed with each method separately are combined using a weighting factor to create reconstructed images with different appearances (i.e., image quality). The internal variables for each reconstruction represent the number of iterations ( and ) and a flag ( and ) to indicate whether the respective reconstructed image was obtained before or after TV minimization. For each bCT exam, a total of 24 images was reconstructed using the above algorithm with different combinations of the variables and . Figure 1 shows how the algorithm performs on an example image. In addition, one clinical reconstruction using the Feldkamp–Davis–Kress (FDK) algorithm34 was added for this study.
Fig. 1.
The IIR algorithm reconstructed images with different image appearances. (a) An image reconstructed by f TV-LSQ . This reconstruction maintains the gray-scale information. (b) An image reconstructed by f TV-δLSQ . This reconstruction provides the edge information. (c)–(e) Final reconstructed images obtained by combining two reconstructions (a) and (b) with different weights (, , and ).
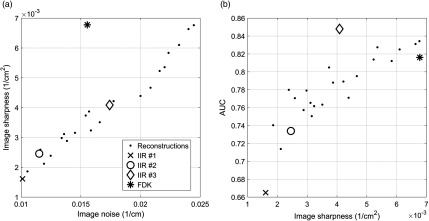
To quantify the appearance of each reconstruction, the standard deviation of a homogeneous portion of breast () was used to characterize noise, and the gradient of a parenchymal portion () was used to characterize sharpness. Since our final reconstruction was the linear combination of two reconstructions with different weights [Eq (1)], all bCT cases would show similar change in the estimated noise and the sharpness values from one reconstruction to another reconstruction. Thus, we used a single representative breast to quantify image appearance of each reconstruction. The image noise values for all reconstructions ranged from 0.01 to , whereas the image sharpness values ranged from 0.002 to . Figure 2 shows the scatter plot between the image noise and sharpness values for all reconstructions considered in this study.
Fig. 2.
The scatter plots of (a) the image noise versus image sharpness and (b) the image sharpness versus the AUC of trained classifiers for all reconstructions that were considered in this study. To compute AUC values, we trained and tested linear discriminant analysis (LDA) classifiers using the quantitative image features extracted from the segmented breast lesions, and then conducted ROC analysis. Section 2.3 explains the details of the ROC analysis on the trained LDA classifiers. The four reconstructions that were selected for the reader study were highlighted with the large markers.
2.3. Quantitative Image Features Analysis
We conducted quantitative image feature analysis to identify a set of reconstruction algorithms that cover a range of image appearances that could affect radiologists’ diagnostic performances. We first segmented all lesions in each of the 24 iterative image and FDK reconstructions using an existing semiautomated segmentation algorithm.35 Then, we computed the segmentation accuracy by comparing the segmentation results of the algorithm to that of a research specialist with more than 15 years of experience in mammography. We utilized the Dice coefficient36 for evaluating segmentation accuracy. Following the existing study’s criteria37 for good segmentation (i.e., Dice ), we removed cases (a total of 10 lesions) that did not meet the criteria for further consideration. In addition, we removed cases (a total of 25 lesions) with missing information (e.g., manual segmentation by the research specialist or seed point for the algorithm) for either IIR or FDK reconstructions. As a result, we utilized 102 breast lesions (62 malignant, 40 benign) for the subsequent feature analysis (Table 1).
We extracted a total of 23 image features from the segmentation results. These 23 image features included both traditional (F1 to F20)28,30,31,38 and newly introduced features (F21 to F23)29 for classifying a breast tumor in bCT images. Table 2 shows the list of image features used for this study. The operators , , and represent the average, the norm of a vector, and the standard deviation, respectively. In addition, , , , , and are the segmented region, its margin, its surface, the distance from the margin voxel from the center, and adipose regions, respectively. Moreover, GV, , , , and are the image gray values, the image gradient vector, its radial component, the semiaxes of an ellipsoid fit to , and the spherical region with the equal volume of , respectively. Three-dimensional (3-D) gray-level co-occurrence matrix (GLCM) refers to the 3-D version of the gray-level co-occurrence matrix, which was used to measure the characteristics of lesion texture. In addition, and refer to maximum and minimum principal curvatures at a given point on , where they represent how much the given surface bends in a certain direction at that point.
Table 2.
List of image features used for this study.
| Feature name | Definition | |
|---|---|---|
| Histogram descriptors | ||
| Average region gray value (HU) | F1 | |
| Region contrast (HU) | F2 | |
| Region gray value variation (HU) | F3 | |
| Margin gray value variation (HU) | F4 | |
| Shape descriptors | ||
| Irregularity | F5 | |
| Compactness | F6 | |
| Ellipsoid axes min-to-max ratio | F7 | |
| Margin distance variation (mm) | F8 | |
| Relative margin distance variation | F9 | |
| Average gradient direction | F10 | |
| Margin volume () | F11 | |
| Margin descriptors | ||
| Average radial gradient (HU) | F12 | |
| Radial gradient index | F13 | |
| Margin strength 1 | F14 | , where |
| Margin strength 2 | F15 | |
| Radial gradient variation | F16 | |
| Texture descriptors | ||
| GLCM|energy | F17 | Energy of 3-D gray-level-co-occurrence matrix |
| GLCM|contrast | F18 | Contrast of 3-D gray-level-co-occurrence matrix |
| GLCM|correlation | F19 | Correlation of 3-D gray-level-co-occurrence matrix |
| GLCM|homogeneity | F20 | Homogeneity of 3-D gray-level-co-occurrence matrix |
| Surface curvature descriptors | ||
| Total curvature | F21 | |
| Mean curvature | F22 | |
| Gaussian curvature | F23 | |
Using a forward feature selection algorithm (“sequentialfs” function in MATLAB) under a leave-one-out-cross-validation (LOOCV), we selected quantitative image features that retained useful information for classifying breast lesions. We repeated the above analysis for 24 IIRs and FDK reconstructions. We selected those features that were selected the most for all LOOCV training samples per each of the 25 reconstructions (i.e., 102 LOOCV training reconstructions, resulting in 2550 feature selections). The selected quantitative image features were F11, F13, and F21 with the corresponding selection frequencies of 59%, 68%, and 96%, respectively, for training and testing a classifier.
Then, we trained and tested classifiers using those three final features and biopsy results of lesions under the LOOCV. We used the AUC as a figure of merit to determine the set of reconstruction algorithms for the reader study. The AUC values of the trained classifiers for all reconstructions ranged from 0.66 to 0.85 (Fig 2). Note that these AUC values were computed from all lesions (). Among the 24 IIRs and FDK reconstructions, we selected the three IIRs (let IIR #1, IIR #2, and IIR #3 denote each of these three IIRs) and FDK reconstructions that covered the range of AUCs for all reconstructions, with corresponding AUCs of 0.66, 0.73, 0.85, and 0.82, respectively. These selected reconstructions spanned a range of smooth, low-noise to sharp, and high-noise image appearance (Fig 2).
2.4. Reader Study I: Performance Study
Under an IRB approved protocol, we recruited a total of six experienced Mammography Quality Standards Act (MQSA) radiologists (15 years or higher in practice), who specialize in breast imaging, for this study. All radiologists have experience reading bCT cases from previous observer studies conducted at our institution (using different cases). To reduce the burden of reading all 102 lesions with four different reconstructions, we further selected a subset of 50 lesions (25 malignant, 25 benign). The 50 lesions selected kept the performance ranking of the selected reconstructions the same as that of the full 102 lesions. The trained classifier’s performance on these 50 lesions was increased in the order of IIR #1, IIR #2, FDK, and IIR #3 with associated AUCs of 0.62, 0.76, 0.85, and 0.96, respectively. Their corresponding 95% confidence intervals (CI) of AUCs estimated from bootstrap sampling over cases () in Table 3 shows good separation between the selected reconstructions. This proved a wide span in classifier performance with the hope of producing a wide span in the radiologists’ performances. A wide span in the radiologists’ performances would increase the statistical power of the experiment.
Table 3.
The diagnostic performances of radiologists on each reconstruction measured in terms of AUC. 95% CI of AUC estimates are given in the brackets.
| Reconstruction type | IIR #1 | IIR #2 | IIR #2 | FDK |
|---|---|---|---|---|
| Image sharpness and noise | Low | → | High | |
| Trained classifier | 0.62 [0.56, 0.75] | 0.76 [0.61, 0.87] | 0.96 [0.88, 0.99] | 0.85 [0.73, 0.93] |
| Radiologist #1 | 0.74 [0.57, 0.87] | 0.79 [0.63, 0.89] | 0.73 [0.56, 0.86] | 0.81 [0.65, 0.91] |
| Radiologist #4 | 0.82 [0.67, 0.92] | 0.84 [0.69, 0.93] | 0.81 [0.66, 0.91] | 0.88 [0.72, 0.96] |
| Radiologist #5 | 0.86 [0.73, 0.93] | 0.77 [0.62, 0.87] | 0.85 [0.73, 0.93] | 0.78 [0.64, 0.88] |
| Radiologist #6 | 0.80 [0.64, 0.90] | 0.71 [0.55, 0.84] | 0.75 [0.59, 0.87] | 0.70 [0.55, 0.83] |
| Radiologist #2 | 0.81 [0.65, 0.91] | 0.78 [0.61, 0.89] | 0.79 [0.62, 0.90] | 0.80 [0.64, 0.91] |
| Radiologist #3 | 0.72 [0.54, 0.85] | 0.70 [0.53, 0.84] | 0.74 [0.58, 0.87] | 0.76 [0.60, 0.88] |
| Averaged across radiologists | 0.78 [0.68, 0.87] | 0.76 [0.66, 0.86] | 0.77 [0.67, 0.86] | 0.77 [0.68, 0.86] |
Before the study session, all radiologists underwent a single training session. We utilized 10 cases (half malignant and half benign), which were independent of the selected 50 cases, with random selection of the four reconstructions (i.e., FDK, IIR1 to IIR3), to help familiarize the radiologists to the range of image appearances of the cases that they would read in the actual reading sessions.
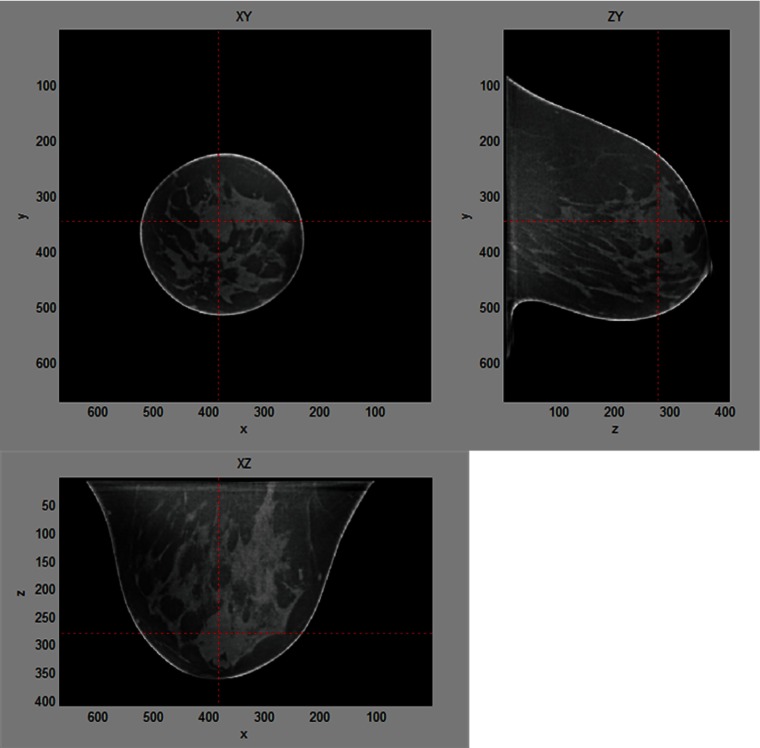
There was a total of four reading sessions and each session consisted of 50 cases with randomized presenting order. Each case was presented once per session and the choice of reconstruction algorithm for each case within the same study session was also randomized. Radiologists were asked to complete up to two sessions during each study visit. To minimize memory effect due to reading the same cases reconstructed by different algorithms, we asked the radiologists to come back at least one week after their last study visit to complete their next session(s). Thus, the above radiologists read 200 cases () and provided the likelihood of malignancy and BI-RADS assessment of the lesion present in the images. Figure 3 shows an example of one lesion case used for this reader study. Radiologists were able to dynamically move through, zoom, and adjust window level of the displayed volume datasets. We used a 27-in. LCD monitor with a resolution of for this reader study. We turned on the display at least 30 min before conducting each reading session to warm up the display. We set the contrast, brightness, and gamma of the display at the factory defaults and kept the same setup for all radiologists.
Fig. 3.
The layout of the viewer used for the reader study 1. Radiologists were able to review entire breast volume by dynamically moving through slices in three different cross-sectional views. Target lesion was highlighted and centered in the viewer.
We conducted empirical ROC analysis using radiologists’ likelihood of malignancy scores of the 50 lesions and their biopsy truth, and computed the corresponding AUC values from the ROC curves. We conducted a multireader-multicases (MRMC) analysis using the OR-DBM MRMC tool39–43 to check if the change in reconstructions affected the radiologists’ diagnostic performances as a group.
2.5. Reader Study II: Preference Study
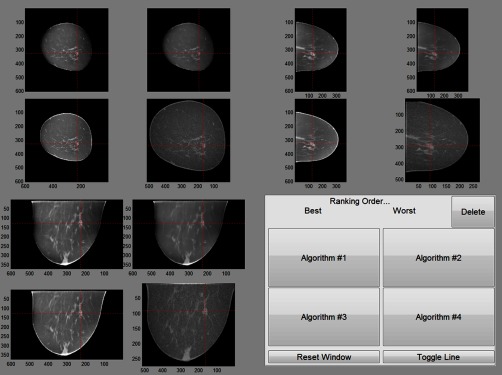
The same group of radiologists participated in a second reader study with a subset of the cases from the first reader study ( lesions, 13 benign, 17 malignant). We selected the cases where they maintained the rank order of the trained classifier’s AUC on each reconstruction. The resulting AUCs for each reconstruction (i.e., IIR1-3 and FDK) were 0.67, 0.76, 0.92, and 0.87, respectively. For each lesion case, we displayed all four reconstructed image data using three different views (sagittal, coronal, transverse views) at the same time on a high-resolution monitor () (Fig. 4). Radiologists were able to zoom and adjust window level of the displayed images, but the individual images were fixed at the lesion center. Then, we asked radiologists to rank image datasets in terms of diagnostic information (or their preference of one appearance over others). We conducted the Kruskal–Wallis test44 on the sum of each reconstruction’s ranking made by the radiologists to check if the six radiologists as a group agreed on which reconstruction they thought was the most diagnostic. We used Kruskal–Wallis test instead of regular parametric one-way analysis of variance, as we were interested in finding the changes in individual radiologist’s preference rankings on the selected reconstructions, not the magnitude of each radiologist’s preference changes on the reconstructions.
Fig. 4.
The layout of the viewer used for the second reader study. Each cross-sectional view of four selected reconstructions was grouped. Target lesion was highlighted. For this reader study, radiologists reviewed the center slice of each view of four selected reconstructions and ranked them in terms of which reconstruction provided the best diagnostic information (or simply their preference of one reconstruction algorithm over others).
3. Results
3.1. Reader Study I: Performance Study
Radiologists’ diagnostic performances (AUC) ranged from 0.70 to 0.89 (Table 3). Note that we ordered radiologists in three groups in terms of the similarity of their diagnostic performance on selected reconstruction methods. The OR-DMB MRMC analysis results for random readers and random cases indicated that the AUCs for reconstruction were not significantly different (). This indicates that there was no effect due to the reconstruction change on radiologists’ performances on average. In addition, we estimated the 95% CI of each radiologist’s diagnostic performance on each reconstruction using 10,000 bootstrap samplings of the cases. Within each radiologist, there was no statistical difference found between his/her performance on the four reconstruction methods.
There was, however, a trend between radiologists (Table 3). Radiologists #1 and #4 tended to show better performance for the sharpest reconstruction, i.e., FDK, whereas radiologists #5 and #6 tended to show better performance for the smoothest reconstruction, i.e., IIR #1. Radiologists #2 and #3 seemed to have the same performance independent of reconstruction algorithm. To check this trend further, we conducted a post hoc analysis to compare the difference in reconstruction AUC values at the two extreme image sharpness values (i.e., difference from the smoothest reconstruction IIR#1 to the sharpest reconstruction FDK) for the above possible groups, bootstrapping over the 50 lesions. Specifically, we first computed the difference between the IIR#1 and FDK reconstruction AUC values for all radiologists. Then, we averaged the AUC differences in each of the above possible groups. We repeated the above process for 10,000 bootstrap samples and computed the difference between the averaged AUC differences among the three groups of radiologists. We then checked if there was a statistical difference between two groups of radiologists (i.e., if 95% and 99% CIs do not include 0), to confirm the trend above. Note that the purpose of this post hoc analysis was to check the aforementioned trend within the six radiologists and 50 cases utilized for this study only, not to generalize our findings to all radiologists and other breast lesion cases.
Table 4 shows the difference in the group averaged AUC differences for the IIR#1 and FDK reconstruction (i.e., ) for the possible pairs of the three groups of radiologists. There was a statistical difference between the radiologist #1 and #4 group and the radiologist #5 and #6 group, as confirmed by both the 95% and 99% CIs. However, there was no statistical difference between the radiologist #2 and #3 group and the radiologist #1 and #4 group and the radiologist #5 and #6 group, which may indicate that the radiologist #2 and #3 group is the random fluctuation of the data (or simply noise). This result may suggest that there exist at least two trends among the six radiologists in diagnostic performances for different reconstructions. As these two trends are completely opposite, it might create considerable interreader variability or disagreement among radiologists in their performances on different reconstructions such that the effect due to the reconstruction change in the diagnostic performance among the six radiologists for this study was canceled out when their AUC values were averaged, as shown in Table 3.
Table 4.
10,000 bootstrap analysis on the difference in the group averaged AUC differences for the IIR#1 and FDK reconstruction (i.e., ) for three possible groups of radiologists.
| Radiologist group | Radiologist group | Mean () | 95% CI | 99% CI |
|---|---|---|---|---|
| Radiologist #1 and #4 | Radiologist #5 and #6 | 0.1528 | [0.0376, 0.3080] | [0.0044, 0.3624] |
| Radiologist #1 and #4 | Radiologist #2 and #3 | 0.0456 | ||
| Radiologist #2 and #3 | Radiologist #5 and #6 | 0.1072 |
3.2. Reader Study II: Preference Study
Although there was disagreement among radiologists on which reconstruction method was diagnostically superior, we found that radiologists agreed on which reconstruction they thought was the most diagnostic; the Kruskal–Wallis test on the sum of each reconstruction’s ranking performed by each radiologist resulted in a -value of 0.002. This result indicates that there is at least one reconstruction method that all radiologists preferred than others. Table 5 shows the ranksum of radiologists’ rankings on each reconstruction. All radiologists, except radiologist #1, preferred the IIR #2. We conducted post hoc tests (i.e., pairwise comparisons among reconstructions) between each pair of reconstructions, via comparing the column-wise differences in aggregated ranksums in Table 5. Note that we used “multcompare” function in MATLAB for the post hoc tests. We used the Tukey’s honest significant difference45 as the multiple comparison correction method for the function. The result in Table 6 showed that IIR #2 was ranked lower than IIR #1 () and the FDK reconstruction (), whereas there was no statistical significant difference between IIR #2 and IIR #3.
Table 5.
The ranksum of each reconstruction ranking in terms of diagnostic information availability. Lower ranksum indicates higher radiologists’ preference over others.
| IIR #1 | IIR #2 | IIR #3 | FDK | |
|---|---|---|---|---|
| Image sharpness and noise | Low | → | High | |
| Radiologist #1 | 69 | 75 | 76 | 80 |
| Radiologist #4 | 89 | 65 | 68 | 78 |
| Radiologist #5 | 80 | 57 | 68 | 95 |
| Radiologist #6 | 74 | 67 | 70 | 89 |
| Radiologist #2 | 84 | 62 | 78 | 76 |
| Radiologist #3 | 89 | 64 | 64 | 83 |
Table 6.
Post hoc comparison between each pair of reconstructions, i.e., analysis on the column-wise differences in aggregated ranksums in Table 5.
| Reconstruction | Reconstruction | Mean () [95% CI] | -value |
|---|---|---|---|
| IIR #1 | IIR #2 | 12 [1.53, 22.47] | 0.017 |
| IIR #3 | 7.3 | 0.273 | |
| FDK | 0.977 | ||
| IIR #2 | IIR #3 | 0.661 | |
| FDK | 0.004 | ||
| IIR #3 | FDK | [19.47, 1.47] | 0.121 |
4. Discussion
In this study, we could not find a statistical difference between radiologists’ diagnostic performances as a group on different reconstructions. It was an unexpected result, as previous studies46–48 for different clinical tasks and images (detection of polyps in CT colonography,46 detection of lung nodules in chest CT,48 and detection of focal lesions in abdominal CT)47 reported that different reconstructions at the same radiation dose level affected radiologists’ performances for the tasks (i.e., detection tasks). It is possible that the differences in imaging modality (i.e., bCT versus CT colonography, chest CT, and abdominal CT), task (classification versus detection), and radiologists’ experiences on imaging modalities could be reasons for our results, but it requires further research to confirm or refute our findings.
However, we observed opposite trends in the diagnostic performances on different subsets of radiologists in this study, which might be a result of a disagreement among radiologists as a group, on which reconstructions are diagnostically superior to others. Our data suggest that there exist at least two trends on radiologists’ diagnostic performances on different reconstructions; one group tended to perform better with the sharpest image reconstruction, whereas another group tended to perform better with the smoothest image reconstruction. These opposite trends of radiologists’ diagnostic performances on different reconstructions could cancel out each other when their diagnostic performances were averaged. We caution that this was a post hoc analysis and needs to be verified in a hypothesis driven study, as we cannot generalize our findings from the post hoc analysis for other radiologists and breast lesion cases.
In our study, we selected four reconstructions out of 25 reconstructions based on the diagnostic performances of the trained classifier on those reconstructions. The diagnostic performances of the classifiers on the selected four reconstructions were ranked in the ascending order of IIR #1, IIR #2, FDK, and IIR #3 (Table 3). However, no subgroup of the six radiologists followed the classifier’s diagnostic ranks on those reconstructions. Instead, as we discussed above, we found opposing trends in diagnostic performances for subgroups in those six radiologists. One of the possible reasons for the low correlation in diagnostic performance between the radiologists and the trained classifiers could be the fact that we trained the classifiers using the biopsy truth, not the radiologists’ malignancy scores. Thus, one could improve the correlation in diagnostic performance between radiologists and the classifier by using the radiologists’ malignancy scores. However, one needs to be cautious about possible variations in malignancy scores among radiologists, which may hinder training of the classifier on an individual radiologist’s diagnostic performance. Nonetheless, the classifier can be trained on malignancy scores from a pool of radiologists, and such a classifier could be useful to estimate the averaged diagnostic performances of radiologists.
Radiologists as a group agreed on which reconstruction method they thought provided the best diagnostic information; radiologists preferred midsharp and midnoise reconstruction methods over other reconstruction methods. However, the reconstruction algorithm preference of an individual radiologist did not match with his/her diagnostic performance. For example, most radiologists preferred IIR #2 (Table 5), but their highest performing reconstructions were either IIR#1 or FDK, not IIR #2 (Table 3). In fact, this disagreement is not a new finding, as previous studies reported similar results on other clinical tasks (screening or detection) on different areas of the body (e.g., CT colonoscopy, cranial CT).49,50
This calls into question the most common method of selecting image quality used for any medical imaging technique, which is the subjective opinion of radiologists on perceived image quality. This study demonstrates that image preference does not necessarily lead to images that deliver the best diagnostic performance. Extrapolating our results, validating observer models may be problematic, because radiologists do not agree on which types of images provide the most diagnostic information. That is, it may be difficult to find a single set of image features that can accurately represent a population of radiologists’ diagnostic performances. Instead, one may need to search multiple sets of image features correlated with a group of radiologists with similar diagnostic performance trends based on reconstruction types or image qualities. Samei et al.26 have shown that they could extract features that correlate with radiologist’s perceived quality of image features.25 However, based on our results (i.e., radiologists’ preferences do not necessarily match their diagnostic performances), this may not lead to model observers that correlate with diagnostic performance.
Given the level of disagreement between the six radiologists, creating a single model observer to represent a population of radiologists may not be advisable, at least for this particular task and imaging modality. The six radiologists can be grouped into at least two trends (Table 3): those that performed best with the noisiest, sharpest images (radiologists #1 and #4); those that performed best with the smoother, less noisy images (radiologists #5 and #6). From this, one may develop at least two different model observers, where they can represent the range in performance preference found in radiologists reading bCT images. Or, it may also be possible to develop a single model observer for all radiologists, if one knows the underlying distribution of radiologists’ aptitudes toward choosing a reconstruction algorithm for them to have the highest diagnostic performance, and model their aptitudes as random terms in the model observer.
This was an unexpected result given how reconstruction algorithms are ultimately determined clinically, i.e., based on radiologists’ subjective impressions. Possible reasons for the disagreement among radiologists on diagnostic performance include: (1) limited experience in reading bCT images, (2) the more variable nature of classification tasks compared to other tasks (e.g., detection tasks), and (3) being specific only to six radiologists recruited for this study. As bCT is a new imaging modality and it is not clinically practiced, radiologists do not have extensive experience in reading bCT images and, therefore, it may be difficult for them to establish the best clinical criteria for breast lesion diagnosis. Furthermore, given the relative newness of the modality, each radiologist may have selected different criteria for what distinguishes a malignant lesion from a benign one. For the case of interpreting screening mammograms, radiologists’ performances increase with the years of clinical practice,51,52 and the annual volume of reading mammograms is positively correlated with radiologists’ performance.51 In fact, many countries regulate the minimum number of mammograms interpreted per year, ranging from 960 to 5000, to meet and maintain the desired level of expertise.51,53,54 Although all radiologists in this study had some experience reading bCT cases in research settings, the number of cases that they read may not have been enough to establish the criteria for breast lesion diagnosis that all radiologists agree on. This lack of clinical criteria may also result in large interreader variability when radiologists diagnose given breast lesions.
It is possible that a classification task is inherently more variable than a detection task. The vast majority of model observer studies are detection tasks and the models are validated against radiologists’ or human observers’ ability to find an abnormality in an image. For these tasks, the target is usually well known to the observer. However, a classification task is less well defined. It is possible that radiologists use different criteria to decide whether a lesion is benign or malignant, and that those differences have different dependence on the quality characteristics of the image. More studies are needed to investigate this postulate.
It is also possible that our finding (i.e., the disagreement among radiologists) was only specific to the radiologists recruited for our study. That is, a different set of six radiologists may agree on which type of reconstruction provided the most diagnostic information, which implies large interobserver variability. Or, it is also possible that we may obtain different patterns from the same radiologists, if we repeat the same reader studies, which implies the large intraobserver variability. However, even if these were true, further investigation with a larger number of radiologists with repeated tests would be needed to conclude that the six radiologists who participated in this study were not representative of a population of radiologists, and they have high or low intraobserver variability on their decisions. Furthermore, if our result is correct, then to develop different types of model observers for each group of radiologists with similar diagnostic performance patterns (e.g., a group of radiologists who perform well with smooth image appearance) will require a larger number of radiologists to be tested.
5. Conclusion
We could not find a statistical difference between radiologists’ diagnostic performances as a group on different reconstructions. We found that this may be due to the disagreement among radiologists on reconstructions. Specifically, we observed opposite trends in the diagnostic performances on different reconstructions for different subgroups of the radiologists in this study, which were canceled out to each other when their diagnostic performances were averaged. This observation has to be verified in a hypothesis driven study. In addition, we found that the radiologists’ preference on reconstructions do not match with their diagnostic performance. Our result indicates that these disagreements may hinder the development of clinical image-based model observers for diagnostic tasks on bCT cases, since the difficulty of validating model observers against radiologists. Future studies with larger numbers of radiologists and cases will be necessary to check, confirm, or refute our findings for this and other imaging tasks.
Acknowledgments
This study was supported in part by grants from the National Institutes of Health R21-EB015053 and R01-CA181081. The authors would like to thank Andriy I. Bandos for his suggestions and help on statistical analyses.
Biographies
Juhun Lee received his PhD in electrical and computer engineering from the University of Texas at Austin in 2014. He is a research instructor at the Imaging Research Laboratory in the Department of Radiology at the University of Pittsburgh. His research interests include algorithm developments for computer-aided diagnosis and breast lesion segmentation for bCT and mammography.
Robert M. Nishikawa received his PhD in medical biophysics from the University of Toronto in 1990. He is currently a professor and a director of the imaging research in the Department of Radiology at the University of Pittsburgh. He is a fellow of the AAPM, SBI, and AIMBE. He has more than 200 publications in breast imaging concentrating on computer-aided diagnosis, technology assessment, and quantitative imaging.
Ingrid Reiser received her PhD in physics from Kansas State University. She is an assistant professor of radiology at the University of Chicago in Chicago, Illinois. Her research interests include computer-aided detection and diagnosis methods for breast cancer in dedicated breast CT and digital breast tomosynthesis, as well as objective assessment of x-ray tomographic x-ray breast imaging systems.
Margarita L. Zuley is a professor of radiology and a vice chair of quality assurance and strategic development in the Department of Radiology at the University of Pittsburgh Medical Center (UPMC), Interim Department chair of radiology UPMC Bedford, and chief of breast imaging of UPMC. She sits on several committees for ACR and SBI; and is a member of several professional organizations including ACR, ARRS, RSNA, and SBI.
John M. Boone received his BA degree in biophysics from the UC Berkeley and his PhD in radiological sciences from the UC Irvine. He is a professor and a vice chair (research) of radiology, and a professor of biomedical engineering at the University of California, Davis. He has research interests in breast imaging, CT, and radiation dosimetry; he is the PI of the breast tomography project, where more than 600 women have been imaged on breast CT scanners fabricated in his laboratory.
Disclosures
Dr. Lee, Dr. Nishikawa, Dr. Reiser, and Dr. Zuley have nothing to declare. Dr. Boone has a research contract with Siemens Medical Systems, and receives royalties from Lippincott Williams and Wilkins (book).
References
- 1.Brenner D. J., Hall E. J., “Computed tomography—an increasing source of radiation exposure,” N. Engl. J. Med. 357(22), 2277–2284 (2007).http://dx.doi.org/10.1056/NEJMra072149 [DOI] [PubMed] [Google Scholar]
- 2.Medicare Payment Authority Commission, A Data Book: Health Care Spending and the Medicare Program, Medicare Payment Advisory Commission; (2015). [Google Scholar]
- 3.Verdun F. R., et al. , “Image quality in CT: from physical measurements to model observers,” Phys. Med. 31(8), 823–843 (2015).http://dx.doi.org/10.1016/j.ejmp.2015.08.007 [DOI] [PubMed] [Google Scholar]
- 4.Thurston J., “NCRP Report No. 160: ionizing radiation exposure of the population of the United States,” Phys. Med. Biol. 55(20), 6327 (2010).http://dx.doi.org/10.1088/0031-9155/55/20/6327 [Google Scholar]
- 5.Barrett H. H., et al. , “Model observers for assessment of image quality,” Proc. Natl. Acad. Sci. U. S. A. 90(21), 9758–9765 (1993).https://doi.org/10.1073/pnas.90.21.9758 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Barrett H. H., Myers K. J., Foundations of Image Science, 1st ed., Wiley-Interscience, Hoboken, New Jersey: (2003). [Google Scholar]
- 7.Gifford H. C., Liang Z., Das M., “Visual-search observers for assessing tomographic x-ray image quality,” Med. Phys. 43(3), 1563–1575 (2016).http://dx.doi.org/10.1118/1.4942485 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Sen A., Kalantari F., Gifford H. C., “Task equivalence for model and human-observer comparisons in SPECT localization studies,” IEEE Trans. Nucl. Sci. 63(3), 1426–1434 (2016).http://dx.doi.org/10.1109/TNS.2016.2542042 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Gifford H. C., “Efficient visual-search model observers for PET,” Br. J. Radiol. 87(1039), 20140017 (2014).http://dx.doi.org/10.1259/bjr.20140017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Popescu L. M., Myers K. J., “CT image assessment by low contrast signal detectability evaluation with unknown signal location,” Med. Phys. 40(11), 111908 (2013).http://dx.doi.org/10.1118/1.4824055 [DOI] [PubMed] [Google Scholar]
- 11.Parages F. M., et al. , “A Naive-Bayes model observer for a human observer in detection, localization and assessment of perfusion defects in SPECT,” in 2013 IEEE Nuclear Science Symp. and Medical Imaging Conf. (2013 NSS/MIC), pp. 1–5 (2013).http://dx.doi.org/10.1109/NSSMIC.2013.6829286 [Google Scholar]
- 12.Parages F. M., et al. , “Machine-learning model observer for detection and localization tasks in clinical SPECT-MPI,” Proc. SPIE 9787, 97870W (2016).http://dx.doi.org/10.1117/12.2217124 [Google Scholar]
- 13.Marin T., et al. , “Numerical surrogates for human observers in myocardial motion evaluation from SPECT images,” IEEE Trans. Med. Imaging 33(1), 38–47 (2014).http://dx.doi.org/10.1109/TMI.2013.2279517 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kalayeh M. M., Marin T., Brankov J. G., “Generalization evaluation of machine learning numerical observers for image quality assessment,” IEEE Trans. Nucl. Sci. 60(3), 1609–1618 (2013).http://dx.doi.org/10.1109/TNS.2013.2257183 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Brankov J. G., et al. , “Learning a channelized observer for image quality assessment,” IEEE Trans. Med. Imaging 28(7), 991–999 (2009).http://dx.doi.org/10.1109/TMI.2008.2008956 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Park S., et al. , “A statistical, task-based evaluation method for three-dimensional x-ray breast imaging systems using variable-background phantoms,” Med. Phys. 37(12), 6253–6270 (2010).http://dx.doi.org/10.1118/1.3488910 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Sidky E. Y., Pan X., “In-depth analysis of cone-beam CT image reconstruction by ideal observer performance on a detection task,” in 2008 IEEE Nuclear Science Symp. Conf. Record, pp. 5161–5165 (2008).http://dx.doi.org/10.1109/NSSMIC.2008.4774398 [Google Scholar]
- 18.Abbey C. K., Boone J. M., “An ideal observer for a model of x-ray imaging in breast parenchymal tissue,” in Digital Mammography, Krupinski E. A., Ed., pp. 393–400, Springer, Berlin, Heidelberg: (2008).https://doi.org/10.1007/978-3-540-70538-3_55 [Google Scholar]
- 19.Abbey C. K., Nguyen N. Q., Insana M. F., “Optimal beamforming in ultrasound using the ideal observer,” IEEE Trans. Ultrasonics Ferroelect. Freq. Control 57(8), 1782–1796 (2010).http://dx.doi.org/10.1109/TUFFC.2010.1616 [DOI] [PubMed] [Google Scholar]
- 20.He X., Park S., “Model observers in medical imaging research,” Theranostics 3(10), 774–786 (2013).http://dx.doi.org/10.7150/thno.5138 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Park S., Zhang G., Myers K. J., “Comparison of channel methods and observer models for the task-based assessment of multi-projection imaging in the presence of structured anatomical noise,” IEEE Trans. Med. Imaging 35(6), 1431–1442 (2016).http://dx.doi.org/10.1109/TMI.2016.2515027 [DOI] [PubMed] [Google Scholar]
- 22.Zhang Y., Pham B. T., Eckstein M. P., “The effect of nonlinear human visual system components on performance of a channelized hotelling observer in structured backgrounds,” IEEE Trans. Med. Imaging 25(10), 1348–1362 (2006).http://dx.doi.org/10.1109/TMI.2006.880681 [DOI] [PubMed] [Google Scholar]
- 23.Witten J. M., Park S., Myers K. J., “Partial least squares: a method to estimate efficient channels for the ideal observers,” IEEE Trans. Med. Imaging 29(4), 1050–1058 (2010).http://dx.doi.org/10.1109/TMI.2010.2041514 [DOI] [PubMed] [Google Scholar]
- 24.Graff C. G., Myers K. J., “The ideal observer objective assessment metric for magnetic resonance imaging,” in Information Processing in Medical Imaging, Székely G., Hahn H. K., Eds., pp. 760–771, Springer, Berlin, Heidelberg: (2011).https://doi.org/10.1007/978-3-642-22092-0_62 [DOI] [PubMed] [Google Scholar]
- 25.Lin Y., et al. , “An image-based technique to assess the perceptual quality of clinical chest radiographs,” Med. Phys. 39(11), 7019–7031 (2012).http://dx.doi.org/10.1118/1.4760886 [DOI] [PubMed] [Google Scholar]
- 26.Samei E., et al. , “Automated characterization of perceptual quality of clinical chest radiographs: validation and calibration to observer preference,” Med. Phys. 41(11), 111918 (2014).http://dx.doi.org/10.1118/1.4899183 [DOI] [PubMed] [Google Scholar]
- 27.Lee J., et al. , “Predicting radiologists’ diagnostic performances using quantitative image features: preliminary analysis,” in Radiological Society of North America 2015 Scientific Assembly and Annual Meeting, Chicago, Illinois: (2015). [Google Scholar]
- 28.Reiser I., et al. , “Automated detection of mass lesions in dedicated breast CT: a preliminary study,” Med. Phys. 39(2), 866–873 (2012).http://dx.doi.org/10.1118/1.3678991 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Lee J., et al. , “Local curvature analysis for classifying breast tumors: preliminary analysis in dedicated breast CT,” Med. Phys. 42(9), 5479–5489 (2015).http://dx.doi.org/10.1118/1.4928479 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Ray S., et al. , “Analysis of breast CT lesions using computer-aided diagnosis: an application of neural networks on extracted morphologic and texture features,” Proc. SPIE 8315, 83152E (2012).http://dx.doi.org/10.1117/12.910982 [Google Scholar]
- 31.Kuo H.-C., et al. , “Impact of lesion segmentation metrics on computer-aided diagnosis/detection in breast computed tomography,” J. Med. Imaging 1(3), 031012 (2014).http://dx.doi.org/10.1117/1.JMI.1.3.031012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Lindfors K. K., et al. , “Dedicated breast computed tomography: the optimal cross-sectional imaging solution?,” Radiol. Clin. North Am. 48(5), 1043–1054 (2010).http://dx.doi.org/10.1016/j.rcl.2010.06.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Antropova N., et al. , “Efficient iterative image reconstruction algorithm for dedicated breast CT,” Proc. SPIE 9783, 97834K (2016).http://dx.doi.org/10.1117/12.2216933 [Google Scholar]
- 34.Feldkamp L. A., Davis L. C., Kress J. W., “Practical cone-beam algorithm,” J. Opt. Soc. Am. A 1(6), 612–619 (1984).http://dx.doi.org/10.1364/JOSAA.1.000612 [Google Scholar]
- 35.Reiser I., et al. , “Evaluation of a 3D lesion segmentation algorithm on DBT and breast CT images,” Proc. SPIE 7624, 76242N (2010).http://dx.doi.org/10.1117/12.844484 [Google Scholar]
- 36.Dice L. R., “Measures of the amount of ecologic association between species,” Ecology 26(3), 297–302 (1945).http://dx.doi.org/10.2307/1932409 [Google Scholar]
- 37.Zijdenbos A. P., et al. , “Morphometric analysis of white matter lesions in MR images: method and validation,” IEEE Trans. Med. Imaging 13(4), 716–724 (1994).http://dx.doi.org/10.1109/42.363096 [DOI] [PubMed] [Google Scholar]
- 38.Chen W., et al. , “Volumetric texture analysis of breast lesions on contrast-enhanced magnetic resonance images,” Magn. Reson. Med. 58(3), 562–571 (2007).http://dx.doi.org/10.1002/mrm.21347 [DOI] [PubMed] [Google Scholar]
- 39.Hillis S. L., et al. , “A comparison of the Dorfman–Berbaum–Metz and Obuchowski–Rockette methods for receiver operating characteristic (ROC) data,” Stat. Med. 24(10), 1579–1607 (2005).http://dx.doi.org/10.1002/sim.2024 [DOI] [PubMed] [Google Scholar]
- 40.Hillis S. L., “A comparison of denominator degrees of freedom methods for multiple observer ROC analysis,” Stat. Med. 26(3), 596–619 (2007).http://dx.doi.org/10.1002/sim.2532 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Hillis S. L., Berbaum K. S., Metz C. E., “Recent developments in the Dorfman–Berbaum–Metz procedure for multireader ROC study analysis,” Acad. Radiol. 15(5), 647–661 (2008).http://dx.doi.org/10.1016/j.acra.2007.12.015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Dorfman D. D., Berbaum K. S., Metz C. E., “Receiver operating characteristic rating analysis. Generalization to the population of readers and patients with the jackknife method,” Invest. Radiol. 27(9), 723–731 (1992). https://www.ncbi.nlm.nih.gov/pubmed/1399456 [PubMed] [Google Scholar]
- 43.Obuchowski N. A., Rockette H. E., “Hypothesis testing of diagnostic accuracy for multiple readers and multiple tests an anova approach with dependent observations,” Commun. Stat. Simul. Comput. 24(2), 285–308 (1995).http://dx.doi.org/10.1080/03610919508813243 [Google Scholar]
- 44.Kruskal W. H., Wallis W. A., “Use of ranks in one-criterion variance analysis,” J. Am. Stat. Assoc. 47(260), 583–621 (1952).http://dx.doi.org/10.1080/01621459.1952.10483441 [Google Scholar]
- 45.Tukey J. W., “Comparing individual means in the analysis of variance,” Biometrics 5(2), 99–114 (1949).http://dx.doi.org/10.2307/3001913 [PubMed] [Google Scholar]
- 46.Shin C.-I., et al. , “One-mSv CT colonography: effect of different iterative reconstruction algorithms on radiologists’ performance,” Eur. J. Radiol. 85(3), 641–648 (2016).http://dx.doi.org/10.1016/j.ejrad.2015.12.030 [DOI] [PubMed] [Google Scholar]
- 47.Pickhardt P. J., et al. , “Abdominal CT with model-based iterative reconstruction (MBIR): initial results of a prospective trial comparing ultralow-dose with standard-dose imaging,” AJR Am. J. Roentgenol. 199(6), 1266–1274 (2012).http://dx.doi.org/10.2214/AJR.12.9382 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Yamada Y., et al. , “Model-based iterative reconstruction technique for ultralow-dose computed tomography of the lung: a pilot study,” Invest Radiol. 47(8), 482–489 (2012).http://dx.doi.org/10.1097/RLI.0b013e3182562a89 [DOI] [PubMed] [Google Scholar]
- 49.Hara A. K., et al. , “ACRIN CT colonography trial: does reader’s preference for primary two-dimensional versus primary three-dimensional interpretation affect performance?,” Radiology 259(2), 435–441 (2011).http://dx.doi.org/10.1148/radiol.11100250 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Venjakob A. C., et al. , “Does preference influence performance when reading different sizes of cranial computed tomography?,” J. Med. Imaging 1(3), 035503 (2014).http://dx.doi.org/10.1117/1.JMI.1.3.035503 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Rawashdeh M. A., et al. , “Markers of good performance in mammography depend on number of annual readings,” Radiology 269(1), 61–67 (2013).http://dx.doi.org/10.1148/radiol.13122581 [DOI] [PubMed] [Google Scholar]
- 52.Miglioretti D. L., et al. , “When radiologists perform best: the learning curve in screening mammogram interpretation,” Radiology 253(3), 632–640 (2009).http://dx.doi.org/10.1148/radiol.2533090070 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Kan L., et al. , “Standardized abnormal interpretation and cancer detection ratios to assess reading volume and reader performance in a breast screening program,” Radiology 215(2), 563–567 (2000).http://dx.doi.org/10.1148/radiology.215.2.r00ma42563 [DOI] [PubMed] [Google Scholar]
- 54.Elmore J. G., et al. , “Variability in interpretive performance at screening mammography and radiologists’ characteristics associated with accuracy,” Radiology 253(3), 641–651 (2009).http://dx.doi.org/10.1148/radiol.2533082308 [DOI] [PMC free article] [PubMed] [Google Scholar]