Collective benefits in traffic during mega events via the use of information technologies

Abstract

Information technologies today can inform each of us about the route with the shortest time, but they do not contain incentives to manage travellers such that we all get collective benefits in travel times. To that end we need travel demand estimates and target strategies to reduce the traffic volume from the congested roads during peak hours in a feasible way. During large events, the traffic inconveniences in large cities are unusually high, yet temporary, and the entire population may be more willing to adopt collective recommendations for collective benefits in traffic. In this paper, we integrate, for the first time, big data resources to estimate the impact of events on traffic and propose target strategies for collective good at the urban scale. In the context of the Olympic Games in Rio de Janeiro, we first predict the expected increase in traffic. To that end, we integrate data from mobile phones, Airbnb, Waze and transit information, with game schedules and expected attendance in each venue. Next, we evaluate different route choice scenarios for drivers during the peak hours. Finally, we gather information on the trips that contribute the most to the global congestion which could be redirected from vehicles to transit. Interestingly, we show that (i) following new route alternatives during the event with individual shortest times can save more collective travel time than keeping the routine routes used before the event, uncovering the positive value of information technologies during events; (ii) with only a small proportion of people selected from specific areas switching from driving to public transport, the collective travel time can be reduced to a great extent. Results are presented online for evaluation by the public and policymakers (www.flows-rio2016.com (last accessed 3 September 2017)).

1. Introduction

Daily traffic has important implications for the functioning of our cities [1–4]. It affects total energy use, equity, air pollution and urban sprawling. Given this impact, master plans of urban transportation need to be technically sound, economically affordable and publicly acceptable [5–11]. This becomes a more pressing need when preparing for large events, which unusually stress the use of the available infrastructures and put at risk the overall success of the event.

In their best attempts, goals of an urban transportation plan seek to: (i) avoid long and unnecessary motorized travel, (ii) shift the movement of people to socially efficient modes, such as walking, biking and public transit, and (iii) improve the technology and operational management of transportation services. To reach these goals, plans today try to promote the use of bus rapid transit (BRT), congestion charging or bike sharing. But much less is done to develop real-time information platforms that provide the value of choices for the social good. Nowadays, the most popular information platforms, such as Waze or Google Transit Feeds, give us individual information about travel times but do not take into account global information, e.g. providing incentives to reduce global costs regarding our route choices. One limitation may be that the main set of infrastructures in urban transportation planning of mature cities were developed in the 1970s, before the information age, and relied on the results of travel diaries, limiting the communication with the majority of the actual travellers. Second, demand management faces the ‘tragedy of the commons’. Space in streets is a shared-resource system where individual users act independently according to their own self-interest, behaving contrary to the common good by depleting that resource. The population, however, may be more prone to take actions for collective benefits while hosting a big event.

We propose demand-management strategies during mega events. Large-scale events happen every year around the world, such as the Olympic Games, world expositions, concerts, pilgrimages, etc. They attract a large number of participants and tourists travelling to one destination, thereby producing increased pressure on transportation, especially for cities with an already large population [12,13]. Past research has tried to estimate the impact of events on the economy and air quality of the host city [14–16]. Moreover, in the face of changing conditions in cities, a new topic—city resilience—has drawn attention from academics and decision-makers in recent years [17–20]. In the case of transportation networks, researchers mainly study the resilience of a network to cope with the unexpected damage or perturbations of transportation facilities [21–24] or guide long-term transportation construction [25,26]. For instance, Donovan and Work quantified the resilience of a transportation system to extreme events using GPS data from taxis [23]. Their model detects the event from historical data, and as a result it cannot forewarn the impact of forthcoming events. In the context of traffic management during large-scale events, previous efforts have focused on ensuring the efficient travel of participants. However, the disruptions to the travel of the local population are not taken into account. Currently, the most frequently used policy to reduce motorized travels is to limit the number of vehicles with a specific-ending plate number, but without efficient strategies to target congested bottlenecks [27,28]. Consequently, the new paradigm is to achieve the collective benefits of all travellers during events by integrating multiple data resources using information technologies to calculate the costs and communicate the benefits of various strategies [29,30].

Specifically, we evaluate the impact of large-scale events on the traffic in the host city and evaluate the impact of strategies to overcome it. We aim at understanding the change of travel demand during large-scale events, and to address reasonable demand-management strategies to mitigate traffic congestion during the event. We take the Summer Olympics 2016 in Rio de Janeiro as a case of study to estimate the impact of large-scale events on the travel of the local population. Rio de Janeiro is one of the most congested cities in the world according to the TomTom report on global traffic congestion [31]. A study released by the Industry Federation of the State of Rio de Janeiro (FIRJAN) confirmed that traffic congestion has resulted in tremendous economic costs. The study found that congestion costs of the cities of Rio and São Paulo added roughly USD43 billion in 2013 alone. The loss amounts nearly 8% of the gross domestic product of each metropolitan area. This is greater than the estimated budget for transport capital investment in Brazil, Mexico and Argentina combined. Traffic congestion originates from the imbalanced development of travel demand of vehicles and the road network supply [32,33]. For a booming city, the traffic congestion can be mitigated through constructing more roadways and transit infrastructure. But for mature urban areas like Rio, opportunities for further investments in transportation infrastructure are often limited [34].

The International Olympic Committee estimates 0.48 million tourists in Rio for Olympics, which is about 7.5% of the population of Rio. To understand the impact of the Olympics, we estimate the travel demand of the local population and their fraction in private vehicles using mobile phone data, also known as call detail records (CDRs) combined with Waze data. The travel times of commuters taking private cars are estimated during the morning and evening peak hours and compared with Google maps in the same hour. During the Olympics, we estimate the origin and destination of tourists using the Olympic Games' schedule, information on the expected audience in each venues, and Airbnb properties [35] and hotels. To estimate the increase in vehicular traffic, we estimate the taxi demand of tourists going to the events each hour and also the reduced capacity in the dedicated Olympic lanes. Both the tourists' taxi demand and the local vehicle demand are assigned to the road network under three routing scenarios: habit, selfish and altruism. The goal is to assess how if certain routing recommendations are followed we can gain collective benefits in vehicular traffic. To evaluate the results, we estimate the travel time of tourists and travel time increment of local commuters' under the three scenarios in the commuting peak hours. In addition, we also propose a mode change strategy, that targets a selected fraction of travellers to change from driving to the metro and BRT. To this end, we uncover the origin–destination (OD) pairs with the most contribution to the collective travel time and consider the overall benefit of taking one vehicle out of that pair. Finally, we demonstrate the effectiveness of the proposed demand-management strategy by comparing it with a benchmark program that reduces the same number of vehicles distributed randomly (which is similar to car reductions by plate numbers). A detailed diagram of the data and modelling pipeline can be found in the electronic supplementary material, figure S1.

2. Results

2.1. Travel demand estimation

2.1.1. Travel demand estimation before the Olympics

Previous studies generated the average hourly travel demand at the census tract scale using CDRs from mobile phones (include the timestamp and location for every phone call or SMS of anonymous users), census records and surveys data in Rio de Janeiro [11,36–38]. In the travel demand estimation framework, the stay locations of each user are recognized and labelled as home, works or other. The most visited place during weekday nights and weekends is labelled as home, the most visited place during weekday working hours is labelled as work, and the rest are labelled as other. Consequently, we classify the trips of each person as: home-based-work (or commuting, includes travel from home to work and from work to home), home-based-other (trips between home and other), and non-home-based (trips between non-home places, e.g. work and other). After aggregating the trips to census tract scale with the geographical locations of their origins and destinations, we get the number of mobile phone users travelling from tract to tract on hourly basis. Then, the travel demand of all residents is estimated by scaling the user demand with an expansion factor, which is defined as the ratio between the actual population of the origin tract from the census and the number of users whose homes are located in that tract. In this way, we get a reasonable person OD matrix with different trip purposes. To assess the traffic in the road network, we need to estimate vehicle demand. Namely the vehicles OD matrix, counting the number of private vehicles used by residents from their origin to their destination tracts. In this work, we only consider the motor vehicles used by residents and thereby simply scale the person demand of each OD pair with the vehicle usage rate in its origin tract. The estimated vehicle demand is 0.44 million from 1.69 million trips of residents during the morning peak hours and 0.44 million vehicles and 1.61 during the evening peak hours in the Rio de Janeiro municipality. The 24-h trip demand with different trip classes is given in the electronic supplementary material, figure S3a,b and note 1.

Next, we extend the vehicle demand to small fluctuations in 5 weekdays, using the records of Waze Mobile [39]. Waze provided the records of Wazers for seven months in 2015. The datasets include the location of user, timestamp, level and duration of jam, average speed and length of the queue. We relate the fluctuations in the average length of the queue of traffic jams in the entire road network as proportional to the fluctuations of the total vehicle demand in this hour (previously estimated with mobile phone data). In other words, we calculate the average queue length in the whole municipality area of Rio in each hour each weekday, and use that value as a global congestion index. Using it to uniformly extend the travel demand of all OD pairs in 5 weekdays (see details in the electronic supplementary material, figures S2c and 4 and note 2).

2.1.2. Travel demand estimation during the Olympics

To build the OD matrices during the Olympics, we need to infer the additional trips, that is, the origins and destinations and the flow between them. During the Olympics, the trips of tourists mainly contain the following three categories: travelling from residences to venues, departing from the venues and others (going to restaurants, shopping areas, scenic regions, etc.). Among them, the trips from residences to venues are more predictable and the most important factor to increase traffic at a particular time. Therefore, we only consider the flow from spectators' residences to the game venues. Figure 1a represents the location of 12 Olympic venues, the distribution of Airbnb properties and hotels, the metro and the BRT lines in Rio. Most of the tourists' residences are distributed in the southeast coastal area. As planned by the municipal government, most venues are located around the metro or BRT stations, which makes public transportation quite convenient for most of the spectators.

Figure 1.

Locations of venues, tourists' residences and the number of spectators per venue per hour. (a) The locations of 12 Olympic venues, the metro and BRT lines in Rio, the locations of hotels and distribution of Airbnb properties. Most venues are near to metro/BRT stations, as well as hotels and most Airbnb properties. We distribute tourists around the 13 400 Airbnb properties and 106 hotels. Metro and BRT will likely be the first choice for most spectators. (b) The number of spectators arriving at each venue per hour on 9 weekdays during the Olympic Games. The largest indoor stadium, Carioca arena is also the busiest one.

The person travel demand equals the sum of local demand before the Olympics and the number of people going to stadiums from their residences in the same time interval. To estimate this increase, the number of spectators arriving at each venue is estimated each hour based on the Olympic game schedule and the expected audience in each venue. For each hour, we add the expected audience of the venue if there are games that start in the venue in the given hour. This information was provided by the city together with the games schedule. Figure 1b shows the results on weekdays during the Olympics. The maximum number of spectators is nearly 0.1 million, which is a considerable fraction of the number of commuters in the peak hour. To determine the departure from hotels/Airbnb places to venues, we make the following assumptions: (i) 30% of spectators depart 1 h ahead; 40% of spectators depart 2 h ahead; the others depart 3 h ahead. (ii) We also use the distribution of Airbnb properties to capture the distribution of origins of the local population that can affords the tickets. Namely, all the spectators are distributed from the Airbnb properties and hotels, and are named tourists in the rest of the paper (see the electronic supplementary material, figure S2d for the distribution of the population density in Rio de Janeiro). As the Airbnb properties and hotels distribute across tracts, we first aggregate them to tracts with their geographical locations and assign an accommodation capacity to each tract. Then, for each tract, we define a factor p_t as the ratio between the accommodation capacity of the tract to the total accommodation capacity in Rio. While the 12 venues are each located in a different tract. Finally, the number of trips from each tract to the venues tract are estimated by scaling the total demand to the venue with the factor p_t in the origin tract (see the electronic supplementary material, figure S5 and note 3).

To estimate the additional vehicle demand during the Olympics, we estimate the travel mode of tourists in each hour. Based on their required travel distances, a considerably fraction of them may use public transportation or taxi which will not affect our vehicle traffic and the subsequent strategies. We allow travel mode of tourists in four categories: walking and Metro/BRT, bike and Metro/BRT, taxi and bus. To that end, we simply take into account the distance to metro/BRT stations, the total travel time and the number of mode transitions. Figure 2a shows the results of travels by mode on 8 August (Monday). As expected, most tourists choose Metro/BRT because both their hotels and venues are near to Metro/BRT stations. Nonetheless, during the daytime, we estimate that about 10 000 tourists choose taxis to the venues per hour, which produces a considerable increase in vehicles added to the streets to only 12 destinations. As it is unlikely that the tourists travel alone, we assume taxi occupancy as 2, that is, two tourists per taxi per trip (see the electronic supplementary material, figure S6).

Figure 2.

Estimated travel mode of tourists and total travel demand during the Olympics. (a) Tourist travel modes on 8 August. A large proportion of tourists used public transportation. About one-third of them may use taxis. (b) Estimates of total trips and vehicle trips per hour on 10 weekdays during the Olympics from August 8 to 19. The total trip estimates add local travellers and tourists going to venues in the given hour. The vehicle trips add the local population in their private cars vehicle and the estimated number of taxis used by tourists.

Figure 2b shows the total trips and the individual car trips on 10 weekdays from 8–19 August. Car trips increase the local vehicle demand for private cars estimated from CDRs and the taxi trips estimated for tourists. The morning peak is around 9.00 and the evening peak is around 18.00. During the peak hour, about 27% of the total trips occur. The number increases to approximately 60 000 trips during the Olympics. Consequently, traffic in the city will be especially congested for the paths from tourists' residences to venues.

2.2. Travel time estimates and analysis of impacts in vehicular traffic

Before the Olympics, we assign the drivers to the routes distributing them via their shortest travel times and taking into account the resulting congestion as streets fill up. This is a common approximation to model the complex problem of route selection. Namely, the user equilibrium (UE) model, which implies no driver can unilaterally reduce his/her travel time by changing routes. In our implementation of the UE model, the travel times of links depend on the volume-over-capacity ratio (VoC), calculated with the Bureau of Public Roads (BPR) function:

2.1

where t_e(v_e) is the average travel time on link e; t^f_e is the free flow travel time on this link; f_s is a scale factor and not less than 1. The coefficients in BPR are calibrated using field data collected by surveillance cameras as f_s = 1.15, α = 0.18, β = 5.0. Finally, we compare our estimated travel times of top commuter OD pairs with the results of the Google maps API in the same hour, finding very good agreement (see the electronic supplementary material, figures S3 and S7, and note 4).

The Olympics will disrupt the routes of a fraction of travellers, especially those with routine routes that follow the paths to the games or trough the reduced capacity of the lanes dedicated to the Olympics. These are lanes in which only buses carrying athletes and staff can travel. In the trips assignment during the Olympics, this reduced capacity also generates traffic.

Our goal is to evaluate the impact on travel times under three types of vehicular route choices: (i) habit: all travellers will follow their routine travel routes even if this route is more congested during the Olympics; (ii) selfish: travellers have good knowledge of the traffic situation and each of them will choose the route with the shortest travel time, which follows the UE model; (iii) altruism: travellers follow the travel routes for the best case scenario for the collective travel time. In this case, the travel route of each traveller is assigned taking into account their effects on the total travel time. We evaluate the results of routing strategy both on taxis and residential vehicles. The traffic states on the roads are diverse under the three scenarios (see the electronic supplementary material, figure S9).

Figure 3a,b is a box plot of the distribution of tourists' travel times during the morning and evening peak hour on 10 weekdays, respectively. The habit scenario always performs worse than selfish and altruism as local travellers will not give way to tourists and their journey times increase considerably. Selfish and altruism scenarios, by contrast, allow travellers to choose their routes towards their own or others' benefit. Interestingly, in the morning peak hour, tourists' travel times under altruism are globally similar than selfish, while they are much worse than selfish and habit in the evening. The reason is that in the morning, the flow direction of tourists (mainly from urban to suburban) is opposite to most of the commuting trips (mainly from suburb to the urban core). While in the evening peak hour, more commuters have a similar direction to the tourists (mainly from the urban core to the suburbs). In this case, under altruism some taxis would detour, taking a longer travel time than selfish and habit.

Figure 3.

Travel times of tourists and impact of the Olympics on the local commuters under three routing scenarios of vehicles. (a,b) Box plot of tourists' taxi travel time during the morning peak on 10 weekdays. In morning peak hour, the average travel time of tourists via the habit, selfish and altruism routes are 66, 44 and 43 min, respectively. In evening peak hour, they are 62, 43, and 47 min, respectively. (c,d) Box plot of commuters' travel time percentage increment on 10 weekdays. The number of commuters is scaled with log function. Negative percentage increments indicate people could reach shorter travel times than before the Olympics. (e,f) Average commuting time percentage increment comparison of three scenarios of 10 weekdays in the morning and evening peak hour, respectively. (g,h) Average percentage increment versus the selfish parameter Λ, representing the fraction of drivers that change their routine routes for a new shortest path during the event.

Furthermore, we evaluate the impact of the Olympics on local commuters, calculating the average percentage increment of commuter's travel times as

2.2

where od is one of all the OD pairs; f^c_od refers to the number of commuters; t^Olym_od and t^before_od refer to the travel time in the od route before and during the Olympics, respectively. I_comm can be negative as selfish or altruism allows that some commuters find shorter paths than before. Figure 3c,d depicts the distribution of commuters travel time in a log scale on weekdays. More people have longer travel times (I_comm > 20%) under the habit scenario than under the selfish or altruism scenarios. Moreover, in contrast with selfish, altruism increases the number of commuters suffering longer travel times but earns overall benefits for the majority of commuters. Figure 3e,f illustrates the average percentage increment per day. The increment with the habit scenario is always larger, followed by selfish and altruism. Furthermore, certain peak hours are subject to the most serious delays, e.g. morning peaks on 9 and 16 August, evening peaks on 12, 15 and 19 August. This is the essence of the altruism strategy: while a small fraction of people suffer longer travel times via detours to less popular routes [11], the overall saving in travel time is larger than in the selfish strategy. While in previous work it was already observed that altruism versus selfish strategies do not produce large differences [11], here we see that both strategies have considerable differences with the habit scenario. This shows the benefits of information technologies to help decrease congestion during the events when people can select alternative routes that are different from their routine routes.

To further evaluate this effect, we see the effects of the interplay between habit and selfish, meaning a fraction of people changing routes towards their shortest travel times, and others keeping their routine routes. To examine such intermediate states, we define a selfish parameter Λ to account for the fraction of selfish travellers. Λ ranges from 0 to 1, where 0 implies the habit scenario, and 1 implies the selfish scenario. Specifically, the travellers in each OD pair seek their shortest travel time with a percentage of Λ and their routes need to be reassigned, others are following their habit routes. Each link can be occupied by habit flow and selfish flow. The habit flow is calculated as v^habit_e · (1 − Λ), where v^habit_e is the link volume under habit scenario. The selfish flow v^selfish_e is obtained by assigning the selfish demand using the UE model. Therefore, the VoC is calculated by

2.3

and the BPR function in equation (2.1) is used to estimate the travel time on each link. For each OD trip, the total commuting time also contains two parts: (1 − Λ) · f^c_od · t^habit_od and Λ · f^c_od · t^selfish_od, where t^habit_od is the travel time under the habit scenario and t^selfish_od is the shortest travel time under the selfish parameter Λ. Figure 3g,h indicates the average increment for commuters on each weekday with different values of Λ. The increment percentage decreases with the increase of Λ, indicating that the impact of the Olympics recedes if more travellers are selfishly looking for their best routes as opposed to using their routine routes.

Most of the transportation planning strategies designed to reduce motorized vehicles are applied independently of origin and destination of the travellers, as a consequence they are very costly in terms of the percentage of car reduction (usually 20% of the cars selected by the ending digit in the plates). They achieve very modest benefits in travel times, usually of the order of 2% [40]. Based on the estimation of travel delays of commuters under the selfish scenario, we explore the spatial impact of the Olympics on commuters. To achieve this, we average the percentage increment of commuter trips to origin and destination zones. Results indicate that commuters who live in the northeast of Rio suffer serious impact in the morning peak hour (see the electronic supplementary material, figure S10). In addition, people working in the eastern coastal area suffer travel delays most in both the morning and the evening peak hours. We also find that the densely populated Governador Island suffers critical delays as one of the two bridges between the island and mainland are set as Olympic lanes.

To facilitate policymaking, we visualize the travel time before and during the Olympics all over the metropolitan area of Rio, as shown in figure 4. From the visualization, travellers can explore their travel time increment during the peak hours due to the Olympics. In addition, the platform provides travel times under different scenarios, which helps travellers and policymakers realize the collective benefits generated by the travel demand-management strategy. To be scalable, this proof-of-concept strategy needs to be managed so that users have reliable access to the information required.

Figure 4.

Interactive visualization of travel times before the Olympics and during the Olympics via various strategies of mobility. The purple hexagon reflects the origin of trips. The white hexagons are associated with the Google travel times for comparison. The colours of other hexagons reflect the travel time from the selected origin to them. Results are presented online at www.flows-rio2016.com.

2.3. Informed mode change

With the aim of mitigating the traffic congestion during the Olympics, the government of Rio de Janeiro has made important investments, such as enhancing the capacity of the traffic network, extensions to the public transportation infrastructures, including construction of new metro and BRT lines. As a complement to those efforts, in this work we propose an efficient strategy to manage the travel demand with the present transport infrastructure; concretely, reducing a fraction of vehicle demand toward relieving congestion during the peak period.

With the purpose of selecting which critical trips to reduce, we evaluate the contribution of each OD trip to the collective travel time. Namely, we consider the following question: how much time will we save collectively if we take one vehicle out from a given OD route? We represent the road network as a directed graph 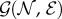, where 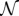is the set of nodes and is the set of directed edges. After assigning the travel demand to the road network, each road segment 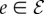is associated with volume v_e and travel time during traffic t_e. First, for a road segment, we estimate the travel time saving of others if we reduce one vehicle using the marginal edge cost, which is the partial gradient of total travel time over the current volume. For each edge, we have

2.4

where the edge travel time t_e is calculated using the calibrated BPR function in equation (2.1). The marginal edge cost MC_e consists of two terms: the first one t_e reflects the travel time of one vehicle and the second would be the saved travel time by other vehicles in the same edge. The travel route p_i,j of each OD trip (i, j) is the set of edges on the path. Consequently, we calculate the marginal path cost of OD pair (i, j) as the sum of MC_e for the edges is traversed by the path:

2.5

where δ_ep is the delta function, which is 1 if edge e is traversed by path p, 0 otherwise.

Larger values of MC_p indicate more collective travel time would be saved if we take the trip out. Consequently, a sensible strategy is to reduce the demand from top-ranked OD pairs. To formulate a feasible strategy, we only consider the trips in which both origins and destinations are located close to the metro or BRT stations, which means these people could switch to public transport rather than driving. In our experiments, we define the maximum distance from the centroid of a zone to the nearest station. We evaluate the effects of this distance defined as 1, 2 or 3 km. First, we select the trips with origins and destinations within a certain distance of the nearest metro or BRT station. Then, we calculate the MC_p for each trip and reduce the demand from the top-ranked trips by 60%. The number of top-ranked trips ranges from 1000 to 10 000. Finally, we reassign the remainder of the demand to the road network and check the reduction of the collective travel time. As a benchmark, we keep the same number of total reduced trips but uniformly distribute them to all OD pairs near Metro and BRT stations.

Figure 5a illustrates the reduction in collective travel times as a percentage of the travel time before the strategy, which approximately follows a linear relationship with the number of reduced OD pairs. Interestingly, in contrast to the uniform benchmark, the strategy based on marginal costs is more effective by a factor of five. For example, reducing 60% of the flow from the selected 5000 OD pairs at the range of 2 km, represents 1.14% of the total vehicle flows. In that case, the reduction in the percentage of collective travel time is more than 10% with the marginal cost strategy and only 2% with the uniform benchmark case. In addition, different distance thresholds produce similar results for the same number of OD pairs. However, as shown in figure 5b, greater distances indicate a lower percentage in the total flow. This is because larger distances provide more options to the collective travel time saving and affects car travel in a less concentrated fraction.

Figure 5.

Informed changes from vehicles to transit during the morning peak hour. (a) Collective travel time reduction under different strategies. The reduction of collective travel time rises linearly over the number of reduced OD pairs. The slopes of the marginal strategy are 1.45 × 10⁻³, 1.64 × 10⁻³ and 1.67 × 10⁻³ for 1 km, 2 km and 3 km, respectively; while the slopes of the uniform benchmark strategies are 0.47 × 10⁻³, 0.39 × 10⁻³ and 0.40 × 10⁻³ for 1 km, 2 km and 3 km, respectively. The informed strategy reduces the collective travel time more than five times the reduction of the uniform case. (b) Reduced demand under different threshold distances. As expected larger number of OD pairs imply a larger percentage of the demand reduced. (c) Added ridership to the metro/BRT line and reduced vehicles around stations with configuration {2 km, 6000 OD pairs}. The width of the metro and BRT line reflects the increased ridership by strategy. Blue and red in different areas reflect the origin and destination of reduced demand, respectively. Darker colours imply more people switching to transit from BRT or metro lines.

Figure 5c presents the spatial distribution of the reduced car demand for {2 km, 6000 OD pairs}. This case reduces the collective travel time by 10.6% at the expense of a 1.4% decrease in the total car demand, and improves the average speed of all vehicles from 37.08 to 39.94 km h⁻¹. Implying that a considerable fraction of the travel times of local commuters and tourists decrease, especially for the travellers with long trips (see the electronic supplementary material, figure S11). Interestingly, the distribution of destinations concentrates a very small area in the Centro of Rio (Downtown). Meanwhile, the distribution of origins concentrates in two areas, the west end of the BRT line and the west end of the metro line. This suggests that people living in two neighbourhoods in the West Zone of Rio (e.g. Santa Cruz and Paciência) and three neighbourhoods in the North Zone of Rio (e.g. Guadalupe, Marechal Hermes and Bento Ribeiro) would have to switch from driving to BRT or metro lines during the morning peak hour, if they work in Downtown. Moreover, figure 5c gives the additional ridership in each segment of the metro and BRT line. As can be seen, the maximum increase is 5000 travellers in the morning peak hour, in contrast with the capacity of the metro and BRT, approximately 30 000 passengers per hour per direction. If the current capacity of BRT cannot meet the needs of the mode change strategy, it is convenient and economical to add buses to the current BRT system. Finally, to investigate the impact in travel times of the proposed strategy on the individuals changing modes, we compared their average driving travel time with the transit time from the Google API (GTFs). Based on these estimates, average travel time would drop from 96.3 to 80.5 min if taking BRT and metro during the morning peak. This may encourage individuals to cooperate with the proposed travel demand-management strategy.

3. Discussion

Mega events can greatly benefit the host city in many aspects, such as attracting investment and tourism and stimulating the economy. Nevertheless, it also disrupts the routine of the city. One of the most feared costs by the population is the increase in travel times, especially for already dense cities, which are more likely to host the event. In the run-up to the Olympics, city planners need estimates on how the traffic will be affected, in order to establish appropriate policies to cope with the impact. However, the current impact evaluation on travellers is mostly confined to qualitative studies with anecdotal experience of events management. We lack quantitative methods to support the strategies. This is mostly due to difficulties regarding data availability to estimate travel demand. In this work, we present a method to estimate urban travel demand and the time increments to commuters during a large event by integrating multiple and large-scale data resources. Moreover, we evaluate the effects of various routing strategies on the increase in congestion.

As a case of study, we analysed the 2016 Summer Olympics in Rio de Janeiro. The large inflow of tourists increases the travel demand while the establishment of Olympic lanes decreases the road network supply. The first task is to estimate the rise in the demand-to-supply ratio on the streets and how this will affect travel times. First, we estimate the person and vehicle travel demands during the Olympics in Rio by estimating the number of tourists and their travel modes. In particular, we expect a greater number of tourists travelling during the morning peaks of 8, 12 and 15 August as well as the evening peaks of 12 and 15–17 August. By estimating the routes of vehicles under three distinct scenarios, habit, selfish and altruism, we assess quantitatively the impact of the Olympics on commuters. We find that the habit scenario produces the greatest travel times, followed by selfish and altruism. For some peak hours, the increment in the percentage of travel times of all commuters can be up to 7% if people follow their routine routes. The selfish scenario, which is the maximum benefit possible via changing routes, still produces about 5% of the increment for the most affected peak hours. This is in agreement with the magnitude of savings reported by Çolak et al. [11] in routine conditions. They showed that the collective travel times could be decreased at most by 4.7–7.7% by routing strategies (altruism).

The most effective strategy to reduce traffic is informed mode change. This improves existing practices of restricting cars by the ending digit of the plate numbers. To generate this strategy, we calculate the contribution of each OD pair to the collective travel time. Namely, the drivers who are mostly involved in traffic bottlenecks are encouraged to change from driving to public transportation. Finally, by reducing 1% of the total cars, but targeting the zones near metro and BRT lines, the decrease in overall travel time reaches about 9%. Wang et al. reported that a 1% target decrease in demand can achieve 14% and 18% decreases in travel times for the San Francisco Bay Area and Boston, respectively [40]. However, the proposed countermeasures did not consider the existing alternatives for travel modes. By contrast, our strategy only targets drivers within 3 km of public transportation both in their origins and their destinations. For incentives, discounts for transit and ridership services in the selected communities could be tested.

Overall, we propose a methodology to give travel recommendations to users towards their collective benefits using information technologies. Specifically, we showed that the use of information to target mode change can be the most cost-effective alternative to increasing capacity in transportation. This information-based approach is convenient not only for relieving congestion, but also potentially increasing the use of public transport, which would deliver better environmental outcomes, stronger communities and more sustainable cities. We have estimated how the travel demand in each zone contributes differently to overall congestion; these results can be helpful for the planning of routes of public transportation. In future studies, we can calculate the reduction in emissions associated with the improvement in travel times when taking one vehicle out from the selected OD pairs, thereby managing vehicle demand to improve air quality. The data resources used in our work are the by-products of the use of communication technologies (CDRs and Waze) or open-source repositories (event schedule, venue property, Airbnb, hotels and OpenStreetMap). Consequently, the proposed methods are portable for events in other cities. Meanwhile, as the data resources are becoming more abundant, our work represents a feasible application for demand prediction and management that improves urban well-being.

We evaluated three ideal scenarios and their impacts during the Olympics. We expect that the most likely routing behaviour to be between habit and selfish, meaning that only a fraction of the population may find their shortest routes while the others will follow their habit routes before the Olympics. To have an idea of such scenarios, we have defined a selfish parameter Λ, and reported the results for different values that go from the habit to selfish case.

An interesting avenue is to estimate empirical routing behaviour [41]. Collecting data about individual route choices before and after the event is useful to understand changes in behaviour during large events. Also, comparing the actual change of traffic conditions from Waze during the Olympics versus our estimates, as well as the comparison of other mitigation strategies, such as ridesharing, and changes in the departure times of travellers, can be key emphasis in the future work.

4. Method

4.1. Datasets

The data resources used in this work are: mobile phone data (CDRs), Waze data, camera data, Airbnb data, hotel data, the Olympic game schedules and information of venues, as well as the OpenStreetMap. CDRs consist of five months of 2.19 million anonymous users and are used to estimate the 24 h routine ODs before the Olympics. Waze datasets contain 4.6 million reports during seven months and are used to extend the 24 h ODs to 5 weekdays. We argue that the larger overall congestion length in the road network relates to the larger number of cars. Also, camera datasets provide the relationship between traffic volumes and average speeds in 85 main streets and are used to calibrate the relationship between volume-over-capacity and actual travel time. Airbnb data sets were reviewed on the website of Airbnb in January 2015 [35], and contain 13 400 properties and each property provides its location and the number of accommodations available. We estimated the distribution of tourists' residences using the Airbnb dataset together with information from 106 hotels. OpenStreetMap provides the road network we used in our demand assignment. Game schedules, and locations and capacities of the venues were used to estimate the tourists' destination and departure times. Among the datasets, CDRs, Waze data and camera data are a by-product of the activity. Other datasets are all publicly available (see the electronic supplementary material, figures S1–S5 and S7, and notes 1–4).

4.2. Tourists travel mode split

In order to estimate the added vehicle demand during the Olympics, the taxi demand of tourists must be calculated from the tourists total demand in each hour. We define four mobility modes for tourists: walking and metro/BRT, bike and metro/BRT, taxi and bus. The reason we merge the metro line and BRT lines together is that they are a closed loop, as shown in figure 1. Walking and metro/BRT implies the origin and destination of tourists is near enough to the stations (1 km). Bike and metro/BRT implies they are near enough for biking (2 km). Tourists will consider bus travel if travel time and the number of transfers are both acceptable (less than 3). Otherwise, they will choose to take a taxi to the venues. We assume the occupancy of taxis by tourists is 2, meaning two tourists will take one taxi on average during the Olympics (see the electronic supplementary material, figure S6 and note 3).

4.3. Travel time estimation

To estimate travellers' delay during the Olympics, we represent their routing trips before and during the Olympics using a traffic assignment model. Traffic assignment aims to estimate the travel time and volume on each road segment. The estimation is implemented by appointing reasonable (usually shortest travel time) travel paths for all of the trips from their origin to destination. Before the Olympics, we assume that all travellers have found their routes with the shortest travel time and assign the demand with the UE model. To validate the estimated travel time, we compare the travel times of the top 5000 commuter OD pairs with Google maps APIs during the morning peak hour. The results show that the estimates are reasonable (see the electronic supplementary material, figure S3). During the Olympics, both the demand and the capacity of the road networks change. For the habit scenario, all of the travellers follow their routes before the Olympics, we update the volume and travel time on each edge only considering the additional tourists flow. Tourists' routes are chosen according to the shortest travel path before the Olympics. For the selfish scenario, we assign the new demand with UE model as before the Olympics. For altruism scenario, we calculate the shortest path with respect to the marginal cost for each OD pair, which makes the entire road network reach system optimum. To obtain more realistic estimates of travellers' journeys during the Olympics, we argue that only a fraction of people can find their shortest path, which means one fraction of the drivers follow their routine routes, while the remaining fraction is assigned using the UE model to the available space (see the electronic supplementary material, figures S9 and 10, and note 5).

Authors' contributions

Y.X. processed and analysed the data. Y.X. and M.C.G. designed the study, wrote the manuscript, and approved the final version of the manuscript.

Competing interests

We declare we have no competing interests.

Funding

The research was partly funded by Ford, the Department of Transportation's grant of the New England UTC Y25, the MIT Portugal Program, the MIT-Brazil seed Grants Program, the Center for Complex Engineering Systems at KACST-MIT and the MIT-QCRI research collaboration.