Synthetic associative learning in engineered multicellular consortia

Abstract

Associative learning (AL) is one of the key mechanisms displayed by living organisms in order to adapt to their changing environments. It was recognized early as a general trait of complex multicellular organisms but is also found in ‘simpler’ ones. It has also been explored within synthetic biology using molecular circuits that are directly inspired in neural network models of conditioning. These designs involve complex wiring diagrams to be implemented within one single cell, and the presence of diverse molecular wires become a challenge that might be very difficult to overcome. Here we present three alternative circuit designs based on two-cell microbial consortia able to properly display AL responses to two classes of stimuli and displaying long- and short-term memory (i.e. the association can be lost with time). These designs might be a helpful approach for engineering the human gut microbiome or even synthetic organoids, defining a new class of decision-making biological circuits capable of memory and adaptation to changing conditions. The potential implications and extensions are outlined.

1. Introduction

A specially important component of adaptation in nature is based on the capacity of some living beings to respond to external signals by a combination of repeated exposure to stimuli and the potential for storing memories. One classical example is provided by early experiments on conditioning, also known as associative learning (AL), and is one particularly important example of a general class of processes involving associative memory [1,2]. In these experiments, a given animal is known to respond automatically to an unconditioned stimulus (US) such as air puff in the eye that leads to eyelid closure. Instead, another stimulus such as a weak noise is unlikely to elicit a response. This would be an example of a conditioned stimulus (CS). In a nutshell, AL occurs when both stimuli are simultaneously presented, in such a way that a repeated exposure to both stimuli creates a cognitive link. At some point the exposure to only CS leads to the response that was originally limited to US: the weak noise triggers eyelid closure.

Conditional learning is part of the enormous potential exhibited by organisms having neuronal systems and might have been a crucial innovation in the evolutionary history of multicellularity [3]. Many forms of adaptation are grounded in neuronal circuits capable of creating correlations between different events, providing a plastic and reliable way of predicting future changes [4,5]. Most of these examples involve the presence of a neural circuitry, but the phenomenon also seems to be at work in non-neural agents. For example, microorganisms are capable of dealing with environmental correlates and can perform decision-making tasks [6–10]. This includes, in particular, molecular mechanisms responsible for information processing [11,12]. A relevant question here is how could we synthetically enhance the cognitive complexity of microorganisms and how can this give insight into the origins and evolution of microbial intelligence [13]?

The potential for designing living systems has been rapidly improved in the last decade. Among the most promising areas where such engineering of microbial intelligence can be crucial is the engineering of the human microbiome [14–16]. Treatments and recovery from disturbance have been shown to be transitions among alternative states [17,18]. Mounting evidence reveals that this complex ecosystem is relevant in many pathological states and that engineered microbes could be designed to detect and cure microbiome-related disorders [19]. Because we often deal with complex diseases, such as inflammatory processes, these engineered microbes need to be ‘smart’, capable of delivering drugs under the required conditions but also able shut off once the inflammation is eliminated. This is more obvious if we take into account the enormous crosstalk that has been identified between microbial and human cells [20] particularly in relation to the gut microbiome and the nervous and immune systems [21]. Engineering such microbial circuits is a major challenge that requires moving beyond the sense-and-deploy framework.

Building complex decision-making circuits within a single cell is a challenging task, but several candidates have been suggested [22–27]. These studies propose different ways of approaching the problem of building synthetic systems capable of diverse levels of bacterial information processing. One example is the AL circuit presented by Fernando et al. that could be implemented in Escherichia coli as a model organism [23]. It was inspired by previous theoretical studies that used model neural networks to explain the process under a minimal set of assumptions. In this case, the problem with the proposed design (as well as many others) is that it requires several interactions to be engineered to tune the connectivity matrix of the molecular network, with all the problems derived from crosstalk [28].

In this paper, we aim to provide a simple short cut to this problem, by using consortia of cells that are used as basic modules, each one containing a small amount of engineering. This approximation has been successful in different contexts [29–34]. In the next section, we describe the logic behind our system design in order to illustrate its simplicity. Next, a potential implementation using a computational model for E. coli will be described.

2. The logic of multicellular learning

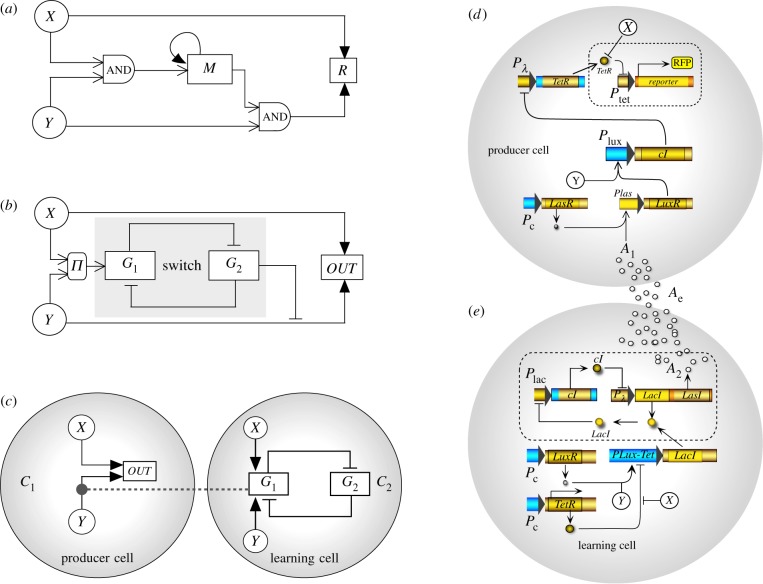
A synthetic circuit capable of AL requires modulation of the internal states through the learning process. Because the circuit responds to one signal (US) but not the other (CS) unless they have been previously presented together, this indicates that the internal states of the underlying molecular circuit must have changed (see table 1). In figure 1a, we show an example of a genetic implementation of AL introduced by Sorek et al. [25]. This work proposed a design inspired in neural networks. Here X can activate the response R whereas Y will do it (when X = 0) only if an intermediate module M (that needs to be previously activated by X + Y) has the right expression level. This kind of design and others of similar inspiration [23] require sophisticated wiring if implemented inside one cell.

Table 1.

Transition table for the simplified Boolean circuit implementing the two-cell circuit shown in figure 1c. The different input pair values given in the two left columns provide the sequence of states (X and Y for the conditional and unconditional inputs) introduced to test the presence of AL, assuming that G₁ = 0 and G₂ = 1 at the beginning.

X (uncond)	Y (cond)	state G1	state G2	output
0	0	0	1	0
0	1	0	1	0
1	0	0	1	1
1	1	1	0	1
0	0	1	0	0
0	1	1	0	1
1	0	1	0	1

Figure 1.

The logic of a two-cell AL circuit. (a) An example of ‘standard’ implementation, following neural network principles, is shown (adapted from [25]). (b) We summarize the basis of the circuit presented here that exploits the presence of a toggle switch (indicated in grey). Two inputs are present, X and Y indicating unconditioned and conditioned signals, respectively. The circuit can be split in two parts corresponding to two engineered cells (c) here indicated as C₁ and C₂, where the molecule G₁ from C₂ is needed to sense the signal Y (indicated with the grey dashed line). (c–d) The proposed implementation of the synthetic consortium is shown. Here the two cells (d, producer, e, learning cell) communicate in one direction by means of a molecular signal (A). Each engineered cell type performs part of the processing required to implement the association mechanism. We have used specific genes, cell–cell communication signals and reporters, but the basic principle can be used in different contexts (see text). (Online version in colour.)

One of the most fundamental requirements for AL is memory, and designing synthetic memory circuits has been an active area [35–41]. A well-known, successful example of a memory circuit is provided by the toggle switch [35,42,43]. This module has been extensively studied and characterized and is one of the best known components in cellular engineering. Because a molecular switch is capable of storing two alternative states, we use it here as a key piece of our proposed multicellular circuit. This introduces a restriction within the design of the system in relation to previous models. In order to illustrate how we perform our implementation, we represent a basic wiring diagram in figure 1b where two inputs are indicated as X and Y, corresponding to the unconditioned and conditioned signals, respectively.

The diagram in figure 1b presents some similarities with the one in figure 1a. We will assume here that the switch has an internal, initial state, with G₁ = 0 and G₂ > 0. If X > 0 and Y = 0, a response will be observed because the response unit receives direct and positive stimulation from X. Instead, since G₂ inhibits the potential activation from Y, a signal coming only from Y will not trigger a response. However, if both X and Y activate G₁, it can toggle the switch, inactivating (or under-expressing) G₂. Once this simultaneous activation occurs, the system is ready to react to Y only. This defines the basic logic of our implementation, but we have split the circuit in two parts (figure 1c) corresponding to a producer cell, C₁, carrying the toggle switch and a learning cell C₂, that is wired to C₁ through a molecular wire A. As can be seen, we maintain the same scheme, but use cells as modules that reduce the complexity of the engineering. In the next section, we make an explicit case for a microbial consortium capable of AL.

Because of the large number of equations involved, mathematical developments can be performed and the solutions will be numerical. However, it is possible to see how the model works (and predict the key outcomes) by using a simple Boolean circuit as the one indicated in figure 1c. Here we use a discrete dynamical system based on a threshold network where all states are either 0 or 1. A reporter signal (OUT) with two possible states provides the result of the computation. In the middle of the circuit, we have located a module involving cross-repression of two elements (G₁ and G₂) one of which can also modulate (through an inhibitory interaction) the effect of Y on the output. We can actually represent these interactions in terms of a Boolean dynamical system, where the state of each element S_i(t) ∈ {X, Y, G₁, G₂, OUT} at a given step t (assuming time is discretized) follows a discrete threshold dynamics: S_i(t + 1) = Φ[W_jiS_j(t) − θ_i]. Here the connections among different pairs are indicated as W_ji and can be positive or negative, indicating activation or inhibition, respectively [4]. The thresholds θ_i provide a condition for the total input in order to trigger a response. This is defined by the threshold function Θ(x) which gives Θ(x) = 1 if x ≥ 0 and 0 otherwise. This ideal function is a discrete, all-or-none version of the standard cooperative functions used in models of genetic networks (see §3).

For the circuit described in figure 1, our (discrete) equations are written as follows:

2.1

2.2

2.3

It is possible to show, following the discrete steps of this Boolean model, that an AL dynamic is being satisfied. The sequence of states associate with the consortium displayed in figure 1c is shown in table 1, where the set of possible input pairs (X, Y) and the (G₁, G₂) the states of the elements defining the memory switch (see table 1).

3. Associative learning in a synthetic microbial consortium

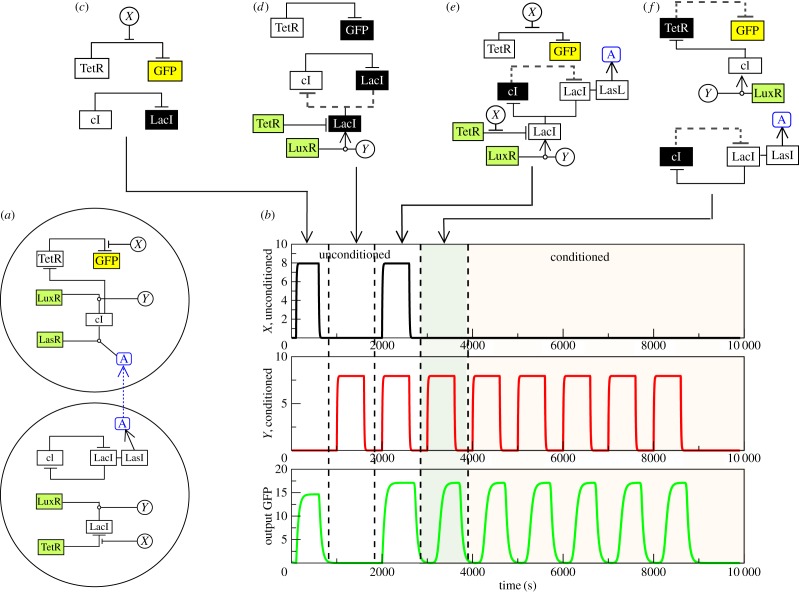
In order to avoid undesirable effects derived from complex constructs, cellular consortia, where different parts of the computation are split into different engineered cells, can be used as an alternative to single-cell designs. An example of such a synthetic consortium is displayed in figure 2a. It combines both constitutive and regulated gene expression and splits the circuit complexity in two separated cells. As summarized in figure 1b–e, the required behaviour is split into two basic modules, each one using different engineering. Although we will assume that the two cell types belong to the same species, this is not a necessary condition. Each cell in the consortia acts as a separated chassis for a subset of the required circuit. In our proposed implementation, we will use available information concerning well-established constructs and parameters gathered from the available literature and take E. coli as our model organism. Several potential candidates could be used as inputs, such as anhydrotetracycline (aTc) as our non-conditional stimulus (X) and acyl-homoserine lactone (AHL) (produced the gene luxI from the Vibrio fischeri quorum sensing system) as a CS (Y). In the presence of this stimulus, there is no response unless the system has established the association between X and Y. In a nutshell, whereas X alone always induces a system's response, Y does not.

Figure 2.

Time series of circuit behaviour under the sequential introduction of the unconditional stimulus X, the two types of stimuli. (a) We show the basic diagram of interactions detailed in figure 1. (b) We show the time series associated with an experiment of classical conditioning at the cell level. The first two are the inputs of X and Y , introduced as pulses for a given period and then removed. The sequence involves X > 0, Y = 0, X = 0, Y > 0, X, Y > 0 and then several pulses of Y-only activation. The upper diagrams (c–f) represent the relevant subgraphs that are changed or activated once the pulse has been introduced and the system stabilized. The dashed lines indicate existing, but not active, inhibitory connections. Here we have used the parameters: γ_TetR = γ_Las = γ_cI = γ_LuxR = γ_LacI = γ_A = γ_λ = γ_GFP = 0.1 μM min⁻¹, β_cI = 0.008 μM, β_Tet = 0.04 μM, θ_Lux = θ_Las = 0.01 μM², 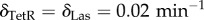, , 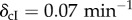, 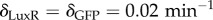μ = 0.025 μM, 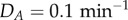. (Online version in colour.)

We have chosen a fluorescent protein as the candidate for the cell's output, although this could be a gene that triggers the delivery of a given therapeutic molecule. LuxR is a transcriptional activator from the V. fischeri quorum sensing system that binds to its cognate promoter Plux activating the expression of genes under its control. The wild-type LuxR is inactive when produced. AHL, produced by another gene, luxI, is an auto-inducer that binds LuxR and increases its activity.

The mathematical model associated with the cellular consortium displayed in figure 2 is decomposed into two sets of equations. Both cells have X and Y as inputs, but the nature of their responses is markedly different.

3.1. Producer cell equations

For the producer cell, we have five coupled differential equations, describing the basic interactions indicated in figure 1d. These equations are standard in the modelling of gene regulation networks [44]. Here we have a feed-forward set of interactions described by

3.1

which is a constitutive gene (here P_c will indicate a constitutive promoter) with a constant production rate γ_LasR. The dynamical equations for the rest of components in our cellular circuit read

3.2

3.3

3.4

The equation for the response dynamics, described by the concentration of our reporter, is defined by

3.5

The molecules are produced with γ rate and their own decay rate associated with the dilution and the loss of function (δ). The non-constant promoters have associated the following Hill functions used here are described by the functions Γ₁([LuxR],[Y]) and Γ₂([LasR],[A]) involving thresholded activation

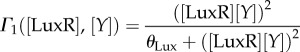3.6

and

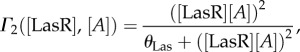3.7

where θ is the threshold of activation for each molecule. And the following Hill inhibition function:

3.8

In particular, we can see that the reporter will be active if no repression from TetR is at work. Either by inactivation of TetR or by the presence of X, the response will be observed. In this function, β and μ are the parameters associated with the binding strength of the TetR and X molecules.

3.2. Learning cell equations

For the learning cell (figure 1e), we consider a different set of equations. Here two genes are expressed constitutively thus involving linear equations

3.9

and

3.10

which provide the gene products that will interact with X and Y within this cell under the nonlinear equations

3.11

We have also the well-known equations for the toggle switch defined by the pair

3.12

and

3.13

which have two alternative states. Finally, the linear equation for the production of the molecule A, used in our first model as the communication signal among the two cells

3.14

3.3. Cell–cell communication wire

A final component needs also to be taken into account: the diffusion of the wiring molecule A responsible for the intercellular connection. The last equation above only considers the production within C₂, but it is shared with cell C₁ by diffusion and is also present in the extracellular medium (A_e). Thus we need to write three equations that account for the dynamics of A in each compartment (see figure 1). The complete equations read

3.15

3.16

3.17

corresponding to the two cells and the extracellular medium, respectively.

3.4. Associative learning dynamics

The previous equations start from an initial condition where the toggle switch is displaced towards cI. This defines the memory state of our system at time 0. Each input is introduced in the system in a pulse-like way. The independent responses of each cell under the presence of the two classes of inputs are shown in the electronic supplementary materials, figures S1 and S2. In figure 2, we show a typical example of the numerical experiment consistent with an AL process. The left diagram (figure 2a) provides a schematic representation of all the interactions, and figure 2b shows the time series obtained from the model. We first start by introducing X but not Y . This leads to a response as shown by the pulse in GFP, which disappears as X is also removed from the system. The positive response is easy to understand, because the only pathway being affected leading to GFP is indicated in figure 2c, where X blocks the inhibition of the reporter from TetR. Afterwards, we do the same experiment with Y, but in this case no active reporter is seen. The repressor of GFP acts with no inhibition (figure 2d), and the paths affected by Y do not propagate. The crucial change occurs when the two inputs are simultaneously correlated. Here the reporter is again activated (top of diagram e) as it happened in the first X-only pulse. However, the effect of the simultaneous input on the toggle switch is that the state of the cI–LacI pair switches to the opposite state, where LacI is now expressed and cI repressed. This is the internal state that has changed as a consequence of the correlated stimulus and will remain in this state once we remove both inputs.

Once the previous pulse has been applied and both inputs removed again, we can see the effect of these correlated input when the conditioned Y signal is introduced in the absence of the unconditioned one. Here the stored memory state in the toggle switch has a very different impact. In this case, this state is not changed but allows the propagation of the effects of Y to the producer cell, where cI is produced, repressing TetR and thus allowing GFP to be expressed. The consortium has created an association (thanks to the toggle) that essentially modifies the system's response to the conditioned state.

The model presented above has been analysed using a given parameter combination. What is the effect of other parameter values on the dynamical response of the consortium to other parameter combinations? Two parameters in particular are relevant to our exploration of the response of the system. These are the production rates γ_Lac and γ_λ. By exploring the (γ_Lac,γ_λ) parameter space (figure 3a) using a wide range of parameter values, i.e. 10⁻⁴≤γ_Lac,γ_λ≤10⁰. Four dynamical phases are found, which are associated with four different types of responses to the incoming stimuli.

Figure 3.

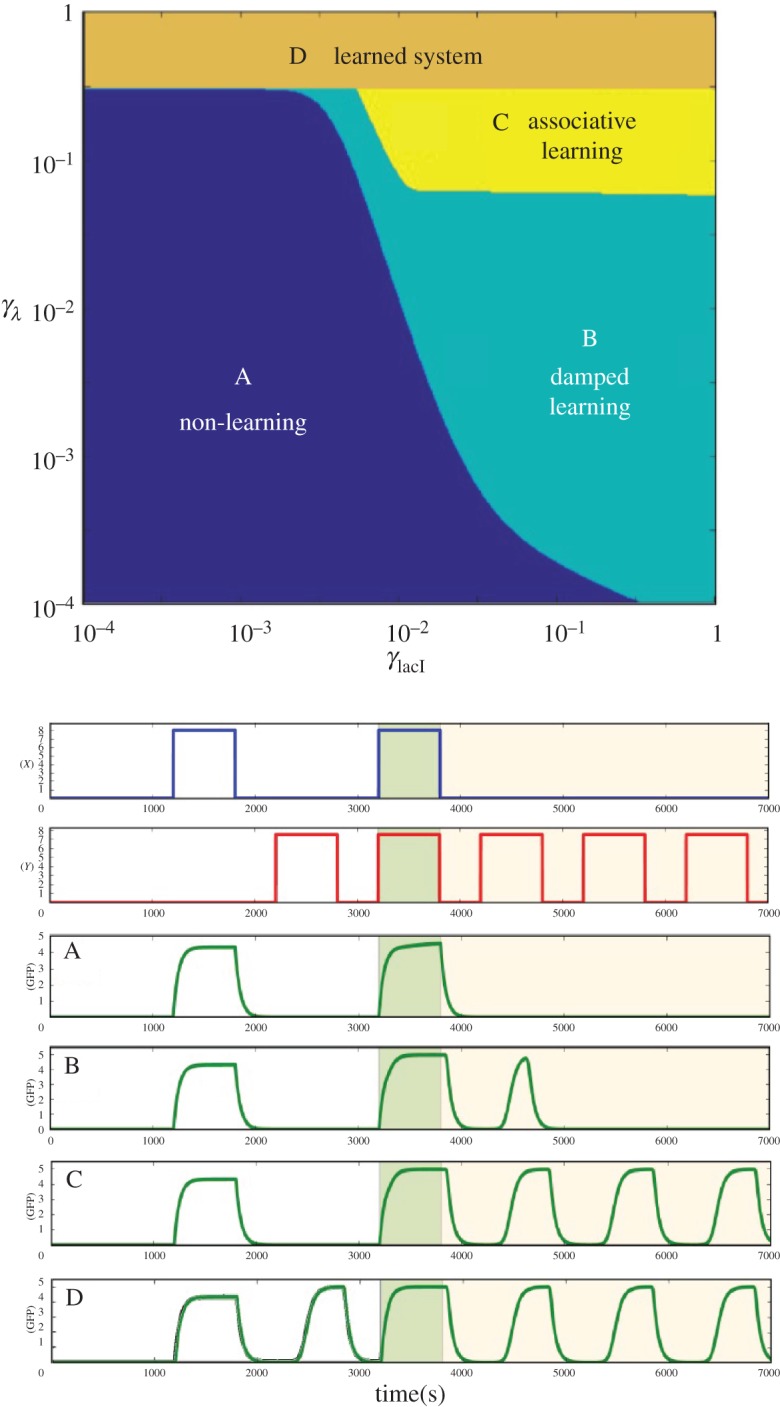
Phase space of the AL two-cell design and their output time series. Depending on the production rate of LacI (γ_LacI) and the production rate of LacI under cI regulation (γ_λ), there are four different response behaviours. (A) Non-learning situation; the system responds to the unconditioned stimulius (X) (blue region), the system is unable to respond to the conditioned signal (Y) even after the conditioning stimulus. (B) Damped learning; the learning cell has a temporal association (turquoise), the producer cells only respond to the conditioned signal for a limited time after the conditioning. (C) AL region (yellow), the learning cell change the state of the toggle switch after the simultaneous stimulation with X and Y signals, then the system has learned. (D) Learned system (orange); the system responds to the unconditioned (X) and conditioned (Y ) signals independently before the conditioning process pulses. The time series of the other variables can be seen in the electronic supplementary material, figures S3–S6. The parameters are the same as in previous figures; the phase space is performed with a 400 × 400 lattice. (Online version in colour.)

As in previous sections, the synthetic consortium receives a sequence of inputs where the unconditioned stimulus X is used first, followed by the conditional one Y and then both together. Afterwards, pulses of Y are introduced and the type of output response is used to classify the circuit's behaviour. The right panel in figure 3 shows examples of the output response for each phase as the sequence of stimuli is introduced. The four classes are captured by the time series associated with each one (A–D) in figure 3 (upper panel). No learning occurs within one phase where there is an unconditional response only. In a second phase (damped learning, B, see figure 3 (lower panel)), a small response is observed suggesting association, but it is rapidly lost after one weak response to the CS. The yellow domain indicates the AL parameter space whereas the domain of learned systems is associated with responses by both stimuli, regardless of how they are presented. The plot has been created on a log–log scale, and thus we can see that a broad range of parameters are consistent with this behaviour.

3.5. Suppressing associative learning

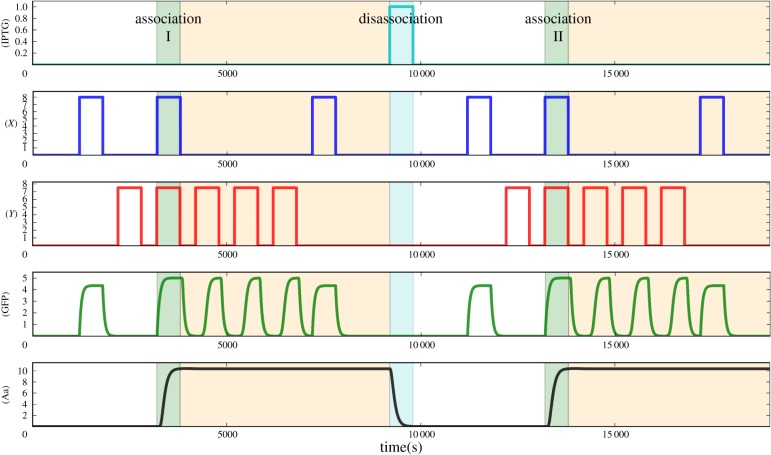
Once the association has been established in our circuit, as it occurs with conditioned learning in animals, the switch is locked in a given state that allows the association to be stable over time. However, if this is a circuit that has been designed to respond to unconditional stimuli once the inputs of both kinds are presented simultaneously, it can be interesting to return to the initial state where the consortium has not yet learned to associate the two stimuli.

The LacI protein has one well-known inhibitor, the IPTG molecule, which

3.18

where ξ = IPTG / β_IPTG. A pulse of IPTG produces inhibition of the LacI function. Then, the cI promoter is active again leading to an inversion of the toggle switch LacI–cI. After this process, the conditioning has been lost, as shown in figure 4.

Figure 4.

Time series of conditioning, memory erase and conditioning again. White regions are the non-conditioned regions; the cells are only able to express the GFP molecule under X signalling. The green regions are regions where the system is being conditioned, there is the association process, simultaneous stimulation with X and Y . Orange regions, the system is conditioned; it is able to respond to the unconditioned stimulus and to the conditioned. When there is a pulse of IPTG (cyan area), there is a loss of memory, a disassociation between signals. The parameters are the same as in the previous figure and β_IPTG = 0.04 and the IPTG pulse is 1 μM of amplitude. (Online version in colour.)

4. Discussion

One of the challenges of synthetic biology is to make possible the reprogramming of cellular behaviour by means of a predictable, engineered manipulation of the available molecular toolkit. The potential of such engineered molecular networks is great, and cover a wide range of areas, from standard biosensors to complex decision-making circuits able to gather a range of external stimuli from the environment and respond according to a predefined set of rules. An important goal is to provide these engineered systems with the appropriate adaptation potential, which necessarily requires the use of learning and memory. In this context, the potential for recapitulating the evolutionary innovations by building synthetic circuits provides a unique opportunity for the study of major transitions [13].

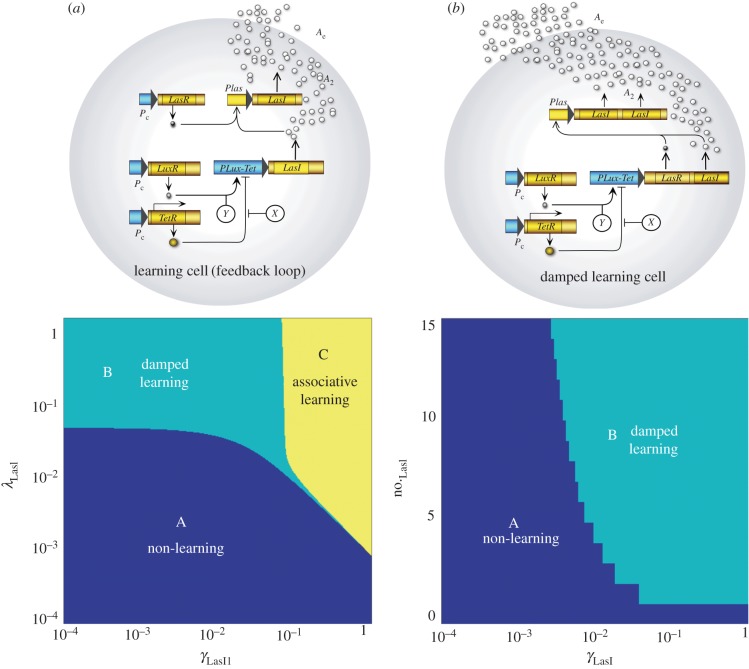
Several possible variations of our multicellular design can be described showing different potential learning behaviours. In figure 5, we suggest two such alternatives. The first (figure 5a) provides the consortium with the capacity to exhibit AL for a wide range of parameter values (as shown in the phase diagram) although it cannot be silenced. Specifically, it can be shown that, once the learning cell is activated by the simultaneous presence of X and Y, the communication molecule (A) will remain auto-activated and always produced in the learning phase (C). An additional example (figure 5b) is provided by another learning circuit. The difference is that in this case, the cell eventually loses its memory after a short time (and thus exhibits damped learning, phase B). These two circuits show that the learning process can be engineered using alternative systems depending on the requirements of the problem.

Figure 5.

Alternative circuits for synthetic memory. (a) AL circuit based on positive feedback loop (figure 1a). (b) Damped learning synthetic circuit. Below each diagram, there is the phase space relating the parameters to the behaviour exhibited. (A) There is response to the unconditioned signal. (B) Damped learning, there is a characteristic time where the two cell system responds to X and Y, afterwards the system does not respond to the unconditioned signal. (C) AL, once the cells are stimulated simultaneously by both molecules (X and Y ), the system responds to either the CS or US. The mathematical models are provided in the electronic supplementary material. The parameters are set to the same values as in figure 2. The phase space are lattices of 400 units per parameter, with the exception of the number of copies of LasI as this parameter is discrete. (Online version in colour.)

The proposed synthetic systems presented here show that the use of cell consortia can help when designing complex decision-making biological circuits capable of coping with external signals and their changes. The human microbiome provides an ideal testbed for these kinds of synthetic designs. If the metaphor of this as a ‘second brain’ becomes valid, then what we are suggesting is to introduce pieces of computational complexity to play an active role within the network of microbial interactions. Our example also combines the internal machinery that responds to external signals (which could be drugs) with a flexible design capable of exploiting the history of previous events. This basic scheme can be generalized to more complex designs. Future work should test the experimental feasibility of our approach as well its scalability. We should also consider the conditions under which the whole consortium will operate properly: we implicitly assume that the external context will act as a proper selection filter, thus maintaining the consortium as a cohesive entity.

The circuits proposed above assume that the two-cell consortium is obtained by engineering the same class of model organism, but this is not required for our purposes. Mixed consortia involving both microbial and human cells could be constructed, and other possibilities are also available, including the design of symbiotic consortia between soil microorganisms and plant cells (or nitrogen-fixing microorganisms living within plant nodules) as potential strategies of ecosystem repair [19,26]. Regarding diseases associated with a malfunctioning microbiome, our results suggest that both permanent and transient modifications of some engineered strains could help to dynamically control some key processes requiring memory and learning. This is an interesting possibility given the feedback existing between both the immune system and the brain as connected with the microbiome [45,46]. Because both immune and brain networks are capable of displaying learning and memory, microbial consortia such as the ones presented here could act as extensions of neural-like decision circuits.

Finally, another interesting possibility concerns the design of synthetic learning circuits (along with other computational structures) that could be incorporated within organoids [47]. This picture was proposed by Jamie Davies, who introduced the concept of synthetic morphology as a hybrid discipline aimed towards the programming of tissues and artificial multicellular assemblies [48]. A closely related view, named morphogenetic engineering, a synthetic biology path, was suggested as a form of shape engineering exploiting both programmed circuits and self-organization [49]. Extra computational complexity can be achieved by introducing synthetic circuits as part of complex multicellular structures. Such enhanced cognitive complexity might be a desirable trait of future designed organoids and allow a move away from natural design principles [50].

Competing interests

We declare we have no competing interests.

Funding

This work has been supported by an ERC Advanced grant no. 294294 from the EU 7th Framework Programme (SYNCOM); the Botin Foundation by Banco Santander through its Santander Universities Global Division; the Secretaria d'Universitats i Recerca del Departament d'Economia i Coneixement de la Generalitat de Catalunya, a grant of MINECO, FIS2015-67616-P and by the Santa Fe Institute.