An algorithm for direct causal learning of influences on patient outcomes

Abstract

Objective

This study aims at developing and introducing a new algorithm, called direct causal learner (DCL), for learning the direct causal influences of a single target. We applied it to both simulated and real clinical and genome wide association study (GWAS) datasets and compared its performance to classic causal learning algorithms.

Method

The DCL algorithm learns the causes of a single target from passive data using Bayesian-scoring, instead of using independence checks, and a novel deletion algorithm. We generate 14400 simulated datasets and measure the number of datasets for which DCL correctly and partially predicts the direct causes. We then compare its performance with the constraint-based path consistency (PC) and conservative PC (CPC) algorithms, the Bayesian-score based fast greedy search (FGS) algorithm, and the partial ancestral graphs algorithm fast causal inference (FCI). In addition, we extend our comparison of all five algorithms to both a real GWAS dataset and real breast cancer datasets over various time-points in order to observe how effective they are at predicting the causal influences of Alzheimer’s disease and breast cancer survival.

Results

DCL consistently outperforms FGS, PC, CPC, and FCI in discovering the parents of the target for the datasets simulated using a simple network. Overall, DCL predicts significantly more datasets correctly (McNemar’s test significance: p ≪ 0.0001) than any of the other algorithms for these network types. For example, when assessing overall performance (simple and complex network results combined), DCL correctly predicts approximately 1400 more datasets than the top FGS method, 1600 more datasets than the top CPC method, 4500 more datasets than the top PC method, and 5600 more datasets than the top FCI method. Although FGS did correctly predict more datasets than DCL for the complex networks, and DCL correctly predicted only a few more datasets than CPC for these networks, there is no significant difference in performance between these three algorithms for this network type. However, when we use a more continuous measure of accuracy, we find that all the DCL methods are able to better partially predict more direct causes than FGS and CPC for the complex networks. In addition, DCL consistently had faster runtimes than the other algorithms. In the application to the real datasets, DCL identified rs6784615, located on the NISCH gene, and rs10824310, located on the PRKG1 gene, as direct causes of late onset Alzheimer’s disease (LOAD) development. In addition, DCL identified ER category as a direct predictor of breast cancer mortality within 5 years, and HER2 status as a direct predictor of 10-year breast cancer mortality. These predictors have been identified in previous studies to have a direct causal relationship with their respective phenotypes, supporting the predictive power of DCL. When the other algorithms discovered predictors from the real datasets, these predictors were either also found by DCL or could not be supported by previous studies.

Conclusion

Our results show that DCL outperforms FGS, PC, CPC, and FCI in almost every case, demonstrating its potential to advance causal learning. Furthermore, our DCL algorithm effectively identifies direct causes in the LOAD and Metabric GWAS datasets, which indicates its potential for clinical applications.

1. Introduction

In medical applications, we often identify variables that are associated with diseases or outcomes. For example, in genome wide association studies (GWAS) we look for single nucleotide polymorphisms (SNPs) that are associated with a particular disease. A SNP results when a nucleotide that is typically present at a specific location on the genomic sequence is replaced by another nucleotide [1]. These high dimensional GWAS datasets can concern over a million SNPs. By looking at single-locus associations, researchers have identified over 150 risk loci associated with 60 common diseases and traits [2-4]. However, most of these studies do not identify actual causative loci. For example, a locus could be associated with the disease due to linkage disequilibrium. Jiang et al. [5] analyzed a late onset Alzheimer’s disease (LOAD) GWAS dataset, and discovered that both APOE and APOC1 are strongly associated with LOAD. However, these genes are in linkage disequilibrium. Although it is well-known that APOE is causative of LOAD [6], without further analysis we cannot say whether this dataset supports that APOC1 is also causative of LOAD. As another example, Curtis et al. [7] developed and analyzed the Metabric breast cancer dataset, which contains data on breast cancer patients, genomic and clinical features of those patients, and survival outcomes. They found, for example, that tumor size, the number of positive Lymph nodes, and tumor grade are all associated with breast cancer-related death. However, perhaps tumor size is associated with survival outcome only due to its association with grade. If we can further analyze such datasets to identify the direct causal influences, it would be helpful both at the level of understanding the mechanisms of disease initiation and propagation, and at the level of patient treatment (i.e. develop and provide treatments that address the causes).

Bayesian networks (BNs) are an effective architecture for modeling causal relationships from passive observational data. Passive observational data is collected without controlling for factors or perturbing the system in question. In contrast, experimental data involves a researcher’s intervention to either control for factors, such as a treatment given or subject groups. Observational data and experimental data are both collected objectively but the former does so in an uncontrolled setting (not subject to controlled experimentation) making it traditionally more difficult to determine causality [8].

We developed a new algorithm, direct causal learner (DCL), for learning causal influences, which concentrates on learning the direct causes of a single target using Bayesian-scoring rather than independence checks. We applied the algorithm to 14,400 simulated datasets, a GWAS LOAD dataset that concerns disease status (present or absent) [6], and to the Metabric breast cancer datasets that concern breast cancer survival outcome over various time-points [7]. We compared the performance of our DCL algorithm to the constraint-based path consistency (PC) and conservative PC (CPC) algorithms, the score-based fast greedy search (FGS) algorithm, and the partial ancestral graphs (PAGs) algorithm fast causal inference (FCI), which are all implemented in the Tetrad package [9].

2. Methods

2.1. Overview of BNs

Since our algorithm concerns BNs, we first review them. BNs [10-12] are increasingly being used for uncertainty reasoning and machine learning in many domains including biomedical informatics [13-18]. A BN consists of a directed acyclic graph (DAG) G = (V, E), whose nodeset V contains random variables, whose edges E represent relationships among the variables, and whose conditional probability distribution of each node X ∈ V is given for each combination of values of its parents. Each node V in a BN is conditionally independent of all its non-descendants given its parents in the BN. Often the DAG in a BN is a causal DAG [11]. Figure 1 shows a BN modeling relationships among variables related to respiratory diseases.

Figure 1.

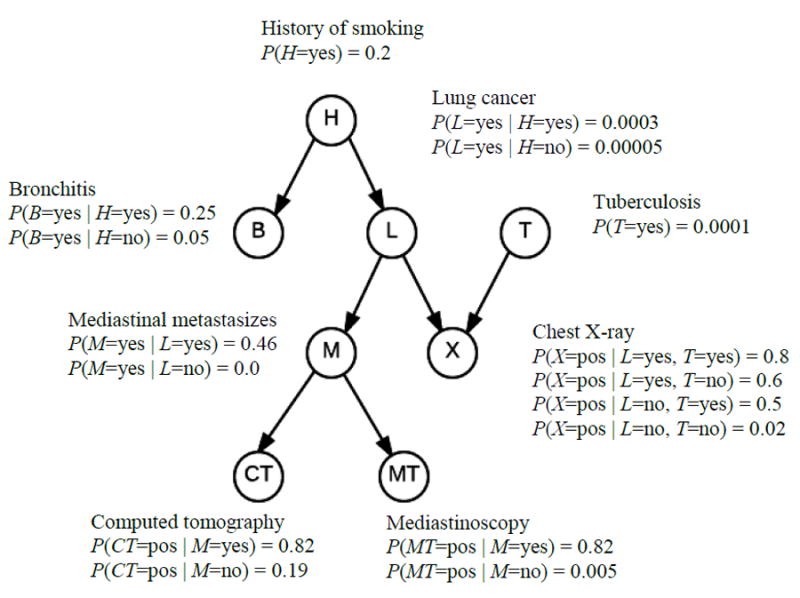
A BN representing relationships among variables related to respiratory diseases.

Using a BN, we can determine probabilities of interest with a BN inference algorithm [11]. For example, using the BN in Figure 1, if a patient has a smoking history (H = yes), a positive chest X-ray (X = pos), and a positive CAT scan (CT = pos), we can determine the probability of the patient having lung cancer (L = yes). That is, we can compute P(L = yes∣ H = Yes, X = pos, CT = pos). Inference in BNs is NP-hard. So, approximation algorithms are often employed [11]. Additionally, learning a BN from data concerns learning both the parameters and the structure (called a DAG model).

2.2. Constraint-based pattern learning

In constraint-based structural learning, a DAG is learned from the conditional independencies suggested by the data [11]. The best known example of a structural learning algorithm which applies a standard statistical method to find variable dependencies is the inductive causation (IC) algorithm, of which the PC algorithm is a refined version [19]. All constraint-based learning algorithms share a similar three-step process based on the IC algorithm. The first step is to learn the Markov blanket of each node in order to reduce the number of possible DAGs. Once all the Markov blankets have been learned, they are checked for symmetry—if node X is an element of the Markov blanket for node Y, then node Y is also an element of the Markov blanket for node X. Asymmetric nodes are then removed from each corresponding node’s Markov blanket. The second step learns the neighbors of each node in the DAG, identifying the arcs connecting pairs of nodes but not their directions. With the exception of the PC algorithm, all other constraint-based algorithms enforce symmetry of the neighbors found. The last step then learns the arcs’ directions [20].

The PC algorithm, one of the classic constraint-based algorithms in causal discovery, assumes that the data’s underlying causal structure is an acyclic graph and contains no latent or unmeasurable variables [21]. PC allows for the specification of a maximum number of parent nodes to reduce the structural learning task’s complexity. Furthermore, PC employs a chi square test to check for independence. The chosen test relies on a pre-specified significance level to learn edges and construct the underlying BN. The PC algorithm tends to output false positive bidirectional edges between pairs of nodes, which indicate uncertainty in their causal relationship, on small samples. Additionally, it is unstable when an error occurs in the early stages of search because it can have a sequential effect on the next iteration of search and can, in turn, result in an extremely different graph than the actual underlying graph representing the data [22].

Conservative PC (CPC), which is a modified version of the PC algorithm, runs under the same assumptions but determines causal relationships in a much more cautious manner than PC [23]. CPC, unlike PC, avoids the tendency to produce many false positives because of its more faithful causal relationship conditions. However, CPC performs the same steps as PC to learn the data’s underlying structure if the data set is large enough. The runtime of CPC is very similar to that of PC.

2.3. Constraint-based learning for PAGs

A Pattern, also known as a Partial DAG or essential graph, is an equivalence class of a DAG, meaning, by definition, every element in a Pattern represents the same set of conditional independence assertions [24]. On the other hand, a PAG represents an equivalence class of Maximal Ancestral Graphs, which is a mixed graph (directed and undirected edges) that contains no directed cycles or almost directed cycles (ancestral) and no inducing paths between any two non-adjacent variables (maximal) [25]. Unlike traditional graphical models, ancestral graphical models are able to represent data that may involve latent confounders and/or selection bias [25].

The fast causal inference (FCI) algorithm, a constraint-based learning algorithm for PAGs, assumes that the underlying causal network is represented by a DAG, similar to the PC algorithm’s assumption, but allows discovery of a model with latent common causes [8]. The FCI algorithm begins with a complete undirected graph of the variables in the data and then deletes edges between non-adjacent vertices. Then the algorithm determines the directionality of the edges and finally deletes edges to remove any existing d-separations within the graph. FCI produces a partially oriented inducing path graph over the data’s variables but, since the algorithm is not complete, we do not know if it produces a maximally informative partially oriented inducing path graph in every case [8]. The FCI algorithm is feasible in datasets with a large number of features if the true graph is sparse and there are not many bidirectional edges.

2.4. Score-based pattern learning

Score-based learning, with respect to constraint-based learning, has often been found to be more effective in learning the network structure from data [11]. In score-based structural learning, we assign a score to a DAG based on how well the DAG fits the data. Cooper and Herskovits [26] introduced the Bayesian score, which is the probability of the data given the model G. A popular variation of the Bayesian score is the Bayesian Dirichlet equivalent uniform (BDeu) score [27], which allows the user to specify priors for the conditional probability distributions using a single hyperparameter α, called the prior equivalent sample size. That score is as follows:

$${\mathit{score}}_{\alpha }(G:\mathit{Data})=P(\mathit{Data}\mid G)=\prod _{i=1}^n\prod _{j=1}^{q_i}\frac{\mathrm{\Gamma }(\alpha /q_i)}{\mathrm{\Gamma }(\alpha /q_i+{\sum }_{k=1}^{r_i}{s}_{\mathit{ijk}})}\prod _{k=1}^{r_i}\frac{\mathrm{\Gamma }(\alpha /r_i{q}_i+s_{\mathit{ijk}})}{\mathrm{\Gamma }(\alpha /r_i{q}_i)}.$$ (1)

where r_i is the number of states of node X_i, q_i is the number of different instantiations of the parents of X_i, and S_ijk is the number of times in the data that X_i took its k th value when the parents of X_i had their j th instantiation. The BN learning problem is NP-hard. So, heuristic search algorithms are often used [11].

The fast greedy search (FGS) algorithm is a modified version of the classic greedy equivalence search (GES) algorithm, which is a score-based structural learning methods. GES defines a scoring function and greedily maximizes the score by first adding and then removing one edge at a time to evaluate how well a BN model fits the data [28, 29]. The GES algorithm, as implemented by David Chickering, performs well in real-world complex problems, such as analyzing television viewer behavior and internet usage [28]. However, its scoring process is extremely redundant and adding n edges to the graph is cubic with respect to the number of variables, even in which the degree of the model is bounded. If the degree of the model is not well bounded, the operation of adding a single edge will be an exponential time complexity and is impractical when there are a large number of variables in the data.

The FGS algorithm improves upon GES’s scalability issues; adding and scoring of the first edge, which is a very expensive step especially for large models, is quadratic in FGS but adding additional edges is linear in the number of variables, enabling the FGS algorithm to run much faster than the GES algorithm. In addition, the scoring of the algorithm has been sped up through parallelization of particular steps that do not rely on the order in which operations are performed [30]. These improvements lead to faster runtimes and more accurate learning in highly complex datasets. We used Tetrad’s command line interface to run the FGS algorithm, which analyzes discrete variables using a discretely analyzable score, such as the BDeu Score.

2.5. A new algorithm for identifying direct causal influences

Our new algorithm, which is designed to discover direct causes of a single pre-specified target and use Bayesian-scoring, follows:

Direct_Causal_Learning(DCL)
procedure remove_ parents(var PA);
i = 0;
repeat
for each Y∈PA
S = set of all sets A∈ PA{Y} such that | A|= i ;	// S contains the empty set Ø when i = 0;
A = first set in S;
while A is not null and Y ∈ PA	// A is null if there are no sets in S.
B = A ∪ {Y};
if deleting some node from B increase score(B;Z)
X = node whose deletion increases score the most;
if Y = X
remove Y from PA;
endif
endif
A = next set in S;	// A is null if there are no sets left in S.
endwhile
endfor
i=i + 1;
until | PA |≤ i or i > R;

Procedure remove_parents removes indirect causes from PA. When i = 2, it checks each two cause model of the form X→Z←Y. If deleting any parent node from this model increases the score, we delete the parent such that the deletion increases the score the most. Variable Y is deleted if and only if there is no edge from Y to Z in the BN model containing the three variables (based on the data). This is the case if and only if X shields Y from Z. By “shield” we mean Y and Z are conditionally independent given X. Next we check each model with three parents (i=3) X, Y, and W of Z. Again if deleting any parent node from this model increases the score, we delete the parent such that the deletion increases the score the most. Variable Y is deleted if and only if there is no edge from Y to Z in the BN model containing the four variables (based on the data). This is the case if and only if X and W together shield Y from Z. We continue in this manner until we have exhausted all possible subsets of PA or until we have checked subsets of size R+1, where R is the assumed maximum number of variables shielding and variable from Z.

3. Experiments

3.1. Simulated data

We developed two simple and two complex BNs, all of which have a single target T, and generated 6 different parameterizations for each network. Figure 2 shows one of the simple and one of the complex structures. For each simple structure, we generated six non-random parameterizations based on a weak-strong schedule. This schedule designated six separate models that vary the strength of the direct and indirect nodes’ relationships to the target. In these models, the direct nodes had either a strong or weak relationship to the target and the indirect nodes had either a strong, weak, or mixed, meaning a combination of strong and weak, relationship to the target. A weak relationship relative to variable X is one in which the conditional probabilities specified for X are close in value, while a strong relationship is one in which the conditional probabilities specified for X vary considerably. We named all direct nodes as Z, Y, X … and all indirect nodes as P1, P2, P3… As for the complex networks, we used TETRAD to randomly generate 6 sets of parameters for each of the complex network structures. We used Hugin Expert’s data simulation function along with its Java application programming interface (API) to implement a mass data generation program, which uses each network parameterization as an input, to generate a pre-specified number of datasets corresponding to the input network parameterization and pre-specified case size.

Figure 2.

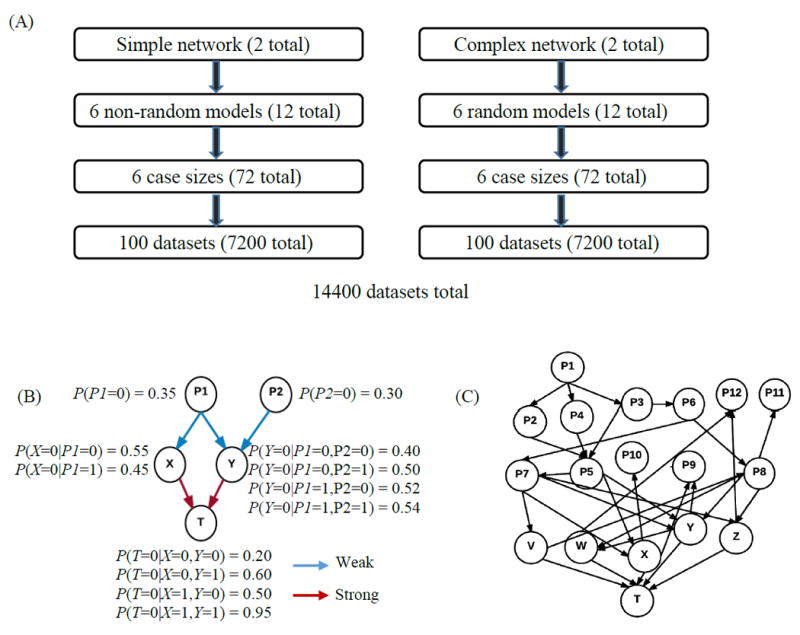
Pictorial representation of the BN parameterizations and models. (A) Detailed outline of the 14,400 datasets. There are two different simple and complex networks, with each simple network having six different parameterizations based on the strong-weak schedule (see supplement S1 for more details) and each complex network having six random parameterizations. Furthermore, each model has 6 different case sizes, and each case size has 100 datasets. The simple and complex networks each have a total of 7200 datasets. (B) A sample diagram of a model of one of the simple networks. X and Y are the parents of T and have a strong causal relationship. P1 and P2 are indirect nodes to T and have a weak relationship to their children, X and Y. (C) A randomly parameterized model of one of the complex networks. V, W, X, Y, and Z are the parents of T, and P1-P12 are indirect nodes to T.

For each parameterization we generated 100 datasets with 300, 600, 1200, 2400, 4800, and 9600 cases. This makes a total of 6 x 6 × 100 = 3600 datasets for each BN and a total of 14,400 datasets for all four networks (Supplementary Information S1 provides more details on how the datasets were generated).

We used the BDeu [27] score in the DCL algorithm, which has a score parameter α called the prior equivalent sample size. We ran DCL with BDeu α = 1, 9, 15, 54, and 108. Similarly, the PC, CPC, and FCI algorithms have a significance parameter β. We ran the each of these algorithms with significance β = 0.01, 0.05, 0.1, and 0.2 (Note: PC, CPC, and FCI call the parameter α, but we do not want to confuse it with BDeu α). We ran FGS with sample prior (smp) = {1, 2} and structure prior (stp) = {1, 2}, leading to four different learning methods.

The accuracy was analyzed in two ways. The first way, called Exact Correct (EC), provides the number of datasets for which the method discovered the direct causes exactly. That is, all true direct causes were discovered, and no other causes were discovered. EC was calculated separately for every 100 datasets of a particular case size and parameterization. The second method uses the Jaccard Index (JI), which is as follows:

$$\mathit{Jaccard}(A,B)=\frac{\#(A\cap B)}{\#(A\cup B)}$$

This index is 1 if the two sets are identical and is 0 if they have no items in common. For each data set, we computed the JI of the set of true causal parents with the set of learned causes. The JI penalizes a scoring method for including additional, incorrect predictors but rewards a scoring method for predicting some, if not all, of the correct predictors.

We also measured the average runtime of each method by averaging all 1200 (all six parameterizations for two networks) runtimes for each case size and then calculated a total runtime by finding the sum of these six average runtimes.

3.2. Real data

3.2.1. LOAD dataset

We ran DCL, FGS, PC, CPC, and FCI on a LOAD dataset (312,316 SNPs and 1,411 samples) developed by Reiman et al. [6] in order to discover the causal influences of LOAD and compare the predictors found among the algorithms. The LOAD dataset was pre-processed and had APOE ε4 carrier status added. Before running the algorithms, we checked the association of each individual SNP with the disease using a chi-square test, and kept those SNPs with p-values < 0.0001 (no Bonferroni correction used). We then ran all five algorithms with these selected SNPs with LOAD status specified as the target.

3.2.2. Metabric dataset

We developed six clinical datasets that predict 5-year, 10-year, and 15-year breast cancer survival and overall breast cancer survival [7]. For each time-point, there are two datasets: breast death and survival death. The former, breast death, contains only cases for breast cancer related morbidities along with those who survived, whereas survival death contains cases for all patients who died along with those who survived. The sample sizes for each of the six datasets are as follows: 5-year breast death (1645), 5-year survival death (1776), 10-year breast death (1146), 10-year survival death (1414), 15-year breast death (677), 15-year survival death (1026). The 13 predictors present in each of these six datasets are age at diagnosis, size, Lymph nodes position, overall grade, histological type, ER category, PR category, HER2 status, inferred menopausal status, overall stage, axillary nodes removed, P53 mutation status, and percent nodes positive. Since the Metabric dataset contained a moderate amount of missing values, we used multivariate imputation by chained equations (MICE) to impute these missing values (see Supplement for more information) [31]. We disregarded overall stage and P53 mutation status in all the datasets and overall grade in only the15-year breast survival death dataset since these predictors had too many missing values to be imputed (> 5%). A summary of the percentages of missing values and brief descriptions for the 13 predictors across all 6 datasets can be found in the Supplementary Material (Tables S3 and S4). For each of the 6 datasets, we ran DCL, FGS, PC, CPC, and FCI and a chi-square test. The MICE imputation and chi-square feature selection were performed using R (version 3.2.3) [32].

3.3. Selecting algorithm parameters

In our summary tables, we included DCL scoring methods using α values of 1, 9, 15, 54, and 108 and PC, CPC, and FCI methods using β values of 0.01, 0.05, 0.1, and 0.2. Since the optimal parameters for each scoring method vary depending on the dataset, we first tested each scoring method using several different parameters on the 2400 case size datasets only, since nearly all of our real datasets had sample sizes between 1200 and 2400. We decided to choose the upper-bound so as to better isolate changes in performance with respect to changes in the parameters’ values, since it is commonly known that performance will increase with larger sample data. We then chose the aforementioned values based on their performance and their coverage of values. Please refer to the Supplementary Material S1 for details.

The FGS algorithm has two parameters: smp, which is required for the Dirichlet prior distribution, and stp, which takes into account the number of parents of a variable in a model [33] We tested values between 1 and 4 for smp and stp on our simulated datasets. We observed that FGS performed optimally at an smp of 1 or 2 and an stp of 1 or 2.

4. Results

4.1. Simulated data results

4.1.1. EC

Table 1 shows the EC values for each method when analyzing the datasets concerning the simple networks. All five DCL learning methods outperformed PC, CPC, FGS, and FCI, with the best and worst DCL methods correctly predicting 4275 (DCL_α=54, 59.38%) and 3942 (DCL_α=9, 54.75%) datasets. After DCL, FGS was the next leading learning method, which correctly predicted 2724 (FGS_{smp2 stp2}, 37.83%) datasets, followed by CPC, PC, and FCI, with each algorithm’s top learning method predicting 2580 (CPC_β=0.1, 35.83%), 1166 (PC_β=0.01, 16.19%), and 54 (FCI_β=0.2, 0.75%) datasets correctly, respectively. When taking into account the strength of the direct predictors’ relationships to the target, all the DCL methods correctly predicted more datasets than any of the other learning methods. For example, in the case of the networks with strong direct predictor relationships to the target, the top non-DCL method correctly predicted 2560 (CPC_β=0.1, 71.11%) datasets, whereas even the lowest performing DCL method, for these same strong-networks, performed better by predicting 3032 datasets (DCL_α=108, 84.22%) correctly. When we consider the EC values for the weak-networks, the relative results are similar; the best and worst performing DCL method in the weak networks correctly predicted 974 (DCL_α=108, 27.06%) and 250 (DCL_α=1, 6.94%) datasets correctly, respectively, whereas the top non-DCL method was only able to predict 223 (FGS_{smp2 stp2}, 6.19%) datasets correctly.

Table 1.

Number of datasets correctly predicted for the simple network models, separated by direct predictor strength and case size (bolded values indicated highest score in each case size)

Learning method		300 cases	600 cases	1200 cases	2400 cases	4800 cases	9600 cases	Total
DCLα=54	Strong	483	567	595	599	600	600	3444
	Weak	35	34	87	132	211	332	831
	Total	518	601	682	731	811	932	4275
DCLα=15	Strong	503	584	600	600	600	600	3487
	Weak	2	15	38	78	153	281	567
	Total	505	599	638	678	753	881	4054
DCLα=108	Strong	328	422	514	572	597	599	3032
	Weak	44	53	99	166	247	365	974
	Total	372	475	613	738	844	964	4006
DCLα=1	Strong	342	461	595	600	600	600	3198
	Weak	0	0	1	7	50	192	250
	Total	342	461	596	607	650	792	3448
DCLα=9	Strong	482	577	600	600	600	600	3459
	Weak	3	9	24	57	131	259	483
	Total	485	586	624	657	731	859	3942
FGSsmp2 stp2	Strong	235	289	430	533	511	503	2501
	Weak	0	0	0	9	54	160	223
	Total	235	289	430	542	565	663	2724
FGSsmp2 stp1	Strong	234	282	426	529	511	503	2485
	Weak	0	0	0	3	35	139	177
	Total	234	282	426	532	546	642	2662
FGSsmp1 stp2	Strong	232	263	379	535	518	501	2428
	Weak	0	0	0	3	33	142	178
	Total	232	263	379	538	551	643	2606
CPCβ=0.1	Strong	159	306	468	530	549	548	2560
	Weak	0	0	1	1	6	12	20
	Total	159	306	469	531	555	560	2580
FGSsmp1 stp1	Strong	230	258	377	530	518	501	2414
	Weak	0	0	0	1	21	115	137
	Total	230	258	377	531	539	616	2551
CPCβ=0.05	Strong	113	253	433	538	576	584	2497
	Weak	0	0	0	0	2	4	6
	Total	113	253	433	538	578	588	2503
CPCβ=0.2	Strong	193	336	428	469	475	473	2374
	Weak	0	0	2	5	15	14	36
	Total	193	336	430	474	490	487	2410
CPCβ=0.01	Strong	54	169	344	516	588	597	2268
	Weak	0	0	0	0	0	0	0
	Total	54	169	344	516	588	597	2268
PCβ=0.01	Strong	209	273	225	160	132	166	1165
	Weak	0	0	0	1	0	0	1
	Total	209	273	225	161	132	166	1166
PCβ=0.1	Strong	137	153	150	144	157	199	940
	Weak	4	2	4	2	1	4	17
	Total	141	155	154	146	158	203	957
PCβ=0.05	Strong	158	157	149	121	160	198	943
	Weak	1	1	3	2	0	2	9
	Total	159	158	152	123	160	200	952
PCβ=0.2	Strong	132	84	114	140	140	177	787
	Weak	8	2	2	2	6	9	29
	Total	140	86	116	142	146	186	816
FCIβ=0.2	Strong	3	3	5	13	16	13	53
	Weak	0	0	0	0	0	1	1
	Total	3	3	5	13	16	14	54
FCIβ=0.1	Strong	3	1	1	3	5	6	19
	Weak	0	0	0	0	0	0	0
	Total	3	1	1	3	5	6	19
FCIβ=0.05	Strong	2	1	0	2	4	4	13
	Weak	0	0	0	0	0	0	0
	Total	2	1	0	2	4	4	13
FCIβ=0.01	Strong	0	1	0	0	1	0	2
	Weak	0	0	0	0	0	0	0
	Total	0	1	0	0	1	0	2

When we look at Table 2, which shows the EC value for each learning method when analyzing the datasets concerning the complex networks, we see that FGS is actually the top method by predicting 1552 (FGS_{smp2 stp2}, 21.56%) datasets correctly and that the top DCL method follows closely by correctly predicting 1502 (DCL_α=15, 20.86%) datasets. In fact, three FGS learning methods are in the top five performing algorithms for the complex networks. However, the top DCL method did outperform the best CPC method, which predicted 1434 (CPC_β=0.2, 19.92%) datasets correctly, and greatly outperformed the best PC and FCI methods, which correctly predicted only 13 (PC_β=0.2, 0.18%) and 10 (FCI_β=0.2, 0.14%) datasets, respectively.

Table 2.

Number of datasets correctly predicted for the complex network models by case size (bolded values indicated highest score in each case size)

Learning method	300 cases	600 cases	1200 cases	2400 cases	4800 cases	9600 cases	Total
FGSsmp2 stp2	0	74	192	338	435	513	1552
DCLα=15	58	120	187	256	369	512	1502
FGSsmp1 stp2	0	52	169	319	425	491	1456
CPCβ=0.2	7	47	111	284	440	545	1434
FGSsmp2 stp1	0	14	160	318	424	497	1413
CPCβ=0.1	0	20	87	242	443	594	1386
DCLα=54	41	84	133	214	379	531	1382
DCLα=9	35	98	172	236	335	490	1366
FGSsmp1 stp1	0	11	140	298	417	479	1345
CPCβ=0.05	0	12	58	180	404	579	1233
DCLα=1	5	34	112	178	243	373	945
DCLα=108	24	56	90	136	239	375	920
CPCβ=0.01	0	0	22	92	268	512	894
PCβ=0.2	0	0	0	0	0	13	13
PCβ=0.1	0	0	0	0	0	12	12
FCIβ=0.2	0	0	0	0	0	10	10
FCIβ=0.1	0	0	0	0	0	9	9
FCIβ=0.01	0	0	0	0	0	0	0
FCIβ=0.05	0	0	0	0	0	0	0
PCβ=0.01	0	0	0	0	0	0	0
PCβ=0.05	0	0	0	0	0	0	0

When we pooled the results from the simple and complex results, which are shown in Table 3, we found that all five DCL learning methods outperformed the other methods, with the best and worst DCL methods predicting 5657 (DCL_α=54, 39.28%) and 4393 (DCL_α=1, 30.51%) datasets correctly. On the other hand, the top FGS, CPC, PC, and FCI methods correctly predicted 4276 (FGS_{smp2 stp2}, 29.69%), 3966 (CPC_β=0.1, 27.54%), 1166 (PC_β=0.01, 8.10%), and 64 (FCI_β=0.2, 0.44%) datasets correctly, respectively.

Table 3.

Number of datasets correctly predicted for both the simple and complex networks combined by case size (bolded values indicated highest score in each case size)

Learning method	300 cases	600 cases	1200 cases	2400 cases	4800 cases	9600 cases	Total
DCLα=54	559	685	815	945	1190	1463	5657
DCLα=15	563	719	825	934	1122	1393	5556
DCLα=9	520	684	796	893	1066	1349	5308
DCLα=108	396	531	703	874	1083	1339	4926
DCLα=1	347	495	708	785	893	1165	4393
FGSsmp2 stp2	235	363	622	880	1000	1176	4276
FGSsmp2 stp1	234	296	586	850	970	1139	4075
FGSsmp1 stp2	232	315	548	857	976	1134	4062
CPCβ=0.1	159	326	556	773	998	1154	3966
FGSsmp1 stp1	230	269	517	829	956	1095	3896
CPCβ=0.2	200	383	541	758	930	1032	3844
CPCβ=0.05	113	265	491	718	982	1167	3736
CPCβ=0.01	54	169	366	608	856	1109	3162
PCβ=0.01	209	273	225	161	132	166	1166
PCβ=0.1	141	155	154	146	158	215	969
PCβ=0.05	159	158	152	123	160	200	952
PCβ=0.2	140	86	116	142	146	199	829
FCIβ=0.2	3	3	5	13	16	24	64
FCIβ=0.1	3	1	1	3	5	15	28
FCIβ=0.05	2	1	0	2	4	4	13
FCIβ=0.01	0	1	0	0	1	0	2

4.1.2. JI

Since EC is a “black and white” method for evaluating accuracy, we decided to use the JI as a measure of how close each learning method was to discovering the direct causes of a target. For the simple networks (Table 4), we found that all five DCL methods were in the top five, with the best and worst DCL methods having total JIs of 5581.87 (DCL_α=54, 77.53%) and 5011.75 (DCL_α=1, 69.61%), respectively. Furthermore, the total JIs for all five DCL methods were much higher than the best FGS, CPC, PC, and FCI methods, each of which had total JIs of only 3178.17 (FGS_{smp2 stp2}, 44.14%), 3172.25 (CPC_β=0.2, 44.06%), 2284.13 (PC_β=0.1, 31.72%), and 487.38 (FCI_β=0.2, 6.77%), respectively.

Table 4.

Total JIs for the simple network models, separated by direct predictor strength and case size (bolded values indicated highest score in each case size)

Learning method		300 cases	600 cases	1200 cases	2400 cases	4800 cases	9600 cases	Total
DCLα=54	Strong	560.67	590.58	598.33	599.67	600.00	600.00	3549.25
	Weak	208.70	236.83	300.92	358.00	426.92	501.25	2032.62
	Total	769.37	827.42	899.25	957.67	1026.92	1101.25	5581.87
DCLα=108	Strong	515.40	549.93	575.92	591.58	599.17	599.75	3431.75
	Weak	213.63	252.20	316.28	384.50	452.92	515.33	2134.87
	Total	729.03	802.13	892.20	976.08	1052.08	1115.08	5566.62
DCLα=15	Strong	566.75	594.67	600.00	600.00	600.00	600.00	3561.42
	Weak	183.75	214.08	261.08	310.42	385.08	473.75	1828.17
	Total	750.50	808.75	861.08	910.42	985.08	1073.75	5389.58
DCLα=9	Strong	559.92	592.33	600.00	600.00	600.00	600.00	3552.25
	Weak	176.17	211.67	253.42	292.42	367.50	459.75	1760.92
	Total	736.08	804.00	853.42	892.42	967.50	1059.75	5313.17
DCLα=1	Strong	510.42	553.67	598.33	600.00	600.00	600.00	3462.42
	Weak	171.67	202.58	236.17	252.00	285.33	401.58	1549.33
	Total	682.08	756.25	834.50	852.00	885.33	1001.58	5011.75
FGSsmp2 stp2	Strong	352.50	424.83	498.83	540.67	515.17	506.50	2838.50
	Weak	2.50	7.67	11.00	24.67	86.67	207.17	339.67
	Total	355.00	432.50	509.83	565.33	601.83	713.67	3178.17
CPCβ=0.2	Strong	324.53	444.47	519.30	535.42	542.67	543.88	2910.27
	Weak	0.75	5.67	13.00	37.67	78.17	126.73	261.98
	Total	325.28	450.13	532.30	573.08	620.83	670.62	3172.25
FGSsmp2 stp1	Strong	341.17	416.50	494.83	537.33	515.17	506.50	2811.50
	Weak	1.00	2.67	7.33	16.00	63.67	184.50	275.17
	Total	342.17	419.17	502.17	553.33	578.83	691.00	3086.67
FGSsmp1 stp2	Strong	314.83	409.67	480.33	545.17	522.17	504.50	2776.67
	Weak	1.00	4.83	8.00	15.50	61.00	182.33	272.67
	Total	315.83	414.50	488.33	560.67	583.17	686.83	3049.33
CPCβ=0.1	Strong	245.50	419.83	532.08	569.08	575.67	576.50	2918.67
	Weak	0.33	0.92	3.17	10.83	33.75	80.75	129.75
	Total	245.83	420.75	535.25	579.92	609.42	657.25	3048.42
FGSsmp1 stp1	Strong	304.83	401.33	480.33	540.17	522.17	504.50	2753.33
	Weak	0.00	1.50	5.17	11.50	45.83	153.33	217.33
	Total	304.83	402.83	485.50	551.67	568.00	657.83	2970.67
CPCβ=0.05	Strong	158.00	355.83	515.17	573.83	588.67	590.00	2781.50
	Weak	0.00	0.67	0.33	4.83	16.33	50.83	73.00
	Total	158.00	356.50	515.50	578.67	605.00	640.83	2854.50
CPCβ=0.01	Strong	64.00	223.33	439.17	559.00	595.83	598.25	2479.58
	Weak	0.00	0.00	0.00	0.67	2.17	10.67	13.50
	Total	64.00	223.33	439.17	559.67	598.00	608.92	2493.08
PCβ=0.1	Strong	312.27	340.27	346.27	337.25	349.48	355.75	2041.28
	Weak	12.08	16.33	26.07	39.57	54.83	93.97	242.85
	Total	324.35	356.60	372.33	376.82	404.32	449.72	2284.13
PCβ=0.05	Strong	324.73	349.28	355.17	337.50	346.97	346.50	2060.15
	Weak	4.75	7.25	19.75	31.92	43.67	69.75	177.08
	Total	329.48	356.53	374.92	369.42	390.63	416.25	2237.23
PCβ=0.2	Strong	289.50	296.02	311.00	316.67	333.13	348.10	1894.42
	Weak	24.08	28.83	33.13	49.82	77.88	121.38	335.13
	Total	313.58	324.85	344.13	366.48	411.02	469.48	2229.55
PCβ=0.01	Strong	323.50	376.67	383.83	371.08	339.67	332.92	2127.67
	Weak	0.00	0.83	9.50	21.50	28.67	40.83	101.33
	Total	323.50	377.50	393.33	392.58	368.33	373.75	2229.00
FCIβ=0.2	Strong	15.58	34.25	56.08	85.75	100.00	129.98	421.65
	Weak	1.17	2.42	3.08	5.17	17.00	36.90	65.73
	Total	16.75	36.67	59.17	90.92	117.00	166.88	487.38
FCIβ=0.1	Strong	5.67	17.17	35.75	63.17	81.17	103.65	306.57
	Weak	0.00	0.00	0.33	2.08	6.17	18.33	26.92
	Total	5.67	17.17	36.08	65.25	87.33	121.98	333.48
FCIβ=0.05	Strong	3.50	7.67	23.50	53.00	71.17	90.58	249.42
	Weak	0.00	0.00	0.00	0.00	2.00	10.08	12.08
	Total	3.50	7.67	23.50	53.00	73.17	100.67	261.50
FCIβ=0.01	Strong	0.00	1.00	10.50	38.17	55.83	72.33	177.83
	Weak	0.00	0.00	0.00	0.00	0.33	1.67	2.00
	Total	0.00	1.00	10.50	38.17	56.17	74.00	179.83

For the complex network data (Table 5), we found all five DCL methods again having the best results, with the best and worst DCL methods having total JIs of 4869.41 (DCL_α=15, 67.63%) and 4441.28 (DCL_α=1, 61.68%), respectively. The best CPC and FGS methods had JIs of 4185.19 (CPC_β=0.2, 58.13%) and 3951.18 (FGS_{smp2 stp2}, 54.88%), respectively, both of which are close to the lowest performing DCL method’s result, but the best PC and FCI methods’ JIs, which were 1035.18 (PC_β=0.2, 14.38%) and 768.32 (FCI_β=0.2, 10.67%), respectively, fell far behind the results of the other three algorithms.

Table 5.

Total JIs for the complex network models by case size (bolded values indicated highest score in each case size)

Learning method	300 cases	600 cases	1200 cases	2400 cases	4800 cases	9600 cases	Total
DCLα=15	665.45	757.70	810.76	831.76	877.03	926.70	4869.41
DCLα=54	665.25	746.21	780.97	819.52	874.83	931.94	4818.71
DCLα=9	641.60	734.24	803.50	832.73	868.33	915.86	4796.26
DCLα=108	616.13	686.78	743.66	781.91	825.57	898.70	4552.76
DCLα=1	537.80	647.40	738.38	813.98	823.88	879.83	4441.28
CPCβ=0.2	379.99	525.76	657.31	786.59	877.45	958.09	4185.19
CPCβ=0.1	333.27	489.02	625.39	778.69	883.77	969.33	4079.47
FGSsmp2 stp2	383.98	522.78	666.85	764.10	803.72	809.75	3951.18
FGSsmp1 stp2	368.63	505.99	645.55	753.39	807.04	804.75	3885.33
CPCβ=0.05	273.69	444.90	590.61	749.22	873.34	952.28	3884.03
FGSsmp2 stp1	357.34	494.30	643.70	751.43	798.21	802.59	3847.58
FGSsmp1 stp1	341.89	475.36	624.04	738.90	804.45	797.71	3782.36
CPCβ=0.01	188.18	351.83	532.85	665.90	812.90	926.02	3477.68
PCβ=0.2	82.98	90.14	114.63	157.06	222.85	367.52	1035.18
PCβ=0.1	82.88	80.78	108.97	139.85	188.74	325.13	926.35
PCβ=0.05	79.68	80.77	105.20	128.05	159.43	274.20	827.34
FCIβ=0.2	48.45	56.93	78.05	116.80	175.55	292.54	768.32
PCβ=0.01	70.42	79.65	91.20	115.05	132.95	204.35	693.62
FCIβ=0.1	40.27	50.86	71.38	101.52	150.77	255.93	670.73
FCIβ=0.05	34.85	50.12	69.70	87.95	126.18	215.77	584.57
FCIβ=0.01	27.15	44.53	60.83	73.40	104.65	162.00	472.57

The combined results in Table 6 once again show all five DCL methods in the top five, with the best and worst DCL methods having overall JIs of 10400.58 (DCL_α=54, 72.22%) and 9453.03 (DCL_α=1, 65.65%), respectively. Similar to the results from the simple networks, the best CPC, FGS, PC, and FCI methods trailed far behind, each of which had overall JIs of 7357.44 (CPC_β=0.2, 51.09%), 7129.34 (FGS_{smp2 stp2}, 49.51%), 3264.73 (PC_β=0.2, 22.67%), and 1255.71 (FCI_β=0.2, 8.72%).

Table 6.

Total JIs for both the simple and complex networks combined by case size (bolded values indicated highest score in each case size)

Learning method	300 cases	600 cases	1200 cases	2400 cases	4800 cases	9600 cases	Total
DCLα=54	1434.62	1573.63	1680.22	1777.19	1901.75	2033.19	10400.58
DCLα=15	1415.95	1566.45	1671.85	1742.18	1862.11	2000.45	10258.99
DCLα=108	1345.17	1488.92	1635.86	1757.99	1877.66	2013.78	10119.38
DCLα=9	1377.68	1538.24	1656.92	1725.14	1835.83	1975.61	10109.43
DCLα=1	1219.88	1403.65	1572.88	1665.98	1709.22	1881.41	9453.03
CPCβ=0.2	705.27	975.90	1189.61	1359.67	1498.29	1628.70	7357.44
FGSsmp2 stp2	738.98	955.28	1176.68	1329.43	1405.55	1523.41	7129.34
CPCβ=0.1	579.10	909.77	1160.64	1358.61	1493.19	1626.58	7127.89
FGSsmp1 stp2	684.46	920.49	1133.88	1314.05	1390.20	1491.58	6934.66
FGSsmp2 stp1	699.51	913.47	1145.87	1304.76	1377.05	1493.59	6934.25
FGSsmp1 stp1	646.72	878.20	1109.54	1290.57	1372.45	1455.54	6753.02
CPCβ=0.05	431.69	801.40	1106.11	1327.89	1478.34	1593.11	6738.53
CPCβ=0.01	252.18	575.16	972.02	1225.57	1410.90	1534.94	5970.76
PCβ=0.2	396.56	414.99	458.76	523.54	633.86	837.01	3264.73
PCβ=0.1	407.23	437.38	481.30	516.67	593.05	774.85	3210.48
PCβ=0.05	409.17	437.30	480.12	497.47	550.07	690.45	3064.57
PCβ=0.01	393.92	457.15	484.53	507.63	501.28	578.10	2922.62
FCIβ=0.2	65.20	93.59	137.22	207.72	292.55	459.43	1255.71
FCIβ=0.1	45.94	68.03	107.47	166.77	238.10	377.92	1004.21
FCIβ=0.05	38.35	57.78	93.20	140.95	199.35	316.43	846.07
FCIβ=0.01	27.15	45.53	71.33	111.57	160.82	236.00	652.40

4.1.3 Runtime

As mentioned before, we used two high-level characteristics, accuracy and runtime, to assess the performance of each scoring method. Accuracy has already been addressed with the EC and JI results. With respect to runtime, we found that for every analysis, DCL had, by far, the fastest runtime. The average runtimes, in seconds, for the fastest and slowest DCL method for the simple network datasets (Table S5) was 0.088 (DCL_α=1) and 0.181 (DCL_α=108), respectively, whereas the fastest CPC, FGS, PC, and FCI methods were 4.522 (CPC_β=0.01), 7.418 (FGS_{smp1 stp2}), 4.991 (PC_β=0.01), and 4.483 (FCI_β=0.05). Similar runtime performances were observed for the complex networks (Table S6), where the fastest and slowest average DCL runtimes were 2.410 (DCL_α=1) and 5.487 (DCL_α=15), respectively, the latter of which was still faster than the quickest non-DCL methods: 7.627 (FGS_{smp2 stp1}), 8.806 (PC_β=0.01), 15.887 (CPC_β=0.01), and 10.326 (FCI_β=0.01). Overall (Table S7), all five DCL methods were a great deal faster than any of the other learning methods. Additionally, when we separated the simple network results by direct predictor relationship strength (Table S8), we found DCL to once again have the fastest runtime among all the learning methods for the strong-datasets—0.096 (DCL_α=1), 4.708 (CPC_β=0.01), 5.565 (PC_β=0.01), 7.535 (FGS_{smp1 stp2}), and 4.432 (FCI_β=0.05)—and also among all the methods for the weak-datasets—0.077 (DCL_α=9), 4.337 (CPC_β=0.01), 4.418 (PC_β=0.01), 7.302 (FGS_{smp1 stp2}), and 4.535 (FCI_β=0.05).

4.1.4. Statistical comparison of the best scoring methods

In order to statistically compare our algorithm’s performance to that of FGS, CPC, PC, and FCI, we performed McNemar’s Test for paired nominal data on how many datasets the best scoring method for each algorithm correctly predicted within each network type. When comparing the best DCL scoring method to that for the other four algorithms for the simple networks and overall, we consistently found a significant difference in accuracy (p ≪ 0.001), as shown in Table 7. However, in the complex networks, when we compared the best FGS method to the best DCL method, the former of which slightly outperformed the latter, we found that there was not a significant different in accuracy (p > 0.05) between FGS and DCL for the complex networks. We also found that there was no significant different in accuracy (p > 0.05) between DCL and CPC for the complex networks even though DCL correctly predicted more datasets than CPC. For PC and FCI, however, DCL performed significantly better in all the network types.

Table 7.

Pairwise comparison of each algorithm’s best learning method to DCL’s best learning method using McNemar’s test

Network type	Learning methods compared	p-value
Simple	DCLα=54 vs FGSsmp2 stp2	0.000
Simple	DCLα=54 vs CPCβ=0.1	0.000
Simple	DCLα=54 vs PCβ=0.01	0.000
Simple	DCLα=54 vs FCIβ=0.2	0.000
Complex	FGSsmp2 stp2 vs DCLα=15	0.269
Complex	DCLα=15 vs CPCβ=0.2	0.053
Complex	DCLα=15 vs PCβ=0.2	0.000
Complex	DCLα=15 vs FCIβ=0.2	0.000
Overall	DCLα=54 vs FGSsmp2 stp2	0.000
Overall	DCLα=54 vs CPCβ=0.1	0.000
Overall	DCLα=54 vs PCβ=0.01	0.000
Overall	DCLα=54 vs FCIβ=0.2	0.000

4.2. Real data results

4.2.1. LOAD dataset

Out of 312,316 SNPs and APOE ε4carrier status (1,411 samples) in the Reiman’s LOAD data, we narrowed down our list of predictors to 77 SNPs and APOE ε4carrier status using a chi-square test with a significant criterion of 0.0001. Then, we ran DCL with α = 1, 9, 15, 54, and 108 to learn which SNPs, from those selected using the chi-square test, are directly causal of LOAD. Table 8 shows the discovered SNPs and their associated genes. APOE is a well-known genetic risk predictor of LOAD. The results from running DCL on the LOAD dataset found APOE at every alpha value. In addition, APOE had the highest BDeu score of any other SNP found as a predictor. At α values of 9, 15 and 54, DCL predicted rs7335085, rs4356530, and rs4394475, found on Chromosomes 13, 17, and 9, respectively, as direct causes of LOAD. At alpha = 1 and 108, DCL discovered two new SNPs as direct causes that were not found at α = 15 or 54: rs6784615 and rs10824310. The former is located on the gene NISCH and the latter on the gene PRKG1 (cGMP-dependent protein kinase type I).

Table 8.

Direct predictors found running DCL on Reiman’s LOAD data

Learning method	SNP	Gene or chromosome	BDeu score
DCLα=1	rs6784615	NISCH	-937.6
	APOE	APOE	-837.8
DCLα=9	rs7335085	Chromosome 13	-939.0
	rs4356530	Chromosome 17	-937.0
	APOE	APOE	-836.0
DCLα=15	rs4356530	Chromosome 17	-936.6
	APOE	APOE	-836.3
DCLα=54	rs4394475	Chromosome 9	-939.5
	APOE	APOE	-839.9
DCLα=108	rs6784615	NISCH	-938.7
	rs10824310	PRKG1	-935.3
	rs4394475	Chromosome 9	-940.2
	APOE	APOE	-845.5

We also ran FGS, PC, CPC, and FCI on the LOAD dataset. PC_β=0.01, PC_β=0.05, and PC_β=0.2 all predicted APOE and each predicted rs732549 (chromosome 3), rs4356530 (chromosome 17), and rs6094514 (EYA2), respectively, as direct causes of LOAD (Table 9). FCI at a beta value of 0.2 predicted just APOE. All the other learning methods were unable to find any predictors of LOAD.

Table 9.

Direct predictors found running PC or FCI on Reiman’s LOAD data

Learning method	SNP	Gene or chromosome
PCβ=0.01	APOE	APOE
	rs732549	Chromosome3
PCβ=0.05	APOE	APOE
	rs4356530	Chromosome17
PCβ=0.2	APOE	APOE
	rs6094514	EYA2
FCIβ=0.2	APOE	APOE

4.2.2. Metabric dataset

We ran the chi-Square test with significance levels of 0.05 and 0.01 on the six Metabric datasets. As shown in Table 10, the chi-Square test returned almost all the variables as significantly associated with breast cancer at a significant level of 0.05. Even when we reduced the significance level to 0.01, our list of predictors was only reduced by one or two variables. For example, in the results for the 10-year breast cancer death dataset, histological type and axillary nodes removed were significant only at a level of 0.05 but not at 0.01. When we ran DCL on these datasets, we found a much shorter list of predictors. For example, with DCL, we found that Lymph nodes pos was found as a direct cause at every α value and for every dataset. In addition, there were some direct causes found that were unique to specific time points. For example, ER category was found by all the DCL learned methods for both 5-year datasets but was not present in the 10-year or 15-year dataset. In the 10-year breast death dataset, HER2 status was found as a direct cause for every learning method except DCL_α=1 but not found as a direct cause for any other dataset.

Table 10.

Direct predictors found running DCL and chi-square test on Metabric data

	5-year breast death	5-year survival death	10-year breast death	10-year survival death	15-year breast death	15-year survival death
DCLα=1	• Lymph nodes pos	• Lymph nodes pos	• Lymph nodes pos	• Lymph nodes pos	• Lymph nodes pos	• Lymph nodes pos
	• ER category	• ER category
DCLα=9	• Lymph nodes pos	• Lymph nodes pos	• Lymph nodes pos	• Lymph nodes pos	• Lymph nodes pos	• Lymph nodes pos
	• ER category	• ER category	• HER2 status	• Age at diagnosis
DCLα=15	• Lymph nodes pos	• Lymph nodes pos	• Lymph nodes pos	• Lymph nodes pos	• Lymph nodes pos	• Lymph nodes pos
	• ER category	• ER category	• HER2 status	• Age at diagnosis
DCLα=54	• Lymph nodes pos	• Lymph nodes pos	• Lymph nodes pos	• Lymph nodes pos	• Lymph nodes pos	• Lymph nodes pos
	• ER category	• ER category	• HER2 status	• Age at diagnosis	• Overall grade	• Age at diagnosis
						• Inferred menopausal status
DCLα=108	• Lymph nodes pos	• Lymph nodes pos	• Lymph nodes pos	• Lymph nodes pos	• Lymph nodes pos	• Lymph nodes pos
	• ER category	• ER category	• HER2 status	• Age at diagnosis	• Histological type	• Histological type
	• PR category	• Age at diagnosis	• PR category
Chi-square	• Age at diagnosis	• Age at diagnosis	• Age at diagnosis	• Age at diagnosis	• Age at diagnosis*	• Age at diagnosis
	• Size	• Size	• Size	• Size	• Size	• Size*
	• Lymph nodes pos	• Lymph nodes pos	• Lymph nodes pos	• Lymph nodes pos	• Lymph nodes pos	• Lymph nodes pos
	• Overall grade	• Overall grade	• Overall grade	• Overall grade	• Overall grade	• PR category*
	• Histological type*	• Histological type*	• Histological type*	• Histological type*	• ER category	• HER2 status
	• ER category	• ER category	• ER category	• ER category	• PR category	• Inferred menopausal status*
	• PR category	• PR category	• PR category	• PR category	• HER2 status	• Percent nodes positive
	•HER2 status	• HER2 status	• HER2 status	• HER2 status	• Percent nodes positive
	•Inferred menopausal status	• Percent nodes positive	• Axillary nodes removed*	• Inferred menopausal status
	• Percent nodes positive		• Percent nodes positive	• Axillary nodes removed*
				• Percent nodes positive

^*significant at α = 0.05 but not α = 0.01

Blue- predictor not found in the previous alpha level for the same dataset

Red- predictor not found in the previous time-point (e.g. found in 10 year but not in 5 year)

Purple- Both red and blue conditions occur

When we ran FGS, PC, CPC, and FCI on the Metabric datasets (Table 11), we also found a smaller number of results than when we ran the Chi-Square test. However, the latter three algorithms found no predictors for a few of the datasets. Moreover, FCI_β=0.01 and FCI_β=0.05 were unable to find any predictors across all the datasets. All the FGS learning methods found Lymph nodes pos for every dataset and the FCI, PC, and CPC methods that did learn predictors found only Lymph nodes pos in many cases. However, PC_β=0.2, CPC_β=0.1, and FCI_β=0.2 were able to find HER2 status as a predictor of 10-year breast cancer survival which DCL found. In addition, CPC_β=0.05 found PR category as a predictor for 5-year survival death and CPC_β=0.05, CPC_β=0.1, and CPC_β=0.2 all found Hormone as a predictor of the 15-year breast death dataset.

Table 11.

Direct predictors found running FGS, PC, CPC, and FCI on Metabric data

	5-year breast death	5-year survival death	10-year breast death	10-year survival death	15-year breast death	15-year survival death
FGSsmp1 stp1	• Lymph nodes pos	• Lymph nodes pos	• Lymph nodes pos	• Lymph nodes pos	• Lymph nodes pos	• Lymph nodes pos
FGSsmp1 stp2	• Lymph nodes pos	• Lymph nodes pos	• Lymph nodes pos	• Lymph nodes pos	• Lymph nodes pos	• Lymph nodes pos
FGSsmp2 stp1	• Lymph nodes pos	• Lymph nodes pos	• Lymph nodes pos	• Lymph nodes pos	• Lymph nodes pos	• Lymph nodes pos
FGSsmp2 stp2	• Lymph nodes pos	• Lymph nodes pos	• Lymph nodes pos	• Lymph nodes pos	• Lymph nodes pos	• Lymph nodes pos
PCβ=0.01	None	•Size	•Size	•Size	None	None
PCβ=0.05	None	None	None	•Size	None	None
PCβ=0.1	None	None	•Size	None	None	None
PCβ=0.2	None	None	•HER2 status	•Lymph nodesps pos	None	None
CPCβ=0.01	• Lymph nodes pos	• Lymph nodes pos	• Lymph nodes pos	• Lymph nodes pos	None	None
	• PR category				• Hormone
CPCβ=0.05	• Lymph nodes pos	• PR category	None	• Lymph nodes pos	• Lymph nodes pos	None
					• Hormone
CPCβ=0.1	None	None	• HER2 status	None	• Lymph nodes pos	None
				• Lymph nodes pos	• Hormone
CPCβ=0.2	None	• Size	None	• Size	• Lymph nodes pos	None
FCIβ=0.01	None	None	None	None	None	None
FCIβ=0.05	None	None	None	None	None	None
FCIβ=0.1	None	None	None	• Lymph nodes pos	None	None
FCIβ=0.2	None	None	• HER2 status	• Lymph nodes pos	None	None

5. Discussion

5.1. Simulated data

In the majority of our analyses, the DCL algorithm is the most accurate causal discovery algorithm using the EC criterion. Viewing the overall performance of each scoring method, we find that the top DCL scoring method correctly discovers the exact causal influences in approximately 1400 more datasets than the top FGS method, 1600 more datasets than the top CPC method, 4500 more datasets than the top PC method, and 5600 more datasets than the top FCI method, while also having the highest EC value for each case size for the simple networks.

When we separated the simple network results based on direct predictor strength, we find that every DCL method, except DCL_α=108, correctly predicts most, if not all, of the strong datasets at case sizes 1200 and above, whereas FGS, CPC, PC, and FCI were unable to correctly predict all the strong datasets for any case size. It is also surprising to see that many of the CPC methods perform better than FGS for the strong datasets since, overall, nearly all the FGS methods correctly predicted more datasets than even the top CPC method (CPC_β=0.1). For example, CPC_β=0.1 and CPC_β=0.05 correctly predicted more datasets than any of FGS methods at case sizes 600 and above, except at 2400 cases where CPC_β=0.1 only predicts more than FGS_{smp2 stp1}. However, CPC falls short of FGS for the weak direct predictors where it correctly predicted no more than 1% of the weak datasets whereas FGS and DCL, both of which performed expectedly worse in the weak datasets than in the strong datasets, were able to correctly predict 4% and 7%, of the weak datasets, respectively, in their least accurate methods. We also see that at every case size, DCL_α=108 correctly predicted the most weak direct predictor datasets than any other method (see Supplement for more information on performance trends with varying alpha values). We also compared the highest scoring DCL method to the highest scoring FGS, CPC, PC, and FCI methods using McNemar’s test, and found that DCL significantly outperforms these four methods for the simple networks and overall.

Even though DCL outperforms FGS for the simple networks and overall, we do find that FGS slightly outperforms DCL for the complex networks according to the total number of correctly predicted datasets. This is consistent with what we know about the FGS algorithm. In our description of FGS, we mention that it performs very well with complex problems. However, if we look closely at the number of datasets correctly predicted across case size, we find that the method correctly predicting the most datasets varies. At case sizes 300 and 600, it is DCL_α=15; at case sizes 1200 and 2400, it is FGS_{smp2 stp2}; and at case sizes 4800 and 9600, it is CPC_β=0.1. Finding the predictors when the dataset is small is a much harder task since it is typically difficult to find real datasets with more than 1200 and 2400 cases, where even these can be quite uncommon. Thus, we find that DCL has a unique advantage in that it is able to correctly predict more datasets than either CPC or FGS at small case sizes. Ultimately, we find that the differences in performance between the best DCL, CPC, and FGS algorithms for the complex networks are not significant, meaning that, overall, these three algorithms perform similarly when given complex datasets.

DCL’s results according to JI are much better (relative to the EC results) as, for every network type, all five DCL methods have the highest total JIs. In addition, contrary to the EC results, the JI results show that CPC_β=0.2 performs almost as well as the best FGS method (FGS_{smp2 stp2}) for the simple networks and performs better than this method for the complex models and overall. Although CPC cannot correctly find all the predictors for the simulated datasets as well as FGS can, it does better than FGS in partially predicting them. For the complex networks, at every case size below 4800, a DCL method has the highest JI but at 4800 and 9600, CPC_β=0.1 has the highest JI, similar to the EC results. This adds to our previous claim that DCL performs better than FGS or CPC at lower case sizes and also that CPC performs better than DCL or FGS at higher case sizes.

For the weak direct predictor datasets in the simple networks, all the DCL methods tend to discover nearly 50% of the predictors, whereas the best FGS and CPC methods are both only able to discover approximately 10% of the predictors. These results indicate that DCL is a substantial advancement in our ability to partially discover the causal influences of a target when the direct predictor strength is weak.

It is clear from our runtime results that the DCL algorithm is much faster than PC, CPC, FGS, and FCI regardless of the parameter or case size. With PC and CPC, there is a clear trend of slower runtimes with larger β values, but there does not seem to be a clear trend between DCL’s runtime and α since, in the complex networks and overall, DCL_α=15 seems to be the slowest DCL method. However, the runtime of a DCL method may in fact be associated with its performance. For example, we can see from the EC and JI results that DCL_α=15 found more predictors than any of the other DCL methods. Additionally, the runtime results show that all DCL methods take, on average, longer to run on the strong datasets than on the weak datasets even though we know DCL performs better on the former than the latter. Discovering more predictors may cause DCL to undergo additional loops, thereby increasing its runtime. This association between performance and runtime is also observed in the FCI runtime results. Since runtime by itself does not necessarily mean an algorithm is performing well, the combination of the fastest runtimes and, in almost all the cases, the most accurate results does show that DCL performs exceptionally well when compared to FGS, CPC, PC, and FCI.

5.2. Real data

5.2.1. LOAD dataset

DCL, PC, and FCI discovered several SNPs to be direct predictors of LOAD. Some of these SNPs, such as rs732549, rs4356530 and rs4394475, are not located on specific genes, but are, more generally, found on chromosome 3, chromosome 17 and chromosome 9, respectively. The PC algorithm also predicted rs6094514, found on the gene of EYA2, as a direct cause of LOAD. However, there are no previous studies that indicate that these SNPs have an effect on LOAD so further study is necessary to investigate whether or not these SNPs are causally linked to Alzheimer’s disease. On the other hand, off the three SNPs found using DCL_α=108, two of them are located on the noteworthy genes NISCH and PRKG1. Two previous studies have indicated that SNP rs6784615, found on NISCH, is associated with LOAD [34, 35]. Furthermore, many GWAS studies have found that PRKG1 is also strongly associated with Alzheimer’s disease [36, 37]. In addition, other GWAS studies have found that PRKG1 (cGMP-dependent protein kinase type I) is associated with neurological diseases, such as onset age of Parkinson’s disease and attention deficit hyperactivity disorder [38, 39]. This is due to PRKG1’s role in regulating neocortical development, brain development, and signal transduction [40-42].

The SNP rs7115850, located on the GRB-associated binding protein 2 (GAB2) gene, has been reported to interact with the APOE gene to have a causal effect on LOAD [6, 43]. Our DCL algorithm did not identify any SNPs on GAB2 as direct causes for LOAD status, as no SNPs on GAB2, including rs7115850, were present in the 77 remaining SNPs after using a chi-square test with a significance criterion of 0.0001. We purposefully included rs7115850 with the 77 SNPs and then ran the DCL algorithm again, but still found that rs7115850 was not identified as a direct cause of LOAD status. This result illustrates the limitations and role of the DCL algorithm. Previous research [6, 43] indicates that APOE and GAB2 interact epistatically to affect LOAD, but GAB2 has little marginal effect. Thus, GAB2 would be eliminated as a cause in the first iteration of the DCL algorithm. In general, the DCL algorithm does not discover a cause with little marginal effect but other causal discovery algorithms such as PC also have this same limitation. The DCL algorithm should be used synergistically with an interaction discovery algorithm. The latter algorithm would first discover interacting variables, and then each set of interacting variables would be transformed to a single variable before running the DCL algorithm.

SNP rs4420638 on APOC1 was the second highest scoring individual SNP after APOE in our previous study [43]. However, it was not discovered as a direct cause by DCL. This result indicates that it may not have a causal effect on LOAD, but rather its strong individual correlation with LOAD is due to its known linkage disequilibrium with APOE.

5.2.2. Metabric dataset

Table 9 shows the various direct causes of breast cancer survival status found by the DCL algorithm, and the predictors learned using chi-square test. We see that DCL found far fewer causes for each dataset and for each α than the number of predictors found using the chi-square test. In addition, the chi-square test found most if not all the variables to be predictors. These results speak to the precision of the DCL algorithm on real data. We see that there are direct causes, as found by DCL, that are distinct to specific datasets or specific time points. One such cause is ER Category, which is found in both 5-year datasets at all five BDeu α values. ER Category refers to the presence or absence (ER+ or ER-, respectively) of estrogen receptors found in breast cancer cells. According to previous studies, five-year survival is about 10 percent better for women with ER+ tumors than for those with ER- tumors. However, after five years, this survival difference begins to decrease and may even disappear [24-25]. In addition, we find that HER2 status is found as a direct cause at every α value for the 10-year breast death dataset. HER-2 is a proto-oncogene whose amplification in breast cancer has been associated with increased cell mortality, cell proliferation, tumor invasiveness, and additional oncogenic cell characteristics [44]. Some studies have shown that only about 60% of patients with HER-2 positive status invasive breast cancer are disease free after ten years, and about 65% survive overall [45-47]. However, patients with negative HER-2 status tumors tend to be disease free at a rate of 75% over ten years and have a slightly higher overall survival rate. As these findings suggest, HER2 status highly have a direct causal effect on breast cancer mortality, and, more so, within the first ten years of acquiring the illness. These previous findings not only substantiate the results of the DCL algorithm, but also highlight the potential DCL has in directing clinical research. The results of DCL give researchers a list of proposed direct causes to experimentally investigate, which could channel resources towards better understanding and possibly tailoring treatments to target the likely direct causes of a disease.

When we ran FGS, PC, CPC, and FCI on the Metabric datasets, we found FGS discovered only Lymph nodes pos across all the datasets and parameter combinations, which DCL also found across all the datasets and alpha values. This may indicate that Lymph nodes pos is a very strong predictor of breast cancer survival across all the time-points but because FGS is unable to learn any other predictors, it gives no additional insight into the predictors of breast cancer survival. Additionally, PC, CPC, and FCI learn no predictors for a large number of the datasets and beta values. In the cases where these three algorithms did learn predictors, a majority of the learned predictors are Lymph nodes pos or predictors that were also found by DCL. However, they do find HER2 status as a predictor, which agrees with the results from previous studies, in the 10-year Breast Death dataset. In contrast, DCL was able to find HER2 status at all alpha values, implying that DCL more confidently determines that HER2 status is a direct predictor of 10-year breast cancer survival. CPC does, in some cases, find predictors that DCL did not find. For example, CPC found PR category and Hormone as a predictor of 5-year and 15-year breast cancer survival, respectively, but we are unable to find previous literature to support these unique findings.

If we assume that the Metabric datasets can be represented by simple BNs, then, taking into account the results from the simulated datasets, DCL’s findings are the most reliable since it had the highest EC and JI for each case size. On the other hand, if we assume that the Metabric datasets are represented by complex BNs, then the results for FGS, CPC, and DCL could be considered the most reliable, and especially FGS and DCL since they performed the best for 600, 1200, and 2400 cases, which most closely resemble the sample sizes for the Metabric datasets. Since FGS is unable to find anything other than Lymph nodes pos, we can only confidently interpret the results of DCL and CPC in this case. However, DCL correctly and partially predicts more simulated datasets at case sizes close to the sample sizes of the Metabric datasets than CPC. In addition, every learning method for CPC found no predictors for at least two of the Metabric datasets, which may suggest that there are no predictors, but more likely suggests that CPC was unable to learn the predictors. Based on these comparisons, we believe that DCL has the highest potential among the learning methods we discuss to effectively learn direct predictors from real datasets.

6. Conclusions

We compared DCL to PC and CPC, the classic constraint-based pattern search algorithms, FGS, another Bayesian-score-based pattern search algorithm, and FCI, a constraint-based PAG search algorithm. DCL performed significantly better on the simple network datasets than all of its counterparts but about equal to FGS and CPC on the complex network datasets when we consider the total number of datasets correctly predicted. However, at small case sizes, DCL performs better than FGS and CPC on complex datasets, which we consider to be a bigger achievement than performing well at large case sizes due to the abundance of small sample-sized real datasets. Additionally, when using a more continuous measurement (JI), we found that DCL performs much better than its counterparts, showing that it can partially discover predictors better than any non-DCL method. Furthermore, DCL had notably faster runtimes than its counterparts, indicating that it improves upon not only the accuracy of popular causal learning algorithms but also the computational speed.

When we applied DCL to a real Alzheimer’s disease dataset, we learned SNPs that were previously determined to have a strong link to LOAD. We also applied DCL to real breast cancer datasets across different time-points and learned clinical predictors proven to be directly causal of breast cancer survival for patients at these specific time-points. It is important to note, however, that DCL may not able to find every predictor known to be linked with the particular target and does find predictors that we are unable to verify through the results of previous studies. Thus, we must approach our real dataset results with caution, understanding that the causes discovered may not all be direct predictors of the specified target. Despite these limitations, we conclude that DCL can still be effective and informative when applied to real data.

DCL makes significant advances in solving the problem of learning causal influences from data, thereby making strides towards the confident use of causal discovery algorithms in practical applications, such as designing medical BN models for decision support. We aim to further develop DCL so that a future version may be able to include expert information, account for latent confounders, and even improve upon its runtime. Nonetheless, our study highlights DCL’s promise in advancing the field of causal discovery and its applications to medicine.

Highlights.

• We propose a new algorithm (DCL) to learn the direct causal influences of a target such as a disease outcome.

• DCL uses Bayesian network scoring and a novel deletion algorithm

• Results show DCL clearly outperforms PC with respect to accuracy and runtime

• Found SNPs directly causal of LOAD on NISCH & PRKG1 and validated by prior studies

• Further Validated ER cat. & HER2 status causal of 5 & 10-year breast cancer survival/death, resp.