Determination of the conformational ensemble of the TAR RNA by X-ray scattering interferometry

Abstract

The conformational ensembles of structured RNA's are crucial for biological function, but they remain difficult to elucidate experimentally. We demonstrate with HIV-1 TAR RNA that X-ray scattering interferometry (XSI) can be used to determine RNA conformational ensembles. X-ray scattering interferometry (XSI) is based on site-specifically labeling RNA with pairs of heavy atom probes, and precisely measuring the distribution of inter-probe distances that arise from a heterogeneous mixture of RNA solution structures. We show that the XSI-based model of the TAR RNA ensemble closely resembles an independent model derived from NMR-RDC data. Further, we show how the TAR RNA ensemble changes shape at different salt concentrations. Finally, we demonstrate that a single hybrid model of the TAR RNA ensemble simultaneously fits both the XSI and NMR-RDC data set and show that XSI can be combined with NMR-RDC to further improve the quality of the determined ensemble. The results suggest that XSI-RNA will be a powerful approach for characterizing the solution conformational ensembles of RNAs and RNA-protein complexes under diverse solution conditions.

INTRODUCTION

RNA's functions in complex cellular machines, in viral function and in the control of gene expression rely on variations in conformational states (1–4). As a result, there is growing interest in resolving these states and their underlying conformational ensembles. Current successes in obtaining RNA conformational ensembles have relied on the measurement of time-averaged NMR residual dipolar couplings (RDC) (5–7). These data provide long-range orientation dynamics information about motions that reorient individual bond vectors relative to an alignment frame describing partial alignment of the molecule relative to the magnetic field (8). Application of this powerful method is non-trivial, requiring NMR assignment and multiple independent molecular alignments (9,10). To date, only one RDC-based ensemble has been reported for an RNA helix-junction-helix motif, that for HIV1 TAR under a single solution condition (5). It can also be difficult to apply these NMR methods to larger RNA systems or RNA–protein complexes. Finally, RDCs are indifferent to conformations that only differ in translational movement of one helix or domain relative to another, an additional component of a complete description of a conformational ensemble. Given these challenges, and the central importance of ensembles for understanding dynamics, thermodynamics, folding and function, it is imperative to develop additional complementary and widely applicable approaches to obtain RNA ensembles.

X-ray scattering interference (XSI) between a pair of Au-nanocrystal probes, site-specifically labelled on a macromolecule, reports the distance distribution between these probes and has been used to determine ensemble properties of helical DNA and model bulged DNAs (11–13) and the structural plasticity of kink-turn RNA and its protein complexes (14). XSI has advantages over more traditional solution techniques as it reports instantaneous rather than time-averaged distances and provides data that can be directly transformed into a distance distribution (15,16). Probe–probe distance distributions have also been obtained through measuring the time dependence of fluorescence energy transfer (17) or spin echo intensity (double electron–electron resonance) (18). These approaches are powerful but have complex relationships between fluorescence or double electron–electron resonance signals and probe–probe distances, which in turn introduces large uncertainties in decomposing the overall signal into contributions from ensemble constituents with different distances.

Au–Au distance distributions can be obtained using fewer samples by collecting anomalous small-angle X-ray scattering of gold (19), but not yet with the precision of the original approach. Larger Au-nanocrystals can increase the signal and allow application to larger complexes (20); however, spherical larger nanocrystals will be needed to increase precision in such measurements. The XSI-based method developed herein to obtain RNA ensembles will also be applicable to XSI data obtained by anomalous scattering or with larger gold particles.

To establish the ability of XSI to obtain RNA ensembles, beyond probing aspects of ensemble properties (14), we calibrated the position of the probes relative to the helix and determined the dynamic properties of the helix itself. We then used a series of XSI measurements to determine the dynamic properties of the structural elements that connect two helices for TAR RNA, a stem loop interrupted by a three-pyrimidine bulge that has previously been shown to kink the axis of the RNA (7,21–22).

MATERIALS AND METHODS

Materials

Au nanocrystals were synthesized and purified as described previously (15). SPDP [succinimidyl 3-(2-pyridyldithio)propionate] was purchased from Thermo Scientific. RNA oligonucleotides were synthesized at the Protein and Nucleic Acids Facility at Stanford University and purified by RNA purification cartridge (Glen Research) followed by anion exchange high pressure (or high performance) liquid chromatography (HPLC) (Dionex DNAPac 100, 10 mM to 1.5 M NaCl in 20 mM sodium borate buffer, pH 7.9). For amino-modified (N2-Amino-Modifier C6 dG, Glen Research) RNA oligonucleotides, we modified the standard post-synthesis procedure to improve the yield of active amino-modifications to above 80% from under 30% (Supplementary Data Notes S1).

Preparation of Au-conjugated RNA oligonucleotides

RNA oligonucleotides with amino-modified guanine (N2-Amino-Modifier C6 dG, Glen Research) were first reacted with 20 μl of an SPDP solution (1 mg/10 μl in dimethyl sulfoxide) in 140 μl of 0.1 M sodium borate buffer, pH 7.9, at 37°C for 30 min. A second 20 μl aliquot of the SPDP solution was added and the reaction was continued for another 30 min. Excess SPDP was removed by ethanol precipitation. The SPDP-modified oligonucleotides were then treated with 100 mM dithiothreitol, 50 mM Tris•HCl, pH 9.0, at 50°C for 30 min to generate a thiol group for conjugation. Excess dithiothreitol was removed by ethanol precipitation and centrifugal filtration. The thiol-containing oligonucleotides were then reacted with a 6-fold molar excess of Au nanocrystals in 20 mM Tris-HCl, pH 9.0, at room temperature for 2 h. Au-coupled oligonucleotides were purified by anion-exchange HPLC (DNAPac 100, 10 mM to 1.5 M NaCl in 20 mM ammonium acetate, pH 5.6) and desalted and concentrated by centrifugal filtration (10 kDa cutoff, Millipore). The purified and desalted oligonucleotide was hybridized with the appropriate complementary strand for 30 min at 40°C, and the resulting double-labelled duplex was purified by anion-exchange HPLC (DNAPac 100, 10 mM to 1.5 M NaCl in 20 mM ammonium acetate, pH 5.6). The samples were then desalted and concentrated by centrifugal filtration (10 kDa cutoff, Millipore) and stored at −20°C until SAXS measurements were carried out. Samples stored for several months showed no signs of breakdown.

SAXS measurements and data processing

Small-angle X-ray scattering measurements were carried out at beamline 4-2 of the Stanford Synchrotron Radiation Lightsource. The data were collected using a sample to detector distance of 1.1 meters at 11 keV (113 pm) over a q-range of 0.02–0.78 Å⁻¹ with a q-step of ∼0.0014 Å⁻¹ (about 540 points). The largest distance probed in this study is less than 100 Å, which is within the d_max limited defined as pi/q_min = 157 Å. The experimental conditions were 15–50 μM RNA, 10 or 150 mM NaCl, 0 or 10 mM MgCl₂, 30 or 70 mM Tris-HCl, pH 7.4, 10 mM sodium ascorbate and 15°C. For each sample, 10 3-s exposures were recorded. The measurement error was calculated as the standard error of the 10 exposures. The labelled RNA concentration was at least 15 μM for the XSI experiments. The X-ray scattering profiles of RNA with two Au-labels (AB), a single Au-label (A and B) and no Au-label (U) and profiles of Au nano-crystals alone (Au) and of buffer (Buf) alone were measured. These profiles were used to calculate the probe–probe scattering interference profile, I_Δ and the probe–probe distance distributions using a previously described procedure (11). Briefly, the probe-probe scattering interference profile, I_Δ, is calculated as the sum of the concentration normalized scattering signal of the double-labelled sample (AB) and non-labelled sample (U) minus the signals of the two single labelled sample (A and B) (Supplementary Figure S1) (11,15–16). The obtained I_Δ is then decomposed into contributions from 200 uniformly spaced probe–probe distances of 1 to 200 Å to generate the probe–probe distance probability distribution using a maximum entropy procedure (Supplementary Figure S1) (11,15–16).

Establishing a solution model for an RNA helix and internally labeled Au nanocrystals

To determine the position of the Au nanocrystal probe relative to its helix attachment point and the solution structure of a RNA helix, we carried out XSI measurements on RNA helices of two different sequences using a total of 20 pairs of Au probes separated by 3 to 20 base steps (Figure 1 and 2A, Supplementary Figure S2–S5). This extensive data set was used to obtain a set of parameters that defines the position of the Au nanocrystals relative to its helix attachment point, the average solution structure of the RNA helix, and the microscopic bending and twisting rigidity of a RNA helix in solution (Supplementary Data Notes S2–4). This solution model of RNA and Au nanocrystal probes, summarized in Supplementary Table S1, enables quantitative prediction of the expected Au–Au distances for a pair of Au nanocrystals site-specially labelled in helices of an RNA with a given structure. A detailed description of the generation of this model follows generally the procedure used previously for DNA (11) and is provided in Supplementary Data Note S4; it is briefly summarized below.

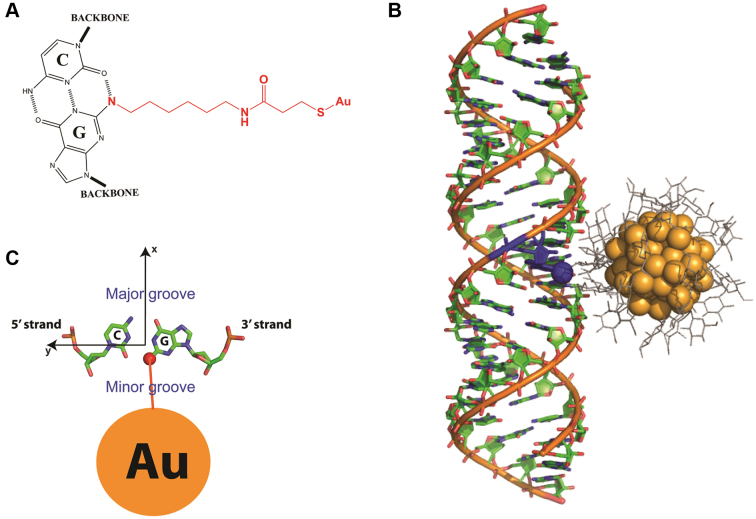
Figure 1.

The position of Au nanocrystals internally labeled to RNA helix. (A) The internally labeled nanocrystals are attached to N2-amino-modifed Gs through SPDP (N-Succinimidyl 3-[2-pyridyldithio]-propionate) linkers. (B) The Au nanocrystal shown in the plane of its attachment to G (seen from top). (C) The XSI-determined model of a thio-glucose (grey) passivated Au nanocrystal (orange) attached to an RNA helix. The attachment is to N2 (blue sphere) of a G residue (blue) as shown in part A, which positions the Au nanocrystals in the minor groove of the RNA helix.

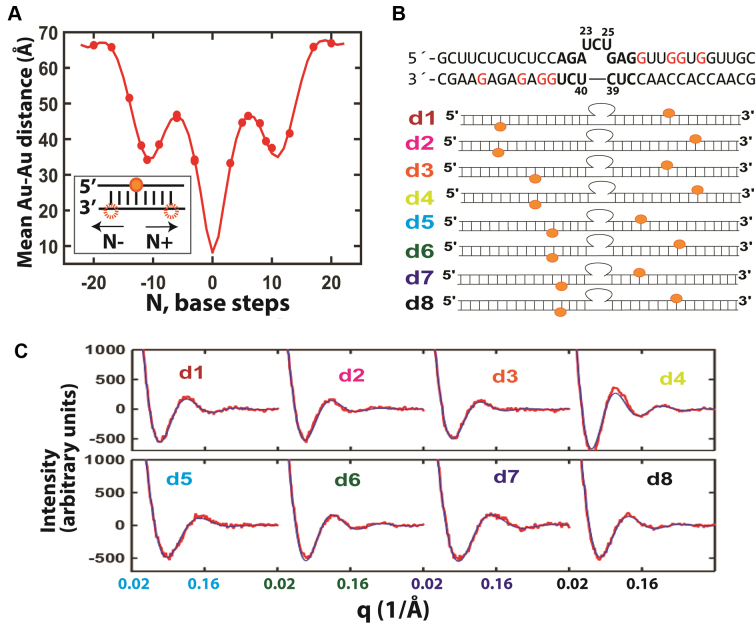
Figure 2.

Using XSI-RNA to resolve TAR RNA ensembles. (A) A solution model of RNA helices labelled with Au nanocrystals was developed from the average distances between two Au nanocrystals as a function of the number of separating base steps (30 mM Tris-HCl, pH 7.4, 150 mM NaCl and 10 mM sodium ascorbate; see Supplementary Figure S3 for RNA sequences). The data (circles) were fitted to a helical model of RNA (line; see Supplementary Data Notes S2–4 and Supplementary Table S1). The twenty sets of data points overdetermine the nine fitting parameters of the model. (B) The RNA constructs used for the TAR RNA XSI measurements. For each construct d1–d8 a pair of Au nanocrystals (orange) were attached to modified G residues (red). (C) The measured Au–Au scattering profiles (red) and the scattering profiles calculated from the resolved TAR ensemble (blue) for the constructs in part B (low salt condition: 30 mM Tris-HCl, pH 7.4, 10 mM NaCl and 10 mM sodium ascorbate; see Supplementary Figure S12 for higher salt profiles and Supplementary Figure S13 for the Au–Au distance distributions). An average value of χ² = 1.5 was obtained for the fits.

RNA helices were modeled as a continuous linear elastic rod (11), where fluctuations of base step parameters, [twist, tilt, roll], are assumed to be governed by elastic potentials. The experimental data were used to parameterize five RNA parameters, including the three helical parameters above (the average twist, tilt and roll per base step) and two elastic parameters, the bending (B) and twisting (C) persistence length. The other three helical parameters, shift, slide and rise, were set to equal to literature values derived from crystal structure database ((23), Supplementary Table S1) as their values are nearly constant across different literature models of RNA (Supplementary Table S2). The position of the internally labelled Au nanocrystal with respect to its helix attachment was modelled using four parameters, D, θ₀, axial₀ and ε_Au, where D, θ₀ and axial₀ determine the average position of the Au probe and ε_Au quantifies the dispersion in Au positions due to linker flexibility (Supplementary Data Note S3) (11,13). The complete model contains nine parameters, five for RNA helix and four for the Au probe. The optimum values for each of the nine parameters (Supplementary Table S1) were obtained by minimizing the χ² statistics that quantify the goodness-of-fit between the mean Au–Au distances and Au–Au distance variances of the model-predicted distributions and the observed distributions (Supplementary Figure S6).

Design and XSI measurement of TAR RNA

The TAR RNA construct used contained the canonical 3 nt bulge flanked by two 15 base pairs stems. The middle section of the construct has the same sequence as the HIV1-TAR RNA, including the CUC bulge and the five base pairs 5΄ to the bulge and three base pairs 3΄ to the bulge (Figure 2B). Each of the eight pairs of Au nanocrystals used spanned the bulge and each nanocrystal was ≥3 nt from the bulge (Figure 2B, d1–d8). The label sites were designed to maximize the sensitivity of Au–Au distance to conformational changes to the TAR bulge by including pairs covering a range of radial and vertical variations and situated as close as possible to the bulge while minimizing Au–Au clashes by their relative placement and placement ≥3 nt from the bulge. The self-consistency of the results, demonstrated by excellent cross-validations, provides strong evidence against a perturbation of the TAR ensemble by one or more of the Au nanocrystal pairs. XSI measurements were carried out under two solution conditions: 70 mM Tris.HCl, pH 7.4, 10 mM sodium ascorbate and 150 mM NaCl (Figure 3, high salt) and 30 mM Tris.HCl, pH 7.4, 10 mM sodium ascorbate and 10 mM NaCl (Figure 3, low salt).

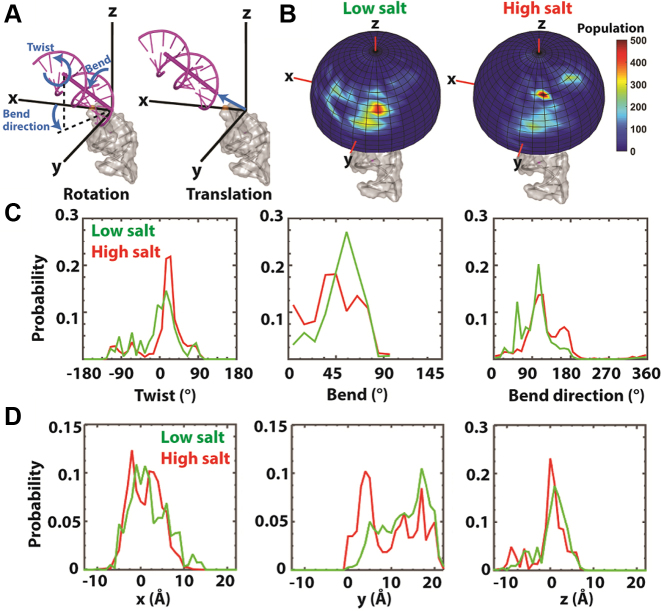
Figure 3.

TAR RNA ensembles obtained by XSI-RNA. (A) The position of a helix (magenta, upper) with respect to a second helix (grey, lower) is defined by a set of rotations (Euler angles) followed by a translation. From a straight position, the set of rotations are defined as follows: i. twist: rotating the upper helix around the z-axis by an amount α + γ; ii. bend: rotating the upper helix by an amount β in the direction defined by the bend direction (γ); subsequently, the helix is translated in the Cartesian coordinate (the xyz space) (see (12) for a more detailed description). (B) The spatial representation of the inter-helical orientation of XSI-resolved TAR ensemble under low (left) and high (right) salt. (Low salt: as in Figure 2C; high salt: 70 mM Tris-HCl, pH 7.4, 150 mM NaCl and 10 mM sodium ascorbate.) The helix 5΄ to the TAR bulge (grey) is fixed along the z-axis as in part A and the probability distribution of the angular orientation of the top helix (without translation) is displayed on the surface of a unit sphere. The (C) inter-helical orientation and (D) translational probability distributions of TAR RNA under the low (green) and high (red) salt solution conditions. Twist, bend and bend direction are as defined in part A and correspond to α + γ, β and γ, respectively, for Euler angle (α, β, γ) of the zyz convention (12).

Generation of a basis set for the conformational space of TAR RNA

A basis set of TAR conformations to use in determining the TAR ensembles was generated using a published MD trajectory of TAR RNA (5) containing 10 000 conformations or frames. For each TAR conformation in the MD trajectory, i in 1–10 000, we first aligned it into the reference coordinate by aligning the bottom (5΄) helix of the TAR RNA to the bottom helix of a standard A-form RNA helix in the reference coordinate. The global conformation of the TAR conformation was defined as the relative position of the 5΄ and the 3΄ helices across the TAR bulge, which is further defined as the movement that aligns the top (3΄) helix in the reference RNA to the top helix of the TAR conformation in the reference coordinate. This transformation, M_i, can be conveniently described as a set of Euler rotations (α, β, γ)_i, followed by translation of (x,y,z)_i. The reference coordinate system is defined as follows: the z axis is along the long axis of the bottom (5΄) helix and the positive z direction is the 5΄ to 3΄ direction of the sequence strand; the x axis points to O3 of the first nucleotide of the top helix on the sequence strand; and the direction of the y axis follows the right-hand rule. The Euler angle convention of zyz was used (12).

Prediction of the XSI data for a single conformation and an ensemble model

In the context of the experimental construct, the distance distribution for a pair of Au-nanocrystal probes has contributions from not only the junction dynamics but also the dynamics of the helices and the Au attachment linker. Thus, each of the 10 000 TAR conformations with a fixed inter-helical orientation corresponds to an Au–Au distribution rather than a single Au–Au distance. To predict the distribution for conformer i (in 1–10 000), we carried out a small-scale simulation of helices and Au linkers based on the models established above (see Establishing a solution model for an RNA helix and internally labelled Au nanocrystals above) using the parameters in Supplementary Table S1. Each simulation results in 2000 coordinates for each of the two Au nanocrytals. The pairwise distances between the two sets of 2000 coordinates were binned in 1 Å units to give the expected Au–Au distance distribution for conformer i, which can then be used to calculate the expected scattering profile for conformer i, I(q,i). With a basis set of conformations 1 to 10 000, an ensemble model is defined as a set of normalized probability weights (w₁, w₂,…w_{10 000}) and the expected scattering profile is the weighted sum of the scattering profiles from all basis conformations, I_ensemble = sum(w_i*I(q,i)).

Estimation of the conformational ensemble using XSI data

To estimate the conformational ensemble of TAR RNA using experimental XSI data, we used a previously described method (12) with modification; we refer to this method as empirical Bayesian sampling (EBS).

Based on a Bayesian principle (24), the optimal ensemble solution has 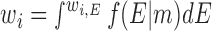, where i = 1 to 10 000, f(E|m) is the probability of having ensemble E given data m, and the integral is for all ensemble solutions. An ensemble solution, E, is a set of weights for the 10 000 basis set conformation, (w_1,E, w_2,E, …w_{10 000,E}). As the number of potential ensemble solutions are infinite and cannot be completely sampled, EBS samples this infinite ensemble solution space with a finite number of ensemble solution groups. An ensemble solution group is a set of different ensemble solutions that satisfies a common condition. In our approach, we define a specific ensemble solution group as ensemble solutions that only contain conformations from a sub-space of the entire conformational space. In other words, for a sub-space of N (N < 10 000) specific conformations out of the entire conformation space (10 000 basis set conformations in total), the corresponding ensemble solution group includes all ensemble solutions in which only the weights for this specific set of N conformations are non-zero and all other basis set conformations have weights of zero. Since the above integral is dominated by high probability ensemble models (i.e. those with high f(E|m)), for each ensemble solution group, only the most probable ensemble solution, the maximum likelihood solution within that ensemble solution group, is used for calculating the integral in EBS. Specifically, we set the size of the sub-space, N, to a constant (e.g. N = 100) and then randomly selecting N conformations to form a sub-space, which corresponds to an ensemble solution group. We then obtain the most probable solution out of this solution group, its maximum likelihood solution, E_j –the ensemble solution that minimizes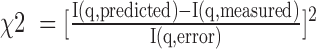. This process is repeated 10⁷/N times and we enforce that each conformation of the 10⁴ total conformations is included exactly the same number of times, 10⁷/10⁴ = 1000 times. In other words, each conformation is given equal chances to be part of a representative ensemble solution and be used in calculating the integral in EBS or the final ensemble solution. In the prior version of this method (12) N was set to 100; here we modified the algorithm to allow N to vary. The optimal N is determined as the value of N that minimizes χ² from a cross-validation test, where we use ensembles generated using seven of the eight data sets (one for each Au–Au pair) to predict the omitted data set. The optimal N was determined to be 200 and 100 for the low and high salt data herein, respectively (Supplementary Figure S7). Ensemble solutions obtained using a wide range of N are similar (Supplementary Figure S8).

Estimation of conformational ensemble using RDC and RDC plus XSI data

EBS was used to generate conformational ensembles with the RDC data from (5) and a combination of RDC data from (5) and the XSI data herein. To combine RDC and XSI data, the RDC data were scaled up by a factor of 19. The value of 19 was chosen so that the sum of χ² (XSI) and χ² (RDC) is at its minimum.

Comparison of the theoretical ensemble-solving capability of XSI and RDC

To compare the intrinsic information content of the XSI-RNA and RDC measurements, we compared their ensemble-solving capabilities using synthetic data sets, i.e. 10 target ensembles were generated by uniformly dividing the MD trajectory into 10 groups of 1000 conformations each. Thus, each ensemble contained 1000 conformations that are relatively more similar in conformation compared to the rest of the 9000 conformations and each ensemble has a conformational probability distribution that is distinct from that for the entire MD ensemble and from one another (Supplementary Figure S9A and B). For each target ensemble, we calculated the expected XSI and RDC data and generated synthetic XSI and RDC data by adding Gaussian experimental noise with magnitudes equal to the actual experimental noise herein and reported in (5). These synthetic data were used to estimate ensembles using EBS. The similarity of the resulting ensembles to the target ensembles were quantified using <Ω> as described in (25).

RESULTS

Establish fundamental XSI-RNA parameters using RNA helices

We attached Au nanocrystals to an RNA helix site-specifically at thiol-functionalized guanines (Figure 1). This labelling strategy positions the Au nanocrystals in the minor groove of the RNA helix (Figure 1C). In order to use these attached probes for quantitative structural analysis, it is necessary to know how they are positioned and fluctuate relative to a canonical unit of RNA secondary structure, the RNA helix. We performed this calibration by carrying out XSI measurements for two RNA helices with a total of 20 different pairs of Au-nanocrystal probes. We used two rather than a single RNA sequence to confirm that the XSI parameters generated are not sequence specific and have general applicability to TAR and other RNAs. We used the data from the two RNA helices to develop a simple model that incorporates basic helix geometry, helix elasticity and motions of the nanocrystal (Supplementary Data Notes S2–4 and Supplementary Table S1). The twenty measured distance distributions over-determine the nine parameters of the model (Figure 2A). XSI measurements were carried out under three salt conditions to establish the salt-dependence of the RNA helix and nanocrystal ensemble, allowing application of XSI-RNA over a range of solution conditions (see Supplementary Data Notes S2–4 for details).

The ability of model parameters obtained from subsets of the XSI data to predict the remaining XSI data (cross-validation) established the precision and accuracy of the XSI-RNA measurements and resulting model (Supplementary Figure S10). Further, it is unlikely that the Au nanocrystal labelling perturbed the RNA helix, because there is no change in circular dichroism spectra of the RNA helix upon introduction of the labels (Supplementary Figure S11; see also Supplementary Table S3). Interactions between the probes are also unlikely, because data at large Au–Au separations accurately predicted Au–Au distances with small Au–Au separations (Supplementary Figure S10). These results and conclusions mirror those previously obtained for DNA helices ((11) and Supplementary Data Note S5).

The RNA helix structural and elastic parameters generated from the XSI data agree well with literature models based on X-ray crystallography (23) and solution NMR data (26) (Supplementary Table S2). Additionally, we found a small but significant effect of Mg²⁺ on the helical conformation and elasticity (Supplementary Table S1).

TAR RNA conformational ensembles

Determining the TAR RNA ensemble by XSI-RNA

We next turned to the TAR RNA conformational ensemble. We used TAR RNA constructs with pairs of Au nanocrystals attached to the helices on either side of the TAR bulge. We measured eight pairs of Au–Au distance distributions for probes positioned across the TAR bulge (Figure 2B and C, see Figure 2B for the sequence). Simulations with synthetic data suggested that additional pairs do not significantly enhance the resolution of the ensemble (Supplementary Figure S9C). We carried out XSI measurements under two solution conditions, a low salt condition similar to the condition used in prior RDC studies (5) and a high salt condition (45 and 220 mM monovalent cation, respectively).

We obtained ensemble models from the XSI-RNA data using a pool of potential conformations as a basis set, analogous to how DNA ensembles were previously constructed (12). For TAR RNA, we first used a published MD trajectory (5) as the pool of basis set conformations, and we calculated the expected XSI for each basis set conformation using the RNA helix model established above (Materials and Methods). We then weighted the MD conformational pool directly against the experimental XSI data, using a previously developed EBS algorithm (12) (Materials and Methods). EBS enables the use of a conformational pool with a large number of basis set conformations (>10⁴), overcoming the limitation of ∼100 conformations typical for standard Bayesian algorithms (27).

The TAR ensemble model obtained accounts for the XSI data well, with average χ² values of 1.5 for both the low and high salt ensembles (Figure 2C, Supplementary Figures S12 and S14). By comparison, the original MD ensemble gave average χ² values of 13 and 5.5 for the low and high salt data set, respectively (Supplementary Figure S14). The quality of the ensemble was further tested by cross-validation, in which the measured XSI of an Au–Au pair was compared with the profile predicted for that pair from the ensemble generated using the remaining seven Au–Au pairs. Excellent agreement was achieved in each case, with average χ² values of 2.0 and 1.8 for the low and high salt data set, respectively (Supplementary Figure S14).

TAR RNA ensembles under two different solution salt conditions

The ensembles obtained for TAR RNA are depicted schematically in Figure 3B, with Figure 3A defining the six degrees of freedom needed to specify the position of one helix with respect to another: three angular degrees of freedom (Euler angles) and three translational degrees of freedom (Cartesian coordinates). The distribution of Euler angles and Cartesian coordinates that describe these ensembles are shown in Figure 3C and D and Supplementary Figures S15 and S16. Under low salt conditions, conformations with bends of about 60° (β) are favored, which mainly comes from an enrichment of a conformation (type X in Supplementary Figure S17B, 35%) that is rarely populated in the MD predicted ensemble (type X in Supplementary Figure S17A, <3%). XSI data resolve only the relative orientations of the two helices emanating from the bulge and not the bulge itself, but the MD conformational library allows generation of models for the bulge from the MD conformations that give the observed helix-helix orientations. For example, orientation type X can form with 3΄-most U of the 3 nt bulge flipped out of the helical stack (Supplementary Figure S17B and C, type X; see also (12)).

The major change in the ensemble at higher salt is an increase in the less bent conformations, i.e. those with bend angles (β) of less than 45° (Figure 3C). This seemingly counter-intuitive result could arise from an increase in conformations with two residues looped-out, which effectively reduces a 4-1 internal loop to a 2-1 internal loop and makes the junction less bent (Supplementary Figure S17A, type 7) (28). Overall, salt-induced changes in the populations within the different regions of the allowed space inversely correlated with TAR RNA phosphate–phosphate distances (Supplementary Figure S18), consistent with increased charge screening from the higher salt reducing phosphate–phosphate charge repulsion and preferentially stabilizing TAR conformations with smaller P–P distances. Earlier NMR RDC studies indicate that the TAR bulge further straightens in the presence of Mg²⁺ (29,30), which may result from diffusive and/or site-bound Mg²⁺.

Comparing RNA ensembles determined by XSI-RNA and NMR-RDC

The XSI ensemble of the TAR RNA in low salt is in close agreement with the ensemble previously derived from RDC measurements under similar conditions (5). This agreement provides strong and independent validation of both methods. Figure 4A shows that the overall distribution of helix orientation angles obtained from these methods follow similar distributions. Both distributions differ substantially from the initial MD-derived ensemble, with more bend, less positive twist and a different maximally occupied bend direction than that in the MD ensemble (Figure 4A and D). The underlying translational conformational distributions for the XSI and RDC ensembles are also quite similar (Supplementary Figure S19). More limited RDC measurements for TAR RNA with increasing concentrations of Na⁺ indicate a decrease in the average bend of TAR RNA (21), also in agreement with the XSI-RNA results herein (Figure 3C, middle), a decrease in the average bending angle of ∼8° by XSI-RNA compared to ∼12° from the limited RDC measurements (21).

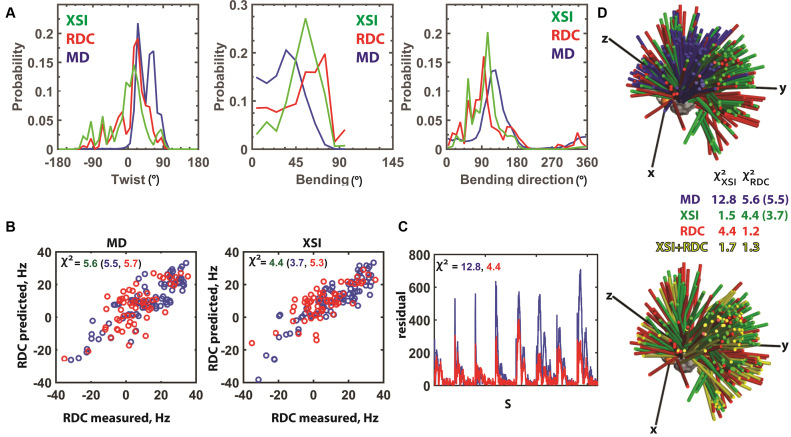
Figure 4.

Comparison of XSI- and RDC-derived TAR RNA ensembles. (A) XSI (green) and RDC (5) (red) TAR ensembles under similar low salt conditions (XSI: 10 mM sodium ascorbate and 30 mM Tris.HCl, pH 7.4 and 10 mM NaCl; RDC: 15 mM Na phosphate, pH 6.4, 25 mM NaCl, 0.1 mM EDTA) and the MD-derived ensemble (5) (blue) (See Supplementary Figure S19 for translational information). (B) Comparison of measured RDC values with RDC values predicted from the MD-derived ensemble (left) and from the XSI-derived ensemble (right). The χ² values were calculated as the average of (RDC_calculated – RDC_measured)²/ RDC_error² for RDC values of all residues (green), of the residues in the flanking helices (blue) and of the residues in the bulge region including the CUC bulge and the two base pairs 5΄ to the bulge (red). (C) Comparison of the residuals between the measured XSI and XSI predicted from the MD-derived ensemble (5) (blue) and XSI predicted from the RDC-derived ensemble (5) (red) for each of the eight Au–Au pairs (Figure 2B). The χ² values were calculated as the average of (XSI_calculated – XSI_measured)²/ XSI_error². (D) Three-dimensional representation of the TAR ensembles derived from MD (5) (blue), XSI (green), RDC (5), (red) and a combination of XSI and RDC (yellow). The colored sticks represent the position of the long axes of the top helix (see Figure 3A), and each stick represents 1% of the total population. The χ² values were determined as described in part B and C; RDC χ² values are for all residues and, in parenthesis, for the flanking helices.

To learn more about the information content of the XSI and RDC data, we compared the ability of ensembles derived from each method to predict the data observed in the other method (Figure 4B and C). As expected, the XSI ensemble predicts RDC data with smaller χ² value for the helix than for bulge residues, as bulge residues are not reported in XSI data (Figure 4B). The predictive ability of the XSI and RDC data was greater than that for the original MD-derived ensemble (Figure 4B and C). Results with synthetic data sets suggest similar accuracies in determining inter-helical ensembles from XSI and RDC data (Supplementary Data Note S6 and Supplementary Figure S20). Results with synthetic data sets also suggest that the information content of XSI data increase with the number of Au pairs measured, plateauing at or above six pairs (Supplementary Figure S9C).

Additional information from combining XSI-RNA and NMR-RDC

From a practical perspective, it may be helpful to combine XSI and RDC data, especially as they in principle contain complementary distance and orientation information (Supplementary Figure S21). Further, there may be different degeneracies in each data (31) that are broken when the two are combined, as an ensemble solution fit to the XSI and RDC data combined gave an ensemble that is similar to the parent ensembles but not simply representing the average of the parent ensembles (Figure 4D and Supplementary Figure S22A and B).

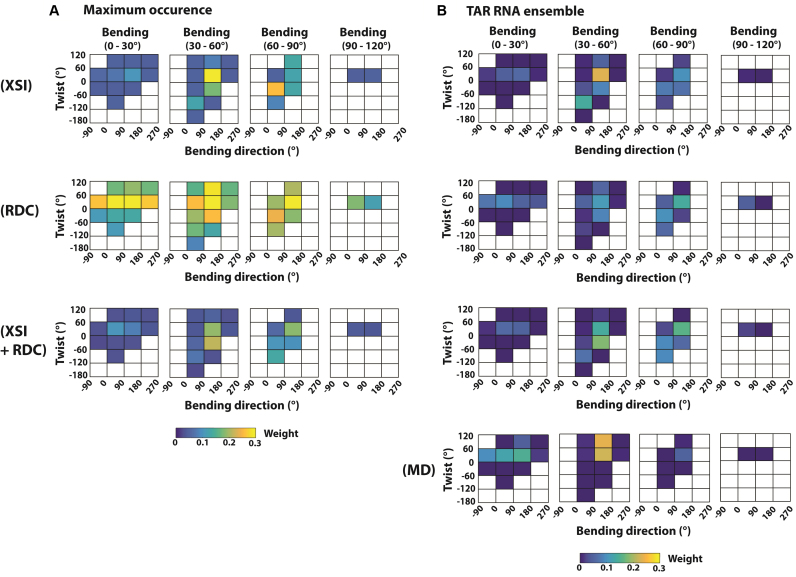
To better understand the potential benefit of combining XSI-RNA and NMR-RDC data, we carried out maximum occurrence analysis to test how effective XSI-RNA, NMR-RDC and their combination is in identifying conformational regions that are inconsistent with the data and accurately determine the population of the major population of the TAR RNA ensemble. The maximum occurrence of a conformational region is defined as the maximum weight of this conformational region among solutions that are consistent with the data, similar to the definition in (32). Here, we set the limit of being ‘consistent’ with XSI data as having a χ² of less than 2.0, the χ² value of cross-validation predictions (Supplementary Figure S14), which is about 0.5 larger than the unconstrained best-fit χ² of 1.5 (Supplementary Figure S14). Similarly, we set the limit of consistency with RDC data as having a χ² of less than 1.5, also about 0.5 larger than the unconstrained best-fit χ²; this Δχ² value is similar to what was used in the literature for maximum occurrence analysis of NMR-RDC of TAR RNA (32).

We found that XSI-RNA can identify 60% of the sampled conformational space as having a maximum occurrence of less than 5% (Figure 5A, top), and these regions also have a low population in the XSI-resolved TAR RNA ensemble, 8.5%, whereas they encompass 60% of conformational space (Figure 5B, top). NMR-RDC data are less effective in excluding conformational regions, as the 60% of the sampled conformational regions with the lowest maximum occurrence have an average maximum occurrence of more than 15% (Figure 5A, middle) and has a combined population of about 15% in RDC resolved TAR RNA. The effectiveness of XSI-RNA in excluding conformational regions likely comes from it measuring distributions, which are more effective in revealing low population regions than measurements of average values. Nevertheless, the low occurrence regions identified by XSI-RNA and NMR-RDC are 89% overlapping, suggesting strong agreement between the two techniques (Figure 5A, top and middle).

Figure 5.

Comparison of maximum occurrence of TAR-RNA conformations defined by data from XSI, RDC and a combination of XSI and RDC. (A) The maximum occurrence and (B) the derived TAR ensembles (Conditions: XSI: 10 mM sodium ascorbate and 30 mM Tris.HCl, pH 7.4 and 10 mM NaCl; RDC: 15 mM Na phosphate, pH 6.4, 25 mM NaCl, 0.1 mM EDTA). Maximum occurrence (part A) is defined as in text: the maximum weight of a conformational region (colored squares) with χ² < 2.0 for XSI (top row); χ² < 1.5 for RDC (middle row); and χ² < 2.0 for XSI and χ² < 1.5 for RDC (bottom row). As maximum occurrence is plotted, the sum can be larger than 1. Twist, bend and bend direction are as defined in Figure 3A and correspond to α + γ, β and γ, respectively, for Euler angle (α, β, γ) of the zyz convention (12). Conformational regions that do not contain any basis set conformations are not sampled and are shown as white.

Combining XSI and RDC data leads to an improvement over the XSI data alone, with 60% of the conformational space with the lowest maximum occurrence (Figure 5A bottom, <5% maximum occurrence) giving a combined population of about 4% in the resolved TAR RNA ensemble (Figure 5B, row three), smaller than 8.5% and 15% from the XSI and RDC data alone, respectively (Figure 5B, top and middle). Combining XSI and RDC data could also improve accuracy in the weight of the highly populated conformational regions. For example, combining XSI and RDC data can provide a more stringent upper limit for the population of high occurrence regions (e.g. Figure 5A, bending 30–60°, twist 0–120° and bending direction 90–180°). Whereas the TAR RNA ensemble determined by XSI and RDC are similar (Figures 4 and 5B), they cannot predict the other data set within the stringent limit set above of χ² = 2.0 (XSI) and 1.5 (RDC) (Figure 4D). By combining XSI and RDC data, we were able to identify a TAR RNA ensemble that is highly consistent both XSI (χ² = 1.7) and RDC (χ² = 1.3) data (Figures 4D, 5B and Supplementary Figure S22).

Effect of the basis set conformations on derived XSI-RNA ensemble

We investigated the impact of the pool of basis set conformations on the XSI-RNA derived ensemble that is obtained, as sampling too narrowly would exclude conformers that are part of the ensemble and sampling too broadly could introduce noise or error, depending on the robustness of the data and method. Above we used a pool of 10 000 MD generated basis conformations (5) that were previously used to generate TAR RNA ensemble by NMR RDC (5). Using the same conformational pool allows a more direct comparison of the two techniques by removing potential complications of having pool dependent differences. To test whether the choice of the basis set conformation actually has a significant impact on the XSI-RNA derived TAR ensemble, we generated a set of an additional 12 000 basis conformations by sampling the entire conformational space that is topologically allowed by the TAR bulge sequence. With the 12 000 additional conformations, the conformation pool is expanded to 22 000 conformations and covers a significantly broader range of inter-helical orientations than the initial pool of 10 000 MD conformations; e.g. the maximum inter-helical bending angle is extended to 163° from 92° (Supplementary Figure S23, black dotted versus red dotted).

We found that the XSI-RNA derived ensemble is largely unchanged when the new extended basis conformation set is used (Supplementary Figure S23, red solid versus black solid), suggesting that the original pool of 10 000 MD conformations adequately covers the range of conformations populated by TAR RNA in solution and that the XSI-RNA solution is not comprised by use of a larger conformational basis set.

We also explored the density of sampling, as too-sparse sampling can reduce the ensemble accuracy and distort its features. For our XSI data, we found the needed sampling density of the Euler space to be about one conformation per 5° or less (Supplementary Figure S24), i.e. requiring about one-third or more of the 10 000 MD conformations.

By simplifying the ensemble of TAR RNA using a small number of parameters, e.g. Euler angles, we were able to obtain a consistent TAR RNA ensemble of inter-helical orientations using XSI and conformation pools generated with or without the constraints of MD (Supplementary Figure S23). While XSI provides no information about the conformation of the non-helical region, information from a pool of MD structures can be used to extract bulge conformations consistent with the observed Euler angles and these models can be further tested experimentally (e.g. (12) and Supplementary Figure S17).

DISCUSSION

We have devised an XSI method, established its self-consistency (Figure 2A, Supplementary Figure S5, S10 and S14) and validated its ability to obtain RNA ensembles (5). XSI-RNA provides ensembles that are similar to and of similar quality to the established NMR RDC method. These approaches provide independent validation of one another, an important accomplishment given the rarity of ensemble methods and their high complexity. RDC measurements provide atomic-level information about each residue, including the bulge residues that are only indirectly probed by XSI, but require high-resolution NMR measurements; XSI measurements require synchrotron radiation. XSI-RNA and NMR-RDC can be combined to improve the quality of the RNA ensemble.

Macromolecules exist as ensembles, and exploration of sub-ensembles is key to folding and function. With a defined structural relationship between RNA helices and Au nanocrystal positions, application of XSI-RNA to additional RNA systems is straightforward (14). XSI-RNA can readily be applied to RNA/protein complexes (14), and can be a valuable tool for measuring the structure and flexibility of RNA nanostructures. The future development of larger monodisperse Au nanocrystals could extend the application of XSI to megadalton macromolecular assemblies (14,20).

We thus expect the XSI-RNA method to be widely applied to RNA and RNA/protein systems, helping to overcome limitations of averaging from traditional structural solution methods and revealing the conformational ensembles and the rigidity and deformability of macromolecules and macromolecular complexes.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

National Institutes of Health [PO1 GM066275 to D.H., DP-OD000429-01 to P.H.]. Funding for open access charge: National Institutes of Health [PO1 GM066275 to D.H., DP-OD000429-01 to P.H.].

Conflict of interest statement. None declared.