Evaluation of Numerical Techniques for Solving the Current Injection Problem in Biological Tissues

Abstract

Accurate computational modeling of electric fields in the human head has become important in clinical research to study or influence brain functionality. While existing numerical approaches have been evaluated against simple geometries with known closed form solutions, the relationship between these approaches in more complex geometries has not been studied. Here, we compare the three most commonly used approaches for bioelectric modeling: the finite element method (FEM), the finite difference method (FDM), and the boundary element method (BEM). Using both isotropic and anisotropic conductivity distributions, we construct and compare bioelectric models for a realistic head geometry. Our results suggest that both FEM and FDM are capable of accurately model voltages in the brain, while computations from BEM result in significantly larger errors, due to the increased simplicity and implicit model assumptions.

1. Introduction

Accurate bioelectric modeling of head tissue is a crucial component of modern diagnostic and therapeutic tools based on the measurement and control of electric fields in the human brain. Non-invasive electrode measurements of scalp voltages with electroencephalography (EEG) are commonly used to study brain activity and reconstruct cortical current sources [1] originating from epileptic brain activity or other neurological diseases [2]. Conversely, scalp electrodes can also be employed to inject low-amplitude currents that modify voltage fields in the human head and modulate brain functionality (transcranial current stimulation (TCS), e.g., [3, 4]). In particular, accurate solution of the current injection problem [5, 6, 4, 7] is crucial for both clinical pre-surgical planning [2], and therapeutic applications [8]. Current injection directly models TCS and also provides the basis for efficient reciprocity-based computation of EEG forward solutions [9].

Volume conduction modeling under quasi-static assumptions requires the solution of Poisson's equation on a geometric representation of the human head. Early head conductor models used concentric spheres to represent different electrically homogeneous tissue types (e.g., scalp, skull, and brain; [10]) and offers closed form solutions that are analytically computable. However, spherical models provide only a rough geometric approximation, and cannot incorporate the spatially varying, potentially anisotropic conductivities that are present in the head. Capturing the complex features of arbitrary head tissues and conductivities [2, 5, 11] requires discretized tissue geometries that combine spatial locations (nodes) and their connections (elements) to form meshes. These meshes can describe regular grids, or be algorithmically generated to adapt to geometric and conductivity requirements [2]. Unlike spherical models, closed form solutions do not exist in these geometries, necessitating the use of numeric solution methods. We focus here on three commonly used numerical approaches for realistic head modeling: the finite element method (FEM), the finite difference method (FDM), and the boundary element method (BEM).

Of those three approaches, the finite element method (FEM) is the mostly adaptable numerical method that can efficiently capture arbitrary geometries and conductivity distributions. The volume is typically subdivided into non-overlapping tetrahedral or hexahedral elements with solved voltage potentials interpolated within each element. This allows smooth tissue boundaries to be modeled, and adaptive meshing to reduce node density within large homogeneous regions, thereby reducing overall computational requirements.

By contrast, the finite difference method (FDM) is more easily implemented, but more computationally expensive when modeling complex head geometries. The computational mesh must be structured as a regular grid in order to construct valid difference equations at all points. Thus doubling spatial resolution in all directions produces an 8-fold increase in the number of computational nodes, regardless of tissue homogeneity. Additionally, restricting the computational geometry to a grid means boundary layers between tissue types will take on a stair-step appearance that may not accurately represent realistic tissue boundaries.

In contrast to FDM/FEM, the boundary element method (BEM) solves Poisson's equation using triangulated surfaces describing the interface layers of head tissues and assumes homogeneous conductivity distributions within [12]. A system matrix is generated to describe the relationship between voltage potentials and normal current vectors on these surfaces. Arbitrary source and sensor locations can be modeled with appropriately generated interpolation matrices mapping sources and sensors to the points associated with this head matrix.

Each of these numerical methods have strengths and weaknesses with regard to the complexity of implementation, the accuracy of the resulting solutions, and the amount of computation required to obtain them. While these numerical techniques have all been demonstrated to be accurate with respect to a spherical shell model [13, 14, 15], to our knowledge they have not been compared to one another in the context of modeling more complex head geometries. An understanding of how these methods differ from one another is important in practical applications regarding accuracy and computational complexity.

In this study, we construct a patient-specific head segmentation including hard and soft skull bone, gray and white matter, cerebrospinal fluid (CSF) and scalp tissue, and compare the relative numerical accuracy of FEM, FDM, and BEM approaches to one another. Using metrics of differences in topography and magnitude, we evaluate the relative performance of each technique, with and without anisotropic conductivities when supported by the approach. Our results suggest that the FEM and FDM techniques produce highly similar answers within the brain, while the BEM, which cannot incorporate tissue anisotropies or complex tissue geometries, produces significantly higher relative errors.

2. Methods

2.1. Data Collection and Initial Processing

T1, T2, and diffusion weighted MRI scans were obtained from a 14 year old control subject using a Siemens Magnetom 3T scanner. The imaging protocol included 3d MPRAGE T1 (1 mm isotropic resolution, 176 × 220 × 220 voxels) and T2TSE (1 mm resolution) structural scans. A 45 direction CUSP scan (2 mm isotropic resolution) was used to collect diffusion data, with tensors estimated using robust least squares. All images were coregistered to a common reference frame, and resampled to the 1 mm resolution of the T1 scan.

A seven tissue segmentation of the head was generated using a combination of automated methods and manual segmentation. A multi-atlas statistical segmentation approach was used to identify the intracranial cavity, and the grey matter, white matter, and cerebrospinal fluid regions therein [16]. Scalp tissue was segmented using a threshold approach followed by manual adjustments for MRI measurement noise and goggles/headphones. The skull was similarly extracted using thresholding, image processing operations (e.g., dilate, erode, etc.), and manual adjustments. Soft skull bone and sinus cavities were identified by thresholding within the skull compartment.

Conductivities for each tissue type in the segmentation were assigned using values established in the literature [4]. Scalp tissue was assigned a isotropic conductivity of 0.43 S/m, hard bone to 0.064 S/m, soft bone to 0.0268 S/m, and sinuses to 1e-6 S/m. Within the intracranial cavity, cerebrospinal fluid was assigned a conductivity of 1.79 S/m, gray matter to 0.33 S/m, and white matter to 0.142 S/m for the isotropic model. To incorporate anisotropic conductivities within the white matter region, diffusion MRI was used to compute individual anisotropic conductivity tensors within each voxel [17]. In conjunction with the head segmentation described above, two separate three dimensional distributions of tissue conductivity are available: one with isotropic conductivities in all tissues, and one with anisotropic conductivities only for white matter tissue.

2.2. Numerical Modeling Approaches

Finite Element Method (FEM)

Based on the head tissue segmentation, each voxel that belongs to a head tissue was subdivided into 5 tetrahedral elements. The final tetrahedral mesh contained 18.8×10⁶/3.7×10⁶ elements/nodes. The mesh was used in two variants, FEM_i and FEM_a, whereas isotropic and (an)isotropic conductivity tensors where assigned to tetrahedral mesh elements respectively.

Finite Difference Method (FDM)

We constructed finite difference models from the isotropic and anisotropic conductivity images using an approach that employs transition layers to permit arbitrary anisotropic conductivities within each individual voxel [18]. This approach places computational nodes at the corners of each volume element, and was constructed at the full 1 mm isotropic resolution of the structural MRI, resulting in a hexahedral mesh with 3.7 × 10⁶/3.8 × 10⁶ elements/nodes respectively. Similar to FEM, for the final FDM mesh, two versions were generated (FDM_i and FDM_a).

Boundary Element Method (BEM)

The boundary element method was implemented using the software tools available from the OpenMEEG project (http://openmeeg.github.io). The model was constructed by identifying three surfaces [19], located at the interfaces between scalp and air, skull and scalp, and intracranial cavity and skull. Tissues conductivities were assigned as 0.43 S/m for the scalp domain, 0.01 S/m for the skull domain, and 0.33 S/m within the brain. The symmetric BEM matrix was constructed, as well as the matrices necessary to appropriately map internal voltages on a 1mm grid and scalp injection currents at electrode locations to the BEM surfaces.

2.3. FDM/FEM/BEM - Forward problem

Despite methodological differences, each of these techniques requires solution of a linear system of equations to obtain interior voltage distributions as A · x = b, with A being the forward problem matrix, x denoting a vector of voltage potentials at each computational node, and b representing the current intensities injected on the scalp surface. Solutions to the resulting linear inverse problems were computed using SCIRun [20] with the MINRES algorithm (Jacobi preconditioning), and allowed to converge to a relative error of 10⁻⁹. Solutions were obtained for each of 72 electrode locations corresponding to the standard 10-10 electrode configuration, with electrode Cz used as the common reference.

3. Results

A total of five head models were constructed for comparison: four modeling (an)isotropic conductivity distributions for finite element and difference method (FEM_i, FEM_a, FDM_i, FDM_a) as well as a BEM model featuring 3 layers of isotropic conductivities. The current injection problem was solved for each electrode in a standard 10-10 array (72 times), using Cz as the fixed reference electrode. A map of nodal voltages was computed for each model and current injection electrode pair. The relative changes in voltage distribution between models were evaluated using the relative difference metric (RDM), which measures changes in voltage topography, and the magnitude difference (MAG), which measures changes in overall signal magnitude ([21]). For each spatial location, these metrics were computed across all electrode pairs to describe overall modelling accuracy at that spatial location.

Figure 1 summarizes the differences for each possible pairing of numerical models using histograms of RDM and MAG. For a better visual assessment, the (min,max) range of voltage values (x-axis) in FEM/FDM have been depicted to be identical in contrast to higher errors achieved with BEM. The lowest errors are seen when comparing the isotropic and anisotropic versions of the FEM and FDM methods. For all comparisons, the BEM model shows significantly higher RDM and MAG errors than the other models, which reflects the increased simplicity necessary to generate a boundary based approach. The BEM model lacks the highly conductive CSF region, and additionally does not differentiate between hard bone, soft bone, and sinus regions. Even provided a high resolution segmentation, identification of sufficiently accurate non-intersecting boundary models for each of these regions is highly challenging, and three surface models are the most commonly employed BEM configuration.

Fig. 1.

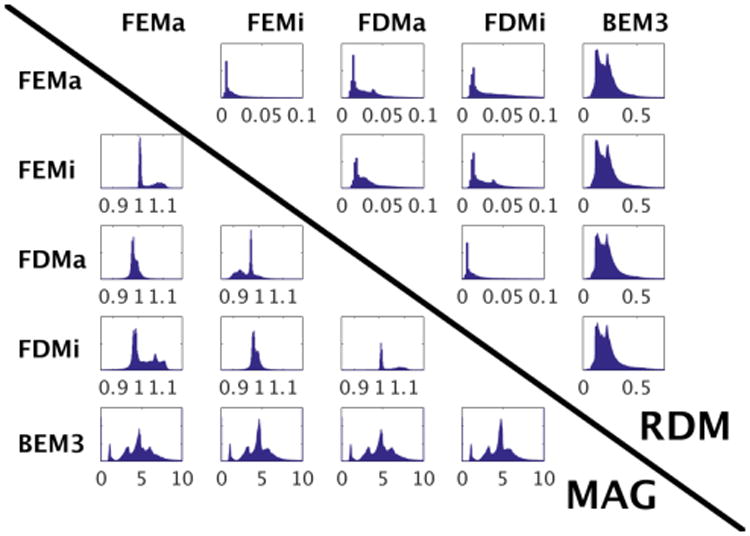
Histogram plots of RDM and MAG error across the entire head. RDM plots are in the upper triangle, MAG plots in the lower.

The spatial distribution of the RDM is displayed in Figure 2. For the FEM_i, FDM_a, FDM_i, and BEM models, voltages were compared to the FEM_a model in terms of RDM. These images demonstrate several common features seen in the computed relative differences. First, using isotropic conductivities, both the FEM and FDM methods produce increased RDM throughout the brain, in particular for deeply located points near the brain stem. The BEM model shows a similar spatial pattern, however, as seen in the histograms above, these differences are on average much higher than those seen between the FEM and FDM models. Peak differences for the two FDM models are seen within the scalp region, immediately adjacent to electrode locations, however these do not translate to local peaks within brain tissue due to volume conduction effects of skull/CSF (as visualized in [4]).

Fig. 2.

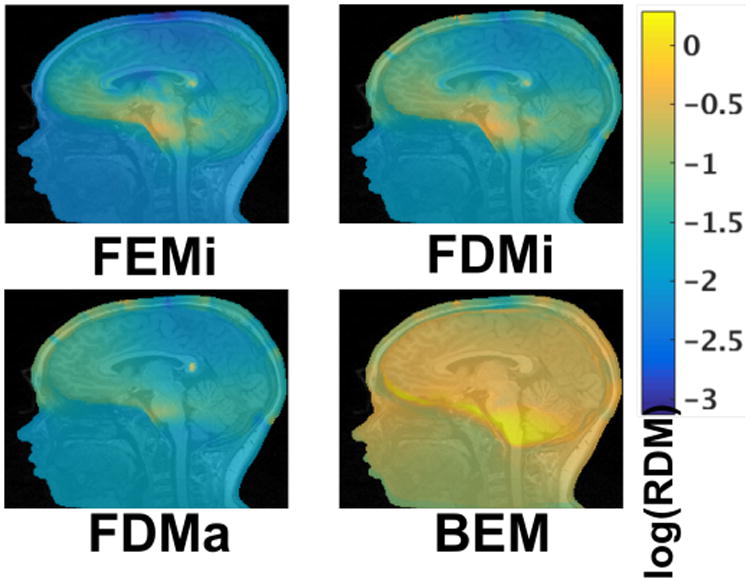
Relative topographic differences (RDM) as compared to the FEM_a model.

Of additional note are the errors seen across all models in the corpus callosum. The white matter is highly anisotropic in this region, producing spatial inhomogeneity in the conductivity. The errors are, however, also localized to the corpus callosum, and unlikely to significantly impact simulated EEG or TCS voltage potentials.

A corresponding set of slices depicting computed MAG values are presented in Figure 3. With both the FEM and FDM approaches, the models using anisotropic conductivity can be seen to exhibit smooth and spatially similar magnitude differences across the cortex. These values are greatest for deep locations near the brainstem. Both isotropic and anisotropic finite difference models show additional magnitude differences within the scalp tissue. These values correspond spatially to those seen in the RDM images, and result from the FDM computing significantly higher voltages at the computational nodes immediately adjacent to current injection points. These results suggest that, assuming FEM to be the more accurate approach, the FDM model may not be well suited to computational scenarios where sensitivities/voltages need to be accurately computed near electrode locations. Finally, similar to RDM, the BEM model shows significantly higher relative magnitude differences than the FEM and FDM models, with the largest errors located primarily within the skull and brain stem.

Fig. 3.

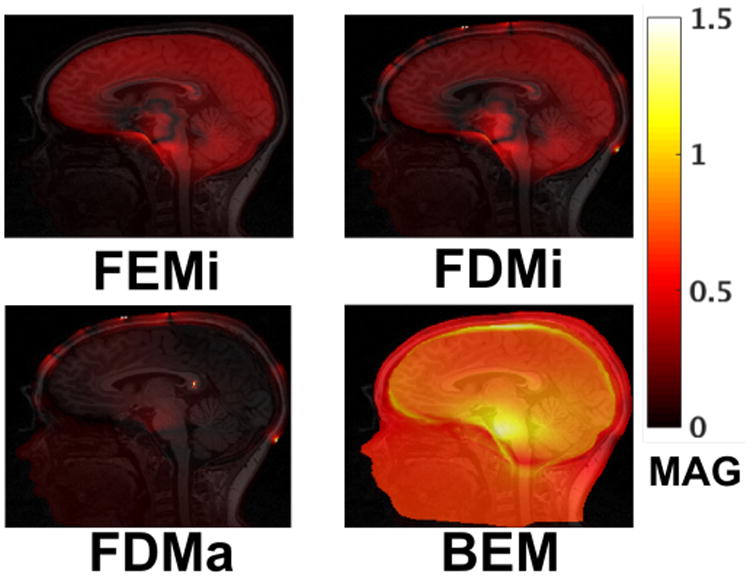
Relative MAG as compared to the FEM_a model. Displayed MAG values were recomputed as exp(abs(log(MAG))) ∈ [1, inf] to better visualize relative changes.

4. Conclusions

We have presented a comparison of three numerical approaches to modeling bioelectric propagation in a complex head model by evaluating maps of voltage potential computed for the current injection problem. Both the finite element and finite difference approaches produce voltage distributions which are highly similar, while the boundary element approach shows consistent differences in voltage intensities and produces larger topographic errors than the other methods. While careful construction of additional tissue boundary meshes may improve BEM accuracy, this is a difficult problem that complicates widespread routine use. The FEM and FDM, by contrast, can easily be constructed on a computational grid that matches available structural imaging, making implementation of these methods relatively straightforward. With the increasing availability of high quality MRI imaging and associated high resolution image segmentations, patient-specific bioelectric models incorporating this additional knowledge should become the standard for both research and clinical use.