Optimizing Stimulus Patterns for Dense Array tDCS With Fewer Sources Than Electrodes Using A branch and Bound Algorithm

Abstract

Dense array transcranial direct current stimulation (tDCS) has become of increasing interest as a noninvasive modality to modulate brain function. To target a particular brain region of interest (ROI), using a dense electrode array placed on the scalp, the current injection pattern can be appropriately optimized. Previous optimization methods have assumed availability of individually controlled current sources for each non-reference electrode. This may be costly and impractical in a clinical setting. However, using fewer current sources than electrodes results in a non-convex combinatorial optimization problem. In this paper, we present a novel use of the branch and bound (BB) algorithm to find sub-optimal stimulus patterns with fewer current sources than electrodes. We present simulation results for both focal and spatially extended cortical ROIs. Our results suggest that only a few (2-3) independently controlled current sources can achieve comparable results to a full set (125 sources) to a tolerance of 5%. BB is computationally 3-5 orders of magnitude less demanding than exhaustive search.

1. Introduction

tDCS uses two or more electrodes to apply electrical currents to the scalp in order to modulate brain function [1]. tDCS has shown promising results in supporting treatments of many brain conditions such as stroke, depression, epilepsy, Parkinson's disease, and Alzheimer's disease [2]. It has been shown that using dense 64 to 256 electrode arrays instead of conventional two patch electrodes yields more focal modulation at target brain ROIs [3, 4]. Several approaches have been studied to optimize stimulus patterns of such arrays [3, 4, 5, 6]. The stimulus patterns found by these approaches, however, assume availability of individually controlled current sources for each electrode, which may be impractical in many settings. Various tDCS systems to date still use only a few current sources to apply electrical currents and thus connecting optimally the electrodes to available current sources for such systems is critical. To the best of our knowledge, there is no optimization study that also imposes constraints on the total number of current sources used in the optimized stimulus patterns.

In this work, we describe an optimization algorithm that finds the sub-optimal stimulus pattern for any complex experimental dense array tDCS scenario using a preset number of current sources. Specifically, given a fixed number of available current sources n and an optimized current pattern for a full set of current sources, we find a sub-optimal stimulus pattern that approximates the optimal pattern and uses at most n sources, while respecting all safety constraints of the original optimization. Each current source is assumed to be capable of sharing its current across any desired number of electrodes. Based on this approach, we devise a BB enumeration tree to efficiently choose the appropriate connections and currents for the available sources. As the enumeration tree grows exponentially in both the number of electrodes and the number of available current sources, we adapted our algorithm to use heuristics such as relative weights of the electrodes in the objective function and optimal stimulus pattern to reduce the computation time.

Simulation studies on a realistic head model with one local and one broadly distributed ROI show that only a few current sources (2-3) may be sufficient to modulate even complex ROIs. Moreover, BB algorithm provides a global solution for the number of current sources considered by evaluating the entire search space of configurations using at most that many current sources.

2. Methods

We first present the optimization problem and our adaptation of the BB algorithm to solve this problem. We then give a high level description of the head model and the two anatomical ROIs used in the simulation studies.

2.1. Original Optimization Problem

As described in our previous study [6], our goal is to maximize the current density along a predefined desired directional field inside the ROI:

$$\underset{\mathrm{I}}{max}{\int }_{{\mathrm{\Omega }}_{\mathit{\text{ROI}}}}\mathbf{J}(\mathbf{r})\cdot \mathbf{d}(\mathrm{r})\mathbf{\text{dr}}$$ (1)

where Ω_ROI represents the ROI, and J(r) and d(r) the induced current density and desired directional field at location r, respectively. I denotes the array of non-reference electrode currents.

In order to ensure subject safety and enforce focality of modulation, we impose three safety constraints on the current power in the brain outside the ROI, on the total injected current, and on individual electrode currents, as shown in (2a), (2b), and (2c), respectively:

$${\int }_{{\mathrm{\Omega }}_{\mathit{\text{brain}}}-{\mathrm{\Omega }}_{\mathit{\text{ROI}}}}{\Vert \mathbf{J}(\mathbf{r})\Vert }_2^2\mathrm{d}\mathbf{r}\le p_{\mathit{\text{max}}})$$ (2a)

$${\Vert \stackrel{\sim }{\mathbf{I}}\Vert }_1\le 2{\iota }_{\mathit{\text{max}}}$$ (2b)

$${\stackrel{\sim }{\mathbf{I}}}_{\mathit{\text{min}}}\le \stackrel{\sim }{\mathbf{I}}\le {\stackrel{\sim }{\mathbf{I}}}_{\mathit{\text{max}}}$$ (2c)

where Ω_brain represents the entire brain, $\stackrel{\sim }{\mathbf{I}}=\left[\begin{array}{c}\mathbf{I}\\ I_{\mathit{\text{ref}}}\end{array}\right]$ denotes the extended electrode current array with reference electrode current included, and ‘‖ ‖₁’ is 1-norm. The variables p_max, ι_max, Ĩ_min, and Ĩ_max represent the constraint bounds.

The optimization problem defined by objective (1) and constraints (2) is convex and thus has a global and unique solution. It can be solved extremely efficiently based on a finite element (FE) discretization with linear basis functions because the objective function (1) and the constraint (2a) become linear and quadratic functions of electrode current array I, respectively [6]. However, when fewer current sources than electrodes are to be used, the problem becomes combinatorial. Thus, we employed a BB algorithm to find sub-optimal solutions with a limited number of current sources.

2.2. BB algorithm to find sub-optimal patterns

We adapted the BB algorithm to find sub-optimal stimulus patterns using at most n current sources. All possible electrode configurations using at most n current sources, after initially truncating the electrode solution space, are split into smaller configuration subsets until they are all evaluated. In other words, we optimize stimulus patterns repeatedly for different electrode configurations with at most n current sources until we exhaust all possible such configurations. The algorithmic description to find the optimal solution with at most n current sources is:

1. Solve the general optimization problem without constraining the total number of current sources. This provides the optimal current injection pattern we need to approximate with fewer current sources.

2. Threshold the current injection intensity values of the solution from the previous step to reduce the number of electrodes over which the BB algorithm is employed. For example, in our work, electrodes with current intensity below 0.01 μA are excluded from the search space.

3. Assign an initial value for the objective function. This value could be i) minus infinity (-∞) if there is no heuristics about the solution, ii) a designated percentage of the optimal value found in the first step if a solution within a tolerance bound is desired, iii) a previously determined feasible value.

4. Decide in which order the electrodes are used in branching a particular configuration into smaller subsets of configurations. Ordering could be done based on i) general unconstrained solution, ii) relative electrode weights in the objective function, or iii) contributions of each electrode to the objective function in the optimal solution.

5. Exhaust all possible configurations in a hierarchical manner via BB algorithm as shown in Algorithm 1.

2.3. Simulations

A realistic head model with 8 million nodes, 47 million elements, and an electrode array of size 126 was used in our simulations [8]. The head model is shown in Fig. 1.

Fig. 1.

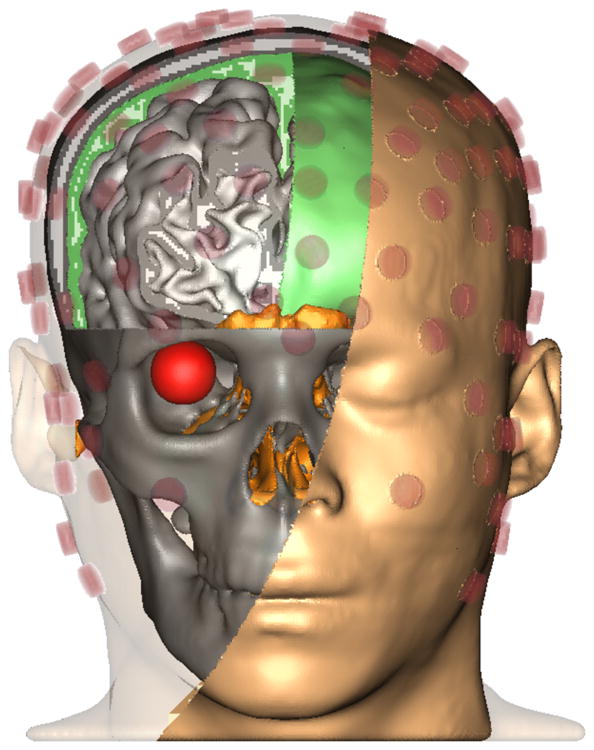
Head model used in the simulations. 8 modeled tissue types were scalp, skull, cerebrospinal fluid, grey matter, white matter, eye, internal air, and electrode sponge.

Both a focal and a spatially extended ROI, shown in Fig. 2, were defined to investigate the effect of ROI complexity on the number of current sources required. The desired directional field for both ROIs was based on the local cortical surface normal. The total injected current bound was set to 1 mA, individual electrode current bounds to 0.15 mA and the current power in the brain outside the ROI to 10^−6.5 A²/m. We found sub-optimal stimulus patterns with 3 and 2 current sources for both ROIs and compared them to the optimal solution with the full set of current sources.

Fig. 2.

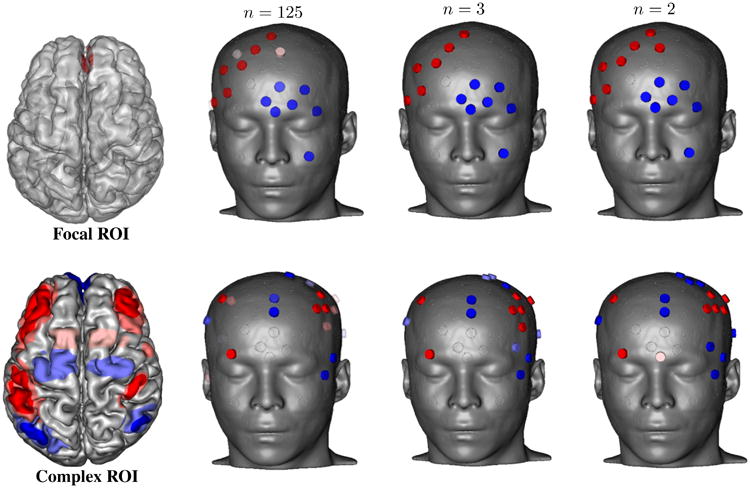
Optimized stimulus patterns with 125, 3, and 2 current sources, along with the anatomical ROIs. Top row shows the results for the focal medial orbitofrontal cortex ROI and bottom row shows the results for the spatially extended cortical ROI based on the cortical correlation mapping in [4].

Algorithm 1: An adaptation of the BB algorithm for dense array tDCS problem. Both the algorithm and the notation given in Table 1 were based on the general BB algorithm in [7].

Table 1.

Notation for Algorithm 1.

ẑ	Objective function value of the current solution
ℒ	The list of all active branches
t	The number of branches generated so far
ℱ0	The set of all possible configurations
r	The index of configuration chosen for branching
p(r)	The number of branches generated from ℱr
xi	The optimal stimulus pattern on relaxed set ℛi
zi	Upper bound on the objective function on ℱi
ℒ + ℱi	The operation of adding ℱi to the list ℒ
ℒ – ℱi	The operation of deleting ℱi from the list ℒ

	Data: Head model, ROI definition, desired directional field, n
	Result: Optimal stimulus pattern with at most n current sources
1	ẑ ← z0 // Initialize objective
2	ℒ ← {ℱ0} //Active set
3	t ← 0
4	while ℒ ≠ ø do
5	determination of r // Next branch
6	ℒ ← ℒ – ℱr
7	determination of p(r)
8	determination of branching
	ℱr ⊂ ℛ1 ⋃ ℛ2 … ℛp(r)
9	for i ← 1 to p(r) do
10	ℱt+i ← ℱr ⋂ ℛi
11	calculation of (xt+i, zt+i)
12	if zt+i > ẑ then
13	if xt+i ∈ ℱ then
14	ẑ ← zt+i
15	else
16	ℒ ← ℓ + ℱt+i
17	t ← t + p(r)

3. Results

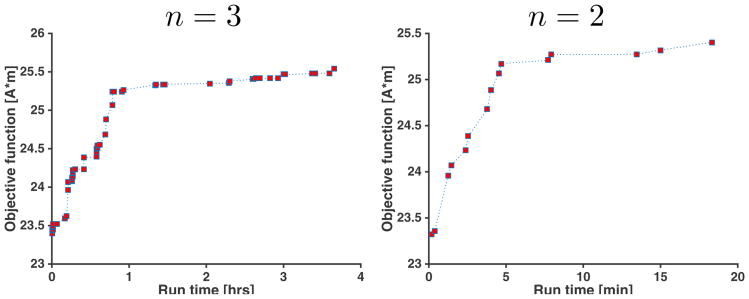
Figure 2 shows the optimized stimulus patterns with different numbers of available current sources for both ROIs. The reduction in the objective function due to using 3 and 2 current sources were 0.7% and 1.2% for the focal target, and 1.6% and 3.8% for the complex target, respectively. This suggests that targeting complex ROIs may require more current sources than localized ROIs to achieve the same percentage of the optimal result.

Objective function updates for the focal ROI as the BB algorithm progresses through the enumeration tree is shown in Fig. 3. The run times of the algorithm on a standard modern desktop were 4 hours and 20 minutes, for n = 3 and n = 2, respectively.

Fig. 3.

Objective function improvement as the BB algorithm progresses for 3 and 2 current sources. Run time increases considerably as we increase the number of available current sources.

4. Discussion

In this study, we approximated fully optimized stimulus patterns with fewer current sources using a branch and bound algorithm. Results indicate that using only a few current sources may be sufficient to induce electrical currents comparable to that of fully optimized stimulus patterns.

The electrodes that are connected to the same current source have the same electrical potential with respect to a common reference. Using this simple fact, we defined the optimization problem such that ‘active’ electrodes have at most n unique potential values. Note, as would be true in practice, the current delivered from a single current source will almost surely not be uniformly distributed across the electrodes connected to it, but rather will depend on where they are connected to the head volume conductor. We impose equality constraints on the potentials of these electrodes, not on their current intensities. Even fully optimized stimulus patterns are typically quite sparse, which let us to exclude many electrodes from the BB search space with minimal cost on the objective function. The decrease in objective function due to this exclusion was on average about 0.01%, which we contend is insignificant in terms of the directional current density in the ROI. One use of our algorithm that may be of particular interest is to determine the number of electrodes needed for adequate stimulation while all remaining electrodes are used for EEG measurements.