Modeling Responses in the Superior Paraolivary Nucleus: Implications for Forward Masking in the Inferior Colliculus

Abstract

A phenomenological model of the responses of neurons in the superior paraolivary nucleus (SPON) of the rodent is presented in this study. Pure tones at the characteristic frequency (CF) and broadband noise stimuli evoke offset-type responses in these neurons. SPON neurons also phase-lock to the envelope of sinusoidally amplitude-modulated (SAM) stimuli for a range of modulation frequencies. Model SPON neuron received inhibitory input that was relayed by the ipsilateral medial nucleus of the trapezoid body from the contralateral model ventral cochlear nucleus neuron. The SPON model response was simulated by detecting the slope of its inhibitory postsynaptic potential. Responses of the proposed model to pure tones at CF and broadband noise were offset-type independent of the duration of the input stimulus. SPON model responses were also synchronized to the envelope of SAM stimuli with precise timing for a range of modulation frequencies. Modulation transfer functions (MTFs) obtained from the model response to SAM stimuli resemble the physiological MTFs. The output of the proposed SPON model provides an input for models of physiological responses at higher levels of the ascending auditory pathway and can also be utilized to infer possible mechanisms underlying gap detection and duration encoding as well as forward masking at the level of the auditory midbrain.

INTRODUCTION

Acoustic information is detected and analyzed by different types of neurons along the auditory pathway. Auditory brainstem neurons are endowed with distinct biophysical characteristics resulting in a range of firing patterns. Neurons of the cochlear nucleus (CN), the first level of the brainstem, can receive convergent information from multiple auditory nerve (AN) fibers as well as from collaterals and descending inputs (both excitatory and inhibitory) (Schofield and Cant 1996; Ryugo and Parks 2003). The superior olivary complex (SOC), the second level of the auditory brainstem, is considered to be the first major stage of binaural processing in the auditory pathway (Harrison and Feldman 1969; Cant and Casseday 1986). The SOC consists of different cell types in the medial superior olive (MSO), the lateral superior olive (LSO), and the medial nucleus of the trapezoid body (MNTB), which have been demonstrated to play a significant role in sound localization (Yin 2002). The superior paraolivary nucleus (SPON) neuron is another cell type within the SOC; however, its role in encoding acoustic information has been less investigated in physiological studies.

SPON neurons are mainly excited by octopus cells, located in the contralateral posteroventral cochlear nucleus (PVCN), which are characterized by onset responses to pure tones (Godfrey et al. 1975; Rhode and Smith 1986; Friauf and Ostwald 1988; Thompson and Thompson 1991; Rhode and Greenberg 1992; Schofield 1995; Kulesza et al. 2003; Bal and Oertel 2007). Multipolar/stellate neurons of the CN also provide excitatory input to the SPON neurons (Schofield 1995); however, because multipolar/stellate cells have heterogeneous characteristics and some are inhibitory (Schofield and Cant 1996; Doucet and Ryugo 2006; Needham and Paolini 2006), octopus cells are considered the most probable source of excitation to SPON neurons. Nonetheless, SPON response properties are dominated by inhibitory postsynaptic potentials (IPSPs) rather than excitatory postsynaptic potentials (EPSPs) (Kulesza et al. 2007; Kopp-Scheinpflug et al. 2011). SPON neurons receive a strong glycine-mediated inhibitory input from ipsilateral MNTB (Moore and Caspary 1983; Helfert et al. 1989; Bledsoe et al. 1990; Banks and Smith 1992; Sommer et al. 1993; Schofield 1994; Smith et al. 1998; Carney et al. 2015) and also receive a GABAergic inhibition, at least in part, from axonal collaterals of SPON neurons (Kulesza and Berrebi 2000). MNTB neurons receive excitatory innervation from globular bushy cells (GBCs) located in the contralateral CN and have response properties similar to those of their excitatory inputs (Banks and Smith 1992; Smith et al. 1998). SPON neurons project GABAergic inhibitory input to the ipsilateral inferior colliculus (IC) (Kelly et al. 1998; Kulesza and Berrebi 2000; Saldaña and Berrebi 2000; Kulesza et al. 2003; Saldaña et al. 2009). This inhibitory innervation originating from SPON neurons has been proposed as a mechanism to explain behavioral forward masking as well as sound duration tuning at the level of the IC (Kulesza et al. 2003; Nelson et al. 2009; Kopp-Scheinpflug et al. 2011).

Physiological response properties of SPON neurons to pure tones at characteristic frequency (CF), broadband noise (BBN), and sinusoidally amplitude-modulated (SAM) tones have been investigated in experimental studies. Almost 87 % of SPON neurons respond to contralateral stimuli and produce an equivalent number of spikes in response to binaural stimuli (Kulesza et al. 2003). SPON neurons show offset responses to pure tones at CF as well as to BBN stimuli and synchronize to the envelopes of SAM stimuli (Behrend et al. 2002; Dehmel et al. 2002; Kulesza et al. 2003; Kadner et al. 2006; Kulesza et al. 2007; Kadner and Berrebi 2008; Felix et al. 2011). SPON neurons also had almost zero spontaneous activity in these physiological studies.

It is noteworthy that SPON neurons had offset responses for stimulus durations ranging from 20 to 500 ms. As a result, a late-arriving excitatory input cannot be the cause of offset activity of SPON neurons. However, a postinhibitory rebound (PIR) mechanism has been suggested as a possible source of generating offset spikes (Kulesza et al. 2003; Kulesza et al. 2007; Kadner and Berrebi 2008; Felix et al. 2011). SPON offset response could play a vital role in encoding sound duration as well as the intensity of the stimulus through the change in magnitude (rate) and first spike latency over a wide range of sound pressure levels (SPLs) (Kadner et al. 2006).

The majority of SPON neurons phase-lock to the envelopes of SAM stimuli for modulation frequencies (MFs) up to almost 100 Hz (Kulesza et al. 2003; Kadner and Berrebi 2008; Felix et al. 2011), with a decline in envelope phase locking at higher MFs. The reduction of SPON discharge rate as a function of MF is stronger than the decrement in vector strength. In addition to the phase-locked discharges during the SAM stimuli, poststimulus-time histograms (PSTHs) of SPON responses contain an offset component (at the termination of the stimulus) for all MFs tested. The response characteristics of the SPON neurons, including offset-type responses to the pure-tone/BBN stimuli and phase-locked response to SAM tones, make them discontinuity detectors that are sensitive to episodes of low stimulus energy such as gaps between tones and troughs of the low-MF SAM tone (Kadner and Berrebi 2008; Saldaña et al. 2009). In the present study, the SPON neuron was hypothesized to be sensitive to the slope of its membrane potential, and only steep slopes during recovery from the hyperpolarization resulted in model discharges.

A phenomenological model of the SPON neuron with a slope detection mechanism is proposed in the current study. This approach is in contrast to the more detailed biophysical models that have been used to describe the underlying ion currents (e.g., Wang et al. 1991; Kopp-Scheinpflug et al. 2011). The benefit of the phenomenological model is that it provides a computationally efficient tool to focus on the potential role of the slope sensitivity of SPON cells in the responses to different types of stimuli. The model was tested with responses to three types of stimuli, pure tones at CF, BBN, and SAM tones, and was validated against physiological recordings from several studies. The model SPON response was then applied as an inhibitory input to a model of the IC neuron to explore the potential role of the SPON in mechanisms of forward masking at the level of the IC. The hypothesized effects of the SPON cell responses on the IC neurons in a forward-masking paradigm could be tested in future studies using intracellular recordings in the IC or by manipulating the function of the SPON during a behavioral experiment. Possible biophysical mechanisms underlying slope detection behavior of the proposed model are also described in the “DISCUSSION” section.

METHODS

Electrophysiological responses of the SPON neuron to a pure tone at CF, BBN, and SAM stimuli were modeled in this study. To provide the required input for the model SPON neuron, physiological responses of the auditory periphery and bushy cells of the VCN were simulated. To this end, the AN model developed by Zilany et al. (2014) and the VCN (bushy cells) model presented by Nelson and Carney (2004) were used as the first and second stages of the proposed model, respectively. The stages of the proposed SPON model are illustrated in Figure 1b. The response of the AN model provided the input to the model VCN neurons, which in turn provided an inhibitory projection to the SPON stage. The slope of this IPSP was computed to model the responses of SPON neurons. Different stages of the proposed model are briefly described in the following sections. AN and VCN signals were continuous rate functions, e.g., the synapse output of the AN model, which could be convolved with simple models for postsynaptic potentials and used as the input to a slope detector. This phenomenological modeling approach omits the details of more accurate neural models but provides an efficient tool for testing hypotheses concerning physiological signal processing. The outputs of this model can be used as inputs to higher-level models, and the efficiency is useful for testing the models with relatively long-duration psychophysical stimuli and population responses.

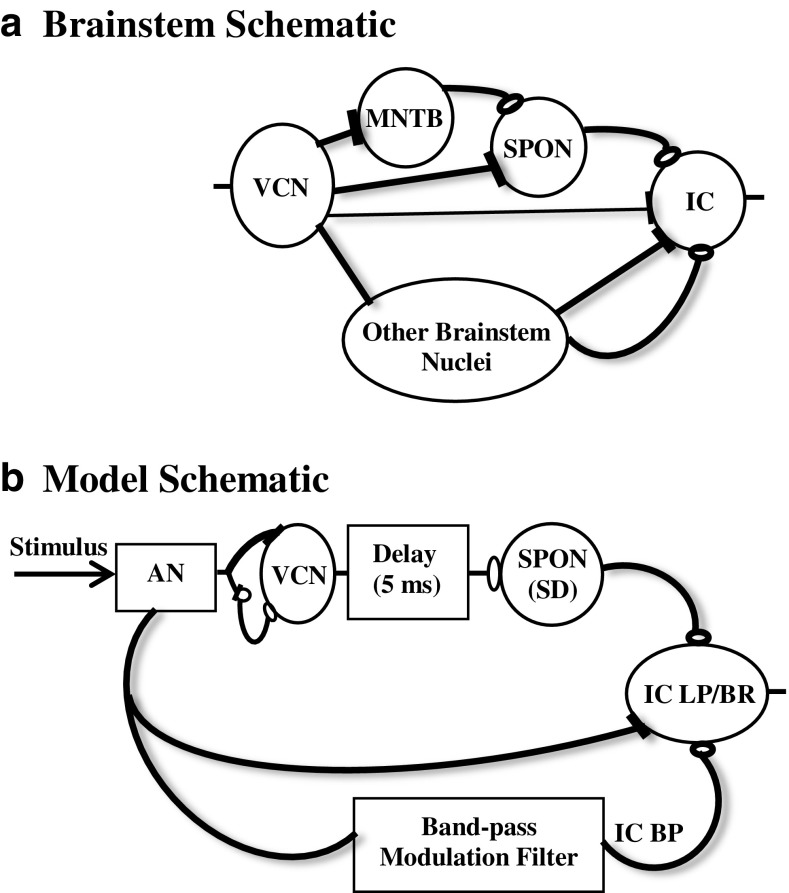
FIG. 1.

a Simplified schematic of the brainstem pathways that are most closely related to the proposed model. Filled “terminals” indicate excitation, and open ones indicate inhibition. For simplicity, crossing of the midline is omitted in this diagram. b SPON model. The AN model provides inputs to the same-frequency inhibition and excitation (SFIE) model used to simulate the responses of VCN bushy neurons (Nelson and Carney 2004; Gai and Carney 2006). A neural delay of 5 ms was included to match the latencies of physiological responses of SPON neurons. The SPON response was modeled using an inhibitory postsynaptic potential (IPSP) originating from the delayed responses of the VCN model and a slope detector (SD) that measures the slope of the membrane potential. The SPON neuron responds with an action potential when the slope exceeds a preset threshold value. IC model. Responses of the AN and SPON models were inputs to a simplified model of IC neurons with band-pass (BP) and low-pass/band reject (LP/BR) modulation transfer functions. The AN and IC BP models provided excitatory and inhibitory inputs, respectively, to the IC low-pass/band reject (LP/BR) neurons. In this study, the output of the SPON model was applied as an additional inhibitory input to the IC LP/BR model to test the potential role of SPON responses in the forward-masking paradigm at the level of the IC.

Model of the AN

An AN model (Zilany et al. 2014) simulated the physiological responses of AN fibers that provided inputs to higher centers. The input to the AN model was the pressure waveform in pascals, and the output of the model was a rate function. In the AN model, the acoustic signal is passed through a middle-ear filter, followed by parallel signal path narrowband (i.e., basilar membrane (BM)) and control path broadband filters. The control path reflects the active processes in the cochlea. The gain and bandwidth of the nonlinear BM filter vary according to the control signal to account for several level-dependent response properties of the cochlea. The output of the BM filter is passed through a transduction function (a static nonlinearity) followed by a seventh-order low-pass filter to replicate the response properties of the inner hair cell (IHC). The IHC output drives the IHC-AN synapse, which provides the instantaneous synaptic release rate as output. The output of the model IHC-AN synapse, r _AN(t), was subsequently used as an input to the next stage of the model. Because the majority of AN fibers (~61 %) have high spontaneous rate (SR) (Liberman 1978), the typical responses of high SR fibers were considered in this study, as in the model of VCN neurons by Nelson and Carney (2004).

Model of the VCN

Physiological responses of bushy cells of the VCN were modeled using the same-frequency inhibition and excitation (SFIE) model (Nelson and Carney 2004), which is consistent with physiological observations at this level of the auditory pathway (Wickesberg and Oertel 1988; Caspary et al. 1994). The effect of the excitatory AN input is stronger, faster, and short lasting (described by an alpha function with a time constant of 0.5 ms) relative to the inhibitory input that is relayed by an interneuron that has an alpha function with a time constant of 2 ms (Oertel 1983). In addition, the inhibitory influence of the model is delayed compared to excitation to reflect the intrinsic disynaptic delay of the inhibitory pathway. The model IHC-AN synapse output was convolved with excitatory and inhibitory alpha functions that were summed to simulate the instantaneous discharge rate of the model VCN neuron, r _CN(t). All values of the model VCN parameters were fixed and consistent with the VCN model stage in Nelson and Carney (2004) (Table 1).

TABLE 1.

Parameters of the model VCN and SPON neurons

VCN	Excitatory time constant	0.5 ms
	Inhibitory time constant	2 ms
	Inhibition delay	1 ms
	Relative inhibitory strength	0.6
	Scaling factor	1.5
SPON	Inhibitory time constant	5 ms
	Neural delay	5 ms
	Scaling factor	75
	Slope threshold	3.95
	Gain	150

Model of the SPON

In general, SPON neurons use GABA as a neurotransmitter and are innervated by a large number of glycinergic and GABAergic synapses from the ipsilateral MNTB and collaterals of SPON axons, respectively. SPON neurons also receive descending inhibitory inputs, presumably GABAergic, from the tectal longitudinal column (Viriuela et al. 2011).The detailed pharmacological study by Kulesza et al. (2007) concluded that glycinergic inhibition is essential to the formation of SPON offset responses, whereas GABAergic inhibition plays a more subtle role by limiting the response magnitude of the SPON neurons during and after the stimulus. Thus, the inhibitory effect of MNTB neurons was considered in this study to be the main cause of SPON offset responses. MNTB neurons receive excitatory input from bushy cells of the contralateral VCN, and the physiological responses of these cells resemble the responses of their excitatory inputs (Banks and Smith 1992; Smith et al. 1998). Thus, the required inhibitory input to model SPON cells originated from the model VCN neuron developed by Nelson and Carney (2004). The total delay between the VCN and SPON stages, including the synaptic delay between MNTB and SPON neurons, was set to 5 ms (Fig. 1b) to match typical SPON latencies.

In this study, the SPON neuron was assumed to be sensitive to rapid positive changes of the membrane potential. To simulate the membrane potential of the SPON neuron, Sin(t), the probability of discharge of the VCN model, (r _CN(t)/F _s), was convolved with an inhibitory alpha function, as shown in Eq. 1. F _s denotes the sampling rate used for the simulations; F _s = 100 kHz was used in this study, as required by the AN model (Zilany et al. 2014). The convolution with the alpha function reflected the membrane and synaptic modifications of the signal (Nelson and Carney 2004) at the SPON stage.

$$S_{\mathrm{in}}\left(t\right)=-{Ate}^{‐t/\mathrm{\tau }}*r_{\mathrm{CN}}\left(t\right)/F_{\mathrm{s}}$$ 1

The time constant (τ) of the alpha function was set to 5 ms. Convolving the model VCN responses with an alpha function that had a relatively long time course (τ = 5 ms) resulted in an IPSP that had slow variations during the stimulus. As a result, the model SPON neurons did not discharge during the stimulus presentation (when the slope was below threshold), as desired in response to pure-tone and BBN stimuli. Note that the single inhibitory time constant of the model should not necessarily be interpreted as a simple time constant of a single IPSP, but rather as an effective time constant describing the overall time course of the inhibitory influence. Moreover, the value of the scaling factor (A) directly affects the amplitude, and thus, the slope of S _in(t). Therefore, the scaling factor had a direct effect on the threshold value. In this study, the model threshold and the scaling factor were adjusted and fixed to achieve the desired offset response and to limit the sustained activity during the stimulus in response to the pure-tone and BBN stimuli. In general, the model SPON parameters were adjusted to obtain the best overall responses across all three types of stimuli used in this study, and then, the parameter values were fixed.

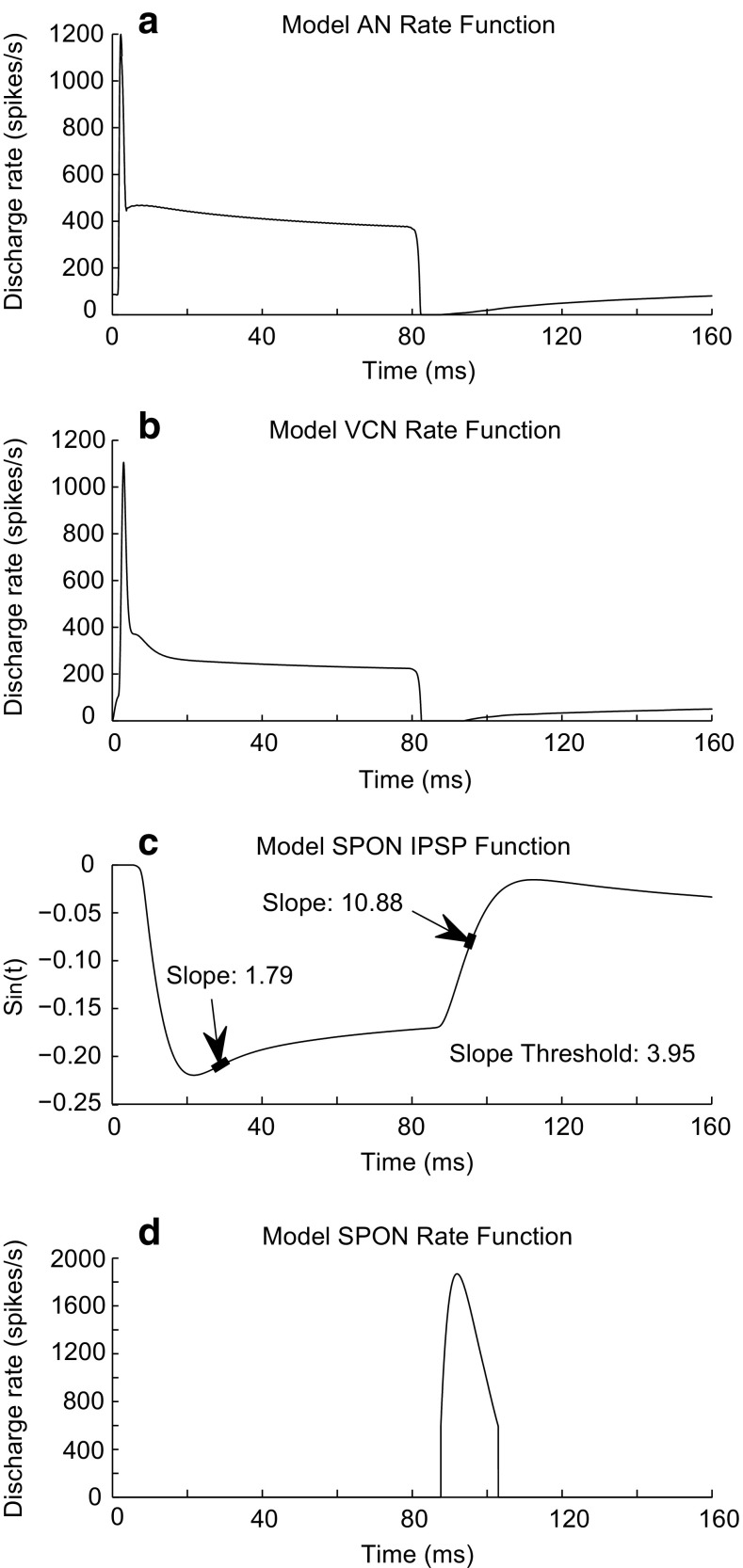
To illustrate how the proposed model works, simulated outputs at different stages of the model are shown in Figure 2. A pure tone at CF (8 kHz) with a duration of 80 ms at 40-dB SPL was applied as an input to the model. The AN model rate function, r _AN(t), (Fig. 2a) was consistent with physiological responses, as previously reported (Zilany et al. 2009, 2014). The VCN model simulated responses of bushy cells that are characterized by the primary-like (PL) response pattern, containing a falling phase at the stimulus offset (Fig. 2b) (Rhode and Greenberg 1992). This falling slope at the offset of the model VCN response resulted in a rising slope at the offset (Fig. 2c) for the model SPON membrane voltage, S _in(t), which was the basis of the discharge activity of the proposed SPON model. Note that the magnitude of model S _in(t) was not adjusted to match the physiological IPSP at the SPON but is scaled at the input to the discharge generator (see in the following).

FIG. 2.

Typical responses at different stages of the proposed model of the SPON neuron. The input to the model was a pure tone at CF (8 kHz) with an intensity of 40-dB SPL. Duration of the stimulus was 80 ms. a, b Rate functions of the AN, r _AN(t), and VCN, r _CN(t), models, which had a primary-like pattern characterized by a falling phase at the stimulus offset. c The model SPON membrane potential after convolving with the inhibitory alpha function, S _in(t) (note: the S _in(t) magnitude was not scaled to resemble the magnitude of the physiological SPON membrane potential). The signal was scaled at the input of the spike generator (see “METHODS” section). Arrows indicate the region of positive slope values resulting from the rising phases of the S _in(t). The SPON model responded only during the rising phase of the membrane potential at the stimulus offset, when the slope exceeded a threshold value of 3.95. d The rate function of the model SPON neuron, r _SPON(t).

The slope of the model membrane potential (dS _in/dt) was the input to a slope detector (SD) (Fig. 2d). Spiking activity of the model SPON neuron was achieved when the slope exceeded a preset threshold value of 3.95. S _in(t) contained two regions of positive slopes: the first one was during the stimulus, and the second one occurred at the stimulus offset (Fig. 2c). Discharge activity of the SPON model occurred during the offset, where the slope was often steep enough (e.g., ~10.88 in Fig. 2c) to exceed the threshold. The slope during the stimulus was typically smaller (e.g., ~1.79 in Fig. 2c) than the threshold. In order to generate spike times for the model SPON, the output of the SD (slope values) was applied as the input to a discharge generator (Jackson 2007). The discharge generator was modeled by a nonhomogeneous Poisson process that includes the effects of absolute and relative refractoriness. The output of the SD was scaled by 150, for a sampling rate of 100 kHz, to obtain discharge rates at the offset comparable to those observed physiologically (e.g., in Fig. 6). The resulting model SPON rate function, r _SPON (t), is shown in Figure 2d. To construct poststimulus-time histograms (PSTHs) of the model responses, the output of the discharge generator was simulated for a large number of repetitions (e.g., 20 or 50) of the input stimulus.

FIG. 6.

Rate-level functions of physiological (top panels) and model (low panels) responses to a 50-ms CF tone. All model rate-level functions (Fig. 6c, d) had small dynamic ranges, as observed for most SPON neurons (Fig. 6a). However, some neurons had a dynamic range of more than 20 dB (Fig. 6b). Physiological data are reproduced from Kulesza et al. (2003) with permission.

The responses of the model AN fibers and VCN bushy neurons have been extensively validated against physiological data in previous studies (Nelson and Carney 2004; Zilany and Bruce 2006, 2007a, b; Zilany et al. 2009; 2014). In this study, the responses of the model SPON neurons, with the fixed parameters (Table 1), were validated against physiological data in response to pure tones at CF, BBN, and SAM stimuli.

Model of the IC

In order to explore the mechanism of forward suppression at the level of the IC, the output of the proposed SPON model was used as an inhibitory input to a model of IC neurons. Models for IC neurons with band-pass (BP) and low-pass/band reject (LP/BR) modulation transfer functions (MTFs) have been developed based on simple interactions of excitatory and inhibitory signals from model VCN neurons (Nelson and Carney 2004; Carney et al. 2015). The same-frequency inhibition and excitation (SFIE) model simulates responses of IC BP neurons receiving inputs from the model VCN neurons. To simulate IC LP/BR responses, model VCN and model IC BP responses were used as the excitatory and inhibitory inputs, respectively (Carney et al. 2015). Parameters of the alpha functions convolved with the IC model inputs can be varied to account for different characteristics of IC neurons (e.g., rate MTFs). Because the SFIE mechanism at the level of the IC acts as a modulation filter, Mao and Carney (2015) passed VCN model responses through a sixth-order BP filter with a Q value of 1, rather than convolving the model VCN output with alpha functions, to simulate IC BP responses. In the current study, the modulation filter of Mao and Carney (2015) was used to model IC responses; details of the modulation filter implementation can be found in their appendix. To simplify the model, AN model responses were directly passed through the modulation filter to model IC BP responses (Fig. 1b) (the same AN model responses that were used for the VCN stage of the SPON model). The function of the VCN stage in the IC model was to increase the synchronization to the SAM envelope (Mao and Carney 2015); as a result, omitting this stage did not affect the results obtained in the forward-masking paradigm, in which pure tones were applied as the stimuli. The best modulation frequency (BMF) of the IC model was set to 160 Hz. IC LP/BR responses were modeled by using the AN model response as the excitatory input and the IC BP model responses as the inhibitory input (Fig. 1b). Only model IC LP/BR responses were used in this study because this IC model provided responses that were most comparable to the physiological IC responses in the forward-masking paradigm reported by Nelson et al. (2009).

RESULTS

This section compares the simulation results of the proposed model to physiological data recorded from SPON neurons in response to simple and complex stimuli. In addition, the effect of using the output of the proposed model as an inhibitory input to a model IC neuron is explored.

Responses to BBN

Figure 3 shows poststimulus-time histograms (PSTHs) constructed from the responses of a representative actual SPON neuron (upper panel) to a 50-ms BBN (Kulesza et al. 2003). Note that in the physiological experiment, the recording was started 10 ms before applying the stimulus. To obtain the corresponding model responses (lower panel), the CF of the model neuron and level of the input signal were set to 10 kHz and 80-dB SPL, respectively. The model SPON neuron responded at the offset of the stimulus, consistent with the vast majority of SPON neurons (~95 %) studied by Kulesza et al. (2003). In addition, spontaneous activity of both physiological and model responses was very low (~zero for the model response). Note that the model’s first-spike latency was adjusted to match the offset responses of SPON neuron to this BBN stimulus, and it was then kept constant for the simulations to all other types of stimuli.

FIG. 3.

Typical physiological (upper panel) and model (lower panel) responses of SPON responses to 20 repetitions of a 50-ms broadband noise (BBN) with a bandwidth of 40 kHz. The stimulus was applied from 10 to 60 ms (black bars) in both the physiological experiment and simulation. The CF of the model neuron was set to 10 kHz, and the stimulus was presented at 80-dB SPL. Offset-type responses were observed in both physiological and model responses. Physiological data are reproduced from Kulesza et al. (2003) with permission.

Responses to Pure Tone at CF

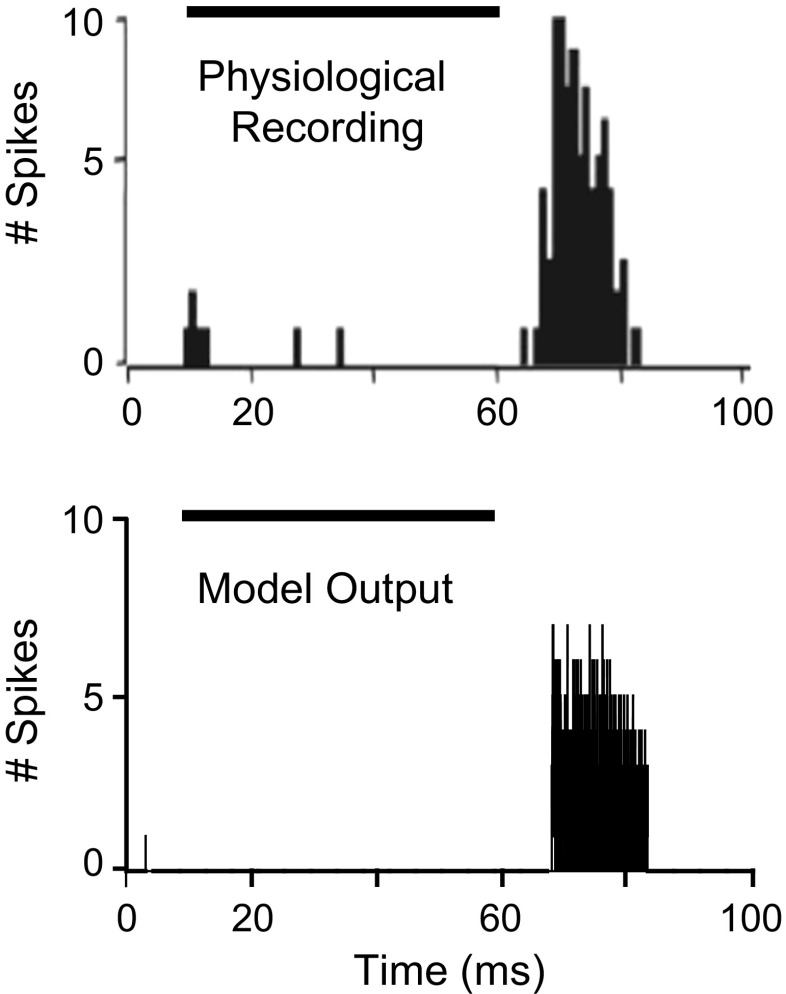
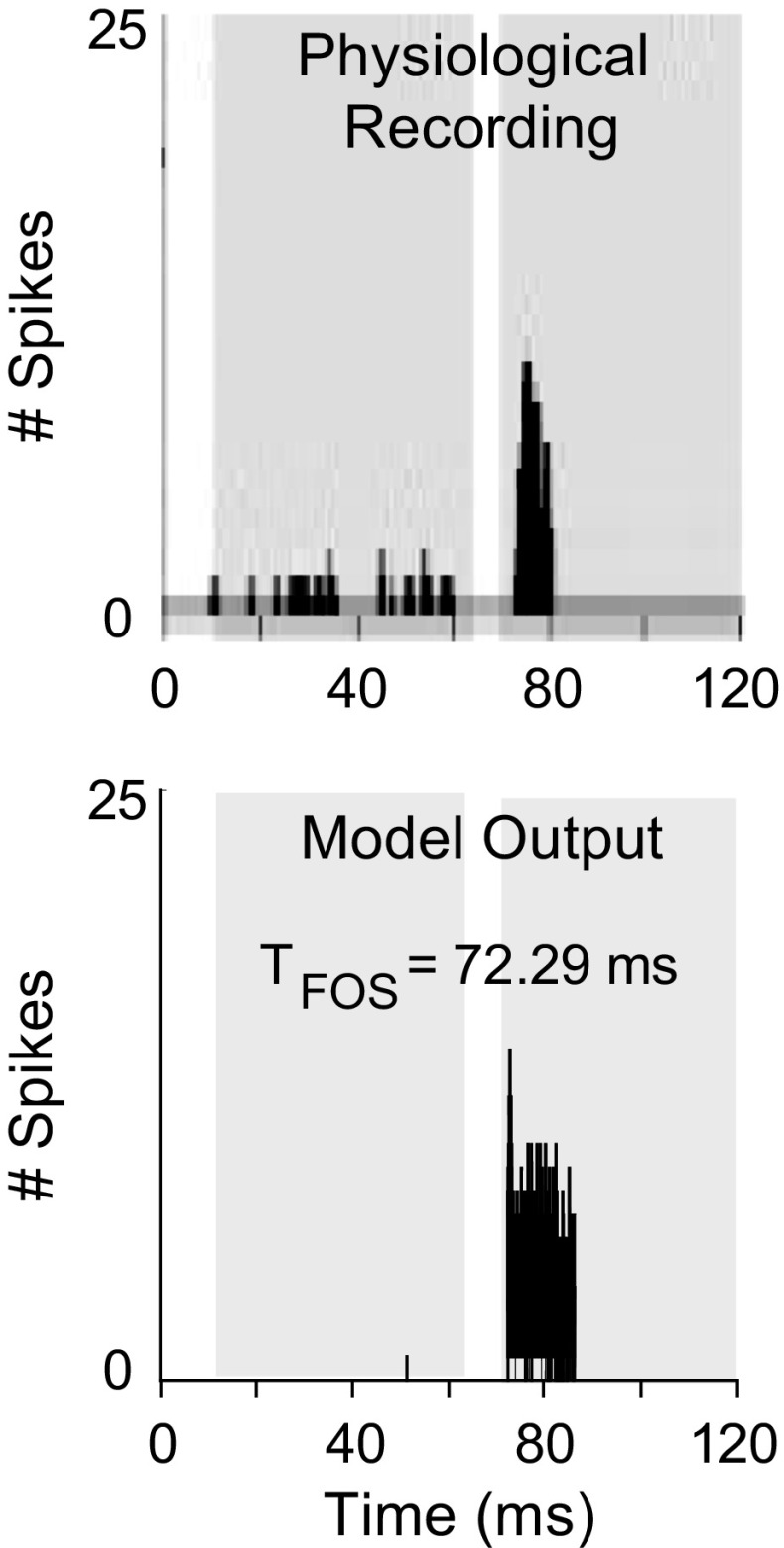
Responses of the proposed model were simulated for tones at CF in different stimulus conditions (Figs. 4, 5, and 6). Figure 4 shows the PSTHs of physiological (upper panel) and model (lower panel) responses to a tone at CF. In both model and physiological responses, 20 stimulus presentations were each started at t = 10 ms with a duration of 55 ms. The physiological response shown in Figure 4 is from Kulesza et al. (2007). The CF of both physiological and model neurons was 3.5 kHz. Response of the model was only at the offset of the stimulus, consistent with the physiological data. Moreover, the time of first offset spike (T _FOS) of the model, computed as an averaged latency across repetitions, was comparable to the T _FOS of actual physiological responses, which was reported to be ~72 ms.

FIG. 4.

Physiological (upper panel) and model (lower panel) responses of an SPON neuron to 20 repetitions of a 55-ms tone stimulus at CF (stimulus was presented with a 10-ms delay in both cases). Physiological data were obtained by setting the sound presentation level to 20 dB above the threshold of the unit. The CF of both model and actual units was 3.5 kHz. The SPON model response was for a stimulus at 30-dB SPL. The first and second gray-shaded regions indicate the peristimulus and poststimulus time windows, respectively. T _FOS is the time of the first offset spike. Physiological data are reproduced from Kulesza et al. (2007) with permission.

FIG. 5.

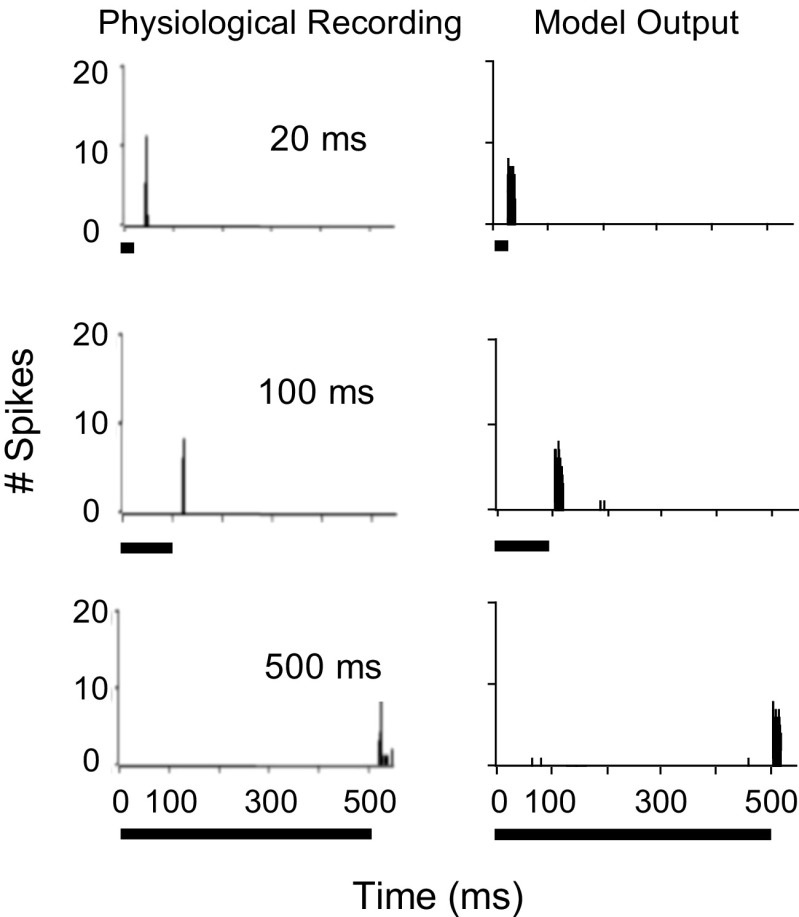
Physiological (left) and model (right) responses of an SPON neuron to 20 repetitions of a 33-dB SPL pure tone at CF (8.3 kHz) with different durations ranging from 20 to 500 ms. Physiological data are reproduced from Kulesza et al. (2003) with permission.

The model SPON cell responses were also simulated to a tone at CF with durations ranging from 20 to 500 ms (Fig. 5). The CF of the model SPON neuron was matched to the CF of the reported physiological unit (8.3 kHz), and the stimulus was presented at 20 dB above threshold. It is obvious that model PSTHs (right panels) showed offset-type responses regardless of the stimulus duration. In addition, the offset spike latency was almost unaffected by duration (T _FOS = 27.2 ms for 20-ms stimulus, T _FOS = 107.4 ms for 100-ms stimulus, and T _FOS = 507.4 ms for 500-ms stimulus), consistent with ~50 % of neurons recorded by Kulesza et al. (2003).

In order to examine the dynamic range of SPON cell responses, the rate-level function was investigated from the offset response of the physiological units. The majority of SPON neurons (~86 % in Kulesza et al. 2003) demonstrated a small dynamic range (less than or equal to 20 dB, Fig. 6a), and only a few cells had dynamic ranges greater than 20 dB (Fig. 6b). Model responses to tones (duration of 50 ms) at CFs matched to the actual neurons (indicated in the corresponding panels) and at sound levels varied from 0- to 70-dB SPL in steps of 10 dB are shown in Figure 6. Note that the level of stimuli for the physiological data was provided in dB attenuation. The rate-level functions of the model responses (Fig. 6c, d) showed narrow dynamic ranges (qualitatively estimated as ~20 dB) for all CFs tested. The discharge rate (spikes per stimulus) of the model responses was close to the rate of actual neurons (compare Fig. 6c, d with Fig. 6a, b).

SPON Model Responses to SAM Stimuli

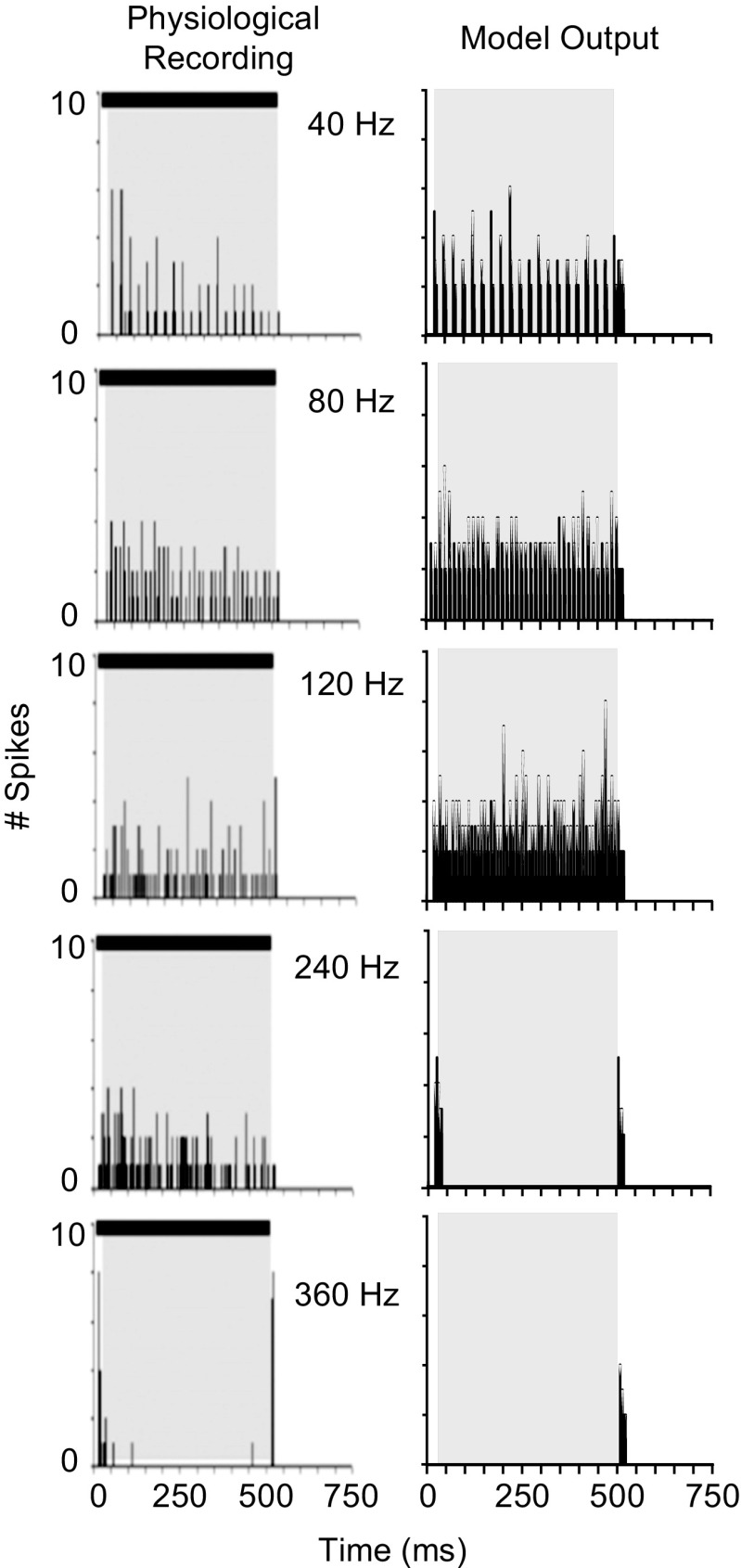
To explore the response properties of SPON neurons to complex sounds, a few studies have investigated the responses to SAM tones at CF (Kulesza et al. 2003; Kadner and Berrebi 2008; Felix et al. 2011). Most neurons synchronize to the envelope of the stimulus for low modulation frequencies (MFs), with decreased phase locking at higher MFs. Responses were simulated using the experimental conditions employed by Kadner and Berrebi (2008). The carrier frequency of the input signal was set to CF (8 kHz), and the model responses were simulated for MFs ranging from 40 to 360 Hz with 100 % modulation. The duration of the SAM stimulus was 500 ms, and the overall sound level was 20 dB above rate threshold. Figure 7 compares the PSTHs obtained from the model responses (right panels) to the actual PSTHs (left panels) (Kadner and Berrebi 2008). Model responses were strongly phase-locked to the SAM stimuli for MFs up to 120 Hz, and the number of phase-locked spikes was substantially reduced at 240 Hz and above. However, the phase-locked responses of the actual neuron can be seen for MFs as high as 240 Hz. For a MF of 360 Hz, both model and actual responses had very low response rates, and the physiological responses from the SPON neuron had onset responses that were not observed in model PSTH responses. Regardless of the MF, both model and actual physiological responses exhibited responses to the offset of each presentation of the 500-ms SAM stimulus.

FIG. 7.

Typical physiological (left) and model (right) responses of SPON neurons to 20 repetitions of a 500-ms 30-dB SPL SAM tone at CF (8 kHz). PSTHs were constructed for modulation frequencies ranging from 40 to 360 Hz (indicated in corresponding panels). Histogram binwidth of the model was 0.5 ms. Both model and actual neurons demonstrated phase locking to the envelope of the stimulus; however, the number of phase-locked spikes in the model response was reduced significantly at 240 Hz, while the actual neural response had synchronized spikes at that frequency. Physiological data are reproduced from Kadner and Berrebi (2008) with permission.

In general, SPON neurons responded to the envelope of the SAM tones (at CF) as if each period of modulation was a separate stimulus and thus discharged only at the offset of each period of the modulated stimulus (i.e., SPON neurons discharged at the waveform troughs) (Kulesza et al. 2003). To show the exact timing of model responses to SAM stimuli, responses of the model SPON neuron for two different MFs (10 and 40 Hz) along with their corresponding stimulus waveforms are illustrated in Figure 8. Responses of the model VCN neuron to the same stimuli are also shown. To simulate model responses, 20 repetitions of 500-ms SAM stimuli were applied. Carrier frequency (CFs of the model units) and stimulus intensity were set to 3.5 kHz and 60-dB SPL, respectively. Both VCN and SPON model responses were phase-locked to the envelope of the SAM stimuli. However, for both MFs, the SPON model responded only at the offset of each period of the SAM stimulus, which was consistent with physiological recordings (Fig. 14 in Kulesza et al. 2003). On the other hand, in the study by Felix et al. (2011), SPON neurons responded mainly at falling phases of the SAM cycles irrespective of the stimulus frequency (Fig. 7 in Felix et al. 2011), which cannot be explained by the proposed SPON model. Note that sharp falling phases in the model VCN responses at the end of each cycle resulted in sharp rising slopes (above the threshold) in the model SPON membrane potential (not shown) and were the basis of the SPON model discharges for both MFs tested. In general, the SPON model discharges occurred at the troughs of the model VCN responses, provided that the slope of the SPON membrane potential exceeded threshold, with an additional delay that was included between the VCN and SPON stages to match physiological latencies. Also, at higher MFs, the slope at the troughs tended to become shallower, and thus, the model SPON discharges decreased.

FIG. 8.

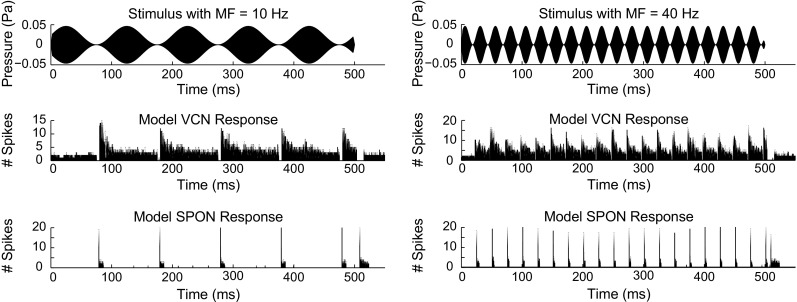
PSTHs of the VCN and SPON model responses to SAM stimuli with MFs at 10 Hz (left panels) and 40 Hz (right panels). Twenty repetitions of 500-ms 60-dB SPL SAM stimuli were applied as the input. CFs of the model units were set to 3.5 kHz. At both MFs, the SPON model followed the synchronized patterns of the VCN model responses. However, the SPON model discharged only at the offset of each cycle of modulation.

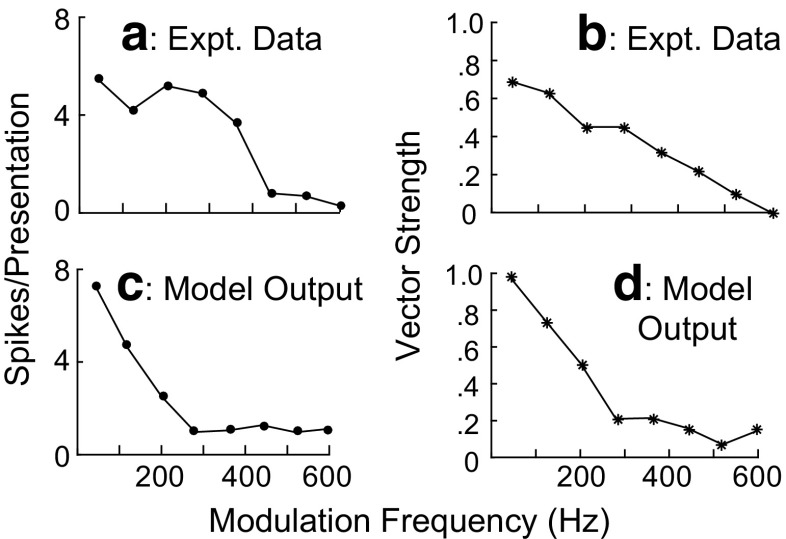
Figure 9 shows the sync MTFs (vector strength as a function of MF) and rate MTFs (number of spikes per stimulus as a function of MF) obtained from neural (upper panels) and model (lower panels) responses to SAM stimuli for MFs ranging from 40 to 600 Hz. The stimulus conditions were the same as in Figure 7. The physiological MTFs (Fig. 9a, b) were the mean of responses recorded from a population of SPON neurons (Kadner and Berrebi 2008). The model MTFs were also shown (Fig. 9c, d) from the mean responses of ten model units with CFs ranging from 3.1 to 33.1 kHz and sound levels ranging between 28.3- and 96.7-dB SPL. The values of CFs and stimulus intensities were extracted from the data of ten neurons illustrated in Figure 4 of Kadner and Berrebi (2008) (sound levels were 20 dB above the corresponding thresholds shown in the figure). The rate MTF of the model responses (Fig. 9c) was low pass in nature, consistent with the physiological rate MTF (Fig. 9a). However, the cutoff frequency of the model rate MTF was much lower than the corresponding cutoff frequency of the physiological rate MTF responses. Sync MTFs of both physiological (B) and model (D) responses were also low pass in nature. Both model and physiological sync MTFs had comparable reductions in vector strength (VS) for MFs from 40 to 200 Hz. The VS of the physiological sync MTF was almost constant for MFs of 200 and 280 Hz, while the VS of the model sync MTF decreased from 200 to 280 Hz. The physiological sync MTF decreased almost monotonically for MFs from 280 to 600 Hz (VS became ~0 for MF = 600 Hz), whereas no remarkable reduction was seen in the model sync MTF for this range of MFs.

FIG. 9.

Rate and sync MTFs for both physiological (a, b) and model (c, d) responses for modulation frequencies of 40 to 600 Hz. The stimulus condition is the same as in Fig. 7. Both rate MTF (c) and sync MTF (d) of the model responses are low pass, which is consistent with the physiological MTFs. Physiological data are reproduced from Kadner and Berrebi (2008).

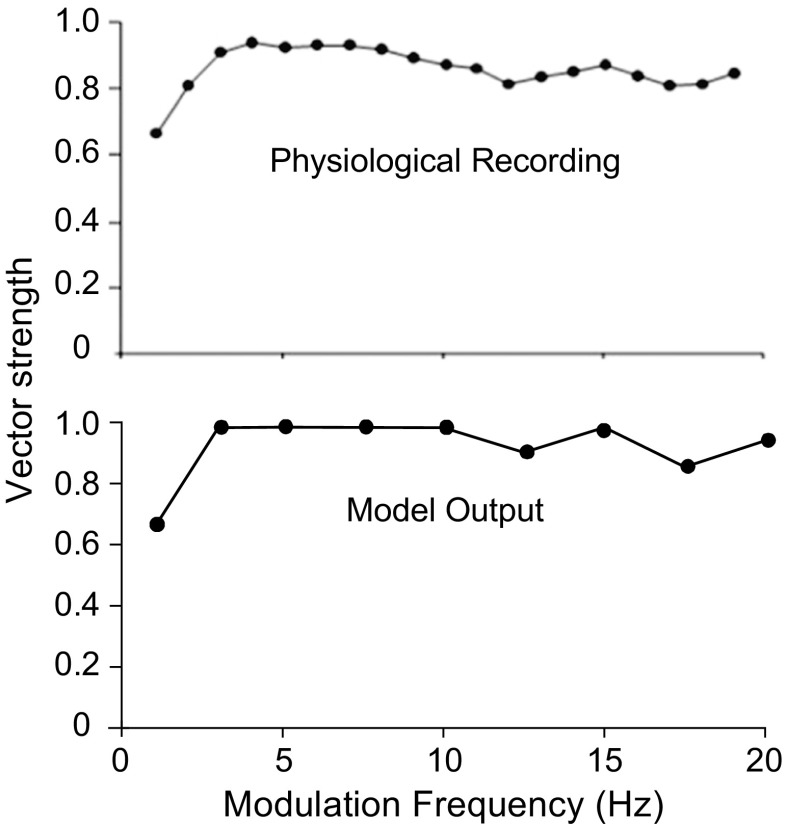
To test the ability of SPON neurons to encode very low-frequency periodic stimuli, Felix et al. (2011) recorded responses of neurons in both young and adult mice with CFs ranging from 11 to 40 kHz. Each unit was presented with SAM tones (duration 2 s) with the carrier frequency set to the unit’s CF, and the MF was systematically varied from 1 to 20 Hz. Two types of responses were observed: one type was marked by a significant phase-locked spiking activity to SAM tones at all MFs from 1 to 20 Hz (all-pass), whereas a significant decline in the phase-locked responses to MFs above 15 Hz was observed in the other type.

SAM stimuli with MFs ranging from 1 to 20 Hz were applied to test the ability of the proposed SPON model to encode the amplitude-modulated sounds with very low modulation rates. Figure 10 illustrates the sync MTF measured in the physiological experiment (upper panel) conducted by Felix et al. (2011) and from the responses of the model SPON neuron (lower panel). Note that the CF of the model SPON neuron was set to 15 kHz, and the sound presentation level was 52-dB SPL. The SPON model simulated the all-pass (not the low pass) type of sync MTF reported in the experimental study.

FIG. 10.

Plots of sync MTF for physiological (top panel) and model (low panel) responses. Twenty repetitions of 52-dB SPL SAM tones at CF (15 kHz) with 2-s duration were applied with modulation rates ranging from 1 to 20 Hz. The SPON model had all-pass sync responses over this range of modulation frequencies, similar to some of the responses recorded by Felix et al. (2011). Physiological data are reproduced from Felix et al. (2011) with permission.

Responses to a Forward-Masking Paradigm at the Level of the IC

Late, long-lasting inhibitions have been commonly observed in the responses of IC neurons, and the time course of this inhibitory component can exceed tens of milliseconds, as illustrated in click responses (Carney and Yin 1989). In order to realize the long-lasting inhibitory component at the level of IC, the output of the proposed SPON model was first convolved with an alpha function and then subtracted from the original IC model response.

Model IC responses were simulated for a forward-masking paradigm for which physiological responses of IC neurons were collected (Nelson et al. 2009). A 200-ms masker tone at CF (4.1 kHz) followed by a 20-ms probe tone (at CF) was applied; the delay between the masker offset and probe onset was set to 10 ms. Responses were computed during a 40-ms window surrounding the probe (probe rate). This window was started at the probe onset in the model responses and at 10 ms after the physical probe onset in the actual neural responses in Nelson et al. (2009) to compensate for acoustical and neural delays. The presentation level of the masker was fixed at 40-dB SPL in both model and actual responses. The probe level was varied from 0- to 80-dB SPL in the model and from −20- to +40-dB SPL in the physiological responses to estimate the rate-level function. The model rates were calculated for higher probe intensities because the simulated rate-level functions were more comparable to the physiological data at this range of probe levels.

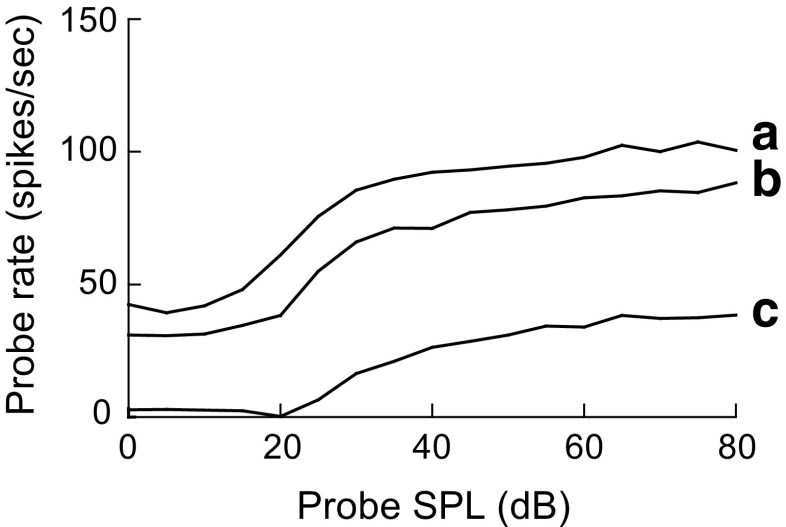
Figure 11 illustrates the probe rate as a function of probe intensity for actual IC responses (Fig. 11a), model IC responses without an SPON input (Fig. 11b), and model IC responses with the SPON inhibitory input responses (Fig. 11c). In the physiological responses (Fig. 11a), applying the probe with a preceding masker (M) led to a reduction in probe rates compared to responses to the probe-only (U) stimuli. This amount of probe rate decrement did not occur in the responses of the IC model without the SPON input (compare Fig. 11b with Fig. 11a). The relatively small probe response reduction observed in the responses of the IC model without the SPON input was also seen in the responses of model AN fibers to a forward-masking paradigm (not shown). However, there was a noticeable difference between masked (M) and unmasked (U) conditions in the responses of the model IC neuron with the inhibitory SPON input (Fig. 11c). In order to explore the effect of the time constant of the alpha function (i.e., duration of the inhibitory input) on the IC model responses to the forward-masked tones, probe rate-level functions were simulated for a range of time constants (indicated in Fig. 11c). It is obvious that increasing the inhibitory time course of model SPON responses from 1 to 4 ms led to more reduction of probe rates for all probe intensities tested.

FIG. 11.

Probe rate as a function of probe stimulus level for a physiological IC neuron (a), model IC responses without an SPON input (b), and model IC responses with an inhibitory input from the model SPON neuron (c). Responses to the unmasked (U) and masked (M) stimuli are shown in each panel. IC model responses to the masked tones were inhibited by the model SPON responses with three different time constants indicated in the c. The model stimulus condition was matched to the physiological study of Nelson et al. (2009). The delay between the masker offset and probe onset was 10 ms. Adding a masker preceding the probe stimulus led to a reduction in the probe rate in both physiological (a) and model IC neuron responses with the SPON input (c). Increasing the time constant of the SPON inhibitory inputs from 1 to 4 ms resulted in stronger probe rate suppression (c). However, a significant suppression was not observed in the probe rate of the model IC neuron without the SPON input (b). Physiological data are reproduced from Nelson et al. (2009) with permission.

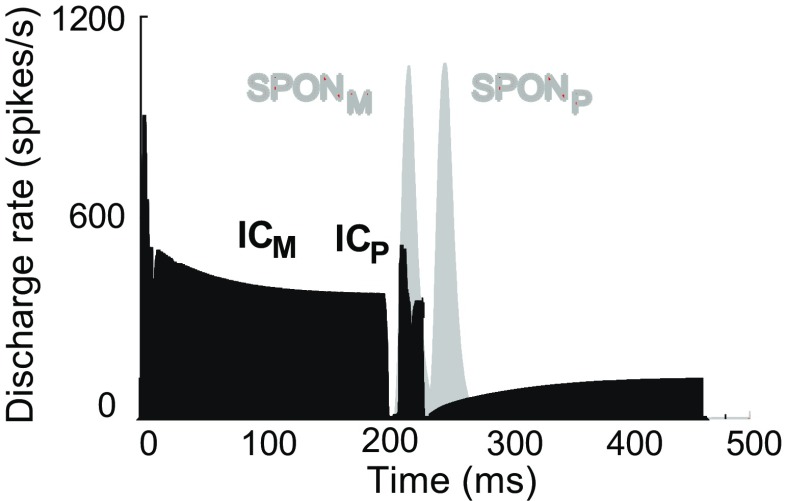
Figure 12 shows the PSTHs (discharge rate as a function of time) for both IC and SPON model responses (after convolving with the alpha function) to the forward-masking paradigm for a probe level of 30-dB SPL and masker-probe delay of 10 ms. Note that IC model responses shown in Figure 12 were responses of the model IC LP/BR (Fig. 1b), which were not yet affected by the SPON model. SPON model responses are shown with an inhibitory time course of 4 ms. IC model responses to the masker and probe stimuli are denoted with IC_M and IC_P, respectively, while SPON_M and SPON_P indicate the responses of the model SPON neuron to the corresponding stimuli. The duration of model SPON response to the masker (SPON_M) was long enough to completely suppress the probe response of the model IC neurons (IC_P) (this suppression results in IC_P = 0, not shown), and thus, the probe rate in the corresponding curve of Figure 11c was zero at the probe level of 30-dB SPL.

FIG. 12.

PSTHs of IC and SPON model responses to the forward-masking paradigm. The IC model responses of the IC LP/BR model (Fig. 1 b) did not include the inhibitory SPON model input. Delay between the masker offset and probe onset was set to 10 ms. IC_M and IC_P represent responses of the IC model to the masker and probe stimuli, respectively. Responses of the SPON model to the masker and probe stimuli are indicated by SPON_M and SPON_P, respectively. By setting the value of the inhibitory time course to 4 ms, IC_P could be totally suppressed by SPON_M (note: IC_P after suppressive effect of the SPON_M is not shown here).

For the stimulus paradigm used in Nelson et al. (2009), the probe stimulus ended at 230 ms for a masker-probe delay of 10 ms. The SPON model response to the probe stimulus (SPON_P) started shortly after the offset of the probe stimulus, and the analysis window to calculate the probe rate ended at 250 ms (40-ms window from 210–250 ms). Taking into account the previously mentioned time course, SPON_P could play a minor role in probe rate reduction by suppressing the spontaneous activity located within the analysis window.

The rate of the model SPON response was also reduced in response to the masked probe compared to the probe-only stimulus, indicating the suppressive effect of the forward masker on responses of the model SPON neuron by itself. Although the level of the masker was 10 dB higher than that of the probe in Figure 12, the SPON model response to the probe-only stimulus (not shown) was stronger than SPON model response to the masker-only stimulus (SPON_M in Fig. 12). Therefore, the SPON model response to the masked probe (SPON_P in Fig. 12) was similar to the SPON_M. This behavior of the SPON model response is discussed in detail in the next section.

Nelson et al. (2009) studied the effect of masker-probe delay on the physiological responses of IC neurons in the forward-masking paradigm. Figure 13 illustrates the masked probe rate-level functions with a 30-ms delay between the masker and the probe stimulus; all other stimulus parameters were the same as in Figure 11. Curve A in Figure 13 represents the IC model responses without inhibition from the model SPON neuron, and curve B was simulated with the inhibitory model SPON inputs with a time course of 4 ms. It is clear that at a 30-ms masker-probe delay, the inhibitory input with a time course of 4 ms did not have a significant effect on the IC model response (compare curve B in Figure 13 with the corresponding curve in Figure 11c). Increasing the inhibitory time course up to 10 ms (curve C in Fig. 13) resulted in probe rate reduction comparable to the physiological responses from the experiment. As a result, a systematic variation of inhibitory time courses can address probe threshold shifts for a range of masker-probe delays in the IC responses to a forward-masking paradigm. At higher masker-probe delays, longer inhibitory inputs are more effective in suppression of probe rates in the model IC neurons.

FIG. 13.

Probe rate-level functions of model IC neurons without (A) and with (B and C) an SPON inhibitory input. Masker-probe delay was 30 ms, and two inhibitory time courses (4 and 10 ms) were used to simulate the responses. Probe rates were considerably reduced in the responses simulated with a 10-ms inhibitory input (C) compared to the responses simulated with an inhibitory time course of 4 ms (b). At higher masker-probe delays, SPON model responses had to be convolved with a longer alpha function in order to simulate realistic IC responses to a forward-masking paradigm.

It is worth noting that the amplitude of the inhibitory alpha function, which was convolved with the model SPON responses, could also contribute to this phenomenon. Increasing the amplitude of the inhibitory alpha function led to a shift in the probe threshold of the model responses at a particular masker-probe delay (not shown). Thus, the interaction between inhibitory strength and time course might play a role in explaining the responses of IC neurons to the forward-masking paradigm, particularly for probe threshold shifts as a function of masker-probe delay and masker level (Nelson et al. 2009).

DISCUSSION

This study proposes a phenomenological model of the SPON neuron that successfully simulates responses to both simple and complex sounds. Offset discharges of the SPON neuron were modeled using a slope detection mechanism, which was sensitive to the positive slope of the repolarizing membrane potential during the decay of the IPSP. Thus, the offset activity of the model SPON neuron was achieved without an excitatory input. The same mechanism could be applied to explain the response properties of OFF neurons located in other auditory structures and/or even nonauditory structures, such as retina and lateral geniculate nucleus (Hubel and Wiesel 1961; Schiller and Malpeli 1978). The proposed model simulates offset responses of SPON neurons to pure tones at CF and BBN stimuli for a wide range of CFs and sound levels. Because the decay of the model SPON IPSP always extended past the stimulus offset, regardless of the stimulus duration, the proposed SPON model had offset responses independent of the sound duration. Modeling offset activity for stimuli with long durations is in agreement with the hypothesis that the SPON offset response is caused by strong inhibitory innervations rather than a long-latency excitatory input (Kulesza et al. 2003). The SPON model response was also evaluated against complex sounds such as SAM tones. In response to the SAM stimulus, the model SPON discharged precisely at the offset of each cycle of the amplitude modulation, similar to physiological responses. As a result, SPON model responses were phase-locked to the envelope of the SAM stimulus for a range of MFs (close to the range of MFs employed in physiological studies). Furthermore, the shape of the model sync and rate MTFs was comparable to that of MTFs obtained in physiological studies.

In this study, responses of the model SPON neuron were simulated using a set of fixed parameters for all types of stimuli. However, using the fixed values of model parameters led to a trade-off between responses of pure tones and SAM tones. Offset discharges in response to pure tones for a wide range of sound levels were ensured at the expense of losing phase-locked activity during the stimulus in response to SAM stimuli with relatively high MFs. The reason for this trade-off can be explained as follows: in response to SAM stimuli, the slope of decaying parts of the IPSP of the model SPON became shallower at higher MFs, and thus, the SPON model did not discharge. Changing the values of the model parameters (e.g., increasing the scaling factor) would increase the slope and result in responses to SAM stimuli at higher MFs. However, this change would also result in higher slopes during the pure-tone stimulus and thus sustained activity during the tone. In this study, the model parameters were first tuned to ensure only offset responses to pure tones and BBN for a wide range of SPLs, and the parameters were further tuned to yield phase-locked responses to SAM stimuli with MFs as high as possible. Thus, with the current set of model parameters, the SPON model did not have phase-locked discharges at high MFs for some model units (e.g., MF = 240 Hz in Fig. 7), and consequently, the cutoff frequency of the model rate MTF was lower than the cutoff frequency of the physiological rate MTF.

As mentioned previously (Fig. 12), the rate of the SPON model response to a 30-dB unmasked probe was higher than that of the SPON model response to a 40-dB masker (SPON_M). However, the model rate function in response to a 40-dB SPL tone should be approximately the same as the rate in response to a 30-dB SPL tone (refer to the model rate-level function in Fig. 6). The reason for this inconsistency in the model response is that presentation of the stimulus after a delay (such as a probe in the forward-masking paradigm) leads to a faster decay of the model SPON IPSP. Because the rate function of the proposed SPON model was proportional to the slope of membrane potential, the model rate was higher when the stimulus was delayed. The probe stimulus used in the model forward masking was also delayed by 210 ms from the onset of the masker, and as a result, the model SPON response to the probe-only stimulus was stronger than that of the SPON_M.

Potential Biophysical Mechanisms Underlying Slope-Sensing Characteristics of the SPON Model

Wang et al. (1991) simulated offset responses to a hyperpolarizing current input using T-type Ca²⁺ and leakage currents. Their model was based on data recorded from the rat thalamocortical relay neurons. Felix et al. (2011) made electrophysiological recordings from SPON neurons and reported the presence of offset responses through a complementary interaction between two ion currents, namely hyperpolarization-activated cation (I _H) and T-type Ca²⁺ (I _TCa) currents. In another study, Kopp-Scheinpflug et al. (2011) demonstrated that I _H activated by a strong IPSP was sufficient to trigger the short-latency offset discharges in the SPON neurons through a fast membrane repolarization, while the I _TCa had a subtle role in determining the number of spikes. In our SPON model, I _H current would also be the possible mechanism behind generating short-latency offset discharges through the detection of sharp rising slopes of the IPSP (during the rapid membrane repolarization). As was discussed earlier, the model IPSP could be an indicator of a net physiological IPSP caused by the inhibitory input and possibly other intrinsic characteristics (e.g., an extreme negative chloride reversal potential, as proposed by Kopp-Scheinpflug et al. 2011). This IPSP was assumed to be strong enough to sufficiently hyperpolarize the membrane potential and in turn activated the I _H. The SPON membrane potential could also be rapidly repolarized (recovered from the hyperpolarization) during the sharp rising phases of the IPSP, which in turn could deactivate the I _H current. The time constant of the I _H deactivation is longer when the membrane potential is strongly hyperpolarized (Fig. 3a, McCormick and Pape 1990). As a result, for fast repolarizations, with sharp positive slopes, the depolarizing effect of the I _H activation could generate discharges before the I _H is sufficiently deactivated. However, at shallow positive slopes, below the slope threshold, I _H would have enough time to deactivate during the slow membrane potential repolarization, and no action potentials would occur. In summary, the SPON spiking activity would occur within the sharp positive slope of the IPSP at the stimulus offset due to a complex interaction between the membrane potential repolarization and kinetics of the I _H current deactivation.

Forward Masking in the IC

Inhibition would play an important role in the rate suppression caused by the masker in IC neurons (Nelson et al. 2009; Gai 2016). In order to investigate the inhibitory effect of the SPON neuron on the forward-masking paradigm at the level of IC, a model of an IC neuron with a low-pass/band reject rate MTF and a sustained response to pure tones was used as the target of our SPON model responses. The responses of the model IC neuron with a BP rate MTF did not produce adequate suppression of probe responses (results not shown) using a similar model structure. The Nelson et al. (2009) study did not include rate MTFs for the IC neurons; thus, it is unknown whether a specific MTF type produced the forward-masking results that they reported. Low-pass/band reject neurons might have different responses to forward-masked stimuli compared to responses from BP MTF neurons, and BMF (best MF) of the neuron may also play a role in responses to the forward-masked stimuli. Nevertheless, two important characteristics of SPON cell responses should be taken into account when interpreting the inhibitory effect of SPON neurons in forward-masking responses: dynamic range and duration of the SPON offset response.

Dynamic Range of SPON Neurons

The probe threshold of IC neurons increases monotonically and linearly as a function of masker level growth (Nelson et al. 2009). Thus, the dynamic range of SPON neurons would be important in realizing this characteristic of forward-masking responses in the IC neurons. In other words, the SPON cell responses caused by the masker, which suppress the IC responses to the probe, should have a large dynamic range. The proposed SPON model has a relatively small dynamic range (~20 dB), consistent with the dynamic range of most SPON neurons analyzed in the experiments. However, Kuwada and Batra (1999) reported a population of OFF neurons from SOC of the rabbits that had large dynamic ranges (up to 65 dB). Note that rabbits have dorsal medial periolivary (DMPO) nucleus rather than SPON, although the two nuclei are presumed to be equivalent. Although the model SPON responses presented here might not account for the shift in probe threshold at high masker levels, collaterals and other ascending inputs (possibly from the dorsal nucleus of the lateral lemniscus (DNLL)) could provide further inhibitory inputs to the postsynaptic IC cell. The time courses of inhibitory influences at the level of the IC are more variable than those observed in the VCN (e.g., Carney and Yin 1989); thus, the inhibitory time constant of the model SPON neuron can be systematically varied to account for the effect of masker level on probe threshold shift in the IC. Furthermore, inclusion of model IC neurons that receive and integrate excitatory and inhibitory inputs with different CFs could also contribute to the probe threshold shift (Nelson et al. 2009).

Duration of SPON Offset Response

Kulesza et al. (2003) showed that offset responses of most SPON neurons, recorded from anesthetized rats, lasted for a short period of time (less than 20 ms), and only offset-sustained neurons (22 % of units) had offset activity that remained active for more than 20 ms (~25–30 ms). In addition, the first spike latency of sustained units was longer than the first spike latency of other units. The offset response of the proposed SPON model lasted for less than 20 ms (consistent with the majority of units recorded in Kulesza et al.’s (2003) physiological experiment). For the default forward-masking condition used in Nelson et al. (2009), the delay between the masker offset and probe onset was set to 10 ms, and the analysis window to measure the neural activity started an additional 10 ms after probe onset (i.e., if the masker-probe delay was 10 ms, the analysis window started 20 ms after masker offset). As a result, either a sustained SPON response with a relatively short IPSP or a nonsustained response with a longer IPSP (as the SPON model proposed in this study) would make the SPON response effective in the default forward-masking condition reported by Nelson et al. (2009). On the other hand, offset responses recorded from awake rabbits (Kuwada and Batra 1999) (presumably from DMPO neurons) lasted for as long as 50 ms. Taking into account the previously mentioned points, one could conclude that either species or anesthetic state might be important in investigating the inhibitory effect of SOC OFF neurons on the forward-masked responses of IC cells.

In our study, IC model responses were inhibited by SPON model responses with different time courses. IC neurons have also previously shown unexpected responses presumably due to an after effect of synaptic inhibition (Sanes et al. 1998). Sanes et al. (1998) reported a prolonged conditioned enhancement and suppression in responses of gerbil IC neurons when a virtual motion stimulus was applied. They suggested GABA_A receptors as the possible postsynaptic mechanism, which could, at least partially, explain unusual responses of IC neurons. Therefore, different time constants of SPON-derived inhibition in our study would be attributable to the dynamics of the GABA receptors. One hypothesis could be that inhibitory inputs projecting to the IC from sources other than SPON (e.g., intrinsic inhibitions, DNLL) could modulate molecular properties of the postsynaptic receptors during the masker stimulus. Then, SPON inhibitory input arrives at the offset of the masker when GABA receptors are modulated, and thus, the effect of the SPON inhibition would be prolonged. Modulation of the GABA receptors might also be time dependent. In this way, GABA receptors could be partially modulated shortly after the masker termination and would be totally modulated after a long period following the masker offset. This idea is in agreement with our results that show a direct relationship between the masker-probe delay and the time constant of the SPON innervation in which a longer time constant was required to suppress the IC model response (to the probe) at higher delays. In conclusion, higher time constants in our model would indicate more GABA receptor modulation, which is required to make the SPON-derived inhibition effective for longer masker-probe delays in the forward-masking paradigm.

In a recent modeling study of SPON neurons, an ON and OFF inhibition was proposed as a potential mechanism of forward masking (Gai 2016) (note that Gai (2016) used frozen noise as the masker, in contrast to the physiological study conducted by Nelson et al. (2009) and the current study, in which the masker was a pure tone at CF). In the Gai study, offset responses of the model SPON (OFF inhibition) were combined with delayed during-stimulus responses of the model DNLL (ON inhibition) to account for observed suppression at the level of the IC. Gai (2016) added an ON inhibition to the model due to the inability of the OFF inhibition to suppress the IC model responses to the probe stimulus for short masker-probe delays (<5 ms). For short delays and for stimuli with no gaps, the SPON offset response to the masker occurred after the IC onset response to the probe, where there was no IC model discharge (onset type) to be suppressed by the OFF inhibition. For this reason, a delayed inhibition from the DNLL was added to suppress the IC model responses to stimuli with short masker-probe delays. Gai’s model (Gai 2016) included only onset-type IC responses; however, for type I (sustained) IC responses, even for stimuli with very short gaps, there will be some spike activity to the probe that can be suppressed by OFF inhibition. Adding DNLL inhibition to the type I IC responses would lead to more rate reduction at short delays compared to the onset units. It is worth pointing out that Nelson et al. (2009) showed the largest threshold shifts caused by the masker for onset units compared to other cell types (this finding was reported for 10-ms masker-probe delay and was not thoroughly discussed for other masker-probe delays, Table 1, Nelson et al. 2009). In conclusion, it is obvious that all types of IC cell responses have to be considered in justifying the potential inhibitory mechanisms underlying forward-masking responses at the level of the IC.

Results obtained from the Gai (2016) study were based on only low-frequency units (~500 Hz) that were of interest for a binaural forward-masking experiment. Nelson et al. (2009) reported the largest threshold shifts for mid-frequency IC cells (4–16 kHz) that were the focus of the current study. SPON units recorded in the electrophysiological experiments (Kulesza et al. 2003; Kulesza et al. 2007) also had much higher CFs compared to the model units in Gai (2016). Moreover, durations of the SPON model responses in Gai (2016) were relatively large (~50 ms), which were closer to the durations reported for DMPO neurons rather than the prevalent duration of the SPON offset responses.

CONCLUSIONS

This study describes a phenomenological model that simulates the physiological responses of SPON neurons to CF tones, BBN, and SAM stimuli. Previously developed models of AN fibers and VCN bushy neurons were used as a front end to model the responses of SPON neurons. Responses of the VCN model were convolved with an alpha function with appropriate parameters to simulate the inhibitory input to SPON neurons. A slope-sensing mechanism inspired by the behavior of phasic neurons was used to simulate the responses of SPON cells. The proposed model successfully simulated the offset-type response to CF tones and BBN as well as phase-locked responses to the envelope of SAM stimuli. To explore a possible mechanism of forward masking at the level of the IC, model SPON responses were used as an inhibitory input to a model of the IC. A systematic variation in the time course of the inhibitory inputs accounted for probe threshold shifts observed physiologically as a function of masker-probe delay. A more complex interaction between SPON and IC model responses in the forward-masking paradigm will be required to explain all physiological response properties for forward masking observed at the level of the IC.