Abstract
The sophistication of the force fields, algorithms and hardware used for molecular dynamics (MD) simulations of proteins is continuously increasing. No matter how advanced the methodology, however, it is essential to evaluate the appropriateness of the structures sampled in a simulation by comparison with quantitative experimental data. Solution nuclear magnetic resonance (NMR) data are particularly useful for checking the quality of protein simulations, as they provide both structural and dynamic information on a variety of temporal and spatial scales. Here, various features and implications of using NMR data to validate and bias MD simulations are outlined, including an overview of the different types of NMR data that report directly on structural properties and of relevant simulation techniques. The focus throughout is on how to properly account for conformational averaging, particularly within the context of the assumptions inherent in the relationships that link NMR data to structural properties.
Keywords: Molecular dynamics, Nuclear magnetic resonance, Protein, Biomolecular simulation
Introduction
In order to understand the function and malfunction of proteins, it is essential to characterise not only their structure but also their dynamics. Biomolecular simulation is an extremely valuable tool for probing these at a detailed molecular level, uniquely allowing direct visualisation. It can suffer, however, from limited force field accuracy and insufficient sampling. Because of this, it is important to check, and, if necessary, improve the relevance of, the structures sampled during a simulation by comparing back-calculated experimentally measurable quantities with experimental data. Nuclear magnetic resonance (NMR) data is particularly useful for such comparisons because it reports on both structure and dynamics, although this information can be encoded in a complex manner.
The focus here is on the use of solution NMR data to validate the ensembles of structures produced by molecular dynamics (MD) simulations of proteins using atomic-level force fields, and to bias such simulations towards structures that are in keeping with the data. Whilst solid state NMR data have recently been utilised for protein structure determination and refinement (Castellani et al. 2002; Andronesi et al. 2005; Siemer et al. 2005; Manolikas et al. 2008; Van Melckebeke et al. 2010), a field in which many of the principles and techniques discussed here are also relevant, these topics are outside the scope of this article.
This review begins by considering the average nature of NMR data, followed by an outline of the relationships that link NMR observables to structural properties of proteins. Subsequently, the use of NMR data to validate MD simulations of proteins is discussed, including factors that affect the agreement between back-calculated and experimental observables. Different means of restraining or biasing simulations to fit NMR data are then described and evaluated. The article ends with a summary of the state of the art, and some thoughts on future developments.
Averaging of NMR data
An important property of NMR data is that they are ensemble-averages over the potentially different conformations of the many molecules present in the experiment, and time-averages over motions that occur faster than the chemical shift difference or the inverse of the coupling constant, depending on the type of NMR experiment (Bryant 1983). This averaging has important consequences when NMR data are interpreted in terms of structural properties, particularly for mobile or disordered states.
The ensemble of different structures sampled by the many molecules present over the duration of the experiment can be thought of in terms of distributions of values of the structural properties, such as dihedral angles or inter-nuclear distances, that are related to NMR observables as outlined in Section 3. These distributions may or may not be correlated to one another. Each value of the structural property in the distribution may give rise to a different value of the related NMR observable; it is the average value of the NMR observable that is measured in an experiment. Because of this, the most naive structural interpretation of an NMR observable in terms of a single value of a structural property back-calculated from the averaged observable is only appropriate if the molecule is rigid (Fig. 1). Reconstruction of the distributions of structural properties, and therefore the ensemble of structures, from the averaged NMR observables is a non-trivial problem, as the relationships linking NMR observables to structural properties are often multiple-valued and non-linear (see Section 3). An advantage of using MD simulations to interpret NMR data is that the shape of the underlying distribution of structural properties described by the data does not have to be assigned a priori as it does when using analytical models. Properly accounting for conformational averaging remains difficult, however, and is therefore discussed throughout this review.
Fig. 1.
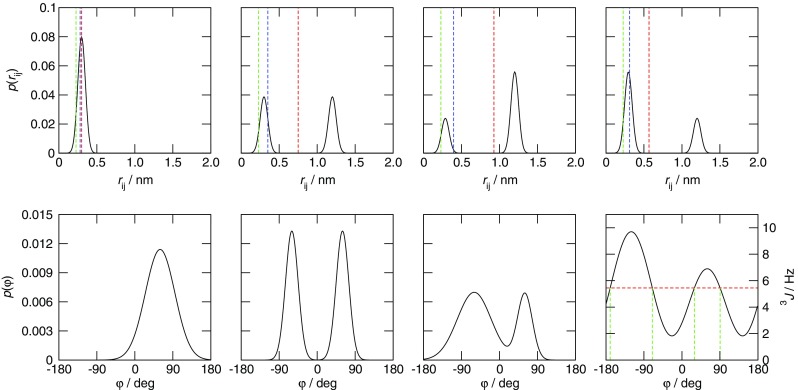
The combined effect of conformational averaging and the non-linear and multiple-valued relationships linking NMR observables to structural properties. Upper row four different distributions of inter-nuclear distances r ij and (dashed lines) the corresponding (red) linearly, (blue) r −3 and (green) r −6 averaged distances. All four distributions have the same r −6 average (0.227 nm) upon which PREs and many NOEs depend, and are therefore indistinguishable at the level of the NMR observable. Lower row three different distributions of values of a dihedral angle ϕ and (rightmost graph) the Karplus relation for the ϕ angle of the protein backbone (Pardi et al. 1984). All three distributions give rise to the same average 3 J-value (5.45 Hz, red dashed line in rightmost graph) and thus are indistinguishable at the level of the NMR observable. (Rightmost graph, green dashed line) the four dihedral angle values that would be predicted from a 3 J-value of 5.45 Hz without allowing for conformational averaging
Relating NMR data to protein structure
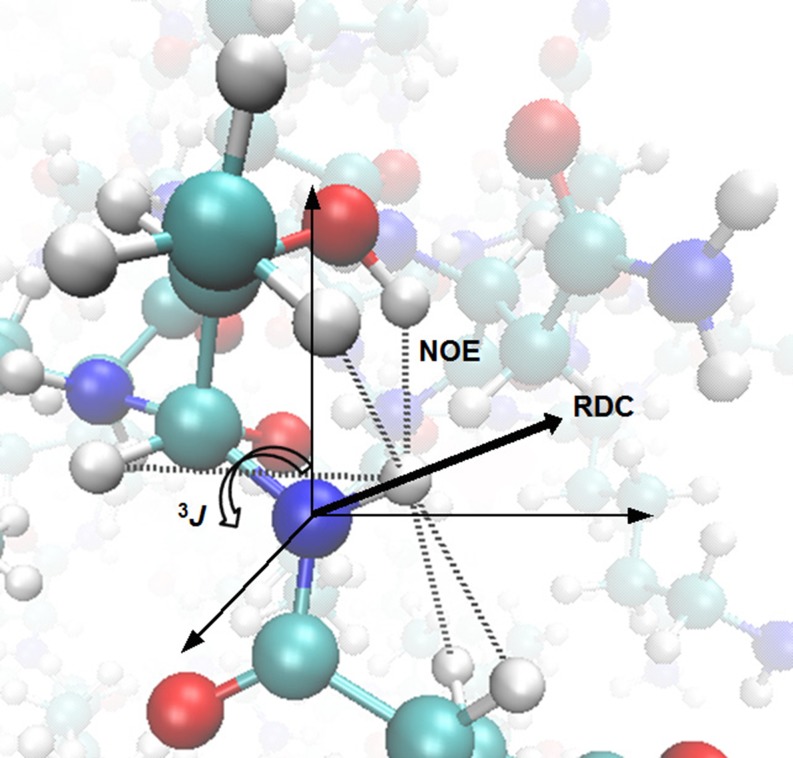
In order to compare MD simulations with NMR data, the value of the NMR observables Q must be calculated from the Cartesian coordinates of the protein r or vice versa. In principle, Q can be calculated from r using quantum-chemical methods (Oldfield 2002; Bühl and van Mourik 2011), but the accuracy that can currently be reached is rather low because a number of approximations must be made due to the expense of the calculations (Mulder and Filatov 2010; Frank et al. 2012). This also renders such calculations too expensive to carry out “on the fly” during an MD simulation. Therefore, protein structure is generally related to observable quantities according to semi-empirical, approximate functions Q(r) and their inverses. These relationships are outlined and discussed below for commonly used NMR observables that provide three main types of structural information: distance, angular, and orientational (Fig. 2).
Fig. 2.
The types of structural information obtained from the NMR observables introduced in Section 3: dashed lines short-range NOE-derived distances, curved arrow dihedral angle ϕ reported on by 3 J HNCαHα-couplings and heavy line the orientation of the N–H bond vector relative to the molecular frame specified by an alignment tensor A attainable from RDCs. The protein atoms are coloured according to type: cyan carbon, blue nitrogen, red oxygen and white hydrogen
Distance information
Short-range distances up to approximately 0.6 nm are obtained from nuclear Overhauser effects (NOEs), the transfer of spin polarisation between nuclei through space via cross-relaxation (Wüthrich 1986). Generally, only semi-quantitative distance information is extracted from NOESY spectra using the isolated spin pair approximation (ISPA)
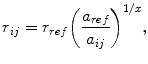 |
1 |
where r ij is the distance between two nuclei i and j, a ij is the cross-peak intensity or volume and x = −3 if internal structural fluctuations are significantly faster than the tumbling time of the molecule, or −6 otherwise (Tropp 1980). a ref is a reference intensity corresponding to an inter-nuclear distance r ref that is known due to internal geometry; these serve to calibrate the conversion. This approach assumes that the mixing time τ m is short, so that the NOE buildup is approximately linear, and that internal motion is negligible. In practise, these expectations are not always met. A short mixing time also limits the effects of spin diffusion (Kalk and Berendsen 1976), one of the major causes of inaccuracy in NOE-derived distances (Keepers and James 1984). In most cases, spin diffusion leads to enlarged NOE intensities and, therefore, under-estimated inter-nuclear distances. A complete description of spin diffusion can only be obtained with a full relaxation matrix formalism, which is computationally very intensive. Nevertheless, several approaches are available for correcting NOE-derived distance restraints for spin diffusion effects during iterative structure refinement (Marion et al. 1987; Boelens et al. 1988; Yip and Case 1989; Borgias and James 1990; Borgias et al. 1990; Post et al. 1990; Edmondson 1992; Leeflang and Kroon-Batenburg 1992; Linge et al. 2004), although these are typically not used in the analysis or biasing of MD simulations.
Distances obtained using Eq. 1 are applied with large tolerances to account for the many sources of uncertainty mentioned above. Often, only an upper bound on the inter-nuclear distance is used, with the sum of the van der Waals radii of the two nuclei involved acting as a proxy for the lower bound. The use of conservative bounds compensates for alteration of cross-peaks by spin diffusion or partial overlap, as well as other possible sources of error. Alternatively, the NOE intensities may simply be sorted into a few groups based on relative peak intensities, with weak, medium and strong intensities corresponding to short, medium and long distances. The upper bounds on the distance for each group are chosen based on cross-peaks stemming from pairs of protons for which the distance can reasonably be estimated, such as those identified as being in regular secondary structure elements according to chemical shift data or a priori structural knowledge. Upper bounds can also be estimated from the maximum distance for which an NOE cross-peak is expected to be observed (0.5−0.6 nm). Whilst a single NOE-derived distance is relatively imprecise, this is compensated for by the large numbers of NOEs typically measured.
In certain cases, such as large proteins or disordered states, long-range distance information may be desirable. Distances in the range 1.2−2.0 nm can be obtained from paramagnetic relaxation enhancement (PRE) experiments, which exploit the change in the relaxation rate of a nuclear spin induced by the presence of a distant paramagnetic group (Solomon 1955; Gillespie and Shortle 1997; Battiste and Wagner 2000; Donaldson et al. 2001; Clore and Iwahara 2009). The paramagnetic relaxation enhancement is quantified by the ratio of the intensities of the cross-peaks with the paramagnetic group present and absent (diamagnetic state), I
para/I
dia. From this, the paramagnetic relaxation rate  can be determined by fitting (Gillespie and Shortle 1997; Battiste and Wagner 2000)
can be determined by fitting (Gillespie and Shortle 1997; Battiste and Wagner 2000)
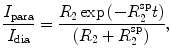 |
2 |
where t is the total INEPT delay time and R 2 is the intrinsic relaxation rate, usually estimated from the half-height linewidth in the diamagnetic state. The electron–proton distance is then calculated according to
| 3 |
where ω H is the Larmor frequency of the proton, τ c is the correlation time of the electron–proton vector and K is a combination of physical constants.
The number of PRE-derived distances obtained is limited by the need to include a paramagnetic centre, which typically requires the creation of many artificial constructs with paramagnetic labels attached. Moreover, the presence of the label must be accounted for when inferring and utilising the inter-nuclear distances.
Angular information
Information regarding dihedral angles spanned by three covalent bonds or the geometry of hydrogen bonds is provided by through-bond 3 J-couplings. These are usually related to the molecular geometry using the Karplus relation: (Karplus 1959)
| 4 |
where θ is the torsion or hydrogen bond angle and A, B and C are empirical parameters. More complex relationships have also been proposed (Haasnoot et al. 1979; Haasnoot et al. 1981; Imai and Osawa 1990; Suardıaz et al. 2007; Schmidt 2007). The constants A, B and C are generally estimated by fitting 3 J-values measured for molecules whose dihedral angle values are presumed to be known. More sophisticated fitting methods such as Bayesian inference have also been used (Habeck et al. 2005). Efforts have been made to incorporate the effects of dynamics and averaging into the parameters by self-consistent fitting (Schmidt et al. 1999; Pérez et al. 2001) and by deriving the parameters from ensembles of structures obtained from MD simulations (Brüschweiler and Case 1994; Lindorff-Larsen et al. 2005b; Vögeli et al. 2007), but such parameters are not necessarily transferable. When the Karplus relation is used, its approximate form and parameters mean that 3 J-couplings should be interpreted with an uncertainty of at least ±1 Hz (Allison and van Gunsteren 2009; Steiner et al. 2012). The multiple-valued nature of this relationship further complicates the extraction of angular information, as a single 3 J-value can be compatible with up to four dihedral angle values (see Fig. 1, lower right graph). Whilst this degeneracy can, in some cases, be resolved by the measurement of 3 J-couplings between different sets of atoms spanning a given dihedral angle (Smith et al. 1991; Schwalbe et al. 2001; Allison and van Gunsteren 2009), for dihedral angles in mobile parts of a protein such as loops or side-chains, the analytical derivation of angular information remains extremely difficult.
Dihedral angle information can also be extracted from the chemical shifts of the protein nuclei, albeit indirectly. Although chemical shifts are influenced by a wide array of structural properties (Wagner et al. 1983; Osapay and Case 1991; Williamson and Asakura 1993; Case 1995; Wishart et al. 1991, 1995), the dependence of Cα and Cβ chemical shifts on the backbone ϕ and ψ dihedral angles (Pastore and Saudek 1990; Spera and Bax 1991; de Dios et al. 1993) is routinely used to infer protein secondary structure (Spera and Bax 1991; Wishart et al. 1991, 1992; Cornilescu et al. 1999; Peti et al. 2001; Yao et al. 2001; Wang and Jardetzky 2002; Eghbalnia et al. 2005; Marsh et al. 2006; Shen et al. 2009). There is no simple analytical relationship linking chemical shifts to protein structure. Methods for calculating chemical shifts using quantum mechanics are improving, but remain too slow to be applicable during simulations (Mulder and Filatov 2010; Frank et al. 2012). A number of fast empirical methods for calculating chemical shifts approximately have been developed (Xu and Case 2001; Neal et al. 2003; Meiler 2003; Shen and Bax 2007; Kohlhoff et al. 2009; Shen and Bax 2010; Han et al. 2011; Nielsen et al. 2012), although even these state-of-the-art programs often result in errors much larger than the deviation between back-calculated and experimental chemical shifts (Kjaergaard and Poulsen 2012), and so should be used with caution.
Orientational information
One source of orientational information is residual dipolar couplings (RDCs) (Tjandra and Bax 1997; Blackledge 2005) between bonded or non-bonded pairs of nuclei. Measurement of RDCs requires the protein to be partially aligned with respect to the magnetic field direction (Bax 2003). Various alignment media have been developed for this task (Sanders et al. 1994; Tjandra and Bax 1997; Clore et al. 1998; Hansen et al. 1998; Sass et al. 1999. 2000; Koenig et al. 1999; Tycko et al. 2000). Partial alignment prevents complete isotropic rotation of the protein, which would average the couplings to zero, but allows sufficient rotation to reduce the dipolar couplings to manageable magnitudes.
RDCs are related to the angle θ between an inter-nuclear vector r ij and the direction of the magnetic field, as well as the length of the inter-nuclear vector r ij , according to:
| 5 |
where γ i and γ j are the gyromagnetic ratios of the two nuclei, μ 0 is the magnetic permeability of vacuum and h is Plancks constant. The inter-nuclear distance r ij is usually assumed to be constant when i and j are bonded, consistent with the constraint of bond lengths in classical atomic-level force fields.
In order to simplify the interpretation of RDCs, the alignment of the protein with respect to the magnetic field is often separated from its internal structure. If the protein is assumed to be rigid, Eq. 5 can be factorised into structural and orientational components by using an alignment tensor, A (Saupe 1968), to describe the non-isotropic alignment of the protein, represented by the molecular frame, and defining the orientation of the inter-nuclear vector with respect to the molecular frame (Blackledge 2005):
| 6 |
where ζ
ij,α is the angle between r
ij and the α-axis of the molecular frame, and the nine components, five of which are independent, of the alignment tensor are given by  , with ξα the angle between the α-axis of the molecular frame and the magnetic field direction. The alignment tensor encompasses averaging over different orientations of the protein. Whilst some have averaged the angles ζ
ij,α over the trajectory prior to fitting A (Markwick et al. 2009), this is not strictly correct, as the derivation of Eq. 6 depends on the assumption that the molecule is rigid. Averaging of ζ
ij,α also requires superposition of the structures, which cannot be done sensibly if the protein undergoes large-scale structural changes during the simulation. Thus, although the use of an alignment tensor greatly simplifies the extraction of structural information from RDCs, the assumptions inherent in its use are not always appropriate. This is particularly pertinent for proteins that are partially or entirely disordered, but even small fluctuations may be sufficient to perturb the alignment (Louhivuori et al. 2007), although such fluctuations appear to be largely uncorrelated with the changes in alignment (Louhivuori et al. 2006). Even when it is appropriate to use an alignment tensor, the extraction of structural information from RDCs is not trivial, due to the degeneracy and non-linearity of Eqs. 5 and 6.
, with ξα the angle between the α-axis of the molecular frame and the magnetic field direction. The alignment tensor encompasses averaging over different orientations of the protein. Whilst some have averaged the angles ζ
ij,α over the trajectory prior to fitting A (Markwick et al. 2009), this is not strictly correct, as the derivation of Eq. 6 depends on the assumption that the molecule is rigid. Averaging of ζ
ij,α also requires superposition of the structures, which cannot be done sensibly if the protein undergoes large-scale structural changes during the simulation. Thus, although the use of an alignment tensor greatly simplifies the extraction of structural information from RDCs, the assumptions inherent in its use are not always appropriate. This is particularly pertinent for proteins that are partially or entirely disordered, but even small fluctuations may be sufficient to perturb the alignment (Louhivuori et al. 2007), although such fluctuations appear to be largely uncorrelated with the changes in alignment (Louhivuori et al. 2006). Even when it is appropriate to use an alignment tensor, the extraction of structural information from RDCs is not trivial, due to the degeneracy and non-linearity of Eqs. 5 and 6.
Validation of MD simulations with NMR data
Comparison of the values of NMR observables back-calculated from and averaged over an ensemble of structures generated by an MD simulation to experimental data allows assessment of both the quality of the structures and the extent of sampling. There are two important points to consider in making such a comparison, however.
Firstly, because there are almost always fewer NMR observables N obs than degrees of freedom of a protein N df, conformational averaging must be accounted for, and the relationships linking observables to structural properties are non-linear and/or multiple-valued, it is likely that many different ensembles of structures can fit the experimental data equally well on average. There are many documented examples of this (Glättli and van Gunsteren 2004; Dolenc et al. 2010; Missimer et al. 2010; Allison et al. 2011, 2012; Eichenberger et al. 2012; Niggli et al. 2012), including several in which the majority of the NMR data are equally compatible with the folded or unfolded states (Daura et al. 1999, 2001; Peter et al. 2003; Zagrovic and van Gunsteren 2006). This insensitivity of NMR observables to the shape of the underlying probability distribution of structural properties has been demonstrated analytically (Bürgi et al. 2001) and is illustrated in the upper panel of Fig. 1. If it is possible to use multiple experimental techniques to measure different observables that report on the same or related structural features, but are subject to different types of averaging, then these can be combined to give more information about the shape of the underlying distribution (Choy et al. 2002; Allison et al. 2009). In general, combining many different datasets to maximise the amount of experimental information is a useful tactic, but is only strictly appropriate if the data were measured at the same or very similar thermodynamic state points.
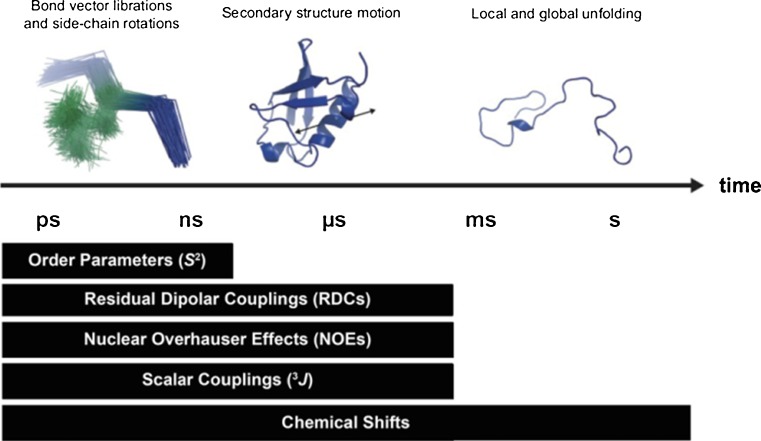
A further concern is the extent of sampling of different conformations. In the limits of an infinitely long simulation, all possible conformations will occur with a relative probability given by the Boltzmann distribution. In practice, however, the length of a simulation is finite and often rather short in comparison to the time-scale encompassed by NMR data. The latter depends on the experiment and on the field strength (Fig. 3). Whilst the length of MD simulations of proteins has increased by several orders of magnitude from the 9.2 ps of the first MD simulation of a protein in 1976 (McCammon et al. 1977), with ns and even μs time-scales now routinely accessible, and ms simulations possible with specialised hardware (Shaw et al. 2009), still longer simulations may be needed for comparison with RDCs and chemical shifts, as well as to obtain statistically good sampling of faster motions. Indeed, earlier studies utilising shorter simulation times mostly, although not always (Philippopoulos et al. 1997), found reasonable agreement with S 2 order parameters, which report on ps–ns motions of bond vectors (Fig. 3), but sometimes struggled to reproduce NMR data averaged over longer time-scales (Brüschweiler et al. 1992; Chandrasekhar et al. 1992; Koerdel and Teleman 1992; Palmer and Case 1992; Eriksson et al. 1993; Smith et al. 1995a, b; Nanzer et al. 1997). Even in more recent studies, the agreement with experimental data is often worst for residues in loops or disordered regions (Wrabl et al. 2000; Tong et al. 2009); in some cases, these regions are simply excluded from the analysis (Showalter and Brüschweiler 2007).
Fig. 3.
The degree of protein conformational motion associated with the time-scales encompassed by the different types of NMR observables discussed here. Note that the scale on the time axis is logarithmic
Further evidence that longer simulations are required is the typically better agreement with experimental data obtained for small systems such as peptides, for which longer simulations have been possible for some time (Trzesniak et al. 2005). Only with the recent construction of ANTON, a massively parallel supercomputer purpose-built for carrying out MD simulations, has it become tractable to run ms-length MD simulations of proteins (Shaw et al. 2009). As well, extensive parallelisation of MD codes (Plimpton 1995; Phillips et al. 2005) and use of GPUs (Schmid et al. 2010; Stone et al. 2010; Brown et al. 2011) have opened up the possibility of conducting hundreds of ns or even μs simulations routinely even without access to supercomputers. Early results from a 1.2 μs simulation of ubiquitin showed that simultaneous consideration of all, rather than solely internal, motions reduced the discrepancies between calculated and experimental S 2 values (Maragakis et al. 2008). More recently, a 200 μs high-temperature simulation aimed at sampling the disordered state of Acyl-CoA-binding protein (ACBP) gave reasonable agreement with experimental NMR relaxation rate data (Lindorff-Larsen et al. 2012b), although the radius of gyration was smaller than the experimental value despite the elevated temperature, and comparison with the PRE-derived distances available for this protein (Teilum et al. 2002) was not made.
Despite being two orders of magnitude longer than previous simulations, the aforementioned simulation of ACBP was not converged, giving some indication of the lengths of simulations that will be required to characterise disordered states and other systems in which large-scale conformational motions are expected. Such long simulation times are required because of the low probability of crossing the high energy barriers that can exist between different conformations that co-exist or interconvert during an NMR experiment. One possible means of counteracting this is to simultaneously run multiple independent simulations of the same protein starting from randomly selected different conformations. So long as the starting conformations are sufficiently different to allow access to all barrier-separated regions of the potential energy surface, averaging over the resulting pooled ensemble of structures should give better agreement with experimental data. This was shown to be the case for NMR data including RDCs, although not 3 J-couplings across hydrogen bonds (Lange et al. 2010). In a similar way, enhanced sampling methods such as replica exchange (Fawzi et al. 2008) also result in improved agreement with experimental data.
Another means of visiting more regions of conformational phase space and crossing barriers that looks to be particularly promising is accelerated molecular dynamics (AMD) (Hamelberg et al. 2004). The potential energy landscape is smoothed by raising the low-energy regions, resulting in accelerated exchange between low-energy conformations whilst retaining the essential details of the landscape. The acceleration level is chosen according to reproduction of experimental data, and the resulting ensemble of structures is reweighted such that the correct canonical Boltzmann distribution is obtained. Due to the acceleration procedure, the time-scale of the motions sampled using AMD is not known explicitly, and can only be inferred indirectly by comparison with the time-scale of the NMR data to which the ensembles of structures are compared. Somewhat remarkably, given the range of time-scales associated with different types of NMR data (Fig. 3), ensembles of structures obtained at the RDC-optimal acceleration level also reproduce experimental 3 J-couplings and order parameters (Markwick et al. 2009) or chemical shifts (Markwick et al. 2010).
A further potential source of discrepancy between back-calculated and experimental NMR data is the quality of the force field. Newly accessible long simulations of proteins are allowing detection of shortcomings in force fields that were not visible in shorter simulations (Klepeis et al. 2009) or in the simulations of small molecules usually used for force field parametrisation (Lindorff-Larsen et al. 2012a). Eight different force fields (Mackerell et al. 1998, 2004; Kaminski et al. 2001; Duan et al. 2003; Mackerell 2004; Hornak et al. 2006; Best and Hummer 2009; Lindorff-Larsen et al. 2010; Piana et al. 2011) were recently used to run 10-μs simulations of ubiquitin and GB3 (Lindorff-Larsen et al. 2012a). Four of the most recent variants produced ensembles of structures in very good agreement with experimental NMR data including 3 J-couplings, RDCs and S 2 order parameters. The key change responsible for the improved agreement with experimental data appears to be modification of the backbone potential, as many other studies using the same and other force fields refined in this way have also shown good agreement with experimental NMR data including 3 J-couplings, RDCs and chemical shifts (Hornak et al. 2006; Buck et al. 2006; Showalter and Brüschweiler 2007; Showalter et al. 2007; Markwick et al. 2007; Trbovic et al. 2008; Li and Brüschweiler 2009; Schmid et al. 2011; Beauchamp et al. 2012; Robustelli et al. 2012).
It cannot be excluded that uncertainty introduced by the use of approximate relationships Q(r) could be causing some of the disagreement between back-calculated and experimental data. For instance, 3 J-couplings calculated using density functional theory rather than the Karplus relation (Eq. 4) from 500 ps simulations agree better with experimental data than those calculated from the X-ray or NMR model structures, despite the short length of the simulations (Markwick et al. 2002). It is likely, however, that limited sampling and force field inaccuracy play the most significant roles. A means of overcoming both of these problems simultaneously is to restrain or bias simulations to fit experimental data, as outlined in the next section. Effectively, the force field is adjusted to favour structures that agree with the experimental data and the sampling is directed towards these structures.
Biasing MD simulations to fit NMR data
To drive simulations to sample areas of conformational space that are in agreement with experimental data, a restraining function V
restr(r(t)) that penalises deviation from the experimental data is added to the physical interaction function term 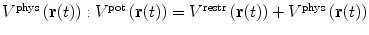 . Conventional restraining terms are harmonic:
. Conventional restraining terms are harmonic:
| 7 |
where  is a user-defined force constant,
is a user-defined force constant, 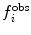 is the value of the i
th observable measured experimentally or the corresponding structural property and
is the value of the i
th observable measured experimentally or the corresponding structural property and  is the value of the observable or structural property back-calculated from the simulation. The more
is the value of the observable or structural property back-calculated from the simulation. The more  deviates from
deviates from 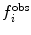 the larger the energy penalty and the resulting forces on the protein. The force constant
the larger the energy penalty and the resulting forces on the protein. The force constant  allows tuning of the strength of the restraint, providing a means of accounting for experimental or other uncertainty.
allows tuning of the strength of the restraint, providing a means of accounting for experimental or other uncertainty.
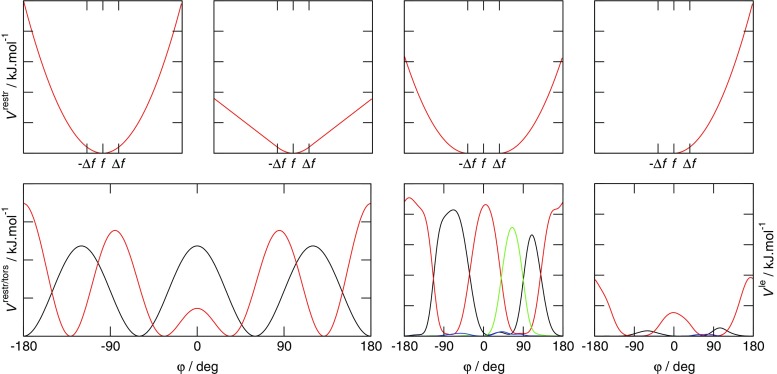
Various modifications of Eq. 7 are possible (Fig. 4). In many applications, the penalty function becomes linear when 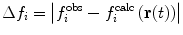 is large to prevent excessive forces. The restraint potential may be made “flat-bottomed” by only enforcing the restraint potential if Δf
i is greater than some threshold value. This is another useful means of accounting for uncertainty in the experimental data or in the relationship that converts between observables and structural properties. For NOE-derived distances, a half-harmonic potential is typically used, so that only distances larger than
is large to prevent excessive forces. The restraint potential may be made “flat-bottomed” by only enforcing the restraint potential if Δf
i is greater than some threshold value. This is another useful means of accounting for uncertainty in the experimental data or in the relationship that converts between observables and structural properties. For NOE-derived distances, a half-harmonic potential is typically used, so that only distances larger than 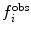 are penalised.
are penalised.
Fig. 4.
Examples of the types of potential functions used to restrain or bias MD simulations to fit experimental data. Upper row, left to right a harmonic potential (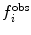 is shown as f for clarity), a harmonic potential that becomes linear when
is shown as f for clarity), a harmonic potential that becomes linear when 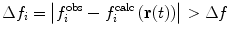 , a "flat-bottomed" harmonic potential that does not penalise deviations of less than Δf from
, a "flat-bottomed" harmonic potential that does not penalise deviations of less than Δf from 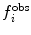 and a half-harmonic potential as used for NOE-derived distances. Lower row, left-hand side potentials from (black) the torsional term of a force field and (red) a harmonic 3
J-value restraint acting on a dihedral angle ϕ. Lower row, right-hand side two sets of local elevation end-point potentials from simulations biased to fit multiple types (shown in black, red, green and blue) of 3
J-values reporting on the same dihedral angle. Left a case in which even allowing for conformational averaging, it is not possible to find a set of dihedral angle values in keeping with all four 3
J-values, so that the local elevation potentials clash with one another and continue to build throughout the simulation. Right a case where after an initial build-up period in which the dihedral angle is biased towards values that on average satisfy the data, the potentials remain static for the remainder of the simulation (Allison and van Gunsteren 2009)
and a half-harmonic potential as used for NOE-derived distances. Lower row, left-hand side potentials from (black) the torsional term of a force field and (red) a harmonic 3
J-value restraint acting on a dihedral angle ϕ. Lower row, right-hand side two sets of local elevation end-point potentials from simulations biased to fit multiple types (shown in black, red, green and blue) of 3
J-values reporting on the same dihedral angle. Left a case in which even allowing for conformational averaging, it is not possible to find a set of dihedral angle values in keeping with all four 3
J-values, so that the local elevation potentials clash with one another and continue to build throughout the simulation. Right a case where after an initial build-up period in which the dihedral angle is biased towards values that on average satisfy the data, the potentials remain static for the remainder of the simulation (Allison and van Gunsteren 2009)
Either the experimental observable or the related structural property may be restrained. In either case, relationships such as those outlined in Section 3 are used to convert between structural properties and experimental observables, thus any inaccuracies or uncertainties in the nature or parametrisation of these relationships cannot be escaped. If the relationship is highly non-linear, a small change in the protein coordinates can have a large impact on the value of the back-calculated observable. For multiple-valued relationships, such as the Karplus relation (Eq. 4), restraining the structural property is only appropriate in cases where additional information exists indicating that only one of the multiple values is possible and specifying which value it is. For both non-linear and multiple-valued relationships, the restraining potential energy landscape is likely to be rugged, and specialised sampling techniques may be required.
The issues discussed at the start of Section 4 mean that restrained simulations tread a fine line between over- and under-fitting. Over-fitting occurs when the restraints are too stringently enforced (see Section 5.1), whereas under-fitting occurs when N df ≫ N obs (Bonvin and Brünger 1995), such that many different ensembles of structures fit the data equally well. A means of checking for under-fitting is cross-validation (Brünger 1992, 1993; Brünger et al. 1993), in which the reproduction of “free” data not used as restraints, which may comprise completely independent data or a randomly excluded subset of the restraint data, as well as of the restraint data, is assessed. Satisfaction of the restraints generally improves with more degrees of freedom, whereas reproduction of the free data becomes worse.
Instantaneous restraining
The most basic restraining method is instantaneous restraining, in which a single copy of the protein is required to fit all of the data simultaneously at each point in time. Whilst this method is widely used, particularly in protein structure determination, it ignores the average nature of NMR data. Even if a protein only samples two different conformations, the structure produced by enforcing the restraints on a single copy will not only be irrelevant, but may well be physically impossible (Kessler et al. 1988). The rarity of examples in which instantaneous restraining fails simply highlights the lack of NMR data relative to the number of degrees of freedom (N obs ≪ N df). Additionally, data pertaining to mobile regions are often omitted. Given that a special feature of NMR data is that they can be measured for dynamic states, it is desirable to account for conformational averaging in the restraining methodology. There are two possible means of doing so: ensemble-averaging (Scheek et al. 1991; Kemmink et al. 1993; Bonvin et al. 1994; Mierke et al. 1994) and time-averaging (Torda et al. 1989, 1990).
Ensemble averaging
In ensemble-averaged restraining, multiple independent replicas are simulated in parallel. At each integration step, the quantity to be restrained is back-calculated from each replica and then averaged over the N rep replicas before comparison with the experimental value:
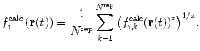 |
8 |
The value of x depends on the type of data and whether the observable or the related structural property is restrained. For 3 J-couplings, the non-linearity is already accounted for by use of the Karplus relation to back-calculate the couplings from the protein coordinates, so x = 1, whereas for NOE- and PRE-derived distances, which are structural properties, x = −3 or −6.
Ensemble-averaging accounts, to some extent, for the average nature of NMR data, although the number of replicas can never be as large as the number of different conformations over which the measured NMR data are averaged, because of the limited amount of experimental data. Averaging over too many replicas results in under-fitting, where the ensemble is primarily determined by the force field. A more elaborate version of ensemble-averaging that attempts to correct for this is the MUMO method (Richter et al. 2007), in which each type of data can be restrained across a different number of replicas. This provides a means by which to represent the different time- and spatial-scales over which each type of data are averaged, but thus far MUMO has only been used in simulated annealing-based structure refinement (Richter et al. 2007; Fenwick et al. 2011).
A further problem with ensemble-averaging is that, although the structures sampled in each individual trajectory will be correctly Boltzmann-weighted, the ensemble of structures drawn from the different trajectories over which the average is calculated at each point in time is not necessarily Boltzmann-weighted. A possible solution to this in which the probability of each replica was treated as a parameter in the simulation was explored, but found to suffer from a number of drawbacks of its own (Fennen et al. 1995).
Despite the aforementioned issues, ensemble-averaging has been used to generate ensembles of structures representative of the dynamics of folded proteins (Hess and Scheek 2003; Best and Vendruscolo 2004; Clore and Schwieters 2004; Lindorff-Larsen et al. 2005a; Clore and Schwieters 2006; De Simone et al. 2009; Robustelli et al. 2010), the variability of the transition-state for folding (Vendruscolo et al. 2001; Paci et al. 2002, 2004; Lindorff-Larsen et al. 2004), molten-globule (Paci et al. 2005) and disordered states (Dedmon et al. 2005; Kristjansdottir et al. 2005; Francis et al. 2006; Allison et al. 2009; Esteban-Martín et al. 2010) of proteins, the conformational equilibrium between major substates (Camilloni et al. 2012) and transiently populated excited states (Robustelli et al. 2010) using NMR and other types of experimental data.
Time-averaging
Another means of accounting for the average nature of NMR data is time-averaging (Torda et al. 1989, 1990, 1993; Bonvin et al. 1994). A single copy of the protein is simulated, and an exponentially-weighted time-average is compared to the experimental observable:
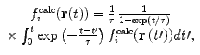 |
9 |
where τ is the memory relaxation time. In this way, more recent structures contribute most to the average, avoiding 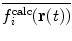 becoming less sensitive to instantaneous fluctuations for increasing values of t (Scott et al. 1998). Time-averaging is computationally more efficient than ensemble-averaging, as only a single copy of the protein needs to be simulated. However the time-scale encompassed by the average is generally much shorter than the time-scale over which the experimental data were averaged, with τ typically on the order of 5–10 ps. This means that the structures contributing to the time-average are likely to be highly correlated, in comparison to ensemble-averaging, where each replica is independent. Thus, whilst time-averaging is efficient at capturing fluctuations up to the time-scales of the averaging time (Hess and Scheek 2003), ensemble-averaging may be a better approach when multiple rather different conformations contribute to the average, as it allows them to co-exist simultaneously (Fennen et al. 1995).
becoming less sensitive to instantaneous fluctuations for increasing values of t (Scott et al. 1998). Time-averaging is computationally more efficient than ensemble-averaging, as only a single copy of the protein needs to be simulated. However the time-scale encompassed by the average is generally much shorter than the time-scale over which the experimental data were averaged, with τ typically on the order of 5–10 ps. This means that the structures contributing to the time-average are likely to be highly correlated, in comparison to ensemble-averaging, where each replica is independent. Thus, whilst time-averaging is efficient at capturing fluctuations up to the time-scales of the averaging time (Hess and Scheek 2003), ensemble-averaging may be a better approach when multiple rather different conformations contribute to the average, as it allows them to co-exist simultaneously (Fennen et al. 1995).
One problem with time-averaging is that 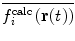 lags behind
lags behind  , thus even if the current conformation of the protein is in keeping with the experimental data, the time-average will not be and the protein will continue to experience a restraining force. This issue is particularly important in the case of 3
J-values. Alternative functional forms for the restraint term have been proposed to overcome this problem. One possibility is to use a biquadratic restraining function (Scott et al. 1998; Christen et al. 2007):
, thus even if the current conformation of the protein is in keeping with the experimental data, the time-average will not be and the protein will continue to experience a restraining force. This issue is particularly important in the case of 3
J-values. Alternative functional forms for the restraint term have been proposed to overcome this problem. One possibility is to use a biquadratic restraining function (Scott et al. 1998; Christen et al. 2007):
| 10 |
In this way, the energy penalty will be zero if either 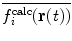 or
or 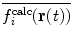 agrees with
agrees with 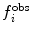 .
.
Rather than weight the time-average and instantaneous values equally, an elliptic restraining function, incorporating a linear combination  and
and 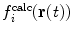 with relative weights specified by the mixing parameter A
ell ∈ [0 . . . 1], may be used (Scott et al. 1998):
with relative weights specified by the mixing parameter A
ell ∈ [0 . . . 1], may be used (Scott et al. 1998):
| 11 |
This method allows the relative weights of 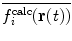 and
and 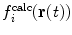 to be adjusted by the user.
to be adjusted by the user.
The particular characteristics of inversion of the Karplus relation inspired further adaptation of the restraining function specifically for 3
J-couplings by introduction of an oscillating factor cos2(ω
restr
t) that scales the torsion angle potential function 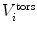 of the dihedral angle associated with the i
th 3
J-coupling as well as the restraining function
of the dihedral angle associated with the i
th 3
J-coupling as well as the restraining function  for a period
for a period 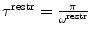 (Keller et al. 2007). The oscillating factor is switched on when the average 3
J-value deviates more than a certain threshold ΔJ from the experimental value, temporarily scaling down the potential energy for the dihedral angle, allowing it to escape from local minima.
(Keller et al. 2007). The oscillating factor is switched on when the average 3
J-value deviates more than a certain threshold ΔJ from the experimental value, temporarily scaling down the potential energy for the dihedral angle, allowing it to escape from local minima.
A related method is local elevation biasing (Christen et al. 2007), based on the local elevation enhanced searching method (Huber et al. 1994). The simulation is driven away from structures that do not fit the experimental data by adding Gaussian functions to a biasing coordinate, usually the structural property related to the NMR observable. For 3
J-couplings, for example, the biasing coordinate is the dihedral angle θ upon which the couplings report. The range of values of θ is divided into N
le bins with midpoints  . At each step, Gaussian functions centered on
. At each step, Gaussian functions centered on  are added if
are added if  and
and 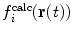 do not match
do not match 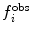 :
:
| 12 |
 is typically orders of magnitude lower than the force constants used in Eqs. 7, 9, 10 and 11. The weight of the k
th penalty term
is typically orders of magnitude lower than the force constants used in Eqs. 7, 9, 10 and 11. The weight of the k
th penalty term 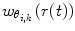 is calculated according to
is calculated according to
| 13 |
where 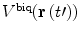 is calculated in the same manner as
is calculated in the same manner as 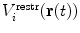 in Eq. 10 and δ is
in Eq. 10 and δ is
| 14 |
Local elevation biasing greatly enhances sampling and has been shown to produce superior agreement with experimental data comprising side-chain 3 J-couplings compared to conventional instantaneous and time-averaged biquadratic restraining methods (Christen et al. 2007; Allison and van Gunsteren 2009; Dolenc et al. 2010; Missimer et al. 2010).
Conclusions
The speed, accuracy and length of MD simulations of proteins have increased markedly over the years, but it remains essential to check the quality of the structures produced and the extent of sampling by comparison with quantitative experimental data. Solution NMR provides a number of observables that can be directly linked to structural properties of proteins and that encompass dynamics on different time-scales. Modern force fields produce ensembles of structures that, on the whole, agree reasonably well with NMR data, particularly when enhanced sampling methods are used. The recent advent of specialised hardware and highly parallelised software capable of simulations of similar lengths to the time-scales encompassed by NMR data has revitalised the field whilst revealing that there is still work to be done. The alternative, biasing or restraining MD simulations to fit experimental data, has also undergone much development over the years, with methods that include enhanced sampling methods showing particular promise. Such methods will always be limited, however, by the need to balance over- and under-fitting.
In the future, the deficiencies in atomic-level protein force fields that are beginning to be exposed by the longer simulations now possible need to be addressed. One possible means of doing so is to utilise the memory of the alterations made to the potential energy surface to improve the agreement between back-calculated and experimentally-measured observables when using techniques such as AMD and local elevation to guide the modification of force field terms. This will involve carrying out such simulations and comparisons with experimental data for a wide range of different proteins, however, to ensure that any changes made to force fields are not specific to a particular system. It would also be desirable to see measurement of more NMR data to improve the ratio of N obs/N df , allow conformational motion to be better accounted for, and increase the potential for cross-validation. Finally, increasing computer power and parallelisation should allow more accurate, perhaps even quantum-chemical, relationships between experimental observables and structural properties to be routinely applied for macromolecules such as proteins.
Acknowledgements
I thank the very many people with whom I have discussed the issues involved in combining NMR data with MD simulations, in particular, Prof. Wilfred van Gunsteren, to whom this article is dedicated on the occasion of his 65th birthday.
Footnotes
Special issue: Computational Biophysics
References
- Allison JR, van Gunsteren WF. A method to explore protein side chain conformational variability using experimental data. Chem Phys Chem. 2009;10(18):3213–3228. doi: 10.1002/cphc.200900400. [DOI] [PubMed] [Google Scholar]
- Allison JR, Varnai P, Dobson CM, Vendruscolo M. Determination of the free energy landscape of α-synuclein using spin label nuclear magnetic resonance measurements. J Am Chem Soc. 2009;131(51):18,314–18,326. doi: 10.1021/ja904716h. [DOI] [PubMed] [Google Scholar]
- Allison JR, Bergeler M, Hansen N, van Gunsteren WF. Current computer modeling cannot explain why two highly similar sequences fold into different structures. Biochemistry. 2011;50(50):10,965–10,973. doi: 10.1021/bi2015663. [DOI] [PubMed] [Google Scholar]
- Allison JR, Hertig S, Missimer JH, Smith LJ, Steinmetz MO, Dolenc J (2012) Probing the structure and dynamics of proteins by combining molecular dynamics simulations and experimental NMR data. J Chem Theory Comput. doi:10.1021/ct300393b [DOI] [PubMed]
- Andronesi OC, Becker S, Seidel K, Heise H, Young HS, Baldus M. Determination of membrane protein structure and dynamics by magic-angle-spinning solid-state nmr spectroscopy. J Am Chem Soc. 2005;127(37):12,965–12,974. doi: 10.1021/ja0530164. [DOI] [PubMed] [Google Scholar]
- Battiste JL, Wagner G. Utilization of site-directed spin labeling and high-resolution heteronuclear nuclear magnetic resonance for global fold determination of large proteins with limited nuclear overhauser effect data. Biochemistry. 2000;39(18):5355–5365. doi: 10.1021/bi000060h. [DOI] [PubMed] [Google Scholar]
- Bax A. Weak alignment offers new nmr opportunities to study protein structure and dynamics. Protein Sci. 2003;12(1):1–16. doi: 10.1110/ps.0233303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beauchamp KA, Lin YS, Das R, Pande VS. Are protein force fields getting better? a systematic benchmark on 524 diverse nmr measurements. J Chem Theory Comput. 2012;8(4):1409–1414. doi: 10.1021/ct2007814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Best RB, Hummer G. Optimized molecular dynamics force fields applied to the helix-coil transition of polypeptides. J Phys Chem B. 2009;113(26):9004–9015. doi: 10.1021/jp901540t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Best RB, Vendruscolo M. Determination of protein structures consistent with nmr order parameters. J Am Chem Soc. 2004;126(26):8090–8091. doi: 10.1021/ja0396955. [DOI] [PubMed] [Google Scholar]
- Blackledge M. Recent progress in the study of biomolecular structure and dynamics in solution from residual dipolar couplings. Prog Nucl Magn Reson Spectrosc. 2005;46(1):23–61. doi: 10.1016/j.pnmrs.2004.11.002. [DOI] [Google Scholar]
- Boelens R, Koning TMG, Kaptein R. Determination of biomolecular structures from proton-proton noe’s using a relaxation matrix approach. J Mol Struct. 1988;173:299–311. doi: 10.1016/0022-2860(88)80062-0. [DOI] [Google Scholar]
- Bonvin AM, Brünger AT. Conformational variability of solution nuclear magnetic resonance structures. J Mol Biol. 1995;250(1):80–93. doi: 10.1006/jmbi.1995.0360. [DOI] [PubMed] [Google Scholar]
- Bonvin AMJJ, Boelens R, Kaptein R. Time- and ensemble-averaged direct noe restraints. J Biomol NMR. 1994;4(1):143–149. doi: 10.1007/BF00178343. [DOI] [PubMed] [Google Scholar]
- Borgias BA, James TL. Mardigras - a procedure for matrix analysis of relaxation for discerning geometry of an aqueous structure. J Magn Reson. 1990;87(3):475–487. [Google Scholar]
- Borgias BA, Gochin M, Kerwood DJ, James TL. Relaxation matrix analysis of 2d nmr data. Prog Nucl Magn Reson Spectrosc. 1990;22(1):83–100. doi: 10.1016/0079-6565(90)80015-A. [DOI] [Google Scholar]
- Brown WM, Wang P, Plimpton SJ, Tharrington AN. Implementing molecular dynamics on hybrid high performance computers - short range forces. Comp Phys Comm. 2011;182(4):898–911. doi: 10.1016/j.cpc.2010.12.021. [DOI] [Google Scholar]
- Brünger AT. Free R value: a novel statistical quantity for assessing the accuracy of crystal structures. Nature. 1992;355(6359):472–475. doi: 10.1038/355472a0. [DOI] [PubMed] [Google Scholar]
- Brünger AT. Assessment of phase accuracy by cross validation: the free R value. Methods and applications. Acta Crystallogr D Biol Crystallogr. 1993;49(Pt 1):24–36. doi: 10.1107/S0907444992007352. [DOI] [PubMed] [Google Scholar]
- Brünger AT, Clore GM, Gronenborn AM, Saffrich R, Nilges M. Assessing the quality of solution nuclear magnetic resonance structures by complete cross-validation. Science. 1993;261(5119):328–331. doi: 10.1126/science.8332897. [DOI] [PubMed] [Google Scholar]
- Brüschweiler R, Case DA. Adding harmonic motion to the Karplus relation for spin-spin coupling. J Am Chem Soc. 1994;116(24):11,199–11,200. doi: 10.1021/ja00103a062. [DOI] [Google Scholar]
- Brüschweiler R, Roux B, Blackledge M, Griesinger C, Karplus M, Ernst RR. Influence of rapid intramolecular motion on NMR cross-relaxation rates. A moleculardynamics study of antamanide in solution. J Am Chem Soc. 1992;114(7):2289–2302. doi: 10.1021/ja00033a002. [DOI] [Google Scholar]
- Bryant RG. The NMR time scale. J Chem Edu. 1983;60(11):933. doi: 10.1021/ed060p933. [DOI] [Google Scholar]
- Buck M, Bouguet-Bonnet S, Pastor RW, MacKerell AD. Importance of the CMAP correction to the CHARMM22 protein force field: dynamics of hen lysozyme. Biophys J. 2006;90(4):L36–L38. doi: 10.1529/biophysj.105.078154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bühl M, van Mourik T. NMR spectroscopy: quantum-chemical calculations. WIREs: Comput Mol Sci. 2011;1(4):634–647. [Google Scholar]
- Bürgi R, Pitera J, van Gunsteren WF. Assessing the effect of conformational averaging on the measured values of observables. J Biomol NMR. 2001;19(4):305–320. doi: 10.1023/A:1011295422203. [DOI] [PubMed] [Google Scholar]
- Camilloni C, Robustelli P, Simone AD, Cavalli A, Vendruscolo M. Characterization of the conformational equilibrium between the two major substates of RNase a using NMR chemical shifts. J Am Chem Soc. 2012;134(9):3968–3971. doi: 10.1021/ja210951z. [DOI] [PubMed] [Google Scholar]
- Case DA. Calibration of ring-current effects in proteins and nucleic acids. J Biomol NMR. 1995;6(4):341–346. doi: 10.1007/BF00197633. [DOI] [PubMed] [Google Scholar]
- Castellani F, van Rossum B, Diehl A, Schubert M, Rehbein K, Oschkinat H. Structure of a protein determined by solid-state magic-angle-spinning NMR spectroscopy. Nature. 2002;420(6911):98–102. doi: 10.1038/nature01070. [DOI] [PubMed] [Google Scholar]
- Chandrasekhar I, Clore GM, Szabo A, Gronenborn AM, Brooks BR. A 500 ps molecular dynamics simulation study of interleukin-1β in water: correlation with nuclear magnetic resonance spectroscopy and crystallography. J Mol Biol. 1992;226(1):239–250. doi: 10.1016/0022-2836(92)90136-8. [DOI] [PubMed] [Google Scholar]
- Choy WY, Mulder FA, Crowhurst KA, Muhandiram DR, Millett IS, Doniach S, Forman-Kay JD, Kay LE. Distribution of molecular size within an unfolded state ensemble using small-angle x-ray scattering and pulse field gradient NMR techniques. J Mol Biol. 2002;316(1):101–112. doi: 10.1006/jmbi.2001.5328. [DOI] [PubMed] [Google Scholar]
- Christen M, Keller B, van Gunsteren WF. Biomolecular structure refinement based on adaptive restraints using local-elevation simulation. J Biomol NMR. 2007;39(4):265–273. doi: 10.1007/s10858-007-9194-2. [DOI] [PubMed] [Google Scholar]
- Clore GM, Iwahara J. Theory, practice, and applications of paramagnetic relaxation enhancement for the characterization of transient low-population states of biological macromolecules and their complexes. Chem Rev. 2009;109(9):4108–4139. doi: 10.1021/cr900033p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clore GM, Schwieters CD. How much backbone motion in ubiquitin is required to account for dipolar coupling data measured in multiple alignment media as assessedby independent cross-validation? J Am Chem Soc. 2004;126(9):2923–2938. doi: 10.1021/ja0386804. [DOI] [PubMed] [Google Scholar]
- Clore GM, Schwieters CD. Concordance of residual dipolar couplings, backbone order parameters and crystallographic B-factors for a small α/β protein: a unified picture of high probability, fast atomic motions in proteins. J Mol Biol. 2006;355(5):879–886. doi: 10.1016/j.jmb.2005.11.042. [DOI] [PubMed] [Google Scholar]
- Clore G, Starich M, Gronenborn A. Measurement of residual dipolar couplings of macromolecules aligned in the nematic phase of a colloidal suspension of rod-shaped viruses. J Am Chem Soc. 1998;120(40):10,571–10,572. doi: 10.1021/ja982592f. [DOI] [Google Scholar]
- Cornilescu G, Delaglio F, Bax A. Protein backbone angle restraints from searching a database for chemical shift and sequence homology. J Biomol NMR. 1999;13(3):289–302. doi: 10.1023/A:1008392405740. [DOI] [PubMed] [Google Scholar]
- Daura X, Antes I, van Gunsteren WF, Thiel W, Mark AE. The effect of motional averaging on the calculation of NMR-derived structural properties. Proteins Struct Funct Bioinform. 1999;36(4):542–555. doi: 10.1002/(SICI)1097-0134(19990901)36:4<542::AID-PROT17>3.0.CO;2-M. [DOI] [PubMed] [Google Scholar]
- Daura X, Gademann K, Schäfer H, Jaun B, Seebach D, van Gunsteren WF. The β-peptide hairpin in solution:conformational study of a β-hexapeptide in methanol by NMR spectroscopy and MD simulation. J Am Chem Soc. 2001;123(10):2393–2404. doi: 10.1021/ja003689g. [DOI] [PubMed] [Google Scholar]
- de Dios A, Pearson J, Oldfield E. Secondary and tertiary structural effects on protein nmr chemical shifts: an ab initio approach. Science. 1993;260(5113):1491–1496. doi: 10.1126/science.8502992. [DOI] [PubMed] [Google Scholar]
- De Simone A, Richter B, Salvatella X, Vendruscolo M. Toward an accurate determination of free energy landscapes in solution states of proteins. J Am Chem Soc. 2009;131(11):3810–3811. doi: 10.1021/ja8087295. [DOI] [PubMed] [Google Scholar]
- Dedmon MM, Lindorff-Larsen K, Christodoulou J, Vendruscolo M, Dobson CM. Mapping long-range interactions in alpha-synuclein using spin-label NMR and ensemble molecular dynamics simulations. J Am Chem Soc. 2005;127(2):476–477. doi: 10.1021/ja044834j. [DOI] [PubMed] [Google Scholar]
- Dolenc J, Missimer JH, Steinmetz MO, van Gunsteren WF. Methods of NMR structure refinement: molecular dynamics simulations improve the agreement with measured NMR data of a C-terminal peptide of GCN4-p1. J Biomol NMR. 2010;47(3):221–235. doi: 10.1007/s10858-010-9425-9. [DOI] [PubMed] [Google Scholar]
- Donaldson LW, Skrynnikov NR, Choy WY, Muhandiram DR, Sarkar B, Forman-Kay JD, Kay LE. Structural characterization of proteins with an attached ATCUN motif by paramagnetic relaxation enhancement NMR spectroscopy. J Am Chem Soc. 2001;123(40):9843–9847. doi: 10.1021/ja011241p. [DOI] [PubMed] [Google Scholar]
- Duan Y, Wu C, Chowdhury S, Lee MC, Xiong G, Zhang W, Yang R, Cieplak P, Luo R, Lee T, Caldwell J, Wang J, Kollman P. A point-charge force field for molecular mechanics simulations of proteins based on condensed-phase quantum mechanical calculations. J Comput Chem. 2003;24(16):1999–2012. doi: 10.1002/jcc.10349. [DOI] [PubMed] [Google Scholar]
- Edmondson SP. NOE R-factors and structural refinement using FIRM, an iterative relaxation matrix program. J Magn Reson. 1992;98(2):283–298. [Google Scholar]
- Eghbalnia HR, Wang L, Bahrami A, Assadi A, Markley J. Protein energetic conformational analysis from NMR chemical shifts (PECAN) and its use in determining secondary structural elements. J Biomol NMR. 2005;32(1):71–81. doi: 10.1007/s10858-005-5705-1. [DOI] [PubMed] [Google Scholar]
- Eichenberger AP, Smith LJ, van Gunsteren WF. Ester-linked hen egg white lysozyme shows a compact fold in a molecular dynamics simulation - possible causes and sensitivity of experimentally observable quantities to structural changes maintaining this compact fold. FEBS J. 2012;279(2):299–315. doi: 10.1111/j.1742-4658.2011.08424.x. [DOI] [PubMed] [Google Scholar]
- Eriksson MAL, Berglund H, Härd T, Nilsson L. A comparison of 15N NMR relaxation measurements with a molecular dynamics simulation: backbone dynamics of the glucocorticoid receptor DNA-binding domain. Proteins Struct Funct Bioinform. 1993;17(4):375–390. doi: 10.1002/prot.340170406. [DOI] [PubMed] [Google Scholar]
- Esteban-Martín S, Fenwick RB, Salvatella X. Refinement of ensembles describing unstructured proteins using NMR residual dipolar couplings. J Am Chem Soc. 2010;132(13):4626–4632. doi: 10.1021/ja906995x. [DOI] [PubMed] [Google Scholar]
- Fawzi NL, Phillips AH, Ruscio JZ, Doucleff M, Wemmer DE, Head-Gordon T. Structure and dynamics of the Aβ21-30 peptide from the interplay of NMR experiments and molecular simulations. J Am Chem Soc. 2008;130(19):6145–6158. doi: 10.1021/ja710366c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fennen J, Torda AE, van Gunsteren WF. Structure refinement with molecular dynamics and a boltzmann-weighted ensemble. J Biomol NMR. 1995;6(2):163–70. doi: 10.1007/BF00211780. [DOI] [PubMed] [Google Scholar]
- Fenwick RB, Esteban-Martíın S, Richter B, Lee D, Walter KFA, Milovanovic D, Becker S, Lakomek NA, Griesinger C, Salvatella X. Weak long-range correlated motions in a surface patch of ubiquitin involved in molecular recognition. J Am Chem Soc. 2011;133(27):10,336–10,339. doi: 10.1021/ja200461n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Francis C, Lindorff-Larsen K, Best RB, Vendruscolo M. Characterization of the residual structure in the unfolded state of the δ131δ fragment of staphylococcal nuclease. Proteins Struct Funct Bioinform. 2006;65(1):145–152. doi: 10.1002/prot.21077. [DOI] [PubMed] [Google Scholar]
- Frank A, Möller HM, Exner TE. Toward the quantum chemical calculation of nmr chemical shifts of proteins. 2. Level of theory, basis set, and solvents model dependence. J Chem Theory Comput. 2012;8(4):1480–1492. doi: 10.1021/ct200913r. [DOI] [PubMed] [Google Scholar]
- Gillespie JR, Shortle D. Characterization of long-range structure in the denatured state of staphylococcal nuclease. I. Paramagnetic relaxation enhancement by nitroxide spin labels. J Mol Biol. 1997;268(1):158–169. doi: 10.1006/jmbi.1997.0954. [DOI] [PubMed] [Google Scholar]
- Glättli A, van Gunsteren WF. Are NMR-derived model structures for β-peptides representative for the ensemble of structures adopted in solution? Angew Chem Int Ed. 2004;43(46):6312–6316. doi: 10.1002/anie.200460384. [DOI] [PubMed] [Google Scholar]
- Haasnoot CAG, de Leeuw FAAM, de Leeuw HPM, Altona C. Interpretation of vicinal proton-proton coupling constants by a generalized karplus relation. conformational analysis of the exocyclic C4’-C5’ bond in nucleosides and nucleotides: Preliminary communication. Recl Trav Chim Pays-Bas. 1979;98(12):576–577. doi: 10.1002/recl.19790981206. [DOI] [Google Scholar]
- Haasnoot CAG, De Leeuw FAAM, De Leeuw HPM, Altona C, Haasnoot CAG, De Leeuw FAAM, De Leeuw HPM, Altona C. Relationship between proton-proton NMR coupling constants and substituent electronegativities. III. Conformational analysis of proline rings in solution using a generalized Karplus equation. Biopolymers. 1981;20(6):1211–1245. doi: 10.1002/bip.1981.360200610. [DOI] [Google Scholar]
- Habeck M, Rieping W, Nilges M. Bayesian estimation of Karplus parameters and torsion angles from three-bond scalar couplings constants. J Magn Reson. 2005;177(1):160–165. doi: 10.1016/j.jmr.2005.06.016. [DOI] [PubMed] [Google Scholar]
- Hamelberg D, Mongan J, McCammon JA. Accelerated molecular dynamics: a promising and efficient simulation method for biomolecules. J Chem Phys. 2004;120(24):11,919–11,929. doi: 10.1063/1.1755656. [DOI] [PubMed] [Google Scholar]
- Han B, Liu Y, Ginzinger S, Wishart D. Shiftx2: significantly improved protein chemical shift prediction. J Biomol NMR. 2011;50(1):43–57. doi: 10.1007/s10858-011-9478-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hansen MR, Mueller L, Pardi A. Tunable alignment of macromolecules by filamentous phage yields dipolar coupling interactions. Nat Struct Mol Biol. 1998;5(12):1065–1074. doi: 10.1038/4176. [DOI] [PubMed] [Google Scholar]
- Hess B, Scheek RM. Orientation restraints in molecular dynamics simulations using time and ensemble averaging. J Mag Reson. 2003;164(1):19–27. doi: 10.1016/S1090-7807(03)00178-2. [DOI] [PubMed] [Google Scholar]
- Hornak V, Abel R, Okur A, Strockbine B, Roitberg A, Simmerling C. Com-parison of multiple amber force fields and development of improved protein backbone parameters. Proteins Struct Funct Bioinform. 2006;65(3):712–725. doi: 10.1002/prot.21123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huber T, Torda AE, van Gunsteren WF. Local elevation: A method for improving the searching properties of molecular dynamics simulation. J Comput Aided Mol Des. 1994;8(6):695–708. doi: 10.1007/BF00124016. [DOI] [PubMed] [Google Scholar]
- Imai K, Osawa E. An empirical extension of the Karplus equation. Magn Reson Chem. 1990;28(8):668–674. doi: 10.1002/mrc.1260280803. [DOI] [Google Scholar]
- Kalk A, Berendsen HJC. Proton magnetic relaxation and spin diffusion in proteins. J Magn Reson. 1976;24(3):343–366. [Google Scholar]
- Kaminski GA, Friesner RA, Tirado-Rives J, Jorgensen WL. Evaluation and reparametrization of the opls-aa force field for proteins via comparison with accurate quantum chemical calculations on peptides. J Phys Chem B. 2001;105(28):6474–6487. doi: 10.1021/jp003919d. [DOI] [Google Scholar]
- Karplus M. Contact electron-spin coupling of nuclear magnetic moments. J Chem Phys. 1959;30(1):11–15. doi: 10.1063/1.1729860. [DOI] [Google Scholar]
- Keepers JW, James TL. A theoretical study of distance determinations from NMR. two-dimensional nuclear overhauser effect spectra. J Magn Reson. 1984;57(3):404–426. [Google Scholar]
- Keller B, Christen M, Oostenbrink C, van Gunsteren WF. On using oscillating time-dependent restraints in MD simulation. J Biomol NMR. 2007;37(1):1–14. doi: 10.1007/s10858-006-9081-2. [DOI] [PubMed] [Google Scholar]
- Kemmink J, van Mierlo CPM, Scheek RM, Creighton TE. Local structure due to an aromatic-amide interaction observed by 1 h-nuclear magnetic resonance spectroscopy in peptides related to the N terminus of bovine pancreatic trypsin inhibitor. J Mol Biol. 1993;230(1):312–322. doi: 10.1006/jmbi.1993.1144. [DOI] [PubMed] [Google Scholar]
- Kessler H, Griesinger C, Lautz J, Mueller A, van Gunsteren WF, Berendsen HJC. Conformational dynamics detected by nuclear magnetic resonance NOE values and J coupling constants. J Am Chem Soc. 1988;110(11):3393–3396. doi: 10.1021/ja00219a008. [DOI] [Google Scholar]
- Kjaergaard M, Poulsen FM. Disordered proteins studied by chemical shifts. Prog Nucl Magn Reson Spectrosc. 2012;60:42–51. doi: 10.1016/j.pnmrs.2011.10.001. [DOI] [PubMed] [Google Scholar]
- Klepeis JL, Lindorff-Larsen K, Dror RO, Shaw DE. Long-timescale molecular dynamics simulations of protein structure and function. Curr Opin Struct Biol. 2009;19(2):120–127. doi: 10.1016/j.sbi.2009.03.004. [DOI] [PubMed] [Google Scholar]
- Koenig B, Hu JS, Ottiger M, Bose S, Hendler R, Bax A. NMR measurement of dipolar couplings in proteins aligned by transient binding to purple membrane fragments. J Am Chem Soc. 1999;121(6):1385–1386. doi: 10.1021/ja9837856. [DOI] [Google Scholar]
- Koerdel J, Teleman O. Backbone dynamics of calbindin d9k: comparison of molecular dynamics simulations and 15N NMR relaxation measurements. J Am Chem Soc. 1992;114(12):4934–4936. doi: 10.1021/ja00038a086. [DOI] [Google Scholar]
- Kohlhoff KJ, Robustelli P, Cavalli A, Salvatella X, Vendruscolo M. Fast and accurate predictions of protein NMR chemical shifts from interatomic distances. J Am Chem Soc. 2009;131(39):13,894–13,895. doi: 10.1021/ja903772t. [DOI] [PubMed] [Google Scholar]
- Kristjansdottir S, Lindorff-Larsen K, Fieber W, Dobson CM, Vendruscolo M, Poulsen FM. Formation of native and non-native interactions in ensembles of denatured ACBP molecules from paramagnetic relaxation enhancement studies. J Mol Biol. 2005;347(5):1053–1062. doi: 10.1016/j.jmb.2005.01.009. [DOI] [PubMed] [Google Scholar]
- Lange OF, van der Spoel D, de Groot BL. Scrutinizing molecular mechanics force fields on the submicrosecond timescale with NMR data. Biophys J. 2010;99(2):647–655. doi: 10.1016/j.bpj.2010.04.062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leeflang B, Kroon-Batenburg L. Crosrel: Full relaxation matrix analysis for NOESY and ROESY NMR spectroscopy. J Biomol NMR. 1992;2(5):495–518. doi: 10.1007/BF02192812. [DOI] [Google Scholar]
- Li DW, Brüschweiler R. Certification of molecular dynamics trajectories with NMR chemical shifts. J Phys Chem Lett. 2009;1(1):246–248. doi: 10.1021/jz9001345. [DOI] [Google Scholar]
- Lindorff-Larsen K, Vendruscolo M, Paci E, Dobson CM. Transition states for protein folding have native topologies despite high structural variability. Nat Struct Mol Biol. 2004;11(5):443–449. doi: 10.1038/nsmb765. [DOI] [PubMed] [Google Scholar]
- Lindorff-Larsen K, Best RB, Depristo MA, Dobson CM, Vendruscolo M. Simultaneous determination of protein structure and dynamics. Nature. 2005;433(7022):128–132. doi: 10.1038/nature03199. [DOI] [PubMed] [Google Scholar]
- Lindorff-Larsen K, Best RB, Vendruscolo M. Interpreting dynamically-averaged scalar couplings in proteins. J Biomol NMR. 2005;32(4):273–280. doi: 10.1007/s10858-005-8873-0. [DOI] [PubMed] [Google Scholar]
- Lindorff-Larsen K, Piana S, Palmo K, Maragakis P, Klepeis JL, Dror RO, Shaw DE. Improved side-chain torsion potentials for the Amber ff99SB protein force field. Proteins Struct Funct Bioinform. 2010;78(8):1950–1958. doi: 10.1002/prot.22711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lindorff-Larsen K, Maragakis P, Piana S, Eastwood MP, Dror RO, Shaw DE. Systematic validation of protein force fields against experimental data. PLoS One. 2012;7(2):e32,131. doi: 10.1371/journal.pone.0032131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lindorff-Larsen K, Trbovic N, Maragakis P, Piana S, Shaw DE. Structure and dynamics of an unfolded protein examined by molecular dynamics simulation. J Am Chem Soc. 2012;134(8):3787–3791. doi: 10.1021/ja209931w. [DOI] [PubMed] [Google Scholar]
- Linge JP, Habeck M, Rieping W, Nilges M. Correction of spin diffusion during iterative automated NOE assignment. J Magn Reson. 2004;167(2):334–342. doi: 10.1016/j.jmr.2004.01.010. [DOI] [PubMed] [Google Scholar]
- Louhivuori M, Otten R, Lindorff-Larsen K, Annila A. Conformational fluctuations affect protein alignment in dilute liquid crystal media. J Am Chem Soc. 2006;128(13):4371–4376. doi: 10.1021/ja0576334. [DOI] [PubMed] [Google Scholar]
- Louhivuori M, Otten R, Salminen T, Annila A. Evidence of molecular alignment fluctuations in aqueous dilute liquid crystalline media. J Biomol NMR. 2007;39(2):141–152. doi: 10.1007/s10858-007-9182-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mackerell ADJ. Empirical force fields for biological macromolecules: overview and issues. J Comput Chem. 2004;25(13):1584–1604. doi: 10.1002/jcc.20082. [DOI] [PubMed] [Google Scholar]
- Mackerell AD, Bashford D, Bellott RL, Dunbrack RL, Evanseck JD, Field MJ, Fischer S, Gao J, Guo H, Ha S, Joseph-McCarthy D, Kuchnir L, Kuczera K, Lau FTK, Mattos C, Michnick S, Ngo T, Nguyen DT, Prodhom B, Reiher WE, Roux B, Schlenkrich M, Smith JC, Stote R, Straub J, Watanabe M, Wiórkiewicz-Kuczera J, Yin D, Karplus M. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J Phys Chem B. 1998;102(18):3586–3616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- Mackerell AD, Feig M, Brooks CL. Extending the treatment of backbone energetics in protein force fields: limitations of gas-phase quantum mechanics in reproducing protein conformational distributions in molecular dynamics simulations. J Comput Chem. 2004;25(11):1400–1415. doi: 10.1002/jcc.20065. [DOI] [PubMed] [Google Scholar]
- Manolikas T, Herrmann T, Meier BH. Protein structure determination from 13 c spin-diffusion solid-state NMR spectroscopy. J Am Chem Soc. 2008;130(12):3959–3966. doi: 10.1021/ja078039s. [DOI] [PubMed] [Google Scholar]
- Maragakis P, Lindorff-Larsen K, Eastwood MP, Dror RO, Klepeis JL, Arkin IT, Jensen MO, Xu H, Trbovic N, Friesner RA, Palmer AG, Shaw DE. Microsecond molecular dynamics simulation shows effect of slow loop dynamics on backbone amide order parameters of proteins. J Phys Chem B. 2008;112(19):6155–6158. doi: 10.1021/jp077018h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marion D, Genest M, Ptak M. Reconstruction of NOESY maps: a requirement for a reliable conformational analysis of biomolecules using 2D NMR. Biophys Chem. 1987;28(3):235–244. doi: 10.1016/0301-4622(87)80094-7. [DOI] [PubMed] [Google Scholar]
- Markwick PRL, Sprangers R, Sattler M. Dynamic effects on j-couplings across hydrogen bonds in proteins. J Am Chem Soc. 2002;125(3):644–645. doi: 10.1021/ja028875w. [DOI] [PubMed] [Google Scholar]
- Markwick PRL, Bouvignies G, Blackledge M. Exploring multiple timescale motions in protein GB3 using accelerated molecular dynamics and NMR spectroscopy. J Am Chem Soc. 2007;129(15):4724–4730. doi: 10.1021/ja0687668. [DOI] [PubMed] [Google Scholar]
- Markwick PRL, Bouvignies G, Salmon L, McCammon JA, Nilges M, Blackledge M. Toward a unified representation of protein structural dynamics in solution. J Am Chem Soc. 2009;131(46):16,968–16,975. doi: 10.1021/ja907476w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Markwick PRL, Cervantes CF, Abel BL, Komives EA, Blackledge M, McCammon JA. Enhanced conformational space sampling improves the prediction of chemical shifts in proteins. J Am Chem Soc. 2010;132(4):1220–1221. doi: 10.1021/ja9093692. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marsh JA, Singh VK, Jia Z, Forman-Kay JD. Sensitivity of secondary structure propensities to sequence differences between α- and γ-synuclein: implications for fibrillation. Prot. Sci. 2006;15(12):2795–2804. doi: 10.1110/ps.062465306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCammon J, Gelin B, Karplus M. Dynamics of folded proteins. Nature. 1977;267:585–590. doi: 10.1038/267585a0. [DOI] [PubMed] [Google Scholar]
- Meiler J. Proshift: protein chemical shift prediction using artificial neural networks. J Biomol NMR. 2003;26(1):25–37. doi: 10.1023/A:1023060720156. [DOI] [PubMed] [Google Scholar]
- Mierke DF, Scheek RM, Kessler H. Coupling constants as restraints in ensemble distance driven dynamics. Biopolymers. 1994;34(4):559–563. doi: 10.1002/bip.360340411. [DOI] [Google Scholar]
- Missimer JH, Dolenc J, Steinmetz MO, van Gunsteren WF. Exploring the trigger sequence of the GCN4 coiled-coil: biased molecular dynamics resolves apparent inconsistencies in NMR measurements. Prot. Sci. 2010;19(12):2462–2474. doi: 10.1002/pro.528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mulder FAA, Filatov M. NMR chemical shift data and ab initio shielding calculations: emerging tools for protein structure determination. Chem Soc Rev. 2010;39(2):578–590. doi: 10.1039/B811366C. [DOI] [PubMed] [Google Scholar]
- Nanzer AP, Torda AE, Bisang C, Weber C, Robinson JA, van Gunsteren WF. Dynamical studies of peptide motifs in the Plasmodium falciparum circumsporozoite surface protein by restrained and unrestrained MD simulations. J Mol Biol. 1997;267(4):1012–1025. doi: 10.1006/jmbi.1997.0911. [DOI] [PubMed] [Google Scholar]
- Neal S, Nip AM, Zhang H, Wishart DS. Rapid and accurate calculation of protein 1 H, 13 C and 15 N chemical shifts. J Biomol NMR. 2003;26(3):215–240. doi: 10.1023/A:1023812930288. [DOI] [PubMed] [Google Scholar]
- Nielsen JT, Eghbalnia HR, Nielsen NC. Chemical shift prediction for protein structure calculation and quality assessment using an optimally parameterized force field. Prog Nucl Magn Reson Spectrosc. 2012;60:1–28. doi: 10.1016/j.pnmrs.2011.05.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Niggli DA, Ebert MO, Lin Z, Seebach D, van Gunsteren WF. Helical content of a β3 -octapeptide in methanol: molecular dynamics simulations explain a seemingdiscrepancy between conclusions derived from CD and \NMR data. Chem Eur J. 2012;18(2):586–593. doi: 10.1002/chem.201102667. [DOI] [PubMed] [Google Scholar]
- Oldfield E. Chemical shifts in amino acids, peptides, and proteins: from quantum chemistry to drug design. Annu Rev Phys Chem. 2002;53(1):349–378. doi: 10.1146/annurev.physchem.53.082201.124235. [DOI] [PubMed] [Google Scholar]
- Osapay K, Case DA. A new analysis of proton chemical shifts in proteins. J Am Chem Soc. 1991;113(25):9436–9444. doi: 10.1021/ja00025a002. [DOI] [Google Scholar]
- Paci E, Vendruscolo M, Dobson CM, Karplus M. Determination of a transition state at atomic resolution from protein engineering data. J Mol Biol. 2002;324(1):151–163. doi: 10.1016/S0022-2836(02)00944-0. [DOI] [PubMed] [Google Scholar]
- Paci E, Friel CT, Lindorff-Larsen K, Radford SE, Karplus M, Vendruscolo M. Comparison of the transition state ensembles for folding of im7 and im9 determined using all-atom molecular dynamics simulations with φ value restraints. Proteins Struct Funct Bioinform. 2004;54(3):513–525. doi: 10.1002/prot.10595. [DOI] [PubMed] [Google Scholar]
- Paci E, Greene LH, Jones RM, Smith LJ. Characterization of the molten globule state of retinol-binding protein using a molecular dynamics simulation approach. FEBS J. 2005;272(18):4826–4838. doi: 10.1111/j.1742-4658.2005.04898.x. [DOI] [PubMed] [Google Scholar]
- Palmer AG, Case DA. Molecular dynamics analysis of NMR relaxation in a zinc-finger peptide. J Am Chem Soc. 1992;114(23):9059–9067. doi: 10.1021/ja00049a043. [DOI] [Google Scholar]
- Pardi A, Billeter M, Wüthrich K. Calibration of the angular dependence of the amide proton-Cα proton coupling constants, 3JHNα, in a globular protein : use of 3 JHNα for identification of helical secondary structure. J Mol Biol. 1984;180(3):741–751. doi: 10.1016/0022-2836(84)90035-4. [DOI] [PubMed] [Google Scholar]
- Pastore A, Saudek V. The relationship between chemical shift and secondary structure in proteins. J Magn Reson. 1990;90(1):165–176. [Google Scholar]
- Pérez C, Löhr F, Rüterjans H, Schmidt J. Self-consistent Karplus parametrization of 3J-couplings depending on the polypeptide side-chain torsion χ1. J Am Chem Soc. 2001;123(29):7081–7093. doi: 10.1021/ja003724j. [DOI] [PubMed] [Google Scholar]
- Peter C, Rueping M, Wörner HJ, Jaun B, Seebach D, van Gunsteren WF. Molecular dynamics simulations of small peptides: can one derive conformational preferences from roesy spectra? Chem. Eur. J. 2003;9(23):5838–5849. doi: 10.1002/chem.200305147. [DOI] [PubMed] [Google Scholar]
- Peti W, Smith L, Redfield C, Schwalbe H. Chemical shifts in denatured proteins: Resonance assignments for denatured ubiquitin and comparisons with other denatured proteins. J Biomol NMR. 2001;19(2):153–165. doi: 10.1023/A:1008307323283. [DOI] [PubMed] [Google Scholar]
- Philippopoulos M, Mandel AM, Palmer AG, Lim C. Accuracy and precision of NMR relaxation experiments and MD simulations for characterizing protein dynamics. Proteins: Struct. Funct. Bioinform. 1997;28(4):481–493. doi: 10.1002/(SICI)1097-0134(199708)28:4<481::AID-PROT3>3.0.CO;2-D. [DOI] [PubMed] [Google Scholar]
- Phillips JC, Braun R, Wang W, Gumbart J, Tajkhorshid E, Villa E, Chipot C, Skeel RD, Kalé L, Schulten K. Scalable molecular dynamics with NAMD. J Comput Chem. 2005;26(16):1781–1802. doi: 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piana S, Lindorff-Larsen K, Shaw D. How robust are protein folding simulations with respect to force field parameterization? Biophys J. 2011;100(9):L47–L49. doi: 10.1016/j.bpj.2011.03.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Plimpton S. Fast parallel algorithms for short-range molecular dynamics. J. Comp. Phys. 1995;117(1):1–19. doi: 10.1006/jcph.1995.1039. [DOI] [Google Scholar]
- Post CB, Meadows RP, Gorenstein DG. On the evaluation of interproton distances for three-dimensional structure determination by NMR using a relaxation rate matrix analysis. J Am Chem Soc. 1990;112(19):6796–6803. doi: 10.1021/ja00175a009. [DOI] [Google Scholar]
- Richter B, Gsponer J, Várnai P, Salvatella X, Vendruscolo M. The MUMO (minimal under-restraining minimal over-restraining) method for the determination of native state ensembles of proteins. J Biomol NMR. 2007;37(2):117–135. doi: 10.1007/s10858-006-9117-7. [DOI] [PubMed] [Google Scholar]
- Robustelli P, Kohlhoff K, Cavalli A, Vendruscolo M. Using NMR chemical shifts as structural restraints in molecular dynamics simulations of proteins. Structure. 2010;18(8):923–933. doi: 10.1016/j.str.2010.04.016. [DOI] [PubMed] [Google Scholar]
- Robustelli P, Stafford KA, Palmer AG. Interpreting protein structural dynamics from NMR chemical shifts. J Am Chem Soc. 2012;134(14):6365–6374. doi: 10.1021/ja300265w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanders CR, Hare BJ, Howard KP, Prestegard JH. Magnetically-oriented phospholipid micelles as a tool for the study of membrane-associated molecules. Prog Nucl Magn Reson Spectrosc. 1994;26(Part 5):421–444. doi: 10.1016/0079-6565(94)80012-X. [DOI] [Google Scholar]
- Sass J, Cordier F, Hoffmann A, Rogowski M, Cousin A, Omichinski J, Lowen H, Grzesiek S. Purple membrane induced alignment of biological macromolecules in the magnetic field. J Am Chem Soc. 1999;121(10):2047–2055. doi: 10.1021/ja983887w. [DOI] [Google Scholar]
- Sass HJ, Musco G, Stahl SJ, Wingfield PT, Grzesiek S. Solution NMR of proteins within polyacrylamide gels: diffusional properties and residual alignment by mechanical stress or embedding of oriented purple membranes. J Biomol NMR. 2000;18(4):303–309. doi: 10.1023/A:1026703605147. [DOI] [PubMed] [Google Scholar]
- Saupe A. Recent results in the field of liquid crystals. Angew Chem Int Ed. 1968;7(2):97–112. doi: 10.1002/anie.196800971. [DOI] [Google Scholar]
- Scheek R, Torda A, Kemmink J, van Gunsteren W (1991) Computational aspects of the study of biological macromolecules by NMR, NATO ASI Series A225. Plenum Press, New York, pp 209–217
- Schmid N, Bötschi M, Van Gunsteren WF. A gpu solvent-solvent interaction calculation accelerator for biomolecular simulations using the GROMOS software. J Comput Chem. 2010;31(8):1636–1643. doi: 10.1002/jcc.21447. [DOI] [PubMed] [Google Scholar]
- Schmid N, Eichenberger A, Choutko A, Riniker S, Winger M, Mark A, van Gunsteren W. Definition and testing of the GROMOS force-field versions 54A7 and 54B7. Eur Biophys J. 2011;40(7):843–856. doi: 10.1007/s00249-011-0700-9. [DOI] [PubMed] [Google Scholar]
- Schmidt J. Asymmetric Karplus curves for the protein side-chain 3J couplings. J Biomol NMR. 2007;37(4):287–301. doi: 10.1007/s10858-006-9140-8. [DOI] [PubMed] [Google Scholar]
- Schmidt JM, Blümel M, Löhr F, Rüterjans H. Self-consistent 3 j-coupling analysis for the joint calibration of Karplus coefficients and evaluation of torsion angles. J Biomol NMR. 1999;14(1):1–12. doi: 10.1023/A:1008345303942. [DOI] [PubMed] [Google Scholar]
- Schwalbe H, Grimshaw SB, Spencer A, Buck M, Boyd J, Dobson CM, Red-field C, Smith LJ. A refined solution structure of hen lysozyme determined using residual dipolar coupling data. Prot. Sci. 2001;10(4):677–688. doi: 10.1110/ps.43301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scott W, Mark A, van Gunsteren WF. On using time-averaging restraints in molecular dynamics simulation. J Biomol NMR. 1998;12:501–508. doi: 10.1023/A:1008306732538. [DOI] [PubMed] [Google Scholar]
- Shaw DE, Dror RO, Salmon JK, Grossman J, Mackenzie KM, Bank JA, Young C, Deneroff MM, Batson B, Bowers KJ, Chow E, Eastwood MP, Ierardi DJ, Klepeis JL, Kuskin JS, Larson RH, Lindorff-Larsen K, Maragakis P, Moraes MA, Piana S, Shan Y, Towles B (2009) Millisecond-scale molecular dynamics simulations on anton. In: Proceedings of the Conference on High Performance Computing, Networking, Storage and Analysis (SC09)
- Shen Y, Bax A. Protein backbone chemical shifts predicted from searching a database for torsion angle and sequence homology. J Biomol NMR. 2007;38(4):289–302. doi: 10.1007/s10858-007-9166-6. [DOI] [PubMed] [Google Scholar]
- Shen Y, Bax A. SPARTA+: a modest improvement in empirical NMR chemical shift prediction by means of an artificial neural network. J Biomol NMR. 2010;48(1):13–22. doi: 10.1007/s10858-010-9433-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen Y, Delaglio F, Cornilescu G, Bax A. TALOS+: a hybrid method for predicting protein backbone torsion angles from NMR chemical shifts. J Biomol NMR. 2009;44(4):213–223. doi: 10.1007/s10858-009-9333-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Showalter SA, Brüschweiler R. Quantitative molecular ensemble interpretation of NMR dipolar couplings without restraints. J Am Chem Soc. 2007;129(14):4158–4159. doi: 10.1021/ja070658d. [DOI] [PubMed] [Google Scholar]
- Showalter SA, Johnson E, Rance M, Brüschweiler R. Toward quantitative interpretation of methyl side-chain dynamics from NMR by molecular dynamics simulations. J Am Chem Soc. 2007;129(46):14,146–14,147. doi: 10.1021/ja075976r. [DOI] [PubMed] [Google Scholar]
- Siemer AB, Ritter C, Ernst M, Riek R, Meier BH. High-resolution solid-state NMR spectroscopy of the prion protein HET-s in its amyloid conformation. Angew Chem Int Ed. 2005;44(16):2441–2444. doi: 10.1002/anie.200462952. [DOI] [PubMed] [Google Scholar]
- Smith LJ, Sutcliffe MJ, Redfield C, Dobson CM. Analysis of φ and χ1 torsion angles for hen lysozyme in solution from proton NMR spin-spin coupling constants. Biochemistry. 1991;30(4):986–996. doi: 10.1021/bi00218a015. [DOI] [PubMed] [Google Scholar]
- Smith LJ, Mark AE, Dobson M, van Gunsteren WF (1995) Comparison of MD simulations and NMR experiments for hen lysozyme. Analysis of local fluctuations, cooperative motions, and global changes. Biochemistry 34(34), 10,918-10,931 [DOI] [PubMed]
- Smith PE, van Schaik RC, Szyperski T, Wüthrich K, van Gunsteren WF. Internal mobility of the basic pancreatic trypsin inhibitor in solution: a comparison of NMR spin relaxation measurements and molecular dynamics simulations. J Mol Biol. 1995;246(2):356–365. doi: 10.1006/jmbi.1994.0090. [DOI] [PubMed] [Google Scholar]
- Solomon I. Relaxation processes in a system of two spins. Phys Rev. 1955;99(2):559–565. doi: 10.1103/PhysRev.99.559. [DOI] [Google Scholar]
- Spera S, Bax A. Empirical correlation between protein backbone conformation and cα and cβ 13 c nuclear magnetic resonance chemical shifts. J Am Chem Soc. 1991;113(14):5490–5492. doi: 10.1021/ja00014a071. [DOI] [Google Scholar]
- Steiner D, Allison JR, van Gunsteren WF (2012) On the calculation of 3Jαβ -coupling constants for side chains in proteins. J Biomol NMR. doi:10.1007/s10858-012-9634-5 [DOI] [PubMed]
- Stone JE, Hardy DJ, Ufimtsev IS, Schulten K. GPU-accelerated molecular modeling coming of age. J Mol Graph Model. 2010;29(2):116–125. doi: 10.1016/j.jmgm.2010.06.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suardıaz R, García de la Vega JM, Fabián JS, Contreras RH. Theoretical Karplus relationships for vicinal coupling constants around χ1 in valine. Chem. Phys. Lett. 2007;442(13):119–123. doi: 10.1016/j.cplett.2007.05.049. [DOI] [Google Scholar]
- Teilum K, Kragelund BB, Poulsen FM. Transient structure formation in unfolded acyl-coenzyme A-binding protein observed by site-directed spin labelling. J Mol Biol. 2002;324(2):349–57. doi: 10.1016/s0022-2836(02)01039-2. [DOI] [PubMed] [Google Scholar]
- Tjandra N, Bax A. Direct measurement of distances and angles in biomolecules by NMR in a dilute liquid crystalline medium. Science. 1997;278(5340):1111–1114. doi: 10.1126/science.278.5340.1111. [DOI] [PubMed] [Google Scholar]
- Tong Y, Ji CG, Mei Y, Zhang JZH. Simulation of NMR data reveals that proteins local structures are stabilized by electronic polarization. J Am Chem Soc. 2009;131(24):8636–8641. doi: 10.1021/ja901650r. [DOI] [PubMed] [Google Scholar]
- Torda A, Scheek R, van Gunsteren WF. Time-dependent distance restraints in molecular dynamics simulations. Chem. Phys. Lett. 1989;157(4):289–294. doi: 10.1016/0009-2614(89)87249-5. [DOI] [Google Scholar]
- Torda AE, Scheek RM, van Gunsteren WF. Time-averaged nuclear overhauser effect distance restraints applied to tendamistat. J Mol Biol. 1990;214(1):223–235. doi: 10.1016/0022-2836(90)90157-H. [DOI] [PubMed] [Google Scholar]
- Torda AE, Brunne RM, Huber T, Kessler H, van Gunsteren WF. Structure refinement using time-averaged J-coupling constant restraints. J Biomol NMR. 1993;3(1):55–66. doi: 10.1007/BF00242475. [DOI] [PubMed] [Google Scholar]
- Trbovic N, Kim B, Friesner RA, Palmer AG. Structural analysis of protein dynamics by MD simulations and NMR spin-relaxation. Proteins Struct. Funct. Bioinform. 2008;71(2):684–694. doi: 10.1002/prot.21750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tropp J. Dipolar relaxation and nuclear oOverhauser effects in nonrigid molecules: the effect of fluctuating internuclear distances. J Chem Phys. 1980;72(11):6035–6043. doi: 10.1063/1.439059. [DOI] [Google Scholar]
- Trzesniak D, Glättli A, Jaun B, van Gunsteren WF. Interpreting NMR data for β-peptides using molecular dynamics simulations. J Am Chem Soc. 2005;127(41):14,320–14,329. doi: 10.1021/ja044285h. [DOI] [PubMed] [Google Scholar]
- Tycko R, Blanco F, Ishii Y. Alignment of biopolymers in strained gels: a new way to create detectable dipole-dipole couplings in high-resolution biomolecular NMR. J Am Chem Soc. 2000;122(38):9340–9341. doi: 10.1021/ja002133q. [DOI] [Google Scholar]
- Van Melckebeke H, Wasmer C, Lange A, Ab E, Loquet A, Bockmann A, Meier BH. Atomic-resolution three-dimensional structure of HET-s(218–289) amyloid fibrils by solid-state NMR spectroscopy. J Am Chem Soc. 2010;132(39):13,765–13,775. doi: 10.1021/ja104213j. [DOI] [PubMed] [Google Scholar]
- Vendruscolo M, Paci E, Dobson CM, Karplus M. Three key residues form a critical contact network in a protein folding transition state. Nature. 2001;409(6820):641–645. doi: 10.1038/35054591. [DOI] [PubMed] [Google Scholar]
- Vögeli B, Ying J, Grishaev A, Bax A. Limits on variations in protein backbone dynamics from precise measurements of scalar couplings. J Am Chem Soc. 2007;129(30):9377–9385. doi: 10.1021/ja070324o. [DOI] [PubMed] [Google Scholar]
- Wagner G, Pardi A, Wüthrich K. Hydrogen bond length and proton NMR chemical shifts in proteins. J Am Chem Soc. 1983;105(18):5948–5949. doi: 10.1021/ja00356a056. [DOI] [Google Scholar]
- Wang Y, Jardetzky O. Investigation of the neighboring residue effects on protein chemical shifts. J Am Chem Soc. 2002;124(47):14,075–14,084. doi: 10.1021/ja026811f. [DOI] [PubMed] [Google Scholar]
- Williamson MP, Asakura T. Empirical comparisons of models for chemical-shift calculation in proteins. J Magn Reson B. 1993;101(1):63–71. doi: 10.1006/jmrb.1993.1008. [DOI] [Google Scholar]
- Wishart DS, Sykes BD, Richards FM. Relationship between nuclear magnetic resonance chemical shift and protein secondary structure. J Mol Biol. 1991;222(2):311–333. doi: 10.1016/0022-2836(91)90214-Q. [DOI] [PubMed] [Google Scholar]
- Wishart DS, Sykes BD, Richards FM. The chemical shift index: a fast and simple method for the assignment of protein secondary structure through NMR spectroscopy. Biochemistry. 1992;31(6):1647–1651. doi: 10.1021/bi00121a010. [DOI] [PubMed] [Google Scholar]
- Wishart D, Bigam C, Holm A, Hodges R, Sykes B. 1H, 1 3C and 15N random coil NMR chemical shifts of the common amino acids. I. Investigations of nearest-neighbor effects. J Biomol NMR. 1995;5(1):67–81. doi: 10.1007/BF00227471. [DOI] [PubMed] [Google Scholar]
- Wrabl JO, Shortle D, Woolf TB. Correlation between changes in nuclear magnetic resonance order parameters and conformational entropy: molecular dynamics simulations of native and denatured staphylococcal nuclease. Proteins Struct. Funct. Bioinform. 2000;38(2):123–133. doi: 10.1002/(SICI)1097-0134(20000201)38:2<123::AID-PROT2>3.0.CO;2-H. [DOI] [PubMed] [Google Scholar]
- Wüthrich K. NMR of proteins and nucleic acids. New York: Wiley; 1986. [Google Scholar]
- Xu XP, Case D. Automated prediction of 15N, 13Cα, 13Cβ and 13C’ chemical shifts in proteins using a density functional database. J Biomol NMR. 2001;21(4):321–333. doi: 10.1023/A:1013324104681. [DOI] [PubMed] [Google Scholar]
- Yao J, Chung J, Eliezer D, Wright PE, Dyson HJ. NMR structural and dynamic characterization of the acid-unfolded state of apomyoglobin provides insights into the early events in protein folding. Biochemistry. 2001;40(12):3561–3571. doi: 10.1021/bi002776i. [DOI] [PubMed] [Google Scholar]
- Yip P, Case DA. A new method for refinement of macromolecular structures based on nuclear overhauser effect spectra. J Magn Reson. 1989;83(3):643–648. [Google Scholar]
- Zagrovic B, van Gunsteren WF. Comparing atomistic simulation data with the NMR experiment: how much can NOEs actually tell us? Proteins Struct Funct Bioinform. 2006;63(1):210–8. doi: 10.1002/prot.20872. [DOI] [PubMed] [Google Scholar]