Abstract
Protein–glycan recognition regulates a wide range of biological and pathogenic processes. Conformational diversity of glycans in solution is apparently incompatible with specific binding to their receptor proteins. One possibility is that among the different conformational states of a glycan, only one conformer is utilized for specific binding to a protein. However, the labile nature of glycans makes characterizing their conformational states a challenging issue. All-atom molecular dynamics (MD) simulations provide the atomic details of glycan structures in solution, but fairly extensive sampling is required for simulating the transitions between rotameric states. This difficulty limits application of conventional MD simulations to small fragments like di- and tri-saccharides. Replica-exchange molecular dynamics (REMD) simulation, with extensive sampling of structures in solution, provides a valuable way to identify a family of glycan conformers. This article reviews recent REMD simulations of glycans carried out by us or other research groups and provides new insights into the conformational equilibria of N-glycans and their alteration by chemical modification. We also emphasize the importance of statistical averaging over the multiple conformers of glycans for comparing simulation results with experimental observables. The results support the concept of “conformer selection” in protein–glycan recognition.
Keywords: N-glycan, Conformational flexibility, Protein–glycan interactions, N-glycan modifications, Conformer selection, Molecular dynamics simulations, Replica-exchange molecular dynamics simulations
Conformational flexibility of glycans
Glycan is an essential molecular component in biological systems. In mammals, there are about ten types of monosaccharides that are used to form glycans. These monosaccharides are linked together by various glycosidic bonds. The addition of branch structures further matures glycans, making them distinct from proteins and DNA (Werz et al. 2007). The co-existence of rigid (saccharides) and flexible (glycosidic linkage) units in the glycan molecule gives rise to distinct multiple conformations in solution. This conformational diversity is also shown in glycans that are covalently attached to proteins and lipids. The glycan-bound proteins and lipids participate in many key biological processes including cell adhesion, molecular trafficking and clearance, receptor activation, signal transduction, and endocytosis (Ohtsubo and Marth 2006).
Most of the biological functions of glycans rely on their binding to receptor proteins like lectin. Single-site-binding affinity in lectin is generally low (with K d values in the micromolar range), but highly specific. The relation between the flexibility of glycans and their specific recognition remains elusive. Protein–glycan interactions have been considered to be based on “conformer selection” (Gabius et al. 2011; Gabius 2008). In contrast to E. Fischer’s lock-and-key idea for common protein–ligand bindings, the multiple conformations of glycans in solution could serve as many “keys” (Fig. 1). Each conformation (“key”) may have biological significance and could bind to a different target protein for a different function (“bunch-of-keys” model; Hardy 1997). There are many cases where the same glycan acts as a ligand for different lectins. A typical example is provided by the common pentasaccharide moiety of ganglioside GM1 being a target both for cross-linking by galectin-1 to inhibit the growth of human SK-N-MC neurobastoma cells (Kopitz et al. 2001) and for the AB5 toxin of Vibrio cholera (Siebert et al. 2003). The different conformations of tetrasaccharide sialyl Lewisx bound to E-selectin seen in different NMR-based analyses serve as another example of the “bunch-of-keys” model (Harris et al. 1999).
Fig. 1.
Schematic illustration of the structural feature of oligosaccharides and their possible binding mechanisms to receptor proteins
Characterization of the conformational states of glycans is a challenging issue due to their labile nature, and leaves details of the binding mechanism elusive. It is now possible to identify the conformational properties of individual glycosidic linkages. Well-established concepts, e.g., the exo-anomeric effect and the gauche effect, help to predict the conformational preference of a particular linkage. However, determination of the overall shape of a large oligosaccharide is still problematic. N-glycans, which are the most abundant oligosaccharide found in cellular proteins, share a common branched pentasaccharide core sequence, Manα1–6(Manα1–3)Manβ1–4GlcNAcβ1–4GlcNAcβ1–Asn–X–Ser/Thr. Additional branches (antennae) complicate the structures. The number of pairs of dihedral glycosidic angles rapidly increases; 22 parameters for typical bianntenary complex-type N-glycan (André et al. 2009). Actually, the number of different conformers of glycans is less than that predicted from the flexibilities of all the individual linkages (Woods et al. 1998).
Due to the inherent flexibility of N-glycans, high-resolution X-ray structures are available only for receptor-bound forms. Fluorescence resonance energy transfer (FRET) experiments provide motions of multiple antennae attached to the core of N-glycans (Rice et al. 1993). They suggest that N-glycan chains undergo a conformational transition between “folded” and “extended” forms. However, FRET experiments are always associated with the possibility that the probes themselves alter the conformational preference. Nuclear magnetic resonance (NMR) spectroscopy has been the most powerful tool to determine glycan conformations. The paucity of parameters describing tertiary structure of glycans makes analysis non-trivial. Recent advances in NMR-based analysis, for example the direct observation of hydroxyl proton exchange by using deuterium isotope shifts on 13C-NMR (Hanashima et al. 2011), prompt an investigation of the various conformational states of N-glycans.
Molecular dynamics simulations of N-glycans
Molecular dynamics (MD) simulations are popular tool in the field of structural biology of proteins, nucleic acids, and lipid bilayers. Recently, they are also becoming popular in the field of glycobiology due to advances in force field accuracy and sampling efficiency—two hallmarks of MD simulations. Development of accurate force fields describing the inherently complex properties of carbohydrates is a nontrivial task. There have been extensive re-parameterization of the general purpose force fields used in CHARMM (Guvench et al. 2009; Hatcher et al. 2009), AMBER (Kirschner et al. 2008), and GROMOS (Lins and Hünenberger 2005), and parameterization of new carbohydrate force fields. Currently, there are high-level carbohydrate force fields that are used for computer simulations (Fadda and Woods 2010). Several easy-to-use Web-tools for modeling carbohydrate 3D structures also prompt investigation of MD simulations (Frank and Schloissnig 2010; Jo et al. 2011).
The conformational phase space of glycans involves multiple minima separated by distinct energy barriers of larger than a few k BT. A well-to-well transition around the glycosidic dihedral angles rarely occurs on the time scale of the few tens of nanosecond that operates in conventional MD simulations (Perić-Hassler et al. 2010). Extensive conformational sampling is required to access the multiple conformers of N-glycans. For this reason, past conventional MD simulations in explicit solvent have been limited to small fragments like mono-, di-, or trisaccharides (Sayers and Prestegaud 2000; Kim et al. 2009; Kirschner and Woods 2001; Almond 2005; Perić-Hassler et al. 2010; Corzana et al. 2004; Landström and Widmalm 2010), or larger fragments with short sampling (Naidoo et al. 1997; Woods et al. 1998; André et al. 2009).
REMD simulations of N-glycan in solution
Many enhanced sampling techniques have been developed for the simulation of biomolecules. The replica-exchange molecular dynamics (REMD) method (Sugita and Okamoto 1999) is one of the simplest and the most widely used methods. This method employs a set of replicated simulations with different temperatures that are exchanged frequently, causing a one-dimensional random walk in temperature space as well as in potential energy space. The random walk in potential energy space avoids each replica simulation being trapped in one of the local energy minimum states, resulting in a significant enhancement of the conformational sampling. The REMD method has been successfully applied to investigate many biophysical issues: protein folding (Yoda et al. 2010; Lei et al. 2007), amyloid aggregation (Miyashita et al. 2009), phase behavior in lipid bilayers (Nagai and Okamoto 2012), etc. A few reports of REMD simulations of carbohydrates have also emerged recently: puckering of the saccharide unit (Babin and Sagui 2010), small saccharides conformations (Campen et al. 2007; Yongye et al. 2008b, a), conformations of cellulose oligomers (Shen et al. 2009), conformation and solvent effects of glycosylated peptides (Mallajosyula and MacKerell 2011; Guardiani et al. 2012), and conformational properties of larger fragments including N-glycans (Beckham et al. 2010; Pan and Song 2010; Ramadugu et al. 2010). These applications give insights into the conformational states of glycans that were not apparent before.
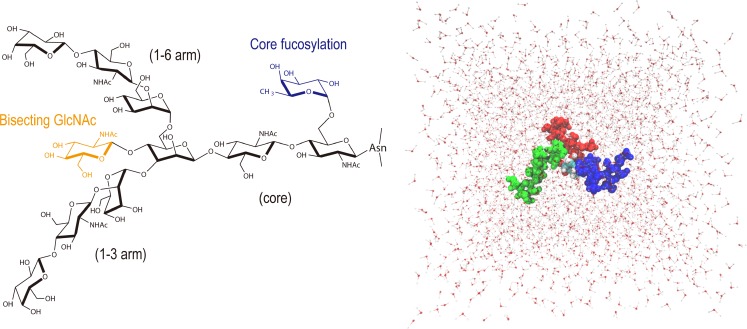
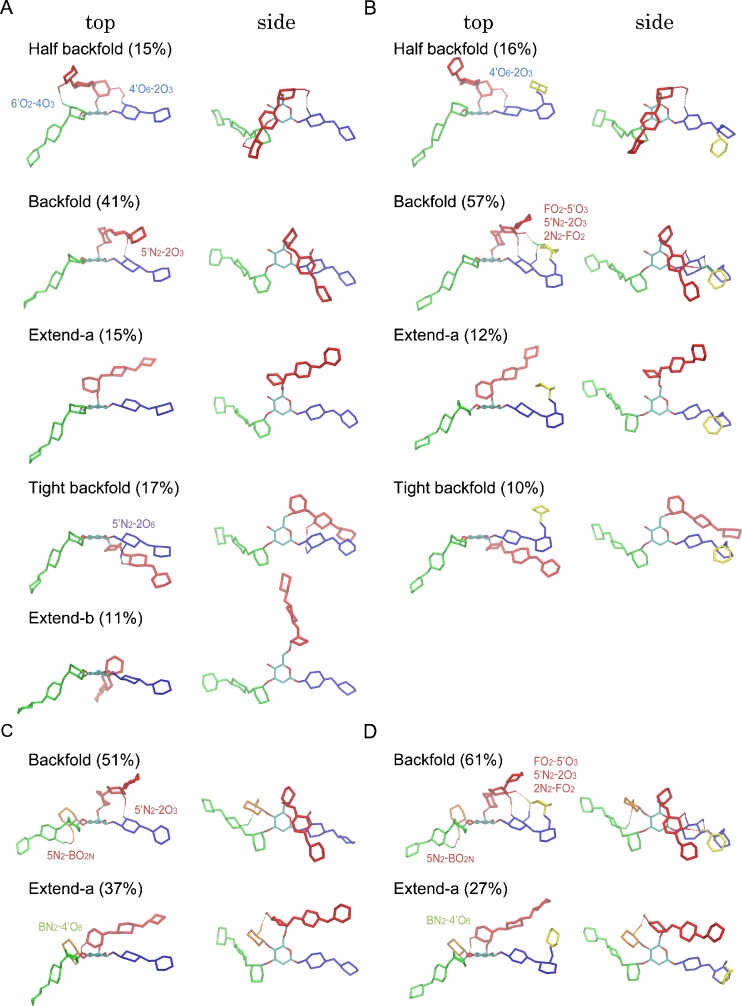
In our research group, we also employ REMD simulations of N-glycans in explicit solvent to characterize their conformational states (Re et al. 2011; Nishima et al. 2012). Our simulations focus on the effect of a branch and modifications to the structures of N-glycans (Fig. 2). Here, we briefly summarize our REMD simulation protocols. We use a GLYCAM06 force field for N-glycans and a TIP3P model for water. An in-house interface program, REIN (Replica-Exchange Interface) (Miyashita et al., in preparation), is used to facilitate REMD simulations. The program is designed to perform REMD simulations with any available software without modification. Currently, two MD programs, NAMD (Phillips et al. 2005) and MARBLE (Ikeguchi 2004) are available in REIN. It can easily interface to other software even quantum chemical packages. The number of replicas and temperature ranges were determined with the aid of a web-protocol (Patriksson and van der Spoel 2008). For N-glycans in explicit solvent, 64 replicas covering the temperature range 300–500 K give an exchange ratio of more than 40 %. A few tens of nanosecond MD run for each replica provides well-converged results. The resultant trajectory is then subjected to a clustering analysis to extract the representative conformations and their relative populations. The above protocol gives five distinct conformers of bianntenary complex-type N-glycan in solution, each of which is characterized by its local orientation of the Manα1-6Man glycosidic linkage (Fig. 3a).
Fig. 2.
Structure of a biantennary complex-type N-glycan (Bi9, black) and its typical modifications: the introduction of bisecting GlcNAc (BiB10, orange), the core fucosylation (BiF10, blue), and both (BiBF11, orange and blue). These modifications are known to change the affinity of protein-glycan interactions. N-glycan solvated within a box of >3,000 TIP3P H2Os used for simulations is also shown (α1,3-arm green, α1,6-arm red, core blue)
Fig. 3.
Structures of distinct conformers (top and side views) found from our REMD simulations for four N-glycans: a Bi9, b BiF10, c BiB10, and d BiBF11. Different colors indicate different arms (α1,3-arm green, α1,6-arm red, core blue, bisect orange, and fucose yellow). The α1,6-arm (red) interacts with either core (blue) or α1,3-arm (green) in the “folded” forms, whereas it is fully solvated in the “extended” forms. Populations of each conformer obtained from the clustering analysis are given in the parentheses. Key inter-residue hydrogen bonds stabilizing each conformer are also shown
Representation of multiple conformers of N-glycan
In order to characterize the conformational states of N-glycans, one needs good representation of their structures. The carb-Rama plots (Salisburg et al. 2009), that extend Ramachandran’s idea of plotting amino acid and ψ angles to the glycosidic , ψ, and ω angles, display the conformational space of each glycosidic linkage. They are readily comparable to experimental NMR data. André and co-workers proposed a single-plot fingerprint-like presentation in polar coordinates for describing the mutual dependence among the many glycosidic angles involved (André et al. 2009).
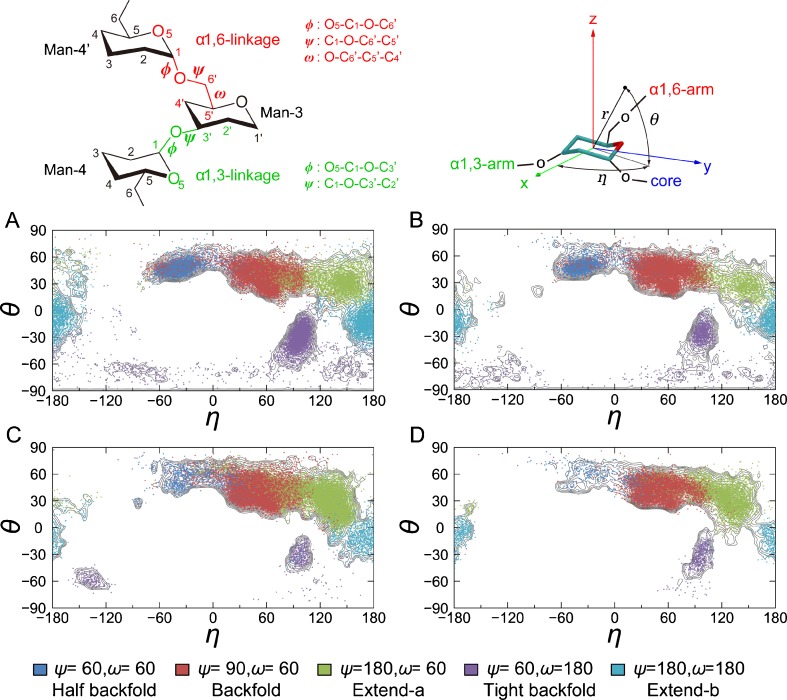
There is no rigorous way to describe the global conformation of an N-glycan. The end-to-end distance between a pair of arms (for example, the α1,6-arm and α1,3-arm) may be used to represent the relative orientation of a particular arm. The xyz population densities of each monosaccharide unit can be mapped on isocontour plots at a certain energy level to visualize the flexibility of global conformation (André et al. 2004). We propose an alternative plot using a spherical coordinate that represents the orientation of the α1,6-arm with respect to the pyranose plane at the branch (Fig. 4) (Nishima et al. 2012). This representation is based on our finding that the five distinct conformers of N-glycan are well characterized by the local orientation of the Manα1-6Man glycosidic linkage (Re et al. 2011). The azimuthal angle, η, represents the swing motion of the α1,6-arm along the polar axis while the polar angle, θ, represents its up–down motion with respect to the x-y plane. The flexibility of the N-glycan conformation is represented by swing and up–down motions of the α1,6-arm. Each motion is in turn correlated with the ψ and ω angles of the Manα1-6Man linkage, respectively, allowing unambiguous characterization of the overall shapes of N-glycans in term of the orientation of the local glycosidic bond (Fig. 4a–d). This Mercator-like plot can be generalized for analyzing the conformational flexibility of N-glycan in terms of the branch orientation.
Fig. 4.
Definition of local dihedral angles (, ψ and ω for α1,6-linkage and and ψ for α1,3-linkage) and the spherical coordinate used to represent the global conformation of N-glycans. The Man-3 structure of each simulation snapshot was superimposed to a plane regular hexagon on the xy plane, with its center at the origin. This allows us to determine a unique orientation of the N-glycan global structure with respect to the Man-3 structure, by reducing the artificial orientation changes arising from distortion of the pyranose ring in the simulation snapshots. The angle η represents swing motion of α1,6-arm around the z (polar) axis, while the angle θ represents up–down motion with respect to the xy-plane. Distribution of five distinct conformers (three “folded” and two “extended” forms, each of which is characterized by different ψ/ω angles of α1,6-linkage) mapped on the spherical coordinates for a Bi9, b BiF10, c BiB10, and d BiBF11. Blue ψ/ω of 60°/60°, red 90°/60°, green 180°/60°, purple 60°/180°, cyan 180°/180°. Free-energy contour lines (gray) are also shown for comparison
Comparison of REMD simulations with experiment
Simulations of glycans are commonly compared with NMR measurements. Nuclear Overhauser Enhancement (NOE) distances and their intensities, average spin coupling constants (3 J CH for /ψ and 3 J HH for ω in 1-6 linkage) are representative experimental parameters. Note that these experimental data provide the averages over multiple conformations of N-glycans in solution, but not the value for the most populated N-glycan conformer. If more than two major conformational states exist in the simulations, we can obtain the NMR measurements for each conformational state separately. Then, we can average over these values for all conformational states, taking the population of each conformer into account. This analysis, the so-called population-weighted average, allows us to compare simulations and experiments directly and make the relationship between the experimental observables and the conformational states clearer (DeMarco and Woods 2009; Yongye et al. 2008b).
Modulation of conformational variety by chemical modification revealed by REMD simulations
Chemical modification of N-glycans is known to modulate the function and regulation of the particular proteins involved. For example, the addition of bisecting GlcNAc by GlcNActransferase III (GnT-III) to the cell adhesion molecules, E-cadherin, and integrins, suppresses cell migration (Zhao et al. 2008). The currently accepted view is that chemical modification changes binding, by way of either switching the major conformation from one to another or inducing a unique bioactive conformation, rather than by making an additional unique binding site. Past studies, including NMR-based-analysis of model oligosaccharides (Homans et al. 1987a), FRET experiments (Stubbs et al. 1996), and molecular modeling followed by systematic bioassays with neoglycoproteins carrying synthetic biantennary N-glycans (André et al. 2009), indicate a switch-like change in the shape of the glycans upon chemical modification.
Figures 3 and 4 show the results of REMD simulations of four N-glycans with and without chemical modification (Nishima et al. 2012). N-glycan modification results in largely equivalent overall conformational space compared to unmodified N-glycan (Bi9). Yongye and co-workers reported a similar effect of chemical modification on the conformational properties of methyl α-(2,8)-di/trisialosides using REMD simulation (Yongye et al. 2008b). This similar outcome implies that the conformational repertoire of the N-glycan is largely determined by its main skeleton. A conspicuous finding of REMD simulations is that the introduction of bisecting GlcNAc and/or core fucosylation reduces the number of major conformers by shifting the conformational equilibria. This finding clearly supports the concept of “conformer selection” for protein–glycan interactions, which has been widely accepted by experimentalists. The switch-like behavior, as suggested previously, now can be understood in terms of the alteration of conformational equilibria by core modification.
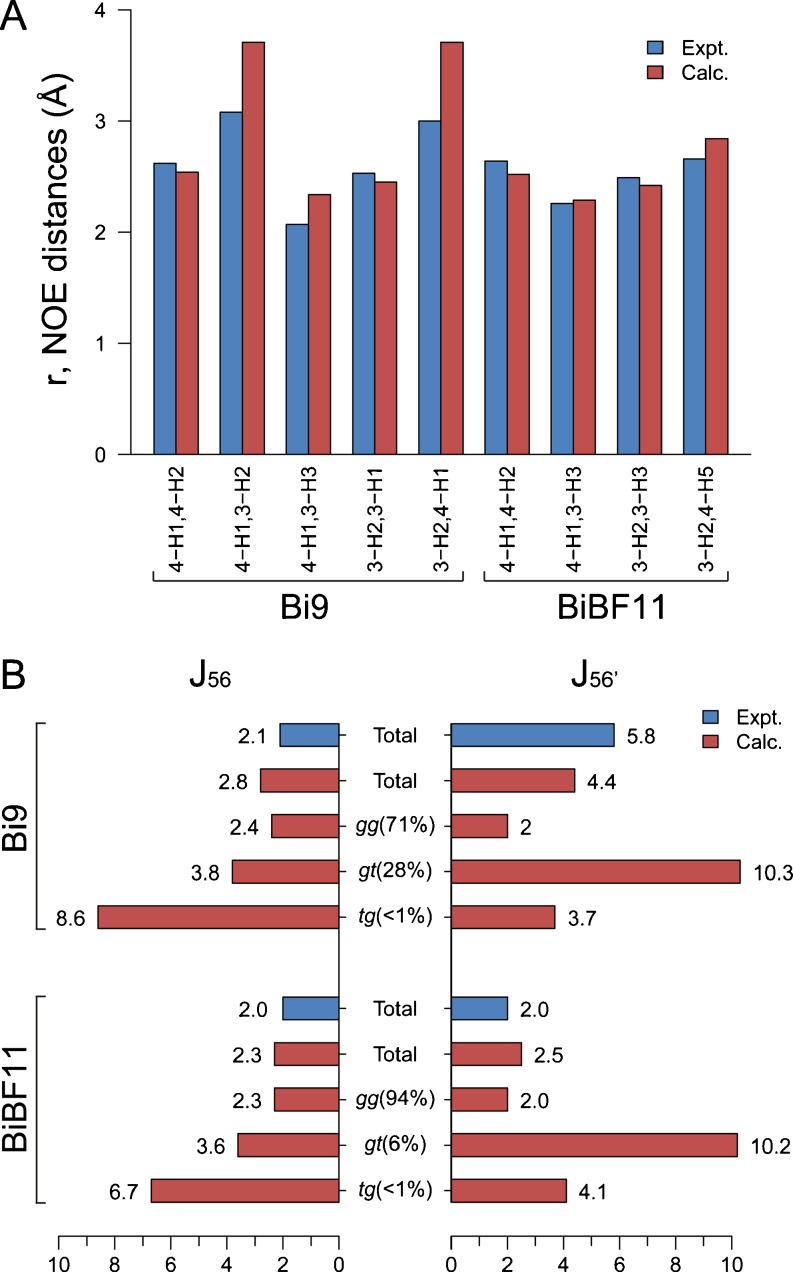
The population-weighed averages of the NMR observables (NOE and J-coupling) calculated from REMD simulations agree well with the experimental values (Homans et al. 1987b, 1986) (Fig. 5). The calculated NOE distances are very close to the experimental values (largest deviation of less than 0.7 Å), confirming the accuracy of the force field in use. More importantly, the REMD simulation well reproduces experimental J-coupling constants (J 56: H5–C5–C6–H6; J 56’: H5–C5–C6–H6’) for the Manα1-6Man linkage when the multiple-conformers are taken into account. Experimentally, two distinct values, 2.1 Hz and 5.8 Hz, were obtained for Bi9, while a single value of ~2 Hz was observed for BiBF11. The calculated J values for three clusters (gauche-gauche (gg), gauche-trans (gt), and trans-gauche (tg) conformers) show that the difference between Bi9 and BiBF11 arises from the non-negligible contribution of gt conformers (MD population of 28 %) in the former. The result agrees with the idea, derived originally from experiment, that Bi9 exists as a mixture of gg and gt conformers and that the introduction of the bisecting GlcNAc and/or the core fucose reduces the diversity.
Fig. 5.
Comparison of calculated and experimental NMR data for Bi9 and BiBF11. a Intra- and inter-residue NOE distances (in Å) of the Manα1-3Man structure, b scalar 3 J-coupling constants (in Hz) of the Manα1-6Man structure
In general, the glycan-binding sites of receptor proteins accommodate only a few sugar residues, typically including a terminal residue, of the whole glycan molecule. The chemical modifications of N-glycans could affect the exposure of those residues. For example, the introduction of bisecting GlcNAc increases the population size of the “extended” form in which the terminal β-linked galactose is exposed to solvent (Fig. 3c). Receptor proteins that preferentially bind to the β-linked galactose could detect such increase in the population. Future simulations of proten–glycan interactions could elaborate on what could be a fundamental principle of the recognition of specific glycans, one based on the natural N-glycan structural diversity and the ability of core modification to alter the conformational equilibria.
Summary and future perspectives
Replica-exchange molecular dynamics (REMD) simulations provide a valuable way to identify the conformational states of N-glycans in solution. A family of N-glycan conformers and their populations can be unambiguously characterized by extensive sampling of their structures followed by clustering analysis. The population-weighted averages of the NMR observables calculated using the multiple conformers well reproduce data derived from experiments, assuring the accuracy of the calculated populations. REMD simulations clearly indicate that the range of specific protein–glycan interactions and affinity changes need to be understood in terms of the conformational diversity of N-glycans and the alteration of conformational equilibria by core modifications.
Such studies could be extended to simulations of protein–glycan interactions. Computer simulation of protein–glycan interactions, including calculations of binding free energy and predictions of binding modes, emerges as a challenging field. A particularly important issue is to incorporate the different conformations of the glycan into the binding process, which is needed for accurate calculation of absolute binding free energy. For instance, to achieve this goal, REMD simulations can be combined with the MM/PBSA (Kollman et al. 2000) or umbrella sampling approach. The application of the REMD method to larger protein–glycan systems requires a large number of replicas. There have been several attempts to reduce the number of replicas, such as using REMD with a hybrid explicit/implicit solvation model (Okur et al. 2006), solute tempering (Liu et al. 2005), and REMD coupled to a high-temperature structure reservoir (Okur et al. 2007). Such methods and further methodological developments could lead to accurate free-energy calculations of protein–glycan binding, and help explore the relationship between the flexibility of glycans and their specific recognition.
Acknowledgements
This research was supported in part by a Grant for Scientific Research on a Priority Area ‘Transient macromolecular complex’ (to Y.S.), the Development and Use of the Next-Generation Supercomputer Project of the Ministry of Education, Culture, Sports, Science and Technology (MEXT) (to Y.S.), the Fund for Seeds of Collaborative Research of the RIKEN (to Y.Y., Y.S., and S.R.), and the Fund from the High Performance Computing Infrastructure (HPCI) Strategic Program of MEXT (to Y.S.). We also thank the RIKEN Integrated Cluster of Clusters (RICC) for providing computational resources.
Conflict of interest
None
Footnotes
Special issue: Computational Biophysics
References
- Almond A. Towards understanding the interaction between oligosaccharides and water molecules. Carbohyd Res. 2005;340(5):907–920. doi: 10.1016/j.carres.2005.01.014. [DOI] [PubMed] [Google Scholar]
- André S, Unverzagt C, Kojima S, Frank M, Seifert J, Fink C, Kayser K, von der Lieth CW, Gabius HJ. Determination of modulation of ligand properties of synthetic complex-type biantennary N-glycans by introduction of bisecting GlcNAc in silico, in vitro and in vivo. Eur J Biochem. 2004;271(1):118–134. doi: 10.1046/j.1432-1033.2003.03910.x. [DOI] [PubMed] [Google Scholar]
- André S, Kožár T, Kojima S, Unverzagt C, Gabius HJ. From structural to functional glycomics: core substitutions as molecular switches for shape and lectin affinity of N-glycans. Biol Chem. 2009;390(7):557–565. doi: 10.1515/BC.2009.072. [DOI] [PubMed] [Google Scholar]
- Babin V, Sagui C. Conformational free energies of methyl-α-L-iduronic and methyl-β-D-glucuronic acids in water. J Chem Phys. 2010;132:104108. doi: 10.1063/1.3355621. [DOI] [PubMed] [Google Scholar]
- Beckham GT, Bomble YJ, Matthews JF, Taylor CB, Resch MG, Yarbrough JM, Decker SR, Bu LT, Zhao XC, McCabe C, Wohlert J, Bergenstråhle M, Brady JW, Adney WS, Himmel ME, Crowley MF. The O-glycosylated linker from the trichoderma reesei family 7 cellulase is a flexible, disordered protein. Biophys J. 2010;99(11):3773–3781. doi: 10.1016/j.bpj.2010.10.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Campen RK, Verde AV, Kubicki JD. Influence of glycosidic linkage neighbors on disaccharide conformation in vacuum. J Phys Chem B. 2007;111(49):13775–13785. doi: 10.1021/jp0730996. [DOI] [PubMed] [Google Scholar]
- Corzana F, Motawia MS, Du Penhoat CH, Perez S, Tschampel SM, Woods RJ, Engelsen SB. A hydration study of (1 −> 4) and (1 −> 6) linked alpha-glucans by comparative 10 ns molecular dynamics simulations and 500-MHz NMR. J Comput Chem. 2004;25(4):573–586. doi: 10.1002/jcc.10405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeMarco ML, Woods RJ. Atomic-resolution conformational analysis of the G(M3) ganglioside in a lipid bilayer and its implications for ganglioside-protein recognition at membrane surfaces. Glycobiology. 2009;19(4):344–355. doi: 10.1093/glycob/cwn137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fadda E, Woods RJ. Molecular simulations of carbohydrates and protein-carbohydrate interactions: motivation, issues and prospects. Drug Discov Today. 2010;15(15–16):596–609. doi: 10.1016/j.drudis.2010.06.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frank M, Schloissnig S. Bioinformatics and molecular modeling in glycobiology. Cell Mol Life Sci. 2010;67(16):2749–2772. doi: 10.1007/s00018-010-0352-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gabius HJ. Glycans: bioactive signals decoded by lectins. Biochem Soc Trans. 2008;36:1491–1496. doi: 10.1042/BST0361491. [DOI] [PubMed] [Google Scholar]
- Gabius HJ, André S, Jiménez-Barbero J, Romero A, Solís D. From lectin structure to functional glycomics: principles of the sugar code. Trends Biochem Sci. 2011;36(6):298–313. doi: 10.1016/j.tibs.2011.01.005. [DOI] [PubMed] [Google Scholar]
- Guardiani C, Signorini GF, Livi R, Papini AM, Procacci P. Conformational landscape of N-glycosylated peptides detecting autoantibodies in multiple sclerosis, revealed by hamiltonian replica exchange. J Phys Chem B. 2012;116(18):5458–5467. doi: 10.1021/jp301442n. [DOI] [PubMed] [Google Scholar]
- Guvench O, Hatcher ER, Venable RM, Pastor RW, Mackerell AD. CHARMM additive all-atom force field for glycosidic linkages between hexopyranoses. J Chem Theory Comput. 2009;5(9):2353–2370. doi: 10.1021/ct900242e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hanashima S, Kato K, Yamaguchi Y. C-13-NMR quantification of proton exchange at LewisX hydroxyl groups in water. Chem Commun. 2011;47(38):10800–10802. doi: 10.1039/c1cc13310a. [DOI] [PubMed] [Google Scholar]
- Hardy BJ. The glycosidic linkage flexibility and time-scale similarity hypotheses. J Mol Struct. 1997;395:187–200. doi: 10.1016/S0166-1280(96)04866-X. [DOI] [Google Scholar]
- Harris R, Kiddle GR, Field RA, Milton MJ, Ernst B, Magnani JL, Homans SW. Stable-isotope-assisted NMR studies on C-13-enriched sialyl Lewis(x) in solution and bound to E-selectin. J Am Chem Soc. 1999;121(11):2546–2551. doi: 10.1021/ja983423y. [DOI] [Google Scholar]
- Hatcher E, Guvench O, Mackerell AD. CHARMM additive all-atom force field for aldopentofuranoses, methyl-aldopentofuranosides, and fructofuranose. J Phys Chem B. 2009;113(37):12466–12476. doi: 10.1021/jp905496e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Homans SW, Dwek RA, Boyd J, Mahmoudian M, Richards WG, Rademacher TW. Conformational transitions in N-linked oligosaccharides. Biochem-Us. 1986;25(20):6342–6350. doi: 10.1021/bi00368a076. [DOI] [PubMed] [Google Scholar]
- Homans SW, Dwek RA, Rademacher TW. Solution conformations of N-linked oligosaccharides. Biochem-Us. 1987;26(21):6571–6578. doi: 10.1021/bi00395a001. [DOI] [PubMed] [Google Scholar]
- Homans SW, Dwek RA, Rademacher TW. Tertiary structure in N-linked oligosaccharides. Biochem-Us. 1987;26(20):6553–6560. doi: 10.1021/bi00394a040. [DOI] [PubMed] [Google Scholar]
- Ikeguchi M. Partial rigid-body dynamics in NPT, NPAT and NP gamma T ensembles for proteins and membranes. J Comput Chem. 2004;25(4):529–541. doi: 10.1002/jcc.10402. [DOI] [PubMed] [Google Scholar]
- Jo S, Song KC, Desaire H, MacKerell AD, Im W. Glycan reader: automated sugar identification and simulation preparation for carbohydrates and glycoproteins. J Comput Chem. 2011;32(14):3135–3141. doi: 10.1002/jcc.21886. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim H, Choi Y, Lee J, Jeong K, Jung S. Conformational analysis of trimannoside and bisected trimannoside using aqueous molecular dynamics simulations. Bull Kor Chem Soc. 2009;30(11):2723–2728. doi: 10.5012/bkcs.2009.30.11.2723. [DOI] [Google Scholar]
- Kirschner KN, Woods RJ. Solvent interactions determine carbohydrate conformation. Proc Natl Acad Sci USA. 2001;98(19):10541–10545. doi: 10.1073/pnas.191362798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kirschner KN, Yongye AB, Tschampel SM, González-Outeiriño J, Daniels CR, Foley BL, Woods RJ. GLYCAM06: a generalizable biomolecular force field. Carbohydrates. J Comput Chem. 2008;29(4):622–655. doi: 10.1002/jcc.20820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kollman PA, Massova I, Reyes C, Kuhn B, Huo S, Chong L, Lee M, Lee T, Duan Y, Wang W, Donini O, Cieplak P, Srinivasan J, Case DA, Cheatham TE. Calculating structures and free energies of complex molecules: combining molecular mechanics and continuum models. Accounts of chemical research. 2000;33(12):889–897. doi: 10.1021/ar000033j. [DOI] [PubMed] [Google Scholar]
- Kopitz J, Reitzenstein C, Andre S, Kaltner H, Uhl J, Ehemann V, Cantz M, Gabius HJ. Negative regulation of neuroblastoma cell growth by carbohydrate-dependent surface binding of galectin-1 and functional divergence from galectin-3. J Biol Chem. 2001;276(38):35917–35923. doi: 10.1074/jbc.M105135200. [DOI] [PubMed] [Google Scholar]
- Landström J, Widmalm G. Glycan flexibility: insights into nanosecond dynamics from a microsecond molecular dynamics simulation explaining an unusual nuclear Overhauser effect. Carbohyd Res. 2010;345(2):330–333. doi: 10.1016/j.carres.2009.11.003. [DOI] [PubMed] [Google Scholar]
- Lei HX, Wu C, Liu HG, Duan Y. Folding free-energy landscape of villin headpiece subdomain from molecular dynamics simulations. Proc Natl Acad Sci USA. 2007;104(12):4925–4930. doi: 10.1073/pnas.0608432104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lins RD, Hünenberger PH. A new GROMOS force field for hexopyranose-based carbohydrates. J Comput Chem. 2005;26(13):1400–1412. doi: 10.1002/jcc.20275. [DOI] [PubMed] [Google Scholar]
- Liu P, Kim B, Friesner RA, Berne BJ. Replica exchange with solute tempering: a method for sampling biological systems in explicit water. Proc Natl Acad Sci USA. 2005;102(39):13749–13754. doi: 10.1073/pnas.0506346102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mallajosyula SS, MacKerell AD. Influence of solvent and intramolecular hydrogen bonding on the conformational properties of O-linked glycopeptides. J Phys Chem B. 2011;115(38):11215–11229. doi: 10.1021/jp203695t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miyashita N, Straub JE, Thirumalai D, Sugita Y. Transmembrane structures of amyloid precursor protein dimer predicted by replica-exchange molecular dynamics simulations. J Am Chem Soc. 2009;131(10):3438–3439. doi: 10.1021/ja809227c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nagai T, Okamoto Y. Replica-exchange molecular dynamics simulation of a lipid bilayer system with a coarse-grained model. Mol Simulat. 2012;38(5):437–441. doi: 10.1080/08927022.2011.564172. [DOI] [Google Scholar]
- Naidoo KJ, Denysyk D, Brady JW. Molecular dynamics simulations of the N-linked oligosaccharide of the lectin from Erythrina corallodendron. Protein Eng. 1997;10(11):1249–1261. doi: 10.1093/protein/10.11.1249. [DOI] [PubMed] [Google Scholar]
- Nishima W, Miyashita N, Yamaguchi Y, Sugita Y, Re S. Effect of Bisecting GlcNAc and Core Fucosylation on Conformational Properties of Biantennary Complex-Type N-Glycans in Solution. J Phys Chem. 2012;116:8504–8512. doi: 10.1021/jp212550z. [DOI] [PubMed] [Google Scholar]
- Ohtsubo K, Marth JD. Glycosylation in cellular mechanisms of health and disease. Cell. 2006;126(5):855–867. doi: 10.1016/j.cell.2006.08.019. [DOI] [PubMed] [Google Scholar]
- Okur A, Wickstrom L, Layten M, Geney R, Song K, Hornak V, Simmerling C. Improved efficiency of replica exchange simulations through use of a hybrid explicit/implicit solvation model. J Chem Theory Comput. 2006;2(2):420–433. doi: 10.1021/ct050196z. [DOI] [PubMed] [Google Scholar]
- Okur A, Roe DR, Cui GL, Hornak V, Simmerling C. Improving convergence of replica-exchange simulations through coupling to a high-temperature structure reservoir. J Chem Theory Comput. 2007;3(2):557–568. doi: 10.1021/ct600263e. [DOI] [PubMed] [Google Scholar]
- Pan D, Song YH. Role of altered sialylation of the I-like domain of beta 1 integrin in the binding of fibronectin to β1 integrin: thermodynamics and conformational analyses. Biophys J. 2010;99(1):208–217. doi: 10.1016/j.bpj.2010.03.063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patriksson A, van der Spoel D. A temperature predictor for parallel tempering simulations. Phys Chem Chem Phys. 2008;10(15):2073–2077. doi: 10.1039/b716554d. [DOI] [PubMed] [Google Scholar]
- Perić-Hassler L, Hansen HS, Baron R, Hünenberger PH. Conformational properties of glucose-based disaccharides investigated using molecular dynamics simulations with local elevation umbrella sampling. Carbohyd Res. 2010;345(12):1781–1801. doi: 10.1016/j.carres.2010.05.026. [DOI] [PubMed] [Google Scholar]
- Phillips JC, Braun R, Wang W, Gumbart J, Tajkhorshid E, Villa E, Chipot C, Skeel RD, Kalé L, Schulten K. Scalable molecular dynamics with NAMD. J Comput Chem. 2005;26(16):1781–1802. doi: 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramadugu SK, Chung YH, Fuentes EJ, Rice KG, Margulis CJ. In silico prediction of the 3D structure of trimeric asialoglycoprotein receptor bound to triantennary oligosaccharide. J Am Chem Soc. 2010;132(26):9087–9095. doi: 10.1021/ja1021766. [DOI] [PubMed] [Google Scholar]
- Re S, Miyashita N, Yamaguchi Y, Sugita Y. Structural diversity and changes in conformational equilibria of biantennary complex-type N-glycans in water revealed by replica-exchange molecular dynamics simulation. Biophys J. 2011;101(10):L44–L46. doi: 10.1016/j.bpj.2011.10.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rice KG, Wu PG, Brand L, Lee YC. Experimental-determination of oligosaccharide 3-dimensional structure. Curr Opin Struc Biol. 1993;3(5):669–674. doi: 10.1016/0959-440X(93)90048-P. [DOI] [Google Scholar]
- Salisburg AM, Deline AL, Lexa KW, Shields GC, Kirschner KN. Ramachandran-type plots for glycosidic linkages: examples from molecular dynamic simulations using the Glycam06 force field. J Comput Chem. 2009;30(6):910–921. doi: 10.1002/jcc.21099. [DOI] [PubMed] [Google Scholar]
- Sayers EW, Prestegaud JH. Solution conformations of a trimannoside from nuclear magnetic resonance and molecular dynamics simulations. Biophys J. 2000;79(6):3313–3329. doi: 10.1016/S0006-3495(00)76563-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen TY, Langan P, French AD, Johnson GP, Gnanakaran S. Conformational flexibility of soluble cellulose oligomers: chain length and temperature dependence. J Am Chem Soc. 2009;131(41):14786–14794. doi: 10.1021/ja9034158. [DOI] [PubMed] [Google Scholar]
- Siebert HC, André S, Lu SY, Frank M, Kaltner H, van Kuik JA, Korchagina EY, Bovin N, Tajkhorshid E, Kaptein R, Vliegenthart JFG, von der Lieth CW, Jiménez-Barbero J, Kopitz J, Gabius HJ. Unique conformer selection of human growth-regulatory lectin galectin-1 for ganglioside GM(1) versus bacterial toxins. Biochem-Us. 2003;42(50):14762–14773. doi: 10.1021/bi035477c. [DOI] [PubMed] [Google Scholar]
- Stubbs HJ, Lih JJ, Gustafson TL, Rice KG. Influence of core fucosylation on the flexibility of a biantennary N-linked oligosaccharide. Biochem-Us. 1996;35(3):937–947. doi: 10.1021/bi9513719. [DOI] [PubMed] [Google Scholar]
- Sugita Y, Okamoto Y. Replica-exchange molecular dynamics method for protein folding. Chem Phys Lett. 1999;314(1–2):141–151. doi: 10.1016/S0009-2614(99)01123-9. [DOI] [Google Scholar]
- Werz DB, Ranzinger R, Herget S, Adibekian A, von der Lieth CW, Seeberger PH. Exploring the structural diversity of mammalian carbohydrates (“Glycospace”) by statistical databank analysis. ACS Chem Biol. 2007;2(10):685–691. doi: 10.1021/cb700178s. [DOI] [PubMed] [Google Scholar]
- Woods RJ, Pathiaseril A, Wormald MR, Edge CJ, Dwek RA. The high degree of internal flexibility observed for an oligomannose oligosaccharide does not alter the overall topology of the molecule. Eur J Biochem. 1998;258(2):372–386. doi: 10.1046/j.1432-1327.1998.2580372.x. [DOI] [PubMed] [Google Scholar]
- Yoda T, Sugita Y, Okamoto Y. Hydrophobic core formation and dehydration in protein folding studied by generalized-ensemble simulations. Biophys J. 2010;99(5):1637–1644. doi: 10.1016/j.bpj.2010.06.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yongye AB, Foley BL, Woods RJ. On achieving experimental accuracy from molecular dynamics simulations of flexible molecules: aqueous glycerol. J Phys Chem A. 2008;112(12):2634–2639. doi: 10.1021/jp710544s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yongye AB, González-Outeiriño J, Glushka J, Schultheis V, Woods RJ. The conformational properties of methyl α-(2,8)-di/trisialosides and their N-acyl analogues: implications for anti-Neisseria meningitidis B vaccine design. Biochem-Us. 2008;47(47):12493–12514. doi: 10.1021/bi800431c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao YY, Sato Y, Isaji T, Fukuda T, Matsumoto A, Miyoshi E, Gu J, Taniguchi N. Branched N-glycans regulate the biological functions of integrins and cadherins. FEBS J. 2008;275(9):1939–1948. doi: 10.1111/j.1742-4658.2008.06346.x. [DOI] [PubMed] [Google Scholar]