Assessment and significance of protein–protein interactions during development of protein biopharmaceuticals

Abstract

Early development of protein biotherapeutics using recombinant DNA technology involved progress in the areas of cloning, screening, expression and recovery/purification. As the biotechnology industry matured, resulting in marketed products, a greater emphasis was placed on development of formulations and delivery systems requiring a better understanding of the chemical and physical properties of newly developed protein drugs. Biophysical techniques such as analytical ultracentrifugation, dynamic and static light scattering, and circular dichroism were used to study protein–protein interactions during various stages of development of protein therapeutics. These studies included investigation of protein self-association in many of the early development projects including analysis of highly glycosylated proteins expressed in mammalian CHO cell cultures. Assessment of protein–protein interactions during development of an IgG1 monoclonal antibody that binds to IgE were important in understanding the pharmacokinetics and dosing for this important biotherapeutic used to treat severe allergic IgE-mediated asthma. These studies were extended to the investigation of monoclonal antibody–antigen interactions in human serum using the fluorescent detection system of the analytical ultracentrifuge. Analysis by sedimentation velocity analytical ultracentrifugation was also used to investigate competitive binding to monoclonal antibody targets. Recent development of high concentration protein formulations for subcutaneous administration of therapeutics posed challenges, which resulted in the use of dynamic and static light scattering, and preparative analytical ultracentrifugation to understand the self-association and rheological properties of concentrated monoclonal antibody solutions.

Introduction

The study and understanding of protein-protein interactions (PPI) have and remain one of the major efforts in modern biology as well as the development of protein therapeutics created by recombinant DNA technology. During the fledgling years of the biotechnology industry, most of the efforts were focused on development of new cloning technology and expression of human proteins in bacterial systems such as E. coli. Although molecular biology technology was refined during these early years, much of the work regarding PPI was of a qualitative nature generally addressing which proteins are interacting with other proteins or cellular components. However, as proteins produced from recombinant DNA technology resulted in marketed products, a greater emphasis was placed on understanding protein solution behavior in order to develop robust processes for fermentation, cell culture, recovery, purification, and eventually formulation into a drug product. The latter aspect of drug development required a better understanding of the chemical and physical properties of these newly developed therapeutics. This review summarizes much of our work investigating PPI that impacted the development of protein therapeutics at Genentech.

Early investigations into protein self-association

Development of proteins into pharmaceuticals requires a good understanding of the physical and chemical properties of the final drug product. One of the major concerns for proteins is their tendency to aggregate (Wang and Roberts 2010; Narhi et al. 2012) with potential consequences for safety, in particular immunogenicity (Singh 2011; Marszal and Fowler 2012). Although proteins are capable of forming irreversible aggregates, they can also undergo concentration dependent reversible self-association, which could be a concern during processing steps such as freezing large volumes leading to concentration gradients or long-term storage of high concentration proteins for the 1.5–2 years typically required for pharmaceuticals. Thus, an understanding of the self-association properties under in-process and final formulation conditions is important.

Self-association of small non-glycosylated proteins

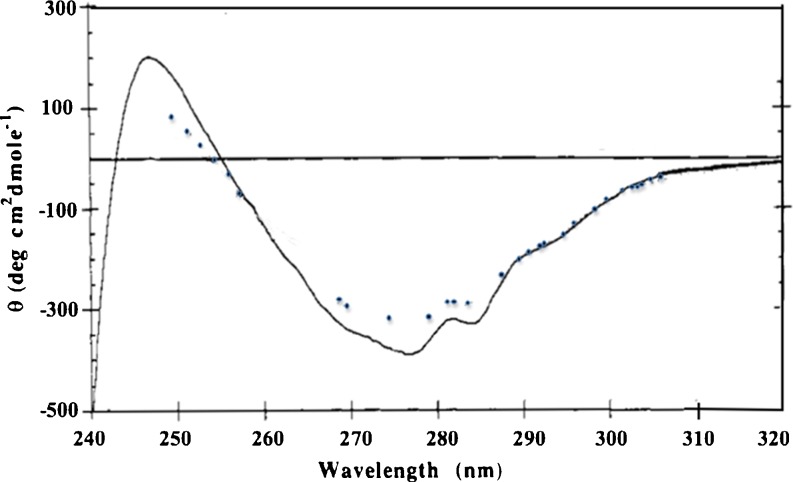
During the formative years of the biotechnology industry, relatively small proteins such as human growth hormone (hGH) and human insulin were produced by recombinant DNA technology and expressed in E. coli. Fortunately, these proteins were available as therapeutics derived from natural sources, and thus a fair amount of characterization and biophysical studies had been previously carried out. Another small protein, relaxin, a pregnancy hormone closely related to insulin in structure, but with very different biological activity, was isolated from pig, and had been previously used to treat scleroderma a rare disorder involving over production of collagen (Casten and Boucek 1958; Nguyen and Shire 1996). Since relaxin as a pregnancy hormone enabled remodeling of cervical tissue, it was hoped that this hormone could be developed as a drug to decrease the need for C-section delivery. This protein is produced naturally as a propeptide, which is cleaved into two chains linked by disulfide bonds. Alignment of the human relaxin sequence with insulin reveals that the cysteine residues involved in the intermolecular linkages are in the same position (Nguyen and Shire 1996). A process was developed at Genentech to express rDNA-derived A and B chains in E. coli and then to recombine the individually purified chains into a biologically functional molecule (Stults et al. 1990). Early characterization of human relaxin by size exclusion chromatography (SEC-HPLC) suggested that the molecule exists in the monomeric form (data not shown). However, studies using sedimentation equilibrium analytical ultracentrifugation (SE-AUC) and circular dichroism (CD) clearly showed that this molecule undergoes concentration dependent self-association, which was not detected by SEC because of the dilution that occurs during the chromatography (Shire et al. 1991). Analysis by circular dichroism before and after dilution resulted in an approximate 5-fold increase in monomer, indicating that there was no difference in the far UV CD spectrum, whereas there were significant decreases in the intensity of the tyrosine CD band near 277 nm and the tyrosine and tryptophan CD band at 284 nm. Moreover, there was little change in the broad band at 295 nm due solely to tryptophan suggesting that the environment of the lone tyrosine rather than the two tryptophans changed upon dilution (Shire et al. 1991) (Fig. 1). These data suggested that dissociation of the human relaxin dimer to monomer was not accompanied by large overall changes in secondary structure or alteration in the average tryptophan environment, whereas there was a significant change in the tyrosine environment. This conclusion was affirmed by the x-ray crystal structure of human relaxin, which crystallized as a dimer with the lone tyrosine from each monomer at the dimer interface (Eigenbrot et al. 1991). Thus, the solution studies were in good agreement with the crystal studies, suggesting that the determined crystal structure is very similar to the structure of the protein in solution.

Fig. 1.

Near-UV circular dichroism of human relaxin at 0.5 mg/mL (solid line), and 20 μg/mL (dotted line). Relaxin at 0.5 mg/mL was thermostated at 20 °C in a 1-cm cell, whereas relaxin at 20 μg/mL was in an unthermostated 10-cm cylindrical cuvette. The temperature in the sample compartment was ∼27 °C during the data collection process. The CD data were collected at 0.25-nm intervals at a spectral bandwidth of 0.5 nm and are the result of an average of three scans using an average time for each single data point collection of 5 s for the 0.5 mg/mL samples and the result of an average of ten scans using an average time for each single data point collection of 10 s for the 20 μg/mL sample. The weight fraction of human relaxin monomer estimated from the determined association constant by sedimentation equilibrium AUC of 100 (g/L)⁻¹ is 0.12 at 0.5 mg/mL and 0.50 at 20 μg/mL. Adapted from Shire et al. (1991)

Self-association of glycosylated proteins

Many of the early human proteins such as hGH, insulin and relaxin that were being developed as therapeutics were relatively small and were produced in E. coli. As more complex glycoproteins were developed using mammalian cell cultures, such as Chinese Hamster Ovary cells, additional characterization studies of self-association needed to be done. Some of these glycoproteins contained a large percentage of sugar residues that posed several challenges in determining accurate molecular weight in solution by SEC-HPLC analysis (Shire 1994). Some of the early studies on glycoprotein using SE-AUC included rgp120, the recombinant DNA-derived envelope glycoprotein of human immunodeficiency virus type 1, being developed as an HIV vaccine, and rhDnase marketed as Pulmozyme^® for the treatment of cystic fibrosis (Shire 1996). Buoyant molecular weights were determined by analyzing the SE-AUC absorbance gradients as a single sedimenting ideal species, and molecular weights were then computed from the buoyant molecular weights using estimated values for the partial specific volume of the glycosylated protein and the densities of the solvent buffers (Shire 1994). The partial specific volumes for rgp120, and rhDNase, were estimated from the amino acid and carbohydrate composition.

Preliminary analysis of rgp120 protein by SEC-HPLC suggested that the molecular weight was that of a dimer, and that the large amount of glycosylation (∼50 % by weight) was responsible for the dimerization (data not shown). The latter conclusion was based on reduction of the SEC retention time after treatment with glycosidases. The SE-AUC data for rgp120 fit well with a single sedimenting ideal species model with determined molecular weight of ∼104 kDa, which is in very good agreement with the expected molecular weight of 102 kDa based on amino acid and average carbohydrate composition. This agreement is quite good considering that the partial specific volume was estimated from amino acid and average carbohydrate composition. The SE-AUC studies convincingly showed that rgp120 does not self-associate in solution and that the apparent high molecular weight determined by SEC was due to the large hydrodynamic size of a protein consisting of 50 % carbohydrate (Shire 1994). In the case of rhDNase, the molecular weight determined by SEC varies from 30 to 40 kDa (Funakoshi et al. 1977; Murai et al. 1978; Love and Hewitt 1979; Ito et al. 1984). Since the expected molecular weight of a monomer based on amino acid and carbohydrate composition is 32,653 Da, the SEC results suggest that rhDNase may be self-associating. Determination of an accurate molecular weight for glycoproteins in solution by SEC was difficult, since the hydrodynamic volume of the glycoprotein was often being compared to unglycosylated standard proteins (Shire 1994). (The improvement in SEC analysis using on-line light scattering detection has alleviated some of these issues.) SE-AUC analysis using a partial specific volume for rhDNase of 0.721 mL/g computed from the amino acid and average carbohydrate composition using the additivity rule and values for the individual amino acid and carbohydrate residues (Cohn and Edsall 1965; Gibbons 1972; Perkins 1986) resulted in a determined molecular weight of 33,200 ± 1,400, in excellent agreement with the molecular weight of 32,653 Da based on the polypeptide sequence and average carbohydrate composition thus demonstrating that rhDNase does not self-associate (Shire 1996).

Self-association of antibody proteins

Including an analysis of protein size distribution, using AUC can give evidence of reversible self-association that cannot be obtained by standard SEC-HPLC techniques. This is especially true when both sedimentation velocity analytical ultracentrifugation (SV-AUC) and SE-AUC are employed. For example, SEC-HPLC analysis of a monoclonal antibody sample resulted in a single monomer peak at 99.6 % with a small amount of aggregate species. However, SV-AUC analysis of this mAb in SEC-HPLC mobile phase resulted in evidence of much larger protein size heterogeniety compared to results from SEC-HPLC. The identification of reversible self-association as the cause was obtained by further studies in PBS buffer that showed increased weight-average sedimentation coefficient with increased protein concentration during the analysis. In addition, an analysis of the same sample by SE-AUC also showed the observed weight-average molecular weight of the antibody increased with increasing protein concentration. Therefore, in this case, using AUC as an additional method for protein size distribution, resulted in the detection of reversible self-association behavior that was not measured by the commonly used SEC-HPLC method alone (Andya et al. 2010).

Interaction of proteins with formulation components

In addition to understanding self-association properties of potential protein therapeutics, it may be necessary to evaluate interactions of proteins with particular excipients added to the formulation. As a case in point, one protein that was being developed as a potential therapy for hemophilia was a recombinant-derived human tissue factor (rhTF), a membrane-bound protein on cell surfaces, which is involved in the coagulation cascade (Nemerson 1988). Since this protein has a hydrophobic region, which is normally inserted into the cell membrane, a non-ionic surfactant, C12E8, was required in the formulation to ensure solubility. Thus, the surfactant essentially replaces the membrane by interacting directly with the transmembrane domain, and characterization of this interaction was carried out using electron paramagnetic resonance (EPR) spectroscopy in conjunction with SE-AUC (Jones et al. 1999). In addition to binding stoichiometries, the possibility of identifying the interacting domains by using two truncated forms of rhTF lacking the cytoplasmic domain was explored. The two recombinant truncated forms of human tissue factor produced in E. coli were formulated in the absence of phospholipids. Recombinant human tissue factor 243 (rhTF 243) consists of 243 amino acids and includes the transmembrane sequences, whereas recombinant human tissue factor 220 (rhTF 220) contains only the first 221 amino acids of the human tissue factor, lacking those of the transmembrane region. Binding of C12E8 to rhTF 243 was detected by both EPR spectroscopy and AUC. Although a unique binding stoichiometry was not determined, EPR spectroscopy greatly narrowed the range of possible solutions suggested by the AUC data. In particular, it was concluded that at least 75 % of the mixed protein surfactant micelles consisted of one rTF243 per micelle. As expected, neither technique revealed an interaction between rhTF 220 and C12E8 because of the lack of a transmembrane domain.

Analysis of large complexes

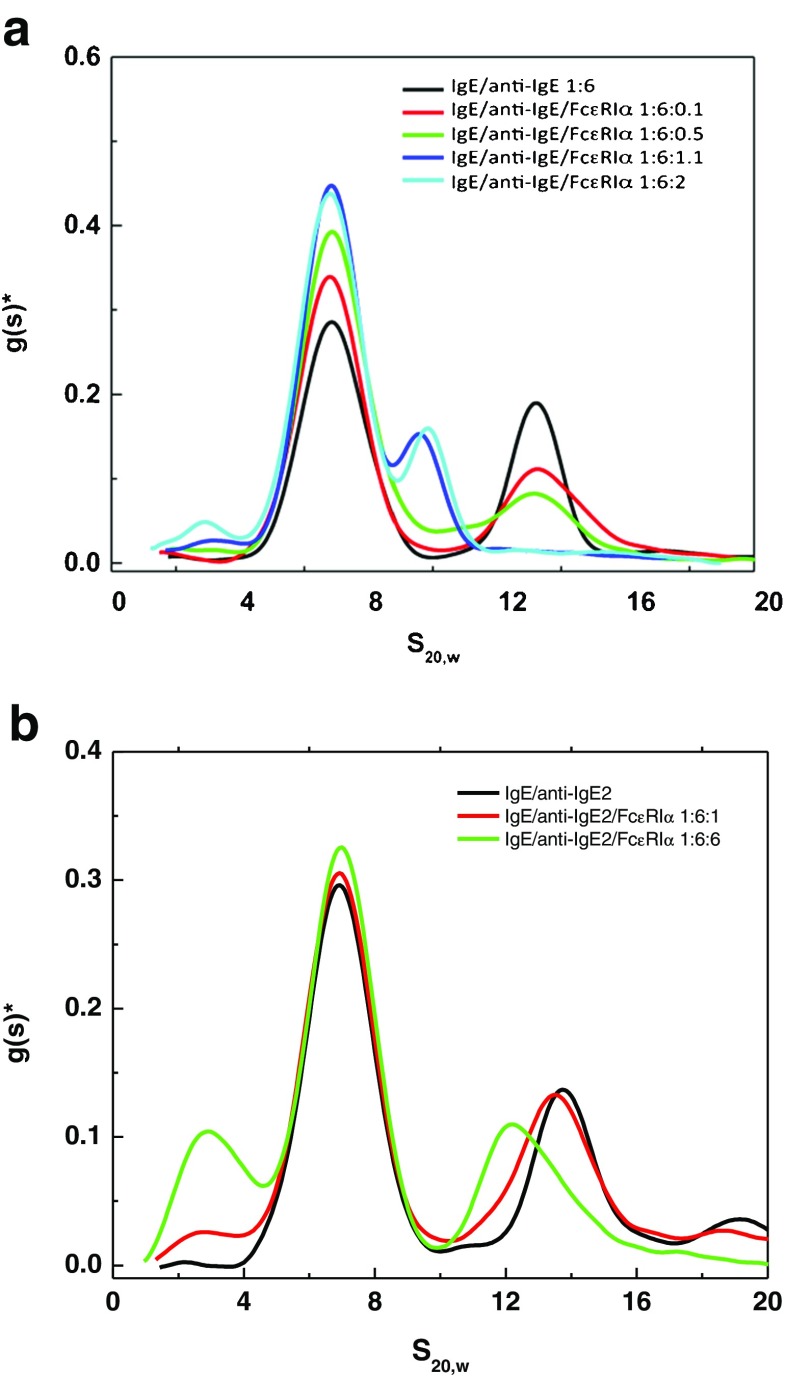
As the biotechnology industry continued to evolve, more attention was concentrated on fulfilling the old dream of using nature’s own immune defenses such as antibodies to treat disease, specifically trying to develop highly specific therapies. Much of the early work was not successful, since the hybridoma technology resulted in murine antibodies, which often generated human antimouse responses. However, as technology evolved to produce humanized versions of the murine antibodies and eventually fully human antibodies, the pharmaceutical industry ramped up efforts to produce therapeutic monoclonal antibodies (MAbs) (Ezzell 2001; Wang et al. 2007). These antibodies have been developed to interact with a variety of targets responsible directly or indirectly for a variety of cancers as well as immunologically based disorders such as multiple sclerosis, arthritis and asthma. Many of the targets are on cell surfaces, but some are also circulating in serum. In one such example, an anti-IgE MAb was developed to treat IgE-mediated allergic disease (Presta et al. 1993, 1994). IgE generated in response to exposure to an allergen can bind to high affinity Fc receptors on the surfaces of mast cells and basophils. Subsequent re-exposure to allergens then results in cross-linking via binding through the IgE Fab regions resulting in release of histamine and leukotrienes, which trigger asthmatic and respiratory symptoms. Since the anti-IgE MAb has two antigen binding sites each of which could combine with one of two sites on the target IgE molecule (located on each Fc heavy chain), the complexes could become very large. SV-AUC and SE-AUC measurements were used to determine weight-average molecular weight and size distribution to clearly show that this did not happen, and that the complexes that formed were of limited size (Liu et al. 1995). The formation of these complexes, which are dependent on the molar ratio of IgE:anti-IgE (Fig. 2a, b) dictates the pharmacokinetics of the drug therapy since IgE has a clearance time of ∼6 h., whereas an IgG1, due to the binding to Fc neonatal receptor (FcRn), has a typical half-life of ∼2 weeks in serum. IgE takes on an extended circulating half-life when it is bound to IgG1 as a complex. Thus, the amount of free IgE circulating in plasma and hence the dose of anti-IgE required to bind to free IgE should be related to the clearance rate of anti-IgE:IgE complexes, free IgE, unbound anti-IgE and the relative binding affinities of high affinity receptor for IgE and that of IgE with anti-IgE.

Fig. 2.

a Schematic diagram of complex formation by IgE and anti-IgE and IgE and soluble high affinity Fc receptor, sFcεRIα (Liu et al. 1995). b Differential sedimentation coefficient distribution of IgE (solid line) and anti-IgE (dotted line) monomers at 0.64 mg/mL (I); IgE and anti-IgE complexes at various molar ratios (II and III) in PBS at 10 °C. The molar ratios of IgE: anti IgE were as follows: (II) 1:1 (solid line), 1:3 (dash-dotted line), 1:6 (dashed line), and 1:10 (dotted line): (III) 1:1 (solid line). 3:l (dash-dotted line), 6:1 (dashed line), and 10:1 (dotted line). The sedimentation coefficients have been corrected to the standard condition of water at 20 C. No faster moving species was observed in early scanning (previously published in Liu et al. 1995)

Competitive binding studies of anti-IgE antibodies to IgE utilizing SV-AUC

Preformed IgE:anti-IgE complexes can be detected using SV-AUC, and can be used to perform competitive binding experiments using analytical ultracentrifugation. A soluble form of the high affinity Fc receptor (sFcεRIα) was added at several molar ratios to preformed anti-IgE:IgE complexes made at a molar ratio of 6:1 where there is an excess of anti-IgE and a predominance of a trimeric species consisting of two anti-IgE molecules bound to one IgE (Fig. 2a, b). The results (Fig. 3a) clearly show that at a molar ratio of 6:1 anti-IgE:IgE all the IgE is incorporated into a trimeric complex at ∼13.3 S and upon addition of soluble receptor to IgE at 0.1:1 (mole:mole) there is a reduction of this 13.3 S peak as well as a slight increase in the baseline between 8 S and 9 S along with an increase of the unbound anti-IgE peak at ∼7 S. As more soluble receptor is added there are additional increases in the anti-IgE peak and the appearance of a peak that is likely the receptor:IgE complex, which was characterized as a dimer (Fig. 2a) in earlier work using sedimentation velocity and equilibrium AUC as well as static light scattering (Liu et al. 1997). These data were generated using the differential sedimentation method of Stafford (1992), which does not take into account diffusion resulting in a broadening of the peak, and is the likely reason that at lower concentrations it is difficult to detect a single peak representative of the receptor:IgE dimer. Another anti-IgE MAb genetically engineered for higher binding affinity to IgE, referred to as anti-IgE2, was also analyzed using the AUC competition binding format. The competition binding analysis shows that anti-IgE2 does indeed have higher affinity since even at a ratio of soluble receptor to IgE at 1:1 there is very little disruption of the complex (Fig. 3b).

Fig. 3.

Differential sedimentation coefficient distribution of anti-IgE, FcεRIα, IgE:anti-IgE, and IgE:FcεRIα complexes (a) and anti-IgE2, FcεRIα, IgE:anti-IgE2, and IgE:FcεRIα complexes (b). Assessment of competition of binding of soluble high affinity receptor, FcεRIα, with either preformed IgE:anti-IgE or IgE:anti-IgE2 complexes using AUC sedimentation velocity

Evaluation of complex formation in vivo

This in vitro example is useful in understanding the size and distribution of large complexes and the impact they have on potential dosing schemes for the MAb therapeutic, but it also would be useful to understand what size distribution and type of complex is formed in vivo. In particular, rather little information on chemical and physical stability is available once the drug is administered to humans, since characterization under physiological conditions requires specialized tools. The recent development and availability of a fluorescence detection system (FDS) for the AUC (MacGregor et al. 2004; Kingsbury and Laue 2011) has enabled studies of complex formation and possible degradation in human serum (Demeule et al. 2009). Such a study was carried out using a fluorescently labeled anti-IgE MAb whereby two main differences were noticed for the anti-IgE binding to IgE in serum versus PBS. The absence of the 21 S peak and the presence of an 8.7 S peak in serum for the anti-IgE complex with IgE, instead of a 7.3 S peak in PBS, were noticeable. The absence of the 21 S peak and the different profile observed in serum compared to PBS underlines the importance to characterize the molecules under physiologically relevant conditions. Additionally, the absence of the 7.3 S peak that is replaced by an 8.7 S peak further confirms the distinct behavior in serum compared to PBS. It is likely that the affinity of an anti-IgE molecule towards IgE was higher in serum compared to that in PBS and that the largest anti-IgE:IgE complex observed in serum was smaller than expected. This higher observed affinity is probably due to the crowding of macromolecular components in serum as discussed by Minton et al. (Minton 2005; Zhou et al. 2008). Overall, AUC equipped with fluorescence optics can be useful to characterize biopharmaceuticals under physiological conditions. Direct characterization in serum may now allow for better drug candidate selection and should be carefully considered during molecular assessment in early research stages.

Analysis of electrostatic interactions and high dose formulations

Viscosity of MAbs and self-association

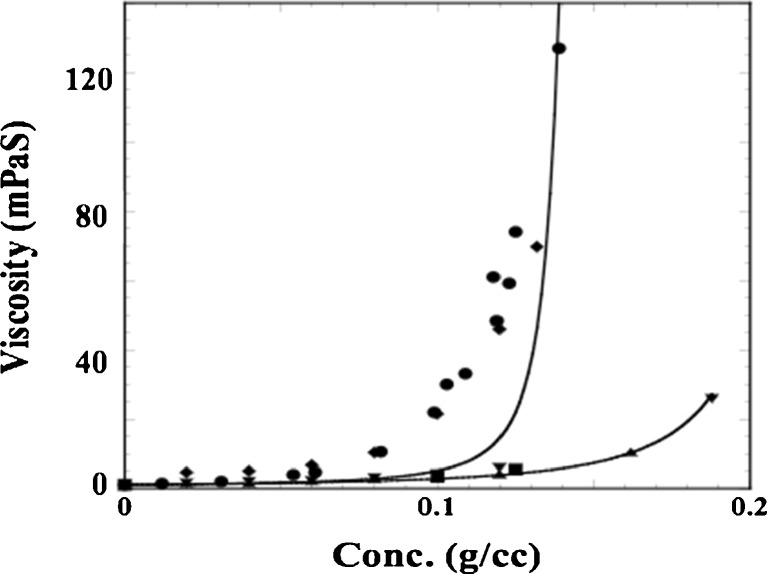
As MAb pharmaceutical development continued to progress, more indications were explored which required dosing in a physician’s office, clinic, or even self-administration by the patient. Many of the MAbs developed to treat cancer were administered by the intravenous route, which would be very inconvenient for out-patient administration. Thus, formulations that could be administered by the subcutaneous (SC) route needed to be developed. Unfortunately, MAbs in general are not given at low doses, typically requiring mg/kg dosing. SC administration is generally restricted to <1.5 mL, necessitating development of MAb formulations at concentrations often exceeding 100 mg/mL. This poses several challenges for manufacturing, stability, and delivery (Shire et al. 2004). In particular, the high viscosities associated with high protein concentrations often limit the concentrations that can be attained by tangential flow filtration (TFF) systems used to concentrate proteins on a large scale as well as the type of autoinjectors commonly used for SC delivery. The limitations of our TFF technology during early development of SC MAb formulations required us to design lyophilization processes whereby, after reconstitution using a smaller volume than the initial load, the high concentration for a SC delivery could be attained. During this development, it was shown that one of the MAbs had a longer reconstitution time than the other two, even though all three were in the same formulation and freeze-dried at the same time, i.e. using the same lyophilization cycle. It was subsequently shown that, under the same formulation conditions, MAb 1 had a substantially greater viscosity than MAbs 2 and 3 (Fig. 4) (Liu et al. 2005). The viscosity of a concentrated protein solution, η as a function of mass concentration, c, can be analyzed by the modified Mooney equation:

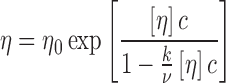1

where η₀ is the solvent viscosity, [η] is the macromolecule intrinsic viscosity, k is a crowding factor, and ν is the Simha parameter related to the ellipsoid of revolution used to model the shape of the protein. Using a typical intrinsic viscosity value for an IgG of 6.3 cm³/g (Hall and Abraham 1984a, b) and a determined solvent viscosity of 1.1 mPas, Eq. 1 can be fitted to the data using k/ν as a single fitting parameter. This equation only takes into account the effect of excluded volume on the viscosity. It is clear that the concentration dependency of the viscosity for MAb 2 and 3 can be accounted for by the hard quasi-spherical model (Fig. 4), which assumes no net attractive protein–protein interactions (PPI) whereas MAb 1 data cannot be fitted with this equation. Analysis of MAbs 1, 2, and 3 by SEC-HPLC showed essentially the same molecular weight of ∼150,000 Da (data not shown). Since the SEC-HPLC experiments are typically run at 0.5–1 mg/mL, the deviations from the Mooney equation suggested that the high viscosity may be due to concentration-dependent reversible self-association. In order to verify this, experiments would have to be done at high concentrations. Such analysis by AUC cannot be done using the light path of commercially available AUC cells because of the high refractive index gradients that result in bending of the exiting light out of the AUC optical path (Gonzalez et al. 2003). Minton has shown that this problem can be circumvented using gasket materials to obtain narrow pathlengths (Minton and Lewis 1981), although this is not easy to do. As an alternative method, it is possible to perform preparative sedimentation equilibrium AUC (SE-AUC) experiments (Minton 1989) where, after attaining equilibrium, the gradient is collected into a plate reader using a commercially available micro-fractionator. The samples are then diluted to obtain absorbances within the dynamic range of the plate reader, and, using a protein absorptivity value, a concentration versus radial displacement plot is obtained (Liu et al. 2005). These data were used to obtain the apparent weight average molecular weight, M_{w, app}, at each radial position with the following equation:

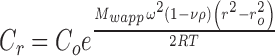2

where C _r is the IgG1 concentration at the radial position r, C _o is the initial loading protein concentration, ν is the partial specific volume, ρ is the buffer density, ω is the angular velocity, r _o is the reference radial position, R is the gas constant, and T is the temperature in ° K. Values of ν for MAb 1 (0.73 mL/g), MAb 2 (0.72 mL/g) and MAb 3 (0.73 mL/g) were calculated from their amino acid and carbohydrate compositions (Durchslag 1986; Perkins 1986). The buffer density, ρ (1.01 g/mL), was determined using a Parr DMA35 digital densitometer (Parr, Austria). Assuming that MAb 2 and 3 exist as monomeric molecules in solution, the non-ideality correction for the charge and excluded volume effects was obtained in the absence of added NaCl for an IgG1 monomer with 150 kDa molecular weight. These corrections were obtained from the relationship (Chatelier and Minton 1987) between apparent molecular weight, M _a at weight/volume concentration c, and actual molecular weight, M:

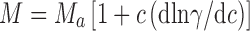3

where γ is the activity coefficient of the monoclonal antibody. Assuming that MAb 2 and 3 are essentially monomeric in solution leads to a multiplicative correction factor as a function of c when M is set equal to 150 kDa. The resulting corrected weight average molecular weights showed that MAb 1 undergoes a reversible self-association, and that addition of NaCl decreases the interactions leading to essentially monomeric MAb (Liu et al. 2005). These results were later corroborated by Scherer et al. using static light scattering (SLS) measurements (Scherer et al. 2010) of MAb 1 and MAb 3 solutions (MAb 3 in Liu et al. 2005 is the same as MAb 2 in Scherer et al. 2010) over protein concentrations from 1 to 275 mg/mL and ionic strengths ranging from 0 to 600 mM. In the work by Scherer et al., the concentration dependence of scattering was analyzed comparatively using three different scattering models, which accounted for intermolecular interactions (in order of increasing model complexity) through steric repulsions alone (simple hard sphere model), steric repulsion with short-ranged attractive interactions (adhesive hard sphere model), and steric and non-steric repulsive interactions as well as interacting (equilibrium self-association) hard sphere species whose relative concentrations may change as a function of total protein concentration. Models of non-interacting and adhesive hard spheres permitted qualitative interpretation of contributions from excluded volume, electrostatic, and van der Waals interactions on net MAb interactions at high concentration as a function of ionic strength. MAb 3 net interactions were found to be generally repulsive and in line with Debye–Hückel theory for charged particles, while MAb 1 interactions were net attractive and longer ranged due to an anisotropic distribution of charge across the molecular surface. More quantitatively, the interacting hard sphere (IHS) mixture models developed by Minton (2007), were able to account for the dependence of scattering for both antibodies over the entire concentration range. At high ionic strength conditions (salt concentrations above 75–100 mM), both mAbs were found to weakly self-associate to form dimer species. IHS models also showed that at low ionic strength mAb 1 self-associated to form oligomers of 4–6 IgG monomers with an affinity that increases substantially with decreasing ionic strength (Scherer et al. 2010). Thus, preparative SE-AUC and SLS yielded the same conclusions that at high concentrations repulsive excluded volume interactions are dominant, and that additional underlying features are salt-dependent to reflect substantial electrostatic contributions to the intermolecular interactions of both mAbs.

Fig. 4.

Viscosity of MAb as a function of protein concentration without any added salt. Non-lyophilized samples prepared by TFF with a composition of 266 mM sucrose and 16 mM histidine at pH 6.0: MAb 1 (♦), MAb 2 () and MAb 3 (). Lyophilized and reconstituted samples: MAb 1 lyophilized and reconstituted (●) and contains 266 mM sucrose, 16 mM histidine, and 0.03 % polysorbate 20 at pH 6; MAb 2 (■) Lyophilized and reconstituted samples are at either 100 mg/mL MAb 2 in 240 mM trehalose, 40 mM histidine, 0.04 % polysorbate 20 or 125 mg/mL in 300 mM trehalose, 50 mM histidine, and 0.05 % polysorbate 20. The solid curves are the result of a non-linear regression of the data to Eq. 1 using a solvent viscosity of 1.1 mPas and intrinsic viscosity of 6.3 cm3/g for an IgG1

These observations suggested that there may be some linkage between reversible protein self-association and the high viscosity observed for MAb 1, and that these interactions appear to be dominated by electrostatic contributions, which could be altered by increasing the ionic strength of the solution. Moreover, these three humanized MAbs were constructed from the same human IgG1 Fc structures, and thus the differences in the CDRs are responsible for the different viscosity behavior dictated by PPI. Details of these PPI and ionic strength dependency were investigated by Kanai et al. (2008). In these studies, the salt dependency of MAb 1 and MAb 3 (referred to as MAb 2 in the paper by Kanai et al.) was determined using either a cationic or anionic series of salts. It was shown that, if the anion was varied using sodium as the common cation, the salt dependency of viscosity for MAb 1 appeared to be related to the Hofmeister series (Hofmeister 1888). In particular, the Hofmeister series for anions tested in this study ranged from kosmotropes to chaotropes where the more chaotropic ions interact preferentially with a protein surface rather than with water (Hribar et al. 2002; Arakawa et al. 2007). This suggested that the chaotropic nature of anions play a major role in altering the attractive PPI for MAb 1, thereby reducing viscosity. Cations, on the other hand, do not affect the viscosity of MAb 1 in a Hofmeister-dependent manner so that the solution viscosity of MAb 1 is reduced upon increasing ionic strength, i.e. a correlation between chaotropic cations and reduction of viscosity was not observed. These results are consistent with the reports that cations have less impact on proteins than anions (Kunz et al. 2004; Arakawa et al. 2007). MAb 2, on the other hand, showed little dependency of viscosity on ionic strength suggesting that electrostatic attractive interactions do not impact the rheology as they do for MAb 1.

The nature of the interactions in MAb 1 and MAb 2 solutions was further explored by generating F (ab)’₂ fragments of each MAb and measuring viscosity of the fragments with and without addition of NaSCN, which was found to be effective in reducing viscosity of full length MAb 1 solutions. It was hypothesized that the high viscosity nature of MAb 1 is due to concentration-dependent reversible self-association that forms an organized network structure. The existence of such network formation has been postulated previously and remains a controversial subject (Stradner et al. 2004; Shukla et al. 2008a, b; Porcar et al. 2010; Stadler et al. 2010). The interactions of MAb 1 that may contribute to network formation may occur either via Fab–Fab interactions, Fab–Fc interactions, or both. MAb 1 and MAb 2 have the same Fc amino acid sequence, thus Fc–Fc interactions cannot explain why only MAb 1 undergoes such reversible self-association. In order to assess the contributions of the interactions of the Fab and Fc regions to the viscosity properties of MAb 1 and MAb 2, the viscosity-concentration profiles of MAb 1 and MAb 2 F(ab’)₂ fragments were determined. If the origin of the high viscosity of MAb 1 is mainly due to the Fab–Fc interaction, then removal of the Fc region should prevent network formation, resulting in reduction of solution viscosity to a similar value as MAb 2 F(ab’)₂. Comparison of the concentration-viscosity profile in the same buffer condition without added salt for F(ab’)₂ fragments of MAb 1 and MAb 2 showed that F(ab’)₂ MAb 1 is more viscous than F(ab’)₂ MAb 2 at high concentrations. This indicates that a significant part of the network interaction remains intact even without the Fc. Moreover, not only does addition of NaSCN reduce the viscosity of full-length MAb 1 to levels of MAb 2 but it also reduces the viscosity of F(ab’)₂ MAb 1 to that of F(ab’)₂ MAb 2, suggesting that this salt is effectively decreasing Fab–Fab interactions responsible for the observed high viscosities of the intact MAb 1.

The details of these interactions were further explored by comparing the viscosity of MAb 1 alone with that of a mixture of MAb 1 and Fab from MAb 2. The addition of MAb 2 Fab did not significantly increase the solution viscosity, and thus it was concluded that MAb 2 Fab fragments do not interact with the network of full-length MAb 1. On the other hand, when Fab from MAb 1 was mixed with the full-length MAb 1, solution viscosity of the mixture increased drastically (Kanai et al. 2008). These data suggested that there are multiple binding sites in the Fab region of MAb 1. In order to ascertain whether Fab–Fc interactions can impact viscosity, the full-length MAb 2 (100 mg/mL) was mixed with either MAb 1 Fab or MAb 2 Fab (100 mg/mL). Since both MAb 1 and MAb 2 were constructed with the same human IgG1 Fc, it was anticipated that the viscosity of MAb 2 solution would increase substantially after adding the MAb 1 Fab if there are significant network interactions between MAb 1 Fab with the Fc. The resulting slight increase in viscosity suggested that MAb 1 Fab alone does not form a significant network interaction with the Fc. If there is any interaction present between the Fab and Fc regions, it is likely to be weak, resulting in limited size for the network. Although these weak interactions do not significantly increase the viscosity of Fab and MAb 2 solutions, it is possible that these interactions may be enhanced by the presence of Fab–Fab interaction for the full-length MAb 1, and therefore partly contribute to the increase of viscosity of full-length antibody. Overall, it was concluded from these studies that Fab–Fab interactions are mainly responsible for the multivalent network interaction of MAb 1.

Investigations into the nature of PPI involved in MAb network formation and relation to viscosity properties

At high solute concentrations, the higher order terms (i.e. virial coefficients that describe multi-body interactions) related to PPI contribute to the solution non-ideality. One of the main contributors to solution non-ideality is the increase in solute volume fractions from 0.2 to 0.3, which increases the activity of the solute from ∼10- to ∼100-fold due to the contribution from the excluded volume effect (Minton 2001), thereby resulting in a dramatic difference in dilute and high concentration solution behavior. For instance, the osmotic pressure of hemoglobin (Hb) solutions with increasing concentration (C _Hb) could be approximated by including contribution from the following virial coefficients; 2nd order at C _Hb < 50 mg/ml, 3rd at C _Hb < 120 mg/ml, 4th at C _Hb < 200 mg/ml, 5th at C _Hb < 280 mg/ml, and 6th at C _Hb < 350 mg/ml (Ross and Minton 1977a, b). In addition to the excluded volume effect, other forces such as electrostatic, hydrophobic, solvation, hydrogen bonding and charge fluctuation also may contribute to the solution viscosity. A better understanding of these interactions is of interest, not only to manage solution viscosity but also towards dealing with issues such as protein solubility (Valente et al. 2005), self-association (Liu et al. 2005; Minton 2005), and aggregation (Saluja et al. 2007). Non-ideality parameters such as the second virial coefficient (B ₂₂) (George et al. 1997a, b) and the interaction parameter (k _D) (Li et al. 2004), measured using conventional techniques such as AUC, SLS and dynamic light scattering (DLS), have been used as a reliable measure of intermolecular interactions in dilute solution conditions as it pertains to relating intermolecular interactions to protein precipitation (Curtis et al. 1998) solubility (Demoruelle et al. 2002; Valente et al. 2005), and crystallization (George et al. 1997a, b).

Second virial coefficient (B₂₂): static light scattering (SLS)

Of all the analytical techniques used to obtain values for B ₂₂, such as SLS (George and Wilson 1994), membrane osmometry (Bonnete et al. 1999), SE-AUC (Behlke and Ristau 1999), self-interaction chromatography (SIC) (Tessier et al. 2002), and SEC-based methods (Bloustine et al. 2003), SLS has been the most widely used technique. SLS measures the time-averaged scattering intensity where the excess Rayleigh ratio, R _θ, i.e. the ratio of the light scattering intensity of a solution in excess of the solvent to the intensity of incident light per unit volume and solid angle, normalized with respect to intensity of incident light, can be related to the weight-average molecular weight, M _w, at low concentration and low observation angle θ by (Magid 1993; Muschol and Rosenberger 1995):

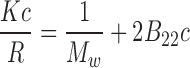4

A positive B ₂₂ value indicates repulsion between molecules such that the protein–solvent interactions are favored over protein–protein interactions and the solvent is generally referred to as a ‘good solvent’. A negative B ₂₂ indicates the presence of intermolecular attraction between molecules and the solvent is termed as a ‘poor solvent’. When the intermolecular attractions balances the repulsive forces, the value of B ₂₂ is zero, and the solvent is referred to as a theta solvent (George and Wilson 1994).

Interaction parameter (k_D): dynamic light scattering (DLS)

The interaction parameter, k _D, can be obtained from DLS experiments. DLS correlates the time-dependent fluctuations in intensity of scattered light to the mutual diffusion of the particles. The interaction parameter, k _D, can be obtained from the mutual diffusion coefficient (D _m) of the particles using the following equation (Brown and Nicolai 1993; Teraoka 2002):

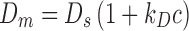5

where D _s, is the self-diffusion coefficient (the value of D _m at c ∼ 0), k _D is the interaction parameter, and c is the concentration of the protein (g/ml). The interaction parameter k _D from Eq. (5) describes interparticle interactions and can be represented as (Liu and Chu 2002; Teraoka 2002):

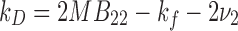6

where M is the molecular weight, ν₂ is the protein partial specific volume, and k _f is the first-order concentration coefficient (ζ ₀ ζ ₁ > 0) in the virial expansion of the frictional coefficient (ζ = ζ ₀ (1 + ζ ₁ c + …)) (Teraoka 2002). Under conditions where measurement times for DLS determinations are long compared to the average molecular collision time, k _D can be expressed in terms of a hydrodynamic [k _H represented by (k _f + 2ν ₂)] and thermodynamic contribution (k _T = 2MB ₂₂) (Bruce 1976; Placidi and Cannistraro 1998):

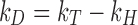7

In the case of a theta solvent (B ₂₂ = 0), the thermodynamic contribution (k _T) → 0 resulting in a negative k _D solely due to hydrodynamic drag (-k _H) and does not represent direct attractive interactions. The contribution of the hydrodynamic interaction under conditions where k _T is zero was shown by Yadav et al. (2012b) to be approximately equal to −5.34 mL/g for MAbs. Thus, in the hydrodynamic regime, only a k _D value of magnitude more negative than ∼−5.34 ml/g depicts attractive interactions, whereas a k _D of less negative magnitude than the theoretically possible value (−5.34 ml/g) suggests contributions from long-range repulsive thermodynamic contributions.

Dilute solution static and dynamic light scattering measurements

Recently, both B ₂₂ and k _D obtained from SLS and DLS have been used extensively to study intermolecular interactions and their subsequent correlation with high concentration viscosity and self-association issues associated with mAb therapeutics ((Yadav et al. 2010a, b, 2011a, b, c, 2012b)). A comparison of high concentration viscosity behavior of four IgG1 MAbs at solution pH 6.0 indicated that, amongst the fundamental molecular aspects such as size and shape, net charge, effective molecular volume, and physical intermolecular interactions, it is the nature and magnitude of the intermolecular interactions that are most critical in regulating the high concentration solution behavior (Yadav et al. 2010b). In particular, the high concentration viscosity profile for different MAbs could not be reasonably justified based on the effective molecular size and excluded volume effects. On the other hand, the interaction parameter (k _D) obtained from DLS measurements indicated that intermolecular interactions, in particular short-range attractive potentials, dictated the high concentration solution behavior (Yadav et al. 2010b). The presence of stronger attractive interactions usually leads to higher solution viscosity as shown in Fig. 5a, b. MAbs A and H with attractive interactions (negative k _D) showed higher viscosity compared to MAb G and E which showed intermolecular repulsions (positive k _D) at pH 6.0 (MAb A and MAb E are MAb 1 and MAb 3, respectively in Liu et al. 2005). Overall, this correlation only holds qualitatively, and quantitative agreements are yet to be established. For instance, MAb A with a higher negative k _D than MAb H in dilute solutions shows a lower viscosity in comparison to MAb H at high concentrations.

Fig. 5.

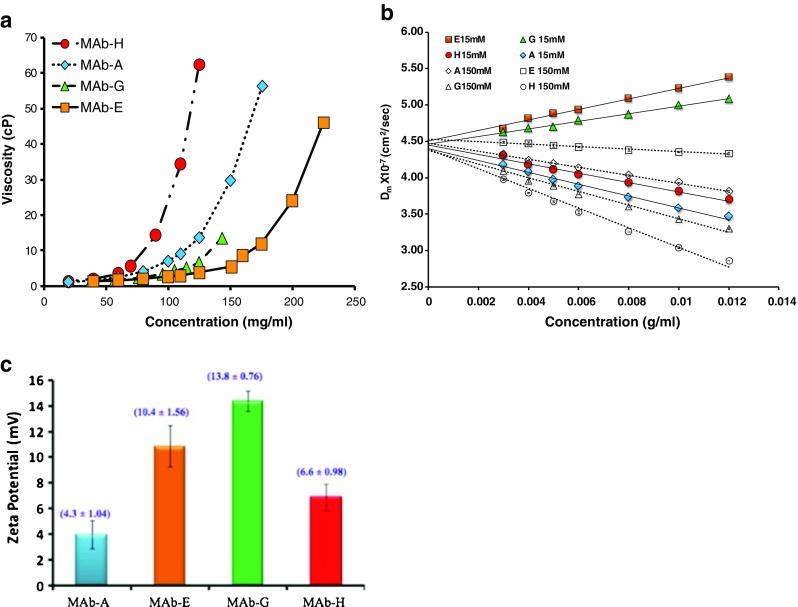
a Viscosity of IgG1 MAbs in pH 6.0, 15 mM ionic strength as a function of concentration. The lines connect the data points to guide the eye and are not the result of model fitting. b Mutual diffusion coefficient (D_m) for four IgG1 MAbs at pH 6.0 at 15 mM ionic strength (solid symbols) and 150 mM ionic strength (open symbols). Ionic strength was adjusted with addition of NaCl. The lines are linear best fits to Eq. (5) with slope and intercept representing D_sk_D and D_s (self-diffusion coefficient), respectively. c Zeta potential of IgG1 MAbs at solution pH 6.0, 15 mM ionic strength. The measurements are performed at a concentration of 5 mg/mL at 25 ± 0.1 °C. The number in parentheses represents the effective charge calculated from Eq. 4 in Yadav et al. (2010b). The result is an average of five measurements. Previously published in Yadav et al. (2010b)

The viscosity dependence on salt for MAb 1 (MAbA) versus MAb 2 suggested that the main attractive interactions were electrostatic. However, the rank order of the viscosity of four IgG₁ molecules at high concentration was not consistent with the rank order of net charge on the molecules (Fig. 5a, c). Investigations into the impact of pH and hence charge on viscosity were extended to a globular protein, Bovine Serum Albumin (BSA) as well as to other mAbs as a function of solution pH (Yadav et al. 2011b, 2012b). The highest solution viscosity at high concentrations was observed closer to the molecular pI. This is contrary to what is typically observed for proteins at lower concentration. In fact, BSA viscosity as a function of pH shows a minimum at the pI when measured ≤40 mg/mL, which is consistent with the electro-viscous effect since the primary and secondary electroviscous effects due to the presence of the double layer around a charged protein are minimized at the pH where the net charge on the protein is zero, i.e. the isoelectric point, pI. However, at the pI, especially when in the range of 5–7, the charge distribution becomes most conspicuous, since Arg, and Lys are generally protonated and most acidic side chains are ionized. This results in a surface distribution of charges which can be sensed as the protein molecules approach closely to each other at high concentration. Thus, at the pI, at high concentration, the protein molecules may align to increase attractive electrostatic interactions resulting in an organized network or clustering of molecules, which can result in a higher viscosity at the pI, as observed for BSA at 200 mg/mL and MAbs at >100 mg/mL. Again, a comparison of the interaction parameters (B ₂₂ or k _D) and solution viscosity indicated that, in many cases, k _D could be used as a qualitative screening tool for predicting high concentration viscosity behavior (Yadav et al. 2011b, 2012b). A higher negative B ₂₂ or k _D generally resulted in a more viscous solution at high concentrations; however, direct quantitative assessment was not possible. This was further corroborated in the recent work correlating the interaction parameter, k _D,, with the high concentration viscosity behavior of ∼16 MAbs (Connolly et al. 2012).

Investigation of electrostatics using charge-swap mutants

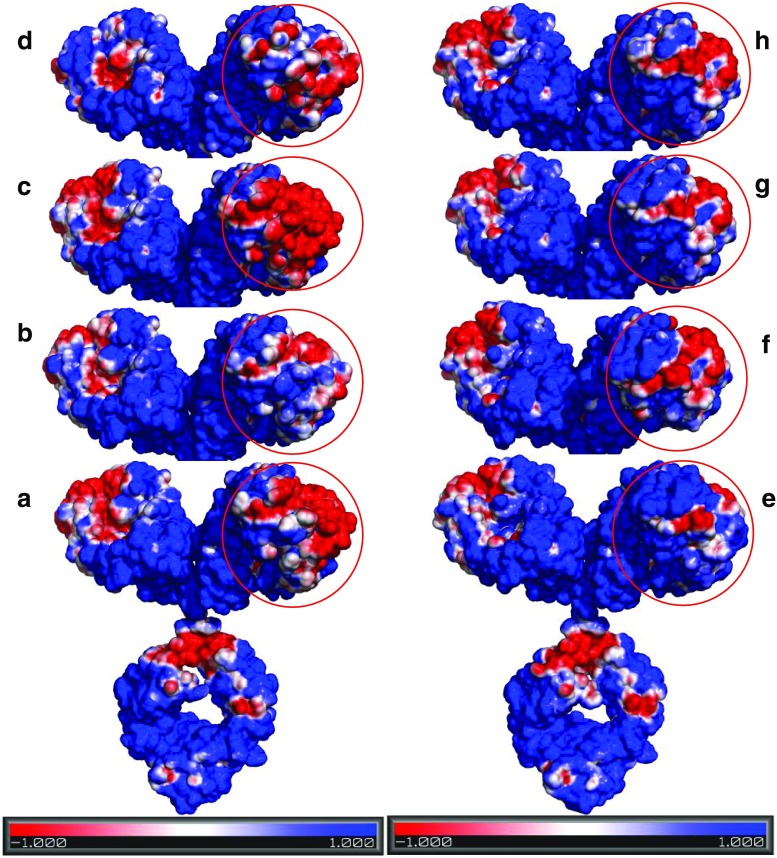
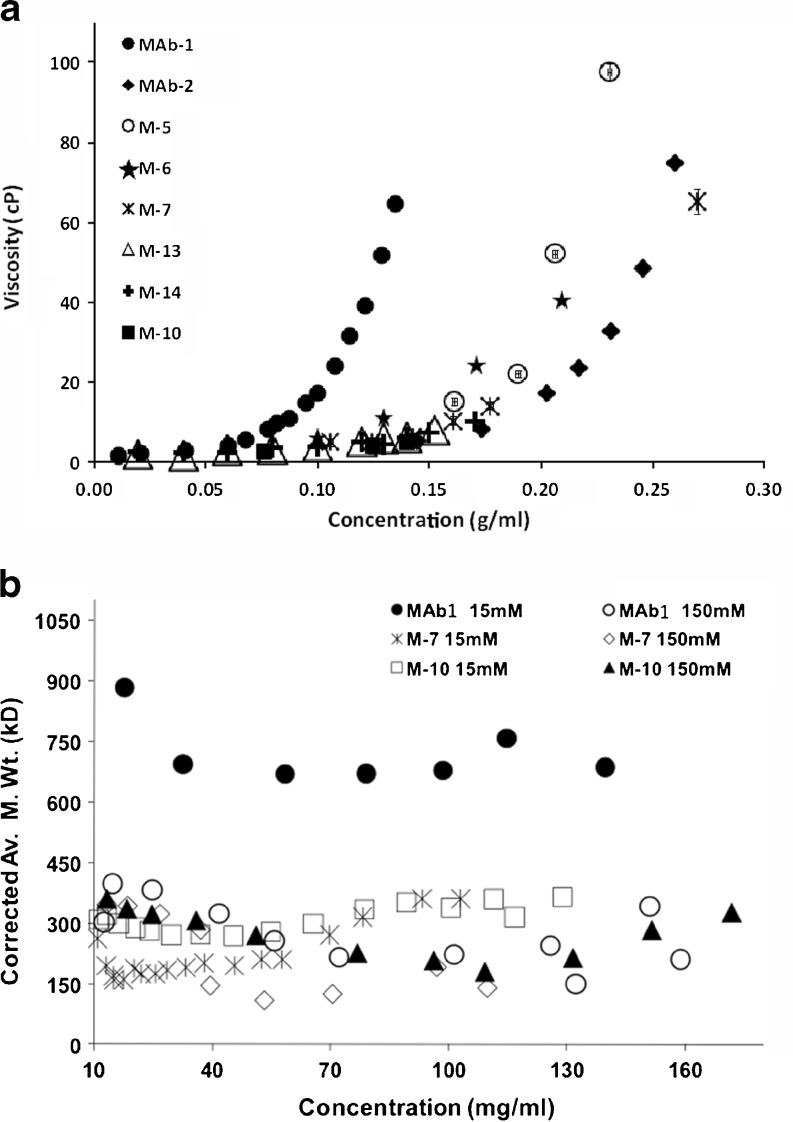
The influence of surface charge distribution in governing the different high concentration solution behavior of MAbs 1 and 2 was assessed in recent work by studying the charge-swap mutants of MAb 1 and MAb 2 (Yadav et al. 2011c, 2012a). The details of these charge-swap mutants, including specific amino acid changes, are discussed in Yadav et al. (2011c). In these studies, MAb 1 showed a relatively more heterogeneous charge surface than for MAb 2 wherein the negative surface on the CDR can interact to attract the positively charged regions (Fig. 6a, e). This is reflected in a negative B ₂₂ for MAb 1 (Fig. 7a) whereby the presence of attractive interactions favors self-association, resulting in higher viscosity for MAb 1 at high concentrations (Fig. 8a). Conversely, the MAb 2 surface exhibits less charge asymmetry (Fig. 6e vs. a) favoring intermolecular repulsions (positive B ₂₂; Fig. 7d), which disfavors self-association and consequently a lower viscosity for MAb 2 (Fig. 8a). When the charge residues in either the variable light (VL) chains, or variable heavy (VH) chains of the MAb 1 CDR were replaced with the corresponding MAb 2 residues, resulting in the charge-swap mutants M-5, and M-6, respectively, there was a decrease in viscosity, but not to the level of MAb 2 (Fig. 8a). However, replacement of the CDR charged residues for both the VL and VH chains resulted in mutant M-7 with similar viscosity concentration profile exhibited by MAb 2 (Fig. 8a). This decrease in viscosity is consistent with the loss of a negative potential surface relative to MAb 1 in the CDR for M-5 and M-7 (Fig. 6a, b, d), and hence the loss of intermolecular attractions resulting in net repulsive interactions for M-5 and M-7 (+ve B ₂₂, Fig. 7a, b) that translate to a loss of long-range order and molecular clustering at high concentration yielding a lower viscosity for M-5 and M-7 (Fig. 8a). The replacement of residues in the sequence of MAb 2 with the corresponding charged residues in the VL and VH chains of MAb 1 CDR (M-10) did result in some additive negative potential in the CDR region; however, not to the same extent as in MAb 1 (Fig. 6a, f). This increased negative potential in the M-10 CDR is reflected as a small decrease in the net repulsive interaction for M-10 (less +ve B ₂₂ of M-10 than MAb-2; Fig. 7d), but still exhibits a similar viscosity as MAb 2 (Fig. 8a). Similarly, M-13 and M-14 showed similar electrostatic potential surface as M-10 (Fig. 6g, h, f) despite replacing the charge residues outside the CDR, thereby still exhibiting a lower viscosity. The apparent linkage of viscosity with self-association is still apparent since M-7 and M-10 have lower degree of self-association compared to MAb 1, as shown by the corrected weight average molecular weight observed from preparative SE-AUC (Yadav et al. 2011c) (Fig. 8b). In addition, the determined k_D (data not shown) and B ₂₂ values at low concentration also show that the M-7 and M-10 mutant net interactions did not become more attractive as the result of the charge changes, again demonstrating the utility of evaluating PPI at low concentrations to predict high concentration behavior (Fig. 7b and d). However, a clear exception to this was the result for M-6 where only the charged residues of the VH of MAb 1 were swapped for the corresponding residues in MAb 2. In that case both k _D (data not shown)and B ₂₂ (Fig. 7c) remained unchanged compared to MAb 1 and the surface charge heterogeneity for M-6 was comparable to MAb 1 (Fig. 6a, c). These observations suggest that the viscosity of M-6 should be similar to MAb 1, whereas the viscosity was decreased and was comparable to the VL chain charge-swap mutant M-5 (Fig. 8a). This behavior of M-6 suggests, in addition to surface charge asymmetry, the proper conformational placement of charge residues may also be important. Additionally, these results illustrate the limitation of dilute solution techniques in quantitatively predicting the high concentration behavior. Despite the inconsistencies in these data, these parameters do have merit, especially because of the number of widely accepted techniques available for dilute solution analysis as well as the requirement for smaller amounts of protein.

Fig. 6.

The electrostatic potential surface for a MAb 1, b M-5, c M-6, d M-7, e MAb 2, f M-10, g M-13, and h M-14 at pH 6.0, 15 mM solution ionic strength generated using APBS plugin in Pymol. The red and blue contours indicate −1 and +1 KT/e isosurface potential. Reproduced from Yadav et al. (2012a)

Fig. 7.

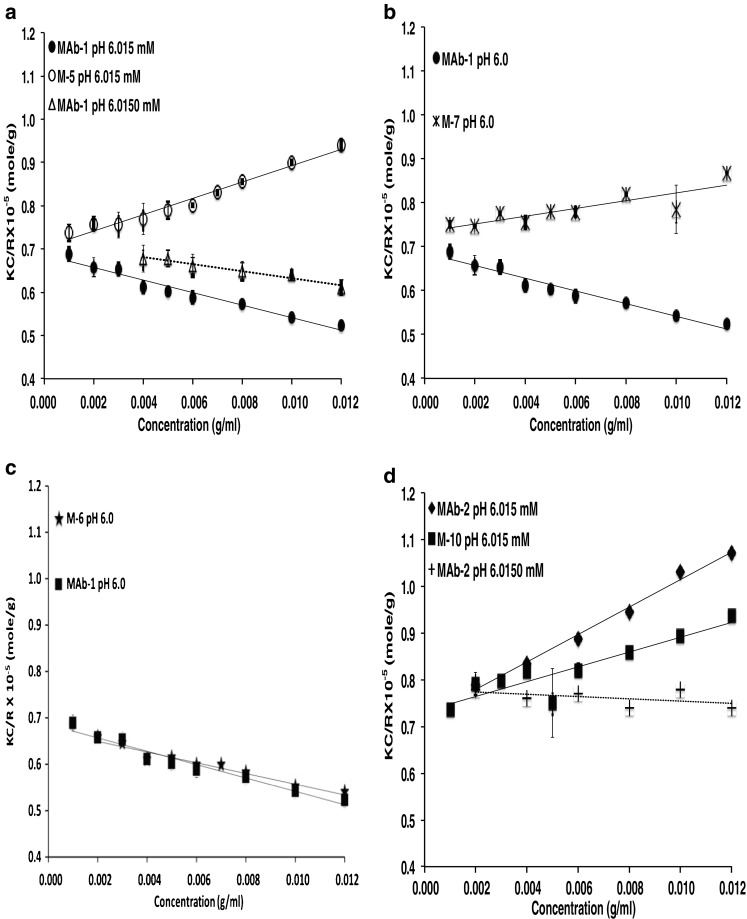
Debye plots for a MAb-1 and M-5, b MAb-1 and M-6, c MAb-1 and M-7, d MAb-2 and M-10. The lines are linear best fits with slope and intercept representing (2B ₂₂) and (1/M _w) respectively. Reproduced from Yadav et al. (2012a)

Fig. 8.

a Viscosity profile of MAb 1, MAb 2 and the designed mutants as a function of IgG concentration at solution pH 6.0, 15 mM ionic strength. The viscosity was measured using a cone/plate measuring system at a shear rate of 1,000/s. Reproduced from Yadav et al. (2012a). b The corrected weight average molecular weights (M _wc) for MAb 1 and Mutants, using the non-ideality corrections for MAb 2 (Eq. 3) from sedimentation equilibrium data. The measurement was conducted at pH 6.0, histidine hydrochloride buffer in 15 and 150 mM ionic strength at 12,000 rpm. Reproduced from Yadav et al. (2011c)

Coarse-grained modeling of the self-association of monoclonal antibodies

The work by Kanai et al. (2008) showed that Fab–Fab interactions played a key role in the transient formation of a self-association network at high MAb concentrations, which are linked to viscosities that are greater than those predicted based solely on excluded volume principles. This network is hypothesized to consist of a transient formation of protein clusters whereby the interactions result in short lifetimes for rearrangement. In the case of MAb 1 and MAb 2, these interactions appeared to be dominated by electrostatics as suggested by the studies by Yadav et al. (2012a). Molecular dynamics simulations can be useful in gaining additional insights into which specific regions of the MAbs are involved in network formation. Although such simulations have come a long way whereby simulation of large molecule such as MAbs is now possible, these computations are limited to short time trajectories and to motions within an isolated molecule in solvent (Brandt et al. 2010). In order to investigate the role of electrostatic interactions in MAb self-association at high concentration, coarse-grained computational models of MAb 1 and MAb 2 were constructed. Two reduced coarse-grained (12- and 26-site) models were constructed for each antibody using either a compact Y-shaped or an extended Y-shaped configuration, and coarse-grained molecular dynamics simulations as described by Chaudhri et al. (2012) were carried out. Overall, the 12- and 26-site models compared very well with each other, and the choice of a compact versus extended structure did not alter the results or conclusions. The resulting simulations of these coarse-grained antibodies that interact through screened electrostatics were done at six different concentrations. It was shown that MAb 1 forms three-dimensional heterogeneous structures with dense regions or clusters whereas MAb 2 does not appear to form such clusters. The formation of such clusters for MAb 1, together with the potential mean force (PMF) and radial distribution functions (RDF) between pairs of coarse-grained regions on MAb 1 and MAb 2, are qualitatively consistent with the significantly higher viscosity for MAb 1 compared to MAb 2, especially at concentrations >50 mg/mL. These simulations also confirmed that the clusters of MAb 1 at high concentrations are formed due to stronger Fab–Fab interactions than in MAb 2. It was also shown that Fab–Fc interactions could be equally important in addition to Fab–Fab interactions. Most importantly, the coarse-grained representations were able to pick up differences based on local charge distributions of domains and make predictions on the self-association characteristics of these protein solutions. Such simulations may be useful in designing MAbs with improved solution behavior at high concentrations since specific regions of interactions can be identified (see figs. 7 and 8 in Chaudhri et al. 2012)

Summary and conclusions

This review covers many different evaluations of PPI for recombinant DNA-derived proteins at Genentech, ranging from determination of solution molecular weight for small proteins and glycosylated proteins to formation of large complexes, and recently to investigation of rheological properties at high protein concentrations. Many of these studies have enabled us to have a better understanding of the solution properties of our therapeutic drugs as well in some cases a clearer understanding of the dosing requirements. Our recent work on linking self-association network formation at high concentration coupled with coarse-grained modeling techniques will be useful in designing MAbs that are not just optimized for potency but also for physical properties such as viscosity that enable easier administration as well as manufacturing at large scale.