Skip to main content
PMC home page
Chemical Science logoLink to Chemical Science
. 2017 Feb 21;8(5):3500–3511. doi: 10.1039/c6sc03738k

Deep learning and 3D-DESI imaging reveal the hidden metabolic heterogeneity of cancer†

Paolo Inglese a, James S McKenzie a, Anna Mroz a, James Kinross a, Kirill Veselkov a, Elaine Holmes a, Zoltan Takats a,✉, Jeremy K Nicholson a,✉, Robert C Glen a,b,✉
PMCID: PMC5418631  PMID: 28507724

graphic file with name c6sc03738k-ga.jpgImaging using 3-D DESI mass spectral data combined with deep learning reveals the topology and heterogeneity of colorectal cancer.

Abstract

Visual inspection of tumour tissues does not reveal the complex metabolic changes that differentiate cancer and its sub-types from healthy tissues. Mass spectrometry imaging, which quantifies the underlying chemistry, represents a powerful tool for the molecular exploration of tumour tissues. A 3-dimensional topological description of the chemical properties of the tumour permits the formulation of hypotheses about the biological composition and interactions and the possible causes of its heterogeneous structure. The large amount of information contained in such datasets requires powerful tools for its analysis, visualisation and interpretation. Linear methods for unsupervised dimensionality reduction, such as PCA, are inadequate to capture the complex non-linear relationships present in these data. For this reason, a deep unsupervised neural network based technique, parametric t-SNE, is adopted to map a 3D-DESI-MS dataset from a human colorectal adenocarcinoma biopsy onto a 2-dimensional manifold. This technique allows the identification of clusters not visible with linear methods. The unsupervised clustering of the tumour tissue results in the identification of sub-regions characterised by the abundance of identified metabolites, making possible the formulation of hypotheses to account for their significance and the underlying biological heterogeneity in the tumour.

Introduction

Intra-tumour phenotypic heterogeneity in human cancer has been associated with tumour progression, treatment resistance and metastasis development.1 3D Mass Spectrometry Imaging (MSI), being able to capture the different molecular patterns present in sub-regions of the tumour tissue, represents a highly promising approach for probing tumour and tumour-microenvironment heterogeneity.2–5 Determining the regions of tumour similarity and heterogeneity is not only crucial to investigate the nature of the diversity of tumours and to classify those into sub-groups, but can provide, through a topological mapping of the heterogeneity, an invaluable tool to understand the possible interactions between those different cell clusters.6 The study of biological interactions in three dimensions is essential,7–9 since biochemical mechanisms occur in a 3-dimensional environment whose complexity and richness may not be captured by the analysis of only a 2-dimensional sample of the tissue. From the point of view of statistical modelling, the lack of the standard state (the ‘normal’ cell type for this tissue) and a comprehensive compendium of the possible tumour cell types represents the biggest obstacle in the identification of tumour sub-types, requiring the employment of unsupervised learning techniques.

Supervised classification of DESI imaging data from brain tumours was used by Eberlin et al. 10 for the identification of molecular patterns related to different types of tumours, but the main limitation of this approach is represented by the impossibility of identification of new tumour sub-types. In a similar vein, previous work has applied unsupervised analysis to MSI datasets to study intra-tumour heterogeneity. In Balluff et al.,11 a set of clustering algorithms were applied to matrix-assisted laser desorption ionization (MALDI) imaging data from gastric and breast carcinoma patients. An agreement-based procedure12 was employed to extract the final segmentation of the images, exploiting the assumption that different algorithms should retrieve real clusters consistently. The main difficulty of this procedure is represented by the selection of the clustering algorithms that should be compared, since some of those could provide similar results as they are founded on a similar concept of a cluster. An example is represented by PCA and k-means, which tend to capture the same kind of structures.13 This would result in an over-optimistic evaluation of the robustness of clusters. A similar difficulty is shown in Lou et al.,14 where similarly, the clusters are defined on the basis of consistency across a set of different algorithms. A further challenge is represented by the selection of the optimal number of clusters.

For this reason, the challenges typical of unsupervised analysis, such as determining the correct number of clusters and the assessment of their validity15,16 can be reduced through inspection of the data structure.17 In order to make the visualisation of high-dimensional data (such as MSI) more straightforward, dimensionality reduction techniques are required.

Several methods are currently available for unsupervised dimensionality reduction.18 Among these, linear techniques, such as Principal Component Analysis (PCA), are widely used to explore the internal relationships of mass spectrometry data.3,19 Unfortunately, these techniques can be inadequate to detect complex relationships between data, suggesting the application of non-linear methods.20,21 Such techniques, however, often make it difficult to extend the non-linear models to unseen data without introducing some degree of approximation.22 This aspect is critical in the case of 3D MSI data, where the datasets can consist of hundreds of thousands of spectra. For example, multi-dimensional scaling (MDS), implemented in Cornett et al. 23 or hierarchical clustering, would hardly be feasible because of the necessity of a complete pairwise distance matrix. Self-organizing maps (SOM), and in particular the extension, generalized self-organizing maps (GSOM), were used in Wijetunge et al. 20 to extract similar ion images from MALDI data. However, a limitation of SOM-based techniques for data dimensionality reduction is exemplified by the fact that high dimensional data are projected on a fixed grid, hence losing the possibility to project and separate ambiguous objects in different regions of the low-dimensional space. This limitation is overcome by Stochastic Neighbour Embedding (SNE) that makes the high dimensional data fixed and determines a continuous mapping for the low-dimensional embedding.24 Application of t-SNE to mass spectrometry imaging data can be found in Fonville et al. 25 and Abdelmoula et al. 26 However, it should be stressed that in those two works, a non-parametric t-SNE was employed. This has two important consequences: (1) the difficulty of projecting unseen data in the low-dimensional space without any approximation or ad hoc assumption, (2) the possibility of obtaining different results as the t-SNE cost function is not convex. The challenges described above can be addressed simultaneously through the application of deep learning based techniques. Firstly, a parametric model can naturally project the unseen high-dimensional data to the low-dimensional space and, secondly, the use of autoencoders trained to reconstruct the original data makes the initial parameters (weights and biases) used during the fine-tuning more stable across different runs. This, in the case of t-SNE, is equivalent to having more stable low-dimensional representations of the high dimensional data.27

We propose a high-throughput computational workflow for large MSI data exploration (consisting of tens of thousands of spectra) to identify possible clusters in the tumour tissue. The proposed workflow is based on the 2-dimensional projection of data using a non-linear technique, parametric t-SNE,28 that combines in one model the flexibility of deep neural networks and the capability of parametric t-SNE to retrieve the local structure of high dimensional data for visualization. The mapped low-dimensional tumour mass spectrometry data are subsequently analysed through both visual inspection and automated clustering techniques. In the work presented here, the low dimensional data points of tumour mass spectrometry data are automatically partitioned by the OPTICS29 algorithm which allows the identification of data structures and the identification of the optimal number of clusters. A similar procedure is found in ACCENSE,30 with the difference that this approach is based on a non-parametric t-SNE model and identifies the density-based clusters using a kernel estimation. This results in a ‘flat’ description of the density properties of the data; in contrast, OPTICS can provide a hierarchical and easily interpretable description of the data structure through the reachability plot.

An evaluation of the performance of the proposed workflow utilises a 3D desorption electrospray ionisation mass spectrometry (DESI-MS) dataset from a human colorectal adenocarcinoma biopsy,31 demonstrating that the reduction of the dimensions of the data using parametric t-SNE is crucial for the identification of tumour sub-types, outperforming the representation of the first two principal components scores. A comparison with a co-expression network analysis of the ion features confirms the presence of the clusters, making it possible to also associate increased weighting of specific ions within the clusters. This has allowed the investigation of the biological significance and interpretation of those sub-regions giving a deeper insight into the nature of tumour heterogeneity. We show that the third dimension can add significant value to the analysis of complex biological systems such as tumour tissues. The third dimension introduces topological constraints that can filter out unrealistic tissue segmentations thereby increasing the robustness of the analysis and additionally we show that 2-dimensional tissue slices, which represent a small portion of the entire tissue, are not able to capture the richness of the biochemical interactions occurring in tumours.

Materials

Human tissue samples were obtained with informed consent under local ethical approval (14/EE/0024). A human colorectal adenocarcinoma biopsy was used to evaluate the performance of the proposed workflow. The tissue specimen was snap-frozen in liquid nitrogen and stored in a freezer at –80 °C. Subsequently the tissue was cryosectioned to 10 μm thick parallel sections, and every tenth section was analysed. The final number of sections was equal to 52. Mass spectrometry data were acquired using a Thermo Fisher Exactive mass spectrometer, in the negative ion mode, in the m/z range of 200–1050. A custom built automated DESI-imaging ion source was employed to acquire the final spectra. Each acquisition consisted of a layer containing 4 tissue sections, resulting in a total number of 13 layers. A more detailed description of the acquisition parameters is available in Oetjen et al. 32 The tissue sections were subsequently contrast enhanced by haematoxylin and eosin (H&E) stains, and optical images were recorded (ESI Fig. 1†). The raw MS (imzML format33) data and the H&E optical images can be freely downloaded from MetaboLights at: ; http://www.ebi.ac.uk/metabolights/MTBLS415.

3D DESI-MS pre-processing

The pre-processing pipeline is aimed at cleaning the data: from the presence of noisy peaks, to reduce the internal variability due to random factors occurring during the acquisition process and to make all the spectra compatible for the application of pattern recognition methodologies. Furthermore, all the sections were co-registered to reproduce the 3-dimensional topology of the tissue.

The 13 slides containing MS data from 4 tissue sections were first pre-processed independently to reduce the internal variability and, following that, all the spectra were pre-processed together. A first smoothing of the spectral profiles was obtained with a 7-point (equivalent to a median of 0.0309 m/z) Savitzky–Golay filter of degree 3. The peak identification algorithm was based on the detection of sign changes of the first derivatives of the spectral profiles.34 Noise peaks were identified through MAD estimation35 and removed. Only the peaks present in more than 0.5% of the entire dataset were retained.

The peak matching, performed using the ‘mspalign’ command from the MATLAB R2016a Bioinformatics Toolbox, was applied independently to the spectra obtained from each slide. The 13 spectra representative of each slide (in which the m/z vectors were the result of peak matching on the individual slide and the intensity of the peaks was defined as the average intensity across the entire slide) were subsequently matched using the same command. In this way, the process could be parallelised with a significant improvement in terms of processing time.

Normalisation of peaks was performed through median fold change scaling,36 with the objective of preserving only the differences due to biological variability.

In order to identify and split the four tissue objects from each slide, the H&E images were aligned with the total-ion-count (TIC) images from the same sections. All the alignments were performed by affine transformations (rotation, translation, shearing) identified through gradient descent. Thereafter, the binary version of the H&E images, obtained through Otsu thresholding,37 were split in rectangular bounding boxes containing the 4 largest non-empty regions. The coordinates of the bounding boxes were projected onto the respective TIC images to identify and split the MS data into the corresponding regions containing the tissue slices.

Afterwards, the H&E images from each slice were sequentially co-registered through affine transformations, using the previous image as a template.

In order to generate the spatially registered MS data, all the ion images were registered with respect to the corresponding H&E optical images. Since the optical images had been already sequentially aligned, this procedure allowed the co-registration of all the MS data.

The final affine transformation was applied to all the ion images of the data to produce a set of aligned MS imaging spectra. In the entire procedure, only one affine transformation was applied to the MS data. The registration procedure, based on the assumption that consecutive tissue sections are similar to each other, was not applied to all the sections between the 33rd and the 52nd because those sections were topologically significantly different (the process of tissue excision and slicing may introduce deformities in the tissue slice) from the previous sections. Those slices were manually aligned with the previous sections applying multiple π/2 rotations and axis inversions when necessary.

As a final step, in order to remove possible batch effects, the ‘removeBatchEffect’ command from the ‘limma’ package for R (available at https://bioconductor.org/packages/release/bioc/html/limma.html) was employed with the batches corresponding to the 13 acquisition slides. After the pre-processing steps, the dataset consisted of 205 556 (59 × 67 × 52) spectra with 391 ion features.

A consultant histopathologist manually annotated the H&E optical images and assigned these to three classes: tumour, healthy, and background, corresponding to ∼11 000 mass spectra.

Methods

Supervised segmentation of the tumour

The manually annotated DESI-MS spectra were used to segment the 3D tissue in the three regions corresponding to tumour, surrounding healthy tissue, and background. The classification performance was tested using four supervised methods: linear support vector machines (SVM), random forest (RF), stacked sparse autoencoder (SSAE), and maximum margin criterion (MMC–LDA). Each classifier performance was evaluated with a 30% hold-out cross validation, repeated 5 times. The method that produced the most accurate predictions was used to train a model on all the labelled spectra in order to assign the class of the remaining unlabelled data. The main purpose of this step was to reduce the number of spectra for subsequent analysis by the unsupervised techniques, since all the non-tumour pixels were discarded. In order to preserve the spectral information related with the tumour tissue, we preferred using strongly distinct tissue types.

Dimensionality reduction of tumour spectra

Heterogeneity of tumour tissue can be captured through the identification of mutual similarity-based partitions from the mass spectrometry data. Several techniques are available to perform reduction of the dimensionality of data. Some of these methods are based on a linear representation of the data in a low-dimensional space, such as Principal Components Analysis (PCA), and others provide a more complex representation based on a non-linear mapping of the data to the low-dimensional space (ISOMAP, LLE, t-SNE, MDS, etc.). It is evident that the linearity of models in some techniques constitutes a severe limitation of their ability to define a faithful low-dimensional representation of the data.25

Also, many of the non-linear techniques refine their models to the training data, making it difficult to use those models to map out-of-sample data without some degree of approximation.22 This, in the case of datasets made up of hundreds of thousands of samples, such as those generated by 3D mass spectrometry imaging technologies, represents a critical factor because this can limit the computational analysis process21 and the capability to apply the model to unseen data.

In contrast the method that is adopted here, parametric t-SNE, combines the advantages of highly non-linear parametric modelling based on a deep neural network model and the capability of t-SNE to capture the similarity relationships in high-dimensional data and represent them in a low-dimensional space.27 For this reason, the trained parametric model can be easily applied to unseen data making it possible to map large datasets such as those produced in 3D MSI. A detailed description of the parametric t-SNE algorithm is given in the ESI.†

Clustering of low-dimensional tumour data points

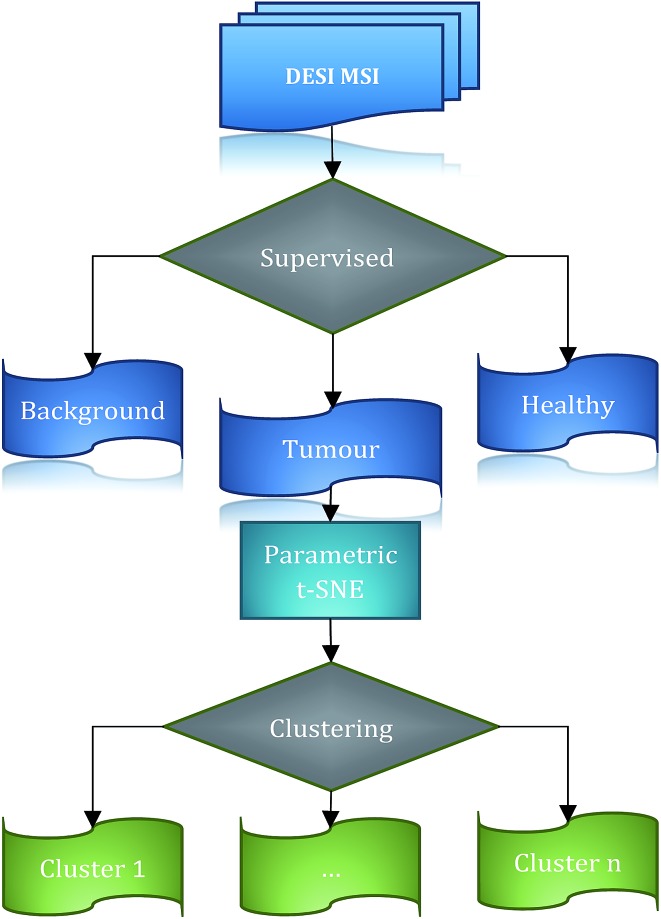
The low-dimensional data points were clustered using the OPTICS algorithm.29 OPTICS is a density-based method based on DBSCAN38 which generates a hierarchical clustering of the data (ESI†). This method has the advantage of providing an intuitive way to examine the structure of the data and identify the optimal number of clusters, through a reachability plot (ESI Fig. 3†). OPTICS requires two parameters: the maximum distance ε to the neighbours of the samples considered, and the minimum number (MinPts) of data points necessary to define a cluster. The reachability plot represents in a compact way the topological properties of the datasets: all the data points are ordered according to their closeness in the data space, and the reachability distance (RD) describes ‘how close’ the adjacent samples are. This means that data points belonging to the same dense cluster will have a smaller RD than points belonging to different clusters. Following this idea, clusters can be easily identified looking at the ‘dents’ (which means that hills and valleys of the reachability plot represent the internal structure of a dataset) of the reachability plot that intersect a specific RD value. Different RD values define different partitions, as the regions in the plot that are greater than the RD value can be in different clusters. In this sense, robust clusters are associated with deep dents. We defined a robust cluster if the dents associated with a partition were deep with a value of at least 0.5. Finally the optimal partition was chosen using the minimum value of the Davies–Bouldin index (DBI).39 A general scheme of the used workflow is shown in Fig. 1.

Fig. 1. Workflow general scheme. DESI imaging data is segmented in 3 classes: background, healthy and tumour. The 2-dimensional representation of the tumour spectra is calculated by parametric t-SNE and clustered using OPTICS.

Fig. 1

Open in a new tab

In order to evaluate the robustness of the clustering results, a co-expression network analysis was performed on only the tumour pixels. Pearson's pairwise correlation matrix between ion variables was used as the adjacency measure. To reduce the effect of correlations due to noise, a threshold of 0.65 was applied. The adjacency matrix was used to define a force-directed graph which was subsequently analysed. All the disconnected sub-networks were automatically identified and the spatial distribution of the ions corresponding to each sub-network was plotted and compared with the spatial distribution of the cluster labels found with OPTICS. The ions found in each sub-network were ranked according to their degree or intra-hub connectivity (the number of connected ion-nodes to a specific ion-node) in the sub-network and a Kruskal Wallis test was performed followed by a multiple comparison Dunn's test to assess if the relative abundance of the most connected ions in each sub-network was significantly different in each spatial region defined by the OPTICS clusters. In this way we could define a quantitative connection between the results of the two methods.

Investigating the importance of 3D in the unsupervised analysis of tumours

There are two questions we wish to address. The first is, does the use of 3D data provide a more complete description of the tumour microenvironment? Secondly, is the clustering (the definition of healthy tissue and tumour sub-types) more robust?

Intuitively, the use of the 3-dimensional environment of a tumour should provide more complete information on the biochemistry and, at the same time, introduce additional topological constraints, which could aid in the identification of e.g. unrealistic partitions.

Indeed, the contiguous nature of the tissue slices implies that, in general, tissue sub-types should change their shape with continuity between slices. Evidently, rapid morphological variations in the tumour sub-regions can still occur, but we would assume that those should coincide with a drastic change of the entire tissue morphology, for example in slices where a portion of tumour begins or ends.

To investigate the importance of 3D versus 2D data, we tested how reliable segmentation methods were in a comparison using 2D and 3D data. Unsupervised analysis was performed on multiple contiguous slices and single 2D slices of tissue independently. The similarity between the tumour sub-regions found with the two datasets was evaluated using the adjusted Rand index (aRI).40

The second assumption was that 3D data can be used to filter out incorrect clusters. For this purpose, we compared the similarity between tumour regions in adjacent slices with sub-regions deduced from three different experiments: slices in the original (proper) order, slices shuffled in order and randomly generated partitions with the original order of the slices maintained. We would expect that realistic clusters would show a more correlated sequence of similarities between adjacent slices using the entire tumour in the correct order compared to using clusters generated when the slice order is permuted or if the same number of clusters are randomly assigned to the pixels. As a similarity measure, the structural similarity index (SSIM)41 was chosen (as additionally we were interested in the similarities between the internal patterns). The correlation between the sequences of SSIM values between pairs of adjacent slices was therefore calculated in order to see if the topological changes present in the entire tumour were reflected in its sub-regions.

Results

Upon testing the prediction accuracy of the four classifiers (the parameter configurations for RF and SSAE are reported in ESI Table 1†), linear SVM was found to perform better than the other classifiers with an average accuracy of 0.99976 ± 0.00025 (ESI Table 2†). The libSVM library from MATLAB was used to generate the linear SVM models,42 whereas MATLAB built-in functions were used to generate the RF and SSAE models. The MMC–LDA model was calculated with an in-house developed MATLAB script.

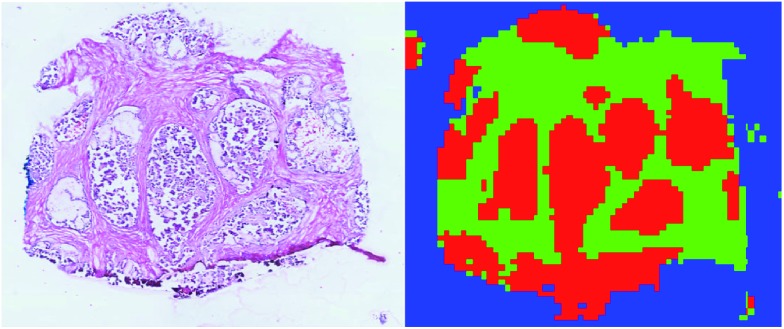
Based on these results, segmentation of the entire 3D DESI-MS dataset was performed using a linear SVM model trained on the ∼11 000 manually labelled spectra to assign the class among tumour, healthy and background classes to all the unlabelled spectra. The result was that 72 261 spectra were classified as tumour (ESI Fig. 4†). A visual inspection of the segmented regions confirmed the validity of the results (Fig. 2).

Fig. 2. Comparison of the H&E image from a tissue slice and the corresponding supervised classification. Tumour is plotted in red, healthy in green, and background in blue.

Fig. 2

Open in a new tab

In order to evaluate the effectiveness of the parametric t-SNE dimensionality reduction, the 2-dimensional representation of the latent space of the entire dataset was compared with that obtained through PCA. The capability of each method to retain the local structure in the latent space was measured using the trustworthiness measure, defined, for n data points, as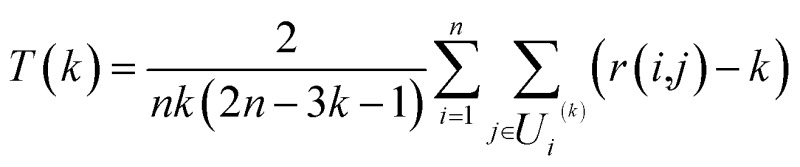Inline graphicwhere k is the number of neighbours considered, r(i,j) is the rank of the low-dimensional jth data point according to the pair-wise distances in the latent space, and U i (k) is the set of data points that are in the k-neighbourhood in the latent space but not in the original high-dimensional space.43 Based on previous work,28,44 a 5-layer parametric t-SNE with a topology of 391-250-250-1000-2 units was applied to the entire dataset. It was trained on 30 000 randomly selected data points (from the entire dataset) and tested on the hold-out data points. The rationale behind the choice of a 2-dimensional latent space was two-fold: (1) this allowed fixing of the number of degrees of freedom of the Students-t distribution45 and (2) the mapped data points could be easily analysed visually (important when the ground truth is not available). The Bernoulli RBMs were trained with 1-step contrastive divergence on mini-batches of 100 samples for 30 epochs. The learning rate was set to 0.01 and the weight regularisation to 0.0002. All the RBMs were trained using logistic sigmoid activations, only the deepest RBM layer was trained using linear hidden activations as described in ref. 45. Fine-tuning for the parametric t-SNE model was performed with a Polak–Ribière conjugate gradient with mini-batches of 5000 samples each and 500 epochs. Perplexity was set to 30 and the degrees of freedom of the Student's t-distribution was set to 1. The analysis was performed using the MATLAB code available at ; https://lvdmaaten.github.io/tsne/code/ptsne.tar.gz. (June 2016).

Over 5 repetitions, the average trustworthiness of the test set with 12 neighbours had standard deviations equal to 0.9485 ± 0.0015 for the parametric t-SNE and 0.9370 ± 0.0016 for the first two principal components, confirming that the data points in the non-linear embedding better represented the similarity relationships of the high-dimensional data. As an additional test, using the SVM predicted labels as ground truth (direct observation), a k-NN model was trained on the 2-dimensional parametric t-SNE data points and the scores of the first 2 principal components.

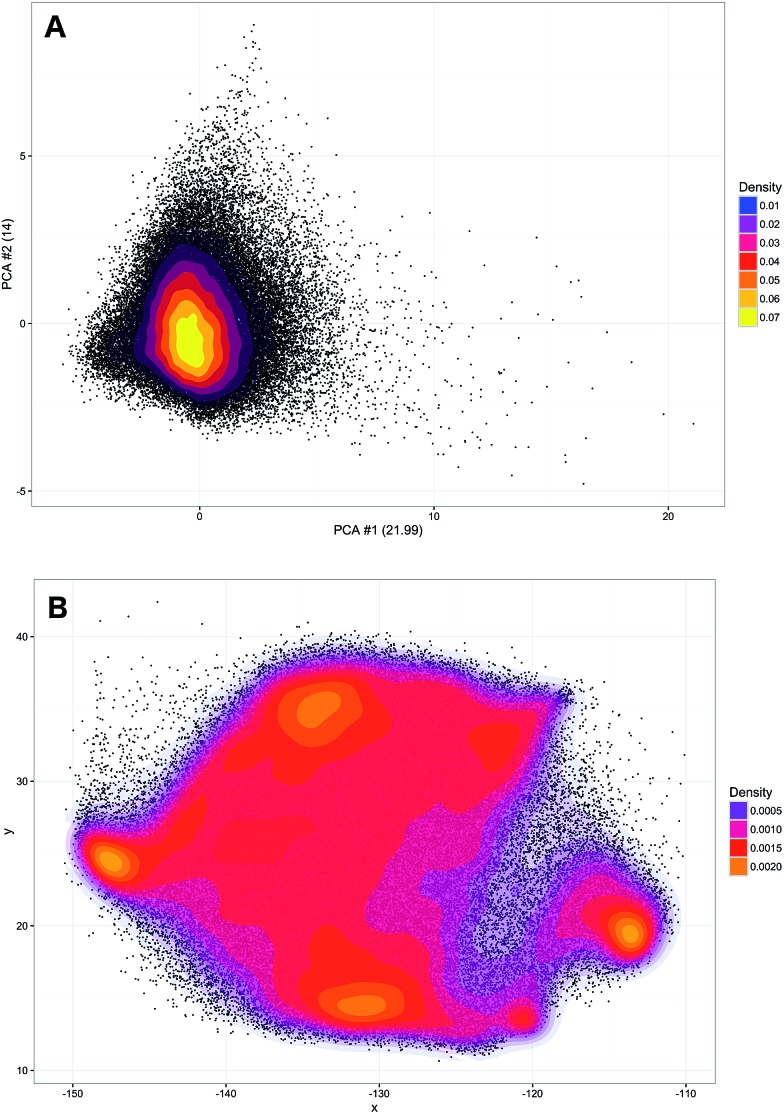
A training set of 30 000 samples randomly selected from the entire dataset was used to fit the model and the test was performed on the hold-out samples. Numbers of neighbours for k-NN in the range of 1–20 were evaluated. Over 5 repetitions it was seen that the average prediction error was always significantly lower for the parametric t-SNE representations (ESI Fig. 5†), confirming that similar spectral patterns (which are expected to belong to the same class) were placed closer in the parametric t-SNE latent space than in the PCA score space. The unsupervised analysis using SVM predicted tumour spectra was carried out by extracting a 2-dimensional representation of the spectra using a 5-layer parametric t-SNE with 391-250-250-1000-2 units. All the learning parameters were set equal to those used in the analysis described previously. A visual inspection of the scatter plots from parametric t-SNE latent space showed the presence of sub-structures (Fig. 3B) that were not visible in the scatter plot of the first two principal components scores (Fig. 3A).

Fig. 3. Scatter plot of the 2-dimensional tumour data points. The first 2 principal components scores (data centred, the axis labels report the percentage of explained variance) are clustered in a single globular shape (A), whereas the parametric t-SNE mapping shows the presence of complex structures (B). Multiple highly dense regions are visible on left and bottom right regions.

Fig. 3

Open in a new tab

Since data scaling can affect the results of PCA, we tested the following set of scaling methods: centring, autoscaling, range scaling, Pareto scaling, vast scaling, and level scaling.46 In all these cases, a scatter plot of the PCA did not show the presence of clusters (ESI Fig. 6†). Additionally, the trustworthiness of parametric t-SNE was always significantly larger than that obtained with PCA (ESI Table 3†).

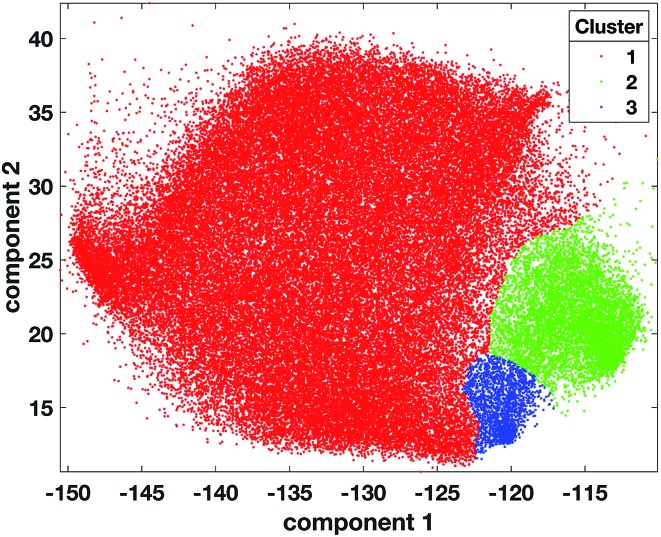
OPTICS was applied on 20 000 randomly selected data points from the 72 261 2-dimensional tumour data points and MinPts set to 200. Three candidate partitions were found with 2, 3, and 4 clusters corresponding to the RD values of 1.68, 1.5 and 1.15 respectively (ESI Fig. 7†). The OPTICS reachability plot was generated using the MATLAB code available at ; http://chemometria.us.edu.pl/download/OPTICS.M. MinPts and the optimal threshold values corresponding to the three possible partitions were used as parameters for DBSCAN to perform clustering, using the ‘DBSCAN’ function available in the Python scikit-learn library47 (; http://scikit-learn.org). After assigning all the tumour data points (comprising those labelled as noise) to the cluster of the closest labelled data point (Fig. 4), the DBIs of the three partitions were calculated and the optimal number of clusters was found to be 3 (ESI Fig. 8†). This result corresponded to dense clusters sufficiently separated to be considered distinct.

Fig. 4. Scatter plot of tumour data points coloured according to cluster 1 = red, cluster 2 = green, cluster 3 = blue, after the projection of labels found with OPTICS on the tumour dataset.

Fig. 4

Open in a new tab

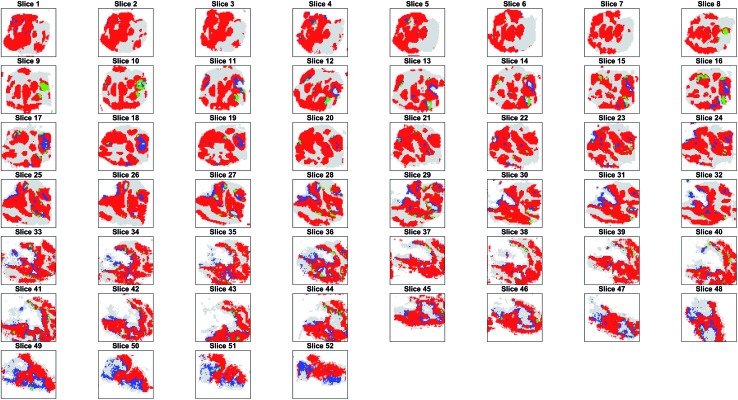
The projection of the clusters on the tissue coordinates is shown in Fig. 5 and the resulting spatial distributions were compatible with the contiguous nature of the tissue slices.

Fig. 5. Segmentation of the tumour into 3 clusters found with OPTICS. The spatial distribution of the 3 clusters (cluster 1 = red, cluster 2 = blue, cluster 3 = green) found in tumour is compatible with the contiguous tissue slices. Healthy tissue is plotted in grey to give an indication of the relative position of the tissues.

Fig. 5

Open in a new tab

The co-expression network was defined using the 391 × 391 pair-wise Pearson's correlation matrix between the ion vectors of the tumour spectra from their adjacency. A threshold of 0.65 was set to define the adjacency matrix for a force-directed graph. Each node of the network represented an m/z value.

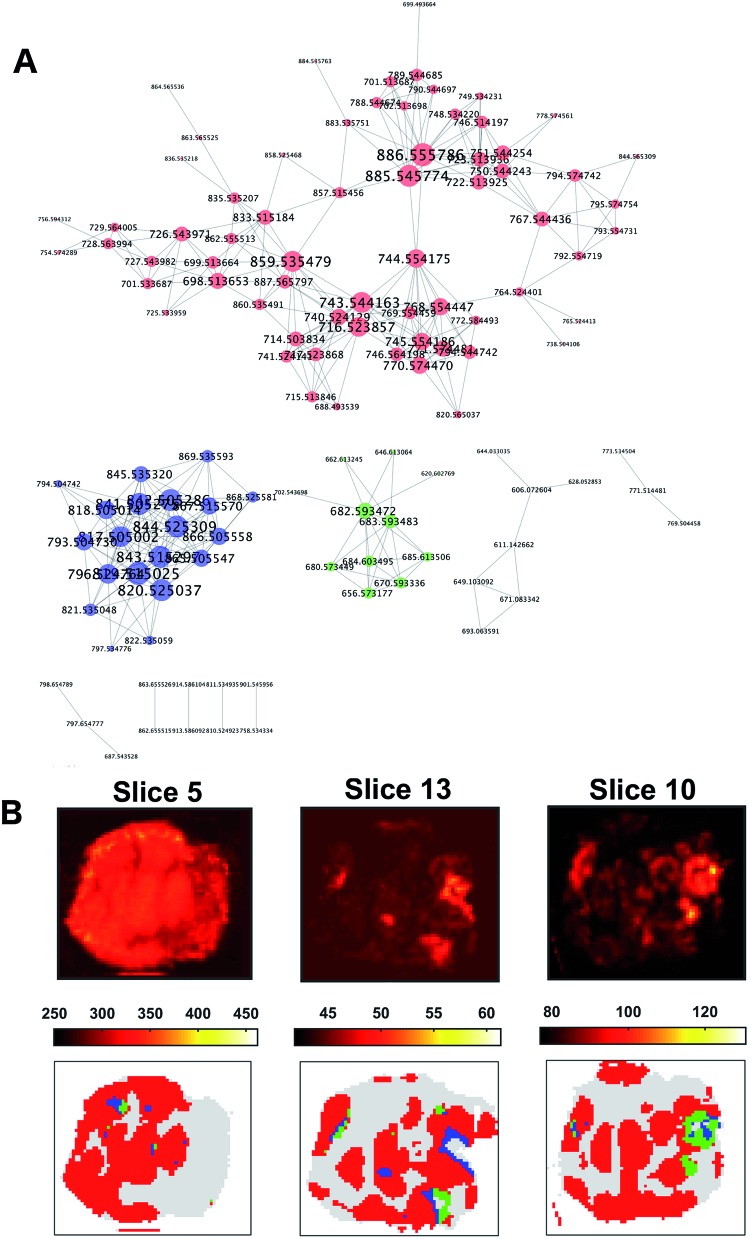
The resulting graph presented a set of 10 disconnected groups of nodes which were identified using the ‘clusterMaker2’48 functionality available in Cytoscape49 ver.3.4.0. The ions belonging to the three largest sub-networks (Fig. 6A) were selected and the corresponding three sum of intensities (SSI) images were plotted (ESI Fig. 9–11†).

Fig. 6. Co-expression network for ion vectors of tumour mass spectra showing 10 disconnected sub-networks (A). Nodes with a degree larger than two are labelled with the relative m/z value in Da. Larger nodes are characterised by a higher degree. The three largest sub-networks are coloured in red, blue and green respectively. The corresponding SSI images showed a spatial distribution compatible with that of the OPTICS clusters (B). The SSI image of the ions from the sub-network 1 (A, red) were compatible with the cluster 1 (B, red), whereas sub-network 2 (B, blue) was compatible with cluster 2 (B, blue), and ions from sub-network 3 (A, green) were similarly distributed to cluster 3 (B, green).

Fig. 6

Open in a new tab

A visual inspection of the SSI images showed that there was a pair-wise correspondence between the spatial distributions of the sum of the ion intensities from the three sub-networks and the regions of the clusters found by OPTICS (Fig. 6B).

The association between clusters and SSI images was confirmed by inspection of the maximum pair-wise Pearson's correlation coefficients (Table 1).

Table 1. Pearson's correlation coefficients between the SSI images corresponding to the three largest sub-networks and the three OPTICS clusters. Each SSI image was significantly more similar to only one of the clustered regions, making it possible to associate the ions of those sub-networks to differences between the clusters.

Cluster 1 Cluster 2 Cluster 3
SSI 1 0.6991 0.0876 0.2071
SSI 2 0.3076 0.5363 0.2440
SSI 3 –0.0556 0.0692 0.4170
Open in a new tab

The ten ions with the largest degree were used as representative ions for each sub-network. In this way, ions were selected with the most similar spatial distribution to that the distribution of the sum of the sub-network ion intensities. In order to annotate those ions, a search over the raw data was performed using a window of ±5 ppm. The median of the m/z values found was used as a representative value for a specific ion. All the queried m/z values were found in at least 34.45% of the entire raw dataset (ESI Table 4†).

A Kruskal–Wallis test followed by a multiple comparison Dunn's test on the 3 ions with the largest degree values in each sub-network considered confirmed that ions from the sub-networks were more abundant in the corresponding cluster region. In particular, ions from the first sub-network were more ubiquitously expressed whereas the ions from the second and third sub-network were more consistent with cluster 2 and 3 (ESI Fig. 12†).

The representative m/z value of the ions were annotated using the ‘Lipid maps’ online search engine50 (ESI Table 5†) if the error was smaller than 5 ppm. After annotation, the most evident molecular difference among the three clusters was the abundance of three different classes of lipids in each sub-region. Cluster one, that was associated with ions expressed more extensively in the entire tumour, was characterised by an abundance of phosphatidylethanolamines (PE), and these high levels have been associated with rapidly proliferating human colorectal cancer in previous work.31,51,52 Additionally, the abundance of phosphatidylinositols (PI) was found only in cluster one, which are also hallmarks of viable cancer tissue. In contrast, phosphatidylglycerols (PG) were found in cluster two, indicating the presence of mucus in mucinous subtype colorectal malignant tissue31,53 as PGs generally serve as surfactants in the human body. The presence of very long acyl chains (n > 18) excludes a bacterial origin and indicates peroxisomal dysfunction in this segment.

Cluster three was characterised by an abundance of ceramides, which indicates the presence of a process of necrosis/apoptosis, in agreement with the gross histological appearance in this sub-region.54 The increased concentration of ceramides is clearly associated with the degradation of sphingolipids in the necrotic cell debris.

An abundance of phosphatidylserine (PS) was found only in cluster two, which has previously been associated with apoptosis of colon cancer cells.55–57

The nature of these two tissue sub-types was established through visual inspection by the consultant histophatologists who confirmed that in cluster 2 there were features typical of nectrotic tissue, whereas those features were not so evident in cluster 3. After careful inspection, it was found that cluster 3 corresponded to a region where an apoptotic process was ongoing.

It is interesting to note that in combining the molecular expressions of clusters two and three with their spatial distributions, it was found that the two clusters were always localised in adjacent regions, suggesting that in this region of the tumour, signalling is having the effect of inducing cell death of adjacent tumour cells. This result supported the hypothesis that an apoptotic process was ongoing in the peripheral regions of the necrotic tissue.

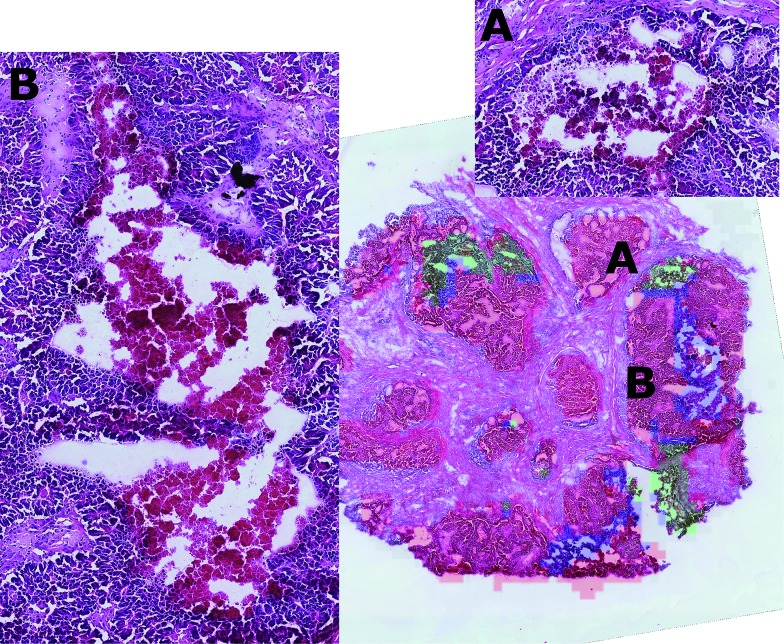
By visual inspection of the H&E images, it was seen that the regions corresponding to clusters two and three were characterised by diverse tissue morphologies compared to cluster one. However these two sub-regions had very similar visual histological characteristics (Fig. 7) and indeed they could be distinguished only after careful analysis driven by the mass spectrometric clustering results. The unsupervised analysis of the mass spectrometric data not only gave an insight into the biochemical heterogeneity (signatures) of the tumour, but also provided a guide for more detailed identification of the tissue sub-types by the histopathologists, suggesting that this approach could be an invaluable tool for the annotation of such massive datasets.

Fig. 7. Approximate projection on the H&E image of the cluster regions (cluster one = red, cluster two = blue, cluster three = green) shows that tissue sub-types 2 and 3 are morphologically different from sub-type 1, but that tissue sub-types 2 and 3 can be distinguished only after careful inspection (A and B). In this way, the unsupervised analysis provides both the molecular description of the two sub-types and represents a tool that can improve the histological analysis of such massive datasets.

Fig. 7

Open in a new tab

The unsupervised analysis of the mass spectrometry data showed that different molecular abundances (signatures) were localised in these regions.

A further test aimed to see if other clustering algorithms were capable of identifying similar partitions. This was performed using k-means with three clusters and three different distance measures (Euclidean, cosine and correlation) and also Gaussian mixture models with 3 clusters. None of these algorithms provided a similar partition to that determined by OPTICS, which resulted in a maximum value of aRI equal to 0.2647 found using the k-means and correlation distance (ESI Fig. 13†). Analogous results were found when applying k-means or GMM on the 2-dimensional parametric t-SNE mapped data points, where the maximum aRI value was 0.0207, found with GMM (shared covariance, full covariance).

Parametric t-SNE followed by OPTICS clustering on individual 2D slices resulted in completely different partitions (ESI Fig. 14†) and, consequently, in disagreement with the results of co-expression network analysis. Also, it was found that the clusters generated by the individual (2D) slices were not topologically compatible with the hypothesis that the clusters should gradually change in adjacent slices, because of the contiguous nature of the tissue (ESI Fig. 15†). This proved that unsupervised analysis of 2D tissue slices cannot guarantee reliable results. Furthermore, when comparing the sequence of SSIM values between the binary images containing only the tumour pixels of pairs of adjacent slices and the images representing the OPTICS clusters it was found that the former were highly correlated, whereas the latter were poorly correlated (ESI Fig. 16†). The randomly assigned clusters still produced a highly correlated SSIM sequence compared to that of the entire tumour, because they shared the overall shape, but their SSIM values were significantly lower than those of the OPTICS clusters, because random clusters could not preserve the internal structures found in the adjacent slices (ESI Fig. 16†).

A Kolmogorov–Smirnov test rejected the null hypothesis that SSIM values of the entire tumour and random clusters were sampled from the same distribution with a significance of 0.05, whereas the null hypothesis could not be rejected when tested against the sequence from the OPTICS clusters.

Finally, a stereoscopic (cross-eyed) reconstruction of the 3D clusters is shown in Fig. 8 demonstrating the complex distribution of tumour subtypes infiltrating normal tissue in the excised sample.

Fig. 8. Stereoscopic (cross-eyed) rendering of the 3D reconstruction of the three clusters. A Laplacian operator is applied four times to smooth the volume. Transparency is added to cluster one to allow the visualisation of the other two inner clusters.

Fig. 8

Open in a new tab

Conclusions

3D mass spectrometry imaging represents a powerful tool to investigate the chemical and biological interactions occurring in tumour tissues. In the experimental and computational workflow shown here, we have demonstrated that inspection of the 3D data derived from deep learning and cluster analysis is a straightforward and more robust approach to identify the presence of tumour subgroups of cells characterised by similar mass spectrometry profiles, providing results that are not captured by visual inspection.

Interestingly, the parametric t-SNE mapping of the 72 261 tumour spectra showed the presence of clusters which were not visible in the scatter plot of the first two principal components. Three clusters were identified using OPTICS, a density based clustering algorithm that allowed the straightforward identification of the optimal number of clusters.

Using this approach, we provided a more detailed description of the chemical and biological interactions occurring in the tumour tissue using a completely unsupervised, data-driven workflow, being able to distinguish the chemical properties of two tumour sub-regions. The association of clusters with the most correlated ions together with the co-expression network analysis gives the opportunity to discover a detailed picture of the molecular distributions and their possible use as biomarkers in the tumour tissue. This permits the discovery of key metabolites in similar tumour sub-types and these can be associated with a probable biological interpretation. These include: phosphatidylethanolamines (which are associated with rapidly proliferating human colorectal cancer), phosphatidylinositols (which are hallmarks of viable cancer tissue), phosphatidylglycerols (which indicate the presence of mucus in mucinous subtype colorectal malignant tissue), the presence of very long acyl chains (n > 18) (which excludes bacterial origin and indicates peroxisomal dysfunction), ceramides (which indicate necrosis/apoptosis and are associated with degradation of sphingolipids in the necrotic cell debris) and phosphatidylserine (which is associated with apoptosis of colon cancer cells).

This approach also represents a useful tool for data-driven histological inspection of massive datasets to assist the histopathologist to identify specific regions for more detailed inspection and characterisation.

We have demonstrated that analysis of 3D data is a straightforward and more robust approach to identify the presence of tumour subgroups of cells characterised by similar mass spectrometry profiles. Indeed, we have demonstrated that the third-dimension is necessary in order to produce reliable results consistent with a co-expression network analysis. The third dimension also introduces topological constraints that, combined with the fact that biochemical interactions are local, can be used to identify unrealistic partitions.

These constraints are absent when analysing 2-dimensional datasets. This result is of invaluable importance because it shows that unsupervised analysis of 2D mass spectrometry imaging data may not be reliable and is sensitive to the specific relative position and orientation of the analysed slice within the entire tumour. Furthermore, we showed that by combining the results of parametric t-SNE with the co-expression network analysis that the tumour clusters not only displayed expression of distinct molecular signatures, but that specific ions were significantly more abundant only in those clusters.

Non-linear techniques usually require more computational power and time to generate a model, in this case 6 hours of CPU time (single Intel i7 processor) was necessary to fit a parametric t-SNE model to the training set. This can be mitigated by more efficient implementations such as GPU-enabled and highly parallel computing environments.

Results provided by unsupervised learning techniques would be further validated if very precise experimental information about the chemical and biological properties of individual differentiated tumour cells58 was available, therefore increased resolution would be beneficial.

Future work will be devoted to the study of 3D DESI-MS data from a broader variety of tumours to investigate the local chemistry and the diverse biological implications of the computational results. Integration of different data sources is fundamental to understand the complex biological mechanisms underlying tumour development; for that reason, studies on the genetics and protein expression of the cells belonging to the sub-regions identified through unsupervised analysis of MSI data are in progress. Furthermore, models trained on larger cohorts of subjects will be studied in order to capture possible relationships between the molecular properties of sub-regions of tumours and the effectiveness of anti-cancer therapies. Ultimately the translational value of MS based tissue imaging will lie in the ability to perform digital pathology using automation to augment clinical decision making. We regard the emergence of 3D MS imaging as an essential technology to help map the 3D variance of tumour chemistry which apart from its value in understanding heterogeneity will underpin the development of tools to assist current 2D MS imaging practice, which is the likely initial deployment mode for this technology in the real pathology laboratory.

Acknowledgments

We would like to acknowledge funding from the Department of Health, National Institute for Health Research, Bowel and Cancer Research, the European Research Council, the Wellcome Trust and the Imperial National Institute of Health Biomedical Research Centre for funding DESI research. Mr Inglese is supported by the Imperial College Stratified Medicine Graduate Training Programme in Systems Medicine and Spectroscopic Profiling (STRATiGRAD). We would like to acknowledge Prof Robert Goldin and Dr Abigail Speller for the manual annotation of the H&E stained images. This work used the computing resources of the UK MEDical BIOinformatics partnership - aggregation, integration, visualisation and analysis of large, complex data (UK MED-BIO) which is supported by the Medical Research Council [grant number MR/L01632X/1].

Footnotes

†Electronic supplementary information (ESI) available. See DOI: 10.1039/c6sc03738k
Click here for additional data file. (3.7MB, pdf)
Click here for additional data file. (9.4MB, wmv)
Click here for additional data file. (67.8KB, pdf)

References

  1. Martinez-Outschoorn U. E., Peiris-Pages M., Pestell R. G., Sotgia F., Lisanti M. P. Nat. Rev. Clin. Oncol. 2017;14(1):11–31. doi: 10.1038/nrclinonc.2016.60. [DOI] [PubMed] [Google Scholar]
  2. Schwamborn K., Caprioli R. M. Nat. Rev. Cancer. 2010;10:639–646. doi: 10.1038/nrc2917. [DOI] [PubMed] [Google Scholar]
  3. Deininger S. r.-O., Ebert M. P., Fütterer A., Gerhard M., Röcken C. J. Proteome Res. 2008;7:5230–5236. doi: 10.1021/pr8005777. [DOI] [PubMed] [Google Scholar]
  4. McCombie G., Staab D., Stoeckli M., Knochenmuss R. Anal. Chem. 2005;77:6118–6124. doi: 10.1021/ac051081q. [DOI] [PubMed] [Google Scholar]
  5. Oppenheimer S. R., Mi D., Sanders M. E., Caprioli R. M. J. Proteome Res. 2010;9:2182–2190. doi: 10.1021/pr900936z. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Ness R. O., Sachs K., Vitek O. J. Proteome Res. 2016;15:683–690. doi: 10.1021/acs.jproteome.5b00911. [DOI] [PubMed] [Google Scholar]
  7. LaBonia G. J., Lockwood S. Y., Heller A. A., Spence D. M., Hummon A. B. Proteomics. 2016;16:1814–1821. doi: 10.1002/pmic.201500524. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Yue X., Lukowski J. K., Weaver E. M., Skube S. B., Hummon A. B. J. Proteome Res. 2016;15:4265–4276. doi: 10.1021/acs.jproteome.6b00342. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Palmer A. D., Alexandrov T. Anal. Chem. 2015;87:4055–4062. doi: 10.1021/ac504604g. [DOI] [PubMed] [Google Scholar]
  10. Eberlin L. S., Norton I., Dill A. L., Golby A. J., Ligon K. L., Santagata S., Cooks R. G., Agar N. Y. R. Cancer Res. 2012;72:645–654. doi: 10.1158/0008-5472.CAN-11-2465. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Balluff B., Frese C. K., Maier S. K., Schöne C., Kuster B., Schmitt M., Aubele M., Höfler H., Deelder A. M., Heck A. J. J. Pathol. 2015;235:3–13. doi: 10.1002/path.4436. [DOI] [PubMed] [Google Scholar]
  12. Jones E. A., van Remoortere A., van Zeijl R. J. M., Hogendoorn P. C. W., BovÈe J. V. M. G., Deelder A. M., McDonnell L. A. PLoS One. 2011;6:e24913. doi: 10.1371/journal.pone.0024913. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Ding C. and He X., Proceedings of the twenty-first international conference on Machine learning, ACM, 2004. [Google Scholar]
  14. Lou S., Balluff B., de Graaff M. A., Cleven A. H. G., Briaire-de Bruijn I., Bovée J. V. M. G., McDonnell L. A. Proteomics. 2016;16:1802–1813. doi: 10.1002/pmic.201500514. [DOI] [PubMed] [Google Scholar]
  15. Handl J., Knowles J., Kell D. B. Bioinformatics. 2005;21:3201–3212. doi: 10.1093/bioinformatics/bti517. [DOI] [PubMed] [Google Scholar]
  16. Milligan G. W., Cooper M. C. Psychometrika. 1985;50:159–179. [Google Scholar]
  17. Halkidi M. and Vazirgiannis M., Data Mining, 2001. ICDM 2001, Proceedings IEEE International Conference, 2001. [Google Scholar]
  18. Van Der Maaten L., Postma E., Van den Herik J. J. Mach. Learn. Res. 2009;10:66–71. [Google Scholar]
  19. Trim P. J., Atkinson S. J., Princivalle A. P., Marshall P. S., West A., Clench M. R. Rapid Commun. Mass Spectrom. 2008;22:1503–1509. doi: 10.1002/rcm.3498. [DOI] [PubMed] [Google Scholar]
  20. Wijetunge C. D., Saeed I., Halgamuge S. K., Boughton B. and Roessner U., 7th International Conference on Information and Automation for Sustainability, 2014. [Google Scholar]
  21. Alexandrov T. BMC Bioinf. 2012;13:S11. doi: 10.1186/1471-2105-13-S16-S11. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Bengio Y., Paiement J.-F., Vincent P., Delalleau O., Le Roux N., Ouimet M. Adv. Neural. Inform. Process. Syst. 2004;16:177–184. doi: 10.1162/0899766041732396. [DOI] [PubMed] [Google Scholar]
  23. Cornett D. S., Mobley J. A., Dias E. C., Andersson M., Arteaga C. L., Sanders M. E., Caprioli R. M. Mol. Cell. Proteomics. 2006;5:1975–1983. doi: 10.1074/mcp.M600119-MCP200. [DOI] [PubMed] [Google Scholar]
  24. Hinton G. E., Roweis S. T. Adv. Neural. Inform. Process. Syst. 2002 [Google Scholar]
  25. Fonville J. M., Carter C. L., Pizarro L., Steven R. T., Palmer A. D., Griffiths R. L., Lalor P. F., Lindon J. C., Nicholson J. K., Holmes E., Bunch J. Anal. Chem. 2013;85:1415–1423. doi: 10.1021/ac302330a. [DOI] [PubMed] [Google Scholar]
  26. Abdelmoula W. M., Balluff B., Englert S., Dijkstra J., Reinders M. J. T., Walch A., McDonnell L. A., Lelieveldt B. P. F. Proc. Natl. Acad. Sci. U. S. A. 2016;113:12244–12249. doi: 10.1073/pnas.1510227113. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Van der Maaten L., Hinton G. J. Mach. Learn. Res. 2008;9:85. [Google Scholar]
  28. Maaten L., International Conference on Artificial Intelligence and Statistics, 2009. [Google Scholar]
  29. Ankerst M., Breunig M. M., Kriegel H.-P. and Sander J., ACM Sigmod Record, ACM, 1999. [Google Scholar]
  30. Shekhar K., Brodin P., Davis M. M., Chakraborty A. K. Proc. Natl. Acad. Sci. U. S. A. 2014;111:202–207. doi: 10.1073/pnas.1321405111. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Gerbig S., Golf O., Balog J., Denes J., Baranyai Z., Zarand A., Raso E., Timar J., Takats Z. Anal. Bioanal. Chem. 2012;403:2315–2325. doi: 10.1007/s00216-012-5841-x. [DOI] [PubMed] [Google Scholar]
  32. Oetjen J., Veselkov K., Watrous J., McKenzie J. S., Becker M., Hauberg-Lotte L., Kobarg J. H., Strittmatter N., Mróz A. K., Hoffmann F., Trede D., Palmer A., Schiffler S., Steinhorst K., Aichler M., Goldin R., Guntinas-Lichius O., von Eggeling F., Thiele H., Maedler K., Walch A., Maass P., Dorrestein P. C., Takats Z., Alexandrov T. GigaScience. 2015;4:1–8. doi: 10.1186/s13742-015-0059-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Schramm T., Hester A., Klinkert I., Both J.-P., Heeren R. M., Brunelle A., Laprévote O., Desbenoit N., Robbe M.-F., Stoeckli M. J. Proteomics. 2012;75:5106–5110. doi: 10.1016/j.jprot.2012.07.026. [DOI] [PubMed] [Google Scholar]
  34. He Q. P., Wang J., Mobley J. A., Richman J., Grizzle W. E. Cancer Inf. 2011;10:65–82. doi: 10.4137/CIN.S6358. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Coombes K. R., Tsavachidis S., Morris J. S., Baggerly K. A., Hung M. C., Kuerer H. M. Proteomics. 2005;5:4107–4117. doi: 10.1002/pmic.200401261. [DOI] [PubMed] [Google Scholar]
  36. Veselkov K. A., Vingara L. K., Masson P., Robinette S. L., Want E., Li J. V., Barton R. H., Boursier-Neyret C., Walther B., Ebbels T. M., Pelczer I., Holmes E., Lindon J. C., Nicholson J. K. Anal. Chem. 2011;83:5864–5872. doi: 10.1021/ac201065j. [DOI] [PubMed] [Google Scholar]
  37. Otsu N. Automatica. 1975;11:23–27. [Google Scholar]
  38. Ester M., Kriegel H.-P., Sander J. and Xu X., Knowledge Discovery in Databases, 1996. [Google Scholar]
  39. Davies D. L., Bouldin D. W. IEEE Trans. Pattern Anal. Mach. Intell. 1979;1:224–227. [PubMed] [Google Scholar]
  40. Rand W. M. J. Am. Stat. Assoc. 1971;66:846–850. [Google Scholar]
  41. Zhou W., Bovik A. C., Sheikh H. R., Simoncelli E. P. IEEE Trans. Image Process. 2004;13:600–612. doi: 10.1109/tip.2003.819861. [DOI] [PubMed] [Google Scholar]
  42. Chang C.-C., Lin C.-J. ACM T. Intel. Syst. Tec. 2011;2:27. [Google Scholar]
  43. Venna J. and Kaski S., ESANN'2006 proceedings – European Symposium on Artificial Neural Networks, Bruges, Belgium, 26–28 April 2006. [Google Scholar]
  44. Hinton G. E., Salakhutdinov R. R. Science. 2006;313:504–507. doi: 10.1126/science.1127647. [DOI] [PubMed] [Google Scholar]
  45. van der Maaten L. Rev. Bras. Med. 2009;500:500. [Google Scholar]
  46. van den Berg R. A., Hoefsloot H. C., Westerhuis J. A., Smilde A. K., van der Werf M. J. BMC Genomics. 2006;7:142. doi: 10.1186/1471-2164-7-142. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Pedregosa F., Varoquaux G., Gramfort A., Michel V., Thirion B., Grisel O., Blondel M., Prettenhofer P., Weiss R., Dubourg V. J. Mach. Learn. Res. 2011;12:2825–2830. [Google Scholar]
  48. Morris J. H., Apeltsin L., Newman A. M., Baumbach J., Wittkop T., Su G., Bader G. D., Ferrin T. E. BMC Bioinf. 2011;12:1. doi: 10.1186/1471-2105-12-436. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Shannon P., Markiel A., Ozier O., Baliga N. S., Wang J. T., Ramage D., Amin N., Schwikowski B., Ideker T. Genome Res. 2003;13:2498–2504. doi: 10.1101/gr.1239303. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Fahy E., Sud M., Cotter D., Subramaniam S. Nucleic Acids Res. 2007;35:W606–W612. doi: 10.1093/nar/gkm324. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Chan E. C. Y., Koh P. K., Mal M., Cheah P. Y., Eu K. W., Backshall A., Cavill R., Nicholson J. K., Keun H. C. J. Proteome Res. 2009;8:352–361. doi: 10.1021/pr8006232. [DOI] [PubMed] [Google Scholar]
  52. Dobrzyńska I., Szachowicz-Petelska B., Sulkowski S., Figaszewski Z. Mol. Cell. Biochem. 2005;276:113–119. doi: 10.1007/s11010-005-3557-3. [DOI] [PubMed] [Google Scholar]
  53. Mandal M. K., Saha S., Yoshimura K., Shida Y., Takeda S., Nonami H., Hiraoka K. Analyst. 2013;138:1682–1688. doi: 10.1039/c3an36554a. [DOI] [PubMed] [Google Scholar]
  54. Morad S. A. F., Cabot M. C. Nat. Rev. Cancer. 2013;13:51–65. doi: 10.1038/nrc3398. [DOI] [PubMed] [Google Scholar]
  55. Koshiji M., Adachi Y., Sogo S., Taketani S., Oyaizu N., Than S., Inaba M., Phawa S., Hioki K., Ikehara S. Clin. Exp. Immunol. 1998;111:211–218. doi: 10.1046/j.1365-2249.1998.00460.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Chaurio R., Janko C., Muñoz L., Frey B., Herrmann M., Gaipl U. Molecules. 2009;14:4892. doi: 10.3390/molecules14124892. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Birge R. B., Boeltz S., Kumar S., Carlson J., Wanderley J., Calianese D., Barcinski M., Brekken R. A., Huang X., Hutchins J. T., Freimark B., Empig C., Mercer J., Schroit A. J., Schett G., Herrmann M. Cell Death Differ. 2016;23:962–978. doi: 10.1038/cdd.2016.11. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Guyon I., Von Luxburg U. and Williamson R. C., NIPS 2009 workshop on clustering theory, 2009. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Click here for additional data file. (3.7MB, pdf)
Click here for additional data file. (9.4MB, wmv)
Click here for additional data file. (67.8KB, pdf)

Articles from Chemical Science are provided here courtesy of Royal Society of Chemistry

RESOURCES