Bivariate Analysis of Age-Related Macular Degeneration Progression Using Genetic Risk Scores

Ding et al. used data from large clinical trials to evaluate the effects of known age-related macular generation (AMD) risk variants on disease progression...

Abstract

Age-related macular degeneration (AMD) is a leading cause of blindness in the developed world. While many AMD susceptibility variants have been identified, their influence on AMD progression has not been elucidated. Using data from two large clinical trials, Age-Related Eye Disease Study (AREDS) and AREDS2, we evaluated the effects of 34 known risk variants on disease progression. In doing so, we calculated the eye-level time-to-late AMD and modeled them using a bivariate survival analysis approach, appropriately accounting for between-eye correlation. We then derived a genetic risk score (GRS) based on these 34 risk variants, and analyzed its effect on AMD progression. Finally, we used the AREDS data to fit prediction models of progression based on demographic and environmental factors, eye-level AMD severity scores and the GRS and tested the models using the AREDS2 cohort. We observed that GRS was significantly associated with AMD progression in both cohorts, with a stronger effect in AREDS than in AREDS2 (AREDS: hazard ratio (HR) = 1.34, P = 1.6 × 10⁻²²; AREDS2: HR = 1.11, P = 2.1 × 10⁻⁴). For prediction of AMD progression, addition of GRS to the demographic/environmental risk factors considerably improved the prediction performance. However, when the baseline eye-level severity scores were included as the predictors, any other risk factors including the GRS only provided small additional predictive power. Our model for predicting the disease progression risk demonstrated satisfactory performance in both cohorts, and we recommend its use with baseline AMD severity scores plus baseline age, education level, and smoking status, either with or without GRS.

AGE-RELATED macular degeneration (AMD) is a common, polygenic, and progressive neurodegenerative disease, which is a leading cause of blindness in the elderly population of developed countries (Congdon et al. 2004; Swaroop et al. 2009). Both common and rare genetic variants associated with AMD risk have been identified in multiple large-scale case–control association studies (Fritsche et al. 2013). In a recent report by The International AMD Genomics Consortium, a total of 34 loci with 52 independent common and rare variants (either from the exome chip or imputed) were discovered or confirmed to have an association with AMD risk (Fritsche et al. 2016).

Some patients with AMD maintain good vision for a long time with little disease progression over time, while others quickly advance to vision-threatening late AMD. Patients can progress to one or both forms of late AMD – central geographic atrophy (GA) and choroidal neovascularization (CNV). Despite remarkable successes in discovering genetic variants associated with AMD risk, the genetic underpinnings of AMD progression have not been well studied. The Age-Related Eye Disease Study (AREDS) was designed to assess risk factors for the development and progression of AMD and to assess the role of micronutrients in delaying the progression to late AMD (Age-Related Eye Disease Study Research 1999). A subsequent randomized clinical trial of additional oral supplements, AREDS2, evaluated progression to late AMD in a cohort of patients who were at higher risk of progression to late AMD (Group et al. 2012; Age-Related Eye Disease Study 2 Research 2013). Both studies collected DNA samples of consenting participants and performed genome-wide genotyping (Fritsche et al. 2016). More recently, other researchers have studied the effects of AMD risk variants on progression using the AREDS data (Seddon et al. 2009, 2011; Farwick et al. 2010; Klein et al. 2011), suggesting that some, but not all, of the known AMD risk variants/loci can influence AMD progression.

Previous studies typically analyzed only one eye per subject for AMD progression, where only the progression time of the faster-progressed eye was analyzed (Seddon et al. 2011; Perlee et al. 2013). Other studies analyzed the progression status of eyes as noted at the final study visit (e.g., no progression, early progression, or late progression) instead of their progression time (Farwick et al. 2010). For the participants who had two eyes free of late AMD at baseline, the progression statuses for both eyes were analyzed accounting for the dependence between eyes. In this setting the progression time was not evaluated due to the short follow-up of their study. Recently, Sardell et al. (2016) analyzed the effects of seven SNPs from four known AMD risk genes on AMD progression (from intermediate AMD to CNV or GA), where they analyzed both eyes using a Cox model that accounted for between-eye correlation.

In this study, we analyzed AMD progression using all eyes that were not in the late AMD stage at baseline. Specifically, we calculated their time-to-progression to late AMD and analyzed them using Cox models that take into account the between-eye correlation, which is similar to the analysis model used in Sardell et al. (2016). In addition to evaluating the effect of each known AMD risk variant on the disease progression, we studied the impact of the AMD genetic risk score (GRS), developed based on a combination of all known 34 AMD risk variants (Fritsche et al. 2016). We performed the analyses in each study cohort separately and compared the results. To explain the differences in the findings from the two studies, we performed additional subgroup analyses. Moreover, we established prediction models based on demographic/environmental factors, baseline eye-level AMD severity scores, and the GRS and used these models to predict the risk of progression to late AMD. The prediction models were established using the AREDS data and validated on the AREDS2 data.

Materials and Methods

Study population and progression data

The main study population consisted of AREDS participants while the AREDS2 cohort was used as an independent validation dataset. AREDS was a multicenter, controlled, randomized clinical trial of AMD and age-related cataract sponsored by the National Eye Institute (Age-Related Eye Disease Study Research 1999). It was designed to assess the clinical course of, and risk factors for, the development and progression of AMD and cataract, and to evaluate the effects of oral supplementation with antioxidant vitamins and minerals on AMD progression and visual acuity. AREDS2 was another large multicenter randomized clinical trial of AMD and age-related cataracts, conducted after AREDS (Group et al. 2012). AREDS2 was designed to evaluate the effect of the refined AREDS formulation on progression to late AMD or cataract. Participants of AREDS2 were selected to have more severe disease at baseline as compared to AREDS and the follow-up time was only about half of that in AREDS. We confined our analyses to the AMD data for this report. Caucasian participants (validated with principal component analysis) with genotype data and at least one follow-up visit were deemed “eligible” for our analysis.

For each eligible participant, the outcome for eye(s) that did not have late AMD at baseline was included in the analysis to study the time-to-late AMD. The detailed AREDS AMD scale (Davis et al. 2005), based upon severity score from 1 to 12, was used to determine whether the eye was in the late AMD stage or not. We define any eye that was not in late AMD at baseline to be a “study eye.” We use “fellow eye” to denote the other eye from the same subject of any given eye. So the two eyes from the same subject mutually serve as the fellow eye of each other. For each study eye, we calculated its time-to-progression, defined as the time from the baseline visit to the first visit when the severity score of the eye reached AREDS AMD scale 9 (noncentral GA) or higher (10: central GA, 11: CNV, and 12: CNV and central GA). If the eye’s severity score did not progress to scale 9 or higher by the end of follow-up, time to the development of late AMD was censored at the last visit.

Other variables we have considered in the progression analysis are: gender, baseline age, education level (≤high school, >high school), baseline smoking status (never, former, current), and treatment group [AREDS: placebo, antioxidants alone, zinc, antioxidants plus zinc; AREDS2: placebo, lutein plus zeaxanthin (L+Z), ω-3 long-chain polyunsaturated fatty acid (LCPUFA), combination of L+Z and LCPUFA]. Body mass index was not included since these data were not collected for AREDS2.

Genotype data

DNA samples from consenting participants in AREDS and AREDS2 were collected and genotyped centrally, as described previously (Fritsche et al. 2016). The risk variants at 34 loci, either confirmed or newly discovered (Fritsche et al. 2016), were analyzed for AMD progression here. We computed a weighted risk score of these 34 variants, with weights determined by their estimated effect size (Fritsche et al. 2016). For each participant, $GRS={\displaystyle {\sum }_{i=1}^{34}\left({\beta }_i{G}_i\right)}/{\displaystyle {\sum }_{i=1}^{34}{\beta }_i},$where β_i is the log(odds ratio) of the risk variant i as provided in Table 1 of Fritsche et al. (2016) and G_i is the corresponding genotype (coded as 0: no risk allele; 1: one copy of risk allele; 2: two copies of risk allele). Note that in this coding all β_i are positive and GRS ranges from 0 to 2.

Statistical analysis of the genetic effects on progression

We analyzed the genetic effects on AMD progression as follows. The time (from baseline) to late AMD was modeled for all study eyes through a multivariable Cox proportional hazards model while using a robust sandwich variance–covariance estimator to account for the intrasubject correlation (which we will refer to as a “robust Cox” model) (Lee et al. 1992). Hence, the individuals with two eyes free of late AMD at baseline contributed two study eyes as a pair (denoted as the “bivariate” outcome). In addition to our primary predictor, i.e., a single genetic variant (treated as a continuous variable with 0, 1, 2 coding) or the GRS, the analysis was controlled for other baseline risk factors. Selection of baseline covariates for inclusion in the multivariable robust Cox model was guided by the results of univariable robust Cox models for each of these covariates, where the variables with univariable P-values < 0.1 were considered for inclusion. The multivariable robust Cox model is formulated as:

$${\lambda }_{ij}\left(t|X_i,Z_{ij}\right)={\lambda }_0\left(t\right)\exp \left\{X_i\alpha +Z_{ij}\beta \right\},$$ (1)

where ${\lambda }_{ij}\left(t\right)$ is the hazard function for progression at time t for the jth eye (j = 1: left, 2: right) in the ith participant, $X_i$ stands for subject-level covariates (e.g., genetic variant or GRS) for the ith participant, and $Z_{ij}$ stands for the eye-level covariate(s) (e.g., baseline severity) for the jth eye in the ith participant. Note that we assume the baseline hazard function ${\lambda }_0\left(t\right)$ to be the same for left and right eyes. After fitting the multivariable analysis on the GRS, we plotted the Kaplan–Meier (KM) curves of progression within three GRS groups determined by genetic score quartiles (low: <25%, medium: 25–75%, high: >75%) with quartiles computed using all participants from AREDS and AREDS2 combined, to visually examine the difference in progression of these three groups.

In addition to examining the progression to any form of late AMD, we separately analyzed the effects of genetic variants on progression to GA and CNV through the same multivariable robust Cox model approach. The eyes progressed to both GA and CNV (coded as 12 in AMD severity score) contributed to both analyses.

Establishing prediction models for progression

To develop progression prediction models, we fitted models to predict eye-level progression risk using ocular, demographic, and genetic information. When predicting the progression risk for an eye (e.g., 5-year probability in progressing to late AMD), here in addition to using its own baseline AMD severity score, its fellow eye’s baseline severity score was also included as a predictor because the AMD severity status of the fellow eye is known to be an important associated factor (Chew et al. 2014). Note that this is different from the robust Cox models for analyzing the genetic effects in the section Statistical analysis of the genetic effects on progression where only the baseline severity score of the eye itself was included as a covariate. Such difference (in the choice of covariates/predictors) is driven by the different focuses of the two analyses. In the first set of analyses aimed at assessing the genetic effects on progression, the primary interest is to get an accurate estimate of the genetic effect and additionally including the baseline severity score from the fellow eye will bias (downward) the effect estimate of a genetic variant (or GRS). In the second set of analyses aimed at establishing prediction models, the estimation of each individual predictor’s effect was not our primary interest; rather we focused on the prediction accuracy of the models. Therefore, all possibly useful predictors were considered for predicting the progression.

We used the AREDS data to train the prediction model and then evaluated its accuracy both within the AREDS cohort (using fivefold cross-validation or bootstrap resampling) and independently in the AREDS2 cohort. We compared and assessed five different prediction models: (A) a model with only demographic and environmental predictors; (B) model A plus the GRS; (C) a model with only baseline AMD severity scores (from both the study eye and its fellow eye); (D) model A plus model C (demographic and environmental factors plus baseline AMD severity scores); and (E) model D plus the GRS.

For each prediction model, we calculated the year-specific (e.g., 10-year progression) Brier score (BrS) and the integrated Brier score (iBrS) (Graf et al. 1999; Gerds and Schumacher 2006). For a fixed time point t*, the BrS measures the mean square error of the prediction: $BrS\left(t*\right)=\left(1/n\right){\displaystyle \sum _{i=1}^n{\left(I\left(t_i>t*\right)-\widehat{\pi }\left(t*|x_i\right)\right)}^2},$ where $I\left(t_i>t*\right)$ is the true progression status at time t* for the ith observation with progression time $t_i,$ and $\widehat{\pi }\left(t*|x_i\right)$ is the predicted progression free probability for the ith observation at time $t*,$ given a prediction model with predictor(s) $x_i.$ When censoring exists (i.e., $t_i$ is not observable for some observations), the weighted version of BrS was proposed by Graf et al. (1999) and Gerds and Schumacher (2006):

$$Br{S}^c\left(t*\right)=\frac{1}{n}{\displaystyle \sum _{i=1}^n\left[{\left(0-\widehat{\pi }\left(t*|x_i\right)\right)}^{2}I\left(t_i\le t*,{\delta }_i=1\right)\frac{1}{\widehat{G}\left(t_i|x_i\right)}+{\left(1-\widehat{\pi }\left(t*|x_i\right)\right)}^{2}I\left(t_i>t*\right)\frac{1}{\widehat{G}\left(t*|x_i\right)}\right]},$$

where ${\delta }_i$ is the censoring indicator for the ith observation (0: censored, 1: progressed) and $\widehat{G}$ is the estimated cumulative distribution function for the censoring variable. Graf et al. (1999) also recommended using an integrated version of the BrS that incorporates quadratic loss averaged over time. The lower the Brier score the better the model predicts. Note that in our case the prediction was on the individual eye-level (instead of joint progression risk on both eyes), so each eye is treated as an observation.

In addition, we calculated the Harrell’s concordance index (c-index) for each prediction model (Harrell et al. 1996). This index calculates the proportion of all “usable” observation pairs in which the predictions and the observed outcomes are concordant. Here “usable” means the observation pairs’ true progression statuses can be ordered (two observations where both are censored, or one is censored and the other is progressed with the censoring time occurring before the progressed time, are not “usable” pairs). The larger the c-index value the better the model predicts.

Besides the BrS and c-index, we also calculated the year-specific AUC (area under the curve) of the Receiver Operator Characteristic (ROC) curves and the integrated AUC (iAUC) over a given time period as secondary metrics for model performance evaluation. The observations that were censored before the time of interest (for the progression prediction) were not used in the ROC curve and its AUC computation, because their true progression statuses were unknown for that time. Moreover, we generated the prediction calibration curves for each prediction model to evaluate the consistency of the predicted and observed progression risks (Pepe and Janes 2013). We also generated the predicted probability density plots for progressors and nonprogressors to visualize the prediction performance (Pepe 2011; Pepe et al. 2013). Finally, for the best prediction model(s), we calculated the sensitivity, specificity, positive prediction value (PPV), and negative prediction value (NPV) in predicting the progression risks. The cutoff value to discriminate the progressors and nonprogressors was determined by the optimal threshold from the ROC curve, where the optimal threshold was defined as the value under which the sensitivity (Sn) and the specificity (Sp) minimize the distance$d=\sqrt{{\left(1-Sn\right)}^2+{\left(1-Sp\right)}^2}.$

Data availability

All the phenotype data of AREDS participants required in this report were obtained from the publicly available website dbGap (accession: phs000001.v3.p1). The phenotype data of AREDS2 participants for this report will be made available to the public on dbGap. The genotype data of these 34 known AMD risk variants on both AREDS and AREDS2 participants are part of the genotype data from Fritsche et al. (2016), which are available from dbGap under accession phs001039.v1.p1.

Results

Descriptive statistics of the study population

The AREDS cohort included 2721 Caucasian participants who had at least one eye free of late AMD at baseline and at least one follow-up visit (Table 1). The mean age of these 2721 participants at baseline was 68.7 years (SD = 4.9), with range from 55.3 to 81.2 years. Fifty-six percent (n = 1527) were females. A vast majority (94%) had either never smoked (n = 1272, 47%) or were former smokers (n = 1288, 47%), and only 6% (n = 161) were current smokers. The mean follow-up time was 10.3 years (SD = 1.7) with the follow-up frequency being every 6 months (in the first 6 years) to 1 year (after year 6). The majority of participants received education higher than high school (67%). In this AREDS cohort, 5017 eyes which were not in the late AMD stage at baseline were analyzed for progression. The mean AMD severity score at baseline was 3.0 (SD = 2.3). The baseline severity score (for eyes that were late AMD free at baseline) was further grouped into three categories: 1–3, 4–6, and 7–8, which represented low, middle, and high severity level. A majority of 5017 eyes from AREDS had low to middle AMD severity scores at baseline (62% with severity score 1–3 and 26% with severity score 4–6). Of the AREDS participants with available DNA, 842 (31%) received placebo, 850 (31%) received antioxidants alone, 507 (19%) received zinc alone, and 522 (19%) received antioxidants plus zinc. Note that more participants received formulations of placebo or antioxidants alone, since the participants with less severe AMD at baseline were only randomized to placebo or antioxidants alone (with equal likelihood) but not to the formulations with the additional dose of zinc (Age-Related Eye Disease Study Research 1999). In comparison, the AREDS2 cohort contained 1700 eligible participants. On average, their median age was 4.5 years older than the AREDS cohort (P = 8.0 × 10⁻⁴³, distribution plot was shown in Supplemental Material, Figure S1 in File S1). The gender and smoking distribution in the AREDS2 participants was not significantly different from that of the AREDS participants (both P > 0.05). The education distributions were statistically different between two cohorts (P = 0.003) but the difference was small. One participant in AREDS and 28 (2%) in AREDS2 did not provide education information and were excluded from the multivariable analysis models where education level was included as a covariate. Note that the mean follow-up time was much shorter in AREDS2 (4.8 years; SD = 0.5) with the frequency of annual follow-up. The 2830 eyes from these AREDS2 participants were late AMD free at baseline and were included in the analysis. On average, the AREDS2 eyes were much more severe than AREDS eyes at baseline (with very small P-values for comparing severity scores either continuously or by categories in Table 1). Almost all eyes in AREDS2 were scored >3 (43% in 4–6 and 53% in 7–8). For AREDS2 participants, 409 (24%) received placebo, 418 (25%) received L+Z, 451 (27%) received LCPUFA, and 422 (25%) received the combination of L+Z and LCPUFA. All AREDS2 participants also received a form of the AREDS supplements in addition to L + Z and/or LCPUFA.

Table 1. Baseline characteristics of the AREDS and AREDS2 cohorts.

	AREDS	AREDS2	P Valuea
Subject-level variables
Number of subjects	N = 2721	N = 1700
Age
Mean (SD)	68.7 (4.9)	71.5 (7.7)	8.0 × 10−43
Median (range)	68.5 (55.3–81.2)	73 (50–86)
Sex (n, %)
Female	1527 (56)	997 (59)	0.11
Male	1194 (44)	703 (41)
Education
≤High school	906 (33)	485 (29)	3.0 × 10−3
>High school	1814 (67)	1189 (70)
Missing	1 (0)	28 (2)
Smoking (n, %)
Never smoked	1272 (47)	739 (43)	0.08
Former smoker	1288 (47)	863 (51)
Current smoker	161 (6)	98 (6)
Treatment	Placebo: 842 (31)	Placebo: 409 (24)
	Antioxidants alone: 850 (31)	L+Z: 418 (25)
	Zinc: 507 (19)	LCPUFA: 451 (27)
	Antioxidants+Zinc: 522 (19)	L+Z plus LCPUFA: 422 (25)
Genetic risk score (GRS)
Mean (SD)	1.00 (0.14)	1.08 (0.13)	8.1 × 10−67
Median (range)	1.01 (0.61–1.45)	1.08 (0.58–1.42)
Follow-up time
Mean (SD)	10.3 (1.7)	4.8 (0.5)
Median (range)	10.9 (1.8–12.6)	4.9 (2.1–5.9)
Eye-level variables
Number of eyes	N = 5017	N = 2830
Baseline AREDS AMD severity score
Mean (SD)	3.0 (2.3)	6.3 (1.3)	<1.0 × 10−300
Median (range)	2 (1–8)	7 (1–8)	<1.0 × 10−300
1–3 (n, %)	3125 (62)	119 (4)	<1.0 × 10−300
4–6 (n, %)	1293 (26)	1211 (43)
7–8 (n, %)	599 (12)	1500 (53)

^aP-values were from two-sided t-test for continuous variables, and were from chi-square test for categorical variables. Wilcoxon rank-sum test was applied to test the median of the eye-level baseline severity score.

We further examined the GRS distributions in both studies. On average, the AREDS2 participants had greater GRSs than the AREDS participants (both mean and median = 1.0 in AREDS vs. 1.1 in AREDS2) with a significant P = 8.1 × 10⁻⁶⁷. GRS distribution in AREDS2 was to the right of the AREDS distribution (Figure S2 in File S1), indicating more AMD risk alleles on average in AREDS2 participants.

From the descriptive analysis (Table 1), the two studies appeared very different in several aspects. Not only were the treatment formulations distinct, but the population characteristics (e.g., participants’ age and AMD severity score at baseline) and the follow-up length and frequency were also different.

Genetic effects on progression to late AMD

We calculated the progression rate (through the entire follow-up time) for all study eyes (eyes that were free of late AMD at baseline in AREDS and AREDS2), categorized by their own and fellow eyes’ baseline severity level. As shown in Table 2, within each data cohort, the study eye progression rate increases with its increasing severity at baseline (AREDS: 3% for severity 1–3, 40% for severity 4–6, and 81% for severity 7–8; AREDS2: 9% for severity 1–3, 19% for severity 4–6, and 50% for severity 7–8). In addition, within each study eye baseline severity category, the progression rate increases as the fellow eye’s baseline severity increases. This holds for all three study eye baseline severity groups (except for the “1–3” group in AREDS2, possibly due to the very small sample size in that group). For example, in AREDS, for the eyes with baseline severity scores in 1–3, the progression rate increases from 2 to 7, 13 and 20% as their fellow eyes’ baseline severity increases from 1–3 to 4–6, 7–8, and 9+, respectively. Thus, an eye’s progression strongly depends on both its own baseline severity and its fellow eye’s baseline severity.

Table 2. Progression counts and rates (from baseline up to the end of follow-up time) by baseline (BL) AMD severity score.

Study eye’s own BL severity score	Fellow eye's BL severity score	AREDS		AREDS2
		N total	N progressed (%)	N total	N progressed (%)
1–3	1–3	2683	61 (2)	36	4 (1)
	4–6	311	23 (7)	49	0 (0)
	7–8	15	2 (13)	4	0 (0)
	9+	116	23 (20)	30	7 (23)
	Any	3123	109 (3)	119	11 (9)
4–6	1–3	311	52 (17)	49	4 (8)
	4–6	684	258 (38)	684	82 (12)
	7–8	142	84 (59)	259	48 (19)
	9+	156	117 (75)	219	91 (42)
	Any	1292	511 (40)	1211	225 (19)
7–8	1–3	15	6 (40)	4	1 (25)
	4–6	142	96 (69)	259	95 (37)
	7–8	290	246 (85)	914	432 (47)
	9+	152	137 (90)	323	229 (71)
	Any	599	485 (81)	1500	757 (50)
Overall		5017	1105 (22)	2830	993 (35)

For AREDS, the follow-up length was up to 12.6 yr with mean follow-up of 10.3 yr; for AREDS2, the follow-up length was up to 5.9 yr with mean follow-up of 4.8 yr.

When the univariable robust Cox modeling was carried out (Table 3), increased baseline age was highly significantly associated with increased progression but gender was not significantly associated with progression. Education was significant in both cohorts with higher education associated with slower progression. Smoking was significant in AREDS, where current smoker or former smoker status was associated with faster progression as compared to never smoker. In AREDS, we performed an “adjusted” univariable analysis for the treatment variable where the baseline AMD severity score of the study eye was included as a covariate in addition to the treatment. This was done because the stratified randomization scheme made the baseline severity of the eyes not balanced across the four treatment groups, as we noted in the “descriptive statistics of the study population” result section. In AREDS2, the standard univariable analysis was done for the treatment variable as there was no such issue. Different treatment groups were not associated with different hazard rates of AMD progression, in either AREDS or AREDS2 (all P > 0.05). The baseline AMD severity score of the study eye was strongly associated with progression in both datasets. The GRS was also found to be significantly associated with progression. However, the significance level was much stronger in AREDS (HR = 1.85, 95% CI: 1.75–1.96, P = 7.1 × 10⁻⁹⁹) than in AREDS2 (HR = 1.14, 95% CI: 1.08–1.21, P = 2.6 × 10⁻⁶).

Table 3. Univariable robust Cox model result on progression to late AMD.

	AREDS		AREDS2
	HR (95% CI)	P Value	HR (95% CI)	P Value
Variable
Baseline age (yr)	1.09 (1.07, 1.10)	2.8 × 10−23	1.06 (1.05, 1.07)	6.6 × 10−29
Sex
Female	Reference		Reference
Male	0.91 (0.78, 1.05)	0.20	0.91 (0.79, 1.06)	0.22
Education
≤High school	Reference		Reference
>High school	0.67 (0.58, 0.78)	2.5 × 10−7	0.78 (0.66, 0.91)	1.8 × 10−3
Baseline smoking
Never	Reference		Reference
Former	1.32 (1.14, 1.54)	3.2 × 10−4	1.21 (1.04, 1.40)	0.01
Current	2.20 (1.65, 2.92)	6.3 × 10−8	1.15 (0.84, 1.57)	0.40
Treatmenta
	Placebo: reference		Placebo: reference
	Antioxidants alone:	0.73	L+Z:	0.52
	0.96 (0.79, 1.19)		0.94 (0.76, 1.15)
	Zinc:	0.07	LCPUFA:	0.56
	1.20 (0.98, 1.48)		1.06 (0.87, 1.30)
	Antioxidants plus zinc:	0.40	L+Z plus LCPUFA:	0.21
	1.09 (0.89, 1.34)		1.14 (0.93,1.40)
Baseline study eye severity score	1.96 (1,89, 2.03)	<1.0 × 10−300	1.89 (1.74, 2.06)	1.0 × 10−47
GRSb	1.85 (1.75, 1.96)	7.1 × 10−99	1.14 (1.08, 1.21)	2.6 × 10−6

^aIn AREDS, in addition to the treatment variable itself, the baseline AMD severity score of the study eye was also included to adjust for the unbalanced disease severity level across treatment groups due to the randomization scheme.

^bFor 0.1 unit increase in GRS.

In the multivariable modeling of progression, based on the univariable results above, baseline age, education level, smoking status, and AMD severity score (of the study eye) were selected as covariates. The corresponding statistical formulation of the multivariable model is given in Equation (2), where ${\lambda }_{ij}\left(t\right)$ stands for the hazard function of progression time for the jth eye in the ith participant, $G{N}_i$ is the genetic variant or GRS of the ith participant, $S{S}_{ij}$ is the baseline severity score for the jth eye in the ith participant, and $A{G}_i$ is the baseline age, ED_i is the education level and $S{M}_i$ is the baseline smoking status of the ith participant. Note that only the severity score is an eye-level variable, while all other variables are participant-level variables.

$$\begin{array}{l}{\lambda }_{ij}\left(t|G{N}_i,S{S}_{ij},A{G}_i,E{D}_i,S{M}_i\right)={\lambda }_0\left(t\right)\exp \{{\beta }_{1}G{N}_i+{\beta }_{2}S{S}_{ij}+{\beta }_{3}A{G}_i\\ +{\beta }_{4}I\left(E{D}_i>HighSchool\right)+{\beta }_5\mathrm{I}\left(S{M}_i=Former\right)+{\beta }_6\mathrm{I}\left(S{M}_i=Current\right)\}\end{array}$$ (2)

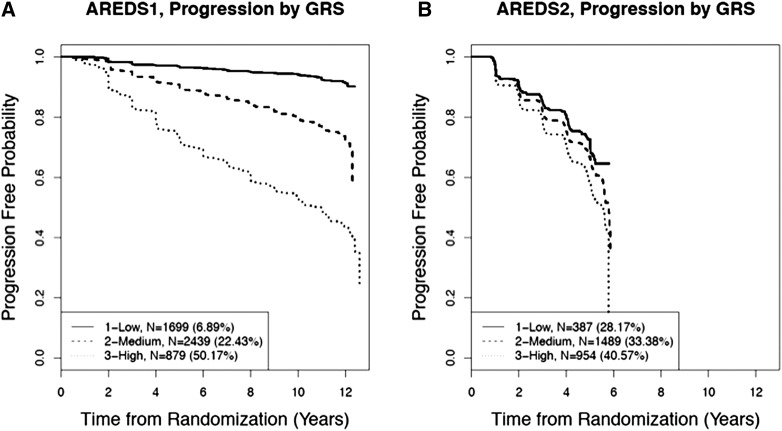
The KM plot (Figure 1) shows a clear separation in the progression profiles for the three GRS groups, especially in AREDS, where the eyes with higher GRSs had faster progression. In AREDS, the progression rates over the entire follow-up time of 12 years increased from 6.9 to 22.4 and 50.2% as the GRSs increased from low to medium and high, respectively. The separation was less obvious in AREDS2, where the progression rates over the shorter entire follow-up time of 6 years were 28.2, 33.4, and 40.6%, respectively.

Figure 1.

KM plots on progression to advanced AMD by GRS groups. (A) AREDS, (B) AREDS2. Eyes were categorized into three groups according to their GRSs: low: 0–25% quartile; medium: 25–75% quartile; high: >75% quartile.

Table 4 presents the multivariable robust Cox model results for AREDS and AREDS2 in the lead variants for the reported 34 AMD-associated loci (Fritsche et al. 2016). In AREDS, 15 variants were associated with progression with P < 0.05 while only eight variants exhibited P < 0.05 in AREDS2. Overall, AREDS2 showed lower significance levels as compared to AREDS. The most significant variant was consistent for AREDS and AREDS2 (rs3750846, locus ARMS2/HTRA1) with an estimated HR = 1.44 and P = 1.3 × 10⁻¹¹ in AREDS and an estimated HR = 1.22 and P = 5.9 × 10⁻⁵ in AREDS2. The second most significant variant in AREDS was in CFH (rs10922109, P = 7.2 × 10⁻⁹) but it was not significant in AREDS2 (P = 0.19). This is perhaps surprising and merits further detailed examination of other variants in the CFH locus. In addition to these two variants, rs10781182 (locus MIR6130/RORB) and rs142450006 (locus MMP9) also showed consistent significant association with AMD progression in the two studies (all P < 0.05).

Table 4. Multivariable robust Cox model results for the 34 top AMD risk variants on progression to late AMD.

Variant	Chr	Major/minor allele	locus namea	Effect on progression (AREDS)		Effect on progression (AREDS2)
				HR	P Value	HR	P Value
rs10922109	1	C/A	CFH	0.69	7.2 × 10−9	1.09	0.19
rs11884770	2	C/T	COL4A3	1.02	0.69	0.86	1.2 × 10−2
rs62247658	3	T/C	ADAMTS9-AS2	1.09	9.9 × 10−2	0.88	9.5 × 10−3
rs140647181	3	T/C	COL8A1	1.64	4.8 × 10−2	0.98	0.91
rs10033900	4	C/T	CFI	0.98	0.67	0.93	0.13
rs62358361	5	G/T	C9	1.06	0.82	0.67	5.4 × 10−2
rs114092250	5	G/A	PRLR/SPEF2	0.61	1.4 × 10−2	0.95	0.80
rs116503776	6	G/A	C2/CFB/SKIV2L	0.75	1.6 × 10−3	0.95	0.61
rs943080	6	T/C	VEGFA	0.94	0.20	0.96	0.37
rs7803454	7	C/T	PILRB/PILRA	1.00	0.99	1.21	2.5 × 10−3
rs1142	7	C/T	KMT2E/SRPK2	1.01	0.83	1.05	0.36
rs79037040	8	T/G	TNFRSF10A	0.95	0.28	0.96	0.42
rs71507014	9	GC/G	TRPM3	0.99	0.86	0.90	2.8 × 10−2
rs10781182	9	G/T	MIR6130/RORB	0.88	2.0 × 10−2	0.90	3.6 × 10−2
rs1626340	9	G/A	TGFBR1	0.92	0.24	0.94	0.32
rs2740488	9	A/C	ABCA1	0.99	0.81	1.04	0.52
rs12357257	10	G/A	ARHGAP21	1.07	0.26	1.10	0.11
rs3750846	10	T/C	ARMS2/HTRA1	1.44	1.3 × 10−11	1.22	5.9 × 10−5
rs3138141	12	C/A	RDH5/CD63	1.18	4.4 × 10−2	0.96	0.58
rs61941274	12	G/A	ACAD10	1.14	0.50	1.00	0.98
rs9564692	13	C/T	B3GALTL	0.83	1.6 × 10−3	0.94	0.24
rs61985136	14	T/C	RAD51B	1.17	6.6 × 10−3	0.98	0.76
rs2043085	15	T/C	LIPC	1.14	1.2 × 10−2	0.99	0.88
rs5817082	16	C/CA	CETP	0.90	6.8 × 10−2	1.08	0.22
rs72802342	16	C/A	CTRB2/CTRB1	0.79	6.3 × 10−2	0.89	0.32
rs11080055	17	C/A	TMEM97/VTN	1.11	3.3 × 10−2	1.08	0.13
rs6565597	17	C/T	NPLOC4/TSPAN10	1.04	0.48	1.01	0.79
rs67538026	19	C/T	CNN2	0.89	3.2 × 10−2	0.90	9.4 × 10−2
rs2230199	19	C/G	C3	0.86	1.6 × 10−2	0.97	0.64
rs429358	19	T/C	APOE	0.95	0.56	1.03	0.73
rs142450006	20	TTTTC/T	MMP9	0.76	1.7 × 10−3	0.76	8.9 × 10−4
rs201459901	20	T/TA	C20orf85	1.05	0.61	0.90	0.38
rs5754227	22	T/C	SYN3/TIMP3	0.90	0.19	0.75	3.3 × 10−4
rs8135665	22	C/T	SLC16A8	0.99	0.86	1.02	0.79

Model was adjusted for baseline age, education, smoking status, and study eye’s baseline AMD severity score.

^aThe locus name is a label of the region using the nearest gene(s), but does not necessarily state the responsible gene.

When progression to CNV or GA was analyzed separately, we observed that 508 eyes developed CNV, 615 eyes developed GA, and 18 eyes developed both CNV and central GA in AREDS; and 457 eyes developed CNV, 536 eyes developed GA, and no eye developed both CNV and central GA in AREDS2. When the genetic effects on progression to CNV or GA were estimated separately, the results were consistent with the combined progression analysis (CNV+GA) for the majority of the variants (Tables S1 and S2 in File S1). Overall, the variants showed higher significance in progression to CNV as compared to GA. There are some exceptions. For example, rs6565597 (locus CNN2) showed consistent significance in progression to GA (P < 0.05 in both cohorts), but was not significant in progression to CNV in either of the two cohorts.

The GRS was significantly associated with AMD progression in both AREDS and AREDS2 using the multivariable robust Cox model (Table 5). However, the significance level was much stronger in AREDS (HR = 1.34, P = 1.6 × 10⁻²²) than in AREDS2 (HR = 1.11, P = 2.1 × 10⁻⁴). This was consistent with the univariable analysis and was expected given the single variant analysis results in Table 4. Nevertheless, this analysis demonstrated that the GRS was significantly associated with AMD progression in two independent cohorts. According to the Wald test results that compared each model coefficient estimate between AREDS and AREDS2 (the last column in Table 5), all the covariates showed consistent effect sizes on progression in both cohorts except for the GRS and current smoker category in the smoking status covariate.

Table 5. Multivariable robust Cox model result on progression to advanced AMD.

	AREDS		AREDS2		Test for differencea
	HR (95% CI)	P Value	HR (95% CI)	P Value	P Value
Variable
Age (yr)	1.05 (1.03, 1.06)	6.4 × 10−10	1.06 (1.05, 1.07)	2.8 × 10−28	0.14
Smoking
Never	Reference		Reference
Former	1.14 (0.98, 1.33)	0.06	1.18 (1.02, 1.37)	0.03	0.75
Current	1.98 (1.51, 2.58)	5.7 × 10−7	1.30 (0.92, 1.81)	0.13	0.05
Education
≤High school	Reference		Reference
>High school	0.87 (0.75, 1.01)	0.06	0.92 (0.78, 1.07)	0.27	0.65
Baseline study eye AMD severity score	1.85 (1.78, 1.92)	4.3 × 10−226	1.90 (1.74, 2.07)	8.7 × 10−48	0.61
GRSb	1.34 (1.26, 1.42)	1.6 × 10−22	1.11 (1.05, 1.18)	2.1 × 10−4	1.0 × 10−5

^aFor each model coefficient estimate [i.e., log(HR)], a Wald test was performed to test whether the coefficient estimates differ between AREDS and AREDS2.

^bFor 0.1 unit increase in GRS.

Prediction models for eye-level progression risk

We used the AREDS data to fit models for predicting progression risk for a given eye using both participant-level and eye-level predictors. We considered different sets of predictors when establishing the prediction models (Table 6). Each model was evaluated in both AREDS (in a resampling fashion) and AREDS2 (as an independent validation dataset). Table 7 presents the BrS for x-year prediction (x = 4 or 10 for AREDS and 4 for AREDS2) and the iBrS (from 0 up to 4 or 10 years) for each prediction model. The c-index values for each prediction model in AREDS (through 50 bootstrapped samples) and in AREDS2 are also presented in Table 7. With only baseline age, education level, and smoking status (model A), the model did not predict well (the c-indices were between 0.61 and 0.62), although the BrSs were small, especially in AREDS. Adding the GRS alone to the predictor list (model B) showed noticeable improvement in AREDS (BrS = 0.058 and 0.123 for 4- and 10-year, respectively; c-index = 0.75) but only small improvement in AREDS2. One reason for this observation could be the fact that the effects of GRS on progression were very different between AREDS and AREDS2, as we found in our multivariable analysis (Table 5). Then, using only baseline severity scores from both eyes (model C) produced obviously better prediction performance compared to models A and B. For example, the 4-year BrS values decreased from 0.058 (model B) to 0.047 (model C) for AREDS and decreased from 0.148 (model B) to 0.134 (model C) for AREDS2; and the c-index increased from 0.75 (model B) to 0.88 (model C) for AREDS, and from 0.63 (model B) to 0.71 (model C) for AREDS2. After including the two baseline severity scores for both the study eye and the fellow eye, adding the demographical/environmental predictors, namely, age, smoking, and education level (model D) or adding both demographical/environmental predictors and the GRS (model E) only improved the prediction by a small amount (0.01 or 0.02 unit increase in c-index values or 0.001–0.003 decrease in BrSs). The results indicate that the baseline disease severity scores from both eyes, developed by AREDS (Davis et al. 2005), are the strongest predictors for AMD progression of a given eye. The other risk factors only provided limited improvement on prediction after including these two in the model. This is not surprising, given progression is directly measured by the severity score.

Table 6. Predictors for each prediction model A–E.

Model index	Model predictors
A	Baseline Age + Education + Smoking
B	Baseline Age + Education + Smoking + GRS
C	Baseline Severity Score (own eye) + Baseline Severity Score (fellow eye)
D	Baseline Age + Education + Smoking + Baseline Severity Score (own eye) + Baseline Severity Score (fellow eye)
E	Baseline Age + Education + Smoking + Baseline Severity Score (own eye) + Baseline Severity Score (fellow eye) + GRS

Table 7. Harrell’s concordance index (c-index) and Brier scores (BrSs) for different prediction models evaluated in all eyes.

Modela	c-indexb	AREDS				AREDS2
		BrSc (4 yr)	BrS (10 yr)	iBrSd (up to 4 yr)	iBrS (up to 10 yr)	c-index	BrS (4 yr)	iBrS (up to 4 yr)
A	0.62	0.079	0.152	0.027	0.079	0.61	0.181	0.074
B	0.75	0.073	0.131	0.026	0.071	0.63	0.179	0.074
C	0.88	0.056	0.083	0.022	0.051	0.72	0.161	0.068
D	0.89	0.055	0.082	0.022	0.050	0.73	0.155	0.067
E	0.89	0.055	0.080	0.022	0.050	0.73	0.154	0.067

These prediction models were established using AREDS data and evaluated on both AREDS and AREDS2.

^aPredictors for each model are given in Table 6.

^bIn AREDS, the c-index values were computed based on bootstrapped samples (average over 50 times).

^cIn AREDS, the Brier scores were computed based on fivefold cross-validation.

^diBrS: integrated Brier score.

The AUCs for AREDS and AREDS2 were presented in Table S3 in File S1. The results showed consistent findings with the BrSs and c-index values (Table 7). Note that the eyes which were censored before year X were excluded from the AUC calculation as their true year X progression statuses were unknown. This in fact led to a biased sample pool for prediction evaluation. Whereas in the calculation of BrSs, the biased sample issue did not exist because an appropriate weighting strategy was implemented in calculating$Br{S}^c\left(t*\right)$ (Graf et al. 1999; Gerds and Schumacher 2006). Therefore, we view the AUC only as a secondary measure in prediction evaluation.

There were substantial performance differences in predicting progression risks in AREDS and AREDS2 (Table 7 and Table S3 in File S1). To explore this further, we made the two datasets more comparable in terms of disease severity by removing the least severe eyes, namely, the eyes with baseline severity scores between 1 and 3, from both datasets. Note that 62% of eyes from AREDS were removed, while only 4% of eyes from AREDS2 were removed. When the least severe eyes were removed, the BrSs for AREDS data clearly increased while the BrSs for AREDS2 did not change much, and the BrS values become much more similar between the two datasets (Table 8). Consistent findings were observed for the c-index values (Table 8) and AUC values (Table S4 in File S1). This is because the “least severe” eyes were mostly predicted to not be progressed, which was consistent with their actual progression statuses. Therefore, removing these easy-to-predict eyes leads to increased BrSs or decreased c-indices. The subgroup analysis presented in Table 8 reflects more realistic model performance in terms of predicting progression risks for eyes with intermediate or more severe AMD at baseline.

Table 8. Harrell’s concordance index (c-index) and Brier scores (BrSs) for different prediction models evaluated in eyes with baseline severity score >3.

		AREDS				AREDS2
Modela	c-indexb	BrSc (4 yr)	BrS (10 yr)	IBrSd (up to 4 yr)	IBrS (up to 10 yr)	c-index	BrS (4 yr)	IBrS (up to 4 yr)
A	0.56	0.170	0.238	0.062	0.152	0.61	0.186	0.076
B	0.63	0.164	0.219	0.061	0.144	0.62	0.184	0.076
C	0.73	0.136	0.178	0.054	0.118	0.71	0.165	0.070
D	0.74	0.134	0.174	0.053	0.117	0.72	0.160	0.069
E	0.75	0.134	0.171	0.053	0.115	0.73	0.159	0.069

^aPredictors for each model are given in Table 6.

^bIn AREDS, the c-index values were computed based on bootstrapped samples (average over 50 times).

^cIn AREDS, the Brier scores were computed based on fivefold cross-validation.

^diBrS: integrated Brier score.

For each prediction model, although its performance on the full AREDS data differed markedly from that on the subgroup AREDS data, we found that the covariate effects estimated from the full AREDS data (Table S3 in File S1) and those from the subgroup data (Table S4 in File S1) were very similar. This reassured us that the prediction models established from the full AREDS data were applicable to predict eyes with different severity levels, including the eyes with more severe AMD. We also specifically looked at the prediction for eyes with intermediate AMD, i.e., the eyes which scored between 4 and 8 and of which the participant had no late AMD in either eye at baseline. All the prediction models produced very similar results to those in Table 8 and Table S4 in File S1. This again is indicative of the performance robustness of the prediction models we established using the full AREDS data.

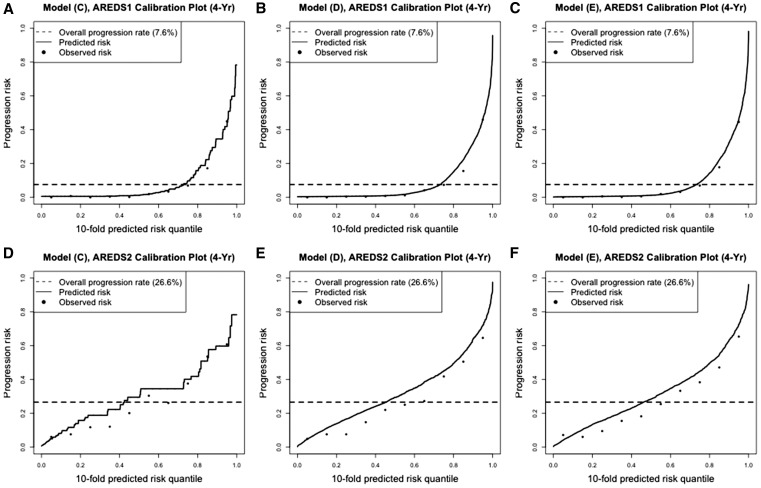
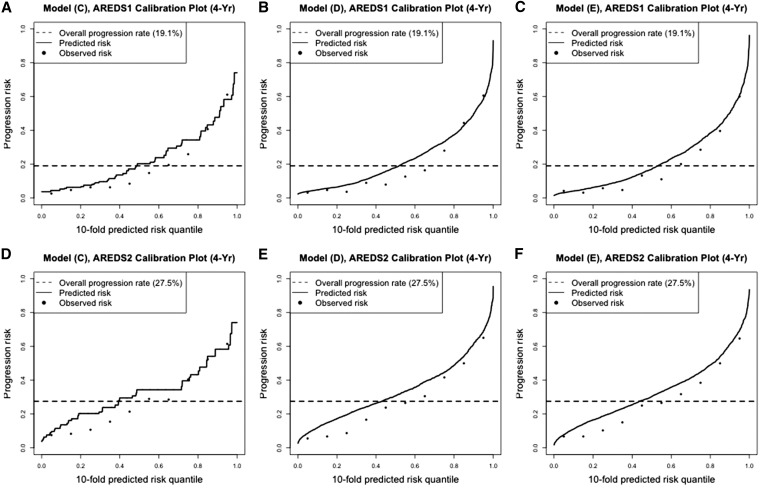
The calibration plots on prediction performance (Pepe 2011; Pepe and Janes 2013) are presented in Figure 2. Such plots allow us to examine the consistency between the predicted risks and the observed risks. For each model prediction, we ordered all evaluable eyes (e.g., eyes with progression statuses known by year X) by their predicted risk and divided them into 10 quantile groups. Within each quantile group, we calculated their mean observed risk. Figure 2 plots the 4-year observed and predicted risks over the risk quantiles, for model C, model D, and model E. For the top panel (corresponding to AREDS), the observed risks and predicted risks were very well matched in all three plots, where the match from models D and E were better. In Figure 2, B and C, the dashed line intersects with the black curve close to where the black curve drastically increases. This also indicates that model D and model E predicted very well since the perfect prediction will yield a smooth predicted curve that is horizontal at zero and then jumps to one at the quantile of (1−overall progression rate). Figure 2, D–F are the corresponding calibration plots when the prediction models were evaluated in AREDS2. In these three cases, the observed risks and predicted risks were less well matched overall. The predicted curves from model C were not smooth since only the baseline severity scores were used and their values were discrete. In the subgroup data where eyes with baseline severity 1–3 were removed, the calibration plots (Figure 3) show that the predicted risks and the observed risks were less well matched compared to those in Figure 2, for AREDS data, which were consistent with the findings from Table 8.

Figure 2.

Calibration plots for model predictions on full data. (A–C) prediction model C, model D, and model E evaluated on 4-year progression risk in AREDS, respectively; (D–F) prediction model C, model D, and model E evaluated on 4-year progression risk in AREDS2, respectively.

Figure 3.

Calibration plots for model predictions on subgroup data for eyes with baseline severity score >3. (A–C) prediction model C, model D, and model E evaluated on 4-year progression risk in AREDS, respectively; (D–F) prediction model C, model D, and model E evaluated on 4-year progression risk in AREDS2, respectively.

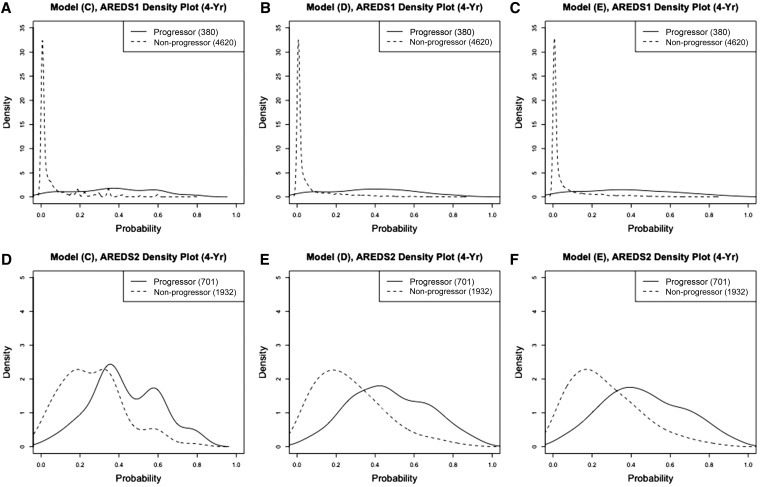
When we examine the density curves of the predicted progression risks separately by nonprogressors and progressors (Figure 4 and Figure 5), we observe that model D and E produced clear separation in predicting the 4-year progression risk in AREDS, especially in the full dataset. The separation was worse in AREDS2 in general, which was consistent with our findings in BrSs and the calibration plots. Similar to those in Figure 2 and Figure 3, model C produced unsmoothed density curves. Therefore, although the prediction performance of model C is close to model D and model E, we recommend using model D or E for predicting the progression risk, since model C is too parsimonious and can only provide a small set of all possible predicted values.

Figure 4.

Density curves of the predicted progression risks for progressors and nonprogressors from full data. (A–C) prediction model C, model D, and model E evaluated on 4-year progression risk in AREDS, respectively; (D–F) prediction model C, model D, and model E evaluated on 4-year progression risk in AREDS2, respectively.

Figure 5.

Density curves of the predicted progression risks for progressors and nonprogressors from subgroup data for eyes with baseline severity score >3. (A–C) prediction model C, model D, and model E evaluated on 4-year progression risk in AREDS, respectively; (D–F) prediction model C, model D, and model E evaluated on 4-year progression risk in AREDS2, respectively.

Finally, to examine the model prediction accuracy in practice, we calculated sensitivities, specificities, PPVs, and NPVs under model D and model E in predicting 4-year progression risks for different datasets. The cutoff value on predicted progression risks was determined by the optimal threshold from the corresponding 4-year ROC plot in the full AREDS data (Figure S6, A and B in File S1). The rationale is that the full AREDS data were used to develop the prediction models and thus they were used as well to decide the cutoff. For model D, the optimal cutoff probability was 0.113 (progression risk >0.113 was determined as progressed; ≤0.113 was determined as not progressed), and the corresponding sensitivity was 0.86 and 0.97 for AREDS and AREDS2, respectively, while the specificity was 0.82 and 0.19, respectively. The PPV was 0.28 and 0.30 for AREDS and AREDS2, respectively; and the NPV was 0.99 and 0.95, respectively. For model E, the optimal cutoff probability was 0.132, and the corresponding sensitivity was 0.84 and 0.95 for AREDS and AREDS2, respectively, while the specificity was 0.84 and 0.25 respectively. The PPV was 0.31 for both studies and the NPV was 0.98 and 0.93 for AREDS and AREDS2, respectively. The low specificity and PPV in AREDS2 was due to nonseparable predicted progression risk values between the true progressors and nonprogressors, as we observed in Figure 4D and Figure 5D. The PPV in AREDS was also low since the percentage of progressors in AREDS was small.

When comparing all five prediction models we have established, model D and model E were found to have a similar prediction performance and outperformed other prediction models. Although the GRS only provided minimal improvement to the prediction performance when added to a model containing the baseline severity scores of both the study and fellow eyes, it was still a significant predictor for AMD progression.

Discussion

We have applied a bivariate statistical approach to rigorously analyze the genetic effects on AMD progression. Our approach has multiple advantages as compared to those existing approaches described earlier. First, time-to-progression is more informative and reliable as compared to progression status, since the progression status may change if the follow-up time is extended. Instead of modeling the categorical progression status, our approach models continuous progression time to study the genetic effects on progression. Second, it is known that the presence and progression of AMD in one eye is strongly associated with the disease in its fellow eye (Barbeito and Herse 1991; Murdoch et al. 1998; Sunness et al. 1999; Pauleikhoff et al. 2002). Instead of only using the faster-progressed eye while ignoring the data from the other eye, our approach takes the advantage of all available data. We used the robust variance estimate in Cox models to appropriately account for the between-eye correlations when evaluating the genetic effects on AMD progression. Note that the traditional Cox model (assuming all the eyes are independent) will produce smaller P-values for the genetic effects, and therefore is inclined to identify false signals. In this study, it is important to use the robust variance estimates when making inferences about genetic effects because strong between-eye correlation was observed in progression.

Overall, we found the genetic effects on AMD progression were much stronger in AREDS than in AREDS2. We believe the major reasons contributing to this finding are: (1) the two study populations differ with regard to distributions of baseline age, baseline severity scores, and GRS; and (2) the study follow-up lengths and frequencies were different. We did a post hoc subgroup analysis where we used the following inclusion criteria to make the two populations similar: (1) participants aged between 55 and 80 years; (2) eyes with baseline severity score of 3 or greater; and (3) follow-up time of up to 6 years with annual frequency. Within this subgroup, the estimated effects of the GRS on AMD progression were much closer between the two cohorts (Table 9, P = 0.16) as compared to those from the original full data analysis (Table 5, P = 1.0 × 10⁻⁵). This supports our explanations for the large differences in the genetic effects we have found for AREDS and AREDS2. Nevertheless, the GRS was shown to be significant in both studies in the full datasets and in the subdatasets. Instead of using all of the top 34 variants from Fritsche et al. (2016) to derive the GRS, we also explored using only the top 5 genetic variants [with the smallest P-values from Table 1 in Fritsche et al. (2016)] to derive a GRS and reanalyzed the data. The results were quite consistent with those obtained using the GRS based on all 34 variants. This suggests that in practice, a GRS composed of a small number of top AMD risk variants can perform well enough in examining the genetic effects on AMD progression.

Table 9. Multivariable robust Cox model results on progression to late AMD using genetic risk score on subgroup data with (1) eyes of baseline severity score >3, (2) age between 65 and 80, and (3) follow-up time of up to 6 yr with annual examination.

	AREDS		AREDS2		Test for differencea
	HR (95% CI)	P Value	HR (95% CI)	P Value	P Value
Variable
Age (yr)	1.04 (1.01, 1.07)	6.7 × 10−3	1.07 (1.05, 1.10)	3.8 × 10−8	0.09
Smoking
Never	Reference		Reference
Former	1.05 (0.85, 1.30)	0.63	1.22 (1.02, 1.47)	0.03	0.28
Current	1.69 (1.17, 2.44)	4.8 × 10−3	1.00 (0.65, 1.52)	0.98	0.06
Education
≤High school	Reference		Reference
>High school	0.87 (0.71, 1.07)	0.18	0.99 (0.81, 1.20)	0.90	0.37
Baseline study eye AMD severity score	1.89 (1.73, 2.06)	7.9 × 10−47	1.97 (1.78, 2.19)	1.7 × 10−36	0.53
GRSb	1.25 (1.15, 1.36)	4.0 × 10−7	1.15 (1.07, 1.24)	2.4 × 10−4	0.16

^aFor each model coefficient estimate [i.e., log(HR)], a Wald test was performed to test whether the coefficient estimates differ between AREDS and AREDS2.

^bFor 0.1 unit increase in genetic risk score.

AREDS contains a large number of normal to early AMD eyes, which have a very small chance of progressing to late AMD. This fact contributes to the very low BrSs or high AUC values achieved from the prediction models. It is worthwhile to caution against the inappropriate interpretation that a low BrS or a high AUC value always indicates that the model predicts well. In the case where the event probability is very low or very high (i.e., the data are skewed in terms of event or nonevent), a low BrS or a high AUC may not necessarily indicate good model prediction, since in this case, even an extreme model that predicts no event (or all events) for all the observations will yield a low BrS and a high AUC.

There are previous studies which analyzed some known AMD risk variants on AMD progression using the AREDS data (Seddon et al. 2007, 2011, 2014). In all these studies, only one eye per participant was used and the analyses were limited to a small set of known AMD risk variants (two to nine). The same groups also established models to predict AMD progression using a set of (six or nine) known AMD risk variants (in addition to demographic, environmental, and ocular predictors) (Seddon et al. 2011, 2013, 2014). Compared with these existing studies, in addition to the differences in the statistical approaches, our model predictors are more parsimonious. For example, instead of using drusen size and/or drusen area, we directly used the composite AMD severity score (developed from AREDS), which was demonstrated to provide better prediction performance than a single ocular variable (detailed results not presented). Also instead of using a set of individual AMD risk variants, we used the composite GRS as a predictor. Another strength of our study is that we thoroughly evaluated our model prediction performance in a large independent AMD cohort (AREDS2) with appropriate additional subgroup analyses. We have discovered that the effect size of the genetic variants (or the GRS) could differ significantly between two study populations when the population characteristics were different. Nevertheless, of the aforementioned differences, we similarly found that variants on loci CFH, ARMS, C3, C2/CFB, COL8A1, and RAD51B have significant effects on AMD progression in the AREDS data, which have been reported previously (Seddon et al. 2007, 2011, 2013, 2014).

Finally, the current GRS is based on the variants and their effects from a case–control meta-analysis for AMD risk (Fritsche et al. 2016), which may not be optimal for AMD progression. In future, it could be useful to use a GRS based on a (potentially different) set of variants that are significantly associated with AMD progression. We are currently investigating this via a genome-wide association analysis of AMD progression using AREDS and AREDS2 data.

Supplementary Material

Supplemental material is available online at www.genetics.org/lookup/suppl/doi:10.1534/genetics.116.196998/-/DC1.