Nonlinear Viscoelasticity of Actin Transiently Cross-linked with Mutant α-Actinin-4

Abstract

Filamentous actin and associated actin binding proteins play an essential role in governing the mechanical properties of eukaryotic cells. They can also play a critical role in disease; for example, mutations in α-actinin-4 (Actn4), a dynamic actin cross-linking protein, cause proteinuric disease in humans and mice. Amino acid substitutions strongly affect the binding affinity and protein structure of Actn4. To study the physical impact of such substitutions on the underlying cytoskeletal network, we examine the bulk-mechanical behavior of in vitro actin networks cross-linked with wild type and mutant α-actinin-4. These networks exhibit a complex viscoelastic response and are characterized by fluid-like behavior at the longest time scales, a feature which can be quantitatively accounted for through a model governed by dynamic cross-linking. The elastic behavior of the network is highly nonlinear, becoming much stiffer with applied stress. This nonlinear elastic response is also highly sensitive to the mutations of α-actinin-4; in particular, we observe that actin networks cross-linked with Actn4 bearing the disease causing K255E mutation are more brittle with a lower breaking stress in comparison to networks cross-linked with wild-type Actn4. Furthermore, a mutation that ablates the first actin binding site (ABS1) in Actn4 abrogates the network’s ability to stress-stiffen. These changes in the mechanical properties of actin networks cross-linked with mutant Actn4 may represent physical determinants of the underlying disease mechanism in inherited focal segmental glomerulosclerosis.

I. INTRODUCTION

The functional behavior of cells is strongly influenced by the mechanical properties of their cytoskeleton; the cytoskeletal elasticity is governed by a complex interplay of biopolymer networks and their associated cross-linking proteins [1-3]. The response of such networks depends sensitively on the timescale on which they are probed and is best quantified by a measure of the frequency-dependent mechanical response or viscoelasticity of the network. The richness of the mechanical behavior of these networks in vivo has led to extensive in vitro studies of networks of individual biopolymers. Many studies have focused on reconstituted networks of filamentous actin (F-actin), which make an essential contribution to the mechanics of the cytoskeleton of many cells [3-12]. Filamentous actin is composed of 42kDa monomers that assemble into double-stranded semiflexible flaments. In the absence of cross-linkers, F-actin forms an entangled network that behaves like a weak viscoelastic solid. However, the addition of a wide-range of cross-linking proteins such as scruin, filamin, fascin, and α-actinin-4, dramatically strengthens these networks [13-27]. Moreover, cross-linked F-actin networks often exhibit strain stiffening; their stiffness increases dramatically upon the application of an external load that induces network strain.

Physiologically, the elastic properties of the actin cytoskeleton are critical to the function of cells. Of particular interest here are podocytes, highly differentiated epithelial cells unique to the kidney. Podocytes possess multiple cellular extensions, known as foot processes, which interdigitate over capillaries, contributing to the kidney’s fltration barrier and preventing deformation due to distensive forces related to blood flow. Each foot process contains an actin-rich contractile apparatus that is cross-linked, in part, by Actn4 [28, 29]. Multiple proteins localize to foot processes and cause proteinuric kidney disease when mutated in humans and mice [30-33].

Mutations in the gene encoding Actn4 cause an inherited form of proteinuric kidney disease, focal segmental glomerulosclerosis [30-32]. The associated actin binding domain of these mutant Actn4 can be generated as GST fusion proteins. Using actin cosedimentation, the dissociation constants of the various forms of Actn4 can be measured, allowing the determination of their binding affinity to actin flaments. The wild-type (WT) dissociation constant is measured to be $K_d^{\mathrm{WT}}=31.72\mu \mathrm{M}$ [35]. By comparison, one particular disease-causing mutation of the lysine residue at position 255 to glutamate (K255E) increases actin affinity, $K_d^{\mathrm{K}255\mathrm{E}}=5.33\mu \mathrm{M}$; this is mediated by the exposure of an additional actin binding site (ABS1) that is normally buried and relatively inactive in the wild-type Actn4 protein [35]. Structural studies of the actin-binding domains of actinin family members and other related proteins suggest a picture in which the actin-binding domain of Actn4 undergoes a conformational change between an “open” configuration, in which ABS1 is exposed, and a “closed” configuration, in which ABS1 is largely buried [36-38]. Consistent with this model, when ABS1 function is ablated with a double amino acid substitution of the glutamine at position 52 and the threonine residue at position 55 (QTAA), there is only a modest effect on Actn4 binding to actin filaments ( $K_d^{\mathrm{QTAA}}=63.31\mu \mathrm{M}$); however, when the QTAA mutation is present in parallel with K255E (K255E/QTAA), the double mutant Actn4 binding affinity reverts back to a level similar to wild-type Actn4, with $K_d^{\mathrm{DM}}=33.06\mu \mathrm{M}$ [35]. These data support the picture that the disease-causing K255E mutation shifts the balance of the Actn4 actin-binding domain towards the “open” configuration.

While this picture based on structural studies provides insight, it is the consequences of these disease-causing mutants on the mechanical properties of the F-actin networks that is most essential. For example, networks cross-linked with the K255E mutant exhibit structural relaxation below a relaxation frequency, which is an order of magnitude lower than those cross-linked with WT Actn4, providing support for the mechanical consequences of this picture [39]. However, while the complex linear viscoelastic behavior demonstrates the richness of the network’s mechanical properties, the functioning of these networks in cells depends not only on their linear properties but also, critically, on their nonlinear properties [3, 7, 9, 18], which remain largely unexplored [15]. An understanding of the structure and viscoelasticity of networks cross-linked with wild-type and mutant α-actinin-4 is essential to elucidate the full consequences of these mutations on the networks and on the mechanical origins of proteinuric kidney disease.

Here, we discuss the results of a detailed, systematic investigation of the linear and nonlinear viscoelastic properties of networks of F-actin cross-linked with Actn4. We utilize four different types of α-actinin-4, including wild-type, K255E, QTAA, and K255E/QTAA double mutant, to explore the effects of mutations on network viscoelasticity. We show that the networks form cross-linked elastic gels and can exhibit strong nonlinearity as applied stress is increased; notably, the presence of the ABS1 binding site plays a crucial role in nonlinear strain-stiffening. In addition, we demonstrate that the K255E mutation results in the formation of more brittle networks with a breaking stress nearly an order of magnitude lower than those of corresponding networks formed with wild-type α-actinin-4. The frequency dependence of the viscoelastic response of both wild-type and mutant Actn4 cross-linked networks is quantitatively described by a network model involving transient cross-links [27, 40], further confirming that network dynamics can be understood within a framework of ABS1 activity.

II. RESULTS AND DISCUSSION

To investigate the microstructure of actin networks cross-linked with wild-type or mutant Actn4, we polymerize purified monomeric actin in vitro in their presence. As actin flaments elongate, they are cross-linked by wild-type Actn4 to form nearly isotropic, finely reticulated three-dimensional networks, as shown in Fig. 1A [35, 39, 46]; crucially, such microscopy demonstrates that the reconstituted networks are free of large-scale inhomogeneities. By comparison, networks polymerized in the presence of K255E Actn4 form a more coarsely reticulated microstructure with a correspondingly smaller mesh size, as depicted in Fig. 1B. These data are consistent with measurements of dissociation constants as well as with previous data showing that K255E Actn4 binds F-actin with a 1:2 stoichiometry as compared with a 1:4 ratio for wild-type Actn4 [35]; indeed, a higher propensity for binding results in a higher fraction of bound linker and hence a correspondingly finer mesh size. The QTAA Actn4, which ablates the functionality of ABS1, generates an actin network similar to wild-type Actn4 but with significantly less reticulation, as shown in Fig. 1C. Interestingly, networks formed with the double mutant K255E/QTAA Actn4 are substantially different than the others with a much looser organization of longer, thicker bundles of actin flaments and very little branching, as depicted in Fig. 1D.; this is especially surprising given that the actin cosedimentation assays indicate a double mutant dissociation constant nearly identical to that of the wild-type cross-linker [47].

Figure 1.

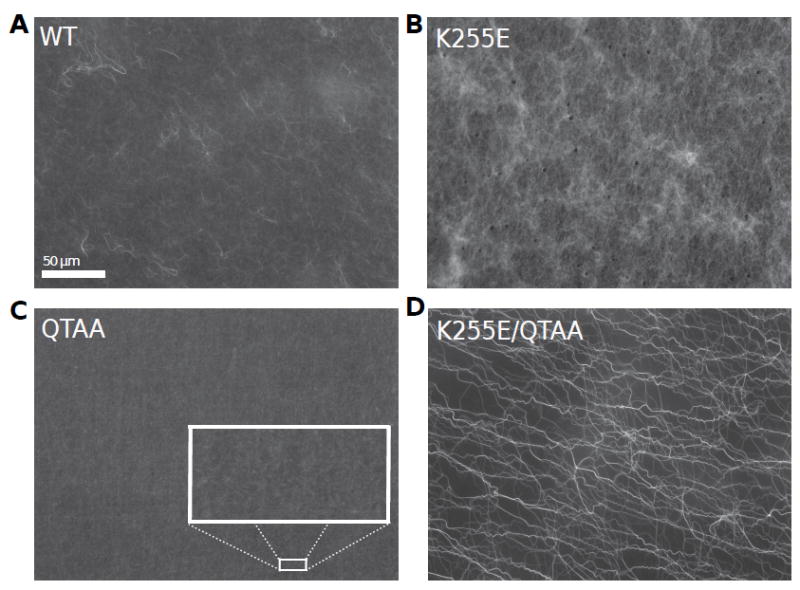
Fluorescence imaging of networks of actin cross-linked with wild-type and mutant Actn4. (A) Depicts the finely reticulated actin network formed in the presence of WT Actn4. (B) Networks formed with the K255E mutant Actn4. (C) Networks formed with the QTAA mutant Actn4 depict minimal reticulation, consistent with the bulk rheological observation that such networks are the weakest viscoelastic solids. (D) Networks formed with the double mutant are characterized by thicker filament bundles.

To relate the microscopic network structure to the macroscopic rheological behavior, we quantify the viscoelasticity of the cross-linked actin networks. We probe the network’s linear viscoelastic moduli during gelation, which lasts approximately one hour; the moduli are initially characterized by a rapid increase and eventually reach a plateau value. To investigate the linear elasticity of the networks, we probe the frequency dependence of G’ and G” for networks cross-linked with various types of Actn4 [6, 16, 23, 39, 40]. For all such networks, both G’ and G” depend sensitively on frequency (0.001 - 10Hz); the elastic modulus is independent of frequency for ω > 1Hz and exhibits relaxation toward a complex, fluid-like behavior at lower frequencies, as shown in Figure 2. This frequency independent elastic plateau regime suggests the existence of a solid-like cross-linked gel and thus, we characterize the network linear response by the plateau modulus, G₀, the value of G’ at 3Hz.

Figure 2.

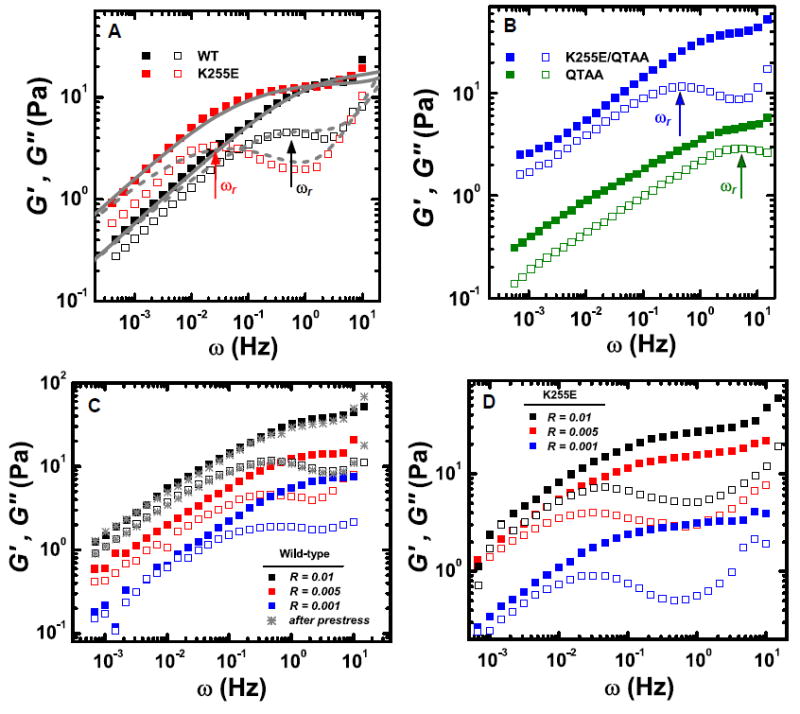
(color online). Linear bulk rheology characterizing the frequency dependence of the viscoelastic moduli for actin cross-linked with wild-type and mutant Actn4. (A) The local maximum of the loss modulus is identified as the characteristic linker unbinding frequency and is highlighted by the associated arrows. Networks formed with the K255E mutant Actn4 depict significantly smaller unbinding frequencies, implying a substantially elongated timescale for linker unbinding; this increased timescale is consistent with a picture of ABS1 governed dynamics since the “open” conformation preferred by the K255E mutant enhances accessibility of the previously buried actin binding site. The viscoelastic dynamics of both WT and K255E networks are accurately captured by the mean-field CGD model and global fits are shown as solid and dashed grey lines [40]. (B) Networks formed with the QTAA mutant depict a substantially increased unbinding frequency, suggesting that a portion of ABS sites are bound in wild-type Actn4. Networks formed with the double mutant revert back to an unbinding frequency comparable to that of wild-type Actn4. (C) Linear viscoelastic moduli of WT networks as a function of frequency for varying R, the molar ratio of Actn4 to actin. The local maximum in the loss modulus remains unaffected by changing R, while the plateau modulus is strongly affected. Naively, mechanical hardening could result from irreversible structural reorganization induced by filament bundling [52]; however, here, the network response is completely reversible, as demonstrated by the recovery of the linear mechanical response (grey stars) following measurements of nonlinear elasticity. (D) Linear viscoelastic moduli of K255E networks as a function of frequency for varying R.

By contrast, in the low frequency regime, all networks exhibit the signatures of structural relaxation: Both the storage and loss moduli exhibit a pronounced frequency dependence, with G” reaching a local maximum before approaching and ultimately attaining the same slope and magnitude as G’ at the lowest frequencies. The frequency of the local maximum in G” is identified as the relaxation frequency ω_r, which characterizes the unbinding rate of cross-linkers [27, 39, 40]; this can be used to compare the network relaxation associated with the various types of Actn4, thereby probing the effect of molecular mutations on linker affinity. The observed network relaxation is reminiscent of the flow of a liquid; however, the network relaxes with a power law G’ ~ ω^β , G” ~ω^η, where β = η = 1/2; this is inconsistent with simple fluid flow, where β = 2 and η = 1. Indeed, the actual relaxation mechanism is consistent with a picture of cross-link governed dynamics (CGD), which is based upon the microscopic unbinding and rebinding of cross-links [40]. On timescales much shorter than the characteristic unbinding time, the length scale of filament fluctuations is constrained to be less than l_c, the typical distance between cross-links. On longer timescales, however, linker-unbinding events lift local constraints on the fluctuating motion of individual flaments. The combined effect of many such local unbinding events allows network relaxation on length scales much longer than l_c and forms the basis of large scale network remodeling, resulting in a frequency dependent shear modulus of the form G’ ~ ω^½ , G” ~ ω^½ below ω_r, as shown by the theoretical curves in Fig. 2A. [40].

The value of ω_r is more than an order of magnitude larger for networks cross-linked with wild-type Actn4 (ω_r ~ 0.6Hz) than for those cross-linked with the K255E mutant (ω_r ~ 0.03Hz), as shown in Fig 2A [39]. The slower relaxation rate observed for networks formed with the K255E mutant is consistent with measurements of a 6-fold lower equilibrium dissociation constant; this is attributed to the exposure of the additional actin binding site, ABS1, due to the propensity for the cross-linker to remain in an “open” conformation [35]. Hence, we hypothesize that the variation in relaxation frequencies between networks cross-linked with WT and K255E Actn4 is governed by the accessibility and activity of ABS1. To ensure that the mutation induced shifts of ω_r are not originating from changes in the fraction of bound Actn4, we vary the molar ratio R of Actn4 to actin over an order of magnitude [17]. Over the full range probed, G’ depends sensitively on R, indicating the that network is as yet far from saturation. Despite this strong dependence of the magnitude of G’, ω_r remains independent of molar ratio for both WT and K255E networks, as shown in Fig. 2C, D, clearly demonstrating that, as expected, ω_r characterizes an intrinsic linker property. However, despite such evidence, it is unclear whether the slower dissociation rate of the mutant results purely from enhanced ABS1 activity or is confounded by other effects of the mutation.

To test our hypothesis and the role of ABS1 in governing variations of binding affinity and hence of ω_r, we further mutate the “open” conformation K255E Actn4 by ablating the ABS1 site (QTAA mutation). This double mutant (K255E/QTAA) Actn4 has both an “open” conformation due to the K255E mutation and a partial ablation of ABS1 activity due to the QTAA mutation. The K255E mutation enhances accessibility and activity of the additional actin binding site by reducing the steric hindrance associated with the “closed” conformation; however, by directly ablating the binding site through the QTAA mutation, it may be possible to offset this enhanced ABS1 activity. Although the relative importance of the two mutations is unknown, the mutations affect the binding dynamics of the ABS1 site in a diametric fashion, implying that the addition of the QTAA mutation may tend to restore the behavior of the K255E mutant to that of the WT linker. Interestingly, the linear rheology of the double mutant confirms this hypothesis and yields a relaxation rate, ω_r ~ 0.5Hz, as shown in Fig. 2B. This value of ω_r coincides with that of the wild-type cross-linked networks suggesting that, strikingly, the partial ablation of the ABS1 site is nearly perfectly compensated by the “open” conformation of the Actn4 molecule. These results also confirm our hypothesis that there are no ancillary effects confounding the variations in relaxation frequency seen among the mutants.

To further explore the role of ABS1 on binding dynamics, we consider the relaxation frequency of networks bound with linkers containing only the QTAA mutation; these mutants effectively retain the WT “closed” conformation while also possessing an ablated ABS1 site. While, the maximum activity of the additional binding site occurs in the K255E mutant which not only has a non-ablated site but also has an “open” conformation, the minimum activity should occur in the QTAA mutant which not only has an ablated ABS1 site but also a “closed” conformation. We find that, for networks cross-linked with the QTAA mutant, ω_r ~ 5Hz, which is a full two orders of magnitude larger than the corresponding relaxation frequency of networks cross-linked with the K255E mutant; moreover, it is also an order magnitude larger than the frequency of wild-type cross-linked networks. Surprisingly, this suggests that even in the wild-type “closed” conformation, a portion of ABS1 sites are active and contribute to the enhanced stability and hence, lower relaxation rate, of WT Actn4 in comparison to the QTAA mutant. Thus, the relaxation frequencies for wild-type and mutant Actn4 linkers are consistent with this picture of ABS1-governed binding dynamics, as shown in Table 1. However, there are also large apparent differences in network structure between the various cross-linkers; this suggests that the network’s nonlinear properties may also be substantially different.

TABLE I.

Relaxation and Nonlinearity

	Mutation			Wild-Type
	K255E	QTAA	K255E/QTAA
ωr (Hz)	0.03	5	0.5	0.6
σC (Pa)	0.4	NA	NA	3
σB (Pa)	1.5	0.67	2.1	8
G0 (Pa)	15.9	3.7	34.9	10.4

To elucidate the role of Actn4 mutations and ABS1 activity on the nonlinear mechanical response of these networks [15], we investigate the nonlinear elastic regime by probing the differential elastic modulus, K’ [45]. Above a critical stress σ_C, networks of wild-type and K255E cross-linked actin display pronounced nonlinear stiffening with applied stress, ex-hibiting a power law of approximately 3/2, as shown in Fig. 3. This is consistent with previous experiments of cross-linked actin networks and with the theory for affine entropic stretching, in which the nonlinear elasticity of the network results from the stretching out of thermal fluctuations between cross-link nodes [3, 7, 48]. Although the double mutant restores the general linear viscoelastic behavior of networks to that of WT cross-linked networks, this does not hold for the nonlinear response. Indeed, networks of actin cross-linked with both the QTAA mutant and the double mutant (K255E/QTAA) exhibit no nonlinear viscoelasticity; instead the networks’ elasticity is strictly linear before reaching the breaking stress, σ_B. This macroscopic breaking stress, which characterizes network rupture, is sensitively dependent on mutations of Actn4 and varies over nearly two decades for the differing mutants, as shown in Table 1. The abrogation of strain-stiffening in both the networks containing the QTAA mutation suggests that ABS1 plays an essential role in governing nonlinear network mechanics. In the case of the single QTAA mutation, network structure, reticulation, and cross-linking are least evident from fluorescence images, and the elastic plateau modulus G₀ ~ 3Pa suggests that the network is the weakest viscoelastic solid of those tested. This not only confirms the previous hypothesis that a fraction of ABS1 is actin-bound in WT networks, but further emphasizes the crucial role that ABS1 plays in network stability, both in the linear regime, where the QTAA elastic modulus is nearly an order of magnitude smaller than the WT elastic modulus, and in the nonlinear regime, where an ablation of the ABS1 site annuls the networks’ ability to stress-stiffen.

Figure 3.

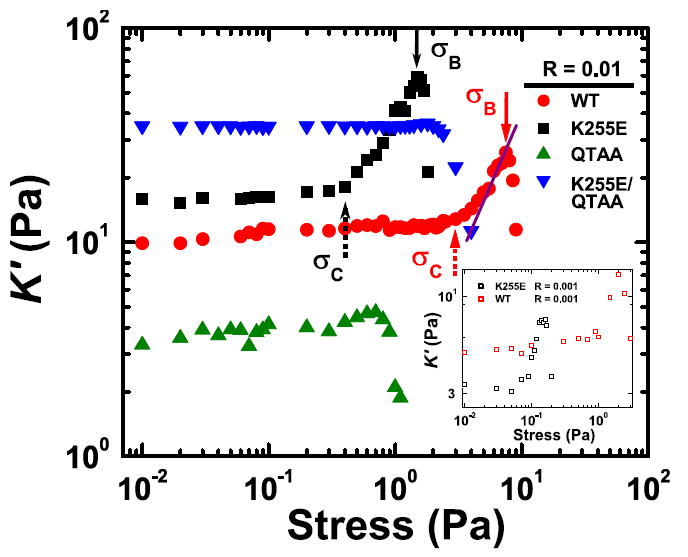
(color online). The differential elastic modulus as a function of applied stress. Both wild-type and K255E linked networks depict pronounced nonlinear stress-stiffening. Interestingly, this nonlinear elastic regime is consistent with a 3/2 power law (purple line) suggesting that the stiffening is entropic in nature [48]. However, despite the apparent similarity in origin, both the onset of nonlinearity, σ_C (dashed arrow), and the breakage stress, σ_B (solid arrow), at which the network ruptures are noticeably different; in particular, networks cross-linked with the K255E mutant Actn4 depict σ_C, σ _B nearly an order of magnitude smaller than their wild-type counterparts. Furthermore, these observations remain robust even for networks with significantly smaller R (molar ratio of Actn4 to actin) as depicted in the inset. Neither the QTAA nor double mutant cross-linked networks depict stiffening as a function of stress. The linear elastic modulus G₀ can also be determined from the differential modulus in the linear regime of K’(σ); this extracted value is given in Table 1.

The structure of networks formed with the double mutant exhibits much thicker bundles and is substantially different from those formed with the WT and K255E mutant. This is consistent with the possibility that non-affine deformations, which thereby avoid entropic filament stretching, are important and could account for the lack of observed strain stiffening [27]. Alternatively, it is possible that for double mutant cross-linked networks, σ_B < σ_C, in which case the network ruptures before the onset of nonlinear behavior. While the double mutant’s apparent inability to stress-stiffen and its bundled microstructure indicate significant differences in comparison to WT networks, its actin binding affinity, as determined through both cosedimentation and rheology, are remarkably similar to WT networks. This incongruence suggests that linker dynamics are unrelated to the origin of the network’s nonlinear stiffening, an observation consistent with the proposed microscopic model of ABS1 governed dynamics. Indeed, while the relative exposure of ABS1 may control the linker’s relaxation rate, it will not affect the flament’s entropic response.

The properties of the two networks which exhibit strain stiffening are similar in most respects; however, they differ significantly in the values of their critical stress, which signifies the onset of network nonlinearity, with networks formed with WT linkers having a substantially larger value of σ_C than those formed with the K255E mutant, as shown in Table 1. Here, it is important to emphasize the distinction between the network’s nonlinear elastic response and its dynamic relaxation. While the relaxation is governed by linker unbinding events, the elasticity of actin networks is governed by the bending fluctuations of the fil-aments [48-50]. We speculate that the microscopic origin of the difference in the critical stress is linked to stress-induced changes in protein conformation, as shown in Fig. 4A-E. To illustrate this behavior we show schematically an undeformed wild-type protein cross-linking two actin filaments in Fig. 4A. Upon application of external load, the protein must first “open” to expose the interaction between F-actin and the ABS1 site, as shown in Fig. 4B. This process of force-induced conformational change precedes the onset of nonlinear elasticity and could hence account for the enhanced critical stress seen in WT networks. By contrast, the K255E mutant linker adopts an “open” conformation even in the absence of load and hence does not require any additional strain to “open” its conformation, as shown in Fig. 4C; consistent with this, its critical stress is reduced. A key assumption of this proposed microscopic mechanism is that ABS1 binding is an essential pre-requisite for network nonlinearity. This is supported by the observation that networks with linkers whose ABS1 site is ablated do not exhibit a nonlinear response, independent of conformation.

Figure 4.

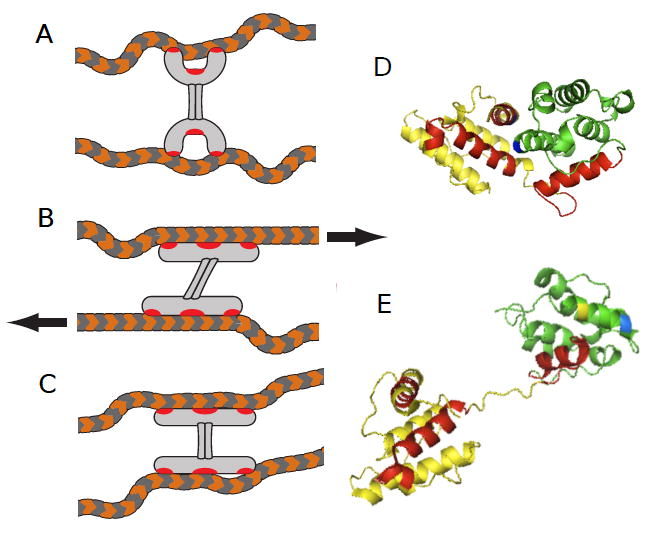
(color online). Schematic representation of effect of Actn4 mutation on the network response to external stress. (A) When the actin network is not under stress, the calponin homology domains of Actn4 adopt a closed conformation, preventing full exposure of its actin binding regions. (B) Under increased stress, the ABD of Actn4 may be forced into a more open conformation, leading to increased exposure of actin-binding regions and greater actin affinity. (C) In the case of networks formed with the K255E mutant Actn4, a more open ABD conformation leads to increased accessibility of actin-binding regions to F-actin, higher affinity, ard a more brittle network. Since the actin binding regions are naturally more accessible, a nonlinear network response is observed for lower values of external stress as compared to WT networks. (D) and (E) Structure of the ABD of Actn4, based on previous models [36, 51], depicting a “closed” and “open” conformation. In our model, the Actn4 ABD adopts a more open conformation under stress and in the presence of human-disease associated mutations.

In addition to differences in the onset of nonlinearity, the networks also exhibit different breakage stresses, with σ_B ≈ 8Pa for the wild-type network, whereas σ_B ≈ 1.5Pa for the K255E network. Interestingly, these differences persist even for networks with a reduced molar ratio of Actn4 to actin, as shown by the inset in Fig. 3.; such differences are particularly surprising given the larger affinity of the K255E mutant, which would otherwise suggest the existence of a stronger network. Indeed, if the dominant network failure results from the rupture of the linker-filament bond, then the higher bound linker fraction of the K255E network would imply a correspondingly larger breakage stress. Contrarily, the data suggests that networks cross-linked with the K255E mutant may be more brittle than those cross-linked with wild-type Actn4. This brittleness appears to be a direct consequence of ABS1 binding; in particular, the K255E mutation causes a decrease in relaxation frequency by over an order of magnitude in comparison to wild-type Actn4. Hence, structural relaxation and stress redistribution, both of which are essential components of the network response to external loads, will occur on significantly longer timescales in networks cross-linked with K255E Actn4. This would cause portions of the network to remain under higher effective loads for longer periods of time, suggesting that the low rate of cross-link unbinding events, caused by the additional binding to ABS1, prevents homogeneous stress redistribution and subsequent network remodeling in the K255E network.

III. CONCLUSION

The ABS1 actin binding site within α-actinin-4 (and other α-actinins) is highly conserved through evolution, suggesting an important role for this domain in the protein’s function. Mutations in Actn4 appear to disrupt the proper folding of the protein, leading to variations in the accessibility of ABS1 and, thus, in the affinity for actin flaments [35]. Such variations in the linkers’ binding kinetics are manifest in network relaxation rates and are consistent with the picture of ABS1-governed binding dynamics. Actin filament networks made with either wild-type α-actinin-4 or the disease-causing K255E mutant show strain-stiffening, despite the large differences in the strength of the actin binding between these two forms of α-actinin. When ABS1 is abolished by mutation, actin networks made with either the wild-type or the K255E form lose this ability to strain harden. This observation, together with the highly conserved nature of ABS1, suggests that this ABS1-dependent strain stiffening is biologically important for normal cell function.

We also observe that actin networks cross-linked with the K255E form of α-actinin-4 are significantly more brittle than networks formed with wild-type α-actinin-4. The podocytes within the renal glomerulus surround glomerular capillaries that undergo cyclical changes in pressure and shape with the cardiac cycle. It seems reasonable to hypothesize that a brittle actin network in vitro may reflect a more brittle cellular structure in vivo, altering the cell’s ability to tolerate physical stress. The data presented here, and the role of α-actinin-4 in human kidney disease, suggest that molecular phenomena controlling physical properties such as brittleness and strain-stiffening may play important roles in a variety of normal biological processes and disease.

IV. MATERIALS AND METHODS

A. Materials and Network Visualization

Purified rabbit muscle G-actin is a kind gift of Fumihiko Nakamura (Brigham and Women’s Hospital, Boston, MA, USA). Full-length human recombinant Actn4 protein is expressed in and purified from baculovirus-infected Sf21 insect cells by ProteinOne (Bethesda, MD). To form fluorescently-labeled actin-Actn4 networks in vitro, actin is diluted to 1 μM in polymerization buffer (100 mM NaCl, 10 mM Tris-HCl pH 7.4, 1 mM MgCl2, 0.5 mM EGTA, 0.5 mM ATP) in the presence of 0.2 units Alexa-Fluor488-phalloidin (Molecular Probes/Invitrogen) and 0.1 μM Actn4 in a total volume of 50 μl. The reaction volume is immediately transferred to a glass slide, and the actin was allowed to polymerize at room temperature in a humidified chamber. After 60 minutes, glass coverslips were placed on the individual droplets, and each Actn4-crosslinked actin network was immediately viewed with an Olympus BX60 microscope using the 40X objective. Images were captured using SPOT Advanced software version 4.6 (Diagnostic Instruments, Inc.). Reproducible images for each mutant form of Actn4 were observed both when duplicate slides were processed in parallel and when the experiment was repeated on separate days with different samples of G-actin.

B. Bulk Rheology

Networks of cross-linked actin are formed by mixing 23.8 μM (1mg/ml) G-actin solution with corresponding WT and mutant α-actinin-4 solution at a molar ratio R = 0.001—0.01 of Actn4 to actin. Polymerization is initiated by the addition of 5x polymerization buffer. The mechanical response of the cross-linked actin networks is measured with a stress-controlled rheometer (AR-G2, TA Instruments) using a 20mm diameter 2 degree stainless steel cone plate geometry and a gap size of 50 μm. We utilize a home-made steel bottom plate to ensure that the networks do not slip and a solvent trap to prevent drying. To measure the linear viscoelastic moduli, we apply an oscillatory stress of the form σ(ω) = A sin(ωt), where A is the amplitude of the stress and ω is the frequency. The resulting strain is of the form γ(ω) = B sin(ωt + δ) and yields the storage modulus G’(ω) = A/B cos(δ) and the loss modulus G^”(ω) = A/B sin(δ). To determine the frequency dependence of the linear moduli, G’(ω), G”(ω) are sampled over a range of frequencies from 0.001 - 10 Hz.

To probe nonlinear behavior, we utilize a differential measurement, an effective probe of the tangent elastic modulus, which for a viscoelastic solid provides consistent nonlinear measurements of elasticity in comparison to other nonlinear methods [41-43]. A small oscillatory stress is superimposed on a steady pre-stress σ₀, resulting in a total stress of the form σ(ω) = σ₀ + |δσ₀| sin(ωt). The resultant strain has an oscillatory response of the form γ(ω) = |δγ₀| sin(ωt + ø); this yields the differential elastic modulus $K^{\prime }({\sigma }_0)=\left|\frac{\delta {\sigma }_0}{\delta {\gamma }_0}\right|\mathrm{COS}(\varphi )$ [44]. Such differential prestress measurements have been shown to be robust and time-independent even in systems that exhibit creep [45]. Here, it is important to note that when the sample is exposed to a prestress, the differential moduli do indeed depict frequency dependence. Over a broad range of frequencies however, the differential elastic modulus exhibits an approximately frequency independent plateau region. The elasticity obtained from this region is quantified as the differential plateau modulus.