Designing Intervention Studies: Selected Populations, Range Restrictions, and Statistical Power

Abstract

An appropriate estimate of statistical power is critical for the design of intervention studies. Although the inclusion of a pretest covariate in the test of the primary outcome can increase statistical power, samples selected on the basis of pretest performance may demonstrate range restriction on the selection measure and other correlated measures. This can result in attenuated pretest-posttest correlations, reducing the variance explained by the pretest covariate. We investigated the implications of two potential range restriction scenarios: direct truncation on a selection measure and indirect range restriction on correlated measures. Empirical and simulated data indicated direct range restriction on the pretest covariate greatly reduced statistical power and necessitated sample size increases of 82%–155% (dependent on selection criteria) to achieve equivalent statistical power to parameters with unrestricted samples. However, measures demonstrating indirect range restriction required much smaller sample size increases (32%–71%) under equivalent scenarios. Additional analyses manipulated the correlations between measures and pretest-posttest correlations to guide planning experiments. Results highlight the need to differentiate between selection measures and potential covariates and to investigate range restriction as a factor impacting statistical power.

Statistical power is an estimate of the probability that a study will detect an effect of a given magnitude given its design parameters. An accurate a priori estimate of the statistical power of a study can conserve resources and ensure that the experiment demonstrates acceptable Type II error rates (i.e., failure to reject the null hypothesis when the alternative hypothesis is true). Power analyses include the manipulation of several parameters, including the number of participants, the magnitude of the expected treatment effect, the effects of participant clustering, and the specified level of alpha (Cohen, 1977; Spybrook & Raudenbush, 2009).

One important approach for improving the statistical power of an experiment is to include covariates that explain variance in the outcome of interest (Bloom, Richburg-Hayes, Black, 2007; Schochet, 2005). For example, the inclusion of pretest performance at the school and person level as covariates can often explain between 80% and 90% of the variance in posttest performance for academic outcomes (Hedges & Hedberg, 2007). However, power estimates that rely on published, unrestricted correlations between pretest and posttest scores may not account for attenuated correlations in samples selected on pretest performance due to restriction of range on the measures of interest (Cole, Haimson, Perez-Johnson, & May, 2011). If the prospective research plan fails to account for this potential range restriction, the power analysis may underestimate the necessary sample size to detect an effect of a given size and jeopardize the experiment. There are at least two types of range restriction: direct and indirect (Sackett & Wade, 1983). Direct range restriction occurs in situations in which the distribution of scores on the measure of analysis is directly truncated. For example, a researcher may include students who scored below the 25^th percentile on a reading comprehension test and exclude all others. In contrast, indirect range restriction occurs in situations in which selection is based on a second, correlated measure and there is no direct truncation of the measure.

Cole et al. (2011) called attention to issues related to range restriction, attenuation of pretest-posttest correlations, and implications for statistical power in randomized control trials (RCTs) utilizing state assessments at both pretest and posttest. Findings indicated that pretest-posttest correlations for homogenous bands of students were attenuated, particularly for low-performing students. The average pretest-posttest correlation for low-performing students was .60, lower than the average correlation of .81 for unrestricted samples. This attenuation of the pretest-posttest correlation has a dramatic effect on statistical power. Assuming a balanced group design, two-tailed t-test at .80 power, p < .05, and d = .25, an 84% increase in sample size would be required to achieve equivalent statistical power with low-performing students when compared to parameters based on correlations observed in unrestricted samples (N = 176 vs. N = 324).

The analyses conducted by Cole et al. utilized a single test administered at multiple time points that served as the selection measure, pretest covariate, and primary outcome. The utilization of multiple measures as possible selection measures, pretest covariates, and outcome variables, all of which may demonstrate some degree of direct and/or indirect range restriction may present a more nuanced picture, as sample size requirements under direct and indirect range restriction differ (Hunter, Schmidt, & Le, 2006; Sacket & Wade, 1983). In the present studies, we investigated these scenarios to better understand the implications of different degrees of range restriction on statistical power and study design.

Rationale for the Present Studies

Appropriate power estimation for RCTs represents a lingering challenge across scientific disciplines (Lipsey, 1990; Spybrook & Raudenbush, 2009; Varnell, Murray, Janega, & Blitstein, 2004). Underpowered experiments yield inflated Type II error rates, resulting in wasted resources and limiting potentially promising lines of inquiry as positive intervention effects are erroneously dismissed. Thus, a nuanced understanding of factors influencing statistical power is of critical importance for experimental design and the advancement of educational science.

In the present studies, we investigated the effects of participant selection criteria and degree of range restriction on pretest-posttest correlations and subsequent implications for statistical power, as indicated by necessary sample sizes, minimum detectable effect sizes (MDES), and expected power. The goal was to provide specific guidance for researchers who conduct treatment experiments with selected samples. The present studies extended the work of Cole et al. (2011) in four primary ways. First, the studies addressed the implications for power for multiple measures that demonstrate direct and/or indirect range restriction, illustrating the differences between range restriction scenarios. Second, the implications of range restriction were reported in MDES, expected power, and necessary sample sizes, providing additional guidance for study design. Third, range restriction was considered across simulations that systematically manipulate the cut point for selection, the correlations of different tests, and the correlations of specific tests, allowing prospective researchers to identify optimal scenarios. Fourth, the present studies described a replicable process for simulating data and determining the implications of range restriction scenarios before conducting a priori power analyses. By improving the precision of parameter estimates for power analysis through simulation, researchers can design more efficient experiments.

The first study illustrates potential issues utilizing empirical results from an RCT conducted with struggling readers (Authors, 2014). In that work, entire schools were screened to identify a sample of fourth grade students at-risk for reading difficulties. The assessment battery included two highly correlated measures of the same latent construct (reading comprehension), one that demonstrated direct range restriction (Gates-MacGinitie Reading Test: Fourth Edition, MacGinitie, MacGinitie, Maria, & Dreyer, 2002) and one that demonstrated indirect range restriction (WJ-III- PC; Woodcock et al., 2001). Differences in the observed pretest-posttest correlations permitted an investigation of the power implications of different measure combinations.

In the second study, we utilized simulated data to investigate issues that may affect pretest-posttest correlations and therefore statistical power under both direct and indirect range restriction, including the degree of range restriction, selection on multiple measures, the inter-correlations between different measures of the same latent construct, and the pretest-posttest correlations for the measures for unrestricted samples.

Study 1: Observed Range Restriction and Statistical Power

Methods

Participants and setting

Participants for study 1 were drawn from a large-scale RCT investigating the effects of an intensive reading intervention with fourth grade students at-risk for reading difficulty (Authors). Participants were drawn from one large urban district (8 participating elementary schools) and two near-urban school districts (9 participating elementary schools) in the southwestern United States.

The Gates-MacGinitie Reading Test (MacGinitie et al., 2002) was administered to all students enrolled in the 4^th grade at participating schools. Students who received a grade-based standard score of 85 or below were eligible for participation in the study. Eligible participants were randomly assigned in a 2:1 ratio to a researcher-designed treatment condition or control condition.

The preliminary sample included 1,695 4^th grade students enrolled at a participating school. From this preliminary sample, 488 students scored at or below the cut point (SS ≤ 85) and were eligible for participation. A total of 93 students who were randomized did not complete posttest because they left the school or were withdrawn from the study. Attrited students did not differ from students who remained at pre-test on the Gates-MacGinitie Reading Test, t (482) = 0.05, p > .05. A total of 395 students (treatment and control combined) completed the posttest assessment. As the goal of the present study requires an evaluation of pretest-posttest correlations under different degrees range restriction, only the 395 students who completed both pretest and posttest assessments are included in the primary analysis.

Among the 395 participants in the present study, 45% were female, and 89% qualified for free or reduced price lunch. The racial/ethnic composition of the sample was 29% Hispanic, 22% African American, 8% White (not Hispanic), and 41% reported a different race or ethnicity, including students listing more than one race or ethnicity. The average age of the sample at pretest was 9.8 years old (SD =.56).

Measures

The two reading measures included in the present study were administered at pretest (fall) and again at posttest (spring). All testing occurred in a quiet location at the participating student’s school. Examiners were trained and were evaluated for proficiency prior to any active data collection.

Woodcock Johnson-III Passage Comprehension (WJ3 PC; Woodcock et al., 2001)

The WJ3 Test of Achievement is a standardized, individually-administered assessment of academic achievement. The Passage Comprehension Subtest is a cloze-based activity in which students read a short passage of text and provide the missing word. Psychometric properties for the WJ3 PC are excellent. Test-retest reliabilities for children aged 8–13 range from .76–.86.

Gates MacGinitie Reading Test- 4^th Edition (GMRT; MacGinitie, et al., 2002)

The GMRT is a standardized, group-administered assessment of reading achievement and vocabulary. The Reading Test consists of expository and narrative passages ranging in length from 3–15 sentences. Students answer three to six multiple-choice questions related to the passage. Internal consistency coefficients range from .91–.93 and alternate form reliability is reported as .80–.87.

Results of Study 1

Descriptive statistics

Descriptive statistics for the sample are reported in Table 1. As expected, scores were lowest on the selection measure (GMRT M = 77.22, SD = 5.99). Scores were higher for the other reading measures, particularly at posttest. In addition to noting that this sample scored well below the published mean observed in the norming sample on all measures, it should be noted that standard deviation statistics for all reading measures were significantly smaller than published standard deviations.

Table 1.

Descriptive Statistics and Correlations at Pretest and Posttest for the Selected Sample

			Correlations
Measure	M	(SD)	1	2	3	4
1. GMRT- Pretest	77.22	5.99	-
2. WJ-III PC- Pretest	82.21	8.8	0.26	-
3. GMRT- Posttest	84.42	8.3	0.29	0.43	-
4. WJ-III PC- Posttest	84	8.91	0.27	0.78	0.52	-

N = 395; GMRT = Gates MacGinitie Reading Test; WJ-III PC = Woodcock Johnson Third Edition Passage Comprehension Subtest; KBIT-2 = Kaufman Brief Intelligence Test- Second Edition.

Correlations

We calculated correlations for the two measures, including the pretest-posttest correlations for the measures. The GMRT, which was the selection measure and therefore demonstrated direct range restriction, exhibited the lowest correlations with all other measures. The pretest-posttest correlation for the GMRT for this restricted sample was .29, much lower than the published correlation of .81 in the GMRT technical report (MacGinitie, et al., 2002). In contrast, the pretest-posttest correlation was .78 for the WJ3 PC, which demonstrated indirect range restriction. This is lower than the published extended test-retest correlation (< 1 year) for students aged 8–18 (r = .91), but is not as attenuated as observed for the GMRT. All correlations are presented in Table 1.

Implications for statistical power

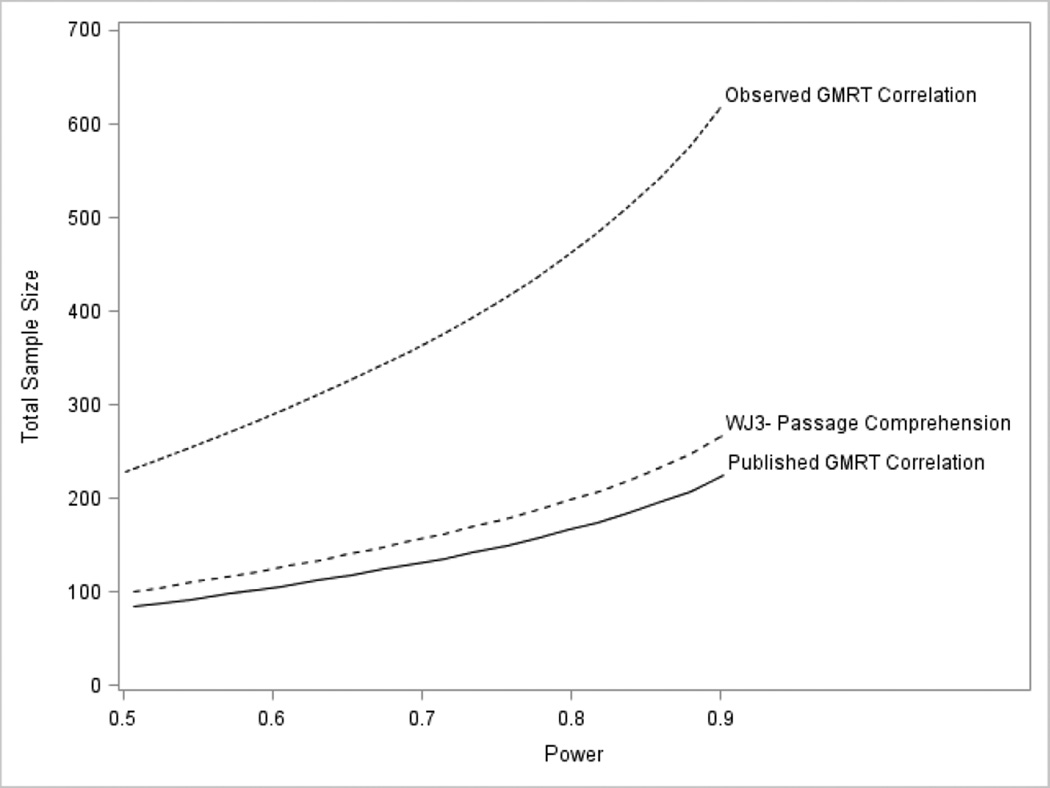
Given the large differences in observed pretest-posttest correlations, we calculated estimates of statistical power given specified parameters to better understand the implications of direct and indirect range restriction. For example, if the study were designed to achieve power of .80 for a two-tailed t-test with p < .05, d = .25 given the published, unrestricted GMRT pretest-posttest correlation of .81 as a covariate, the estimated sample size would be 168 participants. For the observed correlation on the WJ3 PC (.78), the estimated sample size would be 19% larger (N = 200). In contrast, for the observed GMRT correlation (.29), the estimated sample size would be 176% larger (N = 464). Similarly, if the researcher planned an experiment based on published, unrestricted pretest-posttest correlations and recruited 168 participants (two-tailed t-test, p < .05, d = .25) the estimated power utilizing the observed pretest-posttest correlations for the WJ3 PC would drop slightly to .73. However, for the observed GMRT pretest-posttest correlation, estimated power drops precipitously to .39. Figure 1 provides a plot of power by sample size for the published GMRT pretest-posttest correlation in unrestricted samples, the observed WJ3 PC pretest-posttest under indirect range restriction, and the observed GMRT pretest-posttest correlation under direct range restriction given the parameters specified above.

Figure 1. Statistical power under observed scenarios: published correlation, indirect range restriction, and direct range restriction.

WJ3 = Woodcock Johnson Third Edition; GMRT = Gates MacGinitie Reading Test; Note: The observed GMRT demonstrates direct range restriction. The observed WJ3 Passage Comprehension demonstrates indirect range restriction, and the published GMRT correlation is based on the normative sample (MacGinitie et al., 2002).

Study 2: Simulated Datasets under Range Restriction

In response to the observed differences between direct and indirect range restriction and its implications for statistical power, we created a series of data simulations to better understand the issue. All simulated datasets include case-specific values for two related measures administered at two time points (pretest and posttest). We first specified a baseline scenario (described below) and then manipulated four parameters to determine the effect on pretest-posttest correlations and subsequently statistical power: (a) the cut-point utilized for participant selection (scenario 2); (b) the utilization of multiple tests for participant selection (scenario 3); (c) the correlation between the two tests (scenario 4); and (d) the pretest-posttest correlation of the tests (scenario 5).

All data were generated using the IML procedure in SAS 9.4 (SAS Institute, 2008). For each condition, 100,000 simulated observations were generated to ensure adequate precision. Scores were generated for each variable with a mean of zero and standard deviation of one. The correlation matrices utilized to generate the datasets for each condition were derived from a baseline scenario we specified based on our own empirical work and reference to technical manuals of commonly administered assessments of reading. To simplify interpretation, we specified that the two simulated tests would demonstrate equivalent psychometric properties.

For each scenario, power calculations were completed within SAS 9.4 (SAS Institute, 2008) utilizing Proc GLMPower. This procedure permits the calculation of necessary sample sizes given specified parameters or a calculation of expected power given specified parameters including sample size. For estimates of expected power and necessary sample size, we specified a balanced group design, two-tailed t-test with an alpha of .05, and an estimated effect size of .25, which is consistent with the mean meta-analytic effect size (d = .21) for standardized measures for interventions conducted with students in grades 4–12 from 1980–2011 (Scammacca, Roberts, Vaughn, Stuebing, 2013). For estimates of sample size and MDES, a priori power was set at .80. Pretest-Posttest correlations for each analysis within each scenario were utilized to determine the amount of posttest variance explained by the pretest covariate. We report parameter ranges to reflect the upper and lower bounds of all possible correlations for Test 1 pretest and Test 2 posttest, as discussed below. We utilized Optimal Design software (Spybrook, et al., 2013) to verify sample size estimates and calculate MDES given the specified power parameters.

Scenario 1: Baseline

The baseline scenario required specification of three correlations, which were duplicated for both Test 1 and Test 2: (a) the correlation between Test 1 and Test 2 at the same time point; (b) the correlation of pretest and posttest for each test; and (c) the correlation between the pretest of Test 1 and the posttest of Test 2 (and conversely, the correlation of pretest 2 and posttest 1). We set the correlation between Test 1 and Test 2 at the same time point at .75, which is consistent with correlations between standardized reading comprehension measures in late elementary (see for example, the Kaufman Test of Educational Achievement-Normative Update, Kaufman & Kaufman, 1997, p. 133). The same test pretest-posttest correlation for both Test 1 and Test 2 was set at .85, which is consistent with fall-spring correlations reported for the Gates-MacGinitie Reading Test (MacGinitie et al., 2002, p. 63) in late elementary school. We found less guidance on the value of the correlation between Test 1 pretest and Test 2 posttest. Thus, we simulated a range of all possible correlations bound on the lower end by the lowest value that would result in a positive definite correlation matrix and bound on the upper end by the lower value of either the correlation between Test 1 and Test 2 at the same time point or the pretest-posttest correlation for the test. Thus, we report an upper and lower range for all applicable scenarios. For the baseline scenario, we applied a selection criterion of an observed score less than or equal to one standard deviation below the full sample mean on Test 1, matching the selection criterion from the empirical study. The baseline scenario permitted an investigation of restriction of range and pretest-posttest correlations for Test 1 (direct range restriction) and Test 2 (indirect range restriction) under a simulation of realistic parameters.

Scenario 2: Manipulating the Cut Point for Participant Selection

In scenario 2, we utilized data simulated for the baseline scenario, but systematically manipulated the cut point for participant selection to investigate the effect of different magnitudes of range restriction on statistical power. We selected observations with observed z-score values less than or equal to 0, −.33, −.5, −.67, −.75, −1, −1.25, and −1.5.

Scenario 3: Selection based on Multiple Tests

In scenario 3, we applied cut points for participant selection that utilized multiple measures. As in scenario 2, we utilized data simulated under the baseline scenario. The first analysis evaluated participant selection that required observed scores less than or equal to the cut point on both Test 1 and Test 2. As in scenario 2, we systematically manipulated the cut point across a range of observed z-score values. The second analysis evaluated participant selection that required observed scores less than or equal to the cut point on either Test 1 or Test 2 across a range of observed z-score values.

Scenario 4: Manipulating the Correlation between Test 1 and Test 2

In scenario 4, we systematically manipulated the correlations between Test 1 and Test 2 to evaluate the effect on pretest-posttest correlations for the tests under direct and indirect range restriction. For this scenario, we simulated twenty datasets. As in the baseline scenario, three values were necessary to complete the correlation matrix if the psychometric properties of the two tests are equivalent: (a) the correlation between Test 1 and Test 2 at the same time point (manipulated variable); (b) the correlation between pretest and posttest for each test (held constant at .85); and (c) the correlation between Test 1 pretest and Test 2 posttest (and the converse). Parameter a was systematically manipulated at .05 intervals from r = .50–.95, thus 10 intervals were evaluated. Because parameter c is dependent upon parameter a, we simulated an upper and lower range of all possible values for parameter c given specific values of parameters a and b. As in the baseline scenario, the lower bound was the lowest value that would yield a positive definite correlation matrix and the upper bound was the lower value of either the pretest-posttest correlation of the tests or the correlation between the tests at the same time point. The 10 intervals were evaluated at the upper and lower bound of parameter c, requiring 20 simulated datasets. For each of these datasets, the selection cut point was set to z ≤ −1, to match the baseline scenario.

Scenario 5: Manipulating the Pretest-Posttest Correlation

In scenario 5, we systematically manipulated the same test pretest-posttest correlations for both Test 1 and Test 2 (values were the same for each test at each interval). The correlation between Test 1 and Test 2 was held constant at .75. As in scenario 4, 20 datasets were simulated at intervals of r = .05 with values for the pretest-posttest correlation ranging from .50–.95. As in scenario 4, we simulated an upper and lower bound for all possible values for the correlation between Test 1 pretest and Test 2 posttest (and the converse). For each of these datasets, the selection cut point was set to z ≤ −1, to match the baseline scenario.

Results

Descriptive statistics for the baseline scenario and scenario 2 are presented in Table 2 across the range of selection criteria. Means and standard deviations reported in Table 2 represent the mean value for the two datasets (the upper bound simulation and the lower bound simulation for the across time/across tests correlation). Scores for the baseline scenario are presented in bold.

Table 2.

Descriptive Statistics for Baseline Simulation at Different Selection Cut Points (Z-Score Metric)

	Direct Range Restriction				Indirect Range Restriction
	Test 1 Pretest		Test 1 Posttest		Test 2 Pretest		Test 2 Posttest
Cut Point	M	(SD)	M	(SD)	M	(SD)	M	(SD)
No Cut Point	0	(1)	0	(1)	0	(1)	0	(1)
≤ 0	−0.80	(.61)	−0.68	(.74)	−0.60	(.80)	−0.54	(.84)
≤ −.33 SD	−1.02	(.55)	−0.87	(.70)	−0.77	(.78)	−0.69	(.82)
≤ −.5 SD	−1.14	(.52)	−0.97	(.69)	−0.86	(.77)	−0.78	(.81)
≤ −.67 SD	−1.27	(.50)	−1.08	(.68)	−0.95	(.76)	−0.86	(.80)
≤ −.75 SD	−1.33	(.48)	−1.13	(.67)	−1.00	(.75)	−0.90	(.80)
≤−1 SD	−1.53	(.45)	−1.30	(.65)	−1.15	(.74)	−1.04	(.79)
≤ −1.25 SD	−1.73	(.42)	−1.47	(.64)	−1.30	(.73)	−1.17	(.79)
≤ −1.5 SD	−1.94	(.39)	−1.65	(.63)	−1.46	(.73)	−1.31	(.79)

M = 0; SD = 1. Note: Mean scores and standard deviations represent the mean score from the two simulated datasets (i.e. the upper and lower bound). Bold = Baseline scenario (Scenario 1); Test 1–Test 2 r = .75; pretest - posttest r = .85 (both Test 1 and Test 2); Test 1 pretest - Test 2 posttest r = .61 – .75.

Baseline and scenario 2: Manipulating the selection criteria

Table 3 presents the pretest-posttest correlation for Test 1 (direct range restriction) and Test 2 (indirect range restriction), as well as the MDES and the necessary sample size given the pretest-posttest correlations. As would be expected, as the cut point moves toward a more extreme restriction of range, the pretest-posttest correlation becomes more attenuated and statistical power is reduced. However, it is important to note that the pretest-posttest correlations under indirect range restrictions are less attenuated than those observed under direct range restriction at every cut point and the resulting required sample sizes or MDES are smaller.

Table 3.

Scenarios 1 & 2: Manipulating Participant Selection - Statistical Power at Different Cut Points

		Direct Range Restriction				Indirect Range Restriction
Cut Point	Na	Pretest- Posttest r	MDESb	Participants Neededc	Estimated Powerd	Pretest- Posttest r	MDESb	Participants Neededc	Observed Powerd
No Cut Point	100,000	.85	.21	142	.80	.85	.21	142	.80
< 0	49,915	.70–.70	.28–.29	258–262	.54–.55	.77–.80	.24–.25	186–212	.63–.69
< −.33 SD	37,005	.66–.67	.30–.30	284–286	.51–.51	.75–.79	.24–.26	190–222	.61–.68
< −.5 SD	30,860	.64–65	.30–.30	294–298	.49–.49	.74–.79	.25–.27	194–228	.60–.67
< −.67 SD	25,061	.62–.63	.31–.31	306–312	.47–.48	.74–.78	.25–.27	198–230	.59–.66
< −.75 SD	22,564	.61–62	.31–.32	312–318	.46–.47	.74–.78	.25–.27	198–230	.59–.66
< −1 SD	15,815	.58–.60	.32–.32	324–336	.44–.46	.73–.78	.25–.27	202–236	.58–.65
< −1.25 SD	10,569	.56–.57	.33-.33	340–346	.43–.44	.73–.78	.25–.27	202–240	.58–.65
< −1.5 SD	6,666	.53–56	.33–.34	350–362	.42–.43	.72–.77	.25–.27	204–242	.57–.65

^aN is the mean number of observations simulated for the both upper and lower limit parameters;

^bCalculated at p < .05, N = 200; power = .80;

^cCalculated at p < .05, d = .25, power = .80.

^dCalculated at p < .05, d = .25, N =142;

Note: Bold = Baseline scenario (Scenario 1); Test 1–Test 2 r = .75; pretest - posttest r = .85 (both Test 1 and Test 2); Test 1 pretest - Test 2 posttest r = .61 – .75.

Scenario 3: Selection based on multiple tests

Table 4 presents the pretest-posttest correlations when selection is based on multiple tests. Because we specified that Test 1 and Test 2 are psychometrically equivalent for all scenarios, results for Test 1 and Test 2 are statistically equivalent. Therefore, only estimates for Test 1 are reported. As would be expected, when selection is based on either Test 1 or Test 2, there is less attenuation of pretest-posttest correlations and smaller samples or lower MDES are necessary. In contrast, when selection is based on both Test 1 and Test 2, both tests demonstrate direct range restriction and pretest-posttest correlations are more attenuated; larger samples or higher MDES are necessary to achieve sufficient power.

Table 4.

Scenario 3: Manipulating Participant Selection- Selection Based on Multiple Measures

	Selection on Both Measures					Selection on Either of Two Measures
Cut Point	Na	Pretest- Posttest r	MDESb	Participants Neededc	Estimated Powerd	Na	Pretest- Posttest r	MDESb	Participants Neededc	Estimated Powerd
No Cut Point	100,000	.85	.21	142	.80	100,000	.85	.21	142	.80
≤ 0	38,561	.69–.71	.28–.29	250–264	.54–.56	61,408	.74–.78	.25–.27	202–230	.60–.65
≤ −.33 SD	26,252	.66–.68	.29–.30	270–284	.51–.53	47,939	.71–.76	.26–.28	214–252	.56–.63
≤ −.5 SD	20,778	.65–.67	.30–.30	280–294	.49–.51	40,945	.70–.76	.26–.28	218–260	.54–.62
≤ −.67 SD	16,018	.64–66	.30–.31	290–302	.48–.50	34,103	.68–.75	.26–.29	224–270	.53–.61
≤ –.75 SD	14,026	.63–.65	.30–.31	294–308	.48–.50	31,128	.67–.75	.26–.29	226–276	.52–.60
≤−1 SD	8,976	.60–.63	.31–.32	304–322	.46–.48	22,630	.66–.74	.27–.30	232–288	.50–.59
≤ −1.25 SD	5,472	.58–.63	.31–.32	308–336	.44–.48	15,544	.65–.73	.27–.30	236–296	.49–.58
≤ −1.5 SD	3,112	.56–.60	.32–.33	324–348	.43–.46	10,191	.63–.73	.27–.31	238–304	.48–.58

^aN is the mean number of observations simulated for the both upper and lower limit parameters;

^bCalculated at p < .05, N = 200;

^cCalculated at p < .05, d = .25;

^dCalculated at p < .05, d = .25, N =142;

Note: Bold = Baseline (Scenario 1); Test 1–Test 2 r = .75; pretest - posttest r = .85 (both Test 1 and Test 2); Test 1 pretest - Test 2 posttest r = .61 – .75. For selection based on two measures, correlations and power for both Test 1 and Test 2 are equivalent. All statistics reported in Table 4 are for simulations of Test 1.

Scenario 4: Manipulating Test 1–Test 2 correlations

Table 5 presents pretest-posttest correlations under direct (Test 1) and indirect range restriction (Test 2) as the Test 1–Test 2 correlation is manipulated from .95–.50. The pretest-posttest of Test 1, which demonstrates direct range restriction and is unaffected by the correlation with Test 2 is consistent at .58–.59, which was its value at baseline. In contrast, as the correlation between Test 1 and Test 2 drops, the pretest-posttest correlation for Test 2 (indirect range restriction) becomes less attenuated, yielding increased statistical power as evidenced by smaller required sample sizes and lower MDES.

Table 5.

Scenario 4: Statistical Power as Correlations between Test 1 and Test 2 Vary

Simulation Specifications			Direct Range Restriction			Indirect Range Restriction
Test 1– Test 2 r	Pretest - Posttest r	Test 1 Pretest - Test 2 Posttest r	Pretest-Posttest r	MDESa	Participants Neededb	Pretest- Posttest r	MDESa	Participants Neededb
.95	.85	.81–.85	.58	.32	332	.59–.64	.30–.32	296–330
.90	.85	.76–.85	.58	.32	336	.61–.69	.29–.31	264–318
.85	.85	.71–.85	.59	.32	328	.65–.74	.27–.30	232–294
.80	.85	.65–.80	.59	.32	332	.69–.77	.25–.29	210–266
.75	.85	.61–.75	.58	.32	336	.72–.78	.25–.27	200–242
.70	.85	.56–.70	.59	.32	334	.75–.80	.24–.26	188–220
.65	.85	.51–.65	.59	.32	334	.78–.81	.23–.25	178–202
.60	.85	.46–.60	.57	.33	340	.79–.81	.23–.24	172–192
.55	.85	.40–.55	.60	.32	326	.80–.83	.22–.24	160–182
.50	.85	.36–.50	.58	.32	33	.81–.83	.22–.238	156–174

N = 15,788–15,980;

^aCalculated at p < .05, N = 200; power = .80;

^bCalculated at p < .05, d = .25, power = .80;

Note: Participant selection at ≤ −1 SD; Bold = Baseline scenario. Direct restriction range values are from simulation 1 (the lower bound simulation). Values for direct range restriction do not systematically vary in the upper and lower bound simulations.

Scenario 5: Manipulating Pretest-Posttest Correlations

Table 6 presents pretest posttest correlations under direct (Test 1) and indirect range restriction (Test 2) as the same test pretest-posttest correlation for each test is manipulated from .95–.50. As expected, as the correlation between pretest and posttest drops, estimated sample sizes increase and MDES increase. Notably, Test 2 (indirect range restriction) demonstrates superior statistical power at all intervals. The largest pretest-posttest correlation is for Test 2 when both Test 1 and Test 2 demonstrate high correlations between pretest and posttest (good delayed test-retest reliability).

Table 6.

Scenario 5: Statistical Power as Pretest-Posttest Correlations Vary

Simulation Specifications			Direct Range Restriction			Indirect Range Restriction
Pretest- Posttest r	Test 1– Test 2 r	Test 1 Pretest - Test 2 Posttest r	Pretest-Posttest r	MDESa	Participants Neededb	Pretest- Posttest r	MDESa	Participants Neededb
.95	.75	.71–.75	.81	.23	178	.91–.92	.16–.17	84–90
.90	.75	.65–.75	.68	.29	276	.82–.84	.21–.23	148–170
.85	.75	.61–.75	.59	.32	332	.73–.78	.25–.27	198–242
.80	.75	.56–.75	.51	.34	376	.64–.72	.27–.31	244–302
.75	.75	.50–.75	.45	.36	404	.54–.67	.30–.33	280–358
.70	.75	.45–.70	.39	.36	428	.50–.63	.31–.34	304–382
.65	.75	.41–.65	.36	.37	440	.44–.58	.32–.36	336–410
.60	.75	.36–.60	.32	.38	456	.40–.54	.33–.36	360–426
.55	.75	.31–.55	.29	.38	464	.35–.51	.34–.37	376–446
.50	.75	.25–.50	.25	.38	474	.30–.49	.35–.38	386–460

N = 15,738–15,962;

^aCalculated at p < .05, N = 200; power = .80

^bCalculated at p < .05, d = .25, power = .80;

Note: Bold = Baseline scenario. Direct range restriction values are from simulation 1 (the lower bound simulation). Values for direct range restriction do not systematically vary in the upper and lower bound simulations.

Discussion

The goal of this series of studies was to investigate the effects of participant selection criteria, range restriction, and the implications of these factors upon statistical power. We differentiated between direct and indirect range restriction and evaluated impact upon statistical power with empirical and simulated data. The results of both studies demonstrated the dramatic effect of direct and indirect range restriction on statistical power. Under our simulated baseline scenario (z ≤ −1), sample sizes 128%–137% larger were necessary to achieve an acceptable level of statistical power under direct range restriction and sample sizes 42%–66% larger were necessary under indirect range restriction. Even in situations with a relatively high eligibility threshold (z ≤ −0), 78%–85% more participants were necessary to achieve adequate statistical power under direct range restriction compared to 31%–49% more participants necessary under indirect range restriction.

These differences were sufficiently large to jeopardize an experiment if they are unaccounted for in a priori analyses of statistical power. If sample sizes are based on unrestricted pretest-posttest correlations and held constant, estimated power dropped precipitously from .42–.55 for any scenario with direct range restriction. For scenarios under indirect range restriction, estimated power dropped less, but still ranged from .57–.69, values which would be considered unacceptably low when planning an experiment.

Comparisons of results from direct and indirect range restriction were similarly unambiguous, but more encouraging. For every analysis within each scenario, statistical power under indirect range restriction was better than that achieved under direct range restriction. Across different parameters, the effect varied from small (10 fewer participants necessary) to substantial (180 fewer participants necessary). Further, the benefit of indirect range restriction in comparison to direct range restriction was marginally ignorable only in scenarios where the two measures were very highly correlated, a situation unlikely to occur if the design utilizes tests from different published test batteries. In more common designs (e.g. selection at z ≤ −.67 or z ≤ −1; Test 1–Test 2 r = .75), 28%–40% fewer participants were necessary to achieve an acceptable level of statistical power, a substantial difference in person-randomized experiments. Finally, it is important to note that the ranges of necessary sample sizes and MDES reflect all possible correlations for across test pretest-posttest correlations; it is not a range of equally plausible correlations. For these ranges, the higher sample size and MDES estimates were products of our upper bound simulation. All upper bound simulations were bound by either the correlation between Test 1 and Test 2 at the same time point, or the pretest-posttest correlation for the tests. We think it unlikely that the Test 1 pretest and Test 2 posttest correlation would approach these values. Our empirical work suggests that the lower bound and its smaller necessary sample sizes and smaller MDES may be more plausible, reinforcing the advantage for tests demonstrating indirect range restriction over tests demonstrating direct range restriction.

This advantage for the test demonstrating indirect range restriction was strongly related to the correlation between the two tests. As the correlation between the tests demonstrating direct and indirect range restriction dropped, the advantages in statistical power for the indirect measure became stronger. Although this advantage is theoretically maximized when Test 1 and Test 2 are uncorrelated, attention to theory may help the researcher strike an appropriate balance between maximizing statistical power and experimental coherence. Indeed, even at very high correlations between the two tests (~.90), there were potentially large advantages in statistical power for the test demonstrating indirect range restriction.

It is also important to note the critical importance of pretest-posttest correlations for statistical power, even for tests that demonstrate some degree of direct or indirect range restriction. The results of scenario 5 demonstrated that the magnitude of advantage for tests under indirect range restriction was diminished as its pretest-posttest correlation dropped. For example, when the Test 2 (indirect range restriction) pretest-posttest correlation was .90, necessary sample sizes were 54%–62% of those necessary for Test 1 (direct range restriction). In contrast, when the pretest posttest correlation dropped to .65, necessary sample sizes for Test 2 were 76%–93% of those necessary for Test 1.

Implications

The results of the present studies illustrate the importance of drawing a conceptual distinction between selection (screening) measures, pretest covariates, and outcome measures. For some research projects, it may be impossible to avoid utilizing the same measure for selection and as the pretest covariate, as in the study design investigated by Cole et al. (2011) in which state assessments are utilized to evaluate large-scale programs. Studies with this design will require larger participant samples because of direct range restriction. However, for many projects investigating an intervention with selected populations, the research team is present in schools and could administer distinct tests for selection and as a pretest covariate/outcome measure. For example, a planned study could utilize a group-administered assessment such as the GMRT as the selection measure and utilize the properties of the WJ3 Passage Comp under indirect range restriction for the a priori power analysis. Under our baseline parameters, such a design would require up to 134 fewer students. When split equally between control and treatment, this design would require 67 fewer treated students, a significant savings of resources. Further, given the poor expected correlations between the GMRT pretest and a potential posttest, the researcher may wish to conserve further resources by not administering the GMRT at posttest.

Additionally, researchers planning to conduct research with selected samples could utilize the simulation techniques described in study 2 to estimate the expected range restriction and conduct an appropriate power analyses. These steps may help avoid failed studies when working with selected samples. Beyond individual researchers, it is important for funding agencies and grant review officials to understand these issues and prioritize study designs that appropriately address potential range restriction.

Conclusions

Through a series of studies, we investigated participant selection criteria, resulting range restriction, and statistical power to provide guidance for researchers planning intervention research with selected populations. Analyses of empirical and simulated data were unambiguous. Pretest-posttest correlations under direct range restriction were sharply attenuated, resulting in a precipitous drop in statistical power. Prospective researchers should differentiate between selection measures, pretest covariates, and outcome measures whenever possible. In this way, the researcher can maximize the efficiency of the experiment by ensuring that all tests demonstrate good psychometric properties and the pretest covariate and primary outcome do not demonstrate direct range restriction.