The advection of microparticles, MCF-7 and MDA-MB-231 breast cancer cells in response to very low Reynolds numbers

Abstract

The lymphatic system is an extensive vascular network that serves as the primary route for the metastatic spread of breast cancer cells (BCCs). The dynamics by which BCCs travel in the lymphatics to distant sites, and eventually establish metastatic tumors, remain poorly understood. Particle tracking techniques were employed to analyze the behavior of MCF-7 and MDA-MB-231 BCCs which were exposed to lymphatic flow conditions in a 100 μm square microchannel. The behavior of the BCCs was compared to rigid particles of various diameters (η = d_p/H= 0.05–0.32) that have been used to simulate cell flow in lymph. Parabolic velocity profiles were recorded for all particle sizes. All particles were found to lag the fluid velocity, the larger the particle the slower its velocity relative to the local flow (5%–15% velocity lag recorded). A distinct difference between the behavior of BCCs and particles was recorded. The BCCs travelled approximately 40% slower than the undisturbed flow, indicating that morphology and size affects their response to lymphatic flow conditions (Re < 1). BCCs adhered together, forming aggregates whose behavior was irregular. At lymphatic flow rates, MCF-7s were distributed uniformly across the channel in comparison to the MDA-MB-231 cells which travelled in the central region (88% of cells found within 0.35 ≤ W ≤ 0.64), indicating that metastatic MDA-MB-231 cells are subjected to a lower range of shear stresses in vivo. This suggests that both size and deformability need to be considered when modelling BCC behavior in the lymphatics. This finding will inform the development of in vitro lymphatic flow and metastasis models.

I. INTRODUCTION

Lymphatic vessels, which range in size from 10 μm to 2 mm in diameter, serve as routes for transporting immune cells throughout the body and are also exploited by cancerous cells, particularly cancers of epithelial origin, such as breast cancer.¹ Breast cancer is the most frequently diagnosed cancer and one of the leading causes of cancer death among females.² Numerous studies have identified the lymphatics as the primary route for the metastatic spread of breast cancer cells (BCCs),^3–5 however, very little is actually known about the effect these cells have on the lymphatic flow environment, and in turn, the effect these fluidic conditions have on the cells. In the past decade, significant advancements have been made in characterizing lymphatic flow, using both numerical and experimental approaches.^6–25 Accurate measurement of this environment is extremely important as the fluid shear forces and the flow environment surrounding cancer cells can modulate their metastatic potential. Studies have reported that the concentration of Circulating Tumor Cells (CTC) in 1 ml of blood is approximately 1–10 cells;²⁶ however, to the authors' knowledge, no data have been reported on the number of CTCs present in lymph. Lymph is primarily composed of interstitial fluid with a suspension of lymphocytes. The composition of lymph varies depending on the location of the body.²⁷ Lymphocytes make up approximately 20%–40% of all white blood cells in the body which corresponds to 1000–4800 cells/μl of blood and recent experimental work reports that the range of lymphocytes varies from 150 to 35 500 cells/μl in lymph.^25,28 To date, the behavior of BCCs in the lymphatics is relatively unknown; therefore, this study acts as a first step towards investigating and characterizing their behavior through an experimental campaign on their advection in microchannels. There is a considerable wealth of research that examines transport properties and detection of particles and biological cells in microfluidic devices.^29–43 However, there is very limited data available on the behavior of large particles/cells (>10% the channel width) under very low flow rates (0.2–1.7 μl/min) such as those seen in the collecting lymphatics. Lymph contains cells that are 7–10 μm in diameter and BCCs vary from 10 to 40 μm.^36–38,42 The Reynolds number (Re) in the collecting lymphatics is <1,²⁵ which is considerably lower than that used in inertial sorting devices, typically 30 < Re < 300. The Re is defined as

$$\mathrm{Re}=\frac{\rho \overline{u}d}{\mu },$$ (1)

where ρ is the fluid density, $\overline{u}$ is the mean velocity, d is the diameter of the channel, and μ is the fluid viscosity. Particles/cells flowing in a microchannel experience drag and lift forces that result in complex behavior. At Re > 30, despite laminar flow conditions and a tendency to neglect inertial effects in micro-flows, the motion of particles is driven by inertial effects with terminology such as “inertial microfluidics” or “inertial sorting” used to describe the flow phenomena involved. Some recent reviews provide an excellent overview of inertial sorting of cells and particles in microdevices.^44–47 Fluid forces due to shear, wall effects, and particle rotation scale differently depending on the local flow conditions with the effect that low concentration particles suspended in micro-flows move to equilibrium positions. The effect was first reported by Segré-Silberberg who reported an equilibrium location at 60% of the radial distance from the center of a circular tube, and has been exploited extensively in microfluidics for size-based sorting of particles and cells.⁴⁸ Despite the extensive body of experimental, theoretical, and computational studies that Segré-Silberberg's findings initiated, a complete insight into the inertial sorting mechanism is not fully understood.^45–47

At low Re (Re = 21–42), Hur et al. describe the potential for migration due to cell deformability as a potential means to sort cells.⁴⁹ This is where the cell morphologically changes due to the flow environment and enables similar sized cells to be discriminated upon based on their morphological response to the flow. Tanaka et al. examined the inertial migration of MDA-MB-231 cells as a means of identifying CTCs in blood-flow.³⁸ The migration of cells was compared to that of particles in the range of 0.16 < Re_p < 0.62, where Re_p is the particles Reynolds number, defined as

$${\mathrm{Re}}_p=\mathrm{Re}{\left(\frac{d_p}{H}\right)}^2,$$ (2)

where Re is the channels Reynold number, d_p is the particle diameter, and H is the channel height. It was found that the BCCs required a longer channel length to reach an equilibrium state compared to the particles. It is worth noting that the flow rates investigated in the study of Tanaka et al. are orders of magnitude higher than those in the lymphatics (diameter ∼100–300 μm). A study which investigated BCC motility in rat tumors found that three types of motility exist; cohesive motility (groups of cells), collective motility (chains of cells), and single cell motility.⁵⁰ The authors discovered that collective invasion may be used for lymphatic spread as numerous groups of BCCs within the lymphatics were observed. Interestingly, it has recently been shown that in breast cancer transplantation models, clumps of CTCs represent only about 2%–5% of the CTCs, yet they are responsible for almost half of the lung metastases (first capillary bed BCCs encounter when spreading systematically).⁵¹ This demonstrates the considerably higher metastatic potential of clumps of BCCs compared to single BCCs. Therefore, quantifying the behavior of both single cells and cell aggregates travelling in the lymphatics is important to accurately characterize breast cancer metastasis.

This paper describes the particle tracking techniques employed to analyze the behavior of particles, MCF-7 cells and MDA-MB-231 cells which are exposed to lymphatic flow conditions in a 100 μm square channel. A range of BCCs (0.03 < η < 0.81, where η = d_p/H) and rigid particles (0.05 < η < 0.32) were subjected to Poiseuille flow and their response to the flow in terms of speed and spatial distribution was analyzed. The first objective of this research was to determine whether BCC behavior, under lymphatic flow conditions, can be emulated using rigid particles of various diameters that have been used to simulate the various cells contained within lymph. Particle focusing experiments were carried out under a range of Re (Re = 0.02, 5, and 25) to compare both the particle and BCC behavior. Metastatic MDA-MB-231 cells are more deformable than non-metastatic MCF-7 cells, which display stiffer morphological properties;⁵² therefore, the second objective of this study was to investigate if there is a difference in the behavior between the two BCC types, i.e., do the mechanical properties of the BCC affect their flow behavior. Identifying the local velocity gradients and the shear stresses that BCCs are exposed to is crucial to determining their behavior under these specific flow conditions.

II. MATERIALS AND METHODS

A. Microfluidic device

In this study, a 100 × 100 μm topas microchannel (Microfluidic Chipshop, Stockholmer, Germany) with a length of 58.5 mm, was used for the experiments. A square channel was chosen to minimize possible refraction of the light beam at the walls of the microchannel.

B. Particle suspension

To evaluate the performance of the experimental system the flow through the microchannel was measured by seeding distilled water with 0.5 μm fluorescent solid polymer particles (FluoSpheres^® Polystyrene Microspheres, Dublin, Ireland). The particles absorb green light (absorbance peak 580 nm) and emit red light (emission peak 605 nm). The effect of Brownian motion was deemed negligible as a result of calculating the Brownian motion coefficient (0.999). The Brownian motion coefficient is defined as

$$\frac{d_e^2}{d_e^2+8M^2{\beta }^{2}D\Delta t},$$ (3)

where d_e is the image diameter of particles, M is the magnification, β² is a constant of value 3.67, D is diffusivity, and Δt is the time between two lasers pulses. Fluorescent microparticles of 5.2 ± 0.14 μm, 10.22 ± 0.13 μm (Microparticles Ltd., Berlin, Germany), and 27–32 μm (Cospheric, CA, USA) were chosen for testing. These particle sizes were chosen to correspond to the cell sizes seen in the lymphatics in vivo. The particles were mixed at a 0.08% wt fraction in distilled water, with 1 vol. % of Tween-20 surfactant (Sigma-Aldrich, Dublin, Ireland) added to the solution to prevent particle aggregation. The dynamic viscosity and density of distilled water are 1 mPa s and 1000 kg/m³, respectively. Due to the slight density difference between the particles (1050–1090 kg/m³) and distilled water, a percentage of glycerol (22% for the 5.2 μm and 10.22 μm particles and 34% for 27–32 μm particles) was added to the solutions. The viscosity and density of lymph, which are based on values for interstitial fluid from which lymph is derived, are in the range of 0.9–1.5 mPa s and ∼1000 kg/m³ respectively.^24,53–55

C. Breast cancer cell suspension

Two types of BCC lines were used in this investigation: non-metastatic MCF-7 cells and metastatic MDA-MB-231 cells (ATCC, Middlesex, UK). Both cell types were maintained in Dulbecco's Modified Eagle's medium (DMEM), supplemented with 10% fetal bovine serum (Sigma Aldrich, Dublin, Ireland) and 1% penicillin/streptomycin (Sigma Aldrich, Dublin, Ireland) in an incubator kept at 37 °C and 5% CO₂. The cells were fluorescently labelled using CellTrace™ Yellow (Bio Sciences, Dublin, Ireland) before preparing the cell suspension. Prior to testing, the cells were suspended in 55% DMEM and 45% Percoll (Sigma-Aldrich, Dublin, Ireland). Percoll was added to the cell suspension to prevent the cells adhering.⁵⁶ Both DMEM and Percoll are reported to have Newtonian fluid properties.^57–60 Research has reported that Percoll is ideal for use with biological materials and does not affect biological membranes.^60,61 A 2–3 ml solution with a concentration of 500–1000 cells/μl was used for all experiments. BCC concentrations were chosen to be predominantly higher than the actual numbers reported in literature, which are on the scale of 1–10 CTCs per ml of blood, for visualization and data analysis purposes.²⁶ The number of CTCs in lymph has not been reported to date.

D. Experimental apparatus

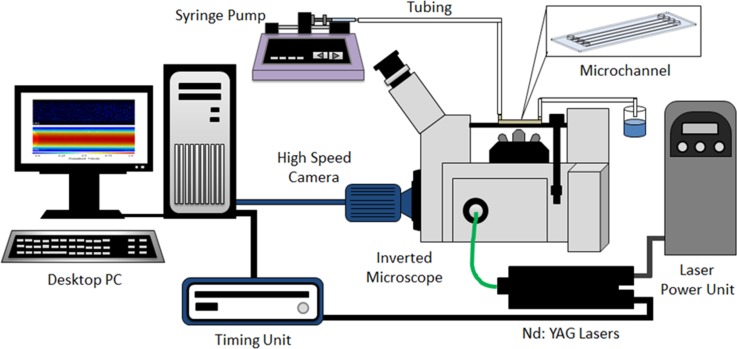
Fig. 1 illustrates the experimental system that was developed for this study which consists of a high speed digital camera (Imager LX, LaVision Ltd., Germany) connected to an inverted microscope (IX71; Olympus, Tokyo, Japan) with illumination provided by dual Nd:YAG lasers (New Wave Research, UK). A 1 ml glass syringe (Sigma Aldrich, Wicklow, Ireland) was connected to the channel via tubing, and the flow rate of the working fluid was kept constant using a syringe Pump (Harvard Apparatus, Holliston, MA, USA). The range of flow rates investigated were Q = 0.233–970 μl/min. The microchannel was illuminated by dual Nd:YAG laser pulses at a wavelength of 532 nm through an objective lens of 20× magnification (M) and a numerical aperture (NA) of 0.5. This objective lens provided a depth of field value of 3.16 μm.

FIG. 1.

The experimental set-up which consists of a high speed camera system connected to an inverted microscope with illumination provided by a double pulse Nd:YAG laser (532 nm).

E. Image acquisition

μPIV imaging techniques were employed using the DaVis image acquisition software (LaVision Ltd., Germany) to capture images of the flow (distilled water seeded with 0.5 μm particles) for validation. The particles were imaged with a resolution of 1608 × 568 pixels, 12-bit greyscale, with a time delay of 2500 μs between consecutive images. For the large particles and BCCs, a series of 500 single frame images were captured at a rate of 15 Hz. The bottom wall of the channel was located using the focusing dial of the microscope and defined as the zero position in the z-direction (channel depth). The fine-focusing dial was then used to scan up 50 μm to locate the center of the microchannel; all measurements were recorded at this depth. The location of both walls in the lateral (y) direction were then set to y = 0 and 1, respectively.

F. Image processing

The μPIV images were processed using DaVis, Version 8.3 (LaVision Ltd., Germany). The series of image pairs were spatially cross-correlated to calculate the velocity vectors of individual particles. A multi-pass, square correlation window with decreasing size, from 64 × 64 to 32 × 32 pixels was used. Using a multi-pass interrogation algorithm, with a 50% overlap, it was possible to obtain the corresponding velocity fields. A pre-processing filter was used to remove the image background noise by subtracting the local minimum from each pixel in the image.

Particle Tracking Velocimetry (PTV) techniques were employed using the plugin Trackmate in the ImageJ software (National Institute of Health, MD, USA) to analyze the large particles and BCCs as the usual flow tracing capabilities of μPIV are not suitable due to the large size of the particles and BCCs. PTV differs from μPIV in that, instead of cross-correlating between interrogation windows, individual particles are identified and tracked from image to image. To acquire the position of the particles/BCCs in-plane (x and y directions), the center of mass of the fluorescent spot was located and related to the zero position located at the channel wall (y direction) using ImageJ. Due to the large size of the particles/BCCs tested and the use of volume illumination, both in-focus and out-of-focus particles/BCCs were recorded. Focused particles have a well-defined outline, with a diameter close to the actual diameter (±10%), while out-of-focus particles have a blurred outline due to the wider intensity distribution, which depends on their distance from the focal plane.³² The image series were converted to grayscale using ImageJ and three criteria were defined to identify in-focus particles for analysis. The spot diameter was set to ±5% the particle diameter, corresponding to depth range of ±0.25–1.5 μm for the particles, the minimum mean intensity value of the fluorescent spot was defined (110 pixels for the η = 0.05 and 0.1 particles and 160 pixels for the η = 0.3 particles), and third, only spots that contained a well-defined outline were used for analysis.⁶² The depth wise measurement uncertainty increases with regard to defining the BCC location due to various shapes and sizes of the BCCs. The BCC sizes recorded were measured using the largest diameter of each individual cell, which was determined following observation over ∼500 μm to factor into account the rotation of the BCCs, and the center of mass of the fluorescent cell was identified and tracked to define its position. The minimum mean intensity value of the BCCs was set to 160 pixels to define in focus BCCs. This value was determined based on experiments carried out on static BCCs (located in a drop of media between two glass slides). Images of the BCCs were obtained at various depths by altering the vertical location of the microscope objective, and their corresponding intensity distributions were recorded. Additionally, to ensure confidence in the measurement technique employed, the depth of field was increased to 7.52 μm using a 10×/0.3 NA objective, and no difference was found in the results.

III. RESULTS AND DISCUSSION

A. Flow visualization

To evaluate the performance of the imaging system in measuring the velocity fields, the results for distilled water seeded with 0.5 μm particles were compared to the analytical solution for steady flow through a long straight square microchannel⁶³

$$u_x\left(y,z\right)=\frac{48\mathrm{Q}}{{\pi }^{3}hw}\left(\frac{\sum _{n,\hspace{0.17em}odd}^{\infty }\frac{1}{n^3}\hspace{0.17em}\left[1-\frac{\cosh (n\pi \frac{y}{h})}{\cosh \left(n\pi \frac{w}{2h}\right)}\right]\text{sin}\left(n\pi \frac{z}{h}\right)\hspace{0.17em}}{\left[1-\sum _{n,\hspace{0.17em}odd}^{\infty }\begin{array}{c}\frac{h}{w{n}^5}\frac{192}{{\pi }^5}\hspace{0.17em}\tanh (n\pi \frac{w}{2h})\end{array}\right]}\right),$$ (4)

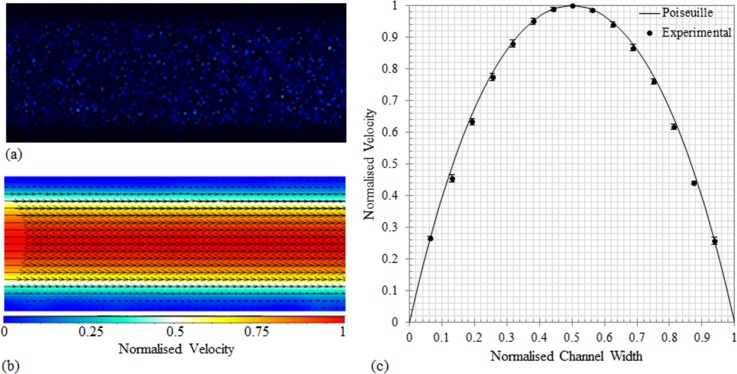
where U_x denotes the fluid velocity in the x-direction, y and z are the directions normal to the flow in the channel, Q is the flow rate, and h and w are the height and width of the channel, respectively. To ensure that the particles faithfully follow the flow, the Stokes number was calculated. The Stokes number is the ratio of the characteristic time of the particle to the characteristic time of the flow. The 0.5 μm particles were found to have a Stokes number of 5.6 × 10⁻⁸; this small value confirms the traceability of the particles. Fig. 2(a) shows the raw image of the flow in the channel and (b) shows the corresponding velocity vector field measurement calculated using cross correlation techniques. To ensure the velocity profiles were fully developed at the time of testing, the data was recorded in the middle of the channel (29.25 mm from the inlet). The experimental measurements and the predicted flow profile obtained using Equation (4) are compared in Fig. 2(c). All velocities and positions are normalized against maximum velocity and channel height, respectively. The data presented here illustrate the ability of the experimental system to obtain accurate results in accordance with the literature, establishing confidence in the measurement techniques employed in this study. The average percentage difference between the experimental velocities and the predicted flow velocities across the channel width (0.06 ≥ w ≤ 0.94) is 3%.

FIG. 2.

(a) Raw image of the 0.5 μm particles flowing in the microchannel, imaged using a 20×/NA = 0.5 objective. (b) The corresponding velocity vectors calculated using the cross correlation method using 500 images pairs. (c) Comparison of the experimental velocity profile, obtained by taking line-by-line averaging along the streamwise direction where the error bars denote standard deviation from the mean, and the analytical solution for Poiseuille flow in a straight square channel. The solid line is the analytical solution for Poiseuille flow. All profiles were acquired at the center of the microchannel at a depth of 50 μm using the same flow conditions.

B. Migration of particles and BCCs subjected to low Re

Particle tracking experiments were carried out to investigate the behavior of rigid particles (η = 0.05 and 0.1), non-metastatic MCF-7 cells (η = 0.03–0.78), and metastatic MDA-MB-231 cells (η = 0.06–0.77), under very low flow rates (Re = 0.02, 5, and 25) within a square microchannel. The BCC diameter, displacement, and location were measured using the image processing software ImageJ. All BCC diameters were normalized by dividing them by the channel height (100 μm). Table I summarizes the size distribution of both BCC types. The BCCs were stratified into two categories: single cells and cell aggregates (defined as two or more BCCs adhered together). The size distribution of both cell types was 0.19 ± 0.09 for the MCF-7 cells and 0.21 ± 0.09 for the MDA-MB-231 cells. A wide variation, in both the size and shape of the cell aggregates, was apparent. Aggregate formation ranged from two to approximately fifteen BCCs, forming a number of geometrical configurations, including spherical clumps and lines of cells, as illustrated in Fig. 3.

TABLE I.

Cell diameters recorded for single cells and cell aggregates for both BCC types. The diameter values were non-dimensionalized by dividing the measured BCC diameter by the channel height (100 μm).

	MCF-7 cells		MDA-MB-231 cells
Cell type	Single cells	Aggregates	Single cells	Aggregates
Number of cells	1856	700	1728	375
Minimum diameter	0.03	0.10	0.06	0.18
Maximum diameter	0.46	0.78	0.36	0.81
Average diameter	0.14 ± 0.04	0.3 ± 0.07	0.18 ± 0.04	0.35 ± 0.05
Total average diameter	0.19 ± 0.09		0.21 ± 0.09

FIG. 3.

Illustration of the types of cells (a) a single BCC, (b) two BCCs adhered together, (c)–(e) three BCCs adhered together in different formations, and (f)–(h) large aggregates of BCCs, found travelling in the microchannel imaged using bright field microscopy (20×/0.5 NA).

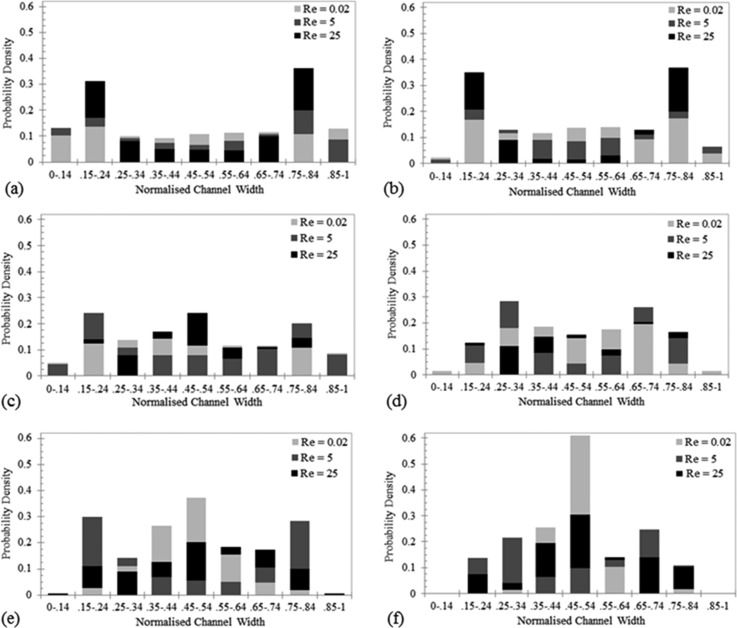
The range of Re_p values for the various experimental flow conditions investigated are summarized in Table II. The response of the particles and BCCs to increasing Re is illustrated in Fig. 4. The BCCs have been stratified into single cells and cell aggregates so that a comparison can be made between their behaviors. Migration is dependent on the size of the particle/cell and the flow rate it is subjected to. Previous work argues that a critical Re of 20–30 is required for migration to occur and the data collected here agrees with this to an extent, as particle migration is noticeably visible for both particle sizes as Re is increased to this range.^34,62,64 Understanding the spatial distributions of BCCs is important to deciphering the shear stresses they are subjected to in vivo. Under lymphatic flow conditions, Re = 0.02, both the η = 0.05 and η = 0.1 particles were distributed uniformly across the channel width, illustrated in Figs. 4(a) and 4(b). As the Re was increased to 5 and then 25, the lift force acting on the particles was increased which permitted them to overcome the viscous drag forces and migrate to equilibrium positions. The location of the equilibrium positions are located by the distinctive peaks of particle distribution and are determined by the imbalance of drag and lift forces acting on the particles. The particles migrate laterally to a radial position of approximately 0.6 times the channel radius (zero position is located at the microchannel center), in agreement with previous works.^42,56–58 A fully developed particle distribution is characterized by the depletion of particles at the channel center, as illustrated by the η = 0.1 particles at Re = 5 and 25. The BCC behavior differs from the particles, Figs. 4(c)–4(f). At Re = 0.02, the single MCF-7 cells (Fig. 4(c)) are distributed uniformly across the entire channel width, in comparison to the single MDA-MB-231 cells which have a distinct peak located at the center of the channel (Fig. 4(e)). Only 5% of single MDA-MB-231 cells travelled near the channel walls (0–0.24 and 0.75–1) versus 37% of the MCF-7 cells. This result suggests that the deformability of the BCCs had an effect on their location within the channel, with the more deformable metastatic MDA-MB-231 cells travelling only at the center of the channel, where the velocity gradient effects are lower than at the walls. The stiffer MCF-7 cells, similarly to the rigid particles, were more evenly distributed across the channel width. The deformability induced lift force increases with increasing BCC deformability which directs the MDA-MB-231 cells away from the channel wall and towards the channel center, to a modified equilibrium position, in agreement with a previous work.⁴⁹ The same behavior is illustrated with the cell aggregates; with 88% of MCF-7 aggregates located in between 0.25 ≤ w < 0.75 and all MDA-MB-231 aggregates located between 0.35 ≤ w < 0.65. This behavior is somewhat expected as the physical size of the aggregates would prevent them from travelling in close proximity of the wall. The results suggest that at lymphatic flow rates BCC aggregates have very little interaction with the walls, corresponding to very little BCC-intimal layer interaction in an in vivo setting. Poiseuille flow has been shown to be an accurate model for describing lymph flow (Re < 1) in a contracting lymphatic vessel model; therefore, the behavior illustrated here could provide an indication of in vivo events.⁵⁴

TABLE II.

Summary of the particle Reynolds number (Re_p) for the particles, MCF-7 cells, and MDA-MB-231 cells for each flow rate.

	Type	Re = 0.02	Re = 5	Re = 25
Particles	η = 0.05	1 × 10−4	0.025	0.125
	η = 0.1	4 × 10−4	0.1	0.5
MCF-7 cells	Single cells	1.3 × 10−4–2.2 × 10−3	0.04–1.06	0.25–2.89
	Aggregates	3.4 × 10−4−5.8 × 10−3	0.05–1.35	0.49–6.76
MDA-MB-231 cells	Single cells	2 × 10−4–2.6 × 10−3	0.04–0.65	0.3–2.89
	Aggregates	6.5 × 10−4–0.013	0.16–1.8	1.0–12.6

FIG. 4.

Lateral probability density of the (a) η = 0.05 particles, (b) η = 0.1 particles, (c) single MCF-7 cells, (d) MCF-7 aggregates, (e) single MDA-MB-231 cells, and (f) MDA-MB-231 aggregates, in response to increasing Re (0.02–25). All data were recorded at the center of the channel (29.2 mm from the inlet) and at a depth of 50 μm.

As Re is increased to 5 both BCC types, single cells and aggregates, migrate towards the channel walls to an extent. However, at Re = 25, the BCCs migrate towards the center of the channel in contrast to the particles. This difference in behavior can be attributed to a number of factors including the varied size, shape, and morphological properties of the BCCs, illustrated in Fig. 3. The deformability of a cell in Poiseuille flow results in an additional lift force, which directs the cell away from the channel wall, creating a modified equilibrium position. BCCs have been successfully separated from fluid suspensions using focusing techniques; however, usually higher flow rates (Re > 30) and specially designed microchannels are utilized to ensure high throughput and efficiency.^{36,41,49,65,66} It has been hypothesized that the deformability of cancer cells affects their inertial focusing; however, the mechanisms responsible remain unclear and warrant further investigation.^49,67 The interesting behaviour of the BCCs in response to the low Re investigated here suggests that the BCCs properties (deformability, size, etc.) play an important role in determining their response in this flow regime (Re < 30).

The densities of the working fluids used in this study (1050–1090 kg/m³ for the particles and ∼1050 kg/m³ for the BCC suspension) are very similar to the values reported in vivo for lymph (∼1000 kg/m³). Due to the nature of the BCC media, in which the cells are suspended, the viscosity value of the BCC working fluid is approximately 4 times higher than that of lymph. This difference in fluid properties represents an experimental limitation for this study. To address this issue, the Re investigated has been matched nondimensionally to take into account this difference in viscosity, and as a result, the non-dimensional velocity values in vivo can be determined using this scaled relationship.

It has been shown that nonspherical particles rotate at frequencies that depend on their largest diameter.⁶⁸ The rotational effects were not quantified in this study; however, the results gathered provide a benchmark for which numerical models can be validated. From the visualization of the BCC motion through the microchannel, fluctuations were present in the flow. Elements of fluid at different distances from the BCCs were not all subjected to the same forces due to the BCC interaction, and both rotational effects and the interaction between neighboring BCCs are important factors to take into account. The response of BCCs to the flow rates present in the lymphatics is unknown, and these results provide the first indication of their behavior under these conditions. By extracting specific information from the experimental measurements and using them as inputs to numerical models, it is possible to quantify the fluidic forces BCCs are exposed to, which influence their advection through the lymphatics. A numerical study investigating the shear stress distribution within the microchannel as a result of the BCCs is currently underway.

Results indicate that the size of the BCC plays an important role in cell motility, dictating both the cell's velocity and its distribution within the channel, which in turn determines the shear stresses BCCs are exposed to. Identifying BCCs that are more likely to metastasis further through the lymphatics based on their geometrical and morphological properties will provide valuable information, which is currently lacking, to lymphatic and breast cancer research.

C. Response of particles and BCCs to lymphatic flow conditions

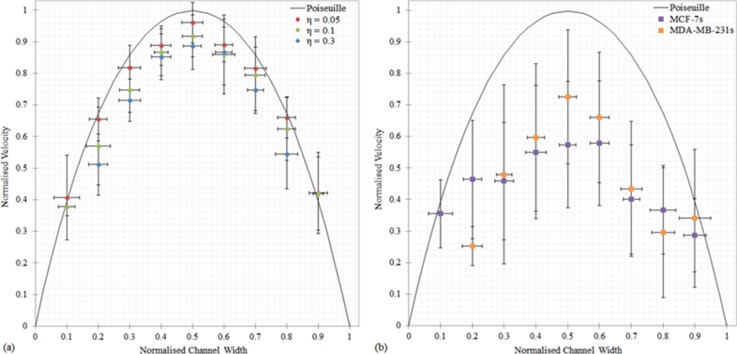
The flow behavior of MCF-7 and MDA-MB-231 cells was investigated to establish if particles could be used to model the flow behavior of BCCs when subjected to lymphatic flow conditions. The time averaged streamwise velocity component profiles for both the particles (η = 0.05–0.32) and the BCCs (η = 0.03–0.78) when subjected to a flow rate of 0.233 μl/min, which is representative of the physiological flow rates present in lymphatics of approximately 100 μm in diameter,²⁵ are shown in Fig. 5. The velocity values were averaged over 10 μm intervals across the channel width. Experimental data illustrate a parabolic form of the horizontal velocity profiles for all particle sizes. However, the flow behavior of both the MCF-7 cells and MDA-MB-231 cells is largely irregular. All particles lagged behind the fluid velocity, with the largest particles travelling at the slowest velocities (Fig. 5(a)). This behavior is in agreement with previous computational work that examined the motion of particles between two parallel plane walls in Poiseuille flow at low Re numbers.^69,70 The decrease in translational velocity from the undisturbed fluid velocity increases with particle size; the η = 0.05, η = 0.1, and η = 0.3 particles travelled at approximately 95%, 91%, and 85% of the undisturbed flow velocity. The increased proximity of the large particles to the channel walls results in a greater retardation force acting on the particle surface due to the velocity gradient found at the walls, as highlighted by Fig. 5(a).

FIG. 5.

Comparison of the flow behavior of (a) the particles (η = 0.05, 0.1, and 0.3), and (b) the MCF-7 (η = 0.03–0.78) and MDA-MB-231 (η = 0.06–0.77) cells, subjected to a flow rate of 0.233 μl/min. All velocities are normalized by dividing them by the maximum velocity and the particle positions are normalized by dividing them by the channel height. The error bars denote the standard deviation from the mean. All profiles were acquired at the center of the channel at a depth of 50 μm.

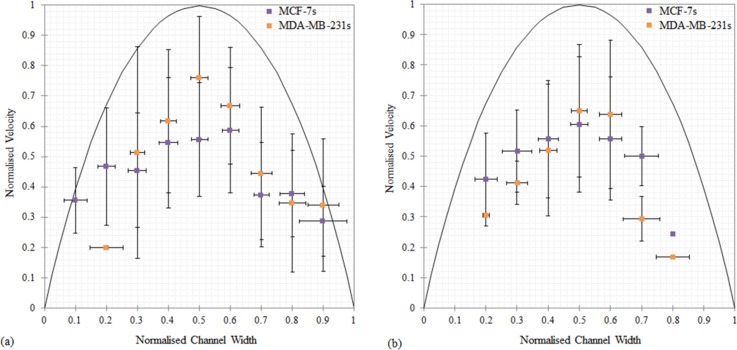
A wide range of velocities were recorded for both BCC types, which can be attributed, at least partly, to the range of BCC sizes tested. Overall, the BCCs on average travelled approximately 40% slower than undisturbed flow velocity; therefore, assuming that BCCs adhere to the bulk flow distribution is incorrect. The MDA-MB-231 cells, on average, travelled at a faster velocity (∼11% faster) than the MCF-7 cells in the center of the channel (0.25 ≤ w < 0.74). While the MDA-MB-231 cells travelled approximately 31% slower than the MCF-7 cells in the near wall regions (w ≤ 0.24 and w ≥ 0.75). This difference in behavior may be attributed to the difference in stiffness of the BCCs. MDA-MB-231 cells are more deformable than MCF-7 cells and deformability introduces additional lift forces to the flow. These forces result in nonlinear effects in the flow field which may cause the MDA-MB-231 cells to be subjected to a different range of shear stresses than the stiffer MCF-7 cells. The corresponding underlying mechanism for this phenomenon is not clear yet and further study is required to shed light on this issue.

The biological significance of aggregates in lymph flow is not documented and it is unknown whether the cells aggregate during circulation or break away from the primary tumor as an aggregate. Circulating aggregates have been found in blood samples from cancer patients⁶⁷ and within lymphatic vessels obtained from mice.⁷¹ In order to take a closer look at the size effects, the BCCs were split up into single cells (Fig. 6(a)) and aggregates (Fig. 6(b)), to examine each type of motion and its consequences with respect to the local flow. In this study, large aggregates (up to 78% of the channel width) were observed to rotate both in and out-of-plane in the flow. The shape of the aggregates influenced their response to the flow, which affected both their advection through, and location in, the microchannel. Due to the wide range of velocities recorded it is difficult to determine whether there is a difference between the behavior of BCC aggregates and single BCCs from this data alone. The presence of BCC aggregates in lymph flow will increase the local velocity gradient and, as a result, generate increased shear stress on the BCC surface. Knowledge of the velocity patterns near the BCCs allows evaluation of shear stress values and thus may provide indications for critical levels of stress that increase the risk of metastasis. The lymphatic flow rate investigated here (Q = 0.233 μl/min) is within the range of flow rates recently found flow rates in lymph nodes (Q = 0.1–0.5 μl/min),¹⁸ where metastatic BCC are known to locate. Experiments that investigate BCCs are typically performed under static, homogeneous conditions, and these static assays do not accurately capture the in vivo conditions experienced by BCCs. These results highlight the varied behavior of BCCs, in response to an in vivo flow rate.

FIG. 6.

Comparison of the flow behavior of (a) the single BCCs (η = 0.03–0.38) and (b) the BCC aggregates (η = 0.2–0.78), at a flow rate of 0.233 μl/min. The purple squares represent the MCF-7 cells, and the orange squares represent the MDA-MB-231 cells. The errors bars denote the standard deviation of the ensemble over which the averaging was performed. The solid line is the analytical solution for Poiseuille flow.

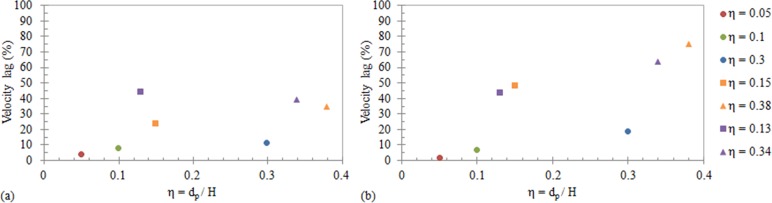
To further highlight the difference in behavior of the particles and the BCCs, Fig. 7 illustrates the average percentage velocity lag of the particles and BCCs (single and aggregates) compared to the local Poiseuille flow in (a) the center of the channel (w = 0.5) and (b) the near wall region (w = 0.8) as a function of size (η). The percentage velocity lag is greatest in all BCC types, compared to the rigid particles, despite their similarity in size. The velocity lag increases when the BCCs are located near the channel wall (Fig. 7(b)). The results demonstrate that BCC behavior is largely different from particles of similar sizes, which are highly predictable and repeatable. Therefore, using rigid spherical particles as models will not provide a true representation of BCC behavior. The size, shape, and deformability of BCCs need to be considered when modelling their behavior in the lymphatics.

FIG. 7.

The percentage velocity lag of the particles (○), single BCCs (□), and BCC aggregates (Δ), in comparison to the undisturbed Poiseuille flow velocity as a function of η, where η = d_p/H, at (a) the center of the microchannel (w = 0.5) and (b) the near wall region (w = 0.8). The purple markers represent the MCF-7 cells, and the orange markers represent the MDA-MB-231 cells. The η values shown are based on the average non-dimensionalised diameters for each particle/BCC grouping.

IV. CONCLUSIONS

An experimental study to investigate the flow behavior of BCCs and rigid particles, when exposed to lymphatic flow conditions in vitro has been carried out. The developed experimental system can facilitate better understanding of the multiphase flow phenomenon of BCC flow at the micro-domain of the lymphatics. Particle tracking experiments were performed to obtain information on the spatial distribution and velocities of a range of particle and BCC sizes subjected to a representative in vivo flow rate (Q = 0.233 μl/min). Parabolic velocity profiles of all particle sizes were found: the larger the particle size, the slower its velocity relative to undisturbed fluid flow. The BCC behavior was highly irregular and both MCF-7 cells and MDA-MB-231 cells travelled at a velocity that was significantly slower (∼40%) than the local fluid velocity.

Varying degrees of lateral migration occurred for both the particles and BCCs as the Re was increased up to 25. At Re = 0.02, single MCF-7 cells were approximately uniformly distributed across the channel width, while the more deformable metastatic MDA-MB-231 cells travelled only at the center of the channel, where the velocity gradient effects are lower than at the channel walls. The flow behavior of both single BCCs and BCC aggregates was compared. The difference in the behavior of the two BCC types suggests that the increased deformability of metastatic BCCs affects their flow behavior, influencing their position in the flow. Results indicate that the BCC size and morphological properties play an important role in cell motility, dictating both the BCCs velocity and its distribution within the channel. These results emphasize the importance of future work focused on investigating BCC deformability and size effects in the lymphatics. The results serve to motivate experimental work focused on linking fluidic conditions to BCC dynamics associated with metastasis. Information gathered here, highlighting the response of BCCs to the lymphatic fluidic environment, could guide the development of novel tools for breast cancer metastasis diagnostics.