Realistic phantoms to characterize dosimetry in pediatric CT

Abstract

Background

The estimation of organ doses and effective doses for children receiving CT examinations is of high interest. Newer, more realistic anthropomorphic body models can provide information on individual organ doses and improved estimates of effective dose.

Materials and methods

Previously developed body models representing 50^th-percentile individuals at reference ages (newborn, 1, 5, 10 and 15 years) were modified to represent 10^th, 25^th, 75^th and 90^th height percentiles for both genders and an expanded range of ages (3, 8 and 13 years). We calculated doses for 80 pediatric reference phantoms from simulated chest-abdomen-pelvis exams on a model of a Philips Brilliance 64 CT scanner. Individual organ and effective doses were normalized to dose-length product (DLP) and fit as a function of body diameter.

Results

We calculated organ and effective doses for 80 reference phantoms and plotted them against body diameter. The data were well fit with an exponential function. We found DLP-normalized organ dose to correlate strongly with body diameter (R²>0.95 for most organs). Similarly, we found a very strong correlation with body diameter for DLP-normalized effective dose (R²>0.99). Our results were compared to other studies and we found average agreement of approximately 10%.

Conclusion

We provide organ and effective doses for a total of 80 reference phantoms representing normal-stature children ranging in age and body size. This information will be valuable in replacing the types of vendor-reported doses available. These data will also permit the recording and tracking of individual patient doses. Moreover, this comprehensive dose database will facilitate patient matching and the ability to predict patient-individualized dose prior to examination.

Introduction

Increased use of computed tomography (CT) has undoubtedly improved the quality of medical care in recent years. However, the rise in the use of CT as a diagnostic tool has increased the collective radiation exposure to the medical patient population [1], which has raised some concerns. For children, there is the possibility of greater radiosensitivity to ionizing radiation, and some authors have implied heightened risks of radiogenic cancers in this population [2–4].

Efforts to reduce the number of examinations and dose per examination, while not negatively influencing image quality, have been introduced [5–8]. Monte Carlo methods have been employed in an attempt to increase the accuracy of patient dose estimates from CT examinations. Many groups have developed codes to simulate CT scanners. Jarry et al. [9] created a CT model of a single-detector GE Healthcare HiSpeed CT/i scanner (GE Healthcare, Waukesha, WI) to estimate radiation dose from spiral CT. DeMarco et al. [10] later expanded these simulations to multidetector systems and modeled GE Healthcare LightSpeed Plus and GE Healthcare LightSpeed 16 CT scanners [10]. Staton et al. [11] developed a simulation of a Siemens SOMATOM Sensation 16 helical multislice computed tomography (MSCT) scanner (Siemens Healthcare, Erlangen, Germany). Li et al. [12] developed a model of a GE Healthcare LightSpeed VCT. In our previous work [13], we developed and validated a model of a Philips Brilliance 64-slice multidetector scanner (Philips Healthcare, Best, The Netherlands) used at the Monroe Carrell Jr. Children’s Hospital at Vanderbilt University. Doses calculated using Monte Carlo simulations are directly applicable to the particular scanner modeled, but some have suggested that doses may also be scanner-independent when normalized by CT dose index – volume (CTDI_vol) [14, 15].

Anthropomorphic phantoms have been used as input into Monte Carlo simulations of CT scans to estimate patient organ and effective doses. Originally, these types of phantoms were constructed with organs defined by mathematical shapes [16–19], consisting of a series of reference pediatric ages (newborn, 1, 5, 10 and 15 years) in addition to an adult male and an adult female. More advanced realistic, anthropomorphic voxel-based computational phantoms have been developed from CT images. The Gesellschaft für Strahlenforschung, Neuherberg, Germany (GSF) family of voxel phantoms consists of 12 voxel phantoms, including pediatric models of an 8-week-old and a 7-year-old [20]. Turner et al. [15] performed Monte Carlo simulations and provided organ dose and effective dose estimates for the GSF phantom series. Patient-specific voxel-based computational pediatric phantoms have been developed for the direct estimation of patient organ dose [21–26]. In a previous work [25], we calculated organ doses for 40 previously scanned pediatric CT patients using our GEometry ANd Tracking version 4 (GEANT4)-based [27] Monte Carlo simulation and manual segmentation techniques to define organs within the scanned image volume [25].

Newer generation reference phantoms, commonly based on non-uniform rational B-splines (NURBS), have improved the ability to estimate CT doses [28]. The University of Florida (UF) hybrid series [29] was developed to provide organ dose estimates for a large series of children receiving CT examinations, and Geyer et al. [30] expanded this organ dose database to also include estimates for obese patients. This work utilizes the enhanced 4D Extended Cardiac-Torso (XCAT) models of Segars [31]. The basis for our library of phantoms presented in this work is the initial set of ten XCAT pediatric reference phantoms created and published by Norris et al. [32], which were matched to ICRP 89 reference values for organ masses [33]. We have expanded these reference 50^th-percentile phantoms to include additional percentiles in height (10^th, 25^th, 75^th and 90^th) and non-reference ages (3, 8 and 13 years) for a total of 80 reference phantoms.

The purpose of this study was to develop a large library of dose estimates for normal-stature children of different ages and heights who receive chest-abdomen-pelvis exams on a Philips Brilliance 64-slice CT system at the Monroe Carrell Jr. Children’s Hospital at Vanderbilt. This study was approved by our institutional review board and informed patient consent was not required. This comprehensive set of organ and effectives doses for NURBS-based pediatric reference phantoms will allow us to assign more accurate radiation dose estimates to children receiving exams. We have also compared our results to a few other published phantom studies [23, 29, 34].

Materials and methods

Phantom development

Our phantoms are based on NURBS surfaces and polygon meshes; these surfaces are easily manipulated to change the size and shape of the body and any organs. Deformation of NURBS surfaces was done using Rhinoceros 3D (Rhino3D) NURBS modeling software version 4.0 (Robert McNeel & Associates, Seattle, WA; http://www.rhino3d.com). Anthropometric data from Centers for Disease Control and Prevention (CDC) growth charts [35, 36] and body measurements of children from the United States National Health and Nutrition Examination Survey (NHANES) [36, 37] were used in the development of these realistic phantoms. To create additional phantoms representing 10^th, 25^th, 75^th and 90^th height-percentiles for normal-stature children, the original 50^th-percentile phantoms for each reference age were initially scaled uniformly to obtain the desired height based on CDC data [35, 36, 38]. All interior organs and structures were scaled together to keep reference anatomy comparable for all phantoms. Care was taken to further scale anterior-posterior (AP) and lateral (LAT) dimensions to match anthropometric data (e.g., waist circumference) [35–38].

To create non-reference aged phantoms, the 50^th-percentile phantoms were initially scaled according to the height-ratio between the non-reference and reference age. The reference-age phantom that was a closest match in height to the target non-reference-age was used as a basis. For example, to create the 8-year-old 50^th-percentile, the 50^th-percentile 10-year-old was scaled down, and similarly the 50^th-percentile 13-year-old was created from the 50^th-percentile 15-year-old phantom. As previously, additional percentiles were created from the 50^th-percentile phantoms using the previous method of initially scaling uniformly by height, and AP and lateral dimensions were matched to anthropometric data. Eighty normal-stature phantoms were generated. This set consists of male and female genders for eight ages and five height-percentiles each (10^th, 25^th, 50^th, 75^th and 90^th). A subset of these is shown in Figure 1 for the 5-year-old phantom series. A program was developed to convert the phantom NURBS surfaces into voxelized phantoms for input into our GEANT4 simulation [13, 27]. Voxel size is a user-defined variable in this program, which was defined as 1.5×1.5×3.0 mm for our phantoms as an appropriate compromise between spatial resolution and computation time and resources. This voxel size is comparable to the pixel size and slice thickness of our clinical pediatric CT images. The program was also used to generate bone marrow cavities within the phantom skeleton. Prior to the voxelization process, the program rendered each bone at high resolution and eroded the outer bone layer by an age-dependent cortical bone thickness [39]. After the bone marrow cavities were generated, individual voxels were seeded with appropriate age-specific and bone-specific distributions of red and yellow marrow within the bone cavities [40].

Fig. 1.

A phantom series for 5-year-olds in the 10th, 25th, 50th, 75th and 90th percentiles in height

Monte Carlo simulation of CT examinations

A GEANT4-based Monte Carlo particle radiation transport code previously described in the literature [13] was used to perform simulations of helical CT examinations. CT scanner properties such as photon-energy spectrum, inherent and bow tie filtration, and geometry were modeled explicitly. An equivalent energy-fluence source model for the simulated CT scanner (Philips Brilliance 64, 64×0.625-mm collimation) was generated following methods in Turner et al. [41]. The CT scanner model also includes the effects of the body bow tie filter, which provides X-ray filtration across the transverse direction of each phantom. Detailed descriptions of the CT scanner properties modeled are provided in Carver et al. [13]. Simulated CT 100-mm dose index (CTDI₁₀₀) values [42] were directly compared to the measured dose indices with overall average agreement within 6%.

Calculation of organ doses

Monte Carlo simulations were performed with a technique of 120 kVp tube voltage, 100 mAs, and a pitch of 1 for all scans. The source moved in one-degree increments and tracked 3.6×10⁶ total photon histories for each tube rotation. The scan length ranged from 2 cm above the apex of the lungs to 2 cm below the bottom of the ischium. This scan length includes one-half of the total beam collimation at each end to account for the overscan distance required for reconstructing helical tomographic images. The relative statistical uncertainties in the simulation for energy deposited in each organ were less than 1%.

The material definitions for tissues used in the simulation (Table 1) were chosen to best represent pediatric anatomy. Soft tissues were taken from body compositions tabulated in International Commission on Radiation Units and Measurements (ICRU) Publication 46 Appendix A [43]. Densities and element compositions for cortical bone, spongiosa, and bone marrow were also selected based on age.

Table 1.

Summary of materials used in the Monte Carlo model [43]

Material	Density (g/cm3)	Chemical composition (% by mass)
		H	C	N	O	Na	P	S	Cl	K	Other
Air	1.21×10−3		0.01	75.5	23.2						1.3 (Ar)
Soft tissuea	1.03	10.5	25.6	2.7	60.2	0.1	0.2	0.3	0.2	0.2
Brainb	1.04	10.7	14.5	2.2	71.2	0.2	0.4	0.2	0.3	0.3
GI tract/intestinesc	1.03	10.6	11.5	2.2	75.1	0.1	0.1	0.1	0.2	0.1
Heartd	1.06	10.3	12.1	3.2	73.4	0.1	0.1	0.2	0.3	0.2	0.1 (Fe)
Kidneye	1.04	10.6	9.4	2.1	77	0.2	0.2	0.1	0.2	0.2
Liverf	1.06	10.2	13.9	3	71.6	0.2	0.3	0.3	0.2	0.3
Lung tissueg	0.26	10.3	10.5	3.1	74.9	0.2	0.2	0.3	0.3	0.2
Mammary glandh	1.06	10.2	15.8	3.7	69.8	0.1	0.1	0.2	0.1	0.1
Ovaryb	1.05	10.5	9.3	2.4	76.8	0.2	0.2	0.2	0.2	0.2
Pancreasb	1.04	10.6	16.9	2.2	69.4	0.2	0.2	0.1	0.2	0.2
Skinb	1.09	10	20.4	4.2	64.5	0.2	0.1	0.2	0.3	0.1
Spleenb	1.06	10.3	11.3	3.2	74.1	0.1	0.3	0.2	0.2	0.3
Testesb	1.04	10.6	9.9	2	76.6	0.2	0.1	0.2	0.2	0.2
Thyroidb	1.05	10.4	11.9	2.4	74.5	0.2	0.1	0.1	0.2	0.1	0.1 (I)
Urinary bladderi	1.04	10.5	9.6	2.6	76.1	0.2	0.2	0.2	0.3	0.3
Cortical bonej (0 y)	1.68	4.7	15.4	4.2	48.5	0.1	8.2	0.2	0.1		0.2 (Mg) 18.4 (Ca)
Cortical bonej (1 y)	1.71	4.5	15.9	4.4	46.7	0.1	8.7	0.3	0.1		0.2 (Mg) 19.1 (Ca)
Cortical bonej (5 y)	1.75	4.3	15.8	4.4	45.7	0.1	9.3	0.3	0.1		0.2 (Mg) 19.8 (Ca)
Cortical bonej (10 y)	1.79	4.0	15.9	4.4	45.0	0.1	9.6	0.3	0.1		0.2 (Mg) 20.4 (Ca)
Cortical Bonej (15 y)	1.83	3.8	16.0	4.4	44.3	0.1	9.9	0.3			0.2 (Mg) 21.0 (Ca)
Red marrow	1.03	10.5	41.4	3.4	43.9		0.1	0.2	0.2	0.2	0.1 (Fe)
Yellow marrow	0.98	11.5	64.4	0.7	23.1	0.1		0.1	0.1

^aICRU 46, Appendix A Adult ICRU-44 male

^bICRU 46, Appendix A Adult

^cICRU 46, Appendix A Adult GI tract

^dICRU 46, Appendix A Adult blood-filled

^eICRU 46, Appendix A Child 2 years

^fICRU 46, Appendix A Adult healthy

^gICRU 46, Appendix A Adult healthy inflated

^hICRU 46, Appendix A Breast-mammary gland Adult #3

ⁱICRU 46, Appendix A Adult empty

^jICRU 46, Appendix A Skeleton-cortical bone

Ar argon, C carbon, Ca calcium, CL chlorine, Fe iron, H hydrogen, I iodine, K potassium, Mg magnesium, N nitrogen, Na sodium, O oxygen, P phosphorus, S sulfur

The Monte Carlo simulation tallied the energy deposited in each voxel, and the 3-D output was converted to absorbed dose using the tissue densities from Table 1. A normalization factor (1.4×10⁶ mGy/100 mAs) was applied to convert simulated data to absolute dose. Absorbed doses to radiosensitive organs were calculated, and the effective dose was determined using tissue-weighting factors from International Commission on Radiological Protection (ICRP) publication 103 [44]. Organ and effective doses were normalized by each phantom’s simulated scan length and the value of CTDI_vol (CT volume dose index) obtained from the 16-cm diameter CTDI phantom (Table 2) and were plotted as a function of phantom average diameter. Because this study focuses only on children receiving exams on a dedicated pediatric CT scanner, the 16-cm diameter CTDI_vol was chosen as reference. Average diameter was determined by calculating the effective diameter (defined as $\sqrt{AP\times \mathit{LAT}}$, where AP is the anterior-posterior dimension, and LAT is the lateral dimension) [45, 46] of each phantom slice and averaging these for slices within the scan range of interest (i.e., CAP [chest, abdomen and pelvis] CT scan length). Regressions of the dose curves were performed as: Dose_norm = exp(α * D_CAP + β), where α and β are fitting parameters, and D_CAP is the average phantom diameter over the corresponding CAP scan length.

Table 2.

CTDI measurements for simulated scan protocol for 16-cm-diameter phantom

Tube potential (kVp)	Pitch	Collimation (mm)	CTDI100 (mGy/100 mAs)		CTDIvol (mGy/100 mAs)
			center	periphery
120	1.0	40 (64 × 0.625)	9.8	14.0	12.6

CTDI CT dose index

CTDI_vol CT dose index – volume

CTDI₁₀₀ CT 100-mm dose index

Results

The GEANT4 output contains dose estimates for more than 120 regions (organs, individual bone and marrow regions, organ walls and contents, and many other structures). The relationship between average diameter and dose-length product (DLP) normalized effective dose is shown in Figures 2–3. A strong correlation between dose and phantom diameter is suggested by high R²-coefficents (R² >0.99) and low root-mean-squared errors (Table 3).

Fig. 2.

Dose-length product-normalized effective dose as a function of average phantom diameter for (a) females and (b) males with exponential fit. Comparison to k-coefficients from Shrimpton et al. [34] for trunk examinations presented as (red squares) for reference children at ages 0, 1 year, 5 years and 10 years developed by Cristy and Eckerman [16–19]. Comparison to k-coefficients calculated by Lee et al. [29] for chest-abdomen-pelvis examinations also shown (blue diamonds)

Fig. 3.

Dose-length product-normalized (32-cm phantom) effective dose as a function of average chest diameter for (a) females and (b) males with exponential fit (dashed line). Plot shows comparison to Li et al. [23] protocol C for chest examination (120 kVp, large body bow tie filter, pitch=1.375, 40-mm beam width) (dotted line) and protocol E for chest examination (120 kVp, pediatric body (small) bow tie filter, pitch=0.984, 40-mm beam width) (dot-dashed line)

Table 3.

Regression fit coefficients for DLP-normalized organ and effective doses for chest-abdomen-pelvis CT reference phantom studies

	α	β	R2	RMSE
Adrenals	−0.0714	−2.41	0.993	7.88×10−4
Bladder	−0.0705	−2.43	0.995	6.47×10−4
Bone	−0.0622	−2.26	0.992	1.03×10−3
Colon	−0.0599	−2.63	0.994	5.88×10−4
Esophagus	−0.0728	−2.49	0.996	5.44×10−4
Gall bladder	−0.0548	−2.73	0.962	1.41×10−3
Heart	−0.0649	−2.46	0.997	5.24×10−4
Kidneys	−0.0694	−2.39	0.993	8.43×10−4
Liver	−0.0625	−2.58	0.991	7.58×10−4
Lungs	−0.0693	−2.46	0.997	5.11×10−4
Pancreas	−0.0687	−2.49	0.997	4.83×10−4
Small intestines	−0.0621	−2.56	0.989	8.76×10−4
Spleen	−0.0684	−2.51	0.950	2.00×10−3
Stomach	−0.0627	−2.61	0.994	6.38×10−4
Prostate	−0.0851	−2.30	0.985	1.24×10−3
Breasts	−0.0682	−2.54	0.926	2.40×10−3
Ovaries	−0.0710	−2.42	0.987	1.09×10−3
Uterus	−0.0721	−2.44	0.984	1.19×10−3
Effective Dose (Females)	−0.0668	−2.63	0.992	7.01×10−4
Effective Dose (Males)	−0.0669	−2.80	0.994	5.38×10−4

α and β are fit coefficients

R² is the coefficient of determination for the fitRMSE is the root-mean-square error, defined as $\sqrt{\frac{1}{n}{\sum }_{i=1}^n{\left({nD}_i-{\widehat{nD}}_{\iota }\right)}^2}$, where ${\widehat{nD}}_{\iota }$ is the DLP-normalized organ dose estimated from the exponential relationship with fit parameters α and β

For comparison, DLP -normalized effective doses from Lee et al. [27] and k-coefficients for trunk exams from Shrimpton et al. [34] for reference children at ages 0, 1 year, 5 years, and 10 years developed by Cristy and Eckerman [16–19] are also plotted on Figure 2. DLP-normalized effective dose is also plotted against average chest diameter in order to compare to results of pediatric chest CT examinations performed by Li et al. [23] for different bow tie filters (Fig. 3). An overall comparison of k-coefficients from Shrimpton et al. [34], Lee et al. [29], and this work is provided in Table 4, with percent differences between 2–23% with an overall mean of 11%.

Table 4.

Comparison of effective doses normalized by dose length product (mSv/mGy-cm) with Shrimpton et al. 2006 [34] and Lee et al. 2012 [29]

		0 yo	1 yo	5 yo	10 yo
Shrimpton et al. 2006		0.044	0.028	0.019	0.014
Lee et al. 2012		0.044	0.029	0.021	0.014
This work	Female	0.037	0.027	0.021	0.016
	Male	0.031	0.023	0.018	0.014

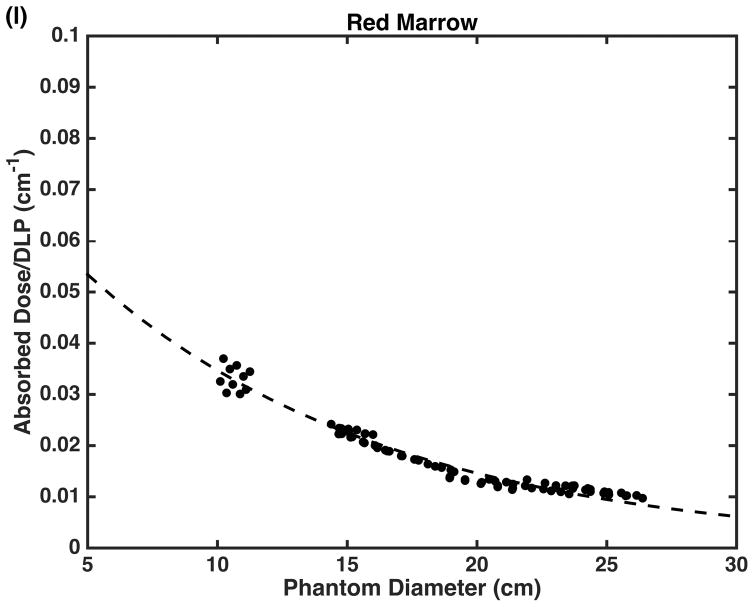
DLP-normalized absorbed doses for organs are plotted as a function of average phantom diameter (Fig. 4). Again, a strong correlation between phantom diameter and dose is demonstrated (R² >0.95 for most organs); Table 3 reports the linear regression fit parameters. Table 5 provides a comparison between our CTDI_vol-normalized organ doses and those of Lee et al. [29] and reports the percent differences on an organ-by-organ basis. Resulting percent differences range between 0 and 33% with an overall mean of 9%.

Fig. 4.

Dose-length product-normalized doses for a few selected organs including (a) adrenals, (b) bladder, (c) breast tissue, (d) colon, (e) cortical bone, (f) esophagus, (g) gall bladder, (h) heart, (i) kidneys, (j) liver, (k) lungs and (l) red marrow shown with exponential fits as a function of average phantom diameter

Table 5.

Percent differences between this work and Lee et al. 2012 [29] for organ doses normalized by CTDI_vol

	% diff NB F	% diff NB M	% diff 1y M	% diff 1y M	% diff 5y F	% diff 5y M	% diff 10 y F	% diff 10y M	% diff 15y F	% diff 15y M
Thyroid	−25.2%	−2.3%	14.0%	1.3%	2.0%	−8.4%	3.9%	−14.5%	−12.9%	9.5%
Esophagus	−13.8%	0.3%	−2.6%	11.8%	1.0%	−22.2%	18.9%	0.5%	−32.6%	23.5%
Thymus	−12.7%	−0.8%	8.0%	1.8%	−0.2%	−5.4%	10.4%	−0.7%	−28.7%	20.9%
Lungs	−17.8%	1.2%	13.8%	−5.5%	−0.1%	−7.2%	8.1%	−0.6%	−18.4%	10.4%
Heart wall	−15.4%	0.5%	9.9%	−1.3%	0.1%	−7.4%	10.9%	−0.7%	−22.7%	19.7%
Stomach wall	−27.0%	1.0%	14.4%	−6.9%	−0.7%	0.9%	3.0%	−0.1%	−13.3%	12.3%
Liver	−27.8%	0.6%	16.2%	−2.3%	0.0%	−6.7%	2.9%	−0.5%	−13.0%	13.8%
Gall bladder	−23.5%	1.9%	13.8%	3.2%	0.3%	−11.5%	3.8%	−0.6%	−13.0%	22.2%
Adrenals	−10.3%	2.2%	−1.8%	11.8%	−1.6%	−20.3%	15.4%	0.4%	−30.4%	22.0%
Spleen	−26.8%	3.1%	16.2%	−20.9%	−0.4%	9.5%	12.7%	−2.4%	−18.8%	−0.9%
Pancreas	−22.4%	3.1%	7.1%	−1.4%	0.3%	−6.7%	8.7%	0.5%	−25.1%	17.9%
Kidney	−16.1%	0.4%	14.2%	−8.5%	0.3%	0.7%	4.4%	−1.8%	−15.8%	7.2%
Small intestine	−17.3%	0.2%	3.3%	6.3%	0.3%	−8.7%	7.9%	−0.7%	−22.1%	21.9%
Colon	−25.5%	−0.1%	14.0%	−3.5%	−0.2%	2.1%	2.4%	−0.5%	−13.2%	9.2%
Skin	−23.3%	1.1%	−1.1%	3.9%	0.8%	−24.6%	−6.6%	−1.0%	−3.7%	−2.1%

CTDI_vol CT dose index – volume

F female

M male

NB newborn

% diff Percent Difference

y year-old

Discussion

The use of CT exams in children is a valuable diagnostic tool, but viable methods for accurately estimating patient dose have been limited. There has been much focus on obtaining patient-specific dose estimates [21–26], but patient-specific 3-D dose calculations can be time-consuming and can only be performed post CT scan rather than as a predictive measure. In this study, we calculated organ and effective doses from chest-abdomen-pelvis scans for a large set of NURBS-based anthropomorphic, anatomically realistic phantoms using a previously validated Monte Carlo model of a Philips Brilliance 64 CT scanner [13]. We also found a strong correlation between DLP-normalized organ and effective dose and average body diameter (R²>0.95 for most organs).

The data generated in this study will allow assignment of higher quality dose estimates for children of different ages and body types, as part of their study record than is currently reported by the CT scanner. Children undergo growth phases at different times during their childhood; hence, age is not the most appropriate metric for predicting patient dose. On the other hand, body diameter correlates very well with patient dose, as demonstrated in this work and others [e.g., 15]. Therefore, a large range of phantom sizes is vital to deliver the best match between patient and phantom and provide patient-individualized estimates organ and effective doses. Preliminary matching of our 40 patient-specific voxel phantoms [25] to the pediatric reference phantoms presented in this work using body diameter has resulted in organ dose agreement between 3% and 22%.

We also compared CTDI_vol-normalized organ doses of completely irradiated organs to results reported by Lee et al. [29]. Generally, we found agreement between results with an average percent difference of 9% with a range of 0% to 33%, with the largest differences corresponding to organs on the edge of the scan range (e.g., thyroid). These differences might be partially accounted for by different scan protocols. The organ doses of Lee et al. [29] were calculated from axial scans of 10-mm nominal beam width. In contrast, our simulation models a fully helical scan with a 40-mm nominal beam width, which is just one factor that could account for higher doses and is supported elsewhere [23]. Additionally, our simulation includes the extra overscan distance on the start and stop ends of the scan that is required for helical image reconstruction. This also would account for higher observed CTDI_vol-normalized doses as a result of increased overall scan length. Furthermore, the two reference phantom series likely have relative anatomical differences, such as phantom diameter. We calculated percent differences between 50^th-percentile reference-aged (newborn, 1, 5, 10 and 15 years) phantom diameters ranging from 2% to 11%.

We have compared our DLP-normalized effective doses to Lee et al. [28], where we saw greater convergence of results at large phantom diameters (Fig. 2). We also compared these results with the k-coefficients derived by Shrimpton et al. [34]. Percent differences ranged from 2% to 23%, with greater agreement for large phantom diameters and greater disagreement for small phantom diameters (Fig. 2). This demonstrates a strong dependence on the model used to derive effective dose. Our comparison to the results of Li et al. [23] for DLP-normalized effective dose revealed similar results. Our data were plotted against average phantom chest diameter in order to compare to Li et al.’s pediatric chest CT examinations. We used their fit for a similar scan protocol using the small pediatric body bow tie filter, as well as their fit for a large bow tie filter. Our results illustrate an overall trend bracketed by the Li et al. data (Fig. 3), with the large body filter trending higher than our results and the pediatric body (small) filter trending slightly lower than our results. Therefore, the specific characteristics of the bow tie filter, especially size, play a major role in the magnitude and shape of the resultant curves, especially for small patients (Figs. 2 and 3). This finding is also supported by Li et al. [23].

The bow tie filter is a factor not necessarily accounted for by a simple normalization of scanner output (i.e. CTDI_vol). The bow tie filter modifies the X-ray spectrum across the patient to take into account differences in body thickness between the center and periphery of the patient. The specific type of bow tie filter chosen (e.g., body or head) will influence the X-ray spectrum greatly and produce significant variations when comparing beam profiles. Our modeled CT scanner, a Philips Brilliance 64, has just one body bow tie filter that is used for all pediatric patients regardless of size. A larger body filter, in contrast to a smaller filter, contributes to higher dose (Figs. 2 and 3).

Our results are limited in that they are specific to the Philips Brilliance 64 CT scanner modeled for this study. These data are potentially applicable to other scanner models, particularly Philips, if physical characteristics such as beam width, total filtration, bow tie filter and detector efficiency are similar. However, further simulation of other scanner models would be necessary to investigate whether this is the case.

There has been much recent interest in the idea of tracking patient radiation doses over time and pediatric patient doses in particular. Dose tracking is especially a concern for patients with a complicated medical history who receive a significant number of X-ray studies, CT examinations, nuclear medicine studies or other exams during a short period of time. Although the benefits of medical imaging often outweigh any potential risks from exposure to ionizing radiation, the cumulative dose from a large number of medical exams using ionizing radiation can approach levels associated with a statistically evident risk of cancer induction.

Although patient dose may be estimated post examination, we can also predict dose prior to a CT scan. We can accomplish this by matching an individual based on their age, stature, and diameter to a reference phantom by employing a dose database. This database could report doses for all clinical protocols: either on an organ-by-organ basis or from direct calculations of organ dose curve fits. Queries of the database could also semiautomatically assign doses for the patient’s medical record. Furthermore, physicians and scientists can use these improved dose estimates in reviews of protocols and exposure parameters at their institution.

The quantity, effective dose, defined by the ICRP, was never intended to be applied to individuals, only to populations. Moreover, assigning a radiogenic lifetime cancer risk based on the effective dose quantity is inappropriate below a cumulative effective dose of 100–200 mSv based on current cancer risk models, which also contain very high uncertainties. However, if effective doses are to be incorporated into individual patient dose records, then calculations based on realistic, individualized anthropomorphic models are preferable to values of CT radiation output determined from simple acrylic phantoms.

Conclusion

A total of 80 deformable pediatric reference NURBS phantoms were developed for ages ranging from newborns to 15-year-olds and included both genders and varying percentiles in height. They were built according to reference anatomies and organ masses of normal-stature children. Absorbed organ and effective doses for children receiving chest-abdomen-pelvis CT exams were calculated, and a strong relationship was observed between organ dose and average patient diameter. The dose estimation methods demonstrated here are vast improvements over the current CT vendor-supplied values, and the organ doses generated by this method may be used to track cumulative patient doses over time.